Abstract
Bimetallic-clad pipes demonstrate exceptional advantages in transporting corrosive oil and gas through the combination of the load-carrying capacity of the base material and the anti-corrosive function of the thin layer of corrosion-resistant alloy. This study investigates the mechanical properties of 24-inch X65 + Alloy625 metallurgically clad pipes through experimental tests and finite element analysis. Uniaxial tensile testing with digital image correlation reveals uniform deformation between the base and clad layers until interfacial failure initiates at an average strain threshold of 34.17%. Microstructural characterization shows continuous metallurgical bonding, with the X65 layer exhibiting polygonal ferrite and bainitic phases, contrasting with the austenitic equiaxed grain structure of Alloy625. In terms of numerical modeling, finite element analyses that consider both initial geometric imperfections and manufacturing-induced residual stresses are performed to evaluate the bending response of the clad pipe. The effect of initial ovality and residual stresses on its bending capacity is also studied.
1. Introduction
With sustained global economic development and growing energy demands, the exploitation of strategic resources such as oil and natural gas has progressively shifted from terrestrial and shallow-water environments to more challenging deep-water and high-corrosion conditions [1,2,3]. Bimetallic clad pipes have emerged as effective solutions in offshore oil and gas extraction, combining the structural integrity of carbon steel base pipes with the corrosion resistance of stainless steel or nickel-based alloy liners through advanced metallurgical bonding techniques [4,5,6,7]. These composite pipes offer superior service life compared to conventional carbon steel pipelines while maintaining cost-effectiveness relative to solid corrosion-resistant alloy pipes [8].
Two primary categories of bimetallic pipes exist based on interfacial bonding mechanisms: mechanical and metallurgical clad pipes. Metallurgically bonded pipes demonstrate enhanced interfacial strength and load-bearing capacity compared to their mechanically bonded counterparts, making them particularly suitable for marine engineering applications [9,10]. However, their complex mechanical behavior and failure mechanisms under operational conditions pose significant challenges to reliability assessment. Although previous studies have made progress in understanding composite pipe behavior, critical knowledge gaps remain regarding the mechanical properties of large-diameter metallurgically clad pipes.
Extensive research has been conducted on mechanically lined pipes through both experimental and numerical approaches. Full-scale tests under axial compression, bending, and reeling loads have been carried out by Hilberink et al. [11,12,13], while Tkaczyk et al. [14,15] investigated the evolution of liner buckling during cyclic bending with and without internal pressure. Yuan et al. [16] performed small-scale four-point bending tests to analyze the effect of local indentation on structural response. Numerical studies by Vasilikis and Karamanos [17], and Yuan and Kyriakides [18,19,20], explored liner wrinkling and local buckling under bending and axial compression, revealing the influence of geometric imperfections. Further investigations [21,22,23] addressed the effects of internal pressure and tension on structural stability during reeling and combined loading, showing good agreement with experimental observations.
Recent investigations by Yoshitake [24] employed centrifugal casting to produce metallurgically bonded pipes with uniform wall thickness. Slany et al. [25] conducted comprehensive analyses of Inconel 625-clad pipes subjected to 0.7D bending deformation. Yang et al. [26] developed a three-dimensional finite element (FE) model incorporating girth welds to evaluate strain capacity under combined internal pressure and bending moments, identifying the heat-affected zone as a critical failure location. Subsequent research by the same group [27] investigated cyclic loading effects on welded metallurgical clad pipes, revealing 120% higher strain concentrations in weld regions during installation. Yuan et al. [28] employed machine learning algorithms to predict collapse pressures of 12-inch mechanically lined pipes, examining the influence of diameter-to-thickness ratios, initial ovality, and material hardening. Overall, prior studies primarily focused on relatively small-diameter pipes (<12 inches), leaving the mechanical behavior of large-diameter clad pipes under deep-sea conditions still poorly understood.
This study focuses on 24-inch X65 + Alloy625 metallurgically clad pipes through experimental characterization and numerical simulation. Unlike most previous studies that concentrate on small-diameter pipes (<12 inches) or simplified boundary conditions, this work investigates large-diameter composite pipes under realistic offshore loading scenarios. The investigation encompasses: (1) geometric characterization via laser scanning and residual stress measurement through the ring-cutting method; (2) uniaxial tensile testing of the base material (X65 steel), clad material (Alloy625), and composite specimens using digital image correlation (DIC) for full-field strain measurement; (3) microstructural analysis through metallography and electron backscatter diffraction (EBSD); and (4) development of a detailed three-dimensional FE model in ABAQUS, incorporating initial ovality and residual stresses to simulate the bending behavior. This comprehensive approach provides new insights into the failure mechanisms and design optimization of large-diameter metallurgical clad pipes in deep-sea environments.
2. Materials and Experimental Methods
2.1. Sample Preparation
A 1.5 m long 24-inch metallurgically clad pipe was sectioned into six segments (340 mm × 1 and 230 mm × 5), as illustrated in Figure 1a,b. Geometric parameters, including length, outer diameter, and wall thickness, were measured at multiple angular positions for each segment, with averaged values presented in Table 1. Specifically, the outer diameter and wall thickness were measured along the circumferential direction at 0°, ±8°, ±30°, ±60°, ±90°, ±120°, ±150°, ±172°, and 180°, taking the weld seam as the 0° reference. The FE model incorporated measured ovality values calculated according to Det Norske Veritas (DNV) specifications, yielding a mean ovality of 0.407%, as detailed in Table 2.

Figure 1.
Pipe segments and 3D scanning: (a) A 1.5 m long 24-inch metallurgically clad pipe; (b) Six segments of the clad pipe; (c) AlphaScan metrology-grade handheld scanner; (d) Scanning process.

Table 1.
Geometric dimensions of pipe segments.

Table 2.
Ovality measurement of pipe segments.
Three-dimensional laser scanning was then performed using an AlphaScan metrology-grade handheld scanner (Insvision Technology Co., Ltd., Hangzhou, China) (Figure 1c) following a standardized protocol: (1) scanner calibration using reference artifacts; (2) validation of measurement accuracy through 300 mm standard specimen testing; and (3) pipeline scanning with pre-applied fiducial markers. The scanning process is depicted in Figure 1d.
2.2. Residual Stress Measurement
Hoop residual stresses were determined through the ring-cutting method following the analytical formulation:
where α represents the opening angle after longitudinal cutting, E is the elastic modulus, t is the wall thickness, and R is the pipe radius. The cutting procedure and angular measurement are shown in Figure 2a,b.
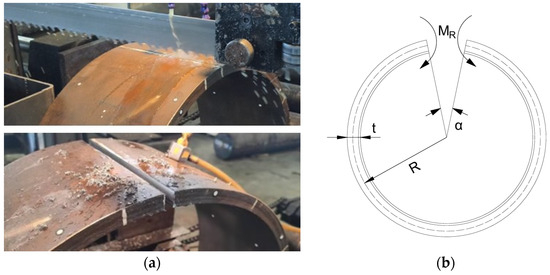
Figure 2.
Longitudinal cutting of pipe segments: (a) Longitudinal cutting procedure; (b) Schematic diagram of the opening angle measurement.
2.3. Tensile Testing
Uniaxial tensile tests were then conducted according to GB/T 228.1-2010 standards [29] for base material (X65), clad material (Alloy625), and composite specimens using a Shimadzu AGX-600 kN universal testing machine (SHIMADZU Corporation, Kyoto, Japan) (Figure 3a).

Figure 3.
Tensile testing equipment: (a) Shimadzu AGX-600 kN universal testing machine; (b) XTDIC-5M digital image correlation system.
Four X65 steel specimens (86 mm parallel length × 20 mm width × 16 mm thickness) were tested at a 2.0 mm/min loading rate, with strain measurement performed using the XTDIC-5M digital image correlation system (XTOP 3D Technology (Shenzhen) Co., Ltd., Shenzhen, China) (Figure 3b) at a 1000 ms acquisition interval, requiring a speckle pattern application on specimen surfaces. Similarly, four Alloy 625 specimens (50 mm × 12.5 mm × 2.7 mm) were tested at a 1.0 mm/min displacement rate using a Y25/10-N extensometer (LISHI (Shanghai) Instrument Co., Ltd., Shanghai, China) with a 25 mm gauge length. To assess strain compatibility between layers, 12 composite specimens (86 mm × 20 mm × 20 mm) were tested at a 1.5 mm/min loading rate, with full-field strain distributions captured by the DIC system, while virtual extensometers recorded engineering strains.
2.4. Microstructural Analysis
Metallographic testing and electron backscatter diffraction (EBSD) scanning analysis were also performed to investigate the microstructures of the base layer, clad layer, and interfacial bonding region. Three specimens with dimensions of 8 × 8 × 4 mm were extracted from the pipe using a wire-cutting method. These specimens were subsequently gradually ground and polished with metallographic sandpaper. One specimen was etched with a corrosive agent after mechanical polishing to prepare a metallographic specimen for microscopic observation, while the other two underwent argon ion polishing for EBSD scanning analysis following mechanical polishing.
3. Experimental Results
3.1. Three-Dimensional Scanning
The six pipe segments were subjected to three-dimensional laser scanning, with Segment 1 selected as the representative case for detailed presentation. Figure 4a displays its three-dimensional scanning results, while Figure 4b shows the two-dimensional cross-sectional profiles with 20× magnification of surface defects. The red contours indicate amplified inner wall imperfections, and the purple contours represent magnified outer wall irregularities. As shown, radial deviations from nominal circular profiles reveal distinct contact zones of the indentation tool on the inner surface during the JCO forming steps. The scanning accuracy was verified through calibration tests on a 300 mm standard specimen, achieving a measurement precision of 0.047%. In addition, the scanned profile was also checked against manual measurements at different angles of the pipe.
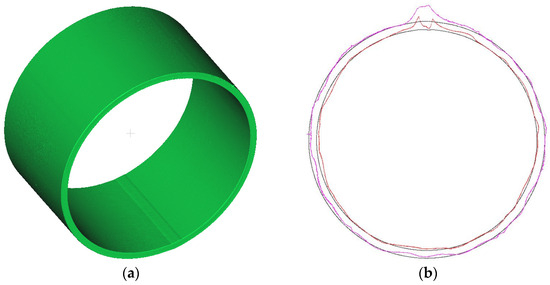
Figure 4.
Scanning Results: (a) Three-dimensional laser scanning result of Segment 1; (b) Cross-sectional profiles of Segment 1 with defects magnified by a factor of 20.
3.2. Residual Stress Measurement Results
Hoop residual stresses were calculated using the ring-cutting method according to Equation (1), with a nominal Young’s modulus of 200 GPa used in the calculation. The measured opening angles and corresponding residual stress values for all six pipe segments are summarized in Table 3. The results indicate consistent residual stress distribution along the pipe circumference, with an average magnitude of 54.58 MPa and a maximum variation of ±15.24 MPa between different pipe sections relative to the mean value.

Table 3.
Measurement of ring-cutting opening and calculated residual stress.
3.3. Tensile Testing Results
3.3.1. Base Material (X65 Steel)
The X65 specimens exhibited typical ductile fracture characteristics during tensile testing. Figure 5a shows the deformed specimens with significant necking. The engineering stress-strain curves obtained through DIC measurement (Figure 5b) reveal a yield strength of 552.08 MPa and an ultimate tensile strength of 618.03 MPa. Detailed mechanical properties are provided in Table 4.
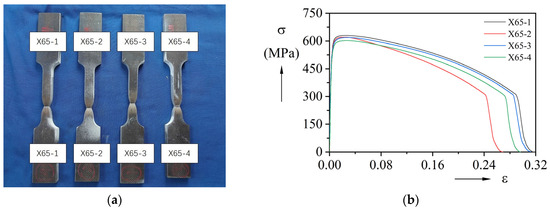
Figure 5.
Tensile testing results of the base material: (a) Specimen of base material after tensile test; (b) Stress-strain curves.

Table 4.
Main material parameters of base material.
3.3.2. Clad Material (Alloy625)
Alloy625 specimens demonstrated superior ductility with significantly higher fracture strains than the X65 counterparts. The deformed specimens are shown in Figure 6a, and the stress-strain curve in Figure 6b displays continuous strain hardening without a distinct yield plateau, characteristic of austenitic alloys. The yield strength reached 679.09 MPa with an ultimate strength of 965.46 MPa and an average strain of 27.90% at peak load, as detailed in Table 5.
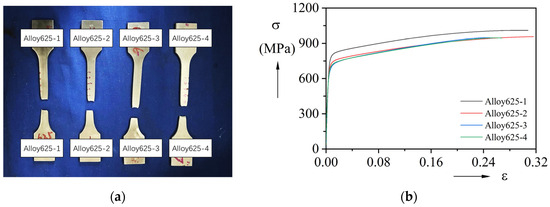
Figure 6.
Tensile testing results of the clad material: (a) Specimen of clad material after tensile test; (b) Stress-strain curves.

Table 5.
Main material parameters of clad material.
3.3.3. Composite Material (X65 + Alloy625)
As to the composite material, the side view of the fractured specimens is presented in Figure 7a (specimen Clad-01 to Clad-12 from left to right). The corresponding nominal stress-strain curves are in Figure 7b. Here, the nominal stress was calculated based on the total area of the cross-section. Interestingly, the composite specimens demonstrated sequential failure characteristics during tensile testing. Initially, the tensile loading induced uniform deformation of the base and clad material. Subsequently, necking originated at peak load, which was followed by audible interface delamination sound. This phenomenon is consistent with the delamination behavior observed in previous studies on bimetallic materials during tensile testing [6]. After continuous loading, a second fracture sound marked clad layer failure after several seconds, while additional loading eventually led to progressive base layer necking until final rupture with complete load drop. This study employed DIC to measure engineering strain during experiments. Unlike previous studies, this approach allows for the acquisition of strain data over the full tensile process, yielding a more complete dataset.
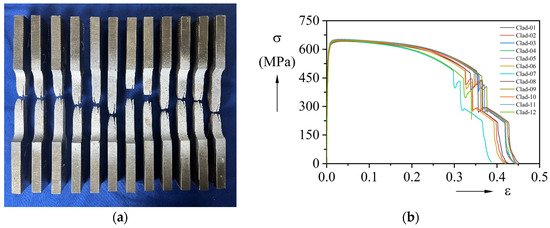
Figure 7.
Tensile testing results of the composite material: (a) Specimen of composite material after tensile test; (b) Stress-strain curves.
For illustration, the stress-strain curve and the corresponding DIC measurement of Clad-01 are specifically displayed in Figure 8 and Figure 9. As shown, the curve exhibits a progressive decline after reaching peak stress. At point a (33.73% strain), interfacial delamination occurs with a sharp stress drop, followed by gradual stress recovery. Subsequently, the clad material Alloy625 fractures at point b (34.23% strain), causing a secondary abrupt decline in stress. Thereafter, only the base layer sustains loading until point c (40.19% strain), where a third stress drop coincides with base material fracture. Key mechanical parameters are summarized in Table 6.
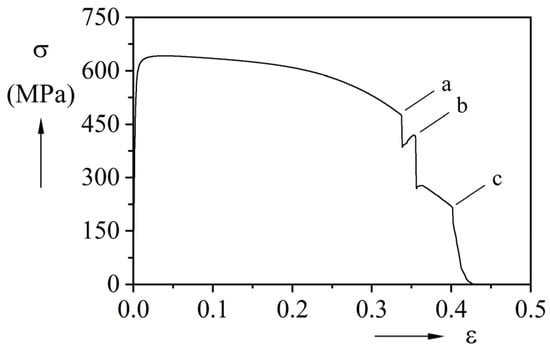
Figure 8.
Stress-strain curve of specimen Clad-01.
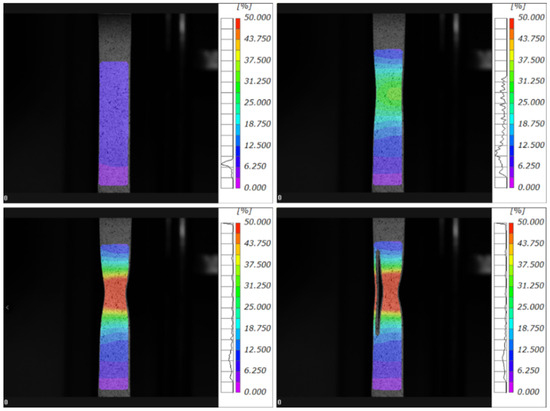
Figure 9.
Measured strain distribution map from DIC.

Table 6.
Main material parameters of composite material.
The strain contour maps obtained through DIC processing are presented in Figure 9. These maps demonstrate a gradual strain localization after necking from both specimen ends toward the central region. The strain initially exhibits uniform distribution across transverse sections, and these identical strain patterns between the base and clad layers confirm their synchronous deformation during tensile loading. Then, delamination takes place, and an extended length of the clad layer separates from the base material, but the strain level of both layers is still almost the same.
3.4. Microstructural Analysis Results
Optical microscopy (OM) observations of X65 steel are presented in Figure 10a (four representative locations). The interface between the two materials appears smooth with minor undulations, but without detectable defects. The X65 region near the interface primarily consists of polygonal ferrite and ferritic bainite structures, with dispersed black M/A (martensite-austenite) constituents within the ferritic bainite. While these M/A phases may induce localized stress concentrations, their limited volume fraction suggests negligible impact on overall toughness.
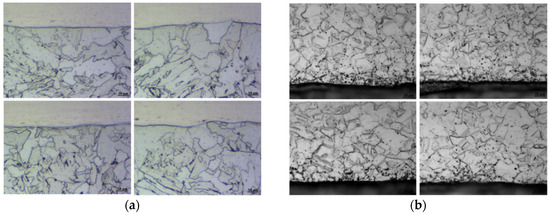
Figure 10.
OM observations results: (a) OM observations of X65 Steel; (b) OM observations of Alloy625.
OM examination of Alloy625 (Figure 10b, four representative locations) reveals a homogeneous single-phase structure composed of fine equiaxed grains at the interface region. The distinct thermal conductivity between ferrite and austenite inevitably induces grain refinement and solid solution strengthening in specific regions of the clad layer, resulting in nanoscale grains and solid solution structures. Dark precipitates are observed within grains and along boundaries, exerting grain boundary-pinning effects that further refine the microstructure. Notably, irregularly distributed dark aggregates concentrate along the bimaterial interface, particularly at edge regions.
Electron backscatter diffraction (EBSD) analysis results are shown in Figure 11. The grain orientation map (Figure 11a) demonstrates clustered fine grains with similar crystallographic orientations in X65 pipeline steel, contrasting with coarse equiaxed grains containing annealing twins in Alloy625. This twin formation likely originates from structural reorganization during recrystallization, where low stacking fault energy promotes twin generation through stacking fault interactions. Near the fusion line, X65 grains exhibit agglomerated distributions resulting from incomplete austenite transformation at elevated temperatures, while regions distant from the interface show typical as-rolled microstructures due to insufficient heating. The phase distribution map (Figure 11b) confirms the dominant ferritic matrix in X65 with minor austenite phases at grain boundaries, whereas Alloy625 maintains primarily austenitic structure containing trace ferrite phases along grain boundaries.
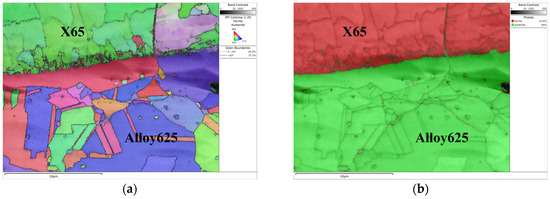
Figure 11.
EBSD analysis results: (a) Grain orientation map; (b) Phase distribution map.
4. Finite Element Analysis
4.1. Model Setup
Bending load represents the most frequent loading condition for subsea pipelines in practical engineering applications. A three-dimensional FE model was developed using ABAQUS 2019 (Dassault Systèmes, Vélizy-Villacoublay, France) commercial software to simulate pipe bending behavior under quasi-static conditions, employing the Static General module.
The FE model replicates a 24-inch metallurgical clad pipe with 609.6 mm outer diameter, 17 mm base layer thickness, 3 mm clad layer thickness, and 1828.8 mm length (equals 3 diameters). Considering dual symmetry characteristics, a quarter model was established with symmetric boundary conditions applied on z = 0 and y = 0 planes (Figure 12). The model employs C3D8 solid elements for the base pipe and S4 shell elements for the clad layer, with four elements through the base wall thickness and a single-layer shell for the clad. This element configuration is consistent with the modeling strategy adopted by Yuan et al. [18] in their study on clad pipes, ensuring accurate representation of mechanical behavior while maintaining computational efficiency. Circumferential and axial directions contain 108 and 99 elements, respectively, incorporating graded axial meshing with refined elements at mid-span regions to balance computational efficiency and accuracy.

Figure 12.
Finite element model.
Experimentally measured material properties were assigned to corresponding inner and outer tubes. In addition, considering the interface delamination takes place at a strain level of 34.17%, the bonding between the two material layers was simulated through tie constraints. Bending moments were applied via reference point rotation coupled with pipe end surfaces. The cross-section at the end plane is free to ovalize while ensuring the plane-remains-plane assumption.
It is worth pointing out that the FE model explicitly incorporates initial ovality of 0.407% and residual stresses of 54.58 MPa from manufacturing processes, utilizing experimentally measured values for both parameters. The residual stress field was introduced via the INITIAL CONDITIONS, TYPE = STRESS option in ABAQUS.
4.2. Bending Simulation
The Mises stress contours of the metallurgically clad pipe before and after bending are presented in Figure 13a,b. The stress distribution along the axial direction remains uniform during bending deformation, while cross-sectional ovalization becomes evident. The moment-curvature and ovality-curvature curves extracted from the pipe’s symmetric plane are shown in Figure 14a,b. Specifically, the moment of the base and clad layer, as well as the value of the composite pipe, are plotted, respectively. As expected, the base material layer carries most of the load. To facilitate comparison, the results are presented in dimensionless form. The normalizing variables are based on the parameters of the base pipe as follows:
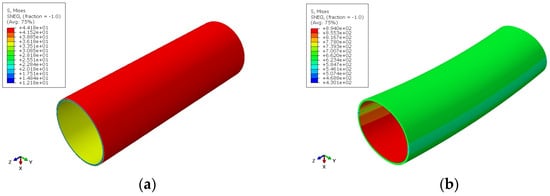
Figure 13.
Mises stress contour of the base case: (a) After the introduction of residual stresses; (b) After bending.
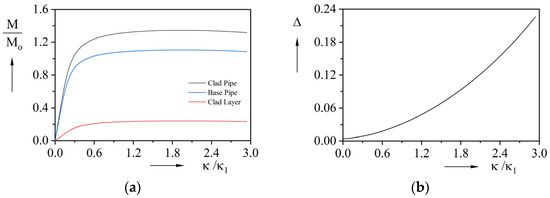
Figure 14.
Finite element results of the base case: (a) Moment-curvature curves (b) Ovality-curvature curve.
As demonstrated in Figure 14a, the bending moment increases linearly with curvature during the elastic stage, followed by a reduced growth rate when plastic yielding occurs. Then, the normalized bending moment reaches its peak value of 1.35 at a normalized curvature of 1.92, followed by a gradual decline. Subsequently, the normalized bending moment gradually decreases with increasing curvature. The normalized curvature at the maximum bending moment is considerably greater than that of mechanically lined pipes [18], indicating enhanced bending resistance. At the same time, the normalized maximum bending moment is also significantly larger. Figure 14b reveals progressive ovality accumulation with curvature, where the curve’s increasing slope indicates an accelerated ovalization rate at higher curvatures.
Comparative analyses of pipes with different initial ovalities are shown in Figure 15 and Figure 16 to further investigate the mechanical behavior under bending loads. Ovalities of 0%, 0.41%, 0.81%, and 1.22% are assigned to the FE model. As observed, Figure 15a demonstrates that higher initial ovality reduces the peak bending moment, indicating weakened load-bearing capacity. However, the reduction is approximately 0.5%, which is relatively small and can be considered negligible. In addition, Figure 15b confirms that initial ovality tends to amplify cross-sectional deformation under identical curvature, which further leads to a reduced moment of inertia and consequent capacity reduction—consistent with findings in Figure 15a.
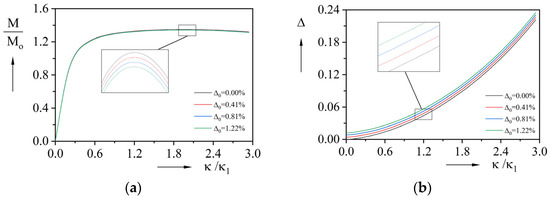
Figure 15.
Finite element results of pipes with different initial ovalities: (a) Moment-curvature curves; (b) Ovality-curvature curves.
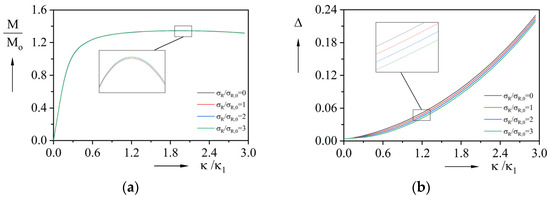
Figure 16.
Finite element results of pipes with different residual stresses: (a) Moment-curvature curves; (b) Ovality-curvature curves.
The residual stress effects were studied by assigning σR/σR,0 = {0, 1.0, 2.0, 3.0} to the FE model. Figure 16a shows negligible variations in peak moments across different residual stress levels, suggesting a limited influence on ultimate bending capacity. Notably, higher residual stresses suppress ovalization growth rates during bending (Figure 16b), despite identical initial ovality conditions. This interesting phenomenon aligns with Kyriakides’ observations of bending-type residual stress-suppressing effects in single-wall pipes [30]. The introduction of residual stress initiates reverse ovalization development during bending-induced plasticization, with strain localization concentrating preferentially in the cross-section’s 0° and 180° orientations.
5. Conclusions
This paper investigates the mechanical properties of X65 + Alloy625 metallurgically clad pipes through experimental and numerical methods. Uniaxial tensile tests demonstrate that the base material (X65 steel) and clad material (Alloy625) exhibit excellent coordinated deformation capability. Interface delamination occurs when the average strain reaches 34.17%, followed by sequential fracture of the clad and base layers. Microstructural analysis reveals well-bonded interfaces with X65, which are primarily composed of polygonal ferrite and ferritic bainite, while Alloy625 consists of austenitic equiaxed grains. Finite element simulations indicate that larger initial ovality reduces ultimate bending moment, whereas residual stresses show limited influence on both load-bearing capacity and ovality progression. In this study, the actual measured initial ovality of the pipe was 0.4066%, and the residual stress was 54.58 MPa. The simulation yielded a maximum normalized bending moment of 1.35, corresponding to a normalized curvature of 1.92. These findings can provide some references for the safe design and engineering application of metallurgically clad pipes in deep-sea environments. Future investigations will address the effects of cyclic loading on interface degradation mechanisms. Moreover, subsequent modeling efforts would also integrate weld joint details, enabling a comprehensive assessment of strain localization and failure risks in girth-welded clad pipe systems.
Author Contributions
Conceptualization, F.W. and L.Y.; Methodology, F.W. and S.Y.; Software, S.Y.; Validation, Y.G. and Z.C.; Formal analysis, Y.G. and Z.C.; Investigation, Y.G., Z.H., S.Y., Z.C. and R.F.; Resources, Z.H. and R.F.; Data curation, Y.G. and Z.H.; Writing—original draft, F.W., S.Y. and R.F.; Writing—review and editing, F.W., Y.G., Z.H., S.Y., Z.C., R.F. and L.Y.; Visualization, Y.G.; Supervision, L.Y.; Project administration, R.F. and L.Y.; Funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant number 52271288).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Feng Wang, Yanan Gao, Zhiguo Hu, Shuo Yang and Zhenying Cui were employed by the company PipeChina Engineering Technology Innovation Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Symbol | Definition |
| α | Opening angle after longitudinal cutting |
| Δ | Ovality |
| Δ0 | Initial ovality |
| ε | Strain |
| εd | Delamination strain |
| εf | Clad fracture strain |
| σ | Stress |
| σR | Residual stress |
| σo | Yield strength of the base pipe |
| σR,0 | Measured average residual stress |
| Agt | Elongation at maximum force |
| D | Diameter |
| E | Elastic modulus |
| fy | Yield strength |
| fu | Ultimate tensile strength |
| L | Length |
| M | Moment |
| R | Pipe radius |
| t | Wall thickness |
| to | Base pipe thickness |
References
- Chee, J.; Walker, A.; White, D. Controlling lateral buckling of subsea pipeline with sinusoidal shape pre-deformation. Ocean Eng. 2018, 151, 170–190. [Google Scholar] [CrossRef]
- Gao, Z.; Han, B.; Li, L.; Ma, G.; Niu, S. Numerical simulation of residual stress in post internal-welding process of bimetal composite pipe and optimization of welding sequence. Int. J. Press. Vessel. Pip. 2022, 199, 104730. [Google Scholar] [CrossRef]
- Hou, D.; Cheng, X.; Wei, L.; Li, Y.; Li, K.; Zhang, Z.; Zhang, H.; Bian, J.; Li, Y.; Si, W. Oil and natural gas geochemistry in offshore China: Advances and challenges. Nat. Gas Ind. B 2024, 11, 631–644. [Google Scholar] [CrossRef]
- Gao, J.; Li, C.-L.; Zhao, S. Optimization of Welding Process for 825 Bimetallic Composite Pipes Based on Corrosion Testing. J. Phys. Conf. Ser. 2024, 2834, 012177. [Google Scholar]
- Wang, F.-C.; Li, W.; Han, L.-H. Interaction behavior between outer pipe and liner within offshore lined pipeline under axial compression. Ocean Eng. 2019, 175, 103–112. [Google Scholar] [CrossRef]
- Liu, X.; Bai, R.; Uy, B.; Ban, H. Material properties and stress-strain curves for titanium-clad bimetallic steels. J. Constr. Steel Res. 2019, 162, 105756. [Google Scholar] [CrossRef]
- Eiselstein, H.; Tillack, D. The invention and definition of alloy 625. Superalloys 1991, 718, 1–14. [Google Scholar]
- Dong, J.; Wang, D.; Guo, Y. Preparation and Performance Evaluation of Erosion Resistant Lining of Bimetallic Composite Pipe. In Proceedings of the International Pipeline Conference, Calgary, AB, Canada, 26–30 September 2022; p. V002T003A021. [Google Scholar]
- Sun, Y.; Yu, S.; Wang, B.; Liu, L.; Liu, E.; Feng, T. Interface Microstructure and Mechanical Properties of Nickel/Steel Bimetal Composite Pipe Fabricated by Explosive Welding. Metals 2024, 14, 1253. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H. Residual stress. Part 1–measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Hilberink, A.; Gresnigt, A.; Sluys, L. Mechanical behaviour of lined pipe during bending: Numerical and experimental results compared. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 401–412. [Google Scholar]
- Hilberink, A.; Gresnigt, A.; Sluys, L. Liner wrinkling of lined pipe under compression: A numerical and experimental investigation. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 311–322. [Google Scholar]
- Hilberink, A.; Gresnigt, A.M.; Sluys, L.J. Mechanical Behaviour of Lined Pipe; Civil Engineering & Geoences: Delft, The Netherlands, 2011; pp. 401–412. [Google Scholar]
- Tkaczyk, T.; Pepin, A. Methods of Reel-Laying a Mechanically Lined Pipe. US8864417B2, 21 October 2014. [Google Scholar]
- Tkaczyk, T.; Pepin, A.L.; Denniel, S. Integrity of mechanically lined pipes subjected to multi-cycle plastic bending. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 255–265. [Google Scholar]
- Yuan, L.; Zhou, J.; Liu, H.; Chen, N.-Z. Buckling of dented bi-material pipe under bending Part I: Experiments and simulation. Int. J. Solids Struct. 2022, 257, 111705. [Google Scholar] [CrossRef]
- Vasilikis, D.; Karamanos, S.A. Mechanical behavior and wrinkling of lined pipes. Int. J. Solids Struct. 2012, 49, 3432–3446. [Google Scholar] [CrossRef]
- Yuan, L.; Kyriakides, S. Liner wrinkling and collapse of bi-material pipe under bending. Int. J. Solids Struct. 2014, 51, 599–611. [Google Scholar] [CrossRef]
- Yuan, L.; Kyriakides, S. Liner wrinkling and collapse of bi-material pipe under axial compression. Int. J. Solids Struct. 2015, 60, 48–59. [Google Scholar] [CrossRef]
- Yuan, L.; Kyriakides, S. Plastic bifurcation buckling of lined pipe under bending. Eur. J. Mech.-A/Solids 2014, 47, 288–297. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, Z.; Chen, N. On the buckling of mechanically lined pipes under combined tension and bending. Ocean Eng. 2022, 262, 111991. [Google Scholar] [CrossRef]
- Yuan, L.; Kyriakides, S. Liner buckling during reeling of lined pipe. Int. J. Solids Struct. 2020, 185, 1–13. [Google Scholar] [CrossRef]
- Focke, E.S.; Gresnigt, A.M.; Hilberink, A. Local buckling of tight fit liner pipe. J. Press. Vessel Technol. 2011, 133, 011207. [Google Scholar] [CrossRef]
- Yoshitake, A.; Torigoe, T. Centrifugally cast bimetallic pipe for offshore corrosion resistant pipelines. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994; p. ISOPE–I-94-115. [Google Scholar]
- Slany, M.; Sedlak, J.; Zouhar, J.; Zemcik, O.; Kouril, K.; Polzer, A.; Pokorny, Z.; Joska, Z.; Dobrocky, D.; Studeny, Z. Analysis of bimetal pipe bends with a bend of 0.7 D with a cladding layer of Inconel 625. Int. J. Adv. Manuf. Technol. 2021, 117, 3859–3871. [Google Scholar] [CrossRef]
- Yang, R.; He, Y.; Zhang, Y.; Duan, M. Strain Capability Analysis of Metallurgically Clad Pipe With Girth Welds Under Combined Loads. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Singapore, 9–14 June 2024; p. V003T004A053. [Google Scholar]
- Yang, R.; He, Y.; Zhang, Y.; Duan, M.; Wang, S.; Wei, S. Strain capacity of metallurgically clad pipes with girth welds during deep-sea reel-lay installation. Ocean Eng. 2025, 325, 120743. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, C.; Luo, Q.; Chen, N. Collapse pressure prediction of mechanically lined pipes using FEM and machine learning techniques. Ocean Eng. 2023, 268, 113418. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2010.
- Kyriakides, S.; Corona, E. Mechanics of Offshore Pipelines: Volume i: Buckling and Collapse; Gulf Professional Publishing: Oxford, UK, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).