Multi-Objective Path Optimization Method for Maritime UAVs Equipped with Inertial Navigation Systems
Abstract
1. Introduction
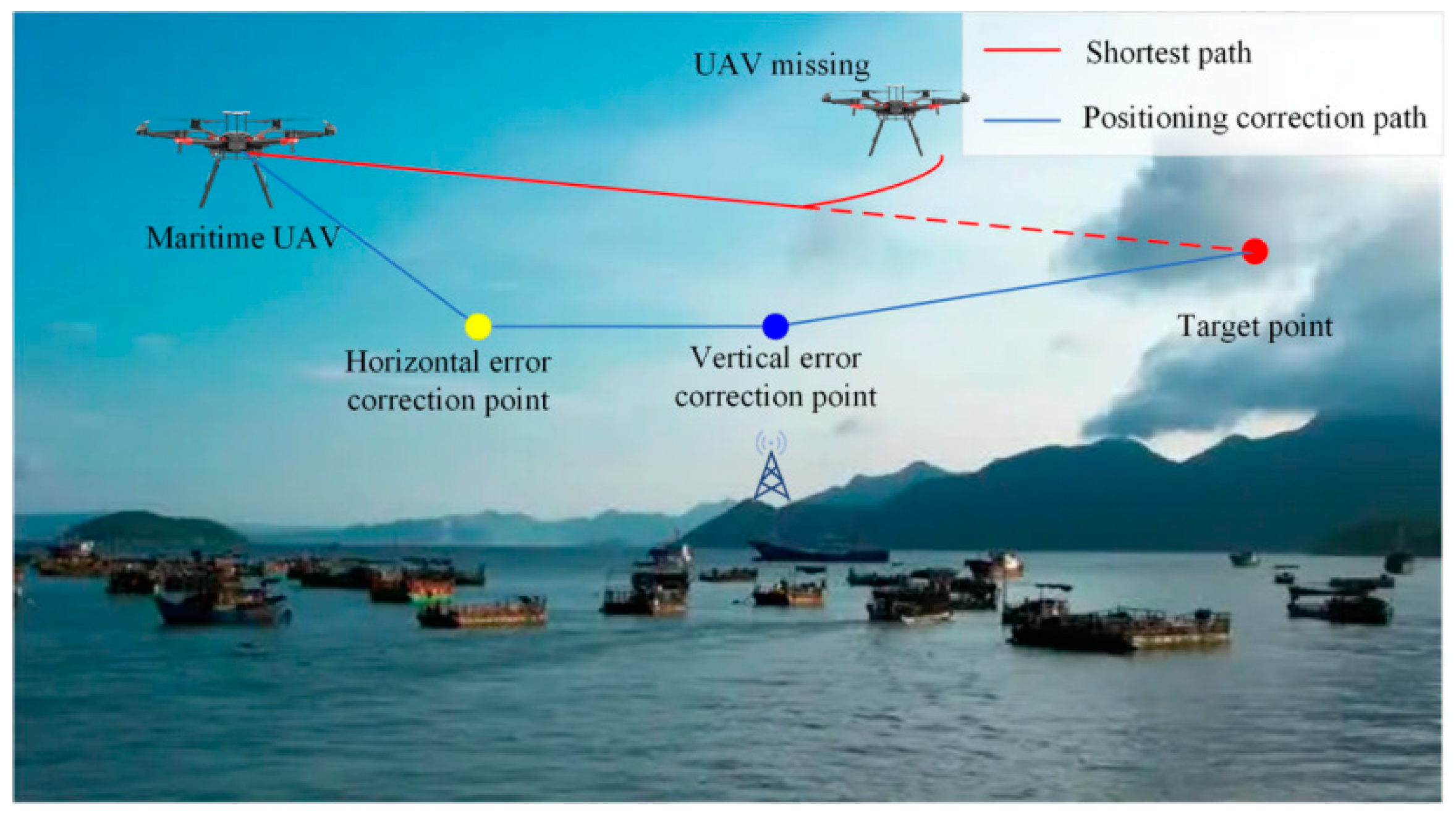
2. Problem Description
3. Mathematical Model
3.1. Model Assumptions
- (1)
- At the starting point, the vertical and horizontal errors of the aircraft are both zero.
- (2)
- When the UAV performs vertical error correction at a vertical error correction point, its vertical error is reset to 0, while the horizontal error remains unchanged.
- (3)
- When the UAV performs horizontal error correction at a horizontal error correction point, its horizontal error is reset to 0, while the vertical error remains unchanged.
- (4)
- During flight, the UAV operates without unexpected disruptions, except as specified in the problem statement.
- (5)
- The UAV can continue to follow the planned trajectory provided that both the vertical and horizontal errors remain below their critical thresholds.
3.2. Model Variables and Parameters
3.3. Maritime UAV Path Planning Model
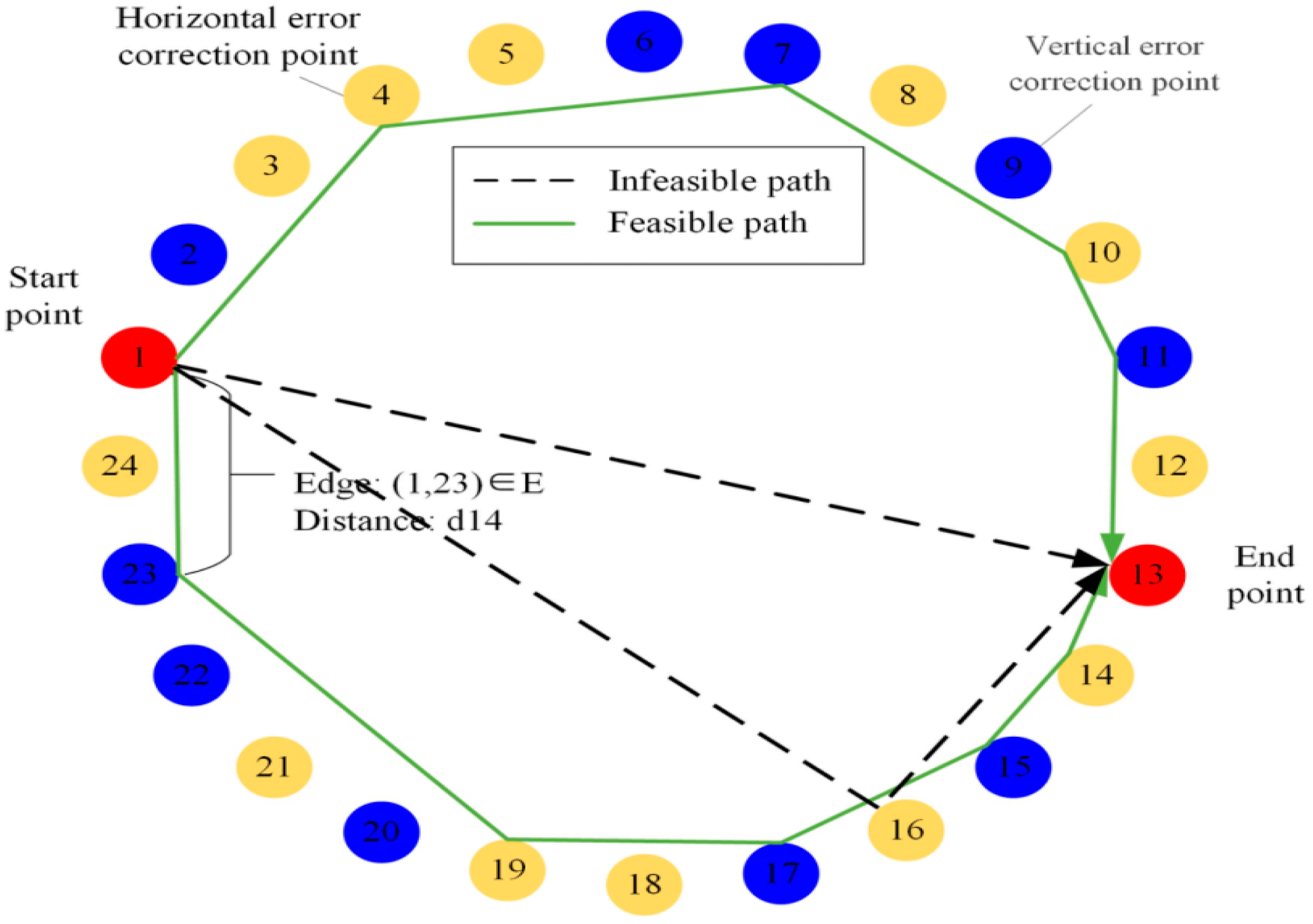
3.3.1. Directed Graph Network
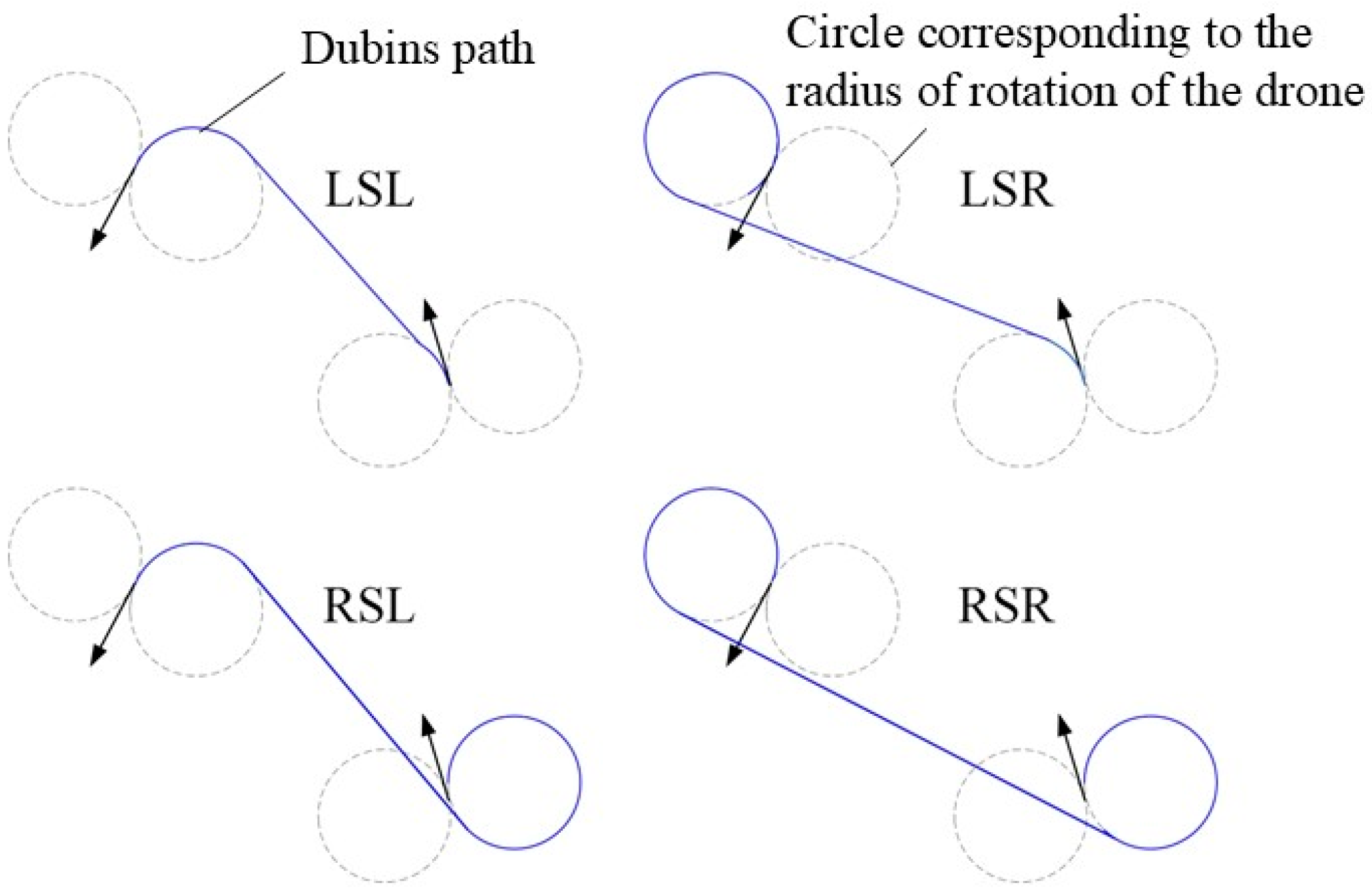
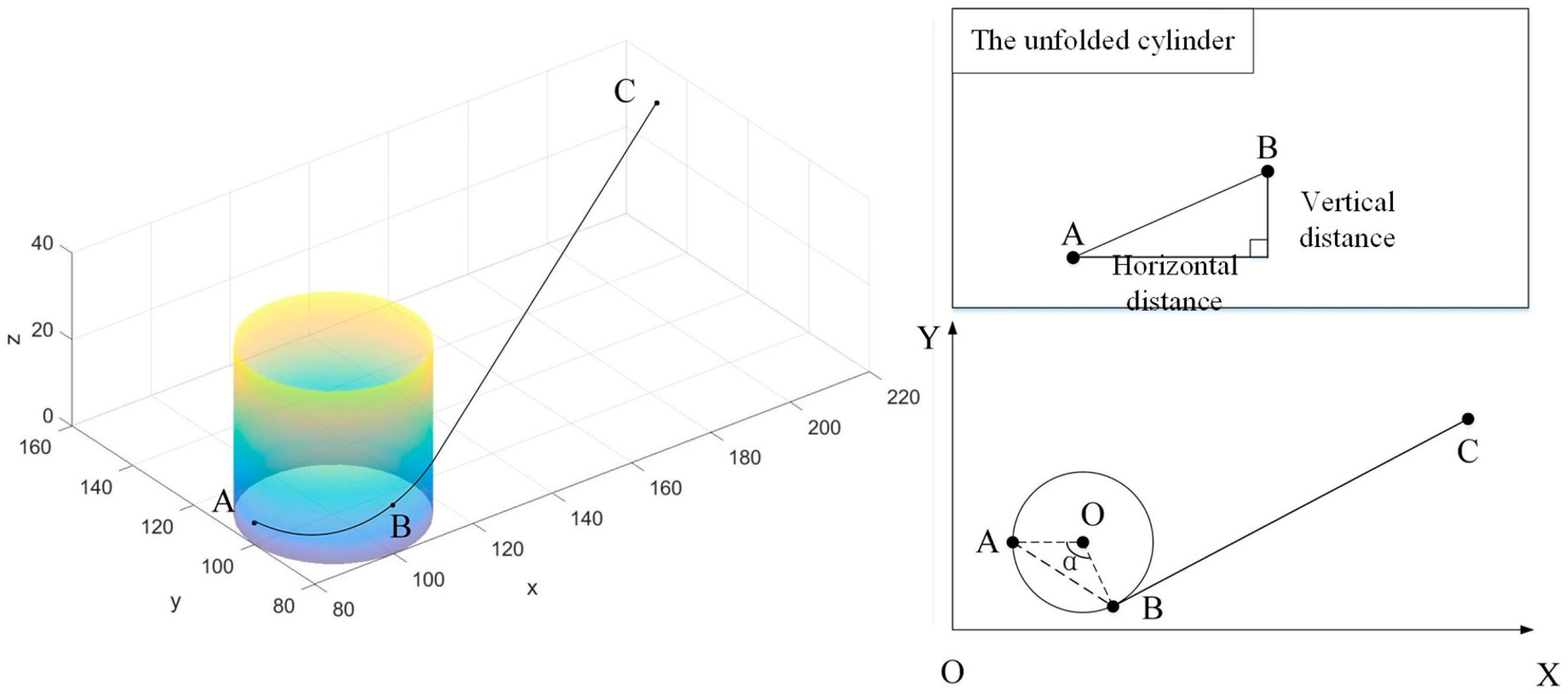
3.3.2. Path Distance Calculation Based on Dubins Curve
3.3.3. Uncertainty of Calibration Error
3.3.4. Objective Model
4. Solution Method
4.1. Model Analysis
4.2. Forward Propagation Multi-Objective Path Planning Algorithm
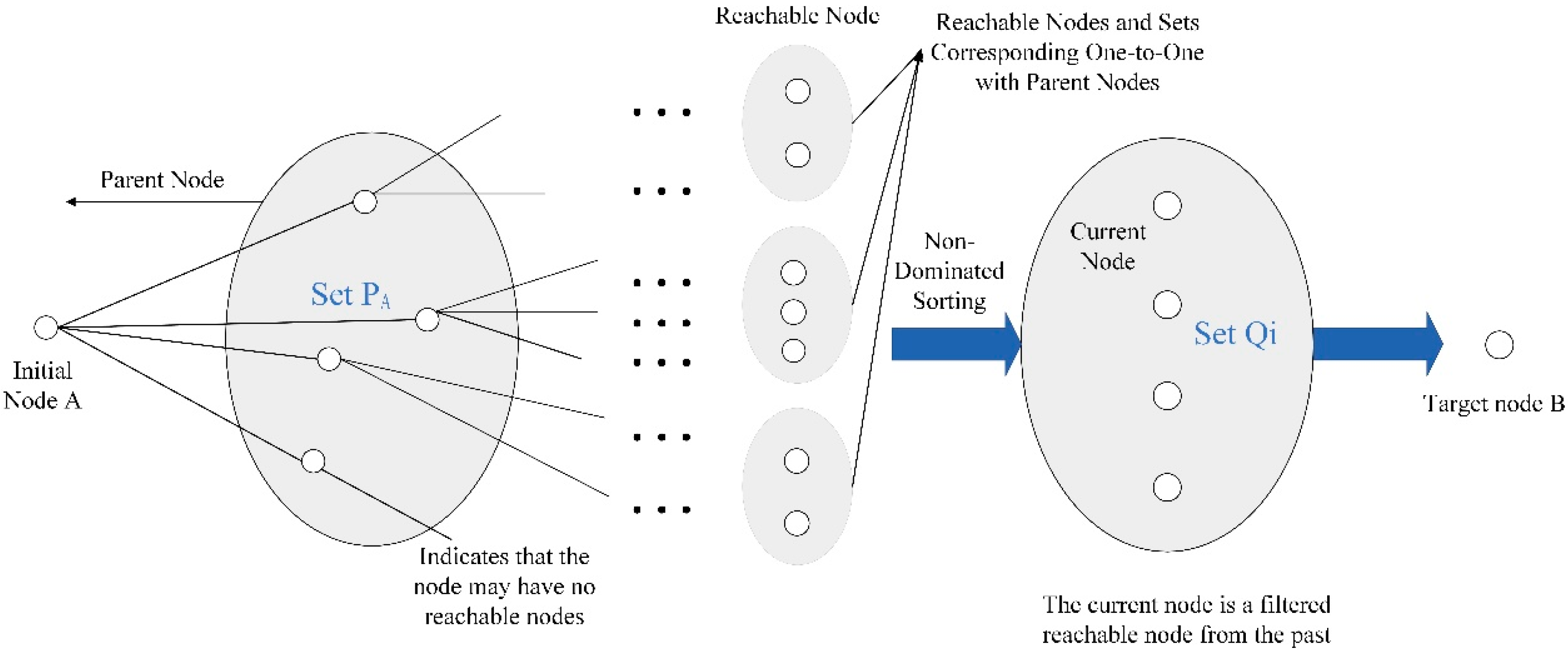
4.2.1. Core Algorithmic Ideas
4.2.2. Core Algorithmic Steps
- Forward Labeling Setup
- 2.
- Heuristic Optimization Strategy
- 3.
- Non-Dominated Sorting Method
| Algorithm 1: Multi-objective path planning algorithm based on forward labels | |
| Input: | Start point s and the target point t. Directed graph G, distance matrix D. |
| Output: | A set of Pareto optimal paths from s to t. |
| Step 1: | Initialize a label set L(v) for each vertex v ∈ V. Each label l ∈ L(v) represents a partial path from ss to vv and stores the following: The cost vector c(l) (e.g., F1, F2, and F3). The predecessor vertex p(l) to reconstruct the path. |
| Step 2: | Add an initial label l0 to L(s) with zero cost and no predecessor. |
| Step 3: | For each vertex u ∈ V in topological order (or using a priority queue) For each outgoing edge (u,v) ∈ E For each label l ∈ L(u) Create a new label l′ for vertex v. Update the cost vector: c(l′) = c(l)+Du,v. Set the predecessor: p(l′) = u. Add l′ to L(v) if it is not dominated by any existing label. Remove any labels in L(v) that are dominated by l′. |
| Step 4 | A label l1 dominates another label l2 if c(l1) is better than or equal to c(l2) in all objectives and strictly better in at least one objective. |
| Step 5: | Only non-dominated labels are kept in L(v)L(v) to ensure Pareto optimality. |
| Step 6: | The algorithm terminates when all vertices have been processed and no further labels can be propagated. |
| Step 7: | The set of labels L(t) at the target vertex tt represents the Pareto optimal paths from s to t. |
| Step 8: | For each label l ∈ L(t), reconstruct the path by backtracking through the predecessors p(l) until reaching the start vertex s. |
5. Case Studies
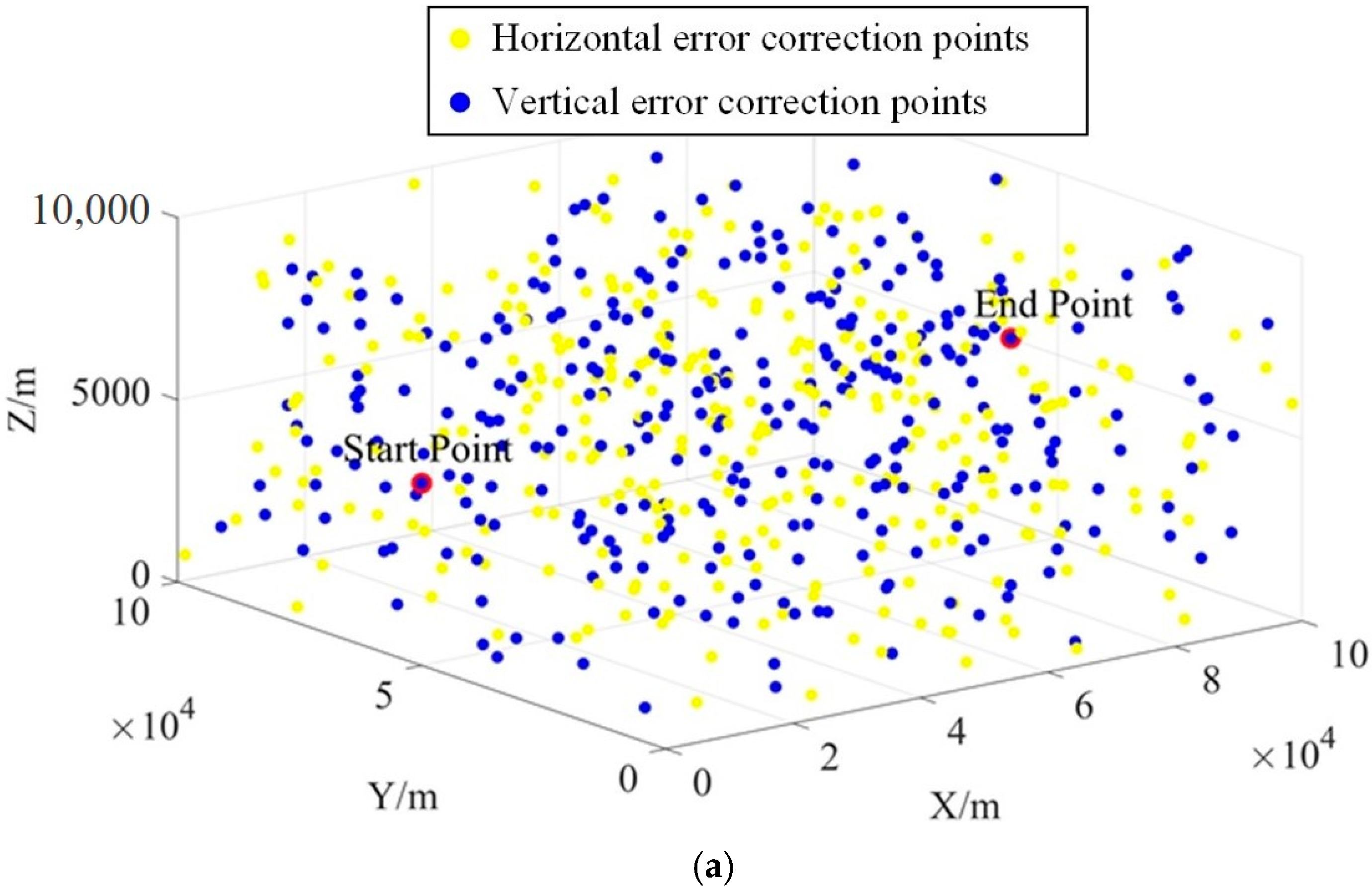
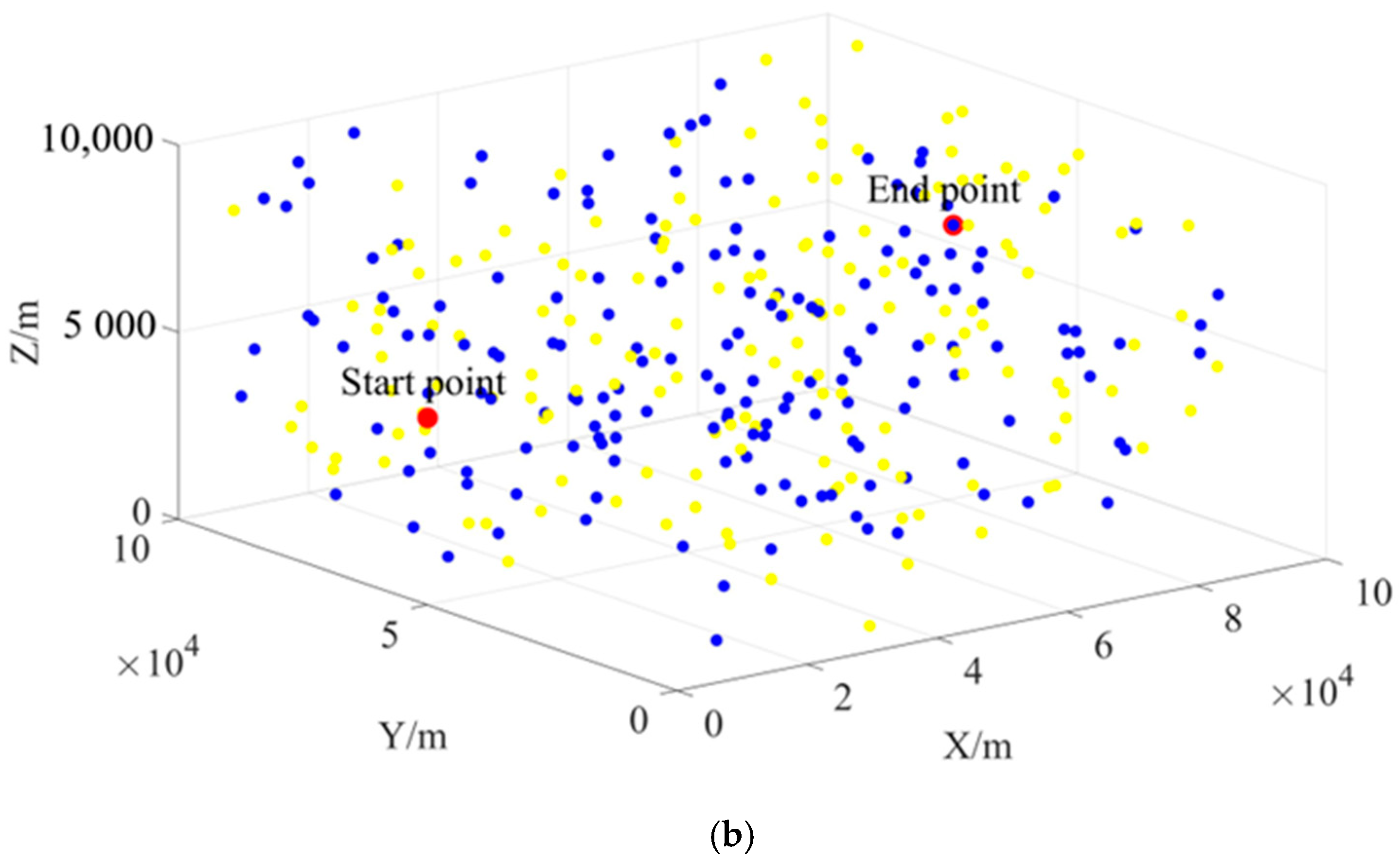
5.1. Definition of Cases
5.2. Results and Discussion
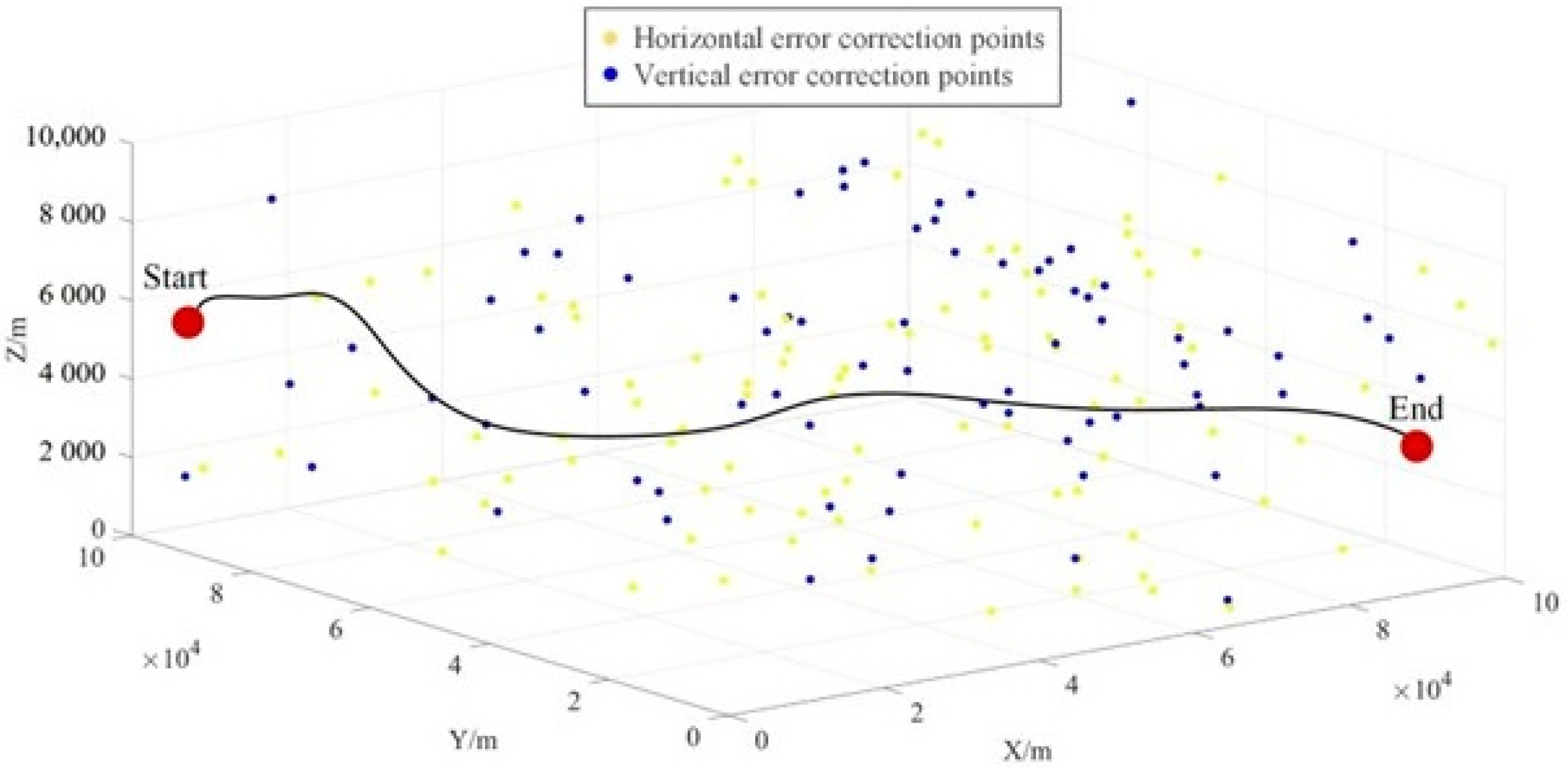
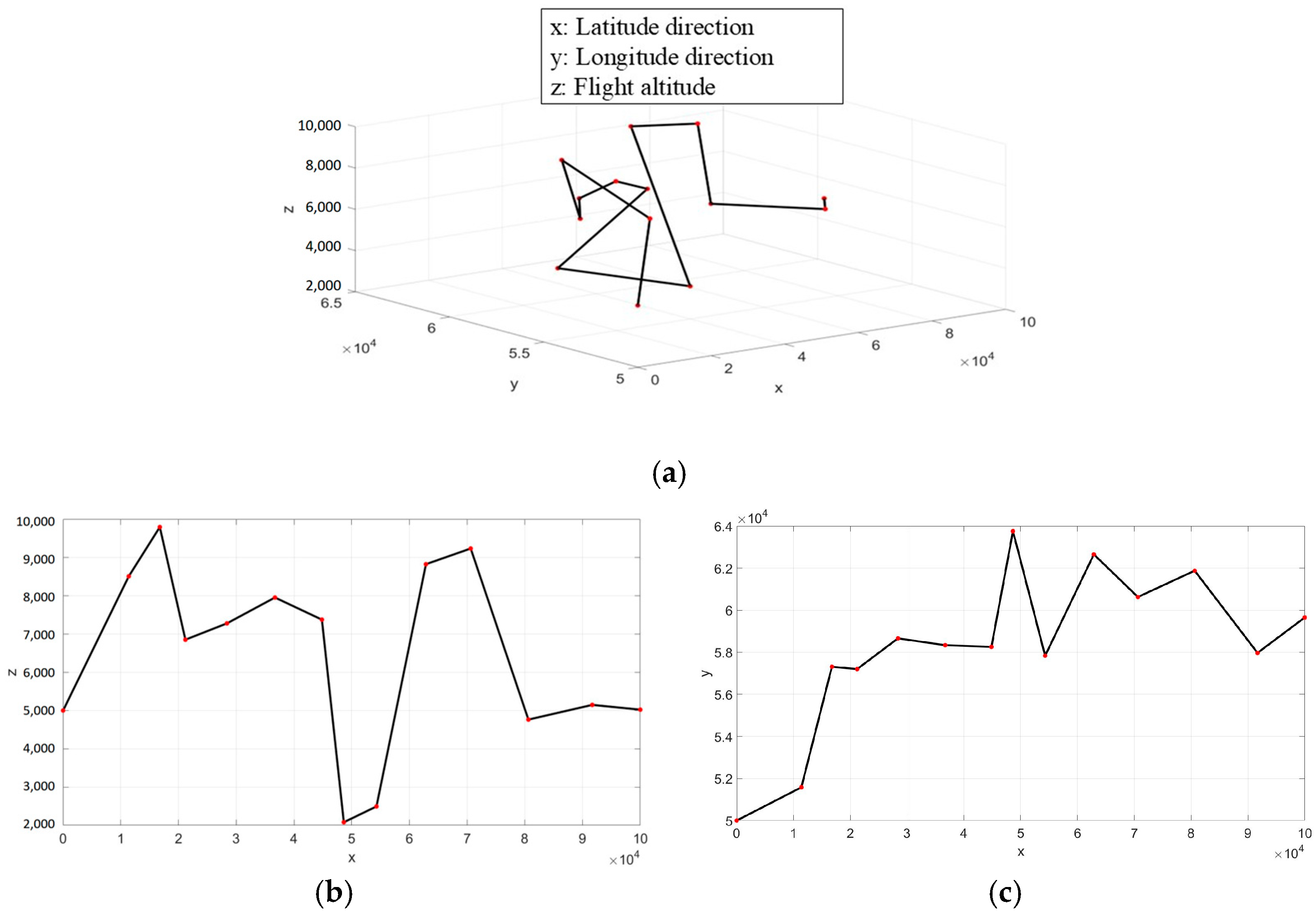
5.2.1. Results of Case 1
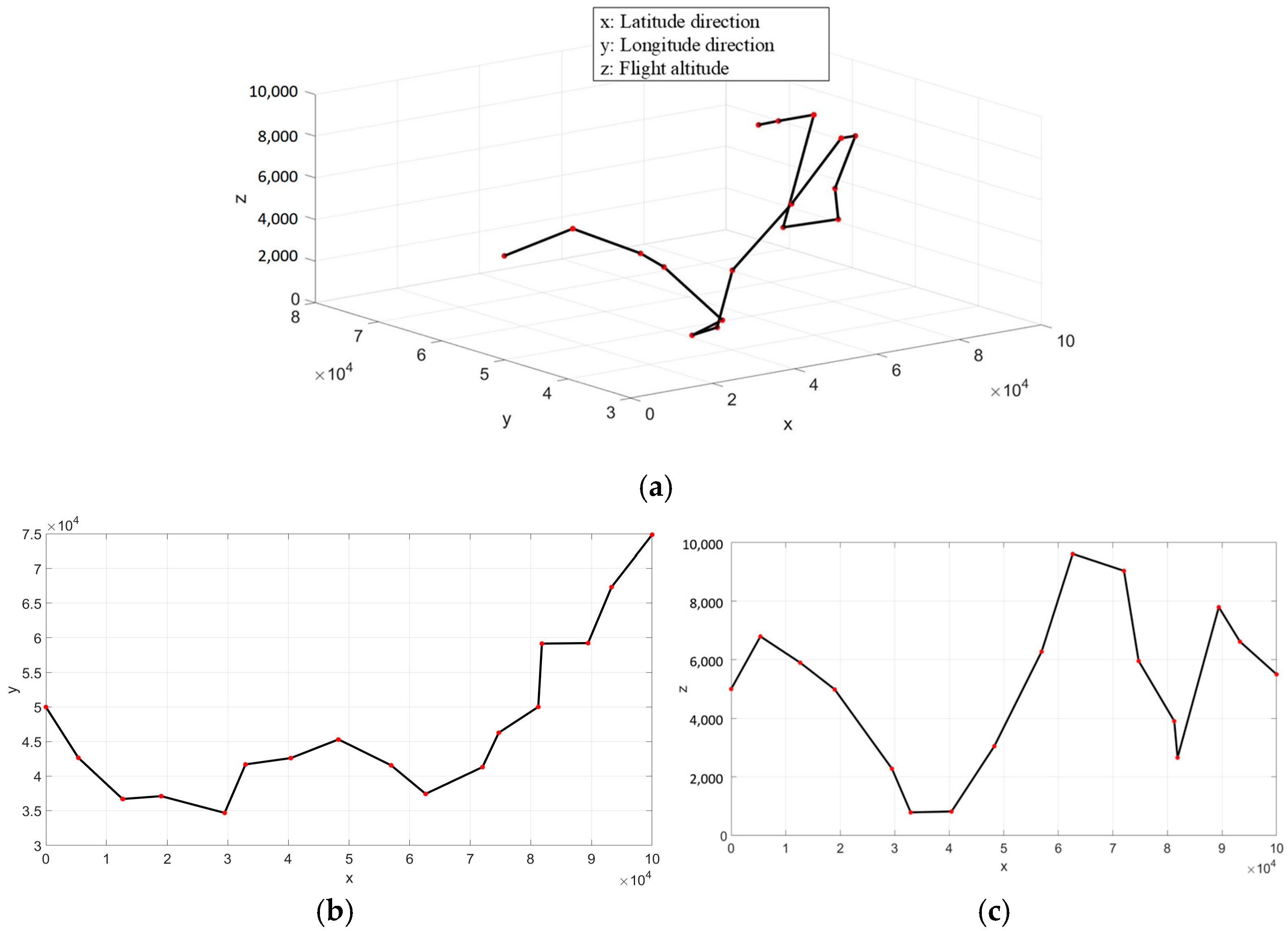
5.2.2. Results of Case 2
5.2.3. Results Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022, 838, 155939. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Ma, W.; Jin, S.; Ma, X. Method for simultaneously optimizing ship route and speed with emission control areas. Ocean Eng. 2020, 202, 107170. [Google Scholar] [CrossRef]
- Ventura, D.; Bonifazi, A.; Gravina, M.F.; Belluscio, A.; Ardizzone, G. Mapping and classification of ecologically sensitive marine habitats using unmanned aerial vehicle (UAV) imagery and object-based image analysis (OBIA). Remote Sens. 2018, 10, 1331. [Google Scholar] [CrossRef]
- Nomikos, N.; Gkonis, P.K.; Bithas, P.S.; Trakadas, P. A survey on UAV-aided maritime communications: Deployment considerations, applications, and future challenges. IEEE Open J. Commun. Soc. 2022, 4, 56–78. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Meng, D.; Dong, M.; Ota, K.; Wang, H. Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment. IEEE Internet Things J. 2021, 9, 5708–5718. [Google Scholar] [CrossRef]
- Taddia, Y.; Corbau, C.; Buoninsegni, J.; Simeoni, U.; Pellegrinelli, A. UAV approach for detecting plastic marine debris on the beach: A case study in the Po River Delta (Italy). Drones 2021, 5, 140. [Google Scholar] [CrossRef]
- Dujon, A.M.; Ierodiaconou, D.; Geeson, J.J.; Arnould, J.P.Y.; Allan, B.M.; Katselidis, K.A.; Schofield, G. Machine learning to detect marine animals in UAV imagery: Effect of morphology, spacing, behaviour and habitat. Remote Sens. Ecol. Conserv. 2021, 7, 341–354. [Google Scholar] [CrossRef]
- Ma, W.; Lu, T.; Ma, D.; Wang, D. Ship route and speed multi-objective optimization considering weather conditions and emission control area regulations. Marit. Policy Manag. 2021, 48, 1053–1068. [Google Scholar] [CrossRef]
- Ma, W.; Ma, D.; Ma, Y.; Zhang, J.; Wang, D. Green maritime: A routing and speed multi-objective optimization strategy. J. Clean. Prod. 2021, 305, 127179. [Google Scholar] [CrossRef]
- Ma, W.; Han, Y.; Tang, H.; Ma, D.; Zheng, H.; Zhang, Y. Ship route planning based on intelligent mapping swarm optimization. Comput. Ind. Eng. 2023, 176, 108920. [Google Scholar] [CrossRef]
- Blasi, L.; D’Amato, E.; Mattei, M.; Notaro, I. UAV path planning in 3-d constrained environments based on layered essential visibility graphs. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 2359–2375. [Google Scholar] [CrossRef]
- Yan, F.; Liu, Y.S.; Xiao, J.Z. Path planning in complex 3D environments using a probabilistic roadmap method. Int. J. Autom. Comput. 2013, 10, 525–533. [Google Scholar] [CrossRef]
- Mokrane, A.; BRAHAM, A.C.; Cherki, B. UAV path planning based on dynamic programming algorithm on photogrammetric DEMs. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–5. [Google Scholar]
- Bauso, D.; Giarré, L.; Pesenti, R. Multiple UAV cooperative path planning via neuro-dynamic programming. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No. 04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 1, pp. 1087–1092. [Google Scholar]
- Radmanesh, M.; Kumar, M. Flight formation of UAVs in presence of moving obstacles using fast-dynamic mixed integer linear programming. Aerosp. Sci. Technol. 2016, 50, 149–160. [Google Scholar] [CrossRef]
- Tu, B.; Wang, F.; Han, X. 3D path planning for UAV based on a hybrid algorithm of marine predators algorithm with quasi-oppositional learning and differential evolution. Egypt. Inform. J. 2024, 28, 100556. [Google Scholar] [CrossRef]
- Wang, G.G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High performance computing for cyber physical social systems by using evolutionary multi-objective optimization algorithm. IEEE Trans. Emerg. Top. Comput. 2017, 8, 20–30. [Google Scholar] [CrossRef]
- Bayili, S.; Polat, F. Limited-Damage A*: A path search algorithm that considers damage as a feasibility criterion. Knowl.-Based Syst. 2011, 24, 501–512. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Yuan, Z.; Gu, Q. An improved A* algorithm for UAV path planning problems. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 958–962. [Google Scholar]
- Meng, B. UAV path planning based on bidirectional sparse A* search algorithm. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; Volume 3, pp. 1106–1109. [Google Scholar]
- Aslan, S. Back-and-Forth (BaF): A new greedy algorithm for geometric path planning of unmanned aerial vehicles. Computing 2024, 106, 2811–2849. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, J.; Han, Y.; Zheng, H.; Ma, D.; Chen, M. A chaos-coupled multi-objective scheduling decision method for liner shipping based on the NSGA-III algorithm. Comput. Ind. Eng. 2022, 174, 108732. [Google Scholar] [CrossRef]
- Duan, H.; Yu, Y.; Zhang, X.; Shao, S. Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Zhao, B.; Huo, M.; Li, Z.; Yu, Z.; Qi, N. Clustering-based hyper-heuristic algorithm for multi-region coverage path planning of heterogeneous UAVs. Neurocomputing 2024, 610, 128528. [Google Scholar] [CrossRef]
- Wu, S.; He, B.; Zhang, J.; Chen, C.; Yang, J. PSAO: An enhanced Aquila Optimizer with particle swarm mechanism for engineering design and UAV path planning problems. Alex. Eng. J. 2024, 106, 474–504. [Google Scholar] [CrossRef]
- Li, L.; Gu, Q.; Liu, L. Research on path planning algorithm for multi-UAV maritime targets search based on genetic algorithm. In Proceedings of the 2020 IEEE International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 6–8 November 2020; Volume 1, pp. 840–843. [Google Scholar]
- Boulares, M.; Barnawi, A. A novel UAV path planning algorithm to search for floating objects on the ocean surface based on object’s trajectory prediction by regression. Robot. Auton. Syst. 2021, 135, 103673. [Google Scholar] [CrossRef]
- Boulares, M.; Fehri, A.; Jemni, M. UAV path planning algorithm based on Deep Q-Learning to search for a floating lost target in the ocean. Robot. Auton. Syst. 2024, 179, 104730. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV autonomous path planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
| Parameters | Meanings |
|---|---|
| G = (V,E) | Directed graph. |
| V | Point set, |V| = n, including the starting point A, the target point B, and the correction points. |
| E | Edge set, |E| = m, the set of edges between points. |
| Vver | The set of vertical error correction points. |
| Vhor | The set of horizontal error correction points. |
| i, j | The node sequence, in a given path, j is the next node corresponding to i. |
| k | Intermediate point between i, j on Dubins curve. |
| (i, j) | An edge from i to j. |
| R | R={2, …, L}, representing the set of feasible path edge counts. |
| r | Sequence of edges in a path. |
| Pi | The set of reachable points corresponding to point i. |
| dij | The length of the edge from node i to j, i.e., the distance between i and j, m. |
| ηijver ηijhor | The vertical error and horizontal error from i to j. |
| δ | For every 1 m of flight, the vertical and horizontal error increments of the UAVs. |
| θ | Upon reaching the end point, the maximum values of vertical and horizontal errors. |
| α1, α2 | The upper bounds for both vertical and horizontal errors, if vertical errors can be corrected. |
| β1, β2 | The upper bounds for both vertical and horizontal errors, if horizontal errors can be corrected. |
| M | Minimum turning radius of the UAV, m. |
| xrij | The binary variable xrij is defined such that xrij = 1 if the edge (i,j) is the r-th segment of a feasible path; otherwise, xrij = 0. |
| Parameters | Symbols | Value |
|---|---|---|
| Vertical error limitation with vertical error can be corrected (dm) | α1 | 25/20 |
| Horizontal error limitation with vertical error can be corrected (dm) | α2 | 15/10 |
| Vertical error limitation with horizontal error can be corrected (dm) | β1 | 20/15 |
| Horizontal error limitation with horizontal error can be corrected (dm) | β2 | 25/20 |
| Vertical and horizontal error increments of the UAV | δ | 0.001 |
| Minimum turning radius of the UAV (m) | M | 200 |
| Serial Number | Calibration Point Number | Vertical Error Before Calibration | Horizontal Error Before Calibration | Calibration Point Type |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | Start point |
| 2 | 578 | 12.0107 | 12.0107 | Horizontal |
| 3 | 417 | 19.9754 | 7.9646 | Vertical |
| 4 | 294 | 5.3257 | 13.2903 | Horizontal |
| 5 | 91 | 12.6804 | 7.3547 | Vertical |
| 6 | 607 | 8.3530 | 15.7077 | Horizontal |
| 7 | 61 | 16.5063 | 8.1533 | Vertical |
| 8 | 193 | 8.5267 | 16.6800 | Horizontal |
| 9 | 375 | 16.7278 | 8.2011 | Vertical |
| 10 | 315 | 11.6958 | 19.8969 | Horizontal |
| 11 | 403 | 19.7218 | 8.0260 | Vertical |
| 12 | 248 | 11.0198 | 19.0458 | Horizontal |
| 13 | 501 | 22.7595 | 11.7397 | Vertical |
| 14 | 612 | 8.4900 | 20.2297 | End point |
| Serial Number | Calibration Point Number | Vertical Error Before Calibration | Horizontal Error Before Calibration | Calibration Point Type |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | Start point |
| 2 | 169 | 9.2705 | 9.2705 | Horizontal |
| 3 | 266 | 18.7485 | 9.4780 | Vertical |
| 4 | 270 | 6.4000 | 15.8780 | Horizontal |
| 5 | 248 | 17.5027 | 11.1027 | Vertical |
| 6 | 194 | 7.9676 | 19.0703 | Horizontal |
| 7 | 205 | 15.5098 | 7.5422 | Vertical |
| 8 | 108 | 8.5901 | 16.1323 | Horizontal |
| 9 | 73 | 18.5680 | 9.9779 | Vertical |
| 10 | 319 | 7.7937 | 17.7716 | Horizontal |
| 11 | 274 | 17.9803 | 10.1866 | Vertical |
| 12 | 12 | 6.4367 | 16.6233 | Horizontal |
| 13 | 216 | 14.2391 | 7.8024 | Vertical |
| 14 | 279 | 9.2184 | 17.0208 | Horizontal |
| 15 | 302 | 18.3551 | 9.1368 | Vertical |
| 16 | 161 | 9.0811 | 18.2179 | Horizontal |
| 17 | 326 | 19.2275 | 10.1464 | End point |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Ma, W.; Pang, H. Multi-Objective Path Optimization Method for Maritime UAVs Equipped with Inertial Navigation Systems. J. Mar. Sci. Eng. 2025, 13, 870. https://doi.org/10.3390/jmse13050870
Li Z, Ma W, Pang H. Multi-Objective Path Optimization Method for Maritime UAVs Equipped with Inertial Navigation Systems. Journal of Marine Science and Engineering. 2025; 13(5):870. https://doi.org/10.3390/jmse13050870
Chicago/Turabian StyleLi, Zhao, Weihao Ma, and Haixiang Pang. 2025. "Multi-Objective Path Optimization Method for Maritime UAVs Equipped with Inertial Navigation Systems" Journal of Marine Science and Engineering 13, no. 5: 870. https://doi.org/10.3390/jmse13050870
APA StyleLi, Z., Ma, W., & Pang, H. (2025). Multi-Objective Path Optimization Method for Maritime UAVs Equipped with Inertial Navigation Systems. Journal of Marine Science and Engineering, 13(5), 870. https://doi.org/10.3390/jmse13050870






