Abstract
Within the 21st century, in the Maritime Silk Road, wave energy, a clean renewable source, is drawing more interest, especially in areas with power shortages. This paper investigates wave energy in ships, particularly in a hybrid electric bulk carrier, by designing a system that supplements the existing power setup with oscillating buoy wave energy converters. The system includes diesel generators (DGs), a wave energy generation system, heterogeneous energy storage (consisting of battery storage (BS) and thermal storage (TS)), a combined cooling heat and power (CCHP) unit, and a power-to-thermal conversion (PtC) unit. To ensure safe and reliable navigation despite uncertainties in wave energy output, onboard power loads, and outdoor temperature, a robust coordination method is adopted. This method employs a two-stage robust optimization (RO) strategy to coordinate the various onboard units across different time scales, minimizing operational costs while satisfying all operational constraints, even in the worst-case scenarios. By applying constraint linearization, the robust coordination model is formulated as a mixed-integer linear programming (MILP) problem and solved using an efficient solver. Finally, the effectiveness of the proposed method is validated through case studies and comparisons with existing ship operation benchmarks, demonstrating significant reductions in operational costs and robust performance under various uncertain conditions. Notably, the simulation results for the Singapore–Trincomalee route show an 18.4% reduction in carbon emissions compared to conventional systems.
1. Introduction
Since its establishment in the late 2nd century BC, the Maritime Silk Road has spanned thousands of years [1], not only facilitating the exchange and integration of civilizations between the East and the West, but also serving as a crucial trade route [2]. Entering the 21st century, the proposal and advancement of the “21st Century Maritime Silk Road” initiative [3] have brought new vitality to this ancient route, attracting the active participation of numerous countries and regions. In this context, for bulk carriers, as an indispensable component of global maritime trade, the optimization of their energy system design is crucial for enhancing operational efficiency, ensuring navigation safety, and responding to environmental protection requirements [4]. Consequently, this paper aims to investigate the dynamic route scheduling and energy management of bulk carriers along the Maritime Silk Road, explore innovative approaches and solutions to achieve the “dual carbon” goals of peak carbon dioxide emissions and carbon neutrality in the shipping industry [5], and provide insights and references for the sustainable development of the global shipping industry.
In recent years, renewable energy technologies like wind and solar power have matured, offering alternatives for bulk carriers and driving the shipping industry’s green transformation [6,7,8]. While wave energy boasts high energy density and predictability, its adoption lags behind that of solar and wind due to technical and operational challenges. Current wave energy systems are primarily fixed installations—e.g., oscillating water column (OWC) systems [9,10,11] and pendulum wave energy converters [12,13,14,15]—or specialized autonomous vessels like AutoNaut [16], which uses wave propulsion for low-energy operations. However, these systems have critical limitations, for example, fixed installations lack mobility, and dedicated wave-powered ships prioritize propulsion over energy storage. Despite the immense potential of wave energy in marine applications, challenges such as immature technology, high costs, and limited adaptability to extreme marine conditions [17] hinder its widespread adoption. Although there have been advancements in wave energy harvesting, existing solutions remain limited to fixed installations or specialized vessels, neglecting the potential of integrating wave energy conversion into mainstream maritime operations. Notably, sections of the Maritime Silk Road—such as the Arabian Sea, Bay of Bengal, and North Indian Ocean—are rich in wave energy resources [18]. For instance, monsoons enhance wave energy density in the Arabian Sea [19,20], while the Bay of Bengal experiences strong winter-monsoon-driven waves [21], and the North Indian Ocean has stable wave patterns due to ocean currents [22]. To address these challenges and leverage regional wave energy potential, this study proposes a dynamic integration of wave energy systems into conventional bulk carriers—a novel approach distinct from fixed facilities or single-purpose vessels. This integration tackles unique challenges, including real-time power coordination with vessel motion (e.g., pitch/roll) and balancing propulsion efficiency with energy storage optimization.
During optimization, we incorporate onboard thermal energy recovery (e.g., waste heat from diesel engines) into the hybrid system [23,24]. However, uncertainties in wave energy output, power loads, and ambient temperature complicate system design. To tackle these, we adopt a two-stage robust optimization framework inspired by prior work [25,26,27,28,29,30]. Yang et al. [25] applied robust optimization to ammonia and waste heat systems in North China, while Fan et al. [31] used KDE and Wasserstein metrics for distributionally robust models. Our approach combines these methods, as follows: a baseline strategy ensures robustness under worst-case scenarios, while real-time adjustments enhance adaptability.
The main contribution of this paper is the innovative design of a parallel hybrid power system tailored for bulk carriers. This system integrates diesel generators (DGs), wave energy converters (WECs), heterogeneous storage (batteries and thermal storage), a combined cooling heat and power (CCHP) unit, power-to-thermal conversion (PtC), and bidirectional interfaces. Given the increasing demand for reducing carbon emissions in the global shipping industry and recognizing the significant potential of wave energy in specific maritime areas, we have initially focused on establishing a feasible technical framework to achieve these goals. The two-stage robust optimization minimizes fossil fuel reliance while maintaining operational efficiency, as demonstrated by simulations of the Singapore–Trincomalee route. The results demonstrate that carbon emissions are 18.4% lower compared to those of conventional systems, proving the feasibility of wave-assisted commercial shipping. However, further exploration is necessary to directly compare the performance and theoretical differences between our proposed wave energy integration system and previous studies involving fixed-installation or dedicated vessel solutions. Future research will aim to address these gaps by comparing our approach with existing technologies, thereby validating its superiority and applicability, enhancing the understanding of various wave energy integration strategies, and fostering technological advancements towards more environmentally friendly and economically efficient shipping solutions.
The structure of the subsequent sections of this paper is as follows: Section 2 presents the wave energy conversion system and energy management strategy of the HEBC. Section 3 examines the optimization framework for maritime operations utilizing a two-stage robust coordination model. Section 4 and Section 5 present the mathematical formulation of the optimization issue and the requisite linearization method for its resolution. Section 6 substantiates the efficacy of the suggested coordination mechanism via a particular case study and illustrates its superiority in enhancing ship operational performance relative to conventional ship operation benchmarks. Section 7 encapsulates the research findings of the report and suggests avenues for future investigation.
2. Wave Energy Conversion and Energy Management for HEBC
2.1. Architecture of Hybrid Power Systems and Wave Energy Conversion
- (1)
- The Parallel Hybrid System and its Dynamic Energy Management Mechanisms
The marine parallel hybrid system may dynamically adjust operational modes and control strategies according to real-time maritime conditions to fulfill energy efficiency and emissions optimization criteria. Multiple modes can be achieved during operation, as follows:
- (1.1)
- Pure motor mode: When functioning under low loads with adequate battery capacity, the motor autonomously propels the propeller while the engine remains inactive;
- (1.2)
- Pure engine mode: Under medium to high load circumstances, the engine alone powers the propeller while deactivating the motor;
- (1.3)
- Hybrid drive mode: Under heavy load conditions, when battery capacity is adequate, the engine collaborates with the motor to jointly propel the system;
- (1.4)
- Charging drive mode: When functioning under low loads with diminished battery capacity, the engine concurrently propels the propeller and generates torque for charging by energizing the motor.
By exercising sound management and intelligent switching between these modes, the energy efficiency of the ship can be maximized and operational costs can be minimized, while simultaneously adhering to environmental protection requirements.
- (2)
- Wave Energy Utilization
In this paper, a wave energy generation system using multiple multi-degree-of-freedom oscillating buoy wave energy converters (OB-WEC) is proposed. The system’s core comprises a series of oscillating buoys positioned at the ship’s base, capable of vertical displacements in reaction to wave motion. The design of these buoys incorporates principles of wave dynamics to optimize wave energy capture. The WEC dynamics are modeled using linear wave theory, assuming small-amplitude waves (H/L < 0.1) to simplify the hydrodynamic interactions [32]. While this linearization assumption simplifies computation, it is valid for small-amplitude waves (steepness < 0.1) under typical operational conditions [32], aligning with sea states such as Beaufort scale 4–5 and enabling tractable energy capture calculations. The system converts wave energy into electricity via two main methods: mechanical linkage and hydraulic transmission. The mechanical linkage converts buoy oscillations directly to generator rotation, while the hydraulic method uses buoy pressure fluctuations to power a hydraulic motor, which drives the generator.
Figure 1 illustrates that the device comprises the Suspension system, the Power Take-off (PTO) system, and the Float system. The buoy moves in response to wave action, transferring heave motion to the PTO, which converts this linear motion into rotational motion to power the generator for electricity. Despite the detailed structural analysis of the OB-WEC system presented in this paper, practical considerations such as installation feasibility, maintenance requirements, and integration with existing ship systems require further exploration. Future research will focus on addressing these practical aspects that were beyond the scope of this study, including investigating the physical and economic challenges of integrating OB-WEC systems into various vessel types, evaluating the long-term maintenance needs of OB-WEC systems and their impact on overall operational efficiency, and ensuring seamless integration with current shipboard power management systems to avoid operational disruptions and enhance overall system performance.

Figure 1.
OB-WEC concept diagram.
This study designs a parallel hybrid power system for bulk carriers, incorporating the system controller, engine, electric motor, battery system, wave energy generation system, gearbox, propeller, and hull models. The gearbox includes clutch mechanisms for flexible power conversion. The wave energy generation system transmits the produced electrical energy to the ship’s internal battery system for storage through cables, guaranteeing power availability when required. Alternatively, the electrical energy may be directly conveyed to the ship’s electric motor to operate various equipment and systems aboard the ship. Figure 2 illustrates the interaction diagram of the aforementioned components. It illustrates how mechanical energy from the engine is transferred through the gear case to drive the airscrew and hull, providing thrust for the ship. Simultaneously, the electrical energy generated by the wave energy generation system is stored in the battery system or directly utilized by the electric motor for propulsion or auxiliary systems. The DC/DC converter ensures compatibility between different electrical components by adjusting voltage levels as necessary. Central to this system is the system controller, which oversees the distribution of both mechanical and electrical energy, manages control signals among components, and optimizes overall efficiency.
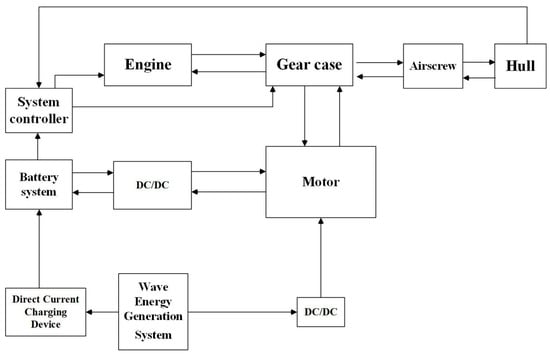
Figure 2.
A ship parallel hybrid power system model.
2.2. Hybrid AC/DC Microgrid Architecture
Figure 3 illustrates the conventional architecture of a hybrid AC/DC HEBC microgrid integrated with energy conversion modules. This microgrid incorporates multiple elements, including DGs, a wave energy generation system, heterogeneous energy storage (consisting of BS and TS), a CCHP unit, a PtC unit, and bidirectional converters. The diesel-fueled CCHP system incorporates the recovery and application of waste heat from the power generation cycle. The TS and PtC units augment the system’s total dispatch flexibility via energy storage, release, or conversion. The wave energy generation system, similar to the CCHP unit, can concurrently generate electricity and heat. DGs generally produce energy by the combustion of diesel fuel. The BS is chiefly employed to avert the recurrent initiation of DGs and to furnish backup power for the system. All components are linked to their corresponding AC or DC busbars and communicate via bidirectional converters.
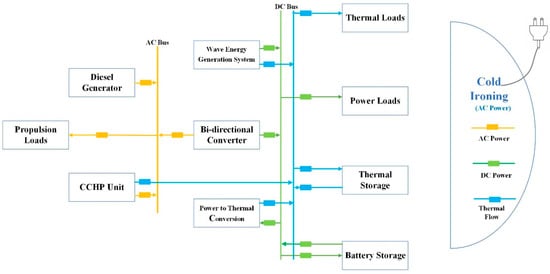
Figure 3.
The hybrid AC/DC HEBC embedded with energy conversion block.
2.3. Ship Voyage Modeling
To guarantee a timely and secure journey, the essential maritime navigation limitations for trip scheduling are as follows:
- (1)
- Ship Speed: The velocity of the ship is adjustable but must remain within specified upper and lower limits to ensure an efficient and safe journey.
- (2)
- Cruising Distance: The cruising distance of the ship is the product of cruising speed and the corresponding time, as indicated in (2). A timely arrival necessitates that the ship arrives in the area of the ports during the designated berthing intervals, as specified in (3).
- (3)
- Power Consumption for Propulsion Motors: The journey is propelled by engines. The associated power usage can be expressed as an exponential function of the cruising speed, as follows:
This document refers to the thermal load model from document [33], which describes the airborne thermal load’s potential for heating or cooling a place.
Here, denotes the heat capacity of the air within the considered space, and denote the indoor and outdoor temperatures at time t, respectively, and stands for the thermal resistance of the building shells.
3. Optimization of Ship Operation Based on a Two-Stage Robust Coordination Model
Diverse uncertainties jeopardize the dependability and economic viability of maritime operations. A two-stage robust coordinated operational method is illustrated in Figure 4, which alleviates their detrimental impacts.
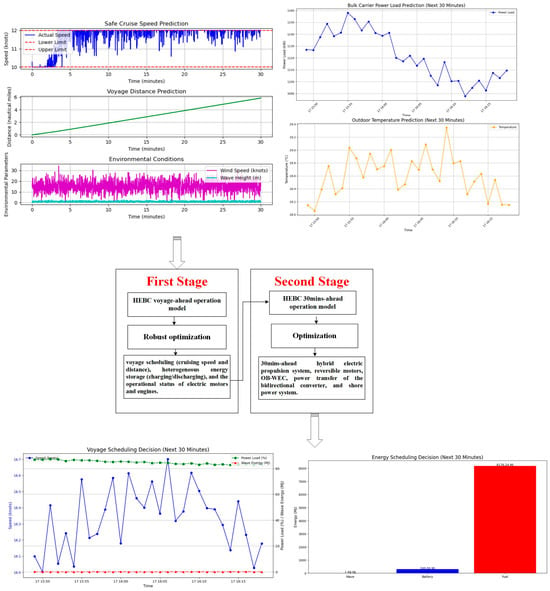
Figure 4.
Two-stage robust coordination model for the HEBC.
In our methodology, to ensure the accuracy and relevance of simulation conditions, we carefully selected and processed data from various sources. The outdoor temperature data were sourced from reliable meteorological databases, focusing on key sections of the Maritime Silk Road such as the Arabian Sea, Bay of Bengal, and North Indian Ocean, incorporating historical records to model realistic seasonal variations. For onboard power load profiles, we adopted a hybrid approach combining actual measurements from existing bulk carriers with assumed values based on industry standards and empirical data to simulate different operational scenarios, including varying sea states and vessel activities (e.g., maneuvering, loading/unloading). To address uncertainties in wave energy output, onboard power loads, and outdoor temperature, we employed advanced forecasting techniques based on historical data and state-of-the-art deep learning methods, as detailed in Section 6.3. These predictive models allowed us to anticipate potential fluctuations and enhance the robustness of our two-stage robust optimization framework.
In Figure 4, the input consists of wave energy generation predictions based on the safe cruising speed and distance range for the ship, onboard power load, outdoor temperature, and navigation information of the ship. Upon the establishment of a two-stage robust coordination model, the ultimate outputs consist of decisions on voyage scheduling and energy dispatch.
This two-stage model’s first stage, termed voyage-ahead operation, functions on an extended scheduling time scale, such as half a day or more. The first stage is optimized using the RO method to ascertain voyage scheduling (cruising speed and distance), heterogeneous energy storage (charging/discharging), and the operational status of electric motors and engines. These decisions will be executed throughout the forthcoming voyage.
The second stage functions on a brief scheduling time scale, such as 30 min (set in this paper), therefore, it is termed the 30-min-ahead operation. This phase utilizes forecasts of diverse uncertainties generated 30 min prior. The output operational decisions include the power output of the DGs, PtC unit, CCHP unit, power transmission through bidirectional converters, cold ironing, and the indoor temperature. These decisions are revised and executed every 30 min to reinforce the initial operations in the face of uncertainty.
4. Mathematical Formulation
4.1. Deterministic HEBC Operation Model
The objective of the parallel hybrid propulsion system is to diminish the operational expenses of ships during navigation. The system’s specific operational mode is as follows:
- (1)
- Objective:
Here, represent the fuel cost, maintenance cost, start-up cost, and power purchasing cost, respectively.
Equation (9) delineates the ship’s operational objective of minimizing total operational costs. Equations (10)–(13) specify that the ship’s operational costs encompass fuel costs (in (10)), maintenance costs (in (11)), start-up costs of DGs (in (12)), and power purchase costs from the grid (in (13)).
- (2)
- Constraints:
Equation (14) includes navigation and temperature constraints; Equations (15)–(18) illustrate the power output limitations, ramp-up restrictions, and minimum start–stop time requirements for DGs; and Equations (19) and (20) delineate the power output constraints for the CCHP unit and PtC unit, respectively. In contrast to DGs, the CCHP unit and PtC unit provide more flexibility in control and initiation, enabling them to shift from zero to maximum power output in seconds, thereby obviating the necessity for ramp-up/down limitations or minimum start–stop durations. Equations (21) and (22) demonstrate the transformation of power into thermal energy for the CCHP unit and PtC unit. Equations (23)–(28) delineate the operational constraints for the BS, with (23) and (24) indicating the maximum charging and discharging power limits, (25) stipulating that the BS cannot charge and discharge concurrently, (26) establishing the correlation between the energy and power for the BS, (27) imposing energy limits for the BS, and (28) guaranteeing consistent dispatch flexibility throughout each voyage. Equations (29)–(34) delineate the operational restrictions for the TS, corresponding to (23)–(28). Equation (35) guarantees that the power assistance from the land during ship berthing remains within a safe range. Equations (36) and (37) delineate power constraints for the bidirectional converter, but Equation (38) precludes concurrent power transfer between the AC and DC sides. Equations (39)–(41) stipulate that the production of AC power, DC power, and thermal energy must consistently satisfy the corresponding demands.
4.2. Model Linearization
The described ship operating model involves a succession of nonlinear equations, including the wave–structure interaction equations, as well as other nonlinear terms in (4), (7), (12), (17), (18), (25), (31), and (38), rendering the optimization of ship operation a difficult, non-convex, nonlinear programming challenge. To address this, nonlinear wave dynamics are first linearized using the small-amplitude wave assumption (H/L < 0.1), transforming the wave–structure interaction equations into a state-space representation, as follows:
where H denotes wave height and L is wavelength. This linearization reduces computational complexity while maintaining accuracy for typical operational conditions. Specifically, the 2D Reynolds-Averaged Navier–Stokes (RANS) equation is considered to account for turbulence effects in the flow field, which is essential for accurately modeling the complex fluid dynamics within the device [32].
- (1)
- Limitations and Future Work
However, the linearization neglects nonlinear effects such as wave breaking or high-frequency turbulence, which are secondary under moderate sea states. These nonlinear extensions will be addressed in future work to improve the model’s applicability under extreme conditions and enhance the representation of real-world wave dynamics.
- (2)
- Additional Linearization Steps
- (2.1)
- For polynomial terms like (4) in the expressions, a piecewise linear function method is employed during the solution process to approximate these original nonlinear functions, as follows:
In this linearization approach, represents the value of the original nonlinear function at a specific point, while denotes the approximated value of the function after linearization at the corresponding point. Here, m serves as the index for the various linear segments (referred to as “blocks”) used to partition the function, with indicating the total number of linear segments. Parameters and represent the slope and intercept of the linear function for the mth linear block, defining the shape and position of that segment. Parameter defines the starting point coordinate of the mth linear block. Additionally, the introduced binary variable m indicates whether the mth linear block is activated at time step t to accommodate the approximation requirements of the function within different intervals.
- (2.2)
- In (7), acknowledging that onboard thermal loads might serve for space heating in winter and space cooling in summer, the numerical values of these thermal loads may be regarded as either positive or negative in real-world situations, thereby obviating the need to take the absolute value. To convey broader thermodynamic relevance and address several potential scenarios, the absolute value sign is preserved in (7) for accurate expression.
- (2.3)
- The max function in (12), which represents the start-up cost that needs to be minimized during system operation, can be effectively decomposed into two separate components, as follows:
- (2.4)
- The steps involved in the simultaneous charging and discharging process of heterogeneous energy storage systems (as shown in (25) and (31)), or in the AC/DC power conversion process (as illustrated in (38)), can be directly omitted or optimized. To elaborate on this theorem, an example (25) is used as a reference for demonstration, as follows:
Due to > 0, it can be concluded that the objective functions (9) and (11) exhibit a monotonically increasing trend with variables and . Therefore, simplifying the objective function by retaining only the terms associated with and , as follows:
Given that is an equivalent cost parameter independent of and , the influence of is disregarded when optimizing these two variables. Therefore, in the optimization process, the objective function can be streamlined to focus on the variations of and . Simultaneously, while maintaining the original constraints’ meanings, (40) can also be simplified to emphasize the terms directly related to and .
where represents the net power independent of and .
Regarding the system objective involving and , as mentioned in (48), it can be reformulated without considering (25) as follows:
or
s.t., > 0, > 0
Given that and are fixed values for the optimization problem concerning and , the optimal solution is only possible when = 0 or = 0. The proof is concluded.
- (2.5)
- The linearization process for the minimum up/down-time constraints in (17) and (18) is illustrated in (50)–(52). It is worth noting that, due to space constraints, only the linearization process for the minimum up-time constraint is detailed here, while the treatment for the down-time constraint is analogous.
Following linearization, the ship coordinated operation model has been converted into a MILP problem, which can be effectively resolved utilizing established solvers like Cplex and Gurobi.
For the sake of clarity in subsequent discussions, the HEBC operation problem after linearization has been reformulated into a concise form and presented in (53) to (56).
Vector x encompasses multiple variables related to the first-stage operation, including and . On the other hand, vector y includes the remaining continuous variables associated with the second-stage operation. Additionally, vector corresponds to the forecasted uncertainties. The term represents the sum of maintenance costs for energy storage devices and start-up costs for DGs. Furthermore, comprehensively represents the power purchasing costs, fuel costs, and maintenance costs of all generators and bidirectional converters. Set χ is defined by (1)–(4), (17) and (18), and (23)–(33) as the feasible range of decisions for voyage-ahead planning. Equation (56) consolidates all energy balance conditions derived from (39) to (41). Finally, Equation (55) succinctly summarizes all linear constraints for the second-stage operation.
4.3. Two-Stage Robust Coordinated Operation Model
Given the robust coordination framework outlined in Section 2.3, the two-stage RO model can be formulated as follows.
where
Here, the symbol represents the uncertainty set consisting of wave energy generator output, onboard power loads, and outdoor temperature. Equations (60) and (61) elaborate on the optimization process of the second stage under a specific uncertainty scenario d, which depends on the first-stage decision x and the constraint Y(x, d), obtaining the second-stage cost L(x, d) by replacing the predicted output of the wave energy generation system . Subsequently, in (57), the uncertainty scenario that maximizes the minimization of L(x, d) is identified given the first-stage decision x. Through this robust planning approach, a solution can be found that minimizes both the first-stage cost and the worst-case second-stage cost.
If the first-stage decision x fulfills the criterion outlined in (59), signifying that, for every conceivable uncertainty scenario , implementing decision x guarantees the system’s functionality and viability, then such a first-stage decision is deemed to be robustly feasible. Conversely, in the absence of a robustly feasible decision x, i.e., when the second stage remains viable across all potential uncertainty scenarios, yet a feasible first-stage solution cannot be identified to uphold system viability, the robust program itself is considered infeasible. Consequently, when the uncertainty set experiences substantial expansion, it is essential to perform a thorough feasibility evaluation of the robust program. If the model does not meet the criteria for robust feasibility in practical applications, it suggests that the HEBC microgrid system requires reconfiguration or planning to address significant variations in uncertainty factors, thus ensuring the resilience and adaptability of the system’s design.
5. Solution Methodology
5.1. Uncertain Set Modeling
The uncertainty set comprises the output of the wave energy generation system, the onboard power load, and the outdoor temperature. This article, referencing [33], addresses the uncertainty set associated with the output of the wave energy generation system, given the significant similarities across these three forms of uncertainty sets.
The uncertainty set for the output of the wave energy generation system can be expressed as follows:
In the uncertainty set, the real wave forcing can vary between the lower () and upper limits (), while the overall variation is controlled by the user-defined lower () and upper () budget level.
5.2. Optimization of the Master Problem in the First-Stage Operation
The coordinated operation model of HEBC can be reformulated into the RO form, with the master problem, as follows:
where is the uncertainty vector obtained from the slave problem.
The resolution of the master problem pertains to the first-stage decisions, represented as x. Given that all constraints are linear, the master issue is categorized as a MILP problem.
5.3. Optimization of the Slave Problem in the First-Stage Operation
According to reference [34], the objective of the slave problem in the C&CG algorithm is to generate the worst-case scenario for the master problem and obtain an upper bound for the first stage. These objectives are accomplished by solving the following separation problem under the first-stage decision from the master problem:
Given , (68)–(70) can determine the worst-case uncertainty scenario d and its corresponding second-stage decision y. According to reference [35], the Karush–Kuhn–Tucker (KKT) conditions are applied to transform the max–min problem in (68)–(70) into a max problem, which is then linearized using the big-M method. Since all constraints are linear, the slave problem can also be classified as a MILP problem.
5.4. Feasibility Check of the First-Stage Operation
For a given decision , it cannot be guaranteed that the slave problem is always feasible, as there might exist a scenario d, such that L(x, d) is infeasible. Therefore, before addressing the slave problem, it is necessary to verify the robust feasibility of the first-stage decision .
The feasibility sub-problem () introduces non-negative slack and surplus variables mc and nc to the system equations with uncertainty sources. These variables are adjusted based on the infeasibility of the slave problem. If () > 0, it implies that there exists an uncertainty scenario where no final feasible solution exists. In such cases, new first-stage decisions should be made, or, in a realistic sense, the ship system should be re-planned. On the other hand, if () ≤ 0, the decision is robustly feasible for all uncertainty scenarios. This feasibility check problem is also a MILP problem, similar to the slave problem.
5.5. Second-Stage Operation
Given the decisions and the realization of uncertainties obtained from the short-lead-time prediction, the second-stage operation model can be formulated as follows:
The second-stage operation can be enhanced by standard deterministic optimization techniques. Once again, the second-stage problem is a MILP problem.
6. Case Study
6.1. Test System
The hybrid AC/DC HEBC configuration, as seen in Figure 3, incorporates a wave energy generation system, a CCHP unit, DGs, a PtC unit, and heterogeneous energy storage to complete the voyage. The cargo ship specializes in bulk transport, departing from Singapore and navigating the Maritime Silk Road northward to the northeastern port of Trincomalee, Sri Lanka. Figure 5 displays the details of the ship’s trip.
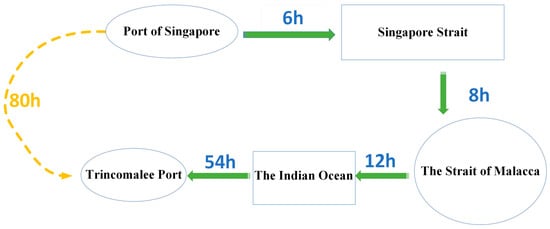
Figure 5.
The voyage information for the test hybrid AC/DC HEBC microgrid.
The direct distance of this route is roughly 900 nautical miles (about 1667 km), with an average speed of 12 knots (nearly 22 km per hour), resulting in an anticipated total journey time of 80 h. This instance presently fails to consider the time wasted during the ship’s berthing period and the effect of crew rest times on overall scheduling efficiency. Future study may integrate these factors to yield a more accurate representation of the actual time management demands in operational contexts.
To ensure energy management during the voyage, the unit scheduling interval is set to half an hour, i.e., Singapore and Trincomalee, Sri Lanka, both lie within the tropical zone, characterized by hot and humid climates. Given the prevailing tropical conditions, it is essential for the ship to incorporate an air conditioning system to regulate high temperatures and humidity, thereby ensuring an appropriate internal environment within the ship’s compartments. The voyage-based interval forecasting of wave energy generating output, onboard power loads, and outdoor temperature, depicted in Figure 6, demonstrates the ranges of these parameters, with the middle line indicating the average values.
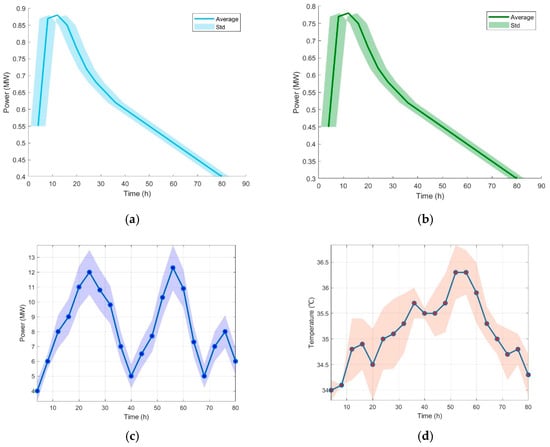
Figure 6.
(a) Wave energy power generation output prediction. (b) Wave energy cooling output prediction. (c) Onboard power loads prediction. (d) Outdoor temperature prediction.
The budgets with varying uncertainty are presented in Table 1. The technical parameters for the generator and energy storage are presented in Table 2 and Table 3. This study, while focused on a specific case, offers a broadly applicable model framework capable of validating any real-world data obtained. The simulation analysis was performed on an Intel(R) Core(TM) i5-11320H 3.20 GHz 64-bit computer with 146 GB of RAM, employing the Cplex solver via the GAMS platform for resolution. The equipment was sourced from Xiaomi Corporation, Beijing, China.

Table 1.
Various uncertainties in the budget.

Table 2.
Generator technical parameters.

Table 3.
Energy storage technical parameters.
6.2. First-Stage Ship Operation Results
Through interval forecasting, the first-stage decision determines the total operational cost of the HEBC to be USD 76,773.5, with the potential for further reduction if the worst-case scenario is avoided in the second stage. Figure 7 illustrates the system energy dispatch under the worst-case scenario.
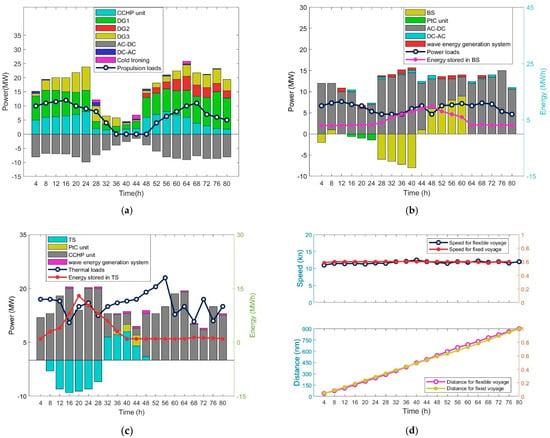
Figure 7.
(a) AC propulsion loads balance condition. (b) DC onboard power loads balance condition. (c) Thermal loads balance condition. (d) Voyage scheduling condition.
Figure 7a–c reveals the coordinated operation of the CCHP unit, TS, and PtC unit under the multi-energy supply in the worst-case scenario. The CCHP unit, due to its high energy efficiency, is capable of continuously generating electricity and heat. The TS decouples the inflexible operating mode of the CCHP unit by storing excess thermal outputs and supplies onboard thermal loads with the PtC unit during berthing, thereby achieving flexible operation of the CCHP unit.
The DGs, serving as the principal energy source for the HEBC, ensure consistent power production while adhering to minimum on-and-off time requirements. To minimize expenses, the BS accumulates electrical power produced by the DGs while docked, thereafter discharging the stored energy during navigation to meet the ship’s energy demands. The bidirectional inverter transforms AC power into DC power, supplying electrical energy for the ship’s electrical apparatus.
The cruise illustrates the complete flexibility of speed and distance, as depicted in Figure 7d. The synchronized operation of the propulsion load with the voyage schedule is maintained by flexibly adjusting propulsion power. The solution time is 23.1 min, satisfying the criteria for voyage-ahead activities in terms of computational efficiency.
6.3. Second-Stage Ship Operation Results
In the second stage of real-time operation, point predictions for the outputs of the wave energy generation system, onboard power loads, and exterior temperature were acquired 30 min in advance. To achieve accurate and reliable predictions, we employed a Long Short-Term Memory (LSTM) network, a specialized type of deep learning model particularly well suited for handling complex time-dependent data sequences [36]. Given that wave energy output is not only influenced by current ocean conditions, but also by historical dynamics over extended periods, LSTM’s ability to “remember” long-term dependencies makes it an ideal choice. By analyzing historical data such as wave height, wave period, and wind speed, the LSTM model effectively captures the intricate nonlinear relationships among these variables, enabling precise forecasts of wave energy output trends. Similarly, for onboard power loads and exterior temperature, which exhibit temporal patterns influenced by factors like operational schedules and weather conditions, LSTM provides robust predictions by leveraging its strength in modeling sequential data. Figure 8 illustrates the decision outcomes of the second stage, along with the results from the first phase for comparison.
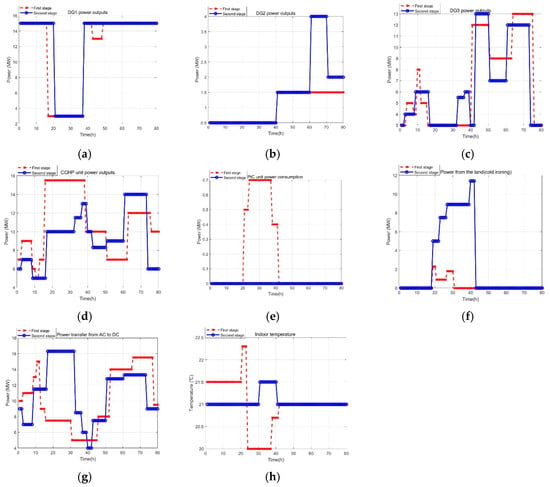
Figure 8.
(a) DG1 power outputs. (b) DG2 power outputs. (c) DG3 power outputs. (d) CCHP unit power outputs. (e) PtC unit power consumption. (f) Power from the land (cold ironing). (g) Power transfer from AC to DC. (h) Indoor temperature.
In light of the varying degrees of uncertainty relative to the worst-case scenario in the initial phase, the HEBC microgrid adjusted the power generation or consumption of the DGs, CCHP unit, PtC unit, ‘cold ironing’, and bidirectional converters (Figure 8a–g). In addition, the indoor temperature was adjusted to different levels (Figure 8h). As a result, HEBC’s final operating expenses were reduced to USD 73,042.40, with a calculation time of just 4.8 s, in line with the ship’s online operations. The results show that the second stage effectively compensates for the first stage and reduces the HEBC operation cost.
6.4. Methods Comparison
To evaluate the effectiveness of the method, two conventional ship operating benchmarks [33] are compared, as follows:
Method 1: Fixed Speed and Temperature Scheduling: This method requires the ship to sustain a consistent rated speed while maintaining a stable indoor temperature.
Method 2: Deterministic Scheduling: This method overlooks uncertainties, asserting that voyage predictions are adequately accurate in order to provide real-time operational modifications.
The operational expenses and computational durations for these approaches are shown in Table 4. All approaches’ computational times correspond closely to the practical operational requirements for ships. Method 1 reduces the operational cost of the ship by flexibly adjusting navigation and thermal loads. Compared to Method 2, our method requires a higher cost in the first stage, but the cost in the second stage is similar to that of the deterministic method. This means that the second stage can effectively compensate for the prediction errors in the first stage, thereby reducing the total operational cost.

Table 4.
Ship operating costs and resolution time.
6.5. Applicability of Linear and Nonlinear Wave Models in the Case Study
The distinction between linear and nonlinear wave models is critical for optimizing ship operations and energy harvesting systems in varying sea conditions. The linearized model demonstrates a robust performance under moderate wave conditions (H/L < 0.1), achieving <5% error in energy capture predictions relative to the nonlinear Boussinesq model. This aligns with the operational requirements of the Singapore–Trincomalee route, which primarily experiences moderate wave conditions (H/L = 0.08), as shown in Figure 9. As shown in Table 5, the linear model’s 60% reduction in simulation time (2 h vs. 5 h for the nonlinear model) enables real-time adjustments for routine operations such as navigation scheduling and thermal load optimization.
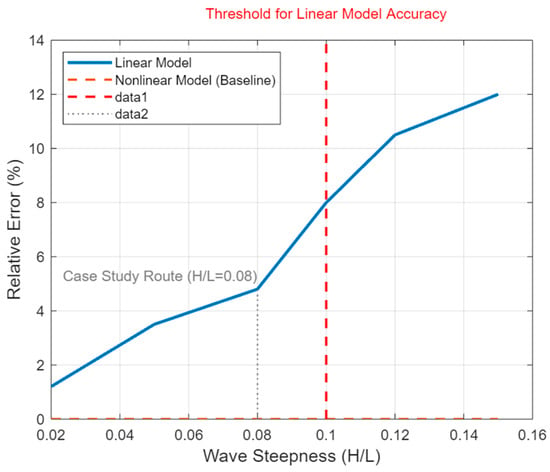
Figure 9.
Comparison of linear and nonlinear models for energy capture error.

Table 5.
Comparison of linear and nonlinear wave models.
However, in extreme sea states (H/L ≥ 0.1), nonlinear effects such as wave breaking and turbulence dominate, introducing 8–12% error in the linear model’s predictions (Figure 9). These phenomena, omitted in linearization assumptions (H ≪ L), are critical for modeling high-wave scenarios but compromise computational speed. For instance, the nonlinear model is indispensable for predicting energy losses due to wave breaking in hypothetical storms along the route (H/L = 0.15), ensuring structural safety and operational reliability in extreme conditions.
The case study further validates the linear model’s feasibility for practical systems. In simulations of an oscillating water column (OWC) device (Figure 10), the linear model accurately captures the spatial distribution of fluid motion—highest near the wave source and diminishing toward the OWC’s interior—as well as the temporal periodicity of wave–structure interactions. These results match the experimental benchmarks for energy capture efficiency (±5% error under H/L < 0.1) and show no numerical instabilities in the OWC’s response, confirming its suitability for real-world implementation.
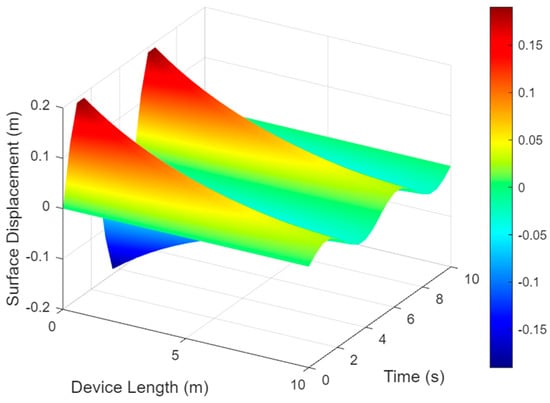
Figure 10.
Free-surface displacement in OWC device (H/L = 0.08).
Practical model selection hinges on operational context, as follows: the linear model is ideal for routine operations under typical sea states (e.g., the Singapore–Trincomalee route’s conditions), while nonlinear models are essential for design-stage analyses of systems exposed to extreme conditions. This framework balances accuracy and computational demands, ensuring cost-effective optimization for moderate scenarios while safeguarding against risks in harsh environments.
The graphical analyses (Figure 9 and Figure 10) play a pivotal role in this discussion. Figure 9 visually demarcates the performance boundary of linear models (H/L = 0.1), showing their reliability under H/L = 0.08 (matching the case study’s conditions) and progressive error escalation in extreme conditions. Figure 10, a 3D surface plot of free-surface displacement in the OWC device, provides empirical validation of the linear model’s spatial and temporal accuracy, reinforcing its practical utility for energy-harvesting systems.
6.6. Feasibility Check
To further demonstrate the advantage of the robustness method over the deterministic approach, a feasibility check was conducted. A set of 1000 scenarios representing uncertainty realizations was generated using Latin Hypercube Sampling (LHS). In all instances of uncertainty, the bottom and upper bounds of the unknown sources aligned with those illustrated in Figure 6. The uncertainty budget for wave power and thermal outputs, onboard power loads, and outdoor temperature is detailed in Table 6. Despite these advancements, future research should address several practical considerations to enhance the model’s applicability, including investigating wave directionality, evaluating wave periodicity, and analyzing ship-type-specific dynamics, which are crucial for optimizing OB-WEC integration across diverse maritime environments.

Table 6.
Feasibility check results.
In Table 6, it can be observed that, during the initial phase, the robustness methods exhibit a higher operational cost in comparison to the deterministic methods. This is primarily due to the design philosophy of robustness methods, which is grounded in the anticipation of the worst-case scenarios. Notably, as we progress into the second phase, the average operational costs of both methods converge and display a significant level of consistency. This conforms to the idea of RO, which stipulates that first-stage decisions are predicated on the worst-case scenario, but the subsequent stage functions as a compensation mechanism. Moreover, concerning feasibility performance, Method 2 is impractical in certain instances, requiring a reduction in a segment of the load to sustain energy equilibrium. This is due to the fact that, in the deterministic scenario, the initial stage of operation failed to consider the influence of many uncertainties. Thus, at the second stage, if a substantial discrepancy exists between the actual uncertainty values and the projected ones, there is insufficient capacity to rectify the flaws, resulting in infeasibility. Conversely, our proposed method is applicable in all cases without necessitating any load reduction, so demonstrating that our robust solution can endure any reality of uncertainty.
6.7. Model Selection Feasibility and Practical Benefits
The feasibility and practical implications of model selection are further explored through an analysis of both operational performance and uncertainty-driven decision-making frameworks. The case study of the Singapore–Trincomalee route underscores the practical advantages of the linearized wave model for routine operations, demonstrating 18.4% lower carbon emissions compared to conventional systems. This is achieved through the model’s capacity for real-time route optimization and thermal load management under moderate sea conditions (H/L < 0.1), supported by its computational efficiency (2 h versus 5 h for nonlinear models). The carbon savings, highlighted in Figure 11, stem from optimized fuel consumption and enhanced energy capture via the OWC device, which the linear model accurately predicts within its operational regime. While nonlinear models remain essential for extreme scenarios (e.g., H/L = 0.15 storms), their computational limitations render them impractical for daily use. The cost–benefit analysis (Table 5) confirms this trade-off, as follows: the linear model’s 60% faster simulation time directly reduces infrastructure and downtime costs, contributing to the overall savings.
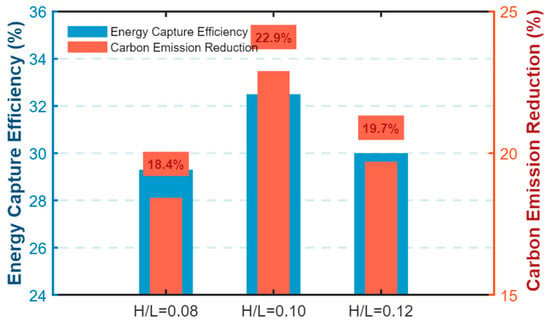
Figure 11.
Energy efficiency and emissions comparison under different sea states.
To evaluate the robustness of the proposed method in uncertain conditions, we analyzed two scenarios characterized by differing levels of uncertainty in the source (Case 1 with elevated uncertainty and Case 2 with diminished uncertainty). Figure 12 and Figure 13 exhibit the voyage-ahead interval forecasts under various uncertainty conditions for both scenarios. The associated uncertainty budgets for each scenario are outlined in Table 7. However, our analysis did not incorporate additional factors such as wave directionality, frequency, or ship-type-specific dynamics. These aspects are critical to understanding the full range of maritime conditions and could provide more comprehensive insights into the system’s robustness and applicability. Despite these limitations, our results highlight the potential of integrating wave energy systems into bulk carriers for enhanced efficiency and environmental sustainability. Future work should aim to address these gaps to further improve the robustness of the proposed model.
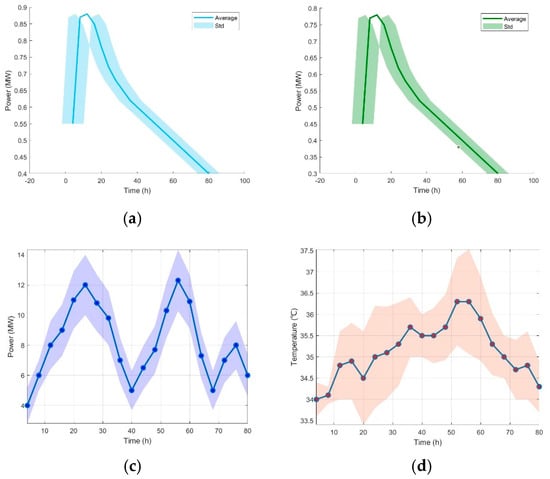
Figure 12.
(a) Wave energy power generation output prediction. (b) Wave energy cooling output prediction. (c) Onboard power loads prediction. (d) Outdoor temperature prediction.
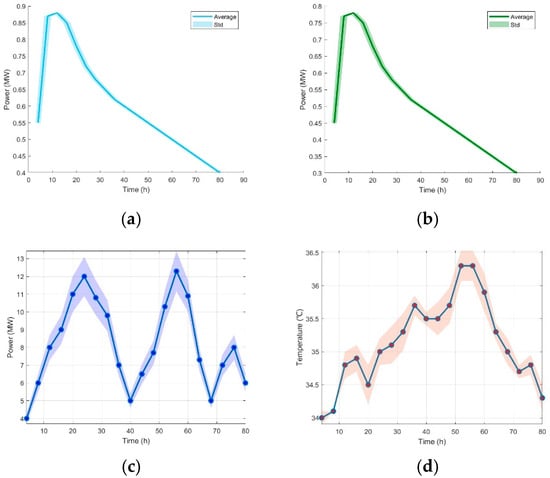
Figure 13.
(a) Wave energy power generation output prediction. (b) Wave energy cooling output prediction. (c) Onboard power loads prediction. (d) Outdoor temperature prediction.

Table 7.
The budgets for the diverse uncertainties in both cases.
Table 8 presents the comparison results of the RO method and Method 2 in Case 1 and Case 2, including the cost and time for both the first and second stages, as well as the average cost of feasible cases in the second stage and the percentage of infeasible cases. The analysis reveals that, in the first stage, the RO method incurs significantly higher costs than Method 2 does in both Case 1 and Case 2; however, in the second stage, the costs of the two methods are similar. Moreover, the average second-stage costs for feasible cases using the RO method and Method 2 are also approximately the same. This phenomenon indicates that, although the RO method requires a higher initial cost, it can reduce costs in subsequent stages. Furthermore, the increase in the initial cost of the RO method with rising uncertainty demonstrates its capability to effectively identify the worst-case realization of uncertainties.

Table 8.
Results of feasibility check for both cases.
The sensitivity analysis outcomes from these trials indicate the following:
- (1)
- The method ensures reliable operation of the ship under various levels of uncertainty, thereby validating its robustness;
- (2)
- The two-stage RO approach is proficient at addressing uncertainty. This is due to the absence of infeasible scenarios in real-time operation when contrasted with the deterministic method (Method 2) across various circumstances;
- (3)
- For the RO method under different scenarios, the cost in the first stage increases with the level of uncertainty. This indicates that the RO method is capable of identifying the worst-case realization of uncertainties, with higher levels of uncertainty leading to more severe worst-case scenarios;
- (4)
- The solution times of the RO method under various scenarios are compatible with its operational requirements. This means that the RO method can solve problems within an appropriate time frame, ensuring efficient and timely decision-making processes regardless of the scenario.
7. Conclusions
This paper investigates a novel hybrid AC/DC HEBC microgrid that incorporates a wave energy generation system and considers flexible voyages and thermal loads. A two-stage RO method is proposed to address various uncertainties. The introduction of the wave energy generation system not only further reduces dependence on diesel and diversifies energy sources, but also significantly decreases energy consumption and environmental pollution, enhancing the sustainability and economic efficiency of the system. The simulation results validate the effectiveness of the two-stage RO method, as follows: under the worst-case scenario, the first stage incurs higher costs; however, under real-time uncertain conditions, the second stage has lower costs, thus compensating for the higher costs in the first stage, and the computational times for both stages fully meet the operational requirements. Flexible voyages and thermal loads increase the scheduling flexibility of the system, significantly reducing the operational costs. Compared to Method 1, the operational costs in the first and second stages are reduced by 8.28% and 8.48%, respectively. Although the costs in the first and second stages are 6.33% and 0.41% higher, respectively, compared to Method 2, the RO method ensures no violation of operational constraints, highlighting its robustness and reliability. Furthermore, the RO method maintains strong robustness under different levels of uncertainty, ensuring reliable ship operation. In summary, the two-stage RO method proposed in this study achieves an optimal balance between low operational costs and robustness. Future work will focus on developing high-fidelity models for onboard equipment, refining microgrid planning using multi-objective evolutionary algorithms, and creating hybrid forecasting models that combine deep learning with traditional statistical methods to better handle uncertainties in ship operations.
Author Contributions
Conceptualization, W.Z.; Methodology, W.Z. and J.C.; Validation, C.B. and J.C.; Formal analysis, W.Z.; Investigation, W.Z. and J.C.; Resources, C.B.; Data curation, W.Z.; Writing—original draft, W.Z.; Visualization, J.C.; Supervision, C.B.; Funding acquisition, C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the open subject fund project of the State Key Laboratory of Maritime Technology and Safety (grant number W24CG000045).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Jianting Chen was employed by the company Shanghai Ship and Shipping Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| BS | Battery storage |
| C&CG | Column-and-constraint generation |
| CCHP | Combined cooling heat and power |
| DGs | Diesel generators |
| HEBC | Hybrid electric bulk carrier |
| KKT | Karush–Kuhn–Tucker |
| LHS | Latin hypercube sampling |
| MILP | Mixed-integer linear programming |
| PtC | Power-to-thermal conversion |
| RO | Robust optimization |
| TS | Thermal storage |
| Sets and Indices | |
| j | Index for the DGs |
| Set of dispatch intervals when the ship is at berth | |
| Set of DGs | |
| Set of dispatch intervals | |
| t | Index for the dispatch interval |
| Parameters | |
| Heat capacity of the air | |
| / | The energy capacity of BS/TS |
| / | Maximal power transfer from AC to DC/DC to AC |
| / | Maximal charging/discharging power of BS |
| Maximal purchasing power from the land | |
| / | Maximal charging/discharging power of TS |
| / | Minimal/maximal power outputs of CCHP unit |
| / | Minimal/maximal power outputs of PtC unit |
| / | Minimal/maximal power outputs of jth DG |
| / | Power ramp down/up limits of jth DG |
| The thermal resistance of the building shells | |
| / | The on/off-time of jth DG before the current period |
| / | The minimal up-/down-time for the jth DG |
| / | Rated ship speed/cruising distance |
| / | Proportional/exponential coefficient in the relationship between ship propulsion loads and speed |
| Unit dispatch period | |
| / | The efficiency of the converter from AC to DC/DC to AC |
| / | Charging/discharging efficiency of BS |
| / | Charging/discharging efficiency of TS |
| / | The thermal efficiency of the CCHP unit/PtC unit |
| / | Minimal/maximal indoor temperature |
| Unit power purchasing cost from the land | |
| / | Unit fuel cost for CCHP unit/jth DG |
| // | Unit maintenance cost for BS/TS/power transfer between AC and DC side |
| // | Unit maintenance cost for CCHP unit/jth DG/PtC unit |
| The unit start-up cost of the jth DG | |
| / | The decay rate of BS/TS |
| / | Minimal/maximal state of charge of BS |
| / | Minimal/maximal distance ratio |
| / | Minimal/maximal state of charge of TS |
| / | Minimal/maximal speed ratio. |
| Variables | |
| / | Fuel/maintenance cost |
| / | Start-up/power purchasing cost |
| / | Energy stored in BS/TS |
| / | Power transfer from AC to DC/DC to AC |
| / | Charging/discharging power of BS |
| Purchasing power from the land | |
| / | Power/thermal outputs of the wave energy generation system |
| / | Thermal outputs of CCHP unit/PtC unit |
| / | Power outputs of CCHP unit/jth DG |
| // | Ship propulsion/service power/thermal loads |
| Power consumption of PtC unit | |
| / | Charging/discharging power of thermal storage |
| Total thermal generation | |
| Binary state for jth DG: 0 denotes that the jth DG are off | |
| / | Ship cruising speed/distance |
| / | Indoor/outdoor temperature |
References
- Xu, S.; Qiao, B.; Yang, Y. The rise of the Maritime Silk Road about 2000 years ago: Insights from Indo-Pacific beads in Nanyang, Central China. J. Archaeol. Sci. Rep. 2022, 42, 103383. [Google Scholar] [CrossRef]
- Wen, L.; Cheng, Y. Evolution and Outlook of Fossil Energy Trade Structure Between China and ASEAN Within the Framework of Twenty-First-Century Maritime Silk Road. In International Association for Engineering Geology and the Environment; Springer Nature: Singapore, 2023; pp. 551–559. [Google Scholar]
- Chang, Y.-C. The ‘21st Century Maritime Silk Road Initiative’ and naval diplomacy in China. Ocean Coast. Manag. 2018, 153, 148–156. [Google Scholar] [CrossRef]
- Ejder, E.; Ceylan, B.O.; Celik, M.S.; Arslanoğlu, Y. Sustainability in maritime transport: Selecting ballast water treatment for a bulk carrier. Mar. Environ. Res. 2024, 198, 106511. [Google Scholar] [CrossRef] [PubMed]
- Runa, A.; Zhang, Z.; Zhang, H. Carbon emission peak and carbon neutrality under the new target and vision. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Maaruf, M.; Khalid, M. Power management and control of an all-electric ship powered by solar photovoltaic and hydrogen energy system. In Performance Enhancement and Control of Photovoltaic Systems; Elsevier: Amsterdam, The Netherlands, 2024; pp. 285–296. [Google Scholar]
- Nyanya, M.N.; Vu, H.B.; Schönborn, A.; Ölçer, A.I. Wind and solar assisted ship propulsion optimisation and its application to a bulk carrier. Sustain. Energy Technol. Assess. 2021, 47, 101397. [Google Scholar] [CrossRef]
- Li, B.; Zhang, R.; Zhang, B.; Yang, Q.; Guo, C. An assisted propulsion device of vessel utilizing wind energy based on Magnus effect. Appl. Ocean Res. 2021, 114, 102788. [Google Scholar] [CrossRef]
- Zhang, F.; Cong, P.; Gou, Y.; Sun, Z. Wave power absorption and wave loads characteristics of an annular oscillating water column (OWC) wave energy converter (WEC) with an attached reflector. Eng. Anal. Bound. Elem. 2024, 169, 105961. [Google Scholar] [CrossRef]
- Zhao, M.; Palmer, H.; Dhamelia, V.; Wu, H. Three-dimensional numerical simulation of a cylindrical oscillating water column (OWC) device placed in a wave flume. Renew. Energy 2024, 231, 120930. [Google Scholar] [CrossRef]
- Rozali, R.H.; Mustapa, M.A.; Ramli, M.A.H.; Mansor, M.N.; Kamal, I.Z.M.; Mohamed, E.A.A.E. Numerical Simulation of a Fixed Oscillating Water Column Wave Energy Converter Device. In Engineering Frontiers: A Multidisciplinary Odyssey; Ismail, A., Zulkipli, F.N., Mohd Daril, M.A., Öchsner, A., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 65–73. [Google Scholar] [CrossRef]
- He, F.; Liu, Y.; Pan, J.; Ye, X.; Jiao, P. Advanced ocean wave energy harvesting: Current progress and future trends. J. Zhejiang Univ. Sci. A 2023, 24, 91–108. [Google Scholar] [CrossRef]
- Gioia, D.G.; Pasta, E.; Brandimarte, P.; Mattiazzo, G. Data-driven control of a Pendulum Wave Energy Converter: A Gaussian Process Regression approach. Ocean Eng. 2022, 253, 111191. [Google Scholar] [CrossRef]
- Cai, Q.; Zhu, S. Applying double-mass pendulum oscillator with tunable ultra-low frequency in wave energy converters. Appl. Energy 2021, 298, 117228. [Google Scholar] [CrossRef]
- Chitumwa, T.; Terrence Hashe, V.; Justin Kunene, T. A Review of the Viability and Development of Ocean Wave Energy Converter Technology. In Proceedings of the International Conference on Engineering, Project, and Production Management, Auckland, New Zealand, 29 November–1 December 2023; Springer Nature: Cham, Switzerland, 2023; pp. 359–379. [Google Scholar]
- Mounet, R.E.G.; Nielsen, U.D.; Brodtkorb, A.H.; Øveraas, H.; Dallolio, A.; Johansen, T.A. Data-driven method for hydrodynamic model estimation applied to an unmanned surface vehicle. Measurement 2024, 234, 114724. [Google Scholar] [CrossRef]
- Chan, C.; Wang, J.; Yang, L.; Zang, J. Wave-assisted propulsion: An experimental study on traveling ships. Phys. Fluids 2024, 36, 027136. [Google Scholar] [CrossRef]
- Zheng, C.-W. Global oceanic wave energy resource dataset—With the Maritime Silk Road as a case study. Renew. Energy 2021, 169, 843–854. [Google Scholar] [CrossRef]
- Anusree, A.; Amrutha, M.M.; Kumar, V.S. Spatial variability in wave characteristics along the eastern Arabian Sea. J. Oceanogr. 2024, 80, 145–160. [Google Scholar] [CrossRef]
- Dwivedi, S.; Pandit, A.K.; Jangid, B.P.; Yesubabu, V.; Ratnam, M.V.; Sathiyamoorthy, V.; Vinoj, V.; Rao, D.N.; Narayanan, M.S. Formation and maintenance of monsoon inversion over the Arabian Sea. Theor. Appl. Climatol. 2024, 155, 2841–2856. [Google Scholar] [CrossRef]
- Ahamed, R.; Alam, W. Documenting Monthly Climatological Mean of Wave Parameters in the Northern Bay of Bengal Using 40 years of ECMWF Reanalysis V5 (ERA5) Data. Thalass. Int. J. Mar. Sci. 2022, 38, 71–86. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, W.; Fan, C.-Q.; Li, L.-G.; Dai, Y.-S. Performance Evaluation of Advanced Wave Energy Converters in the Nearshore Areas of the North Indian Ocean. China Ocean Eng. 2022, 36, 980–993. [Google Scholar] [CrossRef]
- Dikkumbura, R.; Wijewardane, A. Waste Heat Recovery from Marine Engines Using Absorption Chillers for Comfort Application: A Case Study Based on Hamilton and Saryu Ship Classes. In Proceedings of the 2024 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 8–10 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 25–30. [Google Scholar]
- Boodaghi, H.; Etghani, M.M.; Sedighi, K. A novel investigation of waste heat recovery from a stationary diesel engine using a dual-loop organic Rankine cycle. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 369. [Google Scholar] [CrossRef]
- Yang, S.; Wu, H.; Song, J.; Li, H.; Chen, H. Two-stage robust optimization scheduling for integrated energy systems considering ammonia energy and waste heat utilization. Energy Convers. Manag. 2024, 319, 118922. [Google Scholar] [CrossRef]
- Han, F.; Zhao, Y.; Zeng, J.; Zhang, S.; Wu, T. Uncertain parameters adjustable two-stage robust optimization of a rural housing integrated energy system considering biomass on-site utilization. Energy 2024, 296, 131106. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Q.; Ai, Y.; Chen, W.; Benbouzid, M.; Liu, S.; Gao, F. Two-stage distributionally robust optimization-based coordinated scheduling of integrated energy system with electricity-hydrogen hybrid energy storage. Prot. Control. Mod. Power Syst. 2023, 8, 33. [Google Scholar] [CrossRef]
- Haider, H.; Jun, Y.; Rashed, G.I.; Peixiao, F.; Kamel, S.; Li, Y. A robust optimization model for microgrid considering hybrid renewable energy sources under uncertainties. Environ. Sci. Pollut. Res. 2023, 30, 82470–82484. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Improved electrical coupling integrated energy system based on particle swarm optimization. Energy Inform. 2024, 7, 9. [Google Scholar] [CrossRef]
- Mazouzi, A.; Hadroug, N.; Alayed, W.; Hafaifa, A.; Iratni, A.; Kouzou, A. Comprehensive optimization of fuzzy logic-based energy management system for fuel-cell hybrid electric vehicle using genetic algorithm. Int. J. Hydrogen Energy 2024, 81, 889–905. [Google Scholar] [CrossRef]
- Fan, W.; Ju, L.; Tan, Z.; Li, X.; Zhang, A.; Li, X.; Wang, Y. Two-stage distributionally robust optimization model of integrated energy system group considering energy sharing and carbon transfer. Appl. Energy 2023, 331, 120426. [Google Scholar] [CrossRef]
- Ray, A.R.; Koley, S. Hydrodynamic Performance of OWC Under Nonlinear Stokes Wave Theory. In Proceedings of the 2024 Third International Conference on Electrical, Electronics, Information and Communication Technologies (ICEEICT), Tamil Nadu, India, 24–26 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Li, Z.; Xu, Y.; Fang, S.; Zheng, X.; Feng, X. Robust Coordination of a Hybrid AC/DC Multi-Energy Ship Microgrid With Flexible Voyage and Thermal Loads. IEEE Trans. Smart Grid 2020, 11, 2782–2793. [Google Scholar] [CrossRef]
- Habib, S.; El-Ferik, S.; Gulzar, M.M.; Chauhdary, S.T.; Ahmad, H.; Ahmed, E.M. Optimizing Integrated Energy Systems with a Robust MISOCP Model and C&CG Algorithm for Enhanced Grid Efficiency and Profitability. Energy 2025, 318, 134795. [Google Scholar]
- Luo, S.; Chen, C.; Qiu, W.; Ma, J.; Yang, L.; Lin, Z. Bi-layer optimal planning of rural distribution network based on KKT condition and Big-M method. Energy Rep. 2021, 7, 637–644. [Google Scholar] [CrossRef]
- Yin, X.; Jiang, Z. Wave condition preview assisted real-time nonlinear predictive control of point-absorbing wave energy converter based on long short-term memory recurrent neural identification. Mech. Syst. Signal Process. 2023, 188, 109669. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).