Analysis of the Accuracy of a Body-Force Propeller Model and a Discretized Propeller Model in RANS Simulations of the Flow Around a Maneuvering Ship
Abstract
1. Introduction
2. Numerical Methodology
2.1. Governing Equations
2.2. VOF Equations
2.3. Body-Force Propeller Model
2.4. Discretized Propeller Model
2.5. Numerical Discretization
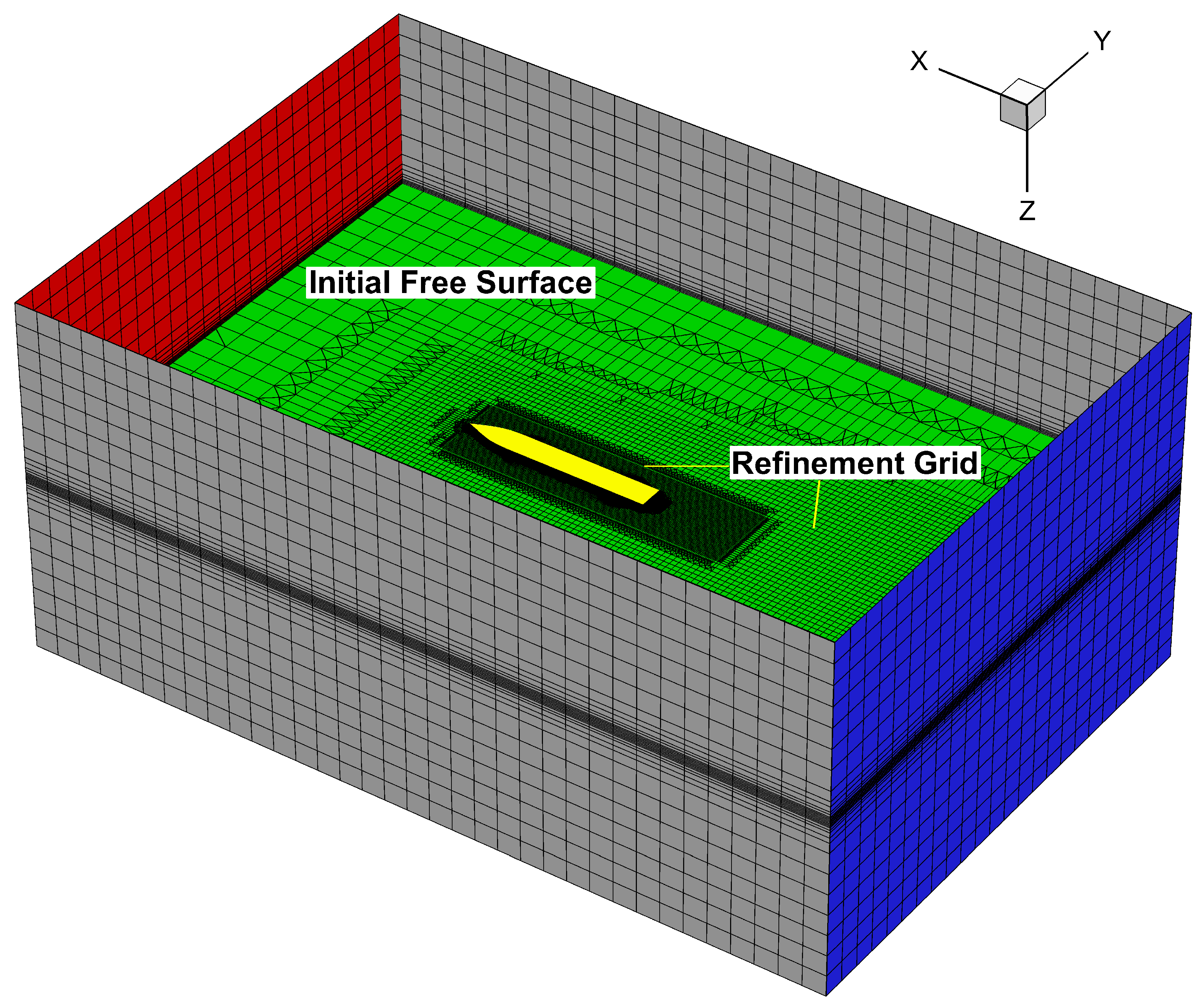
2.6. Computational Domain and Boundary Conditions
3. Ship Data and Computational Cases
4. Verification and Validation
4.1. Preparation
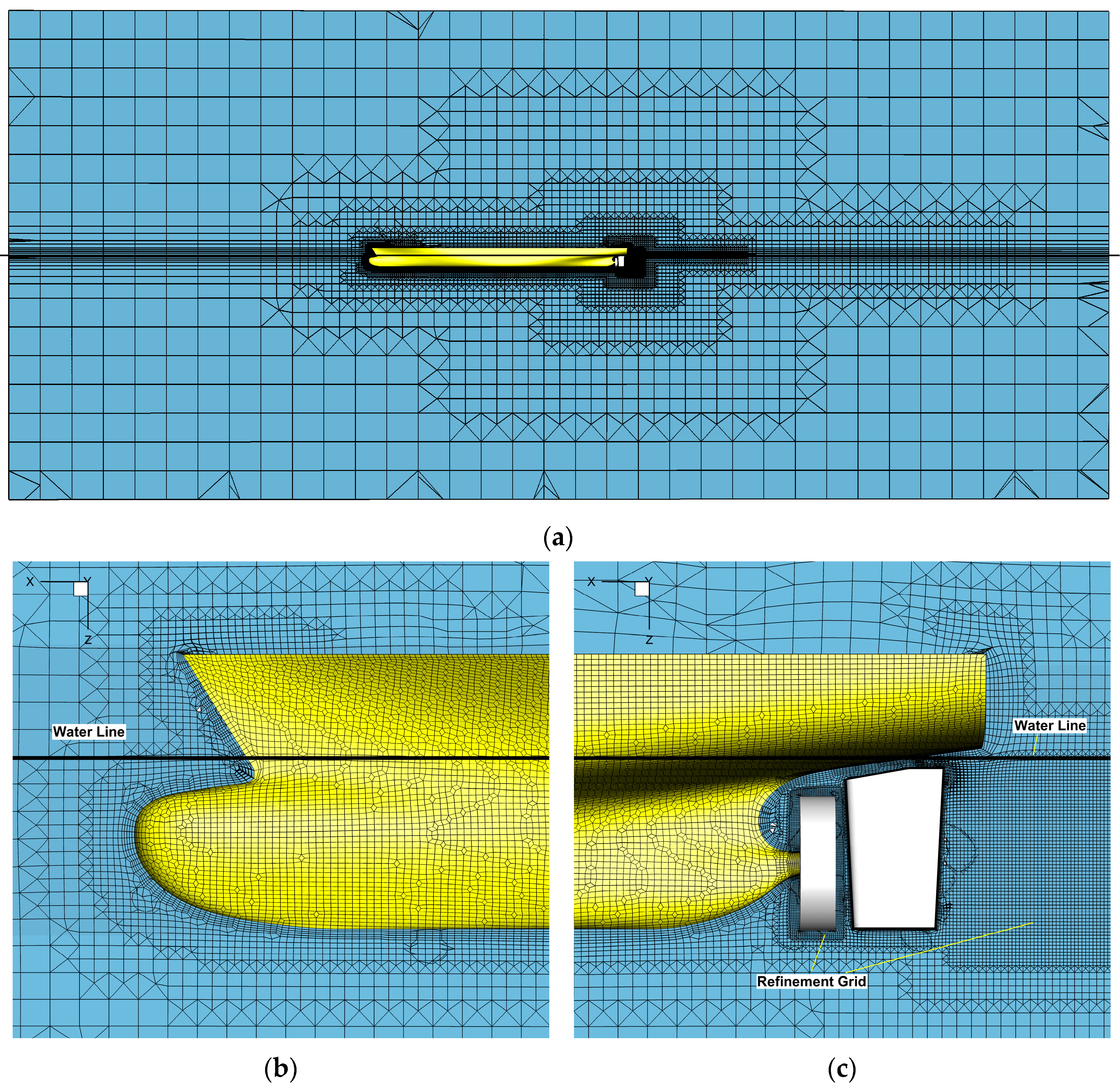
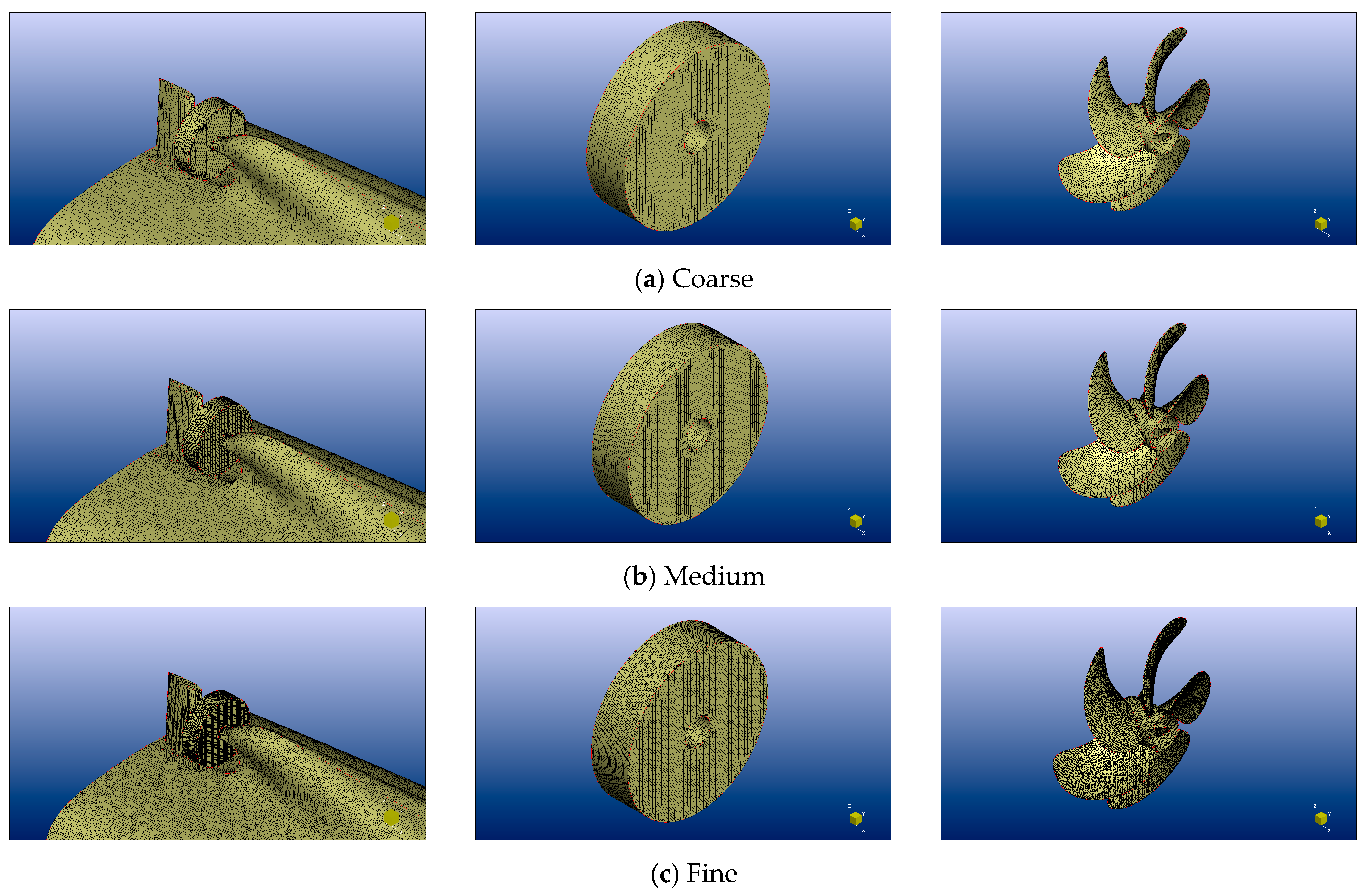
4.1.1. Grid Generation
4.1.2. Grid Spacing
4.1.3. Specification of Cases
4.2. Numerical Uncertainty
4.2.1. Straight-Ahead Motion
4.2.2. Drift Motion
4.2.3. Summary
4.3. Validation Against Experimental Data
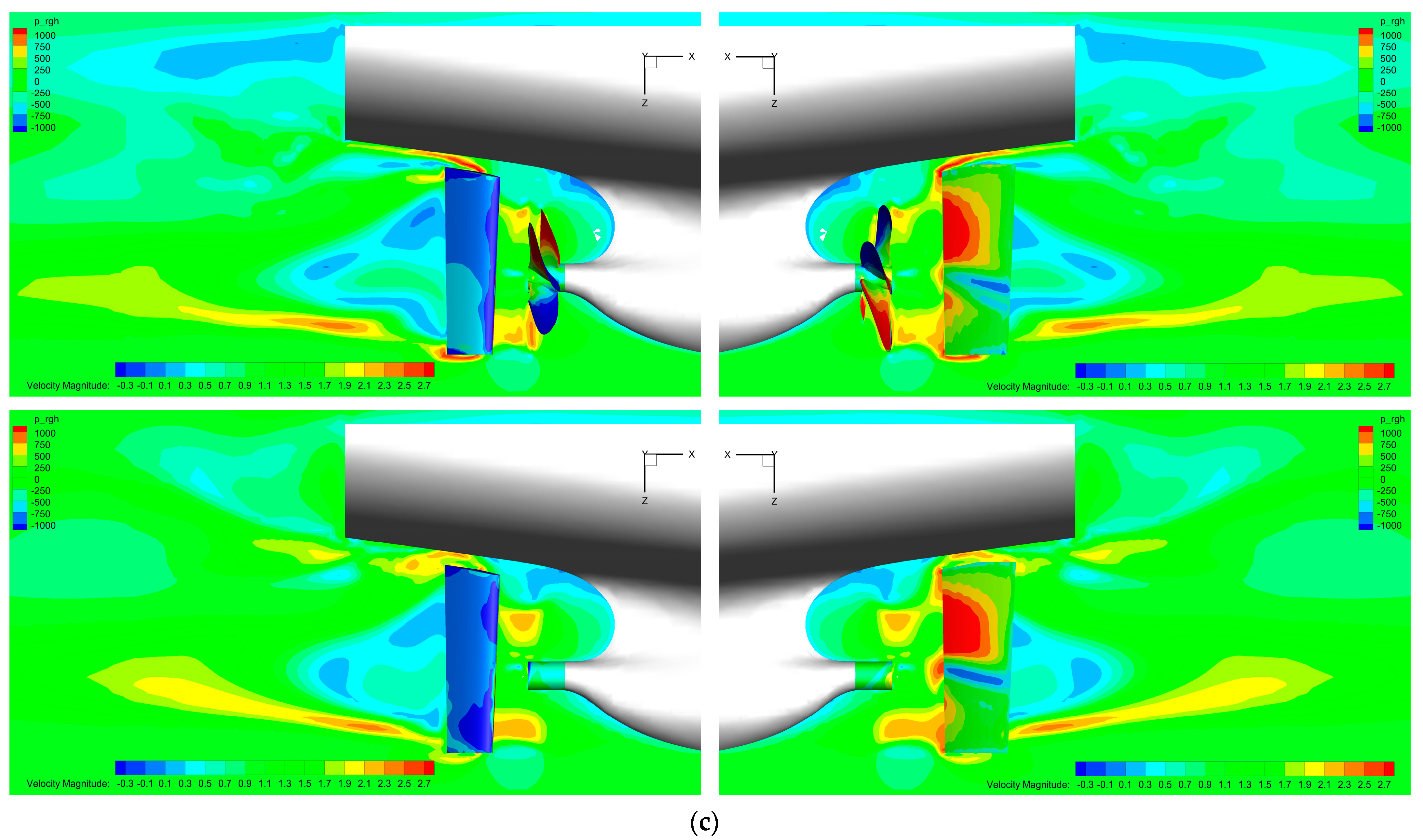
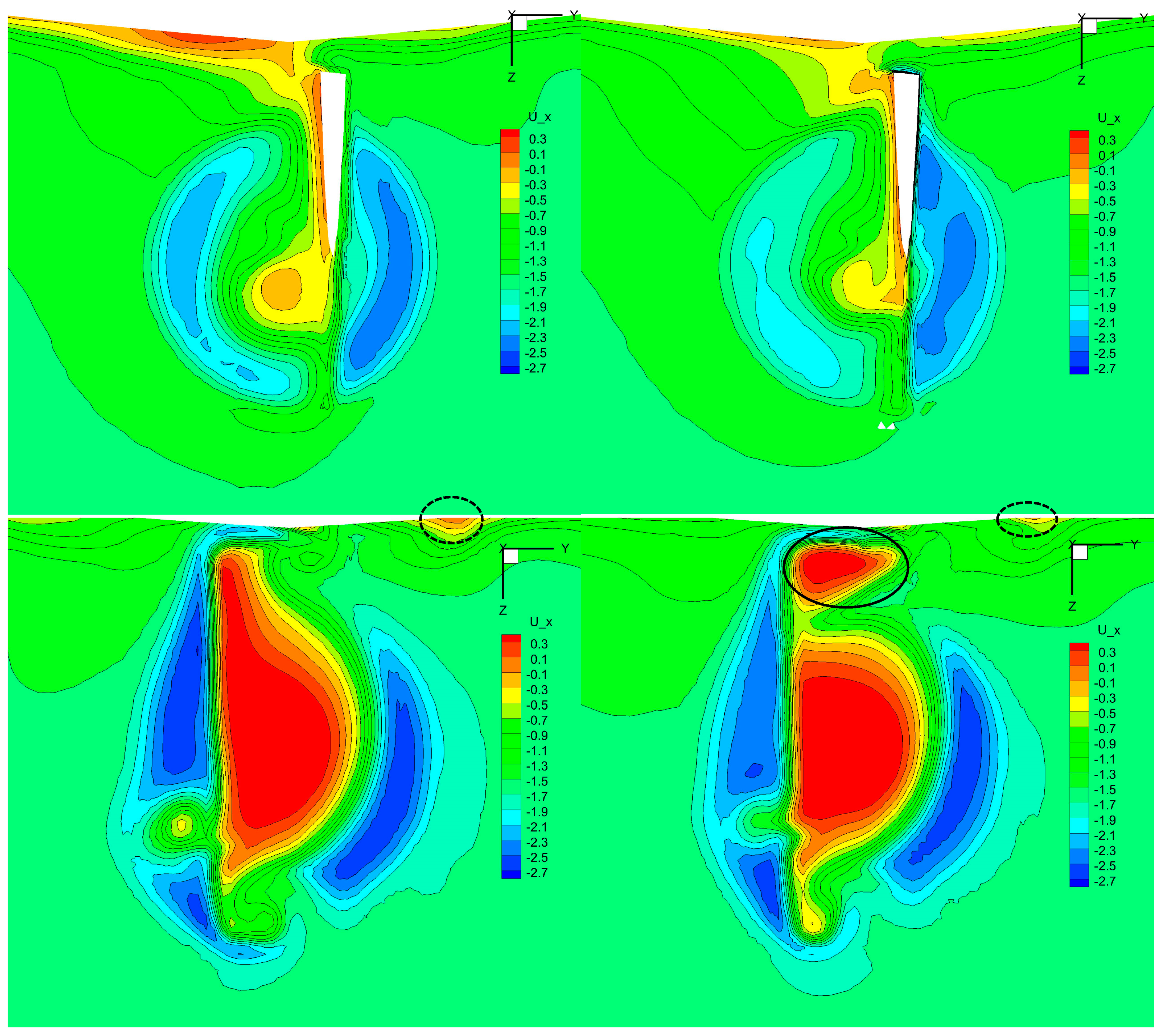
5. Results and Discussion
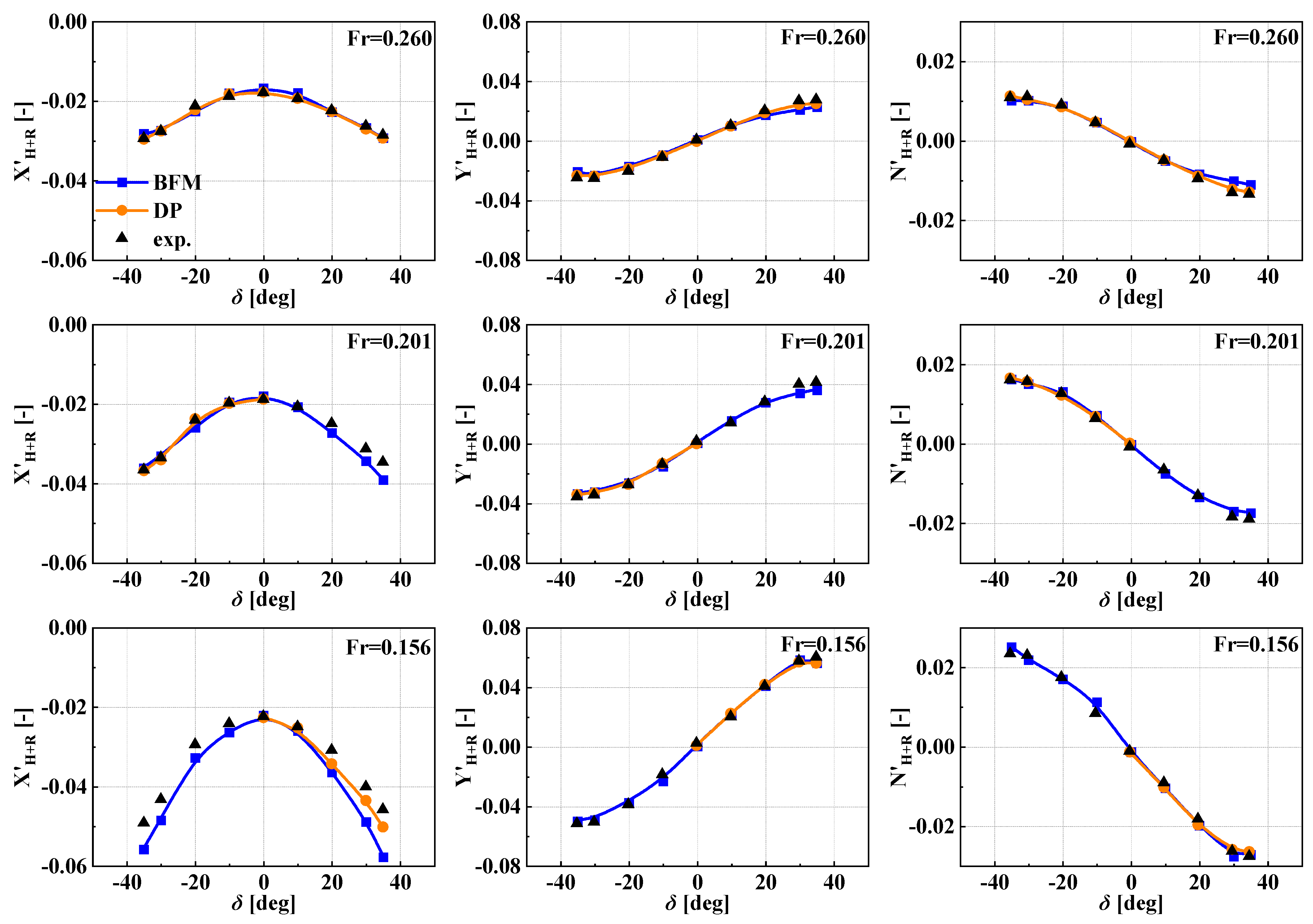
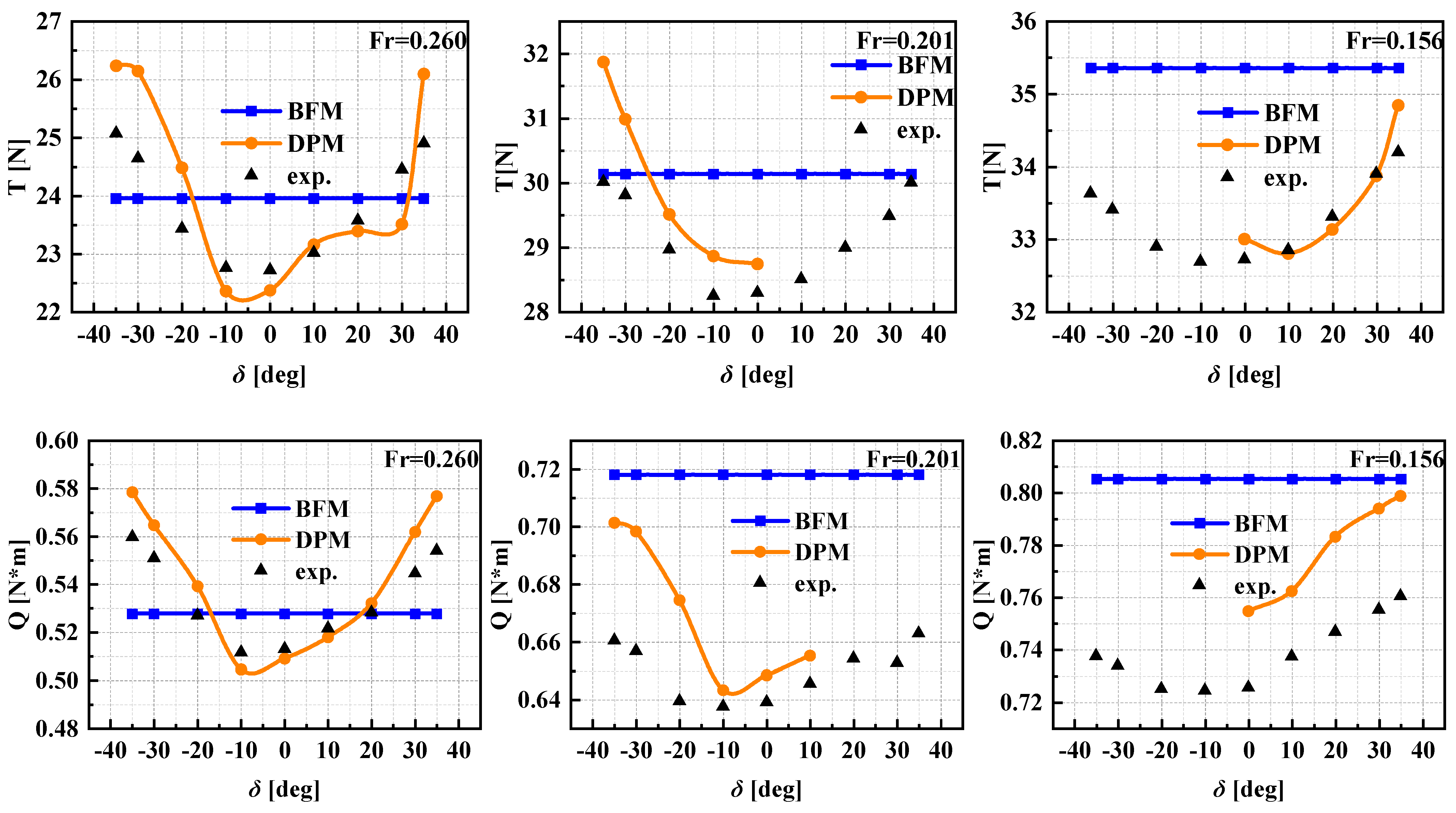
5.1. Static Rudder Force
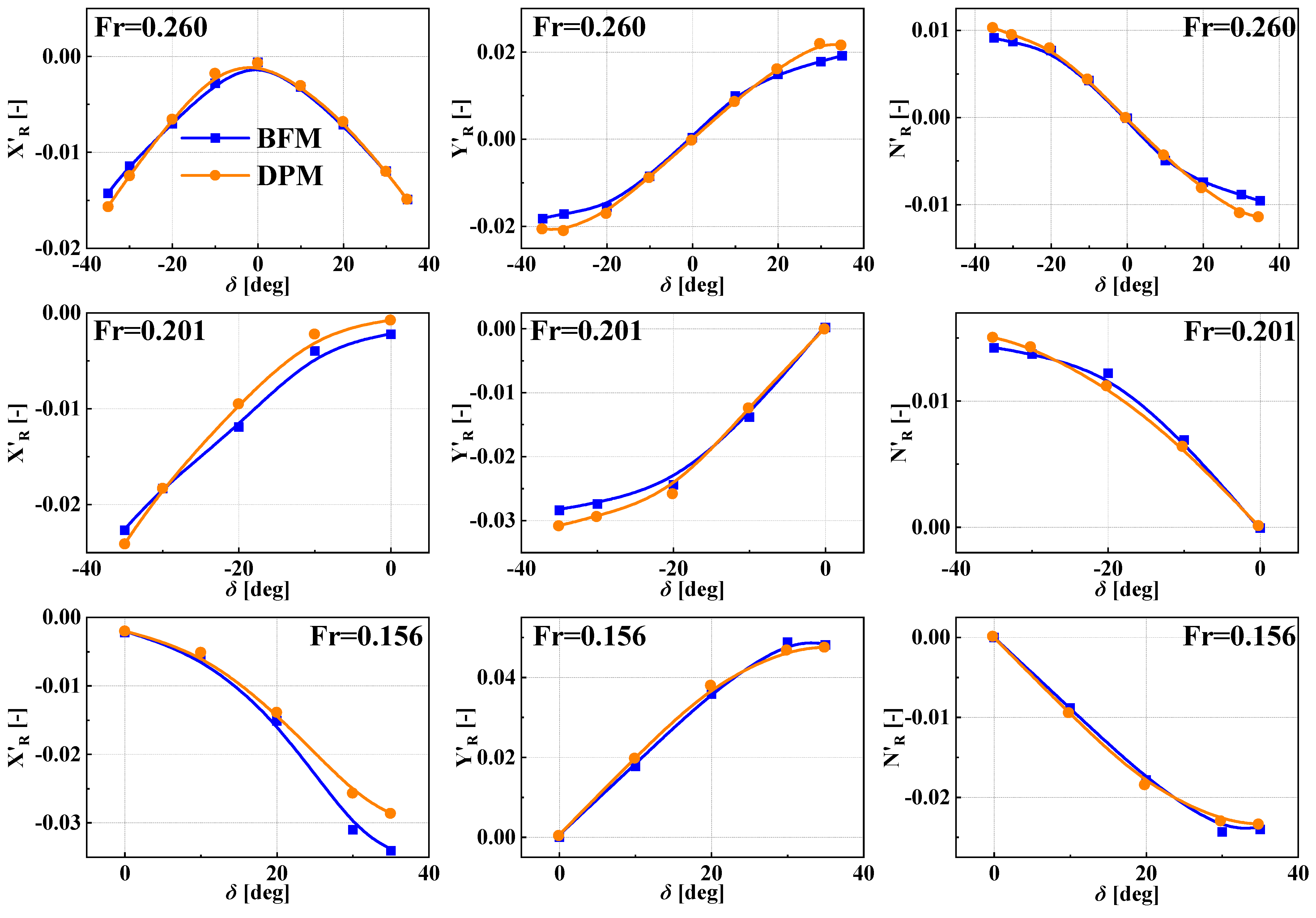
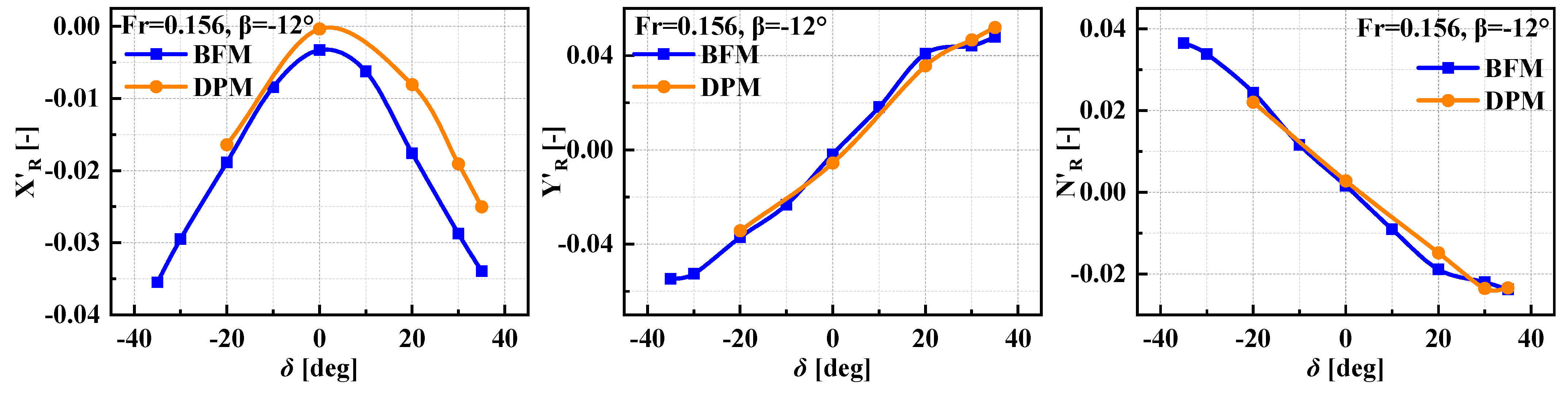
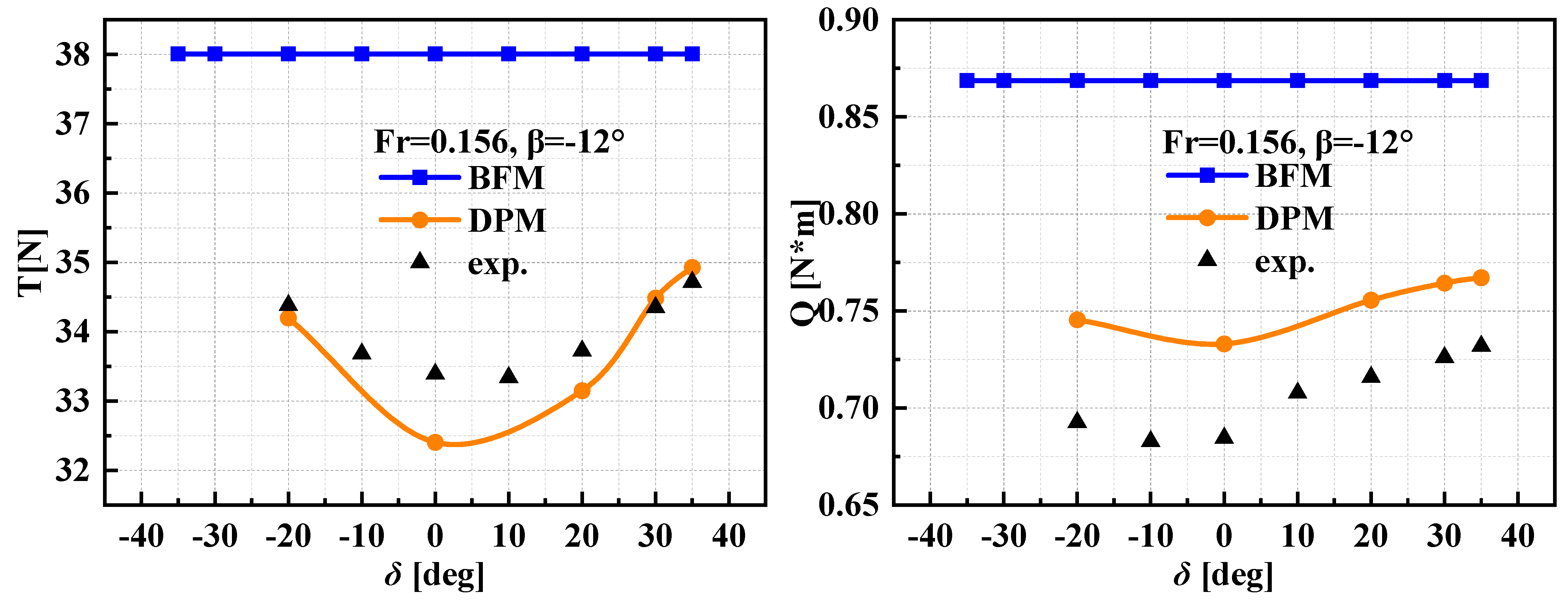
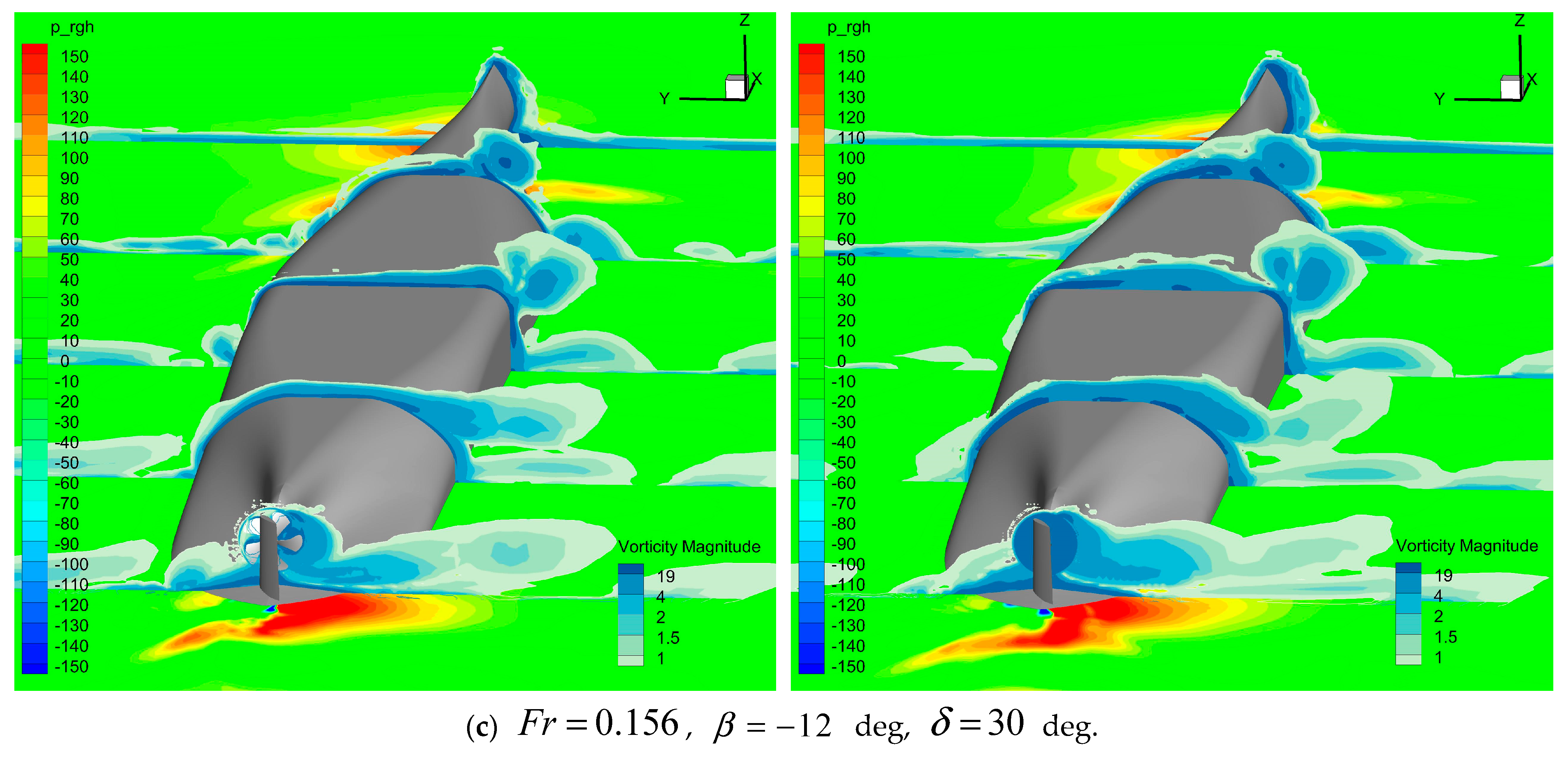
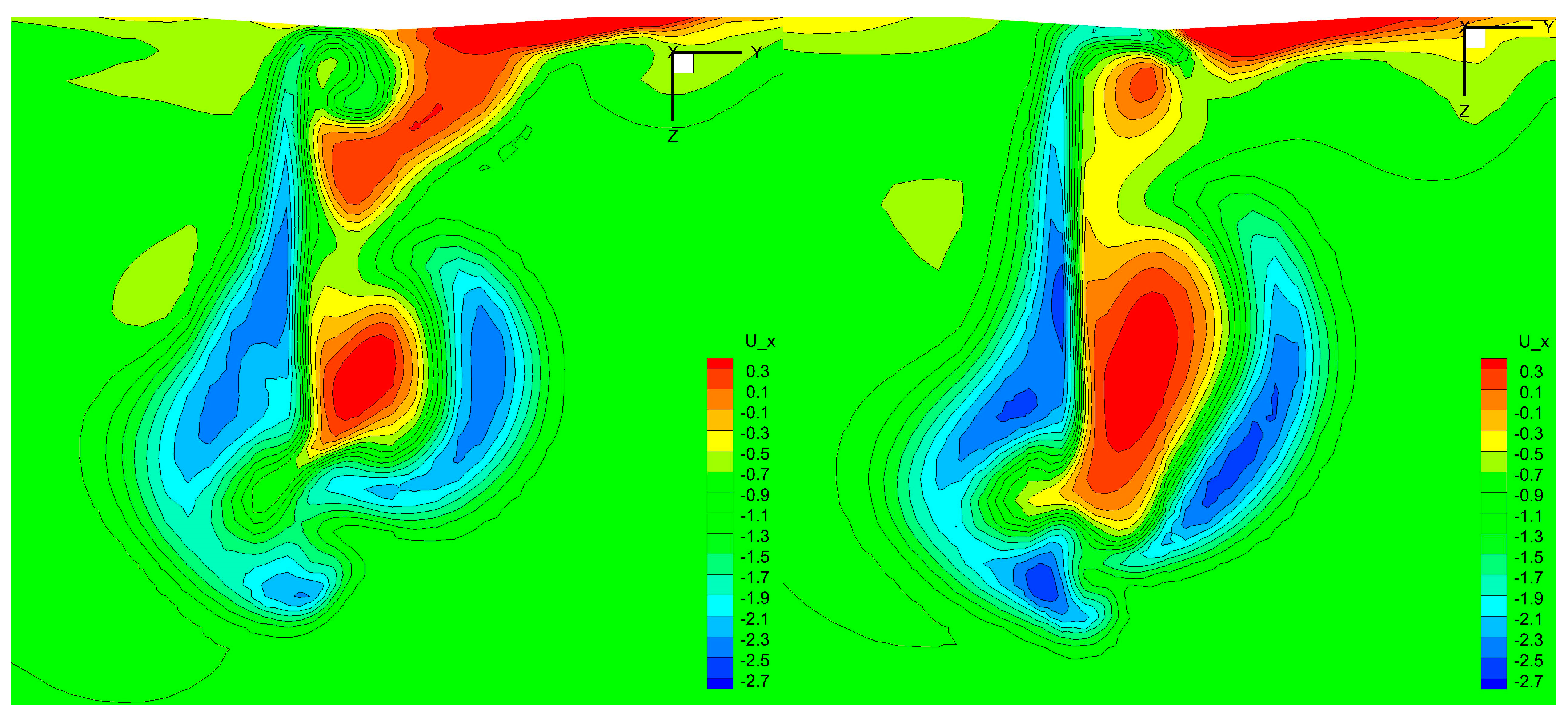
5.2. Static Drift Motion with Rudder Deflection
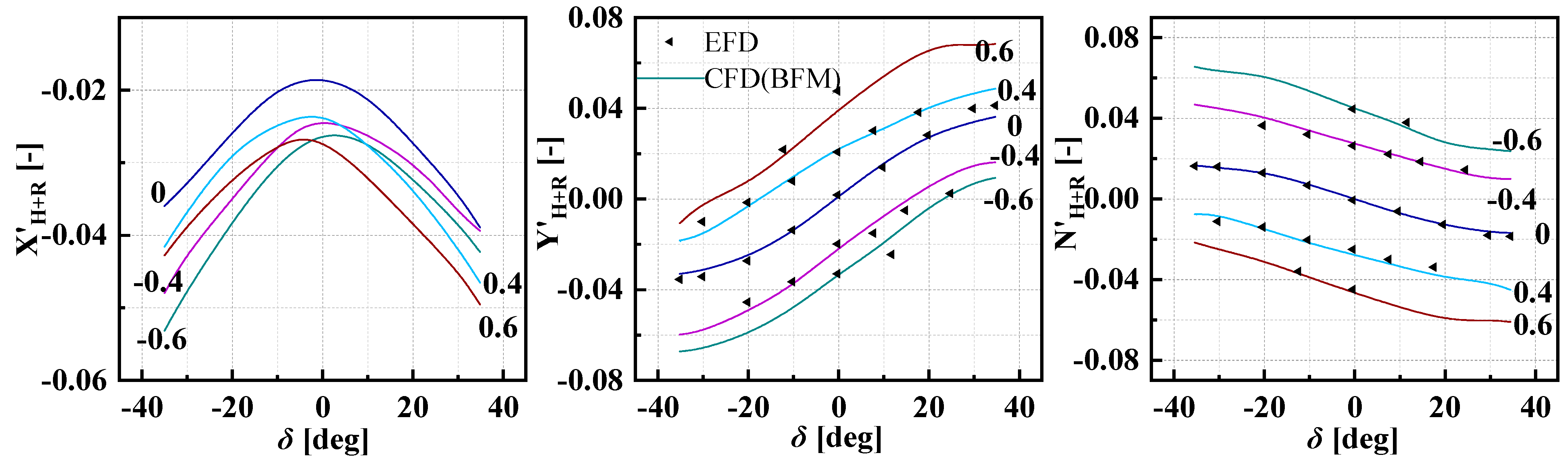
5.3. Static Circular Motion with Rudder Deflection
6. Conclusions
- (a)
- It is feasible to conduct RANS simulations based on the BFM and DPM to predict the hydrodynamic forces and moments of ship hulls. The results of the DPM are more accurate but more time-consuming, with an average computed time for one case close to 35 times that of BFM. However, the BFM exhibits certain inaccuracies in predicting hydrodynamic forces and moments at large rudder angles and/or drift angles. Its longitudinal force values are more sensitive to the drift angle, turning rate, and ship speed, while transverse forces and yaw moments are more sensitive to the rudder angle.
- (b)
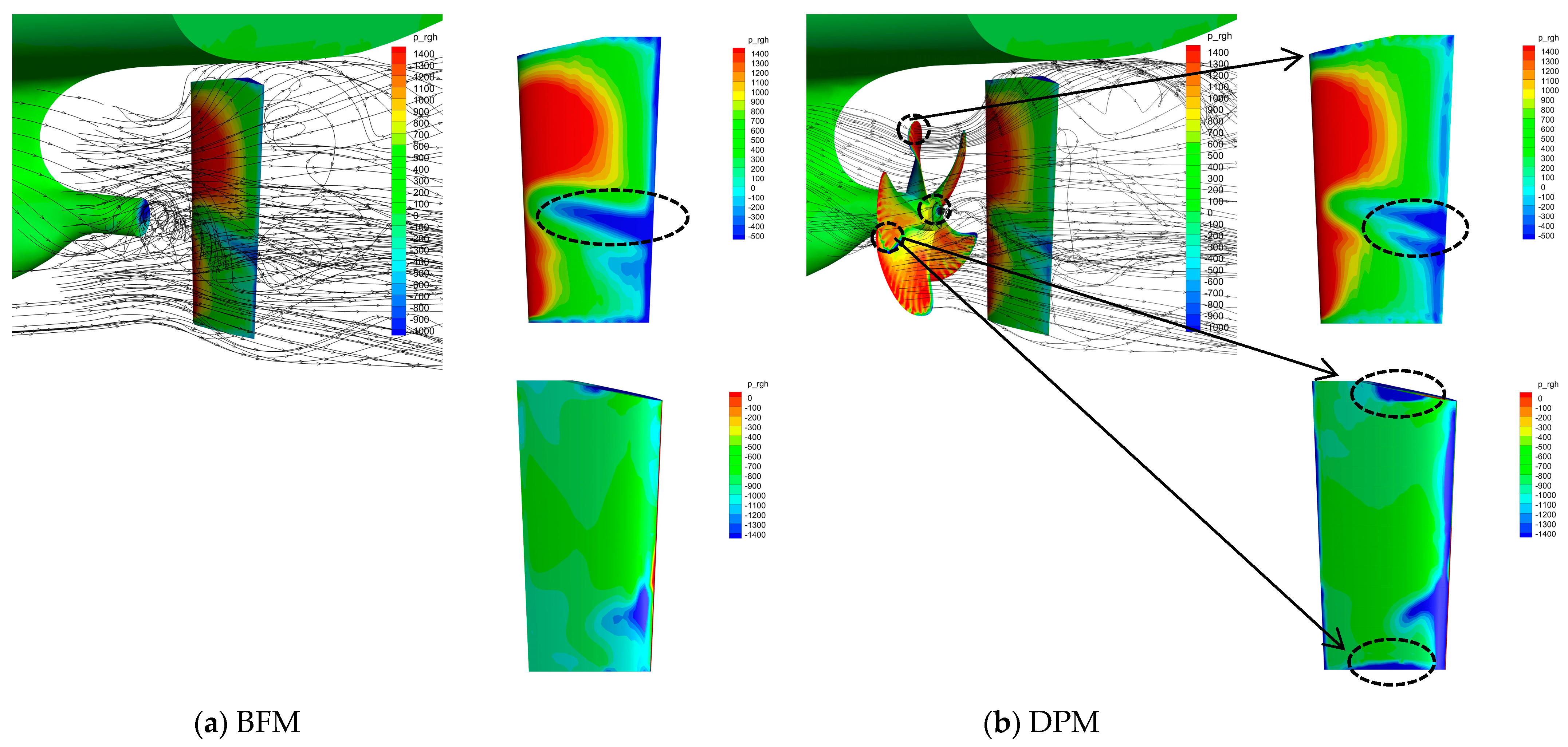
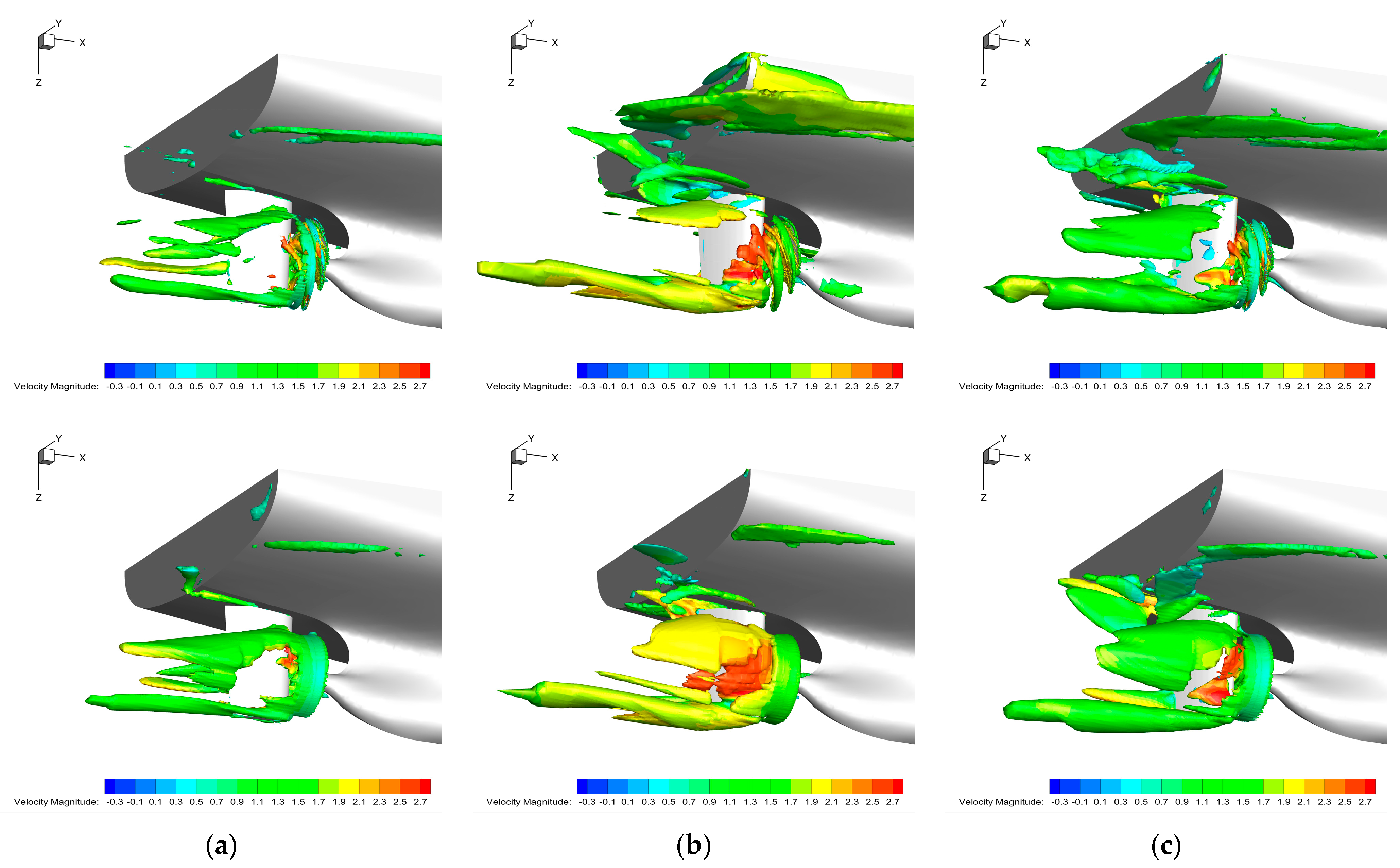
- The main reason for the computed difference between the BFM and DPM methods is the difference in wake field, reflected in the difference in the hydrodynamic force and moment acting on the rudder. Furthermore, there are two sources of error for the results of the BFM method: One is the lack of a physical shape in propeller blades, which means that there is a lack of lather force on the propeller during rotation, leading to the inability to accurately predict the interaction between the propeller-blade root or blade-tip leakage vortices and the rudder. Another issue is the limitation of the adopted model, which makes it impossible to accurately provide the thrust and torque generated by the propeller under actual cases.
- (c)
- The BFM would still be sufficient for calculating linear hydrodynamic derivatives related to rudder angle. The DPM method is more advantageous for complex wake-field simulations, even if the BFM method saves a lot of computation time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IMO. Standards for Ship Maneuverability. Resolution MSC.137(76). 2002. Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/MSCResolutions/MSC.137(76).pdf (accessed on 7 April 2025).
- Yu, J.; Feng, D.; Liu, L.; Yao, C.; Wang, X. Assessments of propulsion models for free running surface ship turning circle simulations. Ocean Eng. 2022, 250, 110967. [Google Scholar] [CrossRef]
- Simonsen, C.D.; Otzen, J.F.; Klimt, C.; Larsen, N.L.; Stern, F. Maneuvering predictions in the early design phase using CFD generated PMM data. In Proceedings of the 29th Symp Naval Hydrodynamics, Gothenburg, Sweden, 26–31 August 2012. [Google Scholar]
- Yoon, H.; Simonsen, C.D.; Benedetti, L.; Longo, J.; Toda, Y.; Stern, F. Benchmark CFD validation data for surface combatant 5415 in PMM maneuvers—Part I: Force/moment/motion measurements. Ocean Eng. 2015, 109, 705–734. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, X.; Wan, D.; Wang, J. Experimental and numerical investigations of advancing speed effects on hydrodynamic derivatives in MMG model, part I: Xvv, Yv, Nv. Ocean Eng. 2019, 179, 67–75. [Google Scholar] [CrossRef]
- Yun, K.; Yeo, D.J.; Kim, D.J. An experimental study on the turning characteristics of KCS with CG variations. In Proceedings of the International Conference on Ship Manoeuvrability and Maritime Simulation (MARSIM 2018), Halifax, NS, Canada, 12–16 August 2018; pp. 12–16. [Google Scholar]
- Yeo, D.J.; Yun, K.; Kim, Y.G. A study on the effect of heel angle on maneuvering characteristics of KCS. In Proceedings of the International Conference on Ship Manoeuvrability and Maritime Simulation (MARSIM 2018), Halifax, NS, Canada, 12–16 August 2018; pp. 1–10. [Google Scholar]
- Jiang, L.; Yao, J.; Liu, Z. Comparison between the RANS simulations of double-body flow and water–air flow around a ship in static drift and circle motions. J. Marine Sci. Eng. 2022, 10, 970. [Google Scholar] [CrossRef]
- Carrica, P.M.; Ismail, F.; Hyman, M.; Bhushan, S.; Stern, F. Turn and zigzag maneuvers of a surface combatant using a URANS approach with dynamic overset grids. J. Mar. Sci. Technol. 2013, 18, 166–181. [Google Scholar] [CrossRef]
- Mofidi, A.; Carrica, P.M. Simulations of zigzag maneuvers for a container ship with direct moving rudder and propeller. Comput. Fluids 2014, 96, 191–203. [Google Scholar] [CrossRef]
- Carrica, P.M.; Mofidi, A.; Eloot, K.; Delefortrie, G. Direct simulation and experimental study of zigzag maneuver of KCS in shallow water. Ocean Eng. 2016, 112, 117–133. [Google Scholar] [CrossRef]
- Prandtl, L. Über die ausgebildete Turbulenz. ZAMM 1925, 5, 136–139. [Google Scholar] [CrossRef]
- Jin, Y.; Duffy, J.; Chai, S.; Magee, A.R. DTMB 5415M dynamic manoeuvres with URANS computation using body-force and discretised propeller models. Ocean Eng. 2019, 182, 305–317. [Google Scholar] [CrossRef]
- Wang, J.; Wan, D.; Yu, X. Standard zigzag maneuver simulations in calm water and waves with direct propeller and rudder. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference (ISOPE 2017), San Francisco, CA, USA, 25 June–1 July 2017; pp. 1042–1048. [Google Scholar]
- Cura-Hochbaum, A. Virtual PMM tests for maneuvering prediction. In Proceedings of the 26th Symposium on Naval Hydrodynamics, Rome, Italy, 17–22 September 2006. [Google Scholar]
- Duman, S.; Bal, S. Prediction of maneuvering coefficients of Delft Catamaran 372 hull form. In Proceedings of the 18th International Congress of the International Maritime Association of the Mediterranean (IMAM 2019), Varna, Bulgaria, 9 September 2019; pp. 167–174. [Google Scholar]
- Visonneau, M.; Guilmineau, E.; Rubino, G. Computational analysis of the flow around a surface combatant at 10° static drift and dynamic sway conditions. In Proceedings of the 32nd ONR Symposium, Hamburg, Germany, 5–10 August 2018; pp. 5–10. [Google Scholar]
- Islam, H.; Guedes Soares, C. Estimation of hydrodynamic derivatives of a container ship using PMM simulation in OpenFOAM. Ocean Eng. 2018, 164, 414–425. [Google Scholar] [CrossRef]
- Silva, K.M.; Aram, S. Generation of hydrodynamic derivatives for ONR Topside Series using computational fluid dynamics. In Proceedings of the STAB 2018, Kobe, Japan, 16–21 September 2018; pp. 16–21. [Google Scholar]
- Sukas, O.F.; Kinaci, O.K.; Bal, S. System-based prediction of maneuvering performance of twin-propeller and twin-rudder ship using a modular mathematical model. Appl. Ocean Res. 2019, 84, 145–162. [Google Scholar] [CrossRef]
- Sakamoto, N.; Ohashi, K.; Araki, M.; Kume, K.; Kobayashi, H. Identification of KVLCC2 manoeuvring parameters for a modular-type mathematical model by RaNS method with an overset approach. Ocean Eng. 2019, 188, 106257. [Google Scholar] [CrossRef]
- Castro, A.M.; Carrica, P.M.; Stern, F. Full scale self-propulsion computations using discretized propeller for the KRISO container ship KCS. Comput. Fluids 2011, 51, 35–47. [Google Scholar] [CrossRef]
- Stern, F.; Yang, J.M. Computational ship hydrodynamics: Nowadays and way forward. Int. Shipbuild. Prog. 2013, 60, 3–105. [Google Scholar] [CrossRef]
- Pankajakshan, R.; Remotigue, S.; Taylor, L.; Jiang, M.; Briley, W.; Whitfield, D. Validation of control-surface induced submarine maneuvering simulations using UNCLE. In Proceedings of the 24th Symp Naval Hydrodynamics, Fukuoka, Japan, 8–13 July 2002. [Google Scholar]
- Cura-Hochbaum, A.; Uharek, S. Prediction of the Maneuvering Behavior of the KCS Based on Virtual Captive Tests; TU: Berlin, Germany, 2014. [Google Scholar]
- Carrica, P.M.; Sadat-Hosseini, H.; Stern, F. CFD analysis of broaching for a model surface combatant with explicit simulation of moving rudders and rotating propellers. Comput. Fluids 2012, 53, 117–132. [Google Scholar] [CrossRef]
- Hough, G.R.; Ordway, D.E. The generalized actuator disk. Dev. Theor. Appl. Mech. 1965, 2, 317–336. [Google Scholar]
- Ohashi, K.; Kobayashi, H.; Hino, T. Numerical simulation of the free-running of a ship using the propeller model and dynamic overset grid method. Ship Technol. Res. 2018, 65, 153–162. [Google Scholar] [CrossRef]
- Bekhit, A.S. Numerical simulation of the ship self-propulsion prediction using body force method and fully discretized propeller model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 042004. [Google Scholar] [CrossRef]
- Win, Y.N.; Wu, P.C.; Akamatsu, K.; Okawa, H.; Stern, F.; Toda, Y. RANS Simulation of KVLCC2 using Simple Body-Force Propeller Model With Rudder and Without Rudder. J. Jpn. Soc. Nav. Archit. Ocean Eng. 2016, 23, 1–11. [Google Scholar]
- Aram, S.; Mucha, P. Computational fluid dynamics analysis of different propeller models for a ship maneuvering in calm water. Ocean Eng. 2023, 276, 114226. [Google Scholar] [CrossRef]
- Feng, D.; Yu, J.; He, R.; Zhang, Z.; Wang, X. Improved body force propulsion model for ship propeller simulation. Appl. Ocean Res. 2020, 104, 102328. [Google Scholar] [CrossRef]
- Yao, J.; Liu, Z.; Song, X.; Su, Y. Ship manoeuvring prediction with hydrodynamic derivatives from RANS: Development and application. Ocean Eng. 2021, 231, 109036. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Proceedings of the Turbulence, Heat and Mass Transfer 4, Antalya, Turkey, 12–17 October 2003. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Stern, F.; Kim, H.T.; Patel, V.C.; Chen, H.C. Computation of viscous flow around propeller-shaft configurations. J. Ship Res. 1988, 32, 263–284. [Google Scholar] [CrossRef]
- Simonsen, C.D. KCS PMM test with appended hull, FORCE 2009-SIMMAN 2014. In Proceedings of the Workshop on Verification and Validation of Ship Manoeuvring Simulation Methods, Copenhagen, Demark, 8–10 December 2014. [Google Scholar]
- Stern, F.; Wilson, R.V.; Coleman, H.V.; Paterson, E.G. Comprehensive approach to verification and validation of CFD simulations—Part 1 and 2: Methodology and procedures. ASME J. Fluids Eng. 2001, 124, 793–802. [Google Scholar] [CrossRef]
- ITTC. Practical Guidelines for Ship CFD Applications. ITTC Recommended Procedures and Guidelines. 7.5-03-02-03. 2014. Available online: https://www.ittc.info/media/8165/75-03-02-03.pdf (accessed on 7 April 2025).
- Yao, J.; Jin, W.; Song, Y. RANS simulation of the flow around a tanker in force motion. Ocean Eng. 2016, 127, 236–245. [Google Scholar] [CrossRef]







| Symbol | ||||||||||
| Value | 0.31 | 0.09 | 0.555 | 0.075 | 0.44 | 0.0828 | 0.85 | 0.5 | 1.0 | 0.856 |
| Items | Full Scale | Model for CFD |
|---|---|---|
| Hull | ||
| Lpp (m) | 230 | 4.3671 |
| Lwl (m) | 232.5 | 4.4141 |
| Bwl (m) | 32.2 | 0.6114 |
| D (m) | 19 | 0.4500 |
| T (m) | 10.8 | 0.2051 |
| Displacement (m3) | 52,030 | 0.3562 |
| CB | 0.651 | 0.651 |
| CM | 0.985 | 0.984 |
| LCB (%), fwd+ | −1.48 | −1.48 |
| Rudder | ||
| S (m2) | 115 | 0.0415 |
| Lather area (m2) | 54.45 | 0.0196 |
| Propeller | ||
| Type | FP | FP |
| No. of blades | 5 | 5 |
| D (m) | 7.9 | 0.150 |
| P/D (0.7R) | 0.997 | 1.000 |
| Ae/A0 | 0.8 | 0.700 |
| Rotation | Right hand | Right hand |
| Hub ratio | 0.18 | 0.227 |
| n (rps) | - | 14 |
| Motions | [-] | [deg] | [-] | [deg] | Cases Number |
|---|---|---|---|---|---|
| Static rudder | 0.156 | 0 | 0 | 0, ±10, ±20, ±30, ±35 | 27 |
| 0.201 | |||||
| 0.260 | |||||
| Static drift and rudder | 0.156 | −12 | 0 | 0, ±10, ±20, 30, 35 | 14 |
| 12 | 0 | 0, ±10, ±20, −30, −35 | |||
| 0.201 | −4 | 0 | 0, ±10, ±20, 30, 35 | 14 | |
| 4 | 0, ±10, ±20, −30, −35 | ||||
| Static circular and rudder | 0.201 | 0 | ±0.4, ±0.6 | 0, ±10, ±20, ±30, ±35 | 36 |
| Total | - | - | - | - | 91 |
| Motions | [-] | [deg] | [-] | [deg] | Cases Number |
|---|---|---|---|---|---|
| Static rudder | 0.156 | 0 | 0 | 0, 10, 20, 30, 35 | 5 |
| 0.201 | 0, −10, −20, −30, −35 | 5 | |||
| 0.260 | 0, ±10, ±20, ±30, ±35 | 9 | |||
| Static drift and rudder | 0.156 | −12 | 0 | 0, ±20, 30, 35 | 5 |
| Total | - | - | - | - | 24 |
| Grid | External Static Part | Mean | Internal Dynamic Part (BFM) | Mean | Internal Dynamic Part (DPM) | Mean |
|---|---|---|---|---|---|---|
| Coarse | 0.56 | 66.51 | 0.03 | 1.22 | 0.21 | 1.15 |
| Medium | 0.96 | 54.73 | 0.09 | 1.20 | 0.38 | 1.13 |
| Fine | 1.88 | 43.33 | 0.26 | 1.16 | 0.76 | 1.10 |
| Grid | Number of ) | CFL | ||
|---|---|---|---|---|
| (1) | 0.59 | 0.02 | 0.026 | 0.025 |
| (2) | 1.05 | 0.01 | 0.026 | 0.033 |
| (3) | 2.14 | 0.005 | 0.026 | 0.026 |
| Grid | Number of ) | CFL | |||
|---|---|---|---|---|---|
| (1) | 0.77 | 0.00035 | 0.026 | 0.000883 | 0.000397 |
| (2) | 1.34 | 0.00035 | 0.026 | 0.001357 | 0.000397 |
| (3) | 2.64 | 0.00035 | 0.026 | 0.001864 | 0.000397 |
| Grid | Diff. (%) | (rps) | |
|---|---|---|---|
| (1) | −0.016768 | - | 14.0607 |
| (2) | −0.017176 | 2.43 | 14.4172 |
| (3) | −0.017336 | 0.09 | 14.5658 |
| Grid | Diff. (%) | (rps) | |
|---|---|---|---|
| (1) | −0.016948 | - | 14 |
| (2) | −0.017427 | 2.83 | 14 |
| (3) | −0.017559 | 0.08 | 14 |
| Quantity | Convergence Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.39 | 2.71 | 1.56 | −0.59 | −0.33 | −0.017459 | 1.25 | Monotonic |
| Quantity | Convergence Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.28 | 3.72 | 2.63 | −0.29 | −0.47 | −0.017691 | 1.22 | Monotonic |
| Grid | Diff. (%) | ||
|---|---|---|---|
| (3) | 0.02 | −0.0180 | |
| 0.01 | −0.0175 | 3.02 | |
| 0.005 | −0.0173 | 1.16 |
| Quantity | Convergence Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.4 | 1.32 | 1.5 | 1.99 | 0.99 | −0.0168 | 3.98 | Monotonic |
| Grid | Diff. (%) | Diff. (%) | Diff. (%) | |||
|---|---|---|---|---|---|---|
| (1) | −0.019458 | - | −0.070236 | - | −0.021487 | |
| (2) | −0.020844 | 7.12 | −0.072119 | 0.27 | −0.022221 | 0.34 |
| (3) | −0.021053 | 1.00 | −0.072483 | 0.05 | −0.022548 | 0.15 |
| Grid | Diff. (%) | Diff. (%) | Diff. (%) | |||
|---|---|---|---|---|---|---|
| (1) | −0.019777 | - | −0.070592 | - | −0.021126 | |
| (2) | −0.020414 | 3.22 | −0.072911 | 3.28 | −0.024420 | 15.59 |
| (3) | −0.020665 | 1.23 | −0.072115 | −1.09 | −0.024000 | −1.72 |
| Quantity | Convergence Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.51 | 1.93 | 0.96 | −3.44 | −0.15 | −0.021794 | 3.75 | Monotonic | ||
| 0.19 | 4.74 | 4.17 | −0.12 | −0.38 | −0.072864 | 0.88 | Monotonic | ||
| 0.49 | 2.33 | 1.24 | −1.17 | −0.28 | −0.022826 | 1.74 | Monotonic |
| Quantity | Convergence Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.39 | 2.69 | 1.54 | −0.79 | −0.42 | −0.020916 | 1.64 | Monotonic | ||
| −0.34 | - | - | - | - | - | −1.61 | Oscillatory | ||
| −0.13 | - | - | - | - | - | −6.86 | Oscillatory |
| Motion | Quantity | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Straight- ahead | (BFM) | −0.0173 | −0.0179 | −3.35 | 1.21 | 3.85 | 4.03 | 5 | 6.42 |
| (DPM) | −0.0176 | −0.0179 | −1.68 | 1.20 | - | 1.20 | 5 | 5.14 | |
| Drift | (BFM) | −0.0211 | −0.0205 | 2.93 | 3.86 | 4.10 | 5.62 | 5 | 7.53 |
| (BFM) | −0.0725 | −0.0726 | −0.14 | 0.88 | 3.97 | 4.07 | 5 | 6.45 | |
| (BFM) | −0.0226 | −0.0241 | −6.22 | 1.63 | 3.73 | 4.07 | 5 | 6.45 | |
| (DPM) | −0.0207 | −0.0205 | 0.98 | 1.66 | - | 1.66 | 5 | 5.27 | |
| (DPM) | −0.0721 | −0.0726 | −0.69 | −1.60 | - | −1.60 | 5 | 5.25 | |
| (DPM) | −0.0240 | −0.0241 | −0.41 | −6.83 | - | −6.83 | 5 | 8.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Yao, J.; Liu, Z. Analysis of the Accuracy of a Body-Force Propeller Model and a Discretized Propeller Model in RANS Simulations of the Flow Around a Maneuvering Ship. J. Mar. Sci. Eng. 2025, 13, 788. https://doi.org/10.3390/jmse13040788
Jiang L, Yao J, Liu Z. Analysis of the Accuracy of a Body-Force Propeller Model and a Discretized Propeller Model in RANS Simulations of the Flow Around a Maneuvering Ship. Journal of Marine Science and Engineering. 2025; 13(4):788. https://doi.org/10.3390/jmse13040788
Chicago/Turabian StyleJiang, Long, Jianxi Yao, and Zuyuan Liu. 2025. "Analysis of the Accuracy of a Body-Force Propeller Model and a Discretized Propeller Model in RANS Simulations of the Flow Around a Maneuvering Ship" Journal of Marine Science and Engineering 13, no. 4: 788. https://doi.org/10.3390/jmse13040788
APA StyleJiang, L., Yao, J., & Liu, Z. (2025). Analysis of the Accuracy of a Body-Force Propeller Model and a Discretized Propeller Model in RANS Simulations of the Flow Around a Maneuvering Ship. Journal of Marine Science and Engineering, 13(4), 788. https://doi.org/10.3390/jmse13040788






