Comparison of Surface Current Measurement Between Compact and Square-Array Ocean Radar
Abstract
1. Introduction
1.1. Background
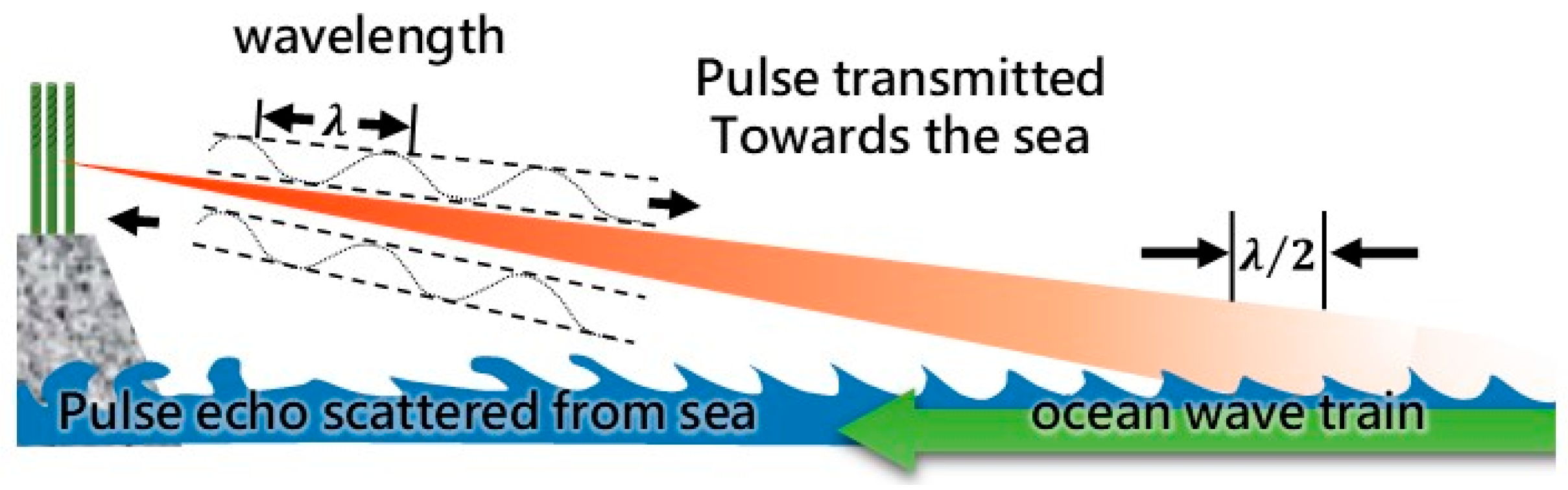
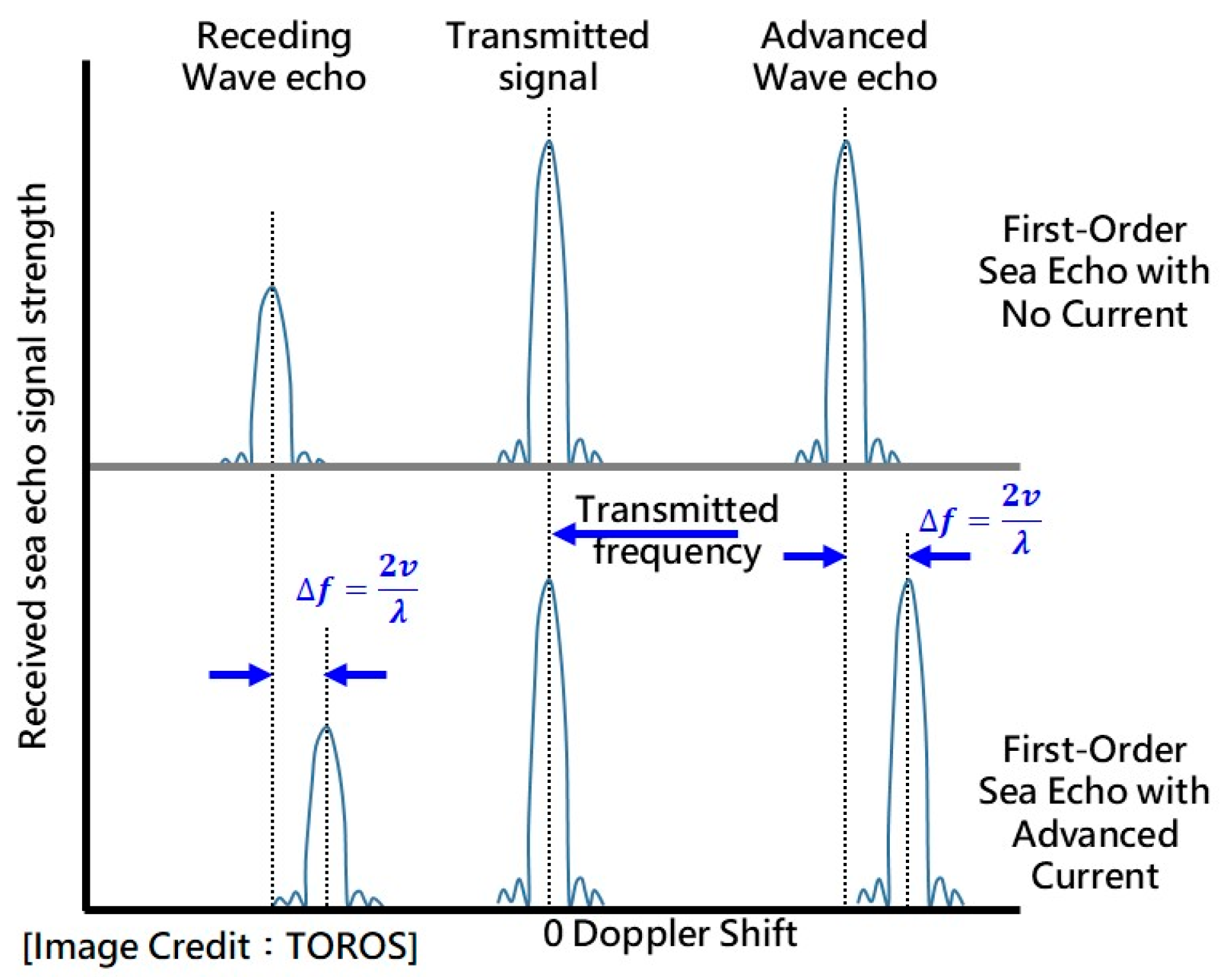
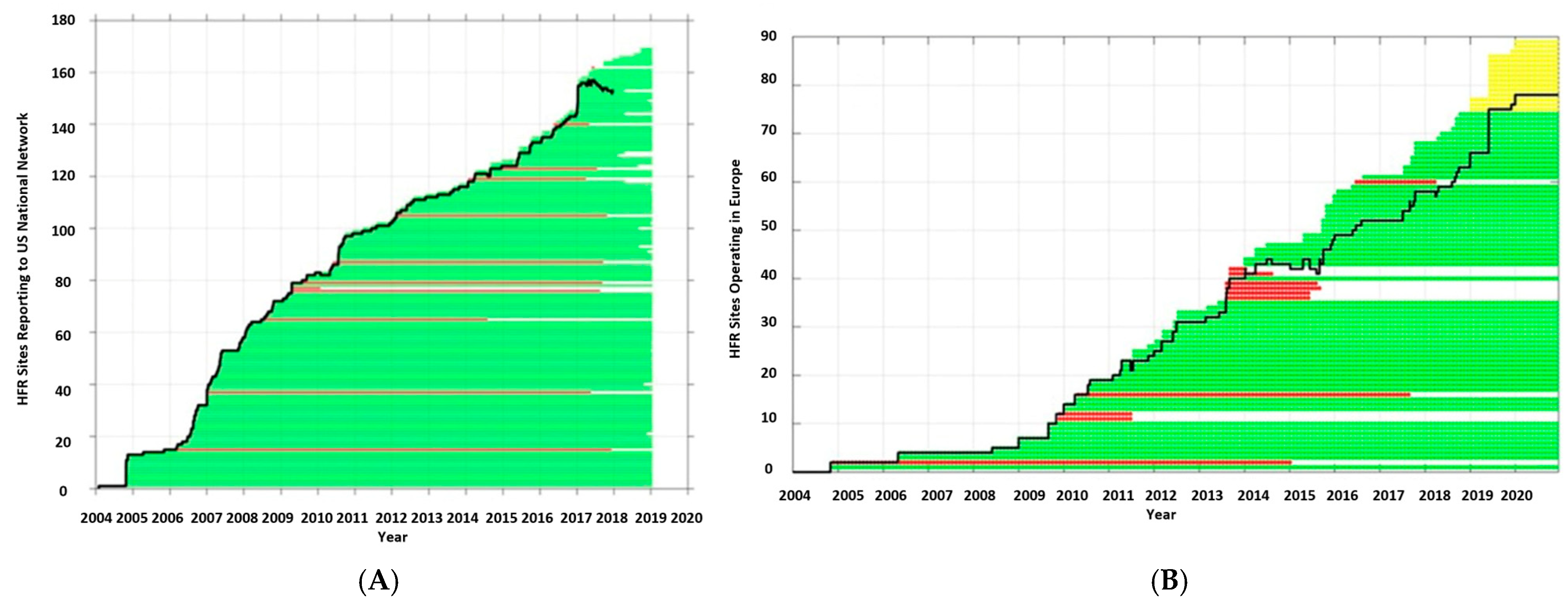
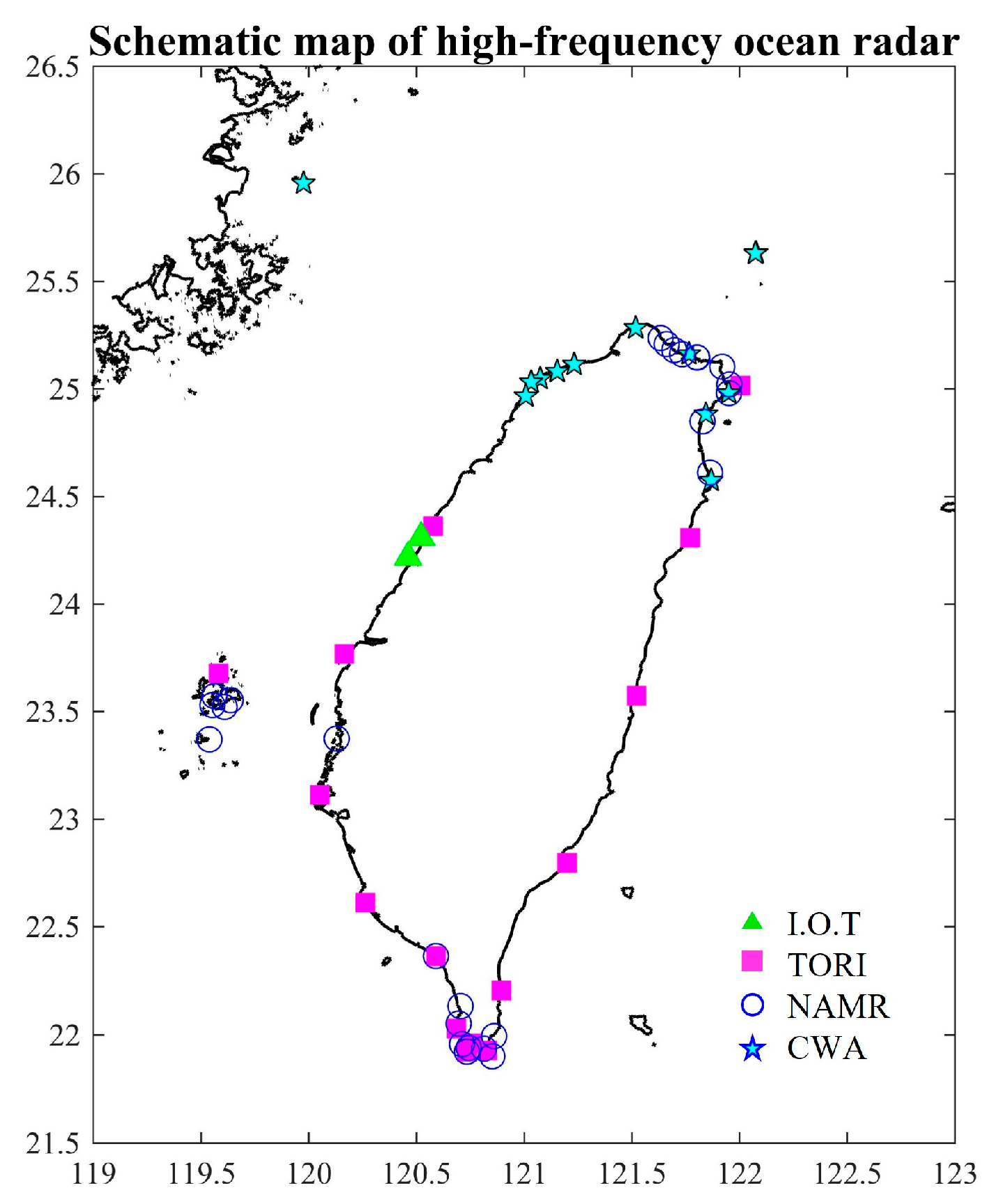
1.2. Introduction of High-Frequency Ocean Radars in Taiwan
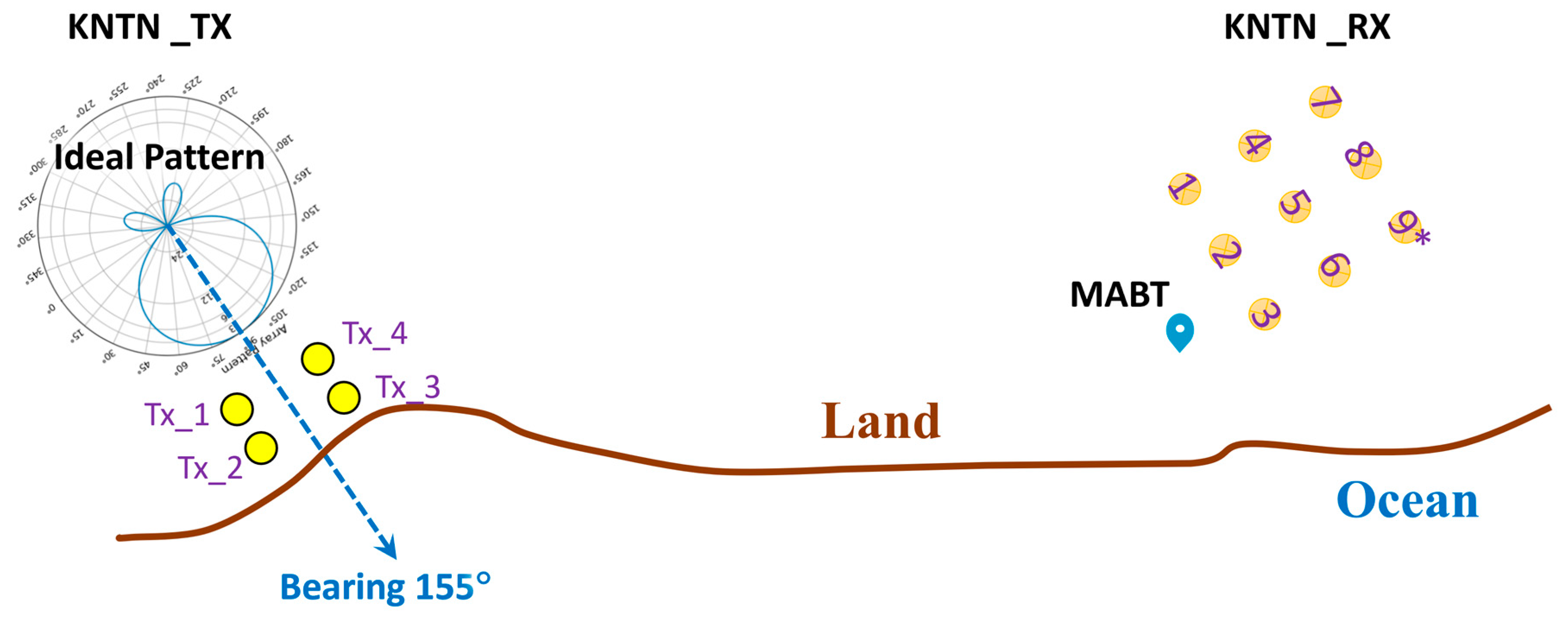
1.3. Overview of the TORI’s Current System at Cape Maobitou
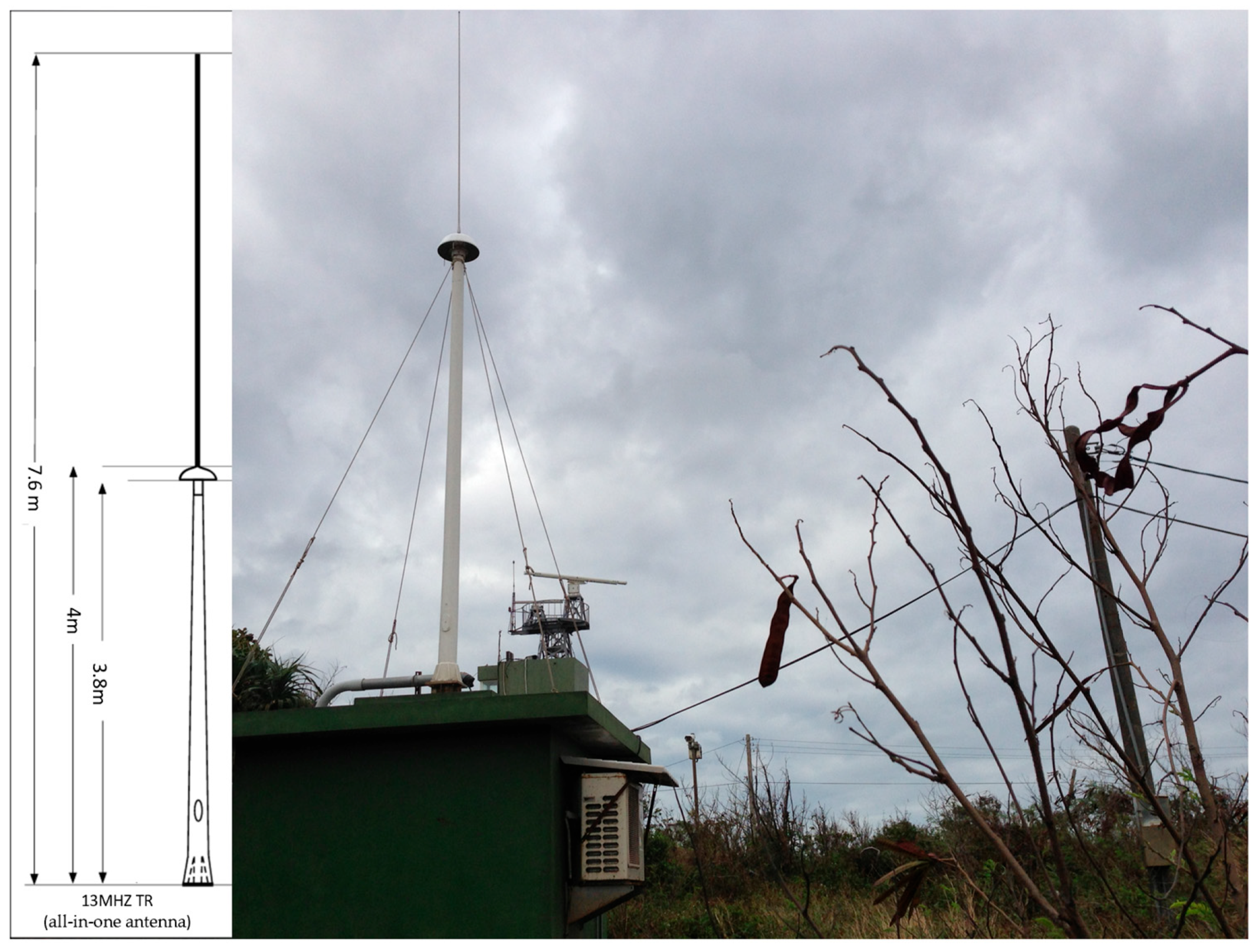
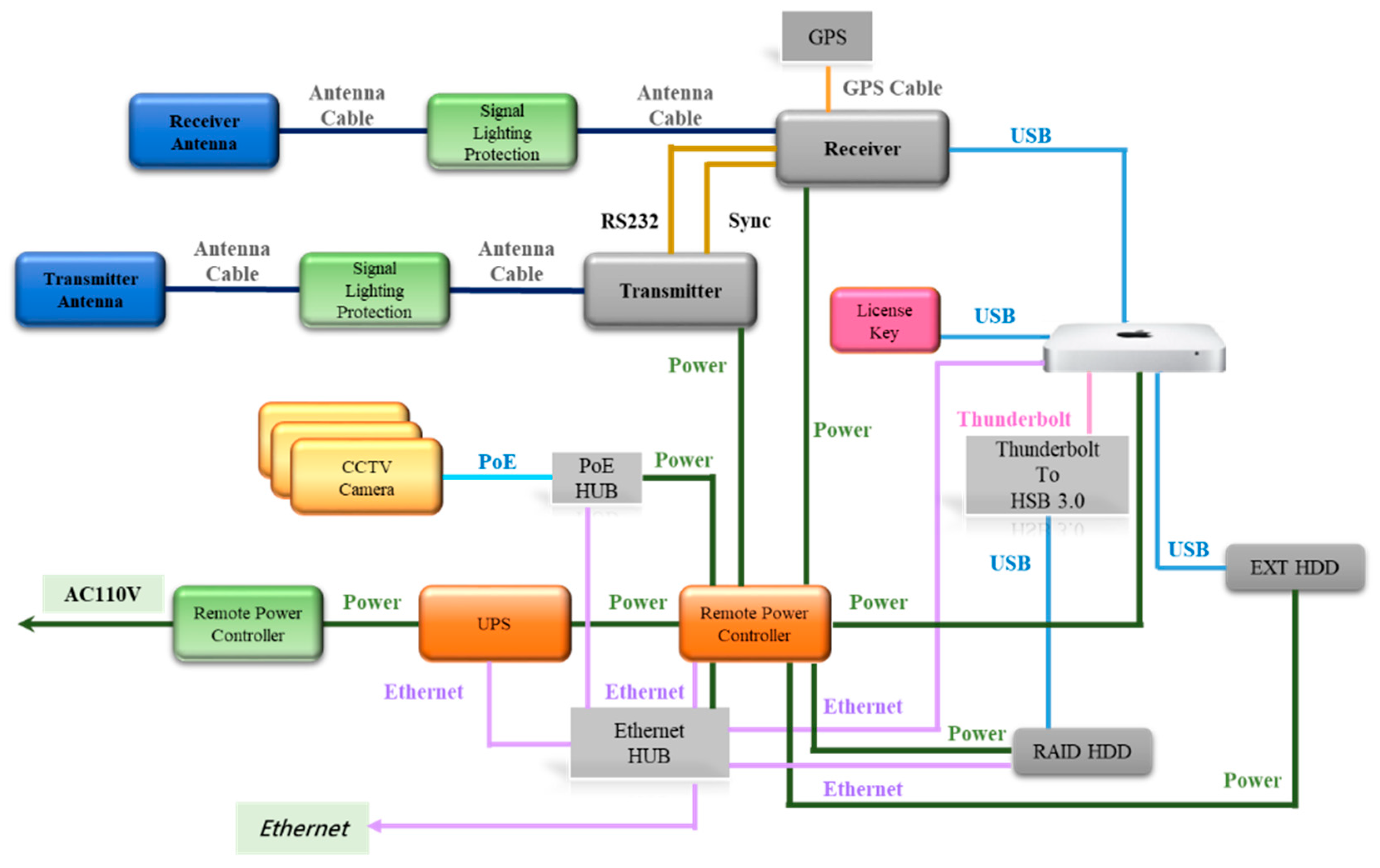
1.3.1. CODAR Systems
1.3.2. LERA (KNTN)
2. Comparison of Compact (MABT) and Square-Array (KNTN) Ocean Radars
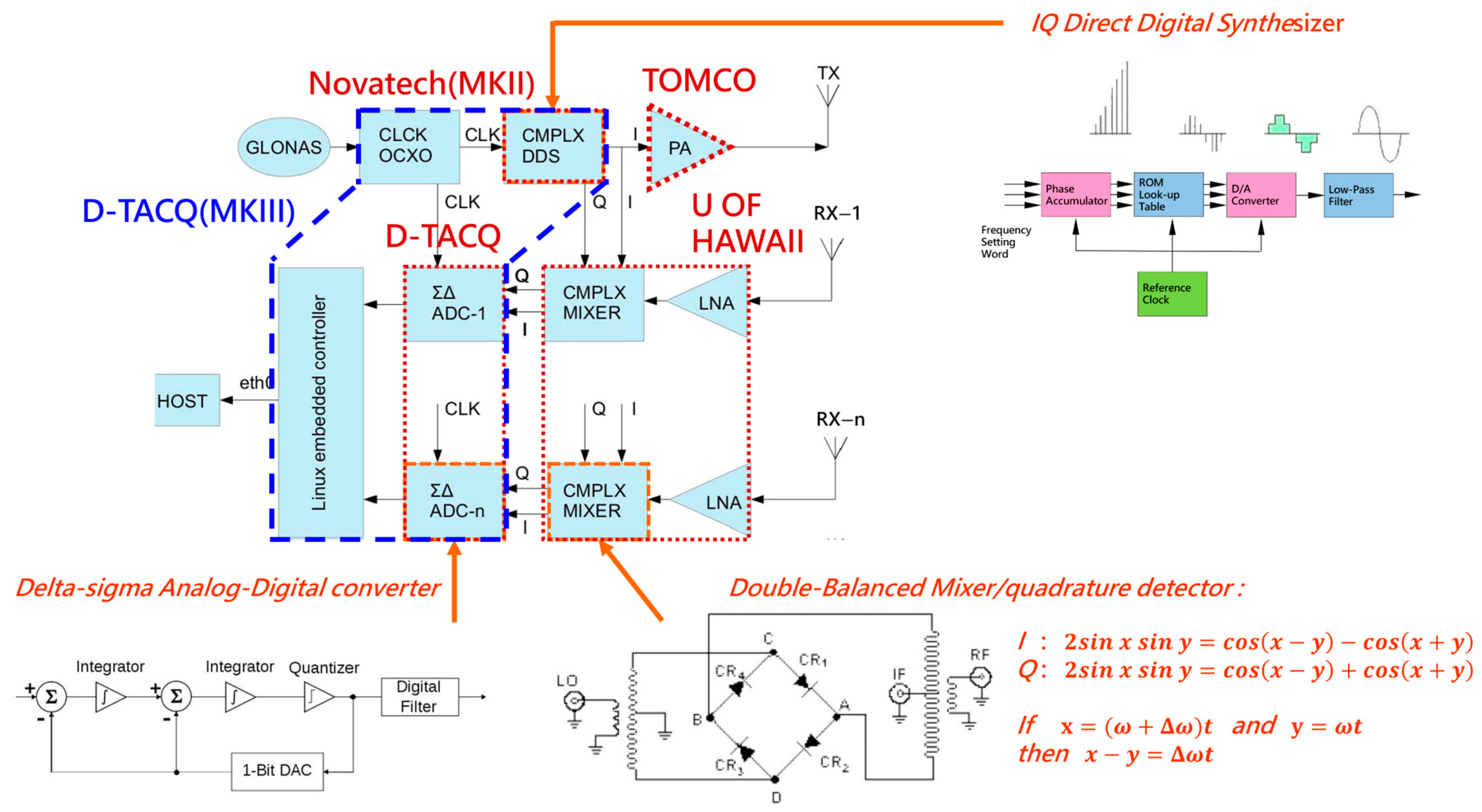
2.1. Hardware Differences
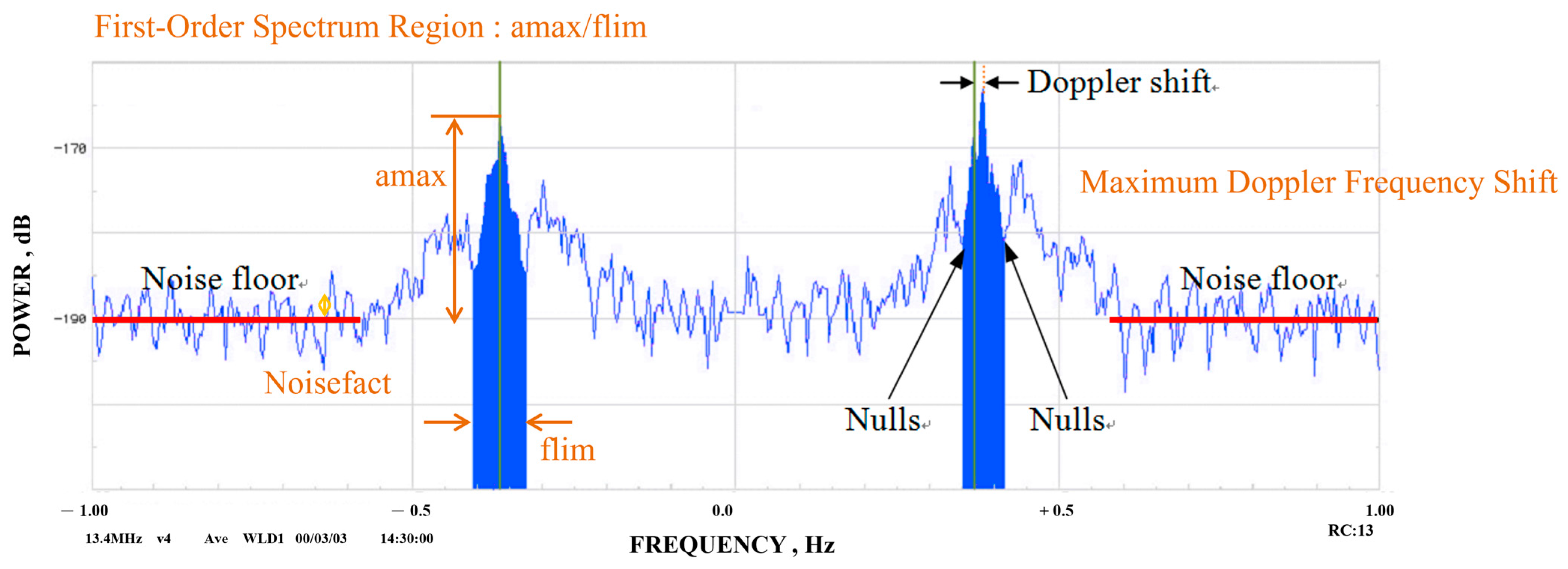
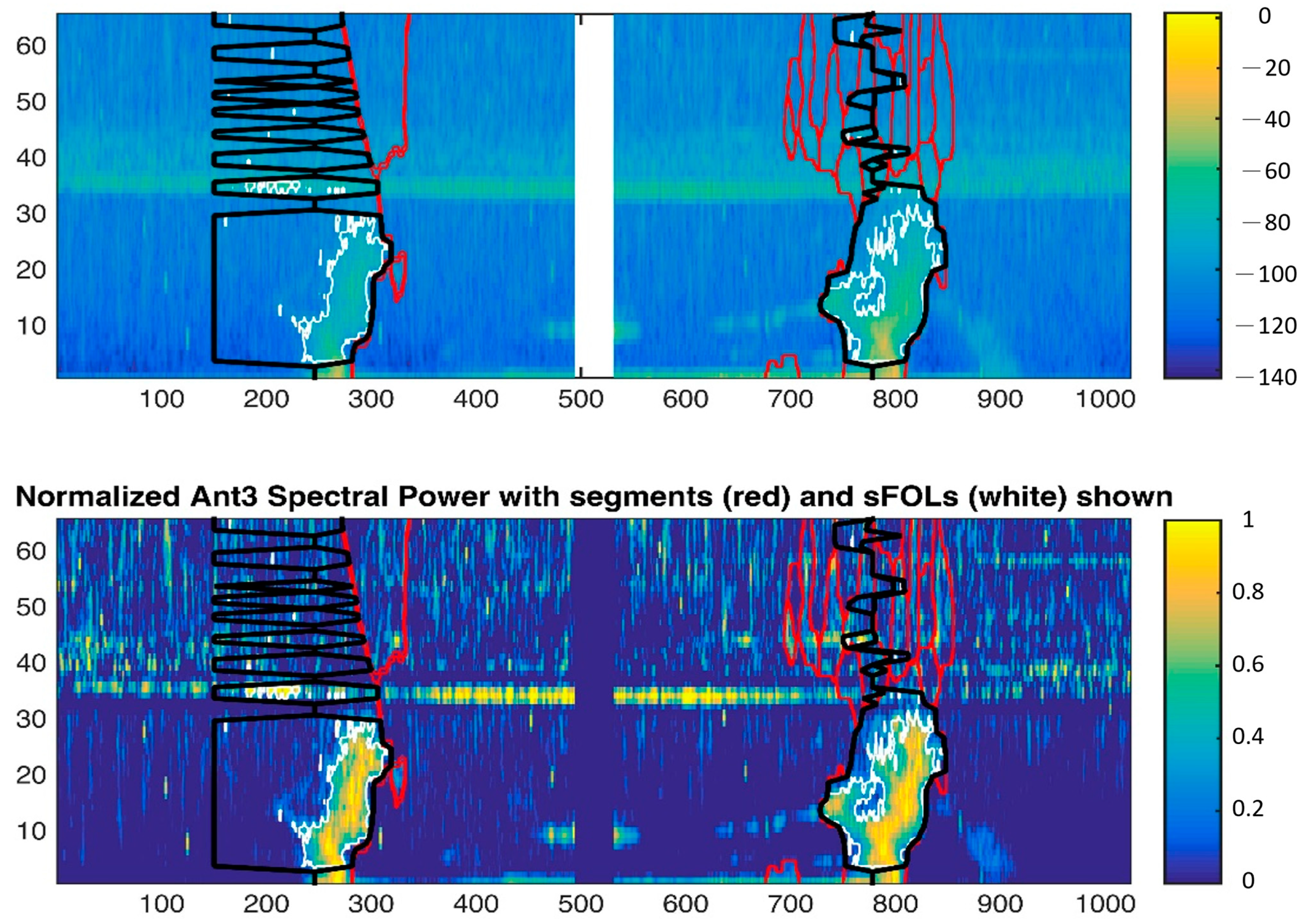
2.2. Algorithm Differences
3. Methodology
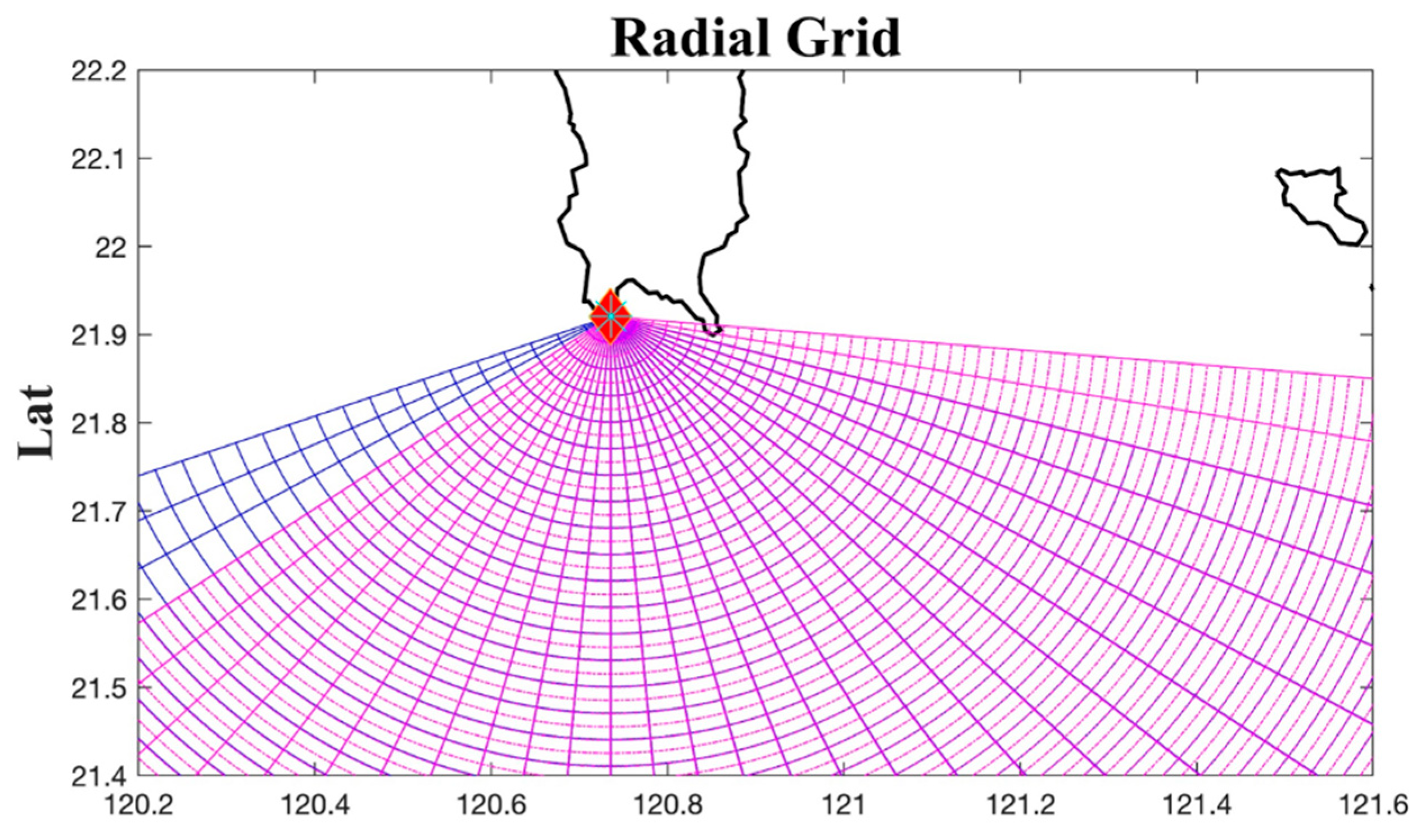
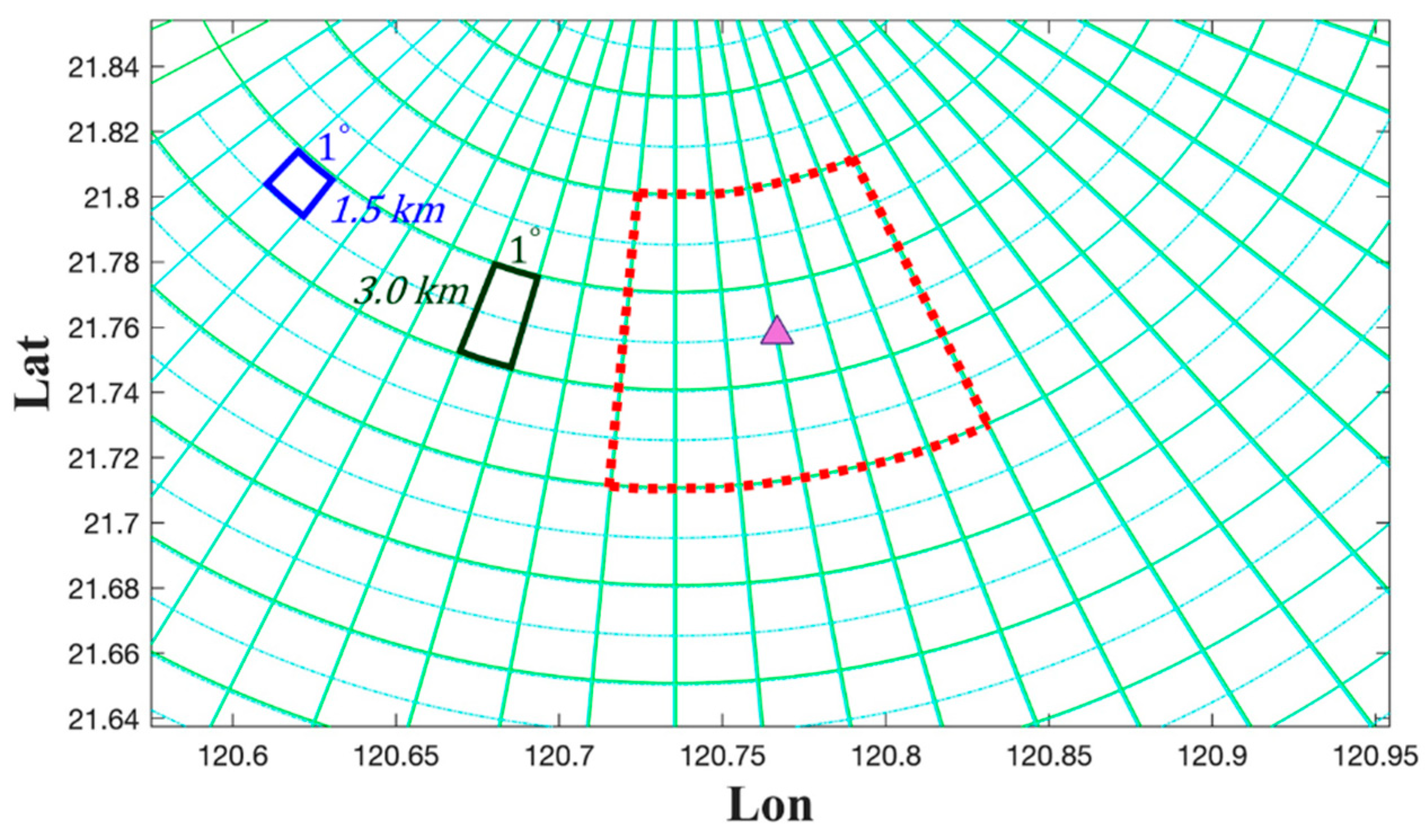
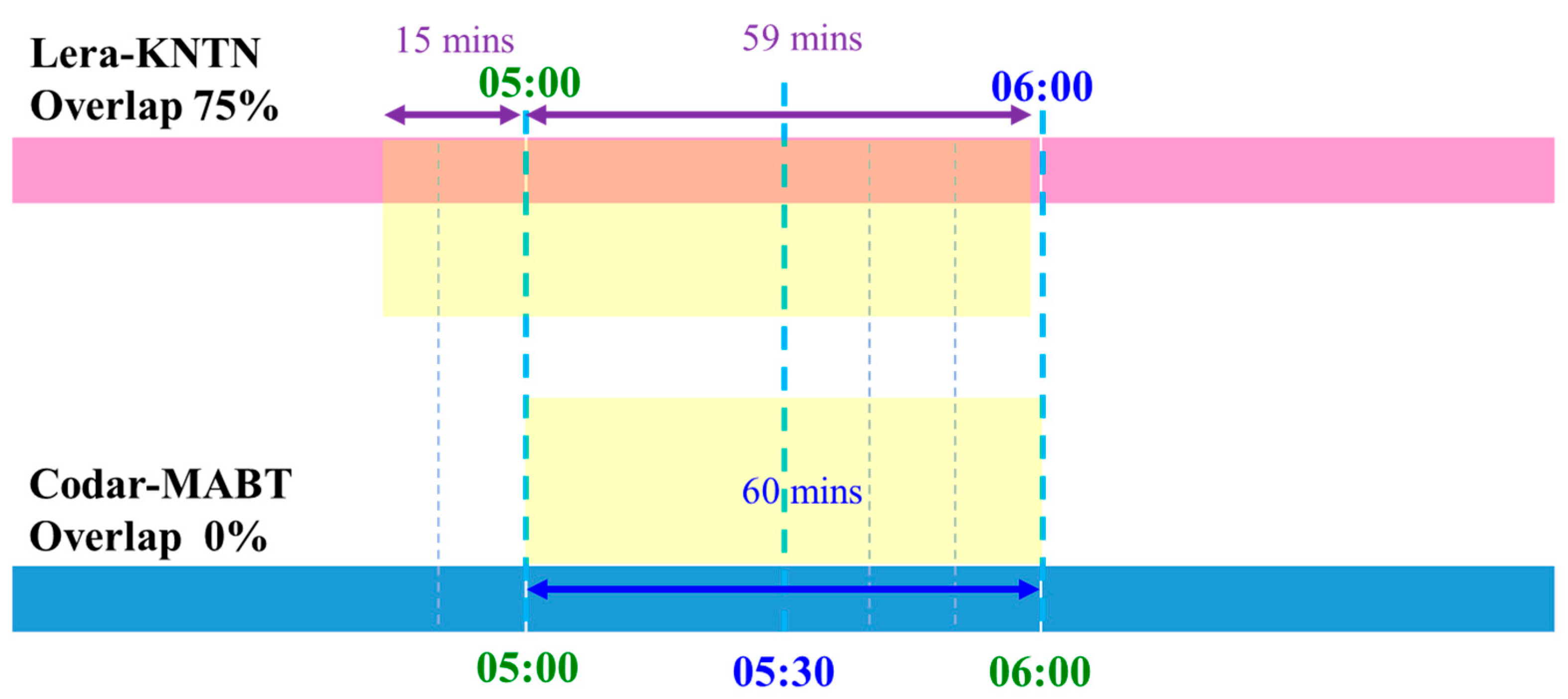
3.1. Methods for Reducing the Impact of Analytical Differences
3.2. Using Drifting Buoys and Data Buoys for Current Measurement to Validate Two Radar-Based Current Measurement Systems
4. Results and Discussion
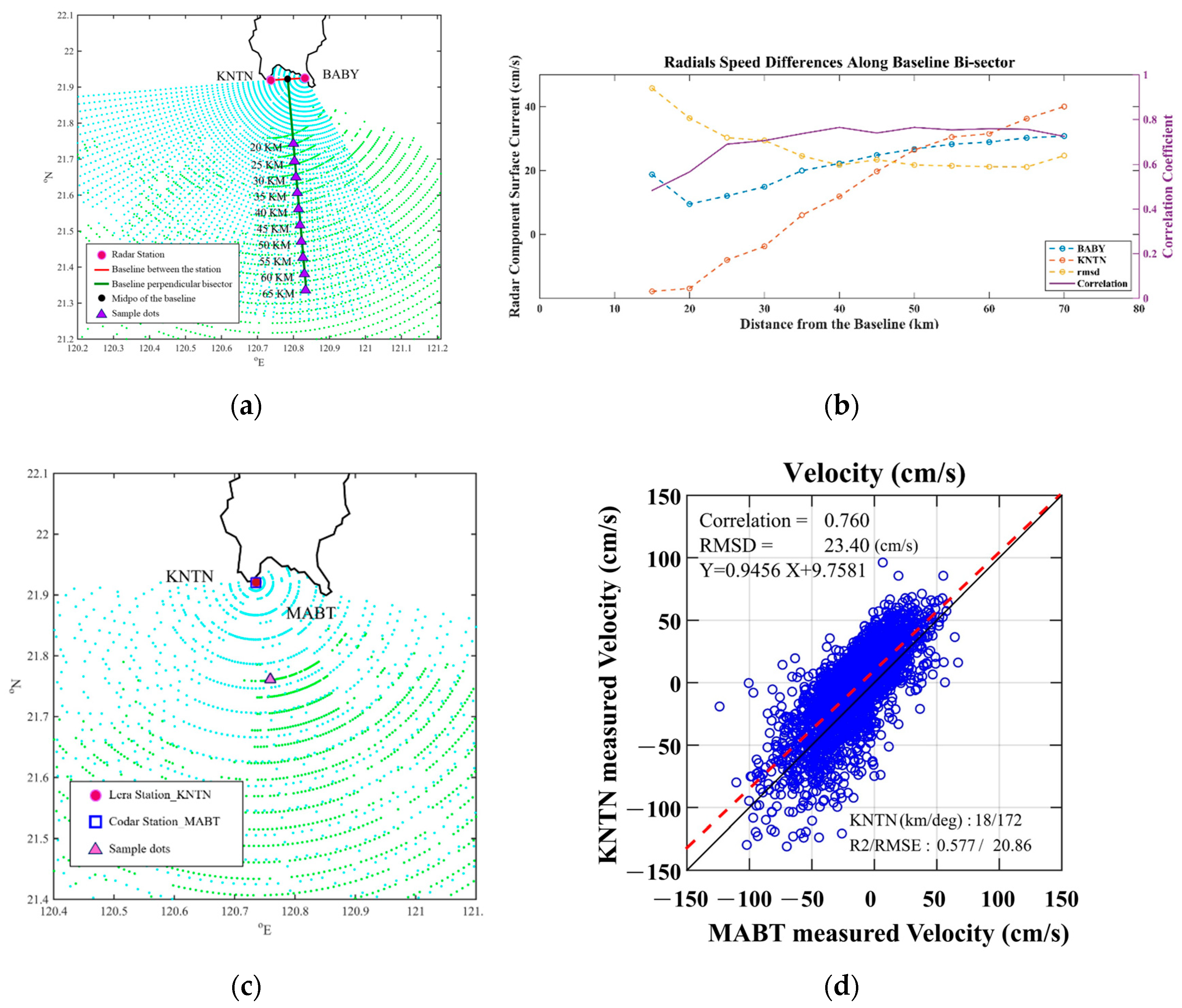
4.1. Differences in Radial Velocity (Baseline Velocity Comparisons)
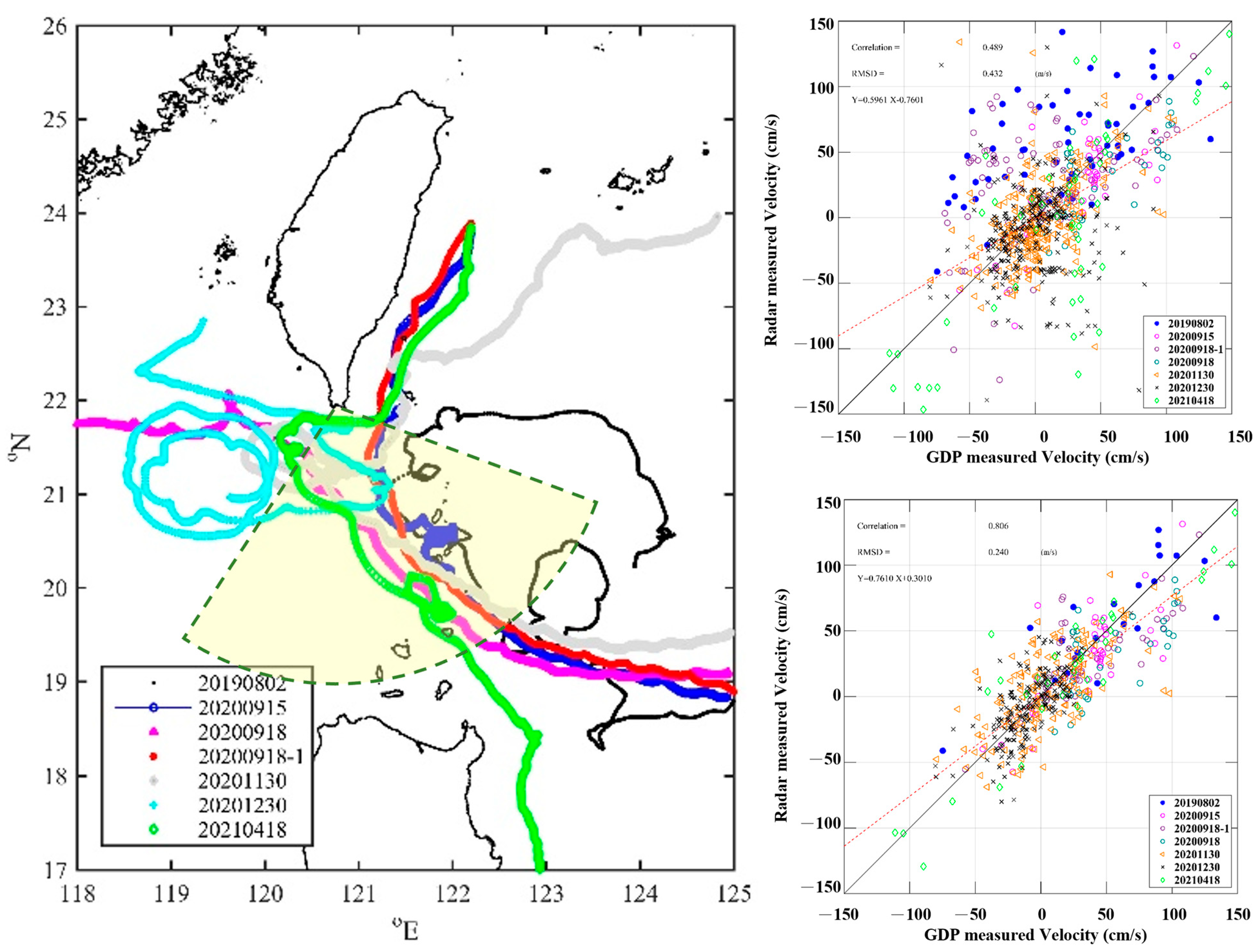
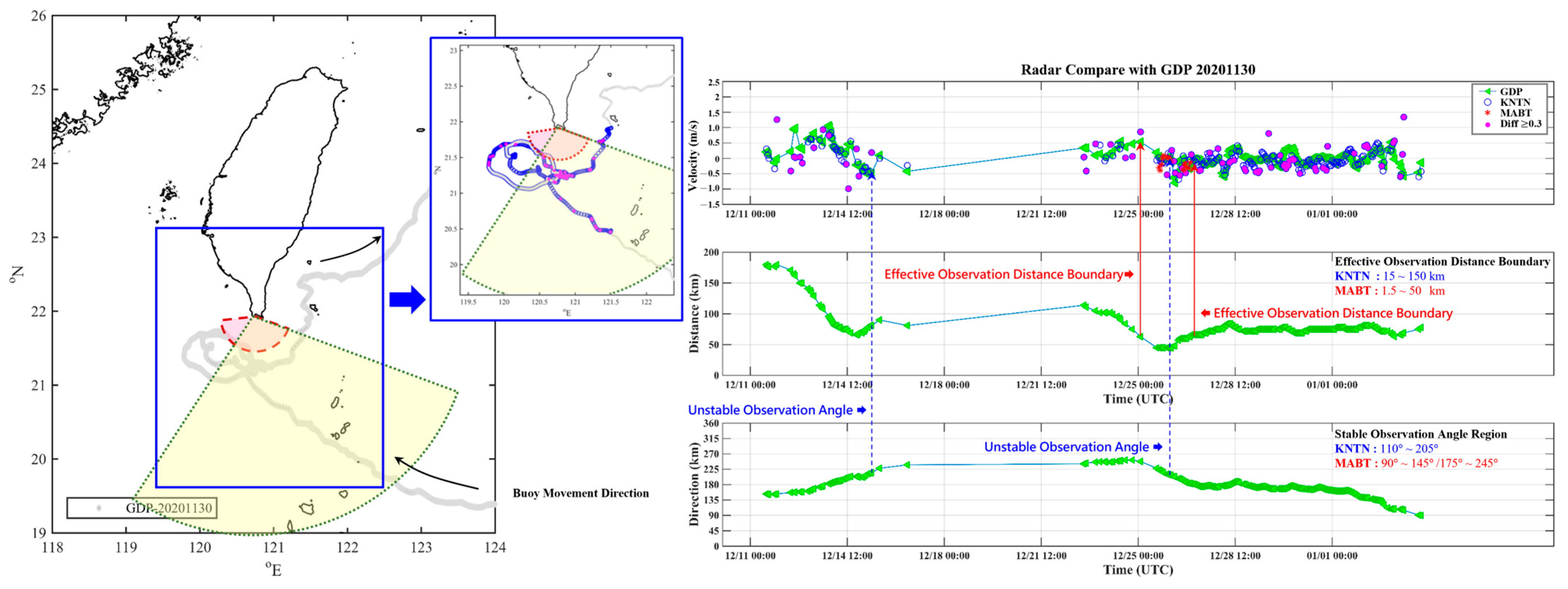
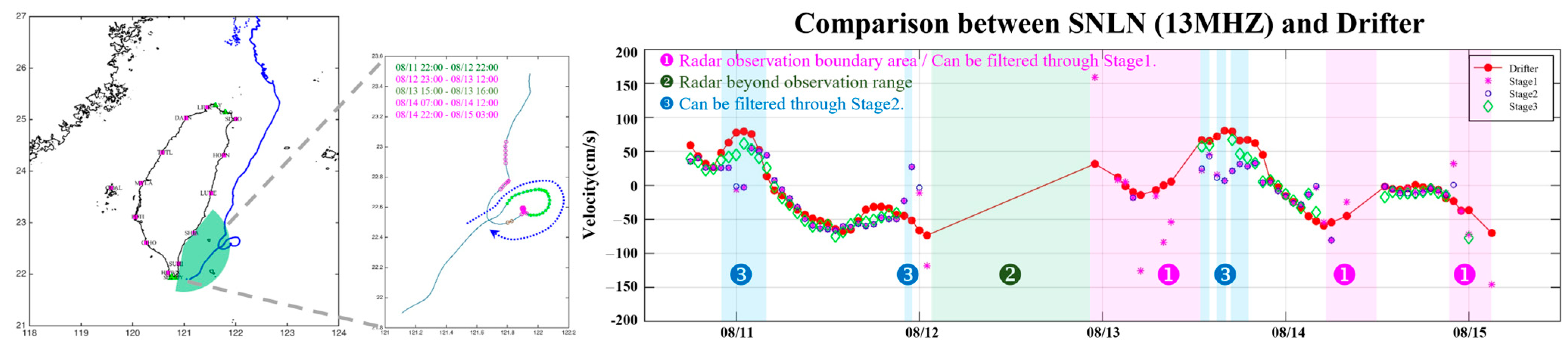
4.2. Drifter-Based Velocity Comparisons
- Data Integrity Verification: This step examines the file headers, footers, and overall data format and content to eliminate errors caused by radar system hardware malfunctions or analytical software anomalies. Additionally, spectral analysis and harmonic analysis are used to assess whether the radar-measured currents conform to the historical tidal characteristics of the observation area and whether the obtained current data follow a normal distribution.
- Data Validity Assessment: Based on the sampling theorem, the effective data production rate for each grid point is calculated to ensure that the produced data accurately reflect tidal variations.
- Anomalous Data Filtering: The mean and standard deviation of the measured current data are analyzed to detect excessively high or low values, ensuring temporal and spatial continuity and reasonability of the dataset.
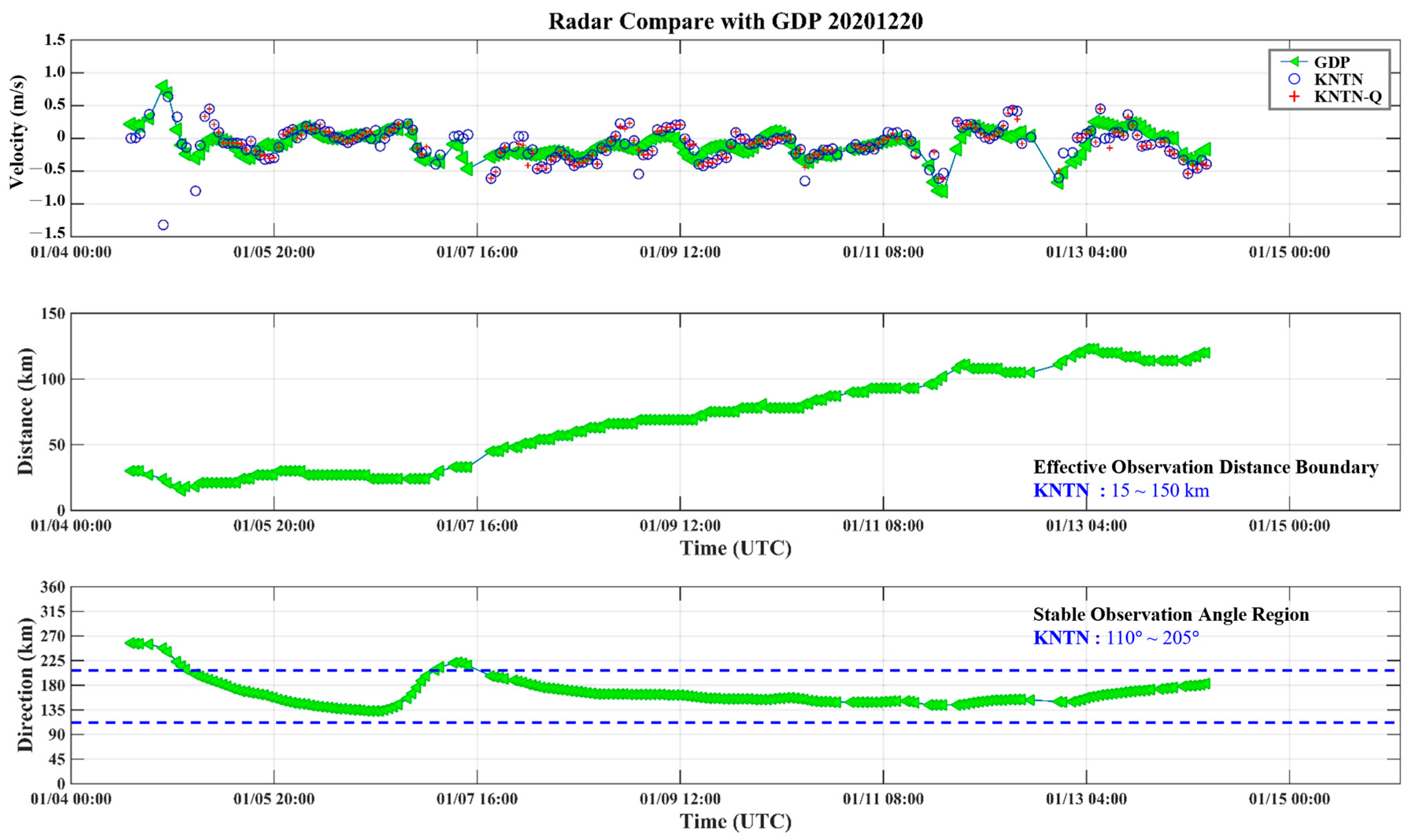
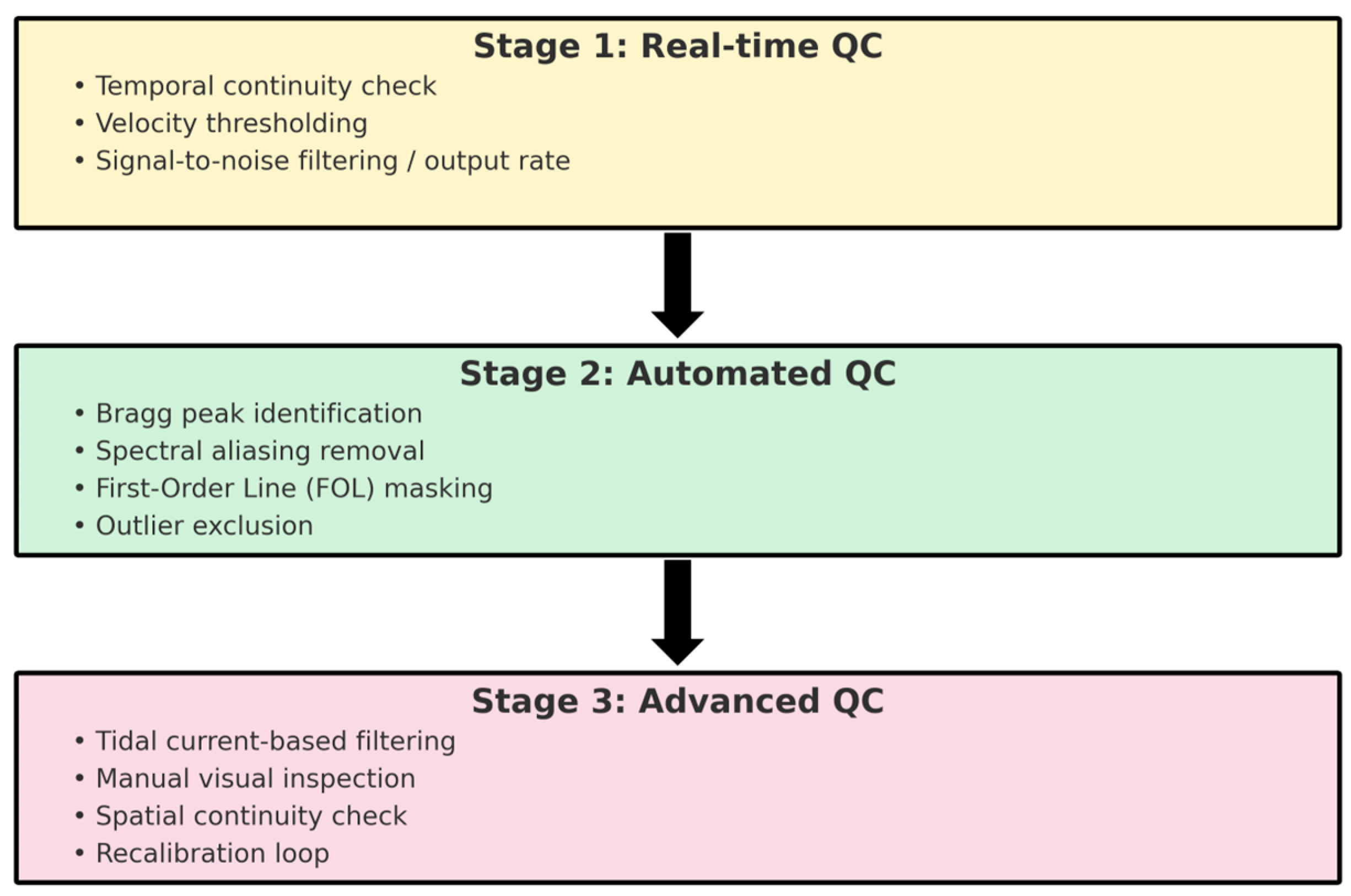
4.3. Differences and Influencing Factors in Surface Current Measurements Between Compact and Phased-Array HF Radars and Drifters
5. Conclusions
- It introduces a locally adapted QC framework designed from empirical operational experience to improve the consistency of radial velocity observations.
- It constructs a rare synchronous dataset from two different HF radar systems operating over the same time and space, with independent validation from drifter observations.
- It examines the effects of operating frequency differences (8 MHz vs. 13 MHz) on data quality and spatial resolution, providing practical insights for multi-frequency data fusion and model assimilation.
- It applies a unified Bragg peak identification algorithm (MUSIC) across both systems, thereby evaluating its performance and consistency across heterogeneous radar platforms.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADCP | Acoustic Doppler Current Profiler |
| BABY | The compact CODAR system in Banana Bay |
| BF | Beamforming |
| DF | Direction-finding |
| DOA | Direction of arrival |
| DDS | Direct Digital Synthesis |
| FMiCW | Frequency-modulated interrupted continuous wave |
| FMCW | Frequency-modulated continuous wave |
| FFT | Fast Fourier Transform |
| GDP | Global Drifter Program |
| HF | High-frequency |
| HFR | High-frequency radar |
| IOOS | Integrated Ocean Observing System |
| I.O.T. | Transportation Technology Research Center |
| KNTN | The square-array phased-array radar system in Maobitou |
| MABT | The compact CODAR system in Maobitou |
| MUSIC | MUltiple SIgnal Classification |
| NAMR | National Academy of Marine Research |
| ONR | Office of Naval Research |
| PA | Power amplifier |
| QARTOD | Quality Assurance/Quality Control of Real-Time Oceanographic Data manual |
| QC | Quality control |
| RC | Radar cell |
| RMSD | Root-mean-square deviation |
| RX | Receiving antenna system |
| RUV | Radial velocity |
| SNR | Signal-to-noise ratio |
| TX | Transmitting antenna system |
| WHOI | The Woods Hole Oceanographic Institution |
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D. First-order theory and analysis of mf/hf/vhf scatter from the sea. IEEE Trans. Antennas Propag. 1972, AP-20, 2–10. [Google Scholar] [CrossRef]
- Barrick, D. Remote sensing of sea state by radar. In Proceedings of the Ocean 72—IEEE International Conference on Engineering in the Ocean Environment, Newport, RI, USA, 13–15 September 1972; pp. 186–192. [Google Scholar]
- Roarty, H.; Cook, T.; Hazard, L.; George, D.; Harlan, J.; Cosoli, S.; Grilli, S. The global high-frequency radar network. Front. Mar. Sci. 2019, 6, 164. [Google Scholar] [CrossRef]
- Barrick, D.E.; Evans, M.W.; Weber, B.L. Ocean surface currents mapped by radar. Science 1977, 198, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.Y.; Su, C.L.; Wu, K.H.; Chu, Y.H. Cross spectral analysis of CODAR-SeaSonde echoes from sea surface and ionosphere at Taiwan. Int. J. Antennas Propag. 2017, 2017, 756761. [Google Scholar] [CrossRef]
- Roarty, H.; Smith, M.; Evans, C.; Handel, E.; Kohut, J.; Glenn, S. Quality control for a network of SeaSonde HF radars. In Proceedings of the IEEE OCEANS 2014, Taipei, Taiwan, 7–10 April 2014. [Google Scholar]
- Haines, S.; Seim, H.; Muglia, M. Implementing quality control of high-frequency radar estimates and application to Gulf Stream surface currents. J. Atmos. Ocean. Technol. 2017, 34, 1207–1224. [Google Scholar] [CrossRef]
- U.S. IOOS—Integrated Ocean Observing System. Manual for Real-Time Quality Control of High-Frequency Radar Surface Currents Data: A Guide to Quality Control and Quality Assurance of High-Frequency Radar Surface Currents Data Observations, Version 2.0; U.S. IOOS—Integrated Ocean Observing System: Maryland, MD, USA, 2016. [Google Scholar]
- Lai, J.-W.; Wu, C.-C.; Huang, Y.-H.; Chen, S.-H. A Proposal and evaluation of data QA/QC processes for Taiwan Ocean Radar Observing System. In Proceedings of the 18th Pacific-Asian Marginal Seas Meeting (PAMS), Okinawa, Japan, 21–23 April 2015. [Google Scholar]
- Kirincich, A.R.; de Paolo, T.; Terrill, E. Improving HF radar estimates of surface currents using signal quality metrics, with application to the MVCO high-resolution radar system. J. Atmos. Ocean. Technol. 2012, 29, 1377–1390. [Google Scholar] [CrossRef]
- Barrick, D.E. FM/CW Radar Signals and Digital Processing; NOAA-TR-ERL-283-WPL-26; National Oceanic and Atmospheric Administration: Boulder, CO, USA, 1973. [Google Scholar]
- Barrick, D.E. First-Order Region Boundaries; Technical Report; CODAR Ocean Sensors Ltd.: Mountain View, CA, USA, 2002; p. 9. [Google Scholar]
- Kirincich, A.R. Improved detection of the first-order region for direction-finding HF radars using image processing techniques. J. Atmos. Ocean. Technol. 2017, 34, 1679–1691. [Google Scholar] [CrossRef]
- Laws, K.E.; Fernandez, D.M.; Paduan, J.D. Simulation-based evaluations of HF radar ocean current algorithms. IEEE J. Ocean. Eng. 2000, 25, 481–491. [Google Scholar] [CrossRef]
- Liu, Y.; Merz, C.R.; Weisberg, R.H.; O’Loughlin, B.K.; Subramanian, V. Data return aspects of CODAR and WERA high-frequency radars in mapping currents. In Observing the Oceans in Real Time; Venkatesan, R., Tandon, A., D’Asaro, E., Atmanand, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 227–239. [Google Scholar] [CrossRef]
- Rayner, R. The U.S. integrated ocean observing system in a global context. Mar. Technol. Soc. J. 2010, 44, 26–31. [Google Scholar] [CrossRef]
- Paduan, J.D.; Kim, K.; Cook, M.; Chavez, F. Calibration and validation of direction-finding high-frequency radar ocean surface current observations. IEEE J. Ocean. Eng. 2006, 31, 862–875. [Google Scholar] [CrossRef]
- Atwater, D.P.; Heron, M.L. HF radar two-station baseline bisector comparisons of radial components. In Proceedings of the IEEE Oceans 2010, Sydney, Australia, 24–27 May 2010; pp. 1–4. [Google Scholar]
- Dao, D.T.; Chien, H.; Lai, J.W.; Huang, Y.H.; Flament, P. Evaluation of HF radar in mapping surface wave field in Taiwan Strait under winter monsoon. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019; Institute of Electrical and Electronics Engineers Inc.: New Jersey, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Kirincich, A.; Emery, B.; Washburn, L.; Flament, P. Improving surface current resolution using direction-finding algorithms for multiantenna high-frequency radars. J. Atmos. Ocean. Technol. 2019, 36, 1997–2014. [Google Scholar] [CrossRef]
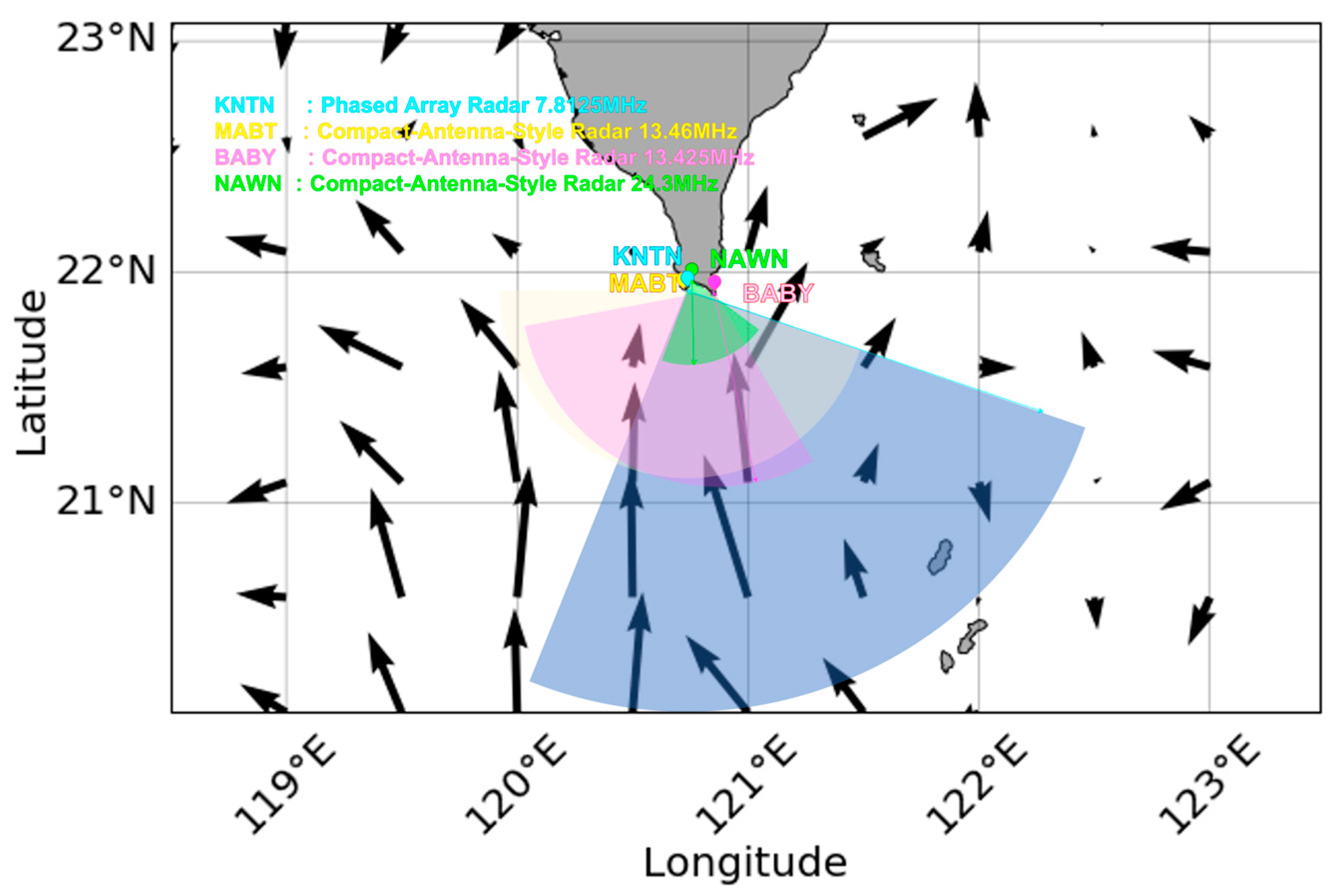





| Parameter | MABT | KNTN |
|---|---|---|
| Signal modulation | FMiCW | FMCW linear sweep |
| Sweep rate | 0.5 s | ~0.455 s |
| Central frequency (MHz) | 13.425 | 7.5125 |
| Location | 120°44′6.54″ E 21°55′13.20″ N | 120°44′6.54″ E 21°55′13.20″ N |
| Signal modulation | FMiCW | FMCW linear sweep |
| Sweep rate | 0.5 s | ~0.455 s |
| MABT | NAWN | BABY | KNTN | |
|---|---|---|---|---|
| Central frequency (MHz) | 13.425 | 24.3 | 13.40 | 7.8125 |
| Location | 120°44′6.54″ E 21°55′13.20″ N | 120°45′41.46″ E 21°57′34.32″ N | 120°49′50.46″ E 21°55′34.02″ N | 120°44′6.54″ E 21°55′13.20″ N |
| Bandwidth (KHz) | 100 | 100 | 100 | 50 |
| Range resolution (km) | 1.5 | 0.7 | 1.5 | 3 |
| RXx antenna type | -length active non-resonant monopoles | Compact type | Compact type | Compact type |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.-H.; Cheng, C.-Y. Comparison of Surface Current Measurement Between Compact and Square-Array Ocean Radar. J. Mar. Sci. Eng. 2025, 13, 778. https://doi.org/10.3390/jmse13040778
Huang Y-H, Cheng C-Y. Comparison of Surface Current Measurement Between Compact and Square-Array Ocean Radar. Journal of Marine Science and Engineering. 2025; 13(4):778. https://doi.org/10.3390/jmse13040778
Chicago/Turabian StyleHuang, Yu-Hsuan, and Chia-Yan Cheng. 2025. "Comparison of Surface Current Measurement Between Compact and Square-Array Ocean Radar" Journal of Marine Science and Engineering 13, no. 4: 778. https://doi.org/10.3390/jmse13040778
APA StyleHuang, Y.-H., & Cheng, C.-Y. (2025). Comparison of Surface Current Measurement Between Compact and Square-Array Ocean Radar. Journal of Marine Science and Engineering, 13(4), 778. https://doi.org/10.3390/jmse13040778






