Research on the On-Line Identification of Ship Maneuvering Motion Model Parameters and Adaptive Control
Abstract
1. Introduction
2. Construction of the Ship Maneuvering Motion Model
2.1. Coordinate System
2.2. Equation of Ship Motion
2.3. Calculation of Ship Maneuverability Index
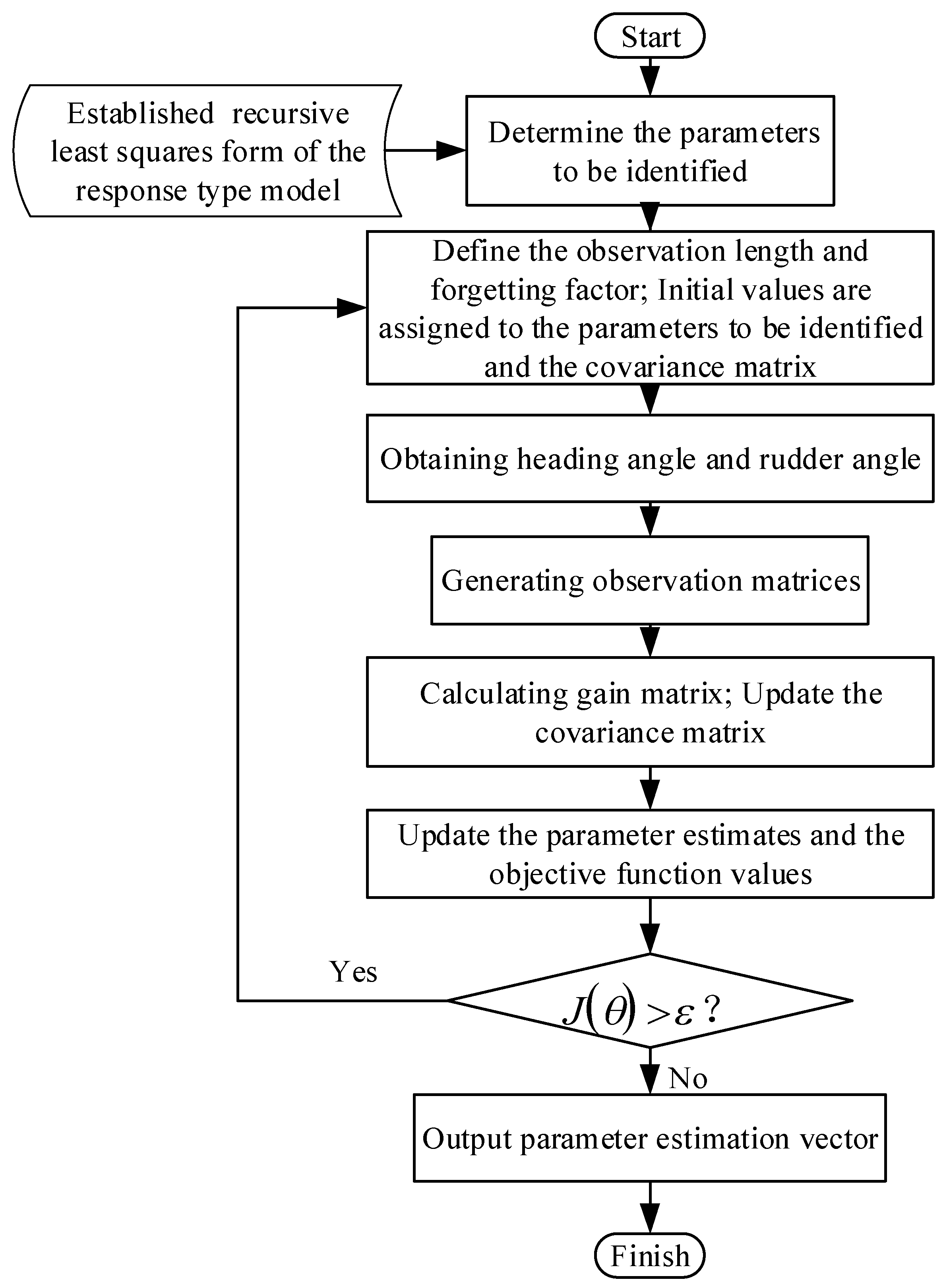
3. Parameter Identification of the Ship Maneuvering Motion Model
3.1. Recursive Least Squares Method
3.2. Recursive Least Square Method with Forgetting Factor
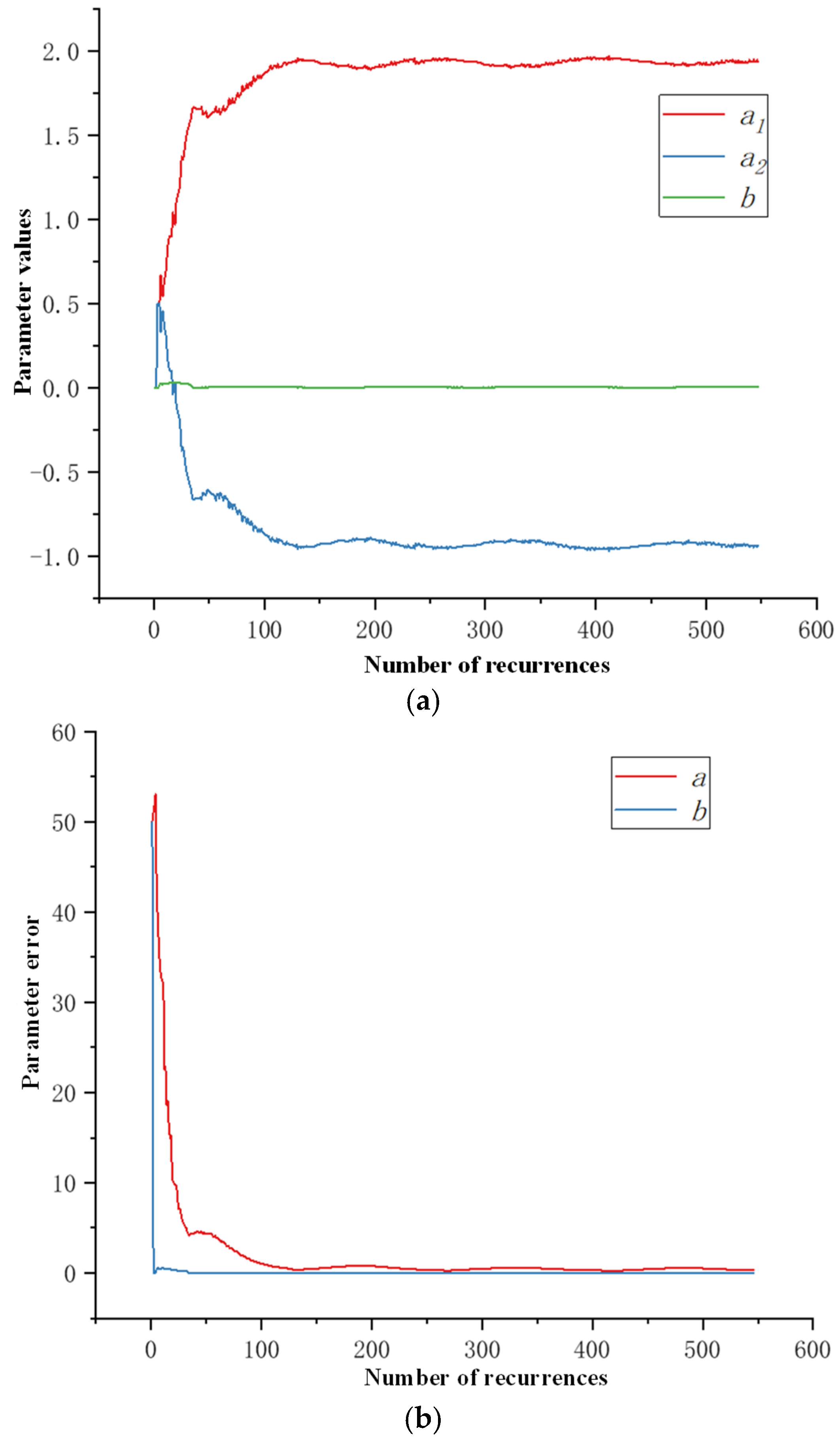
3.3. Parameter Identification of Responsive Ship Motion Model
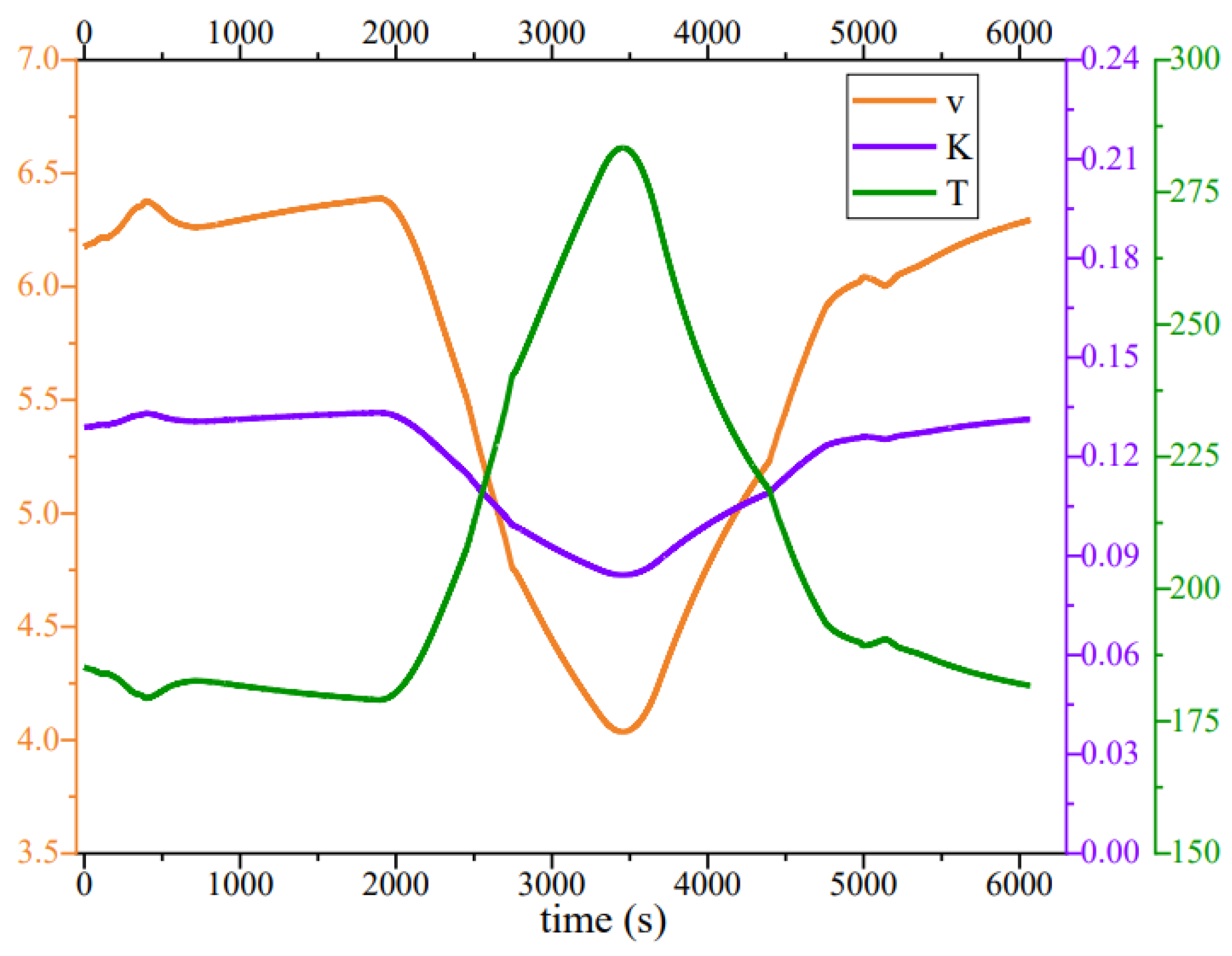
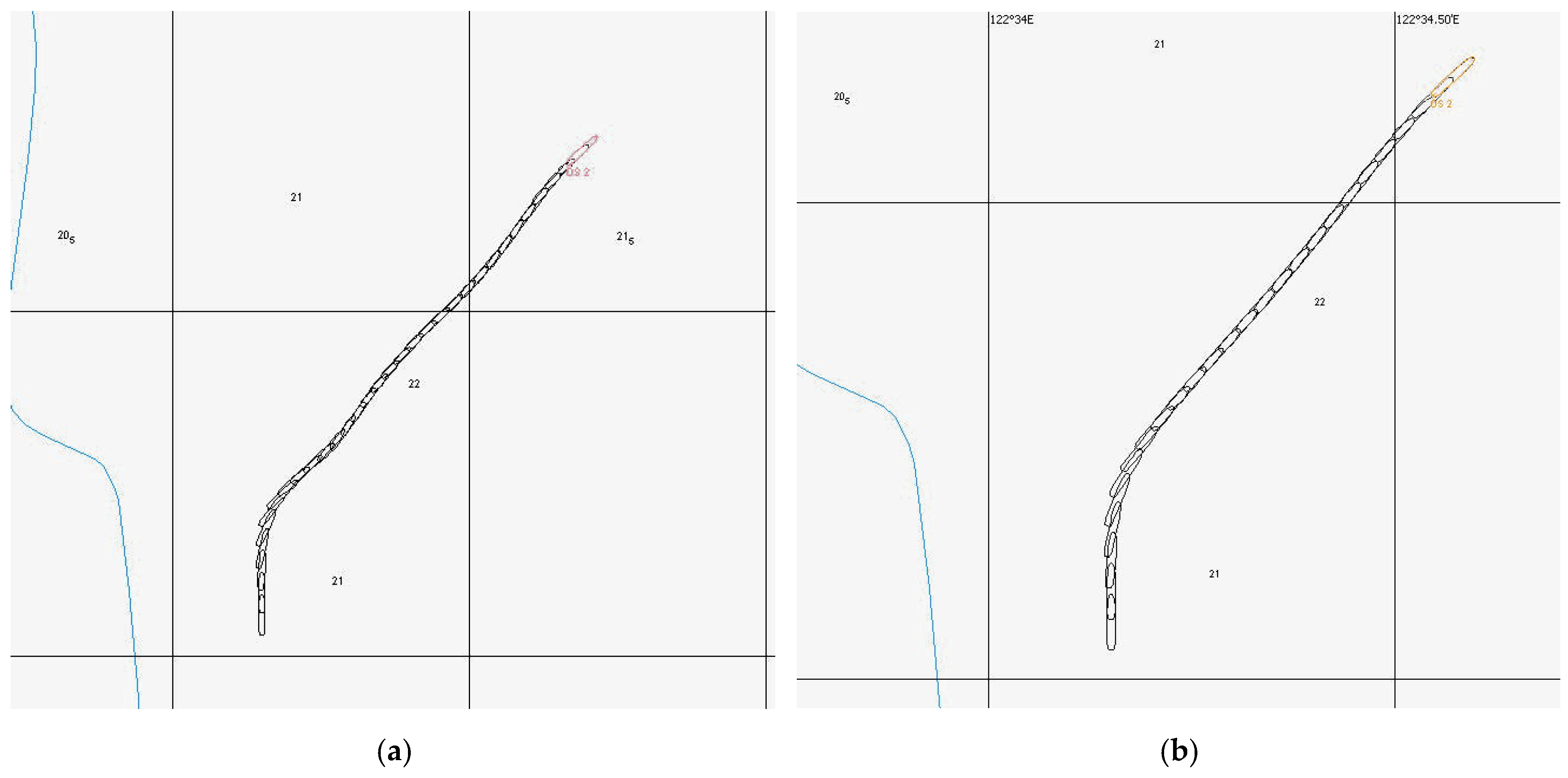
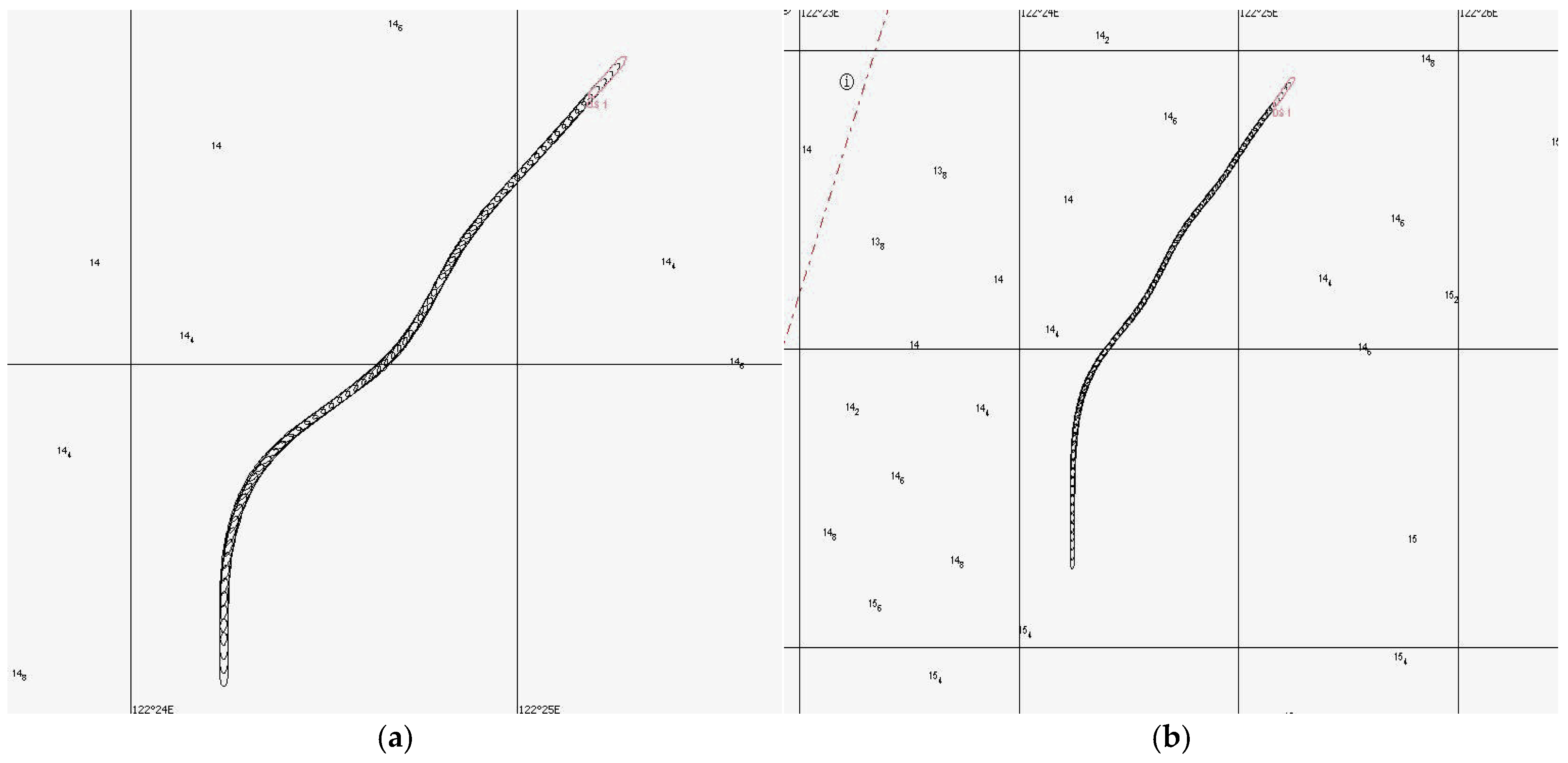
3.4. Analysis of Identification Algorithm Based on Ship Maneuvering Simulator
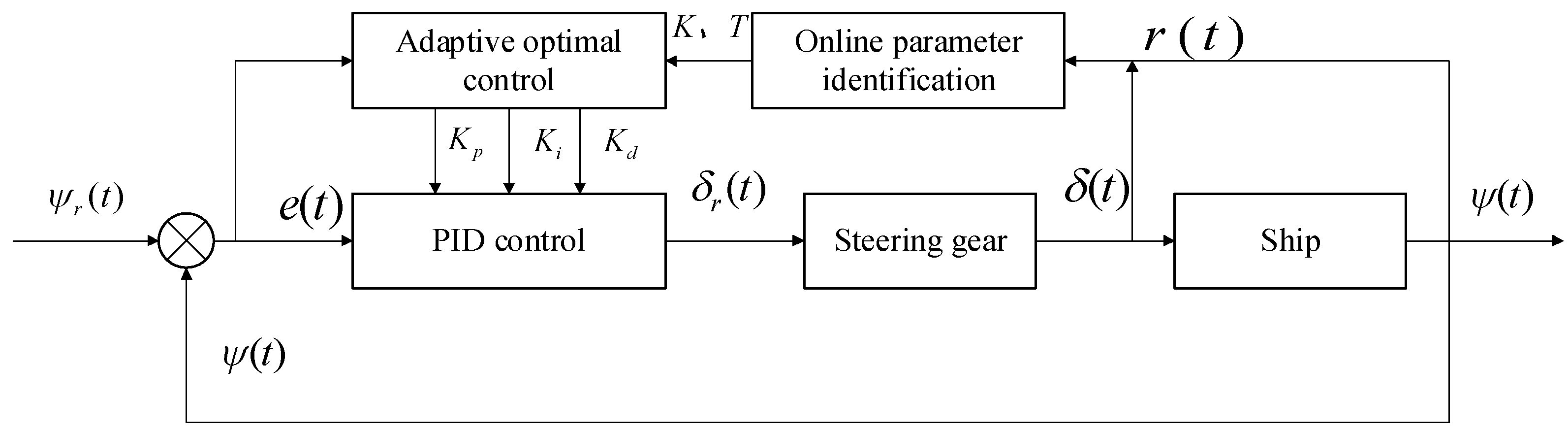
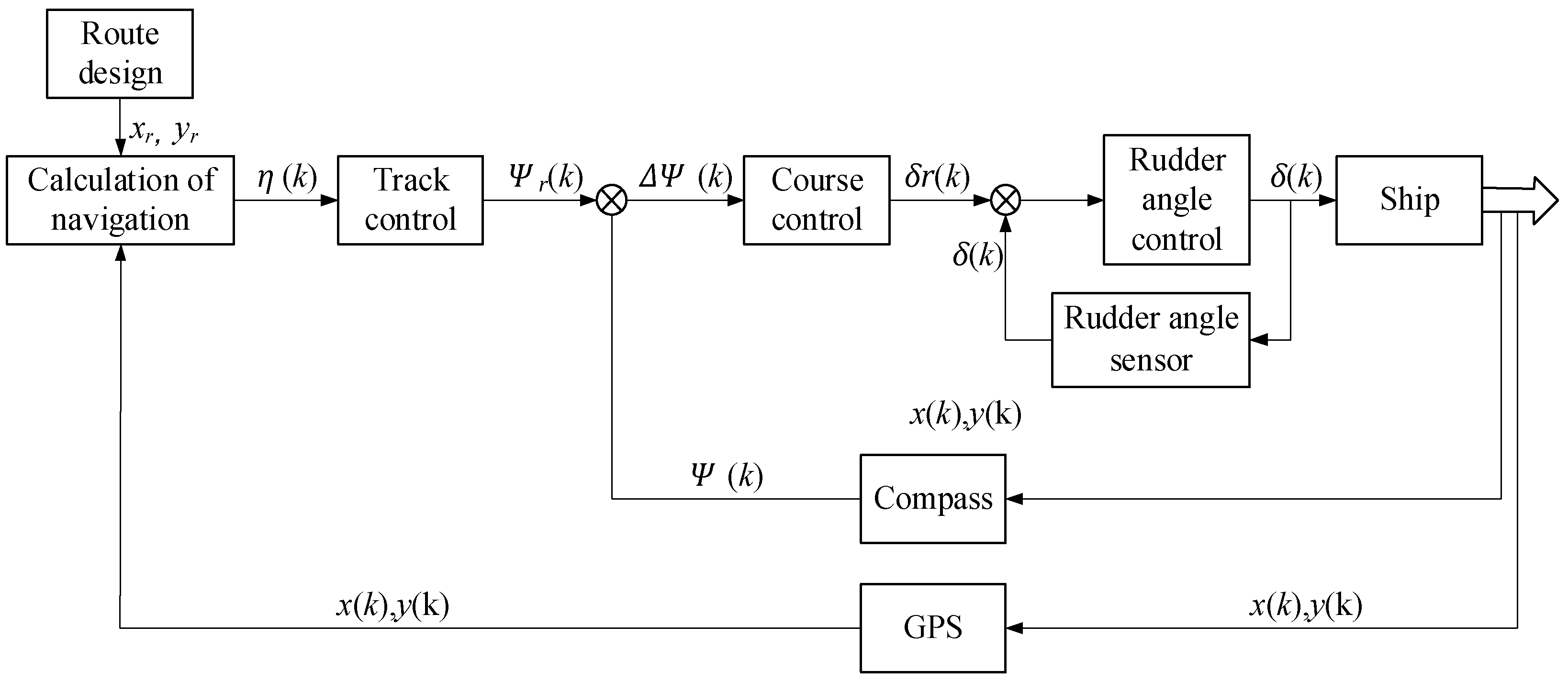
4. Ship Course and Track Control Method
4.1. PID Course Control Method Based on Optimal Control Theory
4.2. Adaptive OP-PID Course Control Method
4.3. Track Control Method
5. Simulation Experiments and Analysis
5.1. Course Control Simulation
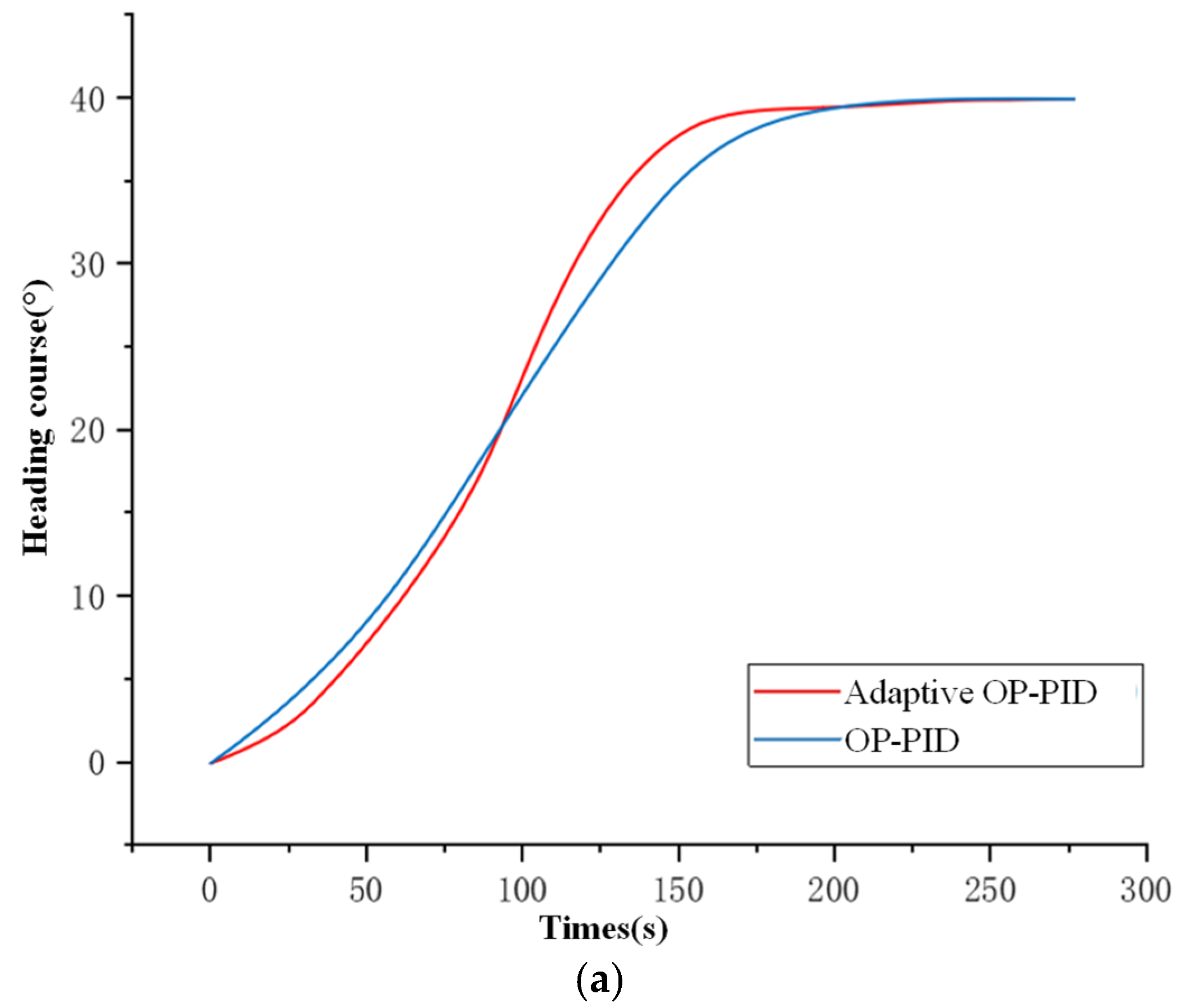
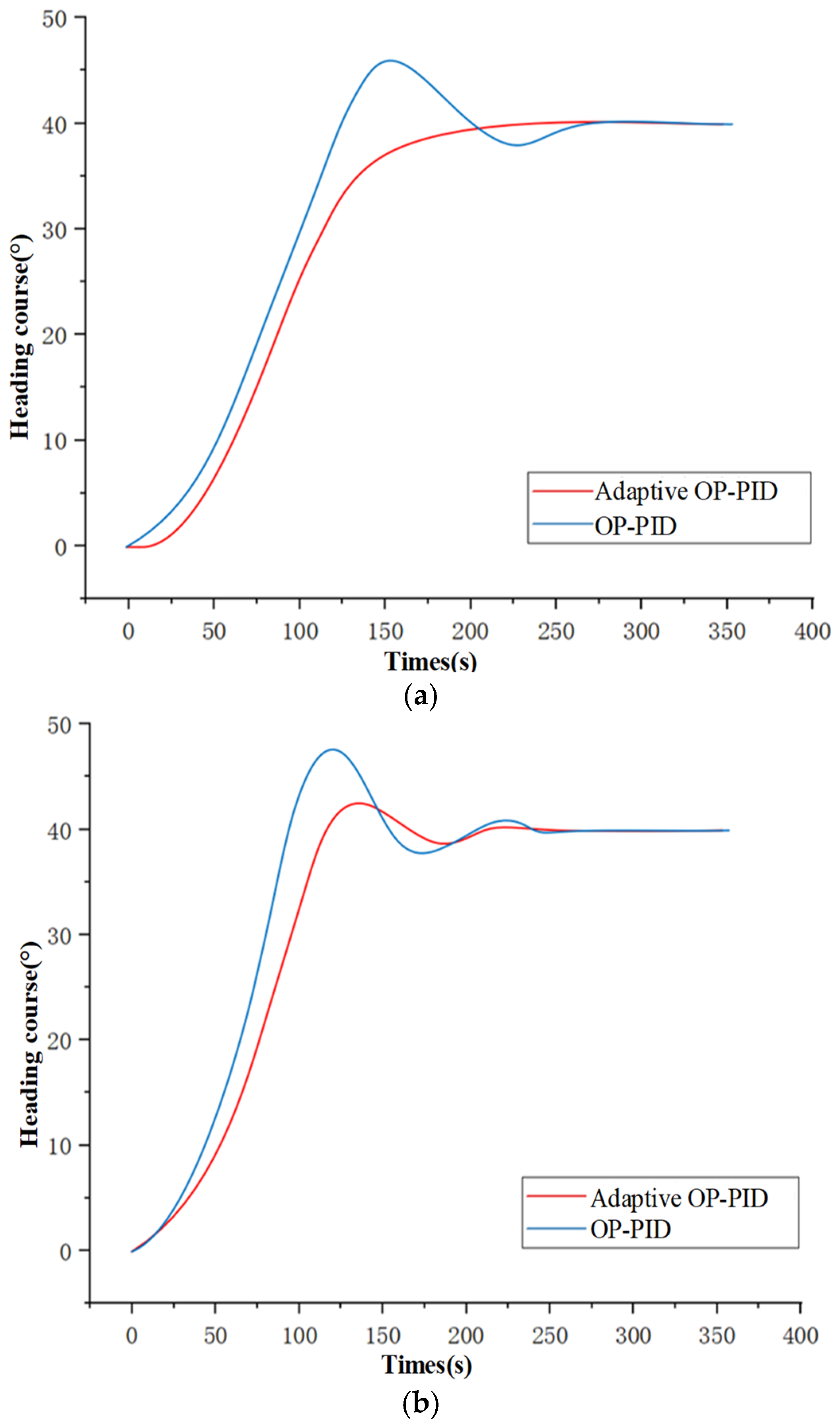
5.1.1. Simulation of Course Control in Still Water
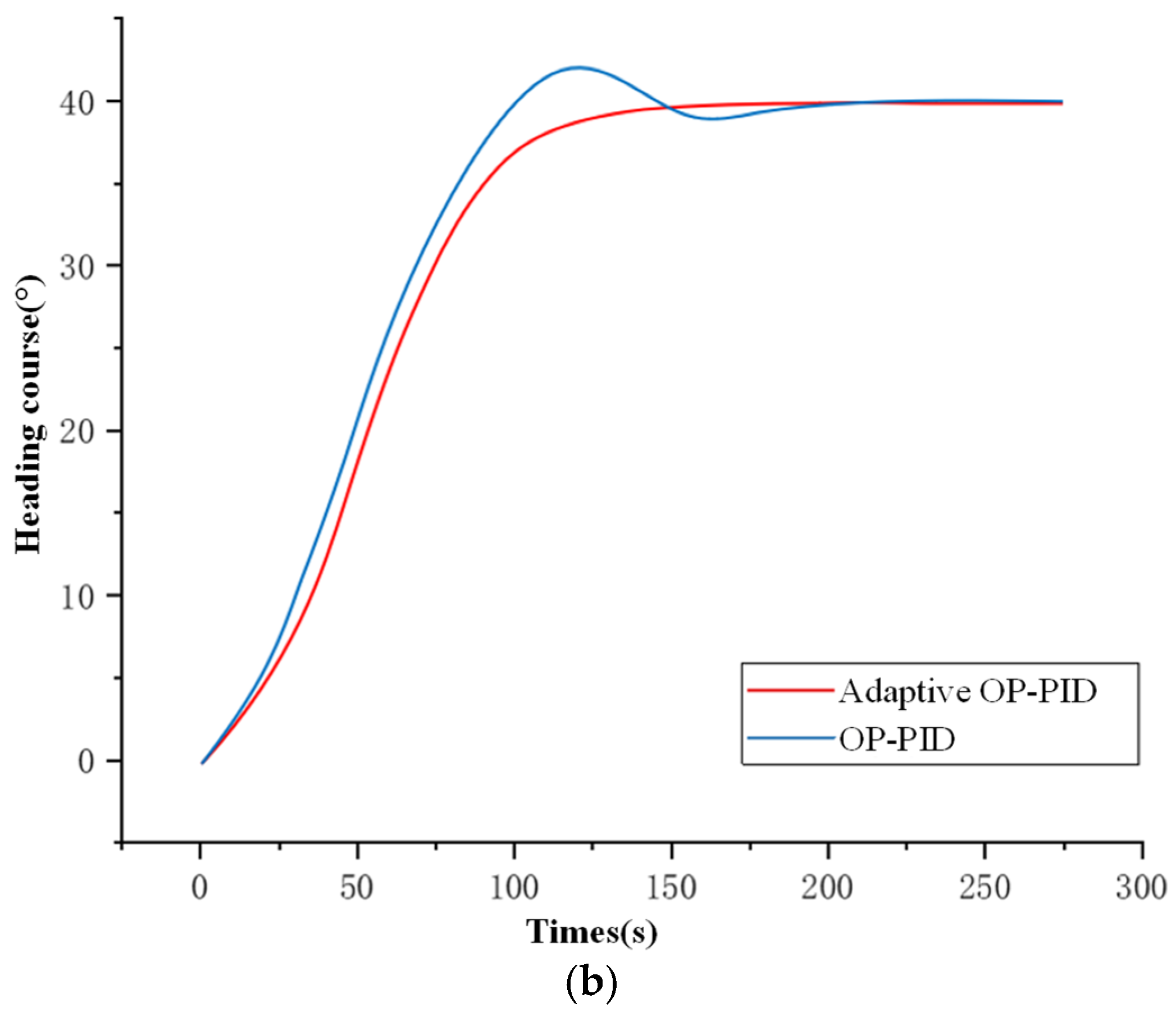
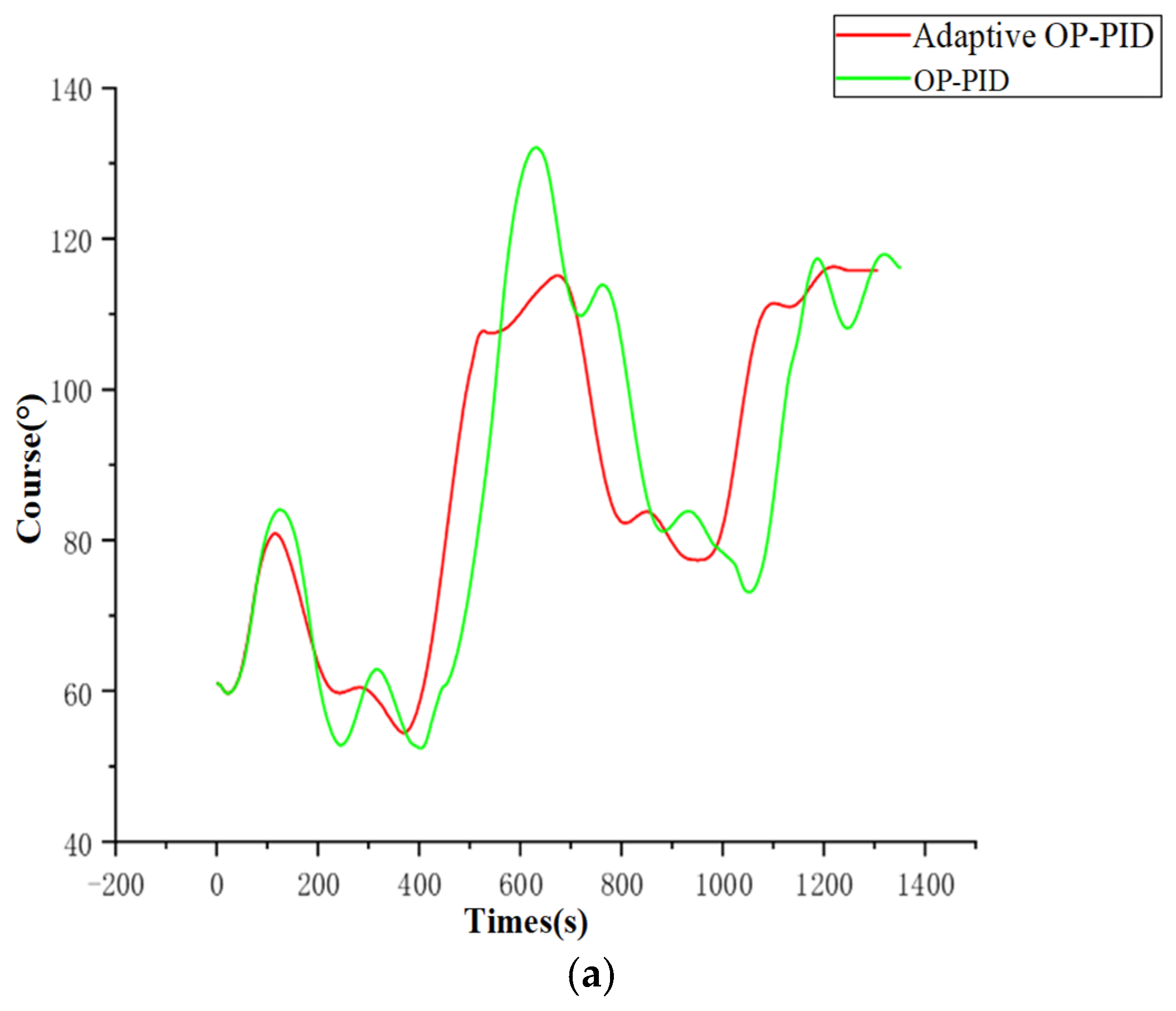
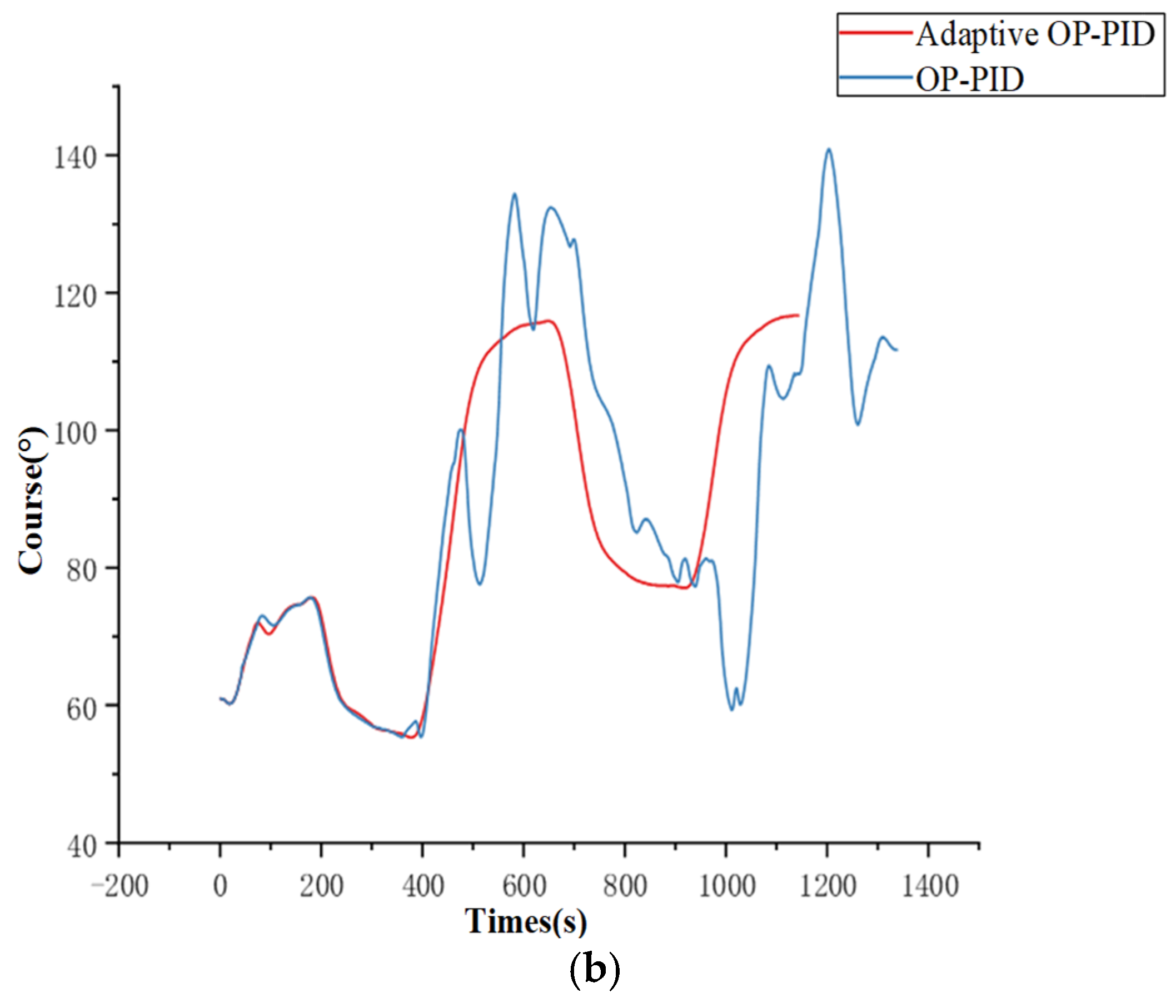
5.1.2. Simulation of Course Control Under Disturbance
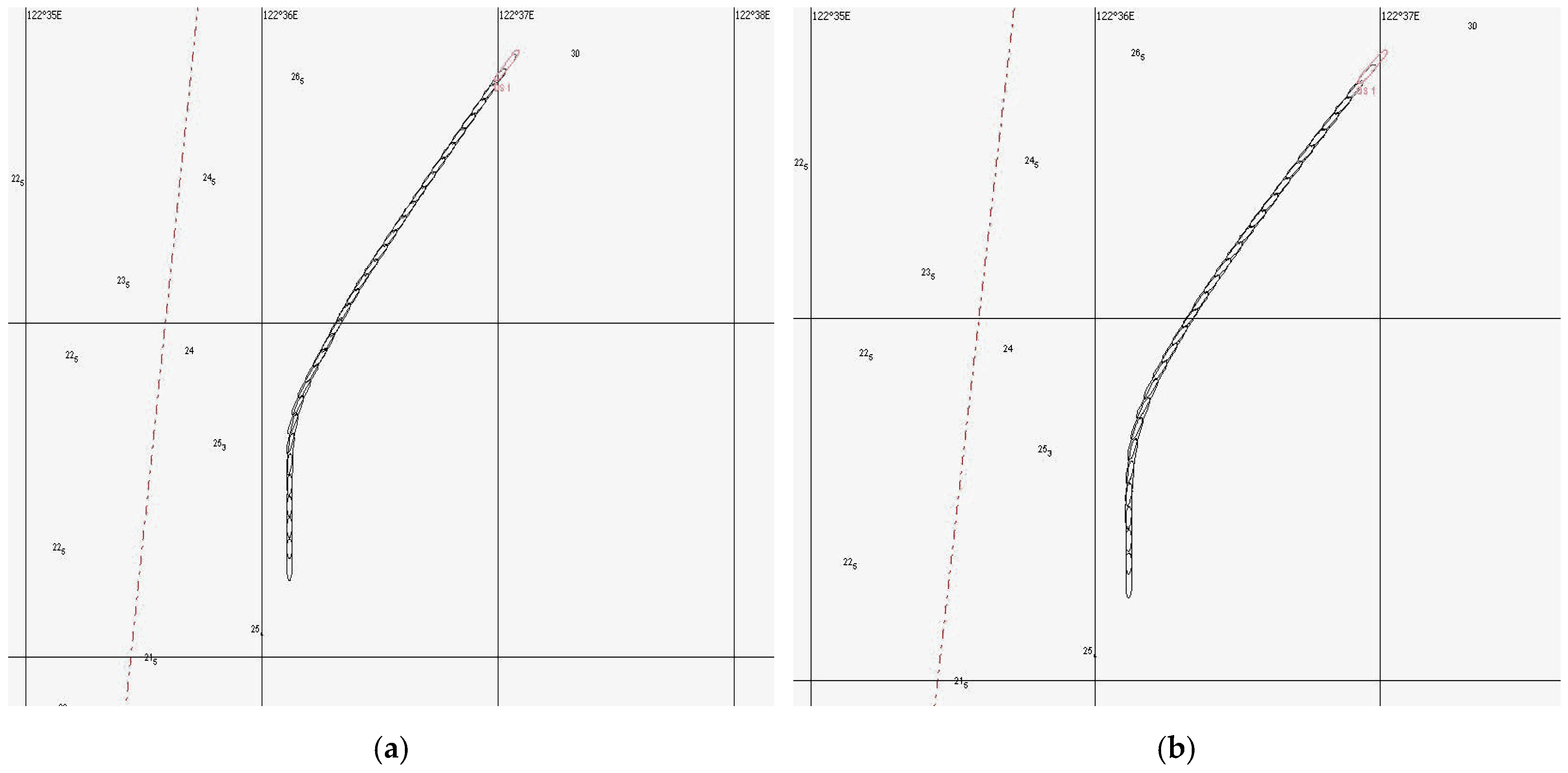
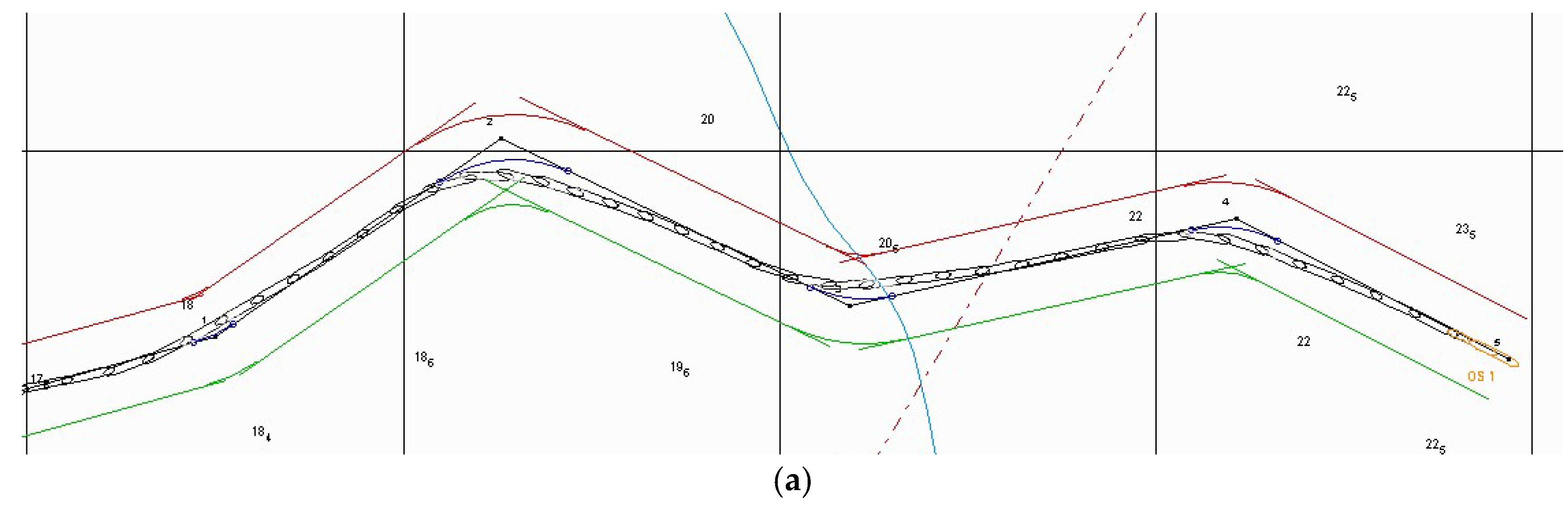
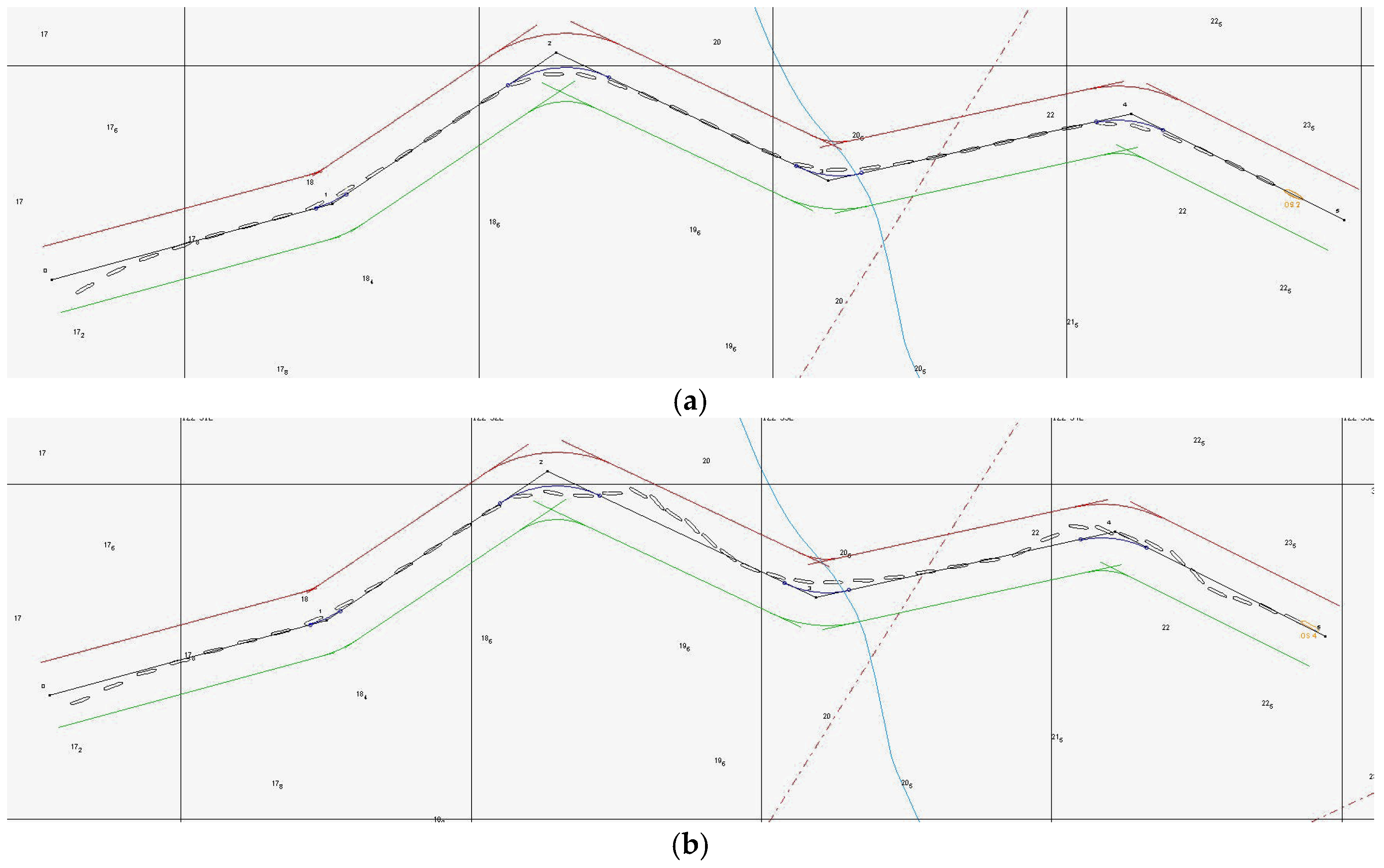
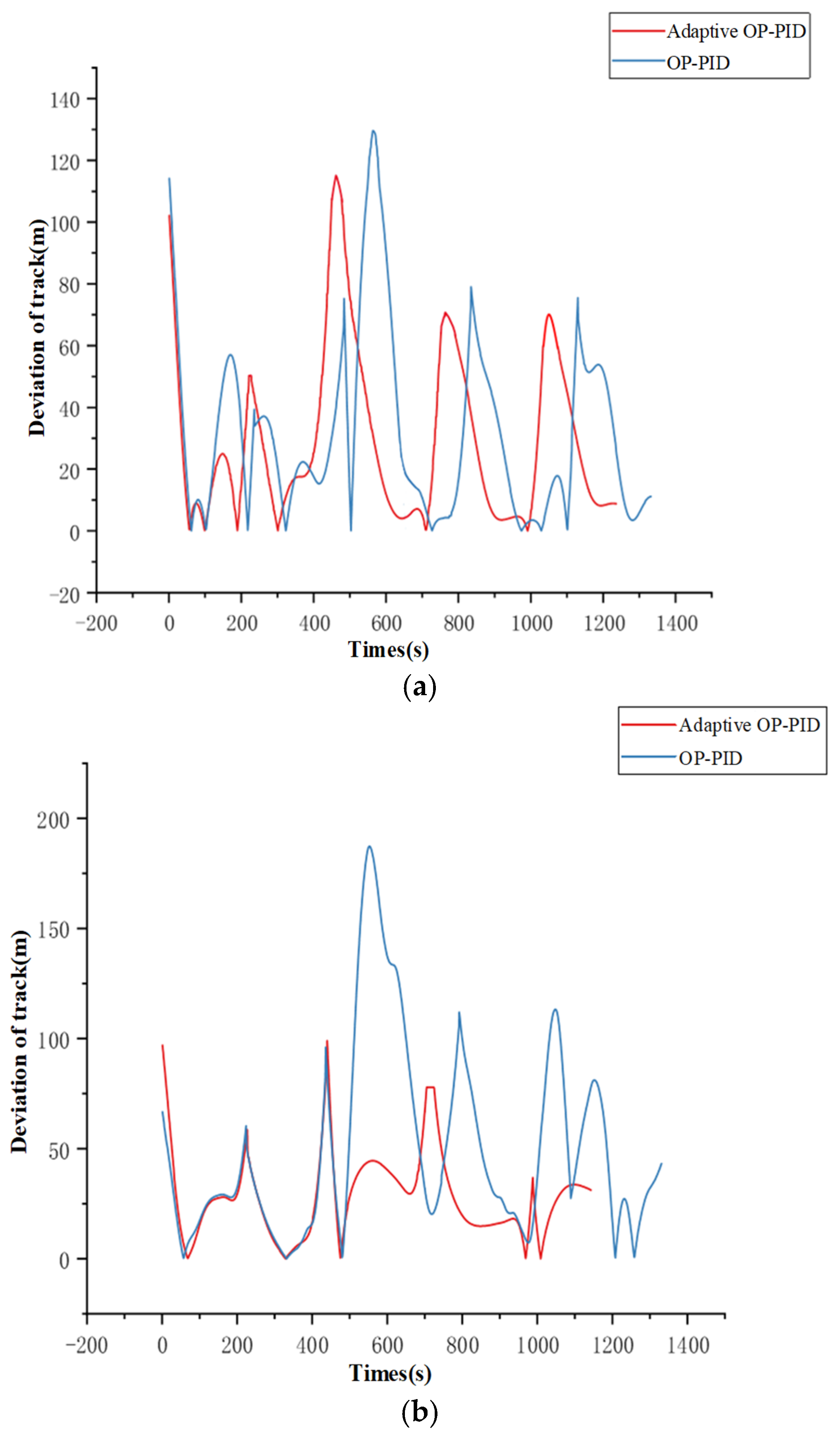
5.2. Track Control Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seung, J.L.; Kwang, H.J.; Namkug, K.; Jaeyong, L. A comparison of regression models for the ice loads measured during the ice tank test. Brodogradnja. 2023, 74, 1–15. [Google Scholar] [CrossRef]
- Mustafayev, V.O.; Mammadov, E.D. Diving vessel speed determination during towing tests. Int. J. Tech. Phys. Probl. Eng. 2024, 16, 333–336. [Google Scholar] [CrossRef]
- Atasayan, E.; Milanov, E.; Dursun, A.A. Application of an offline grey box method for predicting the maneuvering performance. Brodogradnja. 2024, 75, 75304. [Google Scholar] [CrossRef]
- Allotta, B.; Costanzi, R.; Pugi, L.; Ridolfi, A. Identification of the main hydrodynamic parameters of Typhoon AUV from a reduced experimental dataset. Ocean. Eng. 2018, 147, 77–88. [Google Scholar] [CrossRef]
- Yin, Q.; Cai, J.; Gong, X.; Ding, Q. Local parameter identification with neural ordinary differential equations. Appl. Math. Mech. 2022, 43, 1887–1900. [Google Scholar] [CrossRef]
- Luigi, B.; Felice, I.; Ewa, B.W. Weighted least squares collocation methods. Appl. Numer. Math. 2024, 203, 113–128. [Google Scholar] [CrossRef]
- Sabet, M.T.; Fathi, A.R.; Mohammadi, H.R. Optimal design of the Own Ship maneuver in the bearing-only target motion analysis problem using a heuristically supervised Extended Kal-man Filter. Ocean Eng. 2016, 123, 146–153. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Bodson, M.; Athans, M. Real time estimation of ship motions using Kalman filtering techniques. IEEE J. Ocean Eng. 2003, 8, 9–20. [Google Scholar] [CrossRef]
- Cosmo, L.; Minello, G.; Bicciato, A.; Bronstein, M.; Rodola, E.; Rossi, L.; Torsello, A. Graph Kernel Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Esra, Y.; Taskin, K. Deep convolutional neural networks for ship detection using refined DOTA and TGRS-HRRSD high-resolution image datasets. Adv. Space Res. 2024, in press. [Google Scholar] [CrossRef]
- Gao, H.; Zou, Z.; Xia, L. Application of the NIPC-based uncertainty quantification in prediction of ship maneuverability. J. Mar. Sci. Technol. 2021, 26, 555–572. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, N.; Song, J.; Hao, L.; Liu, S.; Han, B.; Qu, K. Math-data integrated prediction model for ship maneuvering motion. Ocean Eng. 2023, 285, 115255. [Google Scholar] [CrossRef]
- Ning, W.; Hui, W.; Yu, Z.; Jia, S.; Ye, L.; Li, H. Self-organizing data-driven prediction model of ship maneuvering fast-dynamics. Ocean Eng. 2023, 288, 115989. [Google Scholar] [CrossRef]
- Wang, N.; Kong, X.; Ren, B.; Hao, L.; Han, B. SeaBil: Self-attention-weighted ultrashort-term deep learning prediction of ship maneuvering motion. Ocean Eng. 2023, 287, 115890. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Willy & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Buerger, J.; Cannon, M. A Constraint Homotopy Active Set Solver for Linear–Quadratic Optimal Control. IEEE Trans. Autom. Control 2024, 69, 7205–7210. [Google Scholar] [CrossRef]
- Liu, J.; Huang, L.; Yu, D.; Xu, L.; He, Y. The control method for ship tracking when navigating through narrow and curved sections. Appl. Ocean Res. 2024, 145, 103943. [Google Scholar] [CrossRef]
- McCue, L. Handbook of Marine Craft Hydrodynamics and Motion Control. IEEE Control Syst. Mag. 2016, 36, 78–79. [Google Scholar] [CrossRef]
- Cao, B. Study on Ship Motion Control Simulation System Based on Model Parameter Identification. Ph.d. Thesis, Ji Lin University, Changchun, China, 2012. [Google Scholar]
- He, Y.; Zhao, X.; Huang, L.; Xu, L.; Liu, J. Control method for the ship track and speed in curved channels. Brodogradnja 2024, 75, 1–27. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, C.; Zheng, C. Design of improved line-of-sight guidance law based on aircraft visual information. Syst. Eng. Electron. 2024, 46, 2779–2788. [Google Scholar]
- Yu, C.; Zhu, J.; Hu, Y.; Zhu, H.; Wang, N.; Guo, H.; Zhang, Q.; Liu, S. Prescribed-time observer-based sideslip compensation in USV line-of-sight guidance. Ocean Eng. 2024, 298, 117177. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Displacement (t) | 69,580 |
| Length (m) | 230 |
| Breadth (m) | 32 |
| Bow draft (m) | 12 |
| Stern draft (m) | 12 |
| Height of eye (m) | 22 |
| Value of the Forgetting Factor | The Error Value of a | The Error Value of a |
|---|---|---|
| 0.99 | 0.117843 | 0.004218 |
| 0.98 | 0.303138 | 0.015827 |
| Parameter | True Value | Equation (8) | FFRLS |
|---|---|---|---|
| K | 0.13 | 0.18 | 0.157 |
| T | 180 | 198 | 192 |
| Wind Speed (m/s) | [0,5] | (5,10] | (10,14] | (14,17] | (17,20] | (20,30] | (30,+∞) |
|---|---|---|---|---|---|---|---|
| m | 0.1 | 4.0 | 8.0 | 8.5 | 9.0 | 9.5 | 10.0 |
| Parameter | Ship Type I | Ship Type II |
|---|---|---|
| Displacement (t) | 69,580 | 8682 |
| Length (m) | 230 | 110 |
| Breadth (m) | 32 | 16.1 |
| Bow draft (m) | 12 | 6.4 |
| Stern draft (m) | 12 | 7.1 |
| Height of eye (m) | 22 | 12 |
| Way Point | Latitude | Longitude | Course | Distance/nm |
|---|---|---|---|---|
| 0 | 30° 08.360 N | 122° 30.540 E | / | / |
| 1 | 30° 08.583 N | 122° 31.500 E | 075 | 0.859 |
| 2 | 30° 09.026 N | 122° 32.260 E | 056 | 0.793 |
| 3 | 30° 08.652 N | 122° 33.186 E | 115 | 0.884 |
| 4 | 30° 08.846 N | 122° 34.216 E | 077 | 0.911 |
| 5 | 30° 08.532 N | 122° 34.938 E | 116 | 0.699 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chang, L.; Xu, L.; He, F.; He, Y. Research on the On-Line Identification of Ship Maneuvering Motion Model Parameters and Adaptive Control. J. Mar. Sci. Eng. 2025, 13, 753. https://doi.org/10.3390/jmse13040753
Liu J, Chang L, Xu L, He F, He Y. Research on the On-Line Identification of Ship Maneuvering Motion Model Parameters and Adaptive Control. Journal of Marine Science and Engineering. 2025; 13(4):753. https://doi.org/10.3390/jmse13040753
Chicago/Turabian StyleLiu, Jinlai, Lubin Chang, Luping Xu, Fang He, and Yixiong He. 2025. "Research on the On-Line Identification of Ship Maneuvering Motion Model Parameters and Adaptive Control" Journal of Marine Science and Engineering 13, no. 4: 753. https://doi.org/10.3390/jmse13040753
APA StyleLiu, J., Chang, L., Xu, L., He, F., & He, Y. (2025). Research on the On-Line Identification of Ship Maneuvering Motion Model Parameters and Adaptive Control. Journal of Marine Science and Engineering, 13(4), 753. https://doi.org/10.3390/jmse13040753






