Security Authentication Protocol for Underwater Sensor Networks Based on NTRU
Abstract
1. Introduction
1.1. Related Work
1.2. Motivation and Contribution
2. Models and Methods
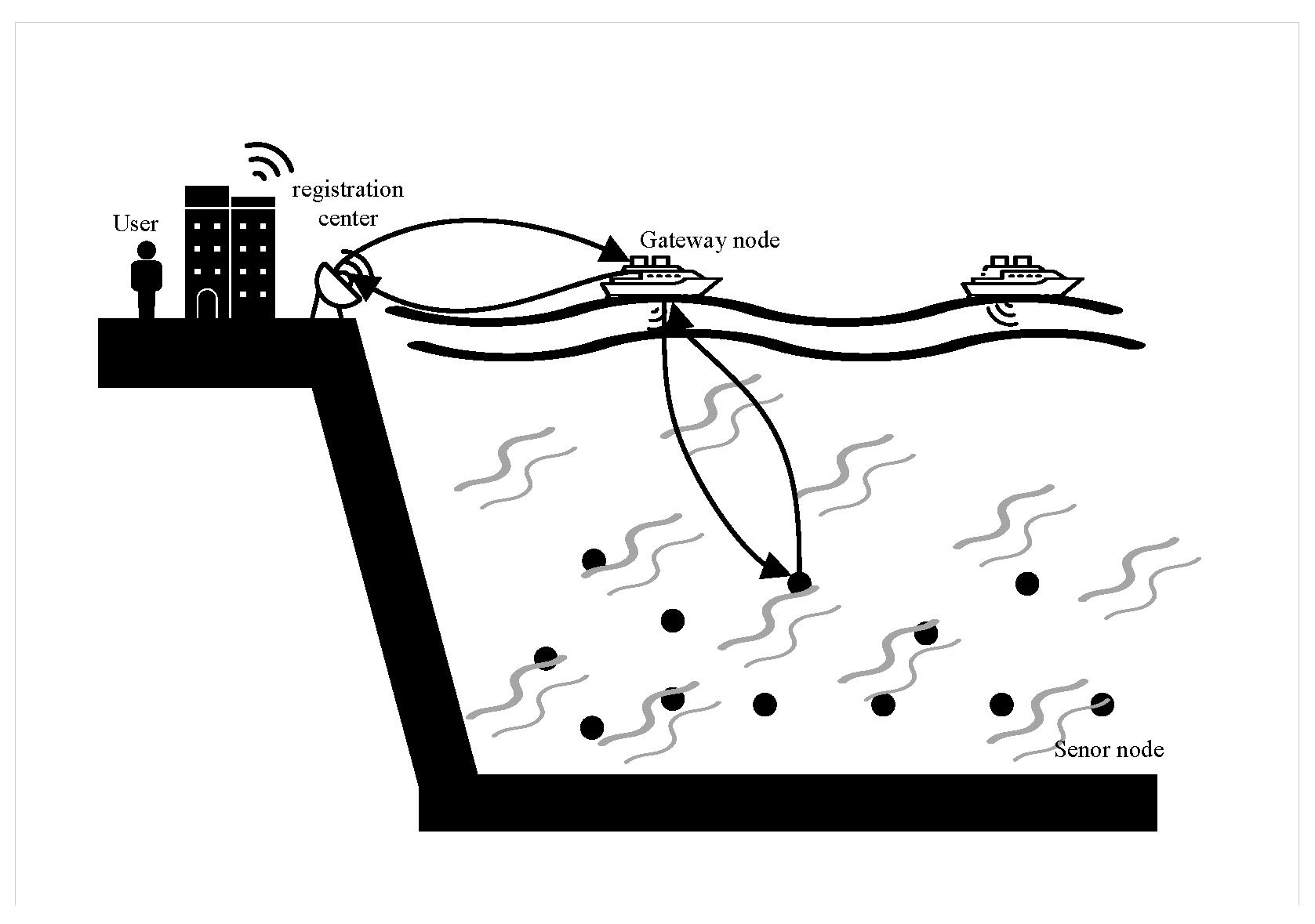
2.1. Underwater Wireless Sensor Networks Model
2.2. Encapsulated Encryption Algorithm
2.3. Node Mobility Model
3. The Proposed Authentication Scheme
3.1. Initialization Phase
3.2. Node Registration Phase
3.2.1. Gateway and Sensor Node Registration
3.2.2. User Node Registration
3.3. Login and Authentication Phase
3.4. Password Update Phase
4. Safety Analysis
4.1. Random Oracle Model Analysis
4.2. Informal Security Analysis
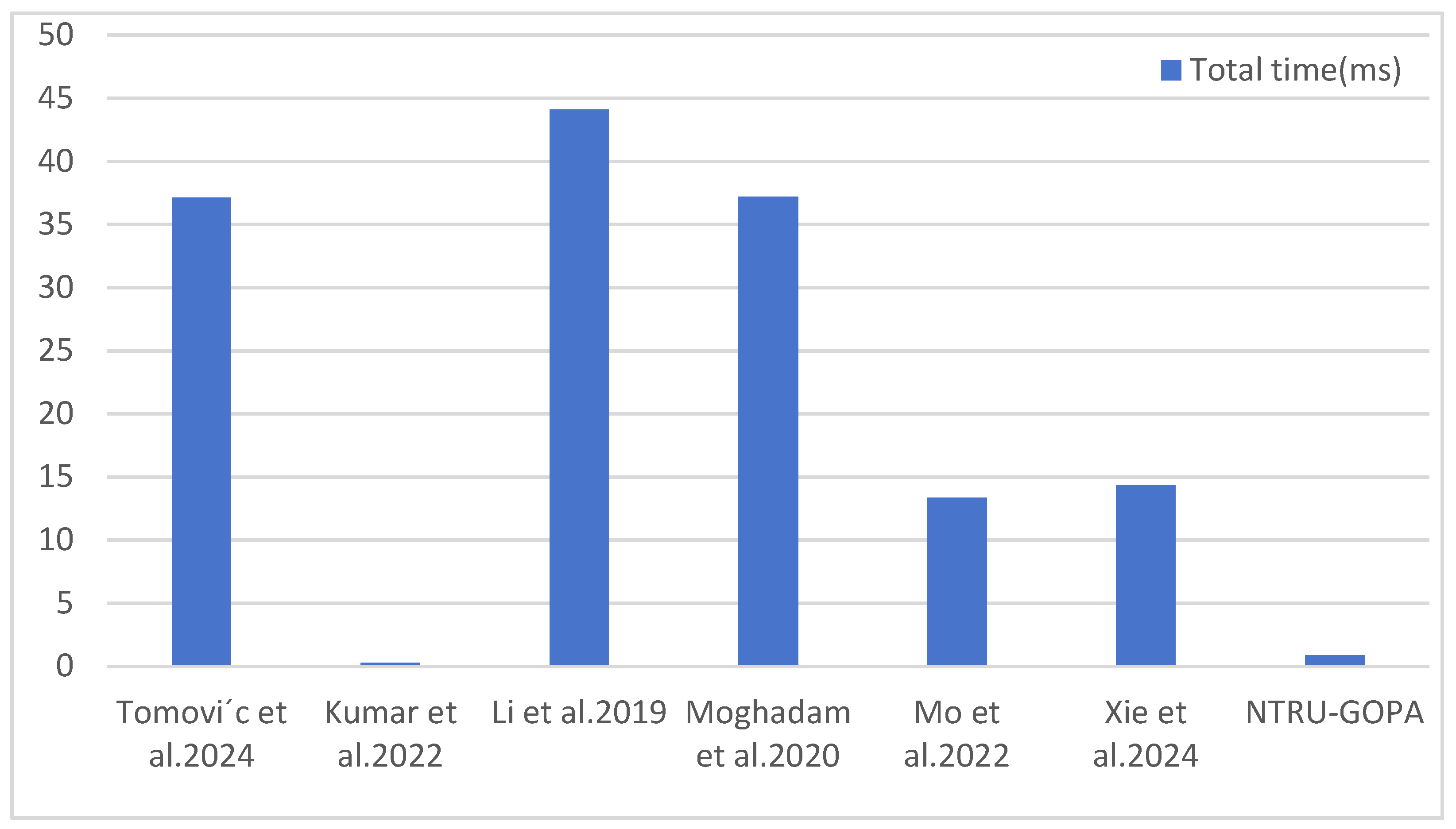
5. Performance Analysis
5.1. Storage Overhead
5.2. Communication Overhead
5.3. Computational Overhead
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, S. On reliable data transfer in underwater acoustic networks: A survey from networking perspective. IEEE Commun. Surv. Tutor. 2018, 20, 1036–1055. [Google Scholar]
- Hamilton, A.; Barnett, J.; Hobbs, A.M.; Pelekanakis, K.; Petroccia, R.; Nissen, I.; Galsdorf, D. Towards secure and interoperable underwater acoustic communications: Current activities in NATO IST-174 research task group. Procedia Comput. Sci. 2022, 205, 167–178. [Google Scholar]
- Gupta, S.; Singh, N.P. Underwater wireless sensor networks: A review of routing protocols, taxonomy, and future directions. J. Supercomput. 2024, 80, 5163–5196. [Google Scholar] [CrossRef]
- Liu, L.; Xi, Z.; Wu, J. Strengthening the achilles’ heel: An AUV-aided message ferry approach against dissemination vulnerability in UASNs. IEEE Internet Things J. 2021, 8, 14948–14958. [Google Scholar]
- Yang, G.; Dai, L.; Si, G.; Wang, S.; Wang, S. Challenges and security issues in underwater wireless sensor networks. Procedia Comput. Sci. 2019, 147, 210–216. [Google Scholar]
- Sliwa, J.; Wrona, K.; Shabanska, T.; Solmaz, A. Lightweight quantum-safe cryptography in underwater scenarios. In Proceedings of the 2023 IEEE 48th Conference on Local Computer Networks (LCN), Daytona Beach, FL, USA, 2–5 October 2023; pp. 1–6. [Google Scholar]
- Tomović, S.; Krivokapić, B.; Nađ, Đ.; Radusinović, I. BEKMP: A blockchain-enabled key management protocol for underwater acoustic sensor networks. IEEE Access 2024, 12, 74108–74125. [Google Scholar]
- Zhou, X.; Wang, S.; Wen, K.; Hu, B.; Tan, X.; Xie, Q. Security-enhanced lightweight and anonymity-preserving user authentication scheme for IoT-based healthcare. IEEE Internet Things J. 2023, 11, 9599–9609. [Google Scholar]
- Kumar, C.M.; Amin, R.; Brindha, M. SafeCom: Robust mutual authentication and session key sharing protocol for underwater wireless sensor networks. J. Syst. Archit. 2022, 130, 102650. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.; Zhong, H.; Cui, J.; Li, J.; He, D. Device-Side Lightweight Mutual Authentication and Key Agreement Scheme based on Chameleon Hashing for Industrial Internet of Things. IEEE Trans. Inf. Forensics Secur. 2024, 19, 7895–7907. [Google Scholar]
- Almuhaideb, A.M.; Al-Khulaifi, D.M. An Efficient Authentication and Key Agreement Scheme for the Internet of Underwater Things (IoUT) Environment. IEEE Access 2024, 12, 175773–175789. [Google Scholar]
- Sadhukhan, D.; Ray, S.; Biswas, G.; Khan, M.K.; Dasgupta, M. A lightweight remote user authentication scheme for IoT communication using elliptic curve cryptography. J. Supercomput. 2021, 77, 1114–1151. [Google Scholar]
- Li, X.; Peng, J.; Obaidat, M.S.; Wu, F.; Khan, M.K.; Chen, C. A secure three-factor user authentication protocol with forward secrecy for wireless medical sensor network systems. IEEE Syst. J. 2019, 14, 39–50. [Google Scholar]
- Moghadam, M.F.; Nikooghadam, M.; Al Jabban, M.A.B.; Alishahi, M.; Mortazavi, L.; Mohajerzadeh, A. An efficient authentication and key agreement scheme based on ECDH for wireless sensor network. IEEE Access 2020, 8, 73182–73192. [Google Scholar] [CrossRef]
- Alotaibi, M. An enhanced symmetric cryptosystem and biometric-based anonymous user authentication and session key establishment scheme for WSN. IEEE Access 2018, 6, 70072–70087. [Google Scholar] [CrossRef]
- Zou, S.; Cao, Q.; Wang, C.; Huang, Z.; Xu, G. A robust two-factor user authentication scheme-based ECC for smart home in IoT. IEEE Syst. J. 2021, 16, 4938–4949. [Google Scholar] [CrossRef]
- Zhang, S.; Du, X.; Liu, X. A secure remote mutual authentication scheme based on chaotic map for underwater acoustic networks. IEEE Access 2020, 8, 48285–48298. [Google Scholar]
- Mo, J.; Hu, Z.; Shen, W. A provably secure three-factor authentication protocol based on chebyshev chaotic mapping for wireless sensor network. IEEE Access 2022, 10, 12137–12152. [Google Scholar]
- Long, Y.; Peng, C.; Tan, W.; Chen, Y. Blockchain-based anonymous authentication and key management for internet of things with Chebyshev chaotic maps. IEEE Trans. Ind. Inform. 2024, 20, 7883–7893. [Google Scholar] [CrossRef]
- Xie, Q.; Yao, Y. PUF and Chaotic Map-Based Authentication Protocol for Underwater Acoustic Networks. Appl. Sci. 2024, 14, 5400. [Google Scholar] [CrossRef]
- Abdi Nasib Far, H.; Bayat, M.; Kumar Das, A.; Fotouhi, M.; Pournaghi, S.M.; Doostari, M.A. LAPTAS: Lightweight anonymous privacy-preserving three-factor authentication scheme for WSN-based IIoT. Wirel. Netw. 2021, 27, 1389–1412. [Google Scholar]
- Deebak, B.D.; Memon, F.H.; Dev, K.; Khowaja, S.A.; Wang, W.; Qureshi, N.M.F. TAB-SAPP: A trust-aware blockchain-based seamless authentication for massive IoT-enabled industrial applications. IEEE Trans. Ind. Inform. 2022, 19, 243–250. [Google Scholar] [CrossRef]
- Heshmati, A.; Bayat, M.; Doostari, M.; Pournaghi, S.M. Blockchain based authentication and access verfication scheme in smart home. J. Ambient Intell. Humaniz. Comput. 2023, 14, 2525–2547. [Google Scholar] [CrossRef]
- Feng, Q.; He, D.; Zeadally, S.; Kumar, N.; Liang, K. Ideal lattice-based anonymous authentication protocol for mobile devices. IEEE Syst. J. 2018, 13, 2775–2785. [Google Scholar] [CrossRef]
- Dabra, V.; Bala, A.; Kumari, S. LBA-PAKE: Lattice-based anonymous password authenticated key exchange for mobile devices. IEEE Syst. J. 2020, 15, 5067–5077. [Google Scholar] [CrossRef]
- Ding, R.; Cheng, C.; Qin, Y. Further analysis and improvements of a lattice-based anonymous PAKE scheme. IEEE Syst. J. 2022, 16, 5035–5043. [Google Scholar] [CrossRef]
- Kumar, U.; Garg, M.; Kumari, S.; Dharminder, D. A construction of post quantum secure and signal leakage resistant authenticated key agreement protocol for mobile communication. Trans. Emerg. Telecommun. Technol. 2023, 34, e4660. [Google Scholar] [CrossRef]
- Ruiqi, L.; Chunfu, J.; Yafei, W. Multi-key homomorphic proxy re-encryption scheme based on NTRU and its application. J. Commun. Xuebao 2021, 42. [Google Scholar]
- Zhang, W.; Han, G.; Wang, X.; Guizani, M.; Fan, K.; Shu, L. A node location algorithm based on node movement prediction in underwater acoustic sensor networks. IEEE Trans. Veh. Technol. 2020, 69, 3166–3178. [Google Scholar] [CrossRef]
- Howgrave-Graham, N.; Silverman, J.H.; Whyte, W. Choosing parameter sets for NTRUEncrypt with NAEP and SVES-3. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 14–18 February 2005; pp. 118–135. [Google Scholar]
- Kim, J.; Park, J.H. NTRU+: Compact construction of NTRU using simple encoding method. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4760–4774. [Google Scholar] [CrossRef]
- Duman, J.; Hövelmanns, K.; Kiltz, E.; Lyubashevsky, V.; Seiler, G.; Unruh, D. A thorough treatment of highly-efficient NTRU instantiations. In Proceedings of the IACR International Conference on Public-Key Cryptography, Atlanta, GA, USA, 7–10 May 2023; pp. 65–94. [Google Scholar]
- Zhang, S.; Du, X.; Liu, X. A novel and quantum-resistant handover authentication protocol in IoT environment. Wirel. Netw. 2023, 29, 2873–2890. [Google Scholar] [CrossRef]
- Liu, Z.; Seo, H.; Großschädl, J.; Kim, H. Efficient implementation of NIST-compliant elliptic curve cryptography for 8-bit AVR-based sensor nodes. IEEE Trans. Inf. Forensics Secur. 2015, 11, 1385–1397. [Google Scholar] [CrossRef]
- Yang, J.; Li, F.; Zhang, Z. Research on ntru-based anonymous authentication and key negotiation protocol for vanets. In Proceedings of the 2022 7th International Conference on Cyber Security and Information Engineering (ICCSIE), Beijing, China, 21–23 October 2022; pp. 104–108. [Google Scholar]
- Zhou, Y.; Wang, L. A lattice-based authentication scheme for roaming service in ubiquitous networks with anonymity. Secur. Commun. Netw. 2020, 2020, 2637916. [Google Scholar]
| Notation | Description |
|---|---|
| Identity and password of user | |
| Set of polynomials i over ring | |
| Random polynomials selected from | |
| Identity and pseudo-identity of the jth gateway node | |
| Identity and pseudo-identity of the ith sensor node | |
| Public/private key of the jth gateway node | |
| Public/private key of the ith sensor node | |
| Public/private key of smart card | |
| Session key between i and j | |
| Random number generated by user | |
| Random number generated by gateway node | |
| Random number generated by smart card and sensor node, respectively | |
| Message X encrypted with public key K | |
| Key encapsulation/decapsulation | |
| ‖ | Concatenate operation |
| ⊕ | XOR operation |
| One-way hash function | |
| Timestamp | |
| The allowable maximum transmission time interval | |
| The initial and current location | |
| The allowable maximum displacement |
| User | Gateway Node |
|---|---|
| Select , | |
| Select random number , | |
| Compute , | |
| Send | |
| Select random number | |
| Compute , | |
| add in Smart Card | |
| Send Smart Card | |
| Compute , , | |
| add in Smart Card |
| User | Gateway Node | Sesnor Node |
|---|---|---|
| Insert SC and input , | ||
| Compute | ||
| Check whether | ||
| Compute | ||
| SC produces a random number | ||
| Encapsulate , encrypt | ||
| Compute , | ||
| Check | ||
| Decrypt , obtain | ||
| GW produces a random number | ||
| Decapsulate , obtain | ||
| Compute , , | ||
| Check | ||
| Encapsulate , encrypt | ||
| Compute | ||
| Check | ||
| Compute | ||
| Decrypt , obtain | ||
| SN produces a random number | ||
| Decapsulate , obtain | ||
| Check | ||
| Encapsulate , encrypt | ||
| Compute | ||
| Check | ||
| Decrypt , verify | ||
| Compare and | ||
| Decapsulate , obtain | ||
| Check | ||
| Negotiate session key | ||
| Encapsulate , encrypt | ||
| Compute , | ||
| Check | ||
| Decrypt , obtain | ||
| Verify the correctness of | ||
| Decapsulate , obtain | ||
| Check | ||
| Negotiate session key |
| Tomović et al. [7] | Kumar et al. [9] | Li et al. [13] | Moghadam et al. [14] | Mo et al. [18] | Xie et al. [20] | NTRU-GOPA | |
|---|---|---|---|---|---|---|---|
| Replay Attack | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Man-in-the-Middle Attack | ✓ | ✓ | × | ✓ | ✓ | ✓ | ✓ |
| User Anonymity | × | × | ✓ | ✓ | ✓ | ✓ | ✓ |
| Untraceability | ✓ | × | × | × | ✓ | ✓ | ✓ |
| DoS Attack | ✓ | ✓ | × | ✓ | ✓ | × | ✓ |
| Offline Password Guessing Attack | ✓ | ✓ | ✓ | ✓ | × | ✓ | ✓ |
| User Impersonation Attack | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Sensor Node Capture Attack | × | × | × | × | ✓ | ✓ | ✓ |
| Quantum Attack Resistance | × | × | × | × | × | × | ✓ |
| Perfect Forward/Backward Security | ✓ | × | ✓ | × | ✓ | ✓ | ✓ |
| Location-Based Authentication | × | × | × | × | × | × | ✓ |
| Scheme | Tomović et al. [7] | Kumar et al. [9] | Li et al. [13] | Moghadam et al. [14] | Mo et al. [18] | Xie et al. [20] | NTRU-GOPA |
|---|---|---|---|---|---|---|---|
| User storage | - | 128 | 1384 | 256 | 256 | 736 | 256 |
| Gateway storage | 704 | 576 | 1312 | 448 | 800 | 704 | 544 |
| Sensor storage | 640 | 448 | 224 | 224 | 224 | 576 | 480 |
| Total storage(bits) | 1344 | 1152 | 2920 | 928 | 1280 | 2016 | 1280 |
| Total communication(bits) | 704 | 1824 | 2720 | 2624 | 1760 | 1408 | 1440 |
| Symbol | Meaning | Time (ms) |
|---|---|---|
| Hash function | 0.0004 | |
| Chebyshev polynomials | 2.226 | |
| Elliptic curve dot product operations | 7.3529 | |
| Elliptic curve Encryption/Decryption | 7.3529 | |
| Symmetric Encryption/Decryption | 0.1303 | |
| NTRU Encryption | 0.13 | |
| NTRU decryption | 0.086 | |
| Polynomial Multiplication | 0.0011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Xu, M. Security Authentication Protocol for Underwater Sensor Networks Based on NTRU. J. Mar. Sci. Eng. 2025, 13, 742. https://doi.org/10.3390/jmse13040742
Jiang F, Xu M. Security Authentication Protocol for Underwater Sensor Networks Based on NTRU. Journal of Marine Science and Engineering. 2025; 13(4):742. https://doi.org/10.3390/jmse13040742
Chicago/Turabian StyleJiang, Fan, and Ming Xu. 2025. "Security Authentication Protocol for Underwater Sensor Networks Based on NTRU" Journal of Marine Science and Engineering 13, no. 4: 742. https://doi.org/10.3390/jmse13040742
APA StyleJiang, F., & Xu, M. (2025). Security Authentication Protocol for Underwater Sensor Networks Based on NTRU. Journal of Marine Science and Engineering, 13(4), 742. https://doi.org/10.3390/jmse13040742