A Numerical Simulation-Based Study on the Impact of Changes in Flow Rate of a Typical River Emptying into the Northern Yellow Sea on Water Environment of the River Estuary and Coastal Waters
Abstract
1. Introduction
2. Material and Method
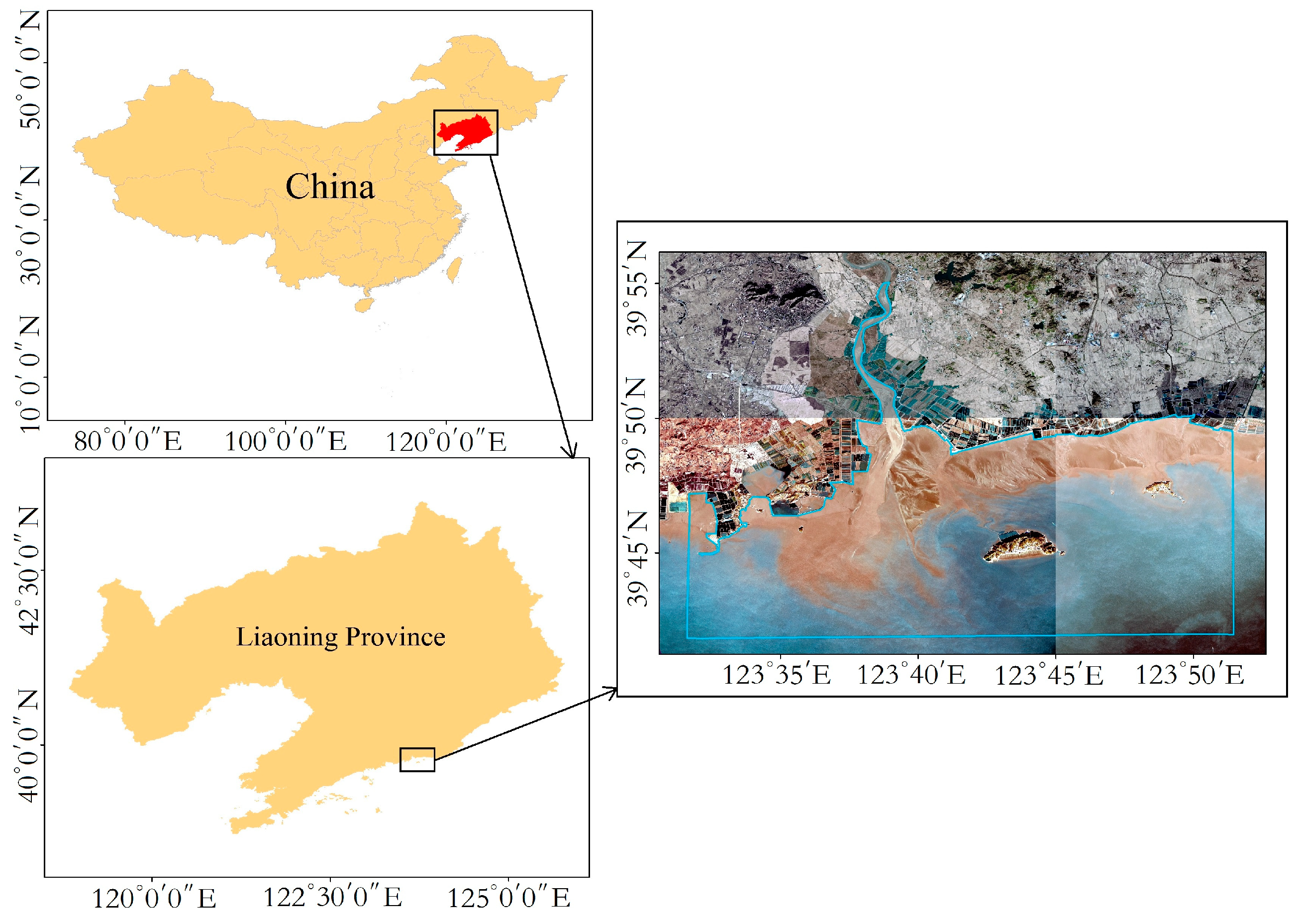
2.1. Investigated Water Area and Observational Data
2.2. Model and Method
2.2.1. Hydrodynamic Model
- (1)
- Initial conditions
- (2)
- Boundary conditions
- (3)
- Numerical discretization of model control equationss
2.2.2. Water Environment Model
2.3. Grid Creation and Model Settings
2.3.1. Grid Creation
2.3.2. Model Settings
3. Results
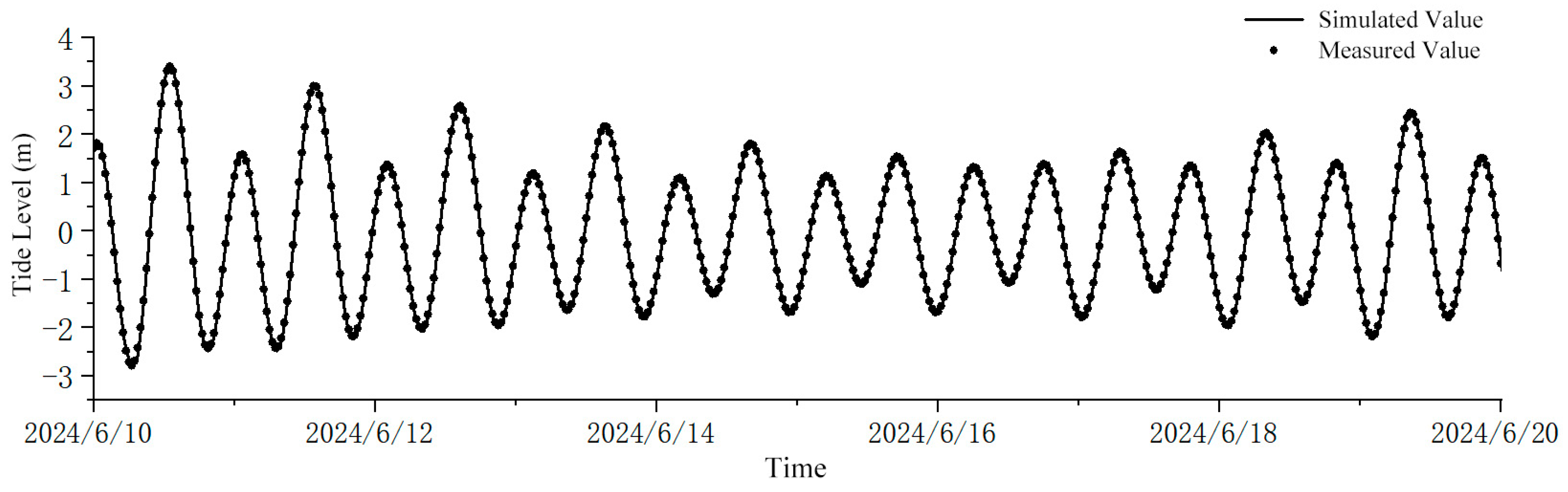
3.1. Model Verification Results
3.2. Simulation Results Under Various Conditions
3.3. Analysis of Water Environment Changes Under Different Schemes
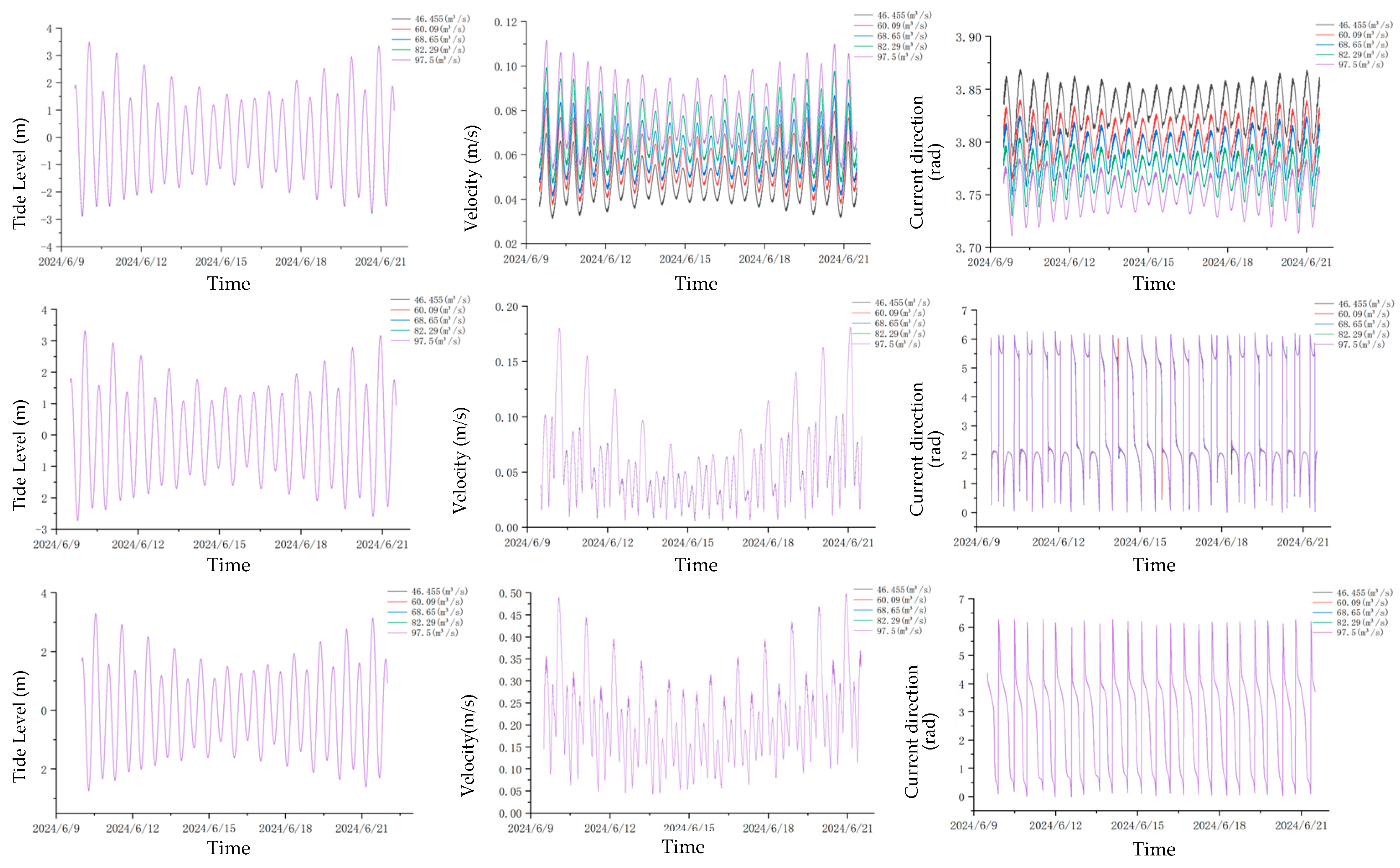
3.3.1. Analysis of Changes in a Hydrodynamic Environment
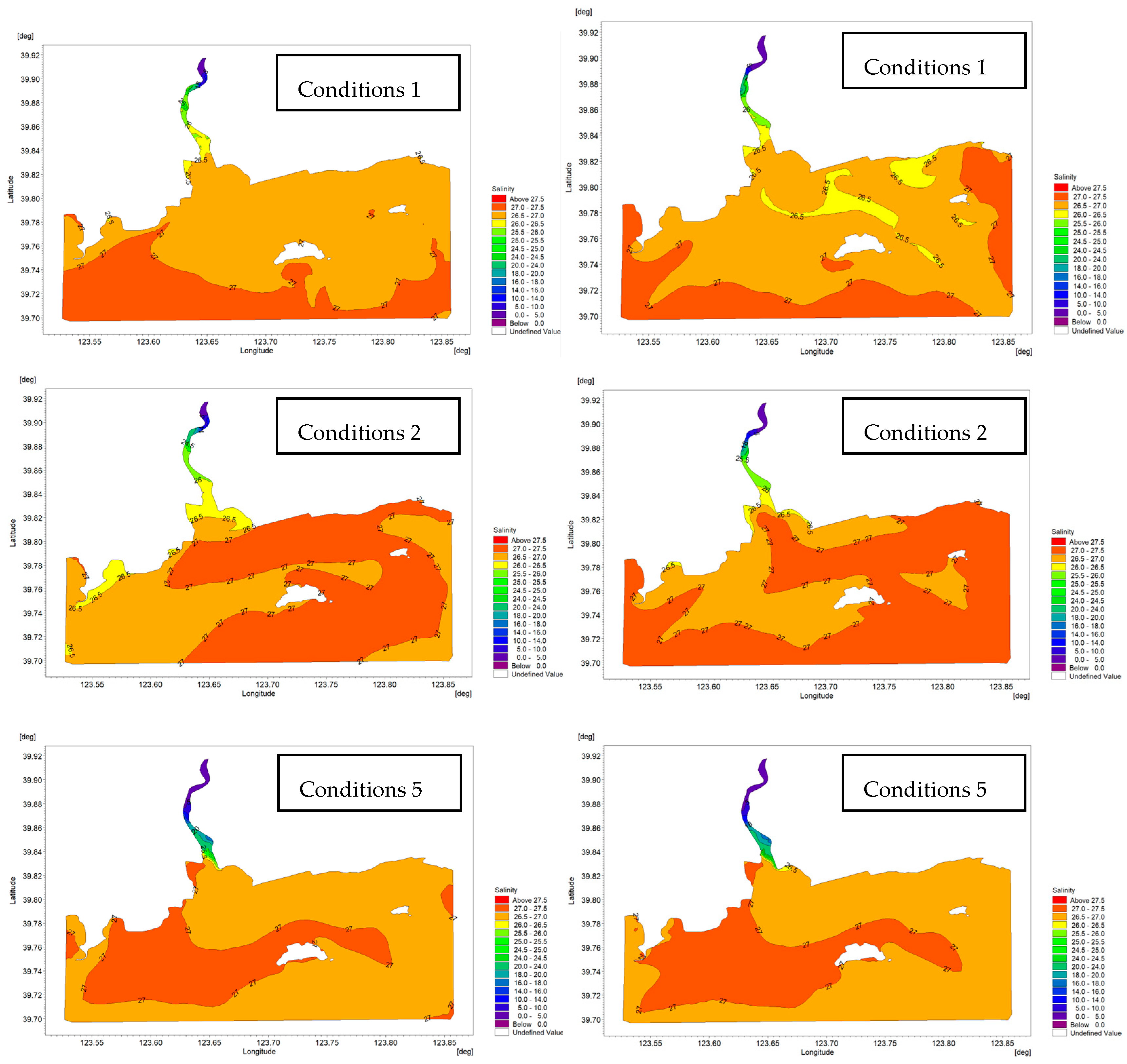
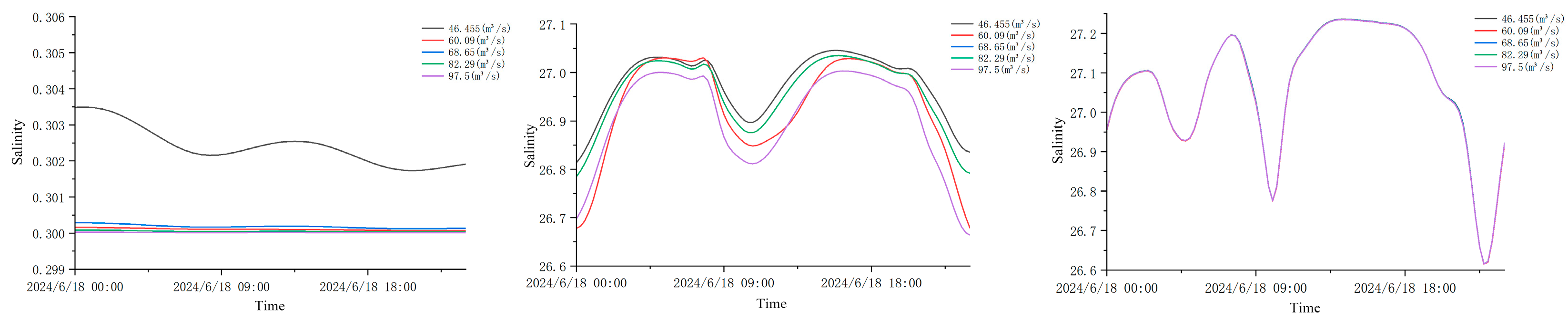
3.3.2. Analysis of Changes in Salinity Distribution
Curve Analysis of Changes in Salinity
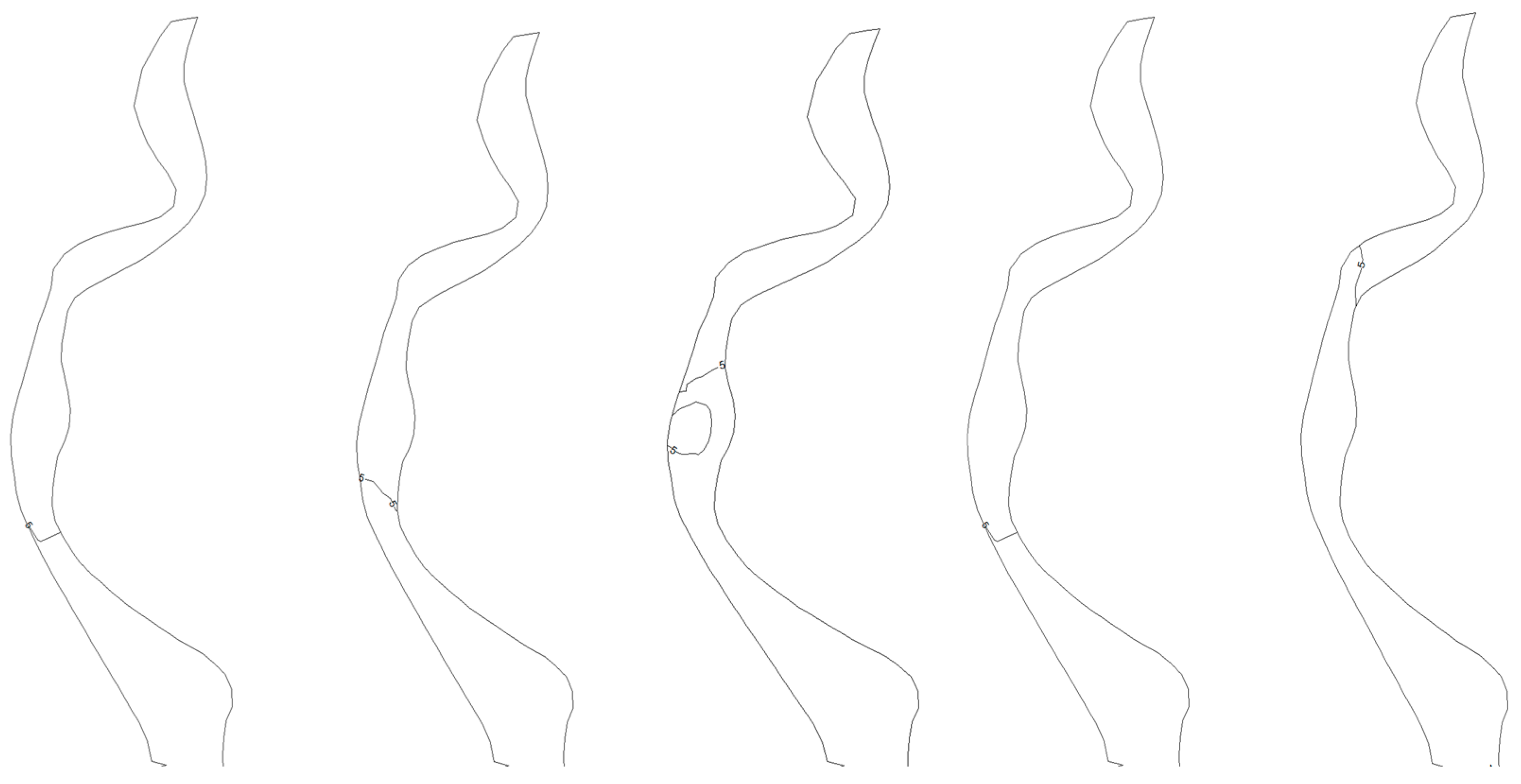
Calculation of Moving Distance of the Isohaline Toward the Estuary
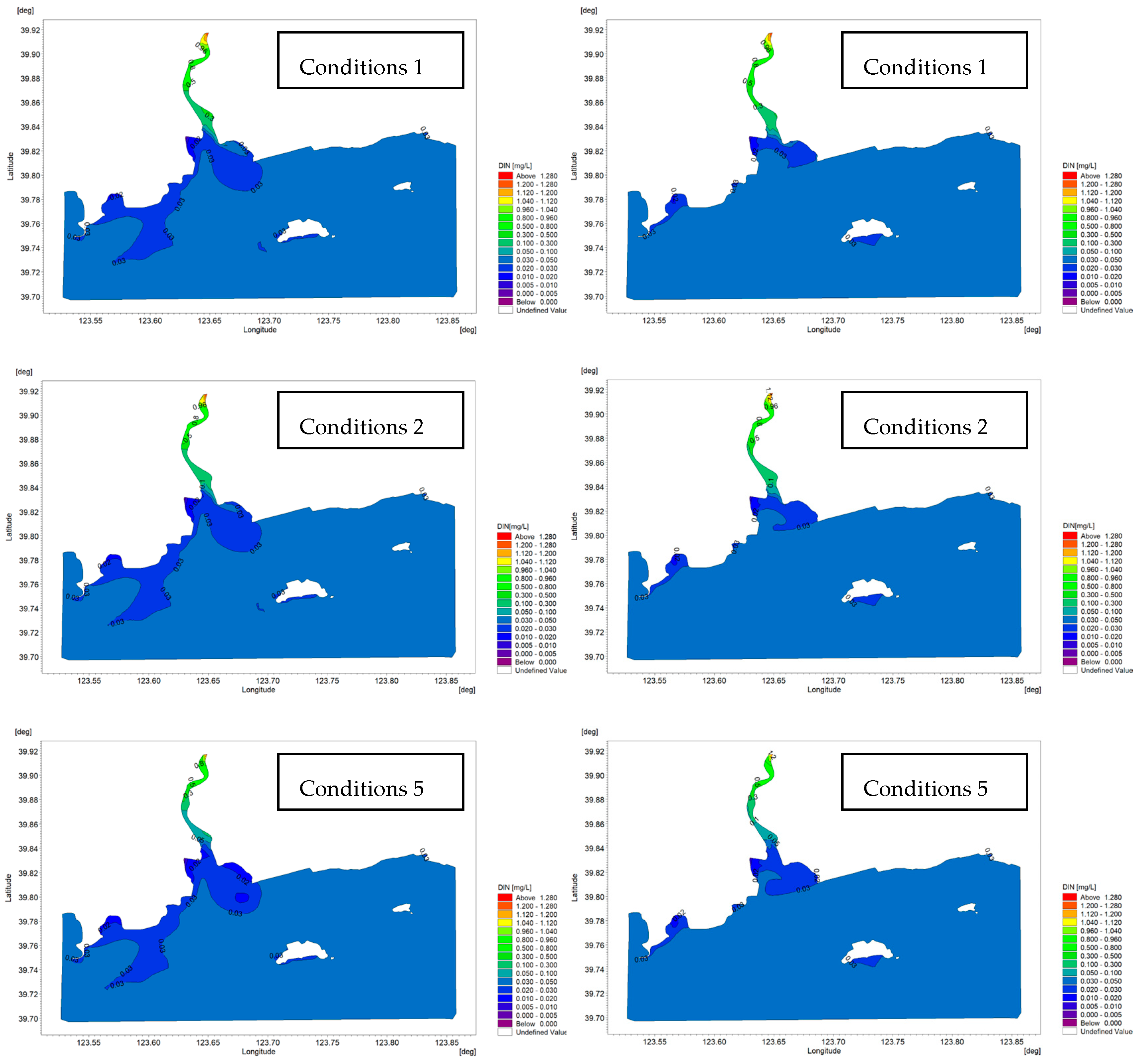
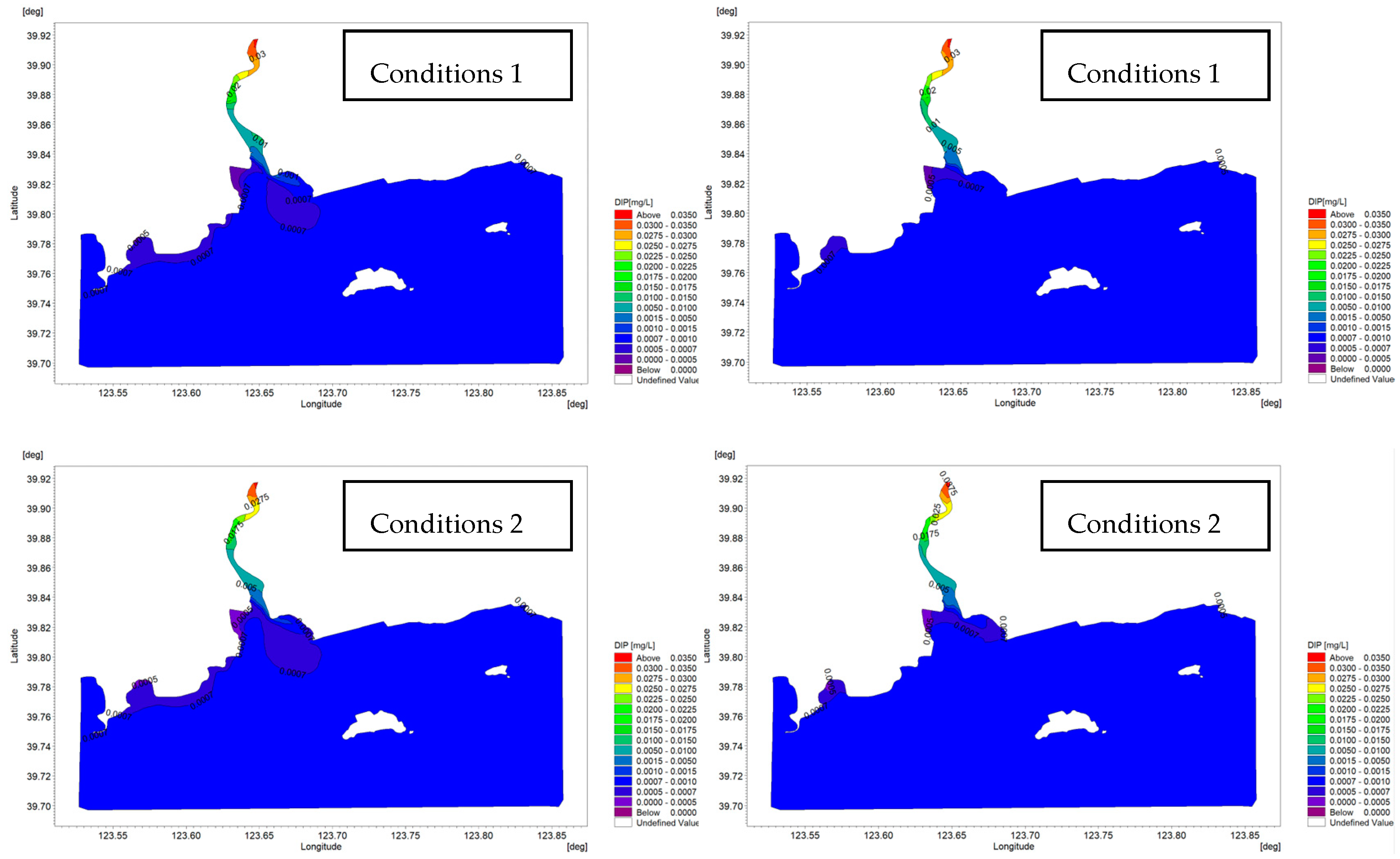
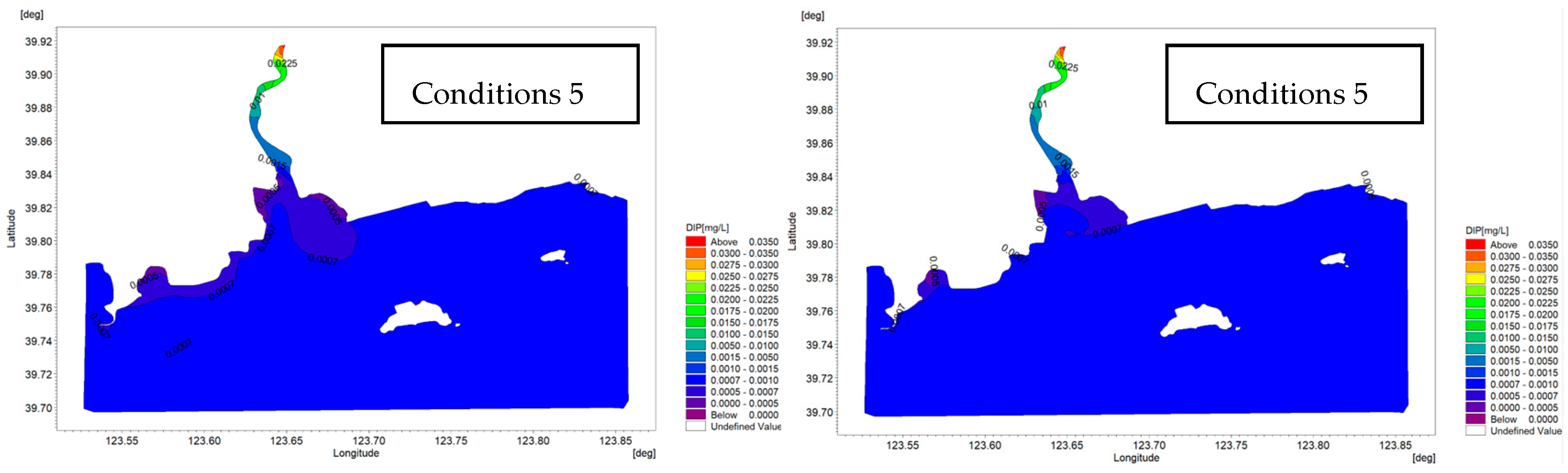
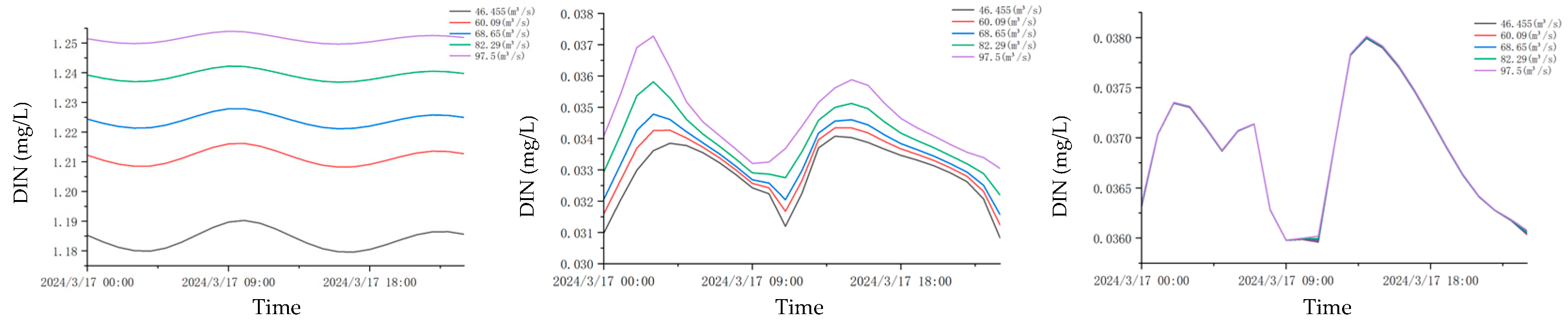
3.3.3. Analysis of Changes in Nutrient Distribution
4. Discussion
4.1. Changes in Hydrodynamic Conditions Before and After Water Interception
4.2. Changes in Salinity Distribution Before and After Water Interception
4.3. Changes in Nutrient Distribution Before and After Water Interception
5. Conclusions
- (1)
- A comparison of the curves of various stations in the sea area under multiple schemes (as shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15) indicates that the changes in tide level and velocity the five schemes before and after interception are not obvious. Through the simulation of the locations of the 5-isohaline under five runoff schemes and calculation of its moving distances compared to the scheme before interception, it is found that changes in runoff indeed have a certain impact on salinity distribution in the estuary. A comparison of the schemes shows that when natural conditions, such as river width and water depth, remain unchanged, under the five interception schemes, with an increase in the interception rate, the moving distance of the 5-isohaline gradually increases, and the amount of reduction in the area of the envelope curve with a salinity of 26.8 increases. There is a certain change in nutrient contents before and after interception, and the amount of change is also related to the interception rate and the distance of a station from the estuary.
- (2)
- Studies on the mechanism of the impact of changes in flow rates of typical rivers emptying into the sea under hydrodynamic conditions must attract sufficient attention from aquaculture operators and people engaging in marine environmental protection. The numerical simulation-based research method used in this paper can provide a technical method for accurately predicting the possible impact of river interception for irrigation on estuarine organisms and coastal wetlands, as well as provide estuarine management authorities with data support to help them learn about changes in water environment, ecological environment, etc., within the scope of coastal wetlands belonging to an estuary in an accurate and real-time manner.
- (3)
- In future studies, we will focus on solving and reducing the impact of changes in runoff of other similar rivers emptying into the sea on water environment across different years and water periods based on numerical simulation methods. We will simulate the impact of high-density cage aquaculture on water environment using non-generalized CFD methods. For example, during ice periods in winter, we may provide quantitative forecasts and early warnings on the amount of changes in water environment indicators, and even try to ensure the stability of water environment indicators by introducing slow-release nutrient fertilizers and externally patented delivery equipment, as well as cooperating with aquaculture operators in ensuring the supply of nutrients required for the growth of organisms. These measures would ensure high yield and quality of organisms [32,33], helping the aquaculture industry pursue sustainable development and providing aquaculture operators with technical support to help them make scientific and effective decisions on aquaculture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sheng, H. The Variations of Water and Sediment Discharge of the Rivers Along the East Coast of Liaodong Peninsula During the Past Millennium: Simulation, Reconstruction and Driving Mechanism Analysis. Master’s Thesis, Nanjing University of China, Nanjing, China, 2018. [Google Scholar]
- Shrestha, S.; Soden, B.J. Anthropogenic Weakening of the Atmospheric Circulation During the Satellite Era. Geophys. Res. Lett. 2023, 50, e2023GL104784. [Google Scholar] [CrossRef]
- Nivesh, S.; Patil, J.P.; Goyal, V.C.; Saran, B.; Singh, A.K.; Raizada, A.; Malik, A.; Kuriqi, A. Assessment of future water demand and supply using WEAP model in Dhasan River Basin, Madhya Pradesh, India. Environ. Sci. Pollut. Res. Int. 2023, 30, 27289–27302. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Wang, J.; Fu, Q.; Chen, L.; Chen, J.; Sun, T.; Li, B. Artificial river flow regulation triggered spatio-temporal changes in marine macrobenthos of the Yellow River Estuary. Mar. Environ. Res. 2024, 202, 106804. [Google Scholar] [CrossRef]
- Rostamzadeh-Renani, M.; Rostamzadeh-Renani, R.; Baghoolizadeh, M. The effect of vortex generators on the hydrodynamic performance of a submarine at a high angle of attack using a multi-objective optimization and computational fluid dynamics. Ocean Eng. 2023, 282, 114932. [Google Scholar] [CrossRef]
- Gong, W.; Lin, Z.; Zhang, H.; Lin, H. The response of salt intrusion to changes in river discharge, tidal range, and based on wavelet in the Modaomen China. Ocean Coastal Manag. 2022, 219, 106060. [Google Scholar] [CrossRef]
- Shou, W.; Zong, H.; Ding, P. A numerical study on the impact of the Yellow River runoff emptying into the sea on the circulation in the Yellow River estuary and nearby waters in summer. Acta Oceanolog. Sin. 2016, 38, 1–13. [Google Scholar]
- Rostamzadeh-Renani, M.; Baghoolizadeh, M.; Sajadi, S.M.; Rostamzadeh-Renani, R.; Azarkhavarani, N.K.; Salahshour, S.; Toghraie, D. A multi-objective and CFD based optimization of roof-flap geometry and position for simultaneous drag and lift reduction. Propuls. Pow. Res. 2024, 13, 26–45. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, J.; Cui, W.; Zhang, H. Impact of the reduction of the Yellow River runoff emptying into the sea on the estuary and marine ecological environment and countermeasures. In Proceedings of the 2003 China Environmental Resources Law Seminar (Annual Conference), Qingdao, China, 2 July 2003; pp. 314–318. [Google Scholar]
- Rostamzadeh-renani, M.; Baghoolizadeh, M.; Rostamzadeh-renani, R.; Toghraie, D.; Ahmadi, B. The effect of canard’s optimum geometric design on wake control behind the car using Artificial Neural Network and Genetic Algorithm. ISA Trans. 2022, 131, 427–443. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, Z.; Liang, R.; Pu, X.; Li, K.; Wang, Y. Impact of changes in runoff in the Beimenjiang River estuary on the water environment at the estuarine reach. Yangtze River 2018, 49, 6. [Google Scholar]
- Quang, N.H.; Sasaki, J.; Higa, H.; Huan, N.H. Spatiotemporal Variation of Turbidity Based on Landsat 8 OLI in Cam Ranh Bay and Thuy Trieu Lagoon, Vietnam. Water 2017, 9, 570. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, X.; Xie, R.; Wy, C. An experimental study on the effect of runoff rate on saltwater intrusion into an estuary and its application. Chem. Eng. Equip. 2020, 3, 11–13. [Google Scholar]
- Liang, J.; Xu, Y.; Zhang, W.; Zhou, R. Effect of runoff change of north river and west river on salt Intrusion in tidal estuary. Sci. Technol. Eng. 2024, 24, 2893–2900. [Google Scholar]
- Gong, Y. A Numerical Simulation-Based Study on the Spatial and Temporal Distribution of Nutrients and Phytoplankton in the Liaohe Estuary; Dalian Ocean University: Dalian, China, 2024. [Google Scholar]
- Wu, Q. A Simulation-Based Study on The Impact of the Yangtze River Runoff on Phytoplankton in the Yangtze River Estuary; Nanjing University of Information Science and Technology: Nanjing, China, 2021. [Google Scholar]
- Wang, Y.; Liu, Z.; Zhang, Y.; Wang, M.; Liu, D. Spatial and temporal variation characteristics of chlorophyll a and environmental factors in Jiaozhou Bay from 2010 to 2011. ACTAOceanolog. Sin. 2015, 37, 103–116. [Google Scholar]
- Shi, F.; Dong, X. Three-dimension numerical simulation for vulcanization process based on unstructured tetrahedron mesh. J. Manuf. Process. 2016, 22, 1–6. [Google Scholar]
- Zhang, P.; Zhang, R.J.; Huang, J.M.; Sheng, Z.; Wang, S. FVCOM model-based study on tidal prism and water exchange capacity of Haizhou Bay. Water Resour. Hydropower Eng. 2021, 52, 143–151. [Google Scholar]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar]
- Zhao, C.; Ren, L.; Yuan, F.; Zhang, L.; Jiang, S.; Shi, J.; Chen, T.; Liu, S.; Yang, X.; Liu, Y.; et al. Statistical and Hydrological Evaluations of Multiple Satellite Precipitation Products in the Yellow River Source Region of China. Water 2020, 12, 3082. [Google Scholar] [CrossRef]
- Marino, M.; Faraci, C.; Jensen, B.; Musumeci, R.E. Turbulent features of nearshore wave–current flow. Ocean Sci. 2024, 20, 1479–1493. [Google Scholar]
- Minhaz, F.A.; Mazlin, B.M.; Chen, K.L.; Nuriah, A.M. Identification of Water Pollution Sources for Better Langat River Basin Management in Malaysia. Water 2022, 14, 1904. [Google Scholar] [CrossRef]
- Liu, X.; Ma, D.G.; Zhang, Q.H. A higher-efficient non-hydrostatic finite volume model for strong three-dimensional free surface flows and sediment transport. China Ocean. Eng. 2017, 31, 736–746. [Google Scholar]
- Stanovoy, V.V.; Eremina, T.R.; Isaev, A.V.; Neelov, I.A.; Vankevich, R.E.; Ryabchenko, V.A. Modeling of oil spills in ice conditions in the Gulf of Finland on the basis of an operative forecasting system. Marine Phys. 2012, 52, 754–759. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar]
- Wang, K.; Li, N.; Wang, Z.; Song, G.; Du, J.; Song, L.; Jiang, H.; Wu, J. The Impact of Floating Raft Aquaculture on the Hydrodynamic Environment of an Open Sea Area in Liaoning Province, China. Water 2022, 14, 3125. [Google Scholar] [CrossRef]
- Wang, K.; Li, N.; Song, L.; Jiang, H. Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture. Water 2023, 15, 3450. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, W. Research progress on the effect of salinity on pond aquaculture. Jiangsu J. Agric. Sci. 2022, 38, 278–284. [Google Scholar]
- Qin, H.; Yang, S.; Wang, B.; Liao, X.; Hu, S.; Zhao, J.; He, Z.; Sun, C. Effects of different salinity levels on biological floccules, prawn growth and enzyme activity. Jiangsu J. Agric. Sci. 2020, 39, 400–406. [Google Scholar]
- Zhang, K. Research on Ph and Salinity Control Technology Fora Culture Environment for Biological Floccules of Prawns; Ocean University of China: Qingdao, China, 2015. [Google Scholar]
- Li, L.; Wu, L.; Yuan, J.; Zhao, X.; Xia, Y. Water Environment in Macro-Tidal Muddy Sanmen Bay. J. Mar. Sci. Eng. 2025, 13, 55. [Google Scholar]
- Al-Mur, B.A. Environmental Assessment Using Phytoplankton Diversity, Nutrients, Chlorophyll-a, and Trophic Status Along Southern Coast of Jeddah, Red Sea. J. Mar. Sci. Eng. 2025, 13, 29. [Google Scholar]
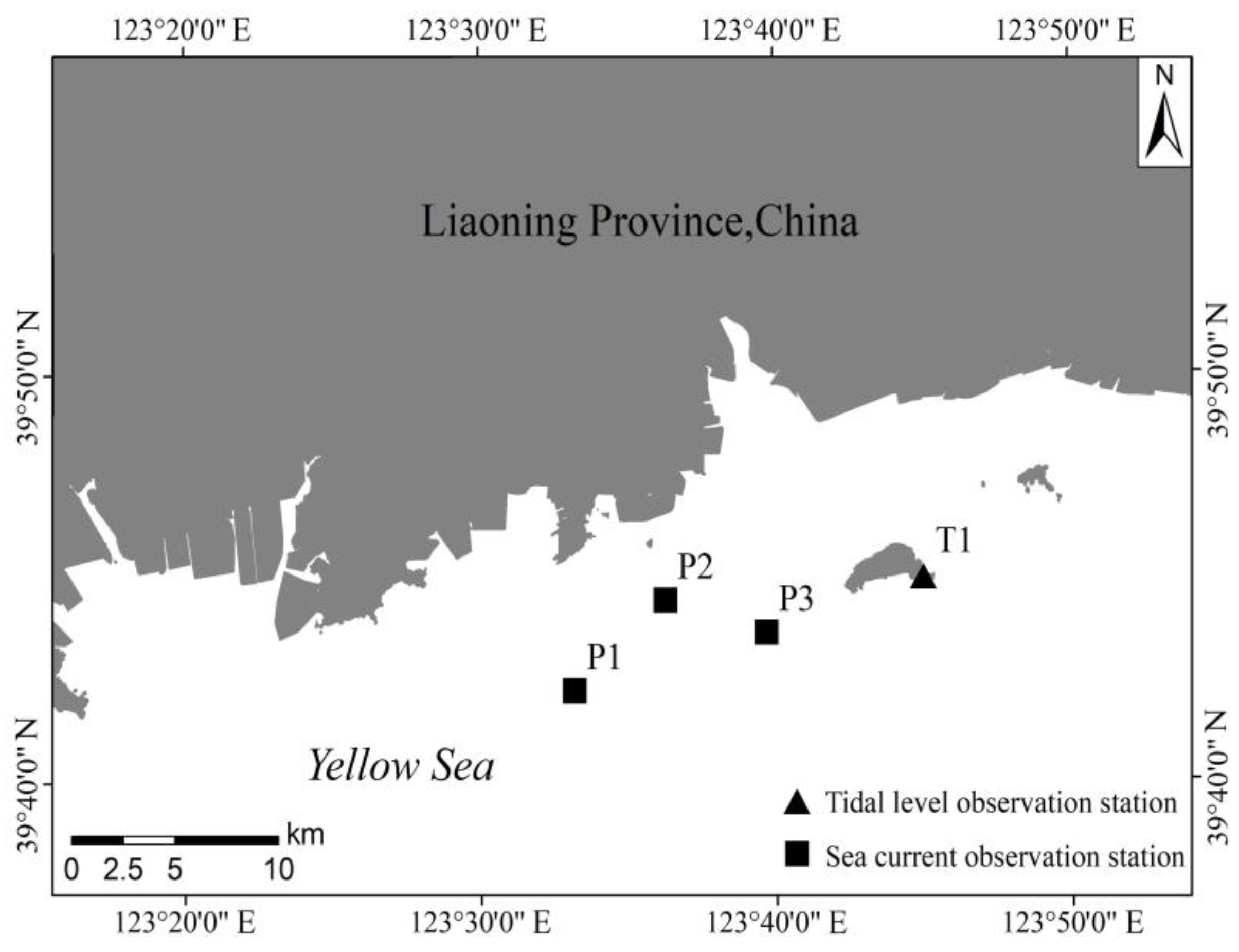






| Station | Longitude | Latitude |
|---|---|---|
| T1 | 123°45′0″ E | 39°45′0″ N |
| P1 | 123°33′10.558″ E | 39°42′14.462″ N |
| P2 | 123°36′15.952″ E | 39°44′26.600″ N |
| P3 | 123°39′41.122″ E | 39°43′38.126″ N |
| Simulation Scheme | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 |
|---|---|---|---|---|---|
| Flow rate (m3/s) | 97.500 | 82.290 | 68.650 | 60.090 | 46.455 |
| Interception rate | 0 | 16% | 30% | 38% | 52% |
| Station | Longitude | Latitude |
|---|---|---|
| 1# | 123°33′10.558″ E | 39°42′14.462″ N |
| 2# | 123°39′13.313″ E | 39°49′29.110″ N |
| 3# | 123°38′52.020″ E | 39°55′1.020″ N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Wu, J.; Hu, C.; He, J.; Song, L.; Li, N.; Liu, Y. A Numerical Simulation-Based Study on the Impact of Changes in Flow Rate of a Typical River Emptying into the Northern Yellow Sea on Water Environment of the River Estuary and Coastal Waters. J. Mar. Sci. Eng. 2025, 13, 736. https://doi.org/10.3390/jmse13040736
Wang K, Wu J, Hu C, He J, Song L, Li N, Liu Y. A Numerical Simulation-Based Study on the Impact of Changes in Flow Rate of a Typical River Emptying into the Northern Yellow Sea on Water Environment of the River Estuary and Coastal Waters. Journal of Marine Science and Engineering. 2025; 13(4):736. https://doi.org/10.3390/jmse13040736
Chicago/Turabian StyleWang, Kun, Jinhao Wu, Chaokui Hu, Jian He, Lun Song, Nan Li, and Yutong Liu. 2025. "A Numerical Simulation-Based Study on the Impact of Changes in Flow Rate of a Typical River Emptying into the Northern Yellow Sea on Water Environment of the River Estuary and Coastal Waters" Journal of Marine Science and Engineering 13, no. 4: 736. https://doi.org/10.3390/jmse13040736
APA StyleWang, K., Wu, J., Hu, C., He, J., Song, L., Li, N., & Liu, Y. (2025). A Numerical Simulation-Based Study on the Impact of Changes in Flow Rate of a Typical River Emptying into the Northern Yellow Sea on Water Environment of the River Estuary and Coastal Waters. Journal of Marine Science and Engineering, 13(4), 736. https://doi.org/10.3390/jmse13040736





