Optimized Deep Reinforcement Learning for Dual-Task Control in Deep-Sea Mining: Path Following and Obstacle Avoidance

Abstract

This study investigates the dual-task control challenge of path following and obstacle avoidance for deep-sea mining robots operating in complex, unstructured environments. To address the limitations of traditional training strategies, we propose an optimized training framework that integrates environmental design enhancements and algorithmic advancements. Specifically, we develop a Dual-Task Training Environment by combining the Random Obstacle Environment with a newly proposed Obstructed Path Environment, ensuring a balanced learning approach. While agents trained solely in the Random Obstacle Environment exhibit unilateral obstacle avoidance strategies and achieve a 0% success rate in randomized obstacle scenarios, those trained in the Dual-Task Environment demonstrate 85.4% success under identical test conditions and acquire more complex bilateral avoidance strategies. Additionally, we introduce a Dynamic Multi-Step Update mechanism, which integrates immediate rewards with long-term returns to enhance deep reinforcement learning (Twin Delayed Deep Deterministic Policy Gradient, TD3) performance without increasing computational complexity. Under the optimal multi-step setting (n = 5), the Dynamic Multi-Step Update mechanism significantly improves path following accuracy, reducing trajectory deviations to 0.128 m on straight paths and 0.195 m on S-shaped paths, while achieving nearly 100% success in multi-directional obstacle avoidance tests. These improvements collectively enhance the adaptability, robustness, and operational performance of deep-sea mining robots, advancing intelligent control strategies for autonomous deep-sea exploration and resource extraction.

1. Introduction

The global demand for critical metals such as nickel, copper, cobalt, and rare earth elements continues to increase, while terrestrial resources are depleting, driving the shift toward deep-sea mineral resources [1]. Although deep-sea mining holds great promise, it faces significant challenges due to the extreme conditions of high pressure, low temperature, and complex seafloor terrain [2]. Mining robots, as illustrated in Figure 1, are central to this process, responsible for both mineral extraction and environmental monitoring. Deep-sea mining robots must possess highly accurate path following and real-time obstacle avoidance capabilities, effectively achieving dual-task control to operate efficiently and safely in such demanding environments [3,4].

In the field of path following for marine unmanned vehicles, Londhe [5] proposed a robust task-space control method based on PID-like fuzzy control, incorporating feed-forward terms and disturbance estimators to handle external disturbances and ensure accurate path following. On the other hand, Dai [6] combined Computational Fluid Dynamics (CFD) with PID control to develop a path following control model for underactuated unmanned underwater vehicles, successfully optimizing path following performance under complex ocean current conditions. Li [7] applied a Model Predictive Control (MPC) method to address track slippage issues, introducing an enhanced path following control strategy that ensures smooth following and stability in challenging environments such as soft sediments. Yan [8] proposed a robust MPC-based path following method utilizing a Finite-Time Extended State Observer (FTESO) to estimate and compensate for system uncertainties, improving the AUV’s disturbance rejection in dynamic environments. Chen [9] introduced a path following controller for deep-sea mining vehicles based on the Improved Deep Deterministic Policy Gradient (IDDPG) algorithm, incorporating slip control and random resistance. The controller demonstrated superior path following performance in simulations, better adapting to the complexities of deep-sea mining environments.

Although significant advancements have been made in path following control methods, a critical challenge remains in practical operations: how to effectively avoid obstacles while maintaining high following accuracy. To address this challenge, many scholars have proposed various path planning and obstacle avoidance algorithms aimed at optimizing underwater robots’ movement control in complex environments. Zhou [10] proposed an autonomous recovery path planning method for unmanned surface vehicles (USVs) based on the 3D-Sparse A* algorithm, optimizing waypoint generation to reduce computational load and improving path smoothness and accuracy during dynamic obstacle avoidance. Lyridis [11] introduced an improved Ant Colony Optimization (ACO) algorithm enhanced by fuzzy logic for local path planning in USVs, significantly improving the efficiency and accuracy of dynamic obstacle avoidance in complex environments. Lu [12] proposed a path planning method for deep-sea mining vehicles based on an improved Particle Swarm Optimization (IPSO) algorithm, which specifically addresses obstacle avoidance, path optimization, and crawler slippage, achieving efficient and safe navigation in complex seabed environments. Wang [13] introduced a speed-adaptive robust obstacle avoidance method based on Deep Reinforcement Learning (DRL) for environmentally driven unmanned surface vehicles (USVs). This approach optimizes the avoidance strategy, significantly improving the USV’s obstacle avoidance capability and adaptability in large-scale, uncertain environments. Li [14] proposed a path planning method for underwater obstacle avoidance in 3D unknown environments based on the Constrained Artificial Potential Field (C-APF) and Twin Delayed Deep Deterministic Policy Gradient algorithm. By combining classical path planning techniques with deep reinforcement learning, this method significantly enhances the obstacle avoidance capability of underwater robots in dynamic and complex environments.

While significant achievements have been made in the single tasks of path following and obstacle avoidance for marine unmanned robots, the challenge of effectively optimizing these dual tasks collaboratively remains unsolved. Wu [15] proposed a trajectory following method for deep-sea mining vehicles based on MPC, addressing track slippage and environmental disturbances, enabling precise path following and effective obstacle avoidance in dynamic deep-sea environments. However, the study was only tested in an environment with a single obstacle and did not consider dual-task collaborative control in dense obstacle scenarios, which limits its applicability in more complex environments. Nevertheless, the study provides a solid technical foundation for solving the dual-task collaborative control problem and lays the groundwork for further algorithm optimization and practical applications.

Although MPC has achieved some results in dual-task control for path following and obstacle avoidance, its application to dual-task collaboration still faces limitations. First, MPC relies on accurate environmental modeling and state estimation, and in dynamic and uncertain environments like the deep sea, the accuracy and real-time computational capacity of the model may be constrained. Additionally, MPC requires trade-offs between different objectives and relies on predefined models and control strategies, making it difficult to adapt to rapidly changing complex environments. In contrast, DRL, as a data-driven approach, overcomes these limitations by learning and optimizing through interaction with the environment. DRL does not rely on precise environmental models and can adjust control strategies in real time, effectively coordinating the trajectory-following and obstacle avoidance tasks. Especially in complex deep-sea mining environments, DRL offers stronger adaptability and robustness. By designing appropriate reward functions, DRL can dynamically optimize the collaboration between the two tasks, achieving more efficient and stable control.

To provide a clearer comparison of existing approaches in marine unmanned robots,

Table 1. Comparison of path following and obstacle avoidance methods for marine unmanned robots.

Method Category	Representative Works	Path Following	Obstacle Avoidance	Dual-Task Collaboration	Adaptability to Dynamic Environments	Suitability for Deep-Sea Mining
PID-Based	Londhe (PID-Fuzzy) Dai (CFD + PID)	Basic	None	None	Low–Medium	Limited
MPC-Based	Li (MPC for Slippage) Yan (MPC + FTESO)	Strong	None	None	Medium–High	Moderate
	Wu (MPC for Dual-Task)	Strong	Limited	Partial	Medium–High	Moderate
Heuristic Path Planning	Zhou (3D-Sparse A*) Lyridis (ACO-Fuzzy) Lu (IPSO)	None	Strong	None	Medium–High	Moderate
DRL-Based	Chen (IDDPG-based) Wang (DRL for USVs)	Strong	Strong	Limited	High	Strong
	This paper	Strong	Strong	Full	High	Strong

summarizes the main methods used for path following and obstacle avoidance. The comparison highlights their respective strengths and limitations, particularly in terms of adaptability, dual-task collaboration, and suitability for deep-sea mining applications.

While progress has been made in single-task control, research on the collaborative control of path following and obstacle avoidance is still limited. Therefore, the primary objective of this study is to develop a dual-task control algorithm that simultaneously optimizes both path following precision and obstacle avoidance performance, addressing the operational demands of deep-sea mining robots in complex and dynamic environments. This approach aims to enhance the overall efficiency and reliability of robotic operations under challenging conditions.

Distinguishing itself from previous works, this study leverages DRL to improve adaptability in the highly nonlinear, unpredictable nature of deep-sea mining operations. While DRL has demonstrated effectiveness in individual tasks of path following and obstacle avoidance, its application to an integrated dual-task framework remains underexplored. To bridge this gap, we propose a dual-task collaborative control framework that optimizes both objectives simultaneously, achieving superior performance within the same training time and computational budget. Furthermore, we introduce a Dynamic Multi-Step Update mechanism, which significantly enhances dual-task coordination while maintaining computational efficiency. By refining the update strategy without introducing substantial overhead, the Dynamic Multi-Step Update mechanism enables more stable and effective policy learning, leading to a marked improvement in the overall operational effectiveness of deep-sea mining robots.

The remainder of the paper is organized as follows: Notations frequently used in this paper are summarized in

Table 2. Nomenclature.

Symbols	Description
DRL	Deep Learning Reinforcement
TD3	Twin Delayed Deep Deterministic Policy Gradient
ROE	Random Obstacle Environment
OPE	Obstructed Path Environment
DTE	Dual-Task Environment
DMSU	Dynamic Multi-Step Update Mechanism
PID	Proportional–Integral–Derivative
CFD	Computational Fluid Dynamics
MPC	Model Predictive Control
FTESO	Finite-Time Extended State Observer
AUV	Autonomous Underwater Vehicle
USV	Unmanned Surface Vehicle
ACO	Ant Colony Optimization
IDDPG	Improved Deep Deterministic Policy Gradient
IPSO	improved Particle Swarm Optimization
C-APF	Constrained Artificial Potential Field

. Section 2 outlines the methodology, including the optimization of dynamics, noise incorporation, and reward design. Section 3 discusses training environments, highlighting the advantages of the Dual-Task Environment. Section 4 details the TD3 algorithm enhanced with Dynamic Multi-Step Update and its performance evaluation. Finally, Section 5 concludes the study and suggests future research directions.

2. Methodology

This section introduces the development methodology of the dual-task control system for deep-sea mining, focusing on two core aspects: modeling and controller design. Section 2.1 presents the simulation model of the deep-sea mining robot and optimizes its dynamic response, providing foundational support for controller development. Section 2.2 details the deep reinforcement learning-based control strategy, including the core principles of the TD3 algorithm, the incorporation of Gaussian noise in input–output design, and the reward function tailored for the dual tasks of path following and obstacle avoidance. All the work was conducted using Python 3.9.18.

2.1. Modeling

This study builds upon the system model of the four-tracked deep-sea mining robot “Pioneer II” developed by Chen [16], with its three-dimensional representation shown in Figure 2. Chen [16] systematically described the kinematic, dynamic, and slippage characteristics of the robot. The four-tracked design overcomes the limitations of two-tracked robots in navigating complex terrains, significantly enhancing the robot’s obstacle-surmounting capability under challenging seabed conditions. This improvement enables the robot to better meet the demanding operational requirements of deep-sea mining. To provide a comprehensive understanding of the robot’s design,

Table 3. The specifications of the four-tracked deep-sea mining robot.

Symbol	Value	Description
$M$	7000 kg	Total mass of the deep-sea mining robot underwater
$I$	34,096 kg$·$m2	Rotational inertia of the deep-sea mining robot
$D$	1.88 m	Center distance of the tracks on both sides of the deep-sea mining robot
$L$	6 m	The length of the deep-sea mining robot
$W$	3 m	The width of the deep-sea mining robot
$H$	2.5 m	The height of the deep-sea mining robot
$l$	1.65 m	The length of one track of the deep-sea mining robot on ground
$d$	0.37 m	The end-to-end distance of two tracks positioned on the same side
$b$	0.55 m	Single track width
$r$	0.31 m	Driving wheel radius of the track

presents the key specifications of “Pioneer II”. These specifications serve as the foundation for analyzing the robot’s dynamic behavior and evaluating its control signal response. Building on this framework, we conducted an in-depth analysis of the control signal response characteristics of “Pioneer II”.

In the model proposed by Chen [16], the robot is assumed to adjust its track angular velocity at a uniform rate after receiving control signals, gradually reaching the target angular velocity within a 0.5 s control cycle. However, actual dynamic behavior during deep-sea operations reveals that “Pioneer II” exhibits a much faster response to control signals, typically approaching the target angular velocity within the first-time step (0.05 s) after the signal is issued, with subsequent velocity adjustments becoming minimal or stabilizing. To better align with this observed behavior, we introduced adaptive modifications to the model, enabling the track angular velocity to rapidly approach the target value during the initial response, rather than adjusting at a uniform rate. This modification provides a more accurate representation of the robot’s real-world dynamic characteristics.

Additionally, to further enhance the model’s realism and adaptability, a randomization mechanism was proposed to introduce variability in the track angular velocity response during each control time step. We formulate the refined model as Equation (1).

$${\omega }_i\left(t+\mathsf{\Delta }t\right)={\omega }_i\left(t\right)+\xi \cdot \left[u_i\left(T\right)-{\omega }_i\left(t\right)\right],$$

(1)

where ${\omega }_i(t)$ denotes the angular velocity of the track driving wheel at time $t$, $u_i(T)$ represents the control signal, corresponding to the target angular velocity, and $\xi$ is a random coefficient governing the rate of angular velocity change during the response time step, with values ranging from 0.8 to 1.0. The variable $\mathsf{\Delta }t$ represents the minimum time step in the robot’s response cycle to the control signal, set to 0.05 s, while $T$ denotes the time at which the control signal is issued.

This improved model not only enhances the dynamic adaptability of the control signal response, but also effectively simulates the nonlinear characteristics induced by complex terrains or environmental disturbances, making the model more representative of the actual dynamic behavior of deep-sea mining robots. However, it should be noted that the model does not account for extreme dynamics caused by sudden track obstructions or highly uneven terrain, which may result in an underestimation of velocity adjustments under such conditions. Future studies will aim to introduce more comprehensive adaptive mechanisms to further refine the model, ensuring greater alignment with real-world deep-sea operational scenarios.

2.2. Controller Design

Building on the previous section’s advancements in mining robot modeling and optimization, this section presents a DRL-based control framework for deep-sea mining robots. The framework employs the Twin Delayed Deep Deterministic Policy Gradient algorithm to achieve stable path following and real-time obstacle avoidance. To account for sensor uncertainties, Gaussian noise is introduced to the robot, target, and obstacle coordinates, enhancing robustness. Additionally, a multi-dimensional reward function is designed to balance path following and obstacle avoidance, optimizing the learning process.

2.2.1. DRL Algorithm

In dual-task control for path following and obstacle avoidance in deep-sea mining robots, the challenging operational environment and task demands place high requirements on the control system. Specifically, the robots need to make real-time decisions in dynamic environments to follow target points while avoiding obstacles. Additionally, the uncertainty of the deep-sea environment, such as sensor measurement errors and path disturbances, further increases the complexity of the control task. Traditional model-based control methods often struggle to address these challenges effectively.

In contrast, DRL offers significant potential in solving dual-task control problems by leveraging its powerful capability for online policy learning and adaptability to complex dynamic systems. By employing a data-driven approach, DRL transforms the problem from direct control to policy optimization, improving robustness against sensor noise and environmental disturbances. Moreover, DRL excels in high-dimensional state spaces, offering more efficient and intelligent solutions tailored for the operational demands of deep-sea mining robots.

This study adopts the TD3 algorithm as the core control framework due to its key advantages, as outlined below.

Smooth Action Generation and Stability: TD3 is based on the Actor–Critic framework and generates smooth and stable control signals for continuous tasks. The Actor network learns the policy by maximizing the estimated Q-value, and its gradient update is formulated as in Equation (2).

$${\nabla }_{\varphi }J(\varphi )=\mathbb{E}\left[{\left.{\nabla }_a{Q}_{{\theta }_1}(s,a)\right|}_{a={\pi }_{\varphi }(s)}{\nabla }_{\varphi }{\pi }_{\varphi }(s)\right],$$

(2)

where the objective function $J\left(\varphi \right)$ is optimized to improve policy performance. The estimated Q-value $Q_{{\theta }_1}(s,a)$, provided by the first Critic network, evaluates how beneficial an action is in a given state. The policy function ${\pi }_{\varphi }\left(s\right)$, parameterized by $\varphi$, determines the action selection strategy. The gradient ${\nabla }_a{Q}_{{\theta }_1}(s,a)$ indicates how the Q-value changes with respect to the action, guiding policy updates, while ${\nabla }_{\varphi }{\pi }_{\varphi }\left(s\right)$ represents the sensitivity of the policy function to its parameters. By incorporating these gradients, TD3 ensures that the Actor network progressively refines the policy toward actions that yield higher expected rewards, ultimately enhancing control smoothness and stability in complex deep-sea environments [17].

High Stability and Sample Efficiency: By utilizing dual Critic networks and delayed policy updates, TD3 effectively mitigates instability during training and accelerates policy convergence. Specifically, the Critic networks estimate the Q-values, and the target Q-value is computed as formulated in Equation (3).

$$y=r+\gamma \underset{\mathrm{i}=1,2}{min}{Q}_{{\theta }_i^{\prime }}\left(s^{\prime },{\pi }_{{\varphi }^{\prime }}\left(s^{\prime }\right)+ϵ\right),$$

(3)

where $y$ represents the target Q-value used to update the Critic network. The reward $r$ is obtained after executing action $a$, while $\gamma$ is the discount factor that determines the importance of future rewards. The function $Q_{{\theta }_i^{\prime }}\left(s^{\prime },a^{\prime }\right)$ represents the estimated Q-value given by the target Critic networks, with two separate networks indexed by $i=1,2$, ensuring the selection of the minimal value to reduce overestimation bias. The next action $a^{\prime }$ is determined by the target policy ${\pi }_{{\varphi }^{\prime }}\left(s^{\prime }\right)$, which adds a clipped noise term $ϵ~clip\left(N\right(0,\sigma ),-c,c)$ to smooth policy updates and enhance training stability. The parameters ${\theta }_i^{\prime }$ and ${\varphi }^{\prime }$ belong to the target networks, which are updated using a soft update mechanism discussed later. This approach significantly improves training stability and sample efficiency, making it particularly suitable for environments with high uncertainty, such as deep-sea mining operations [18].

Environmental Adaptability and Robustness: TD3 improves adaptability to sensor noise and environmental disturbances through the minimum target value selection strategy and delayed policy update mechanism. These enhancements ensure stable decisions and the reliable execution of dual-task operations in complex deep-sea environments. To ensure stable training, soft updates are applied to both the Actor and Critic target networks, as formulated in Equation (4).

$$\left\{\begin{array}{l}{\theta }_i^{\prime }\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }\\ {\varphi }^{\prime }\leftarrow \tau \varphi +(1-\tau ){\varphi }^{\prime }\end{array}\right.,$$

(4)

where ${\theta }_i^{\prime }$ and ${\varphi }^{\prime }$ represent the parameters of the target Critic and target Actor networks, respectively, while ${\theta }_i$ and $\varphi$ correspond to the parameters of the main Critic and Actor networks. The soft update coefficient $\tau$ controls the rate at which the target networks are updated, preventing abrupt changes in the target network, contributing to stable convergence and better performance in dynamic underwater environments [18].

These characteristics make TD3 particularly suited for dual-task control in deep-sea mining robots, providing a robust foundation for achieving efficient and safe operations in underwater conditions. The values of the relevant parameters in the algorithm are listed in

Table 4. Hyperparameter settings of TD3 algorithm.

Parameter	Symbol	Value	Description
Discount Factor	$\gamma$	0.95	Balances immediate rewards and long-term returns
Policy Update Delay	$N_{int}$	2	Delayed policy update frequency
Actor Network Learning Rate Learning Rate	$l_{\alpha }$	0.0001	Learning rate for optimizing the Actor network parameters
Critic Network Learning Rate	$l_{\beta }$	0.0001	Learning rate for optimizing the Critic network parameters
Target Network Soft Update Rate	$\tau$	0.0005	Updates target networks using Exponential Moving Average (EMA)
Replay Buffer Size	$N_{max}$	32,000	Maximum capacity of the experience buffer for storing interaction data
Batch Size	$k_{batch}$	512	Number of samples drawn from the replay buffer per training step
Target Action Noise Scale	${\sigma }_1$	0.2	Standard deviation of Gaussian noise added to the target action for smoothing
Target Action Noise Clipping	$c$	0.5	Limits the amplitude of Gaussian noise to ensure stable target action outputs
Action Noise Scale	${\sigma }_2$	0.1	Standard deviation of Gaussian noise added to the action for exploration
Exploration Noise Decaying Coefficient	${\lambda }_{exp}$	0.9	Reduces the amplitude of action noise during training to transition from exploration to exploitation
Training Episodes	$T$	8000	Defines the total number of training episodes for adequate learning
Random Seed	-	24	Controls the randomness in NumPy (1.26.4), PyTorch (2.4.0), and the environment to ensure reproducibility of experimental results

. The training process of this study is based on the standard TD3 algorithm, with the hyperparameters in Table 4 meticulously fine-tuned from its baseline values to enhance the algorithm’s adaptability and performance in deep-sea mining path tracking and obstacle avoidance.

The design of state and action spaces, as well as the reward function tailored for dual-task control of the deep-sea mining robot, is detailed in Section 2.2.2 and Section 2.2.3.

To ensure the comparability of experimental results in Section 3 and Section 4, a fixed random seed was introduced in this study. The use of a random seed ensures consistency in network initialization, significantly reducing performance fluctuations caused by random variations during initialization. This approach effectively eliminates the influence of stochastic factors, enabling the experimental results to better reflect the actual effects of environment design and algorithm optimization. Consequently, this setup enhances the stability of experimental outcomes and the reliability of the research conclusions.

2.2.2. Robust Noise Injection and Input/Output

In deep-sea mining operations, robots are required to simultaneously perform path following and obstacle avoidance tasks. However, the complex working environment and sensor measurement errors may lead to control system instability. To enhance the controller’s adaptability to sensor errors, this study introduces Gaussian noise to the coordinates of the robot, target point, and obstacles when calculating their relative positions. This approach effectively simulates the impact of sensor measurement errors on positioning accuracy, allowing the controller to maintain stable performance even in the presence of localization deviations. As a result, the reliability and robustness of path following and obstacle avoidance tasks are significantly improved.

When calculating the distance and angular deviation between the robot, the target point, and obstacles, Gaussian noise is applied to the robot’s coordinates $\left(x_R,y_R\right)$, the target point’s coordinates $\left(x_T,y_T\right)$, and the obstacle’s coordinates $\left(x_O,y_O\right)$. The noise-affected coordinates, indicated by a superscript, represent the positions after noise is added, as introduced in Equation (5).

$$\left\{\begin{array}{l}{x}_R^{noise}=x_R+\mu \cdot clip\left(N_1\left(0,1\right),-1,1\right)\\ y_R^{noise}=y_R+\mu \cdot clip\left(N_2\left(0,1\right),-1,1\right)\\ x_O^{noise}=x_O+\mu \cdot clip\left(N_3\left(0,1\right),-1,1\right)\\ y_O^{noise}=y_O+\mu \cdot clip\left(N_4\left(0,1\right),-1,1\right)\\ x_T^{noise}=x_T+\mu \cdot clip\left(N_5\left(0,1\right),-1,1\right)\\ y_T^{noise}=y_T+\mu \cdot clip\left(N_6\left(0,1\right),-1,1\right)\end{array}\right.,$$

(5)

where $N_i\left(0,1\right)\left(i=1,2,\cdots ,6\right)$ represents random variables sampled from a standard normal distribution with mean 0 and variance 1, and $\mu$ is a scaling factor, set to 0.5 in this study. To prevent excessive noise that could cause data to deviate beyond reasonable bounds, a clipping operation $\left(clip\right)$ is applied. This ensures that noise does not overly interfere with the localization data while retaining a degree of randomness to simulate real-world sensor errors. After incorporating Gaussian noise, the distance deviations between the robot and the target point and obstacles, $D_{RT}$ and $D_{RO}$, can be calculated as shown in Equation (6).

$$\left\{\begin{array}{l}{D}_{RT}^{noise}=\sqrt{{\left(x_T^{noise}-x_R^{noise}\right)}^2+{\left(y_T^{noise}-y_R^{noise}\right)}^2}\\ D_{RO}^{noise}=\sqrt{{\left(x_O^{noise}-x_R^{noise}\right)}^2+{\left(y_O^{noise}-y_R^{noise}\right)}^2}-R_O\end{array}\right.,$$

(6)

where $R_O$ is the radius of the obstacle. In this study, $R_O$ ranges from 2 m to 15 m.

Similarly, the heading angle deviations of the robot with respect to the target point and obstacles, ${\phi }_{RT}$ and ${\phi }_{RO}$, are computed based on the noisy coordinates as shown in Equation (7).

$$\left\{\begin{array}{l}{\phi }_{RT}^{noise}={\theta }_{heading}-arctan2\left(y_T^{noise}-y_R^{noise},x_T^{noise}-x_R^{noise}\right)\\ {\phi }_{RO}^{noise}={\theta }_{heading}-arctan2\left(y_O^{noise}-y_R^{noise},x_O^{noise}-x_R^{noise}\right)\end{array}\right.,$$

(7)

where ${\theta }_{heading}$ is the heading angle of the deep-sea mining robot.

To ensure that the angle deviations remain within a valid range, they are restricted to $\left(-\pi ,\left.\pi \right]\right.$, as formulated in Equation (8).

$$\left\{\begin{array}{l}{\phi }_{RT}^{noise}={\phi }_{RT}^{noise}-2\pi \cdot round\left({\phi }_{RT}^{noise}/2\pi \right)\\ {\phi }_{RO}^{noise}={\phi }_{RO}^{noise}-2\pi \cdot round\left({\phi }_{RT}^{noise}/2\pi \right)\end{array}\right.$$

(8)

These calculations ensure that, even with the introduction of random noise, the controller can accurately perceive relative positions and angular deviations, thereby enhancing the system’s robustness in complex operational environments.

To enhance the training efficiency and stability of the deep reinforcement learning (DRL) algorithm, the input states and output actions of the controller were normalized to the range $\left[-1,1\right]$. This normalization not only eliminates the impact of varying data scales on training, but also accelerates convergence and improves algorithm performance. Based on this setup, the controller’s inputs consist of 12-dimensional observational data, while the outputs are 4-dimensional track angular velocity adjustments.

Observation Inputs:

$$input=\left[\begin{array}{l}clip\left(D_{RT}^{noise}/50-1,-1,1\right)\\ clip\left(D_{RO}^{noise}/15-1,-1,1\right)\\ clip\left({\phi }_{RT}^{noise}/\pi ,-1,1\right)\\ clip\left({\phi }_{RO}^{noise}/\pi ,-1,1\right)\\ clip\left(V_L/0.5-1,-1,1\right)\\ clip\left(V_R/0.5-1,-1,1\right)\\ clip\left(\left(A_x+0.4\right)/4.8,-1,1\right)\\ clip\left(A_{\omega }/2.2,-1,1\right)\\ clip\left(i_{L1}/1.0,-1,1\right)\\ clip\left(i_{L2}/1.0,-1,1\right)\\ clip\left(i_{R1}/1.0,-1,1\right)\\ clip\left(i_{R2}/1.0,-1,1\right)\end{array}\right],$$

(9)

where $V_L$ and $V_R$ denote the velocities of the left and right tracks of the deep-sea mining robot, respectively. Additionally, $A_x$ and $A_{\omega }$ denote the forward acceleration and rotational acceleration, respectively, while $i_{L1},i_{L2},i_{R1},i_{R2}$ represent the slippage rates of the four tracks [16].

Notably, during training, the initial distance between the robot and the target point is fixed at 100 m, and the robot’s detection radius is set to 30 m. When no obstacle is detected, ${\phi }_{RO}^{noise}$ is set to $\mathsf{\pi }/2$, indicating that the obstacle is assumed to always be to the robot’s right, thereby not affecting the robot’s path following.

Action Outputs:

$$\left\{\begin{array}{l}{\omega }_{L1}^{signal}={\omega }_{max}\cdot \left(output\left[1\right]+1\right)/2\\ {\omega }_{L2}^{signal}={\omega }_{max}\cdot \left(output\left[2\right]+1\right)/2\\ {\omega }_{R1}^{signal}={\omega }_{max}\cdot \left(output\left[3\right]+1\right)/2\\ {\omega }_{R2}^{signal}={\omega }_{max}\cdot \left(output\left[4\right]+1\right)/2\end{array}\right.,$$

(10)

where ${\omega }_{\max }$ represents the maximum allowable angular velocity for the tracks, with a value of 2.8274 rad/s in this study [16]. The Deep Reinforcement Learning (DRL) model generates a set of actions, denoted as $\mathrm{output}\left[i\right]$ for $i=1,2,3,4$, which serve as the raw control commands. These outputs are subsequently processed and transformed into the actual control signals, ${\omega }_{L1}^{signal},{\omega }_{L2}^{signal},{\omega }_{R1}^{signal},{\omega }_{R2}^{signal}$, ensuring the precise execution of the control strategy.

2.2.3. Reward Design for Dual-Task Control

The design of reward functions is a critical challenge in reinforcement learning, essential for guiding agents to learn effective strategies. Research highlights the importance of balancing informativeness and sparsity in reward design to accelerate learning and maintain simplicity [19,20]. Explicable rewards shaped by potential functions enhance learning efficiency without altering optimal policies [20], while complex tasks can be addressed by decomposing them into subtasks with dedicated reward functions, improving robustness and adaptability [19,21]. Drawing on these principles and prior designs in similar scenarios [16], this study develops a multi-dimensional reward function system. Grounded in the TD3 algorithm and input–output framework, the system allocates reward signals to dynamically balance strategies for path following and obstacle avoidance tasks.

The reward functions are grounded in environmental feedback, avoiding the use of estimated or indirectly observed state information to ensure reliability and practical significance during training.

The reward framework is designed around the core objectives of dual-task control for deep-sea mining robots, integrating key parameters and logical conditions to effectively guide the robot in optimizing its decision-making strategy during training. The path following reward function $r_{TF}$ evaluates the robot’s angular deviation ${\phi }_{RT}$ from the target in real time, as formulated in Equation (11). For small deviations, an exponentially decaying reward is applied to encourage rapid directional adjustments; for deviations exceeding ${\displaystyle \frac{\pi }{2}}$, a fixed penalty is imposed to prevent loss of the target or excessive directional deviation. The parameter $K_1=5$ is introduced to modulate the magnitude of positive rewards in $r_{TF}$, ensuring a balanced trade-off between directional correction and stable path-following behavior.

$$r_{TF}=\left\{\begin{array}{l}{e}^{-K_1{\phi }_{RT}^2}, \mathrm{if} \left|{\phi }_{RT}\right|\le {\displaystyle \frac{\pi }{2}}\\ -1, \mathrm{else}\end{array}\right.$$

(11)

The obstacle avoidance reward function $r_{OA}$ monitors the minimum distance $D_{RO}$ between the robot and obstacles, implementing a dynamic penalty mechanism within the safety threshold, as formulated in Equation (12). When the robot approaches an obstacle closer than $R_{eff}+D_{safe}$ (the specific definitions of the effective radius $R_{eff}$ and the safety distance $D_{safe}$ are illustrated in Figure 3), a penalty is applied to mitigate potential collision risks. Within the safe range, no reward or penalty is issued, maintaining the simplicity and stability of the reward function to support regular cruising behavior.

$$r_{OA}=\left\{\begin{array}{l}-1, \mathrm{if} D_{RO}<R_{eff}+D_{safe}\\ 0, \mathrm{else}\end{array}\right.$$

(12)

The velocity control reward function $r_V$ aims to encourage the robot to maintain an appropriate operating speed during tasks, preventing efficiency losses caused by low-speed operation. In deep-sea mining tasks, the robot’s speed range is defined as 0-1 m/s, with a minimum allowable forward velocity of 0.5 m/s. The reward value is linearly correlated with the velocity deviation, where $K_2=2$. This parameter is selected such that the reward reaches its maximum value of +1 when the speed is 1.0 m/s and decreases linearly to 0 at the minimum allowable speed of 0.5 m/s. A fixed penalty is applied for speeds below this threshold, thereby improving overall task efficiency, as formulated in Equation (13).

$$r_V=\left\{\begin{array}{l}{K}_2\left(V_{heading}-0.5\right), \mathrm{if} V_{heading}\ge 0.5\\ -1, \mathrm{else}\end{array}\right.$$

(13)

The slip reward function $r_{Slip}$ monitors the slip rates of all four tracks to ensure stable operation on complex terrains. A penalty is imposed when the slip rate of any track exceeds 50% [16], reducing the risk of path deviation or task failure, as defined in Equation (14).

$$r_{Slip}=\left\{\begin{array}{l}-1, \mathrm{if}\max \left(i_{L1},i_{L2},i_{R1},i_{R2}\right)>0.5\\ 0, \mathrm{else}\end{array}\right.$$

(14)

The single-step reward function $r_{Step}$ serves as a cornerstone of the dual-task control strategy for deep-sea mining robots, playing a pivotal role in balancing the priorities between path following and obstacle avoidance during reinforcement learning training. This function integrates multiple sub-tasks through a multi-dimensional weighting mechanism, guiding the robot to execute operations efficiently and reliably in complex deep-sea environments. The reward function design holistically incorporates four critical factors: path following, obstacle avoidance, velocity control, and slip detection, establishing a task-oriented and dynamically adjustable multi-task reinforcement learning framework, as formulated in Equation (15).

$$r_{Step}=\left\{\begin{array}{l}-5, \mathrm{if} n_{step}\ge 600\\ 60, \mathrm{elif} D_{RT}\le L/2\\ -120, \mathrm{elif} D_{RO}\le R_{eff}\\ {\displaystyle \frac{{\epsilon }_1{r}_{TF}+{\epsilon }_2{r}_V+{\epsilon }_3{r}_{OA}+{\epsilon }_4{r}_{Slip}}{{\epsilon }_1+{\epsilon }_2}}, \mathrm{else}\end{array}\right.$$

(15)

The reward design incorporates direct rewards and penalties, focusing on balancing goal achievement and obstacle avoidance safety. Penalties are imposed if the task exceeds 600 steps without reaching the goal, preventing inefficient exploration. Rewards are provided when the robot approaches the target within half its body length, encouraging task completion [16]. Additionally, strong penalties are applied if the robot’s distance to an obstacle falls below the inflated radius $R_{eff}$, ensuring timely avoidance and enhancing the robustness of the obstacle avoidance strategy and overall operational safety.

During regular operations, the step reward function dynamically balances sub-task rewards for path following, obstacle avoidance, speed control, and slip detection through weighted integration. The specific weights are assigned as follows: ${\epsilon }_1=2$ for path following, ${\epsilon }_2=1$ for speed, ${\epsilon }_3={\epsilon }_1+{\epsilon }_2=3$ for obstacle avoidance, and ${\epsilon }_4=1$ for slip penalties. By normalizing the positive rewards, the maximum step reward is capped at $+1$, ensuring a rational distribution of reward signals. This approach not only reflects the priority of individual sub-tasks, but also enables the dynamic adjustment of policy tendencies during reinforcement learning, achieving a synergy of safety and efficiency for the robot in complex deep-sea operational environments.

3. Environment Optimization

This section presents a training environment optimization framework aimed at enhancing the robustness and adaptability of the deep-sea mining robot in complex underwater conditions. To this end, a Dual-Task Environment (DTE) is developed, integrating the Random Obstacle Environment (ROE) for generalization and the Obstructed Path Environment (OPE) for structured navigation challenges. By dynamically alternating between these two settings, the DTE ensures a balanced training approach that strengthens both path following accuracy and obstacle avoidance capabilities. The following sections detail the environment design, training methodology, and simulation-based performance evaluation.

3.1. Environment Set Up for Dual-Task

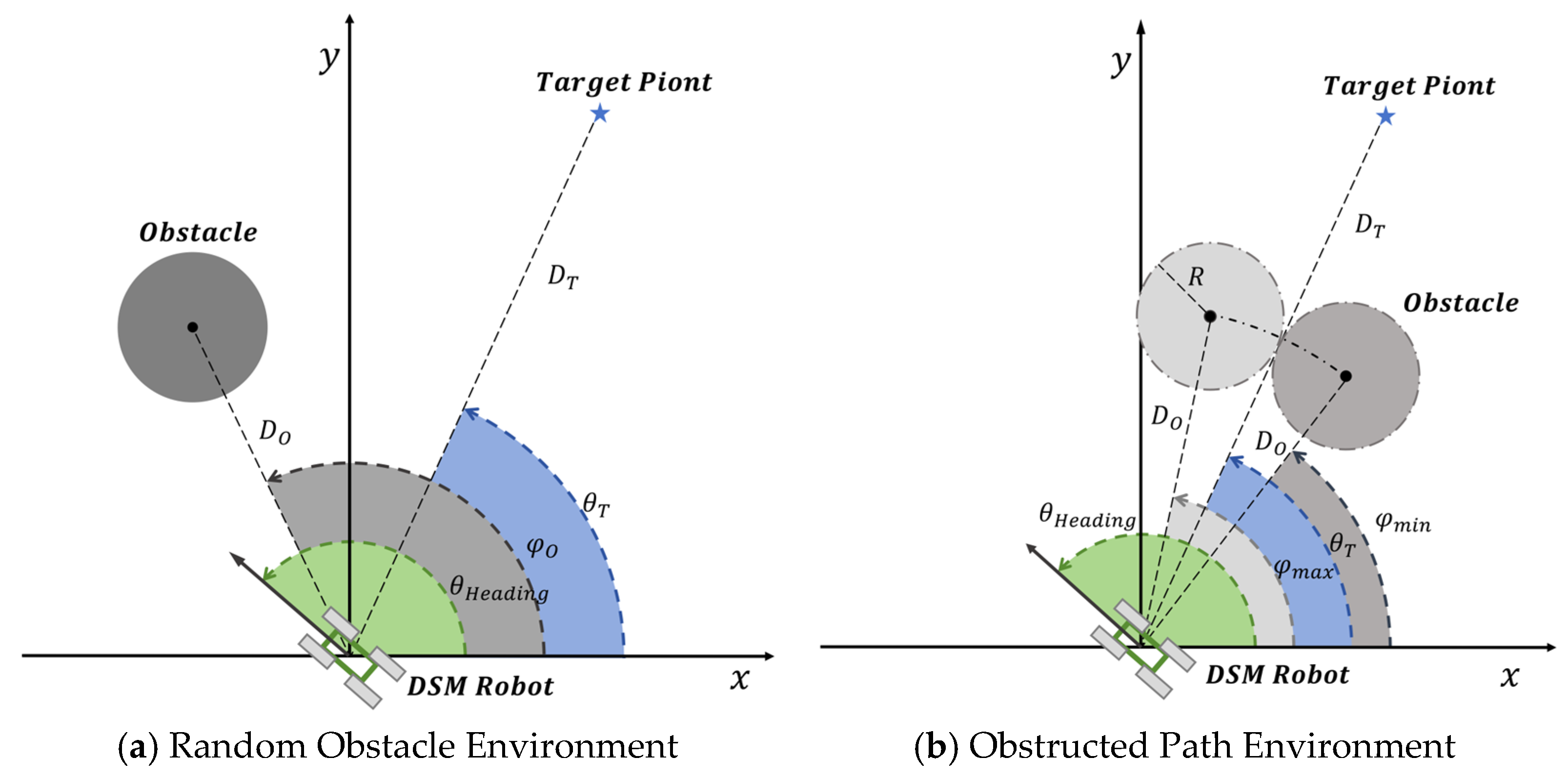
Deep-sea mining robots must simultaneously achieve path following and obstacle avoidance, requiring extensive training across diverse environments to enhance their overall adaptability. This study builds on the conventional Random Obstacle Environment and proposes a novel Obstructed Path Environment. Additionally, a Dual-Task Environment is developed by integrating ROE and OPE to provide tailored training support for reinforcement learning, as illustrated in Figure 4.

The ROE, shown in Figure 4a, is a commonly used setup to evaluate the path following and obstacle avoidance capabilities of intelligent agents. The specific configurations are as follows:

Robot Initial Position: The robot’s initial position is randomly generated within a circular area centered at the origin (0, 0), with an initial heading angle ${\theta }_{Heading}$ uniformly distributed between $0^{\circ }$ and ${180}^{\circ }$.

Target Position: The target is randomly placed on a circular arc 100 m away from the origin, with an angular span ${\theta }_T$ in the range of $\left[0^{\circ },{180}^{\circ }\right]$.

Obstacle Placement: Obstacles are randomly positioned in the potential trajectory area between the robot and the target. The obstacles are distributed along a circular arc with a central angle ${\theta }_O$ spanning [0°, 180°]. To ensure sufficient clearance, obstacles are placed at least 100 m away from both the origin and the target. Their radii range between 2 m and 15 m. While the obstacle placement is random, it rarely blocks the direct path between the robot and the target, occasionally creating hindrances.

ROE provides a simplified environment widely adopted in reinforcement learning for deep-sea mining tasks. While effective for training basic path following strategies, it often lacks the complexity to sufficiently simulate dual-task scenarios, where simultaneous path following and dynamic obstacle avoidance are critical.

To address the limitations of the ROE in training effective obstacle avoidance strategies, this study introduces the OPE. The core idea is to strategically place obstacles in positions that are more likely to directly block the robot’s path to the target, thereby enhancing the robot’s learning potential in complex avoidance tasks. As shown in Figure 4b, the OPE imposes additional constraints on obstacle distribution based on the initial positions of the robot and the target. The valid angular range for obstacle placement is rigorously constrained according to Equation (16).

$$\left\{\begin{array}{l}{\phi }_{min}={\theta }_T-arcsin\left(R_O/D_O\right)\\ {\phi }_{max}={\theta }_T+arcsin\left(R_O/D_O\right)\end{array}\right.$$

(16)

Here, obstacle centers are randomly generated within the range, ensuring that the obstacles intersect with the direct path between the robot and the target.

The OPE enhances the specificity and complexity of avoidance strategy training by carefully controlling obstacle placement. Under OPE conditions, the robot must overcome direct obstructions, thereby improving its ability to handle challenging avoidance scenarios. However, while the OPE increases the complexity and difficulty of avoidance tasks, it may reduce the success rate of path following tasks.

To balance these trade-offs, this study combines ROE and OPE into a unified framework termed the DTE. The DTE is a comprehensive training framework designed to balance the training requirements for both path following and obstacle avoidance. In the DTE, each training episode alternates randomly between ROE and OPE, ensuring that the robot acquires the adaptability and task versatility required for different scenarios. Specifically, the DTE dynamically adjusts obstacle distribution characteristics (as in the OPE) and obstacle randomness (as in the ROE) throughout the training process, enabling the robot to achieve more holistic and robust training outcomes.

The DTE aims to balance the agent’s performance in path following and obstacle avoidance. Section 3.2 will evaluate its effectiveness through training analysis across different environments.

3.2. Training Process

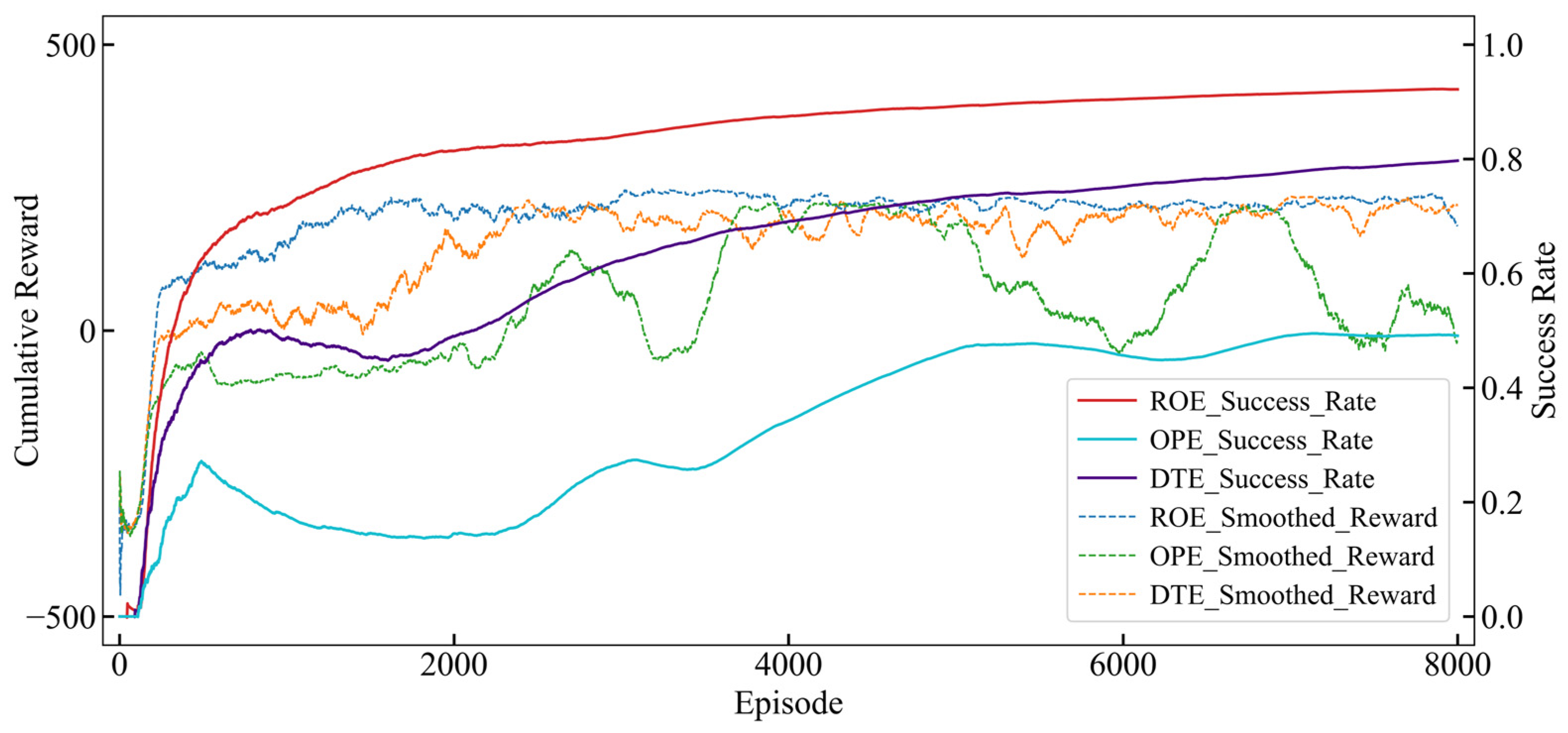
This section presents a comprehensive analysis of the training process across three distinct environments: ROE, OPE, and DTE. The evaluation is conducted using two key performance metrics: cumulative reward and success rate, as illustrated in Figure 5. A rigorous assessment of these metrics provides deeper insights into the learning efficiency and adaptability of the proposed approach in diverse operational scenarios.

In the Random Obstacle Environment (ROE), the agent demonstrated rapid convergence, with a stable increase in cumulative reward. After approximately 2000 episodes, the cumulative reward plateaued at around 230, and the success rate surpassed 80%. This suggests that the relatively straightforward nature of the path following task in the ROE facilitated the agent’s ability to quickly develop effective navigation strategies. However, the limited complexity of obstacles in this environment may have restricted the agent’s capacity to acquire advanced obstacle avoidance skills.

In contrast, the OPE presented significantly greater challenges, as reflected by the instability of cumulative rewards throughout the training process. During the initial training phase, the cumulative reward increased rapidly but soon entered a prolonged stagnation period, during which it remained negative. It was not until approximately 2000 episodes that the reward began to rise again, turning positive at around 2300 episodes. However, due to the heightened complexity of the OPE, the cumulative reward exhibited persistent fluctuations throughout the training process, oscillating between −50 and the stabilized value of 230 observed in the ROE. This instability underscores the increased difficulty posed by the dynamic and obstructed nature of the environment, which required the agent to continuously adjust its strategies. Moreover, the overall success rate declined during the reward stagnation period and only began to recover once the cumulative reward started increasing again. Nevertheless, the final success rate remained below 50%, highlighting the considerable challenges introduced by the intricate obstacle arrangements in the OPE.

The DTE, designed as a hybrid training strategy integrating the characteristics of the ROE and the OPE, enabled the agent to concurrently learn both path following and obstacle avoidance tasks. In the early training phase, the cumulative reward increased rapidly but then entered a stagnation period before 1500 episodes—a characteristic similar to that observed in the OPE. However, due to the mixed training approach, this stagnation phase was significantly shorter, and the cumulative reward remained predominantly positive during this period. As training progressed, the cumulative reward continued to rise, eventually oscillating around 200 after surpassing the stabilized value of 230 observed in the ROE. This indicates that the DTE exhibited greater stability than the OPE while still being slightly less stable than the ROE, with a notably slower convergence rate than the latter.

The success rate in the DTE initially followed a trend similar to that in the OPE, declining during the cumulative reward stagnation period and only beginning to recover once the reward started increasing again. However, a key distinction was that the success rate in the DTE continued to rise steadily throughout the later stages of training, mirroring the trend observed in the ROE. Ultimately, after 8000 episodes, the success rate stabilized at approximately 80%, demonstrating the agent’s ability to adapt to dual-task scenarios. While the training process was inherently more complex, the DTE provided a structured learning framework that enhanced the agent’s capacity to balance path following and obstacle avoidance behaviors under dynamic conditions, contributing to its overall performance across diverse scenarios.

In summary, the ROE facilitated foundational training for path following, while the OPE significantly enhanced the agent’s obstacle avoidance capabilities. By integrating these characteristics, the DTE serves as a robust platform for comprehensive dual-task evaluation. Section 3.3 will further validate the agent’s performance through simulated testing across these environments.

3.3. Dual-Task Simulation Testing

This section evaluates the performance of controllers trained in three environments (ROE, OPE, and DTE) to assess their capabilities in path following and obstacle avoidance tasks. The evaluation consists of two parts: pure path following tests (without obstacles) and randomized obstacle avoidance tests. Each controller was subjected to 500 tests in its respective environment, with each test independently initialized using a randomized starting state and obstacle configuration. This ensures a diverse and unbiased assessment of the controller’s generalization ability across different scenarios.

Path following performance across different training environments: The evaluation of path following tasks was conducted on straight and S-shaped paths in three training environments: ROE, OPE, and DTE. In the context of path following tasks for deep-sea mining operations, the selected path designs aim to rigorously evaluate the robot’s capabilities in both straight-line and turn navigation. The straight path represents stable movement in constrained or relatively flat seabed environments, whereas the S-shaped path effectively simulates the robot’s ability to maneuver through complex terrain and avoid obstacles in operational settings. The performance metrics, including trajectory deviation and average speed, are summarized in

Table 5. Performance evaluation metrics for path following and obstacle avoidance across training environments.

Training Environment	Path Following				Obstacle Avoidance
	Straight Path		S-Shaped Path
	Trajectory Deviation	Average Speed	Trajectory Deviation	Average Speed	Completion Rate	Strategy
ROE	0.169	0.826	0.432	0.806	0%	Unilateral Obstacle Avoidance
DTE	0.409	0.802	0.604	0.794	85.4%	Bilateral Obstacle Avoidance
OPE	0.685	0.810	0.734	0.803	6.6%	Unilateral Obstacle Avoidance

and illustrated in Figure 6.

To further evaluate the effectiveness of controllers trained in different environments, trajectory deviation and speed performance were assessed across both straight and S-shaped path following tasks.

For the straight path scenario, the controller trained in the ROE exhibited the highest precision, with the smallest trajectory deviation of 0.169 m. This indicates that training in a relatively structured environment optimized for path following tasks enabled the agent to achieve superior tracking accuracy. The DTE yielded a moderate trajectory deviation of 0.409 m, reflecting a balanced trade-off between precision and adaptability. In contrast, the controller trained in the OPE exhibited the largest trajectory deviation of 0.685 m, likely due to the increased complexity and dynamic obstacle arrangements encountered during training, which may have prioritized obstacle avoidance over strict trajectory adherence.

A similar trend was observed in the more challenging S-shaped path task. The ROE-trained controller maintained a trajectory deviation of 0.432 m, slightly outperforming the DTE-trained controller, which exhibited a deviation of 0.604 m. Meanwhile, the OPE-trained controller demonstrated the highest deviation at 0.734 m, indicating the heightened difficulty in maintaining precise path tracking under curved and complex trajectories.

Despite these variations in trajectory deviation, the average speed remained consistent at approximately 0.8 m/s across all environments. This suggests that differences in training strategies primarily influenced trajectory precision rather than the controller’s capability to maintain a stable velocity. The results highlight the trade-offs between training environments, with the ROE favoring precision, OPE emphasizing adaptability to complex conditions, and DTE achieving a balance between the two.

Obstacle avoidance performance across different training environments: The obstacle avoidance performance was evaluated by analyzing the completion rate across 500 independently initialized, randomly generated obstacle scenarios for each environment, as detailed in Table 5, with one such scenario illustrated in Figure 7. The completion rate is defined as the proportion of successful target-reaching instances out of 500 independently randomized initialization tests. To ensure a diverse set of obstacle configurations, each environment was uniquely initialized, thereby more accurately simulating the unpredictability and complexity of real-world deep-sea mining operations. This randomized initialization enables a comprehensive assessment of the algorithm’s adaptability to varying environmental conditions. The results indicate substantial performance differences across the three environments, underscoring the distinct challenges posed by different randomized obstacle distributions.

In the ROE, the controller failed to complete any obstacle avoidance tasks, with a completion rate of 0%, highlighting the inadequacy of this setting for training robust obstacle avoidance capabilities. The OPE-trained controller achieved a completion rate of only 6.6%, likely due to constrained obstacle placements increasing task difficulty. Both the OPE and ROE utilize unilateral obstacle avoidance strategies, which limit their effectiveness in handling more complex scenarios. In contrast, the DTE-trained controller significantly outperformed both, achieving a completion rate of 85.4%. This demonstrates the effectiveness of the bilateral obstacle avoidance strategies employed in the DTE, enabling dynamic adaptability to complex obstacle configurations and successful task completion.

3.4. Summary

This section presents a comprehensive investigation into the path following and obstacle avoidance capabilities of deep-sea mining robots, focusing on the design, training, and simulation testing of three distinct training environments: ROE, OPE, and DTE. The ROE is well suited for fundamental path following tasks, demonstrating robust stability and trajectory accuracy. However, its random obstacle distribution limits its training efficacy for obstacle avoidance. The OPE addresses this limitation by refining obstacle placement, significantly enhancing the robot’s obstacle avoidance capabilities. Nonetheless, its support for path following is weaker, and the high complexity of obstacle avoidance tasks reduces overall training efficiency. To achieve a balanced optimization of dual-task performance, this study introduces the DTE, which dynamically integrates the strengths of the ROE and OPE, enabling the robot to achieve a well-rounded performance in both tasks.

During training, the DTE exhibited superior adaptability, achieving relatively high cumulative rewards and success rates among the three environments, underscoring its potential for complex tasks. In path following, the DTE closely matched the ROE in trajectory accuracy and speed. In obstacle avoidance, its success rate far exceeded that of the other environments. Overall, the DTE provides robust support for the stability and operational efficiency of deep-sea mining robots in complex operational scenarios. In the next section, the study will further optimize the algorithm design based on the DTE to address more intricate and dynamic operational demands.

4. Algorithm Optimization

This section introduces an optimization methodology for enhancing the adaptability and decision-making efficiency of the TD3 algorithm in complex dual-task scenarios. To this end, a Dynamic Multi-Step Update mechanism is proposed, which extends the target Q-value estimation to multi-step returns, integrating both immediate rewards and long-term returns to improve policy learning. The mechanism dynamically adjusts trajectory selection during the multi-step return calculation, ensuring a balance between computational efficiency and optimization performance. To evaluate its effectiveness, training performance under different DMSU parameter settings is analyzed, followed by a comprehensive assessment of its impact on path following accuracy, strategy stability in obstacle avoidance, and robustness in multi-directional obstacle scenarios.

4.1. The Principle of Dynamic Multi-Step Update

To further enhance the adaptability and performance of the TD3 algorithm in complex dual-task scenarios, this study introduces the Dynamic Multi-Step Update mechanism. The DMSU extends the calculation range of target Q-values to multi-step returns, integrating immediate rewards with long-term returns to significantly improve the agent’s policy learning capability. Moreover, the DMSU dynamically adjusts the trajectory selection during the multi-step return calculation without imposing additional constraints, ensuring a balance between computational efficiency and effectiveness.

The target Q-value is calculated as shown in Equation (17).

$$Q_{target}\left(s_k,a_k\right)={\displaystyle \sum _{t=k}^{k+n-1}{\gamma }^{t-k}{r}_t}+{\gamma }^{n}min\left(Q_{{\theta }_1}\left(s_{k+n},a_{k+n}\right),Q_{{\theta }_2}\left(s_{k+n},a_{k+n}\right)\right),$$

(17)

where $s_k$ and $a_k$ denote the state and action at time step $k$; $n$ is the hyperparameter of the DMSU, defining the maximum number of steps for multi-step returns; $Q_{{\theta }_1}$ and $Q_{{\theta }_2}$ are the two target Critic networks that evaluate the state–action pairs at time step $k+n$.

During training, the DMSU adjusts the target Q-value calculation based on the trajectory length.

Complete trajectory calculation: When the remaining trajectory steps are greater than or equal to $n$, the full n-step return is computed as shown in Equation (17).

Incomplete trajectory calculation: When the remaining trajectory steps are fewer than $n$, all remaining step rewards are calculated, and the target Q-value for steps beyond $n$ is set to zero. The simplified target Q-value is given by Equation (18).

$$Q_{target}\left(s_k,a_k\right)={\displaystyle \sum _{t=k}^{k+s-1}{\gamma }^{t-k}{r}_t}$$

(18)

This dynamic adjustment mechanism ensures the rationality and stability of target Q-value computation even in the presence of incomplete trajectories, thereby improving the algorithm’s generalization ability.

To visualize the integration of the DMSU into the TD3 algorithm, the improved algorithmic framework is depicted in Figure 8. The framework retains the dual-Critic structure of TD3 while enabling dynamic trajectory adjustment through the DMSU. The trajectories stored in the experience replay buffer are dynamically adapted to the logic of the DMSU, ensuring full utilization of trajectory information and stable training. The detailed algorithmic procedure is presented in Algorithm 1.

Algorithm 1: Optimized TD3 (reducing to the original TD3 algorithm when $n=1$)
Input:	initial critic networks $Q_{{\theta }_1}$, $Q_{{\theta }_2}$ and actor network ${\pi }_{\varphi }$ with random parameters ${\theta }_1$, ${\theta }_2$, $\varphi$
Input:	initial target networks ${\theta }_1^{\prime }\leftarrow {\theta }_1$, ${\theta }_2^{\prime }\leftarrow {\theta }_2$, ${\varphi }^{\prime }\leftarrow \varphi$
Input:	initial replay buffer $B$
Input:	initial hyperparameters: actor network learning rate $l_{\alpha }$, critic network learning rate $l_{\beta }$, target network soft update rate $\tau$, mini-batch size $k_{batch}$, memory pool size $N_{max}$, update actor interval $N_{int}$, discount factor $\gamma$, learning time step $t$, standard deviation ${\sigma }_1$, ${\sigma }_2$, target action noise clipping $c$, exploration noise decaying coefficient ${\lambda }_{exp}$, policy noise ${\xi }_{policy}=clip(normal(0$, ${\sigma }_1))$, $-c$, $c)$, exploration noise ${\xi }_{exp}=normal(0$, ${\sigma }_2{\lambda }_{exp}^{{\displaystyle \frac{t}{5000}}})$, total episodes $T$, random seed 24, max step length $n$
for $t=1$ to $T$ do
	Select action $a_t\leftarrow {\pi }_{\varphi }(s)+{\xi }_{exp}$
	Observe: reward $r_t$, new state $s_{t+1}$, Store trajectory $(s_t$, $a_t$, $r_t$, $s_{t+1})$ in $B$ with max size $N_{max}$
	Sample: mini-batch of $k_{batch}$ trajectories $(s_t$, $a_t$, ${\displaystyle \sum _{k=t}^{t+n-1}{\gamma }^{k-t}}{r}_k$, $s_{t+n})$ from $B$, then update critic using:
	$a_{t+n}^{\prime }\leftarrow {\pi }_{\varphi }^{\prime }(s_{t+n})+{\xi }_{policy}$,
	$y_t={\displaystyle \sum _{k=t}^{t+n-1}{\gamma }^{k-t}}{r}_k+{\gamma }^n\underset{i=1,2}{min}{Q}_{{\theta }_i}^{\prime }(s_{t+n}$, $a_{t+n}^{\prime })$,
	${\theta }_i\leftarrow arg\underset{{\theta }_i}{min}{k}^{-1}{\displaystyle \sum (y_t-Q_{{\theta }_i}(}{s}_t$, $a_t))$, $i=1,2.$
	if $t\mathrm{mod} N_{int}=0$
	Update $\varphi$ by the deterministic policy gradient:
	${\nabla }_{\varphi }J(\varphi )=k^{-1}{\displaystyle \sum {\nabla }_{a_t}}{Q}_{{\theta }_1}(s_t,a_t){|}_{a_t={\pi }_{\varphi }(s_t)}{\nabla }_{\varphi }{\pi }_{\varphi }(s_t)$
	Update target networks by:
	${\theta }_1^{\prime }\leftarrow (1-\tau ){\theta }_1+\tau {\theta }_1^{\prime }$,
	${\theta }_2^{\prime }\leftarrow (1-\tau ){\theta }_2+\tau {\theta }_2^{\prime }$,
	${\varphi }^{\prime }\leftarrow (1-\tau )\varphi +\tau {\varphi }^{\prime }$.
	end if
end for

The Dynamic Multi-Step Update (DMSU) enhances the agent’s ability to optimize long-term objectives by incorporating multi-step returns while ensuring stable target Q-value computation under varying trajectory lengths. This mechanism mitigates the stochasticity of single-step rewards, leading to smoother policy updates and improved adaptability to complex task scenarios. Additionally, the flexibility and compatibility of the DMSU allow it to seamlessly integrate into the TD3 framework, preserving the stability of TD3 while significantly improving its learning efficiency in dual-task scenarios. As the core parameter of the DMSU, the step limit $n$ plays a critical role in balancing short-term and long-term returns. Therefore, subsequent sections investigate the training and testing performance of agents under different $n$ values, providing empirical evidence for optimizing algorithms in deep-sea mining dual-task control scenarios.

4.2. Training Process

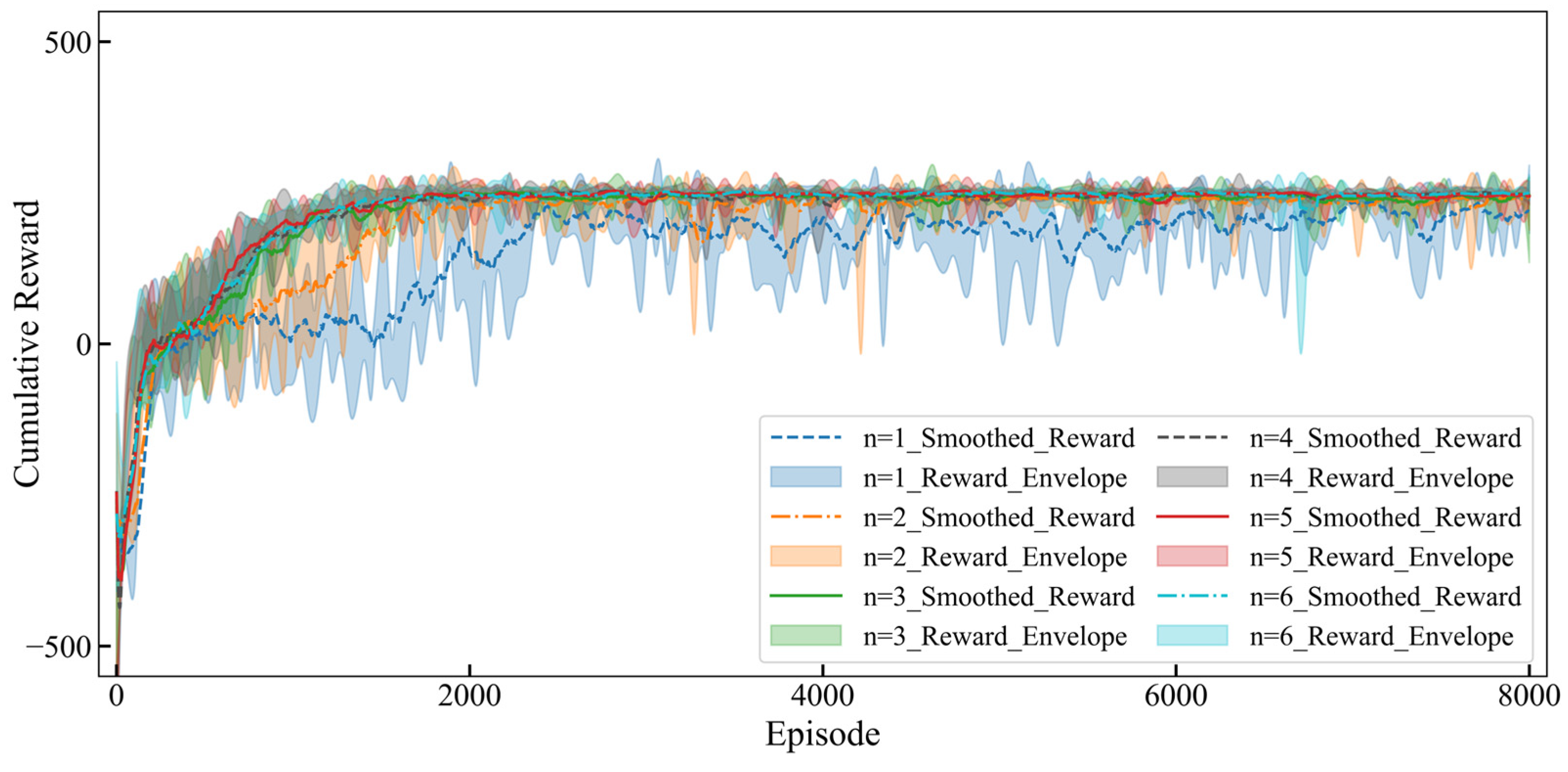
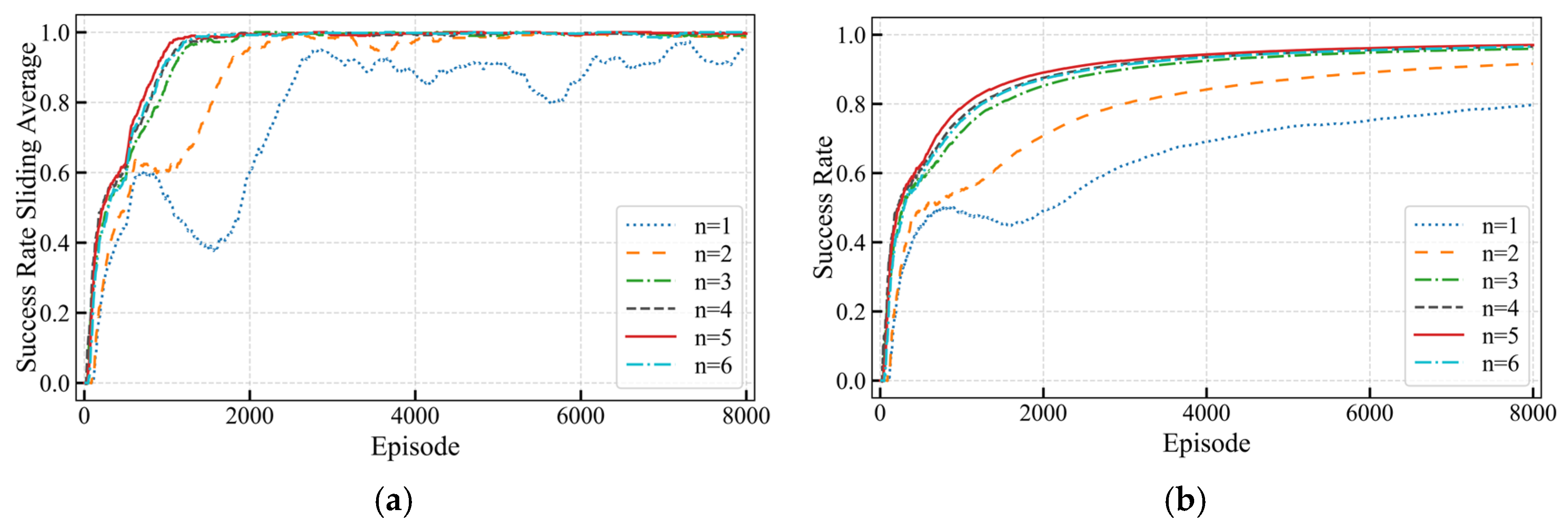
In analyzing the impact of different multi-step settings ($n=1,2,3,4,5,6$) on the training process of the Dynamic Multi-Step Update (DMSU), significant differences in performance were observed through cumulative reward trends and success rates, as illustrated in Figure 9 and Figure 10. The evaluation was conducted over 8000 training episodes for each setting. Figure 9 presents the smoothed reward curves and their envelopes across iterations, while Figure 10 compares the sliding average success rates and overall success rates.

As $n$ increased, the training performance exhibited noticeable variations. For $n=1$, although the cumulative rewards grew slowly in the early stages, the short-term update strategy struggled to adapt to complex tasks, leading to higher reward fluctuations and significantly lower final success rates compared to other settings. When $n=2,3,4$, both reward growth rates and success rates improved noticeably, but some fluctuations persisted during training, suggesting that multi-step updates in this range strike a moderate balance between short-term gains and long-term learning outcomes. At $n=5$, the training achieved its best performance. The reward curve stabilized, and the final success rate reached its peak, indicating outstanding training stability and efficiency in both path following and obstacle avoidance tasks. However, for $n=6$, the increased step count likely introduced more noise due to computational complexity, resulting in larger reward fluctuations and slightly lower final success rates compared to $n=5$.

Overall, $n=5$ emerged as the optimal multi-step update setting, demonstrating a superior balance between stability and efficiency while ensuring long-term benefits for path following and obstacle avoidance tasks. Compared to traditional single-step updates, the DMSU effectively mitigates the impact of single-step reward fluctuations and dynamically enhances the adaptability of the agent to complex task scenarios. In the upcoming Section 4.3, simulation tests will further evaluate the impact of different multi-step settings on control performance and assess the practical effectiveness of the improved DMSU algorithm in path following and obstacle avoidance tasks, providing additional validation for its efficacy.

4.3. Dual-Task Simulation Testing

4.3.1. Path Following Without Obstacles

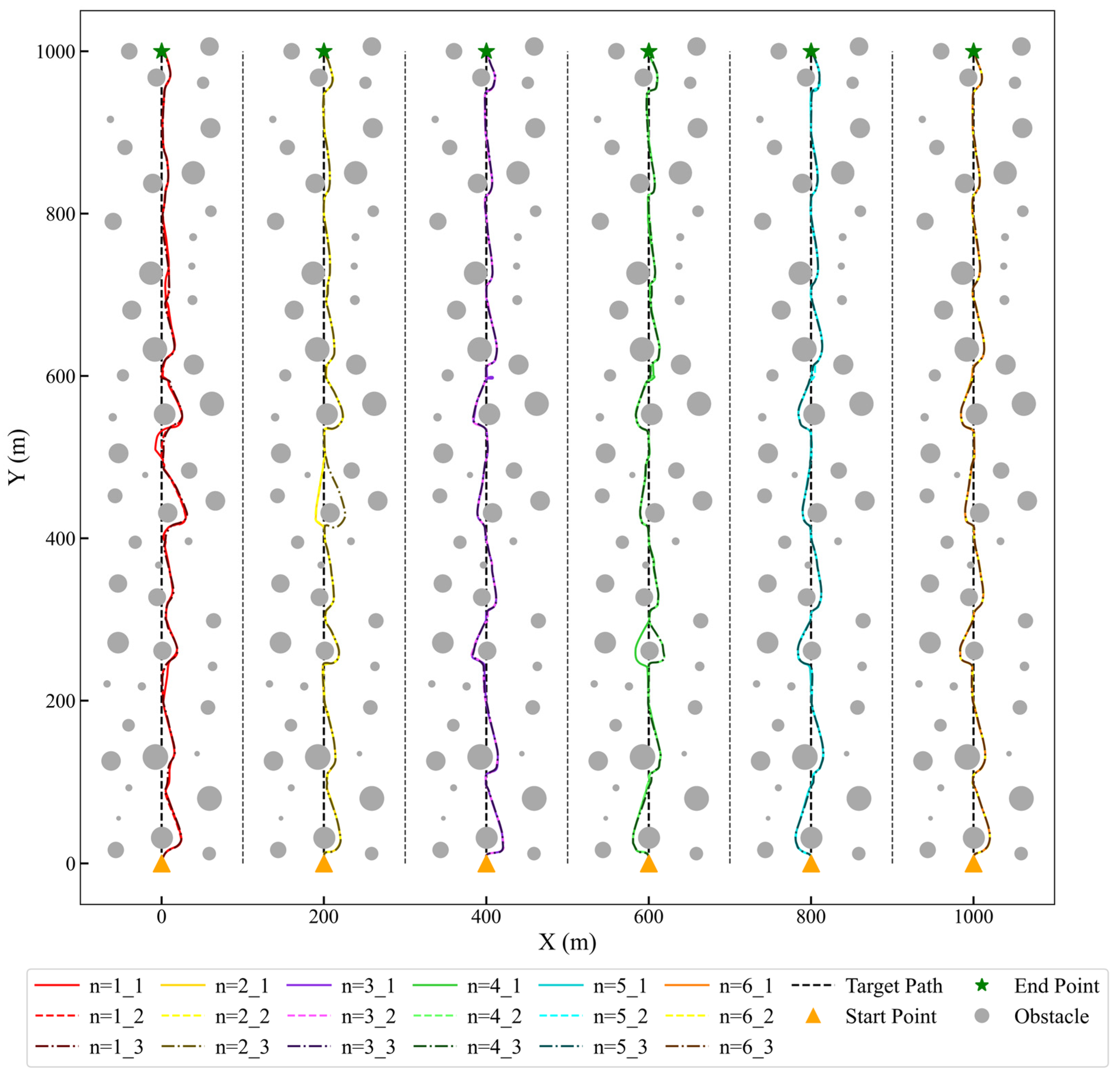
To comprehensively evaluate the performance of the DMSU strategy in path following tasks, this section conducts detailed simulation tests on controllers with varying multi-step update settings. The test paths include a straight path and an S-shaped path. Each controller was subjected to 500 repetitions on each test path to comprehensively assess following accuracy and speed performance in scenarios with varying path complexities. The results are summarized in

Table 6. Performance metrics for path following under different multi-step settings.

Step Limited	Straight Path		S-Shaped Path
	Trajectory Deviation	Average Speed	Trajectory Deviation	Average Speed
$n=1$	0.413	0.803	0.603	0.793
$n=2$	0.149	0.806	0.200	0.801
$n=3$	0.148	0.814	0.223	0.815
$n=4$	0.144	0.820	0.179	0.819
$n=5$	0.128	0.822	0.195	0.814
$n=6$	0.150	0.826	0.282	0.823

, and the following trajectories are visualized in Figure 11.

For the straight path tests, the controller with $n=5$ demonstrated the smallest trajectory deviation of 0.128 m, indicating optimal accuracy. This was closely followed by $n=4$, with a deviation of 0.144 m. In contrast, $n=1$ (representing the original TD3 algorithm) showed a much higher deviation of 0.413 m, significantly underperforming. These results validate the notable improvement in following accuracy achieved through the Dynamic Multi-Step Update strategy. Additionally, the average speed across all settings remained close to 0.8 m/s, with $n=6$ achieving the highest average speed of 0.826 m/s, slightly exceeding $n=5$ at 0.822 m/s.

For the more complex S-shaped path tests, the controller with $n=4$ achieved the lowest trajectory deviation of 0.179 m, showcasing the best following accuracy, followed by $n=5$ with a deviation of 0.195 m, which also falls within acceptable limits. However, the deviation for $n=6$ increased to 0.282 m, likely due to excessive update steps causing instability or disturbances. In terms of speed, all configurations maintained an average speed near 0.8 m/s. The highest average speed of 0.823 m/s was observed for $n=6$, but its reduced accuracy indicates potential trade-offs in performance.

Overall, the results from both the straight and S-shaped paths demonstrate that the Dynamic Multi-Step Update strategy significantly enhances following accuracy in path following tasks. Notably, the configurations with $n=4$ and $n=5$ outperformed the others. $n=4$ achieved the lowest trajectory deviation in complex path scenarios, while $n=5$ delivered the best balance of accuracy and speed, exhibiting superior overall performance. By comparison, $n=1$ (original TD3 algorithm) showed markedly inferior results, further validating the effectiveness of the Dynamic Multi-Step Update strategy. In conclusion, $n=5$ is identified as the optimal multi-step update configuration, providing a solid foundation for high-performing controllers in subsequent tasks. The next section will further evaluate the multi-step update strategy’s performance in obstacle avoidance tasks to comprehensively validate its practical applicability.

4.3.2. Validation of Strategy Consistency and Stability in Obstacle Avoidance

To verify the consistency and stability of the agent’s strategy in obstacle avoidance tasks, we conducted repeated simulations under identical random obstacle distribution environments for different step-length constraints ($n=1,2,3,4,5,6$). For each step-length setting, three trials were performed using a fixed set of randomly generated obstacles in the environment, and their trajectories were recorded to evaluate repeatability and consistency. The results are presented in Figure 12.

As shown in Figure 12, under identical obstacle distribution environments, the three repeated trajectories for different step-length settings exhibited high overlap on the overall path. Particularly for $n=4$ and $n=5$, the trajectories across three trials were nearly identical, demonstrating the agent’s highly stable execution capability in obstacle avoidance tasks under consistent conditions. Even in regions with dense or complex obstacles, the overlap of trajectories remained high, indicating reliable repeatability in complex environments. For $n=1$, the limited step-length constraint reduced the generalization capability of the agent’s strategy, leading to slight deviations in certain regions. However, the overall repeatability remained within an acceptable range, further validating the significant impact of step-length parameters on the stability of the agent’s learning strategy.

The experimental results clearly demonstrate that the agent’s strategies in obstacle avoidance tasks possess a high degree of repeatability and consistency. This underscores the rationality and effectiveness of the training method and experimental design. High trajectory repeatability not only enhances the reliability of the experimental results, but also lays a solid foundation for subsequent tests in more complex environments. The next subsection will further evaluate the robustness and adaptability of the agent’s obstacle avoidance strategies in randomized dynamic obstacle environments.

4.3.3. Robustness Test in Multi-Directional Obstacle Avoidance

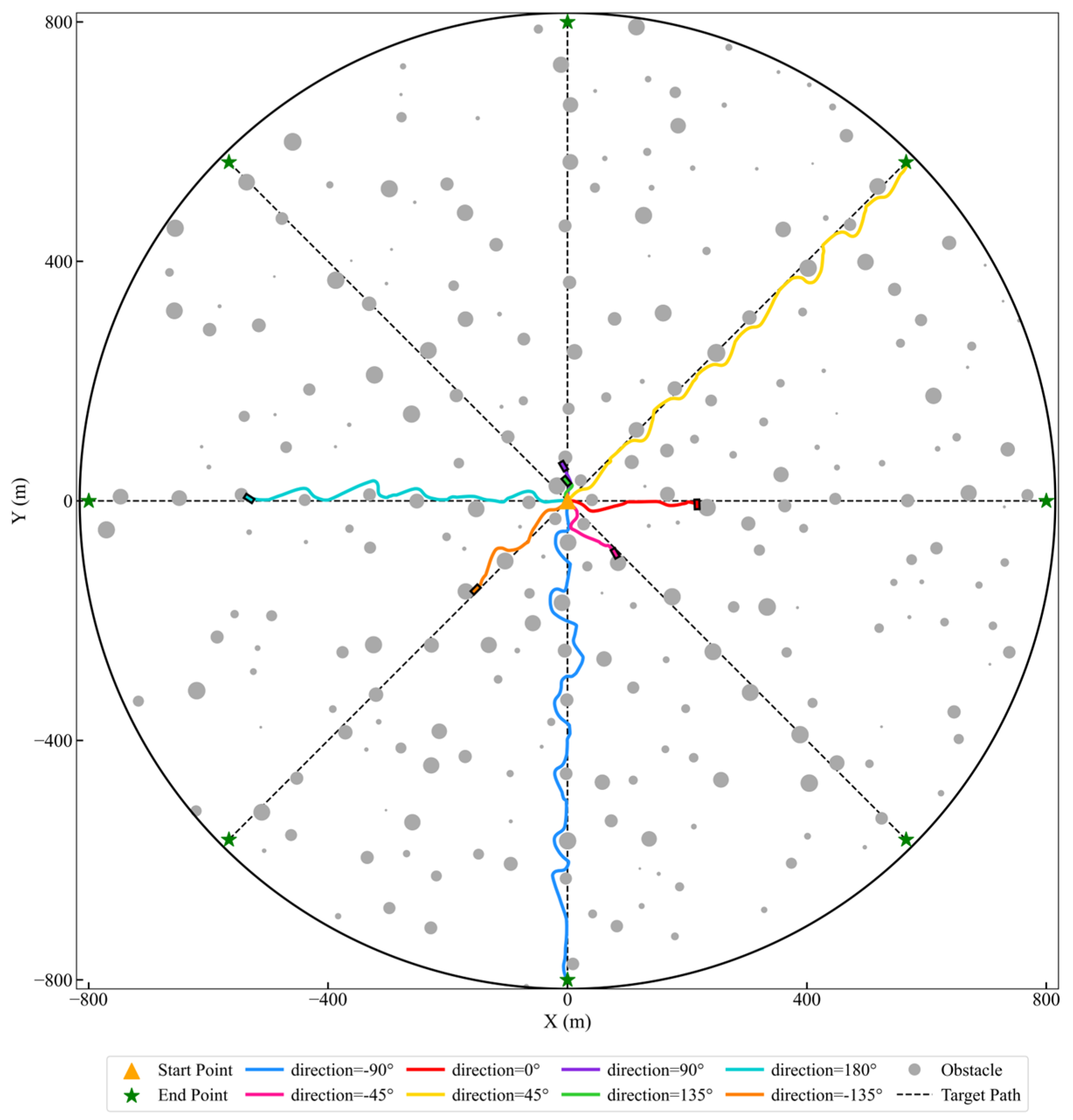
To evaluate the robustness and adaptability of the DMSU strategy in complex multi-directional obstacle environments, we conducted comprehensive tests under eight distinct directional obstacle scenarios, each with varying step-length constraints. For each step-length setting, 500 simulation trials were performed for each direction, with obstacles independently and randomly initialized in every trial. In total, 8 × 500 unique obstacle environments were generated to ensure a diverse and comprehensive assessment of the deep-sea mining robot’s obstacle avoidance capability.

Multi-directional obstacle avoidance evaluation is essential due to the inherent unpredictability of deep-sea mining operations. Variations in environmental disturbances, local flow conditions, and obstacle distributions can lead to non-uniform navigation challenges across different movement directions. A robust obstacle avoidance strategy must maintain consistent performance across diverse orientations to ensure operational reliability. Additionally, unpredictable external perturbations, such as fluctuating water flow, may introduce asymmetries in obstacle encounters, further necessitating a comprehensive multi-directional evaluation.

By systematically analyzing performance across a large set of randomly generated directional scenarios, this study ensures that the proposed method remains effective under varying obstacle configurations and environmental conditions, reinforcing its reliability in practical deep-sea mining applications.

Table 7. Performance metrics for multi-directional obstacle avoidance under different multi-step settings.

Step Limited	Random Obstacle Avoidance Test Completion Rate
	−135°	−90°	−45°	0°	45°	90°	135°	180°	Average
$n=1$	72.0%	71.4%	75.8%	71.8%	74.6%	70.0%	74.4%	71.0%	72.63%
$n=2$	77.4%	77.2%	78.4%	74.2%	78.2%	77.8%	80.0%	79.6%	77.85%
$n=3$	94.6%	95.0%	94.4%	93.4%	94.4%	93.4%	92.8%	92.8%	93.85%
$n=4$	100.0%	99.2%	99.6%	99.6%	99.6%	99.2%	98.8%	99.6%	99.45%
$n=5$	100.0%	99.8%	100.0%	100.0%	100.0%	100.0%	100.0%	100.0%	99.98%
$n=6$	96.0%	96.0%	96.6%	97.6%	97.4%	97.0%	97.2%	96.6%	96.80%

presents the obstacle avoidance completion rates across eight directions under different step-length constraints. The completion rate is defined as the proportion of successful target-reaching instances in 500 independently randomized initialization tests for a given direction and step-length constraint. The results indicate that when the step length was constrained to $n=5$, the completion rate reached 99.98%, demonstrating exceptional robustness and stability. This highlights that a reasonable step-length configuration can effectively optimize the agent’s adaptability to complex dynamic environments. However, for $n=6$, while the overall completion rate remained high, a slight decrease in certain directions (e.g., 135° and 180°) suggests that excessive step lengths might introduce computational complexity, reducing local path-planning efficiency.

The obstacle avoidance trajectories under step-length constraints of $n=1$ and $n=5$ are illustrated in Figure 13 and Figure 14, respectively. For $n=1$, the agent’s trajectories in certain directions, such as −90° and 180°, showed significant deviations from the target path, indicating that shorter step lengths limited the agent’s ability to effectively plan continuous paths. In contrast, for $n=5$, the trajectories across all directions were highly consistent and closely aligned, demonstrating superior path consistency and planning capabilities. This further validates that the controller under $n=5$ exhibits exceptional path-planning stability and robustness in complex obstacle environments.

These findings lead to the conclusion that a well-balanced step-length setting (e.g., $n=5$) effectively ensures both continuity and stability in path planning, enabling the agent to exhibit remarkable adaptability and robustness in complex multi-directional environments. In contrast, excessively short step lengths (e.g., $n=1$) may restrict the agent’s global path-planning capabilities, while excessively large step lengths (e.g., $n=6$) could introduce local inefficiencies due to increased computational complexity. The results underscore the critical role of step-length optimization in enhancing dynamic obstacle avoidance performance, providing a strong foundation for future algorithmic applications in complex environments.

5. Conclusions

This study introduces an optimized Deep Reinforcement Learning algorithm based on the Dynamic Multi-Step Update to systematically investigate and validate dual-task control for path following and obstacle avoidance in deep-sea mining vehicles under complex dynamic environments. By designing three training environments (ROE, OPE, and DTE), the research focuses on analyzing the performance of controllers across different scenarios, ultimately selecting the DTE as the optimal training environment. Under the DTE, the robot demonstrated enhanced capabilities in both path following and obstacle avoidance, overcoming the limitations of single-task environments and exhibiting remarkable balance and adaptability. Furthermore, the step length parameter, as a critical hyperparameter in the DMSU, played a decisive role in improving training efficiency, control precision, and algorithm stability. Systematic simulation tests confirmed that the controller achieved optimal comprehensive performance in path following and obstacle avoidance when the step length was set to a specific value.

In the path following tests, the simulation results under different step-length settings revealed that the controller with the specific step length achieved one of the lowest trajectory deviations on both straight and S-shaped paths, demonstrating the significant impact of the Dynamic Multi-Step Update mechanism on improving following accuracy. Specifically, it achieved the lowest trajectory deviation in the straight path test and the second lowest in the S-shaped path test. In randomized obstacle avoidance tests, the controller with the specific step length achieved a nearly 100% obstacle avoidance success rate across eight directions, with stable and repeatable trajectory performance, showcasing exceptional robustness and task execution capabilities. A comprehensive analysis of the simulation results validated the effectiveness and reliability of the improved algorithm in complex dynamic environments.

While the proposed method demonstrates promising performance in simulation, several aspects require further investigation to bridge the gap between the current study and real-world deep-sea mining operations.

Future research will focus on extending the control algorithm to real-world three-dimensional deep-sea environments, where the presence of complex and irregular seabed topographies poses significant challenges for obstacle avoidance. Additionally, the current study employs a simplified dynamic model with limited consideration of external disturbances, such as ocean currents and sediment dynamics. To enhance the system’s robustness, future work will incorporate more comprehensive hydrodynamic modeling and adaptive disturbance rejection mechanisms.

Furthermore, the proposed framework currently operates in an open-loop manner, lacking real-time perception and environmental feedback. To address this limitation, integrating sonar-based perception and simultaneous localization and mapping (SLAM) techniques will be a key focus. This enhancement will enable the deep-sea mining robot to construct a dynamic environmental representation, facilitating real-time decision-making and adaptive control in unstructured and evolving conditions.

By addressing these limitations, future studies aim to develop a more intelligent and autonomous deep-sea mining robot capable of operating efficiently in complex and unpredictable underwater environments, ultimately contributing to the advancement of deep-sea resource exploration and utilization.