Design of Portable Reefs to Protect Young Mangroves
Abstract
1. Introduction
2. Methodology
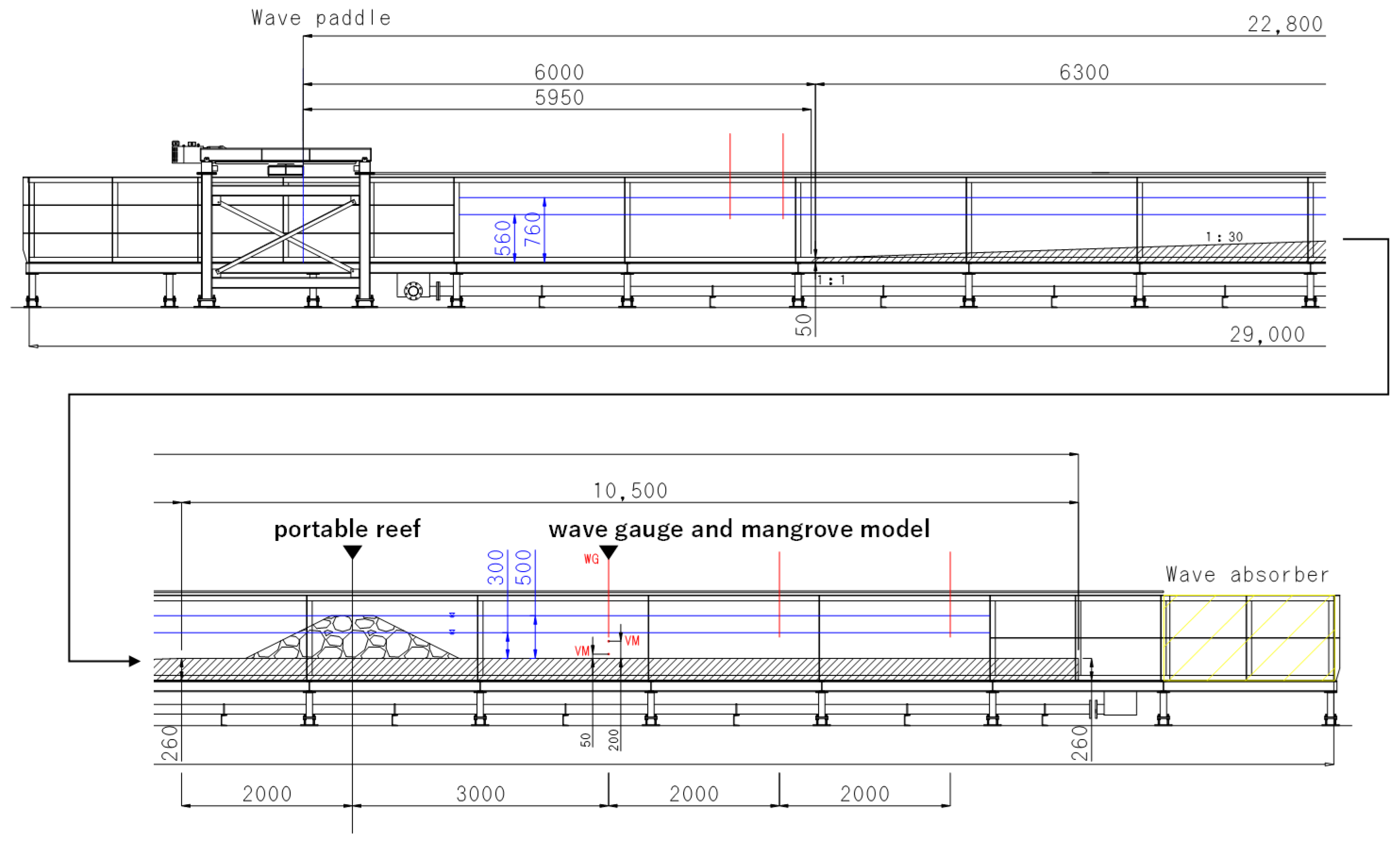
2.1. Wave Flume Experiment
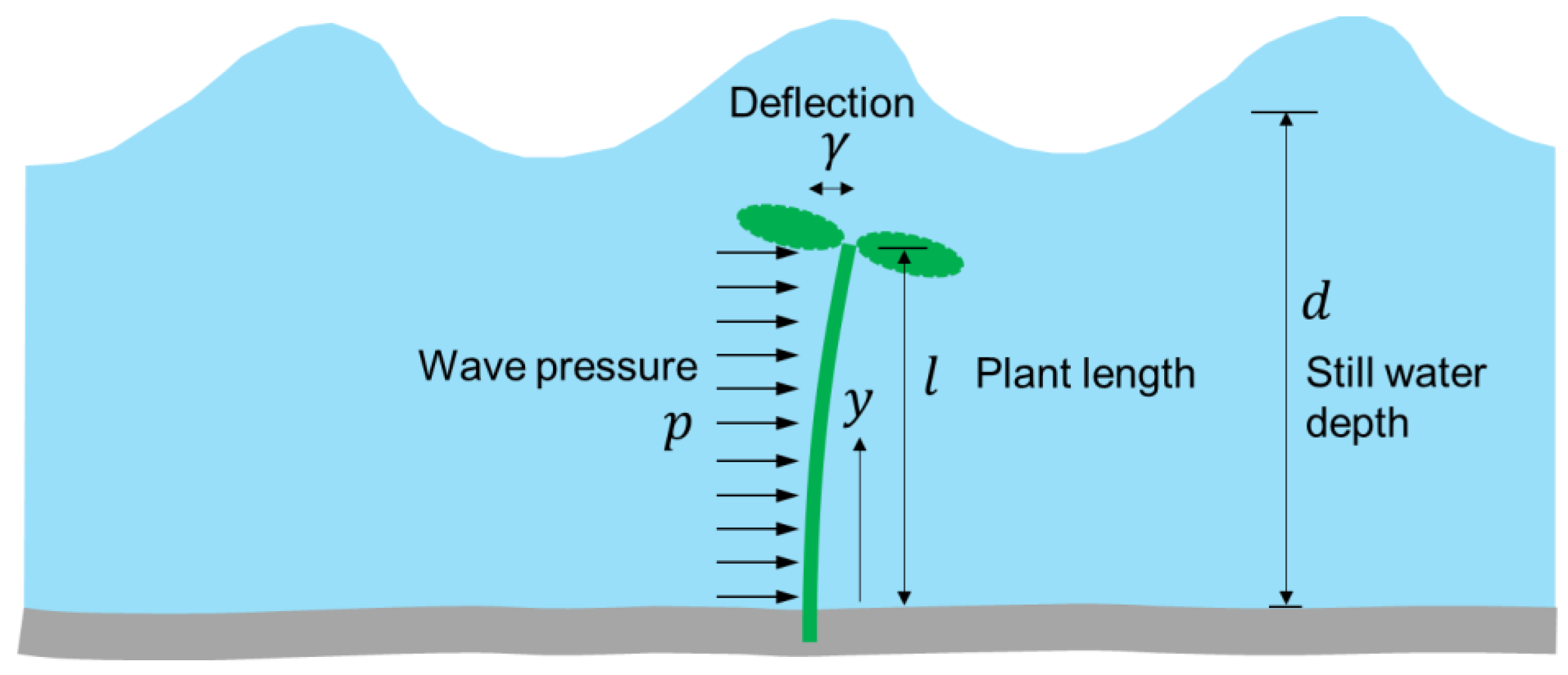
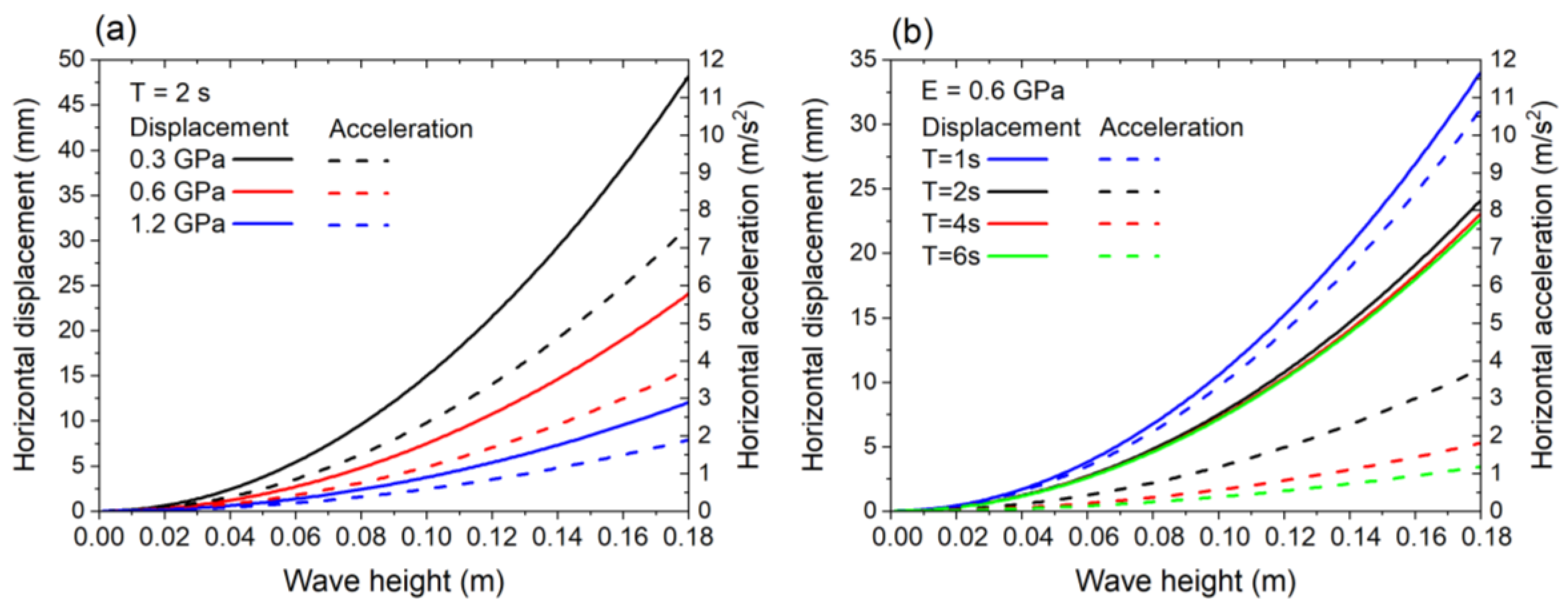
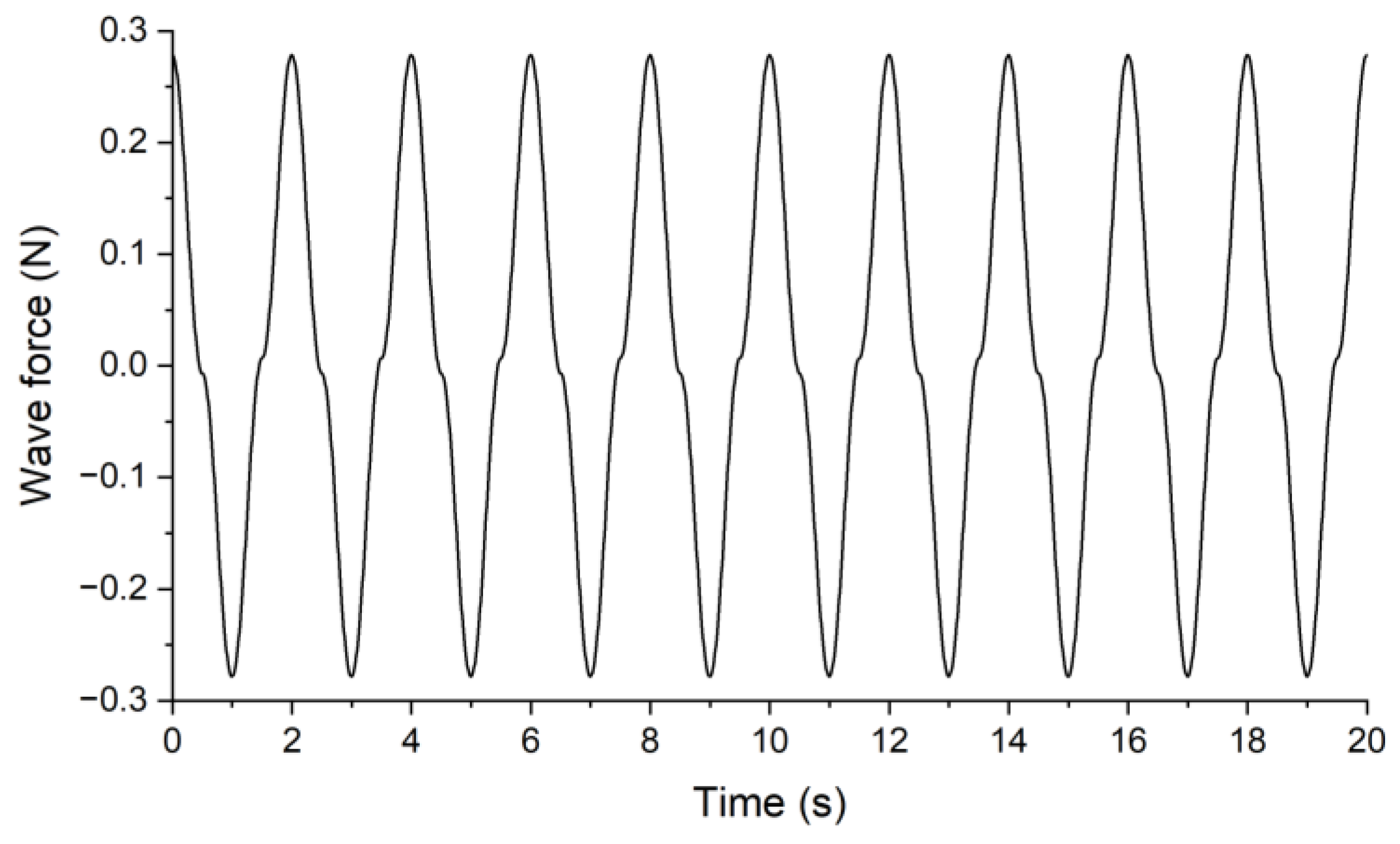
2.2. Analytical Solution for Plant Oscillation
2.3. Applicability of Existing Wave Transmission Formula
3. Results and Discussion
3.1. Summary of Experimental Results
3.2. Detailed Analysis of Oscillatory Characteristics
3.3. Benefits of Reduced Oscillation
3.4. Applicability of d’Angremond Formula to Portable Reefs
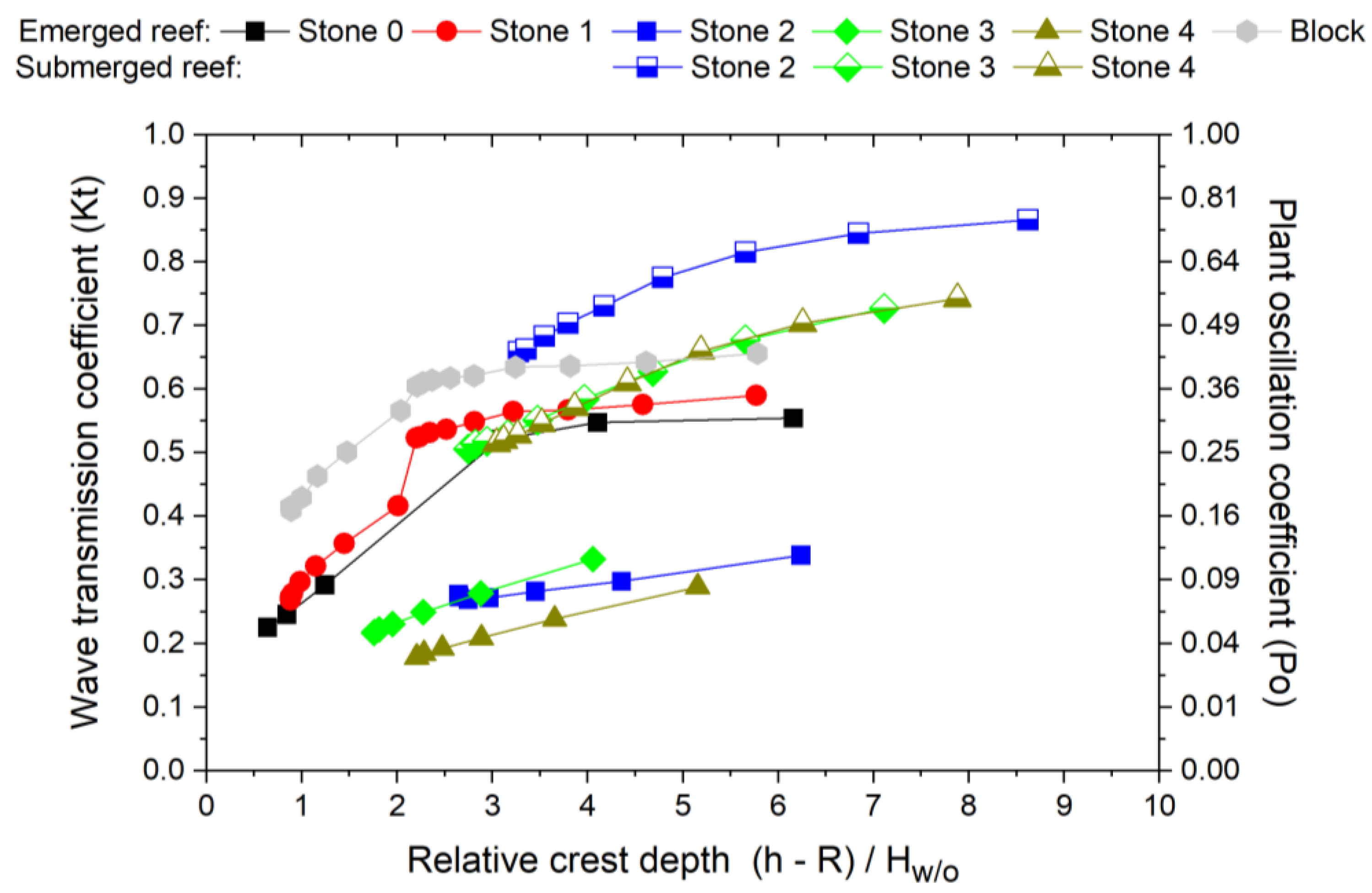
3.5. Wave Transmission Chart for Portable Reef Design
- i.
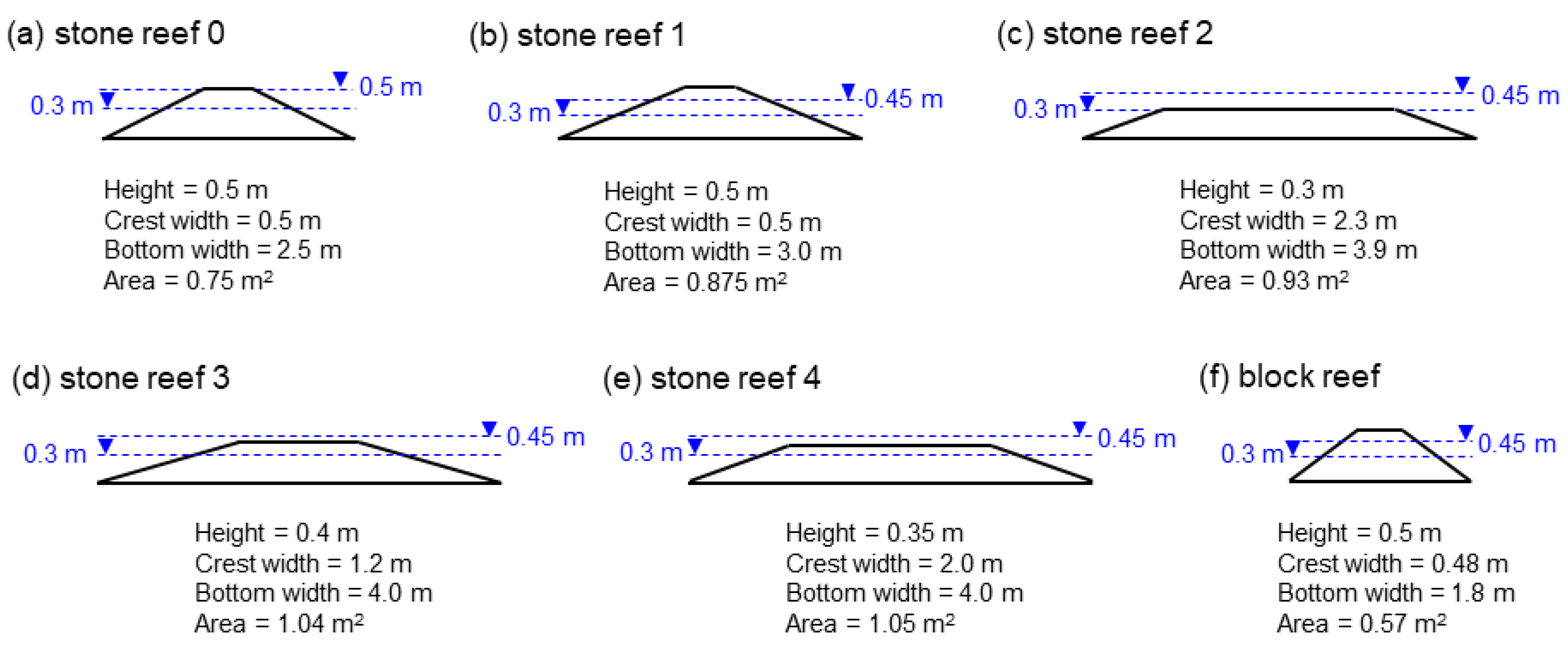
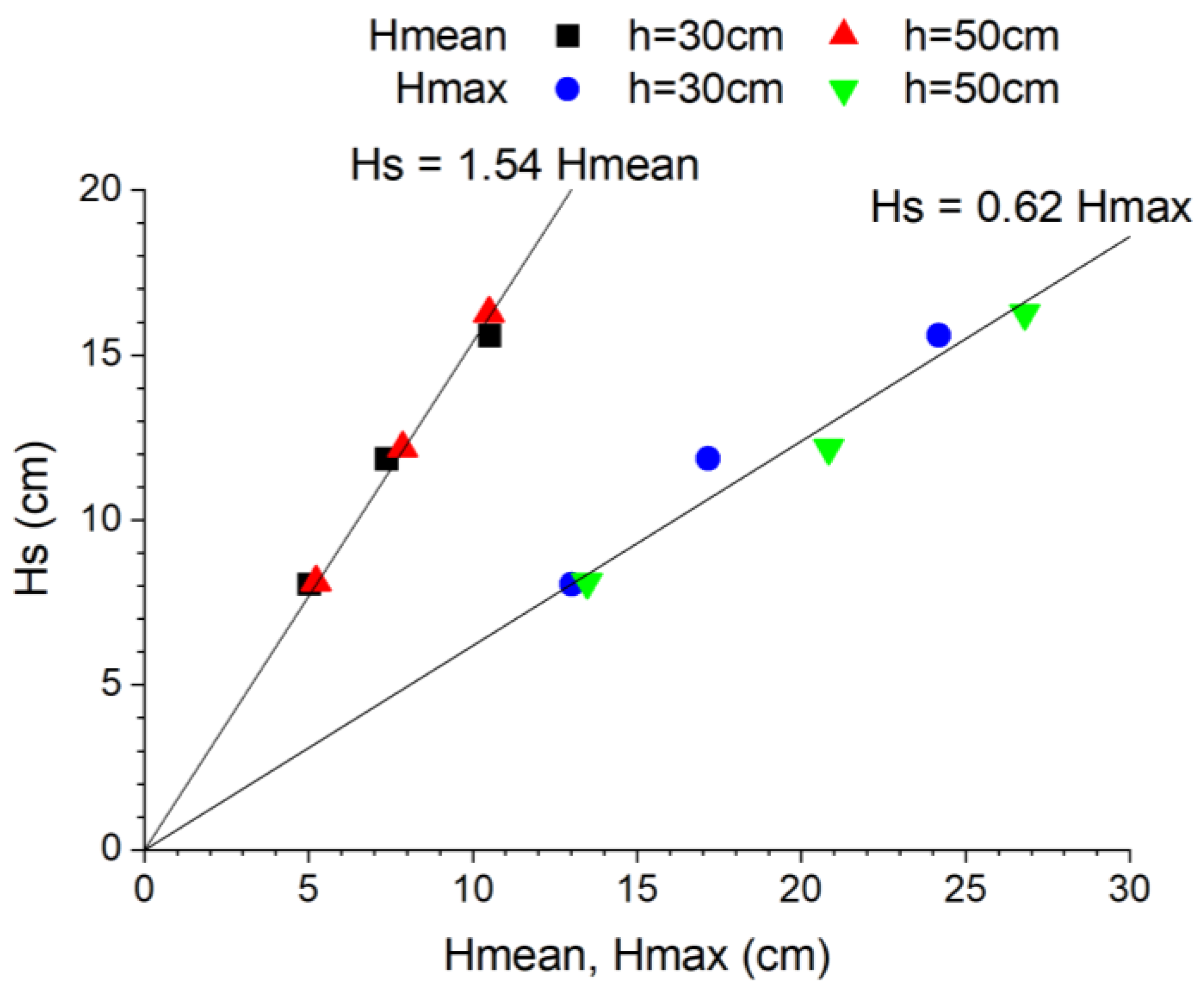
- The water depth and significant wave height at the proposed reef site should be assessed, followed by the calculation of the relative crest depths for six different reef geometries (refer to Figure 7). In cases where only the mean or maximum wave height data are available, this information needs to be converted to the significant wave height, as demonstrated in Figure 18.
- ii.
- Consider whether the reef will be submerged or emergent under the designed tidal conditions. If both submerged and emergent configurations are feasible, one should opt for an emergent reef alternative.
- iii.
- The allowable wave transmission and/or plant oscillations (coefficients Kt and Po) should be calculated for the proposed reef using Figure 17 to ensure compliance with the established allowable limits. If these criteria are not satisfied, the height of the reef crest increases.
4. Conclusions
- ▪
- The present findings indicate that it is possible to reduce the wave transmission coefficient, Kt, to below 0.3 when the reef is in an emerged state. Conversely, Kt exhibits a significant increase when the reef crest is submerged. Although some degree of wave transmission is inevitable, the careful placement of portable reefs can effectively reduce the oscillation experienced by young mangroves to negligible levels. This is because the damping effect on the plant oscillations is greater than the damping of the waves themselves.
- ▪
- The results of our experiments and analytical models provide valuable insights into the various factors that pose risks to young mangroves. Notably, an increase in the short-period wave activity is associated with heightened oscillations in plant structures, which can be detrimental to low-rigidity mangroves at critical early developmental stages. As these young mangroves grow and their leaves rise above the water surface, the oscillation effects diminish.
- ▪
- Existing wave transmission equations such as the d’Angremond formula may not be appropriate for the design of portable reefs, as they tend to overestimate the efficacy of such structures. To address this gap, we have developed a new chart that illustrates the relationship between the wave transmission and the plant oscillations behind portable reefs. Using this chart, the required cross-section can be easily determined based on several parameters, such as the design tide level, wave height, and reef geometries, which will aid in the design and implementation of these protective measures for young mangrove ecosystems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Reef Name | Reef Height (cm) | Crest Width (cm) | Area (cm2) | Depth h (cm) | Crest Elevation R (cm) | Emerge or Submerge | H w/o Reef (cm) | H w/ Reef (cm) | Relative Crest Depth (h-R) /Hw/o | Wave Transmission Coefficient Kt |
|---|---|---|---|---|---|---|---|---|---|---|
| Stone reef 0 | 50 | 50 | 7500 | 30 | 20 | Emerge | 8.05 | 2.35 | 1.24 | 0.29 |
| 30 | 20 | Emerge | 11.85 | 2.91 | 0.84 | 0.25 | ||||
| 30 | 20 | Emerge | 15.59 | 3.51 | 0.64 | 0.23 | ||||
| 50 | 0 | Emerge | 8.12 | 4.50 | 6.16 | 0.55 | ||||
| 50 | 0 | Emerge | 12.18 | 6.67 | 4.11 | 0.55 | ||||
| 50 | 0 | Emerge | 16.26 | 8.47 | 3.08 | 0.52 | ||||
| Stone reef 1 | 50 | 50 | 8750 | 30 | 20 | Emerge | 4.97 | 2.07 | 2.01 | 0.42 |
| 30 | 20 | Emerge | 6.92 | 2.47 | 1.45 | 0.36 | ||||
| 30 | 20 | Emerge | 8.73 | 2.81 | 1.15 | 0.32 | ||||
| 30 | 20 | Emerge | 10.16 | 3.02 | 0.98 | 0.30 | ||||
| 30 | 20 | Emerge | 11.03 | 3.07 | 0.91 | 0.28 | ||||
| 30 | 20 | Emerge | 11.34 | 3.04 | 0.88 | 0.27 | ||||
| 30 | 20 | Emerge | 11.37 | 3.11 | 0.88 | 0.27 | ||||
| 45 | 5 | Emerge | 6.93 | 4.09 | 5.77 | 0.59 | ||||
| 45 | 5 | Emerge | 8.74 | 5.03 | 4.58 | 0.58 | ||||
| 45 | 5 | Emerge | 10.54 | 5.98 | 3.80 | 0.57 | ||||
| 45 | 5 | Emerge | 12.42 | 7.01 | 3.22 | 0.56 | ||||
| 45 | 5 | Emerge | 14.23 | 7.80 | 2.81 | 0.55 | ||||
| 45 | 5 | Emerge | 15.87 | 8.52 | 2.52 | 0.54 | ||||
| 45 | 5 | Emerge | 17.07 | 9.08 | 2.34 | 0.53 | ||||
| 45 | 5 | Emerge | 17.88 | 9.38 | 2.24 | 0.52 | ||||
| 45 | 5 | Emerge | 18.17 | 9.51 | 2.20 | 0.52 | ||||
| Stone reef 2 | 30 | 230 | 9300 | 30 | 0 | Emerge | 4.81 | 1.63 | 6.24 | 0.34 |
| 30 | 0 | Emerge | 6.89 | 2.05 | 4.35 | 0.30 | ||||
| 30 | 0 | Emerge | 8.69 | 2.45 | 3.45 | 0.28 | ||||
| 30 | 0 | Emerge | 10.12 | 2.75 | 2.96 | 0.27 | ||||
| 30 | 0 | Emerge | 10.92 | 2.94 | 2.75 | 0.27 | ||||
| 30 | 0 | Emerge | 11.32 | 3.09 | 2.65 | 0.27 | ||||
| 30 | 0 | Emerge | 11.34 | 3.14 | 2.65 | 0.28 | ||||
| 45 | −15 | Submerge | 6.96 | 6.03 | 8.62 | 0.87 | ||||
| 45 | −15 | Submerge | 8.77 | 7.41 | 6.84 | 0.84 | ||||
| 45 | −15 | Submerge | 10.61 | 8.65 | 5.66 | 0.82 | ||||
| 45 | −15 | Submerge | 12.53 | 9.72 | 4.79 | 0.78 | ||||
| 45 | −15 | Submerge | 14.37 | 10.50 | 4.18 | 0.73 | ||||
| 45 | −15 | Submerge | 15.80 | 11.12 | 3.80 | 0.70 | ||||
| 45 | −15 | Submerge | 16.93 | 11.57 | 3.54 | 0.68 | ||||
| 45 | −15 | Submerge | 17.89 | 11.86 | 3.35 | 0.66 | ||||
| 45 | −15 | Submerge | 18.32 | 12.07 | 3.28 | 0.66 | ||||
| Stone reef 3 | 40 | 120 | 10,400 | 30 | 10 | Emerge | 4.93 | 1.64 | 4.06 | 0.33 |
| 30 | 10 | Emerge | 6.95 | 1.94 | 2.88 | 0.28 | ||||
| 30 | 10 | Emerge | 8.79 | 2.19 | 2.28 | 0.25 | ||||
| 30 | 10 | Emerge | 10.24 | 2.36 | 1.95 | 0.23 | ||||
| 30 | 10 | Emerge | 11.04 | 2.45 | 1.81 | 0.22 | ||||
| 30 | 10 | Emerge | 11.36 | 2.47 | 1.76 | 0.22 | ||||
| 30 | 10 | Emerge | 11.37 | 2.46 | 1.76 | 0.22 | ||||
| 45 | −5 | Submerge | 7.03 | 5.11 | 7.11 | 0.73 | ||||
| 45 | −5 | Submerge | 8.84 | 5.99 | 5.66 | 0.68 | ||||
| 45 | −5 | Submerge | 10.67 | 6.70 | 4.69 | 0.63 | ||||
| 45 | −5 | Submerge | 12.61 | 7.36 | 3.97 | 0.58 | ||||
| 45 | −5 | Submerge | 14.39 | 7.93 | 3.47 | 0.55 | ||||
| 45 | −5 | Submerge | 15.80 | 8.35 | 3.16 | 0.53 | ||||
| 45 | −5 | Submerge | 16.99 | 8.80 | 2.94 | 0.52 | ||||
| 45 | −5 | Submerge | 17.72 | 9.10 | 2.82 | 0.51 | ||||
| 45 | −5 | Submerge | 18.19 | 9.20 | 2.75 | 0.51 | ||||
| Stone reef 4 | 35 | 200 | 10,500 | 30 | 5 | Emerge | 4.85 | 1.40 | 5.15 | 0.29 |
| 30 | 5 | Emerge | 6.84 | 1.63 | 3.65 | 0.24 | ||||
| 30 | 5 | Emerge | 8.67 | 1.81 | 2.88 | 0.21 | ||||
| 30 | 5 | Emerge | 10.10 | 1.94 | 2.48 | 0.19 | ||||
| 30 | 5 | Emerge | 10.95 | 2.01 | 2.28 | 0.18 | ||||
| 30 | 5 | Emerge | 11.32 | 2.02 | 2.21 | 0.18 | ||||
| 30 | 5 | Emerge | 11.34 | 2.02 | 2.20 | 0.18 | ||||
| 45 | −10 | Submerge | 6.98 | 5.18 | 7.88 | 0.74 | ||||
| 45 | −10 | Submerge | 8.79 | 6.18 | 6.26 | 0.70 | ||||
| 45 | −10 | Submerge | 10.60 | 6.99 | 5.19 | 0.66 | ||||
| 45 | −10 | Submerge | 12.45 | 7.59 | 4.42 | 0.61 | ||||
| 45 | −10 | Submerge | 14.23 | 8.12 | 3.87 | 0.57 | ||||
| 45 | −10 | Submerge | 15.64 | 8.53 | 3.52 | 0.55 | ||||
| 45 | −10 | Submerge | 16.84 | 8.88 | 3.27 | 0.53 | ||||
| 45 | −10 | Submerge | 17.64 | 9.16 | 3.12 | 0.52 | ||||
| 45 | −10 | Submerge | 18.06 | 9.29 | 3.05 | 0.51 | ||||
| block reef | 50 | 48 | 5700 | 30 | 20 | Emerge | 4.91 | 2.78 | 2.04 | 0.57 |
| 30 | 20 | Emerge | 6.79 | 3.40 | 1.47 | 0.50 | ||||
| 30 | 20 | Emerge | 8.59 | 3.98 | 1.16 | 0.46 | ||||
| 30 | 20 | Emerge | 10.02 | 4.30 | 1.00 | 0.43 | ||||
| 30 | 20 | Emerge | 11.26 | 4.61 | 0.89 | 0.41 | ||||
| 30 | 20 | Emerge | 11.35 | 4.71 | 0.88 | 0.41 | ||||
| 45 | 5 | Emerge | 6.92 | 4.54 | 5.78 | 0.66 | ||||
| 45 | 5 | Emerge | 8.67 | 5.57 | 4.61 | 0.64 | ||||
| 45 | 5 | Emerge | 10.48 | 6.67 | 3.82 | 0.64 | ||||
| 45 | 5 | Emerge | 12.35 | 7.84 | 3.24 | 0.63 | ||||
| 45 | 5 | Emerge | 14.25 | 8.85 | 2.81 | 0.62 | ||||
| 45 | 5 | Emerge | 15.64 | 9.66 | 2.56 | 0.62 | ||||
| 45 | 5 | Emerge | 16.90 | 10.38 | 2.37 | 0.61 | ||||
| 45 | 5 | Emerge | 17.62 | 10.75 | 2.27 | 0.61 | ||||
| 45 | 5 | Emerge | 18.12 | 10.96 | 2.21 | 0.60 |
References
- Lewis, R.R. Ecological engineering for successful management and restoration of mangrove forests. Ecol. Eng. 2005, 24, 403–418. [Google Scholar] [CrossRef]
- Zimmer, K. Many Mangrove Restorations Fail. Is There a Better Way? Knowable Magazine. 2021. Available online: https://knowablemagazine.org/content/article/food-environment/2021/many-mangrove-restorations-fail (accessed on 1 January 2025).
- Primavera, J.H.; Esteban, J.M.A. A review of mangrove rehabilitation in the Philippines: Successes, failures and future prospects. Wetl. Ecol. Manag. 2008, 16, 345–358. [Google Scholar] [CrossRef]
- IFRC. Breaking the Waves: Impact Analysis of Coastal Afforestation for Disaster Risk Reduction in Viet Nam; International Federation of Red Cross and Red Crescent Societies: Geneva, Switzerland, 2011. [Google Scholar]
- Kodikara, K.A.S.; Mukherjee, N.; Jayatissa, L.P.; Dahdouh-Guebas, F.; Koedam, N. Have mangrove restoration projects worked? An in-depth study in Sri Lanka. Restor. Ecol. 2017, 25, 705–716. [Google Scholar] [CrossRef]
- Fauzi, N.F.M.; Min, T.H.; Hashim, A.M. Assessment of mangrove replanting site at Kg Tanjung Kepah, Lekir, Perak. IOP Conf. Ser. Earth Environ. Sci. 2020, 549, 012054. [Google Scholar] [CrossRef]
- Devaney, J.L.; Marone, D.; McElwain, J.C. Impact of soil salinity on mangrove restoration in a semiarid region: A case study from the Saloum Delta, Senegal. Restor. Ecol. 2021, 29, 13186. [Google Scholar] [CrossRef]
- Sidik, F.; Kusuma, D.W.; Priyono, B.; Proisy, C.; Lovelock, C.E. Chapter 22-Managing sediment dynamics through reintroduction of tidal flow for mangrove restoration in abandoned aquaculture ponds. In Dynamic Sedimentary Environments of Mangrove Coasts; Elsevier: Amsterdam, The Netherlands, 2021; pp. 563–582. [Google Scholar]
- Elster, C. Reasons for reforestation success and failure with three mangrove species in Colombia. For. Ecol. Manag. 2000, 131, 201–214. [Google Scholar] [CrossRef]
- Thompson, B.S. The political ecology of mangrove forest restoration in Thailand: Institutional arrangements and power dynamics. Land Use Policy 2018, 78, 503–514. [Google Scholar] [CrossRef]
- Sreeranga, S.; Takagi, H.; Shirai, R. Community-based portable reefs to promote mangrove vegetation growth: Bridging between ecological and engineering principles. Int. J. Environ. Res. Public Health 2021, 18, 590. [Google Scholar] [CrossRef]
- Takagi, H.; Shirai, R.; Sreeranga, S. Oscillatory characteristics of young mangroves exposed to short-period waves. Sci. Total Environ. 2021, 790, 148157. [Google Scholar] [CrossRef]
- Erickson, A.A.; Saltis, M.; Bell, S.S.; Dawes, C.J. Herbivore feeding preferences as measured by leaf damage and stomatal ingestion: A mangrove crab example. J. Exp. Mar. Biol. Ecol. 2003, 289, 123–138. [Google Scholar] [CrossRef]
- van Bijsterveldt, C.E.J.; van Wesenbeeck, B.K.; Ramadhani, S.; Raven, O.V.; van Gool, F.E.; Pribadi, R.; Bouma, T.J. Does plastic waste kill mangroves? A field experiment to assess the impact of macro plastics on mangrove growth, stress response and survival. Sci. Total Environ. 2021, 756, 143826. [Google Scholar] [CrossRef]
- Holbert, J.; Sudrajat, D.J.; Nurhasybi; Yulianti. Alternative methods for reforestation and land rehabilitation to reduce the plastics waste in forestareas. IOP Conf. Ser. Earth Environ. Sci. 2019, 407, 012007. [Google Scholar] [CrossRef]
- Thampi, A.; Vedharajan, B.; Narayana, S.; Govindarajan, M.; Magalingam, R. Experiment on use of eco-friendly Palmyra nursery bag for mangrove restoration in Palk Bay, India. Restor. Ecol. 2023, 31, e13957. [Google Scholar] [CrossRef]
- Akbar, A.A.; Sartohadi, J.; Djohan, T.S.; Ritohardoyo, S. The role of breakwaters on the rehabilitation of coastal and mangrove forests in West Kalimantan, Indonesia. Ocean Coast. Manag. 2017, 138, 50–59. [Google Scholar] [CrossRef]
- Takagi, H. “Adapted mangrove on hybrid platform”—Coupling of ecological and engineering principles against coastal hazards. Results Eng. 2019, 4, 100067. [Google Scholar] [CrossRef]
- Schmitt, K.; Albers, T. Area coastal protection and the use of bamboo breakwaters in the Mekong Delta. In Coastal Disasters and Climate Change in Vietnam; Elsevier: Amsterdam, The Netherlands, 2014; pp. 107–132. [Google Scholar]
- Cuong, C.V.; Brown, S.; To, H.H.; Hockings, M. Using Melaleuca fences as soft coastal engineering for mangrove restoration in Kien Giang, Vietnam. Ecol. Eng. 2015, 81, 256–265. [Google Scholar] [CrossRef]
- Takagi, H.; Sekiguchi, S.; Thao, N.D.; Rasmeemasmuang, T. Do wooden pile breakwaters work for community-based coastal protection? J. Coast. Conserv. 2020, 24, 31. [Google Scholar] [CrossRef]
- Pranchai, A.; Jenke, M.; Berger, U. Well-intentioned, but poorly implemented: Debris from coastal bamboo fences triggered mangrove decline in Thailand. Mar. Pollut. Bull. 2019, 146, 900–907. [Google Scholar] [CrossRef]
- Saengsupavanich, C.; Ferren, V.; Magdalena, I.; Ariffin, E.H.; Sanitwong-Na-Ayutthaya, S. Using piles for wave reduction and coastal protection: A review. Reg. Stud. Mar. Sci. 2024, 77, 103638. [Google Scholar] [CrossRef]
- Sreeranga, S.; Takagi, H.; Shirai, R.; Kubota, S.; Mitsui, J. Numerical investigation on effectiveness of portable rubble mound breakwater for mangrove restoration. J. Jpn. Soc. Civ. Eng. Ser. B3 (Ocean Eng.) 2021, 77, 61–66. [Google Scholar] [CrossRef]
- Sreeranga, S.; Takagi, H.; Kubota, S.; Mitsui, J. An experimental study on oscillatory characteristics of young mangroves behind a portable reef. Coast. Eng. J. 2022, 65, 110–125. [Google Scholar]
- Frigaard, P.; Brorsen, M. A time-domain method for separating incident and reflected irregular waves. Coast. Eng. 1995, 24, 205–215. [Google Scholar] [CrossRef]
- Takagi, H. Survival of young planted mangroves in a calm bay environment during a tropical cyclone. Nat.-Based Solut. 2023, 4, 100082. [Google Scholar]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. In Proceedings of the 15th Coastal Engineering Conference, Honlulu, HI, USA, 11–17 July 1976; Volume 1, pp. 828–845. [Google Scholar]
- Zhang, X.; Lin, P.; Chen, X. Coastal protection by planted mangrove forest during typhoon Mangkhut. J. Mar. Sci. Eng. 2022, 10, 1288. [Google Scholar] [CrossRef]
- Gijón Mancheño, A.; Vuik, V.; van Wesenbeeck, B.K.; Jonkman, S.N.; van Hespen, R.; Moll, J.R.; Kazi, S.; Urrutia, I.; van Ledden, M. Integrating mangrove growth and failure in coastal flood protection designs. Sci. Rep. 2024, 14, 7951. [Google Scholar]
- Hassanpour, N.; Vicinanza, D.; Contestabile, P. Determining wave transmission over rubble-mound breakwaters: Assessment of existing formulae through benchmark testing. Water 2023, 15, 1111. [Google Scholar] [CrossRef]
- d’Angremond, K.; Van Der Meer, J.W.; De Jong, R.J. Wave transmission at low-crested structures. Coast. Eng. Proc. 1998, 1, 2418–2427. [Google Scholar]
- Tabasi, M.; Mon, A.N.; Mitsui, J.; Kubota, S. Influence of seaside slope angle on stability of wave-dissipating blocks. J. JSCE 2024, 12, 24–17197. [Google Scholar]
- Seabrook, S.R.; Hall, K.R. Wave transmission at submerged rubblemound breakwaters. Coast. Eng. Proc. 1998, 1, 2000–2013. [Google Scholar]
- Kittitanasuan, W.; Goda, Y.; Shiobara, T. Deformation of nonlinear waves on a rectangular step. Coast. Eng. Jpn. 1993, 36, 133–153. [Google Scholar]
- Hang, C.; Pan, J.; Ju, L.; Zhai, B.; Yang, F.; Xie, D. Wave attenuation by juvenile and mature mangrove Kandelia Obovata with flexible canopies. Appl. Ocean. Res. 2025, 155, 104443. [Google Scholar] [CrossRef]
- Jones, H.G. Plants and Microclimate; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Shan, Q.; Liu, W.; Ni, X.; Li, M.; Sun, Y.; Liao, L.; Zheng, C. Serotonin mitigates cold stress-induced damage in Kandelia obovata through modulating the endogenous melatonin- and abscisic acid biosynthesis. Int. J. Mol. Sci. 2025, 26, 1635. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, B.; Dhar, V.; Pawase, A.S. Blue carbon and the role of mangroves in carbon sequestration: Its mechanisms, estimation, human impacts and conservation strategies for economic incentives. J. Sea Res. 2024, 199, 102504. [Google Scholar] [CrossRef]
- Kramer, M.; Burcharth, H. Environmental Design of Low Crested Coastal Defence Structures, Wave Basin Experiment Final form, EU Fifth Framework Programme 1998–2002, Energy, Environment and Sustainable Development, DELOS EVK-CT-2000-00041. 2003. Available online: http://www.delos.unibo.it/Docs/Deliverables/D31.pdf (accessed on 1 January 2025).
- van Gent, M.R.A.; Buis, L.; van den Bos, J.P.; Wuthrich, D. Wave transmission at submerged coastal structures and artificial reefs. Coast. Eng. 2023, 184, 104344. [Google Scholar] [CrossRef]
- CETMEF; CIRIA; CUR. The Rock Manual. In The Use of Rock in Hydraulic Engineering, 2nd ed.; CIRIA: London, UK, 2007; Chapter 5; pp. 487–756. [Google Scholar]
- Van der Meer, J.W.; Daemen, I.F. Stability and wave transmission at low-crested rubble-mound structures. J. Waterw. Port Coast. Ocean. Eng. 1994, 120, 1–19. [Google Scholar] [CrossRef]
- Losada, I.J. Recent advances in the modeling of wave and permeable structure interaction. In Advances in Coastal and Ocean Engineering; Liu, P.L.F., Ed.; World Scientific: Singapore, 2001; pp. 163–202. [Google Scholar]

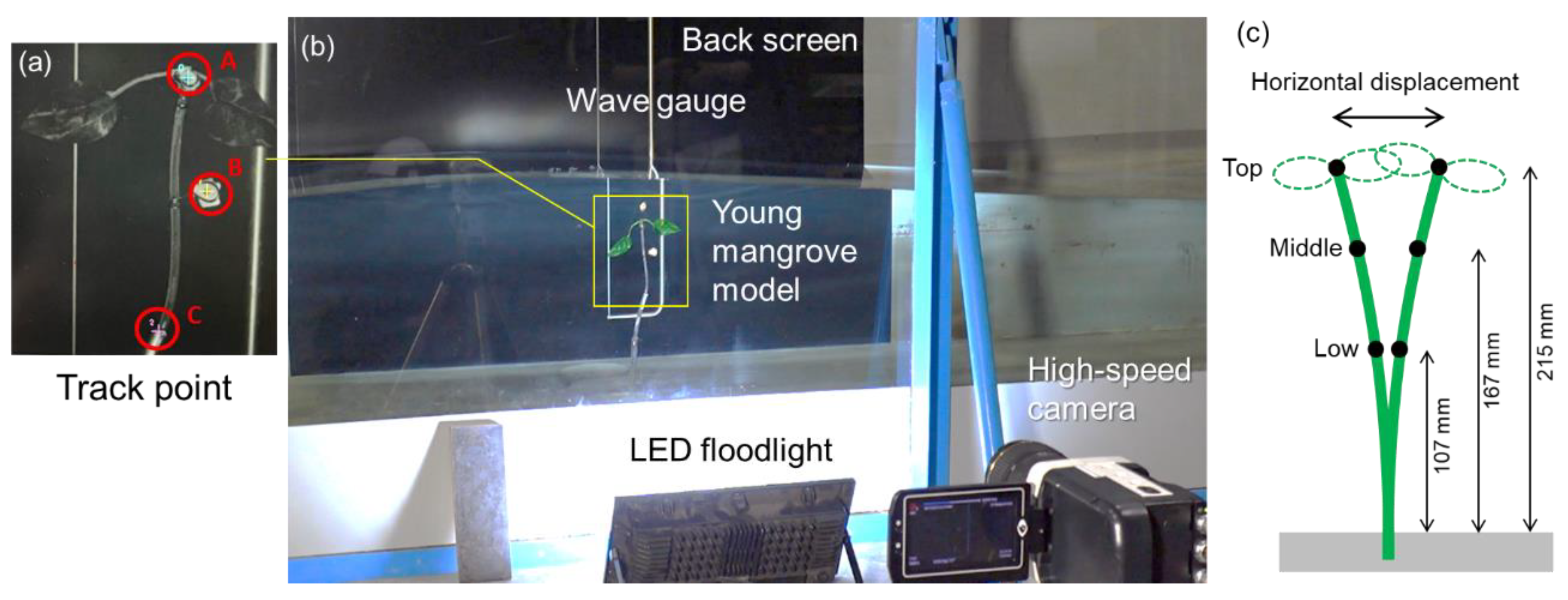




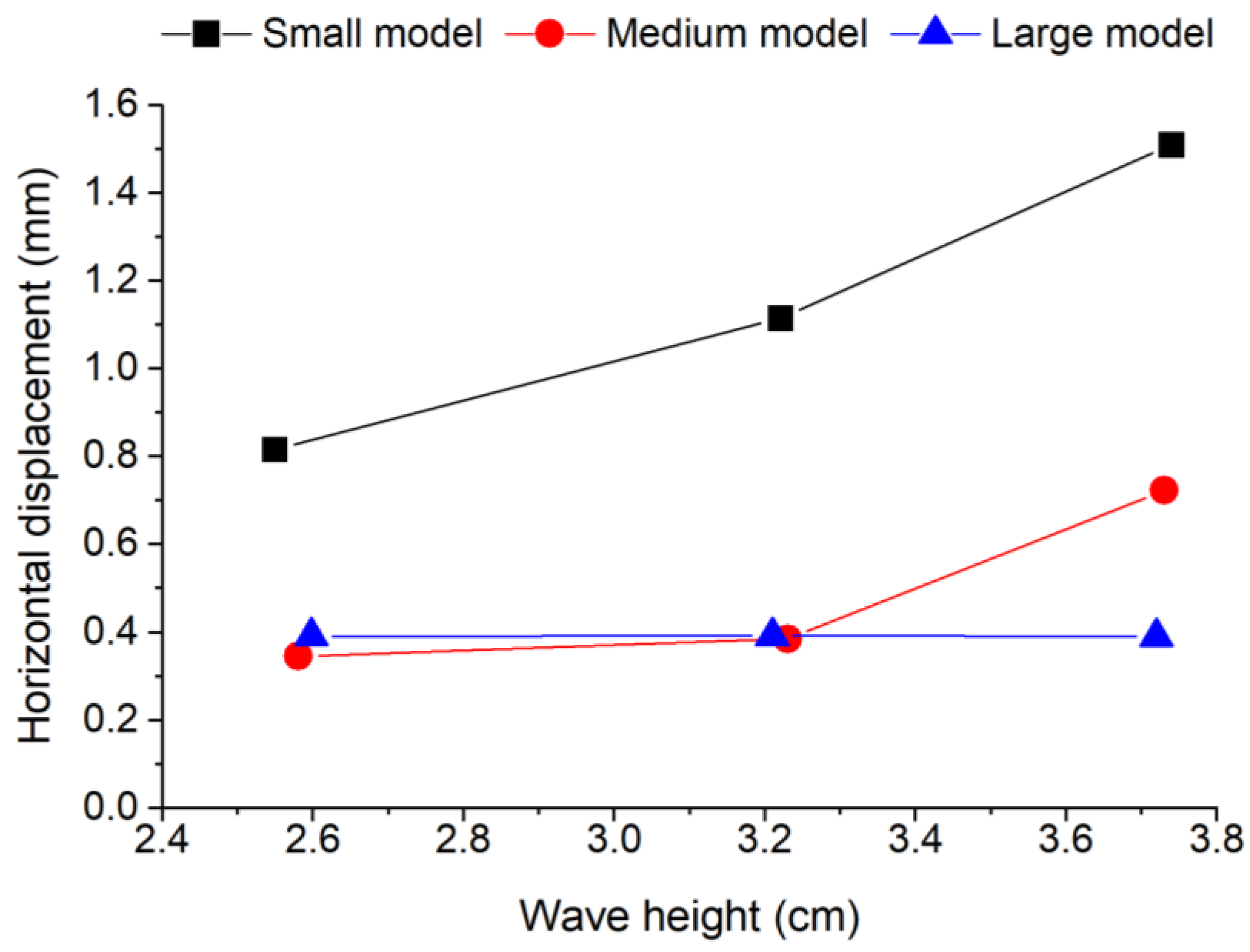

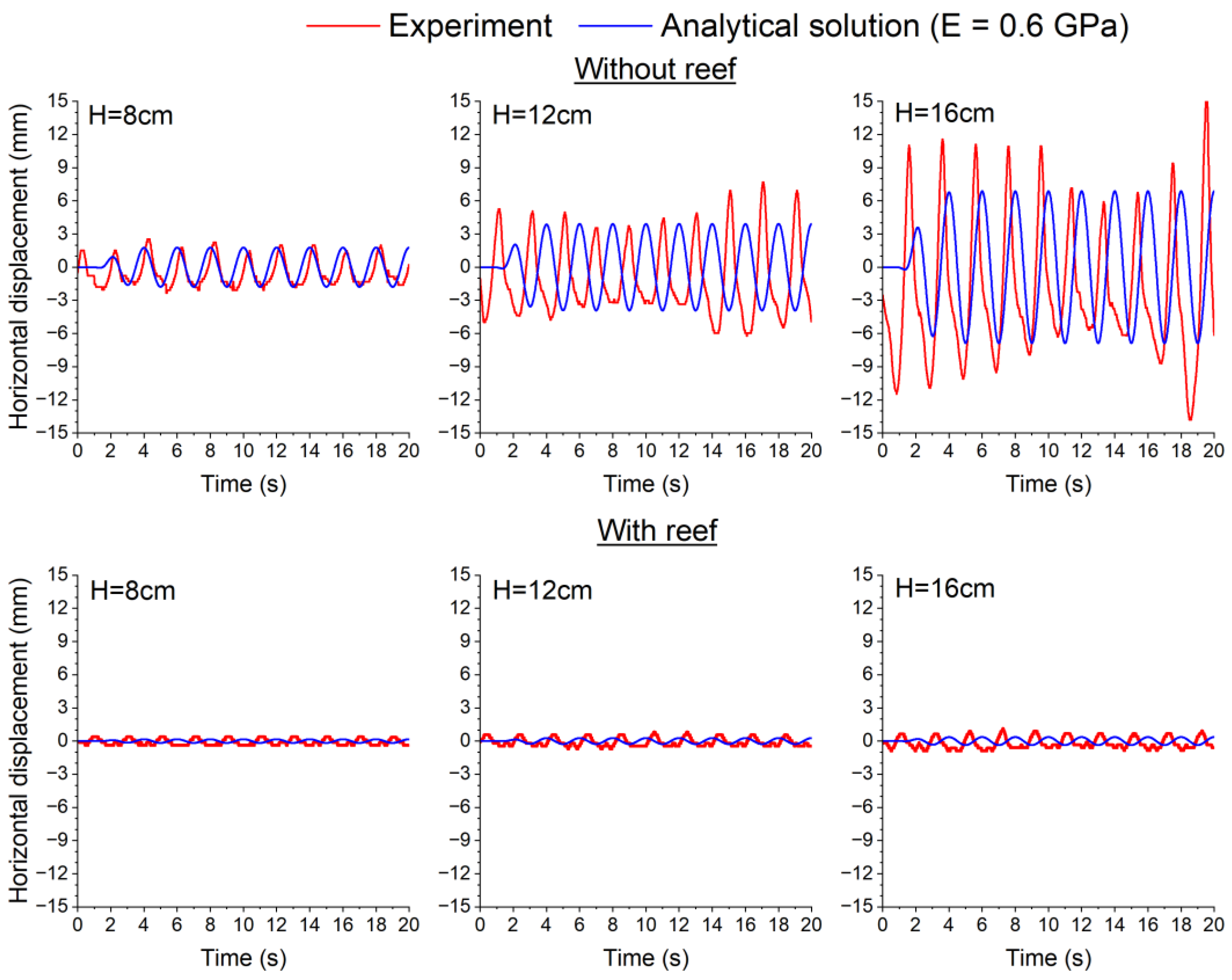


| Small Model (Height of Plant: 215 mm Above the Floor) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure | Without Reef | With Reef | ||||||||||||
| Water Depth | 30 cm | 50 cm | 30 cm | 50 cm | ||||||||||
| Track Point | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | ||
| Target wave height and period | 8 cm | 2 s | A | A | B | A | A | A | A | A | A | A | A | A |
| 12 cm | 2 s | A | A | B | A | A | A | A | A | A | A | A | A | |
| 16 cm | 2 s | A | A | B | A | A | A | A | A | A | A | A | A | |
| Medium model (Height of plant: 290 mm above the floor) | ||||||||||||||
| Structure | Without reef | With reef | ||||||||||||
| Water depth | 30 cm | 50 cm | 30 cm | 50 cm | ||||||||||
| Track point | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | ||
| Target wave height and period | 8 cm | 2 s | A | A | B | N/A | N/A | N/A | A | A | A | N/A | N/A | N/A |
| 12 cm | 2 s | A | B | B | N/A | N/A | N/A | A | A | A | N/A | N/A | N/A | |
| 16 cm | 2 s | A | B | B | N/A | N/A | N/A | A | A | A | N/A | N/A | N/A | |
| Large model (Height of plant: 350 mm above the floor) | ||||||||||||||
| Structure | Without reef | With reef | ||||||||||||
| Water depth | 30 cm | 50 cm | 30 cm | 50 cm | ||||||||||
| Track point | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | Low | Middle | Top | ||
| Target wave height and period | 8 cm | 2 s | A | B | C | N/A | N/A | N/A | A | A | A | N/A | N/A | N/A |
| 12 cm | 2 s | A | B | C | N/A | N/A | N/A | A | A | B | N/A | N/A | N/A | |
| 16 cm | 2 s | A | C | C | N/A | N/A | N/A | A | B | B | N/A | N/A | N/A | |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Wave transmission coefficient | Wave height | ||
| Wave period | Crest elevation | ||
| Crest width | Surf similarity parameter | ||
| Water depth | Elastic modulus | ||
| Plant oscillation coefficient | Significant wave height | ||
| Mean wave height | Maximum wave height | ||
| Wave height without reef |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takagi, H.; Prattoyee, F.T.; Mitsui, J.; Kubota, S.-i. Design of Portable Reefs to Protect Young Mangroves. J. Mar. Sci. Eng. 2025, 13, 734. https://doi.org/10.3390/jmse13040734
Takagi H, Prattoyee FT, Mitsui J, Kubota S-i. Design of Portable Reefs to Protect Young Mangroves. Journal of Marine Science and Engineering. 2025; 13(4):734. https://doi.org/10.3390/jmse13040734
Chicago/Turabian StyleTakagi, Hiroshi, Farhat Tahsin Prattoyee, Jun Mitsui, and Shin-ichi Kubota. 2025. "Design of Portable Reefs to Protect Young Mangroves" Journal of Marine Science and Engineering 13, no. 4: 734. https://doi.org/10.3390/jmse13040734
APA StyleTakagi, H., Prattoyee, F. T., Mitsui, J., & Kubota, S.-i. (2025). Design of Portable Reefs to Protect Young Mangroves. Journal of Marine Science and Engineering, 13(4), 734. https://doi.org/10.3390/jmse13040734






