Vector Form Intrinsic Finite Element Method for Dynamic Response Analysis of Deep-Sea Mining Hose
Abstract
1. Introduction
2. Deep-Sea Mining Hose Modeling
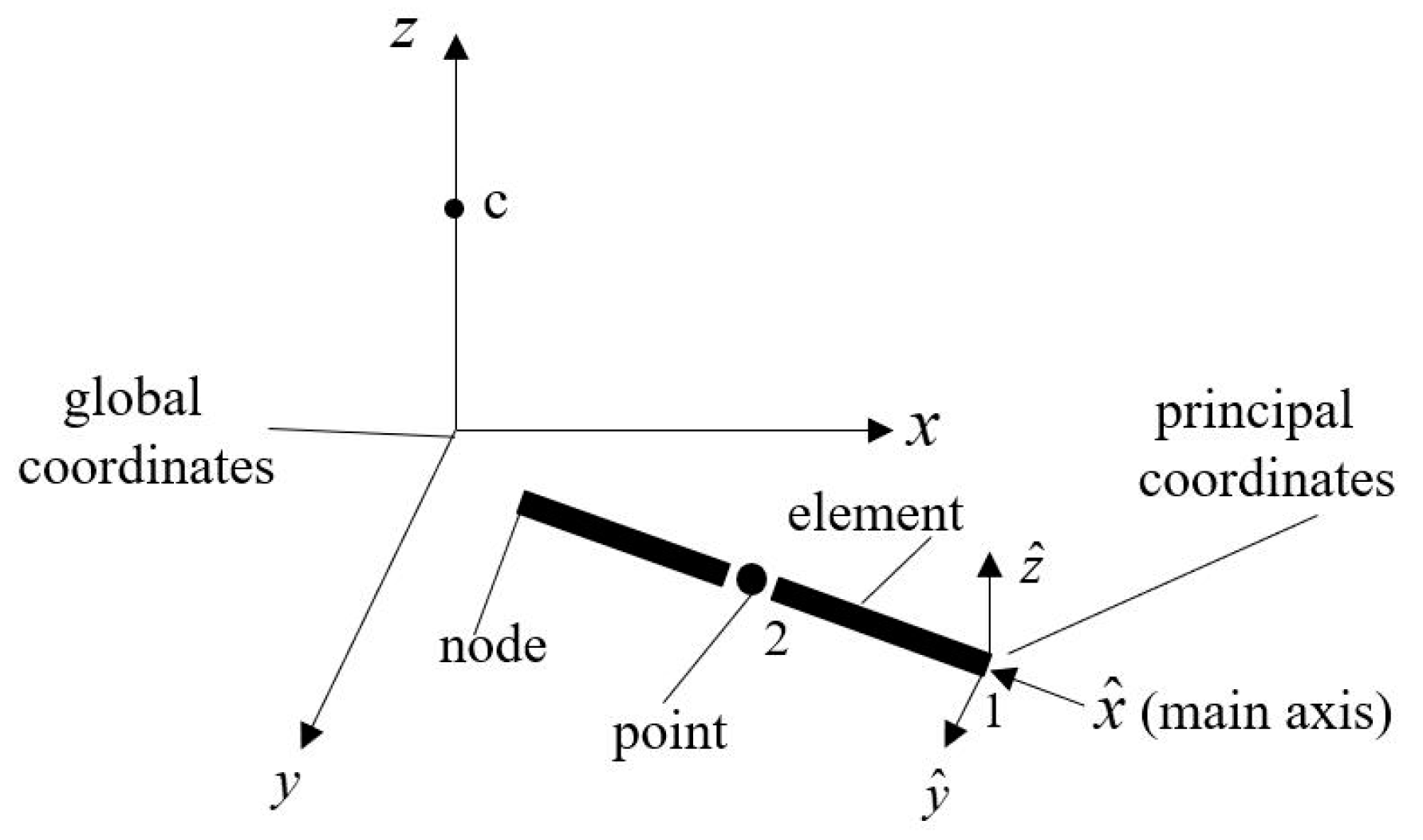
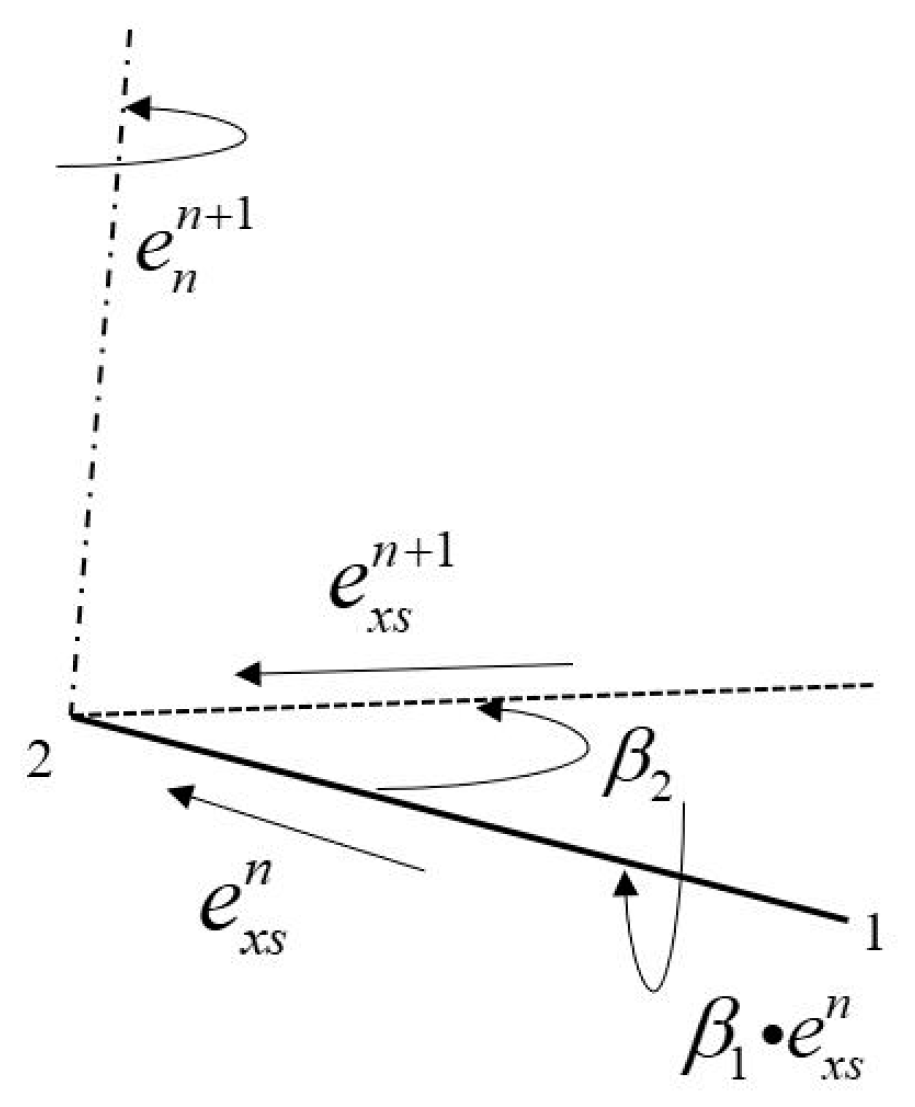
2.1. Point Description and Transformation Matrix
2.2. Force Calculation
2.3. Governing Equation
3. Numerical Calculation and Results
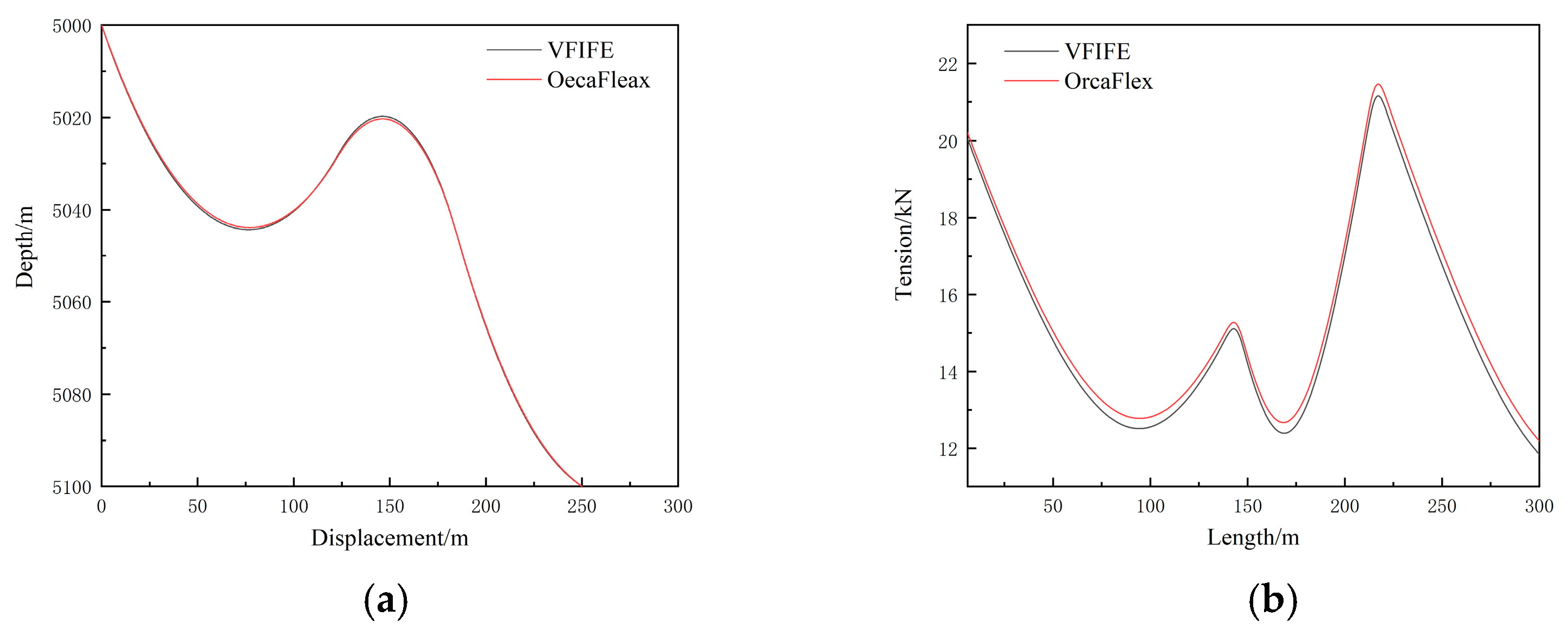
3.1. Verification
3.2. Influence of Different Factors
3.2.1. Current Velocity
3.2.2. Number of Buoyancy Module
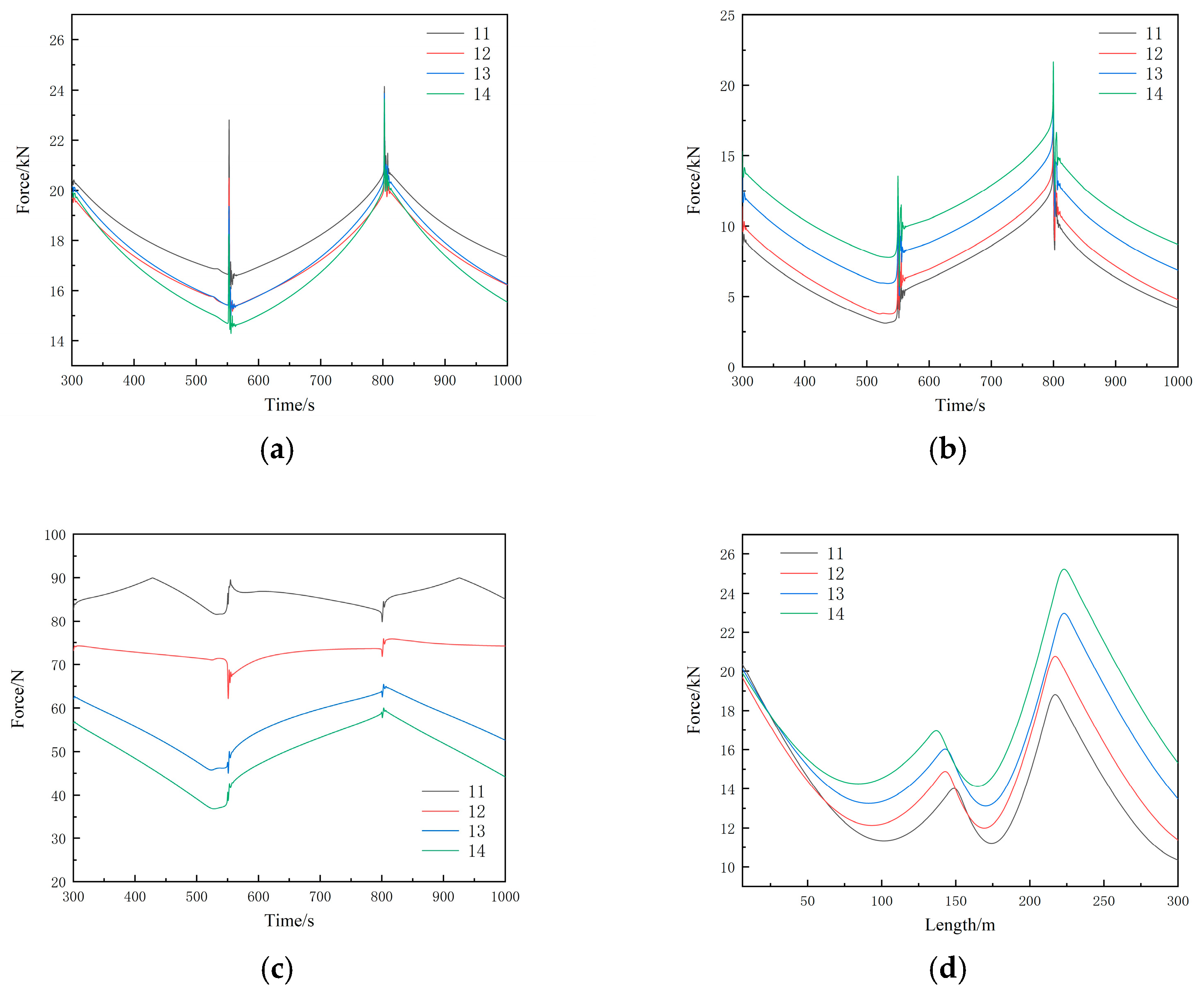
3.2.3. Height of Relay Bin
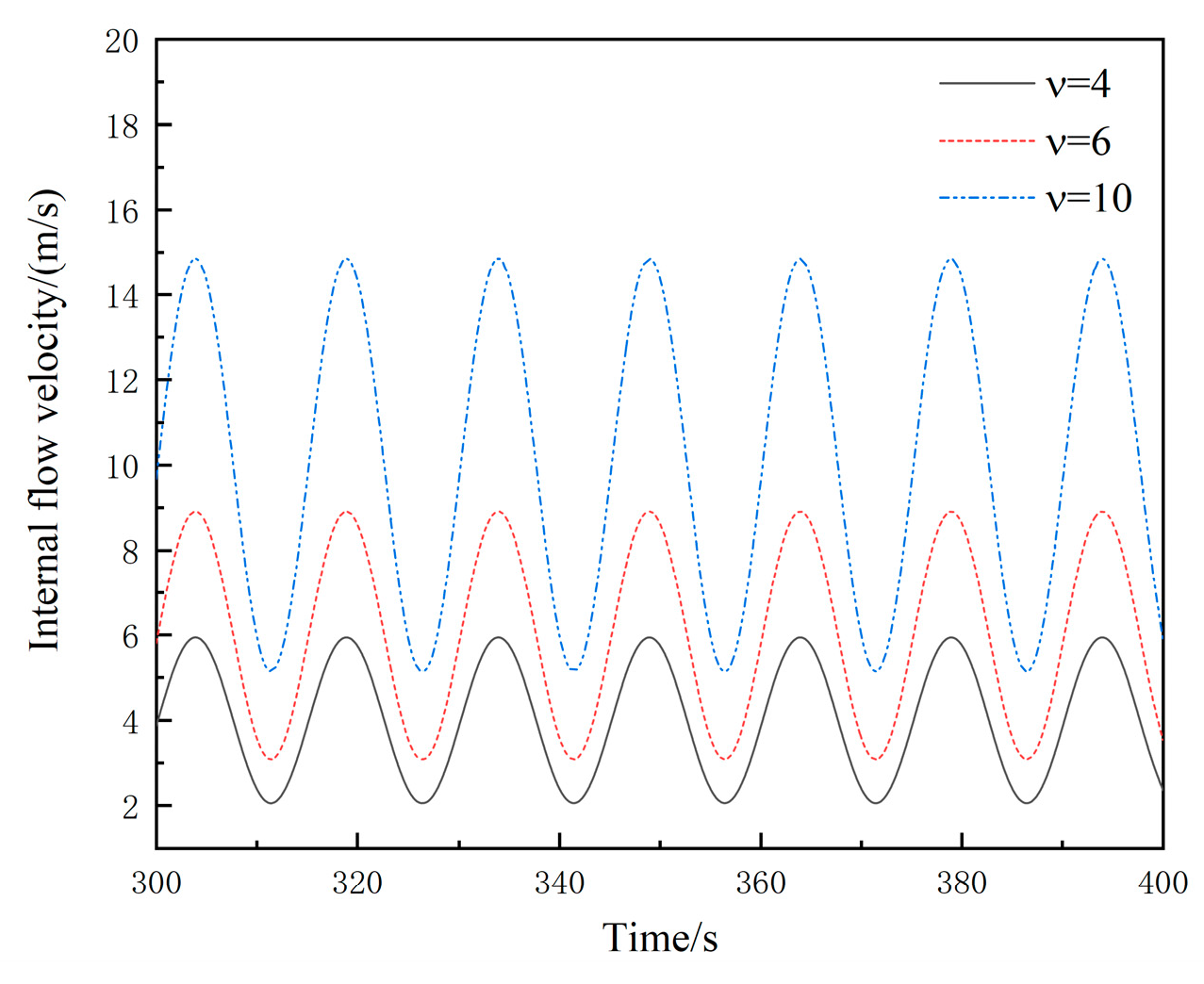
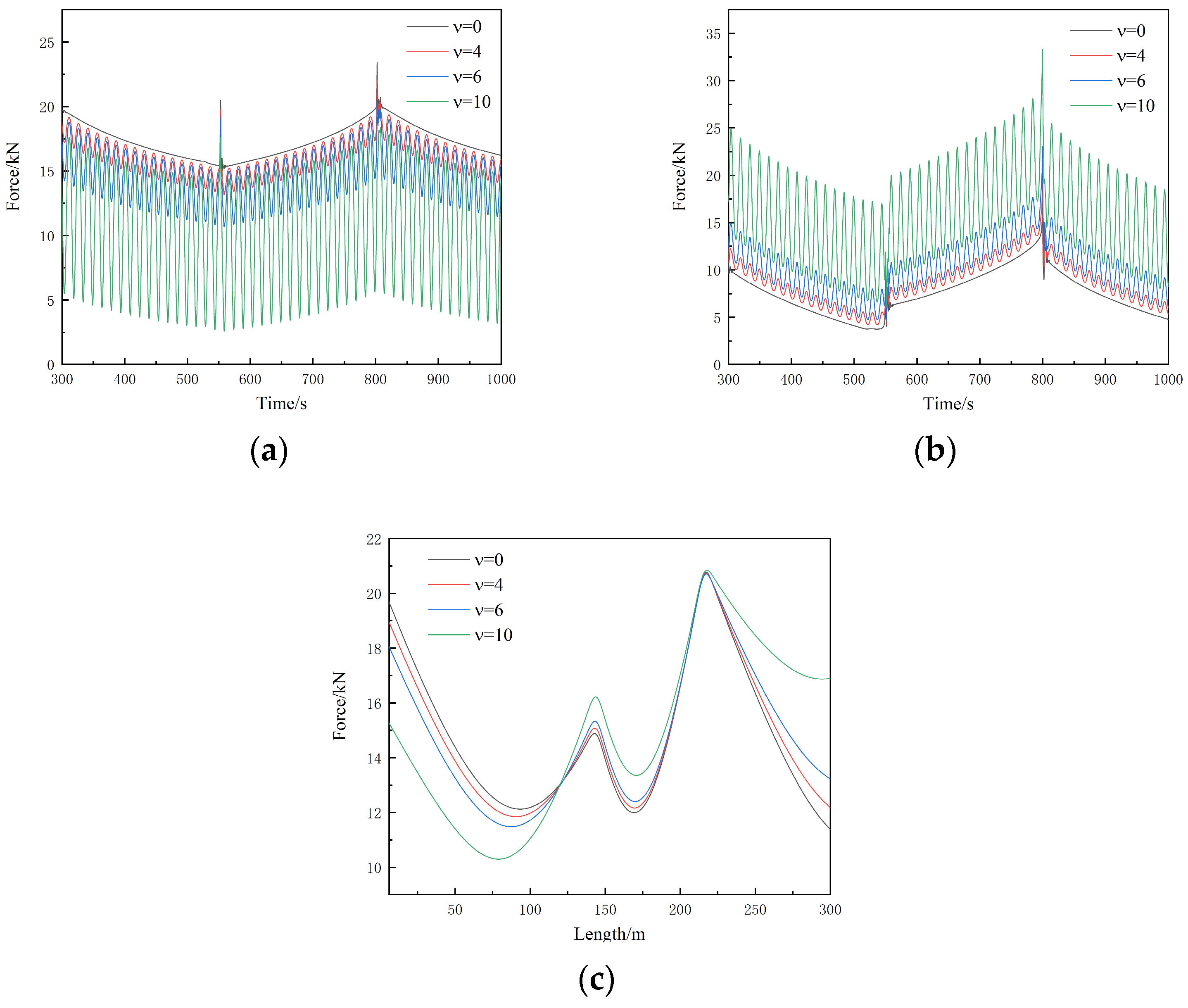
3.2.4. Pulsating Internal Flow Velocity
3.2.5. Movement of Relay Bin
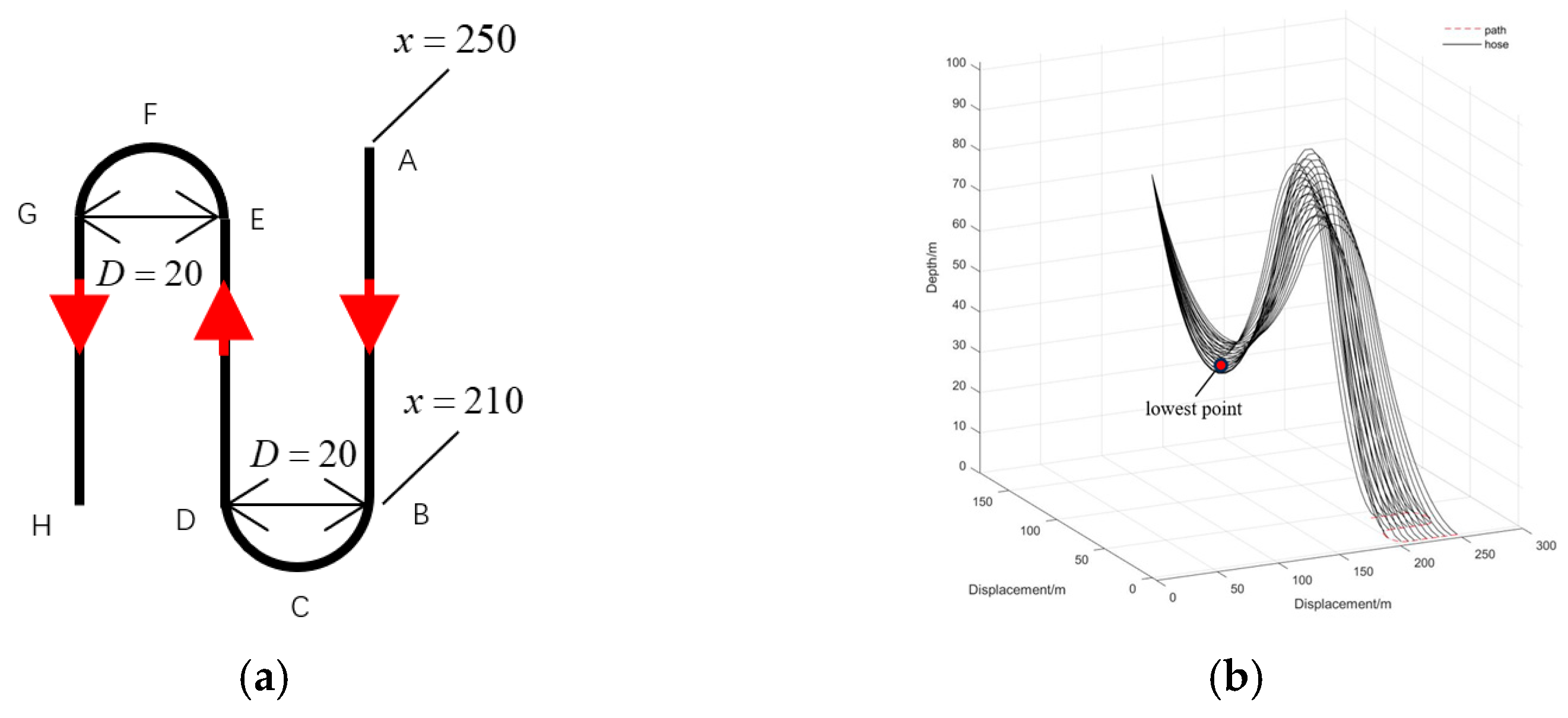
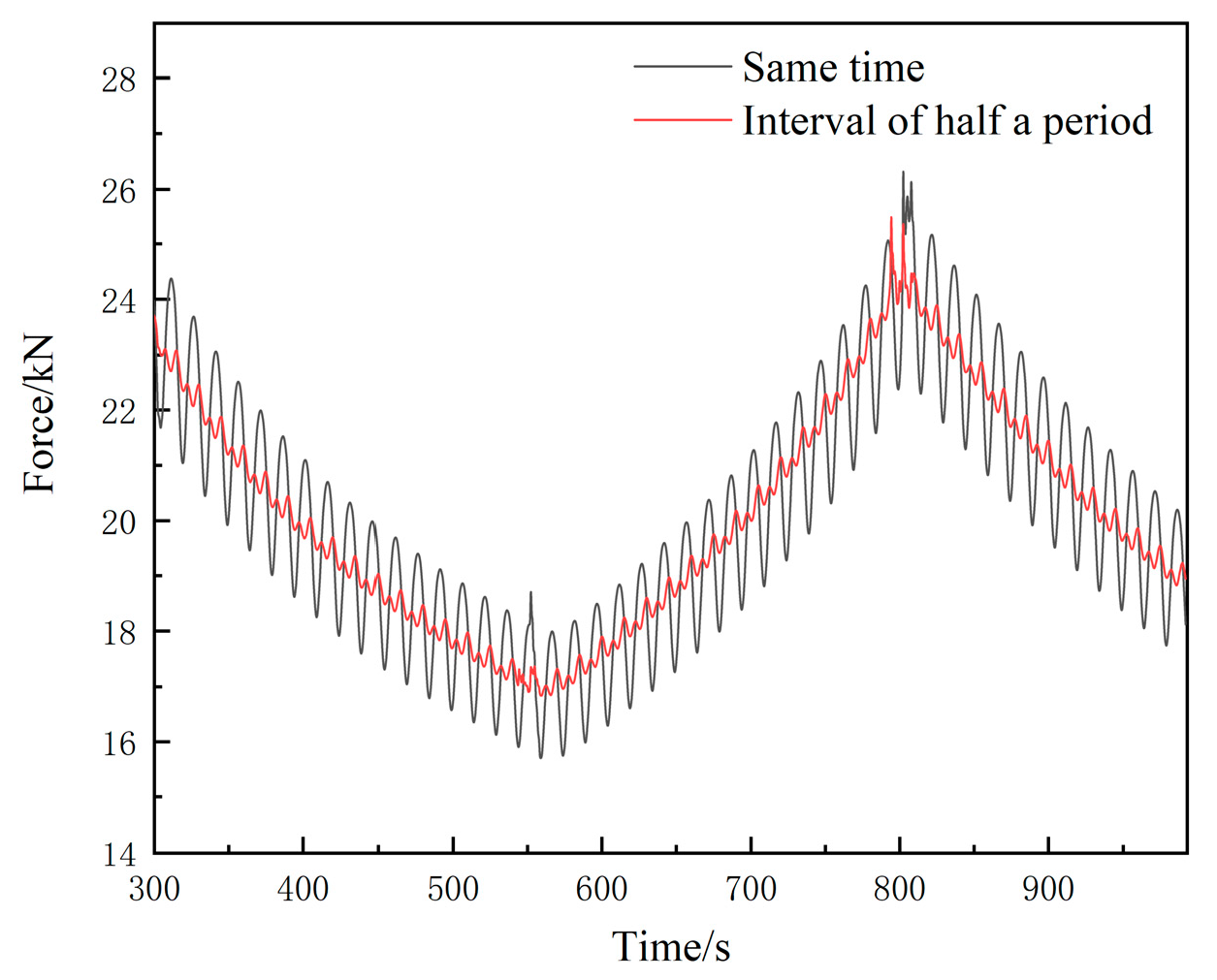
3.2.6. Double-Hose System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, H.H.; Long, G.J. Influence of Mining Vehicle Movement on Sea Mining Flexible Mineral Transporting System. Ocean Eng. 2006, 24, 132–138. [Google Scholar]
- Bernitsas, M.M.; Kokarakis, J.E.; Imron, A. Large Deformation Three-dimensional Static Analysis of Deep Water Marine Risers. Appl. Ocean Res. 1985, 7, 178–187. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.Y. Hydrodynamic Analysis of Marine Flexible Pipe Based on OrcaFlex. China Shiprep. 2024, 37, 54–57. [Google Scholar]
- Tong, Y.; Xia, J. Nonlinear Finite Element Simulation of Flexible Riser System in Deep-sea Mining. Chin. J. Comput. Mech. 2022, 39, 129–134. [Google Scholar]
- Xu, W.H.; Sha, M.; Wang, Y.Y.; Ma, Y.X. Review on The Mechanical Properties of Flexible Pipe Processing Technology in Deep-sea Mining. Mech. Eng. 2024, 46, 532–547. [Google Scholar]
- Song, H.F.; Du, X.G.; Wang, S.; Du, C.Y. Parameter Sensitivity Analysis for Hose Configuration in Deep-Sea Mining Conveying. Shipbuild. China 2020, 61, 154–163. [Google Scholar]
- Yu, Y.; Li, Z.M. Vector Form Finite Element and Its Application in Ocean Engineering; Tianjin University Press: Tianjin, China, 2022; pp. 20–46. [Google Scholar]
- Gu, H.Y. Research on Dynamic Response and Fatigue Damage of Deep-Sea Catenary Riser Based on Vector Form Intrinsic Finite Element. Master’s Thesis, Fuzhou University, Fuzhou, China, 2021. [Google Scholar]
- Yu, Y.; Liu, X.W.; Li, Z.M. Dynamic Characteristics of Lazy Wave Risers under Internal Solitary Waves. J. Ship Mech. 2024, 28, 803–817. [Google Scholar]
- Liu, D.C.; Li, X.M.; Guo, H.Y.; Li, F.H. Influence of Hydro-Pneumatic Tensioner on Static and Dynamic Response of Top Tensioned Riser. Period. Ocean. Univ. China 2023, 53, 161–170. [Google Scholar]
- Li, X.M.; Guo, X.L.; Guo, H.Y. Vector Form Intrinsic Finite Element Method for the Two-dimensional Analysis of Marine Risers with Large Deformations. J. Ocean Univ. China 2018, 17, 498–506. [Google Scholar] [CrossRef]
- Li, X.M.; Guo, X.L.; Guo, H.Y. Vector Form Intrinsic Finite Element Method for Nonlinear Analysis of Three-dimensional Marine Risers. Ocean Eng. 2018, 161, 257–267. [Google Scholar] [CrossRef]
- Chen, D.P.; Gu, H.L.; Li, F.H.; Li, X.M.; Guo, H.Y. Study on Vortex-induced Vibration Characteristics of Catenary Type Riser under Oscillatory Flow. J. Ship Mech. 2022, 26, 1227–1236. [Google Scholar]
- Li, X.M.; Zhang, L.; Niu, J.J.; Han, Y.Q.; Guo, H.Y. Dynamic Response of A Deep-sea Top Tensioned Riser Based on Vector Form Intrinsic Finite Element. J. Vib. Shock. 2016, 35, 218–223. [Google Scholar]







| Parameters | Value | Unit |
|---|---|---|
| length | 300 | m |
| outside diameter | 0.263 | m |
| inner diameters | 0.200 | m |
| modulus | 0.05 | GPa |
| dry weight of unit hose | 38.4 | kg |
| inflow mass density | 1133 | kg/m3 |
| buoyancy of one floating module | 3312.4 | N |
| water velocity | 0.4 | m/s |
| water density | 1025 | kg/m3 |
| drag coefficient | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Li, X.; Zheng, H.; Yan, H.; Zhang, M.; Wang, B. Vector Form Intrinsic Finite Element Method for Dynamic Response Analysis of Deep-Sea Mining Hose. J. Mar. Sci. Eng. 2025, 13, 701. https://doi.org/10.3390/jmse13040701
Xu J, Li X, Zheng H, Yan H, Zhang M, Wang B. Vector Form Intrinsic Finite Element Method for Dynamic Response Analysis of Deep-Sea Mining Hose. Journal of Marine Science and Engineering. 2025; 13(4):701. https://doi.org/10.3390/jmse13040701
Chicago/Turabian StyleXu, Jingchang, Xiaoyan Li, Hao Zheng, Honghao Yan, Ming Zhang, and Bingkun Wang. 2025. "Vector Form Intrinsic Finite Element Method for Dynamic Response Analysis of Deep-Sea Mining Hose" Journal of Marine Science and Engineering 13, no. 4: 701. https://doi.org/10.3390/jmse13040701
APA StyleXu, J., Li, X., Zheng, H., Yan, H., Zhang, M., & Wang, B. (2025). Vector Form Intrinsic Finite Element Method for Dynamic Response Analysis of Deep-Sea Mining Hose. Journal of Marine Science and Engineering, 13(4), 701. https://doi.org/10.3390/jmse13040701






