UUV Cluster Distributed Navigation Fusion Positioning Method with Information Geometry
Abstract
1. Introduction
- An information geometry probabilistic model of underwater navigation for UUVs was established, achieving the standardization of navigation information parameters among UUVs and reducing the impact of asynchronous timing on positioning errors.
- Addressing the issues of poor real-time positioning and the inability to freely aggregate and disperse UUVs, a UUV cooperative positioning method based on information geometry probabilistic fusion was developed, combining the factor graph approach. This method utilizes the information geometry probability of each UUV as positioning information and constructs an information geometry probability factor graph fusion architecture, enabling real-time and high-precision positioning of UUV clusters.
- A testing platform for UUV cluster cooperative fusion positioning was established, and experiments were conducted to evaluate the proposed method under scenarios involving sudden changes in positioning errors and free aggregation and dispersion of UUV clusters. The experimental results matched the simulation results, demonstrating that the proposed unmanned underwater vehicle cluster cooperative fusion positioning method based on information geometry can meet the requirements of real-time positioning and free aggregation and dispersion characteristics of UUV clusters.
2. Related Work
2.1. Current Research Status at Home and Abroad
2.2. Theoretical Foundations of Baseline Methods
2.2.1. Recursive Least Squares (RLS)
2.2.2. Unscented Kalman Filter (UKF)
2.2.3. Backpropagation Neural Network (BPNN)
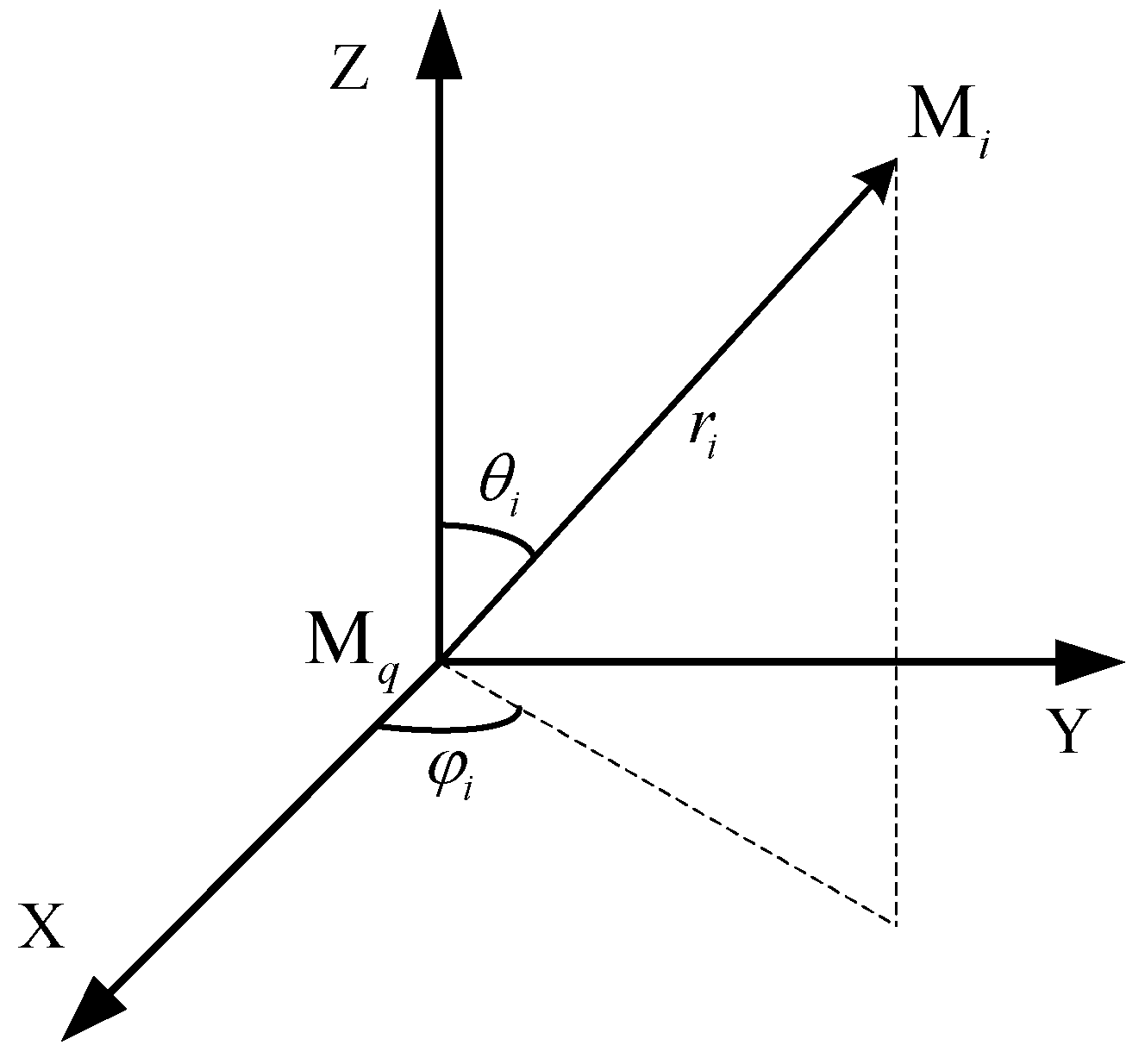
3. System Model
4. Numerical Simulation Setup
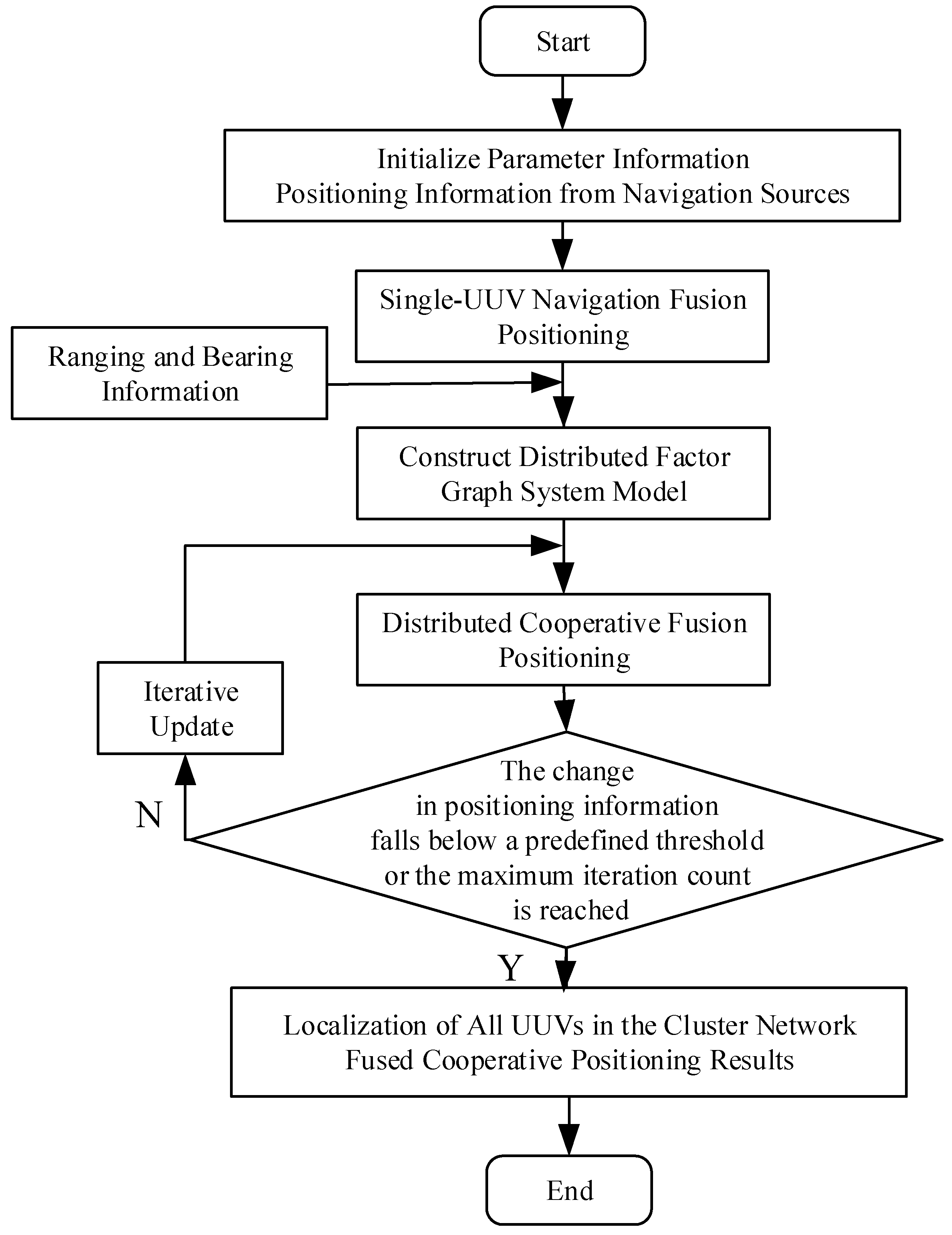
Overall Algorithm Implementation Steps
5. Testing and Results Analysis
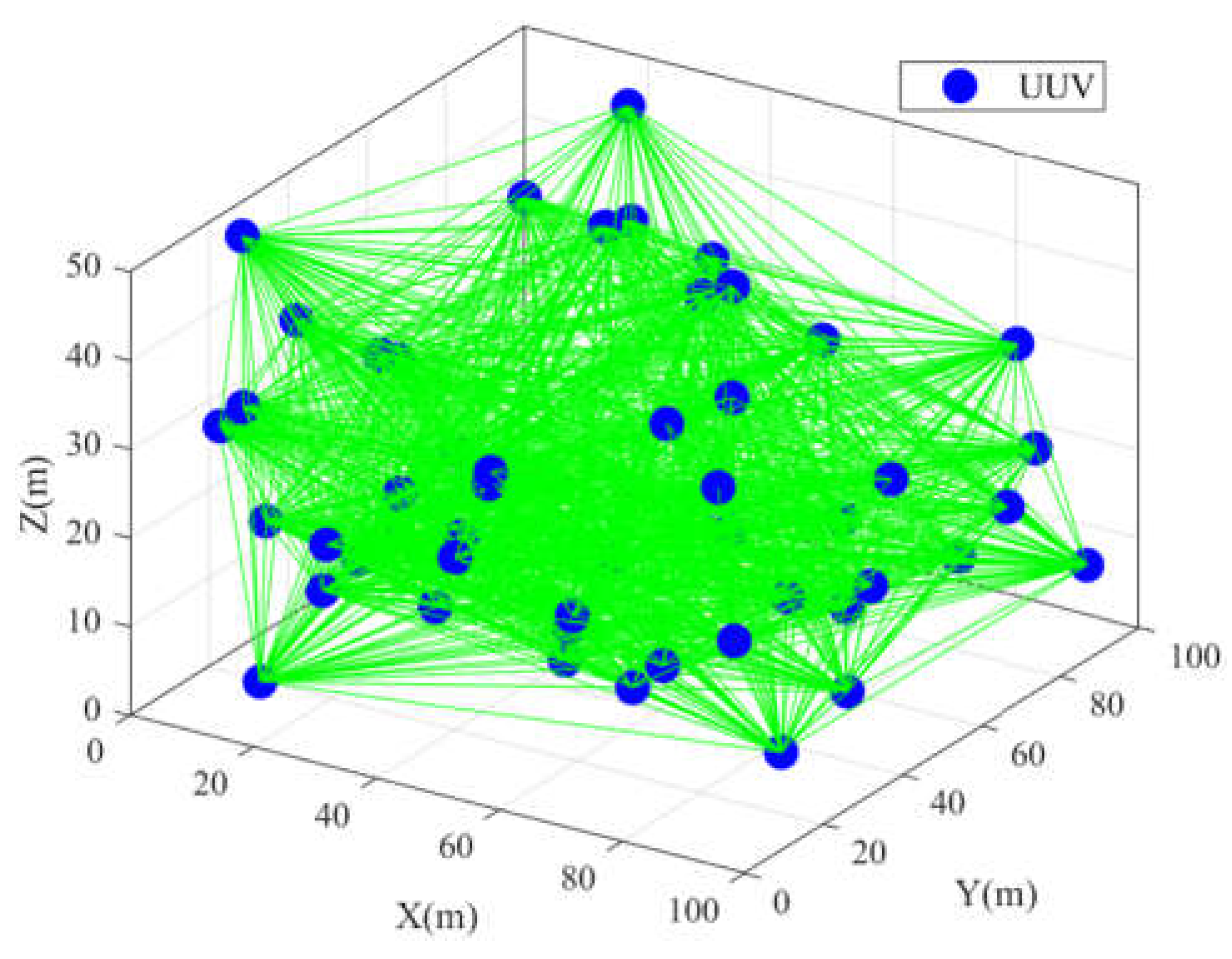
5.1. Simulation Condition Settings
| Simulation Parameters | Parameter Settings |
|---|---|
| Number of underwater base stations | |
| Underwater base station locations | Vertices of the simulation scenario |
| Standard deviation of underwater ranging error | |
| Inertial navigation parameters | Consistent with Table 2 |
| Minimum output time interval | 0.1 s |
| Number of Monte Carlo runs | 10,000 |
| Inertial Unit Parameters | Accelerometer | Gyroscope |
|---|---|---|
| Bias | ||
| Random error standard deviation | ||
| Output rate | ||
| Calibration period | ||
5.2. Ideal Scenario
5.3. Sudden-Change Scenarios
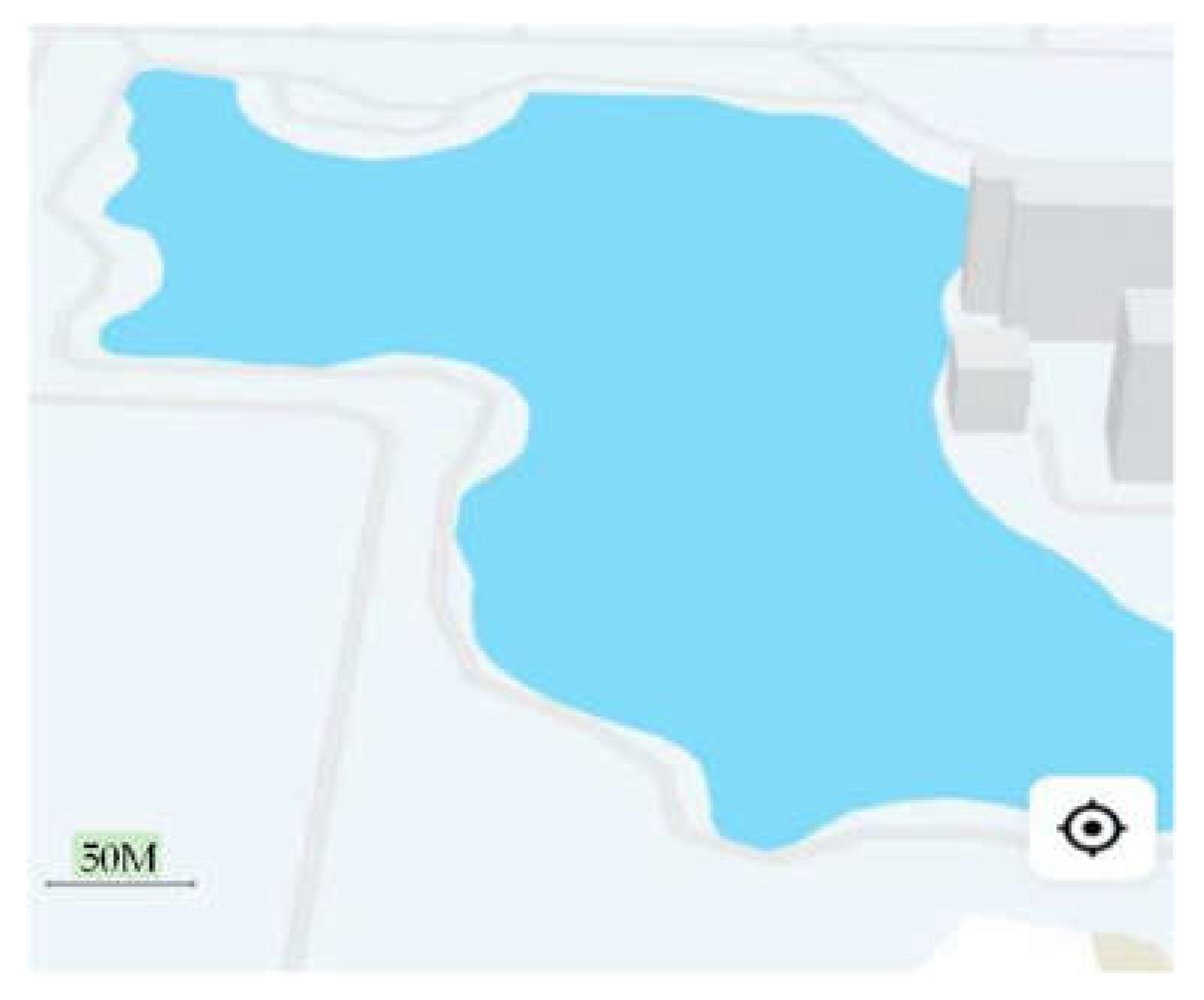
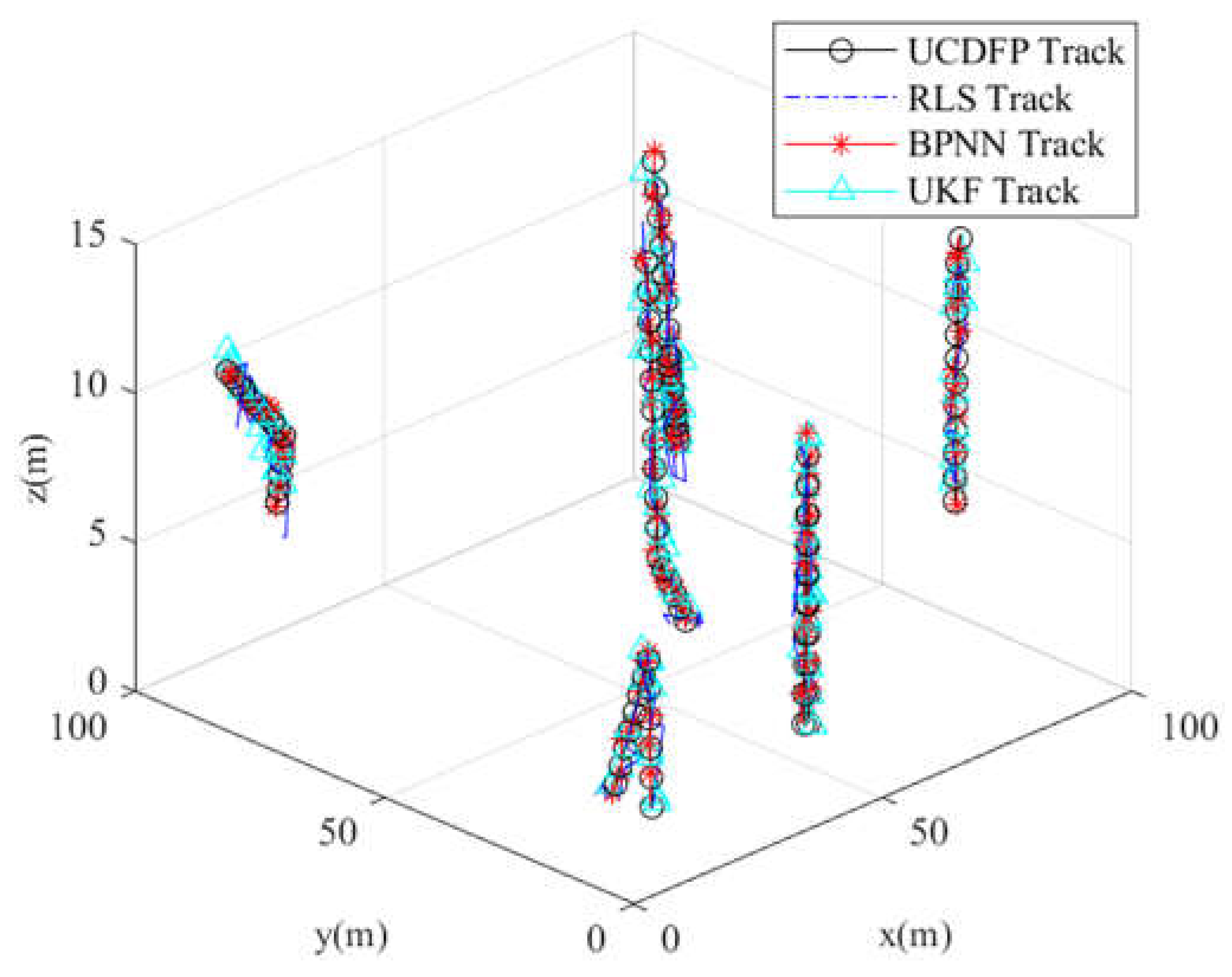
6. Experimental Validation and Results Analysis
Actual Testing Scenario
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, S.; Li, Y.; Bao, F.; Xu, H.; Yang, Y.; Yan, Q.; Zhong, S.; Yin, H.; Xu, J.; Huang, Z.; et al. Marine environmental monitoring with unmanned vehicle platforms: Present applications and future prospects. Sci. Total. Environ. 2022, 858, 159741. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Shang, J.; Luo, Z.; Tang, L.; Zhang, X.; Li, J. Reviews of power systems and environmental energy conversion for unmanned underwater vehicles. Renew. Sustain. Energy Rev. 2012, 16, 1958–1970. [Google Scholar] [CrossRef]
- Bogue, R. Underwater robots: A review of technologies and applications. Ind. Robot. Int. J. 2015, 42, 186–191. [Google Scholar]
- Bai, G.; Chen, Y.; Hu, X.; Shi, Y.; Jiang, W.; Zhang, X. Multi-AUV dynamic trajectory optimization and collaborative search combined with task urgency and energy consumption scheduling in 3-D underwater environment with random ocean currents and uncertain obstacles. Ocean Eng. 2023, 275, 113841. [Google Scholar] [CrossRef]
- Du, Z.; Chai, H.; Xiang, M.; Zhang, F.; Wang, Z. Resilient model of multi-UUVs cooperative localization for detection of sensor fault and outliers. Ocean Eng. 2022, 266, 113216. [Google Scholar] [CrossRef]
- Zhou, Z.; Liang, X.; Shi, Z.; Wang, G.; Lang, J.; Liu, L. An improved comprehensive calibration method for ship strapdown inertial navigation system. Ocean Eng. 2023, 269, 113567. [Google Scholar] [CrossRef]
- Xu, W.; Yang, J.; Wei, H.; Lu, H.; Tian, X.; Li, X. A localization algorithm based on pose graph using Forward-looking sonar for deep-sea mining vehicle. Ocean Eng. 2023, 284, 114968. [Google Scholar] [CrossRef]
- Li, T.; Zhao, J.; Ma, J. A precise underwater positioning method by considering the location difference of transmitting and receiving sound waves. Ocean Eng. 2022, 247, 110480. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, S.; Wang, X.; Shen, P.; Zhang, T. Deep-Sea Underwater Cooperative Operation of Manned/Unmanned Sub-mersible and Surface Vehicles for Different Application Scenarios. J. Mar. Sci. Eng. 2022, 10, 909. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, C.; Gao, L.; Zhang, F. Vessel and Underwater Vehicles Cooperative Localization using Topology Factor Graphs. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, Q.; Fan, S.; Zhang, Y.; Gao, W.; Wei, J.; Wang, Y. A Novel Adaptive Sliding Observation-Based Cooperative Positioning Algorithm Under Factor Graph Framework for Multiple UUVs. IEEE Trans. Ind. Inform. 2022, 19, 8743–8753. [Google Scholar] [CrossRef]
- Yan, Z.; Luan, Z.; Liu, J.; Xing, W. A Cooperative Localization Method for Multiple Unmanned Underwater Vehicles Based on Improved Factor Graph. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Heilongjiang, China, 6–9 August 2023; pp. 894–899. [Google Scholar]
- Liang, Q.; Luo, M.; Wang, Y.; Hao, X. Multi-attacks effectiveness evaluation of UUV based on wake guidance. Ocean Eng. 2022, 266, 112654. [Google Scholar] [CrossRef]
- Wu, Y.; Ta, X.; Xiao, R.; Wei, Y.; An, D.; Li, D. Survey of underwater robot positioning navigation. Appl. Ocean. Res. 2019, 90, 1845–1859. [Google Scholar] [CrossRef]
- Wang, D.; Tang, E.; Li, L.; Peng, H.; Han, Y.; Chen, C.; Chang, M.; Guo, K.; He, L. Temperature and pressure propagation characteristics in multi-media interfaces of PVDF pressure sensor near underwater explosion source. Ocean Eng. 2023, 287, 115810. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, T.; Guo, Q.; Xu, C.; Wang, T.; Peng, D.; Yu, X. Terrain matching positioning method for underwater vehicles based on curvature discrimination. Ocean Eng. 2022, 260, 111965. [Google Scholar] [CrossRef]
- Zhang, L.; An, R. Least square estimation method for the navigation error of the UUVs. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; pp. 775–778. [Google Scholar]
- Wei, Y.; Yu, G.; Qu, F.; Sun, R. AUV-Aided Energy-Efficient Data Collection in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2020, 7, 10010–10022. [Google Scholar] [CrossRef]
- Jia, Z.; Zheng, W.; Yuan, F. A Two-Dimensional Chirp-MFCSK Modulation Method for Underwater LoRa System. IEEE Internet Things J. 2022, 9, 24388–24397. [Google Scholar] [CrossRef]
- Du, Z.; Wang, W.; Chai, H.; Xiang, M.; Zhang, F.; Huang, Z. Configuration analysis method and geometric interpretation of UUVs cooperative localization based on error ellipse. Ocean Eng. 2021, 244, 110299. [Google Scholar] [CrossRef]
- TN, R.; Nherakkol, A.; Navelkar, G. Navigation of autonomous underwater vehicle using extended kalman filter. In Trends in Intelligent Robotics: Proceedings of the 13th FIRA Robot World Congress, FIRA 2010, Bangalore, India, 15–17 September 2010; Proceedings 13; Springer: Berlin Heidelberg, Germany, 2010; pp. 1–9. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, X.; Ma, P. Consistent Extended Kalman Filter-Based Cooperative Localization of Multiple Autonomous Un-derwater Vehicles. Sensors 2022, 22, 4563. [Google Scholar] [CrossRef]
- Bai, M.; Huang, Y.; Chen, B.; Yang, L.; Zhang, Y. A Novel Mixture Distributions-Based Robust Kalman Filter for Cooperative Localization. IEEE Sensors J. 2020, 20, 14994–15006. [Google Scholar] [CrossRef]
- Ullah, I.; Shen, Y.; Su, X.; Esposito, C.; Choi, C. A Localization Based on Unscented Kalman Filter and Particle Filter Localization Algorithms. IEEE Access 2019, 8, 2233–2246. [Google Scholar] [CrossRef]
- Wang, Z.; Xiang, X.; Guan, X.; Pan, H.; Yang, S.; Chen, H. Deep learning-based robust positioning scheme for imaging sonar guided dynamic docking of autonomous underwater vehicle. Ocean Eng. 2024, 293, 116704. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, Y.; Xu, Z.; Zhang, Z.; Chen, L.; Li, C. PL-Net: Towards Deep Learning-Based Localization for Underwater Terrain. In Neural Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–16. [Google Scholar] [CrossRef]
- Zhu, J.; Kia, S.S. Learning-Based Measurement Scheduling for Loosely-Coupled Cooperative Localization. IEEE Robot. Autom. Lett. 2022, 7, 6313–6319. [Google Scholar] [CrossRef]
- Liao, R.; Su, W.; Wu, X.; Cheng, E. Reinforcement Learning Based Mobile Underwater Localization for Silent UUV in Un-derwater Acoustic Sensor Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 1–19. [Google Scholar] [CrossRef]
- Brambilla, M.; Gaglione, D.; Soldi, G.; Mendrzik, R.; Ferri, G.; LePage, K.D.; Nicoli, M.; Willett, P.; Braca, P.; Win, M.Z. Co-operative Localization and Multitarget Tracking in Agent Networks with the Sum-Product Algorithm. IEEE Open J. Signal Process. 2022, 3, 169–195. [Google Scholar] [CrossRef]
- Meyer, F.; Kropfreiter, T.; Williams, J.L.; Lau, R.; Hlawatsch, F.; Braca, P.; Win, M.Z. Message Passing Algorithms for Scalable Multitarget Tracking. Proc. IEEE 2018, 106, 221–259. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Y.; Hao, Q.; Jiang, P.; Yu, C.; Yu, F. Cooperative Positioning for Multi-AUVs Based on Factor Graph and Maximum Correntropy. IEEE Access 2019, 7, 153327–153337. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, S.; Tang, C. Cooperative positioning of underwater unmanned vehicle clusters based on factor graphs. Ocean Eng. 2023, 287, 115854. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, X.; Morelande, M.; Moran, B. Information geometry of target tracking sensor networks. Inf. Fusion. 2012, 14, 311–326. [Google Scholar] [CrossRef]
- Tang, C.; Wang, Y.; Zhang, L.; Zhang, Y.; Song, H. Multisource Fusion UAV Cluster Cooperative Positioning Using Infor-mation Geometry. Remote. Sens. 2022, 14, 5491. [Google Scholar] [CrossRef]
- Braca, P.; Goldhahn, R.; Ferri, G.; LePage, K.D. Distributed Information Fusion in Multistatic Sensor Networks for Underwater Surveillance. IEEE Sensors J. 2015, 16, 4003–4014. [Google Scholar] [CrossRef]
- Ferri, G.; Munafò, A.; Tesei, A.; Braca, P.; Meyer, F.; Pelekanakis, K.; Petroccia, R.; Alves, J.; Strode, C.; LePage, K. Cooperative robotic networks for underwater surveillance: An overview. IET Radar Sonar Navig. 2017, 11, 1740–1761. [Google Scholar] [CrossRef]
- Dell’Erba, R. Determination of Spatial Configuration of an Underwater Swarm with Minimum Data. Int. J. Adv. Robot. Syst. 2015, 12, 61035. [Google Scholar] [CrossRef]
- dell’Erba, R. Distance estimations in unknown sea underwater conditions by power LED for robotics swarms. Contin. Mech. Thermodyn. 2021, 33, 97–106. [Google Scholar]
- dell’Erba, R. The distances measurement problem for an underwater robotic swarm: A semi-experimental trial, using power LEDs, in unknown sea water conditions. Contin. Mech. Thermodyn. 2023, 35, 895–903. [Google Scholar]
- Su, X.; Ullah, I.; Liu, X.; Choi, D. A Review of Underwater Localization Techniques, Algorithms, and Challenges. J. Sensors 2020, 2020, 1–24. [Google Scholar] [CrossRef]
- Amari, S.I. Information Geometry and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]




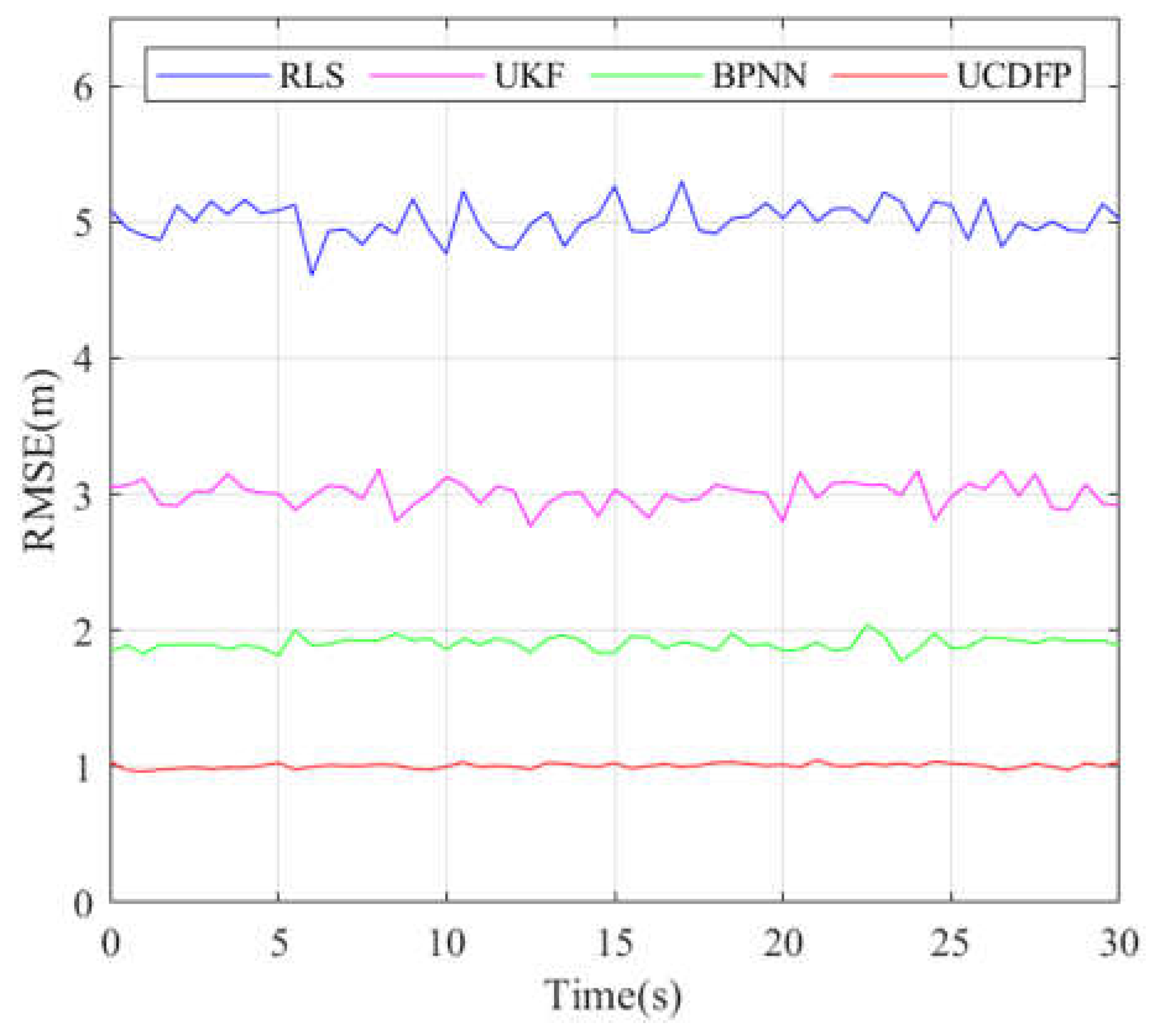



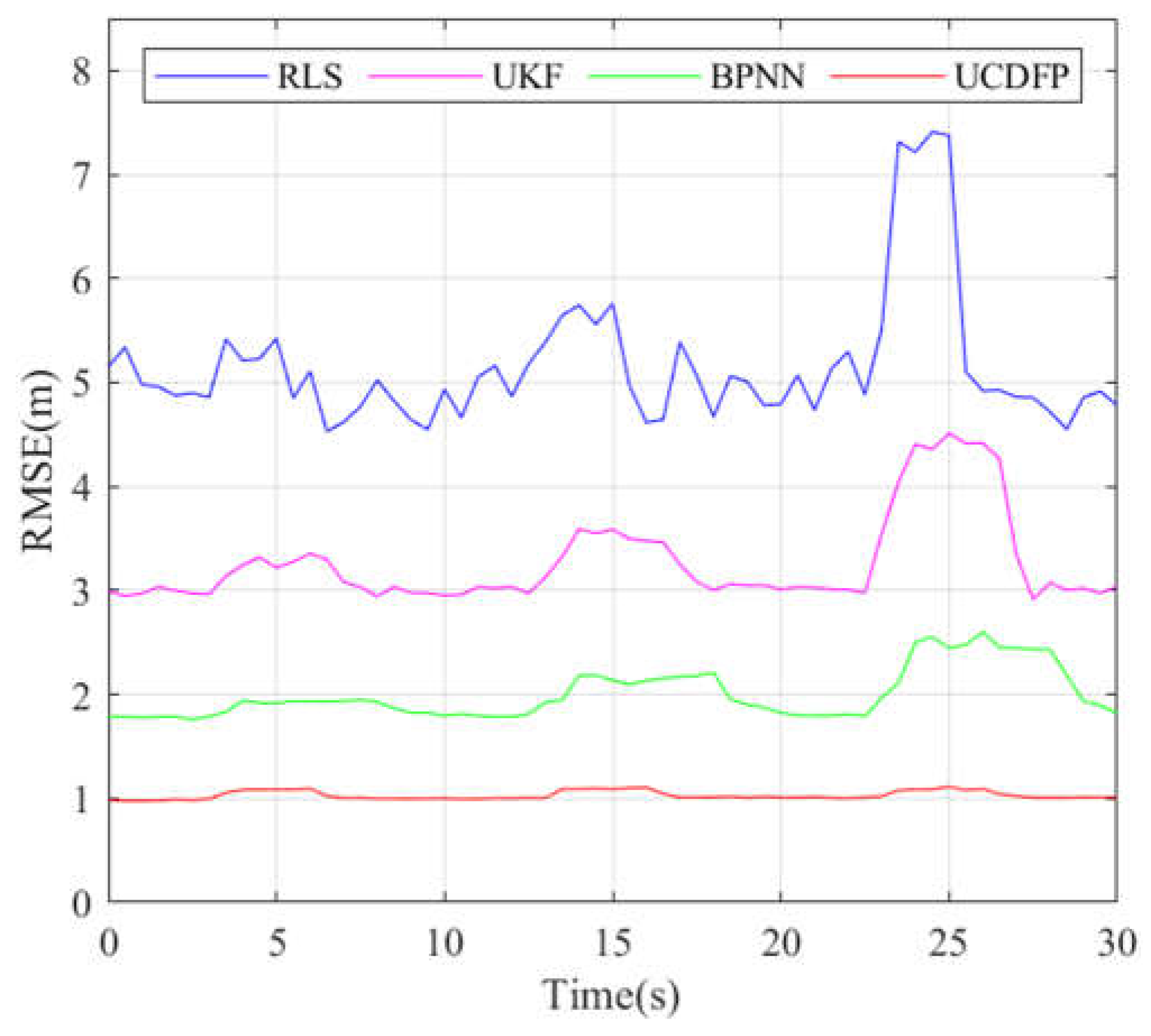


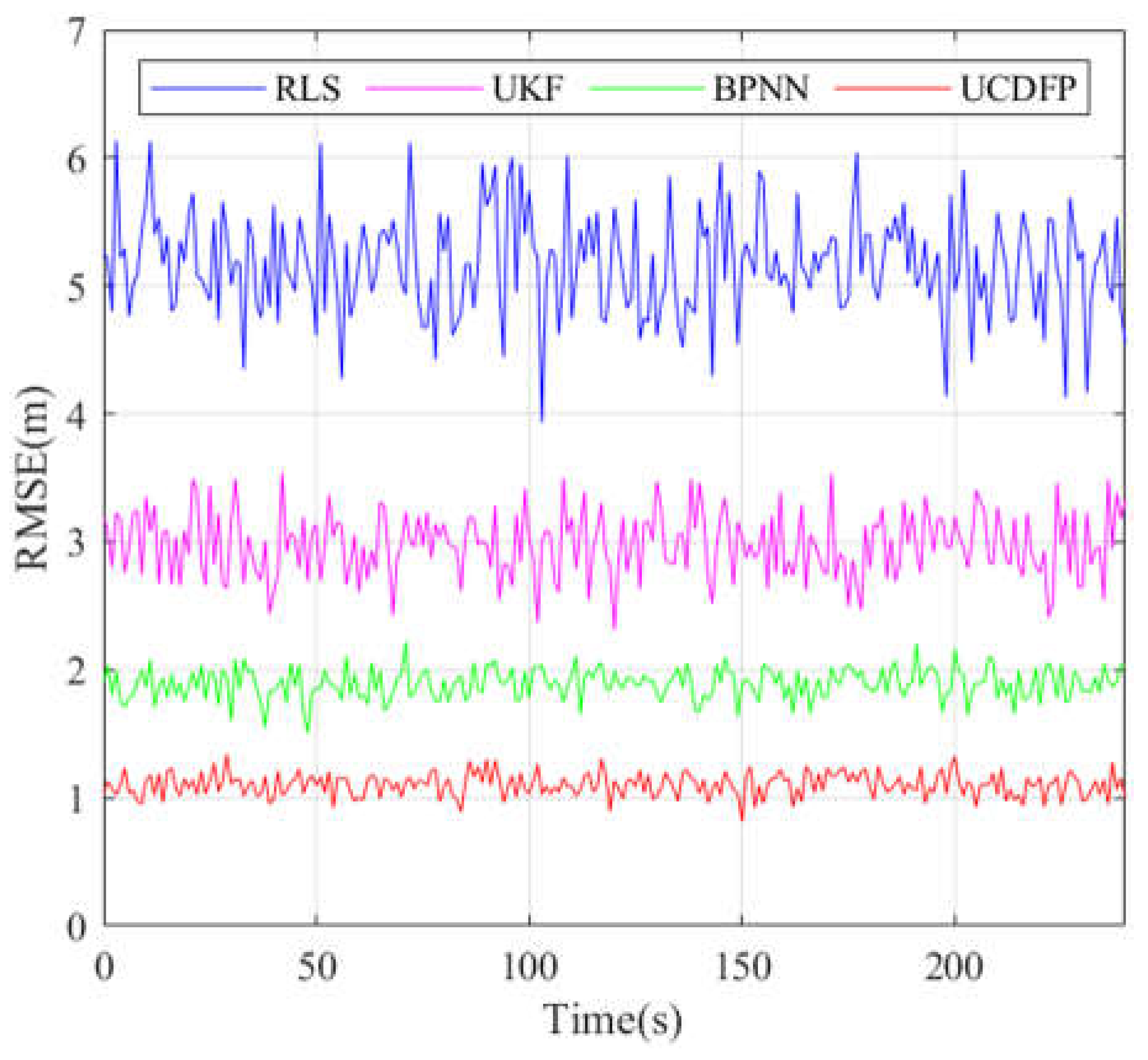

| Method | Average Positioning Error (m) | Error Increment During Dynamic Swarm Changes (m) |
|---|---|---|
| UCDFP | 0.982 | 0.3 |
| RLS | 4.992 | 4.8 |
| UKF | 3.092 | 2.75 |
| BPNN | 1.902 | 1.8 |
| Method | Convergence Time After Sudden Error (s) | Error Increment During Sudden Changes (m) |
|---|---|---|
| UCDFP | 1.5 | 0.352 |
| RLS | 2 | 4.8 |
| UKF | 3 | 2.75 |
| BPNN | 5 | 1.8 |
| Relevant Parameters | Simulation Parameters | Parameter Settings |
|---|---|---|
| Inertial Measurement Unit (IMU) | Model | ADIS16470 (Analog Devices) Shenzhen, China |
| Accelerometer | Bias stability = 1500 μg Noise density = 100 μg/Hz | |
| Gyroscope | Bias stability = 1°/h Noise density = 0.1°/√h | |
| Acoustic Ranging Sensors | Model | Tritech MicronNav |
| Range | 0.1–100 m | |
| Accuracy | ±0.1 m (in still water) | |
| Frequency | 25–50 kHz | |
| Underwater Base Stations (UBSs) | Positioning accuracy | ±0.5 m (static), ±1.2 m (dynamic) |
| Communication | Acoustic modem (WHOI Micro-Modem) | |
| Bandwidth | 4 kHz | |
| Environmental Conditions | Water Properties | Temperature: 10–15 °C; salinity: 35 ppt |
| Sound Speed | 1500 m/s (calculated using Mackenzie’s formula) | |
| Disturbances | Simulated current speed: 0.5–1.0 m/s (random direction); turbidity: 1–5 NTUs (Nephelometric Turbidity Units) | |
| Communication Protocols | Inter-UUV communication | Time-division multiple access (TDMA) |
| Data rate | 500 bps (acoustic), | |
| Packet loss rate | <5% (ideal scenario) <20% (sudden-change scenario) | |
| Experimental Hardware | UUV Platform | Custom-built AUV with 6-DOF thrusters |
| Onboard computer unit | NVIDIA Jetson AGX Xavier | |
| Location | Qixiang Lake (34.1378° N, 108.6594° E) | |
| Depth | 10–15 m | |
| Test duration | 2 h per trial |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wu, S.; Tang, C.; Lin, H. UUV Cluster Distributed Navigation Fusion Positioning Method with Information Geometry. J. Mar. Sci. Eng. 2025, 13, 696. https://doi.org/10.3390/jmse13040696
Zhang L, Wu S, Tang C, Lin H. UUV Cluster Distributed Navigation Fusion Positioning Method with Information Geometry. Journal of Marine Science and Engineering. 2025; 13(4):696. https://doi.org/10.3390/jmse13040696
Chicago/Turabian StyleZhang, Lingling, Shijiao Wu, Chengkai Tang, and Hechen Lin. 2025. "UUV Cluster Distributed Navigation Fusion Positioning Method with Information Geometry" Journal of Marine Science and Engineering 13, no. 4: 696. https://doi.org/10.3390/jmse13040696
APA StyleZhang, L., Wu, S., Tang, C., & Lin, H. (2025). UUV Cluster Distributed Navigation Fusion Positioning Method with Information Geometry. Journal of Marine Science and Engineering, 13(4), 696. https://doi.org/10.3390/jmse13040696







