Variation of Wyrtki Jets Influenced by Indo-Pacific Ocean–Atmosphere Interactions
Abstract
1. Introduction
2. Data
3. Methods
4. Results
4.1. Spatial Distribution and Seasonal Variation Characteristics of WJs
4.2. Selection of ENSO and IOD Events
4.3. General Description of Interannual WJ Variations
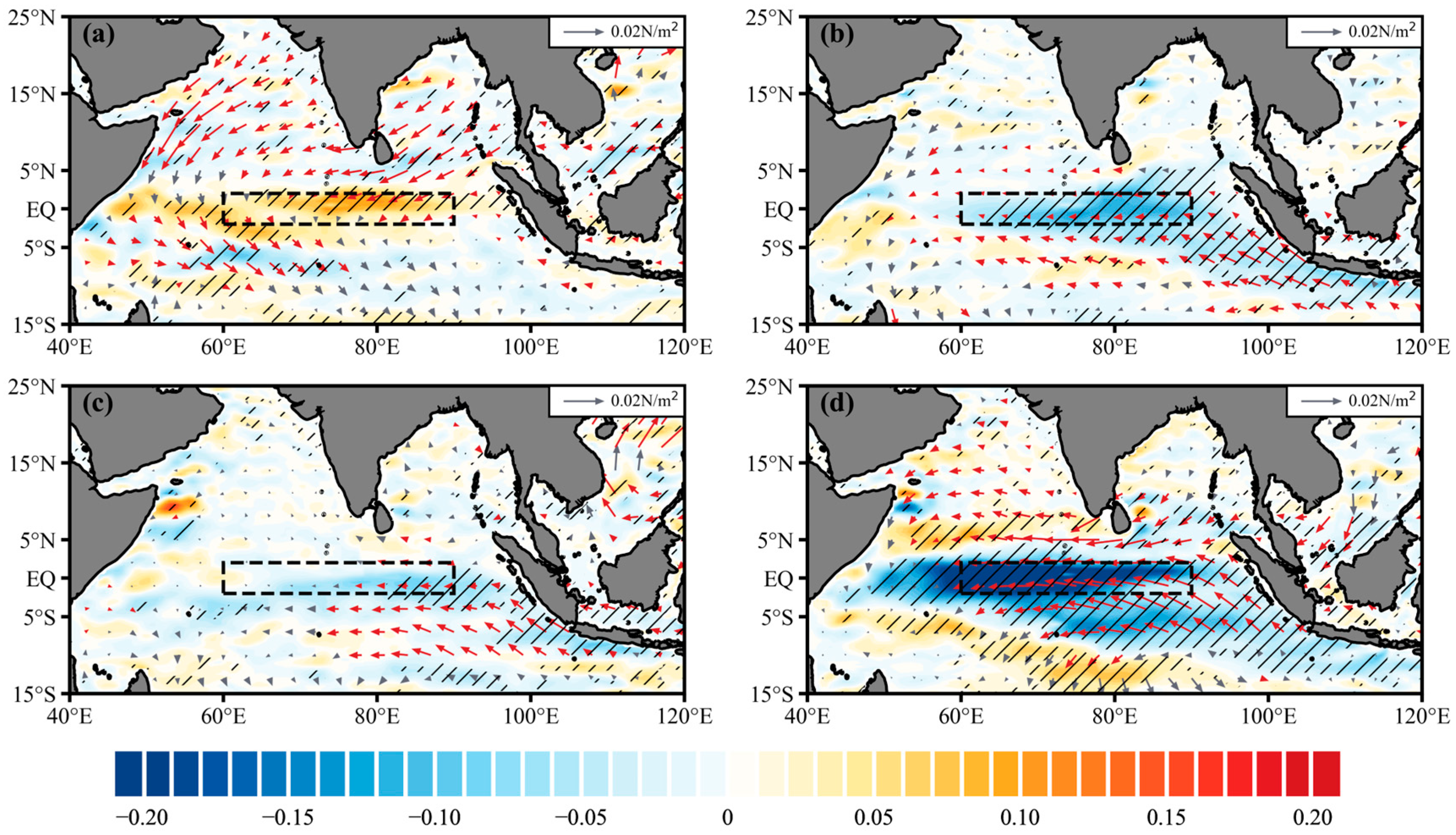
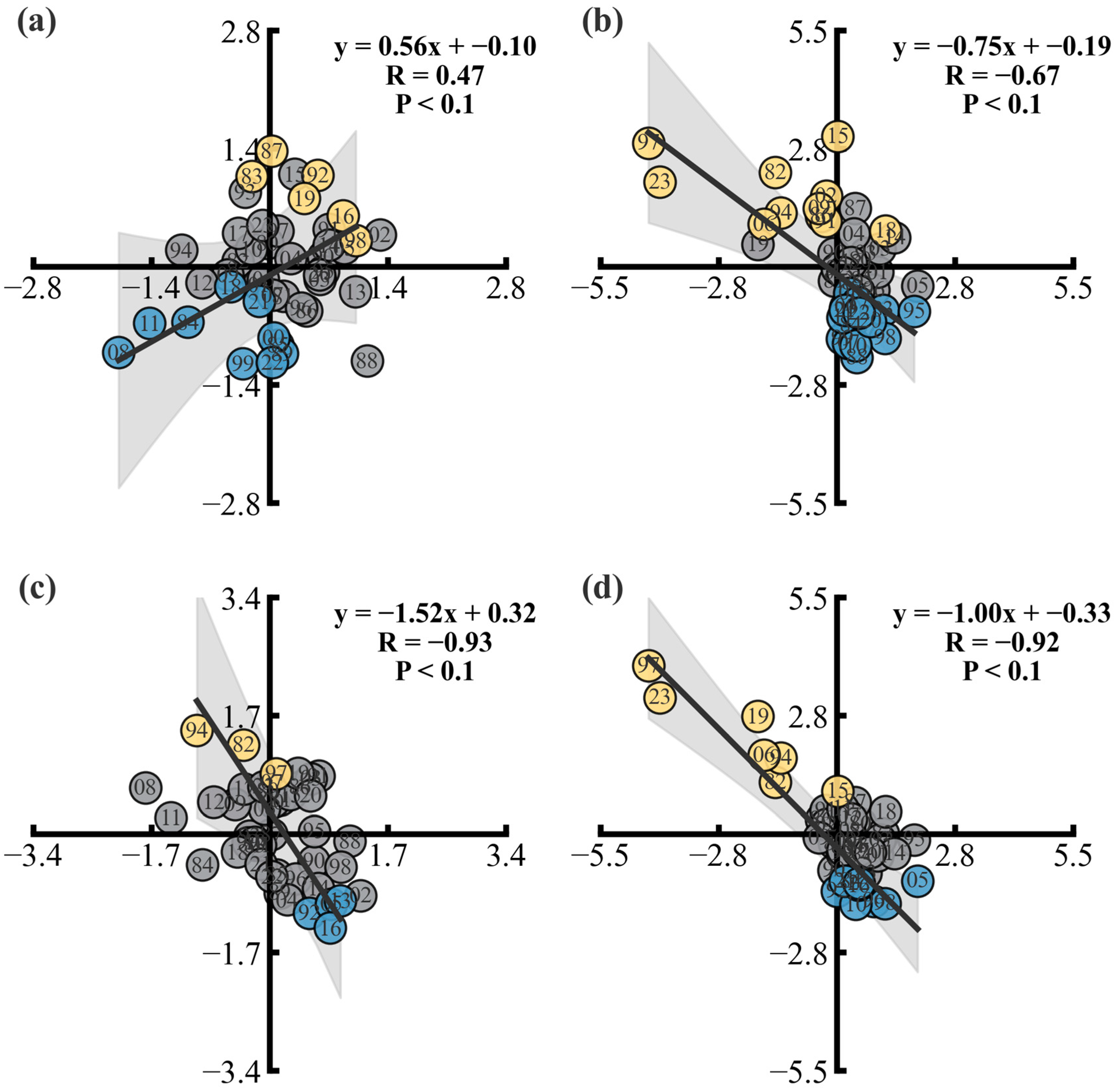
4.4. Influence of IOD and ENSO on WJ Variations
4.5. Regulatory Mechanisms of Abnormal WJs
5. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ENSO | El Niño-Southern Oscillation |
| IOD | Indian Ocean Dipole |
| ONI | Ocean Niño Index |
| DMI | Dipole Mode Index |
| pIOD | positive IOD |
| nIOD | negative IOD |
| WJs | Wyrtki jets |
| ISO | Intraseasonal oscillation |
| SSTAs | Sea surface temperature anomalies |
References
- Schott, F.A.; McCreary, J.P. The Monsoon Circulation of the Indian Ocean. Prog. Oceanogr. 2001, 51, 1–123. [Google Scholar] [CrossRef]
- Schott, F.A.; Xie, S.-P.; McCreary, J.P., Jr. Indian Ocean Circulation and Climate Variability. Rev. Geophys. 2009, 47, RG1002. [Google Scholar] [CrossRef]
- Wyrtki, K. An Equatorial Jet in the Indian Ocean. Science 1973, 181, 262–264. [Google Scholar] [CrossRef]
- Molinari, R.L.; Olson, D.; Reverdin, G. Surface Current Distributions in the Tropical Indian Ocean Derived from Compilations of Surface Buoy Trajectories. J. Geophys. Res. Ocean. 1990, 95, 7217–7238. [Google Scholar] [CrossRef]
- Reppin, J.; Schott, F.A.; Fischer, J.; Quadfasel, D. Equatorial Currents and Transports in the Upper Central Indian Ocean: Annual Cycle and Interannual Variability. J. Geophys. Res. Ocean. 1999, 104, 15495–15514. [Google Scholar] [CrossRef]
- Yuan, D.; Han, W. Roles of Equatorial Waves and Western Boundary Reflection in the Seasonal Circulation of the Equatorial Indian Ocean. J. Phys. Oceanogr. 2006, 36, 930–944. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Hurlburt, H.E. Equatorial Jet in the Indian Ocean: Theory. Science 1974, 184, 1075–1077. [Google Scholar] [CrossRef]
- Nagura, M.; McPhaden, M.J. Wyrtki Jet Dynamics: Seasonal Variability. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Han, W.; McCreary, J.P.; Anderson, D.L.T.; Mariano, A.J. Dynamics of the Eastern Surface Jets in the Equatorial Indian Ocean. J. Phys. Oceanogr. 1999, 29, 2191–2209. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, L.; Yu, W. Behavior of the Wyrtki Jet Observed with Surface Drifting Buoys and Satellite Altimeter. Geophys. Res. Lett. 2009, 36, L18607. [Google Scholar] [CrossRef]
- Jensen, T.G. Equatorial Variability and Resonance in a Wind-Driven Indian Ocean Model. J. Geophys. Res. Ocean. 1993, 98, 22533–22552. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Wang, Y.; Ravichandran, M. Volume Transports of the Wyrtki Jets and Their Relationship to the Indian Ocean Dipole. J. Geophys. Res. Ocean. 2015, 120, 5302–5317. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, L.; Han, G.; Liu, H.; Yu, W.; Yang, G.; Wang, H.; Wang, H.; Liu, Y.; Zahid; et al. Anomalous Behaviors of Wyrtki Jets in the Equatorial Indian Ocean during 2013. Sci. Rep. 2016, 6, 29688. [Google Scholar] [CrossRef]
- Cao, G.; Xu, T.; Wei, Z. Research progress on intraseasonal variability of Wyrtki jet. Prog. Geophys. 2024, 39, 1293–1303. [Google Scholar] [CrossRef]
- Shinoda, T.; Han, W.; Metzger, E.J.; Hurlburt, H.E. Seasonal Variation of the Indonesian Throughflow in Makassar Strait. J. Phys. Oceanogr. 2012, 42, 1099–1123. [Google Scholar] [CrossRef]
- Cao, G.; Xu, T.; Wei, Z. Seasonal Differences of Wyrtki Jet Intraseasonal Variabilities. Front. Mar. Sci. 2024, 11, 1517779. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y. Seasonal Variability of Salinity Budget and Water Exchange in the Northern Indian Ocean from HYCOM Assimilation. Chin. J. Ocean. Limnol. 2012, 30, 1082–1092. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y.; Zheng, S.; Yang, Y.; Cheng, X. Impact of Indian Ocean Dipole on the Salinity Budget in the Equatorial Indian Ocean. J. Geophys. Res. Ocean. 2013, 118, 4911–4923. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y.; Zhang, Y.; Gao, S. Asymmetry of Upper Ocean Salinity Response to the Indian Ocean Dipole Events as Seen from ECCO Simulation. Acta Oceanol. Sin. 2016, 35, 42–49. [Google Scholar] [CrossRef]
- Wang, J. Observational Bifurcation of Wyrtki Jets and Its Influence on the Salinity Balance in the Eastern Indian Ocean. Atmos. Ocean. Sci. Lett. 2017, 10, 36–43. [Google Scholar]
- Xie, C.; Ding, R.; Xuan, J.; Huang, D. Interannual Variations in Salt Flux at 80°E Section of the Equatorial Indian Ocean. Sci. China Earth Sci. 2023, 66, 2142–2161. [Google Scholar] [CrossRef]
- Murtugudde, R.; McCreary, J.P., Jr.; Busalacchi, A.J. Oceanic Processes Associated with Anomalous Events in the Indian Ocean with Relevance to 1997–1998. J. Geophys. Res. Ocean. 2000, 105, 3295–3306. [Google Scholar] [CrossRef]
- Masson, S.; Delecluse, P.; Boulanger, J.-P.; Menkes, C. A Model Study of the Seasonal Variability and Formation Mechanisms of the Barrier Layer in the Eastern Equatorial Indian Ocean. J. Geophys. Res. Ocean. 2002, 107, SRF-18-1–SRF 18-20. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an Integrating Concept in Earth Science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef]
- Guan, C.; Chen, Y.; Wang, F. Seasonal Variability of Zonal Heat Advection in the Mixed Layer of the Tropical Pacific. Chin. J. Ocean. Limnol. 2013, 31, 1356–1367. [Google Scholar] [CrossRef]
- Guan, C.; Hu, S.; McPhaden, M.J.; Wang, F.; Gao, S.; Hou, Y. Dipole Structure of Mixed Layer Salinity in Response to El Niño-La Niña Asymmetry in the Tropical Pacific. Geophys. Res. Lett. 2019, 46, 12165–12172. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A Dipole Mode in the Tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- Chowdary, J.S.; Gnanaseelan, C. Basin-Wide Warming of the Indian Ocean during El Niño and Indian Ocean Dipole Years. Int. J. Climatol. 2007, 27, 1421–1438. [Google Scholar] [CrossRef]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled Ocean–Atmosphere Dynamics in the Indian Ocean during 1997–1998. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef]
- Feng, M.; Meyers, G.; Wijffels, S. Interannual Upper Ocean Variability in the Tropical Indian Ocean. Geophys. Res. Lett. 2001, 28, 4151–4154. [Google Scholar] [CrossRef]
- Rao, S.A.; Behera, S.K.; Masumoto, Y.; Yamagata, T. Interannual Subsurface Variability in the Tropical Indian Ocean with a Special Emphasis on the Indian Ocean Dipole. Deep. Sea Res. Part. II Top. Stud. Oceanogr. 2002, 49, 1549–1572. [Google Scholar] [CrossRef]
- Saji, N.H.; Yamagata, T. Possible Impacts of Indian Ocean Dipole Mode Events on Global Climate. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Feng, M.; Meyers, G. Interannual Variability in the Tropical Indian Ocean: A Two-Year Time-Scale of Indian Ocean Dipole. Deep. Sea Res. Part. II Top. Stud. Oceanogr. 2003, 50, 2263–2284. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Nagura, M. Indian Ocean Dipole Interpreted in Terms of Recharge Oscillator Theory. Clim. Dyn. 2014, 42, 1569–1586. [Google Scholar] [CrossRef]
- Nyadjro, E.S.; McPhaden, M.J. Variability of Zonal Currents in the Eastern Equatorial Indian Ocean on Seasonal to Interannual Time Scales. J. Geophys. Res. Ocean. 2014, 119, 7969–7986. [Google Scholar] [CrossRef]
- Yuan, D.; Liu, H. Long-Wave Dynamics of Sea Level Variations during Indian Ocean Dipole Events. J. Phys. Oceanogr. 2009, 39, 1115–1132. [Google Scholar] [CrossRef]
- Chambers, D.P.; Tapley, B.D.; Stewart, R.H. Anomalous Warming in the Indian Ocean Coincident with El Niño. J. Geophys. Res. Ocean. 1999, 104, 3035–3047. [Google Scholar] [CrossRef]
- Le Blanc, J.-L.; Boulanger, J.-P. Propagation and Reflection of Long Equatorial Waves in the Indian Ocean from TOPEX/POSEIDON Data during the 1993–1998 Period. Clim. Dyn. 2001, 17, 547–557. [Google Scholar] [CrossRef]
- Huang, B.; Kinter III, J.L. Interannual Variability in the Tropical Indian Ocean. J. Geophys. Res. Ocean. 2002, 107, 20-1–20-26. [Google Scholar] [CrossRef]
- Gnanaseelan, C.; Deshpande, A.; McPhaden, M.J. Impact of Indian Ocean Dipole and El Niño/Southern Oscillation Wind-Forcing on the Wyrtki Jets. J. Geophys. Res. Ocean. 2012, 117, C8. [Google Scholar] [CrossRef]
- Joseph, S.; Wallcraft, A.J.; Jensen, T.G.; Ravichandran, M.; Shenoi, S.S.C.; Nayak, S. Weakening of Spring Wyrtki Jets in the Indian Ocean during 2006–2011. J. Geophys. Res. Ocean. 2012, 117, C4. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Zhang, X.; Duan, Y.; Yang, G.; Yang, Y.; Zahid; Oloo, P.; Sagero, P. Different Impacts from Various El Niño Events on Wyrtki Jets in Boreal Autumn Season. Pure Appl. Geophys. 2018, 175, 4567–4577. [Google Scholar] [CrossRef]
- Deng, K.; Cheng, X.; Feng, T.; Ma, T.; Duan, W.; Chen, J. Interannual Variability of the Spring Wyrtki Jet. J. Ocean. Limnol. 2021, 39, 26–44. [Google Scholar] [CrossRef]
- Chu, X.; Han, W.; Zhang, L.; Chen, G. Effects of Climate Modes on Interannual Variability of the Equatorial Currents in the Indian Ocean. Clim. Dyn. 2023, 60, 3681–3694. [Google Scholar] [CrossRef]
- Ueda, H.; Matsumoto, J. A Possible Triggering Process of East-West Asymmetric Anomalies over the Indian Ocean in Relation to 1997/98 El Niño. J. Meteorol. Soc. Japan. Ser. II 2000, 78, 803–818. [Google Scholar] [CrossRef]
- Hendon, H.H. Indonesian Rainfall Variability: Impacts of ENSO and Local Air–Sea Interaction. J. Clim. 2003, 16, 1775–1790. [Google Scholar] [CrossRef]
- Lau, N.-C.; Nath, M.J. Atmosphere–Ocean Variations in the Indo-Pacific Sector during ENSO Episodes. J. Clim. 2003, 16, 3–20. [Google Scholar] [CrossRef]
- Tokinaga, H.; Tanimoto, Y. Seasonal Transition of SST Anomalies in the Tropical Indian Ocean during El Niño and Indian Ocean Dipole Years. J. Meteorol. Soc. Japan. Ser. II 2004, 82, 1007–1018. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Li, T. Atmosphere–Warm Ocean Interaction and Its Impacts on Asian–Australian Monsoon Variation. J. Clim. 2003, 16, 1195–1211. [Google Scholar] [CrossRef]
- Deshpande, A.; Gnanaseelan, C.; Chowdary, J.S.; Rahul, S. Interannual Spring Wyrtki Jet Variability and Its Regional Impacts. Dyn. Atmos. Ocean. 2017, 78, 26–37. [Google Scholar] [CrossRef]
- Gnanaseelan, C.; Deshpande, A. Equatorial Indian Ocean Subsurface Current Variability in an Ocean General Circulation Model. Clim. Dyn. 2018, 50, 1705–1717. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, Y.P.; Huang, R.X. 3D Structure of Striations in the North Pacific. J. Phys. Oceanogr. 2021, 51, 3651–3662. [Google Scholar] [CrossRef]
- Carton, J.A.; Chepurin, G.A.; Chen, L. SODA3: A New Ocean Climate Reanalysis. J. Clim. 2018, 31, 6967–6983. [Google Scholar] [CrossRef]
- Naseef, T.M.; Kumar, V.S. Climatology and Trends of the Indian Ocean Surface Waves Based on 39-Year Long ERA5 Reanalysis Data. Int. J. Climatol. 2020, 40, 979–1006. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Meyers, G.; Ando, K.; Masumoto, Y.; Murty, V.S.N.; Ravichandran, M.; Syamsudin, F.; Vialard, J.; Yu, L.; Yu, W. RAMA: The Research Moored Array for African–Asian–Australian Monsoon Analysis and Prediction*. Bull. Am. Meteorol. Soc. 2009, 90, 459–480. [Google Scholar] [CrossRef]
- Cai, W.; van Rensch, P.; Cowan, T.; Hendon, H.H. Teleconnection Pathways of ENSO and the IOD and the Mechanisms for Impacts on Australian Rainfall. J. Clim. 2011, 24, 3910–3923. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kug, J.-S.; Park, J.-Y. Two Distinct Roles of Atlantic SSTs in ENSO Variability: North Tropical Atlantic SST and Atlantic Niño. Geophys. Res. Lett. 2013, 40, 4012–4017. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Wang, C. Joint Boost to Super El Niño from the Indian and Atlantic Oceans. J. Clim. 2021, 34, 4937–4954. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and Its Possible Teleconnection. J. Geophys. Res. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Hastenrath, S.; Greischar, L. The Monsoonal Current Regimes of the Tropical Indian Ocean: Observed Surface Flow Fields and Their Geostrophic and Wind-Driven Components. J. Geophys. Res. Ocean. 1991, 96, 12619–12633. [Google Scholar] [CrossRef]
- Rasmusson, E.M.; Carpenter, T.H. Variations in Tropical Sea Surface Temperature and Surface Wind Fields Associated with the Southern Oscillation/El Niño. Mon. Weather. Rev. 1982, 110, 354–384. [Google Scholar] [CrossRef]
- Warner, S.J.; Moum, J.N. Feedback of Mixing to ENSO Phase Change. Geophys. Res. Lett. 2019, 46, 13920–13927. [Google Scholar] [CrossRef]
- Guan, C.; McPhaden, M.J.; Wang, F.; Hu, S. Quantifying the Role of Oceanic Feedbacks on ENSO Asymmetry. Geophys. Res. Lett. 2019, 46, 2140–2148. [Google Scholar] [CrossRef]
- Cai, W.; Zheng, X.-T.; Weller, E.; Collins, M.; Cowan, T.; Lengaigne, M.; Yu, W.; Yamagata, T. Projected Response of the Indian Ocean Dipole to Greenhouse Warming. Nat. Geosci. 2013, 6, 999–1007. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Kirtman, B.P. Variability of the Indian Ocean: Relation to Monsoon and ENSO. Q. J. R. Meteorol. Soc. 2003, 129, 1623–1646. [Google Scholar] [CrossRef]
- Annamalai, H.; Xie, S.P.; McCreary, J.P.; Murtugudde, R. Impact of Indian Ocean Sea Surface Temperature on Developing El Niño. J. Clim. 2005, 18, 302–319. [Google Scholar] [CrossRef]
- Li, K.; Liu, Y.; Li, Z.; Yang, Y.; Feng, L.; Khokiattiwong, S.; Yu, W.; Liu, S. Impacts of ENSO on the Bay of Bengal Summer Monsoon Onset via Modulating the Intraseasonal Oscillation. Geophys. Res. Lett. 2018, 45, 5220–5228. [Google Scholar] [CrossRef]
- Li, K.; Yin, Y.; Yang, Y.; Liu, Y.; Yu, W. Dynamic Response of the Spring Wyrtki Jet to the Monsoon Onset Over the Bay of Bengal. Geophys. Res. Lett. 2022, 49, e2022GL101435. [Google Scholar] [CrossRef]
- Huang, K.; Wang, D.; Chen, G.; Nagura, M.; Han, W.; McPhaden, M.J.; Feng, M.; Chen, J.; Wu, Y.; Zhang, X.; et al. Intensification and Dynamics of the Westward Equatorial Undercurrent During the Summers of 1998 and 2016 in the Indian Ocean. Geophys. Res. Lett. 2022, 49, e2022GL100168. [Google Scholar] [CrossRef]
- Srinivas, G.; Amol, P.; Mukherjee, A. Influence of the Extreme Indian Ocean Dipole 2019 on the Equatorial Indian Ocean Circulation. Clim Dyn 2024, 62, 7111–7125. [Google Scholar] [CrossRef]
- Masumoto, Y.; Hase, H.; Kuroda, Y.; Matsuura, H.; Takeuchi, K. Intraseasonal Variability in the Upper Layer Currents Observed in the Eastern Equatorial Indian Ocean. Geophys. Res. Lett. 2005, 32, 2. [Google Scholar] [CrossRef]
- Prerna, S.; Chatterjee, A.; Mukherjee, A.; Ravichandran, M.; Shenoi, S.S.C. Wyrtki Jets: Role of Intraseasonal Forcing. J. Earth Syst. Sci. 2019, 128, 21. [Google Scholar] [CrossRef]
- Wu, R.; Kirtman, B.P. Impacts of the Indian Ocean on the Indian Summer Monsoon–ENSO Relationship. J. Clim. 2004, 17, 3037–3054. [Google Scholar] [CrossRef]
- Krishnan, R.; Ayantika, D.C.; Kumar, V.; Pokhrel, S. The Long-Lived Monsoon Depressions of 2006 and Their Linkage with the Indian Ocean Dipole. Int. J. Climatol. 2011, 31, 1334–1352. [Google Scholar] [CrossRef]
- Roeckner, E.; Oberhuber, J.M.; Bacher, A.; Christoph, M.; Kirchner, I. ENSO Variability and Atmospheric Response in a Global Coupled Atmosphere-Ocean GCM. Clim. Dyn. 1996, 12, 737–754. [Google Scholar] [CrossRef]
- Cai, W.; Borlace, S.; Lengaigne, M.; van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L.; et al. Increasing Frequency of Extreme El Niño Events Due to Greenhouse Warming. Nat. Clim. Change 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Marjani, S.; Alizadeh-Choobari, O.; Irannejad, P. Frequency of Extreme El Niño and La Niña Events under Global Warming. Clim. Dyn. 2019, 53, 5799–5813. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Yang, Y.-M.; Sun, W.; Cane, M.A.; Cai, W.; Yeh, S.-W.; Liu, J. Historical Change of El Niño Properties Sheds Light on Future Changes of Extreme El Niño. Proc. Natl. Acad. Sci. 2019, 116, 22512–22517. [Google Scholar] [CrossRef]
- Yang, S.; Li, Z.; Yu, J.-Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern Oscillation and Its Impact in the Changing Climate. Natl. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Stuecker, M.F.; Timmermann, A.; Jin, F.-F.; Chikamoto, Y.; Zhang, W.; Wittenberg, A.T.; Widiasih, E.; Zhao, S. Revisiting ENSO/Indian Ocean Dipole Phase Relationships. Geophys. Res. Lett. 2017, 44, 2481–2492. [Google Scholar] [CrossRef]

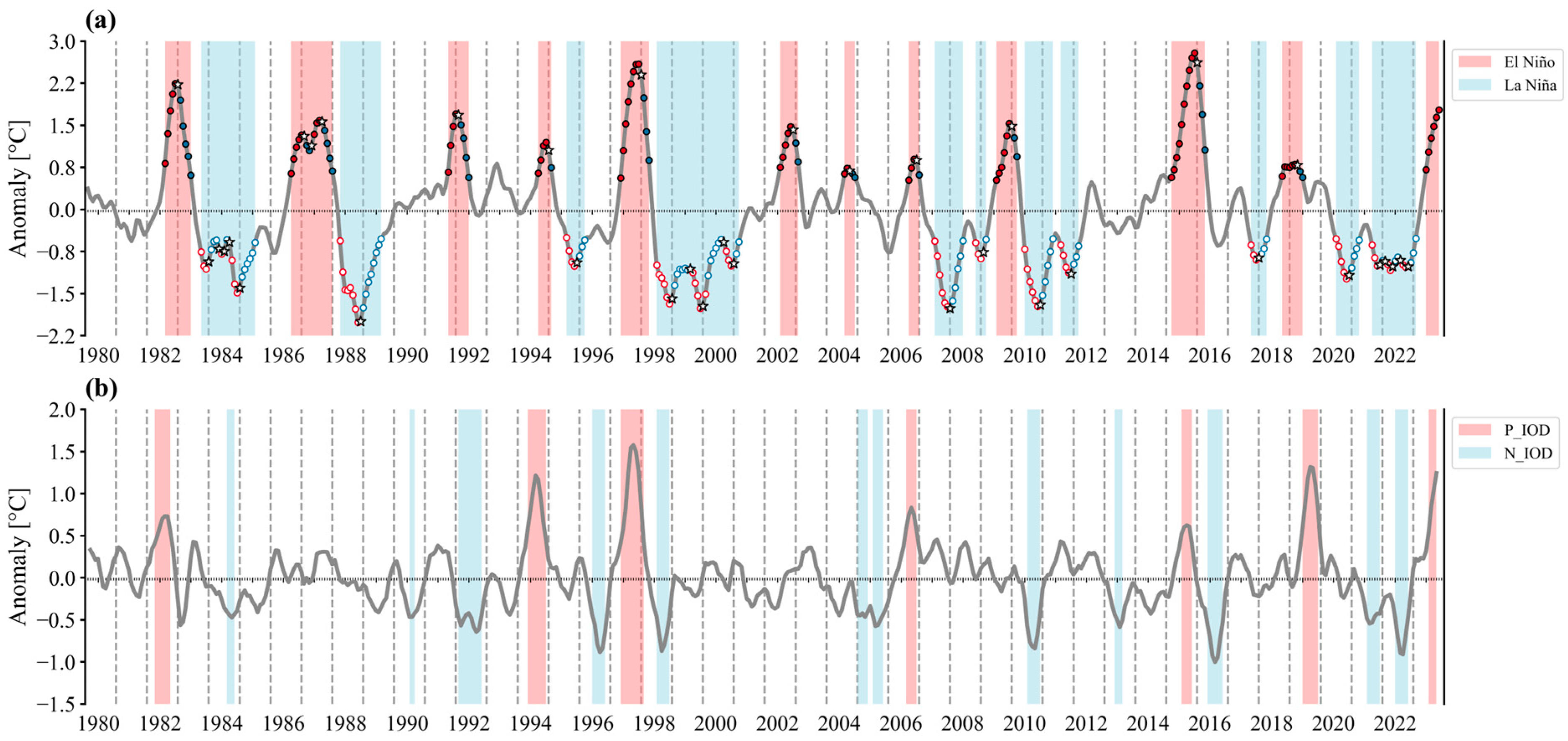

| Phase | Spring Wyrtki Jet | Fall Wyrtki Jet | |
|---|---|---|---|
| ENSO developing | El Niño warming | – | 1982, 1986, 1991, 1994, 1997, 2002, 2006, 2009, 2015, 2018, 2023 |
| La Niña cooling | – | 1983, 1984, 1988, 1995, 1998, 1999, 2000, 2007, 2008, 2010, 2011, 2017, 2020, 2021, 2022 | |
| ENSO decaying | El Niño cooling | 1983, 1987, 1992, 1998, 2016, 2019 | – |
| La Niña warming | 1984, 1985, 1989, 1999, 2000, 2008, 2011, 2018, 2021, 2022 | – | |
| IOD | Positive IOD | 1982, 1994, 1997 | 1982, 1994, 1997, 2006, 2015, 2019, 2023 |
| Neagtive IOD | 1992, 2005, 2013, 2016 | 1984, 1992, 1996, 1998, 2005, 2010, 2016, 2021, 2022 | |
| Model | Spring | Fall | ||
|---|---|---|---|---|
| τx | U | τx | U | |
| Multiple Regression Model | 0.58 | 0.50 | 0.88 | 0.58 |
| Single Regression Model (ONI) | 0.26 | 0.14 | 0.54 | 0.38 |
| ∆ | +0.32 | +0.36 | +0.30 | +0.20 |
| Single Regression Model (DMI) | 0.34 | 0.32 | 0.86 | 0.55 |
| ∆ | +0.24 | +0.18 | +0.02 | +0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Q.; Zhou, J.; Han, G.; Xie, J. Variation of Wyrtki Jets Influenced by Indo-Pacific Ocean–Atmosphere Interactions. J. Mar. Sci. Eng. 2025, 13, 691. https://doi.org/10.3390/jmse13040691
Feng Q, Zhou J, Han G, Xie J. Variation of Wyrtki Jets Influenced by Indo-Pacific Ocean–Atmosphere Interactions. Journal of Marine Science and Engineering. 2025; 13(4):691. https://doi.org/10.3390/jmse13040691
Chicago/Turabian StyleFeng, Qingfeng, Jiajie Zhou, Guoqing Han, and Juncheng Xie. 2025. "Variation of Wyrtki Jets Influenced by Indo-Pacific Ocean–Atmosphere Interactions" Journal of Marine Science and Engineering 13, no. 4: 691. https://doi.org/10.3390/jmse13040691
APA StyleFeng, Q., Zhou, J., Han, G., & Xie, J. (2025). Variation of Wyrtki Jets Influenced by Indo-Pacific Ocean–Atmosphere Interactions. Journal of Marine Science and Engineering, 13(4), 691. https://doi.org/10.3390/jmse13040691






