A Novel Ship Fuel Sulfur Content Estimation Method Using Improved Gaussian Plume Model and Genetic Algorithms
Abstract
1. Introduction
2. Method
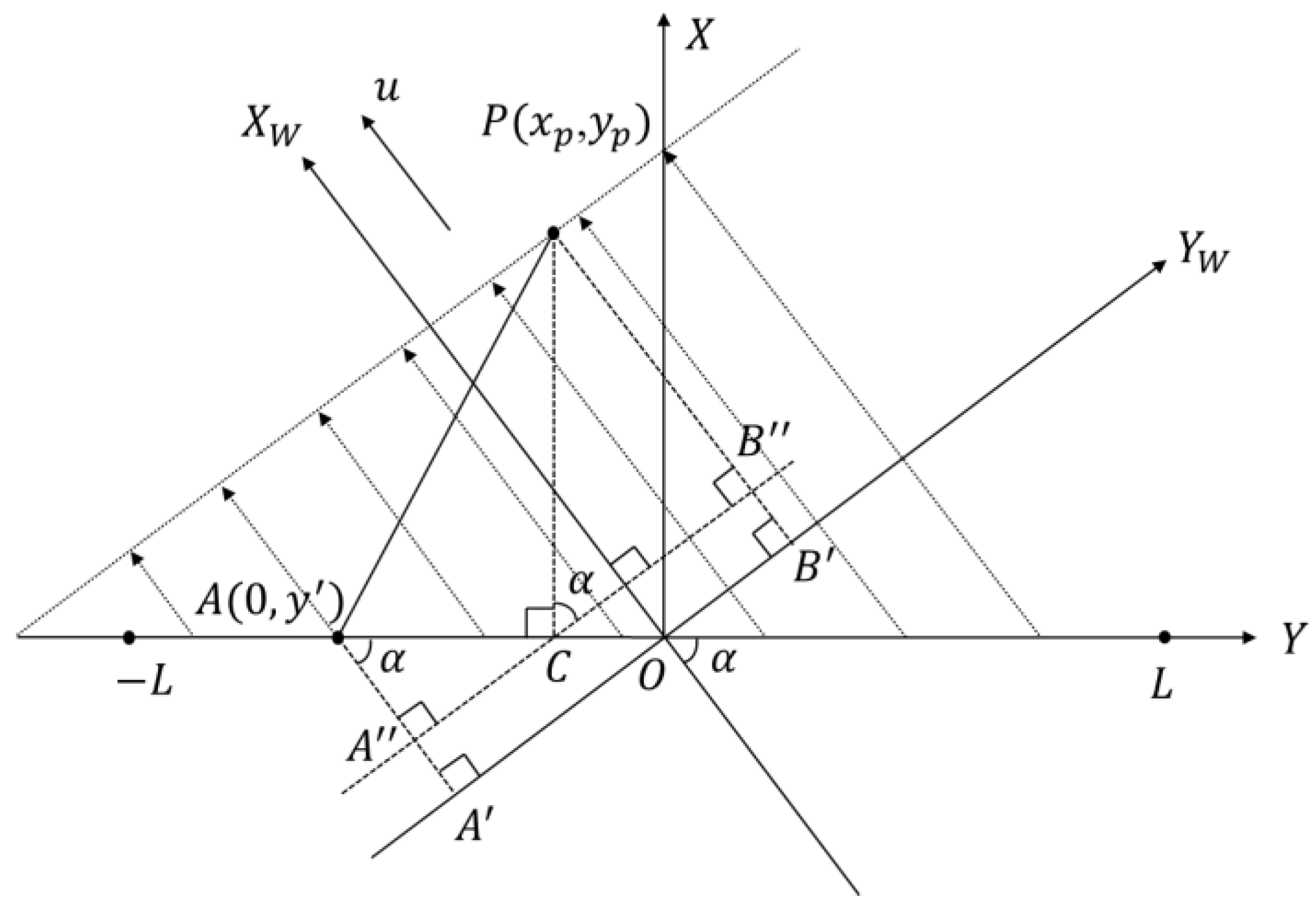
2.1. Gaussian Plume Line Source Model
- (1)
- Emission Source Height Modification
- (2)
- Wind Speed Modification
- (3)
- Dispersion Coefficient Modification
2.2. SO2 Quantitative Inversion of Source Intensity
2.3. Fuel Sulfur Content Estimation
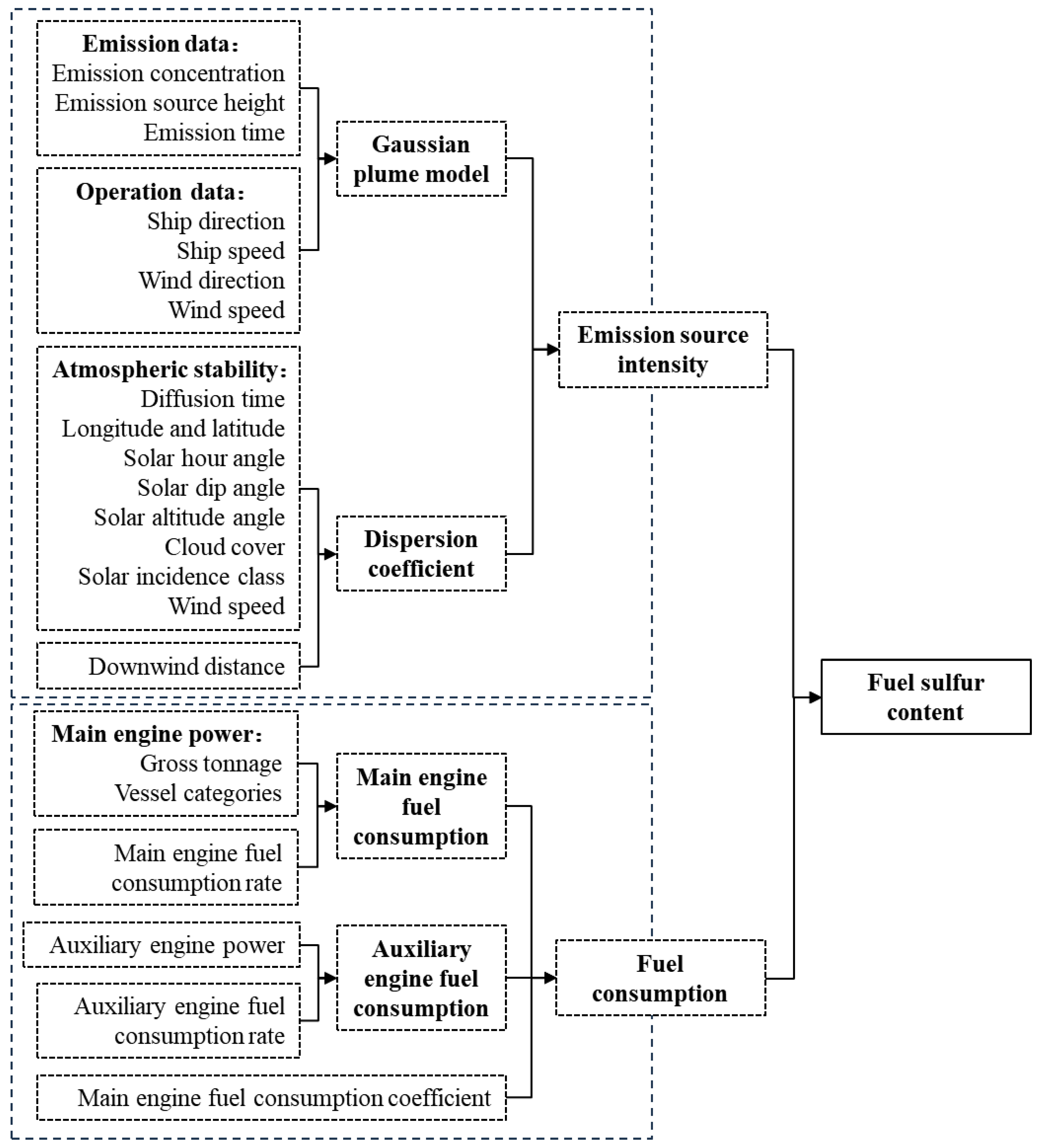
2.4. Overview of the Methodology
3. Data Collection
4. Results and Analysis
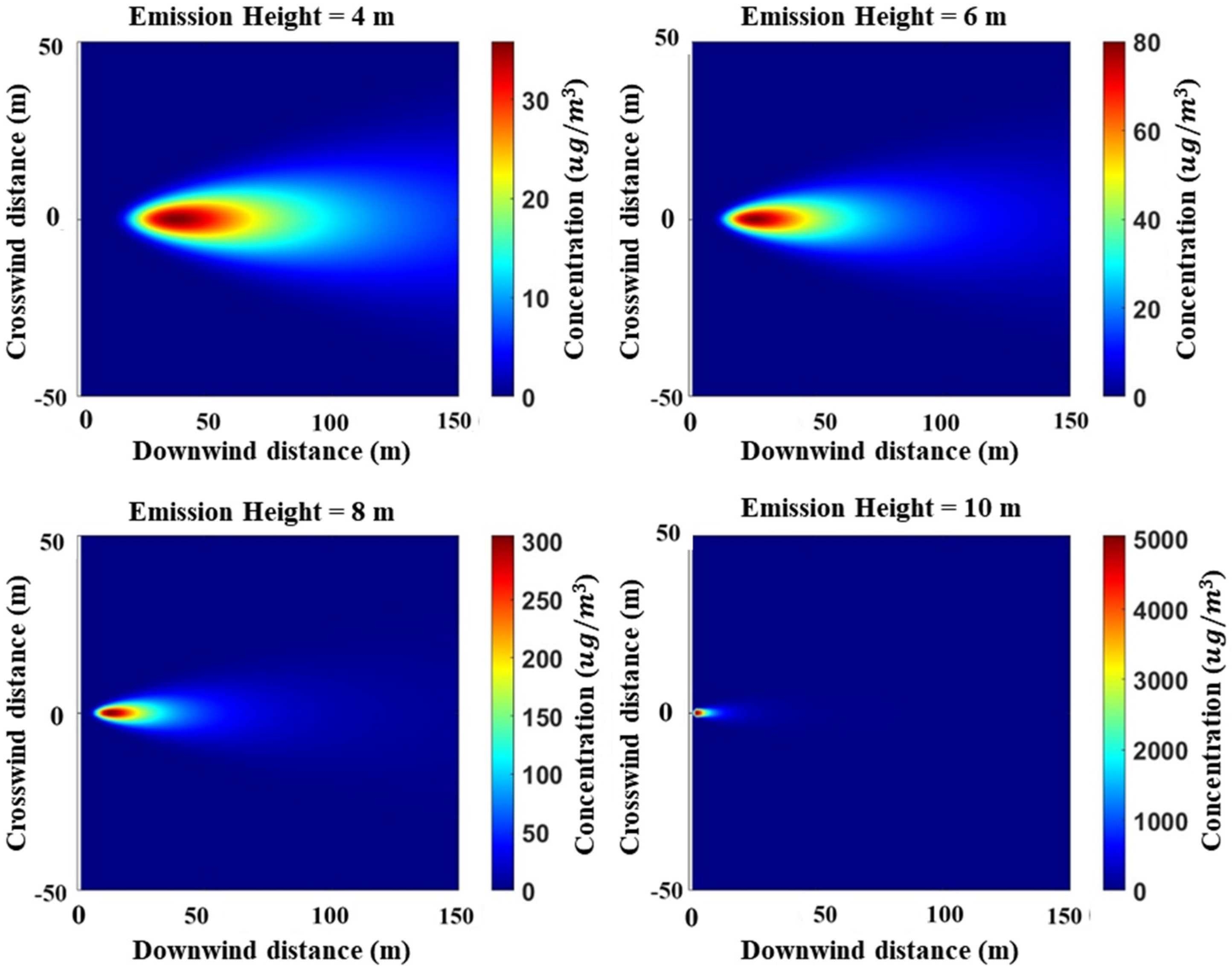
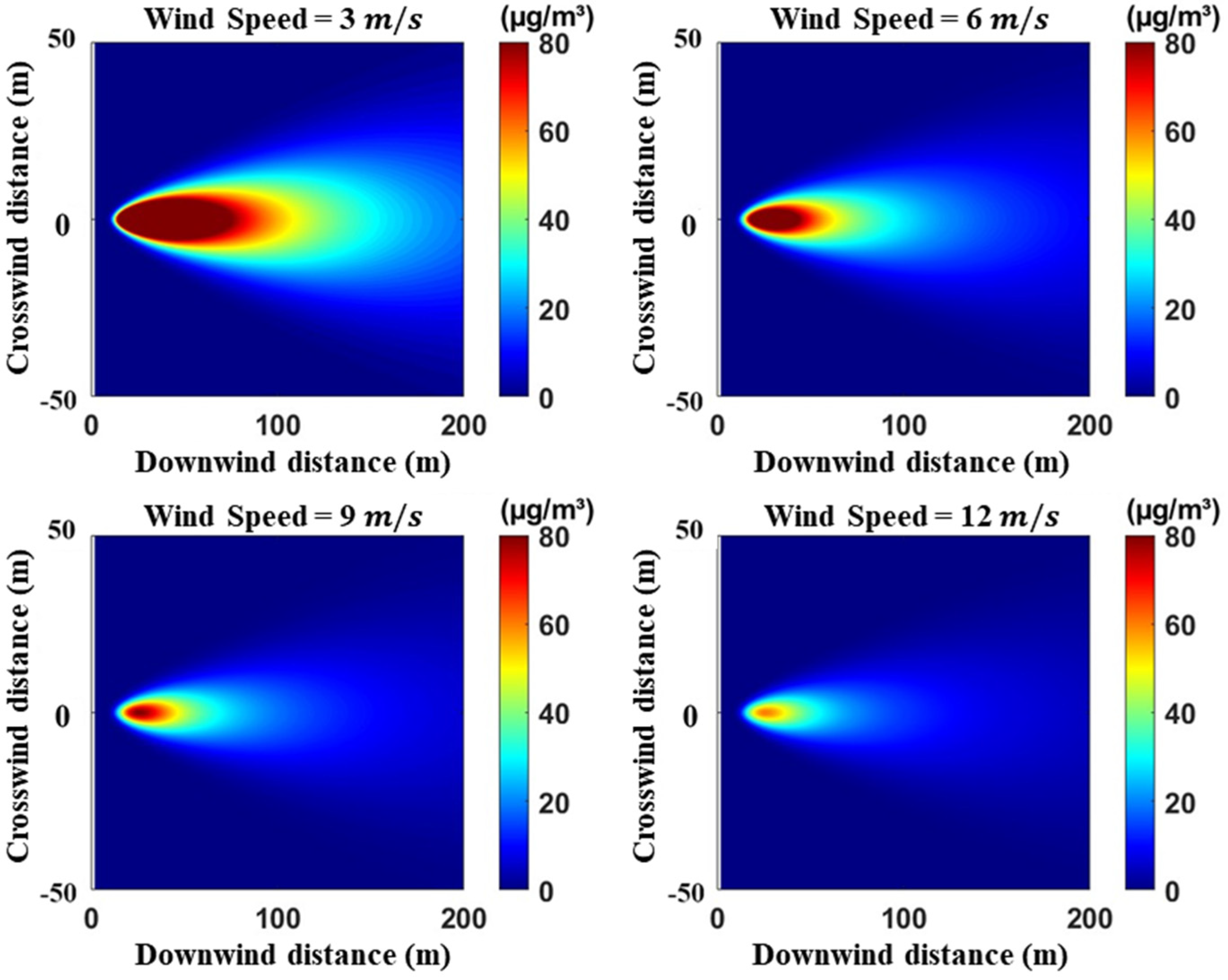
4.1. Simulation Results of Ship Exhaust Gas Diffusion
4.2. An Example to Estimate Fuel Sulfur Content of Ship
4.3. Hyperparameter Adjustment and Impact Assessment of the Genetic Algorithm
4.4. Fuel Sulfur Content Estimation for Exempted Ships
4.5. Assessment of Monitoring Outcomes over a 30-Day Period
5. Conclusions
- (1)
- Selecting one ship detected with sulfur content exceeding the standard to introduce the analysis process of calculating fuel sulfur content without relying on CO2 concentration. The fuel sulfur content of the suspected ship was calculated to be 0.298%. Following sampling and analysis by the maritime department with portable analytical instruments, the actual fuel sulfur content of the ship was found to be 0.26%, resulting in an assessment accuracy of 85.38%.
- (2)
- Using 97 exempted ships’ information provided by the maritime authorities to validate the effectiveness of the quantitative inversion of source intensity and fuel sulfur content estimation method. The results represented that the proposed method could effectively replace the carbon balance method in terms of the detection rate of suspected ships and the outlier rate, with a detection rate of 87.63% and an outlier rate of 2.06%, respectively.
- (3)
- Randomly selecting the operation data for 30 consecutive days to show the actual monitoring effect and evaluate the stability and practicality of this method. Among the 3316 ships, 2743 had their fuel sulfur content detected, with an effective detection rate of 82.72%. In total, 131 ships were suspected of using fuel with high sulfur content, and 111 of them were confirmed to use non-compliant fuel by sampling and detection with portable analytical instruments, with a detection accuracy of 84.73%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- Determining Atmospheric Stability
- (2)
- Determining Ship Emission Source Intensity
- (3)
- Determining Fuel Sulfur Content
References
- Sun, Y.; Zheng, J.; Han, J.; Liu, H.; Zhao, Z. Allocation and reallocation of ship emission permits for liner shipping. Ocean Eng. 2022, 266, 112976. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Wang, C.; Ye, Z. Inverse calculation of vessel emission source intensity based on optimized gaussian puff model and particle swarm optimization algorithm. Mar. Pollut. Bull. 2024, 209, 117117. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Wang, Y.; Hou, L.; An, B. Air pollutant emission factors of inland river ships under compliance. J. Mar. Sci. Eng. 2024, 12, 1732. [Google Scholar] [CrossRef]
- Chen, X.; Dou, S.; Song, T.; Wu, H.; Sun, Y.; Xian, J. Spatial-temporal ship pollution distribution exploitation and harbor environmental impact analysis via large-scale AIS data. J. Mar. Sci. Eng. 2024, 12, 960. [Google Scholar] [CrossRef]
- da Silva, J.N.R.; Santos, T.A.; Teixeira, A.P. Methodology for predicting maritime traffic ship emissions using automatic identification system data. J. Mar. Sci. Eng. 2024, 12, 320. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Patton, A.P.; Ma, W.; Kan, H.; Wu, L.; Fung, F.; Wang, S.; Ding, D.; Walker, K. Projection of ship emissions and their impact on air quality in 2030 in Yangtze River delta, China. Environ. Pollut. 2020, 263, 114643. [Google Scholar] [CrossRef] [PubMed]
- International Maritime Organization. Index of MEPC Resolutions and Guidelines related to MARPOL Annex VI. Resolut. MEPC 2021, 328, 76. [Google Scholar]
- Åström, S.; Yaramenka, K.; Winnes, H.; Fridell, E.; Holland, M. The costs and benefits of a nitrogen emission control area in the baltic and north seas. Transp. Res. Part D Transp. Environ. 2018, 59, 223–236. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Implementation Scheme of the Domestic Emission Control Areas for Atmospheric Pollution from Vessels; Ministry of Transport of the People’s Republic of China: Beijing, China, 2018.
- Bendl, J.; Saraji-Bozorgzad, M.R.; Käfer, U.; Padoan, S.; Mudan, A.; Etzien, U.; Giocastro, B.; Schade, J.; Jeong, S.; Kuhn, E.; et al. How do different marine engine fuels and wet scrubbing affect gaseous air pollutants and ozone formation potential from ship emissions? Environ. Res. 2024, 260, 119609. [Google Scholar] [CrossRef]
- Huang, S.; Li, Y. New exploration of emission abatement solution for newbuilding bulk carriers. J. Mar. Sci. Eng. 2024, 12, 973. [Google Scholar] [CrossRef]
- Anand, A.; Wei, P.; Gali, N.K.; Sun, L.; Yang, F.; Westerdahl, D.; Zhang, Q.; Deng, Z.; Wang, Y.; Liu, D.; et al. Protocol development for real-time ship fuel sulfur content determination using drone based plume sniffing microsensor system. Sci. Total. Environ. 2020, 744, 140885. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Wang, S.; Zhu, J.; Guo, Y.; Zhang, R.; Liu, Y.; Zhang, Y.; Yu, Q.; Ma, W.; Zhou, B. Surveillance of SO2 and NO2 from ship emissions by MAX-DOAS measurements and the implications regarding fuel sulfur content compliance. Atmos. Chem. Phys. 2019, 19, 13611–13626. [Google Scholar] [CrossRef]
- Liu, R.W.; Yuan, W.; Chen, X.; Lu, Y. An enhanced CNN-enabled learning method for promoting ship detection in maritime surveillance system. Ocean Eng. 2021, 235, 109435. [Google Scholar] [CrossRef]
- Van Roy, W.; Schallier, R.; Van Roozendael, B.; Scheldeman, K.; Van Nieuwenhove, A.; Maes, F. Airborne monitoring of compliance to sulfur emission regulations by ocean-going vessels in the Belgian North Sea area. Atmos. Pollut. Res. 2022, 13, 101445. [Google Scholar] [CrossRef]
- Van Roy, W.; Van Roozendael, B.; Vigin, L.; Van Nieuwenhove, A.; Scheldeman, K.; Merveille, J.-B.; Weigelt, A.; Mellqvist, J.; Van Vliet, J.; van Dinther, D.; et al. International maritime regulation decreases sulfur dioxide but increases nitrogen oxide emissions in the North and Baltic Sea. Commun. Earth Environ. 2023, 4, 391. [Google Scholar] [CrossRef]
- Šaparnis, L.; Rapalis, P.; Daukšys, V. Ship Emission measurements using multirotor unmanned aerial vehicles: Review. J. Mar. Sci. Eng. 2024, 12, 1197. [Google Scholar] [CrossRef]
- Van Roy, W.; Merveille, J.-B.; Scheldeman, K.; Van Nieuwenhove, A.; Van Roozendael, B.; Schallier, R.; Maes, F. The role of belgian airborne sniffer measurements in the MARPOL Annex VI enforcement chain. Atmosphere 2023, 14, 623. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, Z.; Li, Y.; Xie, M.; Zheng, W. Surveillance of ship emissions and fuel sulfur content based on imaging detection and multi-task deep learning. Environ. Pollut. 2021, 288, 117698. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Cao, K.; Li, Y. Using a convolutional neural network and mid-infrared spectral images to predict the carbon dioxide content of ship exhaust. Remote. Sens. 2023, 15, 2721. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, C.; Xiao, C.; Wen, Y.; Ma, W.; Wu, L. Identification and detection of high NO x emitting inland ships using multi-source shore-based monitoring data. Environ. Res. Lett. 2024, 19, 044051. [Google Scholar] [CrossRef]
- Krause, K.; Wittrock, F.; Richter, A.; Schmitt, S.; Pöhler, D.; Weigelt, A.; Burrows, J.P. Estimation of ship emission rates at a major shipping lane by long-path DOAS measurements. Atmos. Meas. Tech. 2021, 14, 5791–5807. [Google Scholar] [CrossRef]
- Gao, Q. Research on Back-Calculation of Inland Waterway Sailing Ships Exhaust Emission Source Intensity in Gaussian Mode. Master’s Dissertation, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Liu, J.; Wang, S.; Zhang, Y.; Yan, Y.; Zhu, J.; Zhang, S.; Wang, T.; Tan, Y.; Zhou, B. Investigation of formaldehyde sources and its relative emission intensity in shipping channel environment. J. Environ. Sci. 2024, 142, 142–154. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Z.; Asif, Z. Identification of point source emission in river pollution incidents based on bayesian inference and genetic algorithm: Inverse modeling, sensitivity, and uncertainty analysis. Environ. Pollut. 2021, 285, 117497. [Google Scholar] [CrossRef] [PubMed]
- Tang, H. Research on Exhaust Gas Diffusion of Ships at Sea based on Gaussian Model. Master’s Dissertation, Southeast University, Nanjing, China, 2021. [Google Scholar]
- He, Z.; You, L.; Liu, R.W.; Yang, F.; Ma, J.; Xiong, N. A cloud-based real time polluted gas spread simulation approach on virtual reality networking. IEEE Access 2019, 7, 22532–22540. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Yuan, Y.; Wang, S.; Guo, J.; Wang, L.; Zhou, B. Identification of sulfur content in marine fuel oil based on real-time ship emissions and online monitoring of plumes. Acta Sci. Circumstantiae 2021, 41, 2624–2632. [Google Scholar] [CrossRef]
- Lotrecchiano, N.; Sofia, D.; Giuliano, A.; Barletta, D.; Poletto, M. Pollution dispersion from a fire using a gaussian plume model. Int. J. Saf. Secur. Eng. 2020, 10, 431–439. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Bai, Y.; Zhou, W.; Zhang, Y.; Wei, J. Research on leakage detection technology of natural gas pipeline based on modified gaussian plume model and markov chain monte carlo method. Process. Saf. Environ. Prot. 2024, 182, 314–326. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, Z.; Li, Y.; Zheng, W.; Xie, M. Ship fuel sulfur content prediction based on convolutional neural network and ultraviolet camera images. Environ. Pollut. 2021, 273, 116501. [Google Scholar] [CrossRef]
- Wu, H.; Wang, C.; Chen, E.; Ye, Z. Development of a spectrum-based ship fuel sulfur content real-time evaluation method. Mar. Pollut. Bull. 2023, 188, 114484. [Google Scholar] [CrossRef]
- Fu, J. A Forecasting System and Modeling for Diffusion of Ship Exhaust Emission. Master’s Dissertation, Dalian Maritime University, Dalian, China, 2019. [Google Scholar]
- Sun, J.; Shu, J.; Qiu, B.; Wang, Y.; Wang, Q. An Industry air pollution dispersion system based on Gaussian dispersion model. Available Environ. Pollut. Control. 2005, 7, 50–53. [Google Scholar]
- Fa, G. Turbulent diffusion-typing schemes: A review. Nucl. Saf. 1976, 17, 68–86. [Google Scholar]
- George, S.; Nandanan, D.; Muralikrishna, P. Improving accuracy of source localization algorithms using kalman filter estimator. J. Phys. Conf. Ser. 2021, 1921, 12022. [Google Scholar] [CrossRef]
- Lu, J.; Huang, M.; Wu, W.; Wei, Y.; Liu, C. Application and improvement of the particle swarm optimization algorithm in source-term estimations for hazardous release. Atmosphere 2023, 14, 1168. [Google Scholar] [CrossRef]
- GB/T 7187.2-2010; Fuel Oil Consumption for Transportation Ships, Part 2: Calculation Method for Inland Ships. Standardization Administration of China: Beijing, China, 2010.
- Li, S. The Study on Adhesion Skimmer Design. Master’s Dissertation, Dalian Maritime University, Dalian, China, 2011. [Google Scholar]
- Jalkanen, J.-P.; Brink, A.; Kalli, J.; Pettersson, H.; Kukkonen, J.; Stipa, T. A modelling system for the exhaust emissions of marine traffic and its application in the Baltic Sea area. Atmos. Chem. Phys. 2009, 9, 9209–9223. [Google Scholar] [CrossRef]
- Jalkanen, J.-P.; Johansson, L.; Kukkonen, J.; Brink, A.; Kalli, J.; Stipa, T. Extension of an assessment model of ship traffic exhaust emissions for particulate matter and carbon monoxide. Atmos. Chem. Phys. 2012, 12, 2641–2659. [Google Scholar] [CrossRef]
- Chen, D.; Wang, X.; Li, Y.; Lang, J.; Zhou, Y.; Guo, X.; Zhao, Y. High-spatiotemporal-resolution ship emission inventory of China based on AIS data in 2014. Sci. Total. Environ. 2017, 609, 776–787. [Google Scholar] [CrossRef]
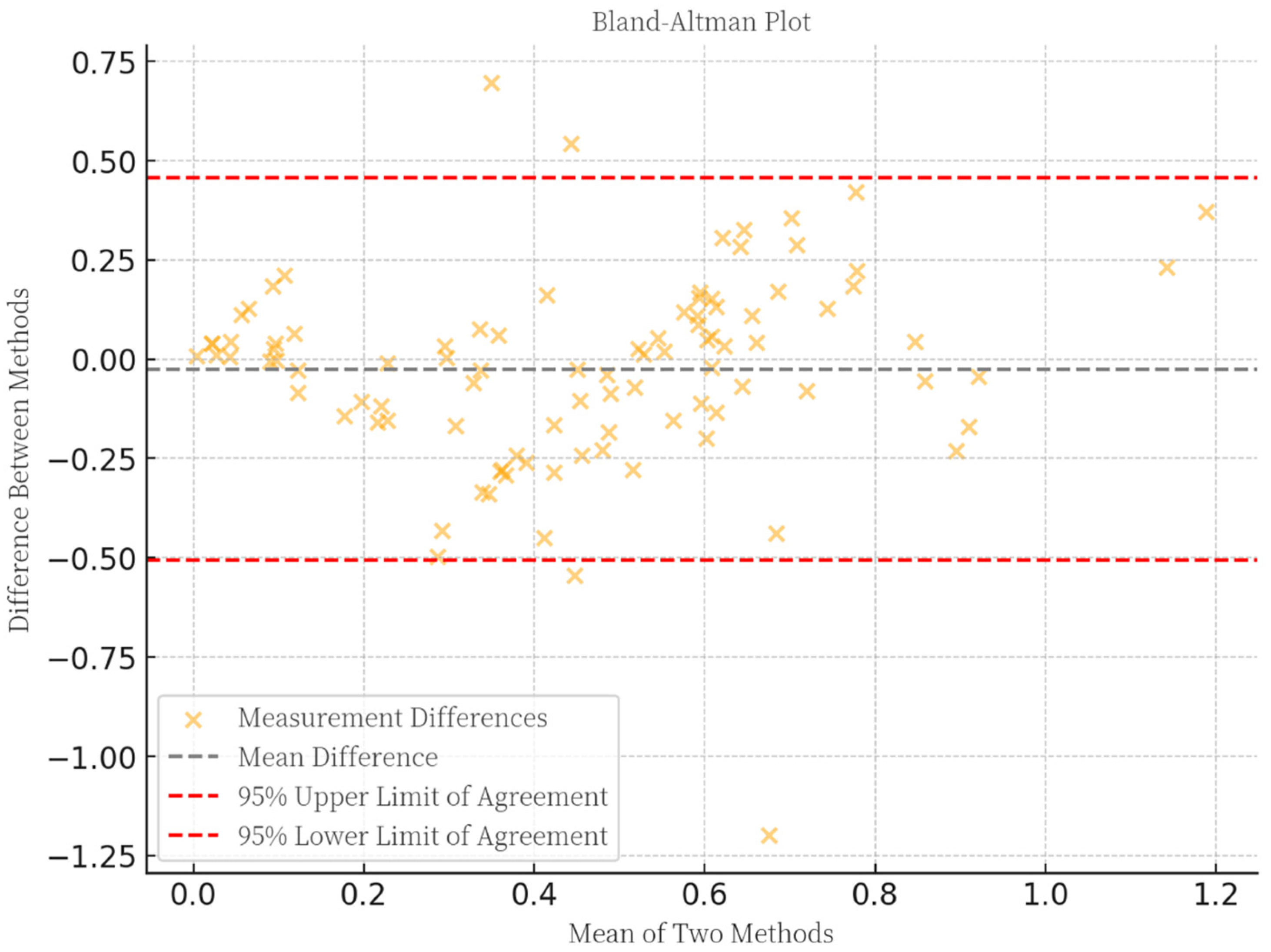
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Qi, S.; Wang, J.; Zhang, X.; Yang, Z.; Xie, Z.; Li, J. Research on monitoring method of fuel sulfur content of ships in Tianjin port. J. Phys. Conf. Ser. 2021, 2009, 12073. [Google Scholar] [CrossRef]

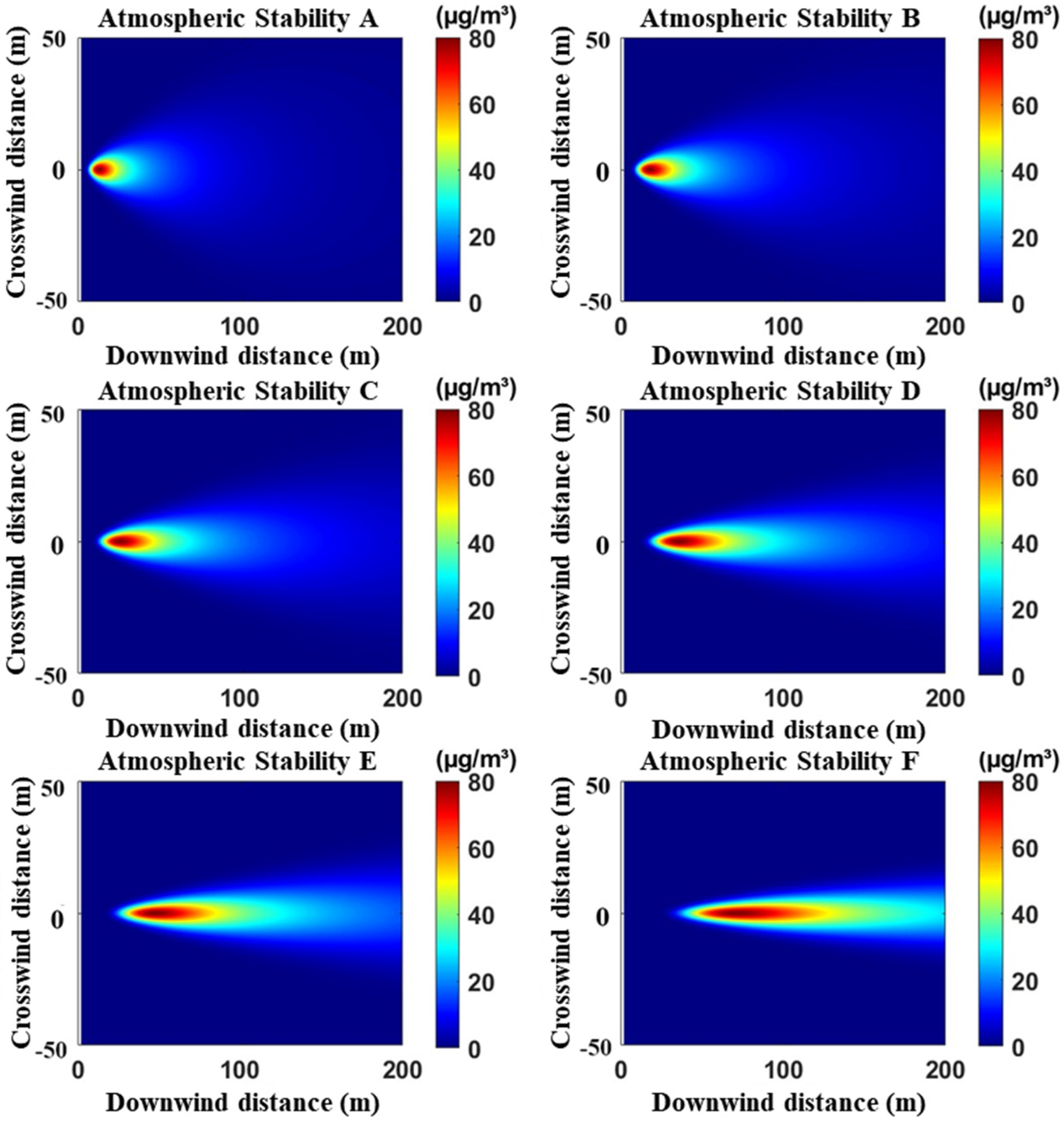

| Atmospheric Stability | |||||||
|---|---|---|---|---|---|---|---|
| Rural condition | A | 0.22 | 0.0001 | 0.5 | 0.20 | 0 | 1.0 |
| B | 0.16 | 0.0001 | 0.5 | 0.12 | 0 | 1.0 | |
| C | 0.11 | 0.0001 | 0.5 | 0.08 | 0.0002 | 0.5 | |
| D | 0.08 | 0.0001 | 0.5 | 0.06 | 0.0015 | 0.5 | |
| E | 0.06 | 0.0001 | 0.5 | 0.03 | 0.0003 | 1.0 | |
| F | 0.04 | 0.0001 | 0.5 | 0.02 | 0.0003 | 1.0 | |
| Ship Categories | Sample Size | Regression Function Between Gross Tonnage (GT) and Main Engine Power | Auxiliary to Main Engine Power Ratios | |
|---|---|---|---|---|
| Cargo-Bulk carrier | 28,320 | 0.947 | ||
| Cargo-Oil tanker | 34,026 | 0.935 | ||
| Cargo-Container | 73,967 | 0.938 | ||
| Cargo-General cargo | 13,809 | 0.802 | ||
| Harbor ship-Tugs | 40,346 | 0.746 | ||
| Cargo-Chemical tanker | 28,147 | 0.929 | ||
| Cargo-Gas tanker | 39,165 | 0.933 | ||
| Cargo-Ro-Ro carrier | 67,838 | 0.731 | ||
| Passenger | 80,998 | 0.746 |
| Parameter | Value | Calculated Source Strength (g/s) | Relative Error of Source Strength (%) |
|---|---|---|---|
| population size | 10 | 0.148310 | 16.27 |
| 20 | 0.146212 | 14.62 | |
| 50 | 0.149235 | 16.99 | |
| crossover rate | 0.6 | 0.150270 | 17.79 |
| 0.8 | 0.146212 | 14.62 | |
| 1.0 | 0.147240 | 15.42 | |
| mutation rate | 0.01 | 0.148255 | 16.21 |
| 0.05 | 0.146212 | 14.62 | |
| 0.1 | 0.149265 | 16.99 | |
| maximum number of iterations | 200 | 0.146212 | 14.62 |
| 300 | 0.146212 | 14.62 | |
| 500 | 0.146212 | 14.62 |
| Comparison of Indices | The Proposed Method | Carbon Balance Method |
|---|---|---|
| Number of exempted ships | 97 | 97 |
| Fuel sulfur content over 0.1% | 85 | 81 |
| Exceeding standard ratio | 87.63% | 83.51% |
| Fuel sulfur content over 1.0% | 2 | 4 |
| Outliers rate | 2.06% | 4.12% |
| Item | Value |
|---|---|
| Valid Sample Size | 97 |
| Mean Value (the proposed method) | 0.442 |
| Mean Value (carbon balance method) | 0.468 |
| Mean (Difference) | −0.026 |
| Standard Deviation (Difference) | 0.247 |
| 95% CI (Difference) | −0.075~0.024 |
| 95% CI (Difference) | −0.510~0.458 |
| t Value (H0: Mean Difference = 0) | −1.023 |
| p Value (H0: Mean Difference = 0) | 0.309 |
| CR Value (Coefficient of Repeatability) | 0.484 |
| Data Type | Sample Size | Maximum | Minimum | Mean | Skewness |
|---|---|---|---|---|---|
| SO2 concentration (ppb) | 367,846 | 99.67 | 0.38 | 8.22 | 5.752 |
| Speed over ground (km/h) | 125,125 | 24.82 | 7.22 | 14.82 | 1.069 |
| Course over ground (°) | 125,125 | 280 | 223 | 245 | 3.954 |
| Wind direction (°) | 384,753 | 360 | 0 | 148 | 0.631 |
| Wind speed (km/h) | 384,753 | 43.92 | 0.36 | 12.24 | 2.033 |
| Total cloud cover | 720 | 10 | 0 | 6.19 | −0.504 |
| Low cloud cover | 720 | 10 | 0 | 1.83 | 1.684 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wu, H.; Wang, N.; Ye, Z. A Novel Ship Fuel Sulfur Content Estimation Method Using Improved Gaussian Plume Model and Genetic Algorithms. J. Mar. Sci. Eng. 2025, 13, 690. https://doi.org/10.3390/jmse13040690
Wang C, Wu H, Wang N, Ye Z. A Novel Ship Fuel Sulfur Content Estimation Method Using Improved Gaussian Plume Model and Genetic Algorithms. Journal of Marine Science and Engineering. 2025; 13(4):690. https://doi.org/10.3390/jmse13040690
Chicago/Turabian StyleWang, Chao, Hao Wu, Nini Wang, and Zhirui Ye. 2025. "A Novel Ship Fuel Sulfur Content Estimation Method Using Improved Gaussian Plume Model and Genetic Algorithms" Journal of Marine Science and Engineering 13, no. 4: 690. https://doi.org/10.3390/jmse13040690
APA StyleWang, C., Wu, H., Wang, N., & Ye, Z. (2025). A Novel Ship Fuel Sulfur Content Estimation Method Using Improved Gaussian Plume Model and Genetic Algorithms. Journal of Marine Science and Engineering, 13(4), 690. https://doi.org/10.3390/jmse13040690





