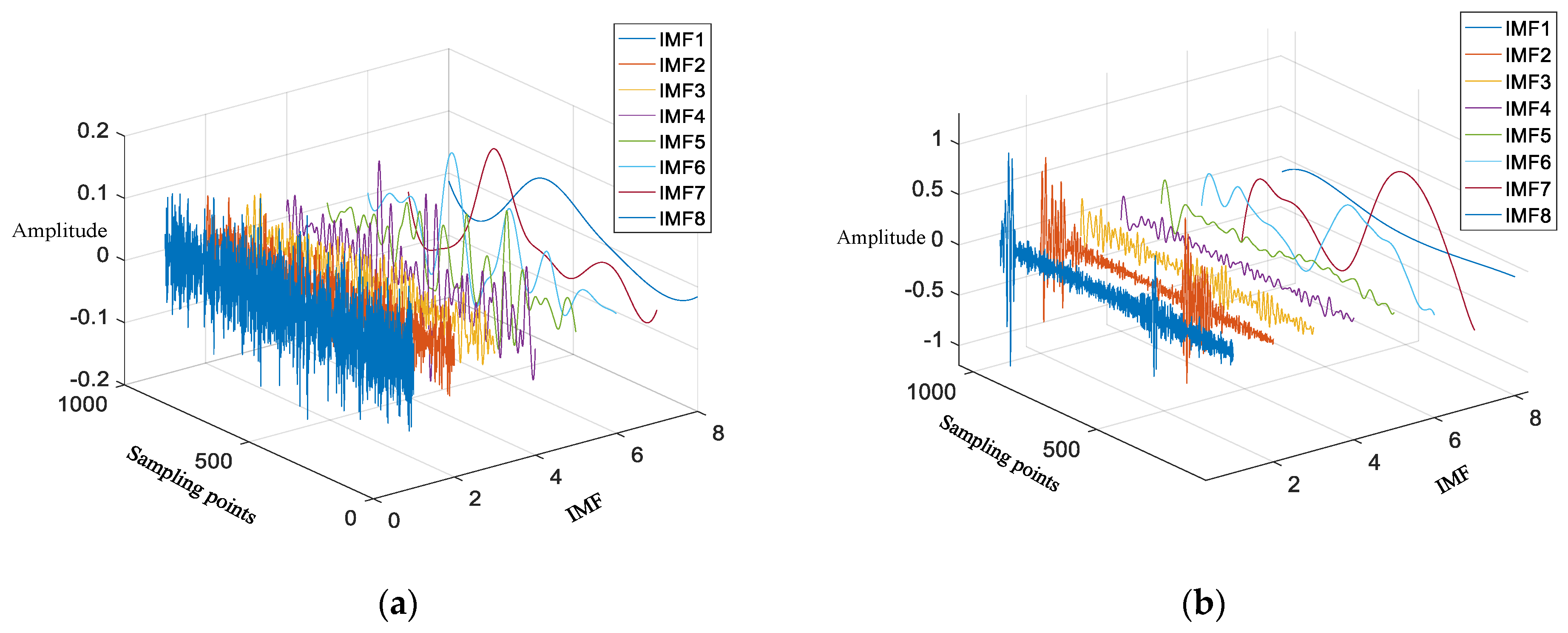
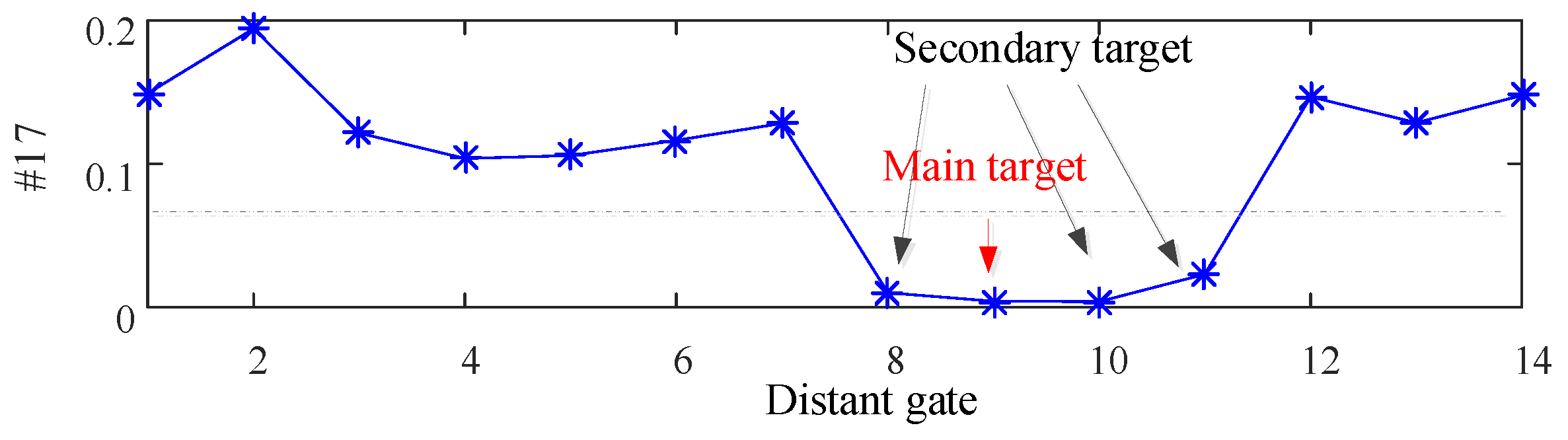
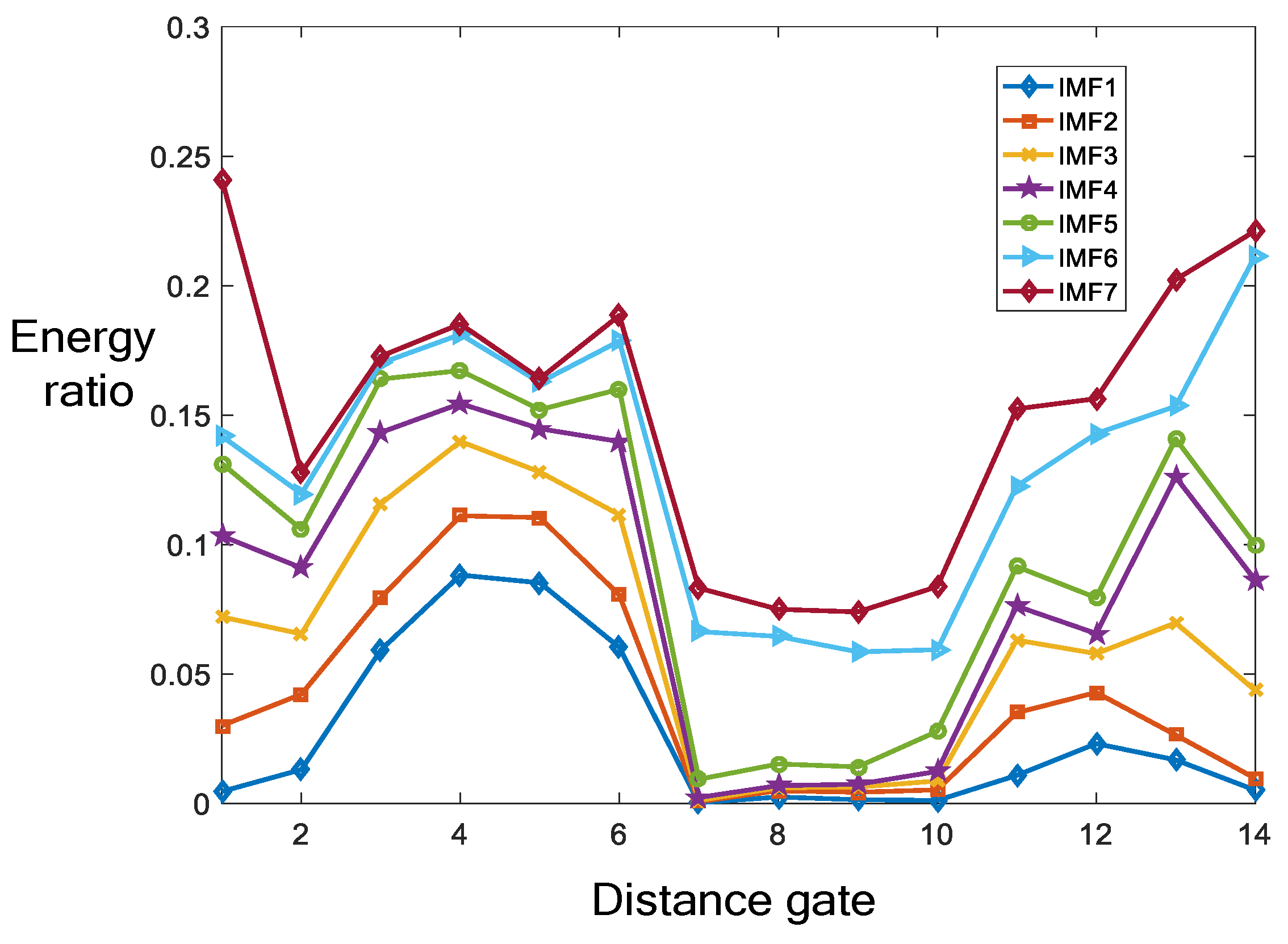
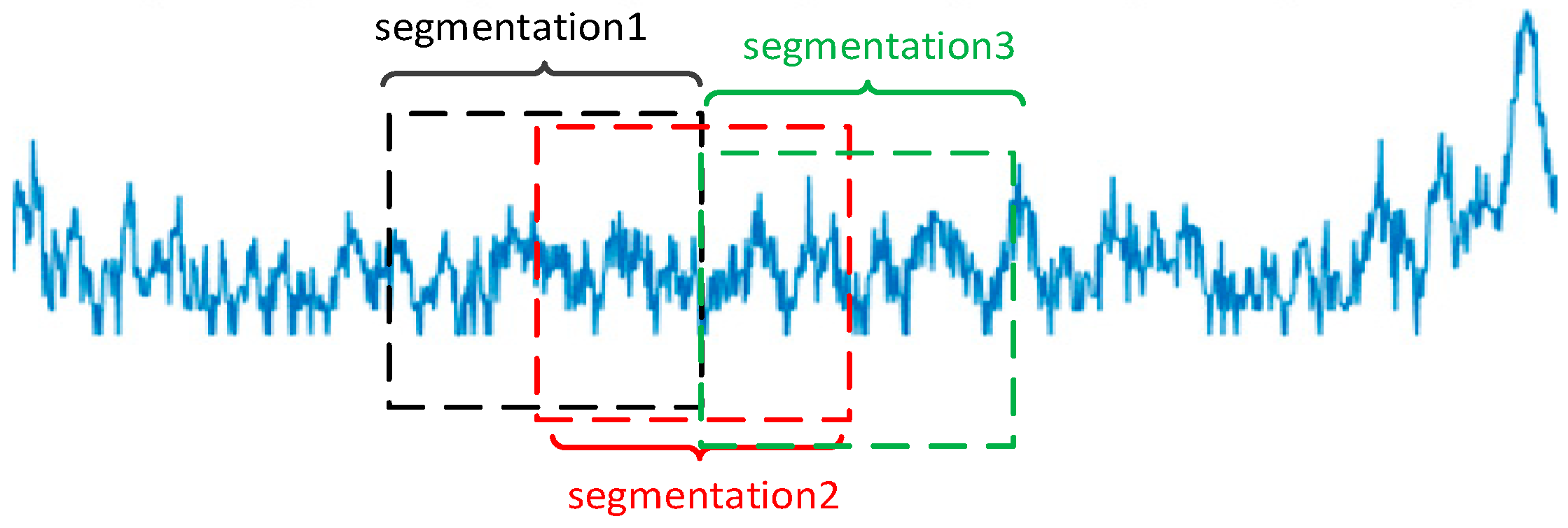
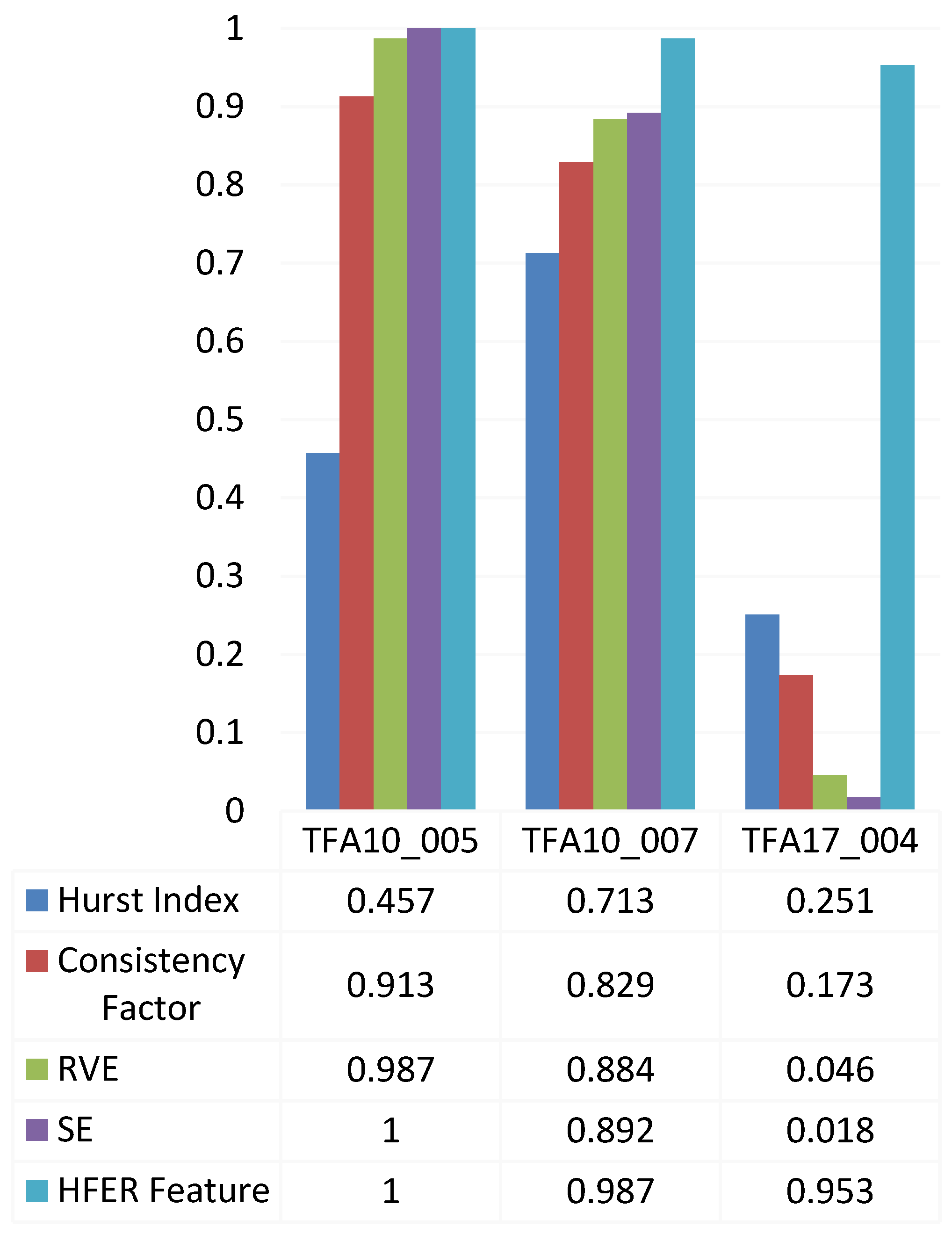
In the detection of weak signals in the background of sea clutter, there are two states of sea clutter: one is to simultaneously receive weak signals and sea clutter, while the other is only sea clutter. The task of sea surface target detection is to determine whether there are weak signals in the received sea clutter, which is simplified as a binary classification problem between clutter units and target units. Therefore, the detection problem is essentially a binary hypothesis test.
After extracting HFER features, we use the XGBoost model with a high computational efficiency and low risk of overfitting to optimize the hyperparameters of XGBoost through SSA. We design an SSA–XGBoost target detection network to transform the problem of detecting weak signals in the sea clutter background into a feature classification problem with or without targets.
4.2. HFER Feature Classification Network Structure Based on XGBoost
XGBoost is a supervised model composed of a series of CART trees.
Figure 8 shows the process of the XGBoost classification network for weak signals undera sea clutter background using five pieces of high-frequency IMF energy ratio data and two tree structures:
XGBoost can automatically utilize the central processing unit for multi-threaded parallel computing [
25]. XGBoost’s new loss function is second-order-differentiable and incorporates a regularization term to find the optimal solution as a whole, in order to balance the decrease in the loss function and the complexity of the model, improve classification accuracy, and avoid overfitting.
Assuming the model has k decision trees, namely,
the loss function is
Among them, represents retaining the model prediction from the previous round, and , is the function space composed of classification regression trees; is the leaf weight; is the number of leaf nodes on the tree; is the structure of each tree, that is, the mapping of sample instances to corresponding leaf node indices; and each corresponds to an independent tree structure and leaf weights , and C is a constant term.
Perform Taylor second-order expansion on the objective function and define two variables for ease of calculation. As shown below,
The objective function can be changed to Equation (11):
When training the model, the objective function can be represented by Equation (12):
Substitute Equation (13) into Equation (12) to obtain Equation (14):
The smaller the value of , the better the performance of the constructed network. The principle of XGBoost is to calculate the first derivative and second derivative of each node and sample, and then sum up the samples contained in each node to obtain and .
Finally, the objective function can be obtained by traversing the decision tree nodes. While it is difficult for general ensemble learning algorithms to specifically list all regression trees, the XGBoost algorithm uses the gradient boosting strategy, constantly adding new trees during the training process to fit the previous learning errors.
4.3. SSA Optimization of HFER Feature Classification Network Based on XGBoost
During the training process, the classification performance of the XGBoost model is easily affected by hyperparameters. The hyperparameter information of the XGBoost model that affects the classification results is shown in
Table 6:
From
Table 6, it can be seen that the selection of numerous hyperparameters determines the training effectiveness of the XGBoost model. Improper selection can seriously affect the classification results. Therefore, it is necessary that we optimize the hyperparameter set of the XGBoost network to obtain a model that is suitable for the training samples and to improve the final detection probability.
During the process of foraging, sparrow populations can be divided into two types: discoverers and followers. Discoverers are responsible for discovering food in the population and informing the entire sparrow population of the next foraging area and direction, while followers obtain food through the information obtained by discoverers.
Individuals in sparrow populations will monitor the behavior of other individuals in the population, and attackers in the population will compete with individuals with a high intake for food resources to increase their predation rate. In addition, when sparrow populations become aware of danger, they will engage in anti-predatory behavior. Based on this intelligent role assignment, the sparrow search algorithm has the advantages of a strong global search ability, short optimization time, and fast convergence speed, and is suitable for optimizing weak signal detection networks under a sea clutter background. The XGBoost hyperparameter set for optimizing the classification of HFER sea clutter features using the sparrow search algorithm can be represented by the following mathematical model.
Equation (15) represents the assumed sparrow population:
In Equation (15), represents the number of sparrows; and represents the dimension of the variable that needs to be optimized.
The fitness value of sparrows is expressed using Equation (16):
In Equation (16), the value of each row in represents the fitness value of each individual.
During the search process, the order in which sparrows obtain food is related to their fitness level, with sparrows that prioritize obtaining food having higher fitness. The leader of the sparrow population is called an explorer. Explorers are responsible for searching for food and providing directions for other sparrows in the population to search for food, thus having the largest range for searching for food.
When the sparrow population is in the absence of predators, the search direction of the explorer is arbitrary. Once a predator appears around the population, the explorer will lead followers to move away from the predator.
The formula for updating the position of the explorer, which is the fitness value, is shown in Equation (17):
In Equation (17), represents the current number of iterations; represents the maximum number of iterations; represents the position information of the i-th sparrow in the j-th dimension; is a random number and ; represents the warning value ; represents the safety value ; is a random number that follows a normal distribution; and is a matrix where all elements are 1.
When , it indicates the presence of danger and predators in the area; when it is the other way around, it indicates that the area is safe and there are no predators present.
In the entire sparrow population, the ratio of explorers to followers is fixed and unchanging. If followers can find better food, they can become explorers, and vice versa. Due to the fact that only explorers in the sparrow population have better foraging environments and larger foraging ranges, followers will constantly observe the explorers’ situation and compete with them for food in order to obtain better food. If followers succeed in the competition, they will obtain the explorers’ food instead of searching for food in farther places. The follower position update formula, Formula (18), is as follows:
In Equation (18), represents the global worst position; represents the best position among the current discoverers; A is an -dimensional matrix with only 1 and −1 elements, and ; and represents the total number of sparrows.
When , it indicates that the fitness of the th follower is low and they have not obtained food, and they need to fly to other directions to search for food.
Vigilantes are randomly generated, so their positions are also random. The number of vigilantes is generally set at 10% to 20% of the entire sparrow population. When vigilantes detect predators around them, the peripheral sparrows will quickly fly to a safe place to obtain a better search environment. The internal sparrows will move within a safe area to reduce the probability of being preyed upon by predators. The location update formula, Formula (19), for the alert is as follows:
In Equation (19), represents the current global optimal position; represents the step size and follows a normal distribution; is a random number ; represents the fitness value of the current sparrow individual; represents the current global optimal fitness value; represents the current global worst fitness value; and is a constant used to avoid the denominator appearing as 0. When , it means that the peripheral sparrows have discovered predators; when it is the other way around, it means that the sparrow inside has discovered a predator.
The steps for classifying sea clutter HFER features using SSA–XGBoost are as follows:
(1) Data preprocessing normalizes the HFER feature sequence to , with the aim of limiting the input sequence to a certain range and solving problems such as inability to converge or slow convergence caused by special sample HFER data. Divide the training set and the testing set.
(2) Determine and initialize the hyperparameter groups Learning_rate, Max_depth, Colsample-bytree, and Subsample to be optimized in the XGBoost network, and initialize the relevant parameters of the sparrow search algorithm.
(3) Calculate the individual fitness value of sparrows, and sort and select the current global best fitness value and worst fitness value , as well as their corresponding positions and .
(4) Update the position of sparrows, based on the warning value and safety value , and update the position of discoverers, joiners, and sparrows that are aware of danger. Obtain the current global best fitness value and the corresponding global best position .
(5) Select the global optimal solution after reaching the maximum number of iterations; otherwise, iterate again.
(6) Take the optimal output solution as the hyperparameter set to be optimized for XGBoost.
(7) Input the test set samples into the optimal XGBoost model and output the classification results.
The flowchart of weak signal detection under a sea clutter background based on the SSA–XGBoost algorithm is shown in
Figure 9: