Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions
Abstract
1. Introduction
2. Methods
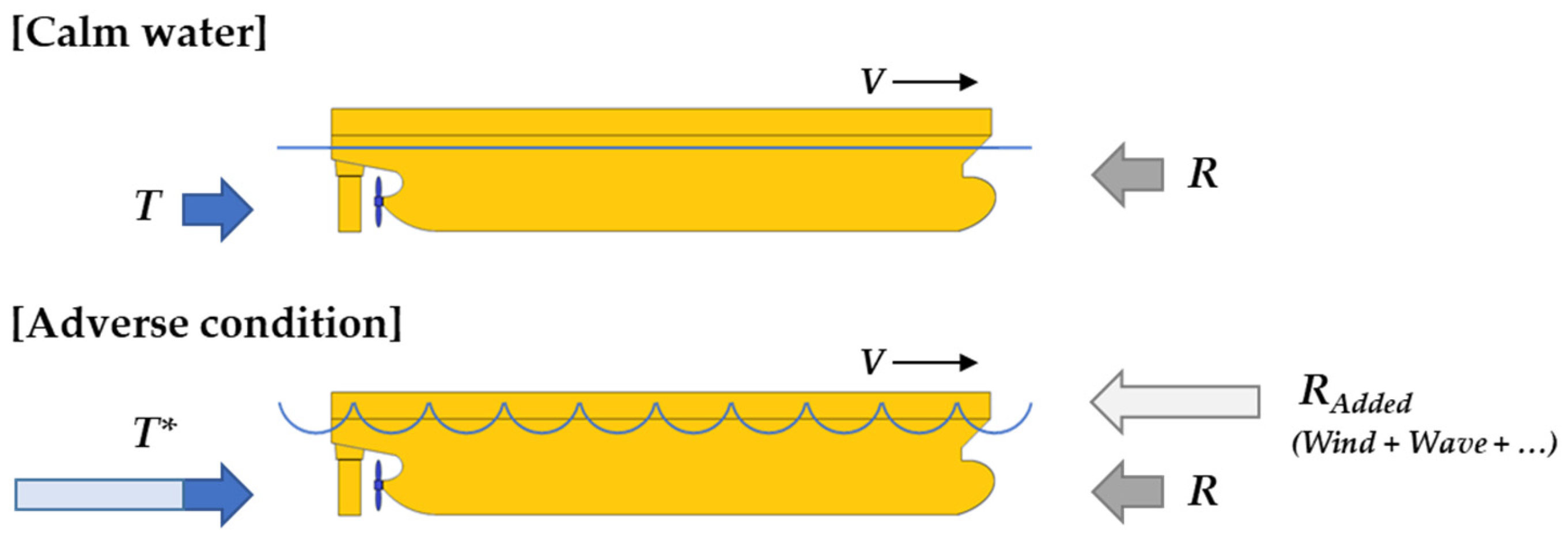
2.1. Assessment in Adverse Conditions
2.2. Overload Test
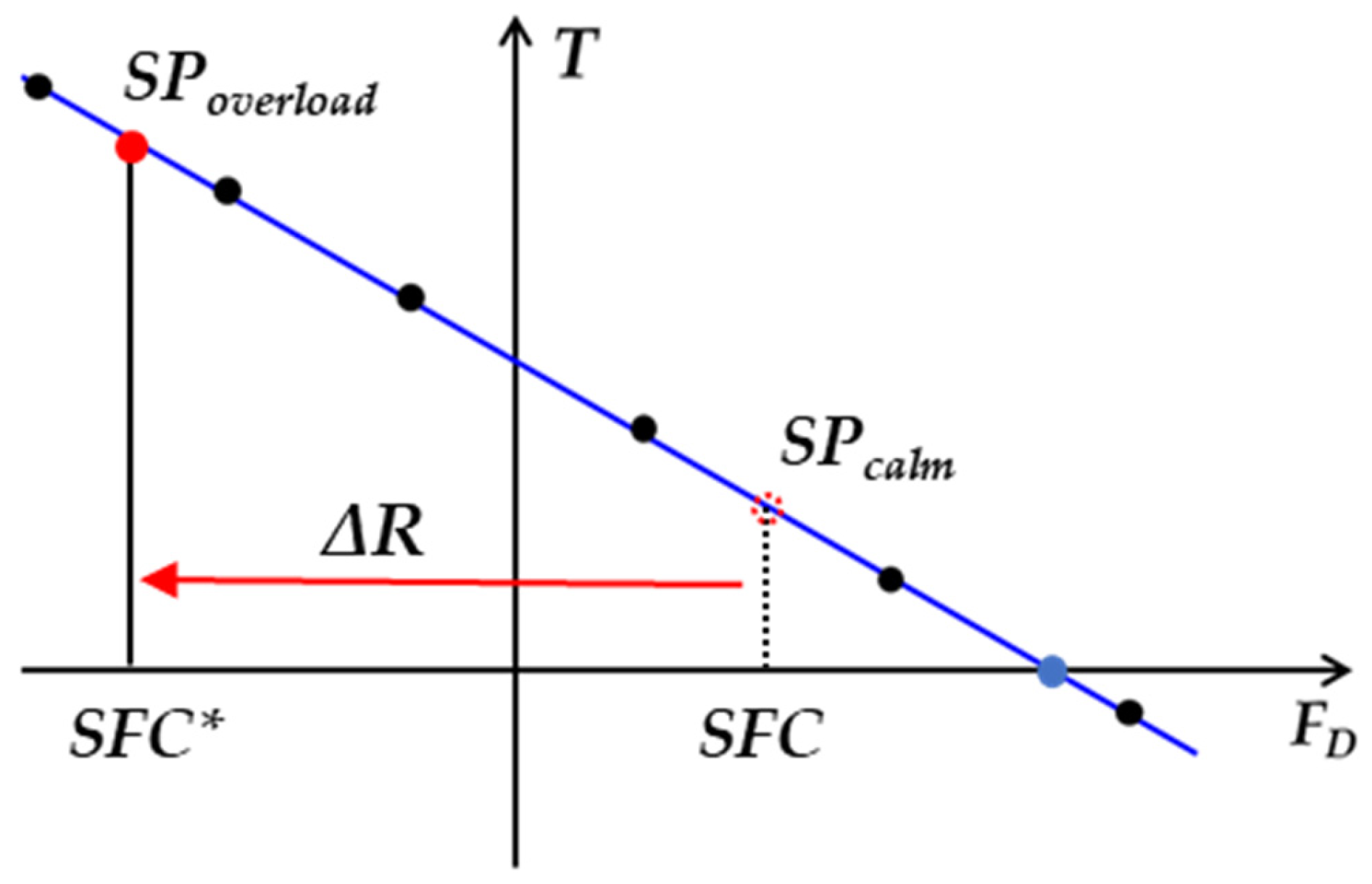
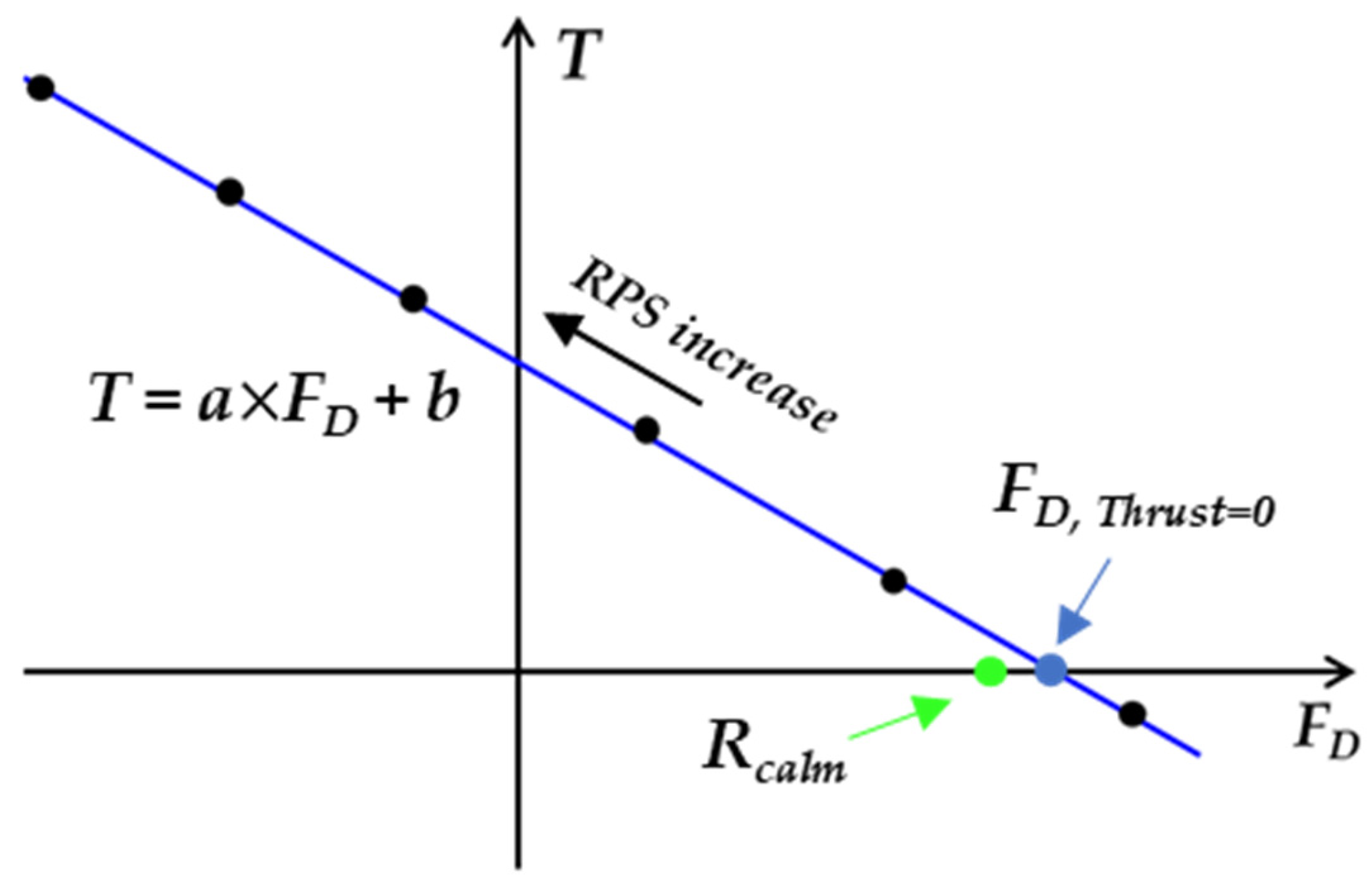
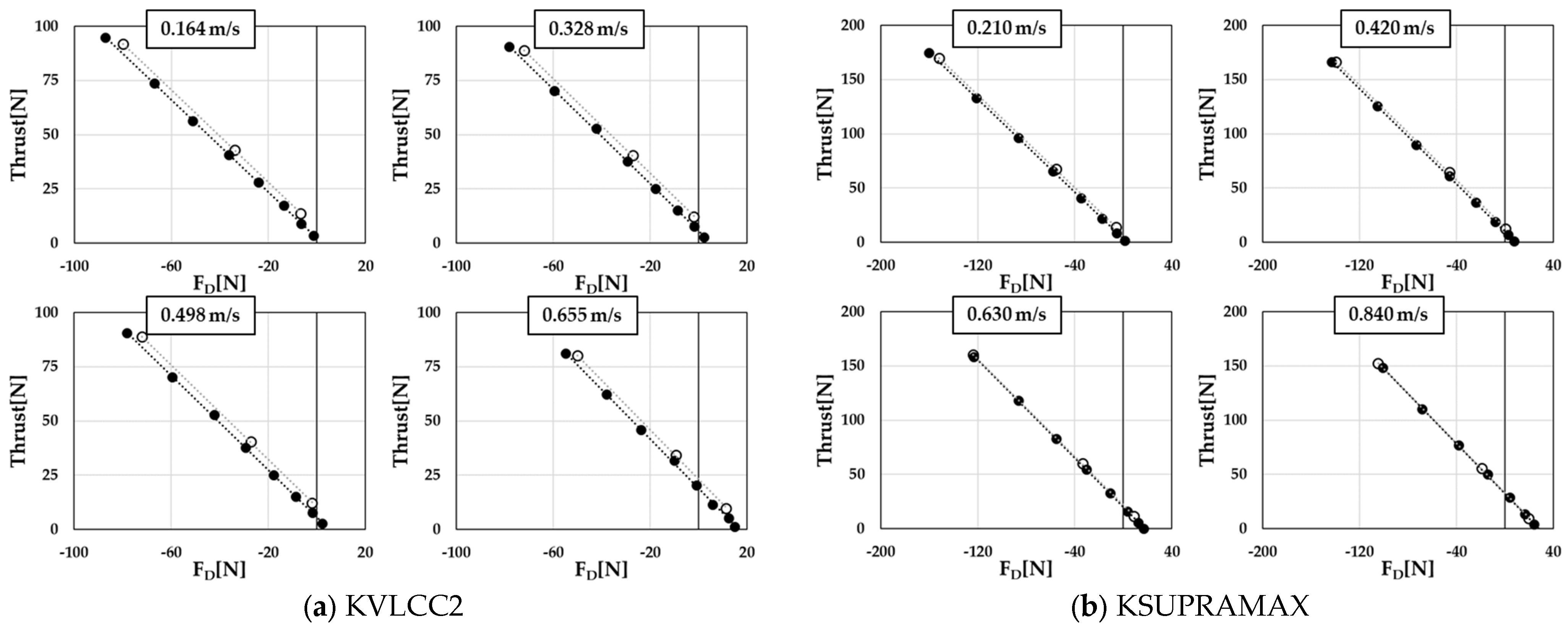
2.2.1. Resistance Derived from the Overload Test
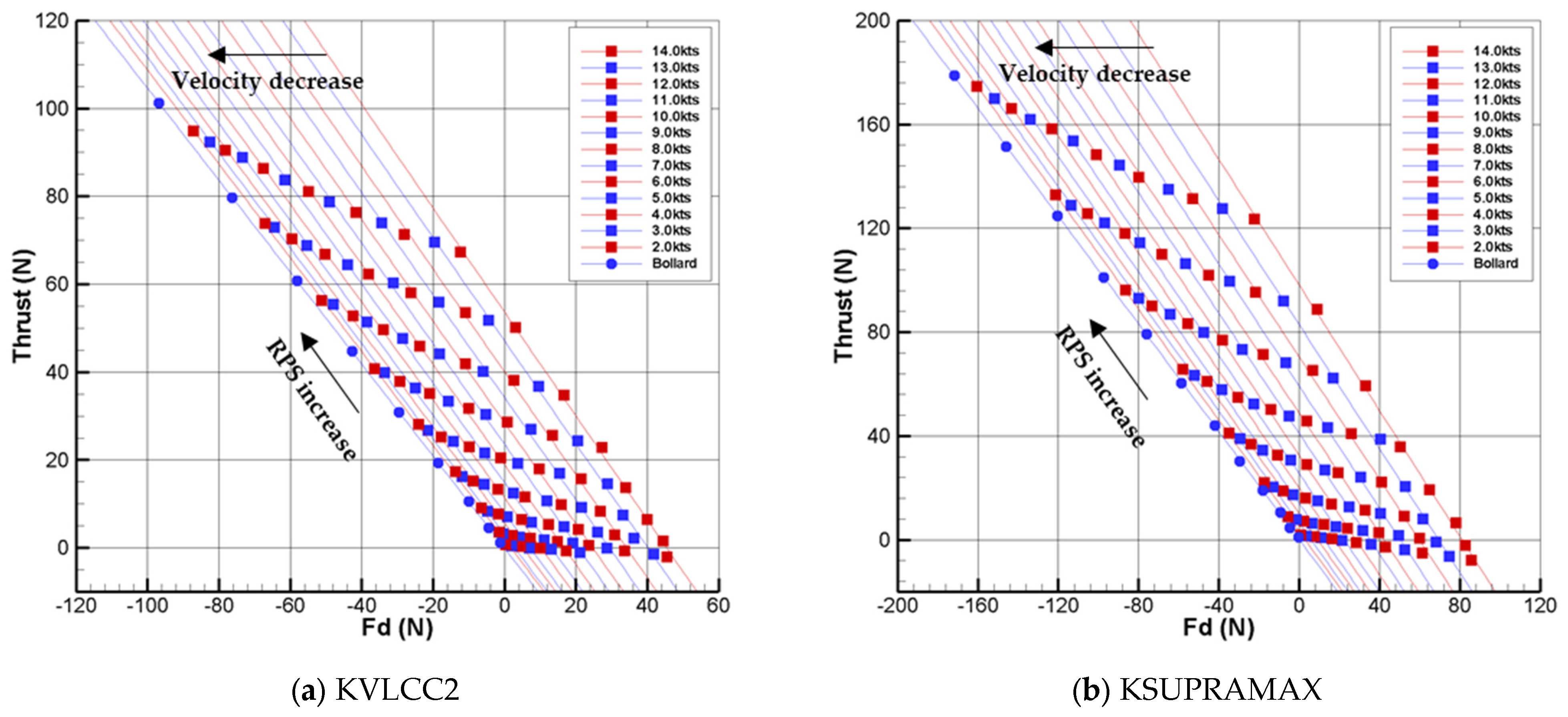
2.2.2. Self-Propulsion Point Considering the Added Resistance
- is the skin friction correction force;
- is the added resistance at the model scale, .
2.3. Model Tests and CFD Simulations
2.3.1. Target Ship and Propeller
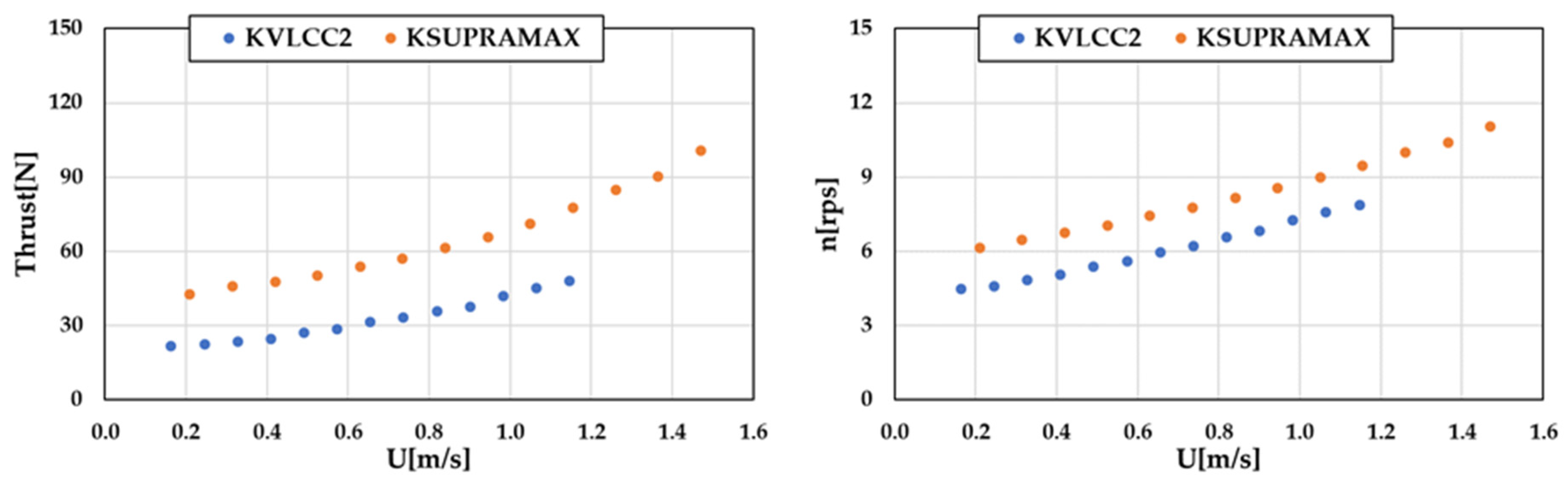
2.3.2. Model Tests
2.3.3. CFD Simulations
3. Results
3.1. Characteristics of Self-Propulsion Factors
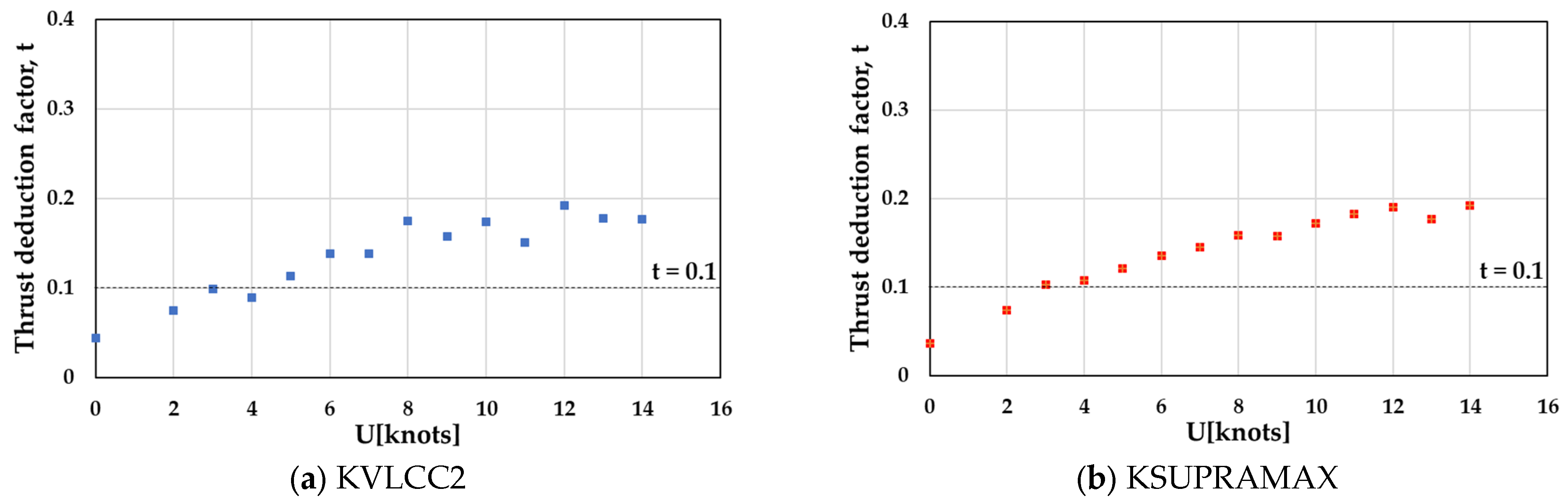
3.1.1. Thrust Deduction Factor
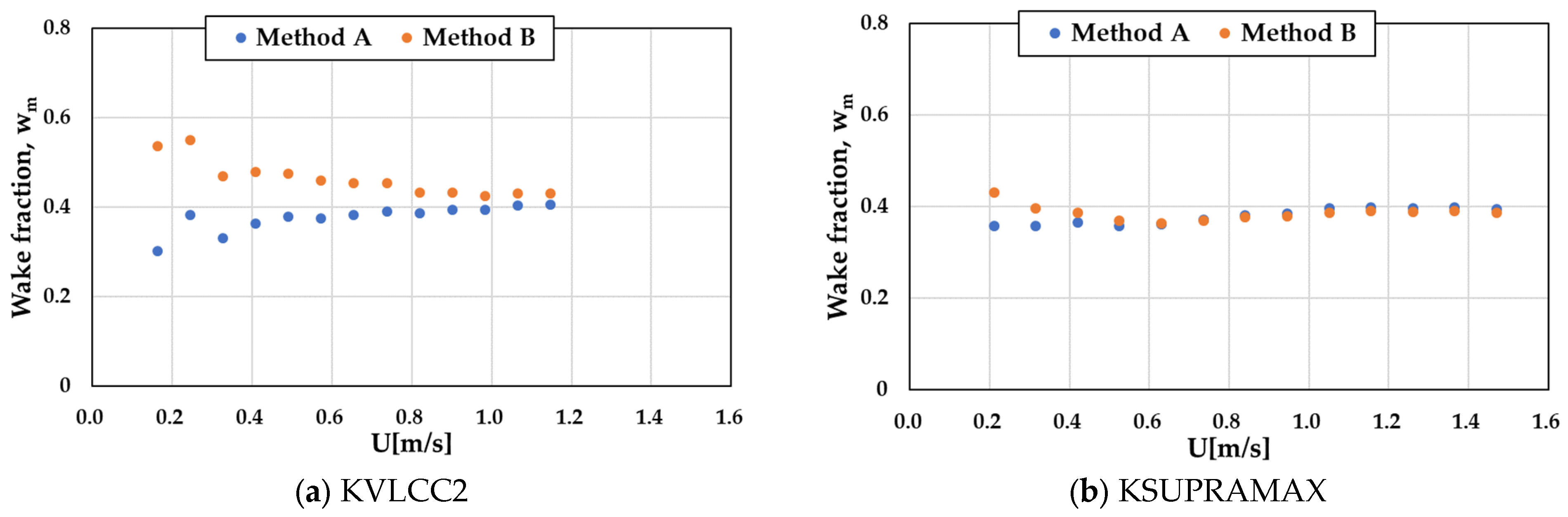
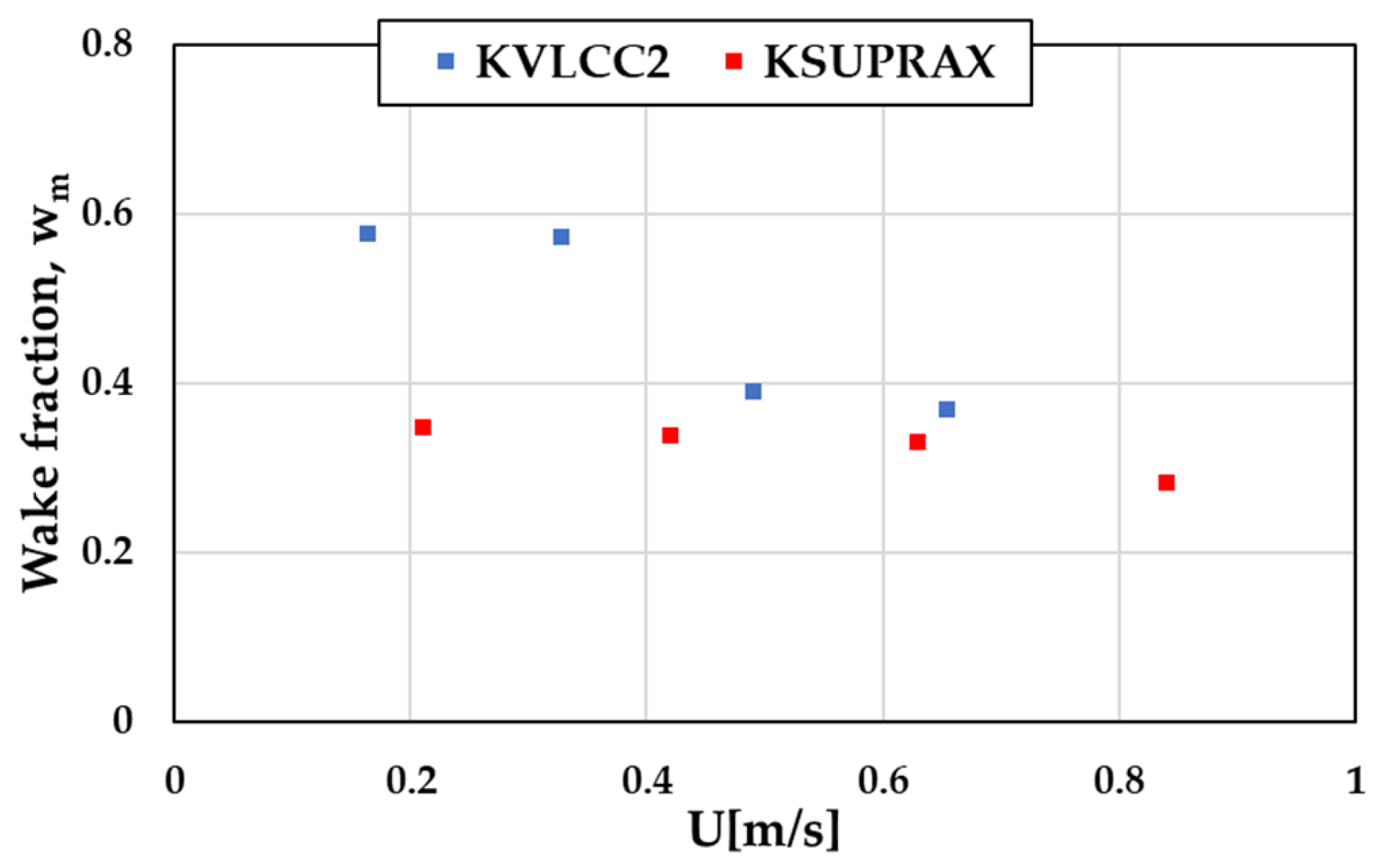
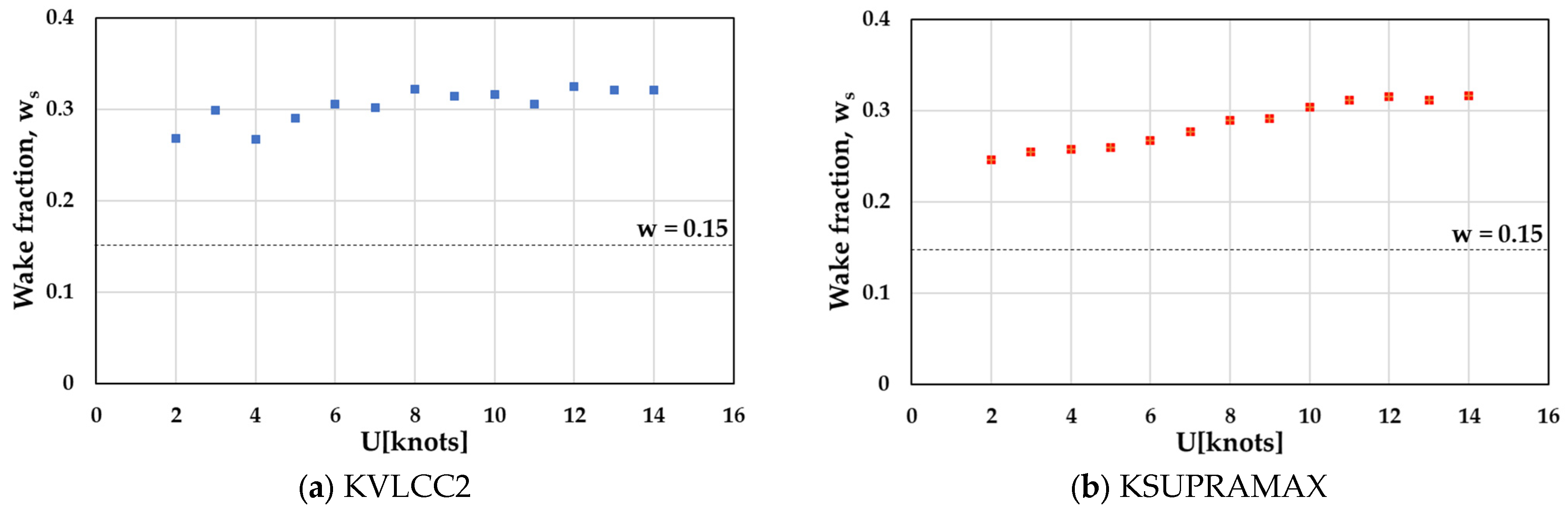
3.1.2. Wake Fraction
- is the thrust at the self-propulsion point.
- is the velocity at the propeller plane, propeller-induced velocity.
- is the velocity far upstream.
- is the velocity far downstream.
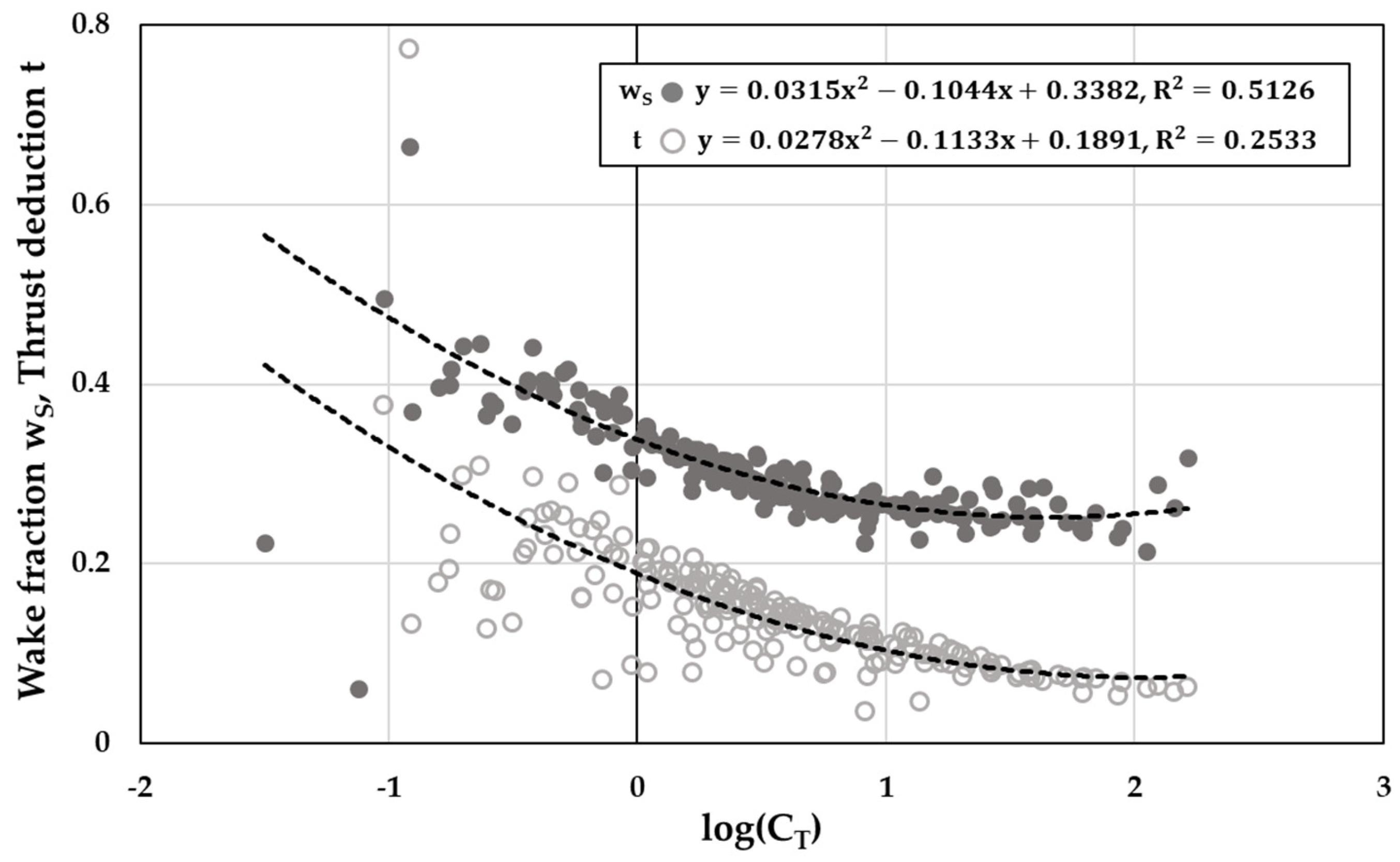
3.1.3. Analysis of Self-Propulsion Factors with Respect to Propeller Load
3.2. Results of the Minimum Propulsion Power
4. Conclusions
- In adverse conditions, with decreasing speed, the proportion of the added resistance becomes larger than that under calm-water conditions. At the required forward speed of 2 knots for the MPP assessment, it increased by more than 30 times.
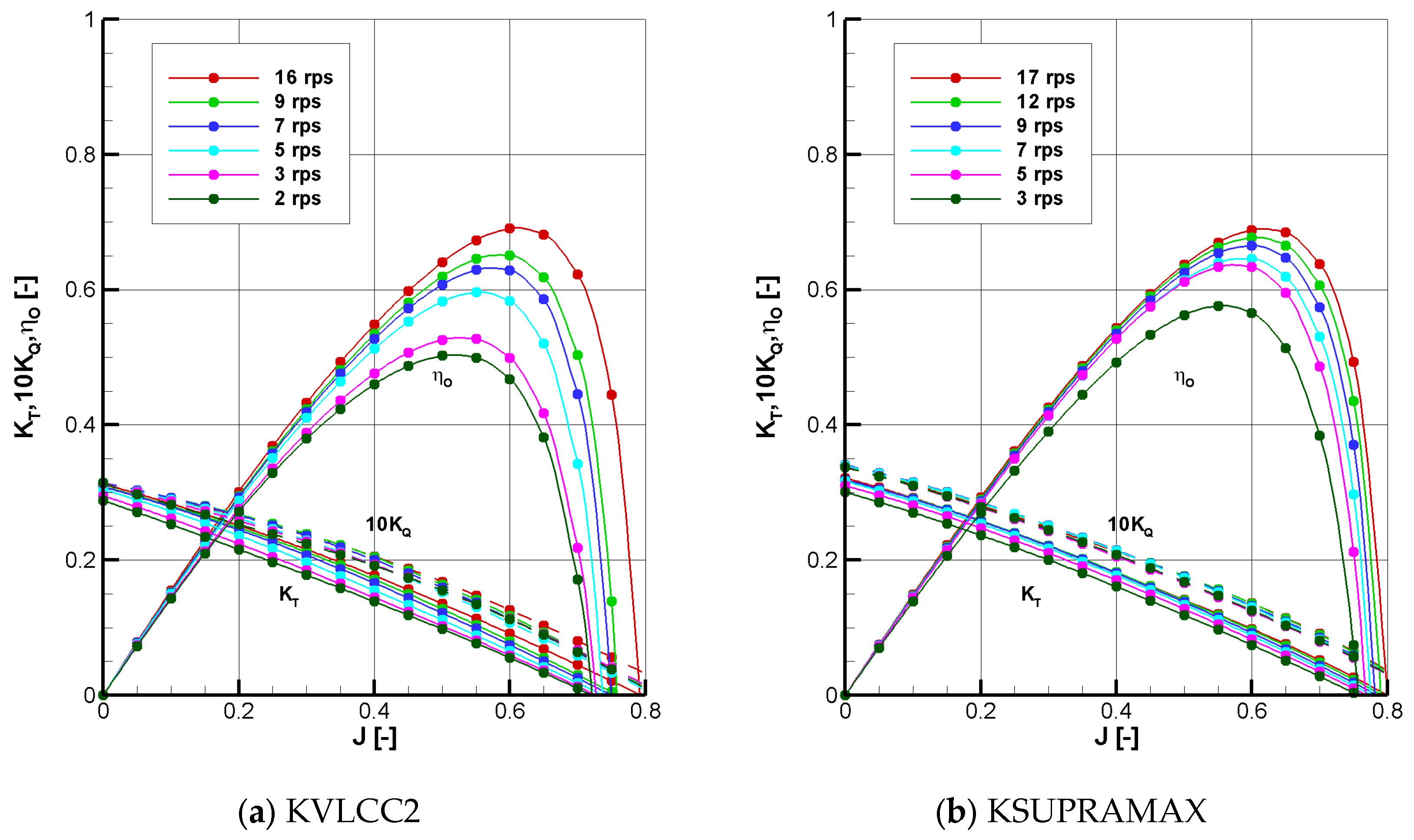
- POW tests were conducted for low Reynolds number conditions for the propeller flow matching those of the self-propulsion point; the propeller open-water efficiency decreased with a decrease in the Reynolds number when the advance ratio was held constant.
- The characteristics of the self-propulsion factors corresponding to Method A (POW results with a high Reynolds number) and Method B (POW results with a Reynolds number matching the self-propulsion point) were analyzed.
- The overload test revealed that the thrust deduction factor decreased with decreasing speed. The wake fraction decreased slightly corresponding to Method A with decreasing speed, whereas it increased corresponding to Method B.
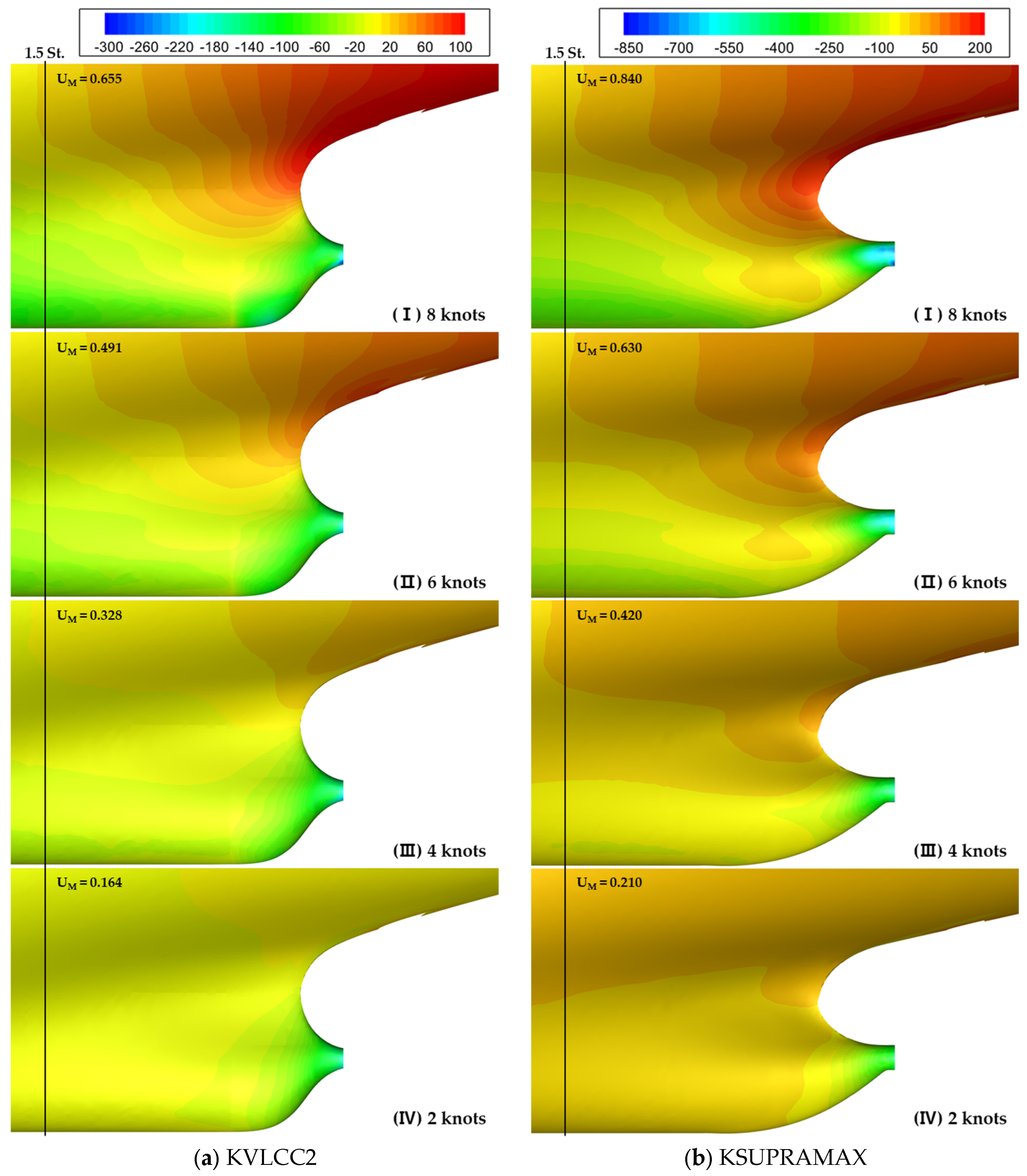
- The physical phenomena in adverse conditions were analyzed using CFD simulations at the model scale. The thrust deduction factor decreased with decreasing speed, attributed to the reduction in propeller suction induced by the decrease in speed, as clearly demonstrated by analyzing the pressure distribution on the hull surface using CFD simulations.
- The flow field induced by the propeller operating on the propeller plane was obtained using CFD simulations. The propeller-induced velocity was calculated using momentum theory, and the effective wake fraction at the model scale was derived indirectly by subtracting it from the flow field. Consequently, the wake fraction increased with decreasing speed, consistent with the trend indicated by the model test results when Method B was considered.
- Full-scale estimation of self-propulsion factors was performed using the results corresponding to Method B. The thrust deduction factor was lower than that given in the MPP guidelines (), whereas the wake fraction was higher ().
- Regression analysis was performed on the self-propulsion factors using the thrust loading coefficient. Self-propulsion factors were demonstrated to decrease with increasing propeller load under full-scale conditions. A more accurate analysis of the correlation between self-propulsion factors and the loading coefficient could lead to an improvement in the MPP guidelines.
- MPP assessments were conducted for the target ships, with the derived self-propulsion factors compared with those in the MPP guidelines. Although the self-propulsion factors were different from each other, some compensation owing to the shift in the advance ratio was observed in the quasi-propulsive efficiency. Consequently, the required brake power derived in this study for the target ships was approximately 4–5% less than that given in MPP guidelines.
- For more reliable and accurate MPP assessments, the self-propulsion factors suggested in the MPP guidelines should be reviewed in more detail to address the absence of model-ship correlation factors in MPP assessment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IMO. Resolution MEPC.203(62). In Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships; International Maritime Organization: London, UK, 1973; As Modified by the Protocol of 1978 Relating Thereto (Inclusion of Regulations on Energy Efficiency for Ships in MARPOL Annex VI), MEPC 62/24/Add.1; p. 2011. [Google Scholar]
- IMO. Resolution MEPC.324(75). In Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships; MEPC 75/18/Add.1; International Maritime Organization: London, UK, 1973; As Modified by the Protocol of 1978 Relating Thereto—Amendments to MARPOL Annex VI (Procedures for Sampling and Verification of the Sulphur Content of Fuel Oil and the Energy Efficiency Design Index (EEDI)); p. 2020. [Google Scholar]
- IMO. Resolution MEPC.328(76). In Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships; MEPC 76/15/Add.1; International Maritime Organization: London, UK, 1973; As Modified by the Protocol of 1978 Relating Thereto—2021 Revised MARPOL Annex VI; p. 2021. [Google Scholar]
- IMO. Resolution MEPC.364(79). In Guidelines on the Method of Calculation of the Attained Energy Efficiency Design Index (EEDI) for New Ships; MEPC 79/15/Add.1; International Maritime Organization: London, UK, 2022. [Google Scholar]
- IMO. Resolution MEPC.350(78). In Guidelines on the Method of Calculation of the Attained Energy Efficiency Existing Ship Index (EEXI); MEPC 78/17/Add.1; International Maritime Organization: London, UK, 2022. [Google Scholar]
- Farkas, A.; Degiuli, N.; Martić, I.; Grlj, C.G. Is slow steaming a viable option to meet the novel energy efficiency requirements for containerships? J. Clean. Prod. 2022, 374, 133915. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Mikulić, A. Benefits of slow steaming in realistic sailing conditions along different sailing routes. Ocean Eng. 2023, 275, 114143. [Google Scholar] [CrossRef]
- Zincir, B. Slow steaming application for short-sea shipping to comply with the CII regulation. Brodogradnja 2023, 74, 21–38. [Google Scholar] [CrossRef]
- IMO. Resolution MEPC.232(65). In Interim Guidelines for Determining Minimum Propulsion Power to Maintain the Manoeuvrability of Ships in Adverse Conditions; MEPC; International Maritime Organization: London, UK, 2013; Volume 65/22. [Google Scholar]
- IMO. Guidelines for Determining Minimum Propulsion Power to Maintain the Manoeuvrability of Ships in Adverse Conditions; MEPC.1/Circ.850/Rev.3; International Maritime Organization: London, UK, 2021. [Google Scholar]
- Sung, Y.J.; Ock, Y.B. Progress of the 2013 interim guidelines for determining minimum propulsion power to maintain the manoeuvrability of ships in adverse conditions. J. Soc. Nav. Archit. Korea 2019, 56, 497–506. [Google Scholar] [CrossRef]
- Gerhardt, F.C.; Kjellberg, M.; Korkmaz, B.; Ljungqvist, K.; Shiri, A. Determining the EEDI “Minimum Propulsion Power”. In Influence of EEDI on Ship Design & Operation; Royal Institution of Naval Architects: London, UK, 2020. [Google Scholar]
- Holt, P.; Nielsen, U.D. Preliminary assessment of increased main engine load as a consequence of added wave resistance in the light of minimum propulsion power. Appl. Ocean Res. 2021, 108, 102543. [Google Scholar] [CrossRef]
- Feng, P.; Liu, S.; Shang, B.; Papanikolaou, A. Minimum propulsion power assessment of a VLCC to maintain the maneuverability in adverse conditions. J. Mar. Sci. Eng. 2021, 9, 1287. [Google Scholar] [CrossRef]
- Liu, S.; Papanikolaou, A.; Shang, B. Regulating the safe navigation of energy-efficient ships: A critical review of the finalized IMO guidelines for assessing the minimum propulsion power of ships in adverse conditions. Ocean Eng. 2022, 249, 111011. [Google Scholar] [CrossRef]
- Bose, N.; Molloy, S. Reliability and accuracy of ship powering performance extrapolation. In Proceedings of the First International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- ITTC. Recommended procedures and guidelines. In Propulsion Tests in Ice; 7.5-02-04-02.2; International Towing Tank Conference: Zürich, Switzerland, 2017. [Google Scholar]
- Jones, S.J. Resistance and Propulsion Model Tests of the USCGC Healy (Model546) in Ice; Laboratory Memorandum (National Research Council of Canada, Institute for Ocean Technology): Sidney, BC, Canada, 2005. [Google Scholar]
- Wang, J.; Jones, S.J. Resistance and propulsion of CCGS Terry Fox in Ice from Model Tests to Full Scale Correlation. In Proceedings of the SNAME 8th International Conference and Exhibition on Performance of Ships and Structures in Ice, Banff, AB, Canada, 20–23 July 2008. [Google Scholar]
- Matsuzawa, T.; Shimoda, H.; Wako, D.; Uto, S.; He, Q.; Watanabe, S. Load-varying methods for ship power estimation in brash ice channel by ice tank model test. In Proceedings of the 24th International Conference on Port and Ocean Engineering Under Arctic Conditions, Busan, Republic of Korea, 11–16 June 2017. [Google Scholar]
- Ji, S.; Tian, Y. Research on overload method based on known ice resistance for self-propulsion test in conventional towing tank. In Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019. [Google Scholar]
- ITTC. Recommended procedures and guidelines. In ITTC Perform. Prediction Method; 7.5-02-03-01.4; International Towing Tank Conference: Zürich, Switzerland, 2021. [Google Scholar]
- Saettone, S.; Taskar, B.; Steen, S.; Andersen, P. Experimental measurements of propulsive factors in following and head waves. Appl. Ocean Res. 2021, 111, 102639. [Google Scholar] [CrossRef]
- Heinke, H.-J.; Hellwig-Rieck, K.; Lübke, L. Influence of the Reynolds number on the open water characteristics of propellers with short chord lengths. In Proceedings of the Sixth International Symposium on Marine Propulsors, Rome, Italy, 26–30 May 2019. [Google Scholar]
- Kim, D.-H.; Jeon, G.M.; Park, J.C.; Shin, M.-S. CFD simulation on predicting POW performance adopting laminar-turbulent transient model. J. Soc. Nav. Archit. Korea 2021, 58, 1–9. [Google Scholar] [CrossRef]
- Grlj, C.G.; Degiuli, N.; Martić, I. Experimental and numerical assessment of the effect of speed and loading conditions on the nominal wake of a containership. Brodogradnja 2024, 75, 75405. [Google Scholar] [CrossRef]
- Molloy, S. Ship Powering Prediction Using Load Varying Self-Propulsion Tests, Degree of Master of Engineering; Memorial University of Newfoundland: St. John’s, NL, Canada, 2001. [Google Scholar]
- Hadler, J.B. The effect of propeller loading on thrust deduction. In Proceedings of the 26th American Towing Tank Conference, New York, NY, USA, 23–24 July 2001. [Google Scholar] [CrossRef]
- Degiuli, N.; Martić, I.; Farkas, A.; Buča, M.P.; Dejhalla, R.; Grlj, C.G. Experimental assessment of the hydrodynamic characteristics of a bulk carrier in off-design conditions. Ocean Eng. 2023, 280, 114936. [Google Scholar] [CrossRef]
- Harvald, S.A. Wake and Thrust Deduction at Extreme Propeller Loadings; Swedish State Shipbuilding Experimental Tank; Scandinavian University Books: Lund, Sweden, 1967. [Google Scholar]
- Harvald, S.A. Resistance and Propulsion of Ships (Ocean Engineering: A Wiley Series), 1st ed.; Wiley Interscience: Hoboken, NJ, USA, 1983; pp. 150–180. [Google Scholar]
- Scragg, C. Wake Scale Effects and Propeller Hull Interaction: State of the Art; Ship Performance Department Report; David W. Taylor Naval Ship Research and Development Center (DTNSRDC): Bethesda, MD, USA, 1980. [Google Scholar]
- Pecoraro, A.; Di Felice, F.; Felli, M.; Salvatore, F.; Viviani, M. Propeller-hull interaction in a single-screw vessel. In Proceedings of the Third International Symposium on Marine Propulsors, Launceston, TAS, Australia, 5–8 May 2013. [Google Scholar]
- Can, U.; Delen, C.; Bal, S. Effective wake estimation of KCS hull at full-scale by GEOSIM method based on CFD. Ocean Eng. 2020, 218, 108052. [Google Scholar] [CrossRef]
- Yao, H.; Zhang, H. Prediction of ship effective wake field using a pure RANS-based methodology. Nav. Eng. J. 2018, 130–132, 47–58. [Google Scholar]
- Sánchez-Caja, A.; Martio, J.; Viitanen, V.M.; Siikonen, T. Simulation of turbulent effective wakes for propellers in off-design conditions by a correction factor approach. J. Mar. Sci. Technol. 2021, 26, 1014–1025. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Jin, W.; Vassalos, D. The calculations of propeller induced velocity by RANS and momentum theory. J. Mar. Sci. Appl. 2012, 11, 164–168. [Google Scholar] [CrossRef]




| Ship Length LPP [m] | Significant Wave Height HS [m] | Peak Wave Period TP [s] | Mean Wind Speed VW [m/s] |
|---|---|---|---|
| Less than 200 | 4.5 | 7.0 to 15.0 | 19.0 |
| 200 ≤ LPP ≤ 250 | Parameters linearly interpolated depending on the ship’s length | ||
| More than 250 | 6.0 | 7.0 to 15.0 | 22.6 |
| Resistance Component | Formula | Explanation |
|---|---|---|
| Total resistance | ||
| Calm-water resistance | U: forward speed, 2 knots | |
| Wind resistance | AF: frontal windage area of the hull and superstructure | |
| Wave resistance | hs: significant wave height | |
| Rudder resistance | t: thrust deduction factor, 0.1 |
| Parameters | KVLCC2 | KSUPRAMAX |
|---|---|---|
| Scale ratio | 39.44 | 24 |
| Length between perpendiculars, LPP [m] | 320.0 | 192.0 |
| Breadth, B [m] | 58.0 | 36.0 |
| Draft, T [m] | 20.8 | 13.0 |
| Block coefficient, CB | 0.8098 | 0.8539 |
| Propeller diameter, D [m] | 9.86 | 6.00 |
| Number of blades | 4 | 4 |
| Target Ship | ||||||
|---|---|---|---|---|---|---|
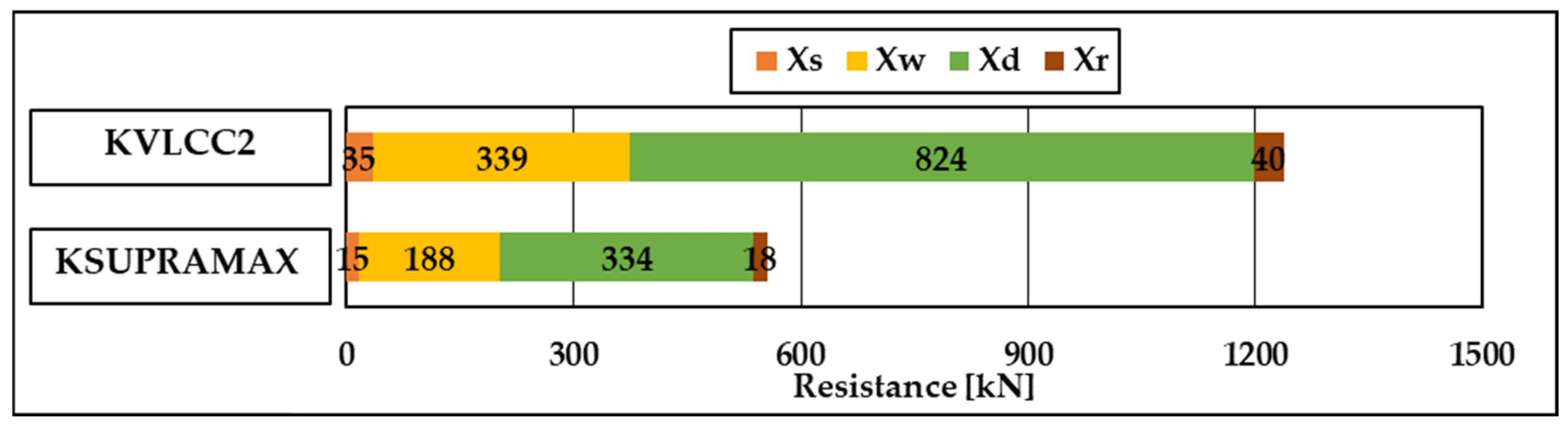
| KVLCC2 | 35 | 339 | 824 | 40 | 1238 | 34.3 |
| KSUPRAMAX | 15 | 188 | 334 | 18 | 555 | 35.3 |
| KVLCC2 | KSUPRAMAX | |
|---|---|---|
| Draft | Design draft * | Scantling draft |
| Speed | 0 (Bollard), 2–14 knots (Interval: 1 knot) | |
| Propeller rotation rate | 2–9 rps (Interval: 1 rps) | 1.5–12 rps (Interval: 1.5 rps) |
| Target Ship | RPS | Target Ship | RPS | ||
|---|---|---|---|---|---|
| KVLCC2 | 16 | KSUPAMAX | 17 | ||
| 9 | 12 | ||||
| 7 | 9 | ||||
| 5 | 7 | ||||
| 3 | 5 | ||||
| 2 | 3 |
| Target Ship | US [knots] | UM [m/s] | RPS |
|---|---|---|---|
| KVLCC2 | 2, 4, 6, 8 | 0.164, 0.328, 0.498, 0.655 | 3, 6, 9 |
| KSUPAMAX | 0.210, 0.420, 0.630, 0.840 | 3, 7.5, 12 |
| Target Ship | Guideline | OLT | Regression | |
|---|---|---|---|---|
| Wake fraction, WS | KVLCC2 | 0.150 | 0.268 | 0.252 |
| KSUPRAMAX | 0.246 | 0.252 | ||
| Thrust deduction factor, t | KVLCC2 | 0.100 | 0.075 | 0.081 |
| KSUPRAMAX | 0.074 | 0.079 |
| Item | [Unit] | Guidelines | OLT | Diff. [%] | Regression | Diff. [%] |
|---|---|---|---|---|---|---|
| EHP | [kW] | 1274 | 1273 | 1273 | ||
| w | [−] | 0.150 | 0.268 | 0.252 | ||
| T | [−] | 0.100 | 0.075 | 0.081 | ||
| J | [−] | 0.123 | 0.109 | 0.111 | ||
| [−] | 0.193 | 0.171 | 0.174 | |||
| [−] | 1.059 | 1.264 | 1.229 | |||
| [−] | 1.000 | 1.000 | 1.000 | |||
| [−] | 0.205 | 0.216 | 0.214 | |||
| RPM | [rev/min] | 43.1 | 42.2 | −2.2 | 42.4 | −1.6 |
| T | [kN] | 1375 | 1337 | −2.8 | 1346 | −2.1 |
| [kN−m] | 1391 | 1347 | −3.2 | 1356 | −2.5 | |
| [kW] | 6282 | 5949 | −5.3 | 6017 | −4.2 |
| Item | [Unit] | Guidelines | OLT | Diff. [%] | Regression | Diff. [%] |
|---|---|---|---|---|---|---|
| EHP | [kW] | 571 | 571 | 571 | ||
| w | [−] | 0.150 | 0.246 | 0.252 | ||
| t | [−] | 0.100 | 0.074 | 0.079 | ||
| J | [−] | 0.114 | 0.103 | 0.102 | ||
| [−] | 0.171 | 0.155 | 0.153 | |||
| [−] | 1.059 | 1.228 | 1.231 | |||
| [−] | 1.000 | 1.000 | 1.000 | |||
| [−] | 0.181 | 0.190 | 0.189 | |||
| RPM | [rev/min] | 76.6 | 75.0 | −2.1 | 75.2 | −1.8 |
| T | [kN] | 617 | 599 | −2.9 | 602 | −2.4 |
| [kN−m] | 398 | 386 | −3.0 | 388 | −2.5 | |
| [kW] | 3191 | 3031 | −5.0 | 3054 | −4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Hwang, S.; Lee, Y.-Y.; Jin, W.-S.; Kim, M.-C. Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions. J. Mar. Sci. Eng. 2025, 13, 595. https://doi.org/10.3390/jmse13030595
Lee J-H, Hwang S, Lee Y-Y, Jin W-S, Kim M-C. Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions. Journal of Marine Science and Engineering. 2025; 13(3):595. https://doi.org/10.3390/jmse13030595
Chicago/Turabian StyleLee, Joon-Hyoung, Seunghyun Hwang, Young-Yeon Lee, Woo-Seok Jin, and Moon-Chan Kim. 2025. "Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions" Journal of Marine Science and Engineering 13, no. 3: 595. https://doi.org/10.3390/jmse13030595
APA StyleLee, J.-H., Hwang, S., Lee, Y.-Y., Jin, W.-S., & Kim, M.-C. (2025). Self-Propulsion Factors for Minimum Propulsion Power Assessment in Adverse Conditions. Journal of Marine Science and Engineering, 13(3), 595. https://doi.org/10.3390/jmse13030595







