Abstract
In ship navigation, determining a safe and economic path from start to destination under dynamic and complex environment is essential, but the traditional algorithms of current research are inefficient. Therefore, a novel differential evolution deep reinforcement learning algorithm (DEDRL) is proposed to address problems, which are composed of local path planning and global path planning. The Deep Q-Network is utilized to search the best path in target ship and multiple-obstacles scenarios. Furthermore, differential evolution and course-punishing reward mechanism are introduced to optimize and constrain the detected path length as short as possible. Quaternion ship domain and COLREGs are involved to construct a dynamic collision risk detection model. Compared with other traditional and reinforcement learning algorithms, the experimental results demonstrate that the DEDRL algorithm achieved the best global path length with 28.4539 n miles, and also performed the best results in all scenarios of local path planning. Overall, the DEDRL algorithm is a reliable and robust algorithm for ship navigation, and it also provides an efficient solution for ship collision avoidance.
1. Introduction
Maritime transportation has long been the primary mode of international trade, supporting 90% of global trade [1]. In 2022, the global fleet grew by 3.2%, culminating in 105,493 ships (each over 100 tons) as of January 2023, with a total deadweight tonnage of 2.27 billion [1]. However, this substantial volume of maritime transport has led to increased ship density, posing significant navigation challenges, resulting in ship collision avoidance being an imperative task for navigation safety at sea [2]. The rise of intelligent ships has underscored the critical importance of ship collision avoidance in ensuring maritime safety, alongside various technical complexities [3]. Research on ship collision avoidance emphasizes both intelligent decision-making and path planning. The problem of path planning is categorized into local and global path planning [4]. Intelligent decision-making for ship collision avoidance imitates the processes of a seasoned crew by perception, cognition, and decision-making [5].
Traditional path planning algorithms, such as sampling, searching, and optimizing algorithms, are widely used for solving ship collision avoidance problems [6]. Gu et al. developed a novel RRT algorithm that merges automatic identification system information with the Douglas–Peucker technique, thereby enhancing ship path planning efficiency [7]. By incorporating maritime navigation regulations, He et al. formulated a dynamic collision avoidance path planning algorithm, leveraging the A-star algorithm for its design [8]. Xue proposed a sine cosine particle swarm optimization method that is quasi-reflection-based for the purpose of ship grounding avoidance [9]. Furthermore, some researchers studied hybrid traditional algorithms for better performance. Sui et al. created a bi-layer hybrid algorithm, which melds the particle swarm optimization, ant colony optimization, and A-star algorithms, thereby achieving a path that is not only collision-free but also shorter and safer [10]. However, traditional path planning algorithms face considerable challenges due to their slow convergence rates, excessive number of turning points, and the production of non-smooth paths. These inherent issues complicate the process and necessitate further refinement [11].
In the realm of maritime applications, recent years have seen a significant increase in studies that utilize techniques from machine learning, with a special focus on deep reinforcement learning (DRL), as well as other methods of reinforcement learning [12]. Yang et al. enhanced the experience replay and parameter update processes of the actor–critic algorithm, applying it to collision avoidance in complex marine environments [13]. Chen et al. proposed a Q-learning-based adaptive method for tuning active disturbance rejection control parameters in ship course control [14]. Guan et al. proposed an intelligent decision-making system based on an improved proximal policy optimization algorithm for ships navigating and avoiding collisions [15]. However, there are some weakness still remaining in these methods, like the problem of it being easy to fall into local optimum, long training time, and discrete motion space [16].
This paper proposes a novel differential evolution deep reinforcement learning (DEDRL) algorithm to address the aforementioned challenges. The DE algorithm is newly integrated into the realms of DRL and ship collision avoidance, where it is combined with Deep Q-Network (DQN) for global path planning and optimization. Specifically, the DQN detects and records nodes in each episode, subsequently returning the path that maximizes the reward upon completion. The DE algorithm is then employed to refine the returned path, rendering it shorter and more efficient. In the context of dynamic multi-ship scenarios for local path planning, the DQN utilizes the proposed Course-Punishing Reward Mechanism (CPRM) within the agent’s reward function, action space, and state space, taking into account the course angle and continuous position. Experimental results demonstrate that DEDRL outperforms other algorithms, achieving a distance of 28.4539 n miles in ship collision avoidance. Furthermore, this paper addresses the existing research gap in heuristic hybrid models within this field. And the primary contributions are as follows:
- The DQN is utilized to search for paths in global path planning. Subsequently, the DE algorithm is introduced to optimize and smooth the detected path, ultimately achieving a shorter global path length through the integration of the DE and DQN algorithms.
- A CPRM is proposed for local path planning, considering the course angle and position. This model is integrated with DQN to restrict the agent, enabling it to execute fewer steps and efficiently reach its destination in dynamic multi-ship local path planning.
- DEDRL is evaluated against six other algorithms, including various reinforcement learning and intelligent algorithms, to assess its effectiveness, showcasing superior performance across all comparisons.
This paper is organized as follows: Section 2 describes the DQN, DE, COLREGs, and dynamical collision risk detection. Section 3 introduces the proposed algorithm in detail. The experimental results and analysis are described in Section 4. In Section 5, the ablation experiment and analysis of the proposed algorithm are carried out. Finally, Section 6 concludes the paper.
2. Materials and Methods
2.1. Global and Local Path Planning
Path planning can be divided into global and local path planning based on the mastery of environmental information [17]. Global path planning requires the mobile robot to create and understand a comprehensive map model, utilizing search algorithms to find the optimal or suboptimal path. This path then directs the robot safely to the target location in the real environment [18]. On the contrary, local path planning offers greater flexibility, but its main drawback is that it may result in a path that is only locally optimal, without ensuring global optimality. In some cases, the target point may even be unreachable [19].
Global path planning involves designing a safe, economical, and collision-free path from the starting point to the destination, based on fixed geographical information, route data, and obstacle locations [20]. Chen et al. proposed a collision risk-integrated FM2 algorithm for planning the global path of autonomous ships, taking into account both environmental obstacles and vessel velocity [21]. Hu et al. devised a ship path planning algorithm using heuristic adaptive rapid search technology to heuristically and adaptively plan global navigation paths [22]. Huang et al. introduced a self-adaptive neighborhood search A-star algorithm and utilized it for global path planning of mobile robots on a known static map [23].
Local path planning involves a robot operating in a partially or completely unknown environment, focusing on immediate responses to dynamic obstacles, such as other vessels and weather changes, while utilizing real-time environmental information [24,25,26]. Zhang et al. proposed a path planning technique using a soft actor–critic algorithm to address the local path planning problem of autonomous underwater vehicles in unknown, complex marine environments [27]. Xin et al. proposed a solution named Color to enhance the training efficiency and generalization capability of DRL in local path planning [28]. Wang et al. developed a risk assessment and mitigation-based local path planning algorithm that uses predicted trajectories of surrounding vehicles [29].
In the field of path planning, it is crucial to develop an integrated system that merges strategies for global path planning, which focus on identifying a globally optimal trajectory and providing the foundational framework, with techniques for local path planning [30]. The latter are designed to enable real-time obstacle avoidance and navigation as supplement.
2.2. Deep Q-Network
In the last decade, Mnih V. et al. developed an advanced DRL algorithm known as DQN, which integrates reinforcement learning with a specific type of artificial neural network called deep neural networks [31]. Owing to its ability to develop a broad range of competencies across diverse challenging tasks, DQN has been effectively applied in various fields. For example, Zhao et al. introduced a data-driven BC-MP-DQN algorithm for energy-constrained multi-period production scheduling in the dietary supplement manufacturing sector [32]. Additionally, Li et al. proposed a DQN-based content caching strategy aimed at improving cache hit ratios, reducing transmission delays, and alleviating return link loads in content caching problems [33]. Furthermore, DQN has been applied to coordinated intelligent control problems [34], stock market forecasting [35], and long-term depolarized interactions [36], among others.
Recent advances in deep neural networks, which utilize multiple layers of nodes to create progressively more abstract representations of data, have enabled artificial neural networks to learn concepts such as object categories directly from raw sensory data. The DQN employs a deep convolutional network, utilizing hierarchical layers of convolutional filters to mimic the effects of receptive fields. This approach effectively exploits local spatial correlations present in images and enhances robustness to natural transformations such as changes in viewpoint or scale.
The DQN framework addresses tasks where an agent interacts with an environment through sequences of observations, actions, and rewards. The agent’s objective is to select actions that maximize cumulative future rewards. The DQN approximates the optimal action–value function through the employment of a deep convolutional neural network.
where the maximum sum of discounted rewards, denoted as , is determined by the discount factor at each time-step t. This sum represents the cumulative rewards achievable under a behavior policy , subsequent to observing a state s and executing an action a.
A deep convolutional neural network is utilized within the DQN framework to estimate the value function . For the purpose of implementing experience replay, the sequence of experiences encountered by the agent at each time-step t is stored within the dataset . Subsequently, the DQN conducts Q-learning updates using samples drawn randomly from stored samples. The update rule at iteration i is governed by the following loss function:
where the parameters are the parameters of the target network utilized for computing the target at iteration i, while represent the Q-network parameters at iteration i. The target network parameters, , are updated synchronously with the Q-network parameters () every C steps, remaining constant during the intervals between updates. The denotes the discount factor that governs the agent horizon.
2.3. Differential Evolution
DE, as a population-based optimization method proposed by Storn [37], is renowned for its simplicity and ease of coding, which has led to its widespread use in solving various optimization tasks including multi-objective optimization problems [38], nonlinear equation systems [39], and multimodal optimization issues [40]. The steps involved in the DE algorithm are outlined as follows:
- (1)
- Initialization: The population is initialized at random within the search domain, adhering to the following formula:where the j-dimension is indicated by the subscript j, while the current individual is referenced by the subscript i. And is a random scalar that falls within the interval [0, 1]. Additionally, and are used to signify the upper and lower bounds, respectively.
- (2)
- Mutation: The DE algorithm involves the generation of a mutant vector for each individual in the current population. This process utilizes a prevalent mutation operators, which is as follows:“DE/rand/1”:where F denotes a scaling factor that varies between 0 and 1, while , , and represent distinct individuals that are randomly selected from the population.
- (3)
- Crossover: The trial vector is produced from the mutated vector according to the following equation:where the crossover rate, denoted as , falls within the interval [0, 1]. is a random number from the range [0, 1], and is a randomly selected index from the set [1, 2, …, D].
- (4)
- Selection: During the selection process, the target vector is potentially supplanted by the trial vector. This occurs when the trial vector fitness surpasses that of the target, adhering to a greedy approach for vector replacement.
2.4. COLREGs and Ship Maneuverability Restriction
2.4.1. COLREGs
The Convention on the International Regulations for Preventing Collisions at Sea (COLREGs), adopted in 1972 and entering into force in July 1977, has been accepted by numerous states [41]. Compliance with COLREGs is essential when addressing multi-ship collision avoidance. The COLREGs dictate that the vessel responsible for giving way must execute evasive maneuvers when sailing vessels are heading towards a potential collision [42].
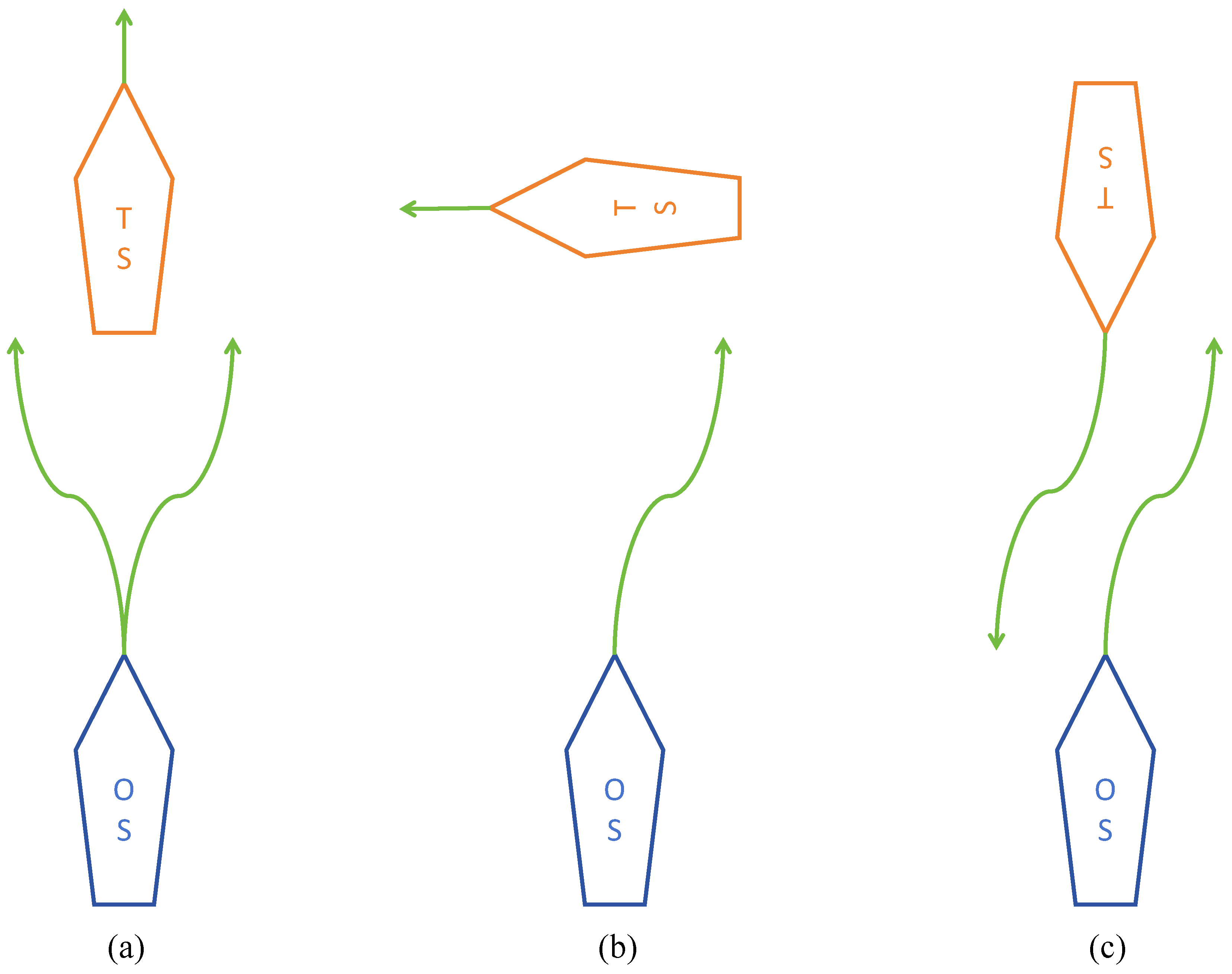
Particularly, this paper focuses on Rules 13–15 of the COLREGs [43], which primarily address head-on, overtaking, and crossing situations, as depicted in Figure 1.
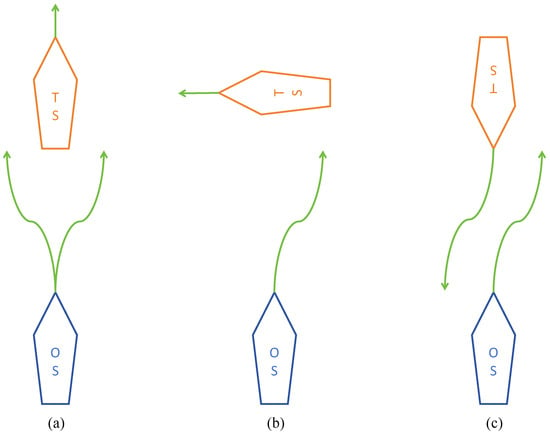
Figure 1.
The directions for avoiding ship collisions in various situations: (a) Overtaking, (b) Crossing, and (c) Head-on.
The detail description of three scenarios are as follows:
- Overtaking: To avoid a potential collision, the Own Ship (OS) is required to modify its heading to starboard or port when it finds itself in an overtaking scenario. This occurs when the OS is following the Target Ship (TS) directly from behind, a situation that is deemed overtaking if the approach is from a direction more than 22.5 degrees abaft the TS’s beam.
- Crossing: In cases where two power-driven vessels are at risk of collision due to their crossing paths, the vessel with the other on her starboard side is responsible for yielding way. The OS must adjust its course towards starboard when it encounters another vessel on its starboard side during navigation. This maneuver is necessary in a scenario deemed a starboard-side crossing. Furthermore, this vessel should strive to avoid crossing ahead of the other vessel whenever the circumstances permit.
- Head-on: A head-on scenario is identified when the OS and the TS are on courses that are directly opposite or nearly so, resulting in one vessel being observed ahead or nearly ahead of the other. To avert a collision, it is necessary for both the OS and TS to alter their courses to starboard, ensuring that each vessel passes on the port side of the other.
2.4.2. Ship Maneuverability Restriction
For a ship to navigate successfully along a planned route, the path must be designed to align with the ship maneuvering characteristics and to effectively assess collision avoidance. Failure to do so may prevent the ship from adhering to the intended course. Therefore, it is crucial to incorporate turning angle limitations based on the distance between adjacent path nodes. This constraint minimizes turning angles to ensure the ship capability to stay on course.
The path planning algorithm incorporates these maneuverability constraints. It selects potential path nodes where the turning angle remains within a specified range. This approach ensures that the turning angles throughout the entire path are appropriate, enabling the ship to follow the planned route within the bounds of its maneuverability limitations. The approach restricts the maximum turning angle between nodes to 10 degrees, and the simulation findings from the motion model [42] suggest a distance step of 0.2 n miles.
2.5. Dynamical Collision Risk Detection
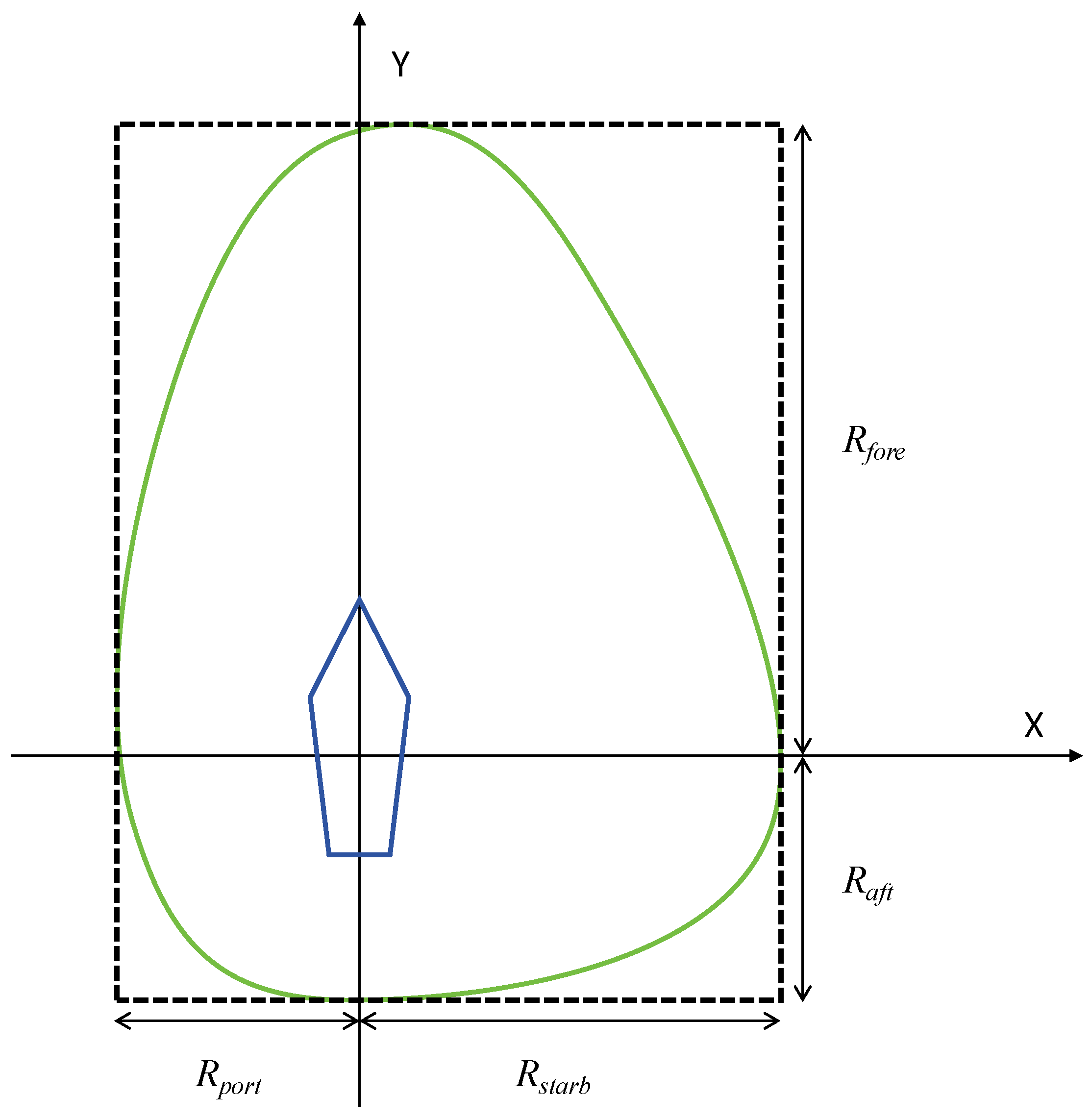
A variety of elements, such as the size and speed of the vessel, visibility conditions, traffic density, and maneuverability constraints, determine the configuration and dimensions of a ship’s navigational domain [44]. This study introduces a quaternion-based model of the ship domain to assess dynamic collision risks, taking into account the COLREGs and utilizing distinct safety radii for various bearing angles. The quaternion ship domain is depicted in Figure 2, with the parameters described as follows:
where the parameter L represents the length, and v denotes the speed. The ship maneuverability is influenced by the gain coefficients and , which are specific to the advance and tactical diameters, respectively. These parameters are calculated as follows:
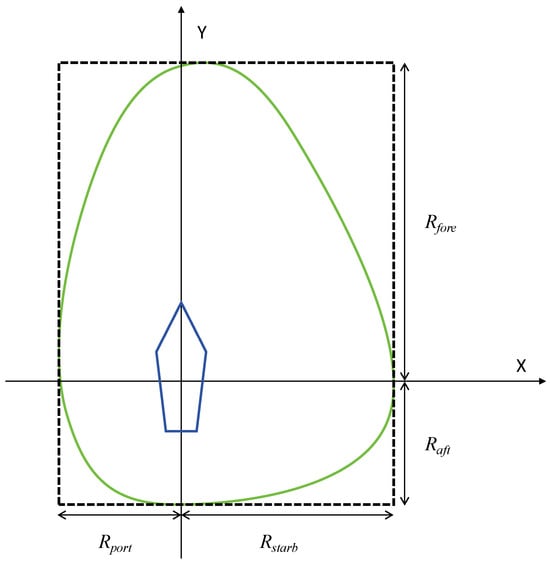
Figure 2.
The diagram of quaternion ship domain.
In contrast to other ship domains, the quaternion ship domain provides navigators with enhanced reliability and versatility in decision-making. This domain is defined by a quaternion consisting of four radii (fore, aft, starboard, and port), which encapsulate various factors influencing the domain, such as the ship speed, course, and maneuverability. Furthermore, the quaternion ship domain shape is characterized by an additional parameter that enhances flexibility. This parameter allows the ship boundary to be adaptable, taking on either linear or nonlinear forms, as well as varying in width from thin to broad.
3. Proposed DEDRL Algorithm
To address the challenge of finding an economically viable and safe path from the start to the destination, this paper proposes a DEDRL algorithm that integrates deep reinforcement learning with differential evolution. First, the DQN is employed to identify the shortest global path during global path planning. Next, the DE algorithm is introduced to refine the obtained global path. Finally, a course-punishing reward mechanism is proposed to complement the DQN, enabling the detection of the shortest paths in three dynamic multi-ship scenarios for local path planning.
3.1. Global Path Planning Utilizing DQN and DE
Global path planning involves an integration of DQN and DE to design an effective and optimal path for a ship sailing from the start node to the end node. In the global map, ten static obstacles of various irregular shapes are placed in the water area between the start and destination. Initially, the DQN is employed to identify available paths and prevent collisions with static obstacles during navigation. However, the detected paths are often convoluted and inefficient. Consequently, DE is introduced to refine the path by optimizing node combinations. Ultimately, the DEDRL algorithm yields an effective and viable global path.
3.1.1. State Space
In global path planning, the state of the agent consists of two-dimensional coordinates, x and y. These coordinates characterize the agent’s state in terms of achieving a available point, reaching a destination, or encountering a collision. The state space is defined as follows:
where S is the set of possible states, x is the horizontal coordinate of the agent, and y is the vertical coordinate of the agent.
3.1.2. Action Space
The action space comprises all possible actions available to the agent. And the action space is discretized into five distinct directions representing five discrete actions of the agent: up, upper left, upper right, right, lower right.
where A is the set of possible agent actions, a is the action executed by the agent, and m represents the step length of the agent.
3.1.3. Reward Function
The rewards associated with these actions are consistently negative, promoting the agent to take fewer steps. Furthermore, the reward approaches relative huge number when the agent encounters a ship collision or reaches its destination.
Algorithm 1 details the pseudocode for the global path planning algorithm.
3.2. Local Path Planning with CPRM
Local path planning utilizes DQN to prevent collisions with multiple ships and to navigate around static obstacles, ensuring the vessel adheres to its global route. Meanwhile, the proposed CPRM enables the ship to minimize operations, thereby ensuring an economical path. Furthermore, detailed specifications for DQN and CPRM, including the reward function, state space, and action space, are provided below.
3.2.1. State Space
The agent and environment primarily consist of the ship and obstacle coordinates, the ship course angle, the start point, the destination, and the map boundaries. First, the OS, TS, and static obstacles have coordinates, which enable the calculation of distances between them and the determination of potential collisions. Additionally, the OS is characterized by an additional course angle, allowing the agent to move within a continuous range. If the agent crosses the map boundary, its coordinates will be reset to align with the boundary. Overall, the state space of the agent is composed of three dimensions, defined as follows:
where x is the horizontal coordinate of the agent, y is the vertical coordinate of the agent, and represents the navigating course angle of the agent.
| Algorithm 1: DEDRL (Global path planning) |
 |
3.2.2. Action Space
The actions of the agent are randomly generated from a continuous set of actions. The agent moves a specified step length while shifting towards a randomly selected angle. To ensure that the ship does not deviate from the global path, the randomly selected angle is approximately aligned with the angle from the intended destination to the starting point of local path planning.
where is the angle from start to destination. Therefore, the state of the agent can be observed after taking action.
where is the next state, and is the previous state, while m is the given step length of the agent.
3.2.3. Reward Function
The reward function considers both the efficiency of the path and the ship maneuverability. The agent receives a positive huge reward upon reaching the local destination and a negative enormous reward when colliding with obstacles. Notably, the agent incurs a negative reward based on the chosen angle and the current distance from the destination. This reward mechanism assists the agent in converging towards obstacles while also progressing closer to the destination. Consequently, the agent is encouraged to take fewer steps without colliding and to achieve its objective.
where is the local destination horizon coordinate and is the local destination vertical coordinate.
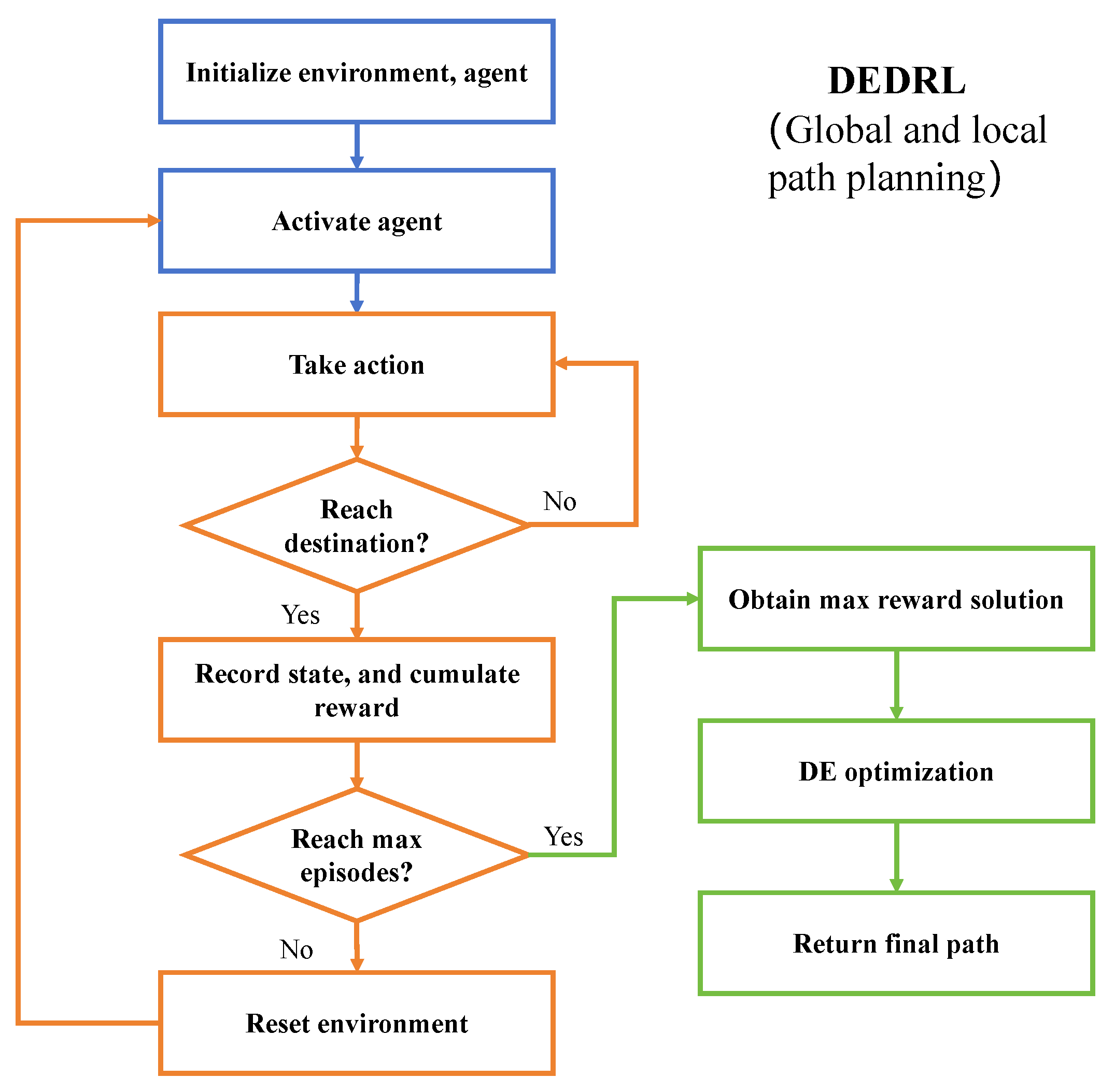
The DEDRL procedure is illustrated in Figure 3 and the pseudocode is presented in Algorithm 2. The blue section represents the normal setting steps, the orange section depicts the DQN execution, and the green section encompasses the DE optimization steps. Initially, the parameters, environment, and agent for DEDRL are initialized. The agent then begins to take actions while executing the ship collision checking program. Upon reaching the destination, the state comprising horizontal and vertical coordinates along with the reward is returned. To optimize the smoothness of the path, the solution with the highest reward is selected, thereby reducing the number of nodes in the path through the application of DE.
| Algorithm 2: DEDRL (Local path planning) |
 |
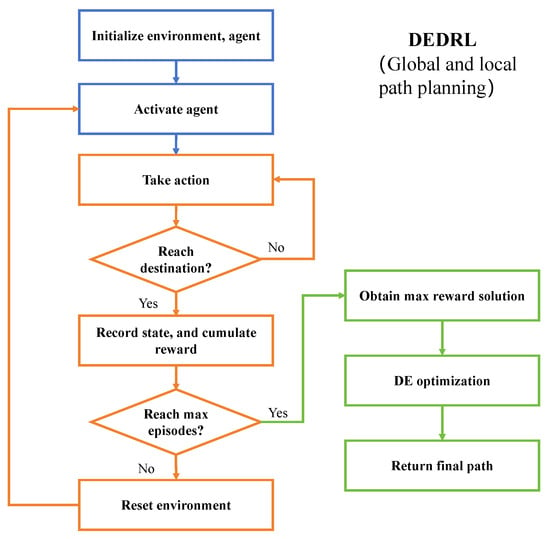
Figure 3.
The flowchart of DEDRL algorithm.
4. Experimental Results
In this experiment, a seabed map is developed using charted depths, while a navigable map is produced by integrating grounding risks. Both grounding and collision risks are mitigated through local and global path planning. The experiments were executed on a computer featuring an Intel i3-12100F CPU, an NVIDIA 1660 Super GPU, 16 GB of RAM, and the experiments were conducted using Python 3.8. All hardware was sourced from China.
4.1. Environment Map Construction
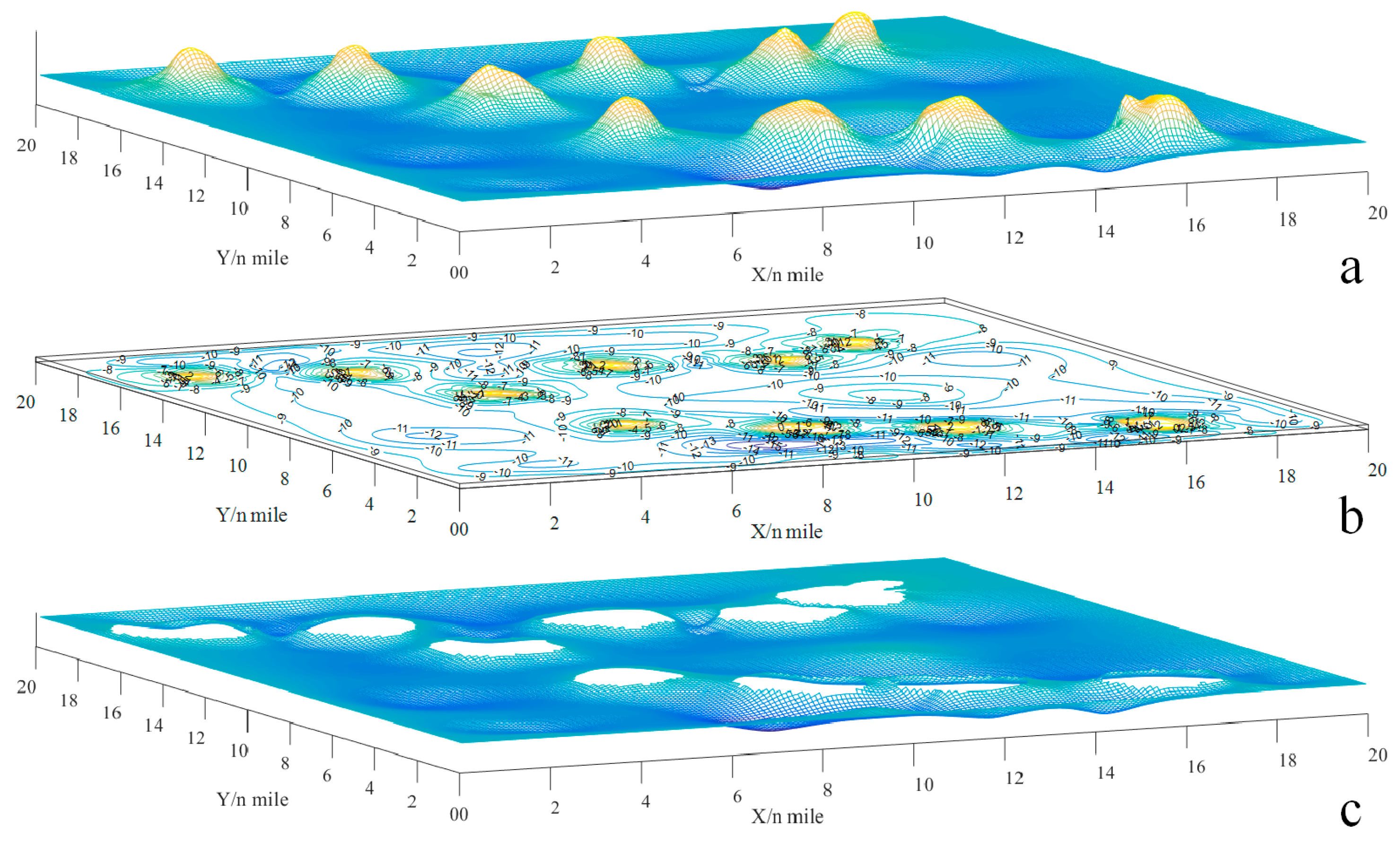
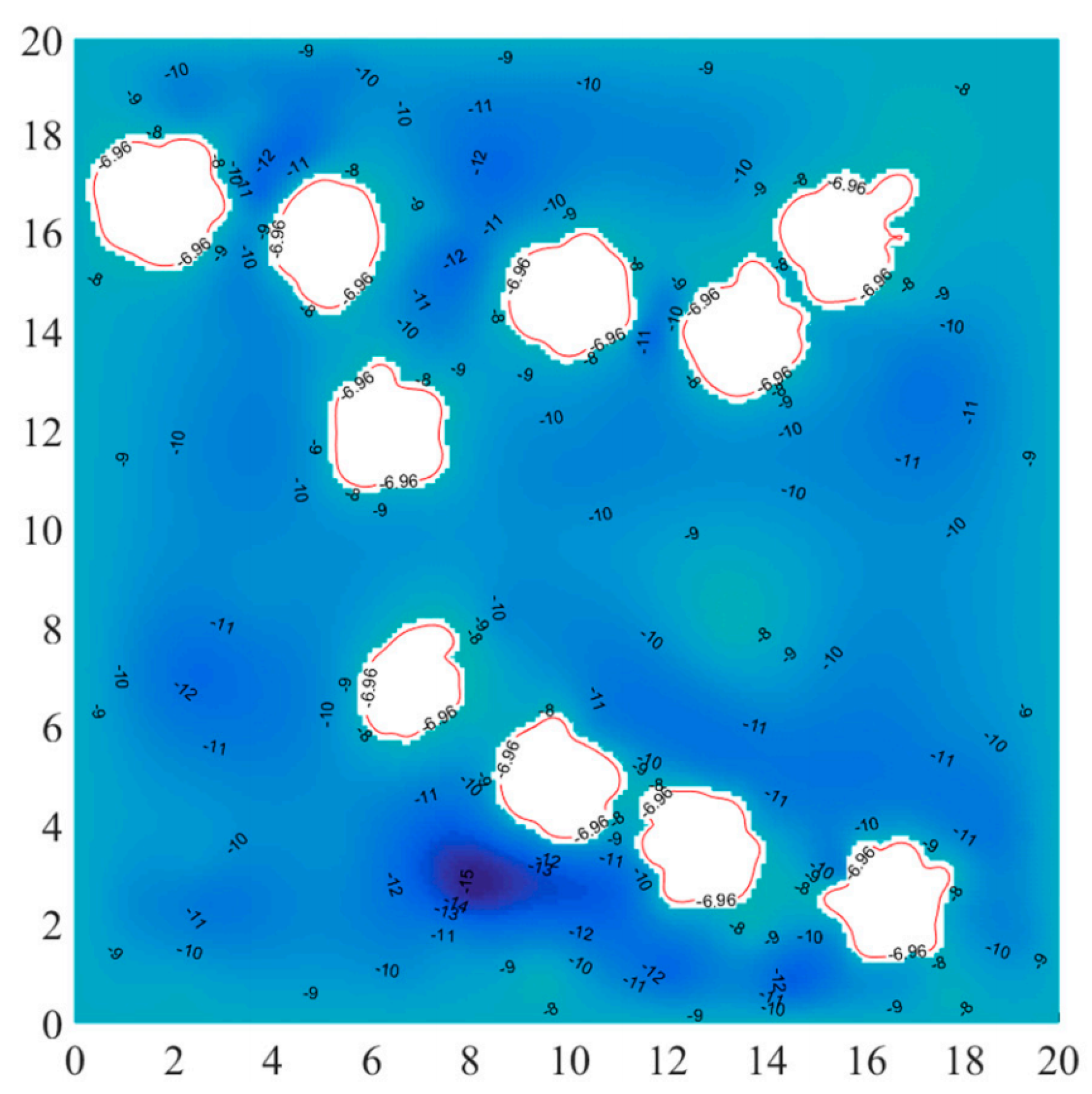
The vessel OS, classified as a general cargo ship, boasts dimensions of 96 m in length and 16.6 m in breadth, with a loaded draft reaching 5.8 m. To ensure safe navigation, the minimum water depth must be at least 6.96 m, as determined by the equations and , where k is the factor for the UKC relative to the draft. A topographic map spanning 20 by 20 n miles, which includes details of water depth, has been created to serve as a comprehensive environmental information resource. To avoid side grounding, the safety distance is maintained at 0.1 n miles, or 185.2 m, which exceeds the ship breadth by a factor of ten. Figure 4a–c provides visual representations: (a) depicts the topographic map, (b) shows the contour map, and (c) highlights the navigable map, taking into account the risks of grounding.
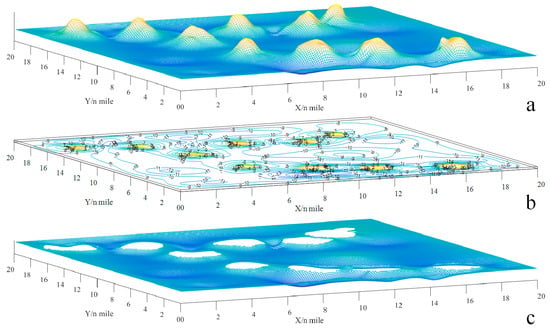
Figure 4.
The schematic of the navigable map: (a) topographic map; (b) contour map; (c) navigable map [42].
Figure 5 illustrates the relationship between minimum water depth and navigable maps, with the red line representing the minimum water depth boundary.
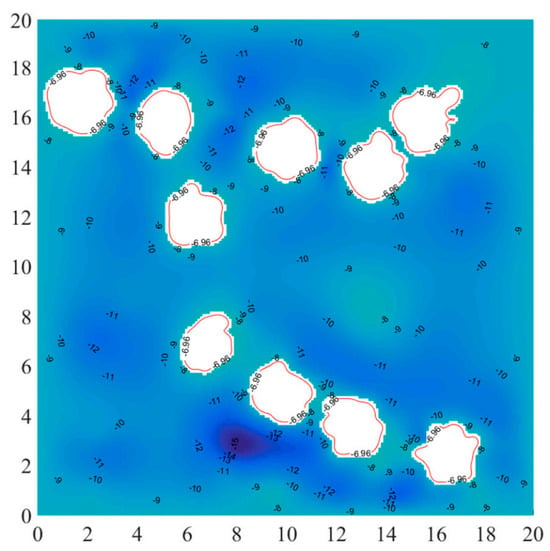
Figure 5.
The navigable map and minimum water depth [42].
In global planning, coordinates (0, 0) and (100, 100) are designated as the start point and destination, respectively, to validate the proposed DEDRL using a navigable map. Subsequently, scenarios involving head-on, overtaking, and crossing encounters between TS and OS are incorporated to assess the performance of collision avoidance decision-making.
4.2. Evaluation Metrics and Parameters Setting
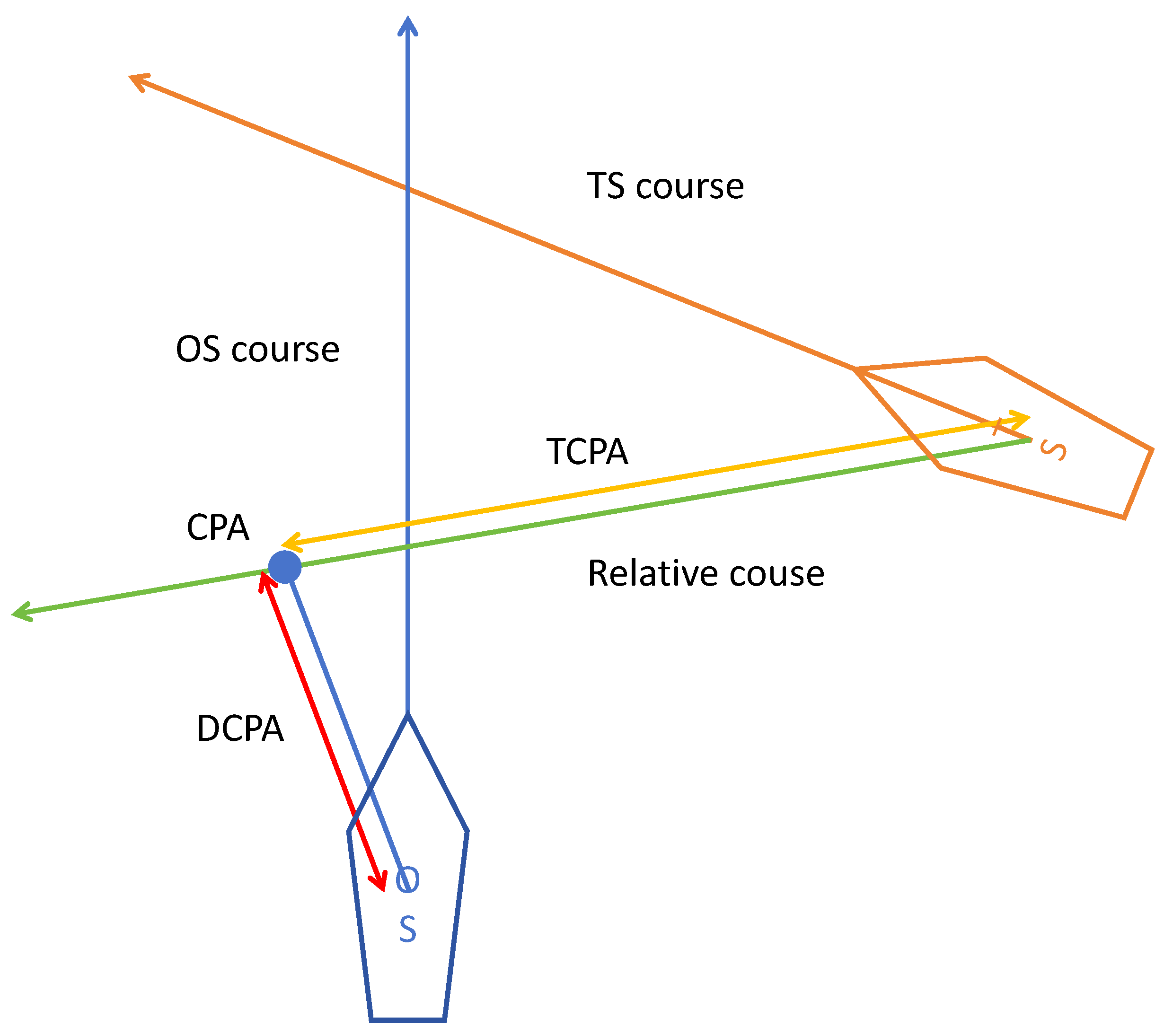
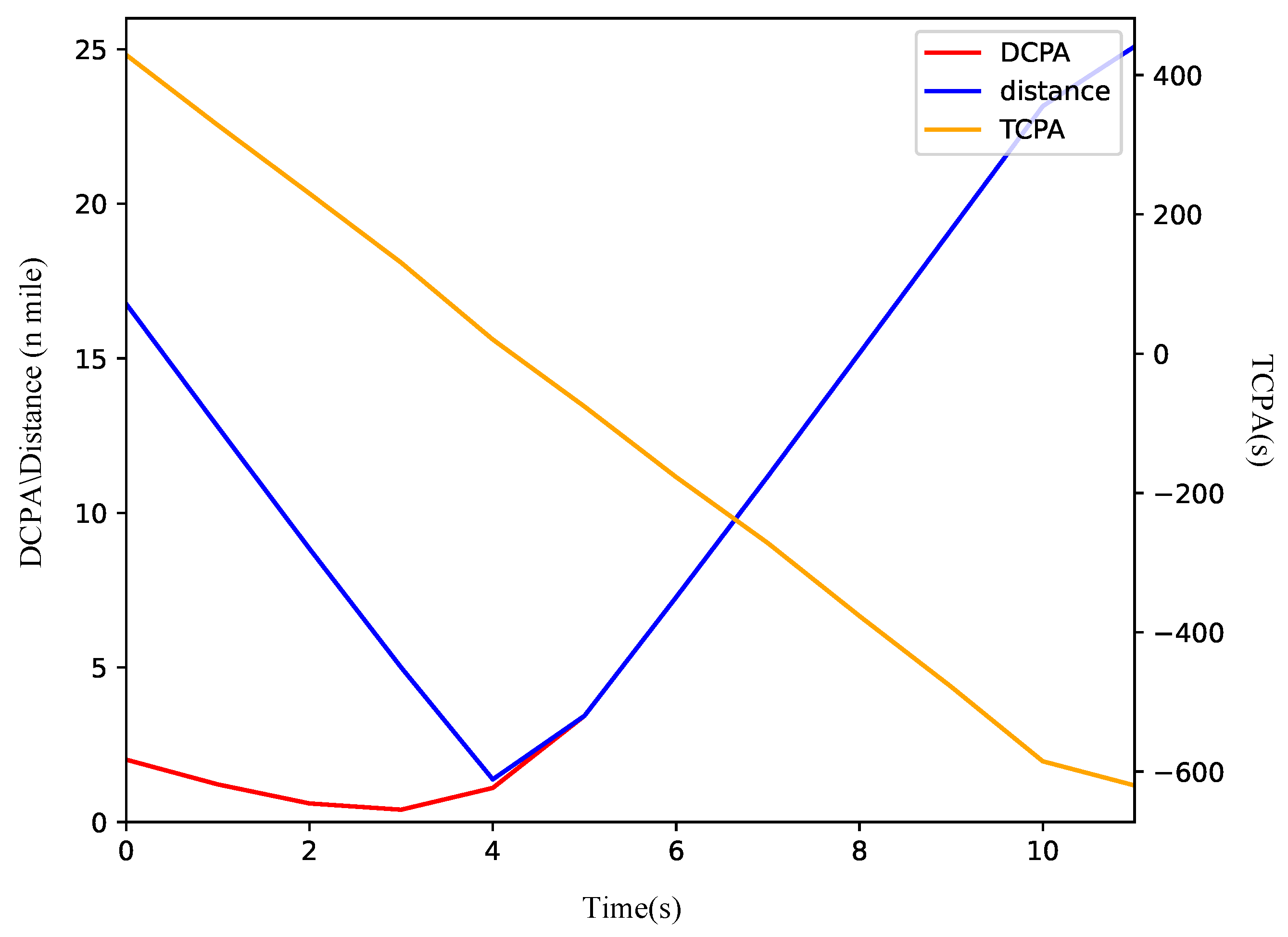
The three most commonly used ship probability risk evaluation metrics, the Closest Point of Approach (CPA), the Time to the Closest Point of Approach (TCPA), and the Distance to the Closest Point of Approach (DCPA), are employed in these research experiments [45]. To compare the performance of different algorithms, total global path length and time consumption in local path planning are utilized as evaluation metrics for the experiments. The schematic diagram of DCPA and TCPA is illustrated in Figure 6.
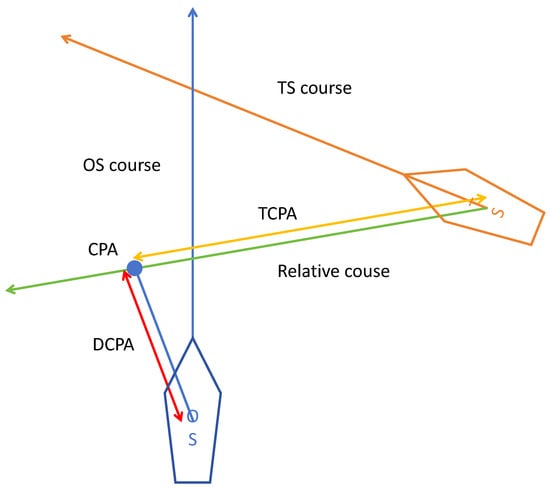
Figure 6.
DCPA and TCPA schematic diagram.
The main agent parameters are as follows: the iterative update value is 8, the maximum number of episodes is 50, the decay factor is 0.5, the batch size is 128, and the replay buffer size is 1000. The environment parameters include a maximum allowed step of 1000 and a threshold distance to the terminal of 10. Detailed parameters are categorized into global and local path planning settings, due to the discrete and continuous states and actions of the agent in the two path planning experiments, respectively. In global path planning, the agent has five actions, as mentioned in Section 3, and the step range is a discrete value of 9. In contrast, for local path planning, the agent has only one action, represented by a random continuous angle, and the step range is set to 3. The initial course angles of the ship are denoted as , where represents the angles from the start node to the end node in the global path, which are divided into two parts: and .
4.3. Algorithms Comparison in Global Path Planning
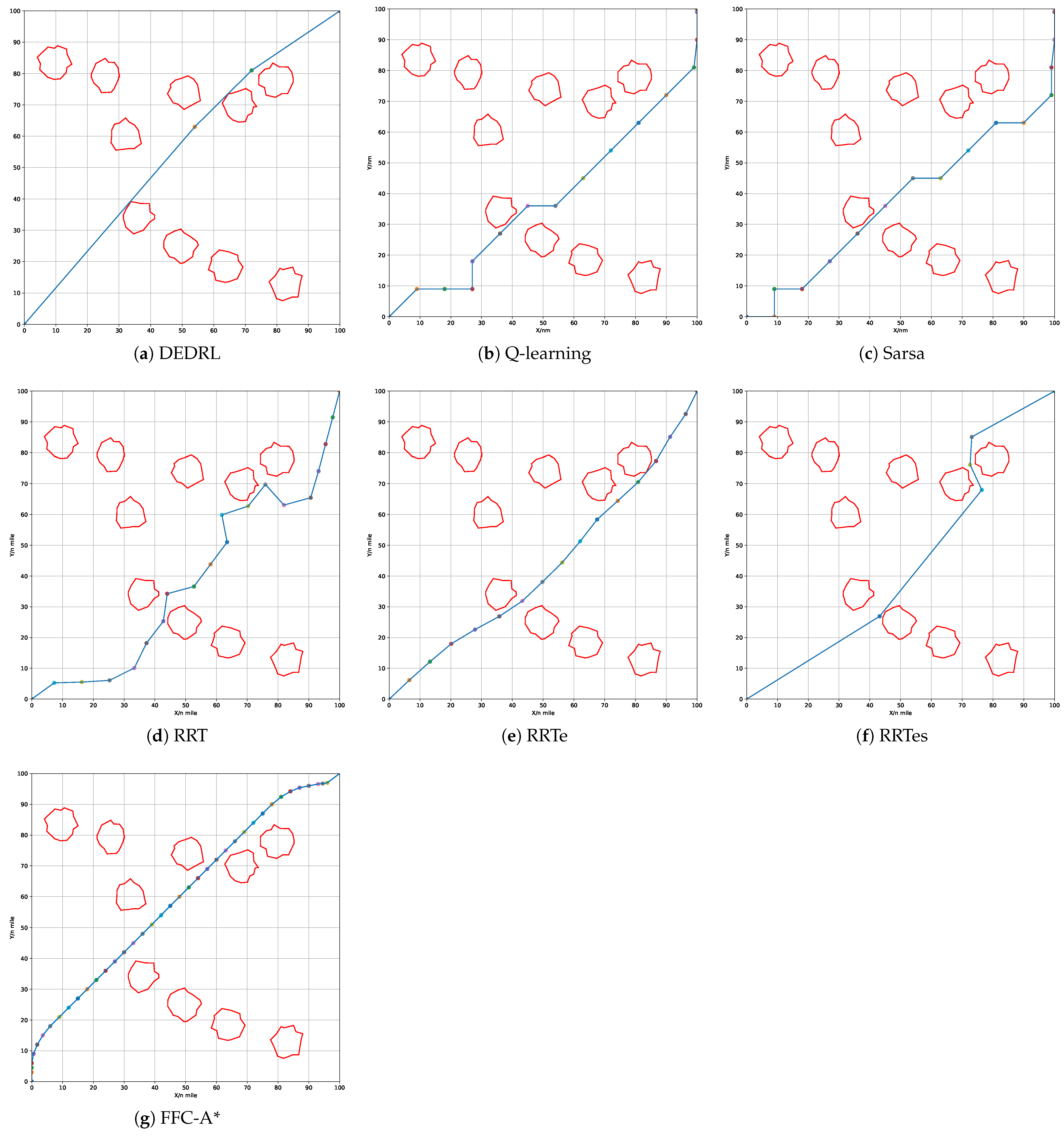
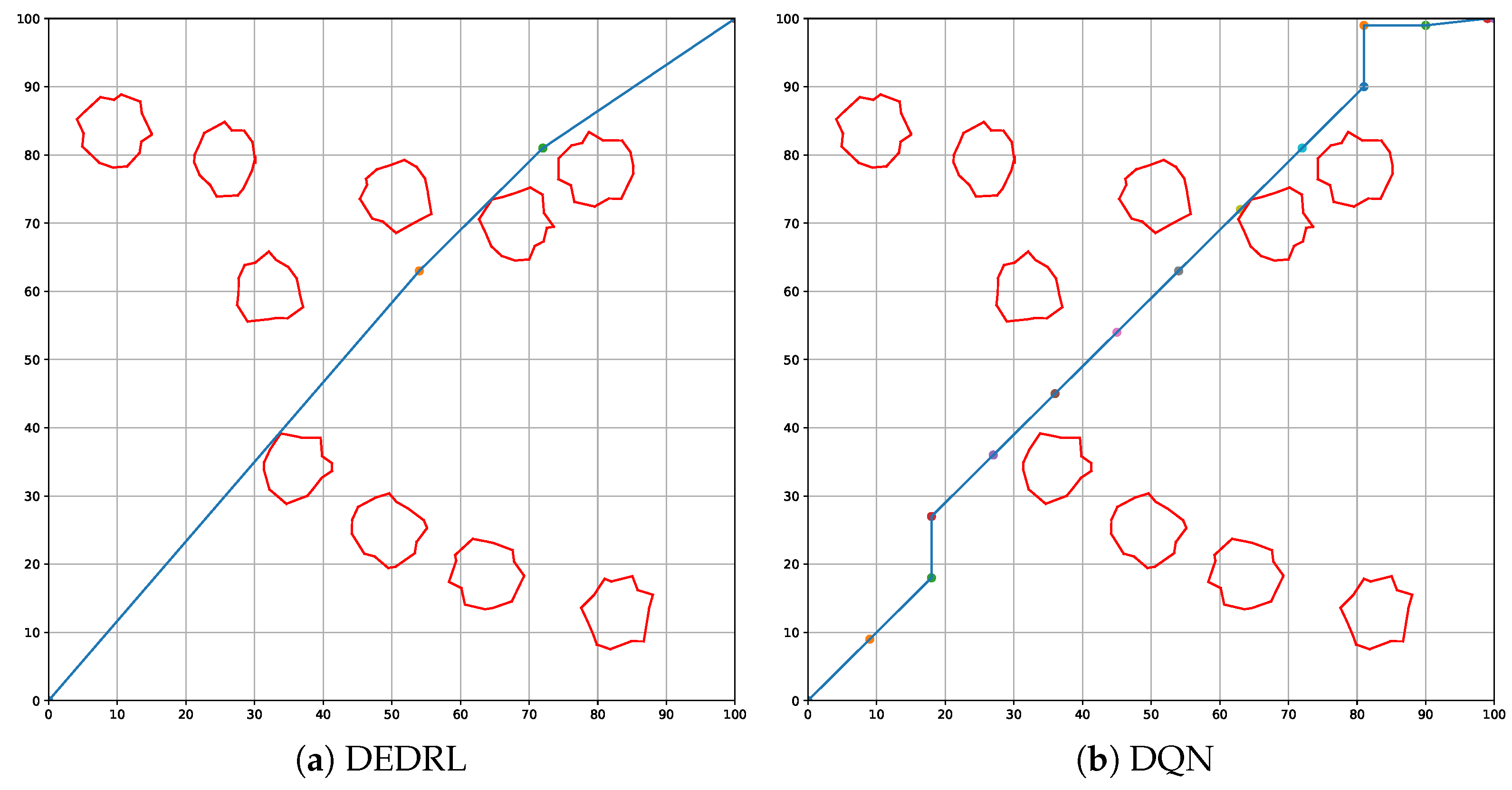
Figure 7 demonstrates that all algorithms effectively identify a available path by accounting for grounding risk and utilizing the navigable map. The red line marks static obstacles, the blue line indicates the global route, and colored circles represent path nodes. The global path planning outcomes for each algorithm: DEDRL, Q-learning, Sarsa, RRT, RRTe, RRTes, and FFC-A*, are presented in Figure 7 (a) through (g), respectively. Notably, DEDRL achieves the shortest path length of 28.4539 n miles, benefiting from effective path detection and the advantages of DE optimization. In contrast, the reinforcement learning algorithms Q-learning and Sarsa yield the longest path lengths of 30.3213 n miles each. The sampling algorithms RRT, RRTe, and RRTes perform better than the aforementioned reinforcement learning algorithms but are outperformed by DEDRL, with medium path lengths of 31.2561, 28.6456, and 29.0754 n miles, respectively. Finally, FFC-A* gains 29.2346 n miles.
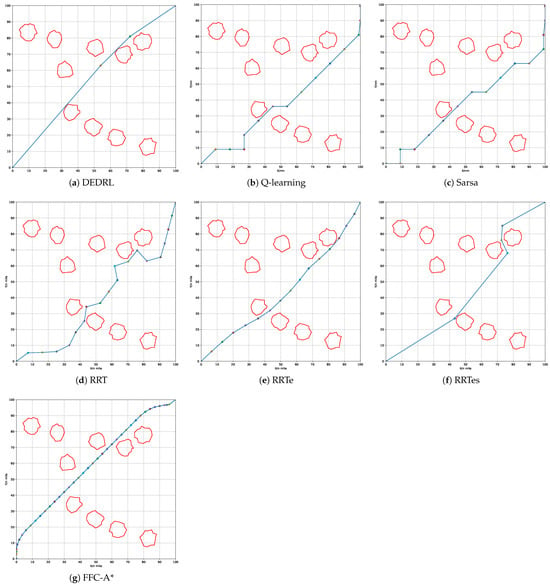
Figure 7.
Compare the performance of different algorithms.
Two experimental metrics, namely time consumption and path length, are illustrated in Table 1. It is worth noting that DEDRL achieves the shortest path of 28.4539 n miles in global path planning. Additionally, the average path length of 28.6943 n miles and a maximum of 28.9354 n miles for DEDRL further demonstrate its robustness and reliability compared to other algorithms. Conversely, traditional reinforcement learning algorithms and sampling algorithms exhibit inferior performance. While RRTe obtains a path length of 28.6456 n miles, slightly less than DEDRL, it still outperforms Q-learning, Sarsa, RRT, RRTes, and FFC-A*, which are around 30 n miles.

Table 1.
Experimental results of different algorithms.
4.4. Algorithms Comparison in Local Path Planning
COLREGs are usually applied in local path planning for collision avoidance and are not involved in global path planning. The experimental figures of local path planning presented below illustrate several key elements: the green line corresponds to the newly generated local path, the red line represents static obstacles, the blue line indicates the global route, and the various colored circles denote local path nodes. Additionally, the black and orange lines represent the ship domains of the TS and OS, respectively. And the exact information of the OS and TS are given in Table 2 as follows:

Table 2.
Parameters of OS and TSs in encounter scenarios.
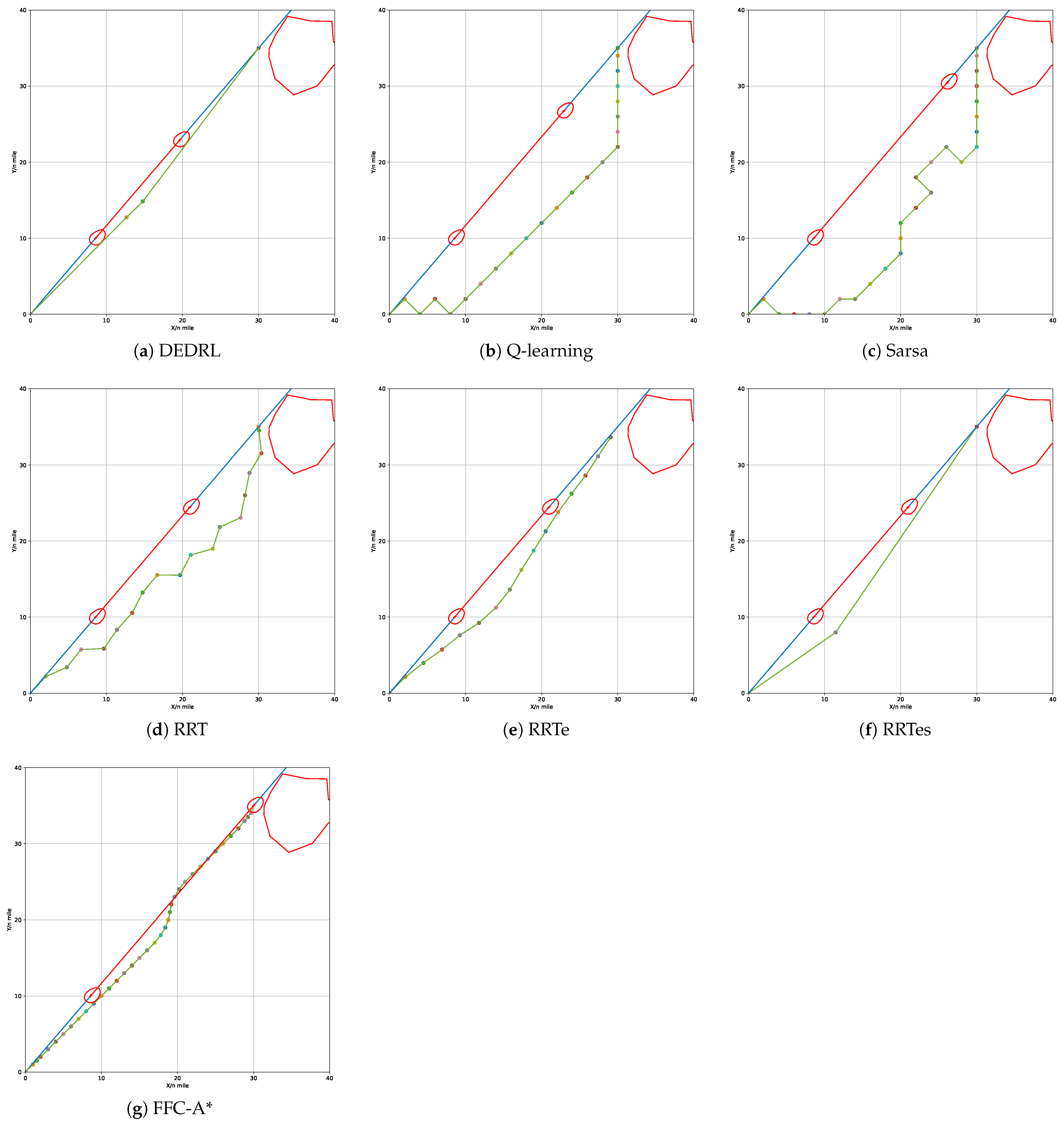
In the overtaking scenario, the OS begins at coordinates (0, 0) and traverses to (30, 35) with a course angle of lean to the global path. The TS departs from coordinates (8.5714, 10) and follows a similar course along the global path but operates at a lower speed. If the OS maintains a constant course angle and speed, a collision with the TS is inevitable in this scenario. According to Rule 13 of the COLREGs, the TS is observable by the OS, which is assumed to take actions to avoid collision as it approaches the TS. The OS is determined to alter its course to the starboard side to avoid a collision. The results of the replanned path generated by all algorithms are illustrated in Figure 8.
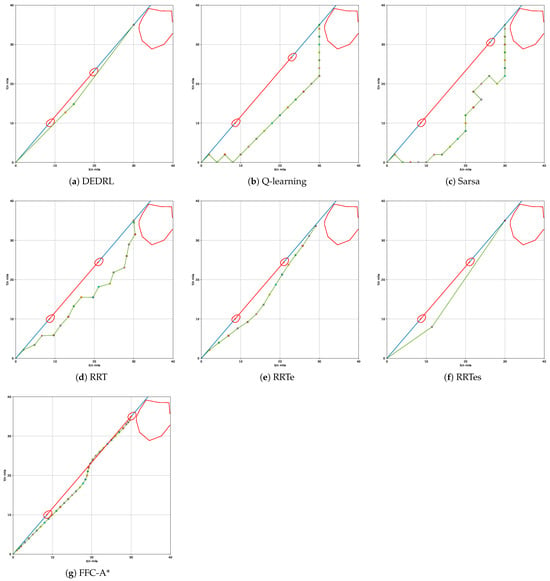
Figure 8.
Performance comparison of different algorithms in overtaking scenario.
The regenerated local path length is illustrated in Table 3 as experimental metrics. It is worth noting that DEDRL achieves the shortest path of 9.2335 n miles in the overtaking scenario, leveraging the advantages of DE optimization and DQN searching capabilities. Additionally, the average path length of 9.2443 n miles and a maximum of 9.2643 n miles for DEDRL further demonstrate its robustness and reliability compared to other algorithms. FFC-A* achieves 9.3373 n miles, making it slightly weaker than DEDRL. Conversely, traditional reinforcement learning algorithms and sampling algorithms exhibit inferior performance. While RRTe achieves a path length of 9.3180 n miles, slightly less than DEDRL, it still outperforms Q-learning, Sarsa, RRT, and RRTes, which have lengths around 12 n miles.

Table 3.
Experimental results of different algorithms in overtaking scenario.
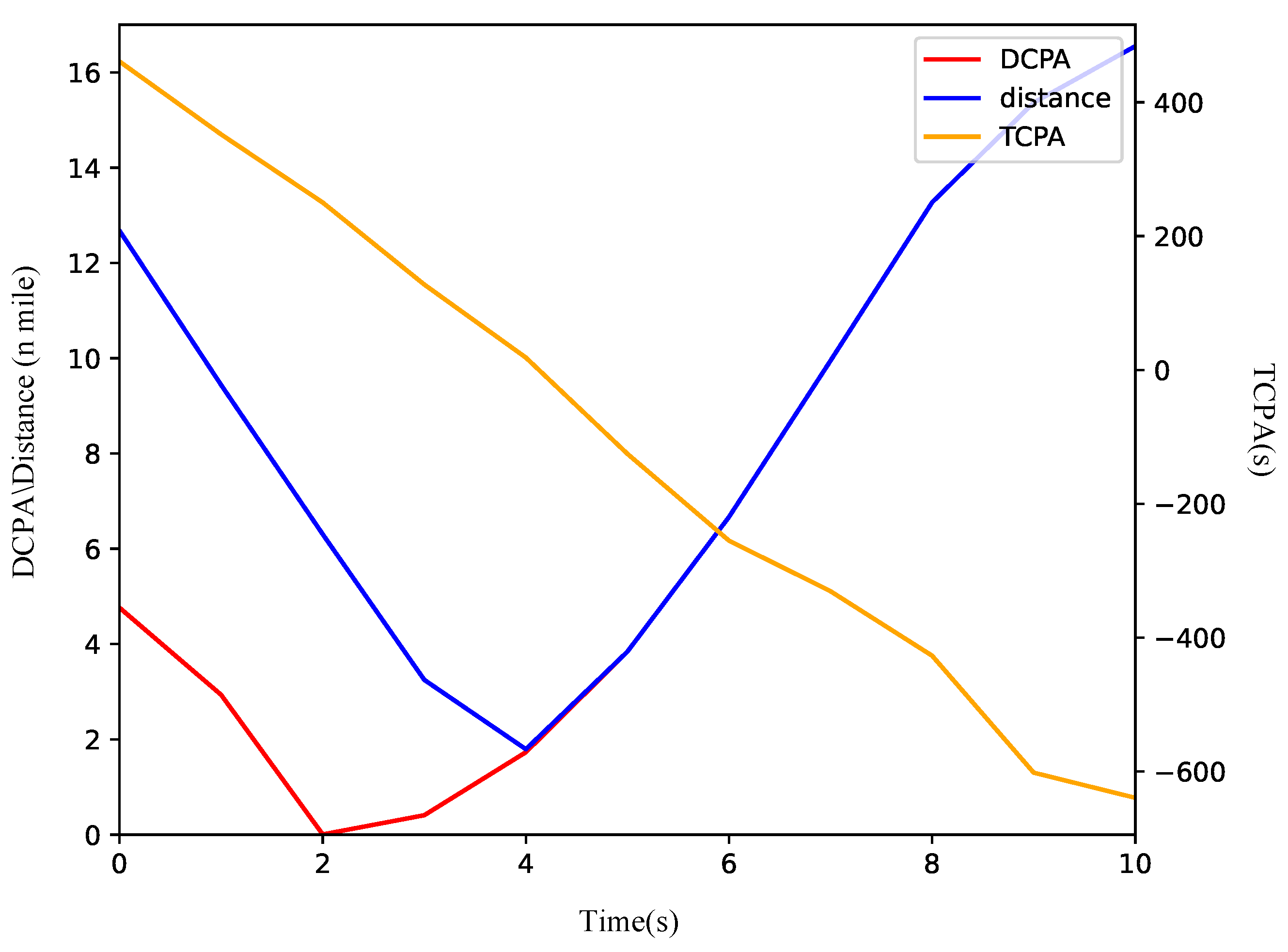
Figure 8a shows that the ship modifies its course to starboard to evade the TS. A review of the COLREGs suggests that either a port or starboard turn is permissible during the overtaking scenario. Initially, the relative bearing of the TS from the OS is 0. Within the QSD framework, the port side is narrower than the starboard side. Therefore, turning starboard facilitates a safer passage around the TS with a reduced amplitude of collision avoidance. As depicted in Figure 9, the DCPA is 0.9 n miles at the onset and increases swiftly following the execution of the collision avoidance maneuver. The vessels keep a minimum distance of 1.7 n miles at the sixth node, after which the OS reverts to its original heading towards waypoints (30, 35).
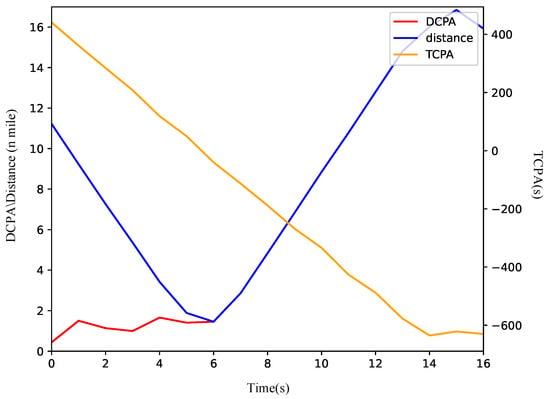
Figure 9.
The variation curve of ship encounter parameters in overtaking scenario.
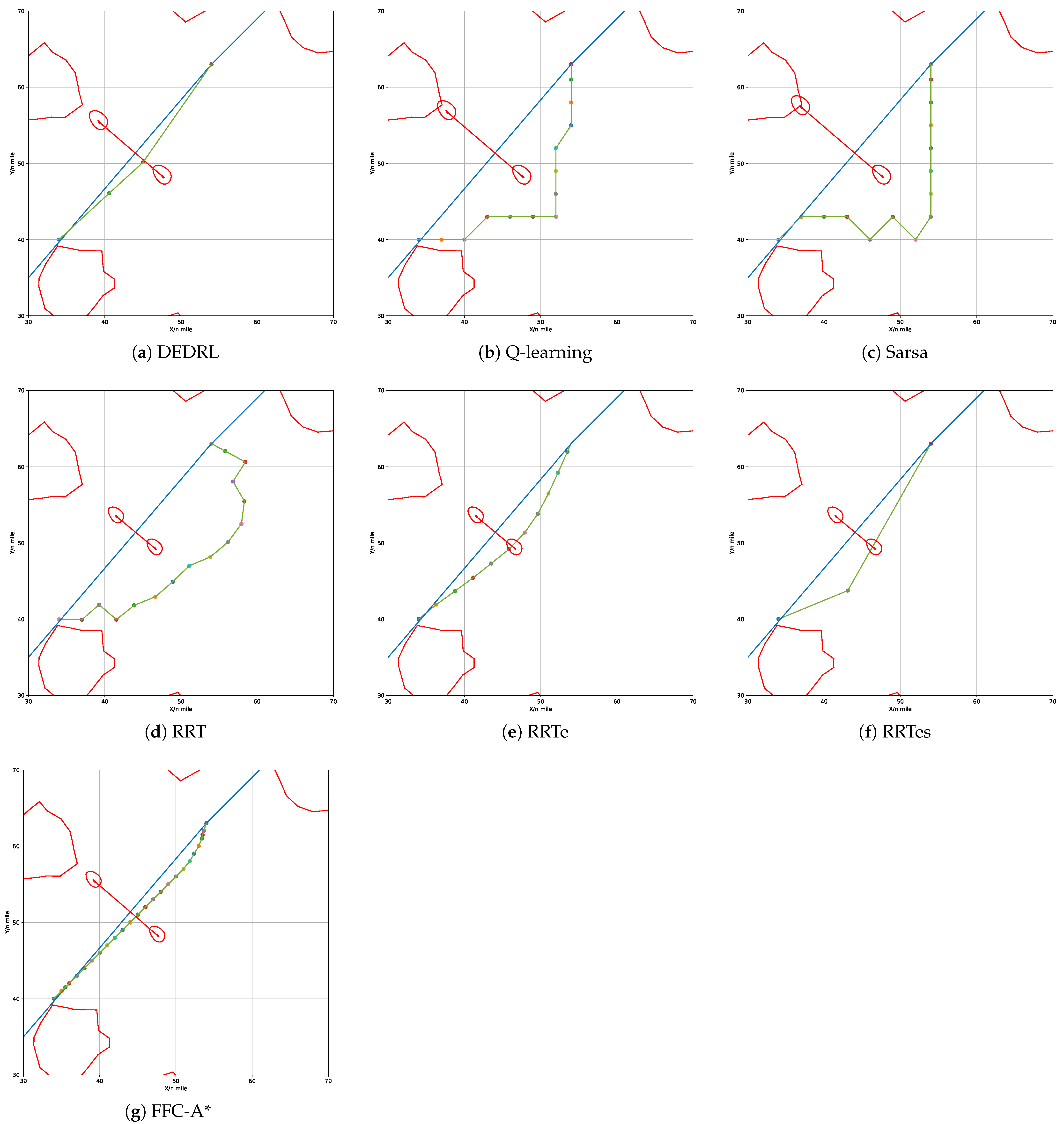
In the crossing scenario, the OS initiates its movement from coordinates (34, 40) towards (54, 63) at a course angle of relative to the global path. Concurrently, the TS departs from coordinates (47.65, 48.24) at an almost vertical angle to the global path. Given the OS’s constant course angle and speed, a collision with the TS is unavoidable in this scenario. According to Rule 15 of the COLREGs, when two vessels are crossing and there is a risk of collision, the OS must keep out of the way and, if circumstances permit, avoid crossing ahead of the other vessel. It is reasonable that the OS will take proactive measures to navigate behind the TS in order to avert a collision as it approaches. The updated path results from all algorithms are shown in Figure 10.
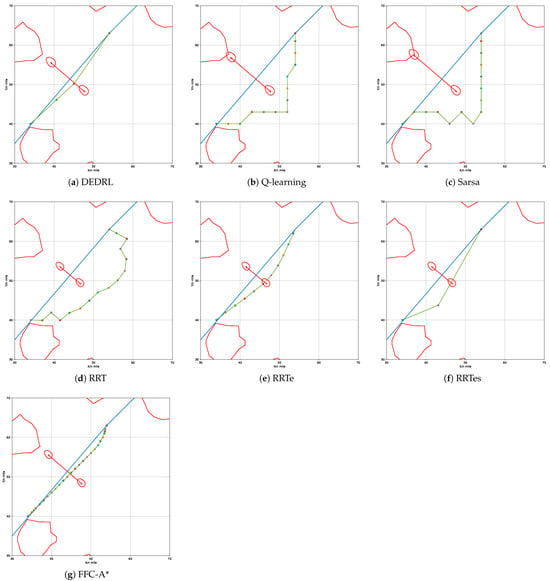
Figure 10.
Performance comparison of different algorithms in crossing scenario.
The experimental metric path length is presented in Table 4. Notably, DEDRL achieves the shortest path of 6.1371 n miles in crossing scenario, attributed to the advantages of DE optimization and DQN searching capabilities. Furthermore, the average path length for DEDRL is 6.1476 n miles, with a maximum of 6.1693 n miles, both of which surpass those of competing algorithms, further proving its stability. In contrast, traditional reinforcement learning and sampling algorithms exhibit inferior performance. Only RRTe and FFC-A* achieve path lengths of 6.2237 and 6.1645 n miles, respectively, which are slightly worse than those of DEDRL but better than Q-learning, Sarsa, RRT, and RRTes, all of which approximate 7 n miles; thus, these methods fall short.

Table 4.
Experimental results of different algorithms in crossing scenario.
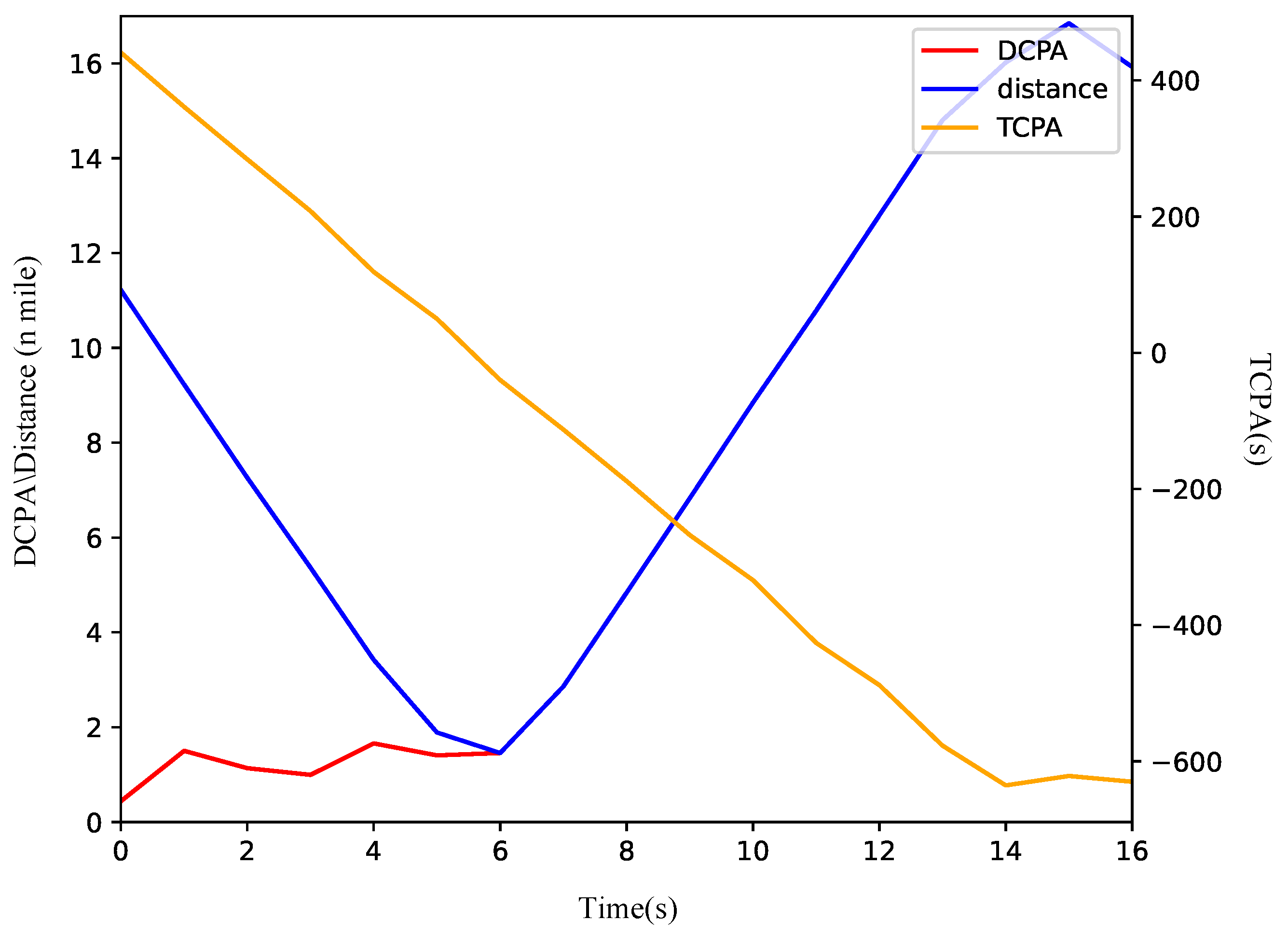
Based on Figure 10a, the OS turns starboard to maintain clearance from the TS, consistent with the requirements of the COLREGs in crossing situations. Initially, the distance between the vessels exceeds 12 n miles. The starboard turn enables the OS to safely make a detour behind the TS. As illustrated in Figure 11, the DCPA is 1.1 n miles at the initial moment and stabilizes between 1 and 2 n miles thereafter. The vessels maintain a minimum distance of 2.1 n miles at the fifth node, after which the OS resumes its heading towards waypoints (54.00, 63.00).
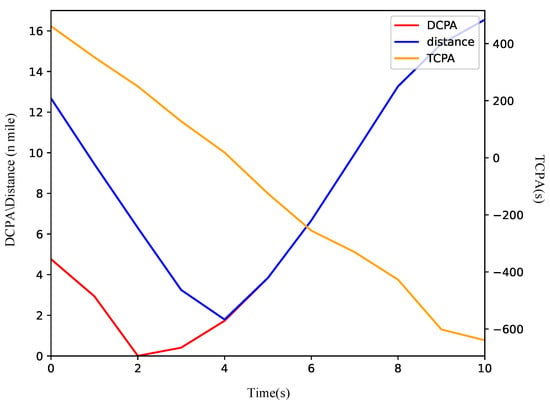
Figure 11.
The variation curve of ship encounter parameters in a crossing scenario.
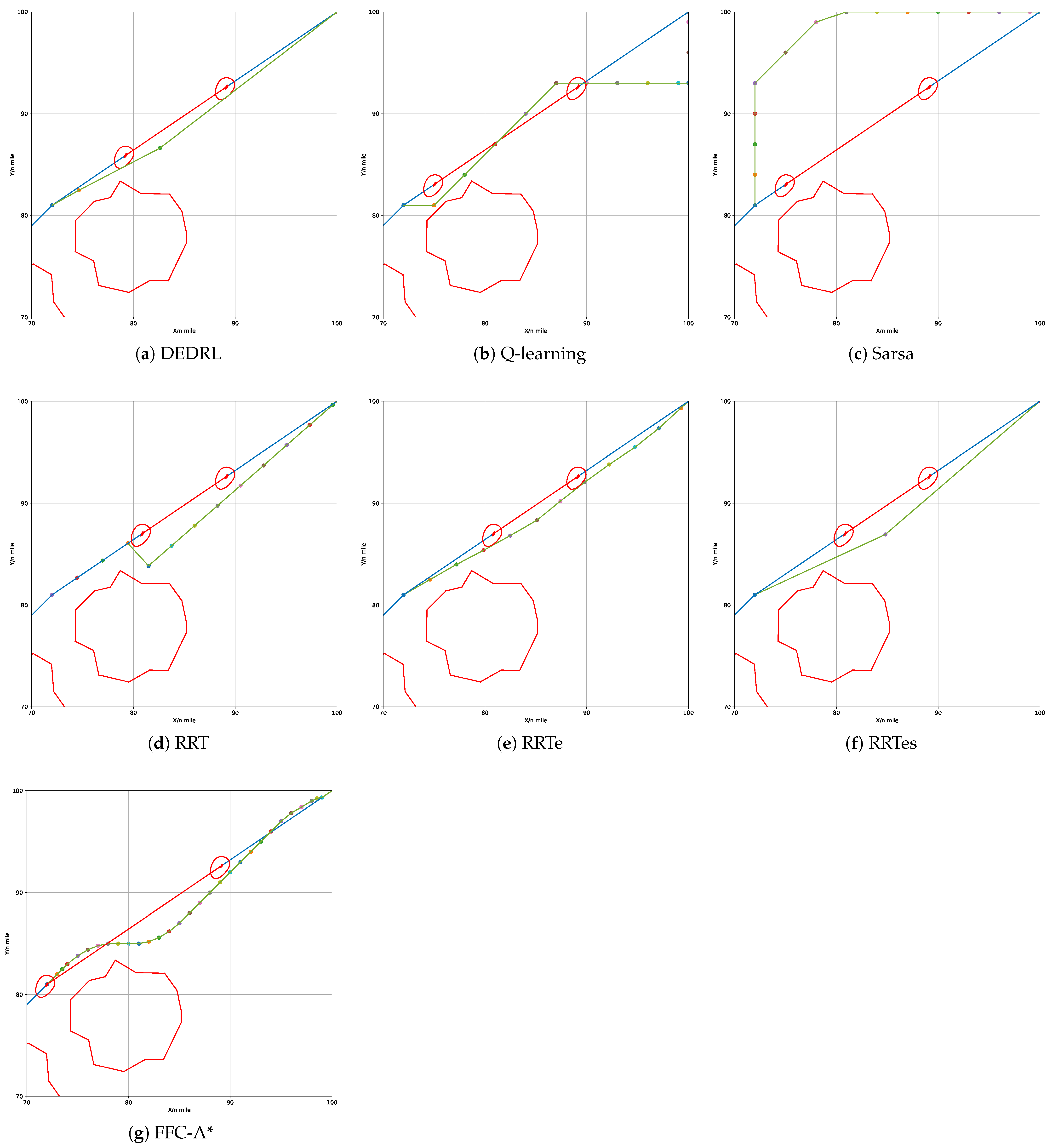
In the head-on scenario, the OS initiates its movement from coordinates (72, 81) towards (100, 100) at a course angle of relative to the global path. Simultaneously, the TS departs from coordinates (89.17, 92.65) at an opposite course angle to that of the OS along the global path. The OS having a collision with the TS is inevitable in this situation, if the OS keeps its origin course angle and speed. According to Rule 14 of the COLREGs, when two vessels are on reciprocal or nearly reciprocal courses that present a risk of collision, the OS must alter its course to starboard so that both may pass on the port side of one another. It is determined that the OS will implement proactive measures to maneuver behind the TS in order to avert a collision as it approaches. The replanned path results produced by all algorithms are illustrated in Figure 12.
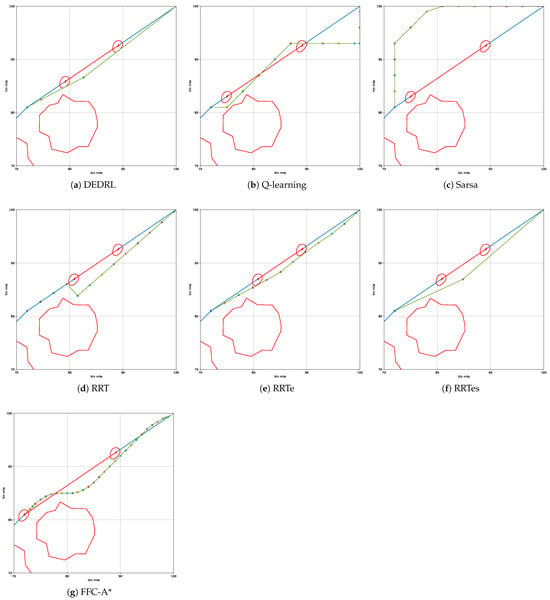
Figure 12.
Performance comparison of different algorithms in head-on scenario.
The path length of the head-on scenario is presented in Table 5 and is the same as the former.It is noteworthy that the combination of DE and DQN allows DEDRL to achieve the shortest path of 6.7869 n miles in global path planning. Furthermore, the average path length of 6.7938 n miles and the maximum of 6.8015 n miles for DEDRL, which surpass those of other algorithms, also represent its dependability. In contrast, traditional reinforcement learning algorithms and sampling algorithms display inferior performance. Except for RRTe and FFC-A, which yield performance metrics of 6.7905 and 6.9877 n miles, respectively, falling slightly short of DEDRL yet surpassing Q-learning, Sarsa, RRT, and RRTes, all of which approximate 8 n miles, the remaining methods are found to be deficient.

Table 5.
Experimental results of different algorithms in head-on scenario.
As shown in Figure 12a, only the OS turns starboard to maintain clearance for simplified maneuvering. Initially, the distance between the vessels exceeds 16 n miles. The OS alters course to starboard to ensure safe passage on the port side of the TS. As illustrated in Figure 13, the DCPA is 2.3 n miles at the initial moment and stabilizes between 0 and 2 n miles thereafter. The vessels stay at a minimum distance of 2.5 n miles at the fifth node, after which the OS resumes its heading towards waypoints (100.00, 100.00).
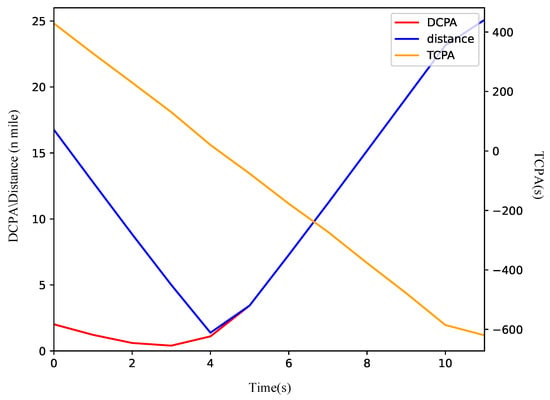
Figure 13.
The variation curve of ship encounter parameters in head-on scenario.
In summary, the proposed DEDRL algorithm outperforms other comparative algorithms in both local and global path planning scenarios. However, because of the evolutionary process in DE, the DEDRL algorithm achieves slightly more runtime than the others. These results highlight both the robustness and efficiency, as well as the limitations of the DEDRL algorithm.
5. Discussion
Ablation Analysis
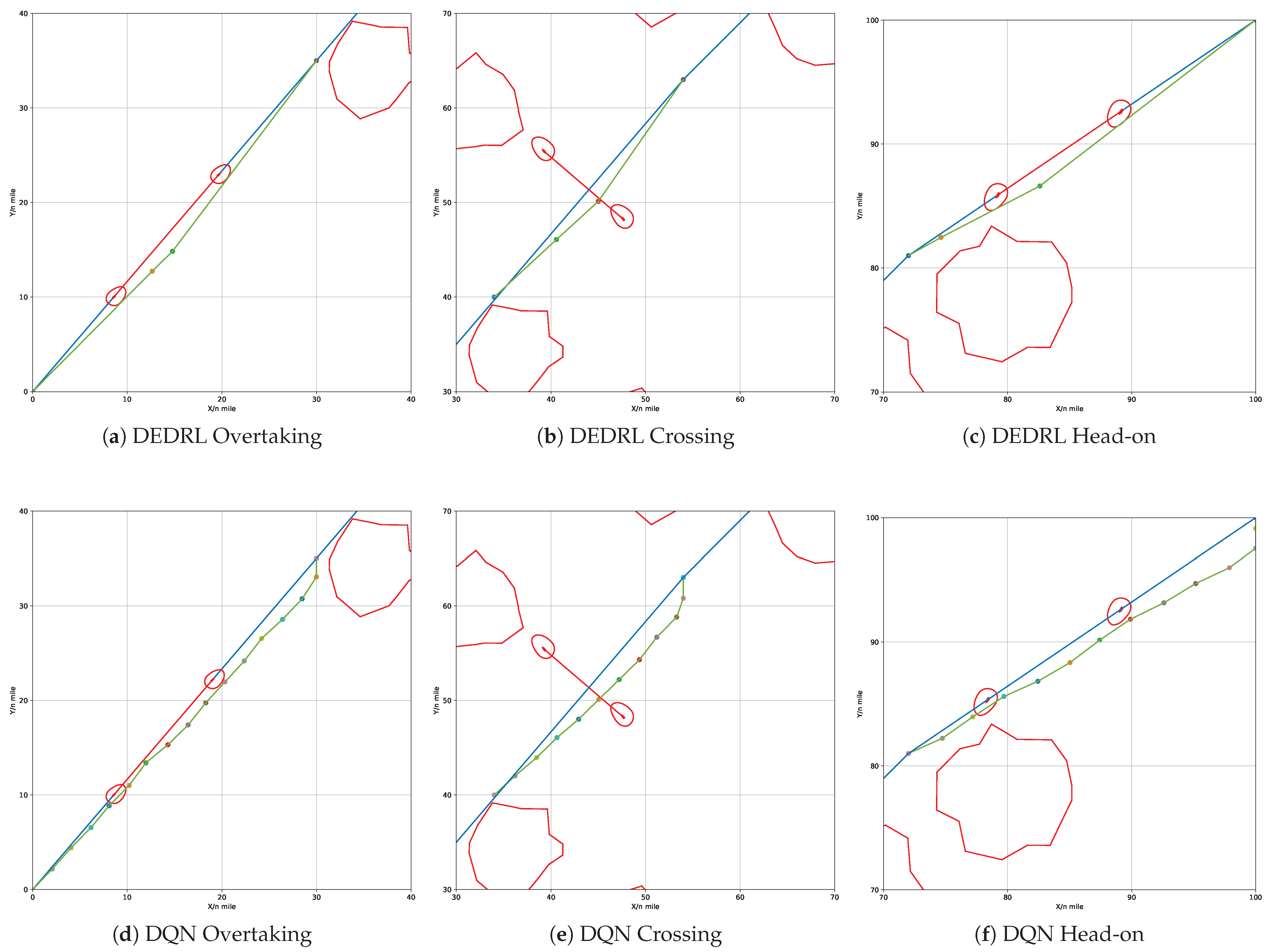
This section presents an ablation analysis of DEDRL, emphasizing the contribution of DE to the collision avoidance algorithm. As illustrated in Figure 14, figures (a) and (b) depict the global paths planned by DEDRL and DQN, respectively. It is evident that DEDRL significantly outperforms DQN, achieving a shorter global path length of 2.9219 n miles, as shown in Table 6. This improvement is attributable to the benefits provided by DE optimization.
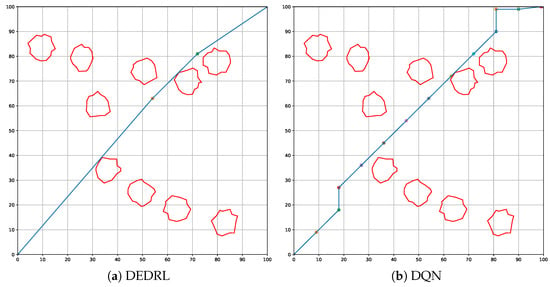
Figure 14.
Global path planning: discuss the contribution of DE.

Table 6.
Ablation analysis of DEDRL.
DE significantly reduces the number of route nodes in local path planning, resulting in a smoother trajectory. Meanwhile, CPRM contributes to constraining the agent, requiring fewer steps. Figure 15 illustrates the local path planning performance of DEDRL in overtaking (a), crossing (b), and head-on (c) scenarios. In contrast, figures (d), (e), and (f) display DQN’s performance in the same contexts, providing a comparative analysis of DE and CPRM’s isolated effects within DEDRL. Notably, DEDRL consistently outperforms DQN across all scenarios due to DE’s role in optimizing local path length. Specifically, DEDRL surpasses DQN by 0.0694, 0.003, and 0.0511 in the three scenarios, as detailed in Table 6.
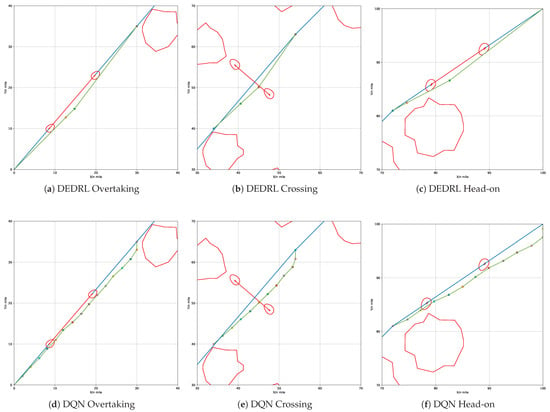
Figure 15.
Local path planning: discuss the contribution of CPRM.
Table 6 presents the detailed results from the ablation experiment, which includes ten runs for each scenario. As observed, DEDRL consistently shows improvement across average, maximum, and minimum statistics for both local and global path planning. DEDRL achieves a maximum path length that is shorter than DQN in global path planning, as well as in overtaking and head-on scenarios. Additionally, the average path lengths of DEDRL with 28.6943, 9.2443, 6.1476, and 6.7938 demonstrate its robust performance in the ship collision avoidance algorithm across all comparisons.
6. Conclusions and Outlook
To address the inefficiencies of the existing algorithms in the field of ship collision avoidance and to enhance the performance of path planning algorithms, this paper proposes a novel DEDRL algorithm. This algorithm integrates DE and DQN to incorporate evolutionary techniques into path planning and ship collision avoidance. Experimental results demonstrate that DEDRL outperforms existing algorithms, achieving the best performance with a global path distance of 28.4539 n miles. In local path planning, DEDRL also shows significant improvements, yielding distances of 9.2335, 6.1371, and 6.7869 n miles in overtaking, crossing, and head-on scenarios, respectively. Additionally, an ablation analysis discusses DE’s main contributions, highlighting its effectiveness in both global and local path planning.
However, the proposed DEDRL algorithm requires slightly more runtime than other reinforcement learning algorithms, indicating potential for improvement. In future work, this issue will be considered to be addressed further, and the DEDRL algorithm should be applied to various path planning and ship collision avoidance scenarios. Additionally, efforts will concentrate on real-world validation and assessing the feasibility of deploying this approach in maritime navigation.
Author Contributions
Conceptualization, Y.S. and Z.L.; methodology, Y.S. and D.C.; software, Y.S.; validation, Z.L. and D.C.; formal analysis, D.C.; investigation, Z.L.; resources, Z.L. and D.C.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, Z.L. and D.C.; visualization, Y.S. and Z.L.; supervision, D.C.; project administration, Z.L. and D.C.; funding acquisition, Z.L. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Shared Voyage Program on 2025 Beibu Gulf Scientific Research Expedition (No. NORC2054-11), the National Natural Science Foundation of China (No. 62362001), and the Key Research Base of Humanities and Social Sciences of Universities in Guangxi Zhuang Autonomous Region (No. BHZXSKY2305).
Data Availability Statement
The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhu, Q.; Xi, Y.; Weng, J.; Han, B.; Hu, S.; Ge, Y.E. Intelligent ship collision avoidance in maritime field: A bibliometric and systematic review. Expert Syst. Appl. 2024, 252, 124148. [Google Scholar] [CrossRef]
- He, Y.; Liu, X.; Zhang, K.; Mou, J.; Liang, Y.; Zhao, X.; Wang, B.; Huang, L. Dynamic adaptive intelligent navigation decision making method for multi-object situation in open water. Ocean Eng. 2022, 253, 111238. [Google Scholar] [CrossRef]
- Pietrzykowski, Z.; Wołejsza, P.; Nozdrzykowski, Ł.; Borkowski, P.; Banaś, P.; Magaj, J.; Chomski, J.; Maka, M.; Mielniczuk, S.; Pańka, A.; et al. The autonomous navigation system of a sea-going vessel. Ocean Eng. 2022, 261, 112104. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The review unmanned surface vehicle path planning: Based on multi-modality constraint. Ocean Eng. 2020, 200, 107043. [Google Scholar] [CrossRef]
- Jiang, L.; An, L.; Zhang, X.; Wang, C.; Wang, X. A human-like collision avoidance method for autonomous ship with attention-based deep reinforcement learning. Ocean Eng. 2022, 264, 112378. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Chen, P.; Negenborn, R.R.; van Gelder, P. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Gu, Q.; Zhen, R.; Liu, J.; Li, C. An improved RRT algorithm based on prior AIS information and DP compression for ship path planning. Ocean Eng. 2023, 279, 114595. [Google Scholar] [CrossRef]
- He, Z.; Liu, C.; Chu, X.; Negenborn, R.R.; Wu, Q. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl. Ocean Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Xue, H. A quasi-reflection based SC-PSO for ship path planning with grounding avoidance. Ocean Eng. 2022, 247, 110772. [Google Scholar] [CrossRef]
- Sui, F.; Tang, X.; Dong, Z.; Gan, X.; Luo, P.; Sun, J. ACO+PSO+A*: A bi-layer hybrid algorithm for multi-task path planning of an AUV. Comput. Ind. Eng. 2023, 175, 108905. [Google Scholar] [CrossRef]
- Gao, P.; Zhou, L.; Zhao, X.; Shao, B. Research on ship collision avoidance path planning based on modified potential field ant colony algorithm. Ocean Coast. Manag. 2023, 235, 106482. [Google Scholar] [CrossRef]
- Rawson, A.; Brito, M. A survey of the opportunities and challenges of supervised machine learning in maritime risk analysis. Transp. Rev. 2023, 43, 108–130. [Google Scholar] [CrossRef]
- Yang, X.; Han, Q. Improved reinforcement learning for collision-free local path planning of dynamic obstacle. Ocean Eng. 2023, 283, 115040. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, B.; Sun, M.; Sun, Q. Q-Learning-based parameters adaptive algorithm for active disturbance rejection control and its application to ship course control. Neurocomputing 2020, 408, 51–63. [Google Scholar] [CrossRef]
- Guan, W.; Luo, W.; Cui, Z. Intelligent decision-making system for multiple marine autonomous surface ships based on deep reinforcement learning. Robot. Auton. Syst. 2024, 172, 104587. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.Y. Ship collision avoidance anthropomorphic decision-making for structured learning based on AIS with Seq-CGAN. Ocean Eng. 2020, 217, 107922. [Google Scholar] [CrossRef]
- Cheng, C.; Sha, Q.; He, B.; Li, G. Path planning and obstacle avoidance for AUV: A review. Ocean Eng. 2021, 235, 109355. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, Q.; Prorok, A. Mobile Robot Path Planning in Dynamic Environments Through Globally Guided Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 6932–6939. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Jang, D.u.; Kim, J.s. Development of Ship Route-Planning Algorithm Based on Rapidly-Exploring Random Tree (RRT*) Using Designated Space. J. Mar. Sci. Eng. 2022, 10, 1800. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P. Global path planning for autonomous ship: A hybrid approach of Fast Marching Square and velocity obstacles methods. Ocean Eng. 2020, 214, 107793. [Google Scholar] [CrossRef]
- Hu, W.; Chen, S.; Liu, Z.; Luo, X.; Xu, J. HA-RRT: A heuristic and adaptive RRT algorithm for ship path planning. Ocean Eng. 2025, 316, 119906. [Google Scholar] [CrossRef]
- Huang, J.; Chen, C.; Shen, J.; Liu, G.; Xu, F. A self-adaptive neighborhood search A-star algorithm for mobile robots global path planning. Comput. Electr. Eng. 2025, 123, 110018. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.S. Collision Risk Inference System for Maritime Autonomous Surface Ships Using COLREGs Rules Compliant Collision Avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Namgung, H. Local Route Planning for Collision Avoidance of Maritime Autonomous Surface Ships in Compliance with COLREGs Rules. Sustainability 2022, 14, 198. [Google Scholar] [CrossRef]
- Ohn, S.W.; Namgung, H. Requirements for Optimal Local Route Planning of Autonomous Ships. J. Mar. Sci. Eng. 2023, 11, 17. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, W.; Bi, W.; Huang, Z. A path planning method based on deep reinforcement learning for AUV in complex marine environment. Ocean Eng. 2024, 313, 119354. [Google Scholar] [CrossRef]
- Xin, J.; Kim, J.; Li, Z.; Li, N. Train a real-world local path planner in one hour via partially decoupled reinforcement learning and vectorized diversity. Eng. Appl. Artif. Intell. 2025, 141, 109726. [Google Scholar] [CrossRef]
- Wang, H.; Lu, B.; Li, J.; Liu, T.; Xing, Y.; Lv, C.; Cao, D.; Li, J.; Zhang, J.; Hashemi, E. Risk Assessment and Mitigation in Local Path Planning for Autonomous Vehicles With LSTM Based Predictive Model. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2738–2749. [Google Scholar] [CrossRef]
- Jang, D.u.; Kim, J.s. Map Space Modeling Method Reflecting Safety Margin in Coastal Water Based on Electronic Chart for Path Planning. Sensors 2023, 23, 1723. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, S.; Mo, X.; Xu, X. Data-driven optimization for energy-constrained dietary supplement scheduling: A bounded cut MP-DQN approach. Comput. Ind. Eng. 2024, 188, 109894. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Luo, Y. DQN-enabled content caching and quantum ant colony-based computation offloading in MEC. Appl. Soft Comput. 2023, 133, 109900. [Google Scholar] [CrossRef]
- Xu, W.; Li, Y.; Pei, B.; Yu, Z. Coordinated intelligent control of the flight control system and shape change of variable sweep morphing aircraft based on dueling-DQN. Aerosp. Sci. Technol. 2022, 130, 107898. [Google Scholar] [CrossRef]
- Carta, S.; Ferreira, A.; Podda, A.S.; Reforgiato Recupero, D.; Sanna, A. Multi-DQN: An ensemble of Deep Q-learning agents for stock market forecasting. Expert Syst. Appl. 2021, 164, 113820. [Google Scholar] [CrossRef]
- Lechiakh, M.; El-Moutaouakkil, Z.; Maurer, A. Towards long-term depolarized interactive recommendations. Inf. Process. Manag. 2024, 61, 103833. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yu, X.; Hu, Z.; Luo, W.; Xue, Y. Reinforcement learning-based multi-objective differential evolution algorithm for feature selection. Inf. Sci. 2024, 661, 120185. [Google Scholar] [CrossRef]
- Liao, Z.; Zhu, F.; Gong, W.; Li, S.; Mi, X. AGSDE: Archive guided speciation-based differential evolution for nonlinear equations. Appl. Soft Comput. 2022, 122, 108818. [Google Scholar] [CrossRef]
- Liao, Z.; Mi, X.; Pang, Q.; Sun, Y. History archive assisted niching differential evolution with variable neighborhood for multimodal optimization. Swarm Evol. Comput. 2023, 76, 101206. [Google Scholar] [CrossRef]
- Stepien, B. Towards a New Horizon: 1972 COLREG in the Era of Autonomous Ships. Ocean Dev. Int. Law 2024, 55, 170–184. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Liu, J.; Wu, D.; Soares, C.G. A Two-Stage Path Planning Algorithm Based on Rapid-Exploring Random Tree for Ships Navigating in Multi-Obstacle Water Areas Considering COLREGs. J. Mar. Sci. Eng. 2022, 10, 1441. [Google Scholar] [CrossRef]
- International Maritime Organization. Convention on the International Regulations for Preventing Collisions at Sea, 1972 (COLREGs). 1972. Available online: https://www.imo.org/en/About/Conventions/Pages/COLREG.aspx (accessed on 28 August 2024).
- Liu, K.; Yuan, Z.; Xin, X.; Zhang, J.; Wang, W. Conflict detection method based on dynamic ship domain model for visualization of collision risk Hot-Spots. Ocean Eng. 2021, 242, 110143. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Yang, Z.; Wan, C.; Zhang, M. A novel data-driven method of ship collision risk evolution evaluation during real encounter situations. Reliab. Eng. Syst. Saf. 2024, 249, 110228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).