Dual-Vector-Based Model Predictive Current Control with Online Parameter Identification for Permanent-Magnet Synchronous Motor Drives in Marine Electric Power Propulsion System
Abstract
1. Introduction
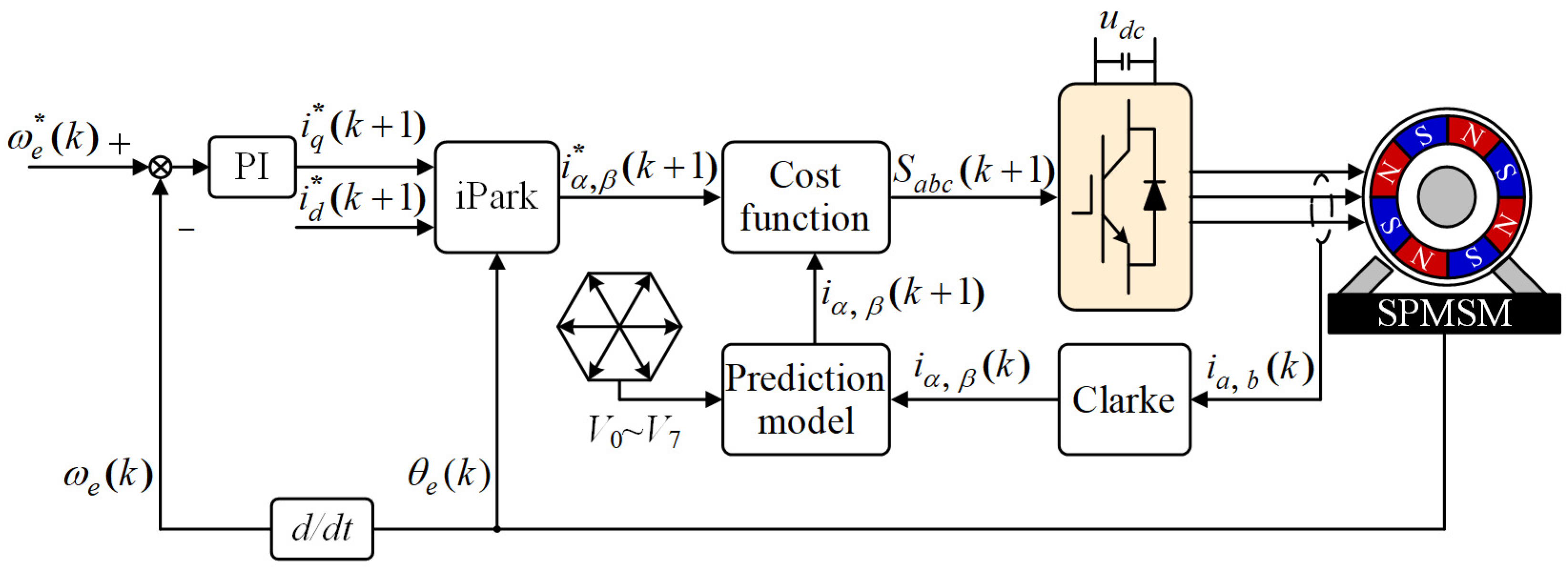
2. Basic Principle of FCS-MPCC
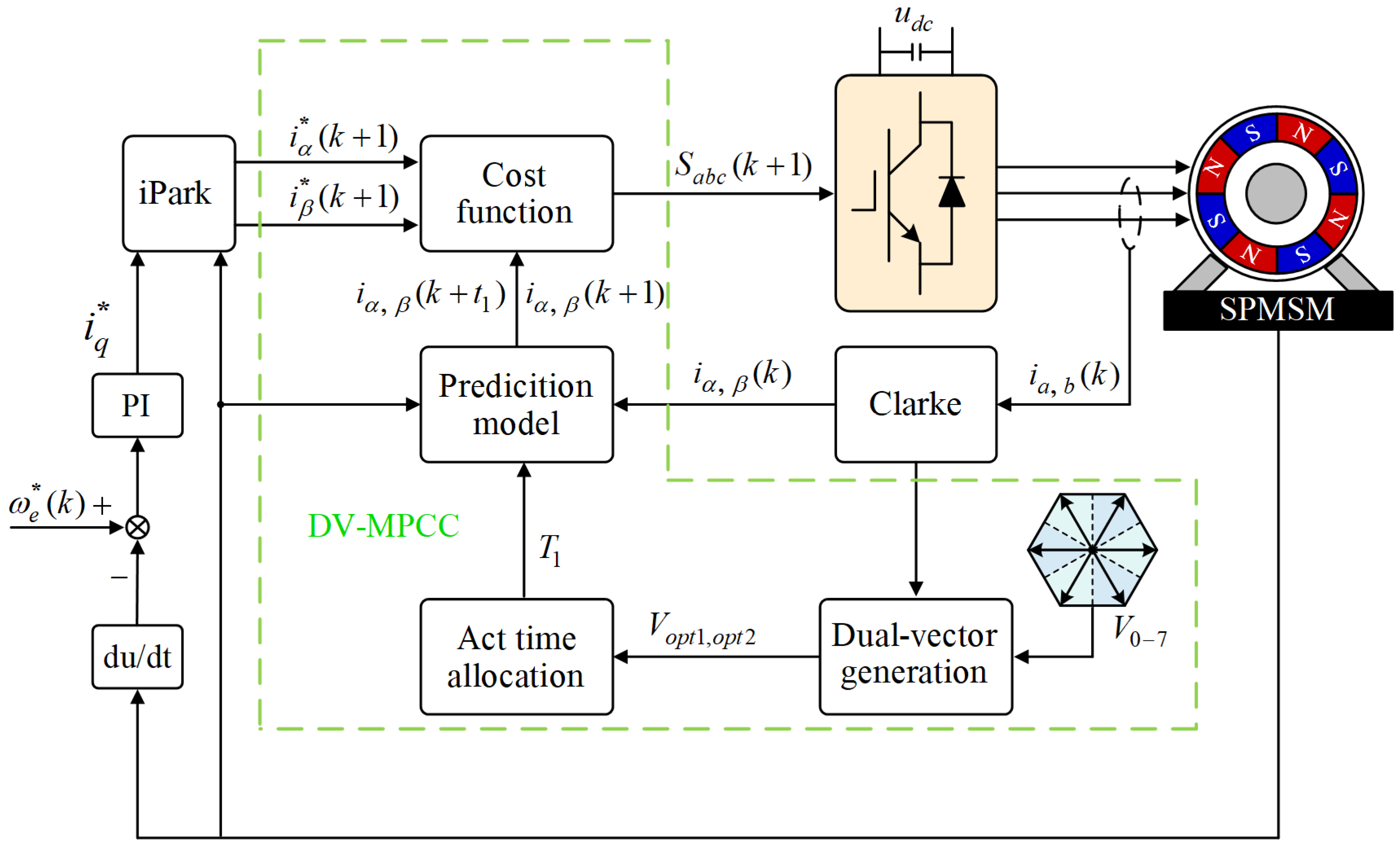
3. An Improved MRAS-Based DV-MPCC
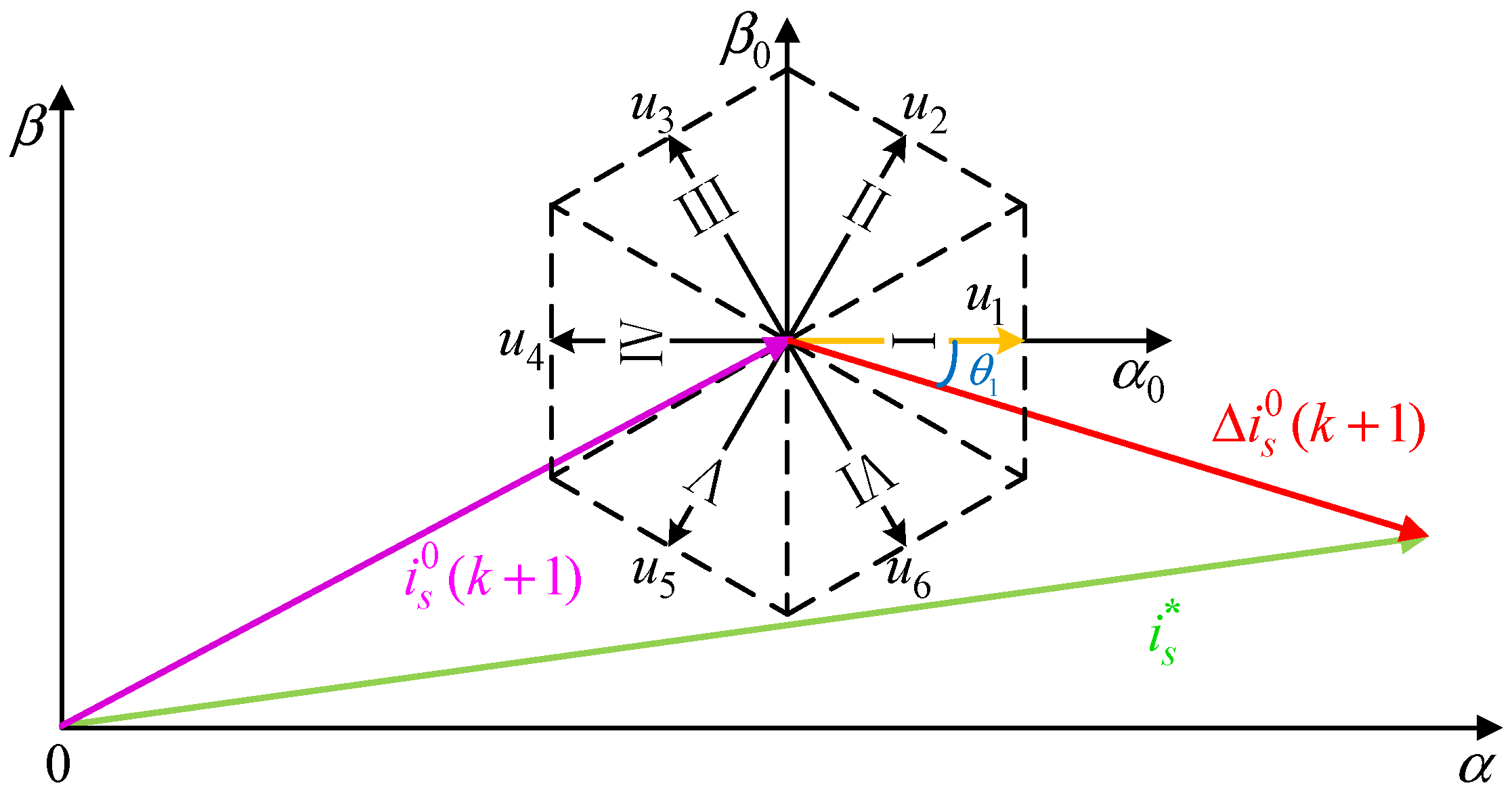
3.1. Error Current Vector-Based DV-MPCC
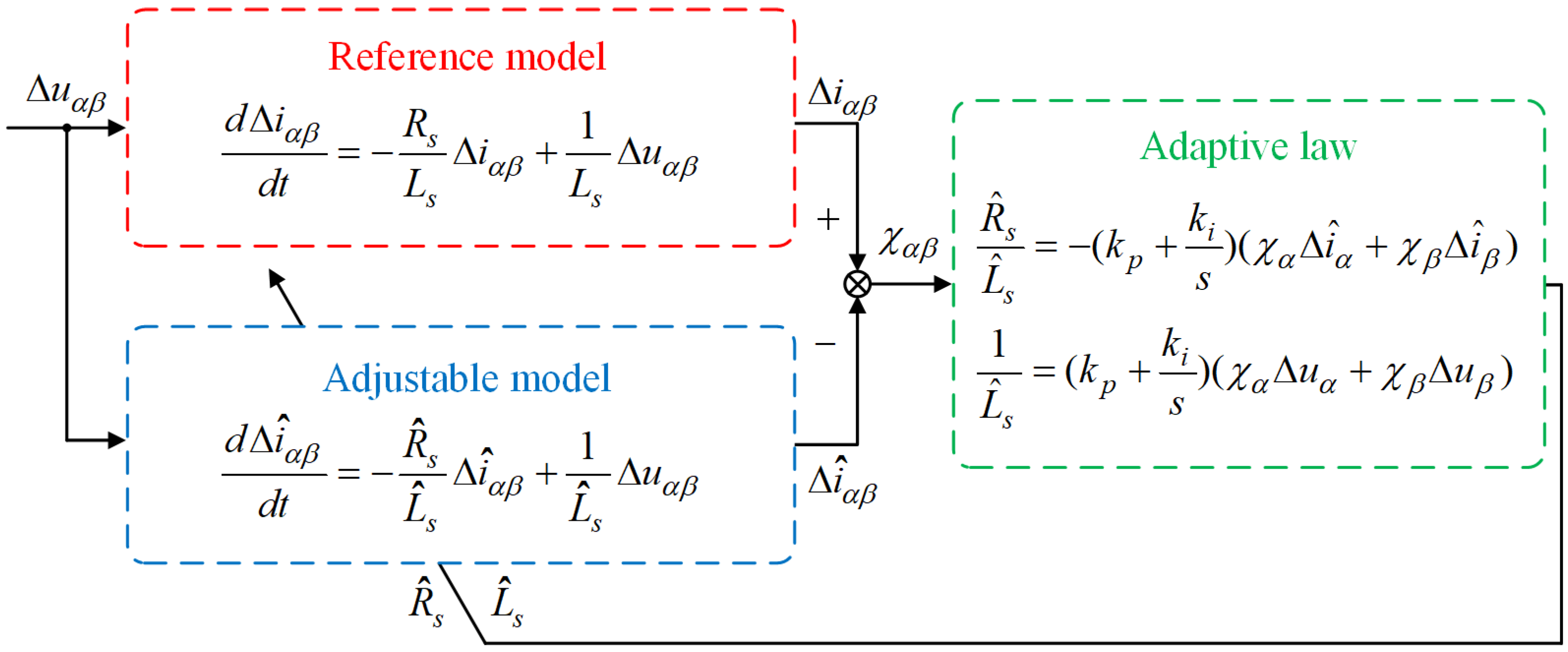
3.2. Incremental State Equation-Based MRAS Parameter Identification Method
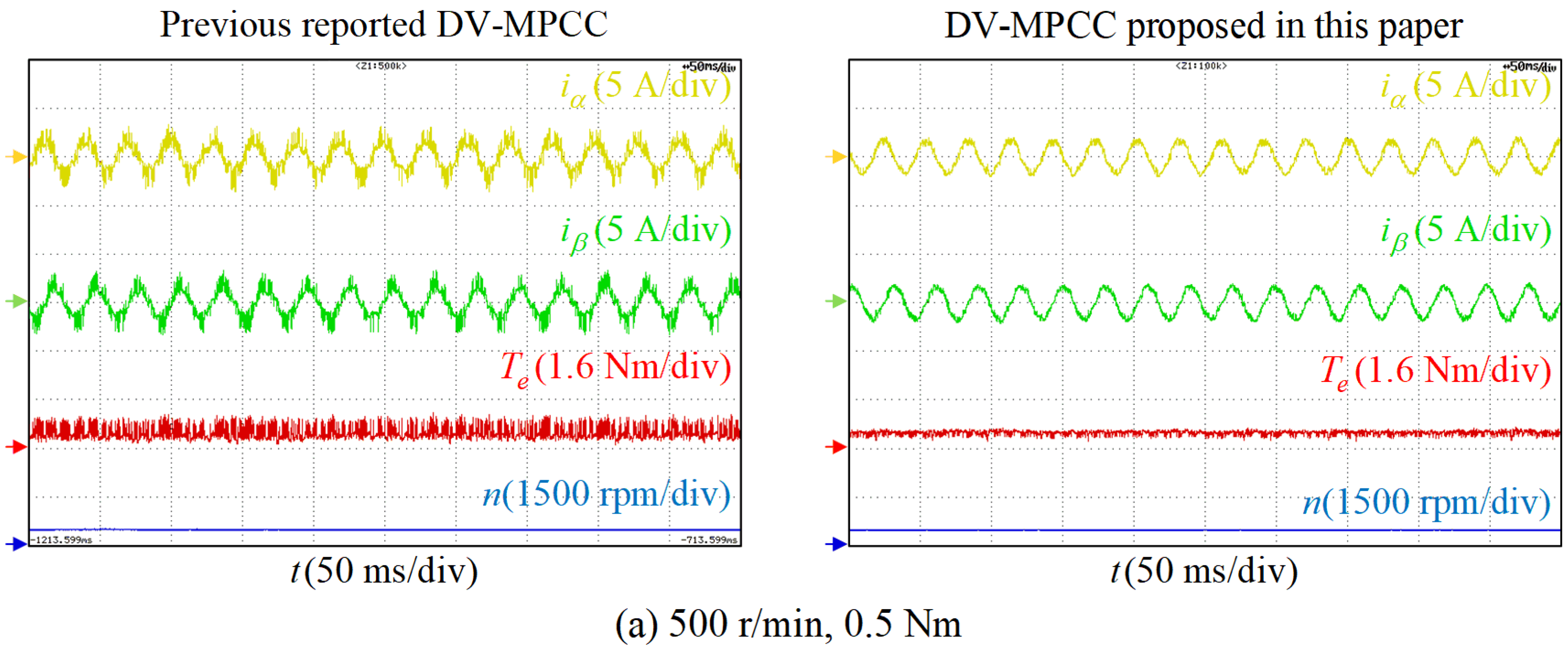
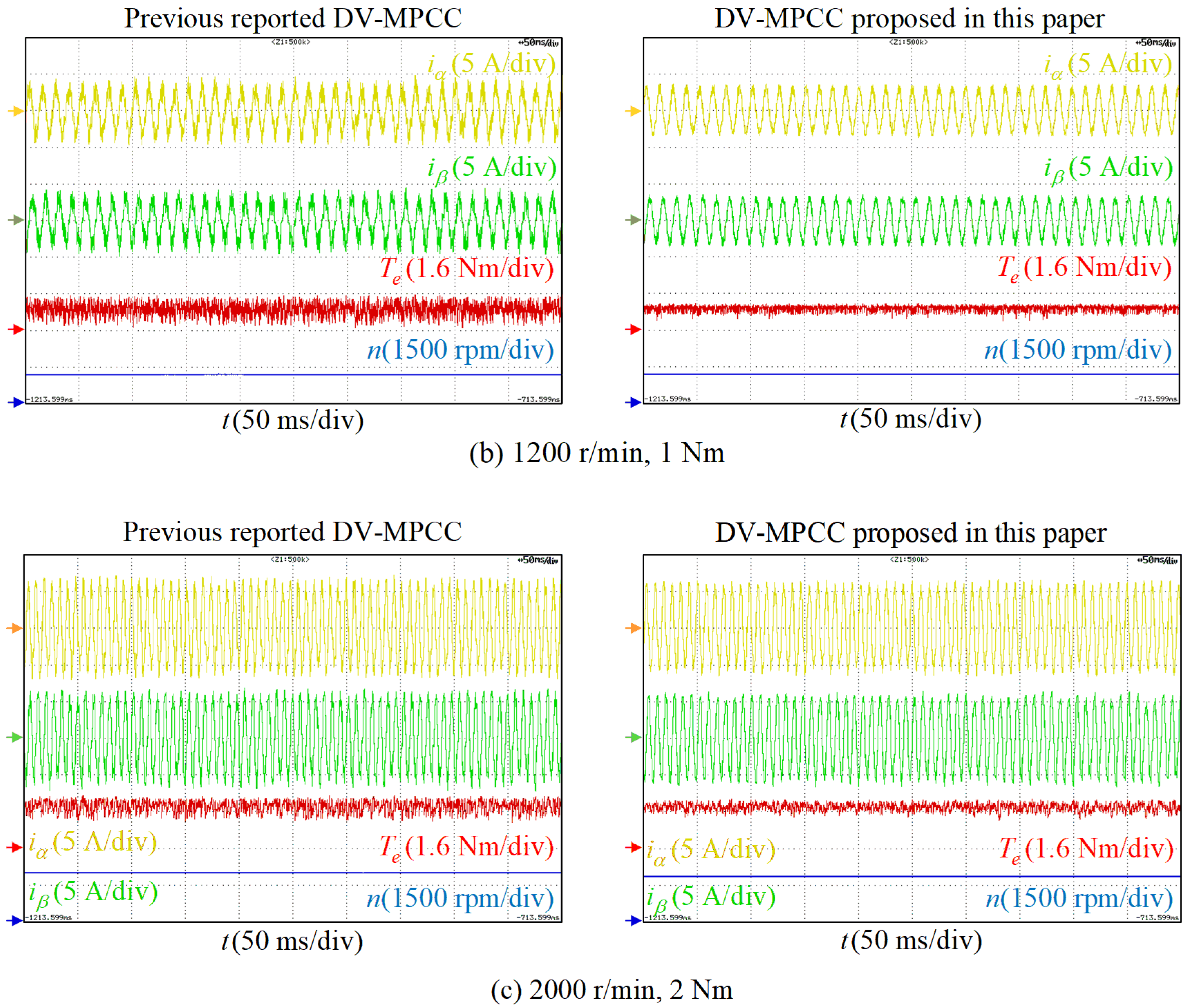
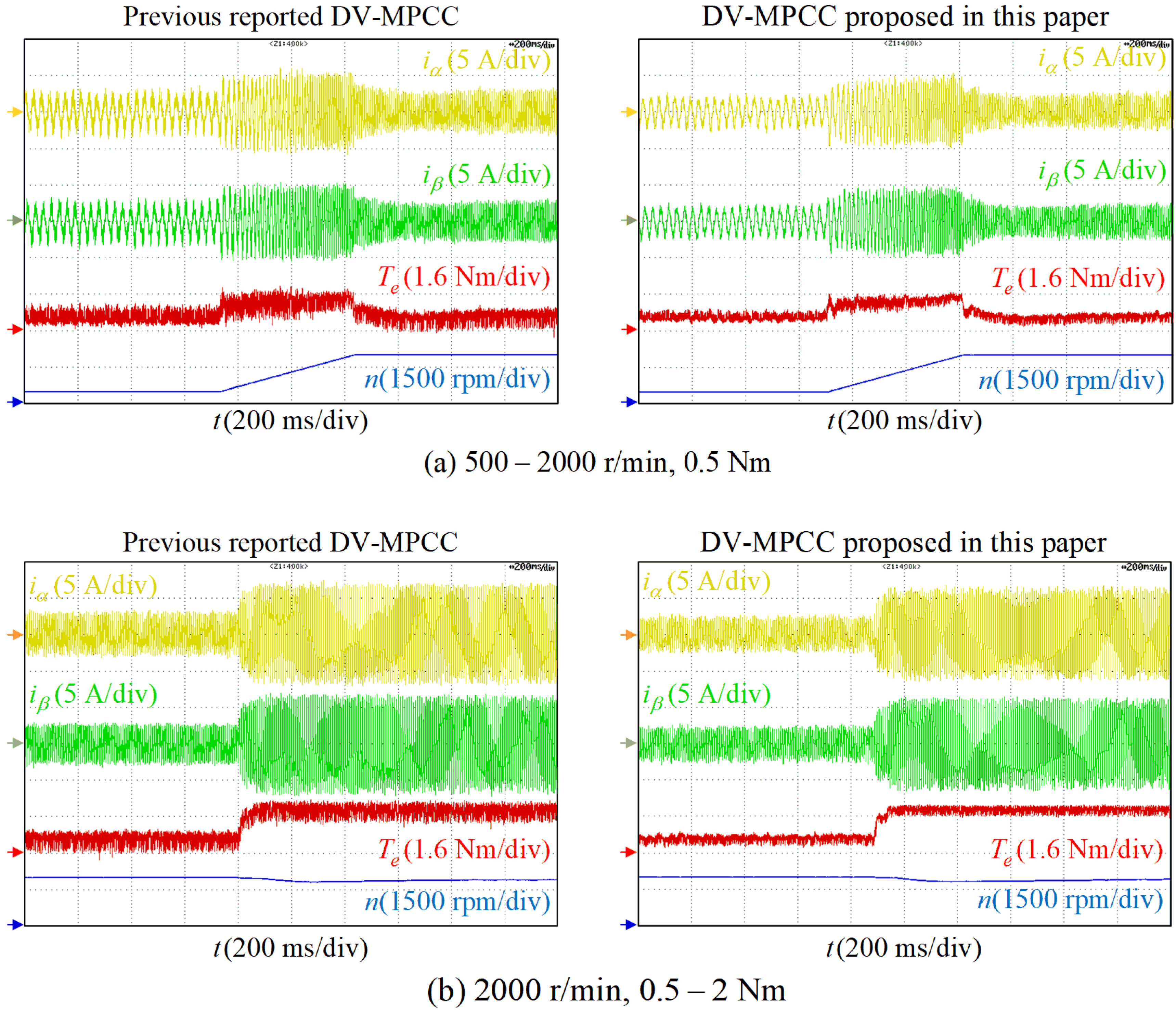
4. Experimental Validations
4.1. Improved DV-MPCC Control Performance Validation
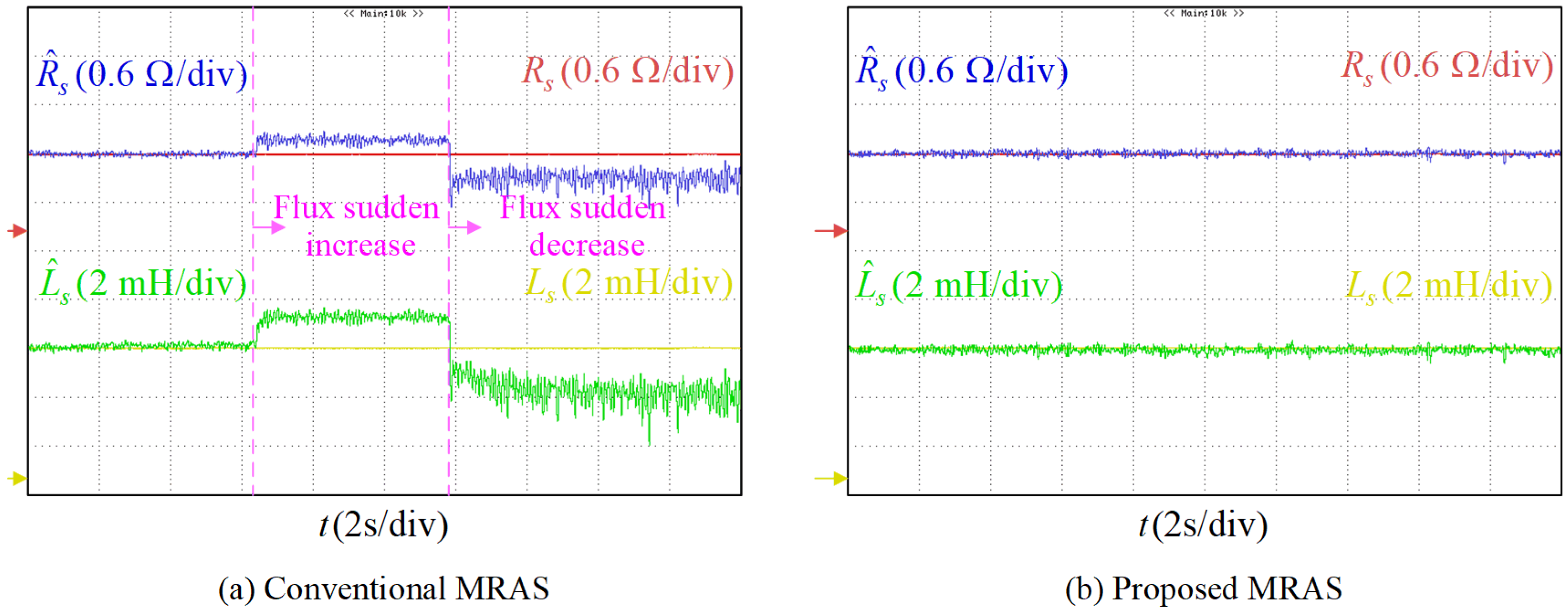
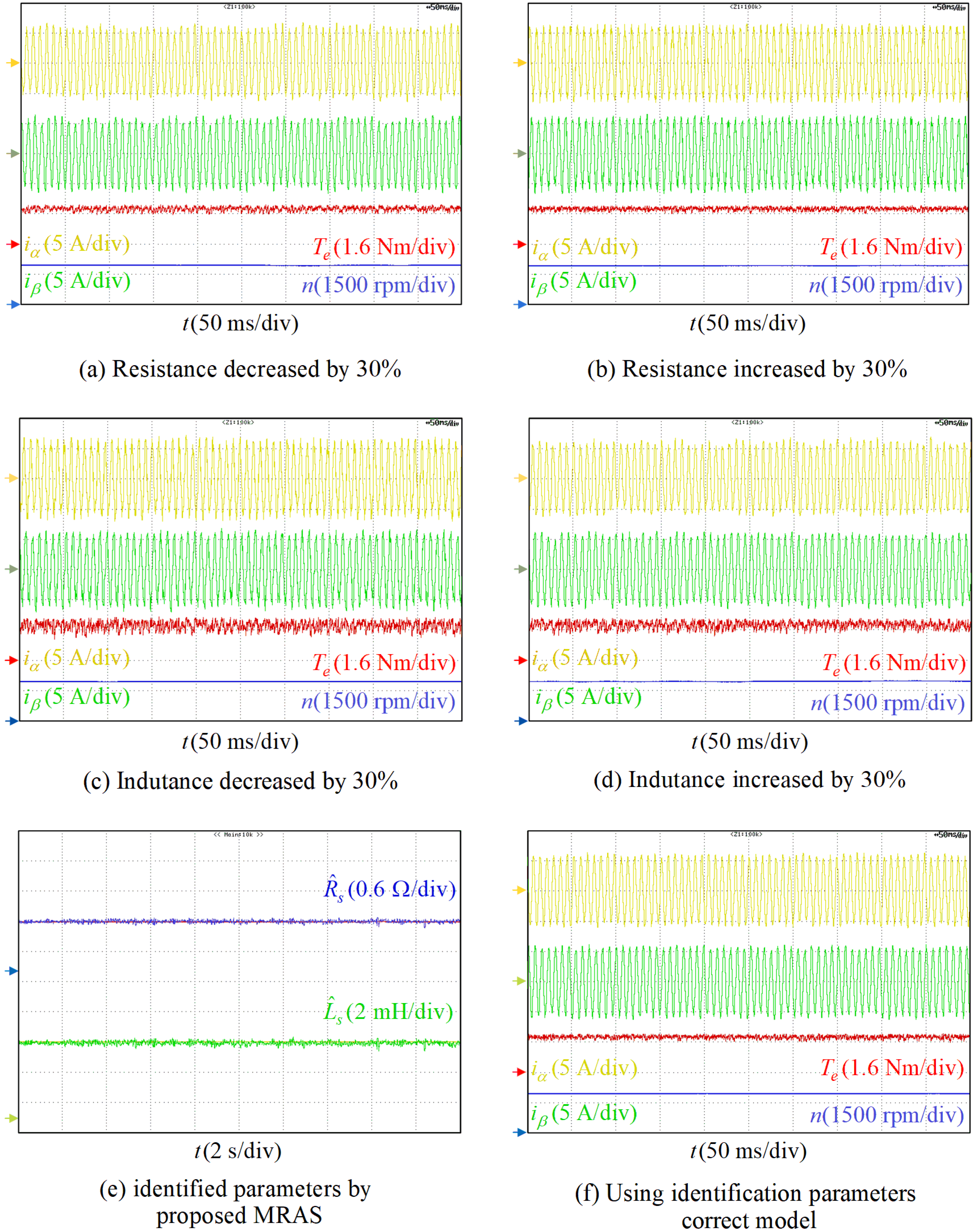
4.2. Improved MRAS Parameter Identification Performance Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, X.; Yao, X.L.; Liao, Y.F. Full Operating Range Optimization Design Method of LLC Resonant Converter in Marine DC Power Supply System. J. Mar. Sci. Eng. 2023, 11, 2142. [Google Scholar] [CrossRef]
- Kim, S.; Jeon, H. Comparative Analysis on AC and DC Distribution Systems for Electric Propulsion Ship. J. Mar. Sci. Eng. 2022, 10, 559. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Zhao, W.X.; Ji, J.H.; Zhu, S.D.; Hu, Q.Z. Zeroth-Order Vibration Analysis and Mitigation in Integral-Slot IPMSMs by Rotor Static Modulation Theory for Electrified Ship Propulsion. IEEE Trans. Transp. Electrif. 2024, 10, 7667–7678. [Google Scholar] [CrossRef]
- Mirzaeva, G.; Mo, Y.X. Model Predictive Control for Industrial Drive Applications. IEEE Trans. Ind. Appl. 2023, 59, 7897–7907. [Google Scholar] [CrossRef]
- Elmorshedy, M.F.; Xu, W.; El-Sousy, F.F.M.; Islam, M.R.; Ahmed, A.A. Recent Achievements in Model Predictive Control Techniques for Industrial Motor: A Comprehensive State-of-the-Art. IEEE Access. 2021, 9, 58170–58191. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.D.; Lei, G.; Guo, Y.G.; Yang, Z.B.; Zhu, J.G. Finite-Control-Set Model Predictive Control of Permanent Magnet Synchronous Motor Drive Systems—An Overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Morel, F.; Lin-Shi, X.F.; Retif, J.-M.; Allard, B.; Buttay, C. A Comparative Study of Predictive Current Control Schemes for a Permanent-Magnet Synchronous Machine Drive. IEEE Trans. Ind. Electron. 2009, 56, 2715–2728. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Yang, H.T. Generalized two-vector-based model-predictive torque control of induction motor drives. IEEE Trans. Power Electron. 2015, 30, 3818–3829. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Yang, H.T. Two-vector-based model predictive torque control without weighting factors for induction motor drives. IEEE Trans. Power Electron. 2016, 31, 1381–1390. [Google Scholar] [CrossRef]
- Petkar, S.G.; Thippiripati, V.K. Enhanced Predictive Current Control of PMSM Drive with Virtual Voltage Space Vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 3, 834–844. [Google Scholar] [CrossRef]
- Parvathy, M.L. An Effective Modulated Predictive Current Control of PMSM Drive with Low Complexity. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 10, 4565–4575. [Google Scholar] [CrossRef]
- Ma, C.W.; Rodríguez, J.; Garcia, C.; De Belie, F. Integration of Reference Current Slope Based Model-Free Predictive Control in Modulated PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1407–1421. [Google Scholar] [CrossRef]
- Zhang, X.G.; Zhang, L.; Zhang, Y.C. Model predictive current control for PMSM drives with parameter robustness improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Jung, J.W. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed Range. IEEE Trans. Ind. Informat. 2020, 16, 4747–4758. [Google Scholar] [CrossRef]
- Lian, C.Q.; Xiao, F.; Liu, J.L.; Gao, S. Parameter and VSI Nonlinearity Hybrid Estimation for PMSM Drives Based on Recursive Least Square. IEEE Trans. Transp. Electrific. 2023, 9, 2195–2206. [Google Scholar] [CrossRef]
- Li, X.Y.; Kennel, R. General formulation of kalman-filter-based online parameter identification methods for VSI-fed PMSM. IEEE Trans. Ind. Electron. 2021, 68, 2856–2864. [Google Scholar] [CrossRef]
- Odhano, S.A.; Pescetto, P.; Awan, H.A.A.; Hinkkanen, M.; Pellegrino, G.; Bojoi, R. Parameter Identification and Self-Commissioning in AC Motor Drives: A Technology Status Review. IEEE Trans. Power Electron. 2019, 34, 3603–3614. [Google Scholar] [CrossRef]
- Usama, M.; Kim, J. T Robust adaptive observer-based finite control set model predictive current control for sensorless speed control of surface permanent magnet synchronous motor. Trans. Inst. Meas. Control. 2021, 43, 1416–1429. [Google Scholar] [CrossRef]
- Usama, M.; Choi, Y.O.; Kim, J. Speed Sensorless Control based on Adaptive Luenberger Observer for IPMSM Drive. In Proceedings of the IEEE 19th International PEMC, Gliwice, Poland, 25–29 April 2021; pp. 602–607. [Google Scholar]
- Liu, Z.H.; Wei, H.L.; Li, X.H. Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO. IEEE Trans. Power Electron. 2018, 33, 10858–10871. [Google Scholar] [CrossRef]
- Boileau, T.; Leboeuf, N.; Nahid-Mobarakeh, B.; Meibody-Tabar, F. Online Identification of PMSM Parameters: Parameter Identifiability and Estimator Comparative Study. IEEE Trans. Ind. Appl. 2011, 47, 1944–1957. [Google Scholar] [CrossRef]
- An, X.K.; Liu, G.H.; Chen, Q.; Zhao, W.X.; Song, X.J. Adjustable Model Predictive Control for IPMSM Drives Based on Online Stator Inductance Identification. IEEE Trans. Ind. Electron. 2022, 69, 3368–3381. [Google Scholar] [CrossRef]
- Nalakath, S.; Preindl, M.; Emadi, A. Online multi-parameter estimation of interior permanent magnet motor drives with finite control set model predictive control. IET Electri Power Appl. 2017, 11, 944–951. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, S.; Zhang, C.; Zhou, Y. An Improved Deadbeat Predictive Current Control Based on Parameter Identification for PMSM. IEEE Trans. Transp. Electrific. 2024, 10, 2740–2753. [Google Scholar] [CrossRef]
- Liu, Y.; Ran, Q.; Zhao, S.P. Parameter Identification of Permanent Magnet Synchronous Motor Based on Improved MRAS Algorithm. J. Phys. Conf. Ser. 2023, 2456, 012050. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Xu, D.L.; Liu, J.L. Performance improvement of model-predictive current control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Sun, X.D.; Hu, C.C.; Lei, G. Speed sensorless control of SPMSM drives for EVs with a binary search algorithm-based phase-locked loop. IEEE Trans. Veh. Technol. 2020, 69, 4968–4978. [Google Scholar] [CrossRef]





| Parameter | Variable | Value |
|---|---|---|
| P | kW | 0.75 |
| np | / | 4 |
| Rs | Ω | 0.901 |
| Ls | mH | 5.445 |
| ψf | Wb | 0.113 |
| Ts | μs | 100 |
| Udc | V | 311 |
| TN | Nm | 2.4 |
| Performance Metric | DV-MPCC Proposed in [9] | DV-MPCC Proposed in This Paper | Performance Improvement |
|---|---|---|---|
| Steady-state performance | |||
| 500 rpm, light load | Te Ripple: 0.401 Nm ia THD: 21.9% | Te Ripple: 0.238 Nm ia THD: 15.8% | Ripple: 40.6% reduction; THD: 27% reduction |
| 1200 rpm, middle load | Te Ripple: 0.567 Nm ia THD: 24.4% | Te Ripple: 0.279 Nm ia THD: 16.7% | Ripple: 50.8% reduction; THD: 24% reduction |
| 2000 rpm, high load | Te Ripple: 0.443 Nm ia THD: 20.7% | Te Ripple: 0.284 Nm ia THD: 18.4% | Ripple: 35.9% reduction; THD: 19% reduction |
| Dynamic-state performance | |||
| Acceleration response time | 0.6 s | 0.6 s | Remains consistent |
| Load variation response time | 0.15 s | 0.15 s | Remains consistent |
| Execution Time | 26.5 us | 16.5 us | 38% reduction |
| Steady-State Performance | DV-MPCC Proposed in [10] | DV-MPCC Proposed in [11] | DV-MPCC Proposed in This Paper |
|---|---|---|---|
| 500 rpm, light load | iq Ripple: 0.995 A ia THD: 20.7% | iq Ripple: 0.597 A ia THD: 19.4% | iq Ripple: 0.352 A ia THD: 16.1% |
| 1200 rpm, middle load | iq Ripple: 0.778 A ia THD: 22.3% | iq Ripple: 0.466 A ia THD: 18.5% | iq Ripple: 0.410 A ia THD: 16.9% |
| 2000 rpm, high load | iq Ripple: 0.704 A ia THD: 19.8% | iq Ripple: 0.436 A ia THD: 18.1% | iq Ripple: 0.365 A ia THD: 17.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Zhang, Y.; Shi, L.; Huang, Y.; Chang, B. Dual-Vector-Based Model Predictive Current Control with Online Parameter Identification for Permanent-Magnet Synchronous Motor Drives in Marine Electric Power Propulsion System. J. Mar. Sci. Eng. 2025, 13, 585. https://doi.org/10.3390/jmse13030585
Huang S, Zhang Y, Shi L, Huang Y, Chang B. Dual-Vector-Based Model Predictive Current Control with Online Parameter Identification for Permanent-Magnet Synchronous Motor Drives in Marine Electric Power Propulsion System. Journal of Marine Science and Engineering. 2025; 13(3):585. https://doi.org/10.3390/jmse13030585
Chicago/Turabian StyleHuang, Shengqi, Yuanwei Zhang, Lei Shi, Yuqing Huang, and Bin Chang. 2025. "Dual-Vector-Based Model Predictive Current Control with Online Parameter Identification for Permanent-Magnet Synchronous Motor Drives in Marine Electric Power Propulsion System" Journal of Marine Science and Engineering 13, no. 3: 585. https://doi.org/10.3390/jmse13030585
APA StyleHuang, S., Zhang, Y., Shi, L., Huang, Y., & Chang, B. (2025). Dual-Vector-Based Model Predictive Current Control with Online Parameter Identification for Permanent-Magnet Synchronous Motor Drives in Marine Electric Power Propulsion System. Journal of Marine Science and Engineering, 13(3), 585. https://doi.org/10.3390/jmse13030585






