Nonlinear Sliding-Mode Super-Twisting Reaching Law for Unmanned Surface Vessel Formation Control Under Coupling Deception Attacks
Abstract
1. Introduction
- (1)
- A new nonlinear sliding-mode surface is designed for nonlinear fitting modeling of attacks coupled with actuator failures. Due to the physical limitation of system control ability, the redundancy information is saturated to improve the robustness of the system.
- (2)
- Based on the traditional approach law, a nonlinear super-twisting reaching law is designed. The nonlinear time-varying gain can be adjusted according to the system state, which effectively solves the dynamic change of error when it approaches and reaches the sliding surface, and can better control the sliding surface and reduce jitter.
- (3)
- In order to solve the saturation filtering problem, a dynamic error of the saturation filter is designed, and an adaptive nonlinear fault-tolerant filtering control mechanism is introduced to effectively deal with coupling attacks and actuator failures, to improve system stability and control accuracy.
2. Formation Model and Related Theory
2.1. USV Model
2.2. Attack Model
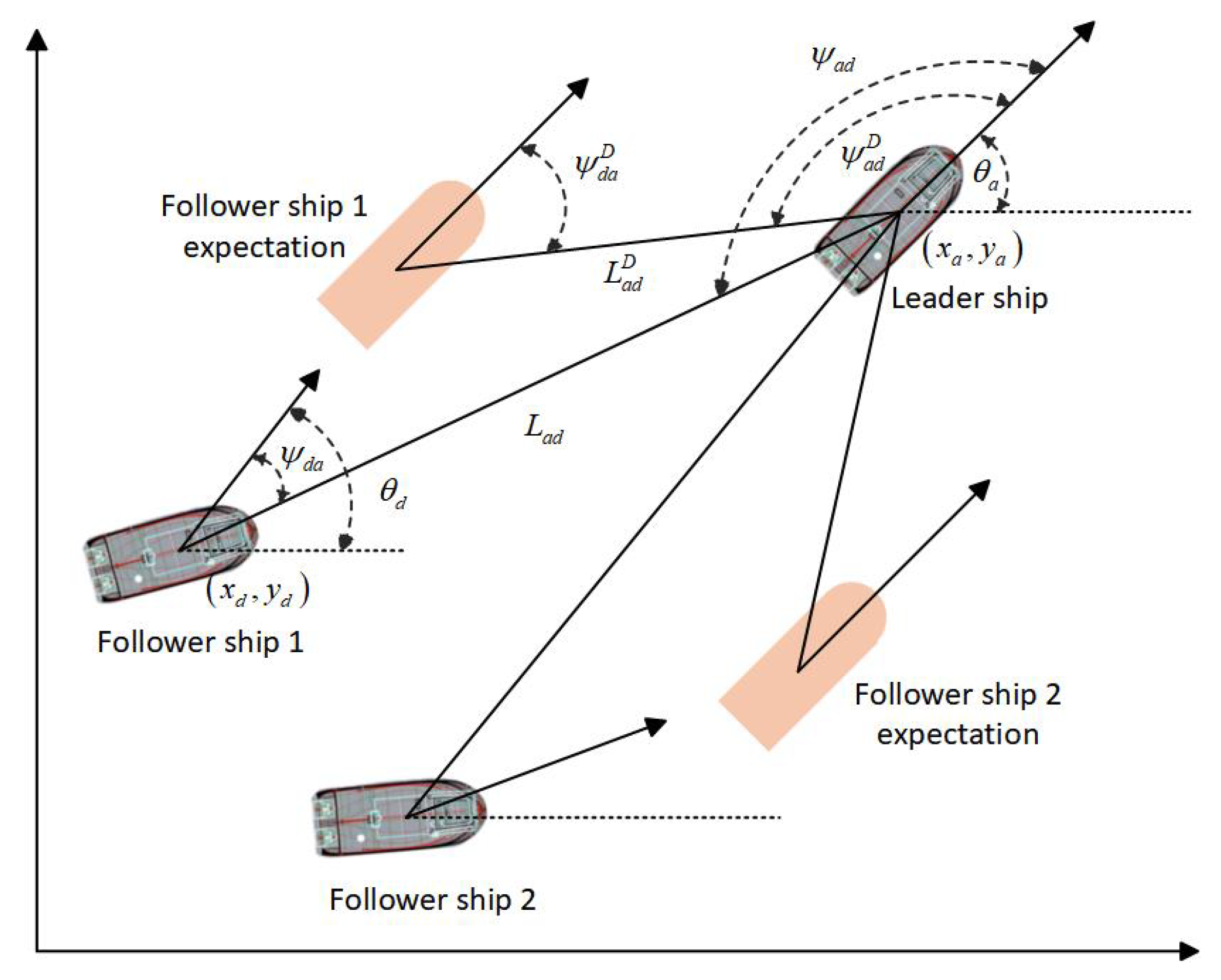
2.3. Formation Design
2.4. Related Lemmas
3. Controller Design
3.1. Nonlinear Sliding Surface Design
3.2. Improved Super-Twisting Reaching Law Algorithm Design
3.3. Improved Design of Super-Twisting Reaching Law Controller
4. Stability Analysis
4.1. Kinematic Stability Analysis
4.2. Kinetic Stability Analysis
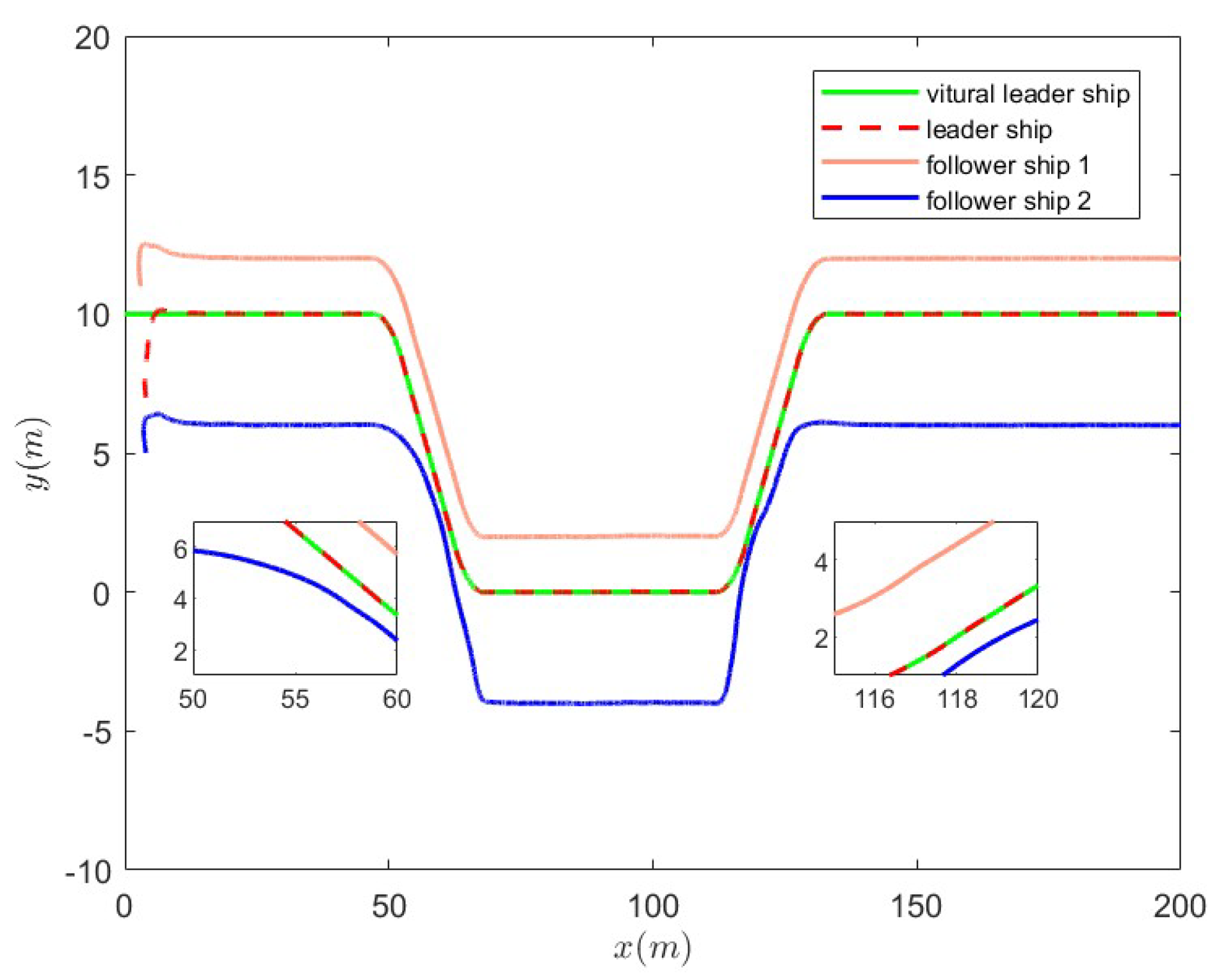
5. Simulation Analysis
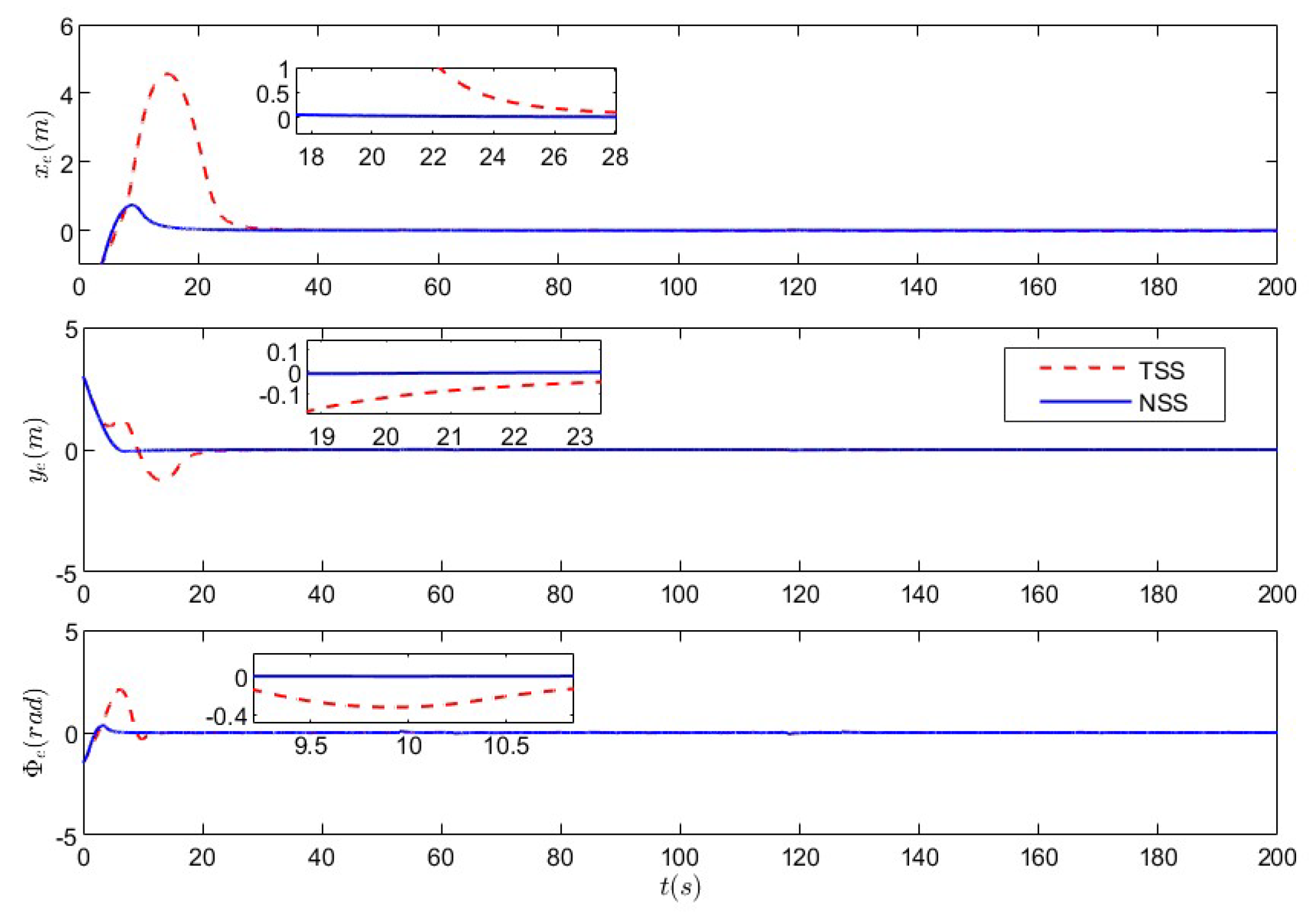
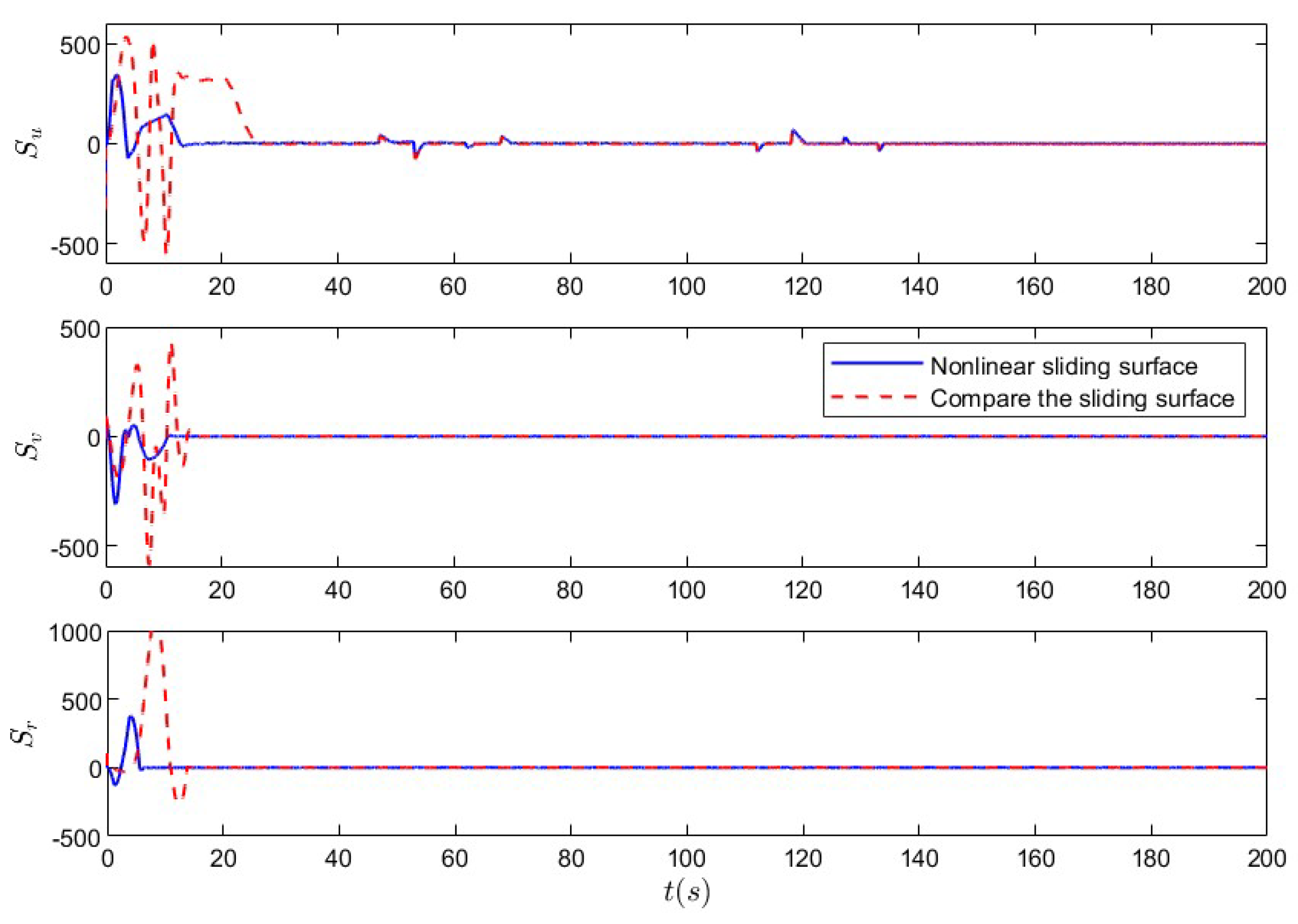
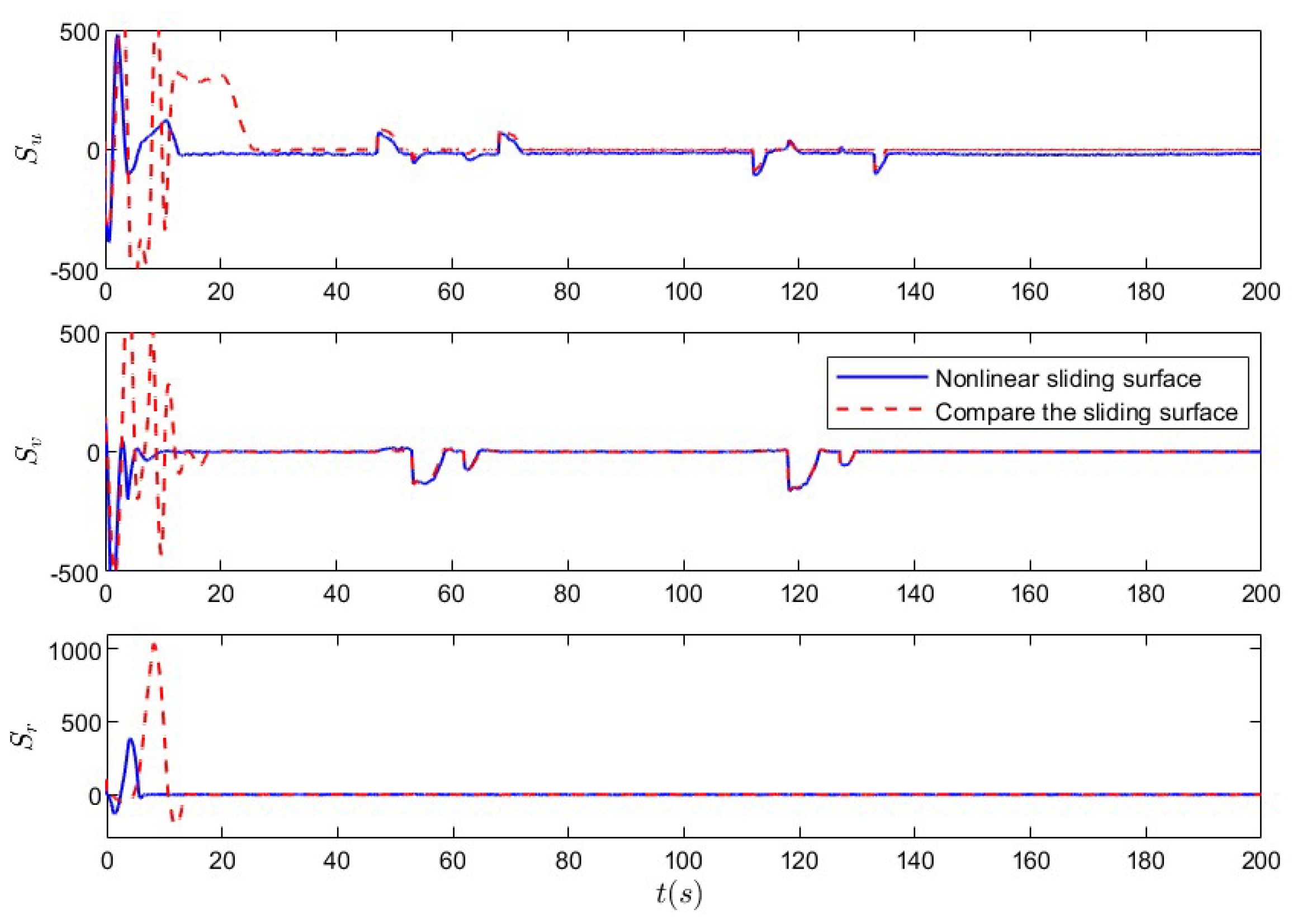
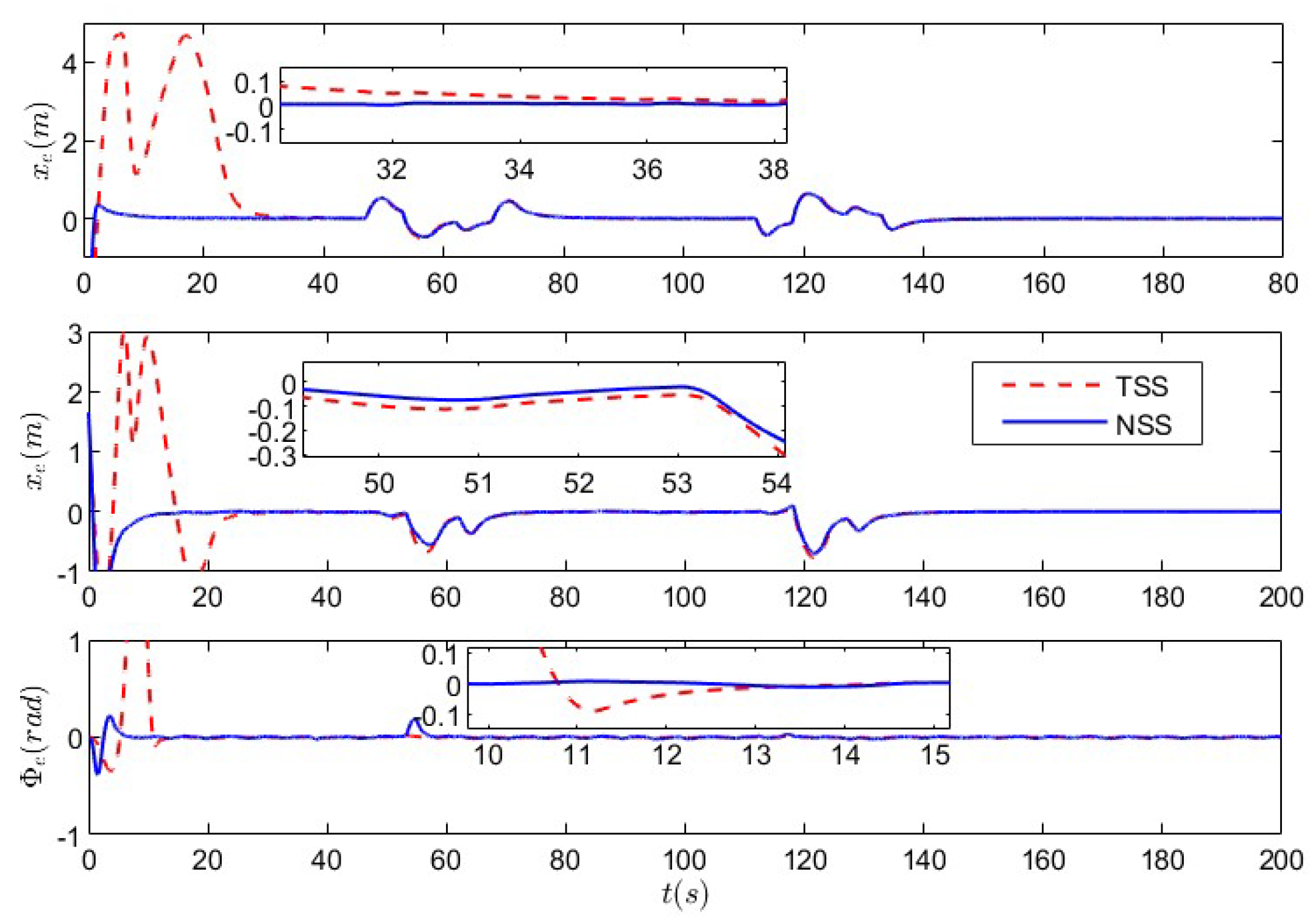
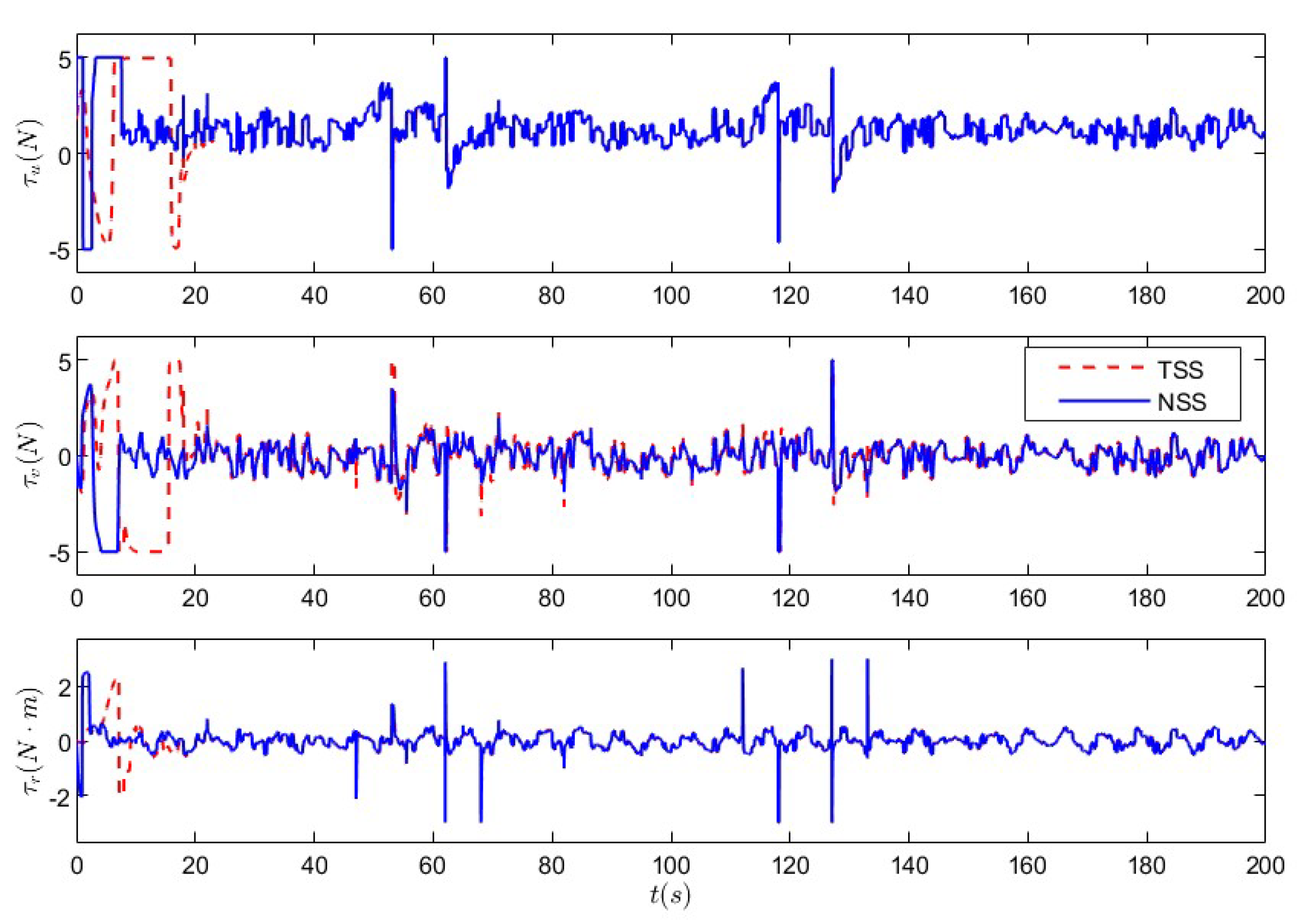
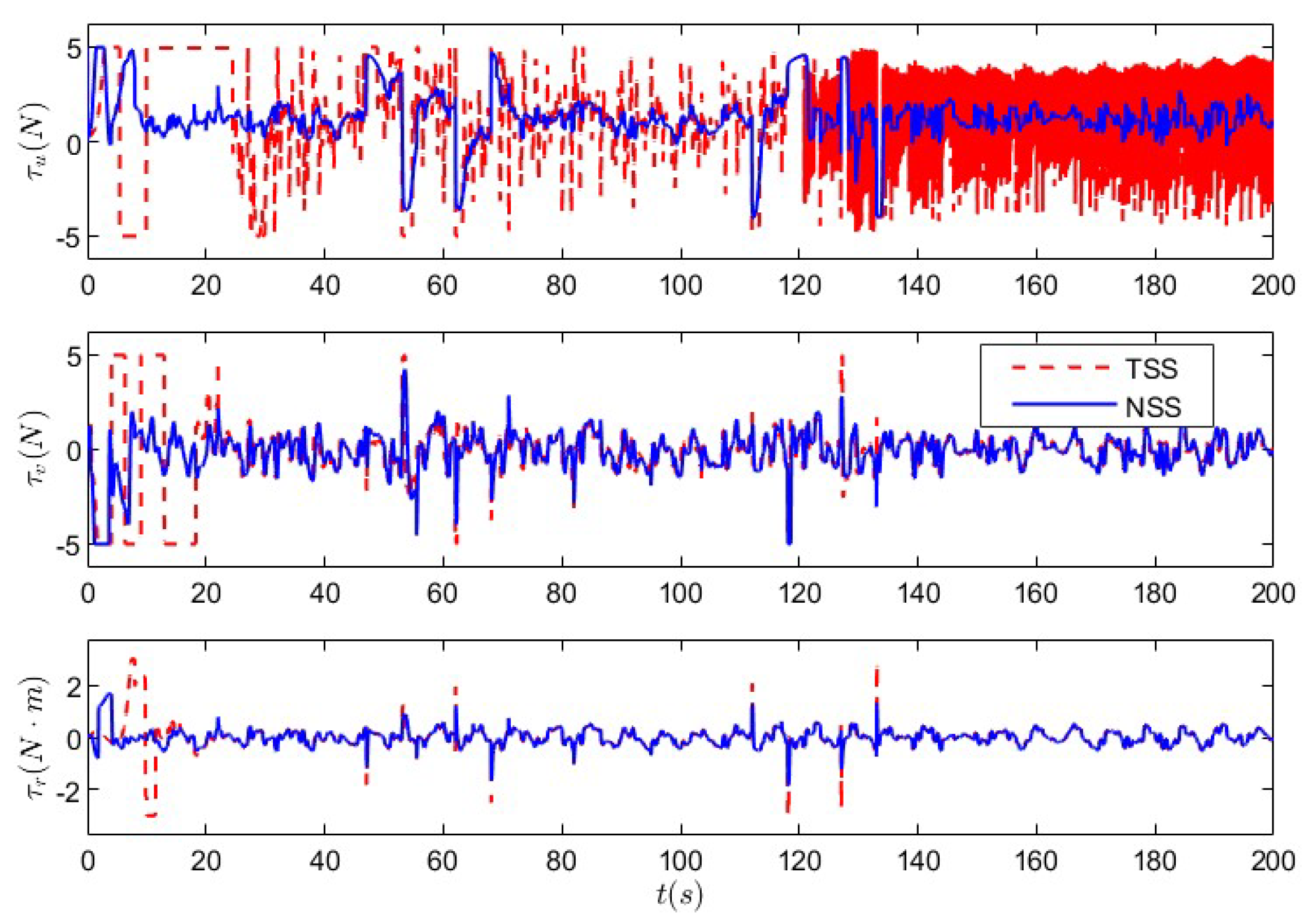
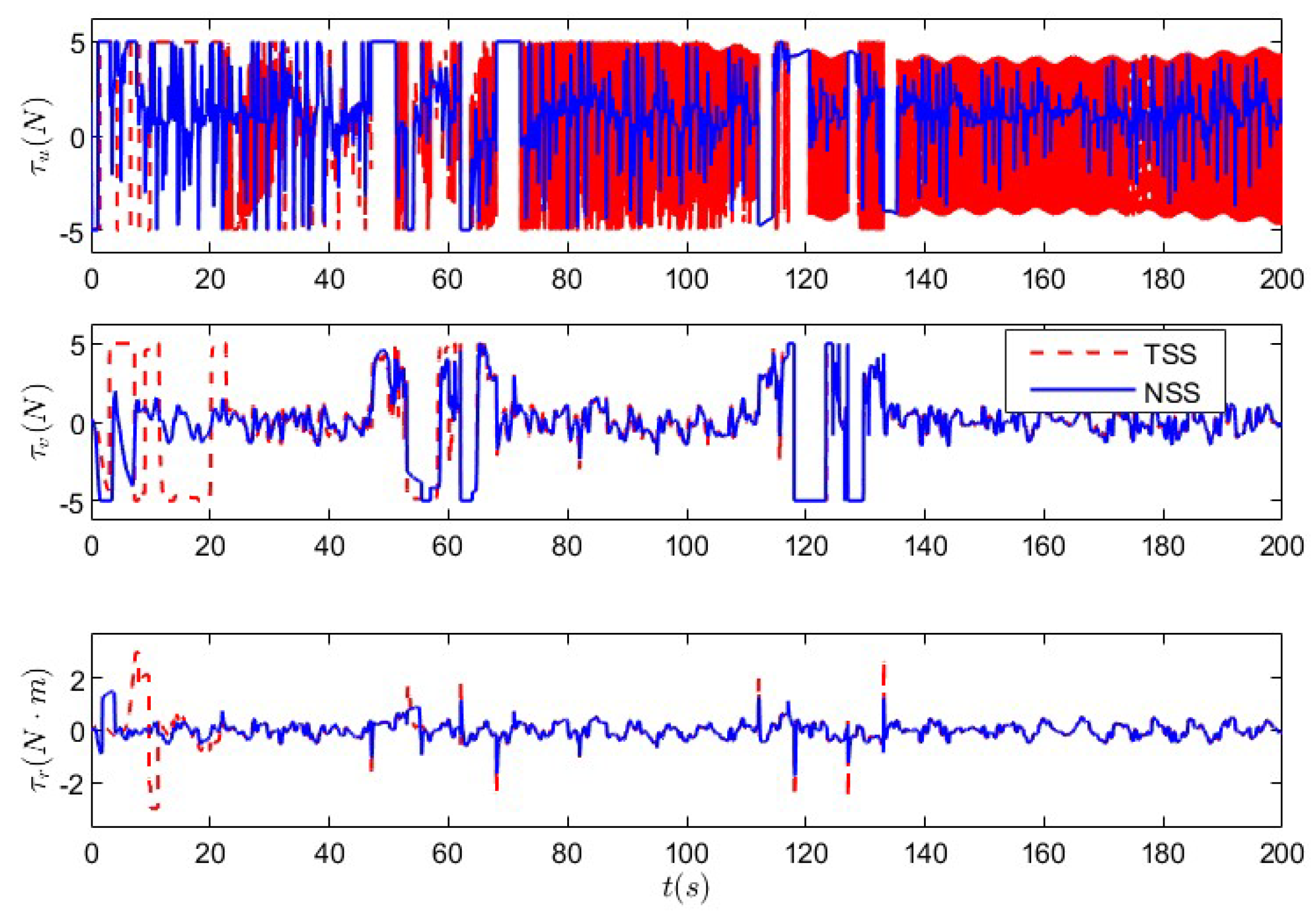
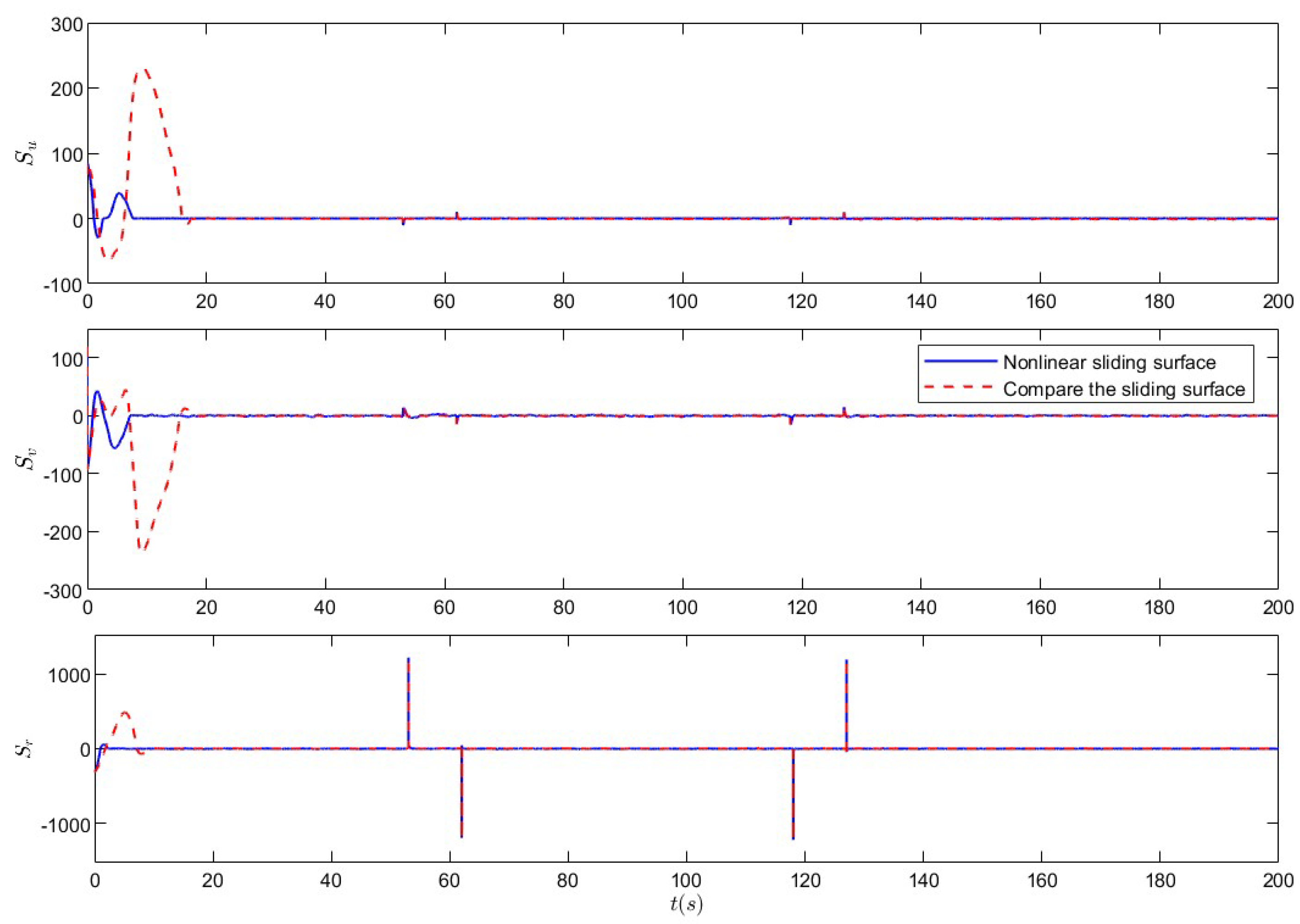
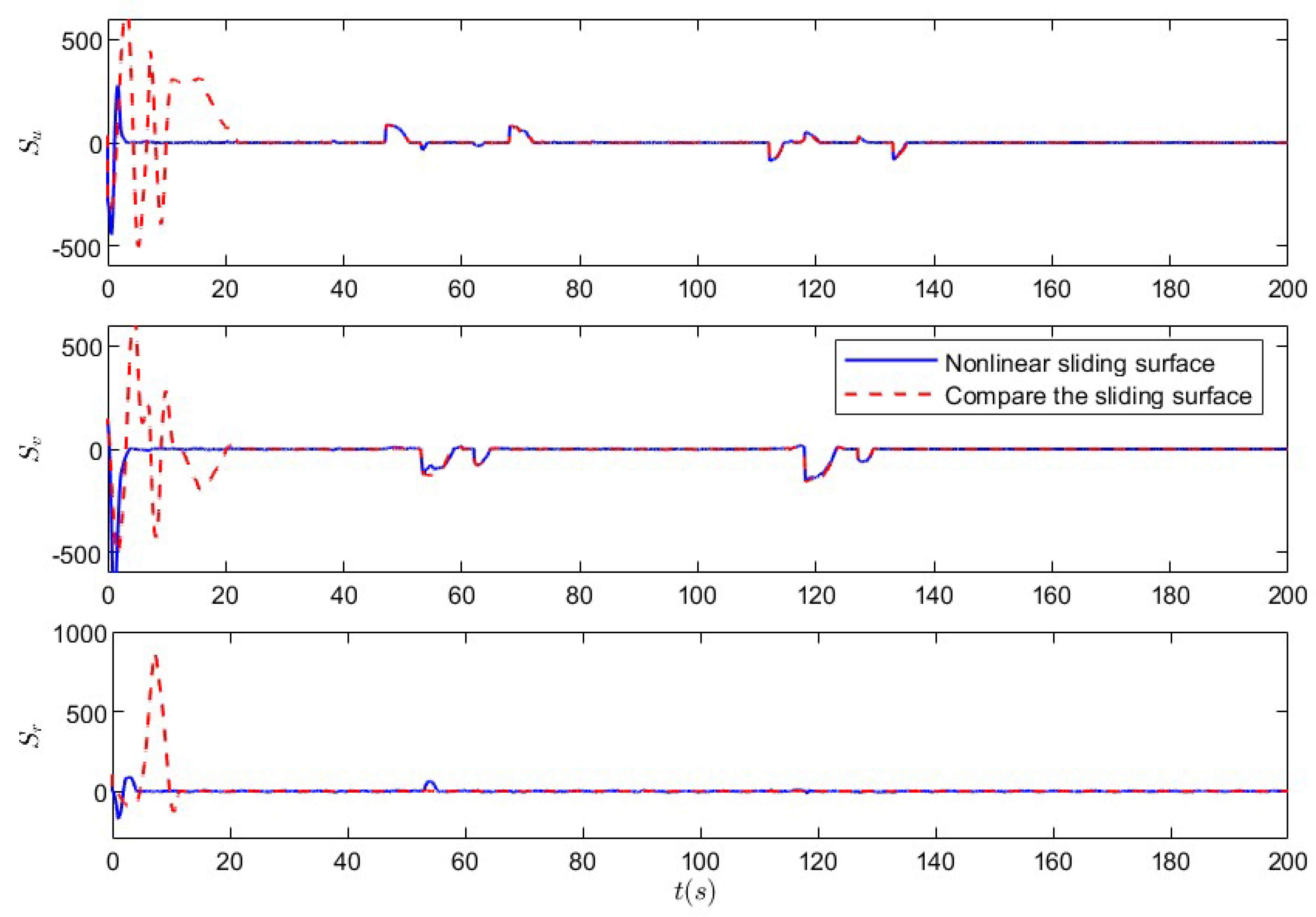
5.1. Nonlinear Sliding-Mode Super-Twisting Reaching Law Control Under Non-Deception Attack
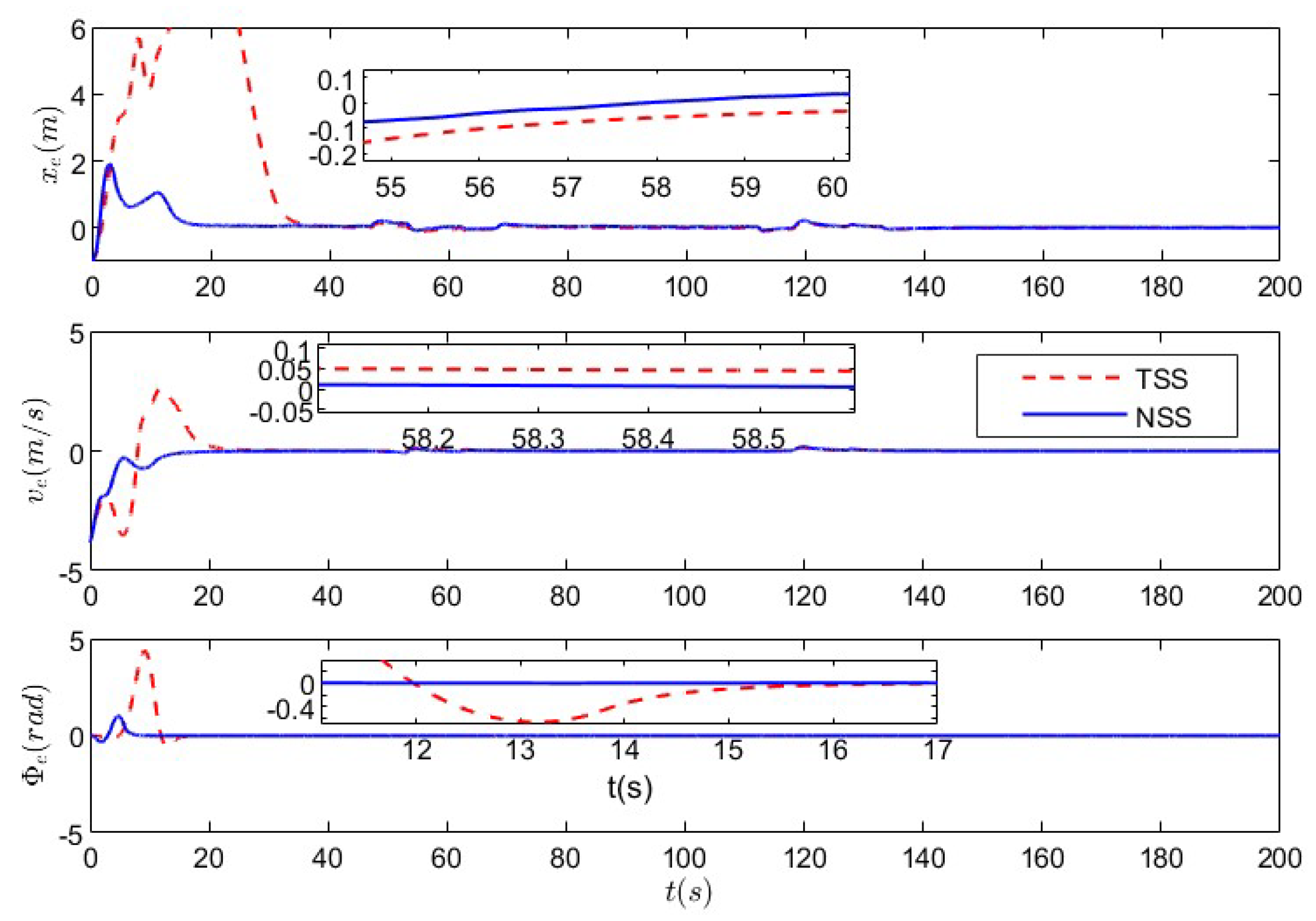
5.2. Nonlinear Sliding-Mode Super-Twisting Reaching Law Control Under Coupled Deception Attack
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NSTRL | Nonlinear super-twisting reaching law |
| PRL | Power reaching law |
| ERL | Exponential reaching law |
| TSS | Traditional sliding surface |
| NSS | Nonlinear sliding surface |
References
- Bai, X.E.; Li, B.H.; Xu, X.F.; Xiao, Y.J. A review of current research and advances in unmanned surface vehicles. J. Mar. Sci. Appl. 2022, 21, 47–58. [Google Scholar] [CrossRef]
- Khanmeh, J.; Wanderlingh, F.; Indiveri, G.; Simetti, E. Design and Control of a Cooperative System of an Autonomous Surface Vehicle and a Remotely Operated Vehicle (ASV-ROV). In Proceedings of the 2024 20th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Genova, Italy, 2–4 September 2024; pp. 1–7. [Google Scholar]
- Qiao, Y.; Yin, J.; Wang, W.; Duarte, F.; Yang, J.; Ratti, C. Survey of Deep Learning for Autonomous Surface Vehicles in Marine Environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3678–3701. [Google Scholar] [CrossRef]
- Zhao, C.; Thies, P.R.; Johanning, L. Investigating the winch performance in an ASV/ROV autonomous inspection system. Appl. Ocean. Res. 2021, 115, 102827. [Google Scholar] [CrossRef]
- Du, J.; Jiang, B.; Jiang, C.; Shi, Y.; Han, Z. Gradient and channel aware dynamic scheduling for over-the-air computation in federated edge learning systems. IEEE J. Sel. Areas Commun. 2023, 41, 1035–1050. [Google Scholar] [CrossRef]
- Ding, L.; Guo, G. Formation control for ship fleet based on backstepping. Control Decis. 2012, 27, 299–303. [Google Scholar]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances. Ocean Eng. 2018, 167, 36–44. [Google Scholar] [CrossRef]
- Lin, A.; Jiang, D.; Zeng, J. Underactuated ship formation control with input saturation. Acta Autom. Sin. 2018, 33, 1496–1504. [Google Scholar]
- Van, M. An enhanced tracking control of marine surface vessels based on adaptive integral sliding-mode control and disturbance observer. ISE Trans. 2019, 90, 30–40. [Google Scholar] [CrossRef]
- Martin, S.C.; Whitcomb, L.L. Nonlinear model-based tracking control of underwater vehicles with three degree-of-freedom fully coupled dynamical plant models: Theory and experimental evaluation. IEEE Trans. Control Syst. Technol. 2018, 26, 404–414. [Google Scholar] [CrossRef]
- Ma, Y.; Qi, X.; Li, Z.; Hu, S.; Sotelo, M.Á. Resilient Control for Networked Unmanned Surface Vehicles With Dynamic Event-Triggered Mechanism Under Aperiodic DoS Attacks. IEEE Trans. Veh. Technol. 2024, 73, 5824–5833. [Google Scholar] [CrossRef]
- Li, M.; Yu, C.; Zhang, X.; Liu, C.; Lian, L. Fuzzy adaptive trajectory tracking control of work-class ROVs considering thruster dynamics. Ocean Eng. 2024, 267, 113232. [Google Scholar] [CrossRef]
- Li, T.; Zhao, R.; Chen, C.L.P.; Fang, L.; Liu, C. Finite-Time Formation Control of Under-Actuated Ships Using Nonlinear sliding-mode Control. IEEE Trans. Cybern. 2018, 48, 3243–3253. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhang, Y.; Zhang, Y.; Nie, Y.; Tang, J.; Zhu, S. Disturbance-observer-based sliding-mode control design for nonlinear unmanned surface vessel with uncertainties. IEEE Access 2019, 7, 148522–148530. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, Z.; Yin, G.; Wang, H. A recurrent neural network based fuzzy sliding-mode control for 4-DOF ROV movements. Ocean Eng. 2022, 256, 111509. [Google Scholar] [CrossRef]
- Schauer, S.; Kalogeraki, E.M.; Papastergiou, S.; Douligeris, C. Detecting sophisticated attacks in maritime environments using hybrid situational awareness. In Proceedings of the 2019 International Conference on Information and Communication Technologies for Disaster Management (ICT-DM), Paris, France, 18–20 December 2019; pp. 1–7. [Google Scholar]
- Li, S.; Cheng, X.; Shi, F.; Zhang, H.; Dai, H.; Zhang, H.; Chen, S. A novel robustness-enhancing adversarial defense approach to AI-powered sea state estimation for autonomous marine vessels. IEEE Trans. Syst. Man Cybern. Syst. 2024, 55, 28–42. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, M.; Xu, J.; Zhang, W. Robust neural event-triggered control for dynamic positioning ships with actuator faults. Ocean Eng. 2020, 207, 107292. [Google Scholar] [CrossRef]
- Hu, S.; Chen, X.; Li, J.; Xie, X. Observer-Based Resilient Controller Design for Networked Stochastic Systems Under Coordinated DoS and FDI Attacks. IEEE Trans. Control. Netw. Syst. 2024, 11, 890–901. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, X.; Ma, Y.; Li, Z.; Malekian, R.; Sotelo, M.A. Path Following Optimization for an Underactuated USV Using Smoothly-Convergent Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6208–6220. [Google Scholar] [CrossRef]
- Erbas, M.; Khalil, S.M.; Tsiopoulos, L. Systematic literature review of threat modeling and risk assessment in ship cybersecurity. Ocean Eng. 2024, 306, 118059. [Google Scholar] [CrossRef]
- Tam, K.; Hopcraft, R.; Moara-Nkwe, K.; Misas, J.P.; Andrews, W.; Harish, A.V.; Giménez, P.; Crichton, T.; Jones, K. Case study of a cyber-physical attack affecting port and ship operational safety. J. Transp. Technol. 2021, 12, 1–27. [Google Scholar] [CrossRef]
- Bhatti, J.; Humphreys, T.E. Hostile control of ships via false GPS signals: Demonstration and detection. Navig. J. Inst. Navig. 2017, 64, 51–66. [Google Scholar] [CrossRef]
- Gao, S.; Peng, Z.; Liu, L.; Wang, D.; Han, Q.-L. Fixed-time resilient edge-triggered estimation and control of surface vehicles for cooperative target tracking under attacks. IEEE Trans. Intell. 2023, 8, 547–556. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Hamdan, M.M.; Baroudi, U.A. Modeling and control of cyber-physical systems subject to cyber attacks: A survey of recent advances and challenges. Neurocomputing 2019, 338, 101–115. [Google Scholar] [CrossRef]
- Ubaleht, J. Importance of Positioning to MASS: The Effect of Jamming and Spoofing on Autonomous Vessel. Master’s Thesis, University of Turku, Turku, Finland, 2022. [Google Scholar]
- Elsisi, M.; Yu, J.T.; Lai, C.C.; Su, C.L. A drone-assisted deep learning based IoT system for monitoring ship emissions in ports considering adversarial attacks. IEEE Trans. Instrum. Meas. 2024, 73, 9506111. [Google Scholar] [CrossRef]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 26, 1292–1306. [Google Scholar] [CrossRef]
- Ohn, S.W.; Namgung, H. Requirements for optimal local route planning of autonomous ships. J. Mar. Sci. Eng. 2022, 11, 17. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.S. Collision risk inference system for maritime autonomous surface ships using COLREGs rules compliant collision avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Chen, X.; Jia, T.; Wang, Z.; Xie, X.; Qiu, J. Practical fixed-time bipartite synchronization of uncertain coupled neural networks subject to deception attacks via dual-channel event-triggered control. IEEE Trans. Cybern. 2023, 54, 3615–3625. [Google Scholar] [CrossRef]
- Yang, W.; Shi, Z.; Zhong, Y. Robust time-varying formation control for uncertain multi-agent systems with communication delays and nonlinear couplings. Int. J. Robust Nonlinear Control. 2024, 34, 147–166. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, S. Disturbance observer-based prescribed performance super-twisting sliding-mode control for autonomous surface vessels. ISA Trans. 2023, 135, 13–22. [Google Scholar] [CrossRef]
- Feng, C.; Chen, W.; Tao, R.; Zhu, D.; Chu, K. Adaptive Super-Spiral Trajectory Tracking sliding-mode Control for Unmanned Vessels. Electron. Meas. Technol. 2024, 47, 37–44. [Google Scholar]
- Liu, W.; Du, J.; Li, J.; Li, Z. Robust Control of Shipborne Stable Platforms Based on Hyperhelix Slip Mode. Syst. Eng. Electron. Technol. 2022, 44, 1662–1669. [Google Scholar]
- Liu, Y.; Xu, C.; Zhao, Y.; Liu, S.; Liang, X. Tracking Control of Underdriven Vessels Based on Hyperhelical sliding-mode. Inf. Control. 2022, 49, 578–584, 597. [Google Scholar]
- Sonnenburg, C.R.; Woolsey, C.A. Modeling. identification, and control of an unmanned surface vehicle. J. Field Robot. 2013, 30, 371–398. [Google Scholar] [CrossRef]
- Dong, Z.; Qi, S.; Yu, M.; Zhang, Z.; Zhang, H.; Li, J.; Liu, Y. An improved dynamic surface sliding-mode method for autonomous cooperative formation control of underactuated USVs with complex marine environment disturbances. Pol. Marit. Res. 2022, 29, 47–60. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Zhang, Z. Adaptive finite-time stabilization of stochastic nonlinear systems subject to full-state constraints and input saturation. IEEE Trans. Autom. Control. 2020, 66, 1306–1313. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L. Event-triggered dynamic output feedback control for networked control systems. IET Control Theory Appl. 2014, 8, 226–234. [Google Scholar] [CrossRef]
- Fallaha, C.J.; Saad, M.; Kanaan, H.Y.; Al-Haddad, K. Sliding-Mode Robot Control With Exponential Reaching Law. IEEE Trans. Ind. Electron. 2011, 58, 600–610. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Mobayen, S. Adaptive global sliding-mode control of underactuated systems using a super-twisting scheme: An experimental study. J. Vib. Control. 2019, 25, 2215–2224. [Google Scholar] [CrossRef]


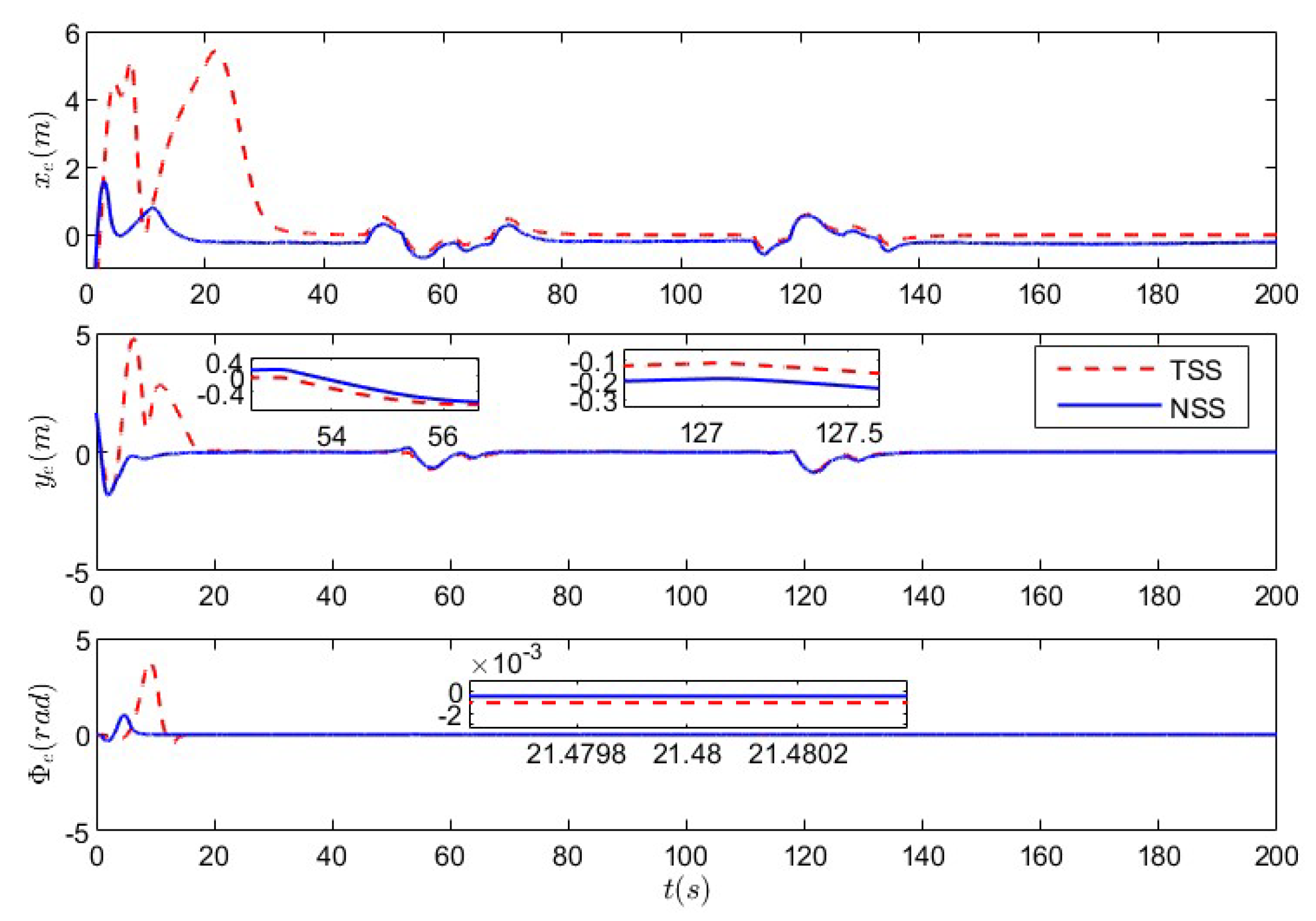
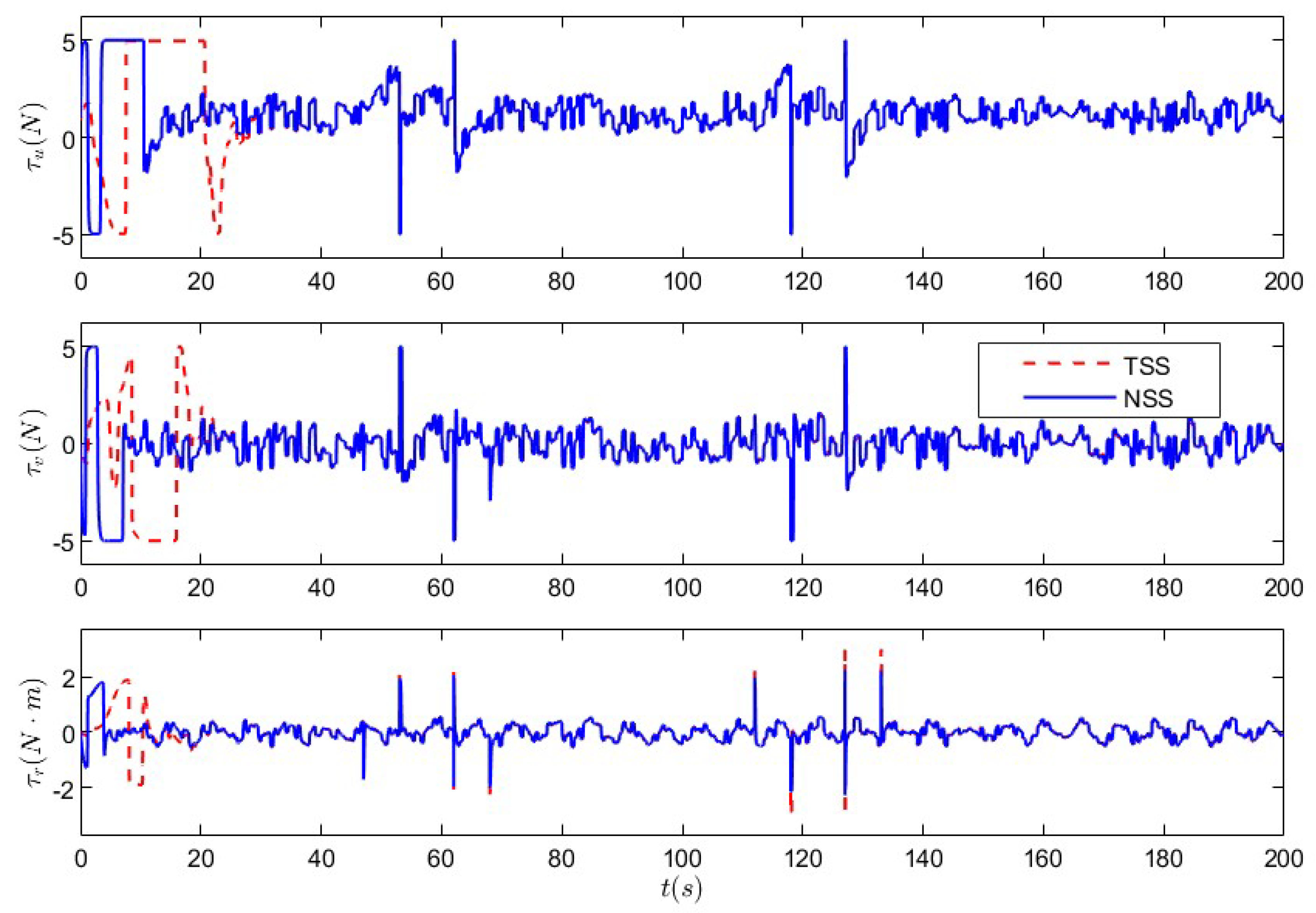
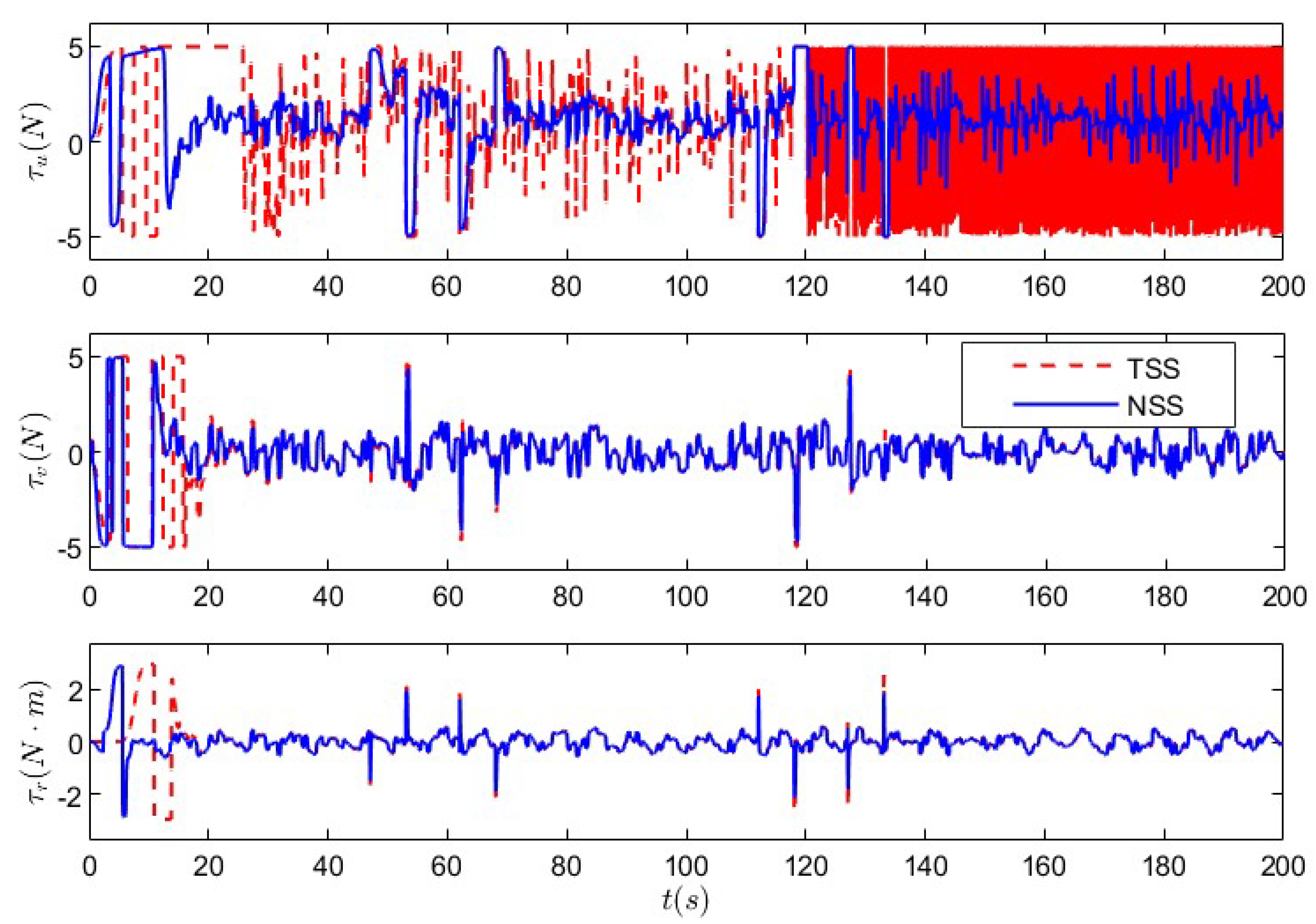

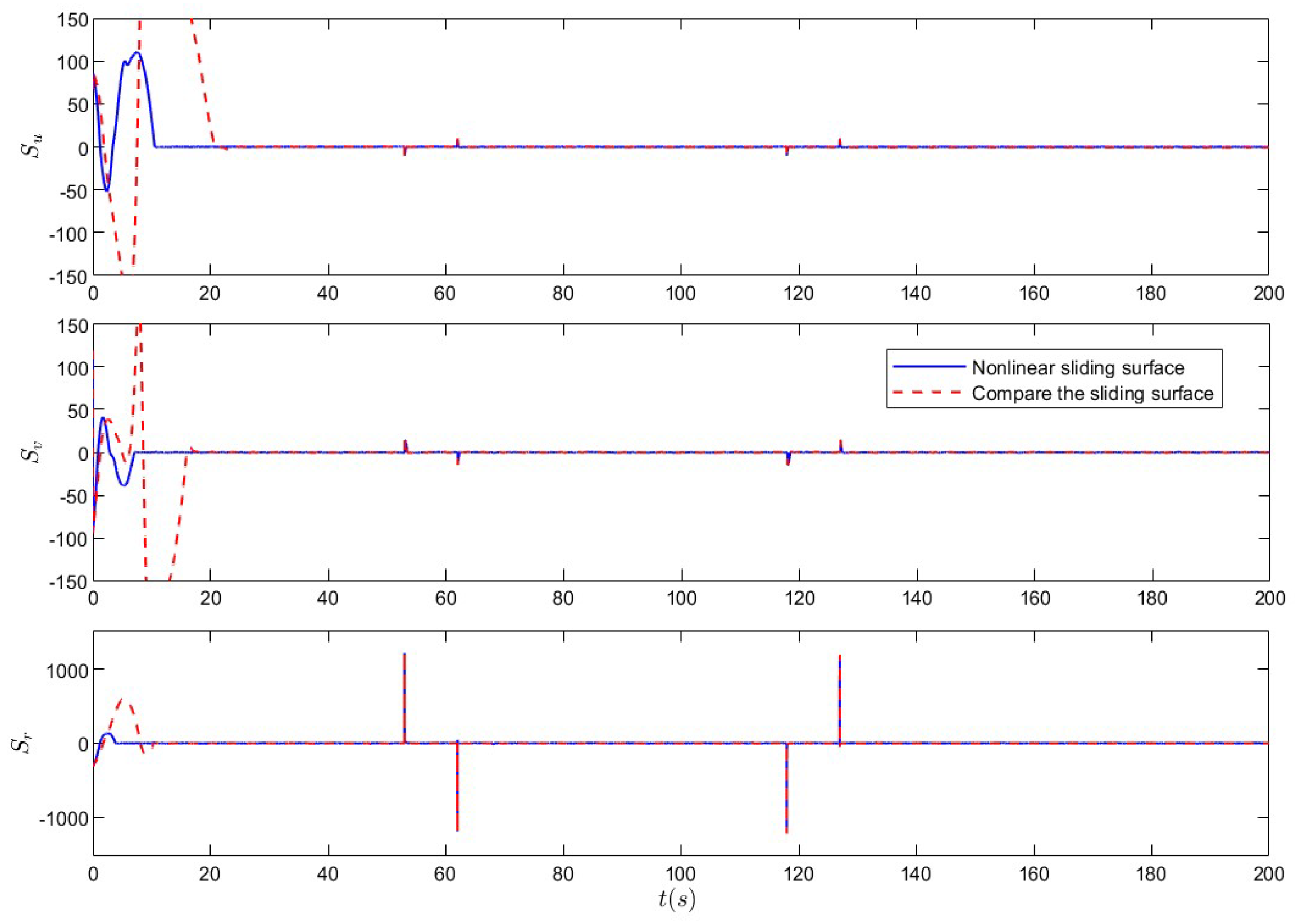




| Improvement Rate | Improvement Rate | Improvement Rate | ||||
|---|---|---|---|---|---|---|
| Leader ship | 7 s | 72% | 8 s | 70.4% | 2 s | 80.0% |
| Comparison leader ship | 25 s | 27 s | 10 s | |||
| Follower ship 1 | 12 s | 64.7% | 12 s | 55.6% | 5 s | 64.3% |
| Comparison follower ship 1 | 34 s | 27 s | 14 s | |||
| Follower ship 2 | 8 s | 76.5% | 12 s | 55.6% | 6 s | 53.8% |
| Comparison follower ship 2 | 34 s | 27 s | 13 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Q.; Zhu, Y.; Hu, Y.; Hu, X. Nonlinear Sliding-Mode Super-Twisting Reaching Law for Unmanned Surface Vessel Formation Control Under Coupling Deception Attacks. J. Mar. Sci. Eng. 2025, 13, 561. https://doi.org/10.3390/jmse13030561
Wang Y, Zhang Q, Zhu Y, Hu Y, Hu X. Nonlinear Sliding-Mode Super-Twisting Reaching Law for Unmanned Surface Vessel Formation Control Under Coupling Deception Attacks. Journal of Marine Science and Engineering. 2025; 13(3):561. https://doi.org/10.3390/jmse13030561
Chicago/Turabian StyleWang, Yifan, Qiang Zhang, Yaping Zhu, Yancai Hu, and Xin Hu. 2025. "Nonlinear Sliding-Mode Super-Twisting Reaching Law for Unmanned Surface Vessel Formation Control Under Coupling Deception Attacks" Journal of Marine Science and Engineering 13, no. 3: 561. https://doi.org/10.3390/jmse13030561
APA StyleWang, Y., Zhang, Q., Zhu, Y., Hu, Y., & Hu, X. (2025). Nonlinear Sliding-Mode Super-Twisting Reaching Law for Unmanned Surface Vessel Formation Control Under Coupling Deception Attacks. Journal of Marine Science and Engineering, 13(3), 561. https://doi.org/10.3390/jmse13030561







