Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process
Abstract
1. Introduction
2. Methodology of the Trawl System (TS) Model
2.1. The Lumped Mass Model
2.2. Equivalent of Trawl Net
2.3. Modeling of the Beam Trawl System in OrcaFlex
2.4. Validation
3. Results and Discussion
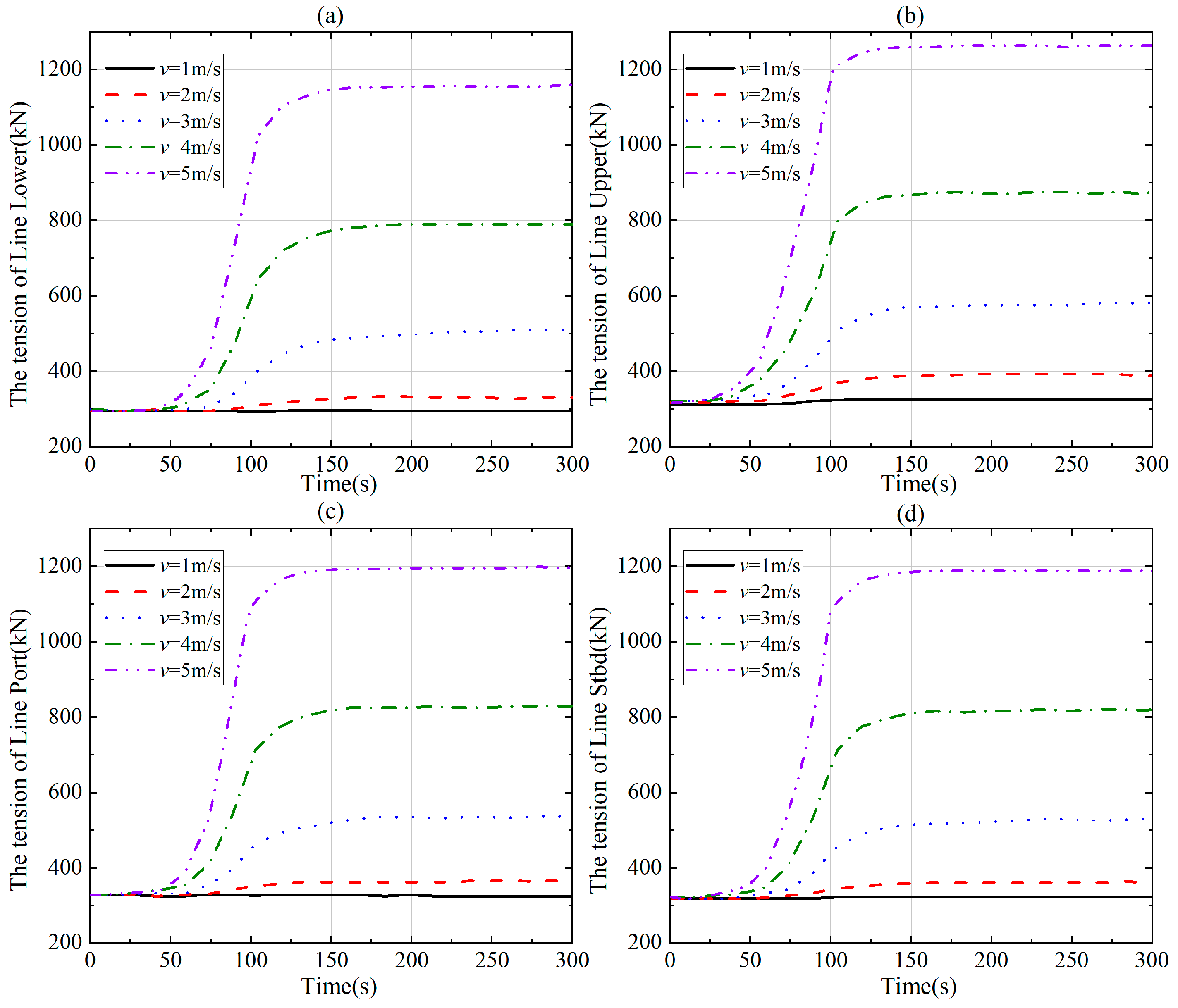
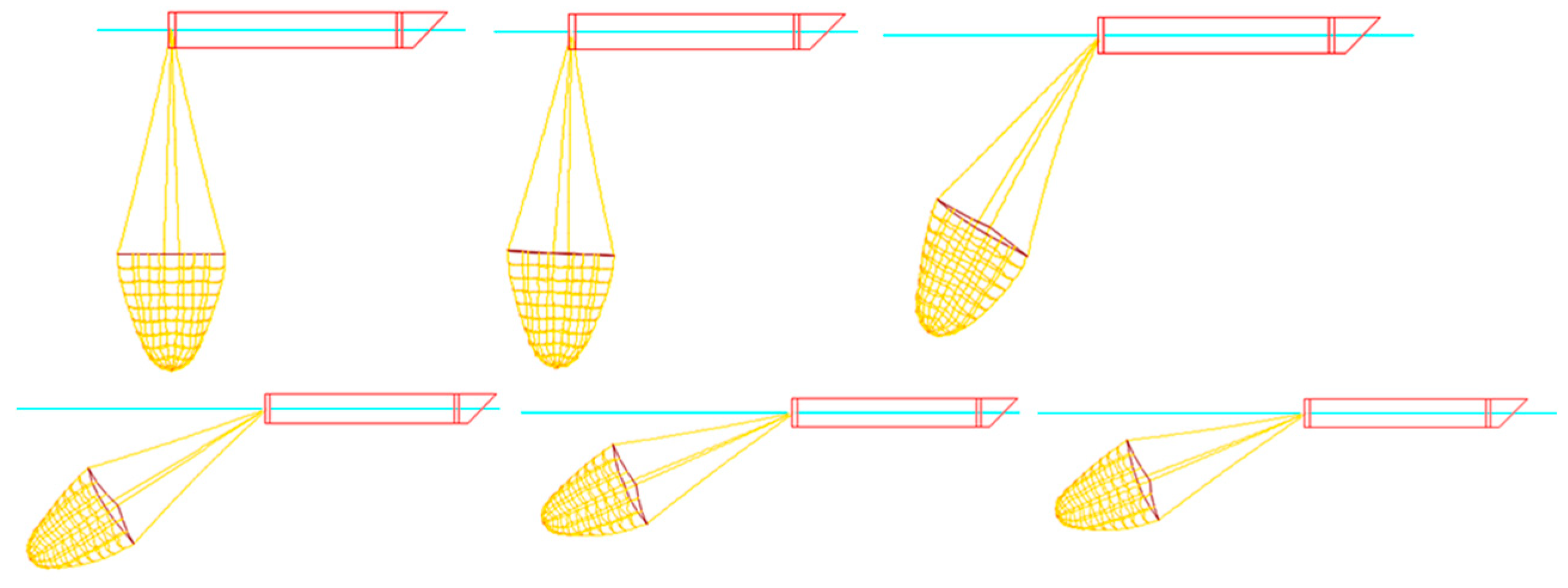
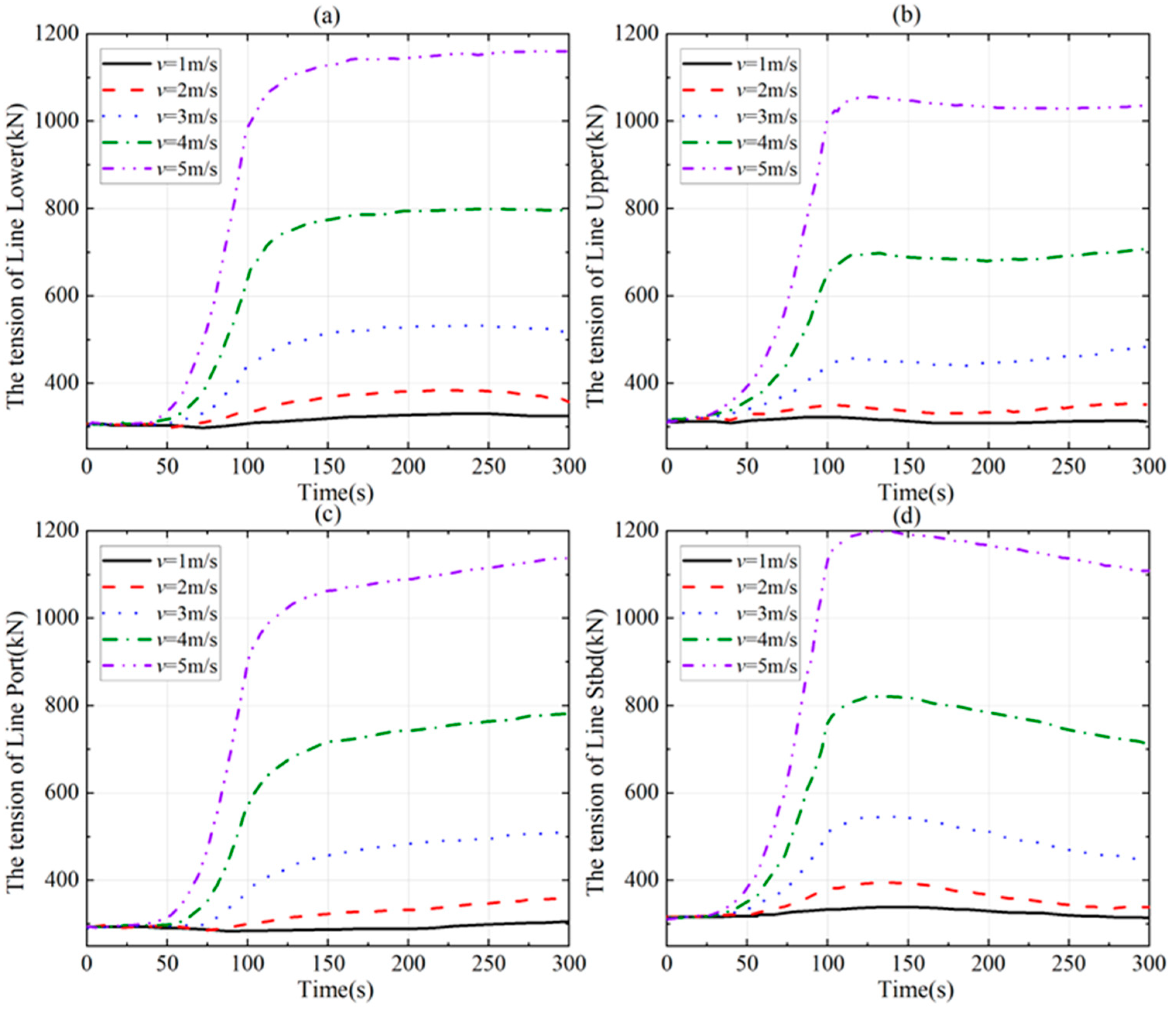
3.1. Effects of the Speeds During Straight-Line Towing
3.2. Effects of the Speeds Under a Fixed Turning Radius
3.3. Effects of the Speeds Under Fixed Angular Velocity
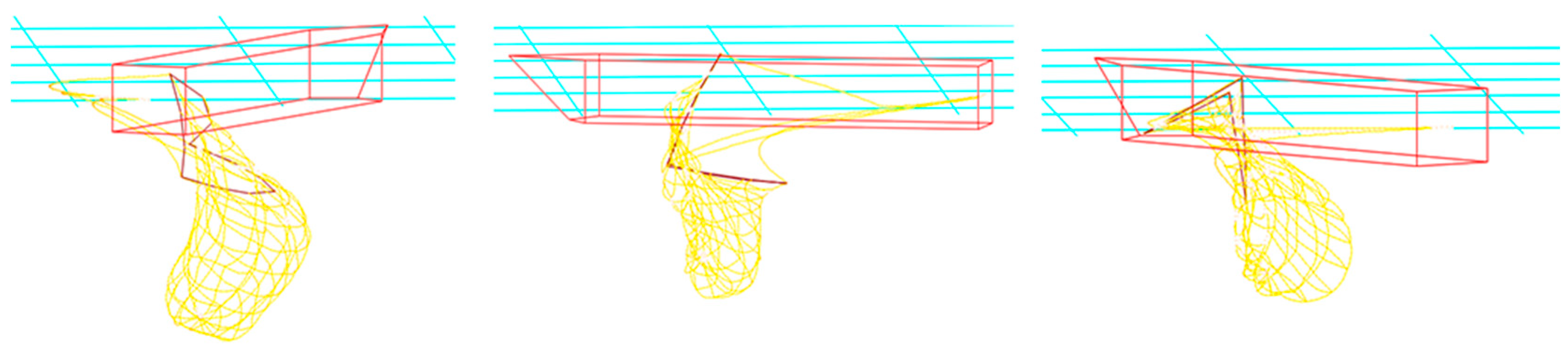
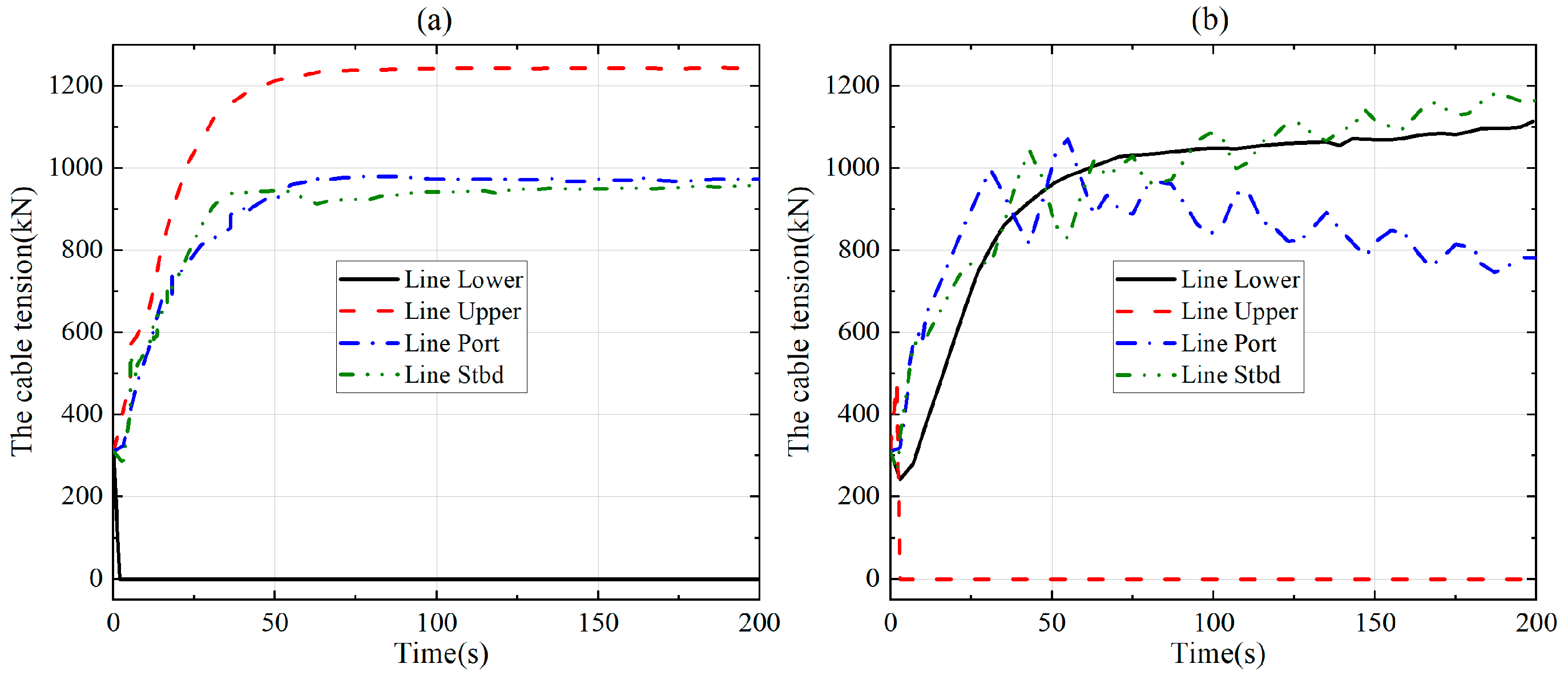
3.4. Dynamic Response of Line Fracture Failure in Startup Phase
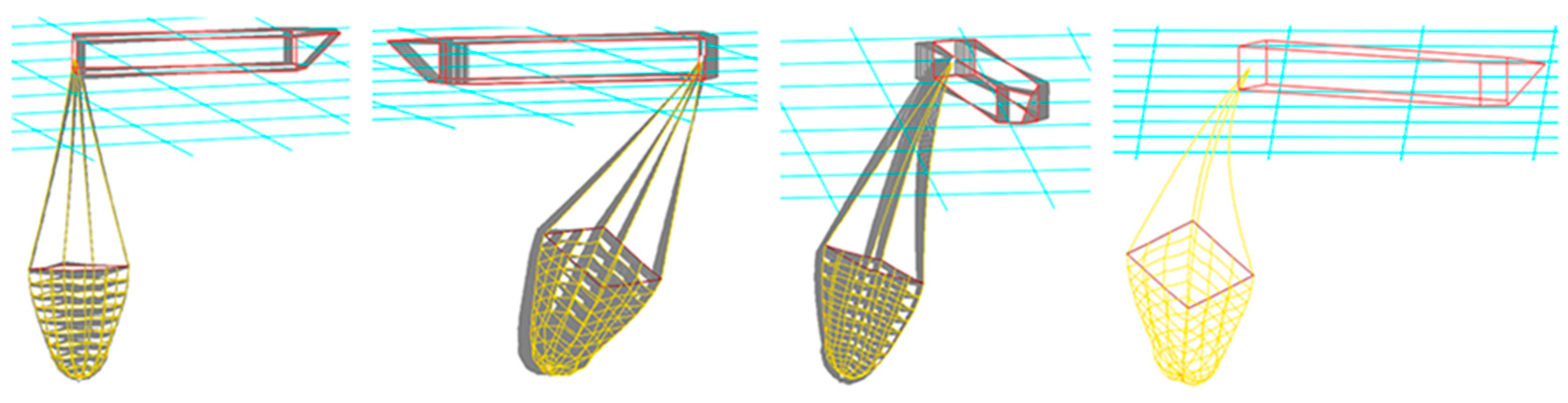
3.5. Dynamic Response of Line Fracture Failure During Straight-Line Towing
4. Conclusions
- (1)
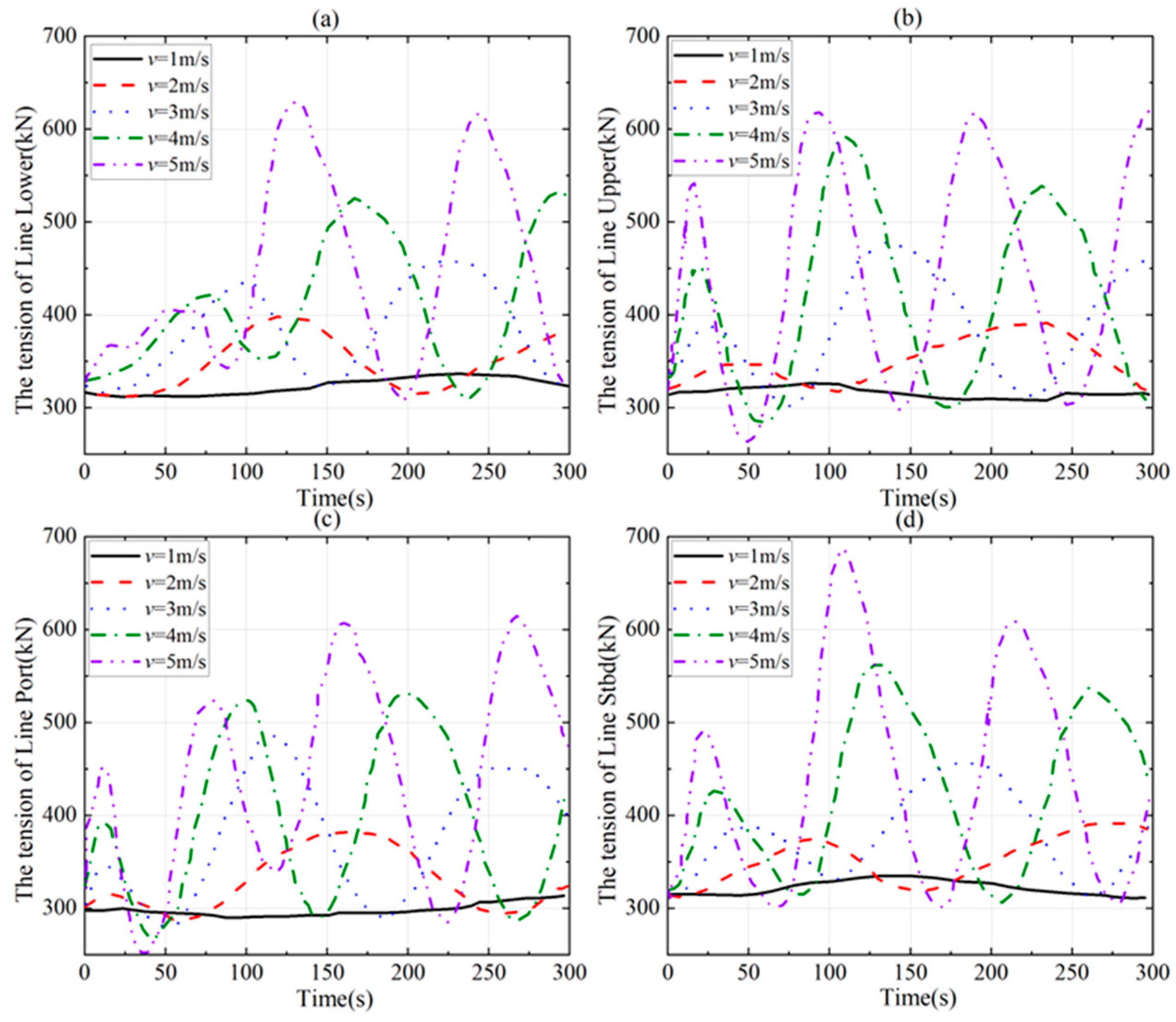
- As the linear towing speed increases, so does the line tension. This increased tension causes the line to stretch along its length, leading to minimal bending deformation during straight-line towing. Thanks to its strong truss structure, changes in towing speed have little impact on the trawl’s shape. At a towing speed of 5 m/s, the maximum axial tension in the four cables reaches 1280 kN (Line Upper). Under a fixed turning radius (57.32 m), angular velocities exceeding 20°/s induce centrifugal overload, driving line tensions to exceed 1200 kN;
- (2)
- During the initial phase of rotational towing, the line tension experiences significant changes, followed by frequent fluctuations over time. As the towing speed increases, the trawl’s overall horizontal floating distance progressively expands. Concurrently, the rate of change in the horizontal turning angle escalates, which in turn amplifies the trawl’s outward floating distance;
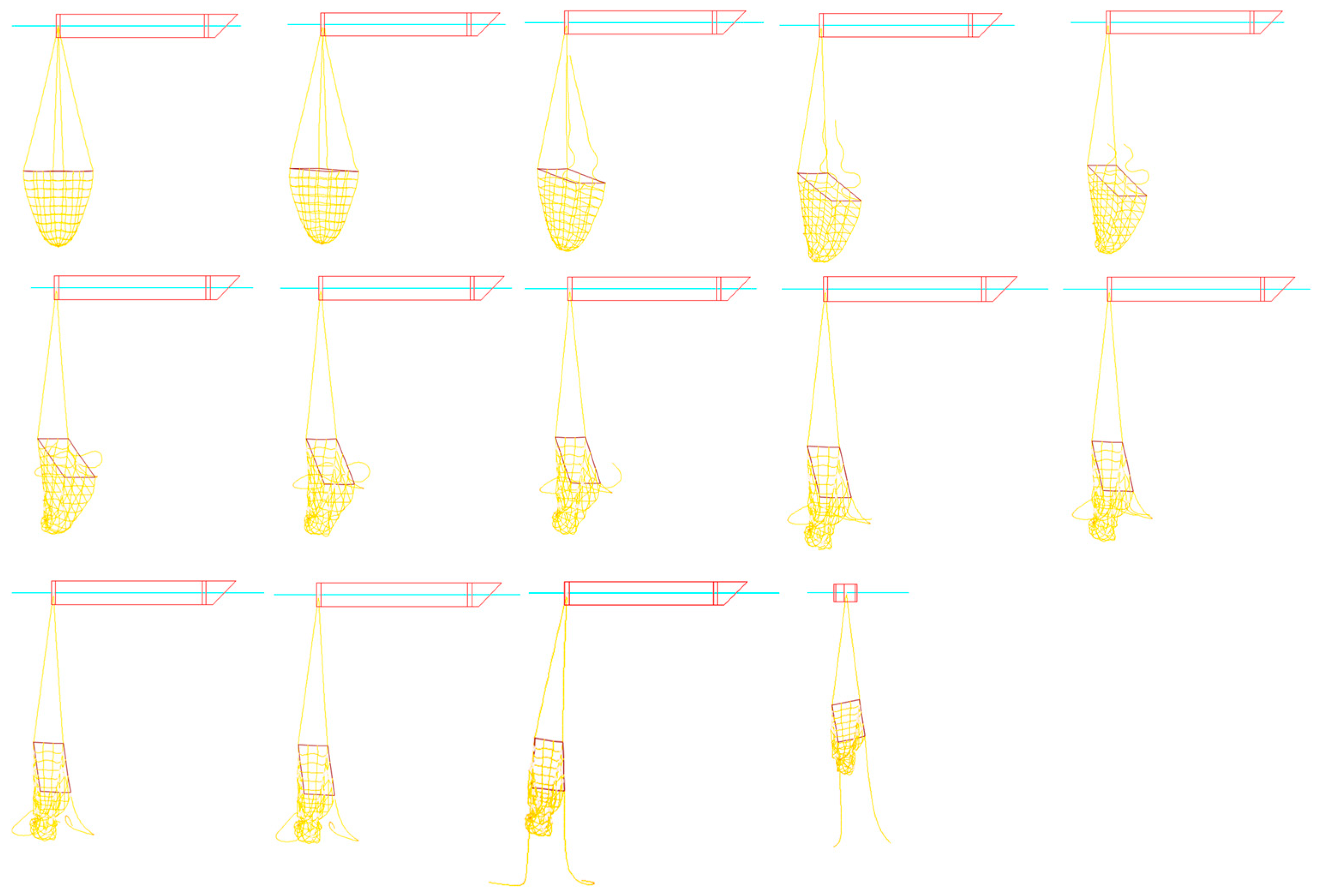
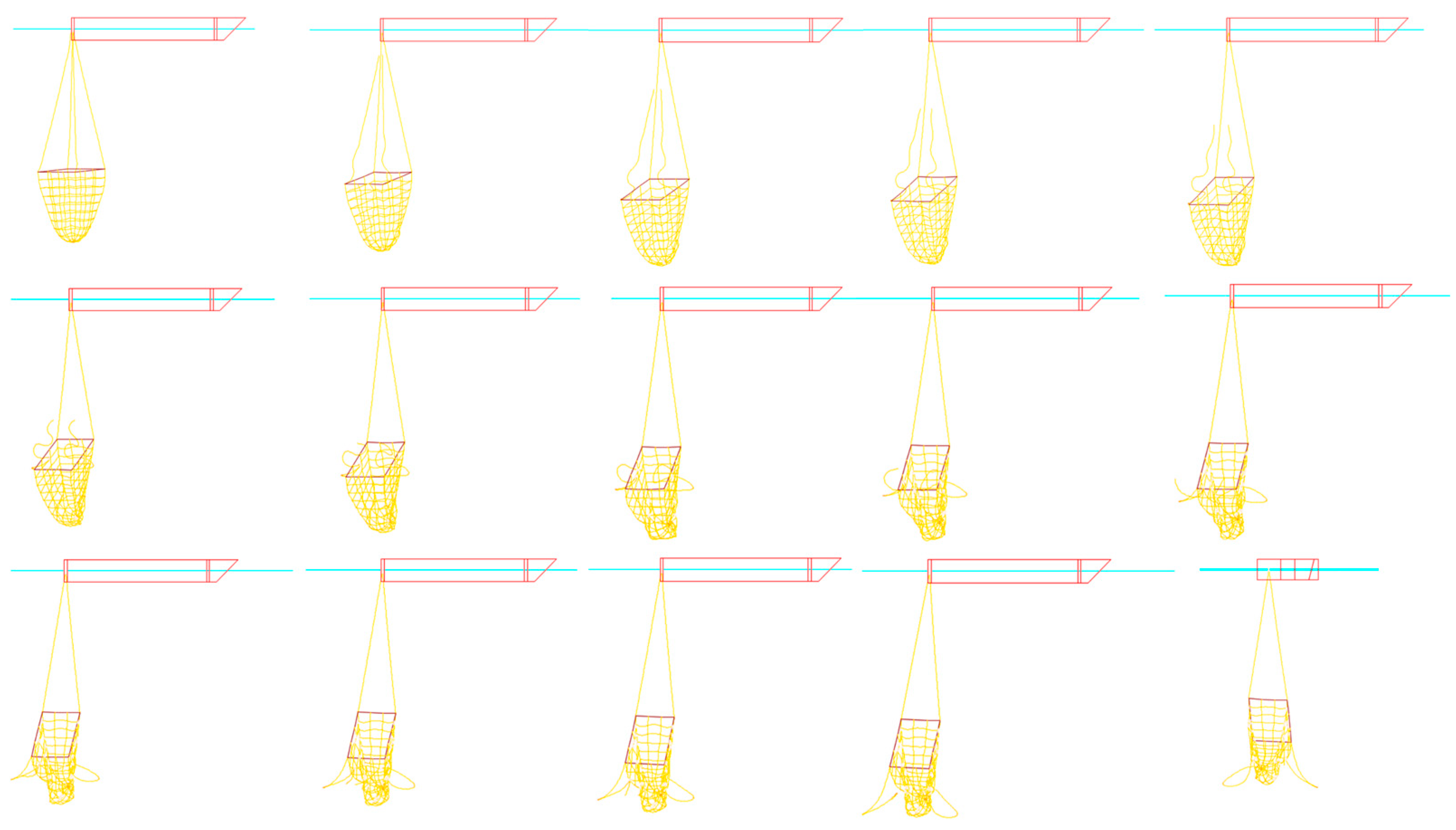
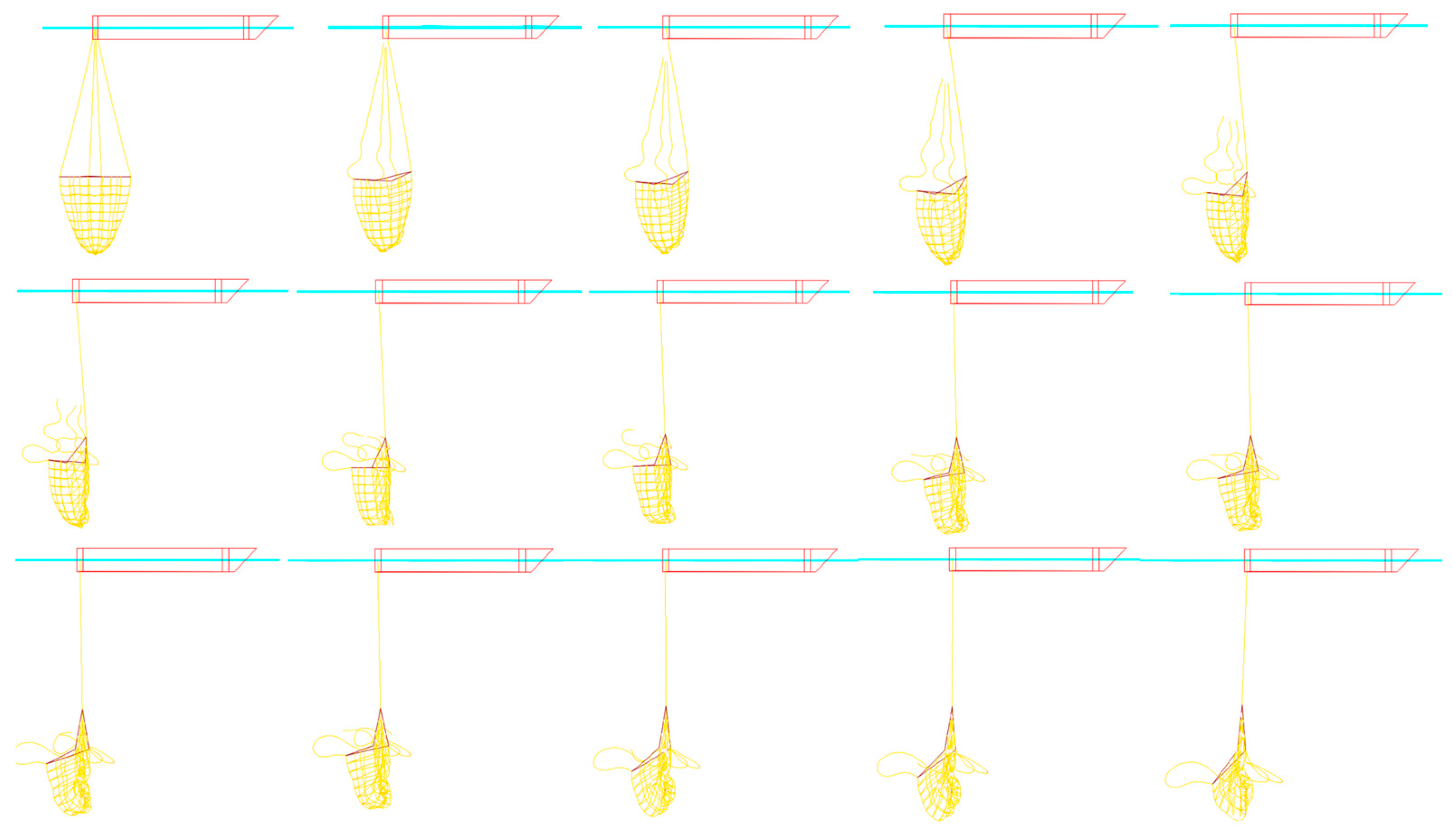
- (3)
- The integrity and operational safety of the trawl system are significantly compromised when the line breaks. No matter which line fails at commencement, the towing box starts to distort quickly as the tensile impact of the line is gone. If two symmetrical lines fail, the trawl quickly collapses from the outside into the interior before flattening out. The square frame of the trawl, which is made up of four stiff frame edges, remains unchanged if two asymmetrical lines break;
- (4)
- During straight-line towing, the fracture of one line leads to a lack of constraints to maintain the edge center of the rigid frame. If one line breaks, the tension on the other lines will be redistributed. These results provide quantitative guidelines for operational parameter optimization: recommended towing speeds ≤ 4 m/s, angular velocities ≤ 20°/s, and redundant cable designs to mitigate abrupt failures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clarke, T.M.; Wabnitz, C.C.; Striegel, S.; Frölicher, T.L.; Reygondeau, G.; Cheung, W.W. Aerobic growth index (AGI): An index to understand the impacts of ocean warming and deoxygenation on global marine fisheries resources. Prog. Oceanogr. 2021, 195, 102588. [Google Scholar] [CrossRef]
- Bax, N.; Novaglio, C.; Maxwell, K.H.; Meyers, K.; McCann, J.; Jennings, S.; Frusher, S.; Fulton, E.A.; Nursey-Bray, M.; Fischer, M.; et al. Ocean resource use: Building the coastal blue economy. Rev. Fish Biol. Fish. 2021, 32, 189–207. [Google Scholar] [CrossRef]
- Zhang, Y.-Z.; Xue, C.; Wang, N.; Chen, G. A comparative study on the measurement of sustainable development of marine fisheries in China. Ocean Coast. Manag. 2023, 247, 106911. [Google Scholar] [CrossRef]
- Konar, M.; Ding, H. A sustainable ocean economy for 2050: Approximating its benefits and costs. In The Blue Compendium: From Knowledge to Action for a Sustainable Ocean Economy; Springer International Publishing: Cham, Switzerland, 2023; pp. 681–714. [Google Scholar]
- Zhuang, X.; You, X.; Kumazawa, T.; Ito, S.; Shiode, D.; Hu, F. Dynamic performance of strategy for transitioning from conventional bottom otter trawling to semi-pelagic trawling through towing tank experiments and numerical simulations. Ocean Eng. 2024, 300, 117436. [Google Scholar] [CrossRef]
- Chu, W.; Cui, S.; Zhai, M.; Cao, Y.; Zhang, X. The influence of flow field bottom effect and sand cloud effect on the hydrodynamic performance and stability of bottom trawling otter board under tilted attitudes. Appl. Ocean Res. 2024, 152, 104176. [Google Scholar] [CrossRef]
- Zhang, D.; Bai, Y.; Soares, C.G. Dynamic analysis of an array of semi-rigid “sea station” fish cages subjected to waves. Aquac. Eng. 2021, 94, 102172. [Google Scholar] [CrossRef]
- Tang, M.F.; Dong, G.H.; Xu, T.J.; Zhao, Y.P.; Bi, C.W. Numerical simulation of the drag force on the trawl net. Turk. J. Fish. Aquat. Sci. 2017, 17, 1219–1230. [Google Scholar]
- Thierry, N.N.B.; Tang, H.; Achille, N.P.; Xu, L.; Hu, F. Unsteady turbulent flow developing inside and around different parts of fluttering trawl net in flume tank. J. Fluids Struct. 2021, 108, 103451. [Google Scholar] [CrossRef]
- Nyatchouba Nsangue, B.T.; Tang, H.; Liu, W.; Xu, L.; Hu, F. Turbulent flow interacting with flexible trawl net structure including simulation catch in flume tank. Sci. Rep. 2023, 13, 6249. [Google Scholar] [CrossRef]
- Thierry, N.N.; Tang, H.; Liuxiong, X.; You, X.; Hu, F.; Achile, N.P.; Kindong, R. Hydrodynamic performance of bottom trawls with different materials, mesh sizes, and twine thicknesses. Fish. Res. 2020, 221, 105403. [Google Scholar] [CrossRef]
- Dealteris, J.T.; Recksiek, C.W.; Fahfouhi, A.; Liuxiong, X. Comparison of the Performance of Two Bottom-Sampling Trawls. Trans. Am. Fish. Soc. 1989, 118, 119–130. [Google Scholar] [CrossRef]
- Buxton, N.; DeAlteris, J. Quantification of water flow and net drag in midwater trawls. Fish. Res. 1993, 16, 165–178. [Google Scholar] [CrossRef]
- Fuxiang, H.; Matuda, K.; Tokai, T.; Kanehiro, H. Dynamic Analysi of Midwater Trawl System by a Two-Dimensional Lumped Mass Method. Fish. Sci. 1995, 61, 229–233. [Google Scholar] [CrossRef]
- Sangster, G.I.; Breen, M. Gear performance and catch comparison trials between a single trawl and a twin rigged gear. Fisheries Research 1998, 36, 15–26. [Google Scholar] [CrossRef]
- Reite, K.-J.; Sorensen, A. Mathematical Modeling of the Hydrodynamic Forces on a Trawl Door. IEEE J. Ocean. Eng. 2006, 31, 432–453. [Google Scholar] [CrossRef]
- Sala, A.; Farran, J.D.P.; Antonijuan, J.; Lucchetti, A. Performance and impact on the seabed of an existing- and an experimental-otterboard: Comparison between model testing and full-scale sea trials. Fish. Res. 2009, 100, 156–166. [Google Scholar] [CrossRef]
- Sun, X.; Yin, Y.; Jin, Y.; Zhang, X.; Zhang, X. The modeling of single-boat, mid-water trawl systems for fishing simulation. Fish. Res. 2011, 109, 7–15. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Gui, F.-K.; Xu, T.-J.; Chen, X.-F.; Cui, Y. Numerical analysis of dynamic behavior of a box-shaped net cage in pure waves and current. Appl. Ocean Res. 2013, 39, 158–167. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhao, B.; Ma, Y.; Si, K. Exploring subsea dynamics: A comprehensive review of underwater pipelines and cables. Phys. Fluids 2024, 36, 101304. [Google Scholar] [CrossRef]
- Zhang, D.; Yan, J.; Zhu, K. Hydrodynamic characteristics of deep sea station cage under different failure modes of mooring cables. J. G. Ocean U. 2022, 42, 107–116. (In Chinese) [Google Scholar]
- Li, F.; Song, L.; Hua, C.; Zhu, Q. Numerical and experimental investigation on hydrodynamic performance of the stick-held dip net in Pacific saury fishery. Front. Mar. Sci. 2022, 9, 985086. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, F.; Wan, R.; Wang, Y.; Guo, S.; Yan, H.; Zhou, C. Hydrodynamic characteristics of frustum-type depressor for sampling midwater trawl. Ocean Eng. 2024, 295, 117009. [Google Scholar] [CrossRef]
- Guan, Q.; Zhu, W.; Feng, C.; Chen, F.; Tang, W.; Liu, L.; Chen, J. Hydrodynamic interactions between a sorting grid and a demersal trawl. Ocean Eng. 2024, 304, 117837. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, X.; Guo, Y.; Fu, Z. Study on ice resistance of Antarctic krill ship with trawl under floating ice sea conditions. Front. Mar. Sci. 2024, 11, 1357331. [Google Scholar] [CrossRef]
- O’Neill, F.; Breddermann, K. The contribution of mesh opening angle to the drag of netting panels. Ocean Eng. 2024, 305, 117959. [Google Scholar] [CrossRef]
- Tang, H.; Thierry, N.N.B.; Pandong, A.N.; Sun, Q.; Xu, L.; Hu, F.; Zou, B. Hydrodynamic and turbulence flow characteristics of fishing nettings made of three twine materials at small attack angles and low Reynolds numbers. Ocean Eng. 2022, 249, 110964. [Google Scholar] [CrossRef]
- Nsangue, B.T.N.; Tang, H. Flow field and nonlinear dynamics of the gillnet structures under steady flow using a one-way coupling model. Ocean Eng. 2024, 309, 118380. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Wang, Z.; Zhang, X.; Wang, L.; Zhang, Y.; Ma, S.; Qi, G.; Wang, Y. Study on the Hydrodynamic Performance of the Beam Used in the Antarctic Krill Beam Trawl. Fishes 2023, 9, 17. [Google Scholar] [CrossRef]
- Rijnsdorp, A.D.; Depestele, J.; Molenaar, P.; Eigaard, O.R.; Ivanović, A.; O’neill, F.G. Sediment mobilization by bottom trawls: A model approach applied to the Dutch North Sea beam trawl fishery. ICES J. Mar. Sci. 2021, 78, 1574–1586. [Google Scholar] [CrossRef]
- He, R.; Zheng, H.; Ma, S.; Wu, Y.; Yang, S.; Dai, Y.; Wang, Y. Hydrodynamic simulation and experiment of depth adjustable beam trawl for Antarctic krill. J. Mar. Sci. Technol. 2023, 28, 399–409. [Google Scholar] [CrossRef]
- Sen, D. A Study on Sensitivity of Maneuverability Performance on the Hydrodynamic Coefficients for Submerged Bodies. J. Ship Res. 2000, 44, 186–196. [Google Scholar] [CrossRef]
- Kristiansen, D.; Faltinsen, O.M. Non-linear wave-induced motions of cylindrical-shaped floaters of fish farms. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2009, 223, 361–375. [Google Scholar] [CrossRef]
- Orcina. OrcaFlex Manual 2015. Available online: http://www.orcina.com/SoftwareProducts/OrcaFlex/Validation/index/.pdf (accessed on 25 December 2024).
- Suzuki, K.; Takagi, T.; Shimizu, T.; Hiraishi, T.; Yamamoto, K.; Nashimoto, K. Validity and visualization of a numerical model used to determine dynamic configurations of fishing nets. Fish. Sci. 2003, 69, 695–705. [Google Scholar] [CrossRef]
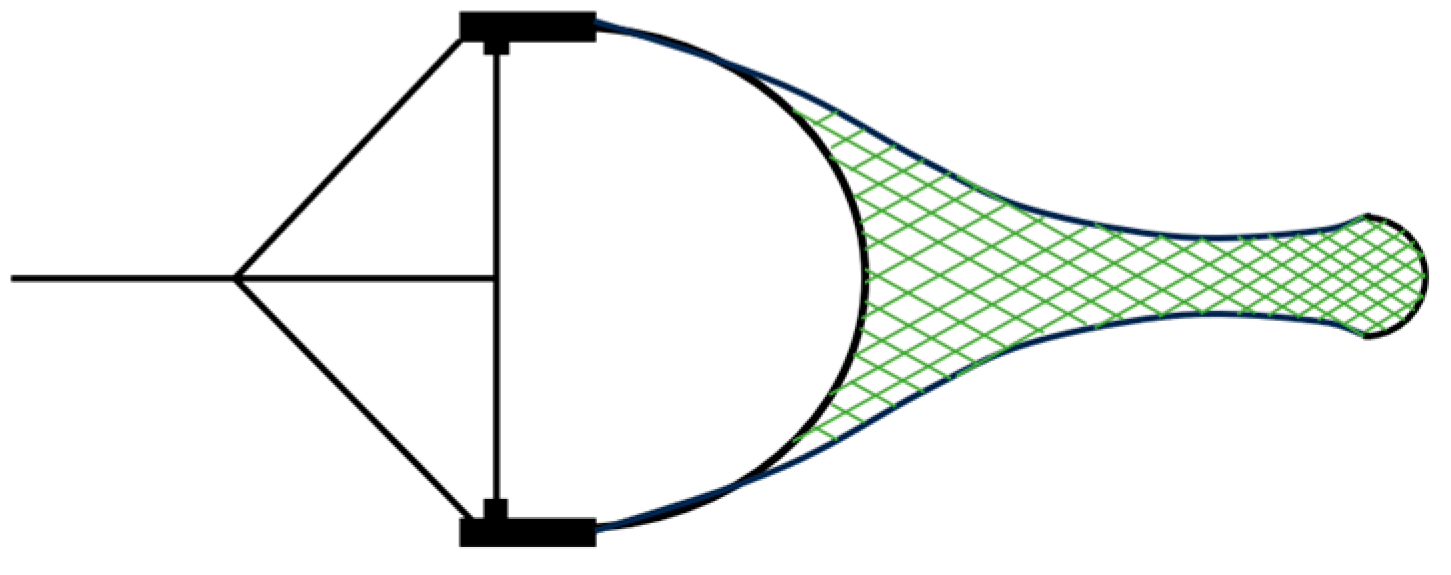

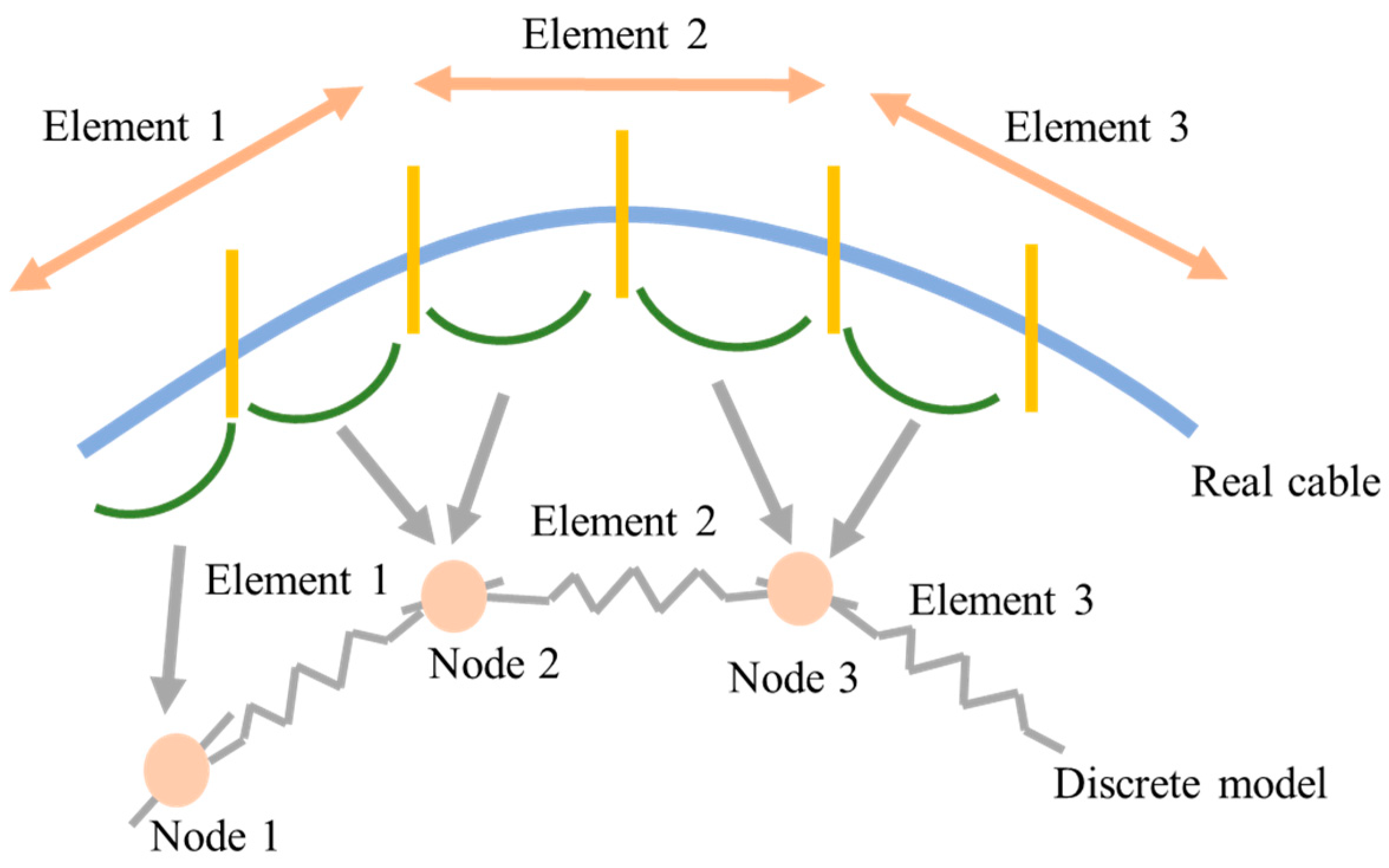
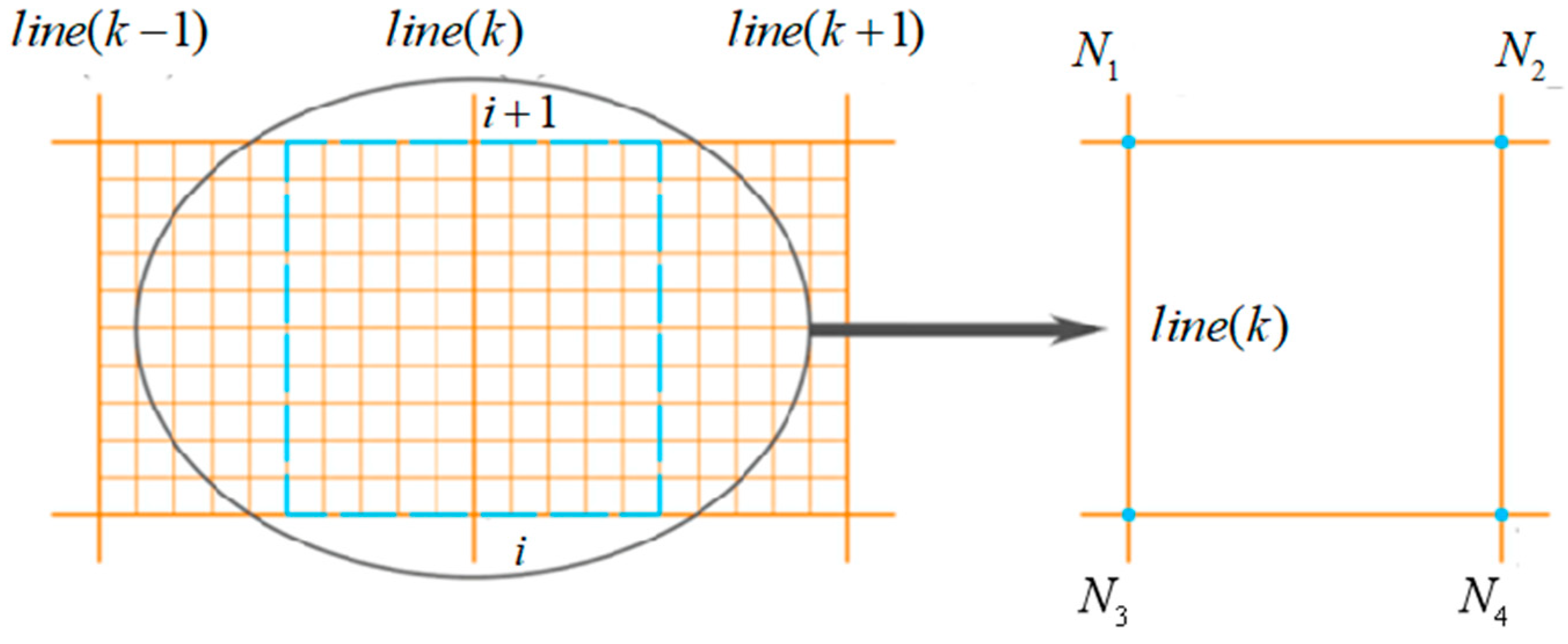
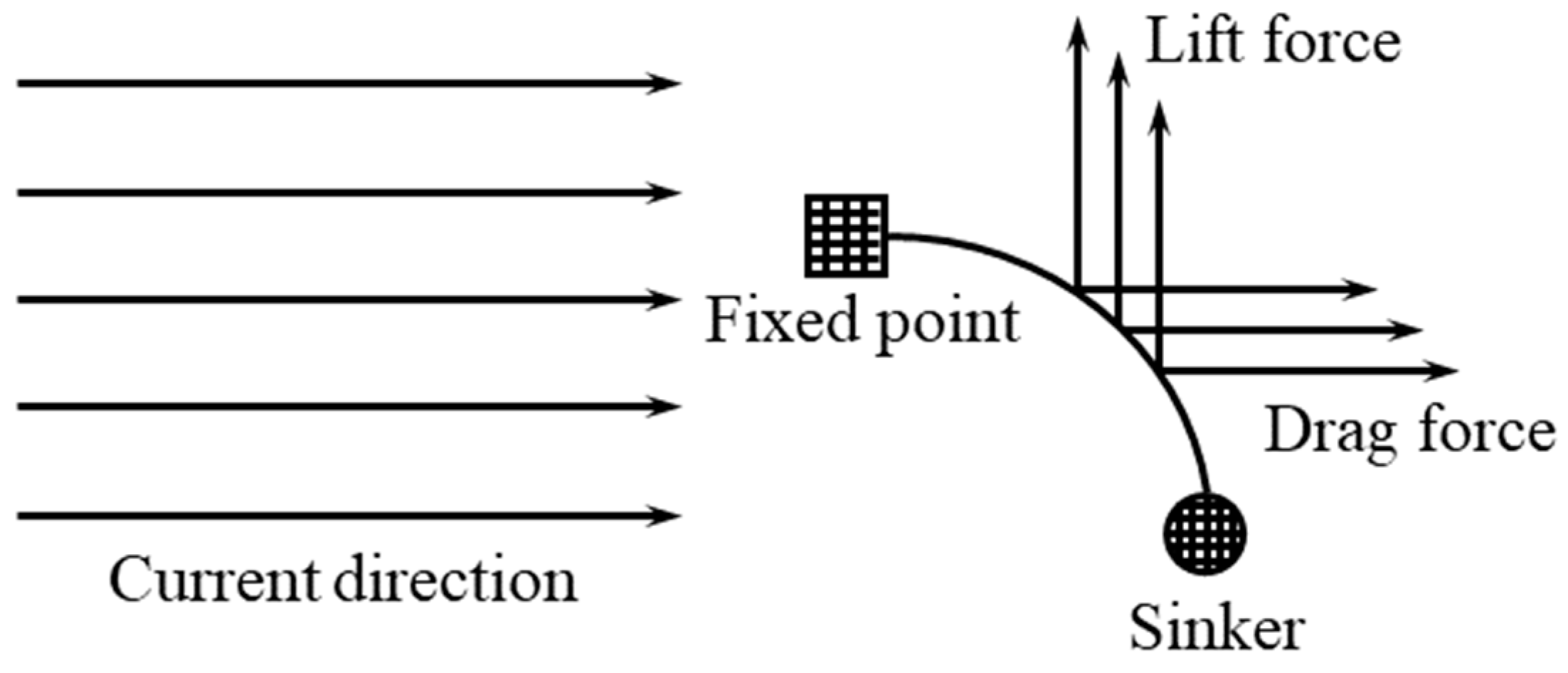
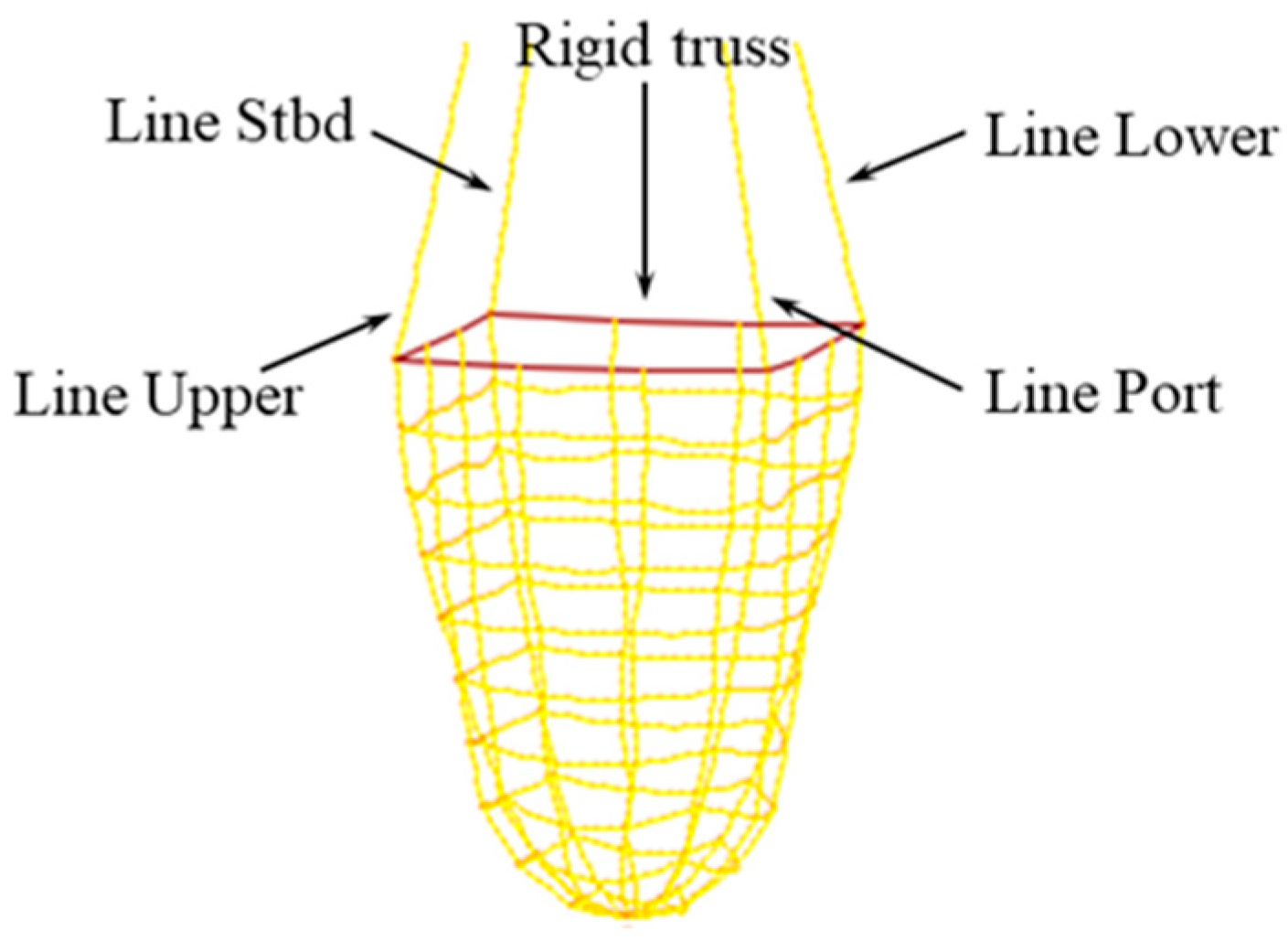

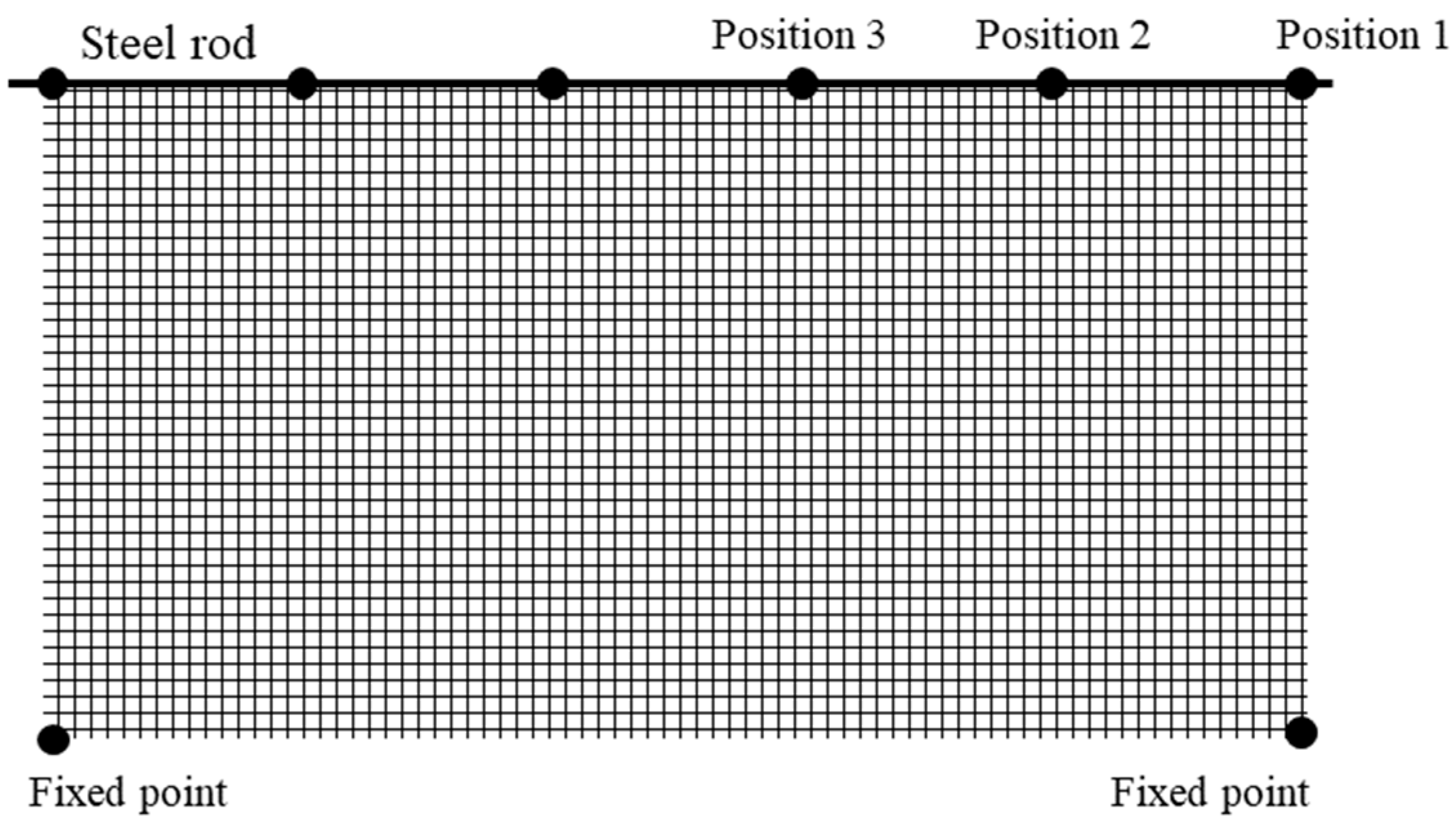
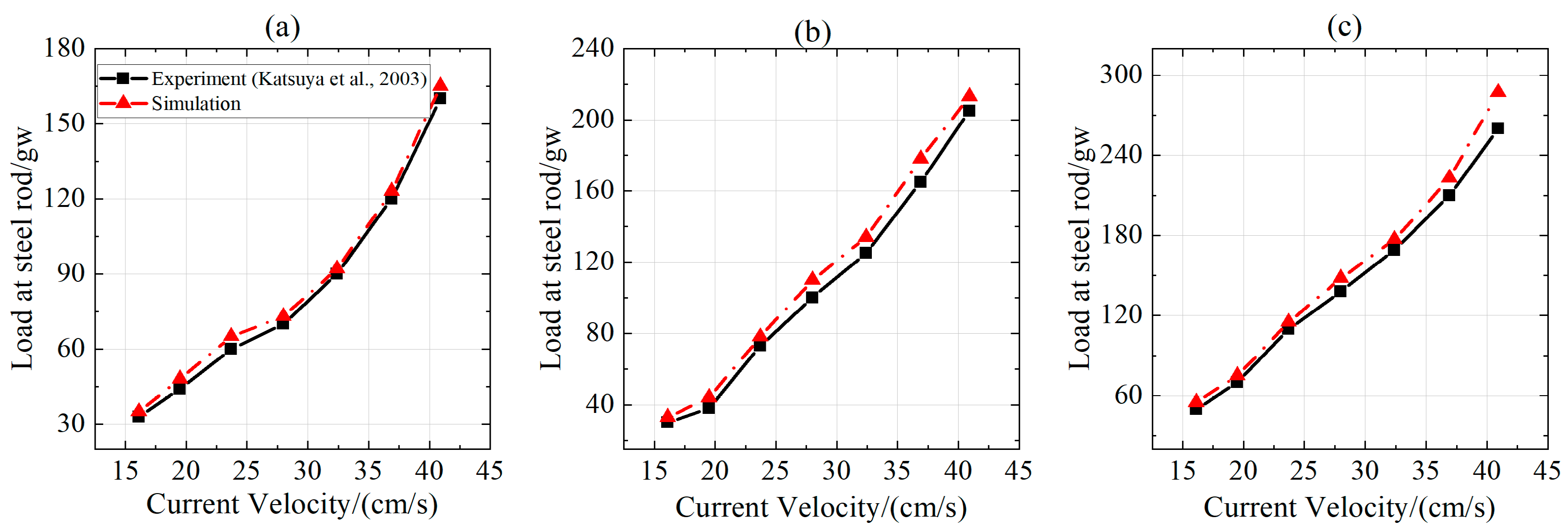
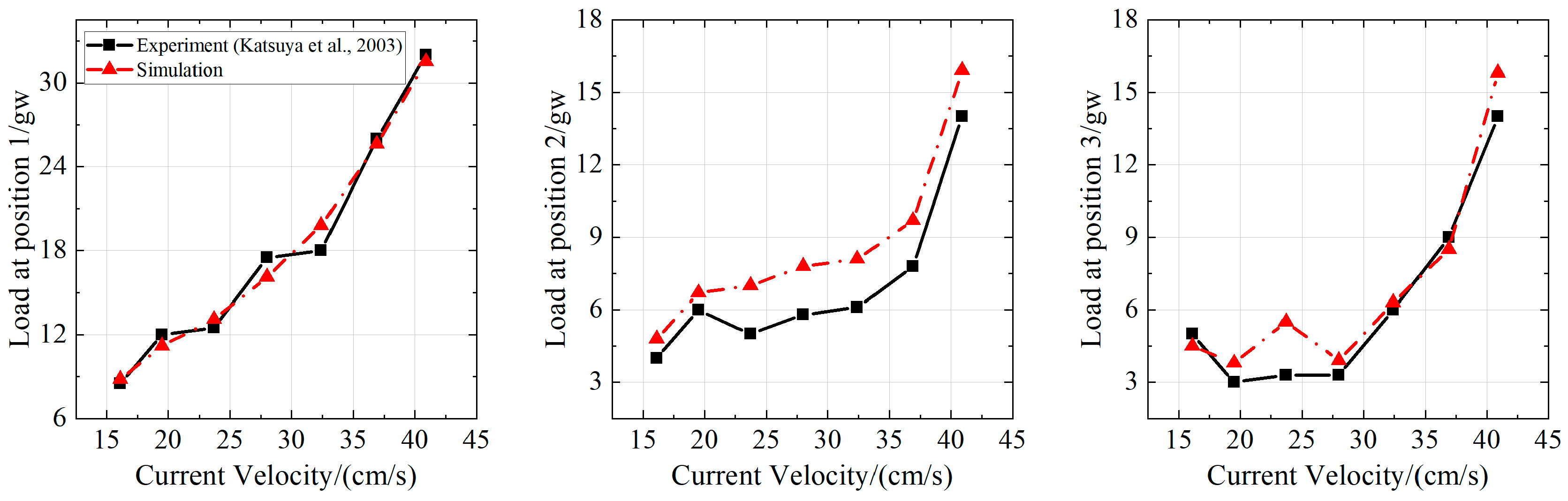
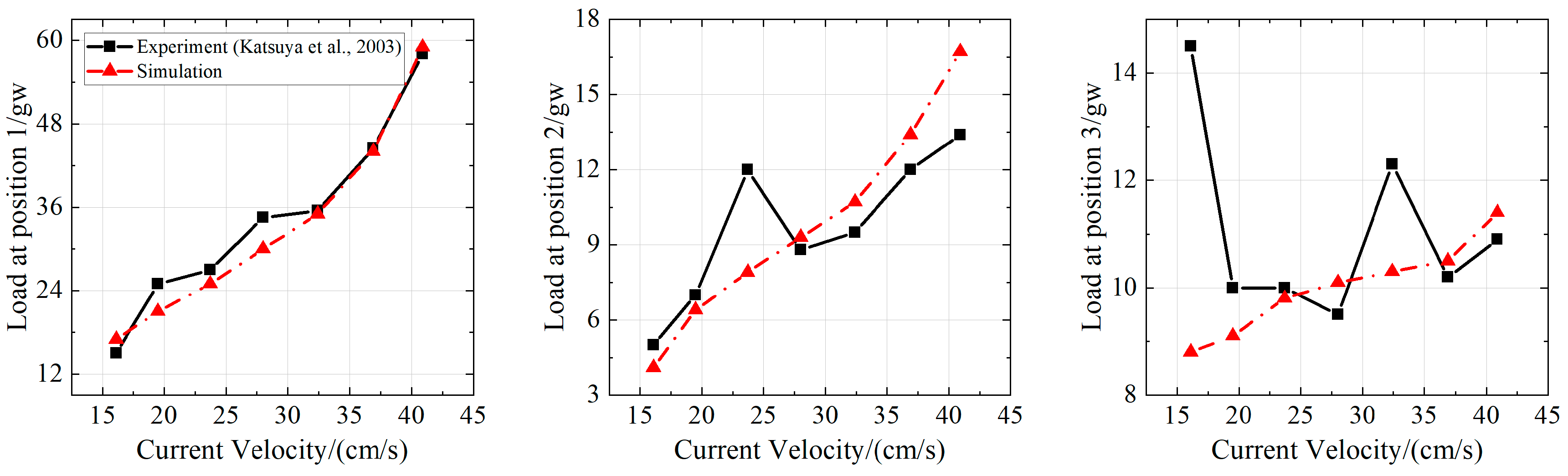






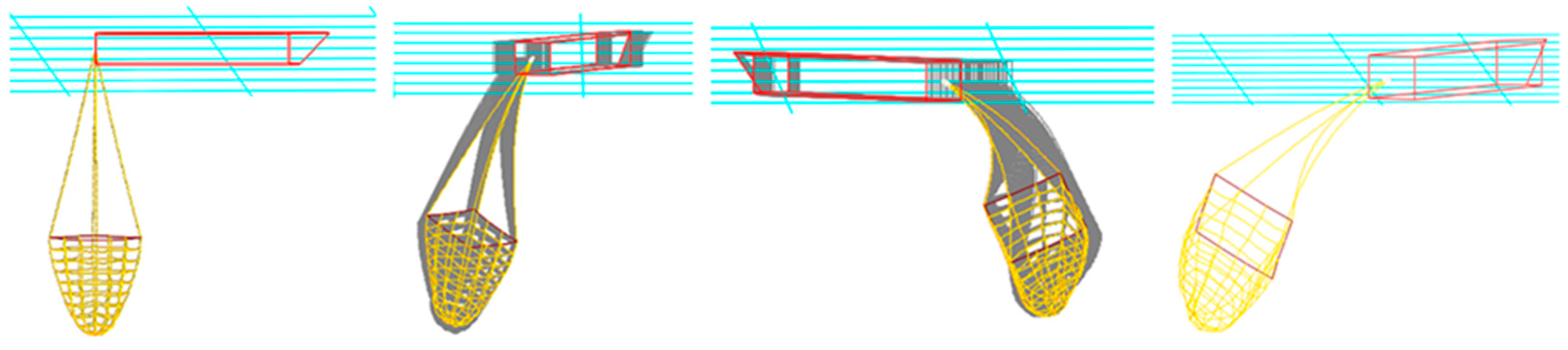
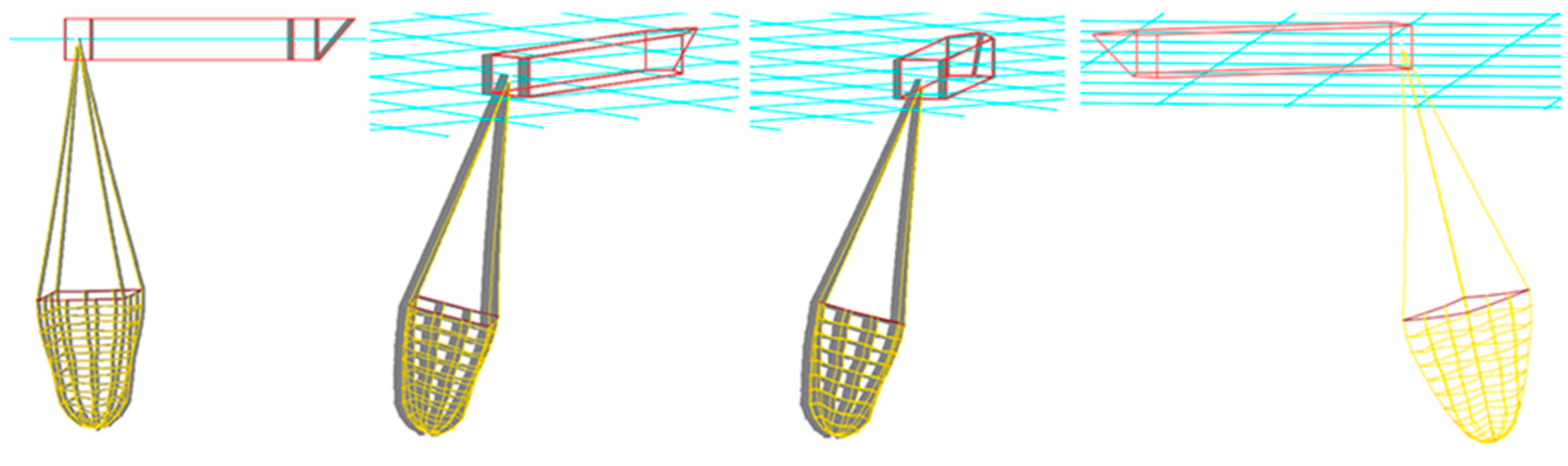
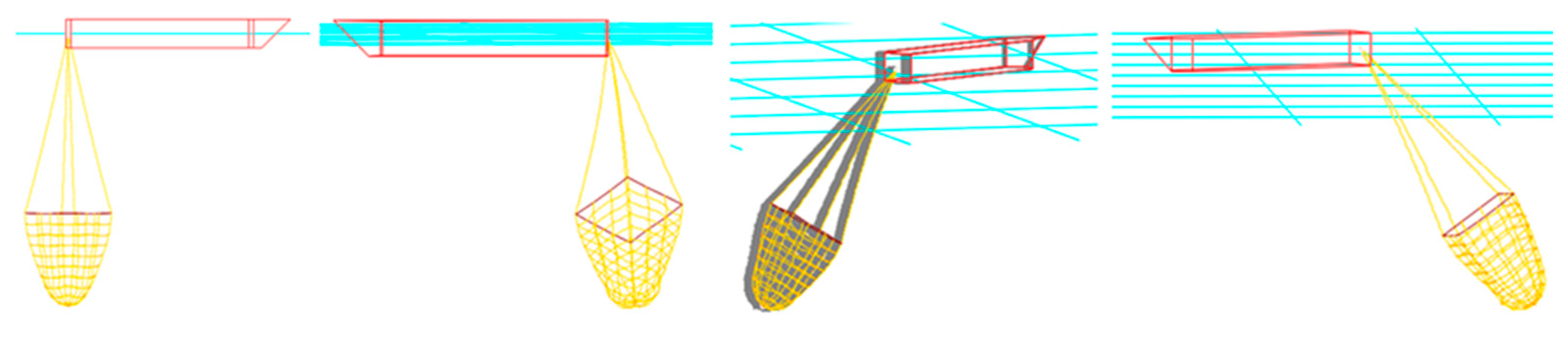
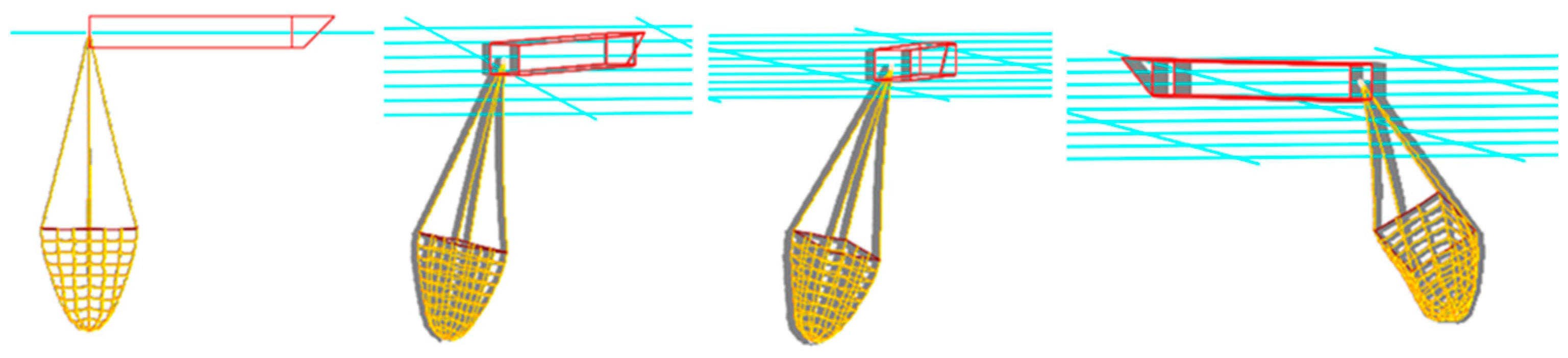


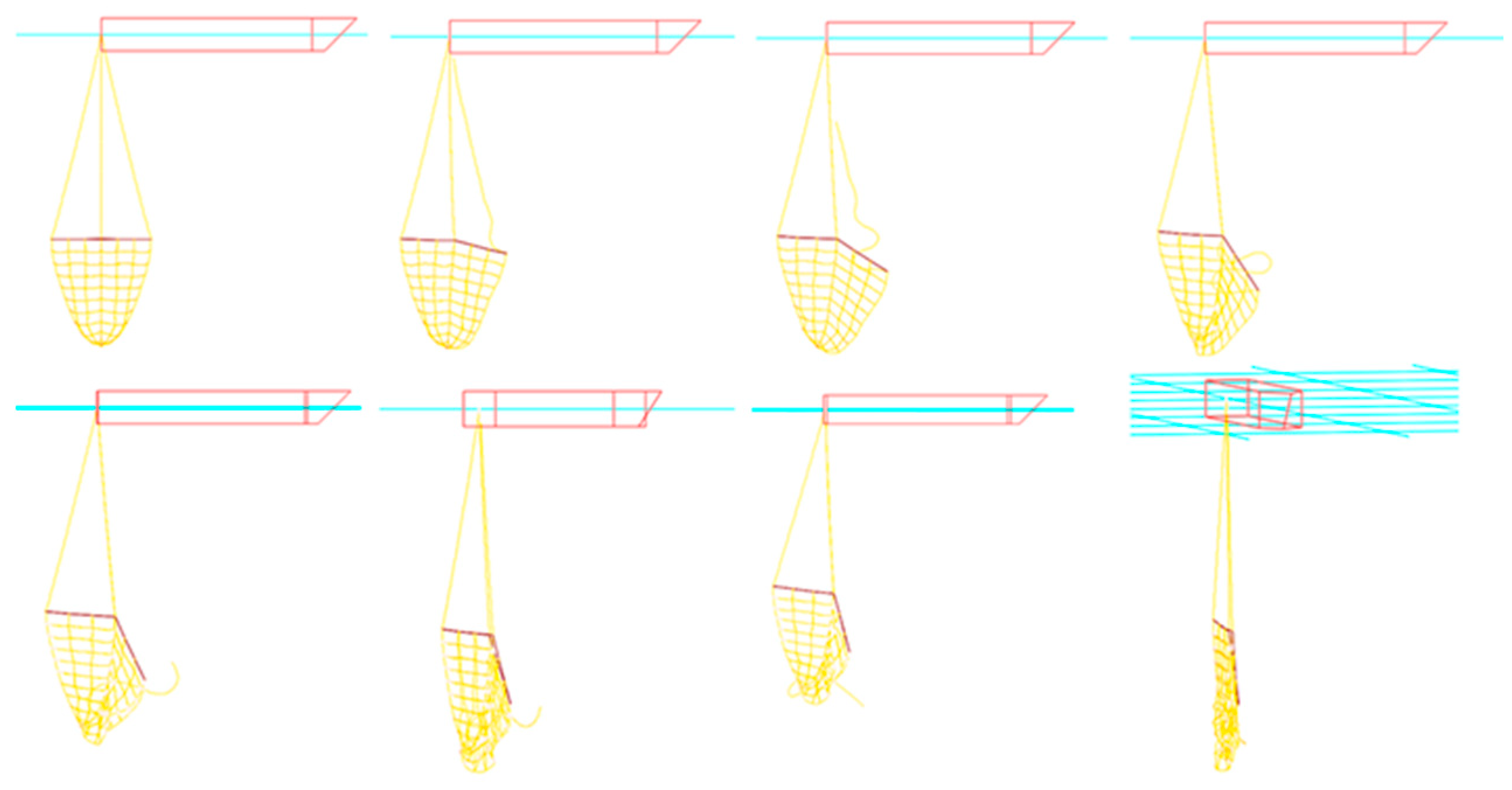

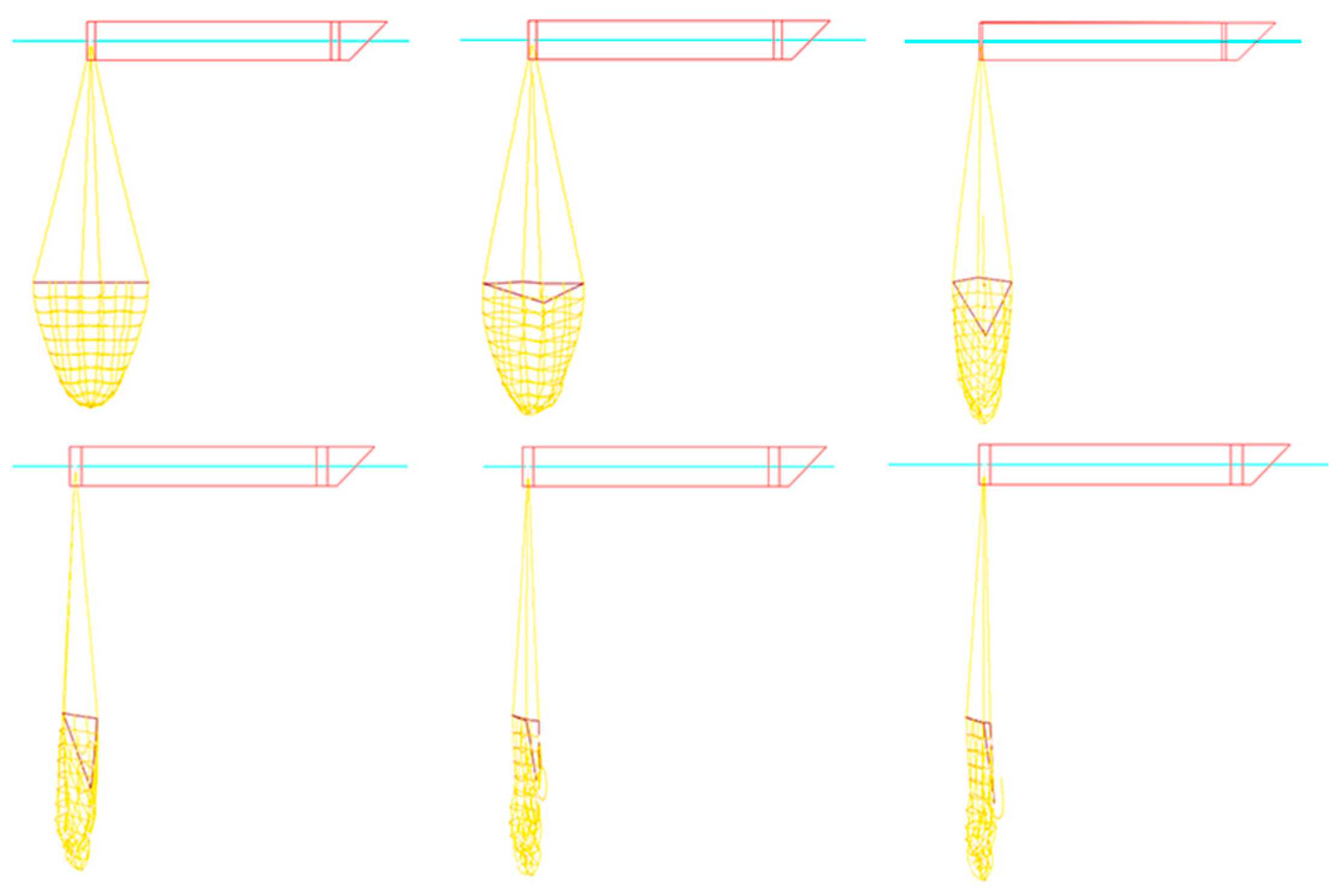
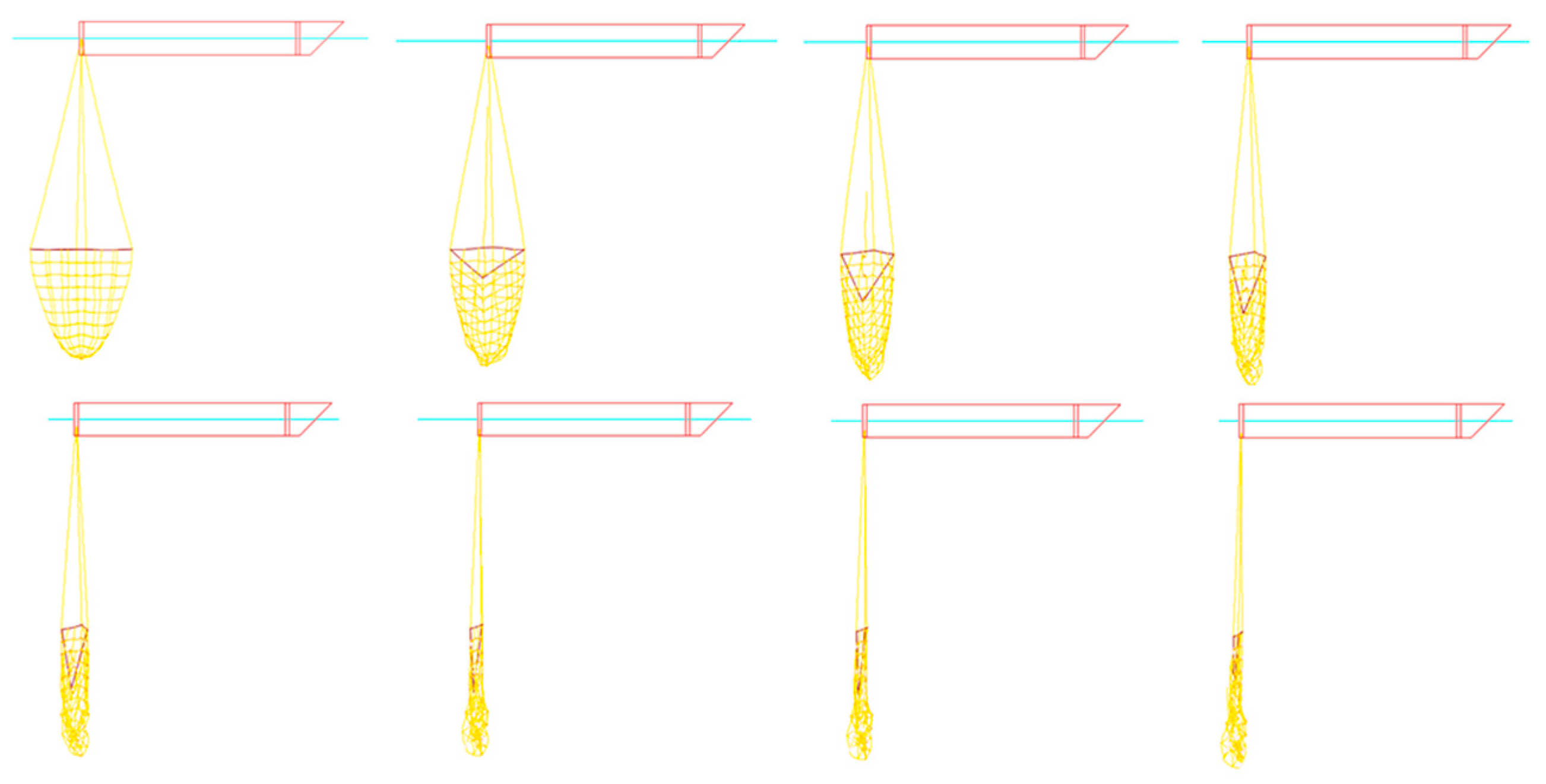
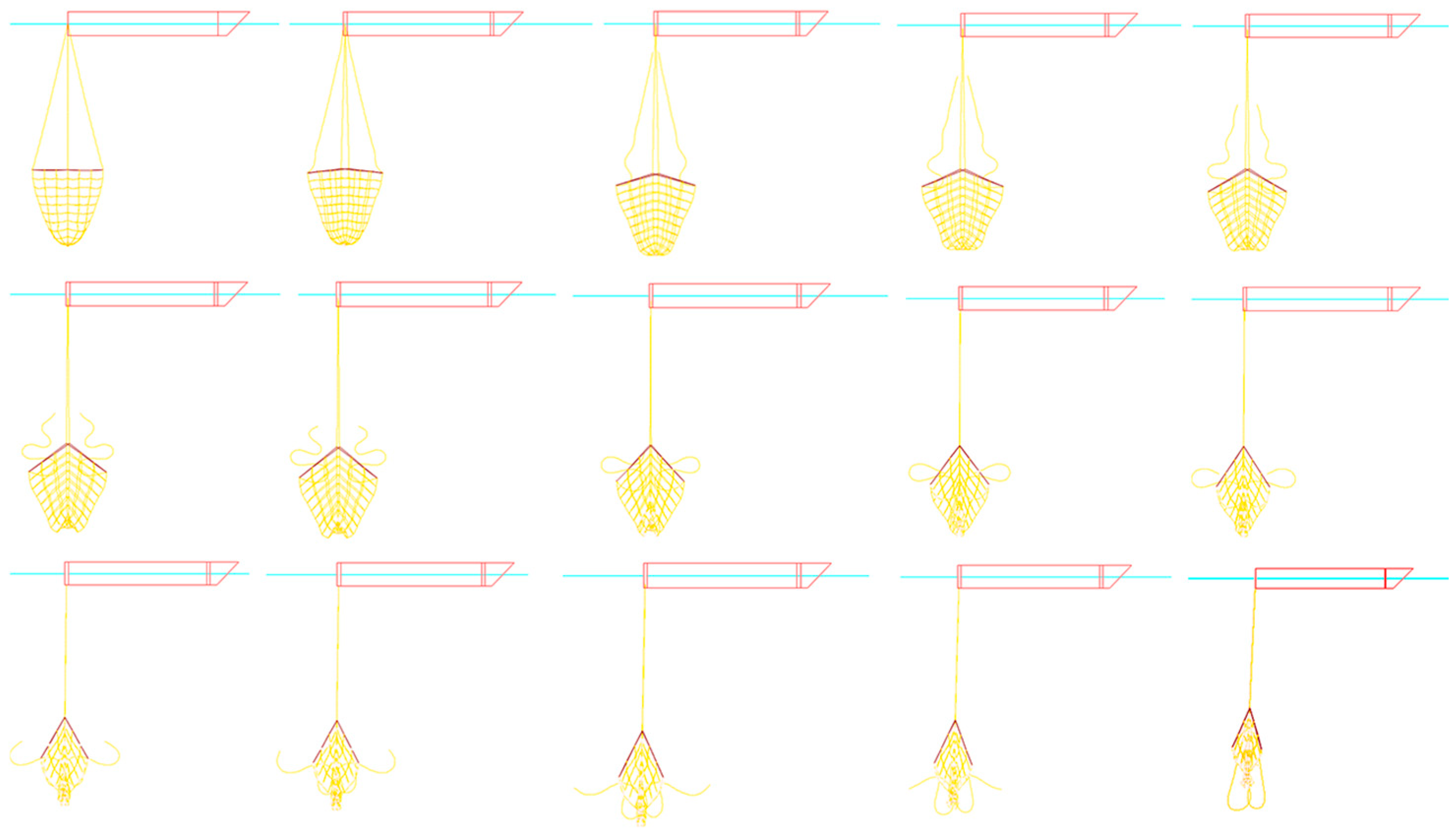
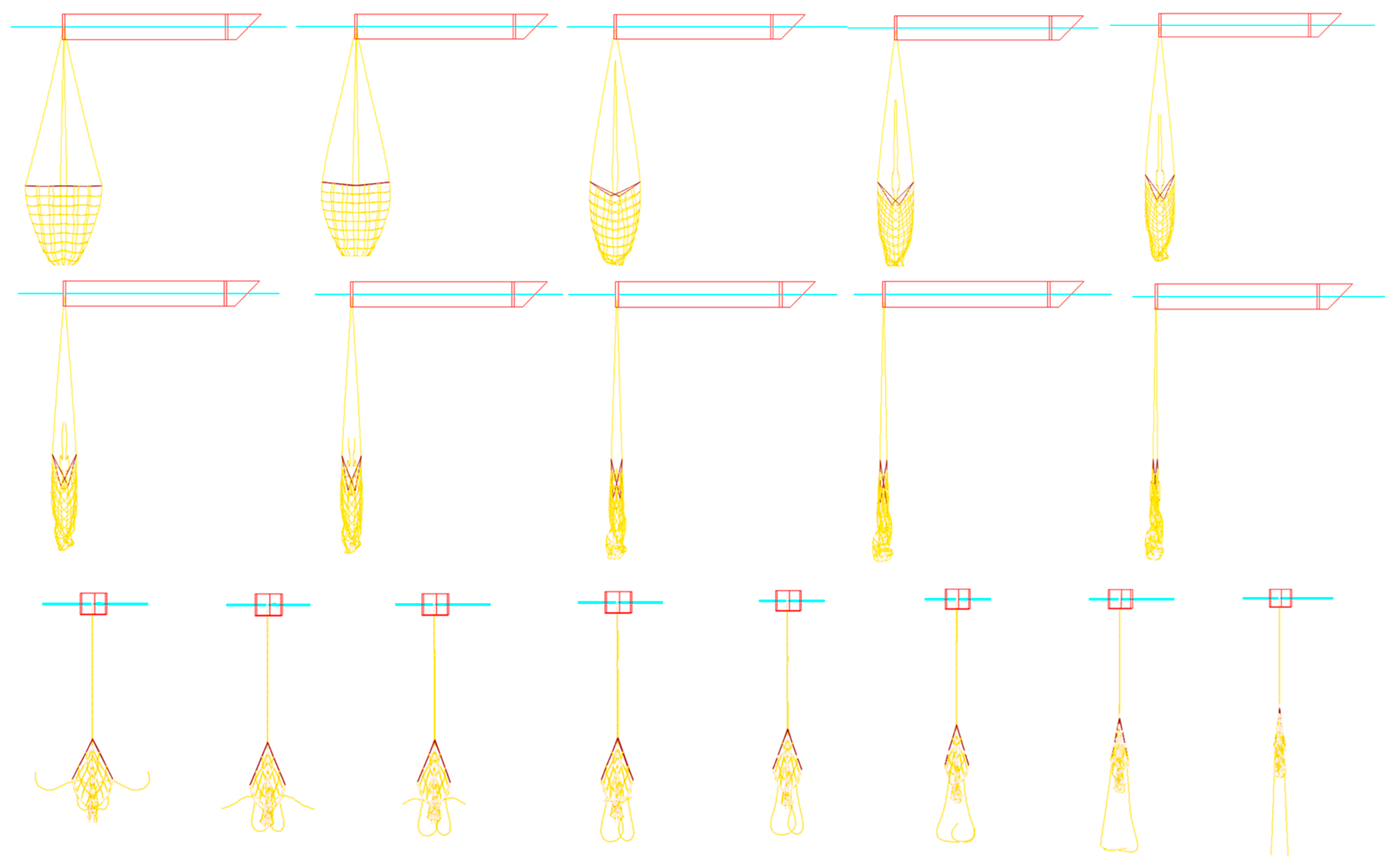
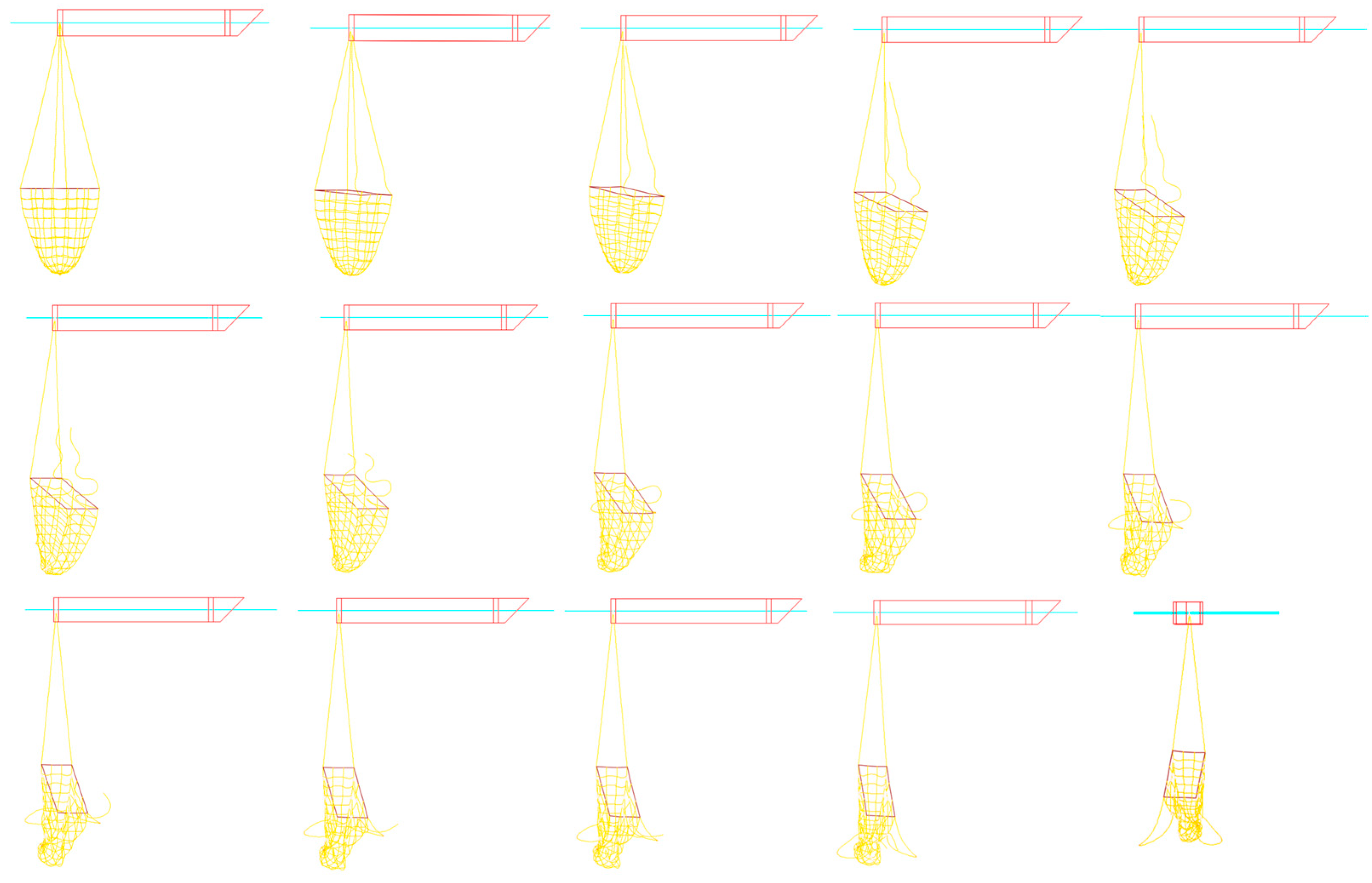
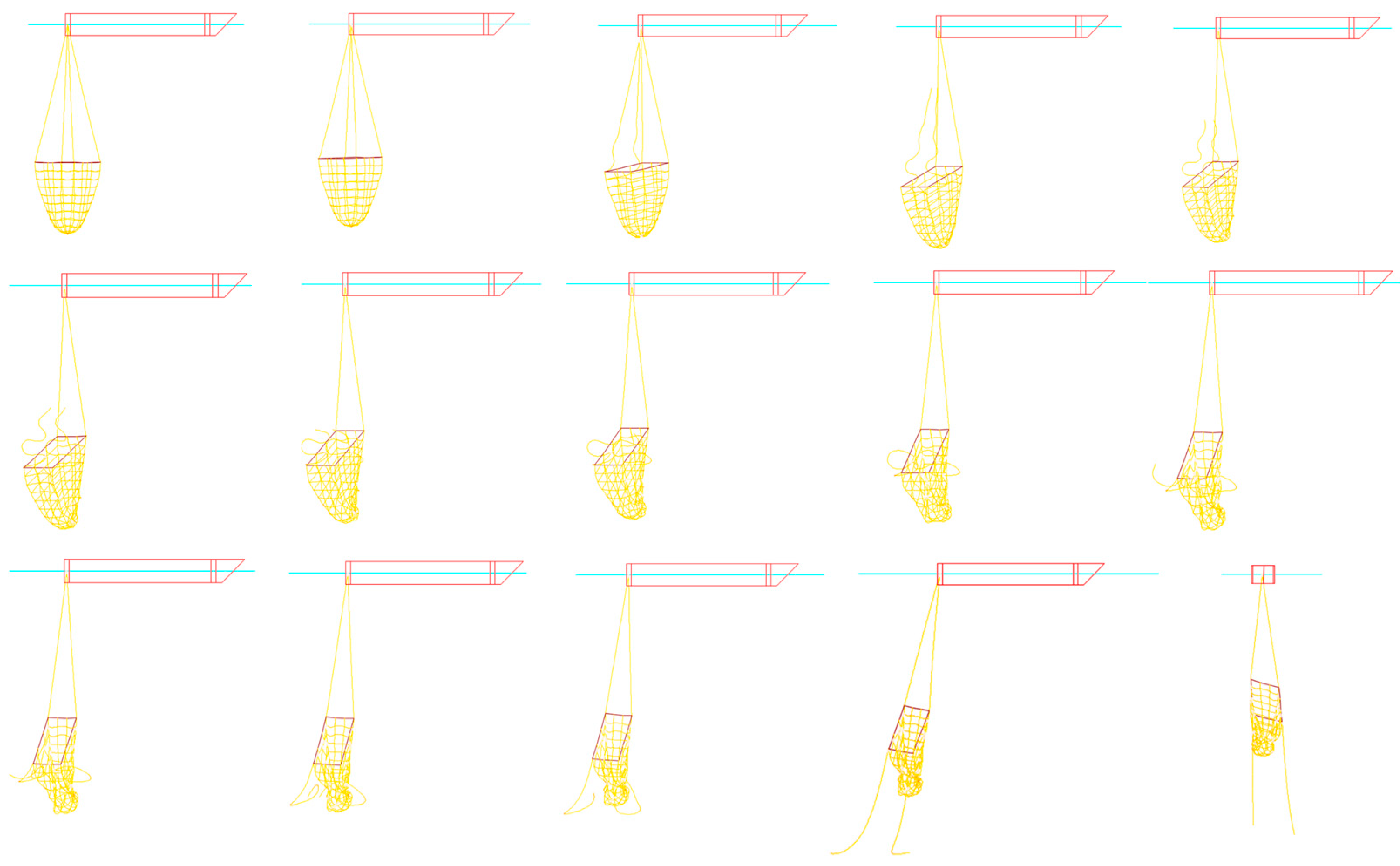
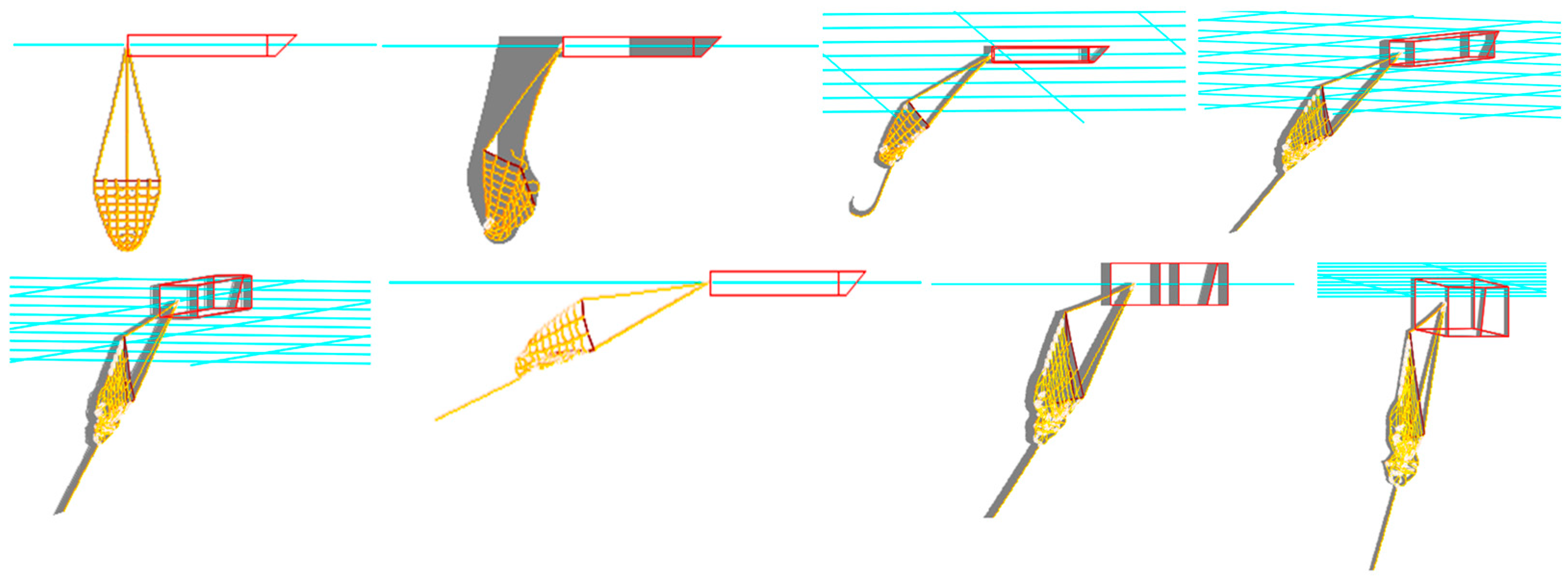
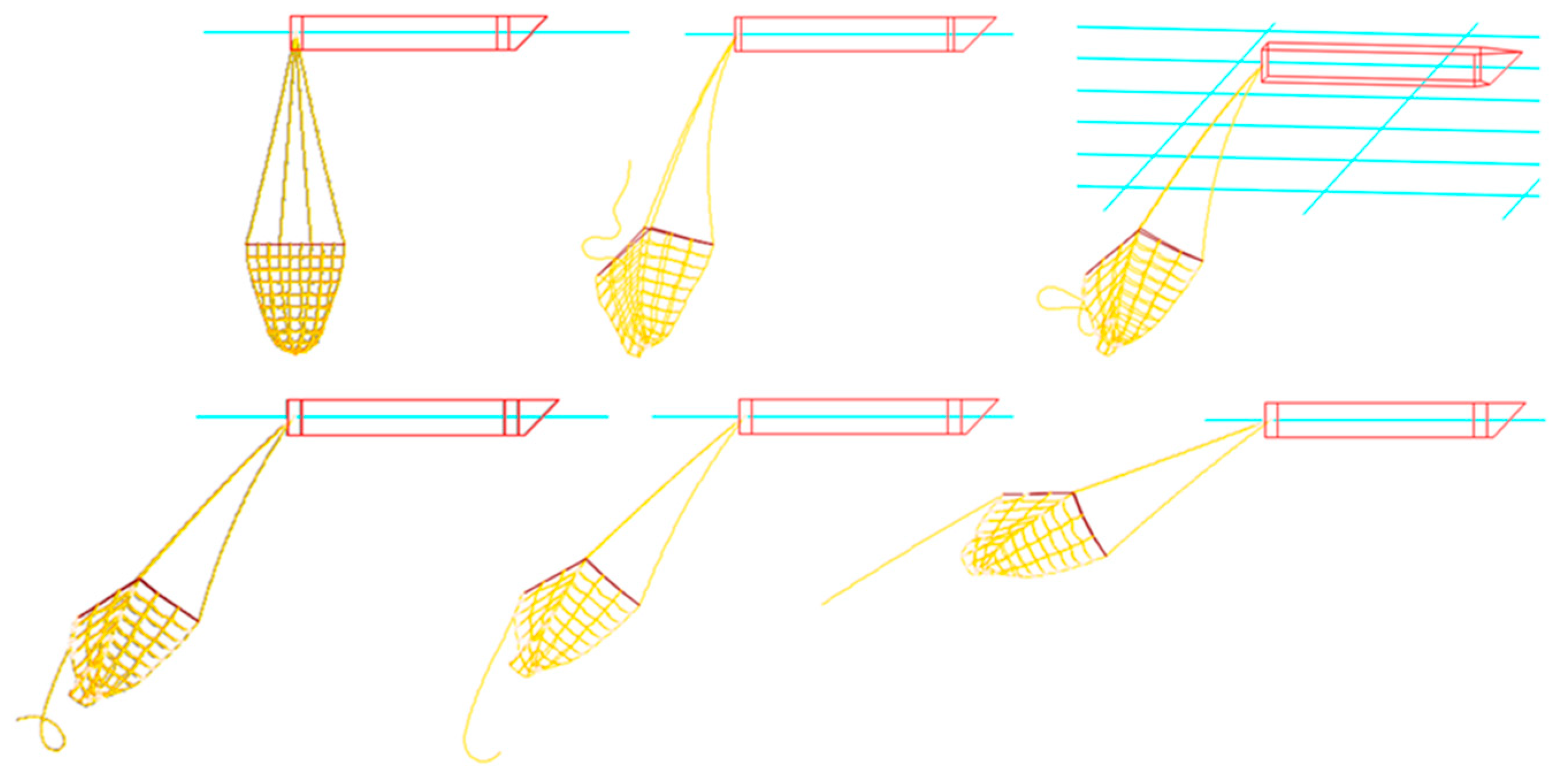
| Net Type | Twine Diameter (mm) | Mesh Size (mm) | Total Mass (g) |
|---|---|---|---|
| A | 0.348 | 75 | 9.91 |
| B | 0.348 | 50 | 14.68 |
| C | 0.348 | 40 | 22.31 |
| Loads on the Steel Rod/(gw) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Velocity | Type A | Type B | Type C | ||||||
| Simulation | Experiment | Error | Simulation | Experiment | Error | Simulation | Experiment | Error | |
| 16.10 | 34.55 | 31.63 | 9.23% | 49.85 | 47.95 | 3.95% | 72.92 | 67.21 | 8.49% |
| 19.50 | 47.62 | 43.27 | 10.07% | 61.28 | 56.22 | 8.99% | 91.00 | 86.11 | 5.68% |
| 23.70 | 64.34 | 59.98 | 7.27% | 93.15 | 87.41 | 6.57% | 127.98 | 123.90 | 3.29% |
| 28.00 | 72.70 | 69.78 | 4.19% | 121.81 | 112.22 | 8.55% | 157.62 | 148.58 | 6.08% |
| 32.40 | 91.93 | 89.73 | 2.45% | 143.47 | 135.83 | 5.62% | 186.38 | 178.97 | 4.14% |
| 36.90 | 122.79 | 119.87 | 2.44% | 183.56 | 170.86 | 7.43% | 229.06 | 218.39 | 4.89% |
| 40.90 | 164.58 | 160.22 | 2.72% | 215.43 | 208.43 | 3.36% | 288.20 | 261.97 | 10.01% |
| Loads at position 1/(gw) | |||||||||
| 16.10 | 8.63 | 8.55 | 0.98% | 16.87 | 15.06 | 12.04% | 8.56 | 9.13 | −6.28% |
| 19.50 | 10.83 | 11.93 | −9.22% | 20.99 | 25.11 | −16.39% | 10.96 | 9.96 | 10.04% |
| 23.70 | 12.87 | 12.28 | 4.79% | 24.62 | 27.08 | −9.11% | 13.03 | 12.03 | 8.31% |
| 28.00 | 16.00 | 17.53 | −8.72% | 30.05 | 34.82 | −13.70% | 20.07 | 22.14 | −9.33% |
| 32.40 | 19.73 | 17.78 | 10.96% | 34.66 | 35.33 | −1.89% | 28.28 | 29.02 | −2.57% |
| 36.90 | 25.50 | 26.01 | −1.97% | 44.22 | 44.72 | −1.13% | 29.76 | 27.44 | 8.45% |
| 40.90 | 31.51 | 31.86 | −10.8% | 59.37 | 58.07 | 2.25% | 32.09 | 31.34 | 2.38% |
| Loads at position 2/(gw) | |||||||||
| 16.10 | 3.86 | 4.69 | −17.61% | 3.95 | 4.94 | −19.98% | 3.17 | 2.27 | 39.78% |
| 19.50 | 5.85 | 6.58 | −11.03% | 6.34 | 6.92 | −8.38% | 6.62 | 10.85 | −38.97% |
| 23.70 | 4.93 | 6.92 | −28.73% | 7.80 | 11.92 | −34.57% | 8.55 | 16.37 | −47.74% |
| 28.00 | 5.75 | 7.74 | −25.63% | 9.30 | 8.79 | 5.82% | 10.73 | 10.09 | 6.30% |
| 32.40 | 6.04 | 8.03 | −24.75% | 10.66 | 9.47 | 12.58% | 22.01 | 21.10 | 4.27% |
| 36.90 | 7.74 | 9.68 | −20.04% | 13.32 | 11.99 | 11.07% | 29.06 | 29.06 | 0.00% |
| 40.90 | 13.94 | 15.83 | −11.95% | 16.69 | 13.38 | 24.67% | 36.87 | 34.82 | 5.87% |
| Loads at position 3/(gw) | |||||||||
| 16.10 | 4.41 | 4.99 | −11.66% | 8.79 | 14.51 | −39.40% | 8.49 | 9.90 | −14.28% |
| 19.50 | 3.69 | 3.01 | 22.57% | 9.09 | 9.98 | −8.97% | 10.02 | 10.26 | −2.38% |
| 23.70 | 5.53 | 3.20 | 72.80% | 9.77 | 9.96 | −1.89% | 13.56 | 12.15 | 11.64% |
| 28.00 | 3.88 | 3.25 | 19.41% | 10.09 | 9.52 | 5.93% | 19.33 | 18.27 | 5.82% |
| 32.40 | 6.31 | 6.01 | 4.88% | 10.30 | 12.30 | −16.28% | 26.28 | 24.99 | 5.19% |
| 36.90 | 8.49 | 9.03 | −5.92% | 10.46 | 10.15 | 3.08% | 33.35 | 31.94 | 4.43% |
| 40.90 | 15.77 | 14.03 | 12.45% | 11.36 | 10.90 | 4.21% | 38.89 | 38.66 | 0.60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhao, B.; Zhang, Y.; Zhu, K.; Yan, J. Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process. J. Mar. Sci. Eng. 2025, 13, 586. https://doi.org/10.3390/jmse13030586
Zhang D, Zhao B, Zhang Y, Zhu K, Yan J. Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process. Journal of Marine Science and Engineering. 2025; 13(3):586. https://doi.org/10.3390/jmse13030586
Chicago/Turabian StyleZhang, Dapeng, Bowen Zhao, Yi Zhang, Keqiang Zhu, and Jin Yan. 2025. "Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process" Journal of Marine Science and Engineering 13, no. 3: 586. https://doi.org/10.3390/jmse13030586
APA StyleZhang, D., Zhao, B., Zhang, Y., Zhu, K., & Yan, J. (2025). Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process. Journal of Marine Science and Engineering, 13(3), 586. https://doi.org/10.3390/jmse13030586







