Investigation on the Welding Residual Stress Distribution in Multi-Segment Conical Egg-Shaped Shell
Abstract
1. Introduction
2. Multi-Segment Egg-Shaped Shell
2.1. Design of the Segmented Egg-Shaped Shell
2.2. Egg-Shaped Shell Finite Element Model
2.2.1. Material
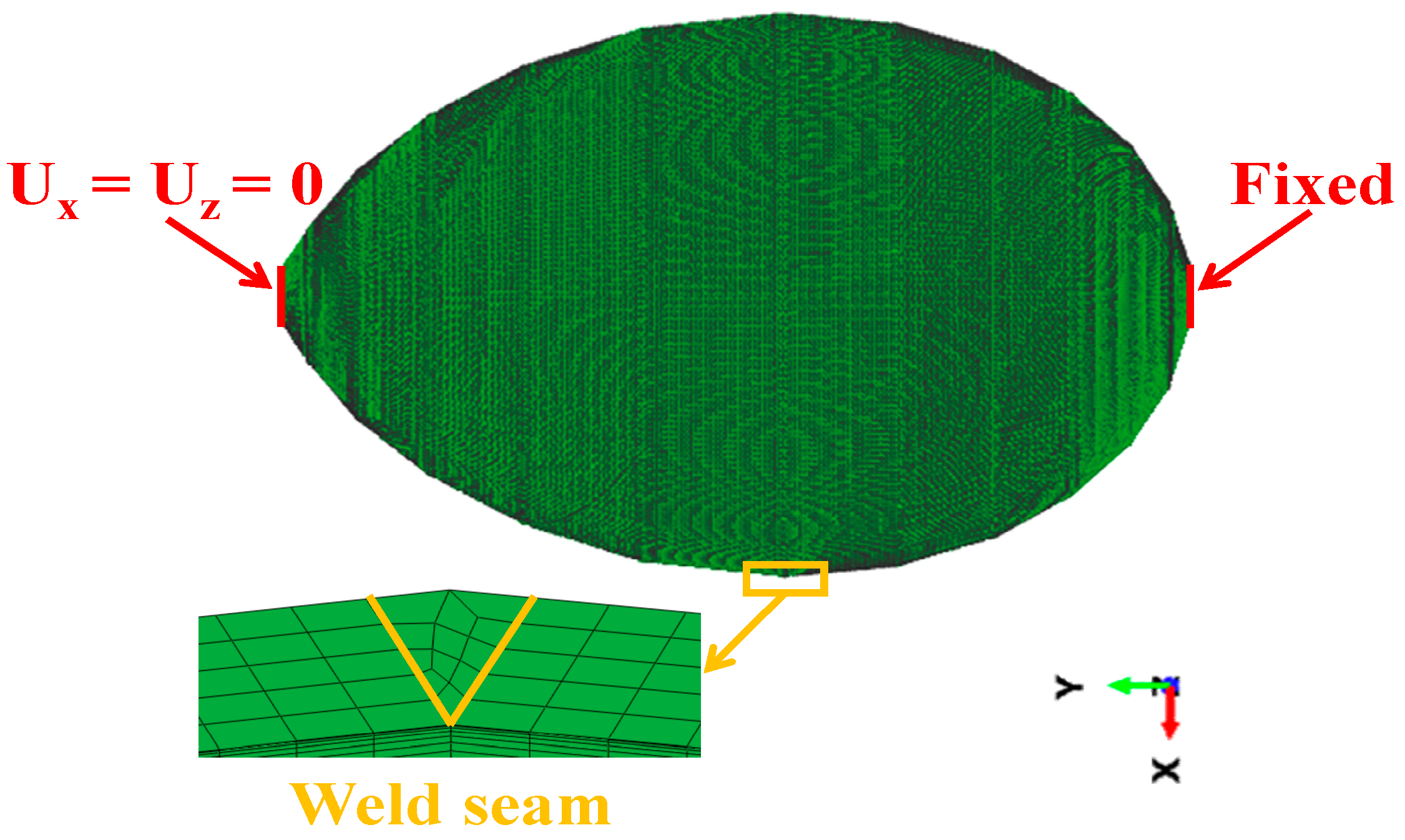
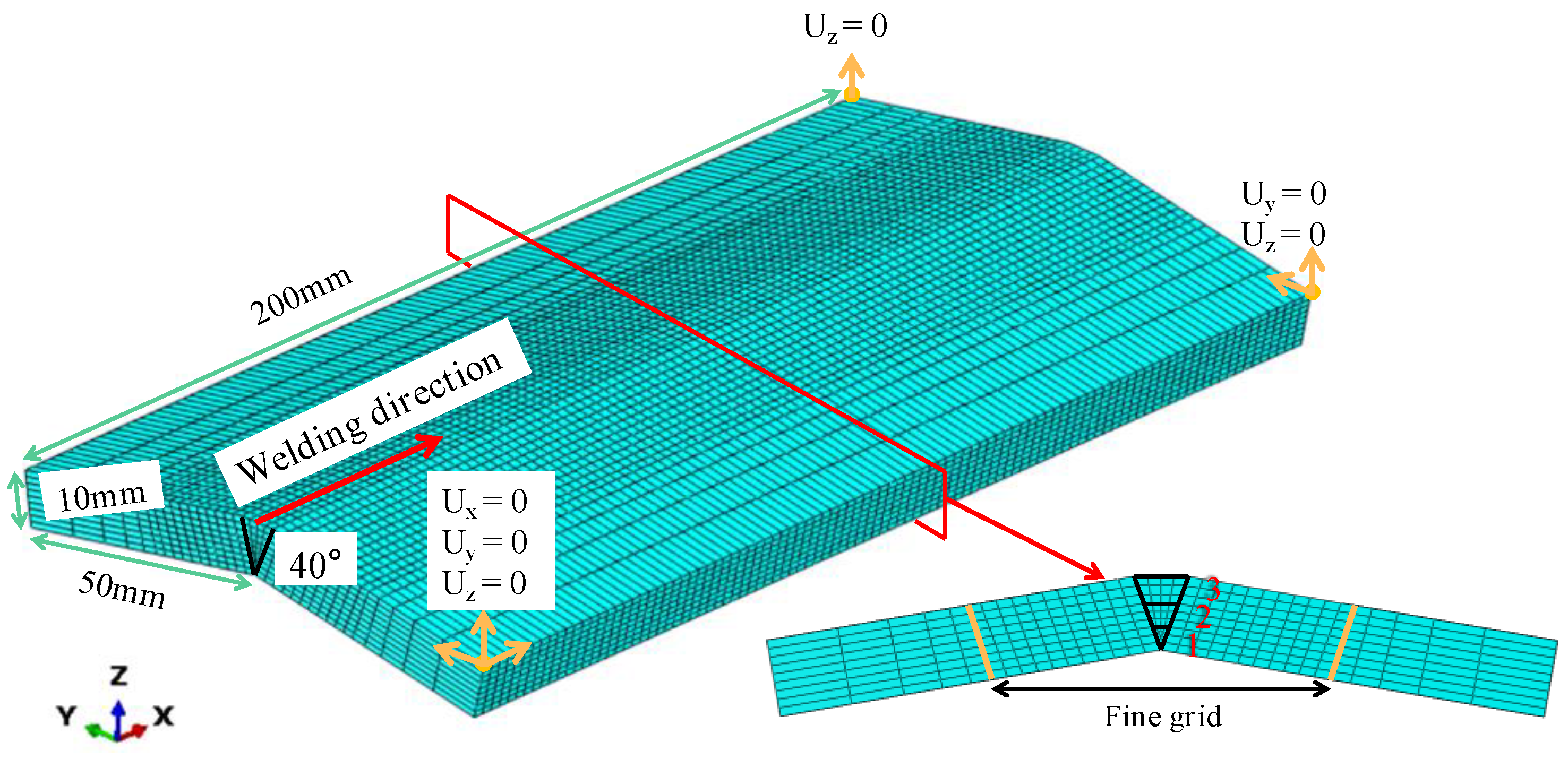
2.2.2. Boundary Conditions
2.2.3. Heat Source Model
3. Welding Residual Stress of Egg-Shaped Shells
3.1. Residual Stress Distribution on the Outer Surface
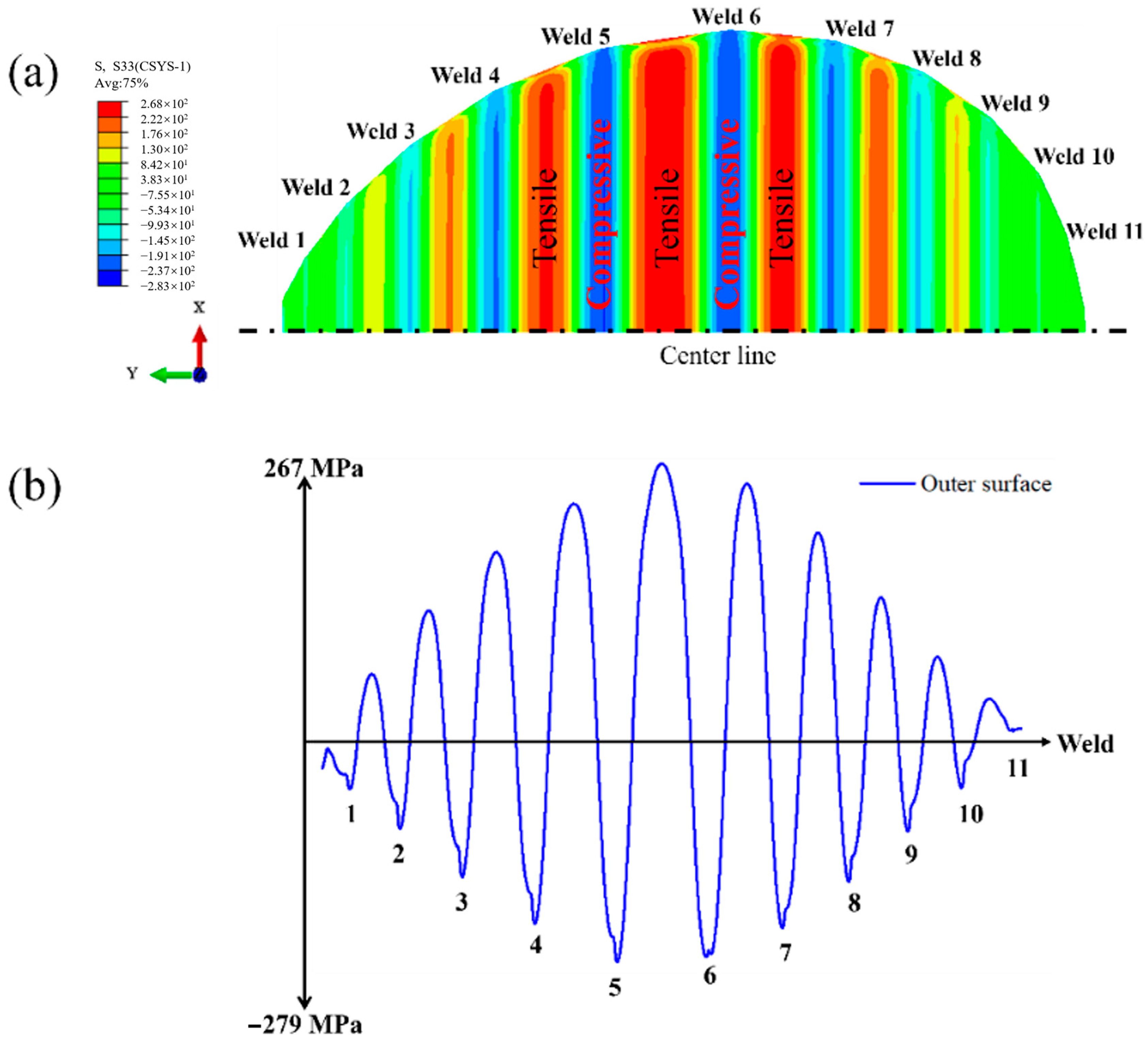
3.1.1. Circumferential Residual Stress on the Outer Surface
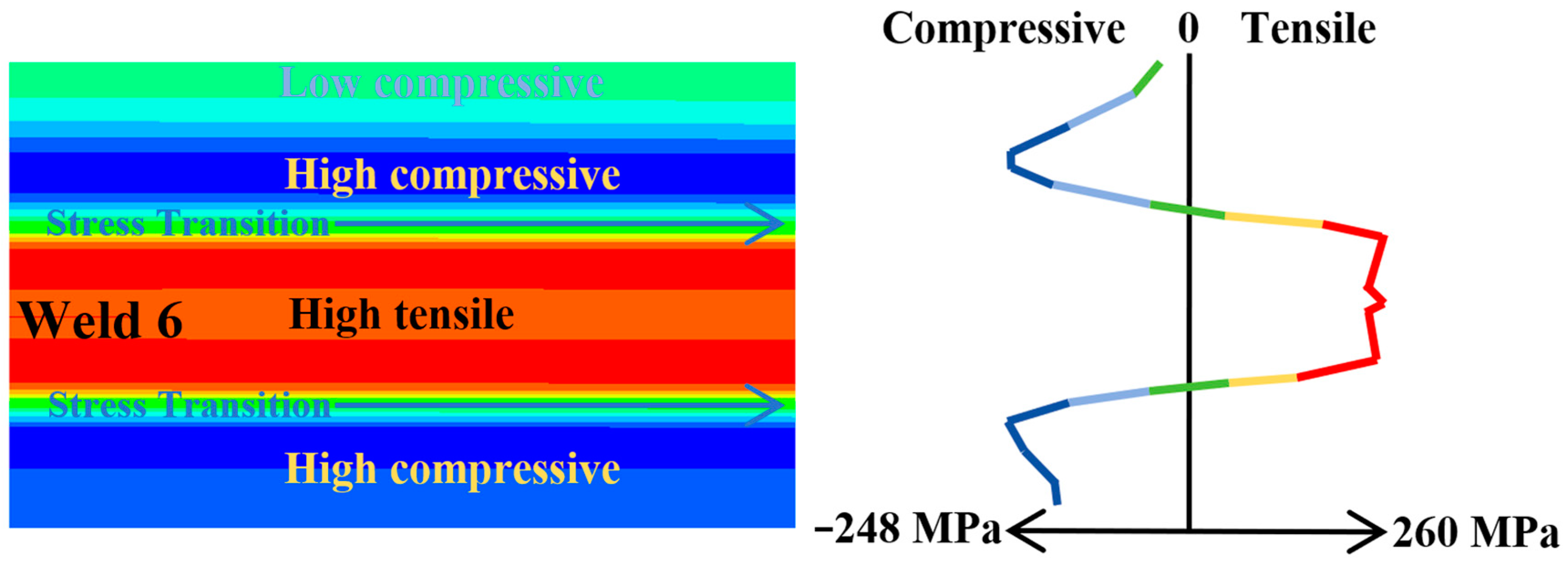
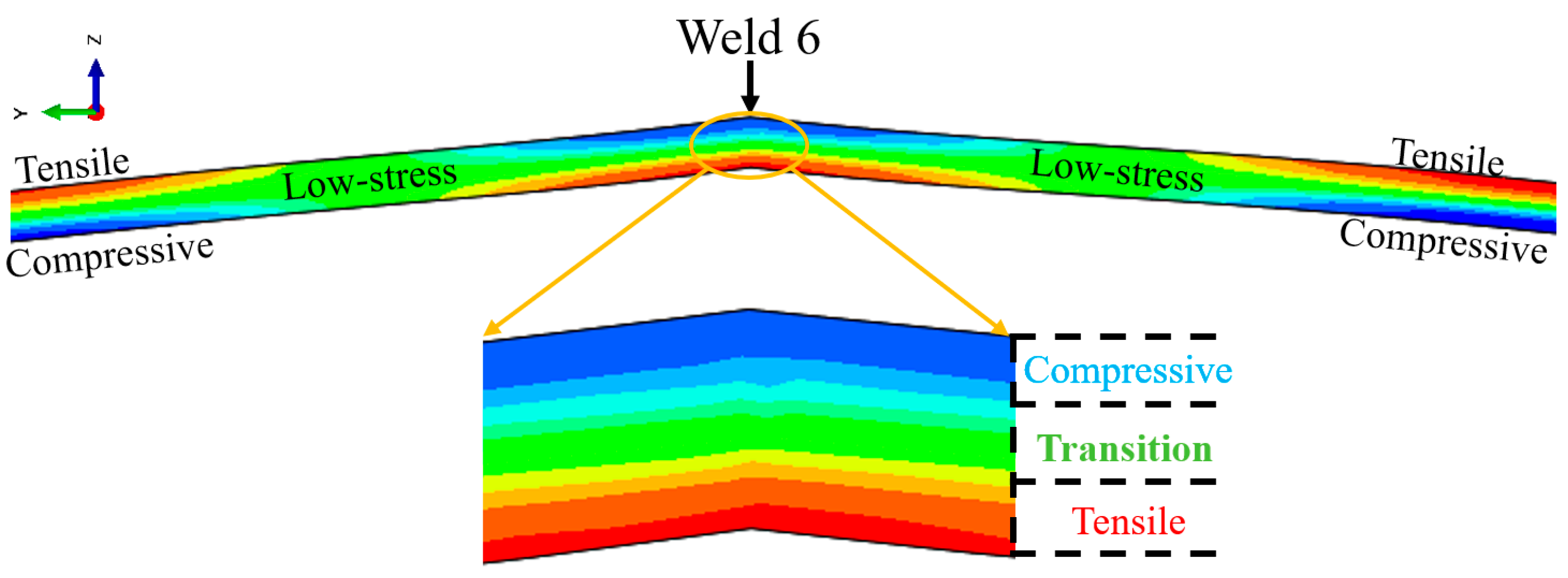
3.1.2. Axial Residual Stress on the Outer Surface
3.2. Residual Stress Distribution on the Inner Surface
3.2.1. Circumferential Residual Stress on the Inner Surface
3.2.2. Axial Residual Stress on the Inner Surface
4. Experiments
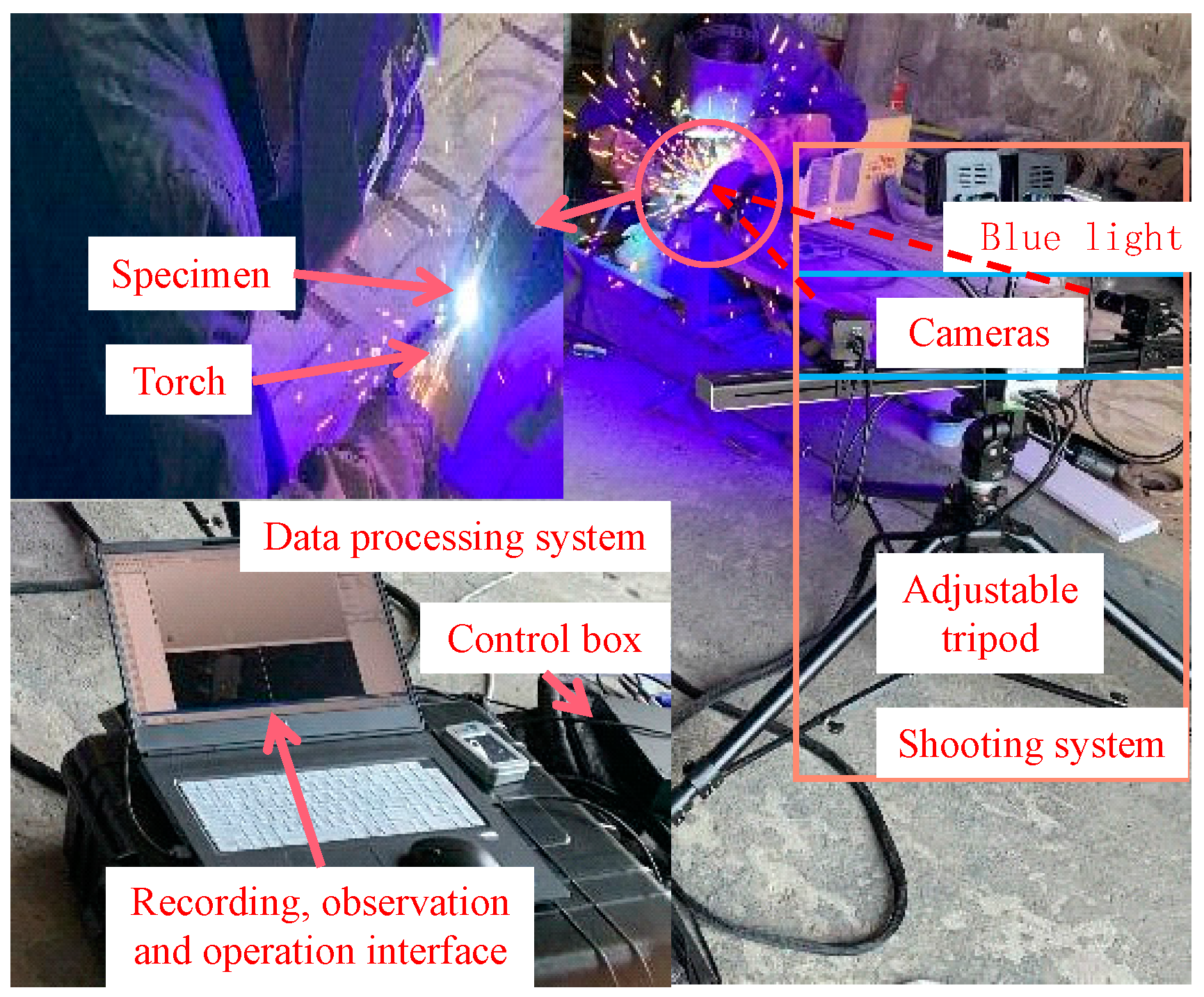
4.1. Equivalent Sample Experiment
4.2. The Numerical Model of the Equivalent Specimen
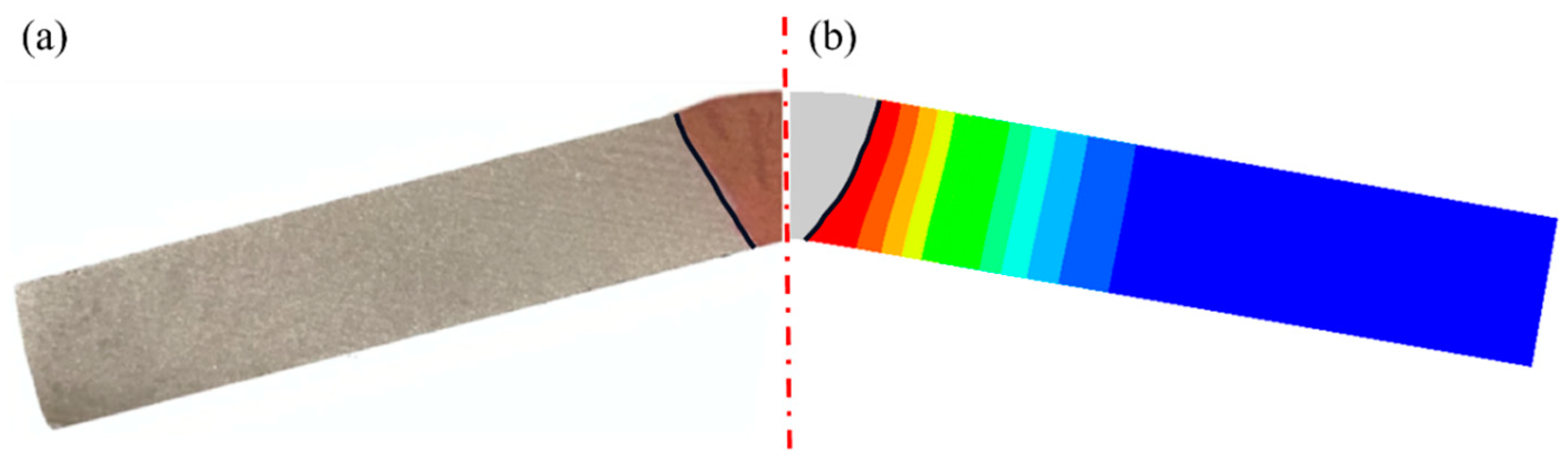
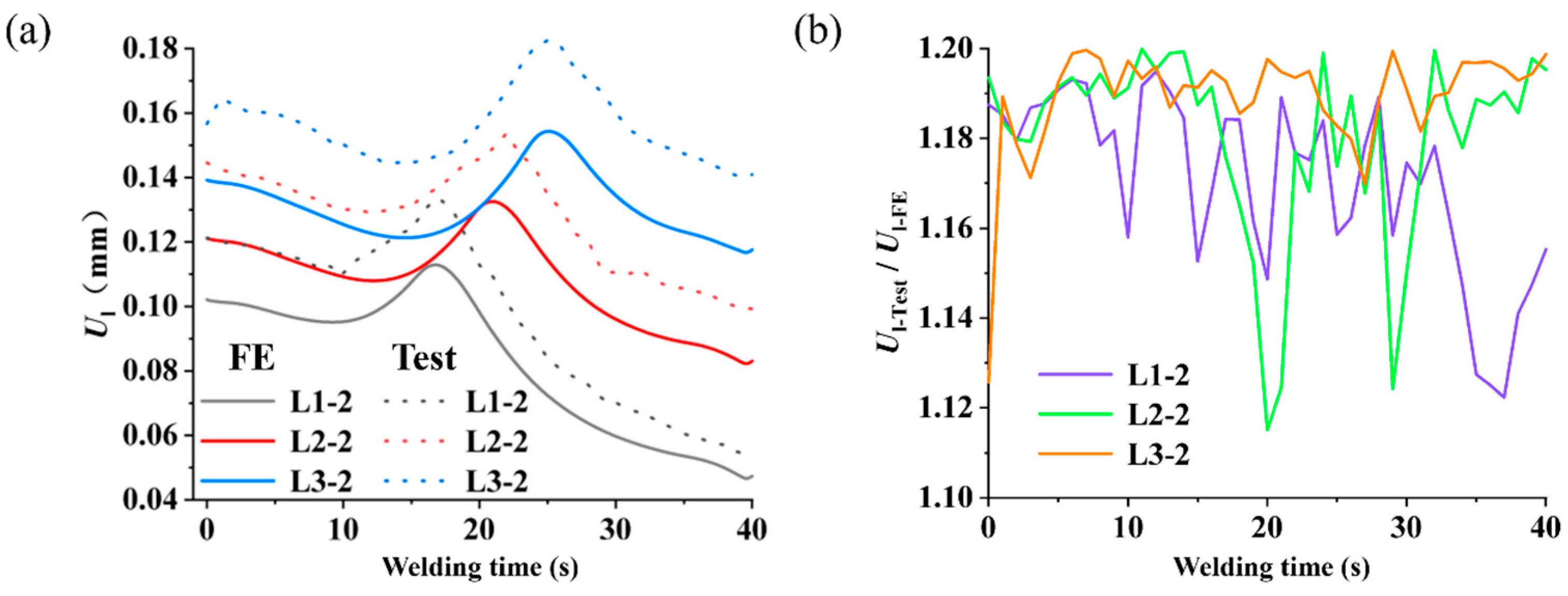
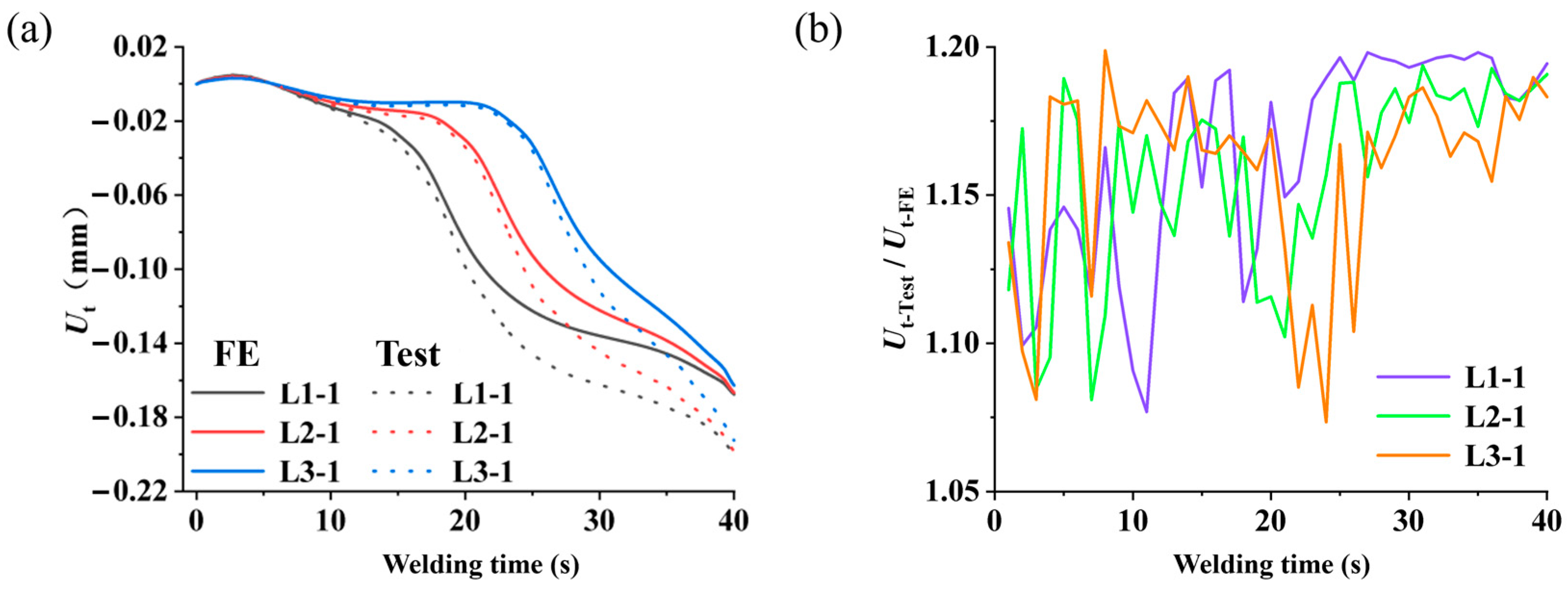
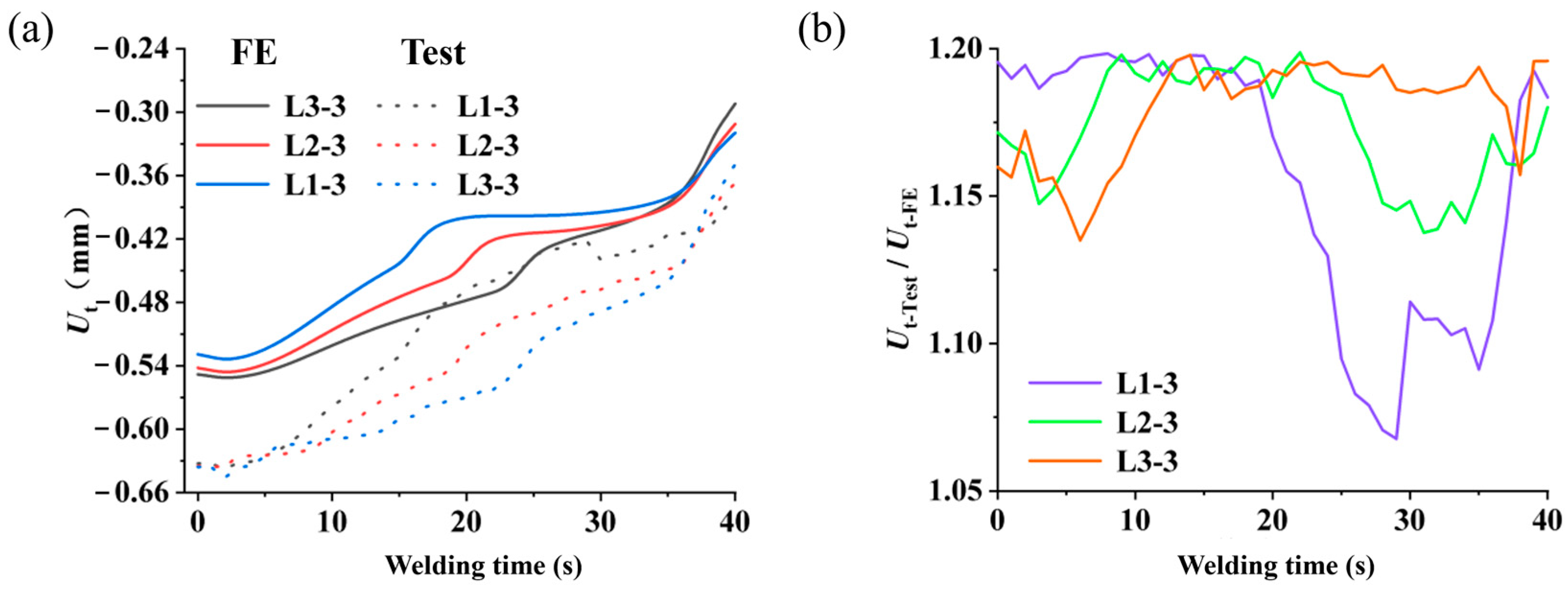
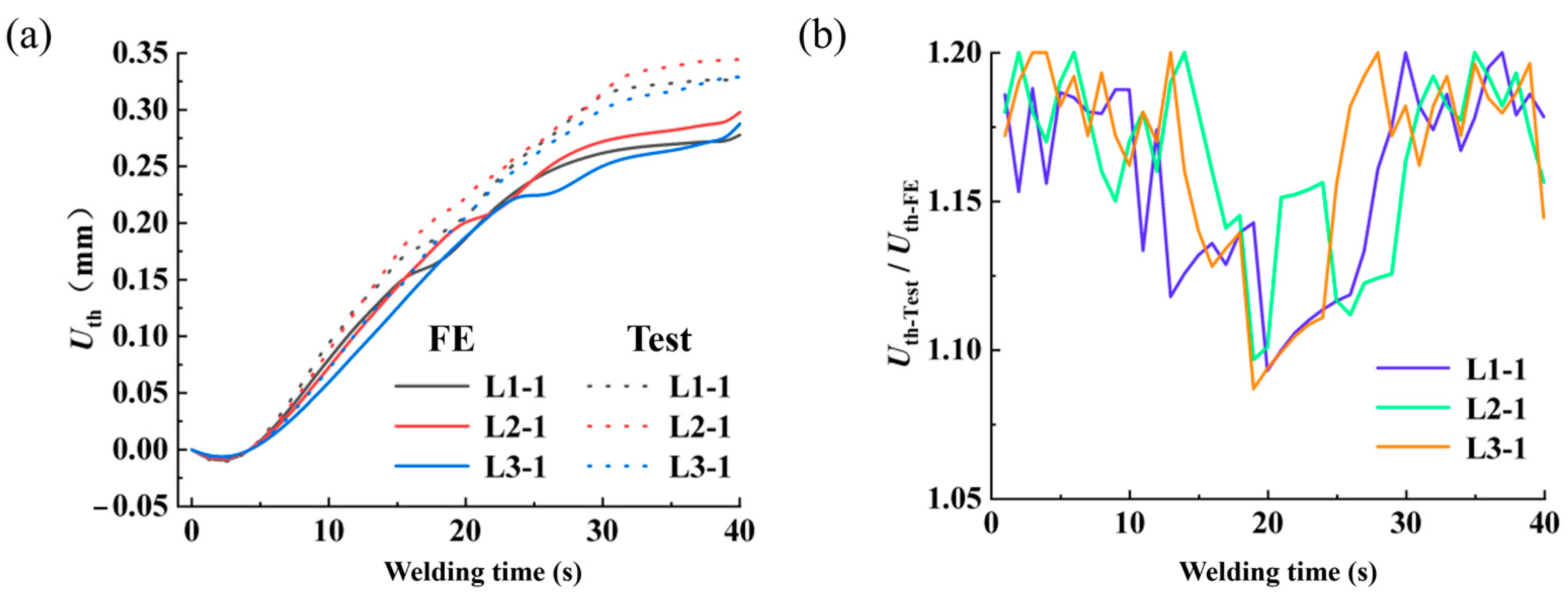
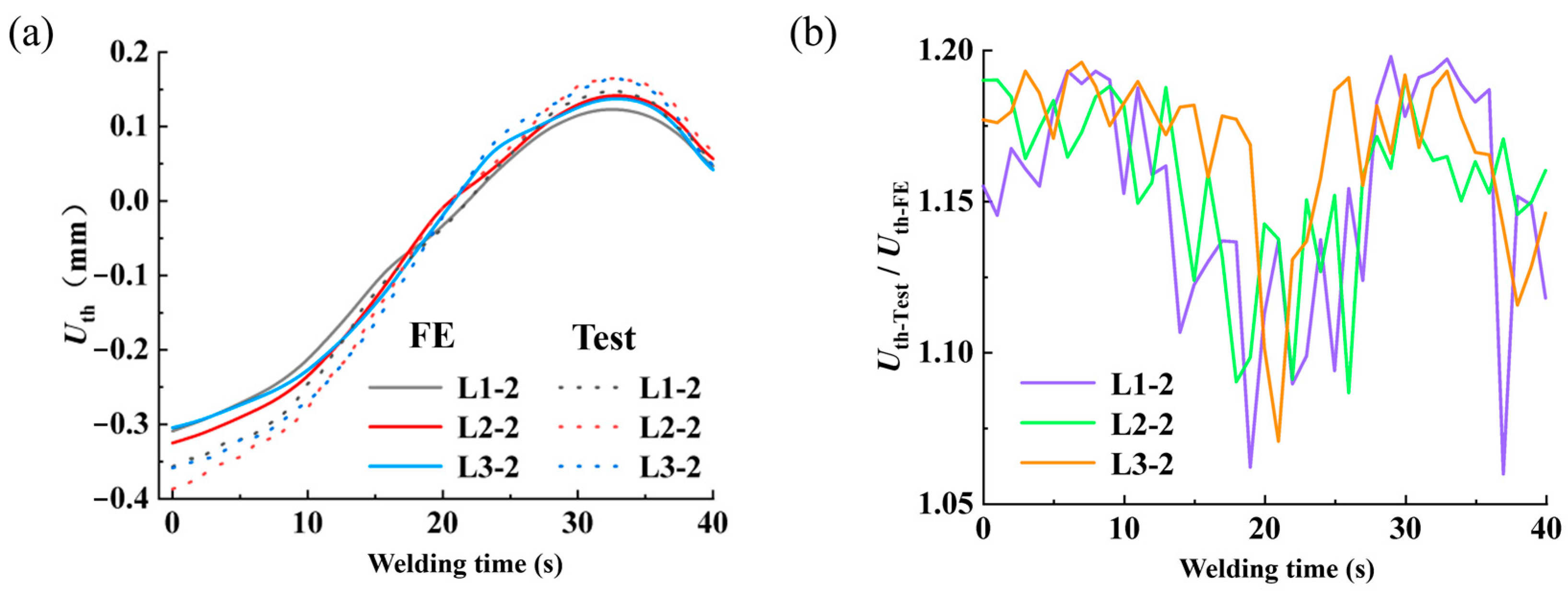
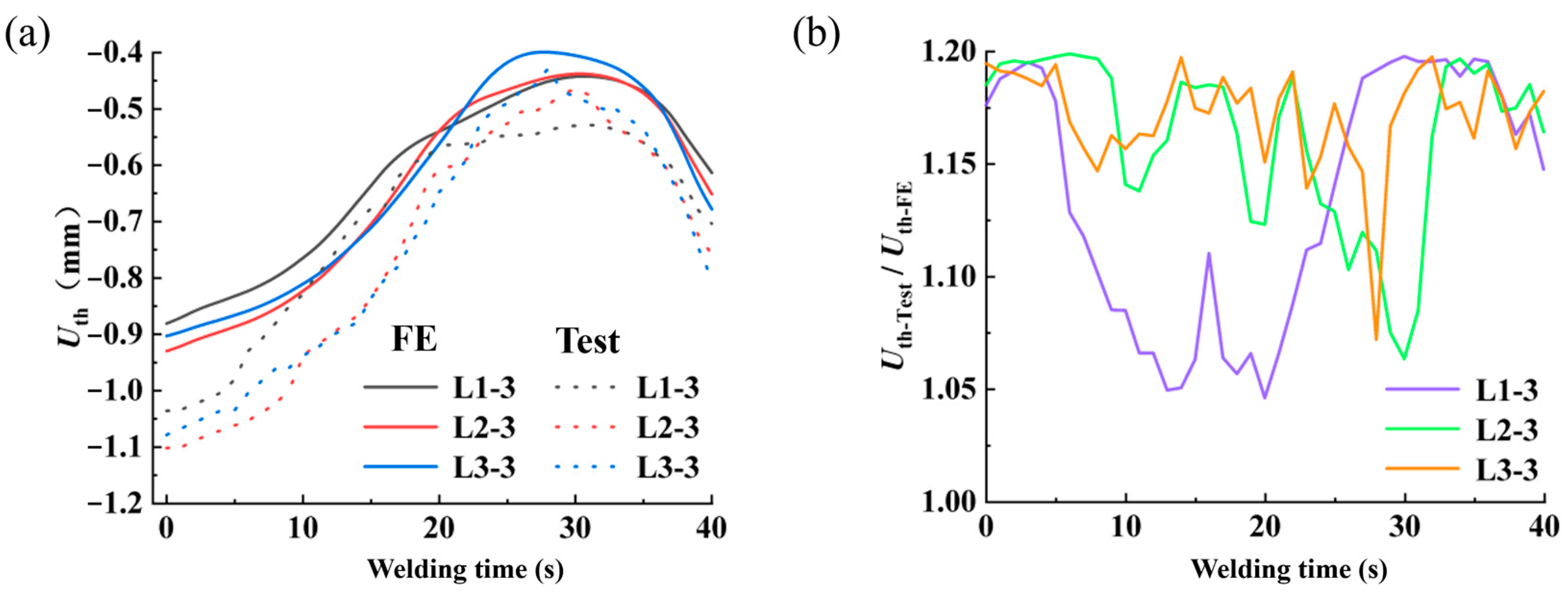
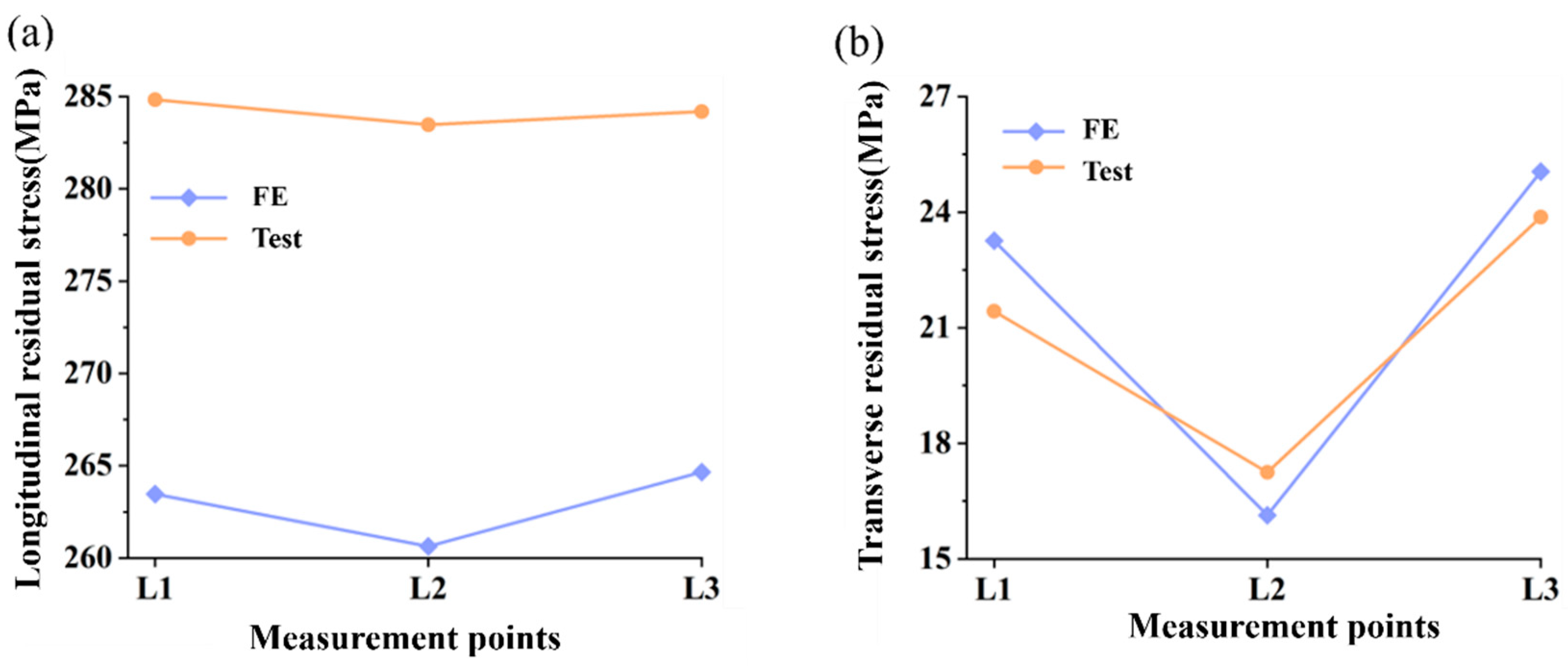
4.3. Comparison of Experimental Results
5. Conclusions
- (1)
- On the outer surface of the shell, the circumferential residual stresses around the welds and their adjacent areas follow a distinct pattern: compressive stress is followed by tensile stress. The axial residual stresses are tensile, and their distribution near the welds and adjacent regions is not influenced by the length of the cone’s generator line. As we move from the welds toward the adjacent cone segments, the circumferential residual stresses form a striped pattern of compressive–tensile–compressive stresses, with the stress magnitudes resembling a W-shape. In contrast, the axial residual stresses exhibit a compressive–tensile striped pattern, with stress magnitudes resembling a V-shape.
- (2)
- On the inner surface of the shell, the residual stresses around the welds and adjacent areas are tensile, while those on both sides are compressive. The length of the cone’s generator line and the relative welding angle influence both the magnitude and the merging effect of the circumferential residual stress distribution region. As for the axial residual stresses, these factors primarily affect the stress magnitude. Notably, the residual stresses in the middle section of the shell are higher than those at the ends.
- (3)
- The numerical simulation of the fused region morphology for the equivalent sample closely matches the experimental results, with an average deformation deviation of approximately 16.6%. The numerical results for residual stress show deviations of less than 10% when compared to the experimental data, and both exhibit consistent trends. Additionally, the residual stress distribution around the weld in the stable welding sections of the equivalent model is similar to that of the shell’s welding residual stress distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hauber, M.E. The Book of Eggs: A Life-Size Guide to the Eggs of Six Hundred of the World’s Bird Species; University of Chicago Press: Chicago, IL, USA, 2014; ISBN 978-0-226-05781-1. [Google Scholar]
- Imran, M.; Shi, D.; Tong, L.; Waqas, H.M.; Uddin, M. Design Optimization of Composite Egg-Shaped Submersible Pressure Hull for Minimum Buoyancy Factor. Def. Technol. 2021, 17, 1817–1832. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, J.; Tang, W.; Zhao, X.; Zhu, Y. Experimental and Numerical Collapse Properties of Externally Pressurized Egg-Shaped Shells under Local Geometrical Imperfections. Int. J. Press. Vessel. Pip. 2019, 175, 103893. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W. Buckling of Egg-Shaped Shells Subjected to External Pressure. Thin-Walled Struct. 2017, 113, 122–128. [Google Scholar] [CrossRef]
- Yuan, S.J.; Teng, B.G.; Dong, X.Y.; Wang, R.W. Progress in Large Vessel Forming: Introduction of Some Innovations of Prof. Z.R. Wang. J. Mater. Process. Technol. 2004, 151, 12–17. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, M.; Wang, F.; Tang, W.; Zhao, X.; Zhu, Y. Theoretical and Experimental Study of the Free Hydroforming of Egg-Shaped Shell. Ships Offshore Struct. 2022, 17, 257–267. [Google Scholar] [CrossRef]
- Barsoum, Z.; Barsoum, I. Residual Stress Effects on Fatigue Life of Welded Structures Using LEFM. Eng. Fail. Anal. 2009, 16, 449–467. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.; Bao, Y.; Bu, Y.; Luo, Y. Fatigue Life Evaluation of Welded Joints in Steel Bridge Considering Residual Stress. J. Constr. Steel Res. 2019, 153, 509–518. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, X.; Wang, T.; Zhang, X.; Tu, S.-T.; Wang, J.; Zhao, X. Fatigue Life Prediction of 316L Stainless Steel Weld Joint Including the Role of Residual Stress and Its Evolution: Experimental and Modelling. Int. J. Fatigue 2021, 143, 105997. [Google Scholar] [CrossRef]
- Ngoula, D.T.; Beie, H.T.; Vormwald, M. Fatigue Crack Growth in Cruciform Welded Joints: Influence of Residual Stresses and of the Weld Toe Geometry. Int. J. Fatigue 2017, 101, 253–262. [Google Scholar] [CrossRef]
- Deng, D. FEM Prediction of Welding Residual Stress and Distortion in Carbon Steel Considering Phase Transformation Effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Li, L.; Bao, H.; Wan, Z.; Li, Y.; Sun, K.; Luo, G. Influence of Residual Stress Due to the Equatorial Weld on the Ultimate Strength of a Ti80 Spherical Pressure Shell. Int. J. Adv. Manuf. Technol. 2021, 116, 1831–1841. [Google Scholar] [CrossRef]
- Lu, W.-L.; Sun, J.-L.; Su, H.; Chen, L.-J.; Zhou, Y.-Z. Experimental Research and Numerical Analysis of Welding Residual Stress of Butt Welded Joint of Thick Steel Plate. Case Stud. Constr. Mater. 2023, 18, e01991. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, L.; Du, J.; Cao, Y. Analysis of Residual Stresses in Electron Beam Welding with Filler Wire of Ti62A Alloy. J. Mater. Res. Technol. 2023, 23, 985–997. [Google Scholar] [CrossRef]
- Yu, D.; Yang, C.; Sun, Q.; Dai, L.; Wang, A.; Xuan, H. Impact of Process Parameters on Temperature and Residual Stress Distribution of X80 Pipe Girth Welds. Int. J. Press. Vessel. Pip. 2023, 203, 104939. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Niu, Y.; Du, S.; Shen, C. Investigation on Welding Residual Stress and Vibration Characteristics of Ring-Stiffened Cylindrical Shell. Chin. J. Ship Res. 2023, 18, 208–215. [Google Scholar] [CrossRef]
- Yuelai, Z.; Zhangzhu, P.; Maochun, C.; Long, H.U.; Guochang, P.N.; Bo, X.U. Numerical simulation of residual stress in complex aluminum alloy welded structure. HJXB 2021, 42, 91–96. [Google Scholar] [CrossRef]
- Pu, X.; Zhang, C.; Li, S.; Deng, D. Simulating Welding Residual Stress and Deformation in a Multi-Pass Butt-Welded Joint Considering Balance between Computing Time and Prediction Accuracy. Int. J. Adv. Manuf. Technol. 2017, 93, 2215–2226. [Google Scholar] [CrossRef]
- GB/T 985.1-2008; Recommended Joint Preparation for Gas Welding, Manual Metal Arc. Standards Press of China: Beijing, China, 2008. Available online: https://www.codeofchina.com/standard/GBT985.1-2008.html (accessed on 30 November 2024).
- Dai, M. Study on the Free Hydroforming and Buckling Analysis of Egg-Shaped Pressure Shells. Ph.D. Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2021. [Google Scholar]
- Nedomova, S.; Severa, L.; Buchar, J. Influence of hen egg shape on egg-shaped shell compressive strength. Int. Agrophysics 2009, 23, 249–256. [Google Scholar]
- Sun, J.; Liu, X.; Tong, Y.; Deng, D. A comparative study on welding temperature fields, residual stress distributions and deformations induced by laser beam welding and CO2 gas arc welding. Mater. Des. 2014, 63, 519–530. [Google Scholar] [CrossRef]
- Ahn, J.; He, E.; Chen, L.; Wimpory, R.C.; Dear, J.P.; Davies, C.M. Prediction and measurement of residual stresses and distortions in fibre laser welded Ti-6Al-4V considering phase transformation. Mater. Des. 2017, 115, 441–457. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, G.; Pu, X.; Deng, D. Influence of welding sequence on residual stress distribution and deformation in Q345 steel H-section butt-welded joint. JMR T 2021, 13, 144–153. [Google Scholar] [CrossRef]
- Wang, Y. Investigation and Application on the Analysis Methods of Welding Distortion in Large-Scale and Complex Marine Structures. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2015. [Google Scholar]
- Xiong, X.; Lu, M.; Lu, Y. Numerical simulation of longitudinal residual stress distribution in welded T—Section of Q690 high strength steel. J. Taiyuan Univ. Technol. 2023, 54, 107–116. [Google Scholar]
- Yang, J.; Li, Y.; Peng, Y. Numerical analysis on welding residual stress in Q690 high—Strength steel pipe. Eng. Mech. 2014, 31, 108–115. [Google Scholar] [CrossRef]
- Huang, X.; Shi, D. Experiment on Fatigue Behavior of Surface Cracks at Weld Toe under Combination Stresses of Compressing and Bending. J. Ship Mech. 2002, 6, 37–43. [Google Scholar]
- Shajan, N.; Kumar, R.; Manik, R.; Asati, B.; Dhagde, S.; Dhangi, D.; Kumar, S.; Mohan Mahapartra, M.; Singh Arora, K. Role of residual stress in the failure of HF-ERW welded tubes. Eng. Fail. Anal. 2024, 161, 108342. [Google Scholar] [CrossRef]










| Parameters | Value |
|---|---|
| Major axis, L (mm) | 2561 |
| Minor axis, B (mm) | 1767 |
| Egg-shaped coefficient, SI | 0.69 |
| Thickness, t (mm) | 10 |
| Segment | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Major (mm) | 95.7 | 227.5 | 425.3 | 689.0 | 1018.6 | 1414.1 |
| Minor (mm) | 221.6 | 387.7 | 561.4 | 719.1 | 837.4 | 886.2 |
| Segment | 7 | 8 | 9 | 10 | 11 | 12 |
| Major (mm) | 1735.1 | 2002.5 | 2216.5 | 2376.9 | 2483.9 | 2537.4 |
| Minor (mm) | 851.8 | 761.5 | 630.5 | 470.3 | 290.3 | 100.0 |
| Temperature, T (°C) | Expansion Coefficient, α (10−5/K) | Yield Strength, σs (MPa) | Elastic Modulus, E (GPa) | Poisson’s Ratio, Ν | Density, ρ (g/cm3) | Specific Heat, C (J·kg−1·K−1) | Conductivity, λ (W·m−1·K−1) |
|---|---|---|---|---|---|---|---|
| 20 | 1.67 | 265 | 200 | 0.29 | 7.80 | 465 | 15.0 |
| 100 | 1.70 | 237 | 190 | 0.30 | 7.79 | 500 | 15.1 |
| 300 | 1.83 | 170 | 168 | 0.31 | 7.75 | 512 | 18.0 |
| 500 | 1.95 | 142 | 157 | 0.32 | 7.65 | 546 | 20.4 |
| 700 | 2.00 | 122 | 151 | 0.33 | 7.57 | 589 | 22.9 |
| 900 | 2.02 | 68 | 120 | 0.33 | 7.50 | 615 | 25.5 |
| 1100 | 2.03 | 36 | 76 | 0.33 | 7.47 | 647 | 29.5 |
| 1300 | 2.10 | 17 | 20 | 0.34 | 7.35 | 697 | 33.0 |
| 1500 | 2.13 | 8 | 10 | 0.39 | 7.33 | 704 | 32.0 |
| Weld | Voltage (V) | Current (A) | Thermal Efficiency | Welding Speed (mm/s) | Heat Input (J/mm) |
|---|---|---|---|---|---|
| 1 | 18 | 80 | 0.8 | 5 | 230.4 |
| 2 | 21 | 110 | 0.8 | 5 | 369.6 |
| 3 | 23 | 130 | 0.8 | 5 | 478.4 |
| Directions | Uth-test/Uth-FE | Average | |
|---|---|---|---|
| Longitudinal | First layer | 1.001–1.200 | 1.144 |
| Second layer | 1.115–1.200 | 1.181 | |
| Third layer | 1.109–1.200 | 1.180 | |
| Transverse | First layer | 1.073–1.199 | 1.160 |
| Second layer | 1.107–1.199 | 1.175 | |
| Third layer | 1.068–1.199 | 1.170 | |
| Thickness | First layer | 1.093–1.200 | 1.161 |
| Second layer | 1.060–1.198 | 1.158 | |
| Third layer | 1.046–1.199 | 1.156 | |
| Measurement Point | Longitudinal | Transverse | ||||
|---|---|---|---|---|---|---|
| Numerical Results (MPa) | Test Results (MPa) | Ratio | Numerical Results (MPa) | Test Results (MPa) | Ratio | |
| L1 | 263.5 | 284.8 | 1.08 | 23.3 MPa | 21.4 | 0.92 |
| L2 | 260.6 | 283.5 | 1.09 | 16.1 MPa | 17.2 | 1.07 |
| L3 | 264.7 | 284.2 | 1.07 | 25.1 MPa | 23.9 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Sun, A.; Zhou, L.; Wang, L.; Zhao, X. Investigation on the Welding Residual Stress Distribution in Multi-Segment Conical Egg-Shaped Shell. J. Mar. Sci. Eng. 2025, 13, 578. https://doi.org/10.3390/jmse13030578
Zhu Y, Sun A, Zhou L, Wang L, Zhao X. Investigation on the Welding Residual Stress Distribution in Multi-Segment Conical Egg-Shaped Shell. Journal of Marine Science and Engineering. 2025; 13(3):578. https://doi.org/10.3390/jmse13030578
Chicago/Turabian StyleZhu, Yongmei, Ao Sun, Longbo Zhou, Lihui Wang, and Xilu Zhao. 2025. "Investigation on the Welding Residual Stress Distribution in Multi-Segment Conical Egg-Shaped Shell" Journal of Marine Science and Engineering 13, no. 3: 578. https://doi.org/10.3390/jmse13030578
APA StyleZhu, Y., Sun, A., Zhou, L., Wang, L., & Zhao, X. (2025). Investigation on the Welding Residual Stress Distribution in Multi-Segment Conical Egg-Shaped Shell. Journal of Marine Science and Engineering, 13(3), 578. https://doi.org/10.3390/jmse13030578






