A Low-Complexity Path-Planning Algorithm for Multiple USVs in Task Planning Based on the Visibility Graph Method
Abstract
1. Introduction
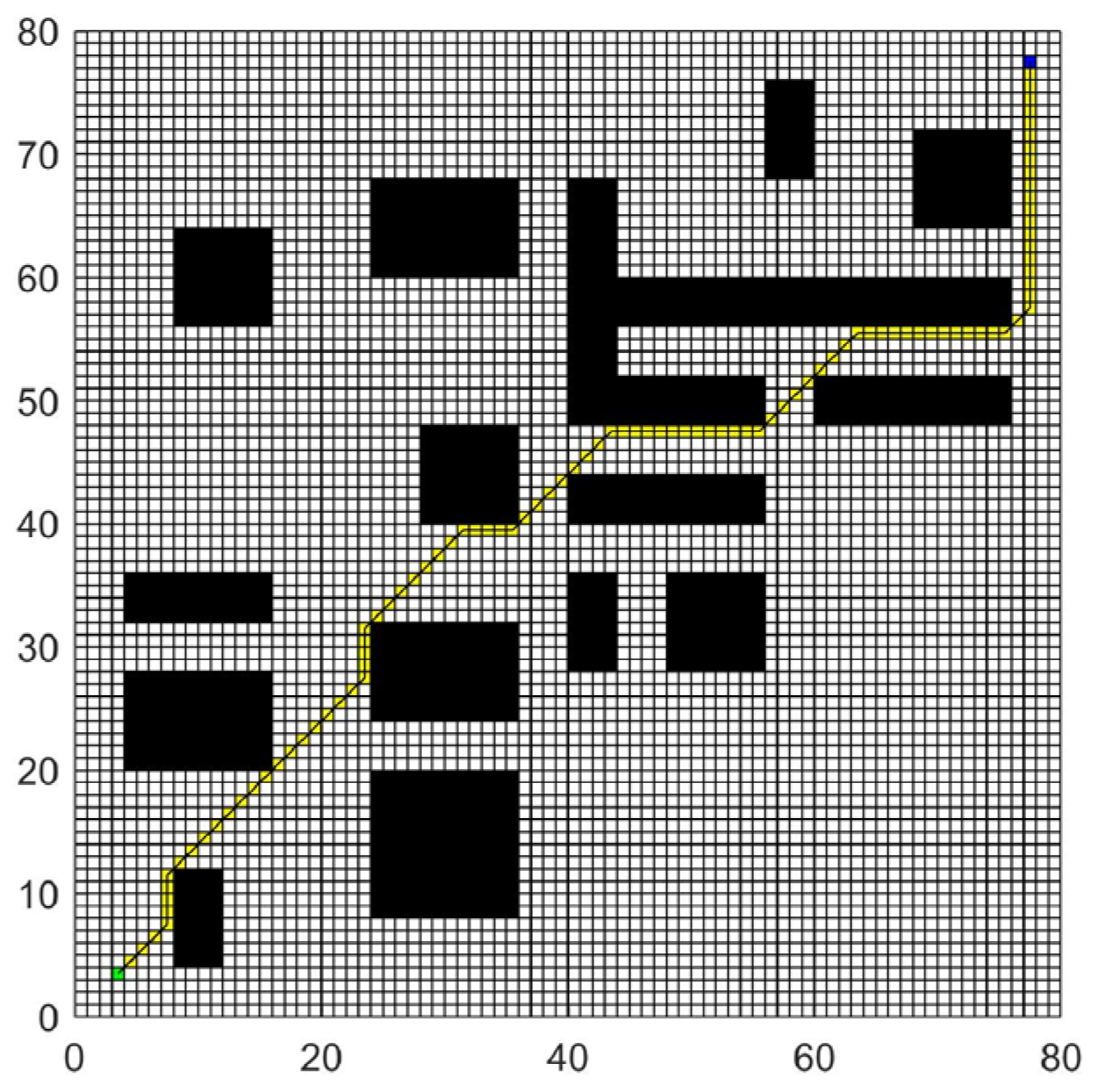
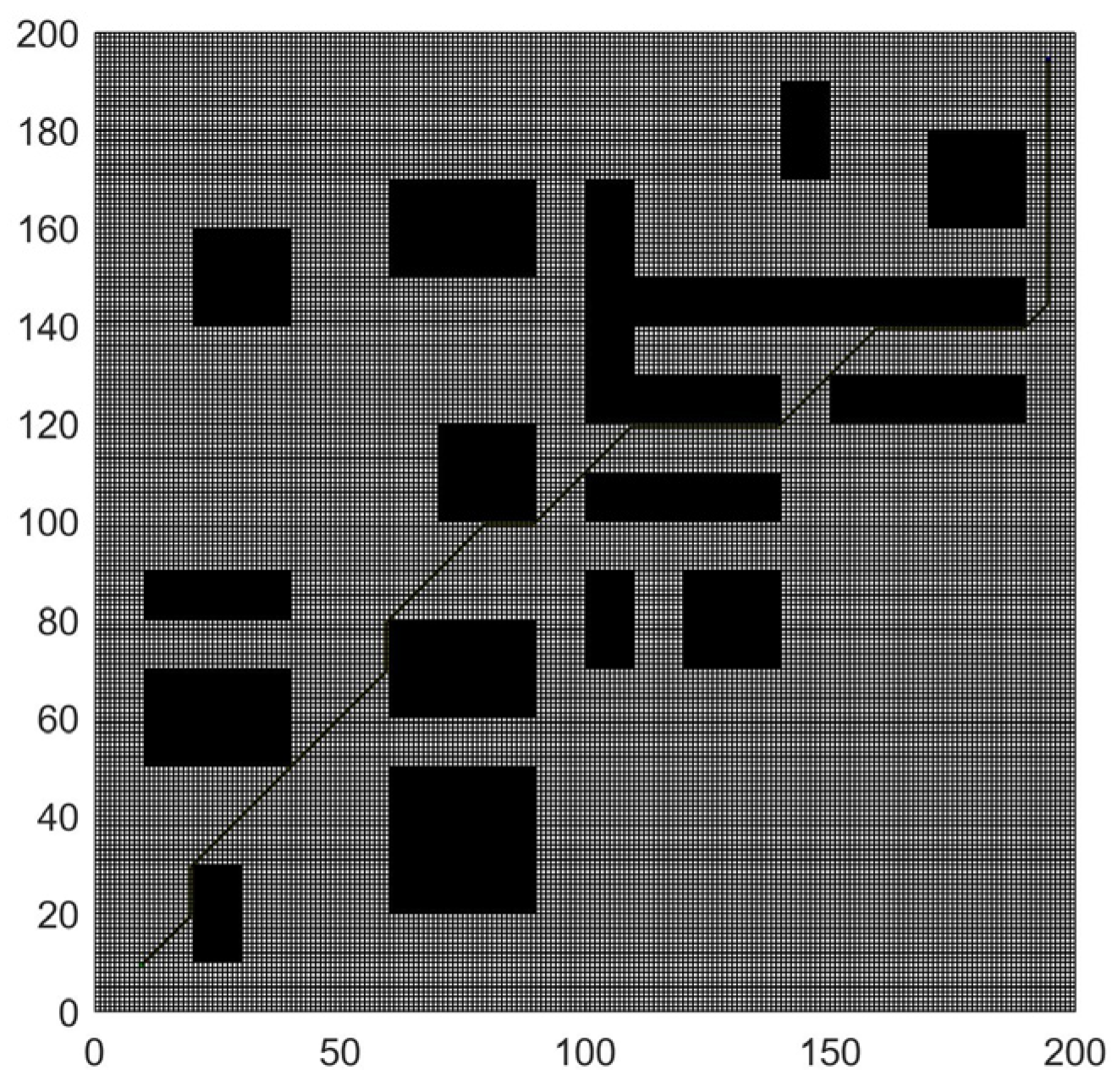
- A low-complexity path-planning algorithm (LCPP) for multiple USVs is proposed based on the visibility graph method, which reduces the computational complexity from to .
- The parameters of the adaptive line-of-sight (ALOS) guidance algorithm are optimized using the simulated annealing algorithm to enhance the safety of each USV traveling along the edge of obstacles.
2. Problem Modeling
3. Path Planning with Low-Complexity and Optimized Guidance in Task Planning
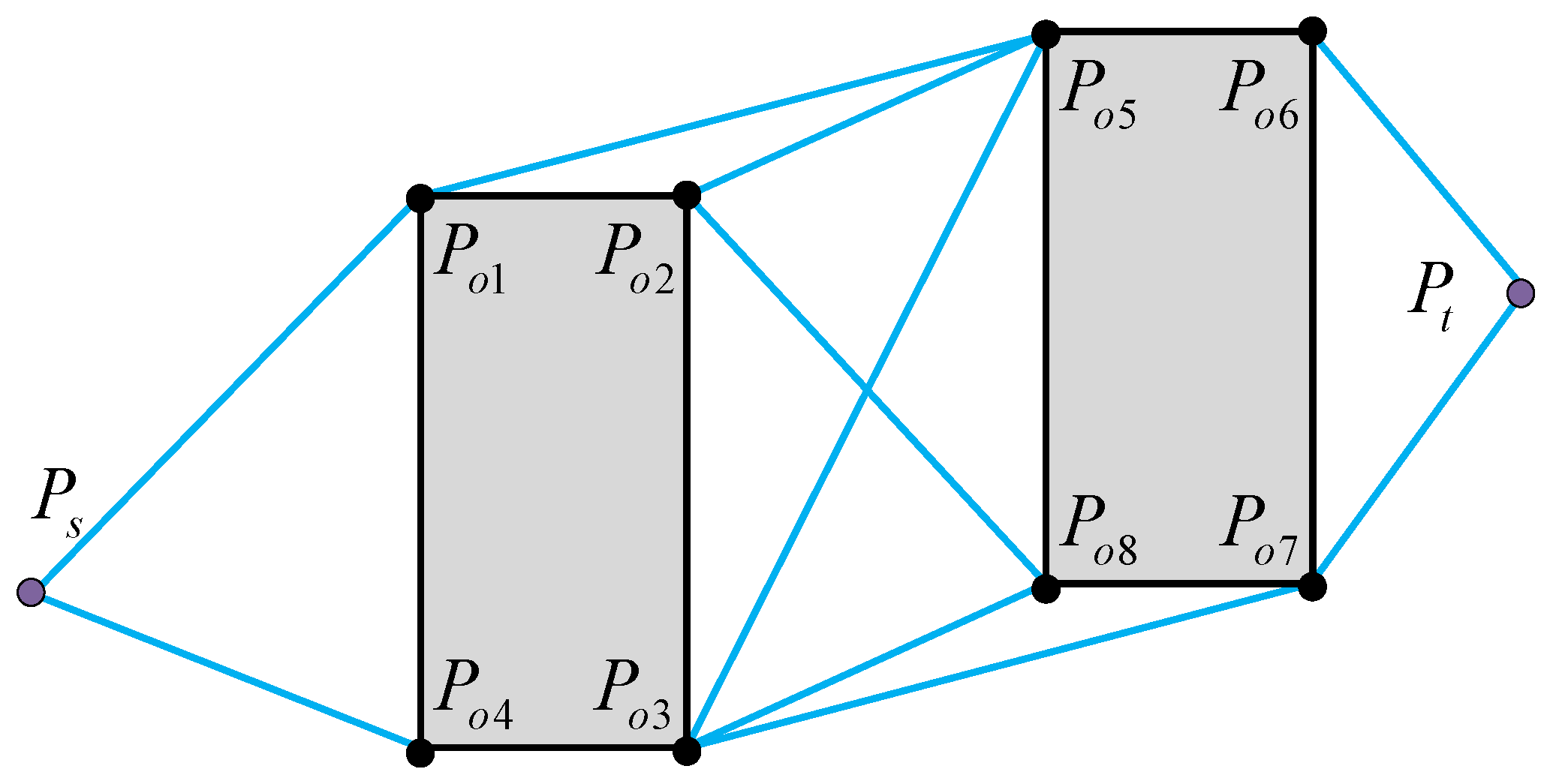
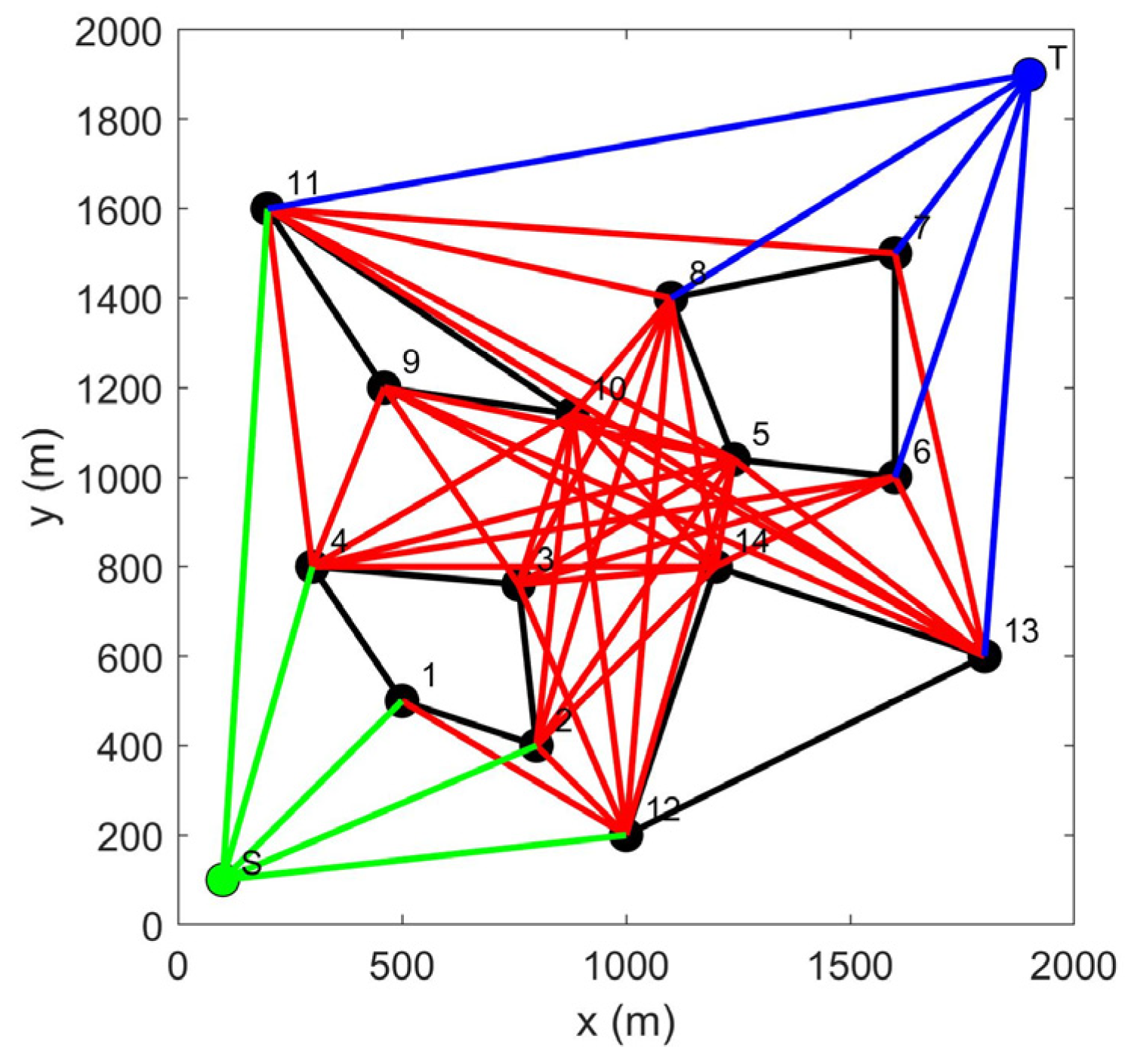
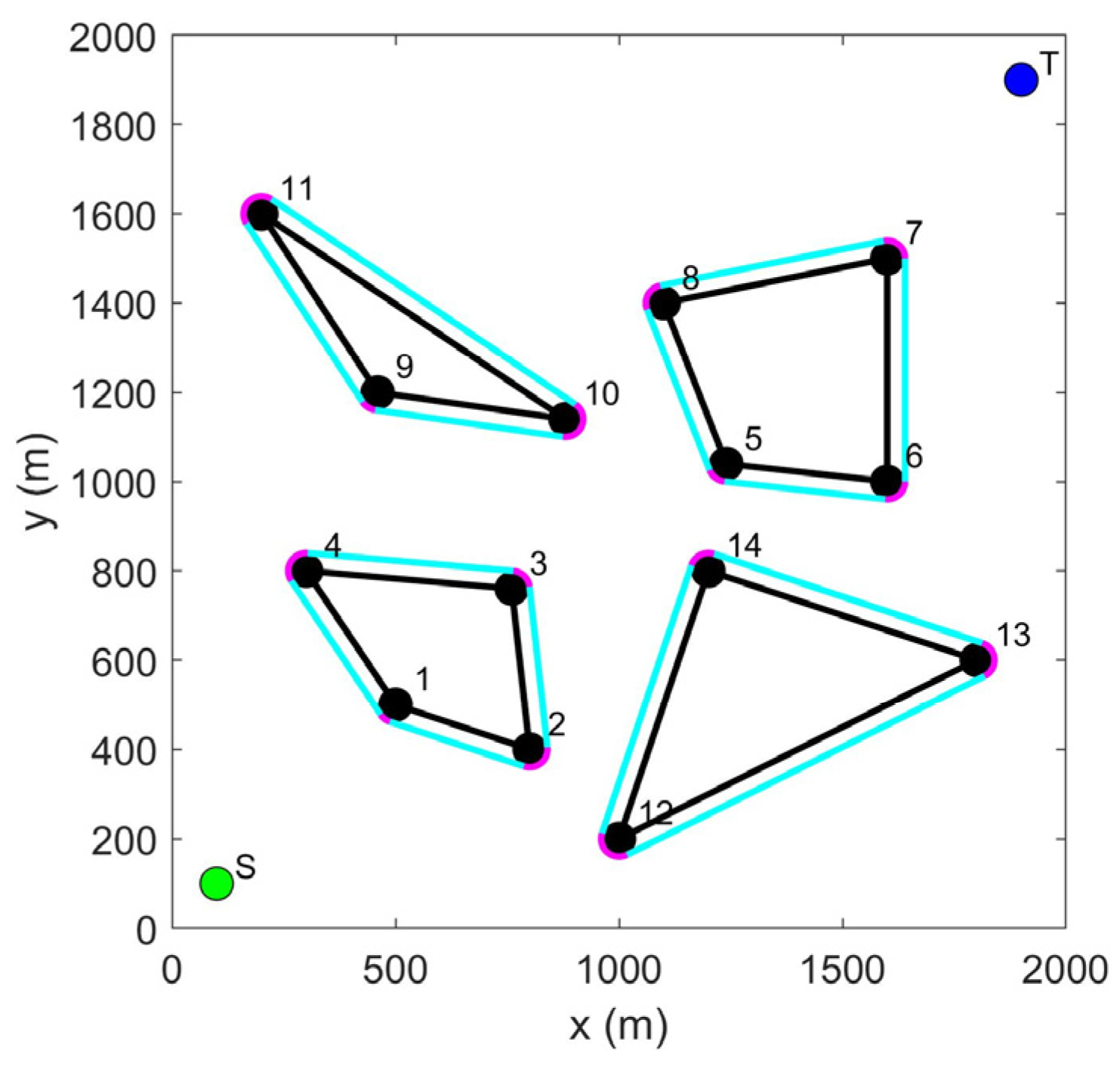
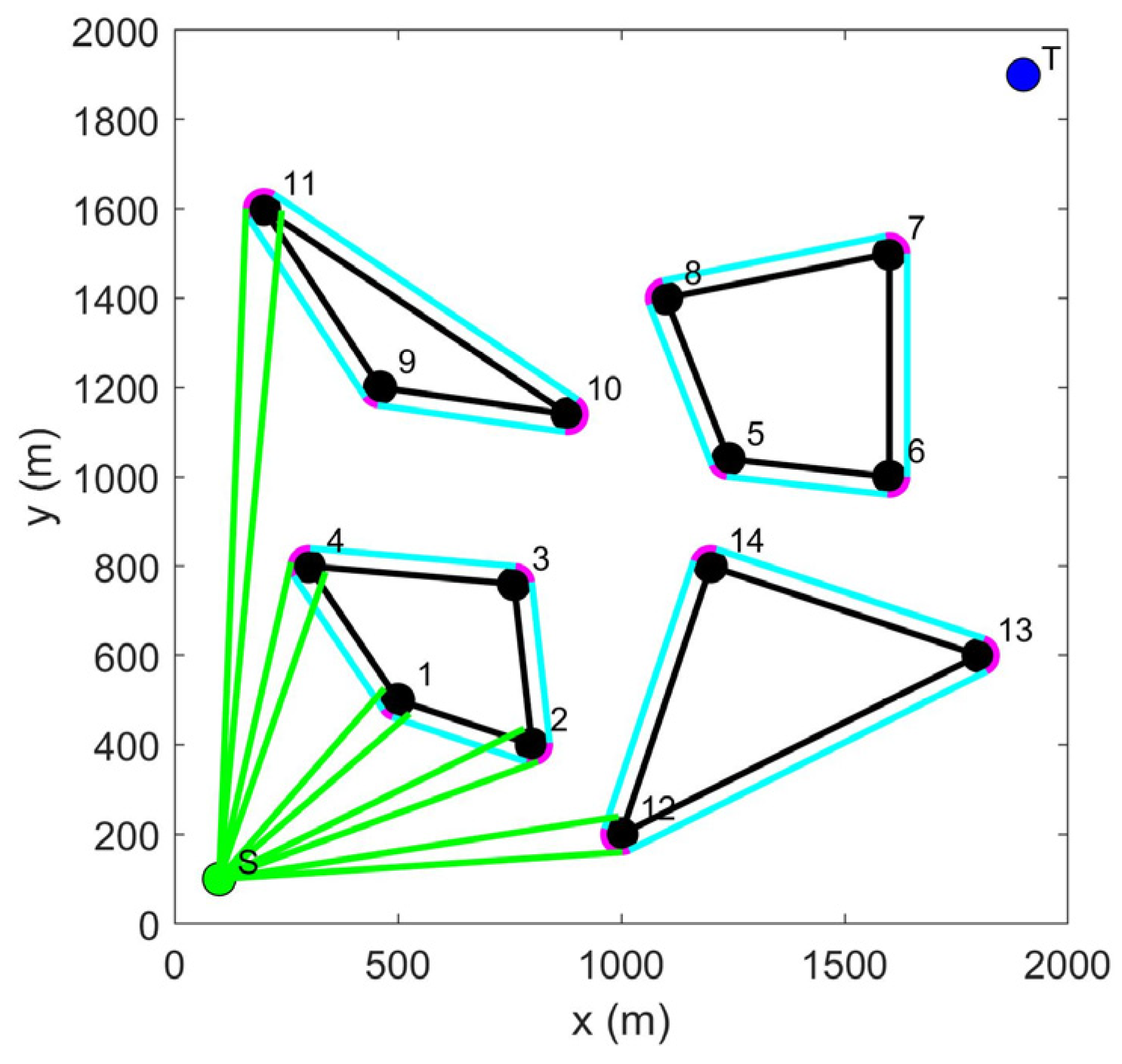
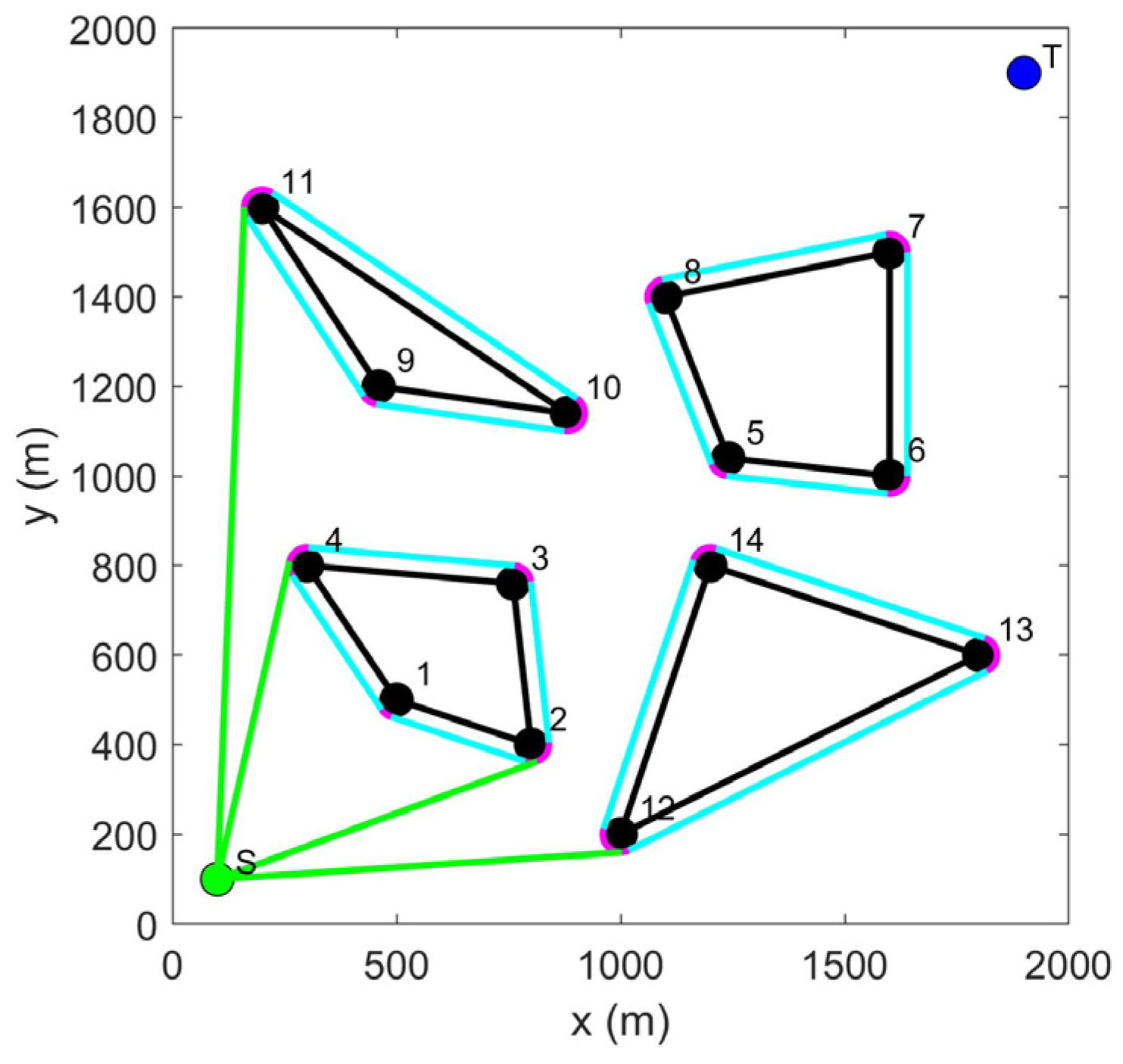
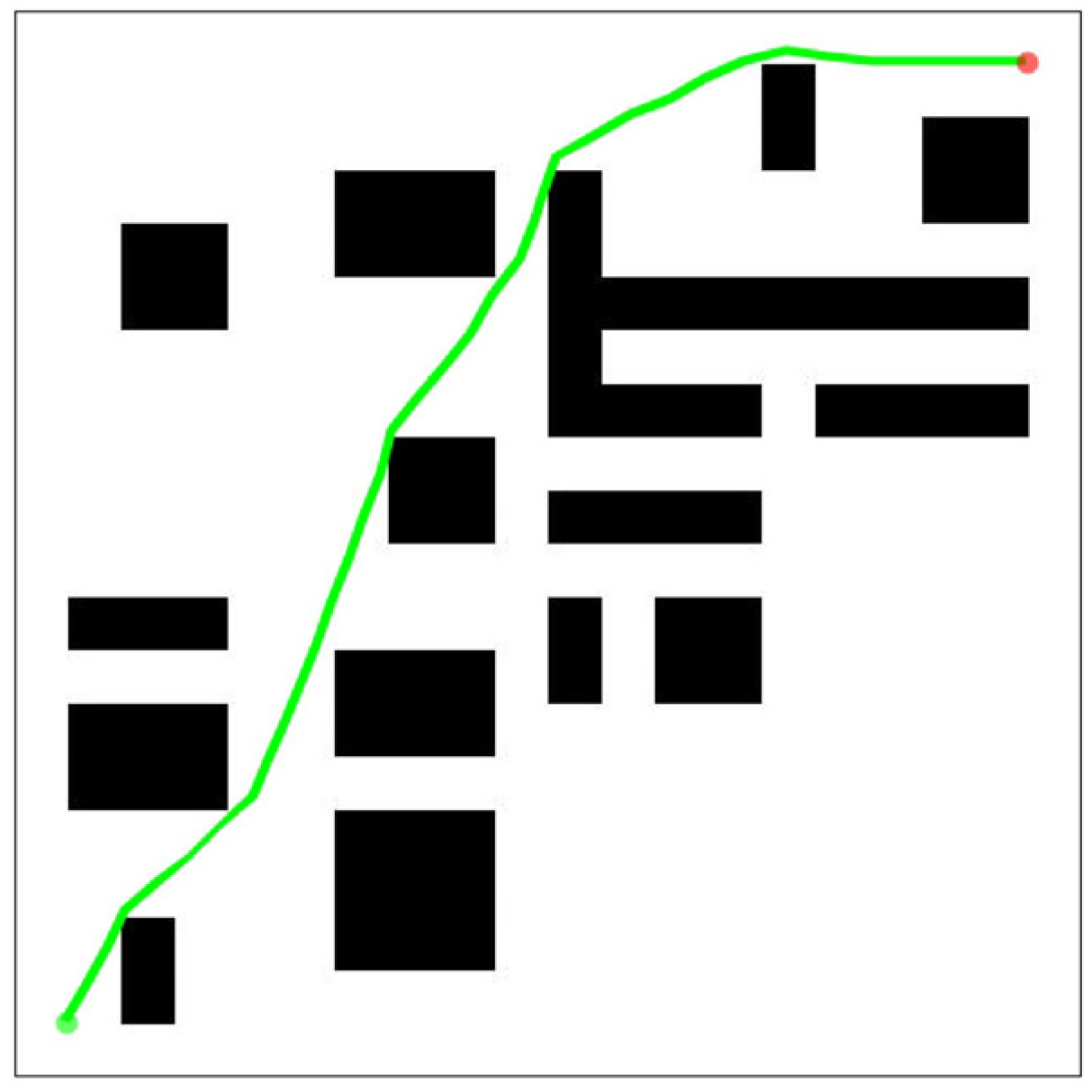
3.1. LCPP for Path Planning of Multiple USVs
- (1)
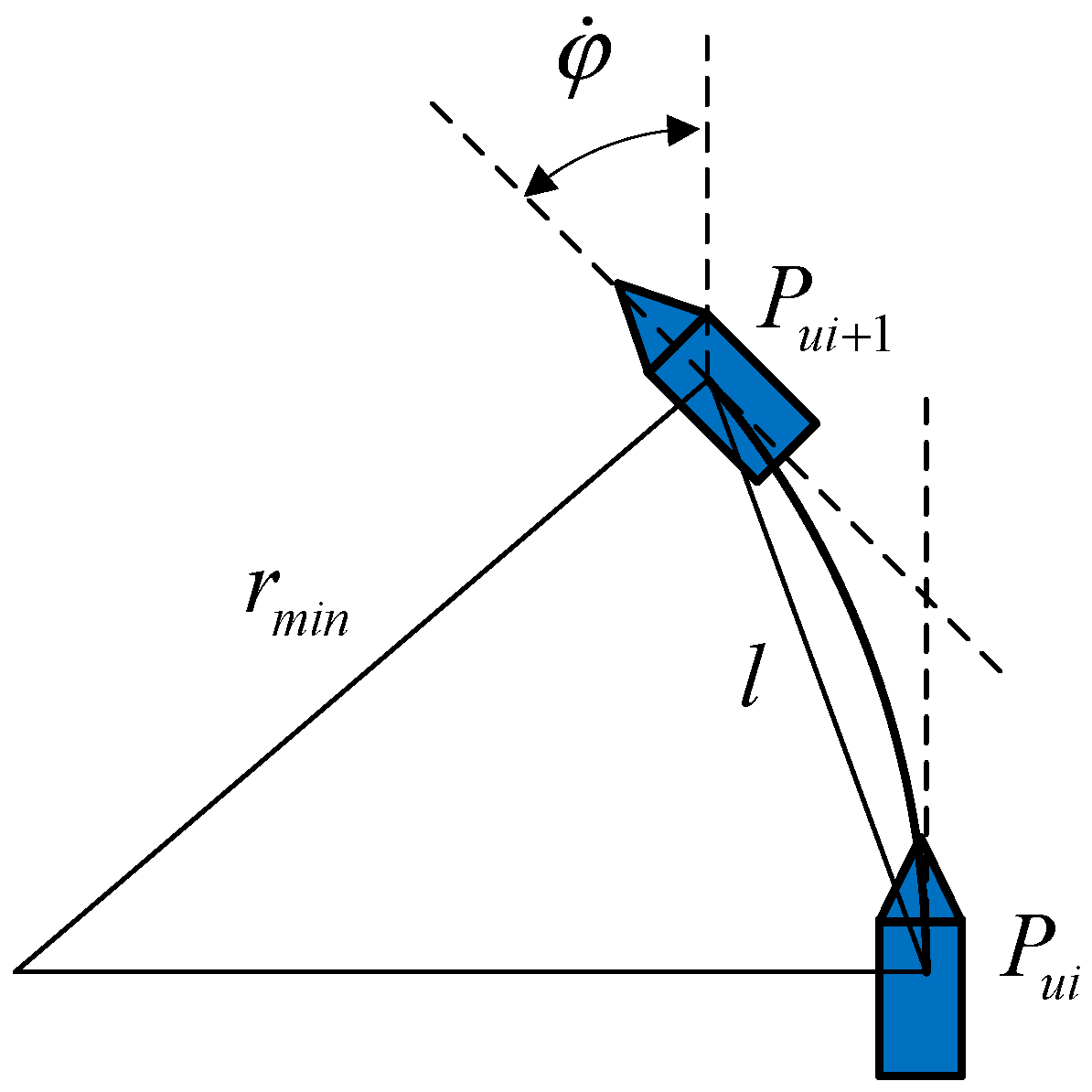
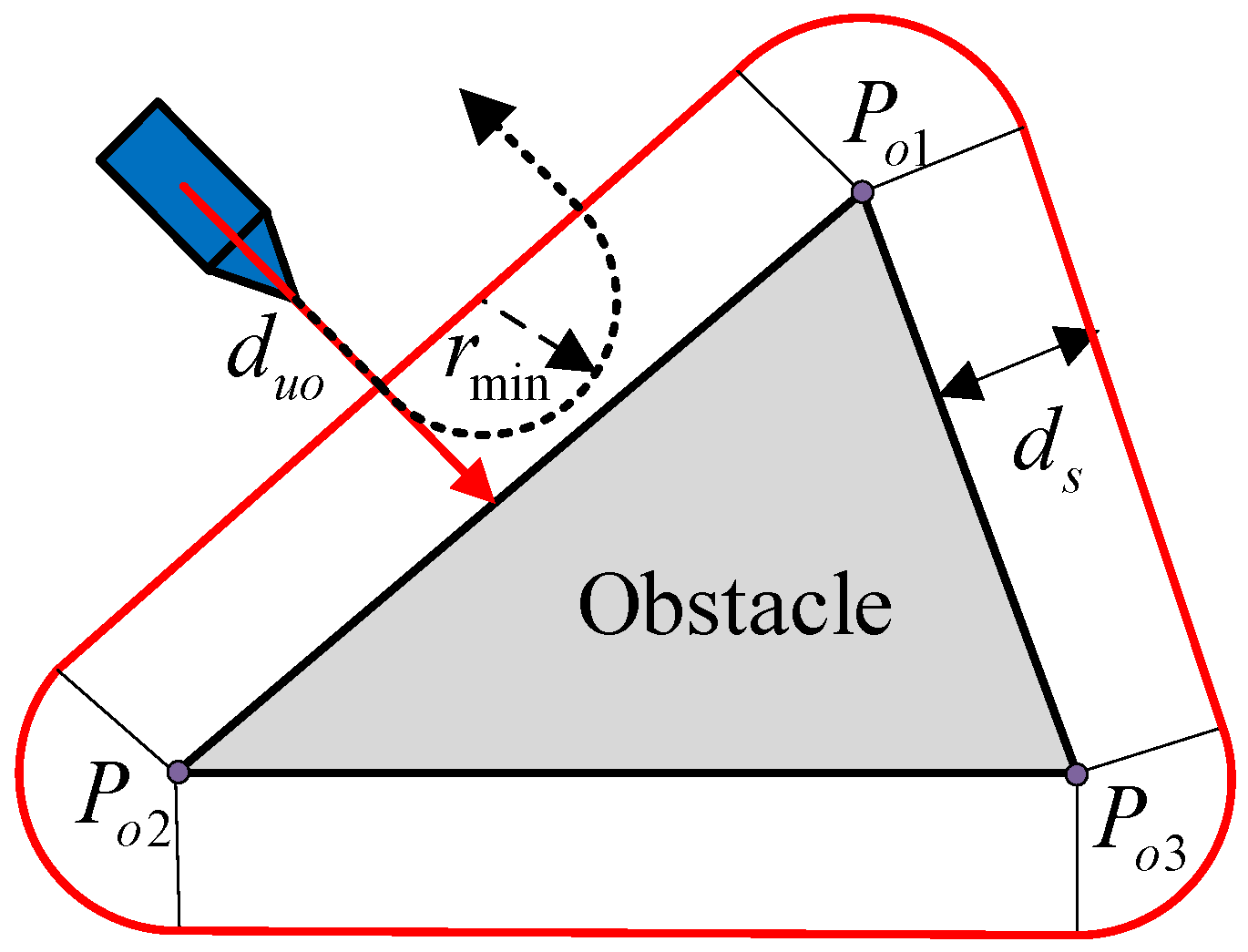
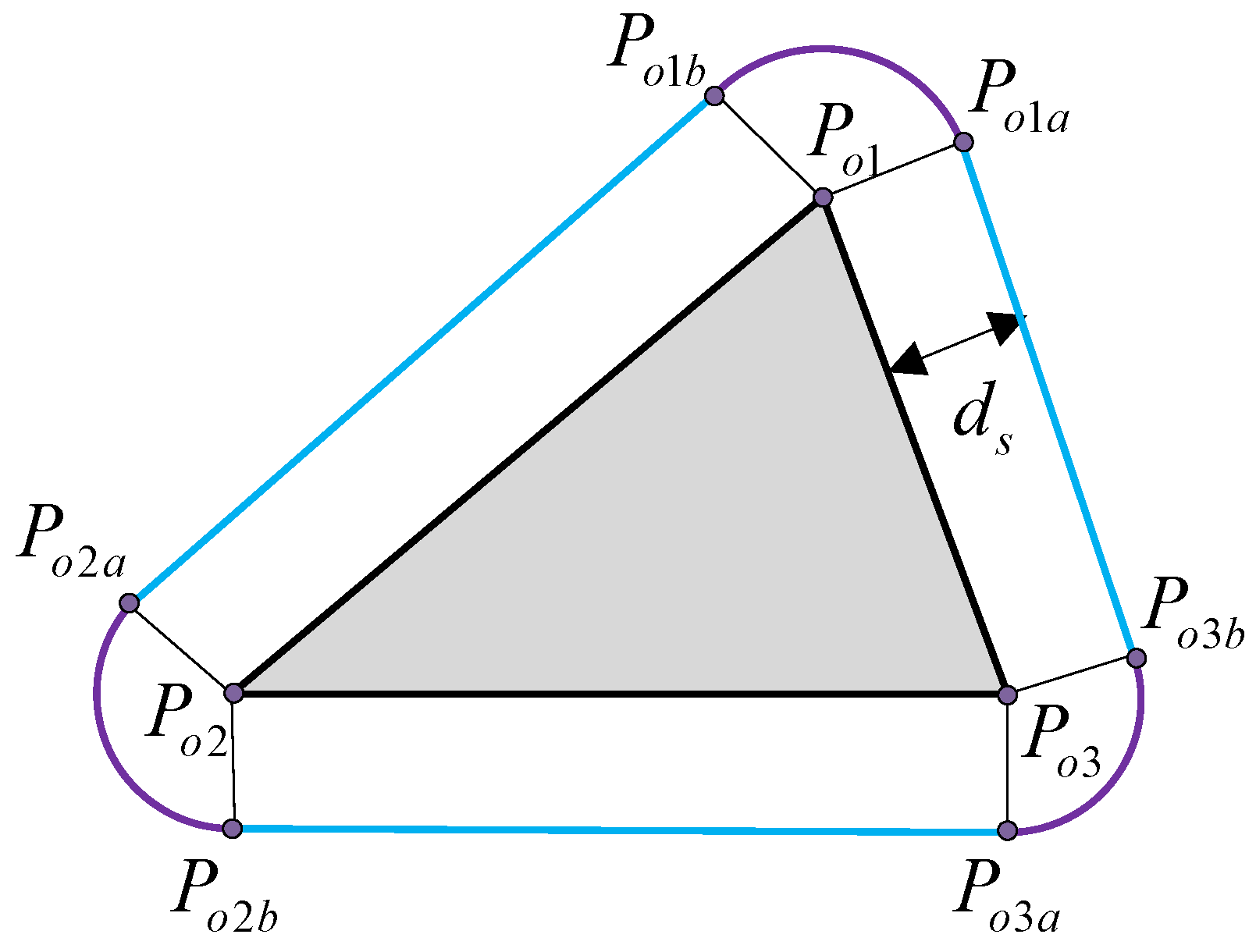
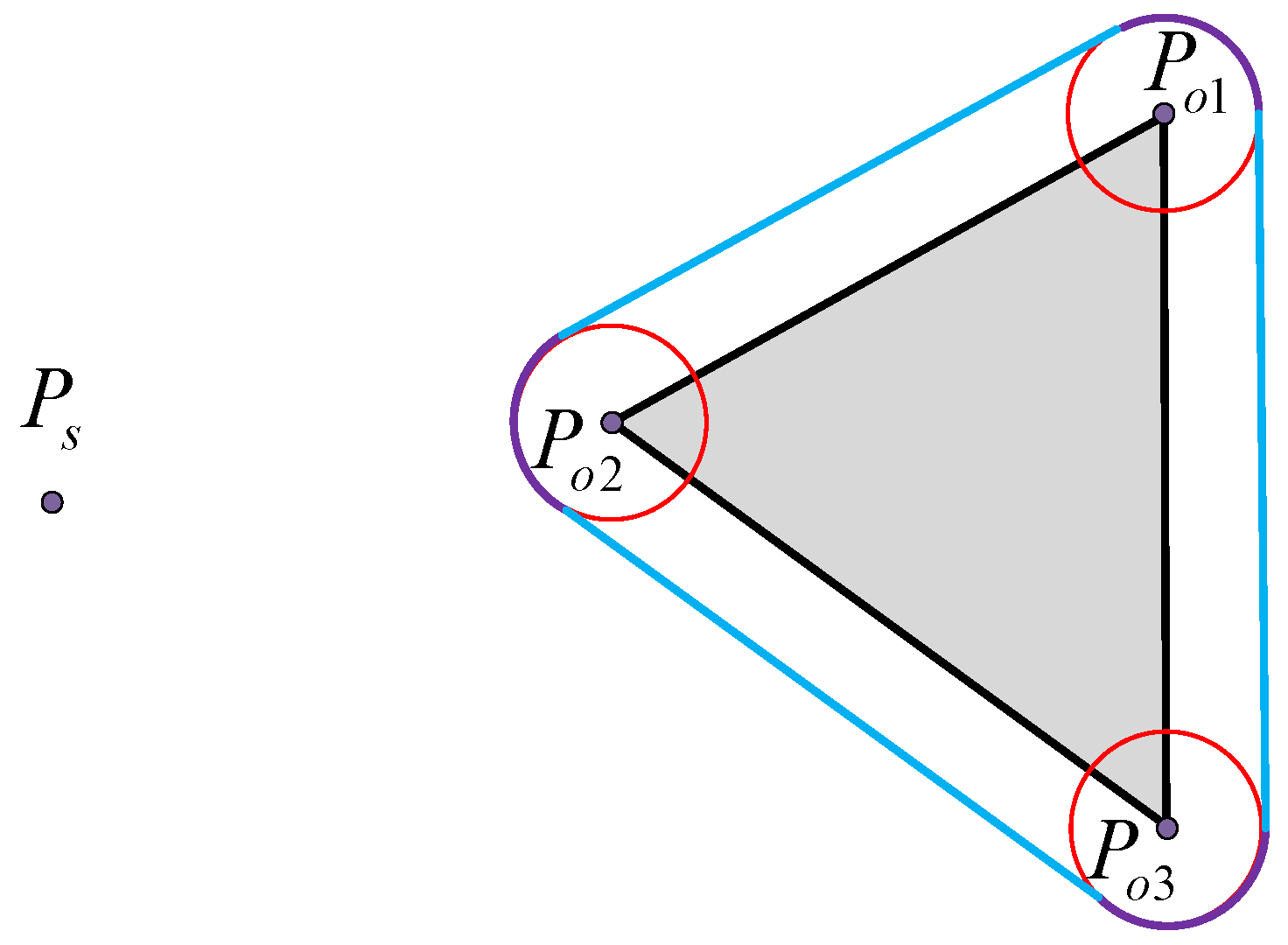
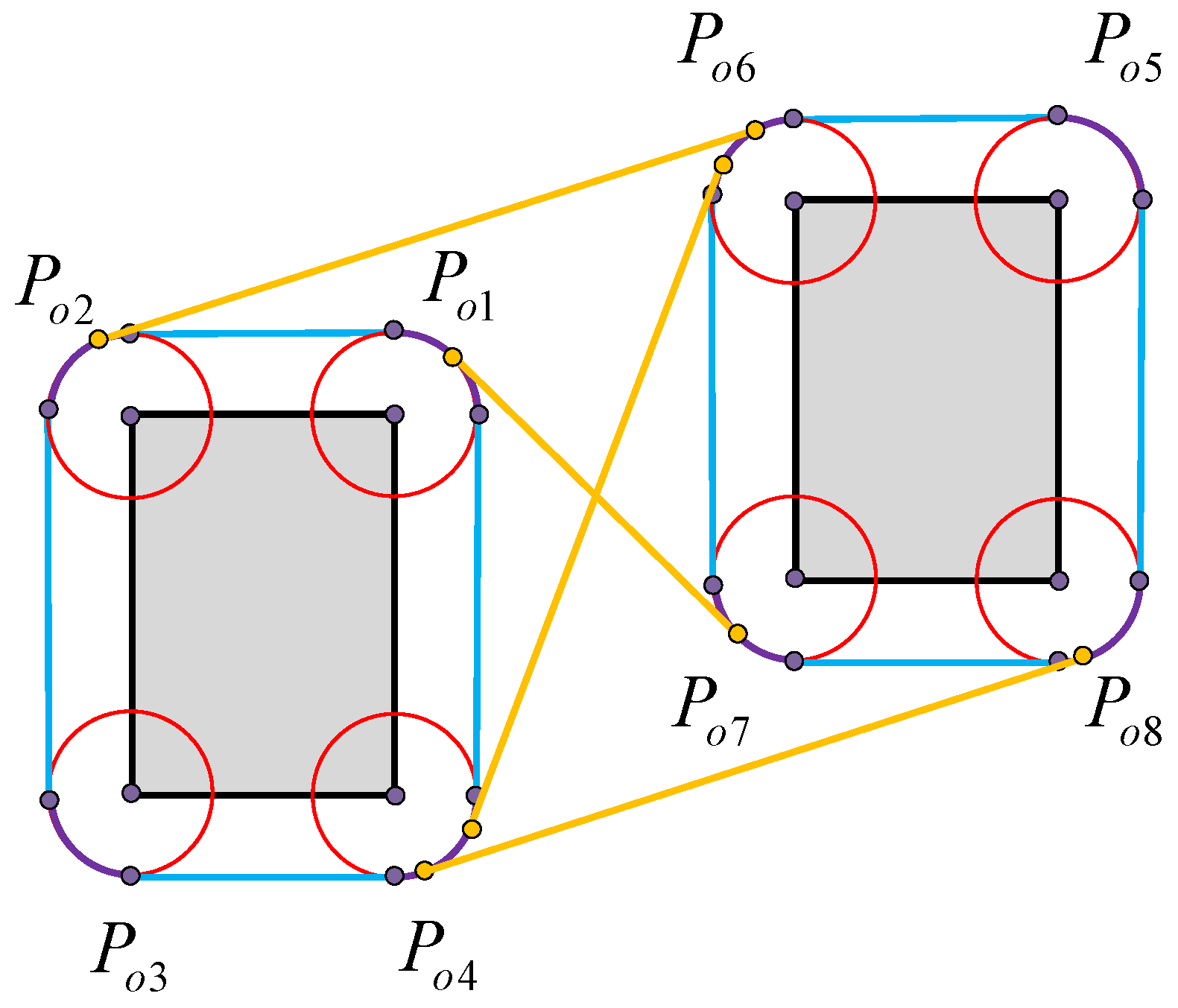
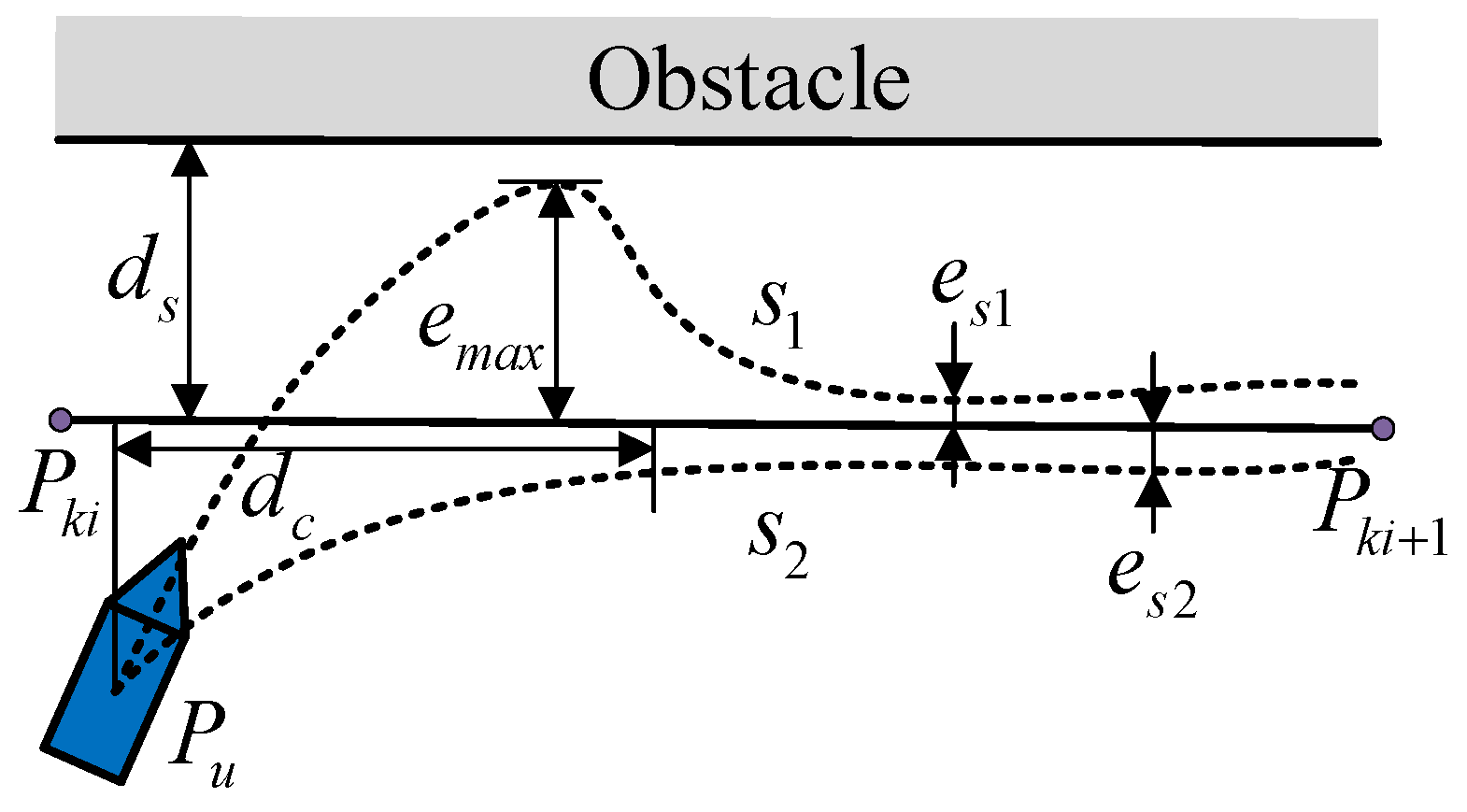
- The path along the safety boundary of obstacles. The safety boundary of the obstacle vertex is represented by a circular arc and is tangential to the safety boundary of the connected straight line.
- (2)
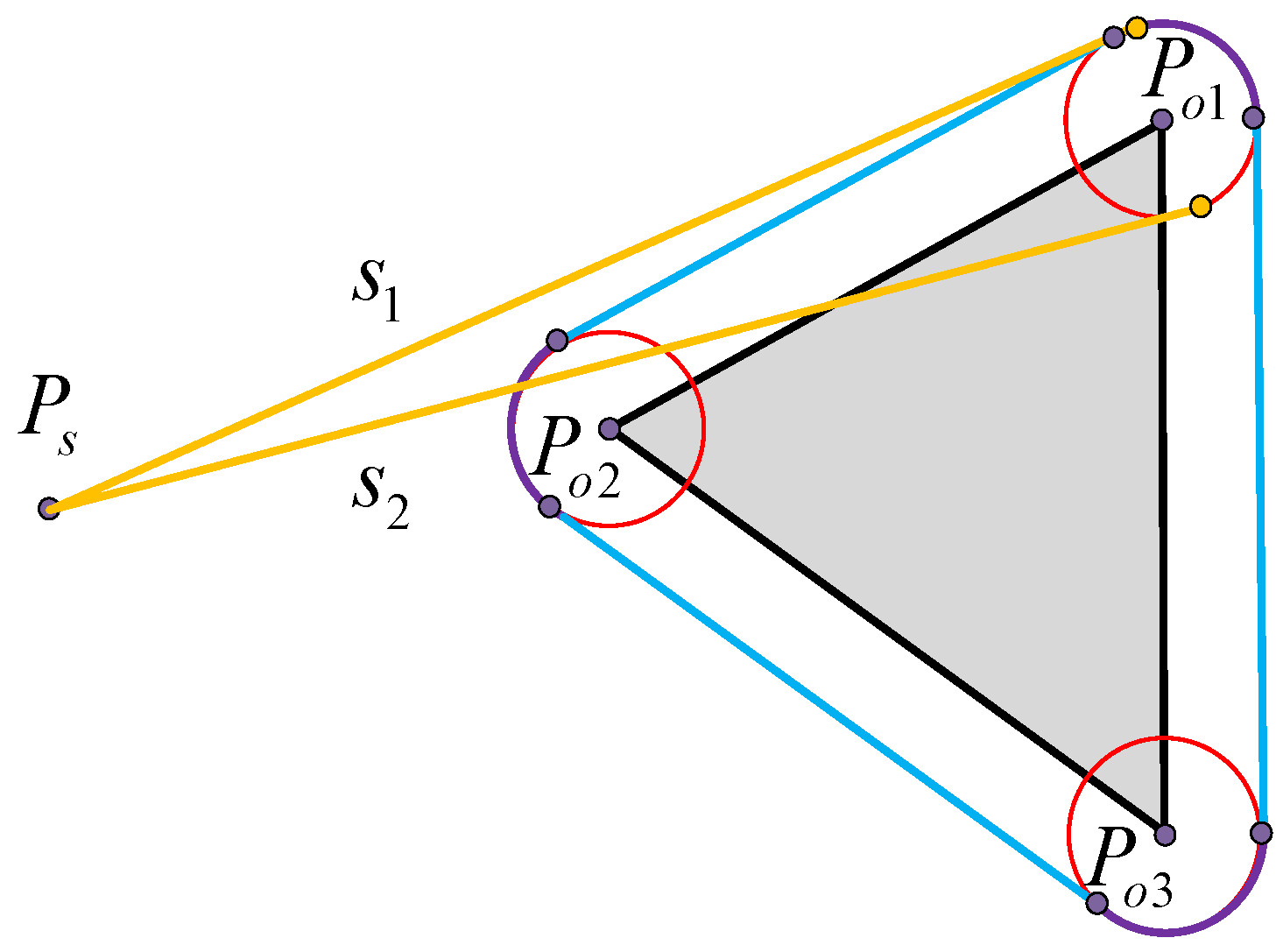
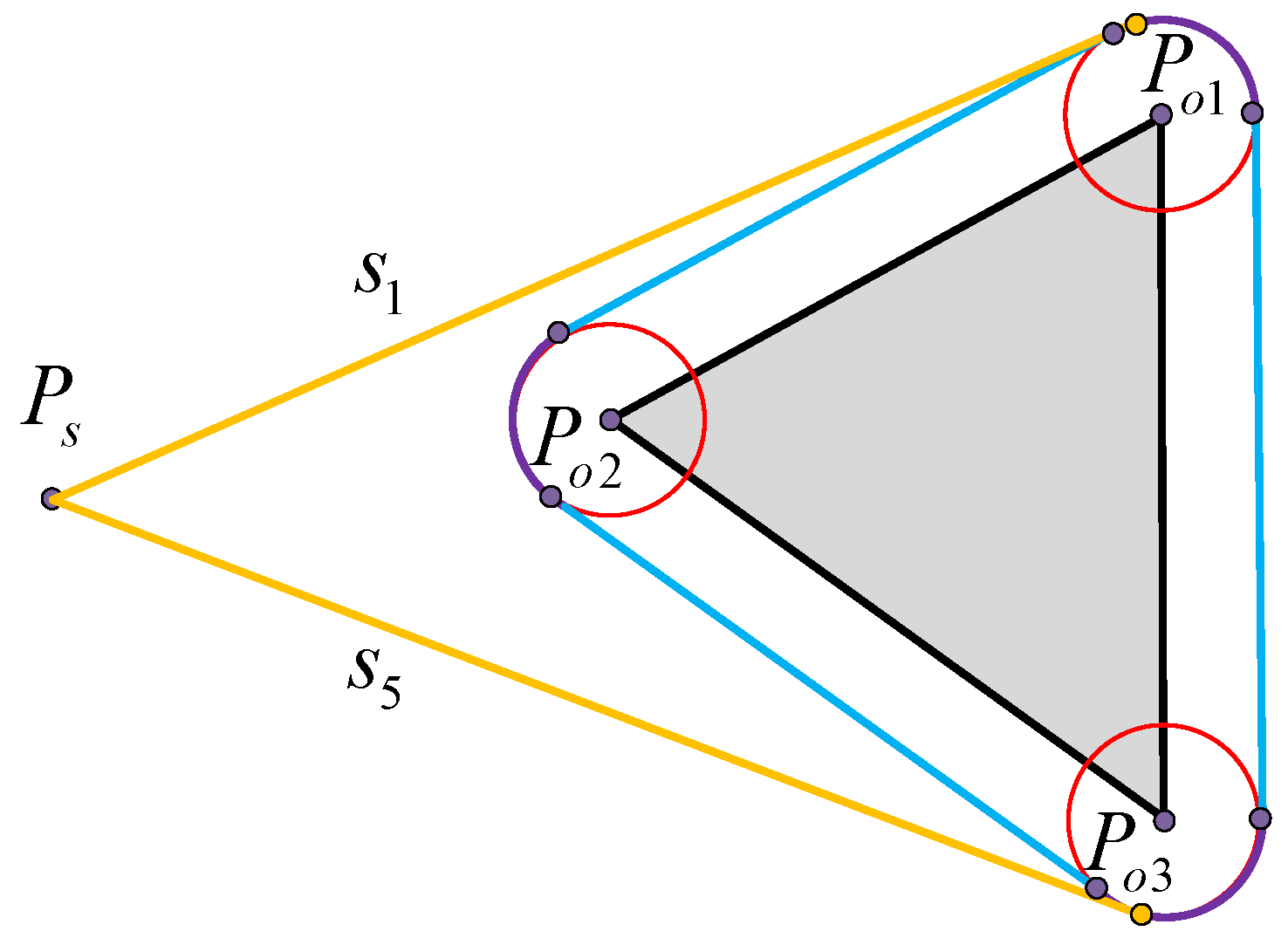
- The path from the start point and target point to the vertex of the obstacle. Because the starting and target points are the locations where USVs depart and arrive, the path from the start and target points to the obstacle vertex should be the tangent of the arc from the start and target points to the obstacle vertex. When the tangent point of the tangent falls on the safe arc corresponding to the vertex, the tangent is an optional path. When the USV moves toward the target point, if it needs to update the path, the path from the USV to the obstacle vertex needs to be recalculated because the USV has moved from the start point to a new position. The target point is always stationary, so there is no need to recalculate the path from the target point to the obstacle vertex.
- (3)
- The path between the vertices of obstacles. The path between obstacle vertices is based on VG to select feasible theoretical paths, construct a safe circle for obstacle vertices, construct four tangents between vertex safe circles, and observe the position of the tangents. If both tangent points of the tangent line are on the safe arc, then the path is an optional path and other paths are unsafe and unselected abandoned paths. Judging the path between obstacle vertices in this way not only increases the safety of the path but also eliminates nonselectable paths in advance, reducing the filtering range for subsequent selectable path selections.
3.2. ALOS with the Optimized Parameter
| Algorithm 2. Calculate evaluation parameter | |
| Input: , USV motion model , USV control algorithm , LOS algorithm , weighting function , end time of LOS , initial position , initial speed , and initial heading of USV, desired path , , | |
| Output: evaluation parameter | |
| 1: | ; |
| 2: | While |
| 3: | ; // track error |
| 4: | ; // desired heading |
| 5: | ; // desired rudder angle |
| 6: | ; // USV travels |
| 7: | ; |
| 8: | End |
| 9: | ); |
| 10: | ; |
| Algorithm 3. Parameter selection of LOS using Simulated Annealing | |
| Input: Initial temperature , final temperature , attenuation coefficient , initial solution , length of Markov chain , random function , | |
| Output: Best solution | |
| 1: | ; ; ; ; |
| 2: | While && |
| 3: | ; |
| 4: | If |
| 5: | ; |
| 6: | Else if |
| 7: | ; |
| 8: | End |
| 9: | |
| 10: | ; |
| 11: | End |
4. Simulation
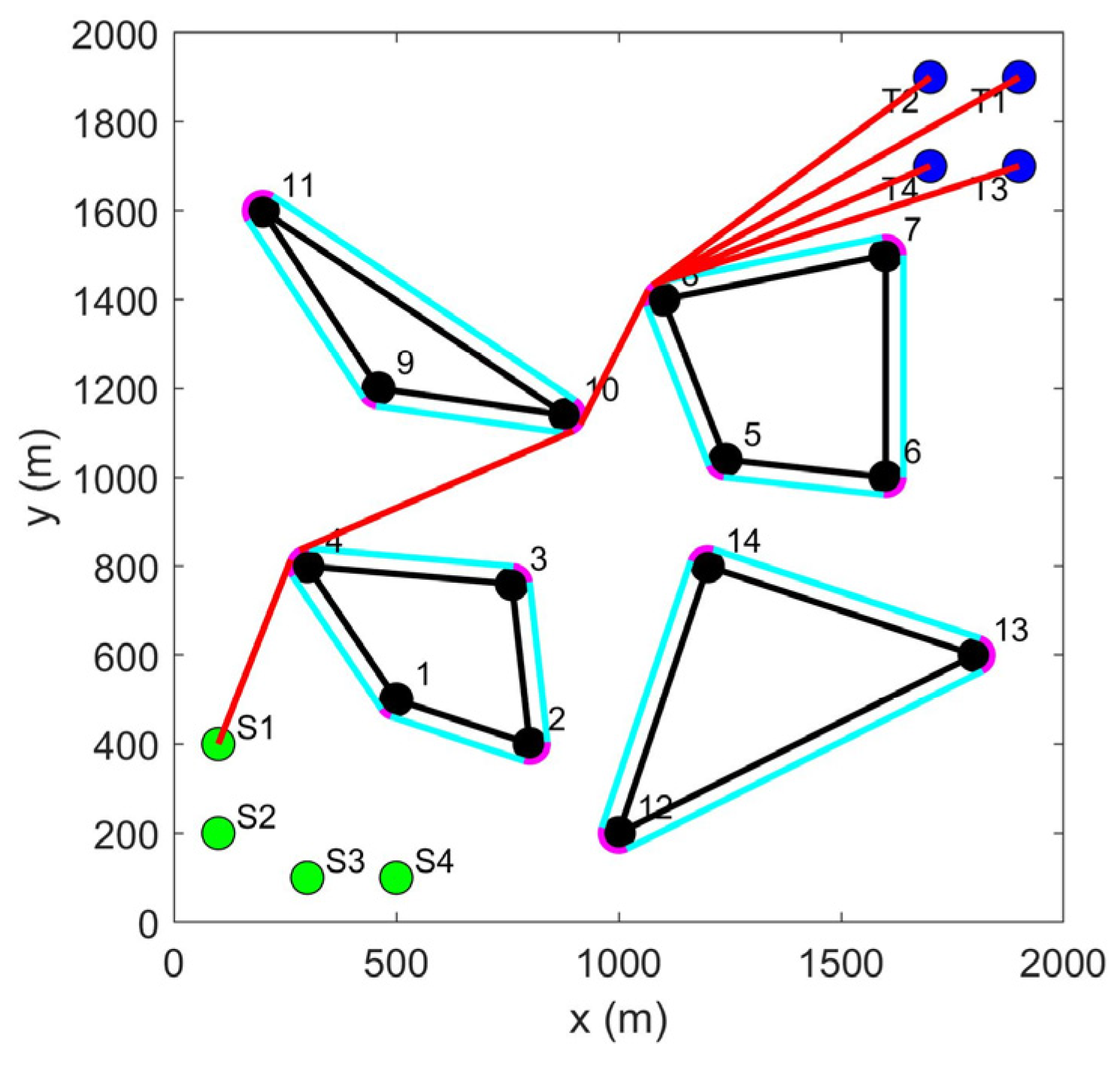
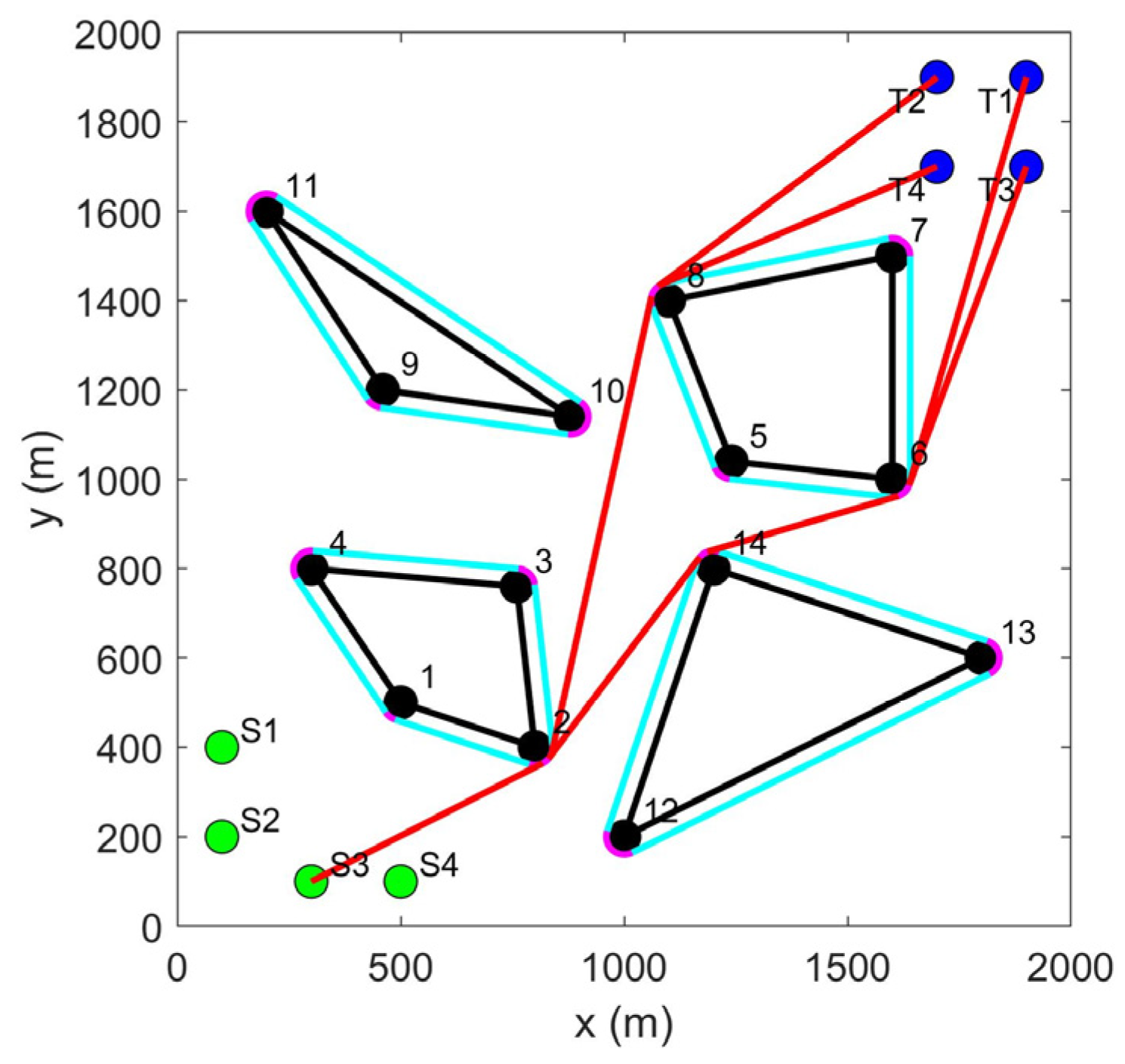
4.1. LCPP for Path Planning of Multiple USVs
- (1)
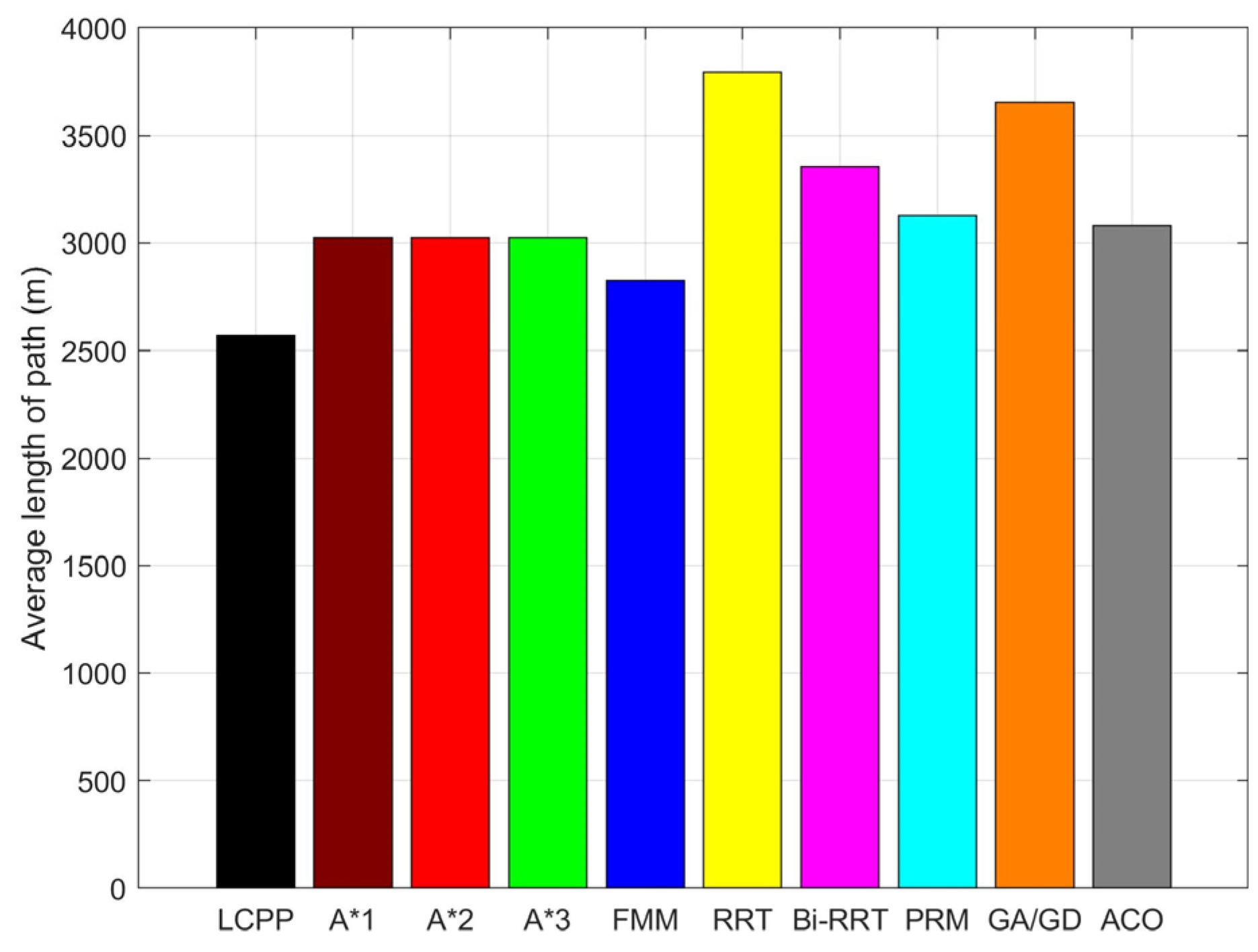
- Calculation time and path length of path planning for the single USV
- (2)
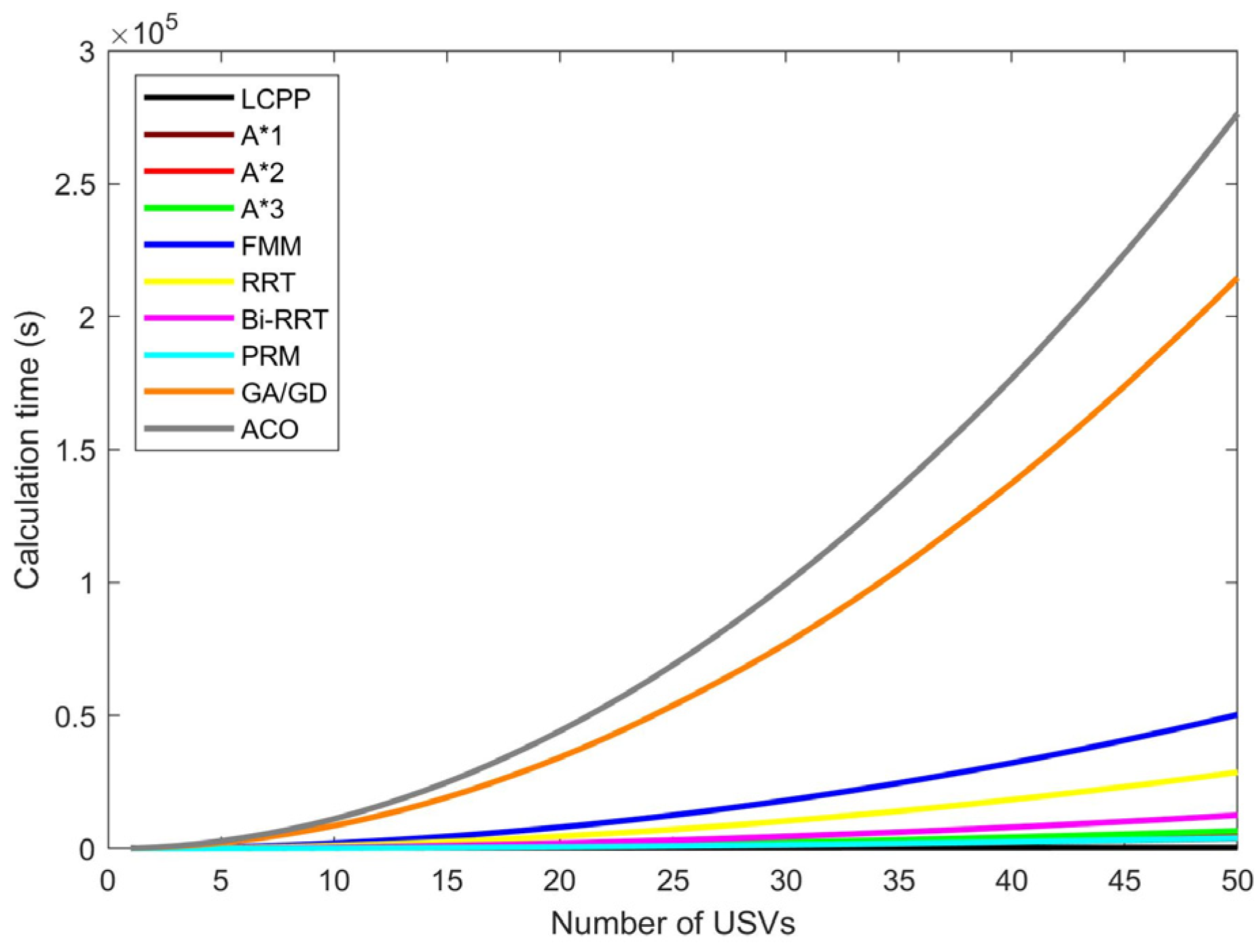
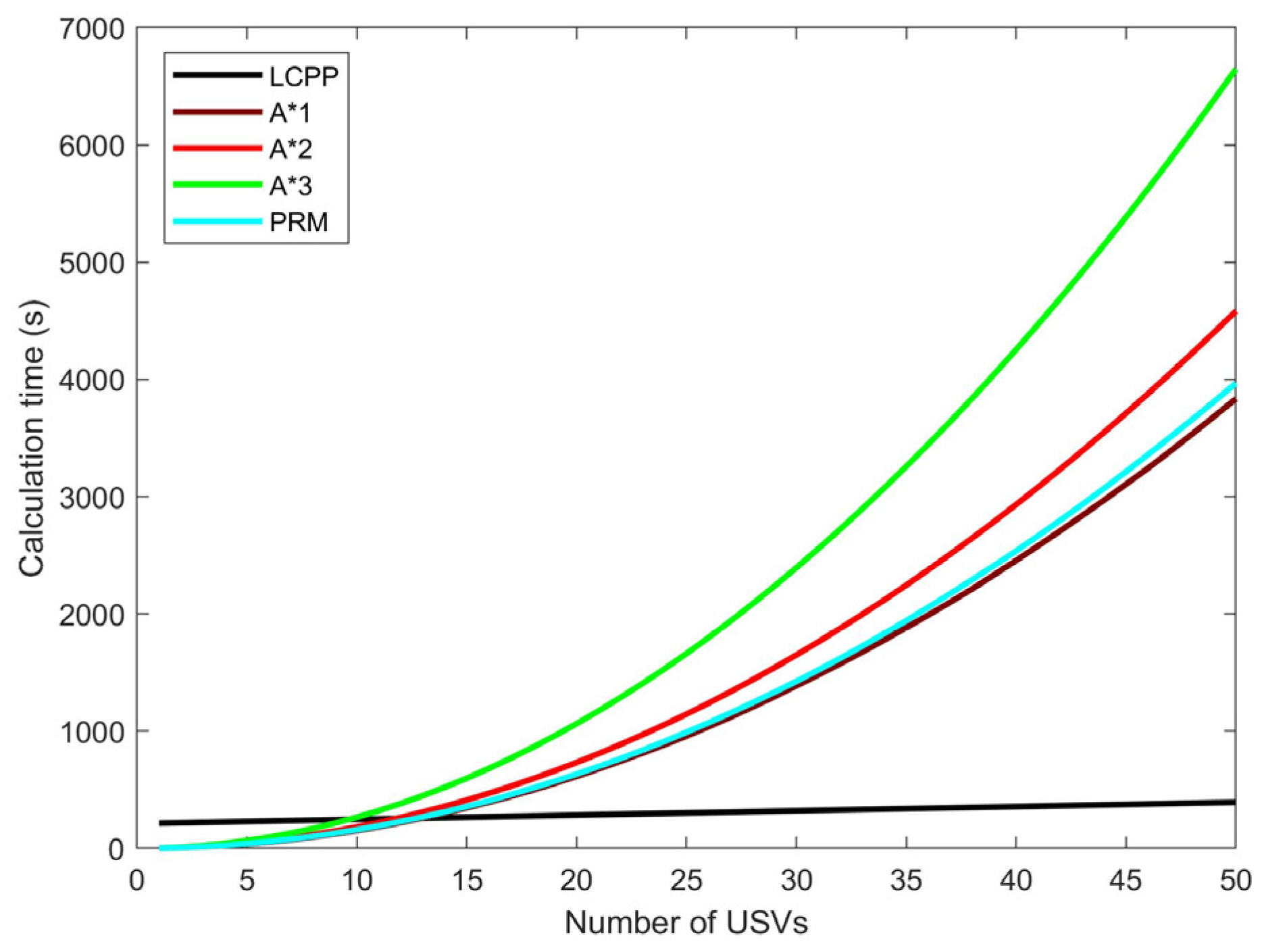
- Calculation time and path length of path planning for multiple USVs.
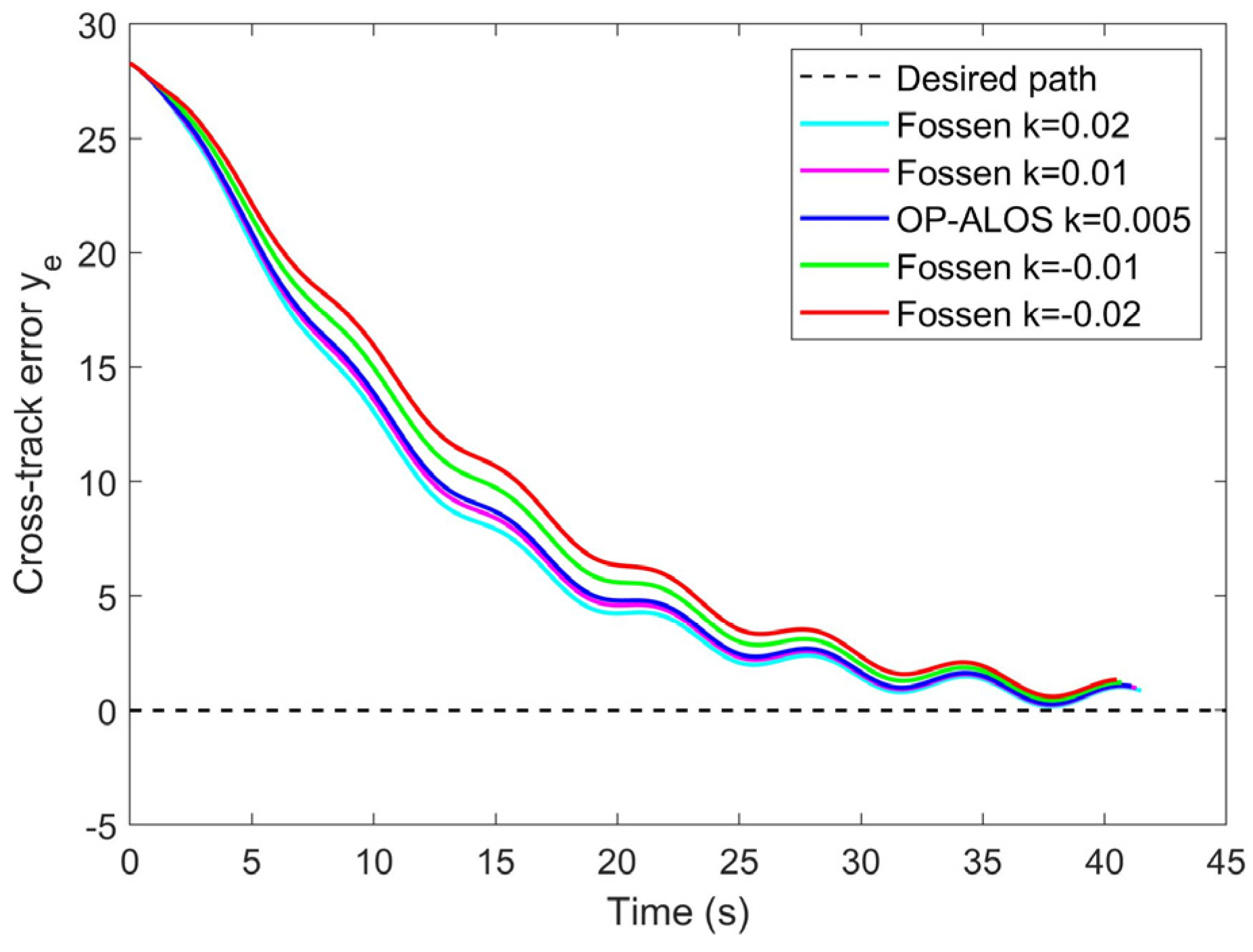
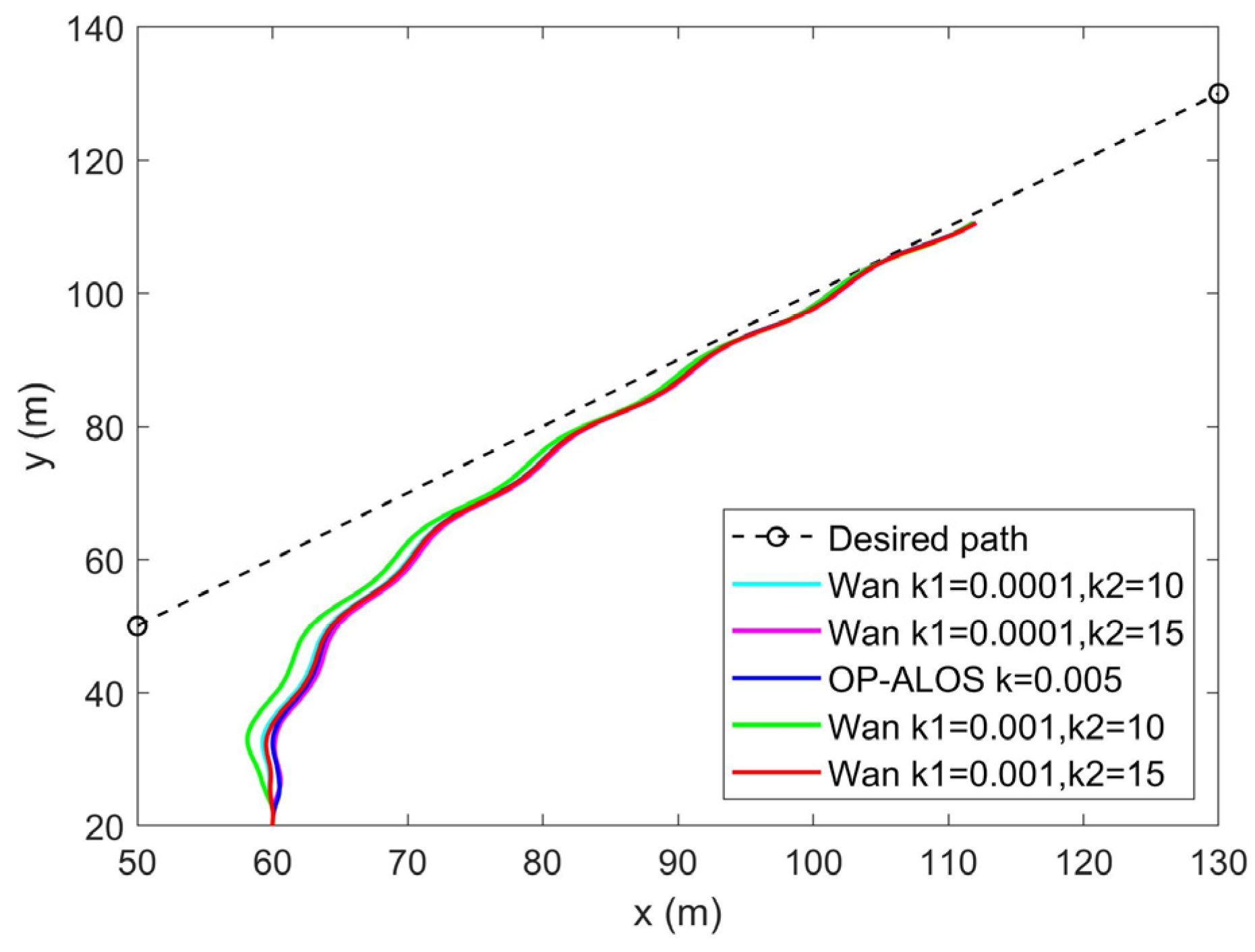
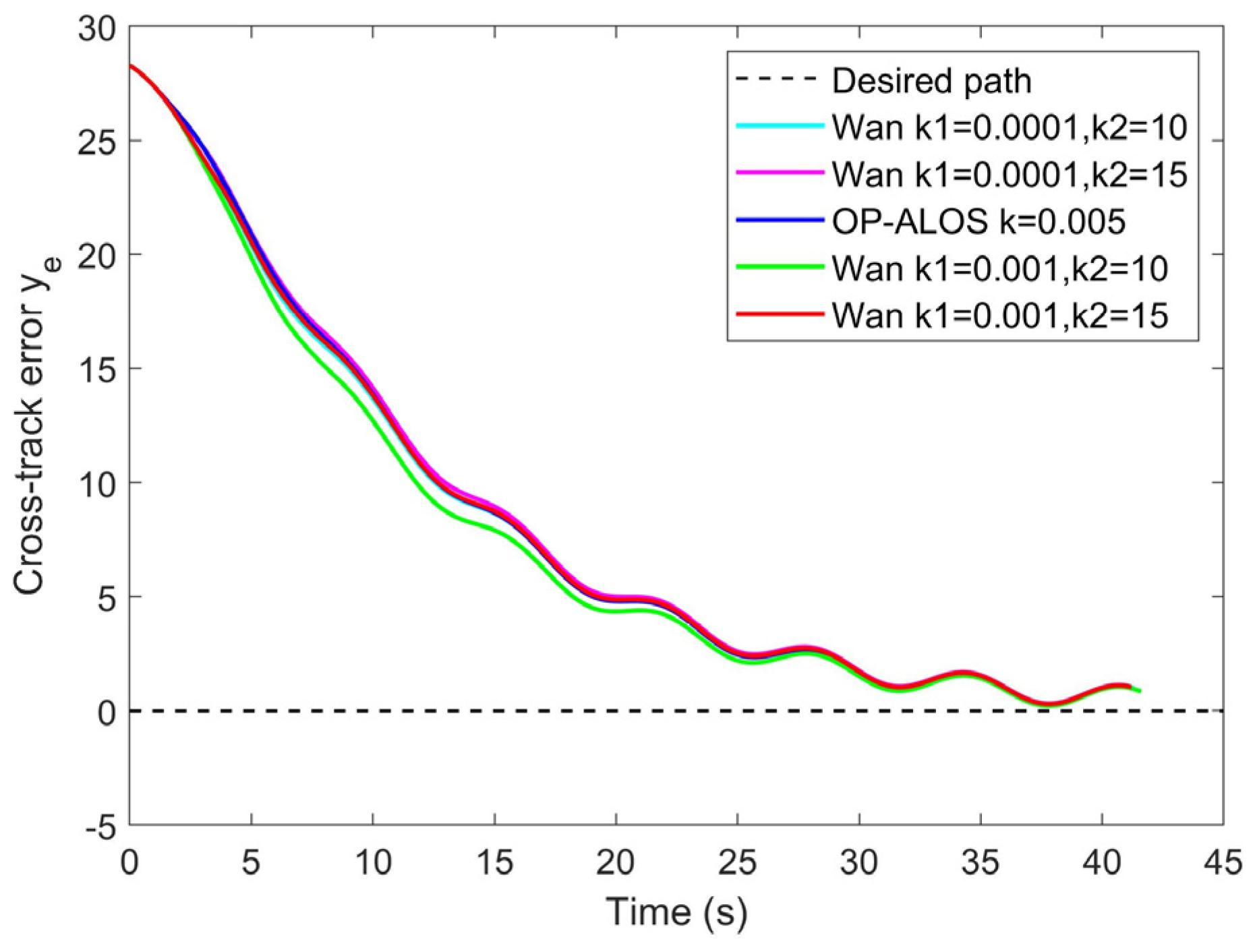
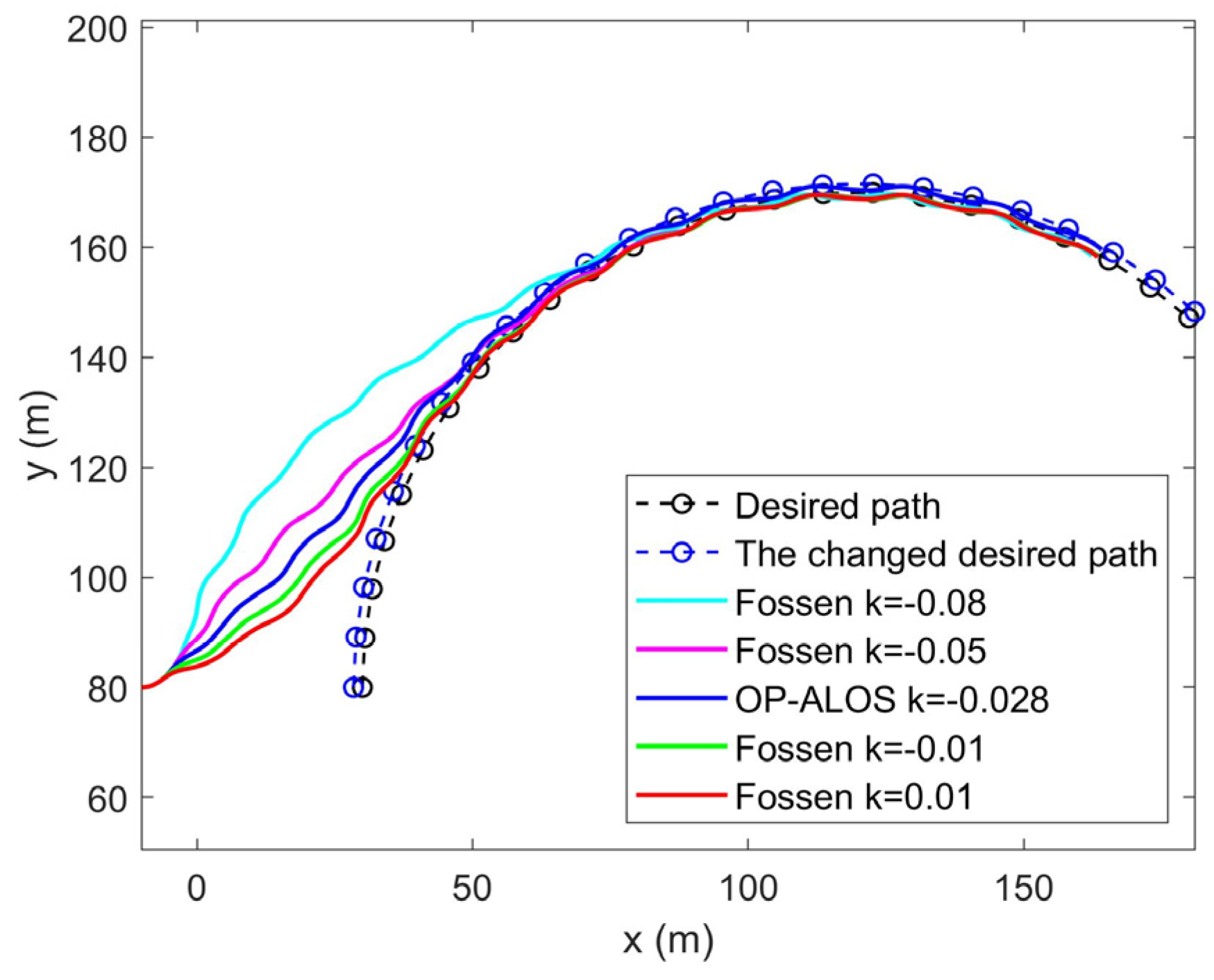
4.2. ALOS with the Optimized Parameter
- (1)
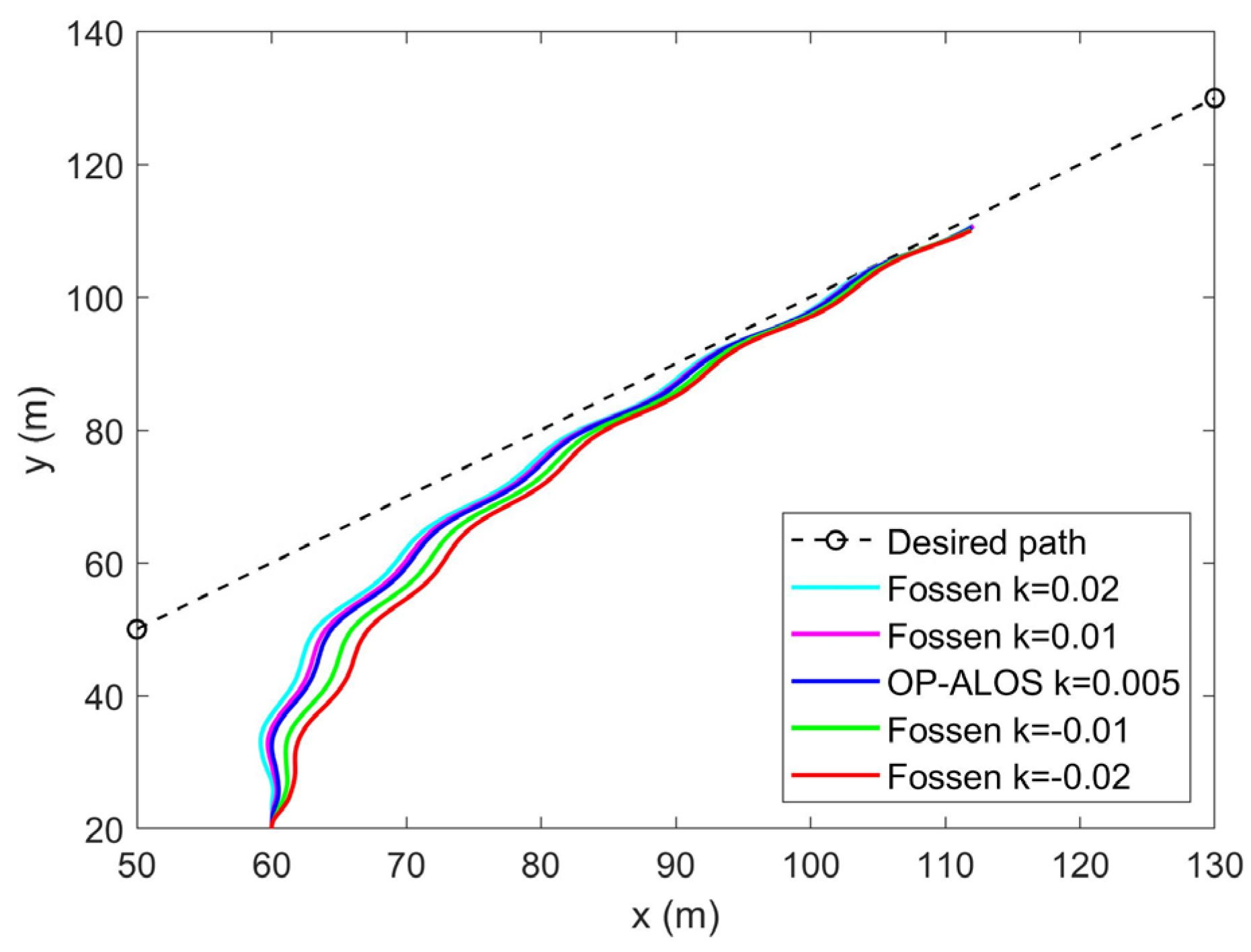
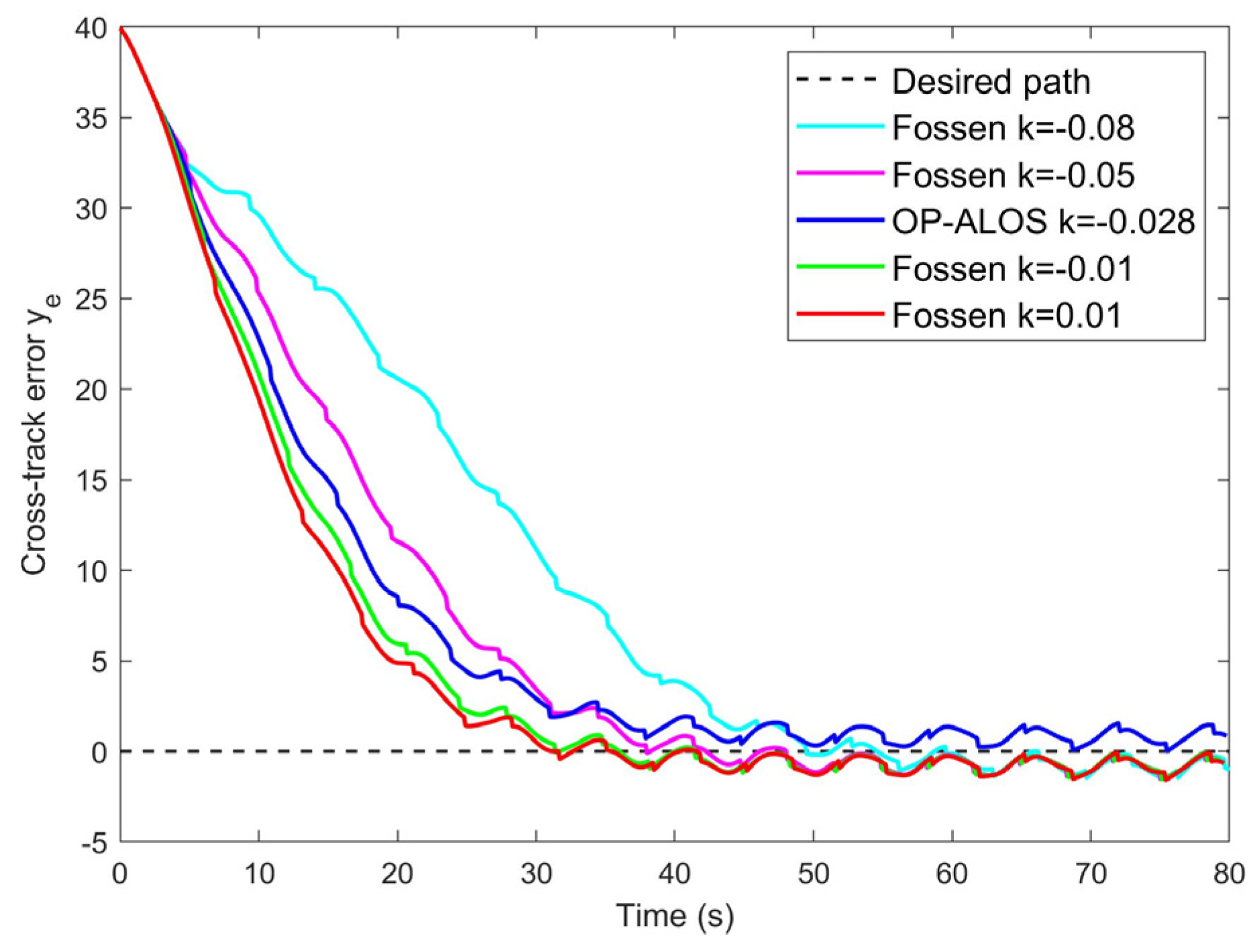
- Trajectory and cross-track error of the straight desired path
- (2)
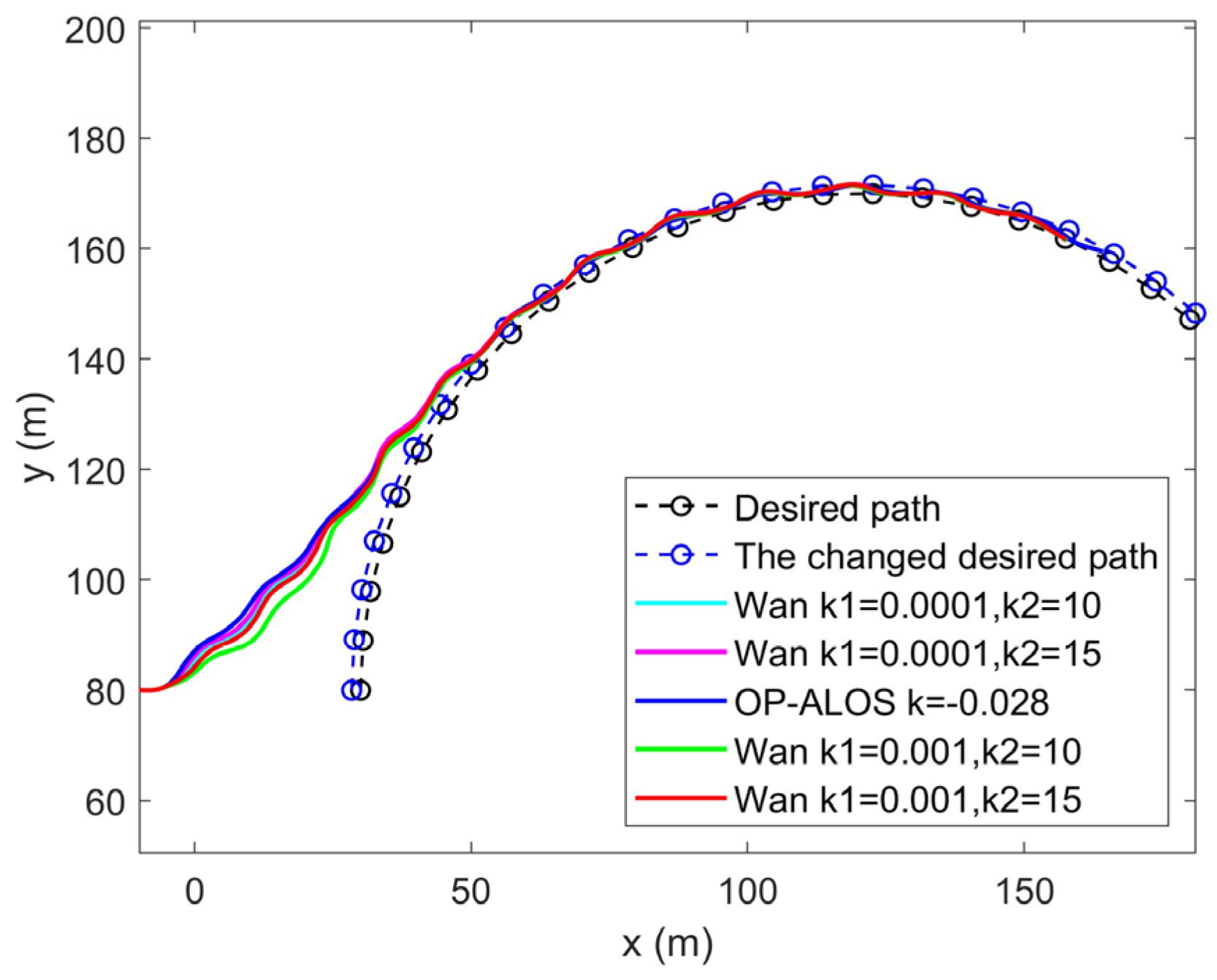
- Trajectory and cross-track error of the curve desired path
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Salima, B.; Assia, B.; Ghalem, B. HA-UVC: Hybrid approach for unmanned vehicles cooperation. Multiagent Grid Syst. 2020, 16, 1–45. [Google Scholar] [CrossRef]
- Zhong, J.B.; Li, B.Y.; Li, S.X.; Yang, F.; Li, P.; Cui, Y. Particle swarm optimization with orientation angle-based grouping for practical unmanned surface vehicle path planning. Appl. Ocean Res. 2021, 111, 102658. [Google Scholar] [CrossRef]
- Dvorak, M.; Dolezel, P.; Stursa, D.; Chouai, M. Genetic Algorithm-Based Task Assignment for Fleet of Unmanned Surface Vehicles in Dynamically Changing Environment. Cybern. Syst. 2023, 55, 1314–1331. [Google Scholar] [CrossRef]
- Zwolak, K.; Wigley, R.; Bohan, A.; Zarayskaya, Y.; Bazhenova, E.; Dorshow, W.; Sumiyoshi, M.; Sattiabaruth, S.; Roperez, J.; Proctor, A.; et al. The Autonomous Underwater Vehicle Integrated with the Unmanned Surface Vessel Mapping the Southern Ionian Sea. The Winning Technology Solution of the Shell Ocean Discovery XPRIZE. Remote Sens. 2020, 12, 1344. [Google Scholar] [CrossRef]
- Wu, G.X.; Xu, T.T.; Sun, Y.S.; Zhang, J. Review of multiple unmanned surface vessels collaborative search and hunting based on swarm intelligence. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221091885. [Google Scholar] [CrossRef]
- Xing, B.W.; Yu, M.J.; Liu, Z.C.; Tan, Y.; Sun, Y.; Li, B. A Review of Path Planning for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 1556. [Google Scholar] [CrossRef]
- Liu, Y.C.; Bucknall, R. Efficient multi-task allocation and path planning for unmanned surface vehicle in support of ocean operations. Neurocomputing 2018, 275, 1550–1566. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, P.; Du, G.L.; Li, F. Ant Colony Optimization Based Memetic Algorithm to Solve Bi-Objective Multiple Traveling Salesmen Problem for Multi-Robot Systems. IEEE Access 2018, 6, 21745–21757. [Google Scholar] [CrossRef]
- Liu, Y.C.; Song, R.; Bucknall, R.; Zhang, X. Intelligent multi-task allocation and planning for multiple unmanned surface vehicles (USVs) using self-organising maps and fast marching method. Inf. Sci. 2019, 496, 180–197. [Google Scholar] [CrossRef]
- Ning, Q.; Tao, G.P.; Chen, B.C.; Lei, Y.; Yan, H.; Zhao, C. Multi-UAVs trajectory and mission cooperative planning based on the Markov model. Phys. Commun. 2019, 35, 100717. [Google Scholar] [CrossRef]
- Lusk, P.C.; Cai, X.Y.; Wadhwania, S.; Paris, A.; Fathian, K.; How, J.P. A Distributed Pipeline for Scalable, Deconflicted Formation Flying. IEEE Robot. Autom. Lett. 2020, 5, 5213–5220. [Google Scholar] [CrossRef]
- Xia, G.Q.; Sun, X.X.; Xia, X.M. Multiple Task Assignment and Path Planning of a Multiple Unmanned Surface Vehicles System Based on Improved Self-Organizing Mapping and Improved Genetic Algorithm. J. Mar. Sci. Eng. 2021, 9, 556. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, Y.J.; Li, Z.X.; Bi, H.; Wang, J.; Malekian, R.; Sotelo, M.A. CCIBA*: An Improved BA* Based Collaborative Coverage Path Planning Method for Multiple Unmanned Surface Mapping Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19578–19588. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Zhu, B.; Zhou, Y.; Yao, P.; Yu, J. Cooperative Path Planning of Multiple Unmanned Surface Vehicles for Search and Coverage Task. Drones 2023, 7, 21. [Google Scholar] [CrossRef]
- Yao, P.; Wu, K.Q.; Lou, Y.T. Path Planning for Multiple Unmanned Surface Vehicles Using Glasius Bio-Inspired Neural Network With Hungarian Algorithm. IEEE Syst. J. 2022, 17, 3906–3917. [Google Scholar] [CrossRef]
- Yu, J.B.; Chen, Z.H.; Zhao, Z.Y.; Yao, P.; Xu, J. A traversal multi-target path planning method for multi-unmanned surface vessels in space-varying ocean current. Ocean Eng. 2023, 278, 114423. [Google Scholar] [CrossRef]
- Pei, M.; An, H.; Liu, B.; Wang, C. An Improved Dyna-Q Algorithm for Mobile Robot Path Planning in Unknown Dynamic Environment. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4415–4425. [Google Scholar] [CrossRef]
- Zhang, J. Path Planning for a Mobile Robot in Unknown Dynamic Environments Using Integrated Environment Representation and Reinforcement Learning. In Proceedings of the 2019 Australian & New Zealand Control Conference (ANZCC), Auckland, New Zealand, 27–29 November 2019; pp. 258–263. [Google Scholar]
- Wu, K.; Wang, H.; Esfahani, M.A.; Yuan, S. Achieving Real-Time Path Planning in Unknown Environments Through Deep Neural Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2093–2102. [Google Scholar] [CrossRef]
- Qin, Y.M.; Liu, J.X.; Shao, X.; Duan, S. Rapid path planning for Unmanned Surface Vessels. In Proceedings of the SPIE 11th International Symposium on Multispectral Image Processing and Pattern Recognition (MIPPR)—Remote Sensing Image Processing, Geographic Information Systems, and Other Applications, 2019, Wuhan, China, 14 February 2020; Volume 11432, pp. 279–285. [Google Scholar]
- Lozano-Pérez, T.; Wesley, M.A. An Algorithm for Planning Collision Free Paths Among Polyhedral Obstacles. Commun. ACM 1979, 22, 560–570. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Line-of-Sight Guidance for Path Following of Marine Vehicles. Adv. Mar. Robot. 2013, 5, 63–92. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control. Guidance Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 240–284. [Google Scholar]
- Lekkas, A.M.; Fossen, T.I. Integral LOS Path Following for Curved Paths Based on a Monotone Cubic Hermite Spline Parametrization. IEEE Trans. Control. Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws. Automatica 2014, 50, 2912–2917. [Google Scholar] [CrossRef]
- Liu, L.S.; Wang, B.; Xu, H. Research on Path-Planning Algorithm Integrating Optimization A-Star Algorithm and Artificial Potential Field Method. Electronics 2022, 11, 3660. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.F.; Gu, J.D.; Li, F. A Path-Planning Strategy for Unmanned Surface Vehicles Based on an Adaptive Hybrid Dynamic Stepsize and Target Attractive Force-RRT Algorithm. J. Mar. Sci. Eng. 2019, 7, 132. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Wu, H.B.; Zhou, H.; Song, Y.; Chen, Y.; He, K.; Gao, J. Recovery Path Planning for Autonomous Underwater Vehicles Using Constrained Bi-RRT*-Smart Algorithms. In Proceedings of the OCEANS Conference, Limerick, Ireland, 5–8 June 2023. [Google Scholar]
- Liu, C.Y.; Xie, S.B.; Sui, X.; Huang, Y.; Ma, X.; Guo, N.; Yang, F. PRM-D* Method for Mobile Robot Path Planning. Sensors 2023, 23, 3512. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, Y.A.; Ali, E.S.; Osman, T.E.; Khalifa, O.O.; Mohamed, Z.O.; Saeed, R.A.; Saeed, M.M. Multi-Drones Energy Efficient Based Path Planning Optimization using Genetic Algorithm and Gradient Decent Approach. In Proceedings of the 9th International Conference on Mechatronics Engineering (ICOM), Kuala Lumpur, Malaysia, 13–14 August 2024; pp. 171–176. [Google Scholar]
- Hu, J.H.; Er, M.J.; Liu, T.H.; Wang, S. A Hybrid Algorithm Based on Ant Colony and Genetic Algorithm for AUV Path Planning. In Proceedings of the 2nd Conference on Fully Actuated System Theory and Applications (CFASTA), Qingdao, China, 14–16 July 2023; pp. 888–893. [Google Scholar]
- Mu, D.; Wang, G.; Fan, Y.; Sun, X.; Qiu, B. Modeling and Identification for Vector Propulsion of an Unmanned Surface Vehicle: Three Degrees of Freedom Model and Response Model. Sensors 2018, 18, 1889. [Google Scholar] [CrossRef]
- Helma, S. Surprising Behaviour of the Wageningen B-Screw Series Polynomials. J. Mar. Sci. Eng. 2020, 8, 211. [Google Scholar] [CrossRef]
- Faramin, M.; Goudarzi, R.H.; Maleki, A. Track-keeping observer-based robust adaptive control of an unmanned surface vessel by applying a 4-DOF maneuvering model. Ocean Eng. 2019, 183, 11–23. [Google Scholar] [CrossRef]




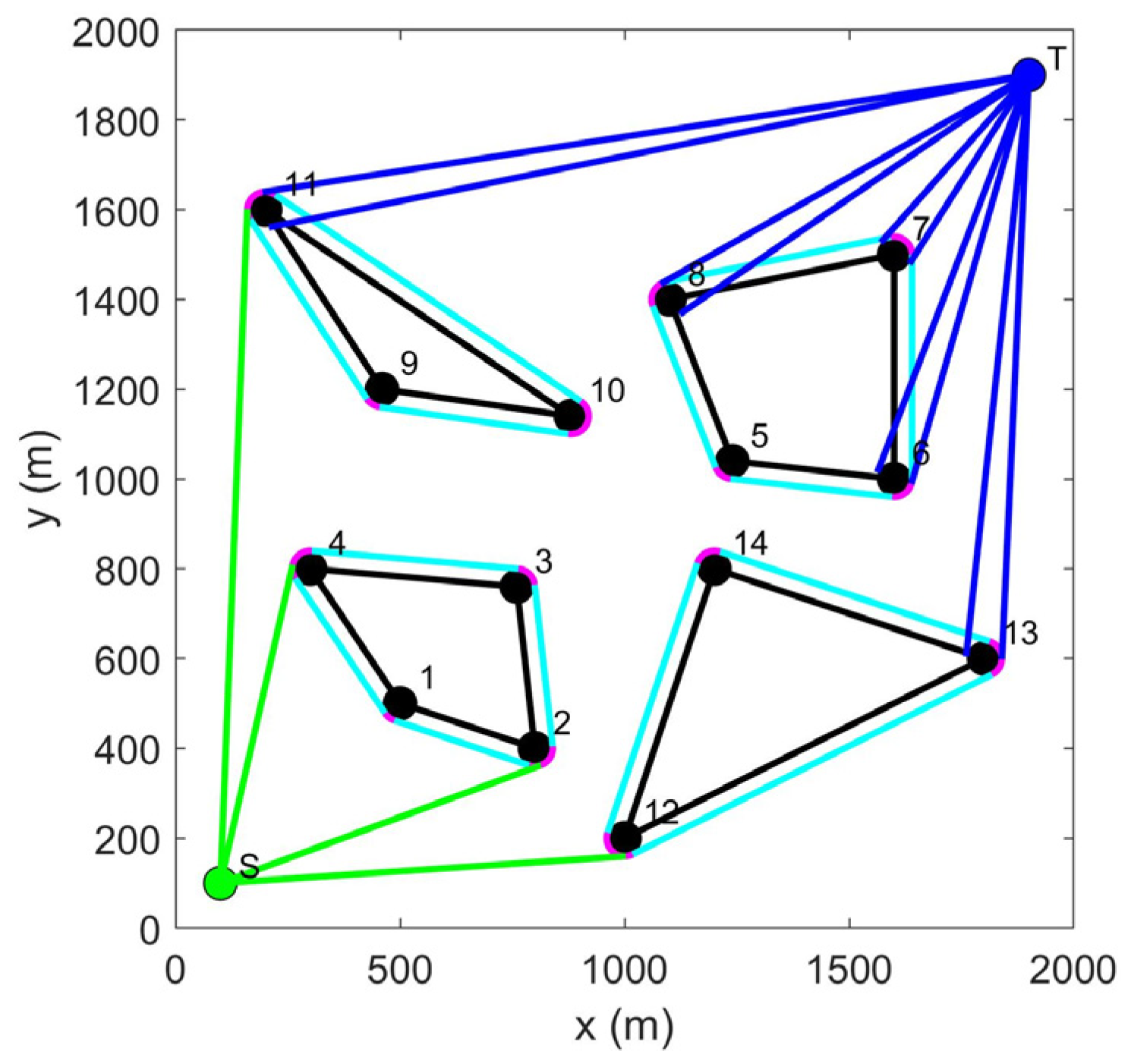
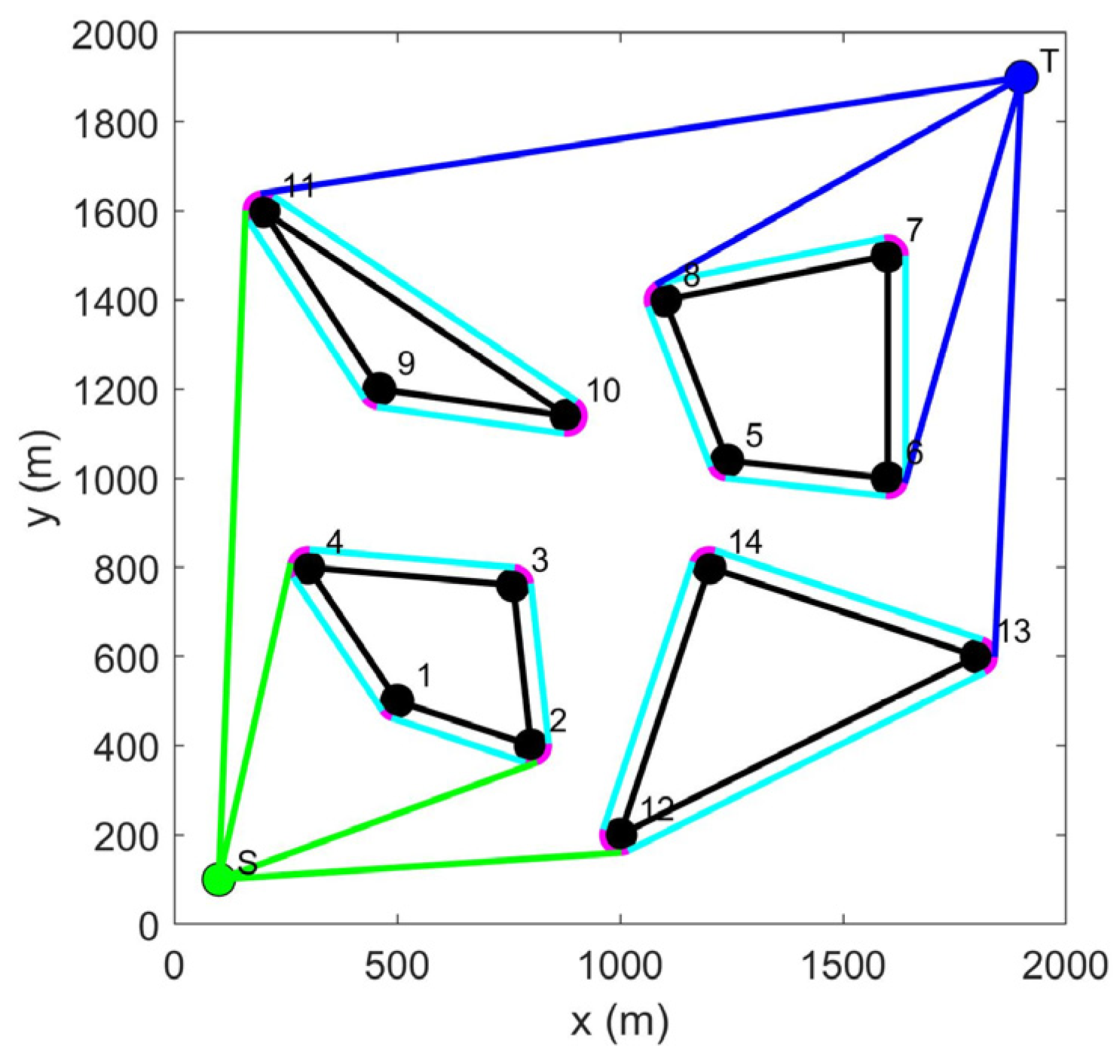

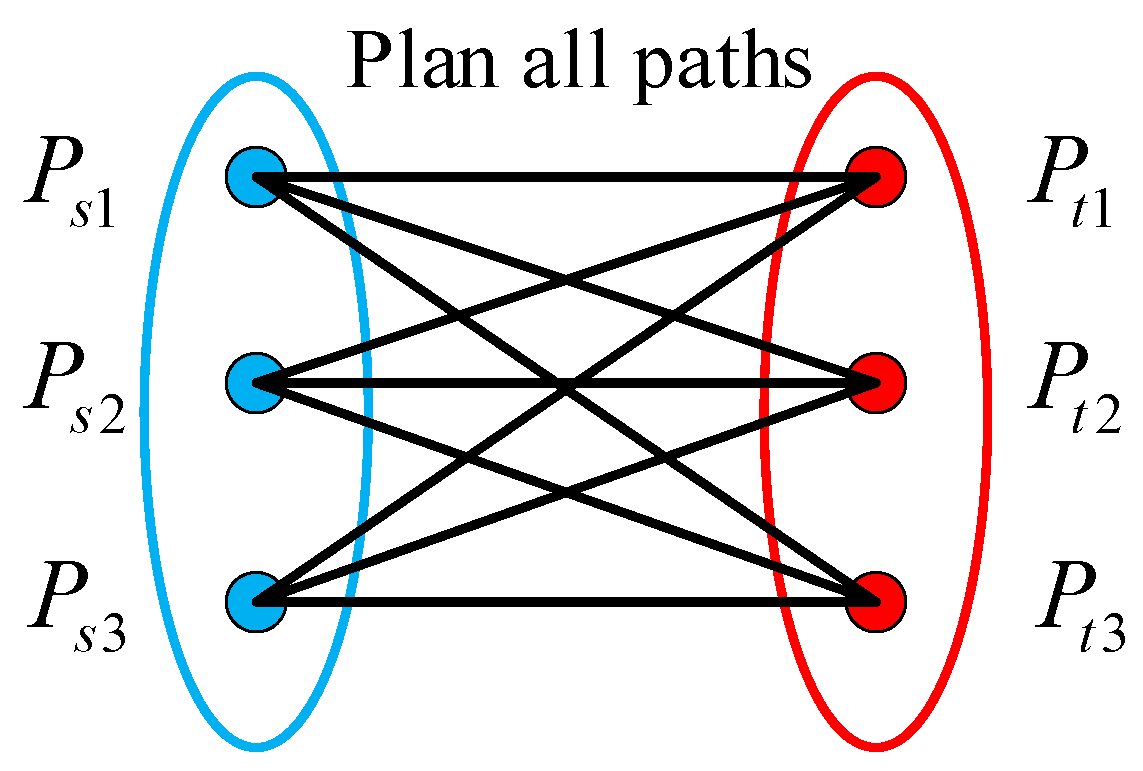
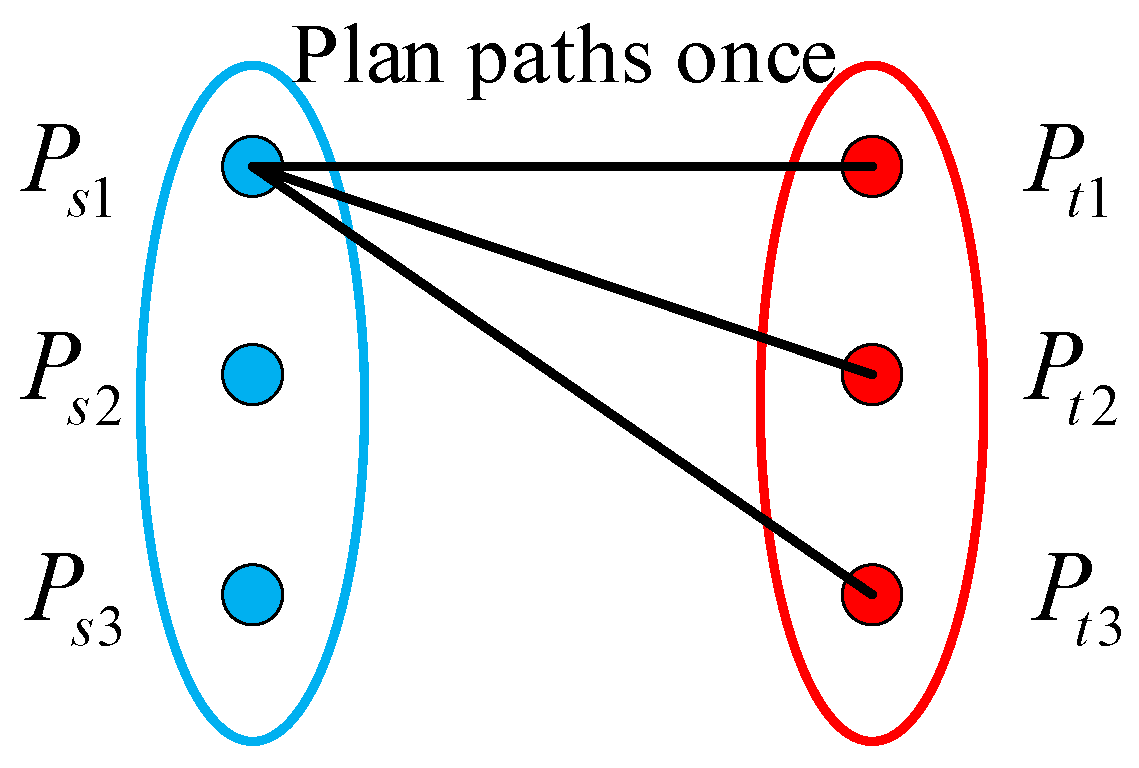








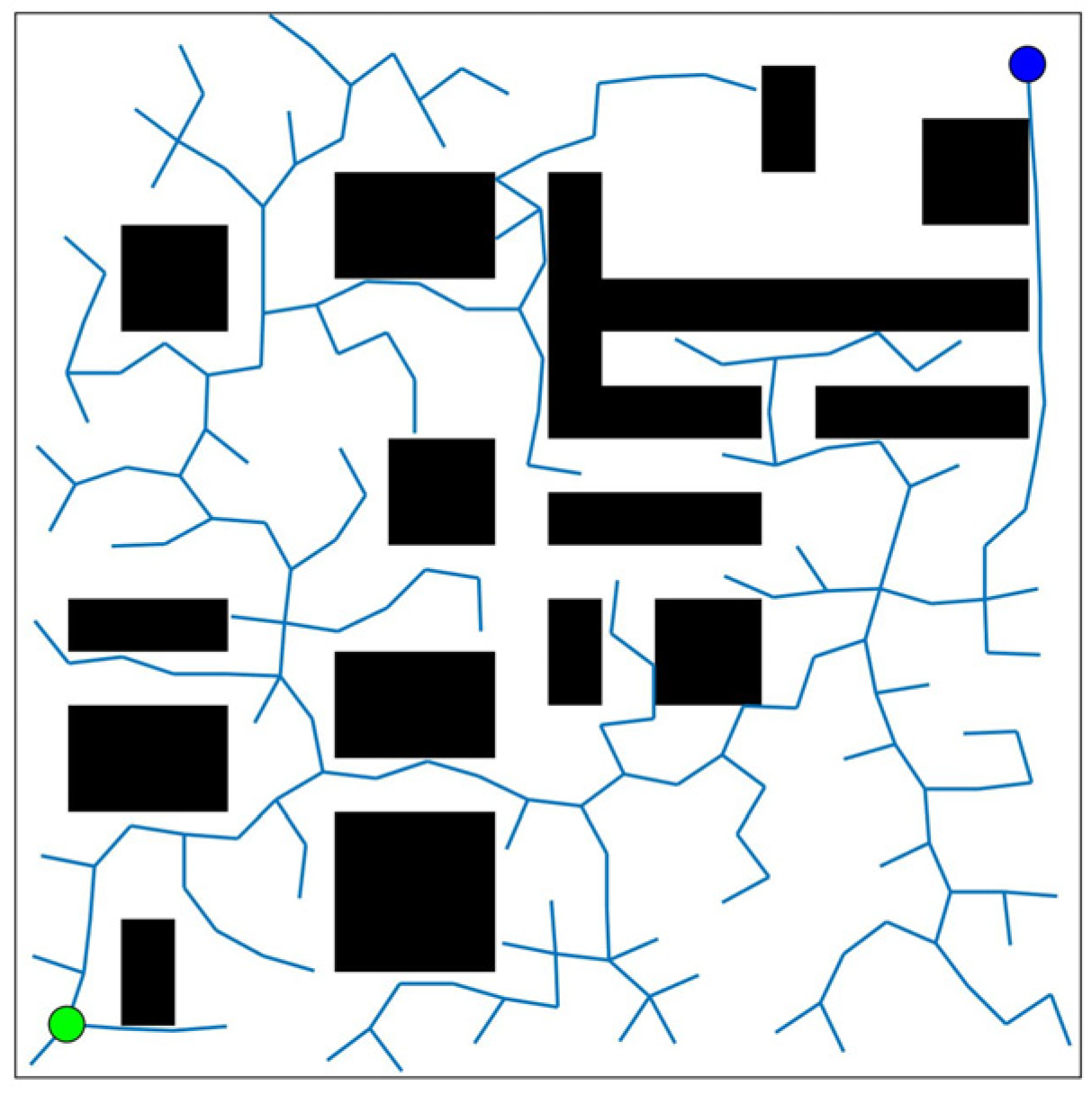
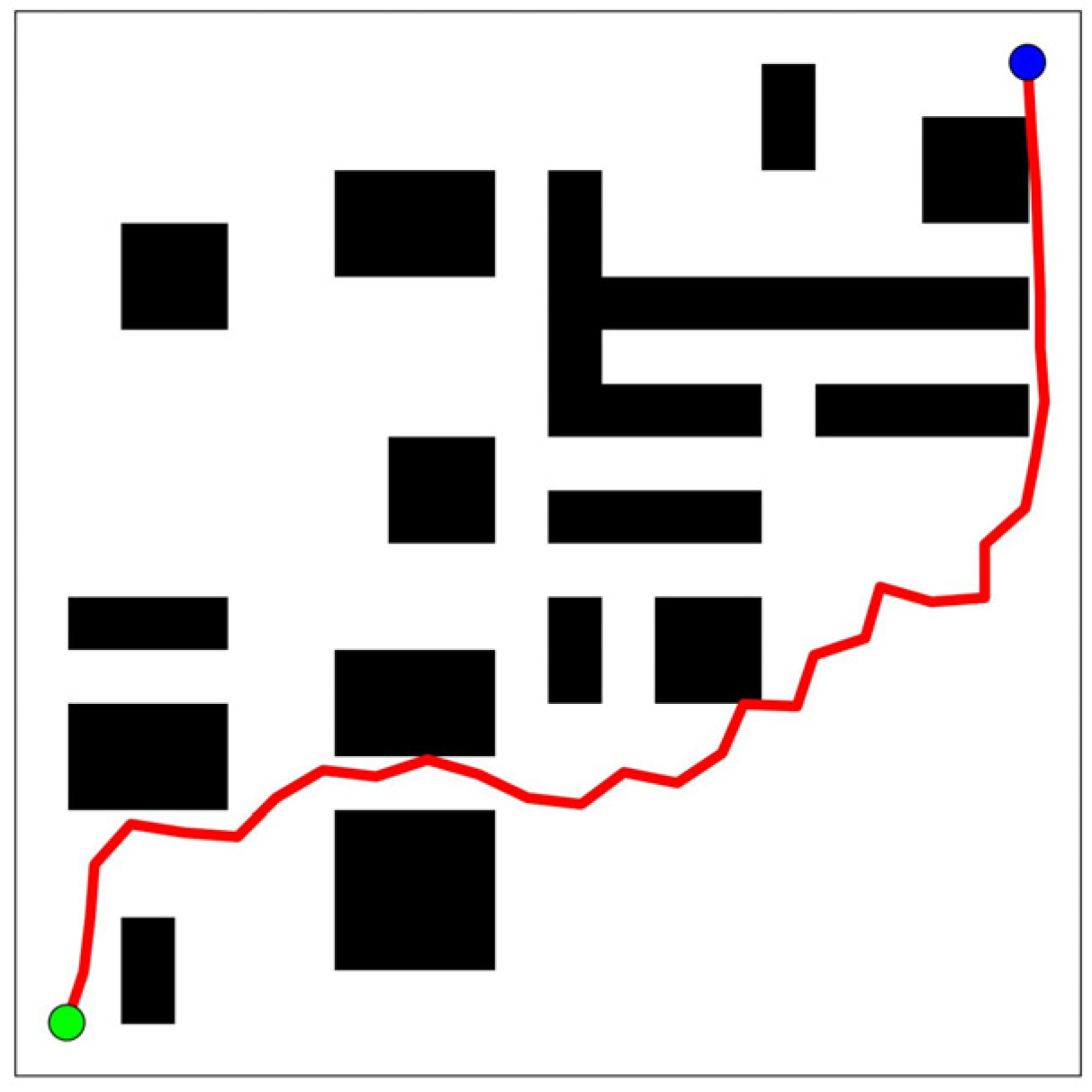
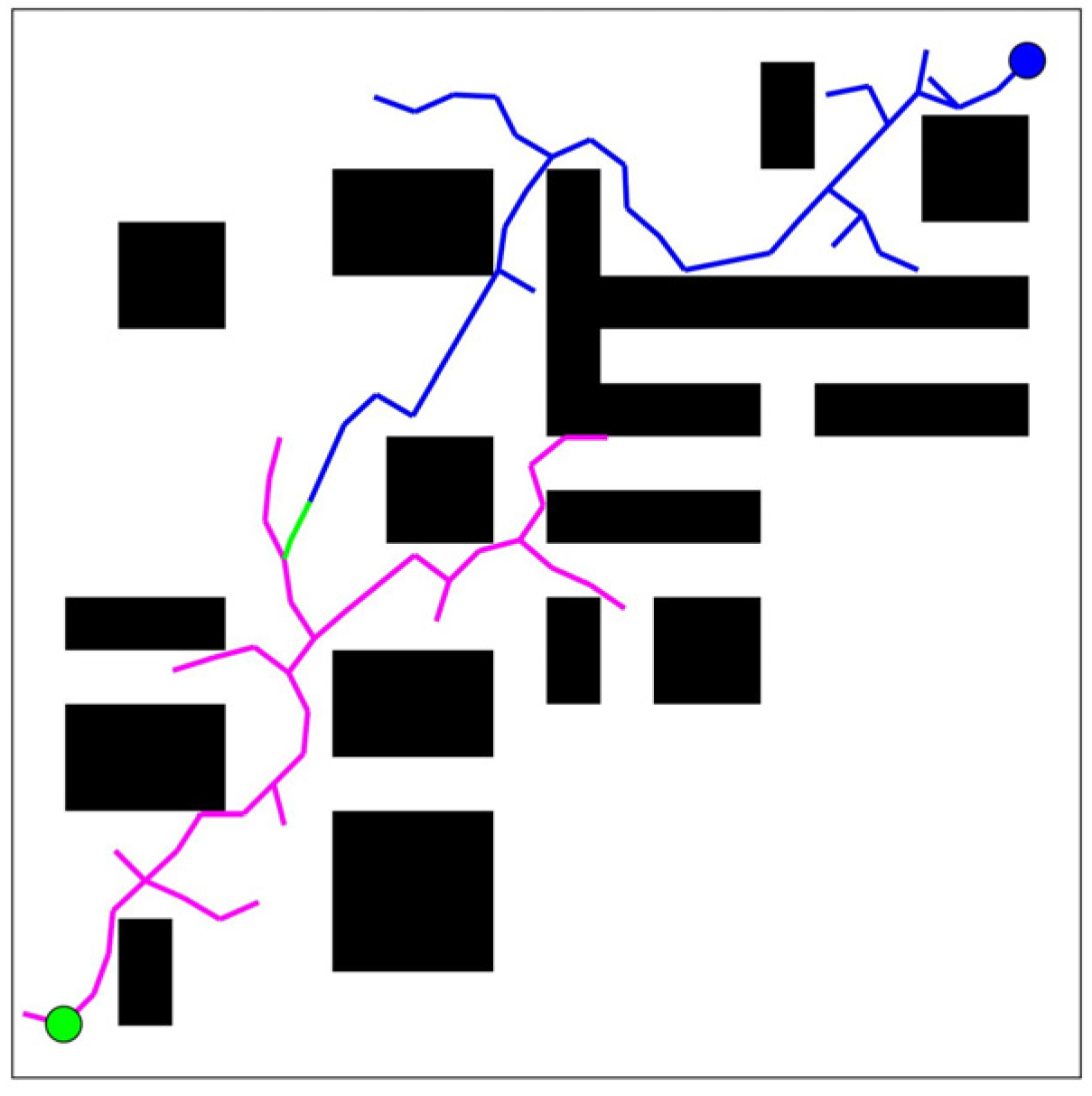

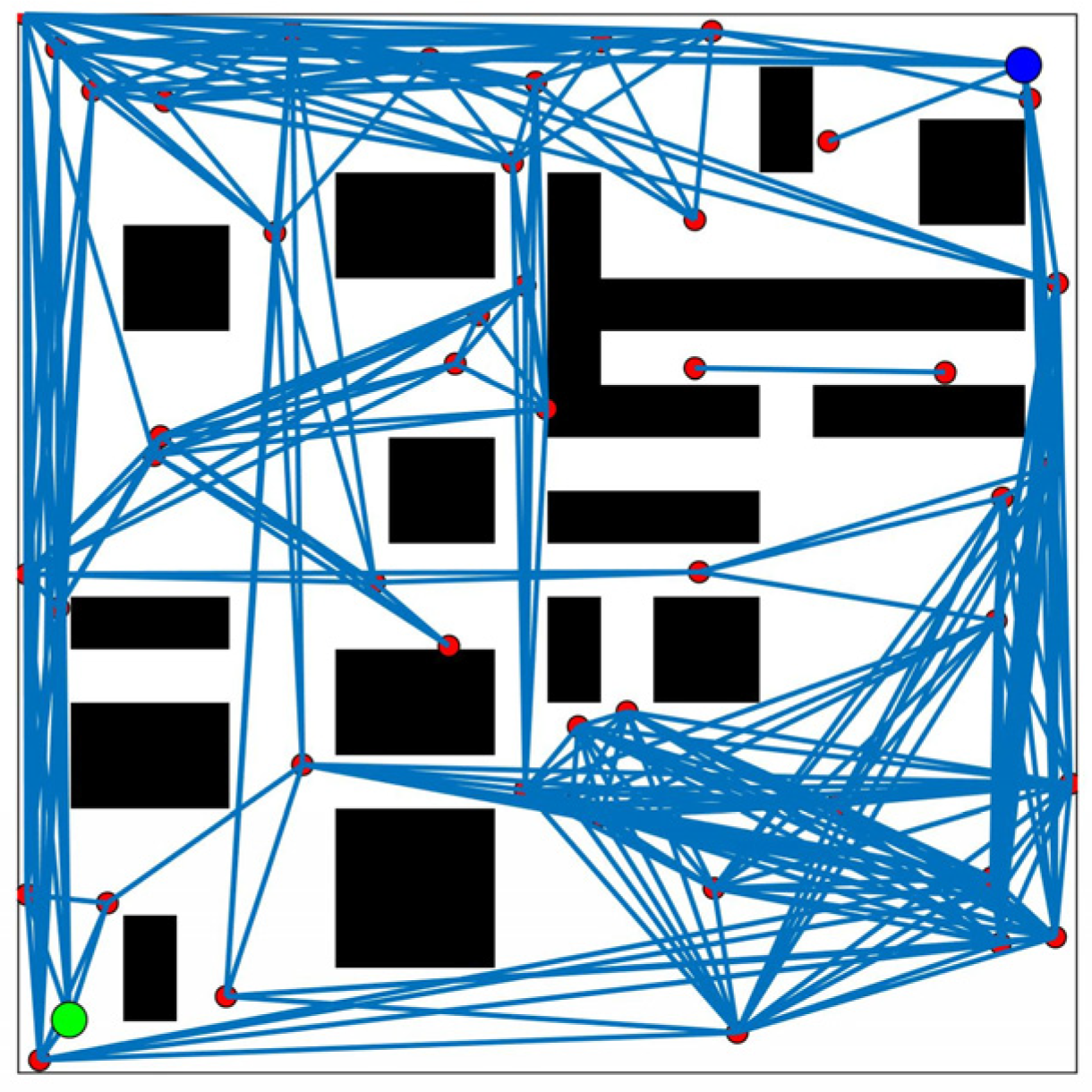

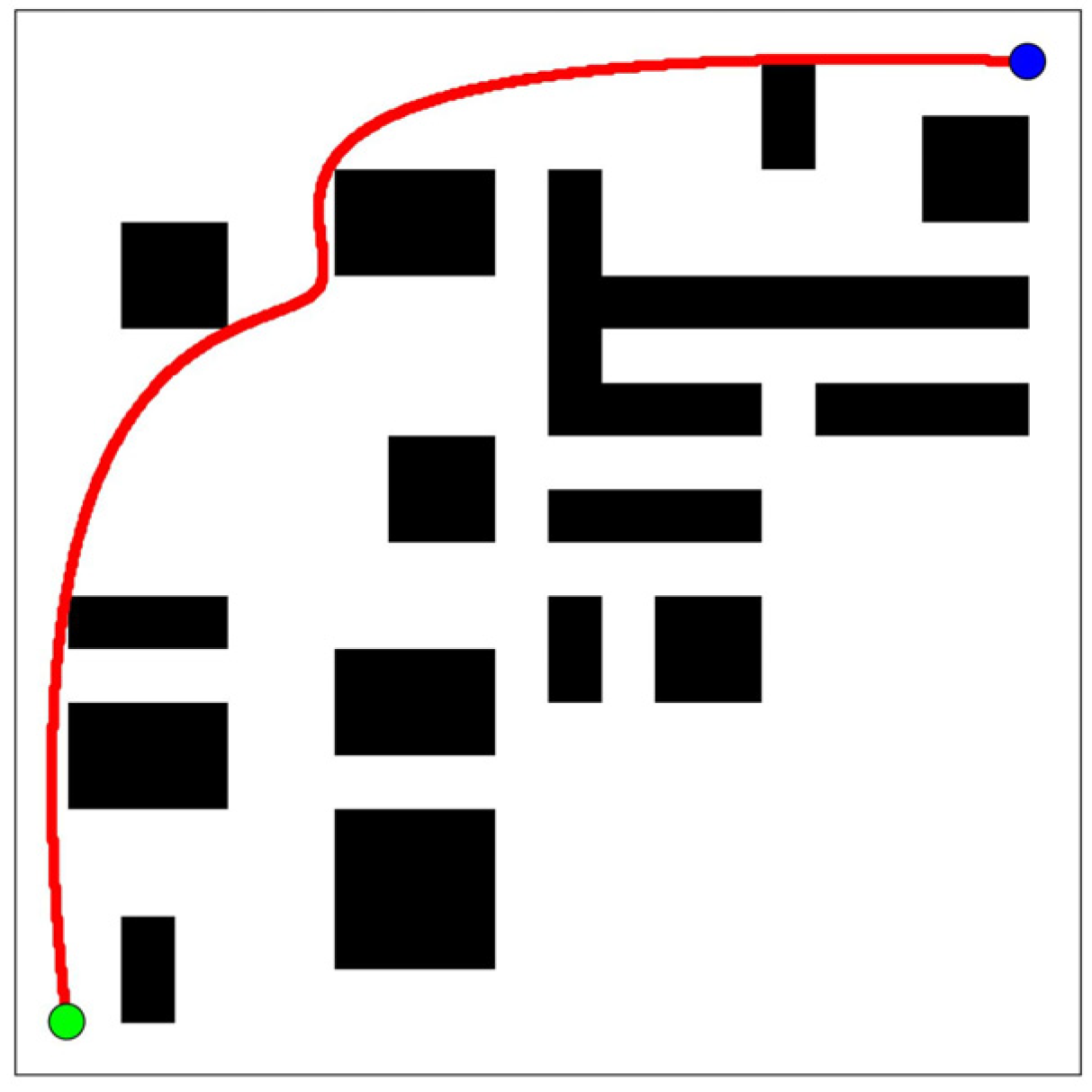


| The Traditional Path-Planning Algorithms | A Low-Complexity Path Planning Algorithm | |
|---|---|---|
| The planned path | Plan paths (from start points to target points). | Plan possible paths and find the shortest path |
| Computational complexity | Plan possible paths: Find the shortest paths: (Obstacles are stationary and have a fixed number) | |
| Calculation time | Exponential growth | Linear growth |
| Notations | The Meaning of Notations |
|---|---|
| Position of the start point | |
| Position of the target point | |
| Position of the USV | |
| Position of edge points of the obstacle | |
| Position of the desired path point |
| Algorithm | Note |
|---|---|
| LCPP | Based on VG and using Dijkstra algorithm. |
| A*1 | The grid is 50 m × 50 m |
| A*2 | The grid is 25 m × 25 m. |
| A*3 | The grid is 10 m × 10 m. |
| FMM | Based on potential field. The minimum potential field unit is 10 m × 10 m, and step length is 80 m. |
| RRT | Initial step length is 100 m. The minimum step length is 80 m. |
| Bi-RRT | Step length is 80 m. |
| PRM | The number of key nodes is 20. |
| GA/GD | Population size 100, iteration times 1000. |
| ACO | Population size 100, iteration times 1000. |
| Algorithm | The First Calculation | The Second Calculation | The Third Calculation | |||
|---|---|---|---|---|---|---|
| Calculation Time (s) | Path Length (m) | Calculation Time (s) | Path Length (m) | Calculation Time (s) | Path Length (m) | |
| LCPP | 215.169 | 2568.2 | The same start point: 0.269 Different start points: 3.960 | 2568.2 | The same start point: 0.721 Different start points: 3.541 | 2568.2 |
| A*1 | 1.720 | 3026.3 | 1.494 | 3026.3 | 1.392 | 3026.3 |
| A*2 | 1.847 | 3026.3 | 1.826 | 3026.3 | 1.827 | 3026.3 |
| A*3 | 2.686 | 3026.3 | 2.652 | 3026.3 | 2.641 | 3026.3 |
| FMM | 19.981 | 2826.0 | 19.362 | 2826.0 | 21.035 | 2826.0 |
| RRT | 12.570 | 4111.0 | 12.060 | 3831.9 | 9.799 | 3447.6 |
| Bi-RRT | 6.137 | 3267.2 | 4.588 | 3431.0 | 4.366 | 3366.3 |
| PRM | 1.513 | 3084.2 | 1.533 | 3032.2 | 1.716 | 3273.8 |
| GA/GD | 74.840 | 3548.0 | 91.038 | 3744.0 | 91.408 | 3664.0 |
| ACO | 113.545 | 3090.1 | 101.123 | 3033.6 | 105.098 | 3123.3 |
| The Data of the USV | Value |
|---|---|
| Mass | |
| Length | |
| Width | |
| Sea water density | |
| Distance between thrusters | (Single thruster) |
| Propeller diameter | |
| Propeller speed | |
| Rudder angle | |
| Rudder rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, K.; Huang, Z.; Wang, P.; Xu, Z.; Kong, D. A Low-Complexity Path-Planning Algorithm for Multiple USVs in Task Planning Based on the Visibility Graph Method. J. Mar. Sci. Eng. 2025, 13, 556. https://doi.org/10.3390/jmse13030556
Xue K, Huang Z, Wang P, Xu Z, Kong D. A Low-Complexity Path-Planning Algorithm for Multiple USVs in Task Planning Based on the Visibility Graph Method. Journal of Marine Science and Engineering. 2025; 13(3):556. https://doi.org/10.3390/jmse13030556
Chicago/Turabian StyleXue, Kai, Zhiqin Huang, Ping Wang, Zeyu Xu, and Decheng Kong. 2025. "A Low-Complexity Path-Planning Algorithm for Multiple USVs in Task Planning Based on the Visibility Graph Method" Journal of Marine Science and Engineering 13, no. 3: 556. https://doi.org/10.3390/jmse13030556
APA StyleXue, K., Huang, Z., Wang, P., Xu, Z., & Kong, D. (2025). A Low-Complexity Path-Planning Algorithm for Multiple USVs in Task Planning Based on the Visibility Graph Method. Journal of Marine Science and Engineering, 13(3), 556. https://doi.org/10.3390/jmse13030556






