Three-Dimensional Numerical Simulation of the Vortex-Induced Motion Response of Semi-Submersible Platforms Under Wave-Current Coupling Effect
Abstract
1. Introduction
2. Overview of Platform and Model
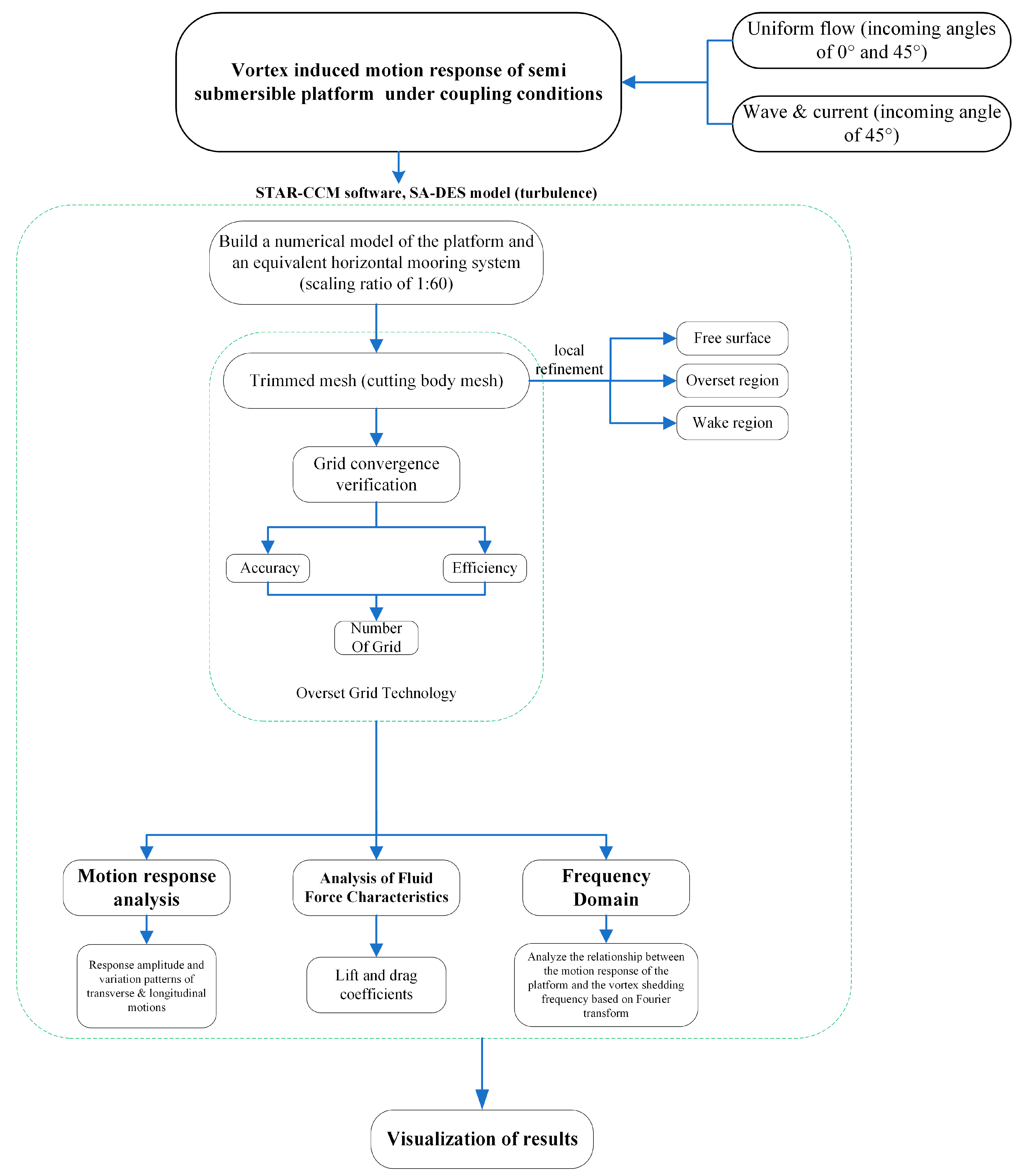
3. Numerical Modeling Method
3.1. Numerical Theory
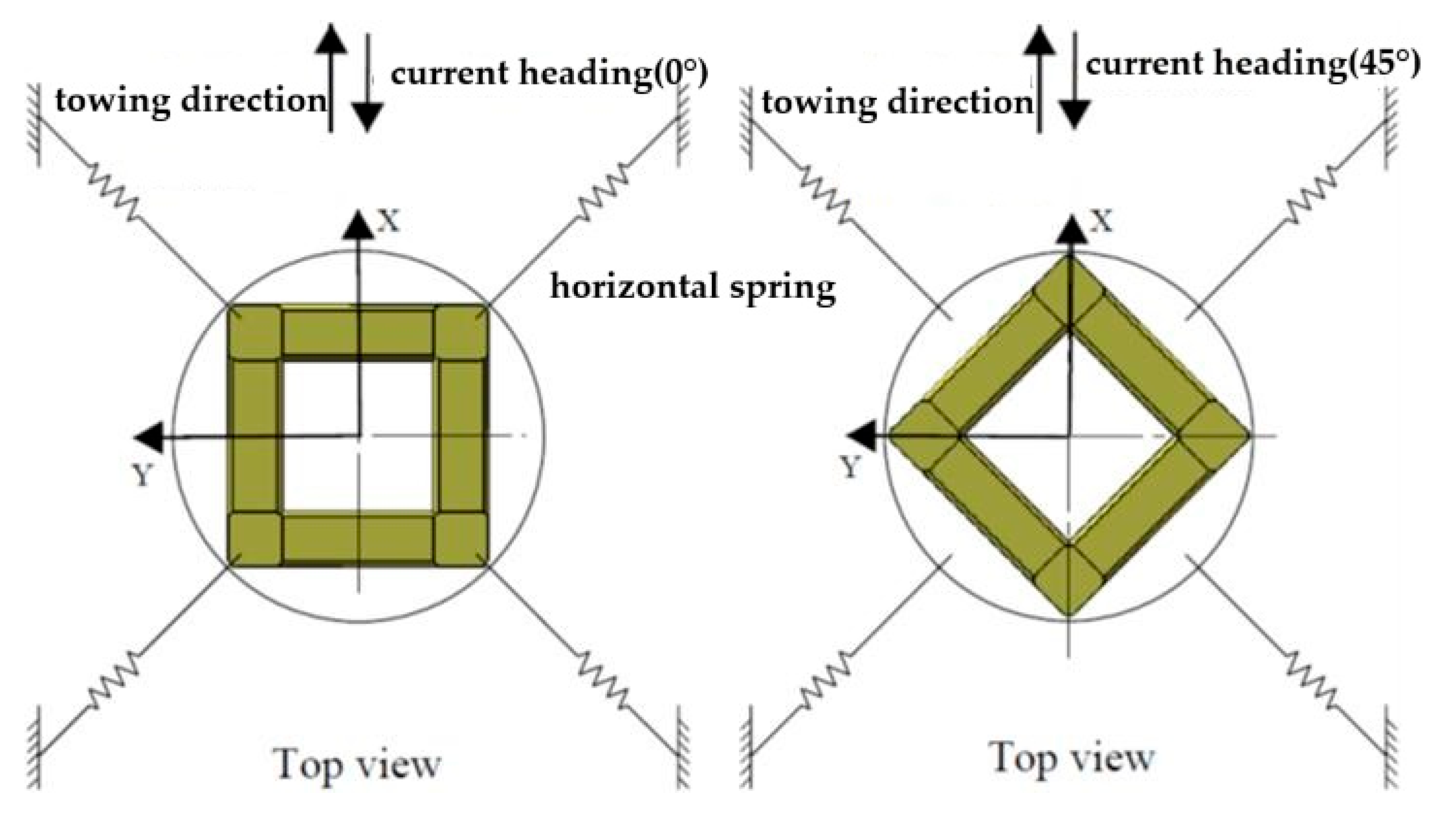
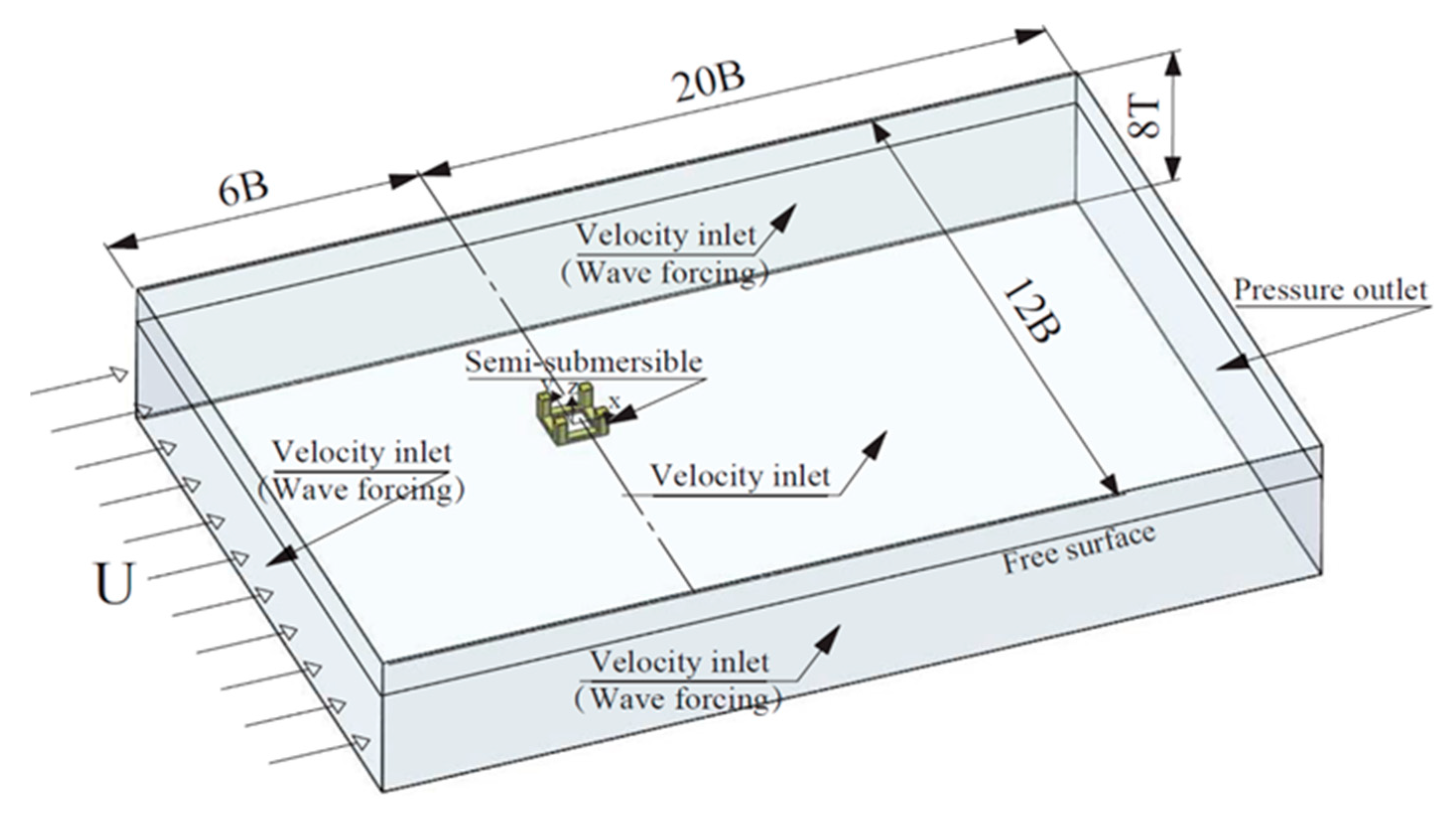
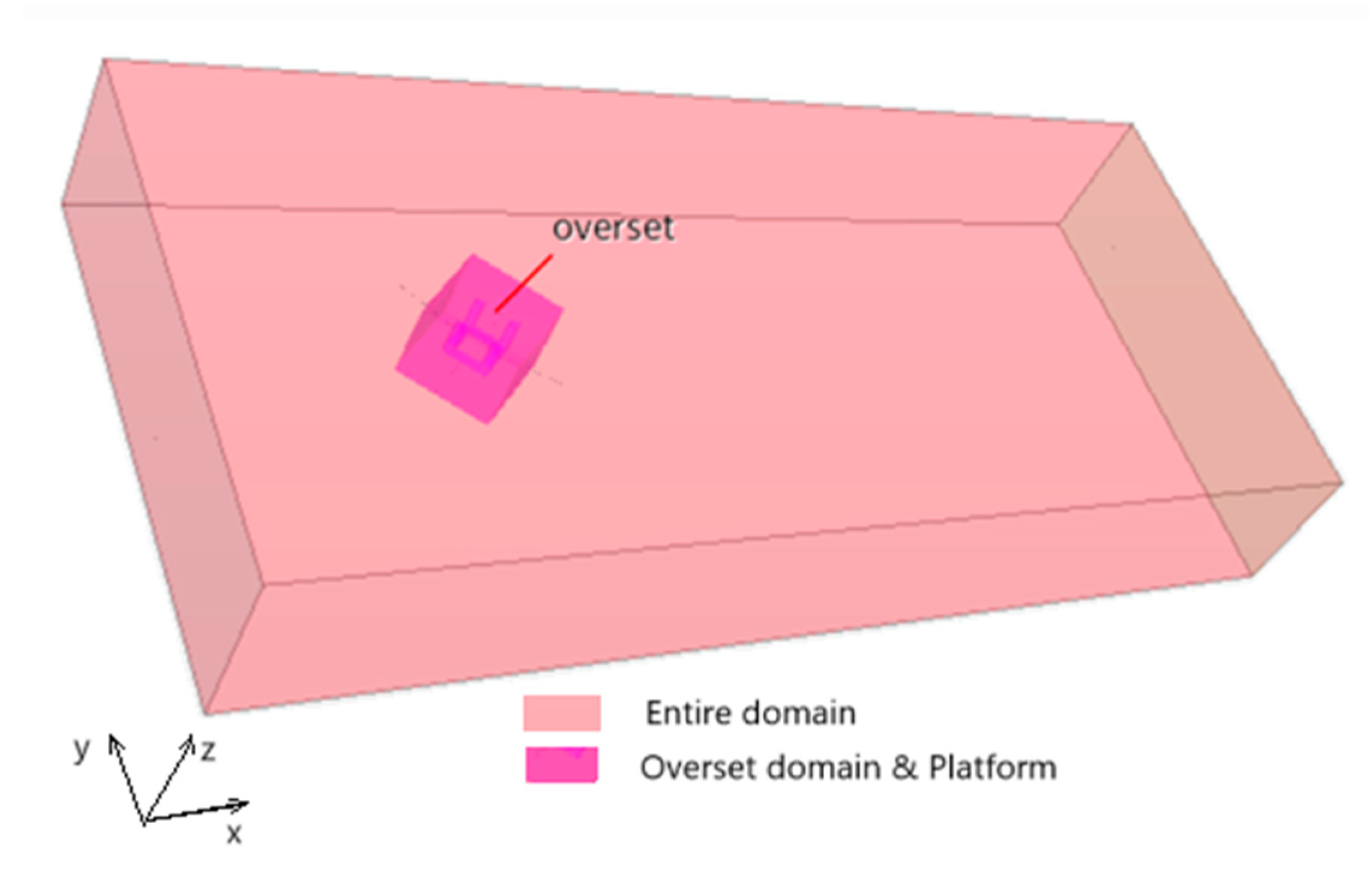
3.2. Computational Domain and Boundary Conditions
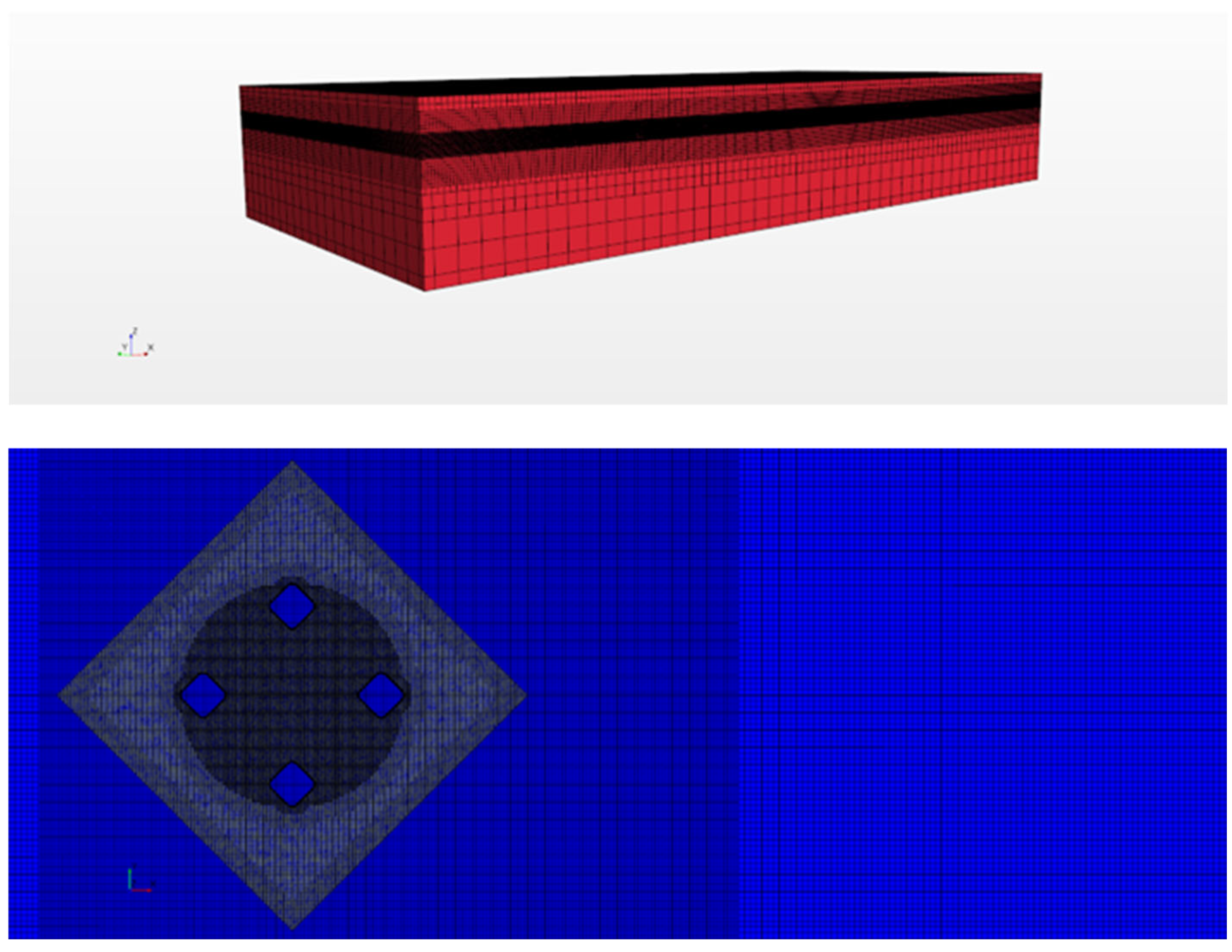
3.3. Overset Domain Generation and Grid Division
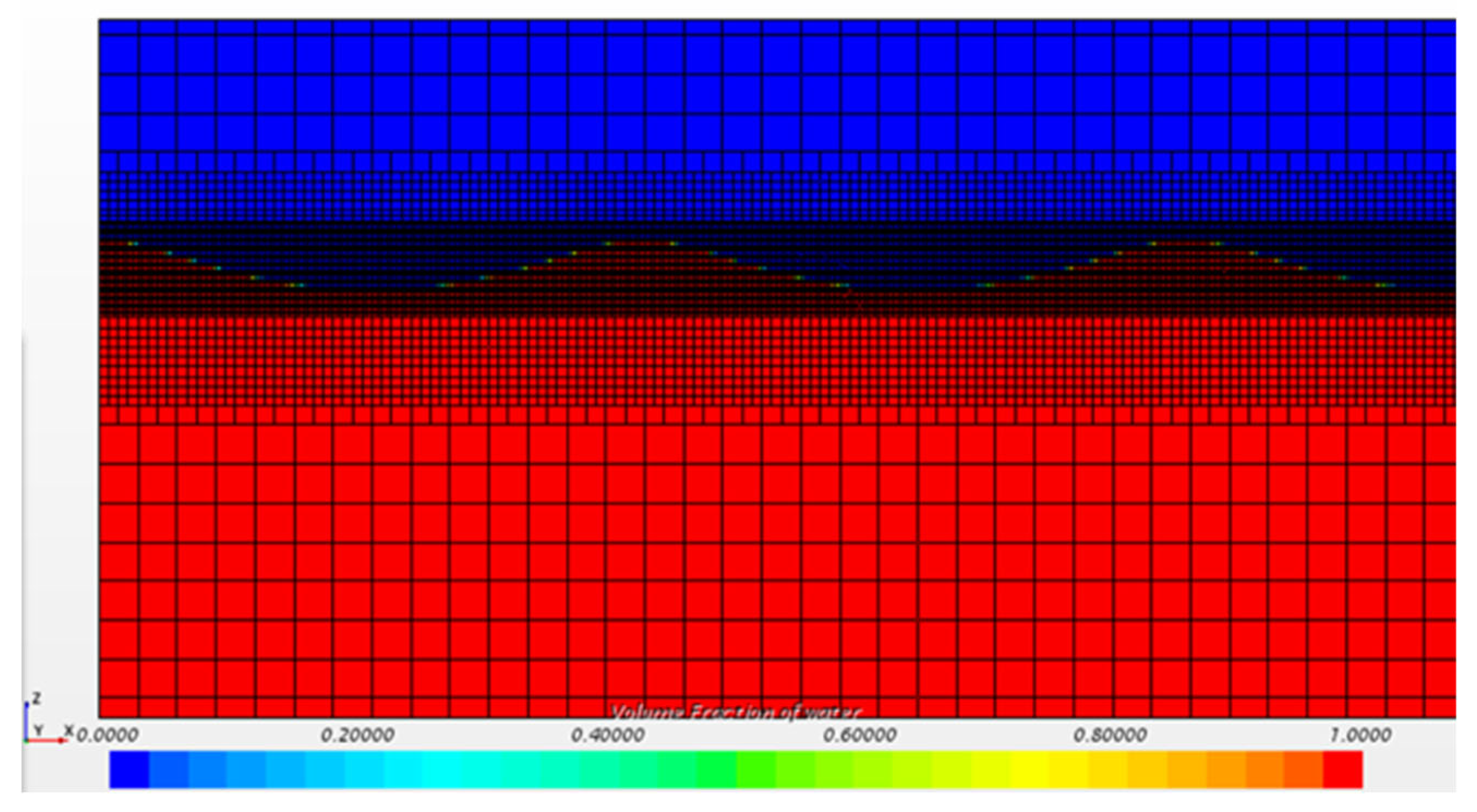
3.4. Two-Dimensional Numerical Simulation Verification of Waves
4. Simulation Results and Analysis
4.1. Simulated Conditions
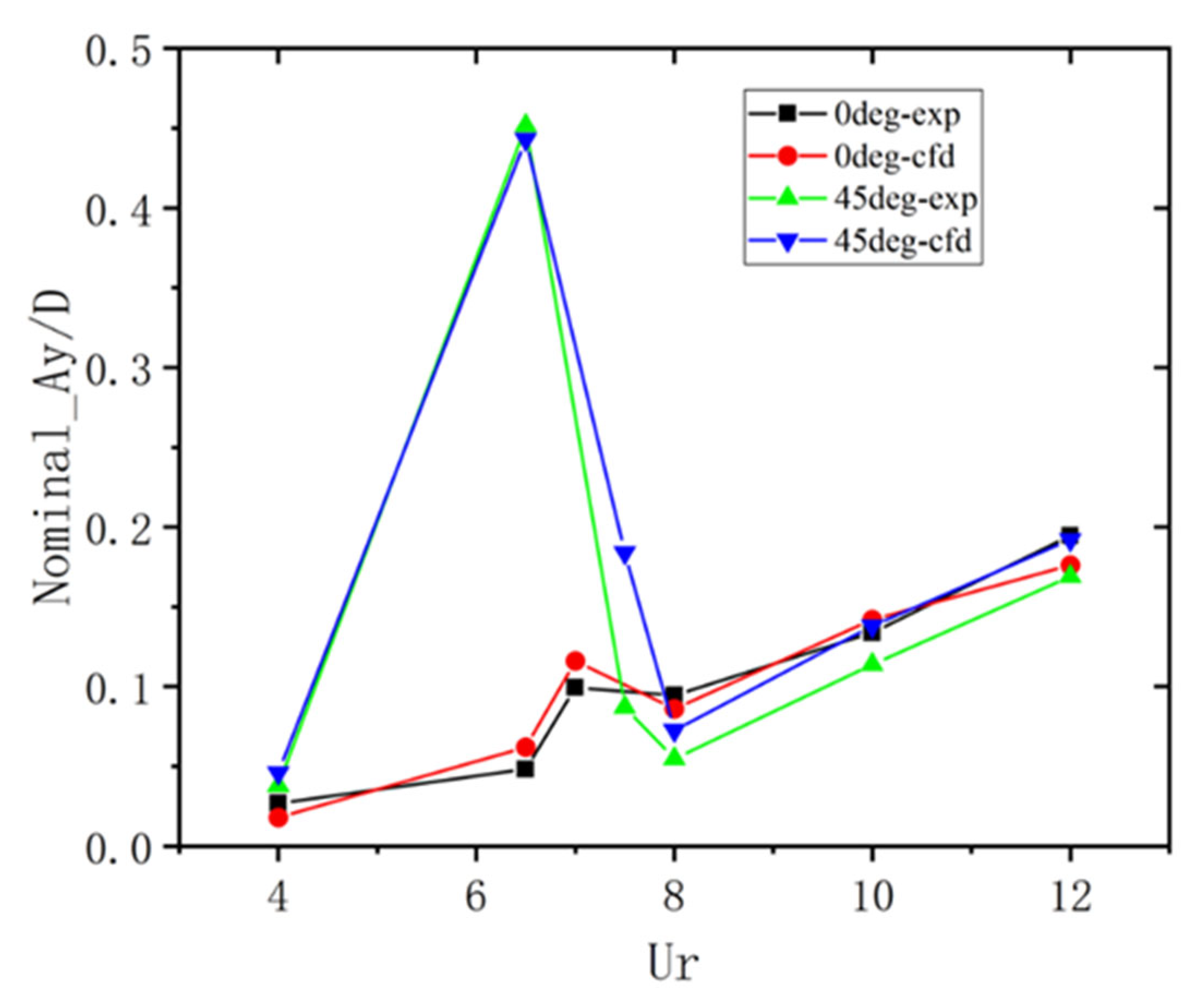
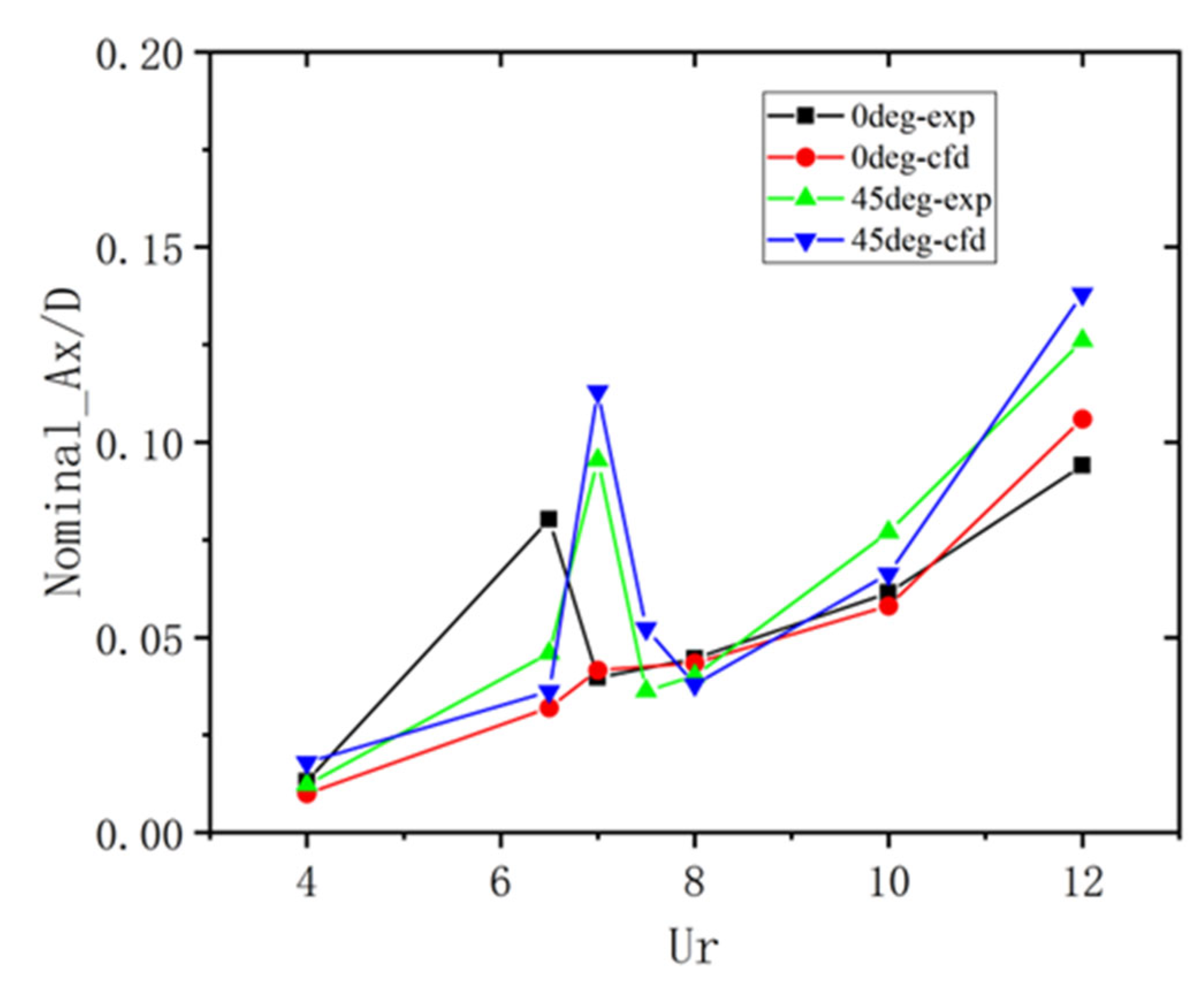
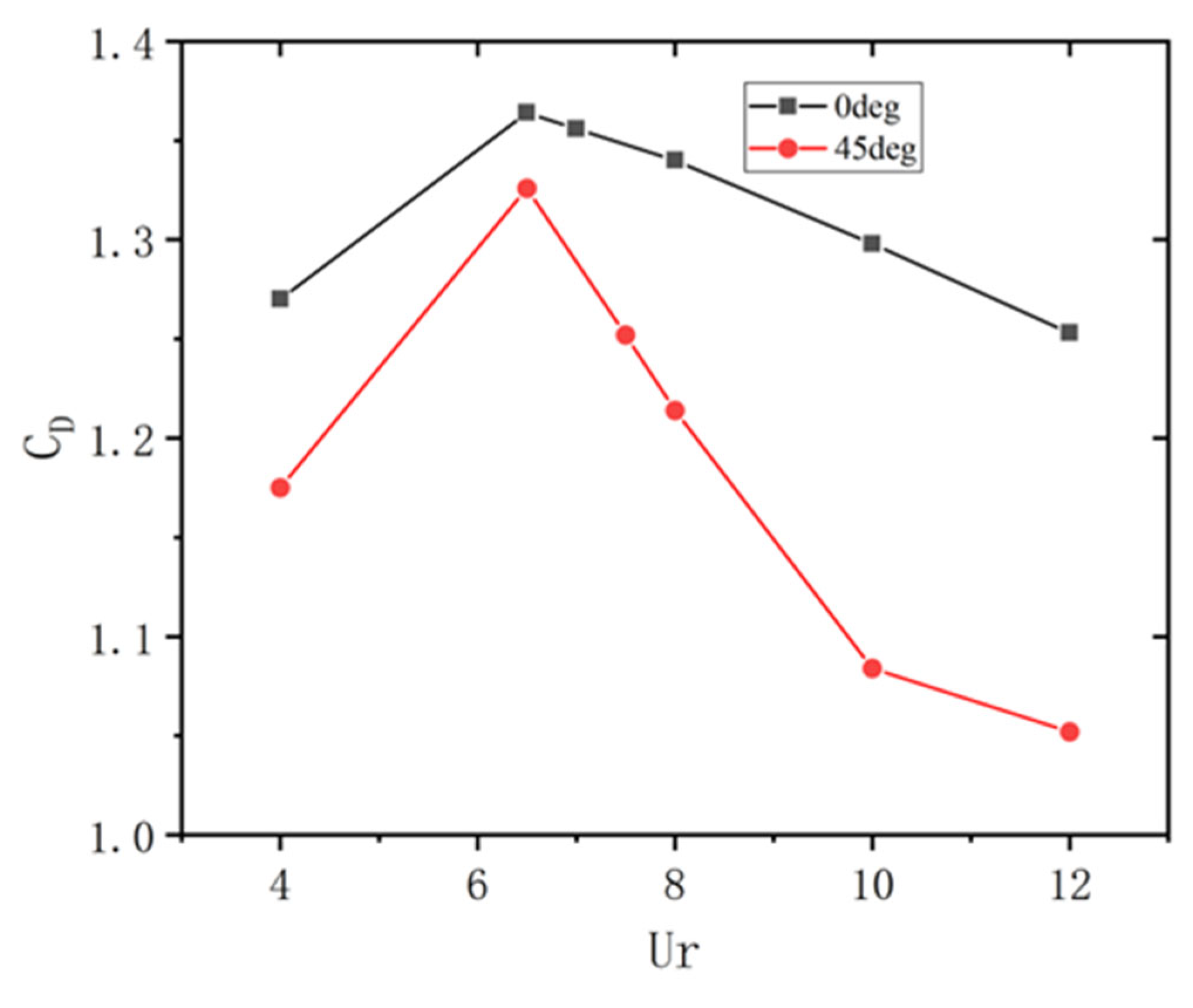
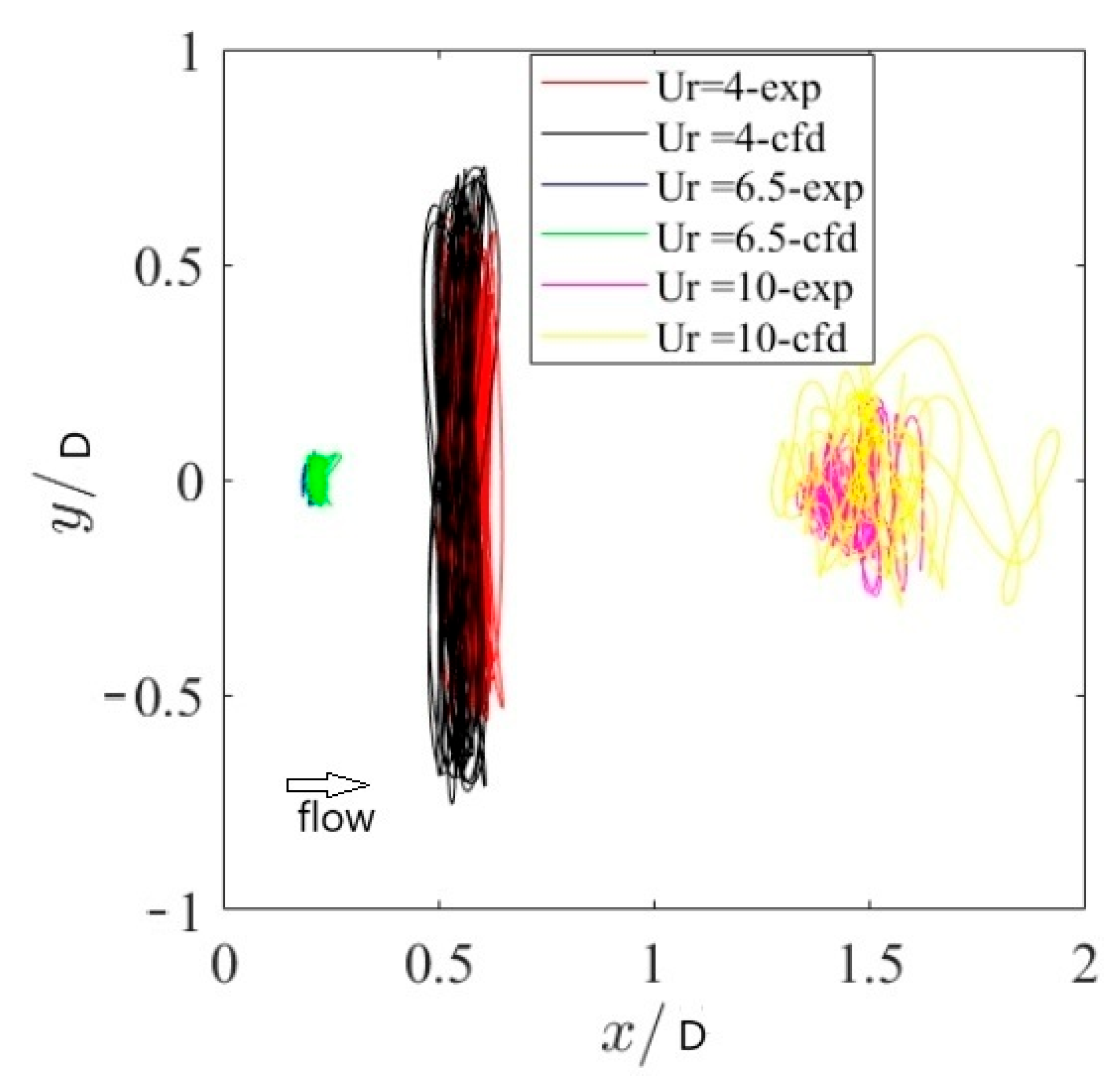
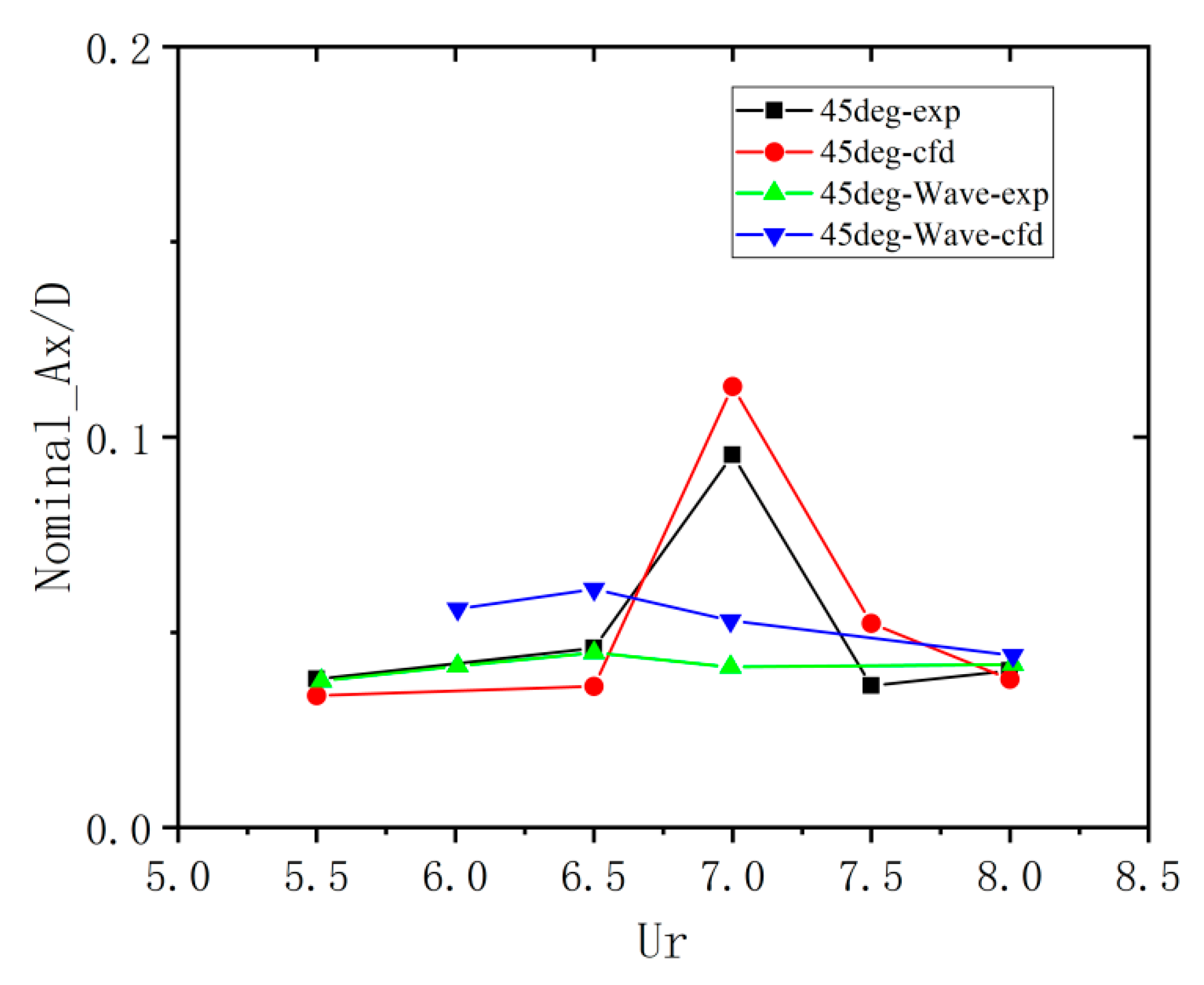
4.2. Motion Response Under Uniform Flow
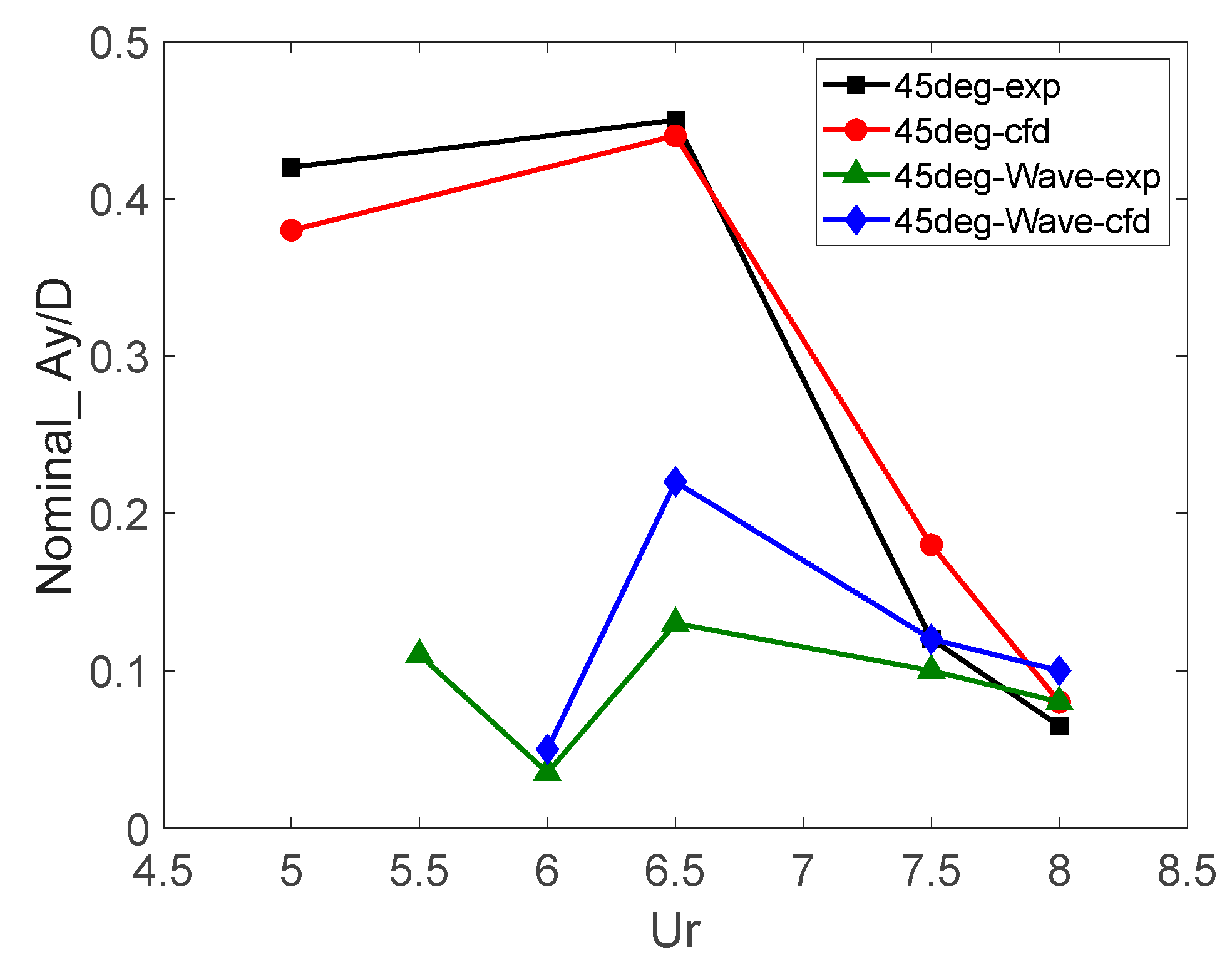
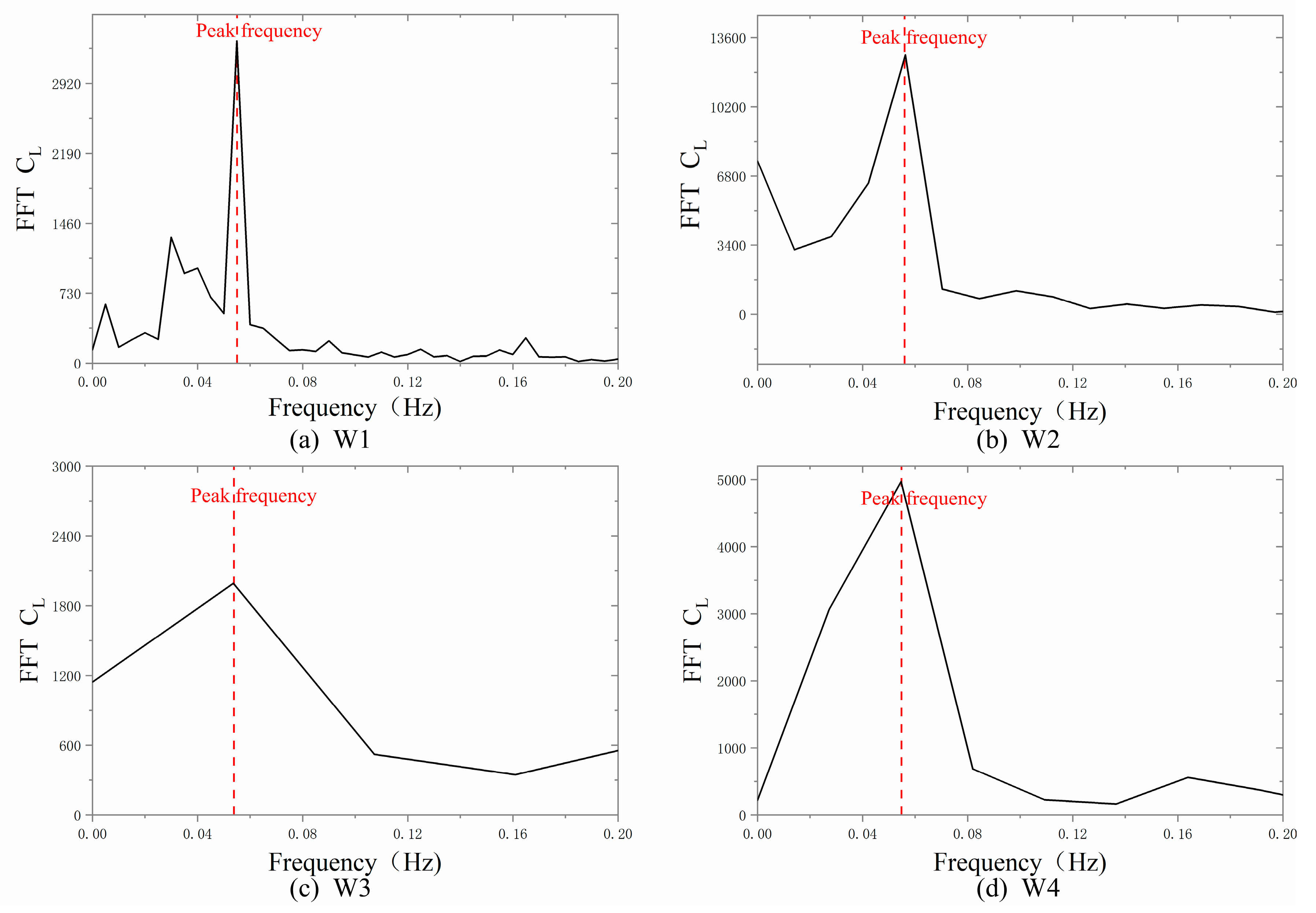
4.3. Motion Response Under Wave Current Coupling
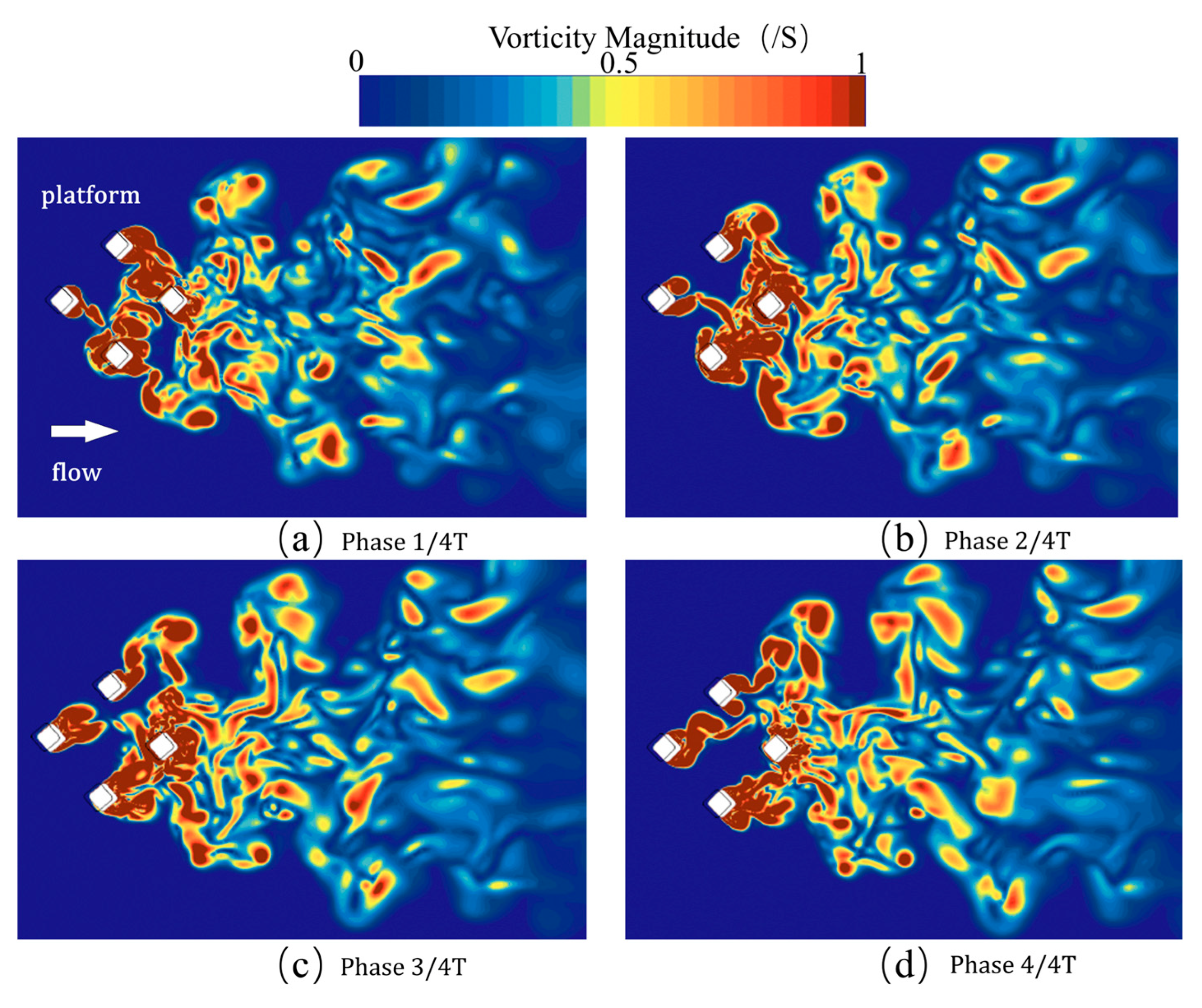
4.4. Instantaneous Flow Field
5. Conclusions
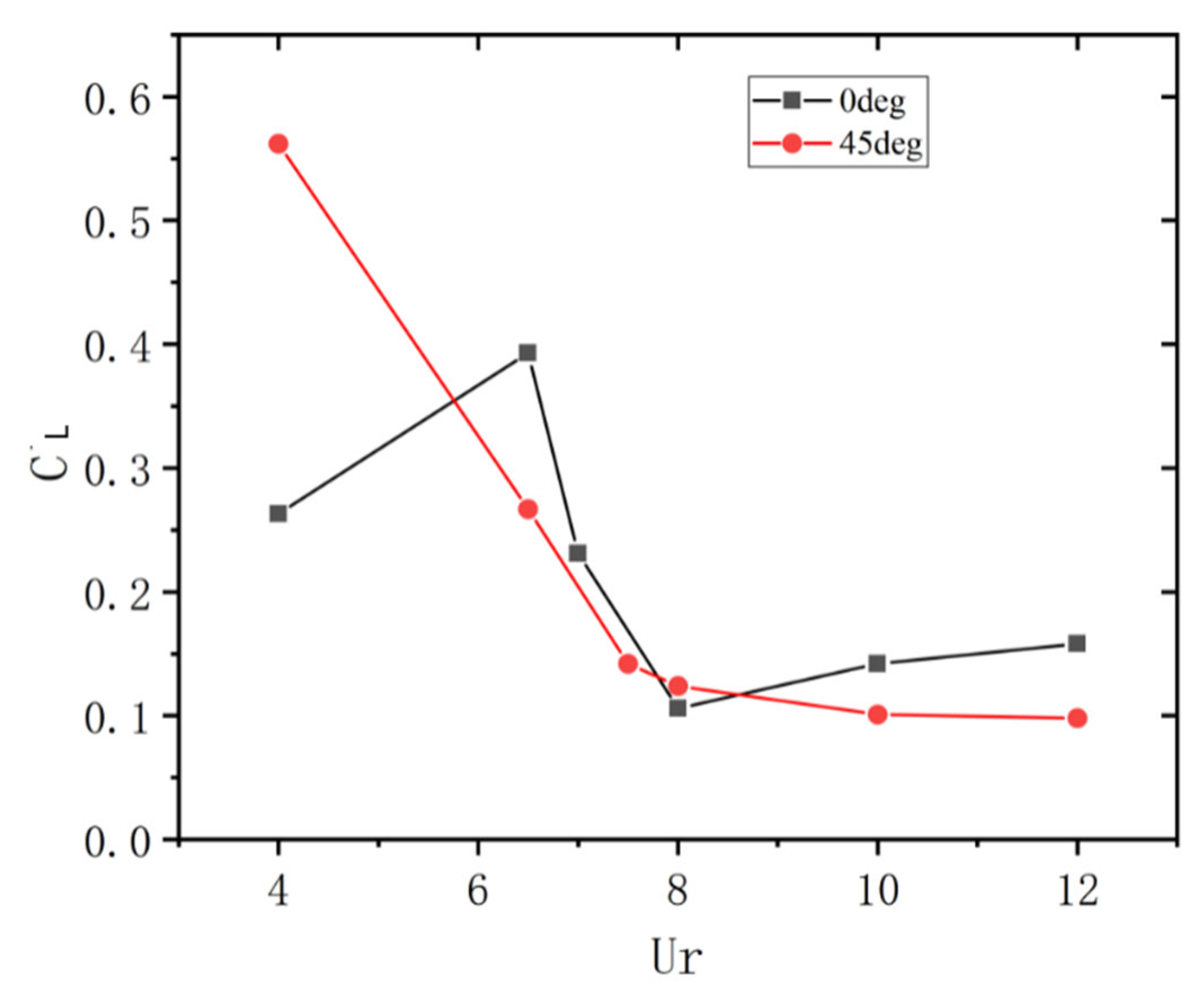
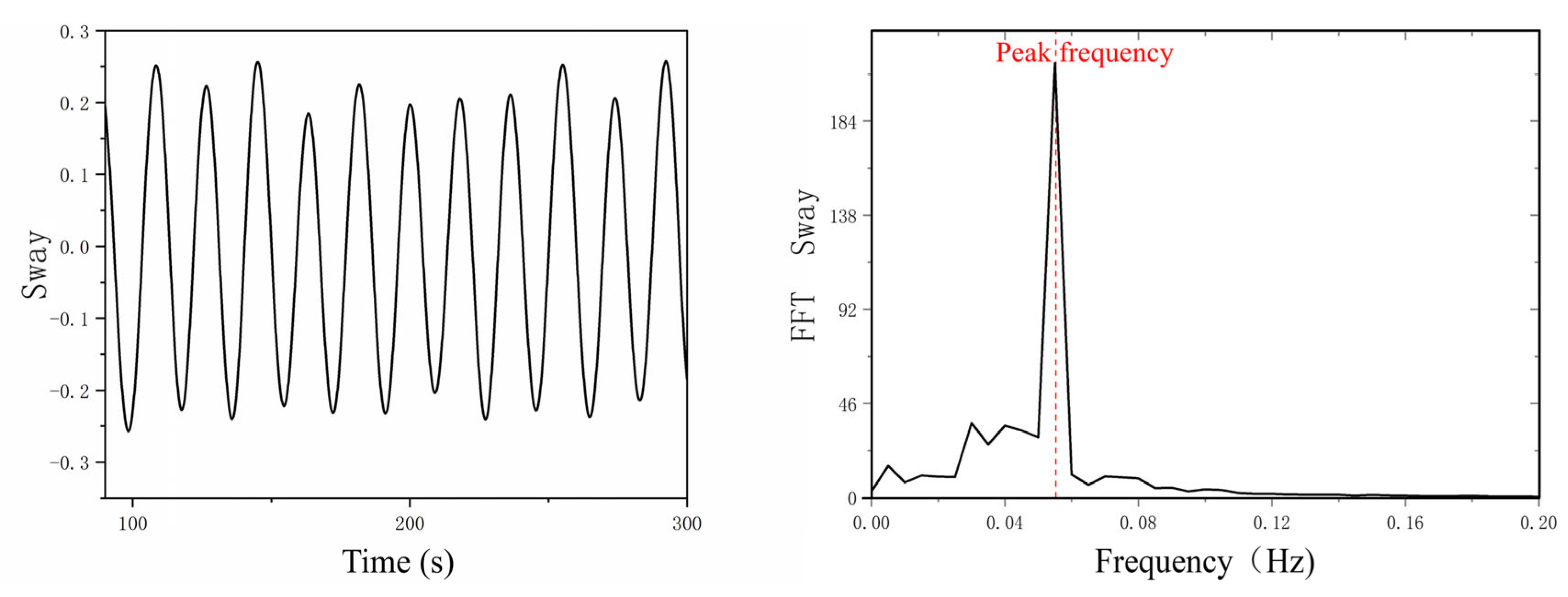
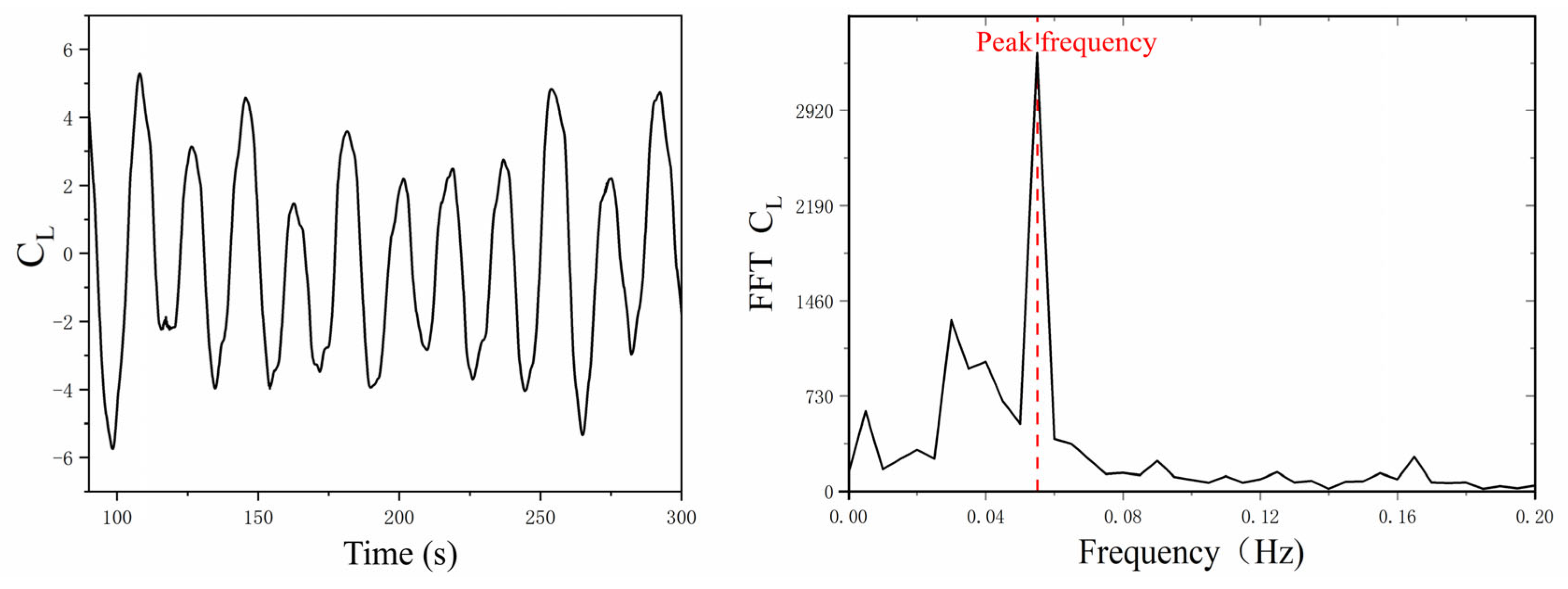
- Under the single action of uniform flow, the transverse motion perpendicular to the incoming flow direction dominates the vortex-induced motion. Regardless of the incoming flow angle of 0° or 45°, there is a significant “LOCK-IN” phenomenon in the range of reduced velocity , and a peak response amplitude appears near the reduced velocity = 7. When the inflow angle is 45°, the amplitude of the transverse motion response is larger than that at 0°. In terms of fluid force characteristics and response frequency, the transverse motion response frequency is the same as the vortex shedding frequency, which indicates that the transverse motion response of a semi-submersible platform is dominated by pulsating lift force. Within the range of reduced velocity , the vortex shedding frequency is roughly the same as the natural period of the platform, which is the fundamental reason for the “LOCK-IN” phenomenon in the transverse motion.
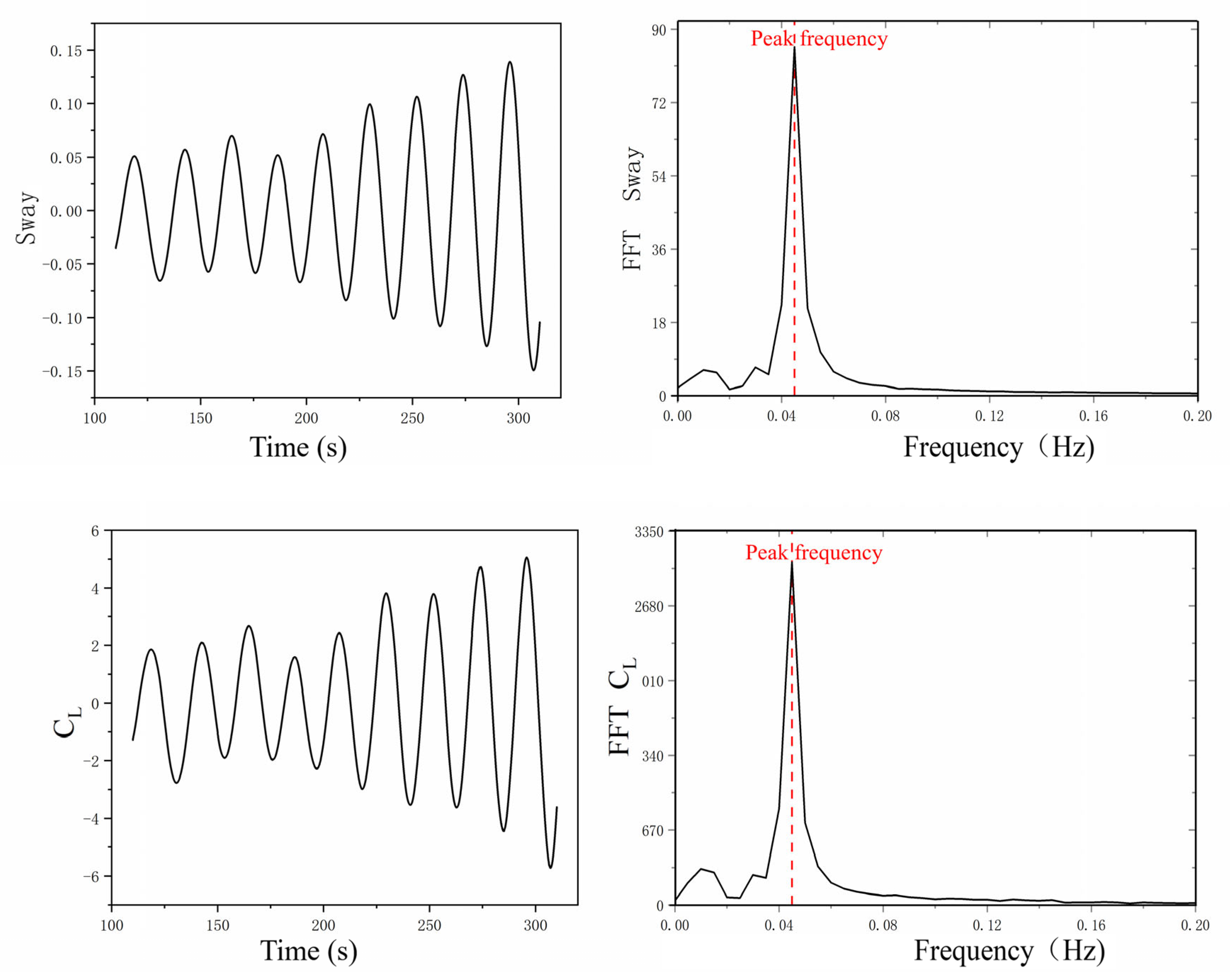
- Under identical wave-type coupling with varying reduced velocities (), the cross-flow motion response amplitude exhibits a characteristic rise to peak amplitude followed by gradual attenuation with increasing . For fixed with varying wave types, the response amplitude remains lower than the uniform flow condition. The vortex shedding frequency remains phase-locked to the platform’s natural frequency across all conditions, demonstrating wave-independent synchronization. However, the attenuated response amplitude reveals wave-induced suppression of vortex-induced motion through flow oscillation.
- Comparative analysis between numerical simulations and physical model tests demonstrates the following: Under uniform flow conditions, numerical results exhibit strong agreement with experimental measurements, validating the computational grid accuracy and physical model configurations. In wave-current coupling scenarios, while maintaining consistent dynamic trends, numerical models demonstrate notably higher response amplitudes, necessitating refinements in wave spectrum parametrization and grid convergence criteria. The complementary integration of numerical simulations (providing vorticity/velocity field visualization) and experimental benchmarks effectively mitigates individual limitations, enhancing result reliability and enabling in-depth investigation of vortex-induced motion mechanisms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Waals, O.J.; Phadke, A.C.; Bultema, S. Flow induced motions on multi column floaters. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 669–678. [Google Scholar]
- Hong, Y.; Choi, Y.; Lee, J.; Kim, Y. Vortex-induced motion of a deep-draft semi-submersible in current and waves. In Proceedings of the Eighteenth (2008) International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008; pp. 453–459. [Google Scholar]
- Gonçalves, R.T.; Rosetti, G.F.; Fujarra, A.L.; Oliveira, A.C. Experimental study on vortex-induced motions of a semi-submersible platform with four columns, Part I: Effects of current incidence angle and hull appendages. Ocean. Eng. 2012, 54, 150–169. [Google Scholar] [CrossRef]
- Zheng, G.; Shi, J.; Li, L.; Li, Q.; Gu, Z.; Xu, W.; Lu, B.; Wang, C. Fluid-solid coupling-based vibration generation mechanism of the multiphase vortex. Processes 2023, 11, 568. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, J.; Wang, J.; Mao, Y. Time-frequency analysis of the vortex motion in a cylindrical cyclone separator. Chem. Eng. J. 2019, 373, 1120–1131. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, W. A comprehensive assessment on detached eddy simulation and delayed detached eddy simulation approaches in large-scale rotating separated flow in a centrifugal impeller under small flow rate. Phys. Fluids 2023, 35, 105111. [Google Scholar] [CrossRef]
- Li, J.; Ho, M.T.; Borg, M.K.; Cai, C.; Li, Z.H.; Zhang, Y. Pore-scale gas flow simulations by the DSBGK and DVM methods. Compute Fluids 2021, 226, 105017. [Google Scholar] [CrossRef]
- Ho, M.T.; Li, J.; Wu, L.; Reese, J.M.; Zhang, Y. A comparative study of the DSBGK and DVM methods for low-speed rarefied gas flows. Comput. Fluids 2019, 181, 143–159. [Google Scholar] [CrossRef]
- Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Prog. Aerosp. Sci. 2020, 114, 100597. [Google Scholar] [CrossRef]
- Menter, F.; Hüppe, A.; Matyushenko, A.; Kolmogorov, D. An overview of hybrid RANS–LES models developed for industrial CFD. Appl. Sci. 2021, 11, 2459. [Google Scholar] [CrossRef]
- Zheng, X.; Montazeri, H.; Blocken, B. CFD simulations of wind flow and mean surface pressure for buildings with balconies: Comparison of RANS and LES. Build. Environ. 2020, 173, 106747. [Google Scholar] [CrossRef]
- Shastri, R.; Brar, L.S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation. Sep. Purif. Technol. 2020, 249, 117149. [Google Scholar] [CrossRef]
- He, X.; Zhao, F.; Vahdati, M. Detached eddy simulation: Recent development and application to compressor tip leakage flow. J. Turbomach. 2022, 144, 011009. [Google Scholar] [CrossRef]
- Kumar, R.; Padhee, S.S.; Samanta, D. Aerodynamic performance and flow mechanism of 3D flapping wing using discrete vortex method. J. Fluids Struct. 2024, 127, 104128. [Google Scholar] [CrossRef]
- Oliveira, M.A.d.; Moraes, P.G.d.; Andrade, C.L.d.; Bimbato, A.M.; Alcântara Pereira, L.A. Control and suppression of vortex shedding from a slightly rough circular cylinder by a discrete vortex method. Energies 2020, 13, 4481. [Google Scholar] [CrossRef]
- Faure, T.M.; Dumas, L.; Montagnier, O. Numerical study of two-airfoil arrangements by a discrete vortex method. Theor. Comput. Fluid Dyn. 2020, 34, 79–103. [Google Scholar] [CrossRef]
- Masdari, M.; Tahani, M.; Naderi, M.H.; Babayan, N. Optimization of airfoil Based Savonius wind turbine using coupled discrete vortex method and salp swarm algorithm. J. Clean. Prod. 2019, 222, 47–56. [Google Scholar] [CrossRef]
- Díaz-Carrasco, P.; Croquer, S.; Tamimi, V.; Lacey, J.; Poncet, S. Advances in numerical Reynolds-Averaged Navier–Stokes modelling of wave-structure-seabed interactions and scour. J. Mar. Sci. Eng. 2021, 9, 611. [Google Scholar] [CrossRef]
- Chen, W.; Xiang, Q.; Li, Y.; Liu, Z. On the mechanisms of pressure drop and viscous losses in hydrofoil tip-clearance flows. Energy 2023, 269, 126712. [Google Scholar] [CrossRef]
- Heinz, S. The large eddy simulation capability of Reynolds-averaged Navier-Stokes equations: Analytical results. Phys. Fluids 2019, 31, 021702. [Google Scholar] [CrossRef]
- Heinz, S.; Mokhtarpoor, R.; Stoellinger, M. Theory-based Reynolds-averaged Navier–Stokes equations with large eddy simulation capability for separated turbulent flow simulations. Phys. Fluids 2020, 32, 065102. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Lin, P.; Zhu, Z. An improved detached eddy simulation method for cavitation multiphase flow. Ocean. Eng. 2024, 313, 119359. [Google Scholar] [CrossRef]
- Chen, J.; Yang, R.; Huang, Z.; Li, G.; Qin, X.; Li, J.; Wu, X. Detached eddy simulation on the structure of swirling jet flow field. Pet. Explor. Dev. 2022, 49, 929–941. [Google Scholar] [CrossRef]
- Zhai, L.J.; Chen, H.X.; Ma, Z. A delayed detached eddy simulation model for the simulation of complex turbulent flow. J. Appl. Fluid Mech. 2022, 15, 1111–1124. [Google Scholar]
- Qian, G.W.; Ishihara, T. Numerical study of wind turbine wakes over escarpments by a modified delayed detached eddy simulation. J. Wind. Eng. Ind. Aerodyn. 2019, 191, 41–53. [Google Scholar] [CrossRef]
- Mukha, T.; Rezaeiravesh, S.; Liefvendahl, M. A library for wall-modelled large-eddy simulation based on OpenFOAM technology. Comput. Phys. Commun. 2019, 239, 204–224. [Google Scholar] [CrossRef]
- Ren, X.; Su, H.; Yu, H.-H.; Yan, Z. Wall-modeled large eddy simulation and detached eddy simulation of wall-mounted separated flow via OpenFOAM. Aerospace 2022, 9, 759. [Google Scholar] [CrossRef]
- Zhou, T.; Yang, Q.; Yan, B.; Deng, X.; Yuan, Y. Detached eddy simulation of turbulent flow fields over steep hilly terrain. J. Wind. Eng. Ind. Aerodyn. 2022, 221, 104906. [Google Scholar] [CrossRef]
- Li, J. Efficient prediction of gas permeability by hybrid DSBGK-LBM simulations. Fuel 2019, 250, 154–159. [Google Scholar] [CrossRef]
- Li, J.; Cai, C.; Li, Z.H. Efficient DSBGK simulations of the low speed thermal transpiration gas flows through micro-channels. Int. Commun. Heat Mass Transf. 2020, 119, 104924. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M.; Allmaras, S.R. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Zhang, D.; Zhang, L.; Tang, H.; Yuan, S.; Wang, H.; Chen, S.N.; Zhao, Y. A novel fluid–solid coupling model for the oil–water flow in the natural fractured reservoirs. Phys. Fluids 2021, 33, 036601. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, C.; Liu, H.; Kou, Y.D.; Shi, B. A multi-field and fluid–solid coupling method for porous media based on DEM-PNM. Comput. Geotech. 2023, 154, 105118. [Google Scholar] [CrossRef]
- Xue, Y.; Feng, Y.; Zheng, X. Assessment of Compressibility Corrections on Spalart–Allmaras Turbulence Model for High-Mach-Number Flows. AIAA J. 2024, 62, 92–107. [Google Scholar] [CrossRef]
- Polewski, M.D.; Cizmas, P.G.A. Several cases for the validation of turbulence models implementation. Appl. Sci. 2021, 11, 3377. [Google Scholar] [CrossRef]
- Tang, Q. Experimental Study on Vortex-Induced Motion of a Platform Considering Wave-Current Coupling Effects. Ocean Eng. Equip. Technol. 2024, 11, 75–84. (In Chinese) [Google Scholar]
- Kim, J.W.; Magee, A.; Guan, K.Y.H. CFD simulation of flow-induced motions of a multi-column floating platform. In Proceedings of the ASME 2011 30th International Conference on Ocean, Off-Shore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2011; pp. 319–326. [Google Scholar]
- Liu, M. Research on the Flow Characteristics and Vortex-Induced Motions of Deep-Draft Semi-Submersibles; Shanghai Jiao Tong Universuity: Shanghai, China, 2016. (In Chinese) [Google Scholar]
- Liu, M.; Xiao, L.; Yang, J.; Tian, X. Parametric study on the vortex-induced motions of semi-submersibles: Effect of rounded ratios of the column and pontoon. Phys. Fluids 2017, 29, 055101. [Google Scholar] [CrossRef]
- Bai, Z.N.; Xiao, L.F.; Cheng, Z.S.; Lai, Z.M. Experimental study on Vortex Induced Motion response of a deep draft semi-submersible platform. J. Ship Mech. 2014, 18, 377–384. (In Chinese) [Google Scholar]
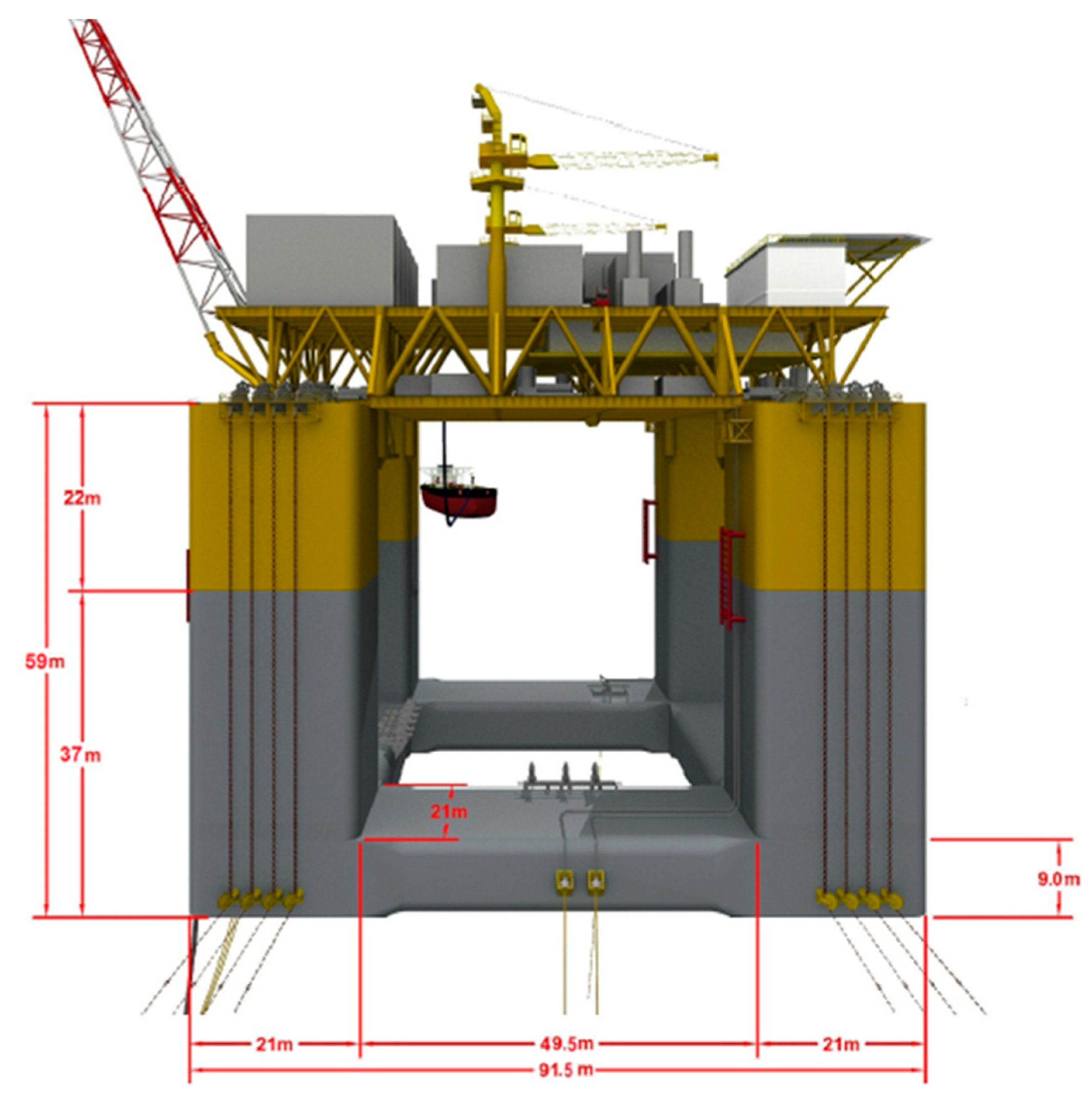




| Name | Unit | Prototype Value | Model Values |
|---|---|---|---|
| Column diameter | m | 21 | 0.350 |
| Pontoon height | m | 9 | 0.150 |
| Pontoon width | m | 21 | 0.350 |
| Center distance of columns | m | 70.5 | 1.175 |
| Draft | m | 35 | 0.583 |
| Displacement | ton | 101,100 | 0.456 |
| Height of center of gravity | m | 31.9 | 0.532 |
| Grid Name | Number of Grids (in Millions) | Relative Deviation from Finest Grid (M4) | Relative Deviation from Finest Grid (M4) | ||
|---|---|---|---|---|---|
| M1 | 0.94 | 0.457 | −17.5% | 0.212 | −26.1% |
| M2 | 1.53 | 0.472 | −14.8% | 0.222 | −22.6% |
| M3 | 3.87 | 0.548 | −1.1% | 0.275 | −4.2% |
| M4 | 5.37 | 0.554 | - | 0.287 | - |
| Angle | Ur | 4.00 | 6.50 | 7.00 | 8.00 | 10.00 | 12.00 |
|---|---|---|---|---|---|---|---|
| 0° | U (m/s) | 0.081 | 0.131 | 0.141 | 0.161 | 0.201 | 0.242 |
| 45° | U (m/s) | 0.114 | 0.185 | 0.213 | 0.228 | 0.285 | 0.342 |
| Condition | Flow Angle | Flow Reduced Velocity (Ur) | Wave Types | Wave Amplitude (m) | Wave Period (s) |
|---|---|---|---|---|---|
| 1 | 45° | 7.5 | W1 | 0.08 | 1.03 |
| 2 | W2 | 0.08 | 1.29 | ||
| 3 | W3 | 0.08 | 1.56 | ||
| 4 | W4 | 0.08 | 1.90 |
| Conditions | Flow Angle | Flow Reduced Velocity (Ur) | Wave Types | |
|---|---|---|---|---|
| 1 | 45° | 7.5 | W1 | 0.112 |
| 2 | W2 | 0.096 | ||
| 3 | W3 | 0.036 | ||
| 4 | W4 | 0.043 | ||
| 5 | Uniform flow | 0.182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Yan, J.; Deng, C.; Zhang, D. Three-Dimensional Numerical Simulation of the Vortex-Induced Motion Response of Semi-Submersible Platforms Under Wave-Current Coupling Effect. J. Mar. Sci. Eng. 2025, 13, 550. https://doi.org/10.3390/jmse13030550
Yin Y, Yan J, Deng C, Zhang D. Three-Dimensional Numerical Simulation of the Vortex-Induced Motion Response of Semi-Submersible Platforms Under Wave-Current Coupling Effect. Journal of Marine Science and Engineering. 2025; 13(3):550. https://doi.org/10.3390/jmse13030550
Chicago/Turabian StyleYin, Yankun, Jin Yan, Chushan Deng, and Dapeng Zhang. 2025. "Three-Dimensional Numerical Simulation of the Vortex-Induced Motion Response of Semi-Submersible Platforms Under Wave-Current Coupling Effect" Journal of Marine Science and Engineering 13, no. 3: 550. https://doi.org/10.3390/jmse13030550
APA StyleYin, Y., Yan, J., Deng, C., & Zhang, D. (2025). Three-Dimensional Numerical Simulation of the Vortex-Induced Motion Response of Semi-Submersible Platforms Under Wave-Current Coupling Effect. Journal of Marine Science and Engineering, 13(3), 550. https://doi.org/10.3390/jmse13030550







