Prescribed-Time Formation Tracking Control for Underactuated USVs with Prescribed Performance
Abstract
1. Introduction
- (1)
- A distributed prescribed-time control strategy is introduced for achieving formation among underactuated USVs. This scheme guarantees that, despite the presence of unknown USV velocities, the tracking errors converge to a preset range within a certain timeframe.
- (2)
- A unique performance function is intended to ensure guaranteed transient and steady-state performance within a certain timeframe.
- (3)
- A suggested formation control strategy incorporates the observer, a prescribed performance technique, and a dynamic surface control algorithm. The designed approach guarantees accurate tracking control by allowing the formation tracking error to converge to a certain precision within a designated timeframe.
2. Preliminaries
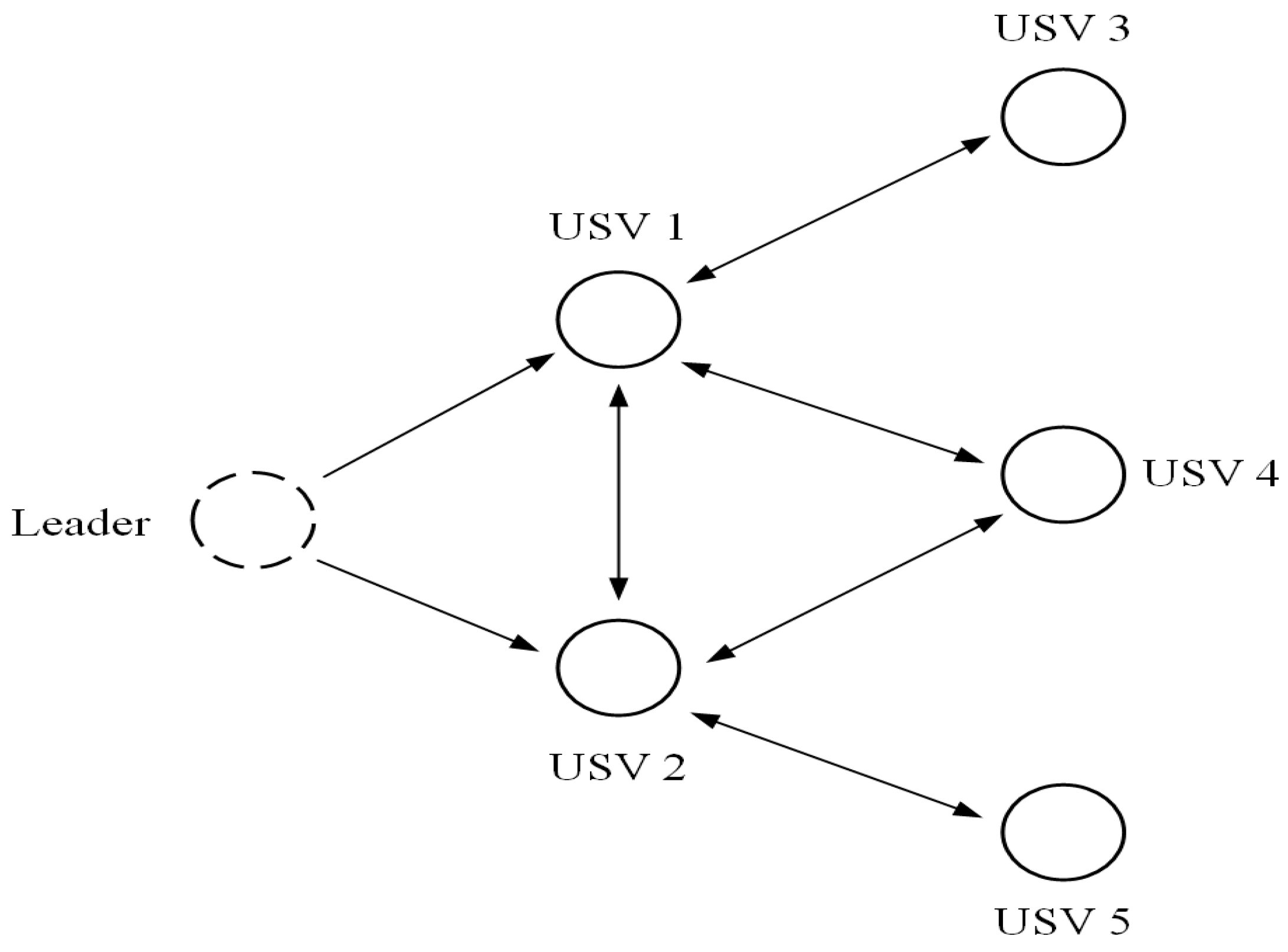
2.1. Graph Theory
2.2. USV Dynamics
2.3. Prescribed-Time Prescibed Performance Function (PTPPF)
2.4. Lemma and Assumption
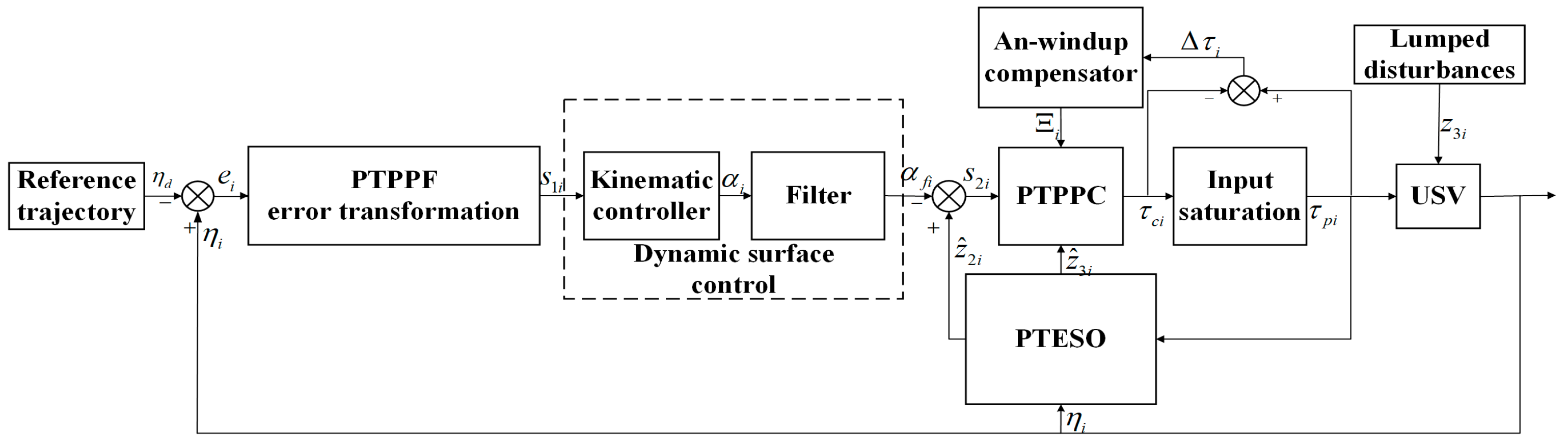
3. Main Results
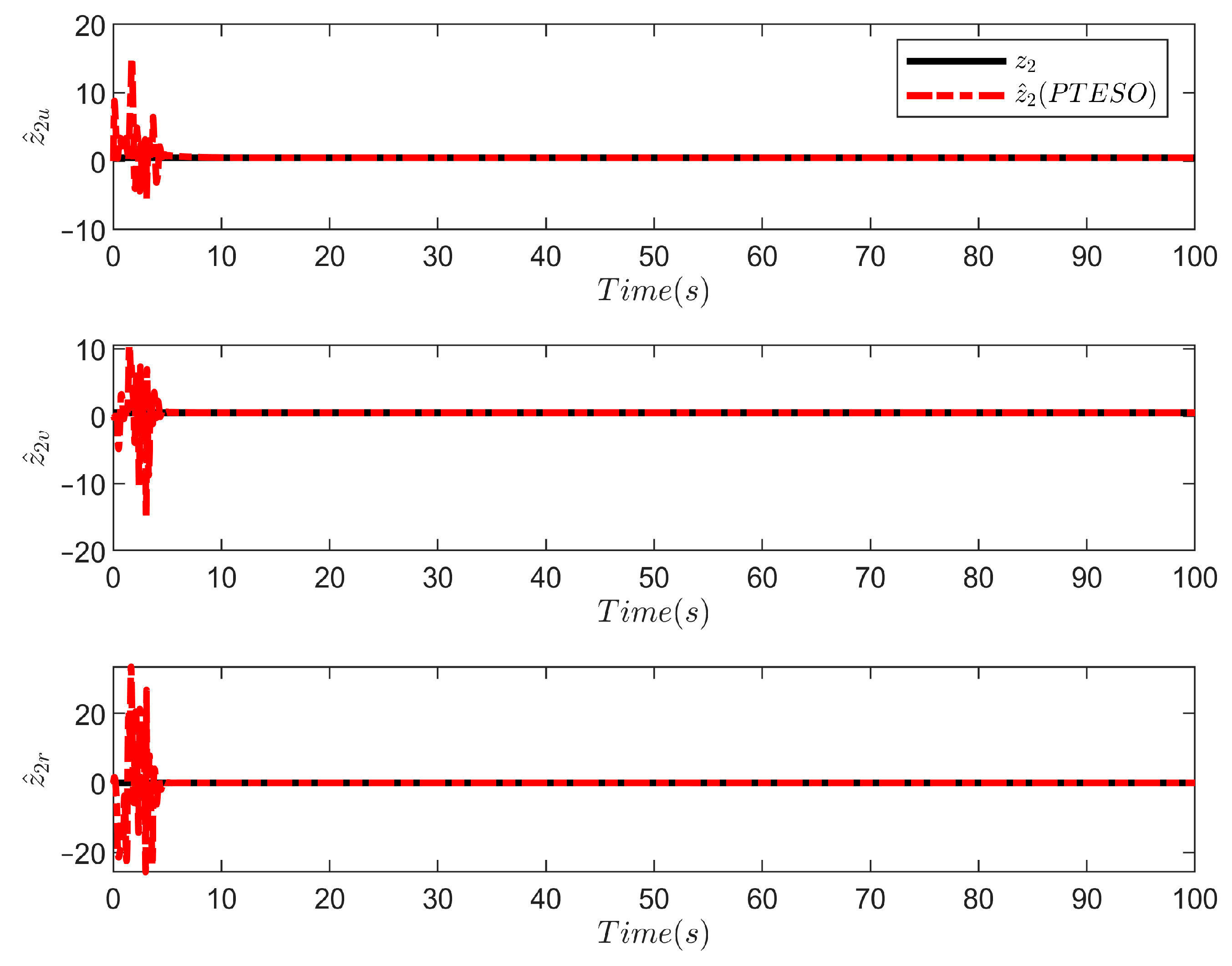
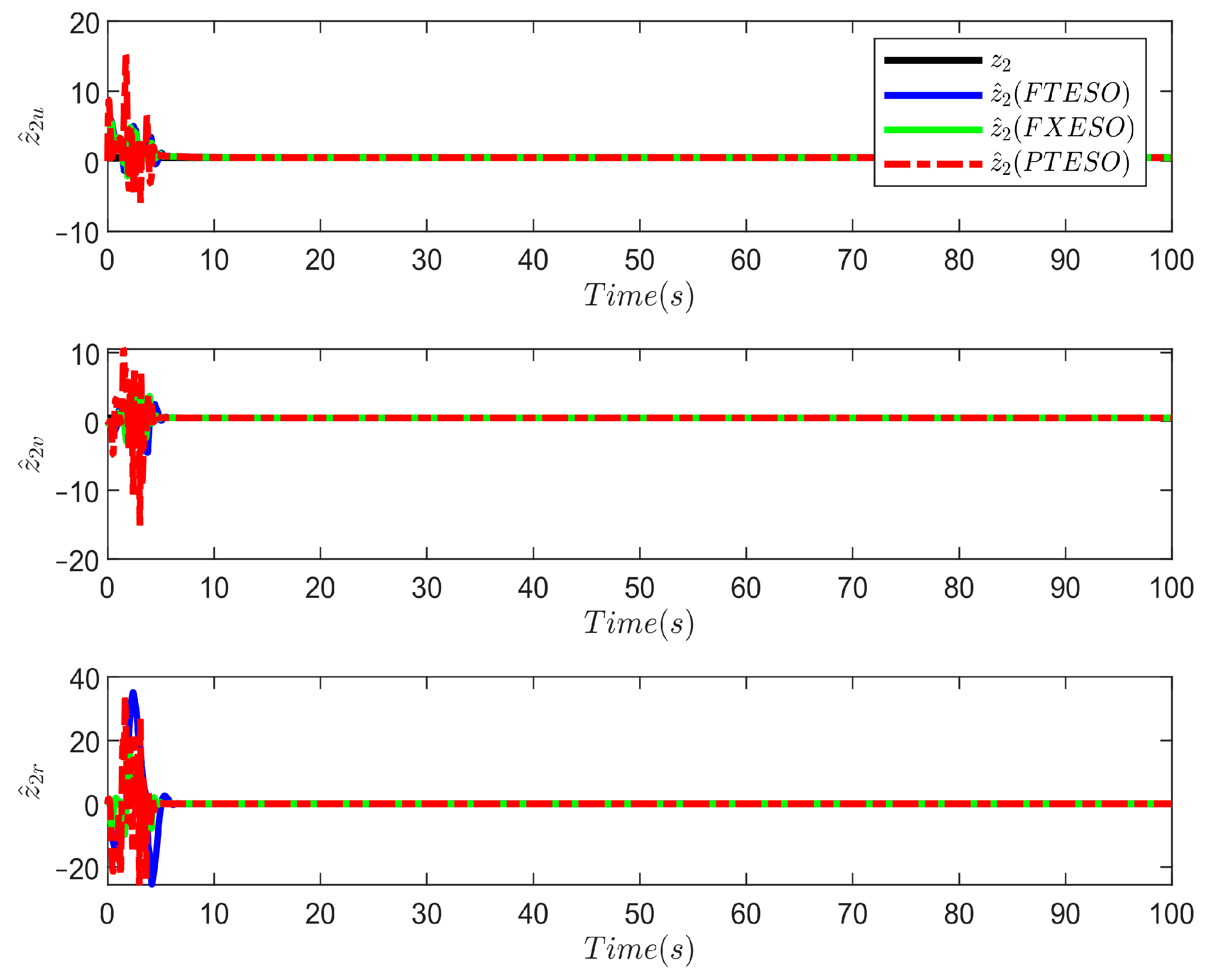
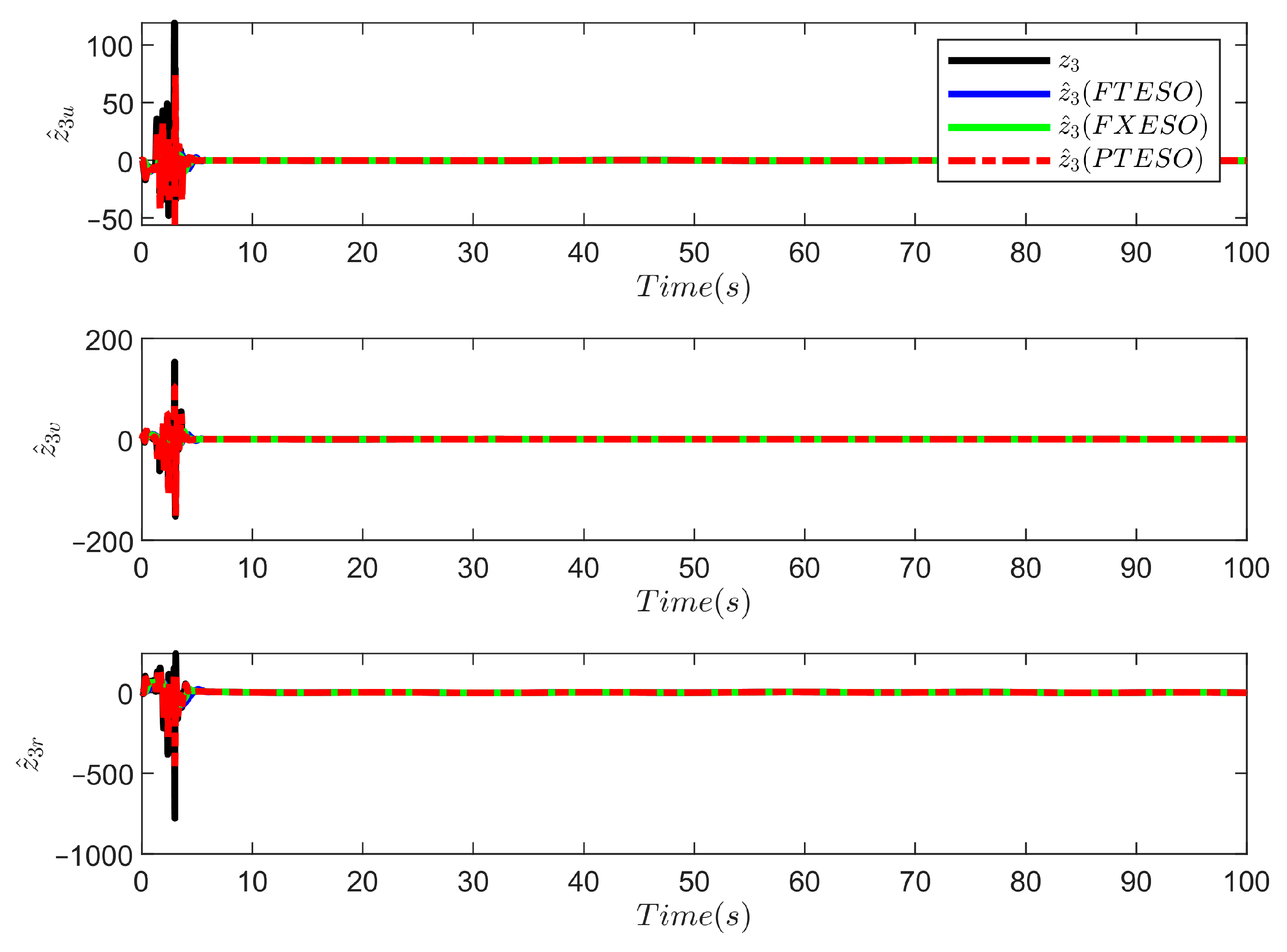
3.1. Prescribed-Time Extended State Observer (PTESO)
3.2. Controller Design and Stability Analysis
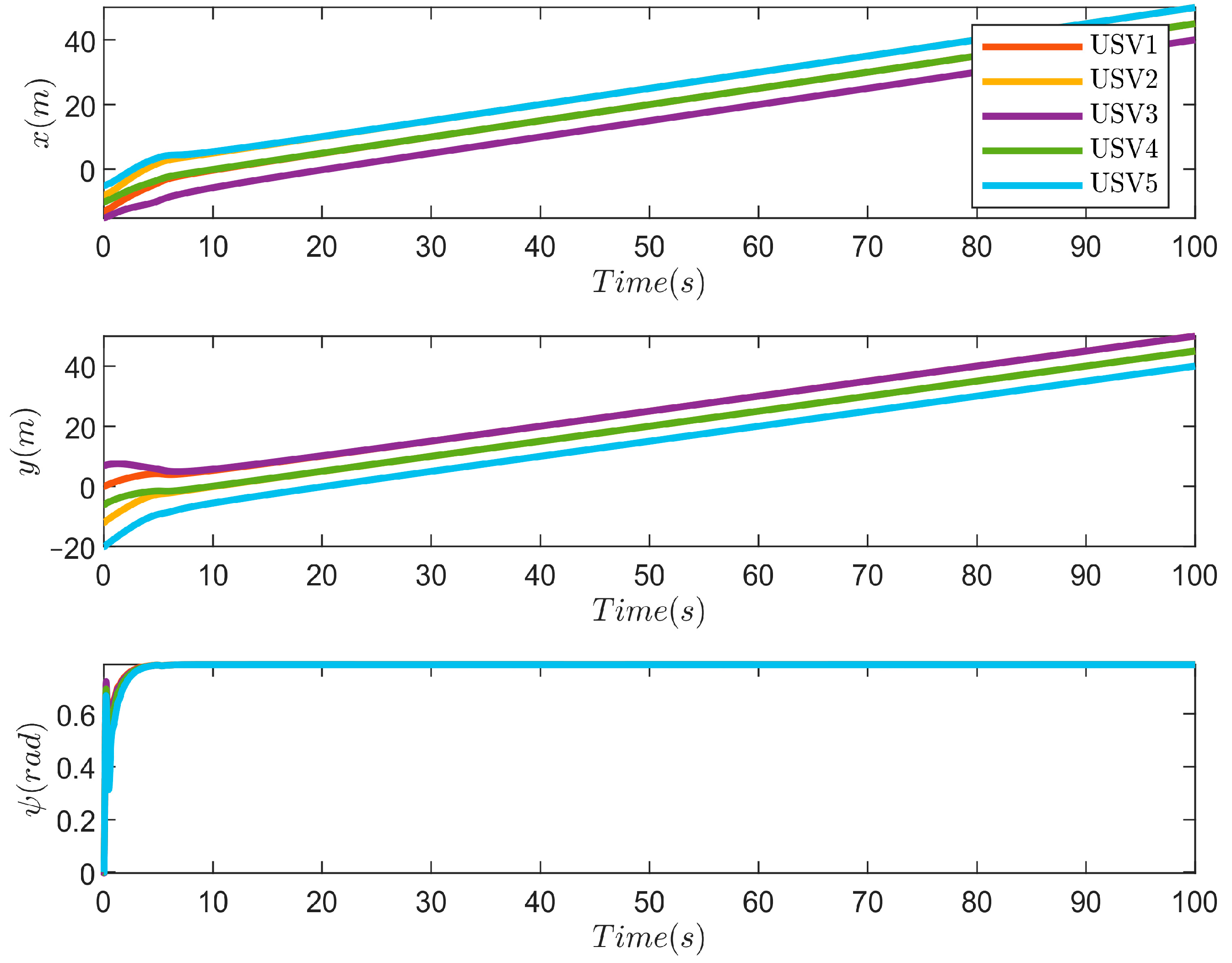
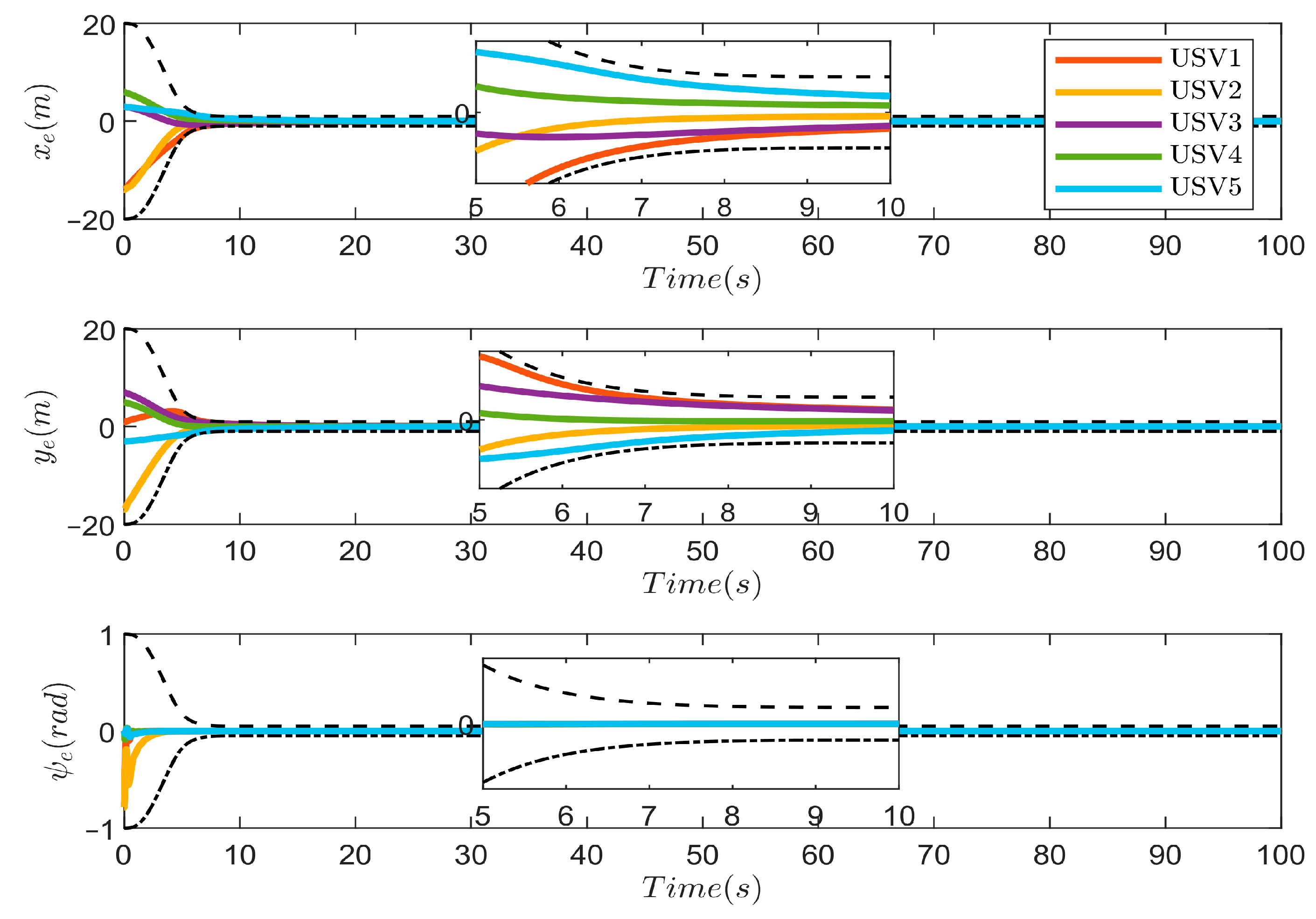
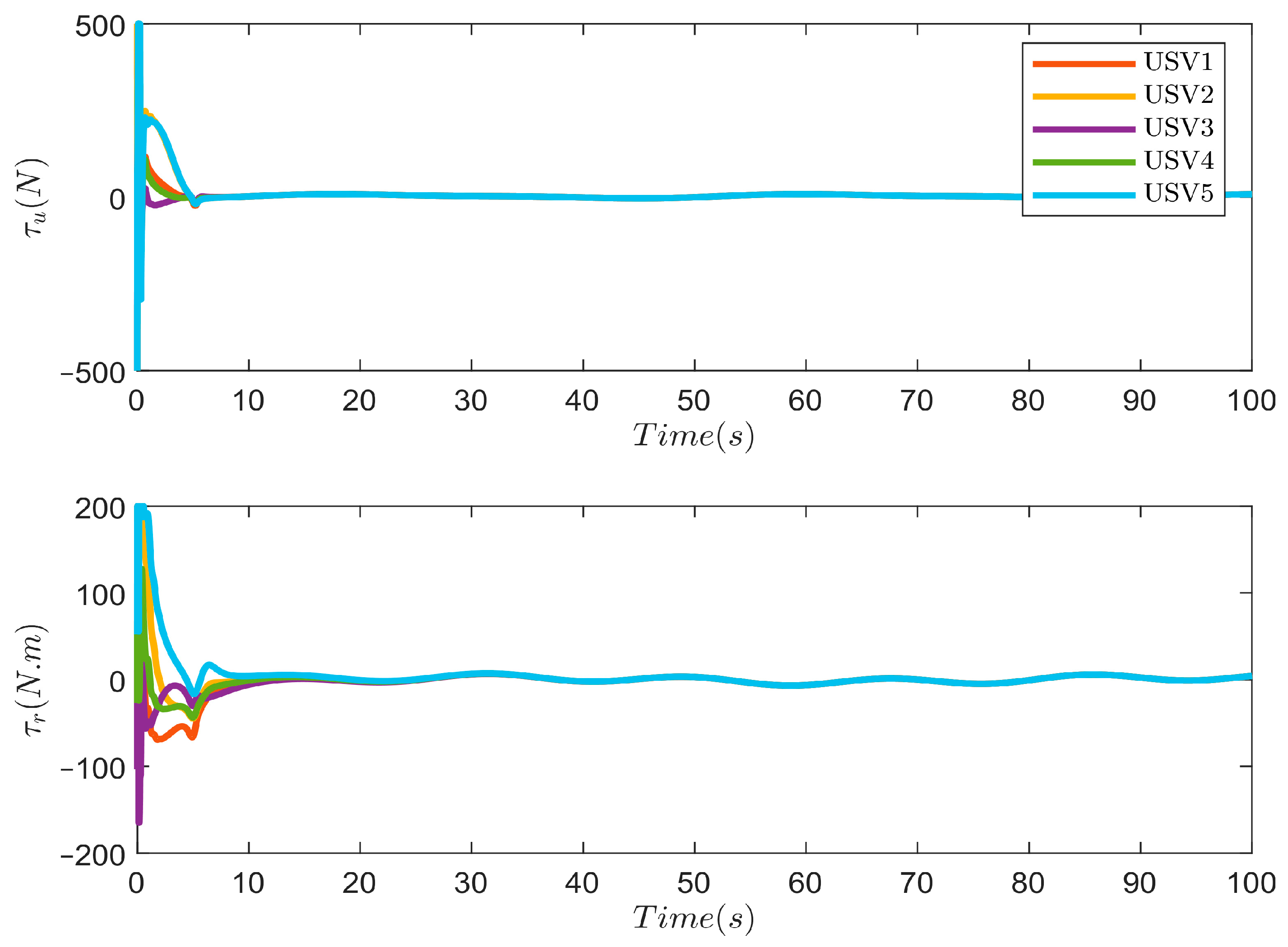
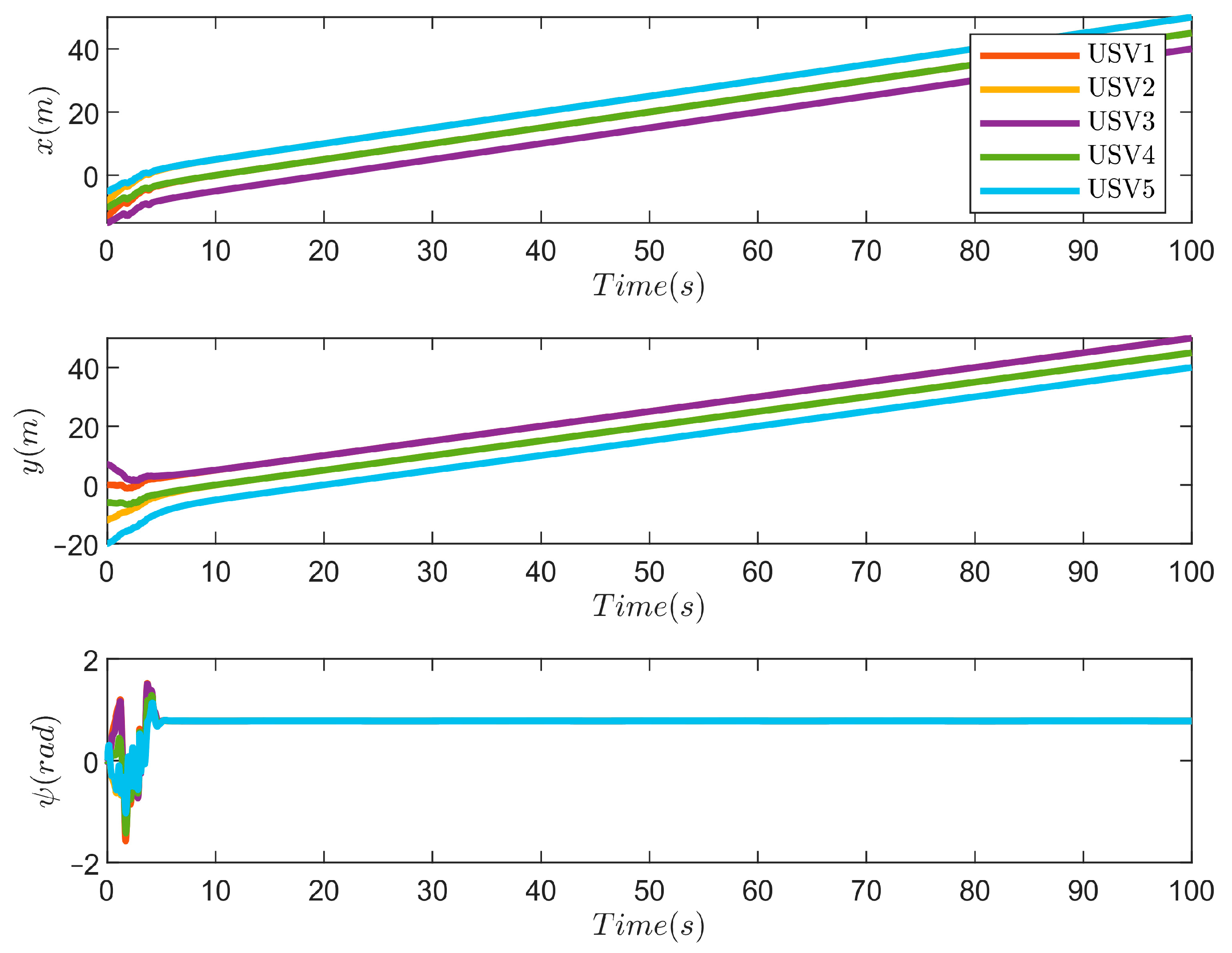
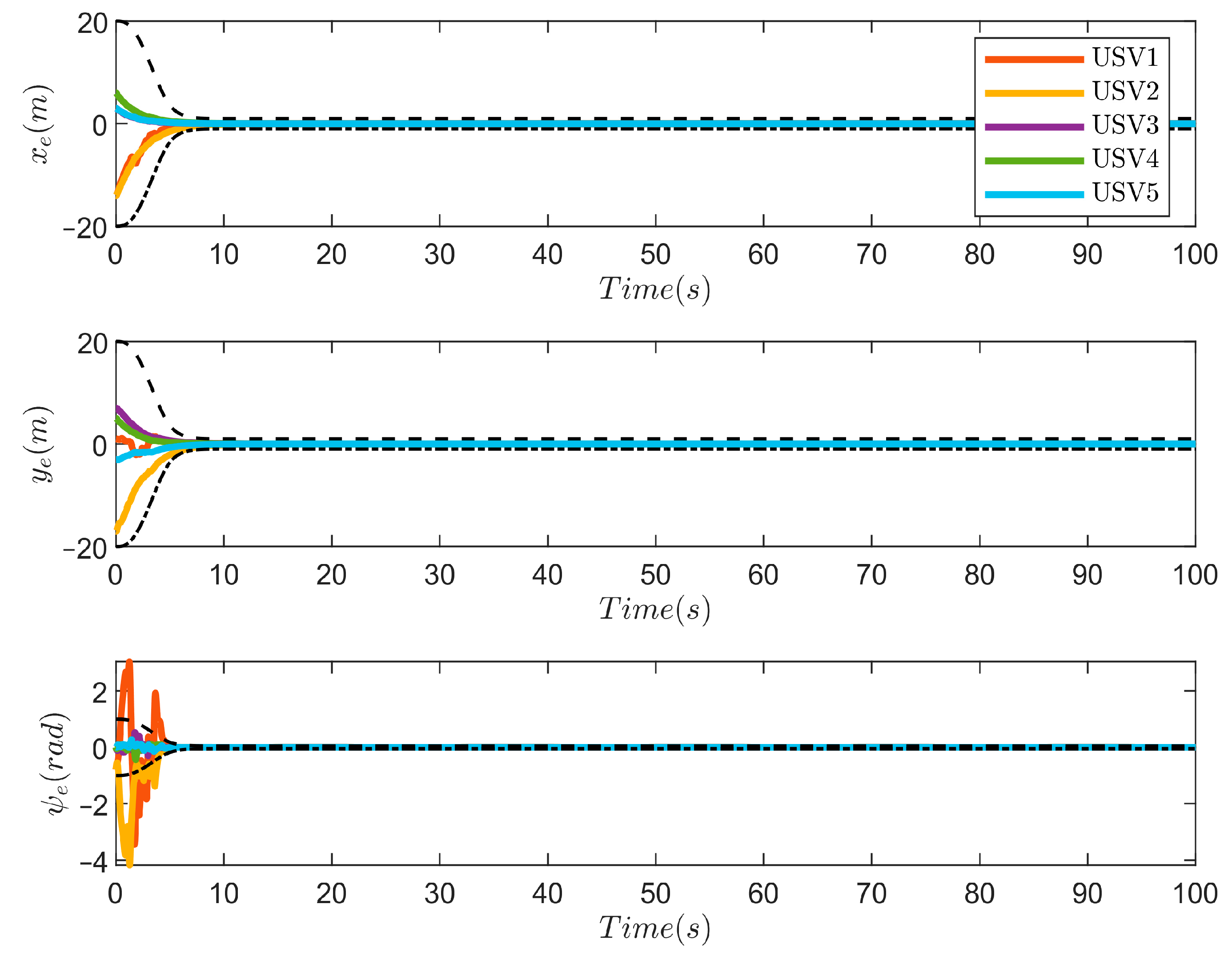
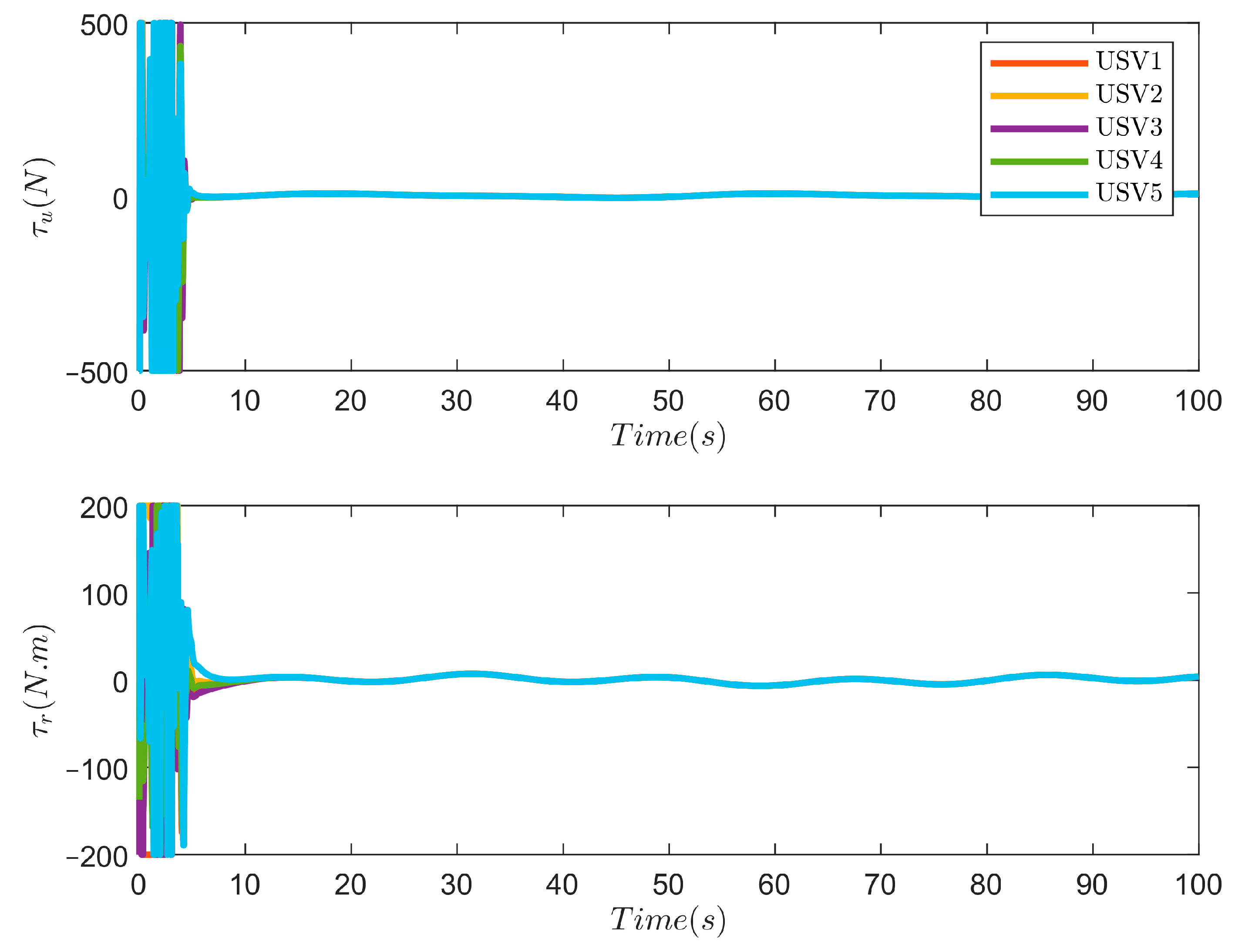
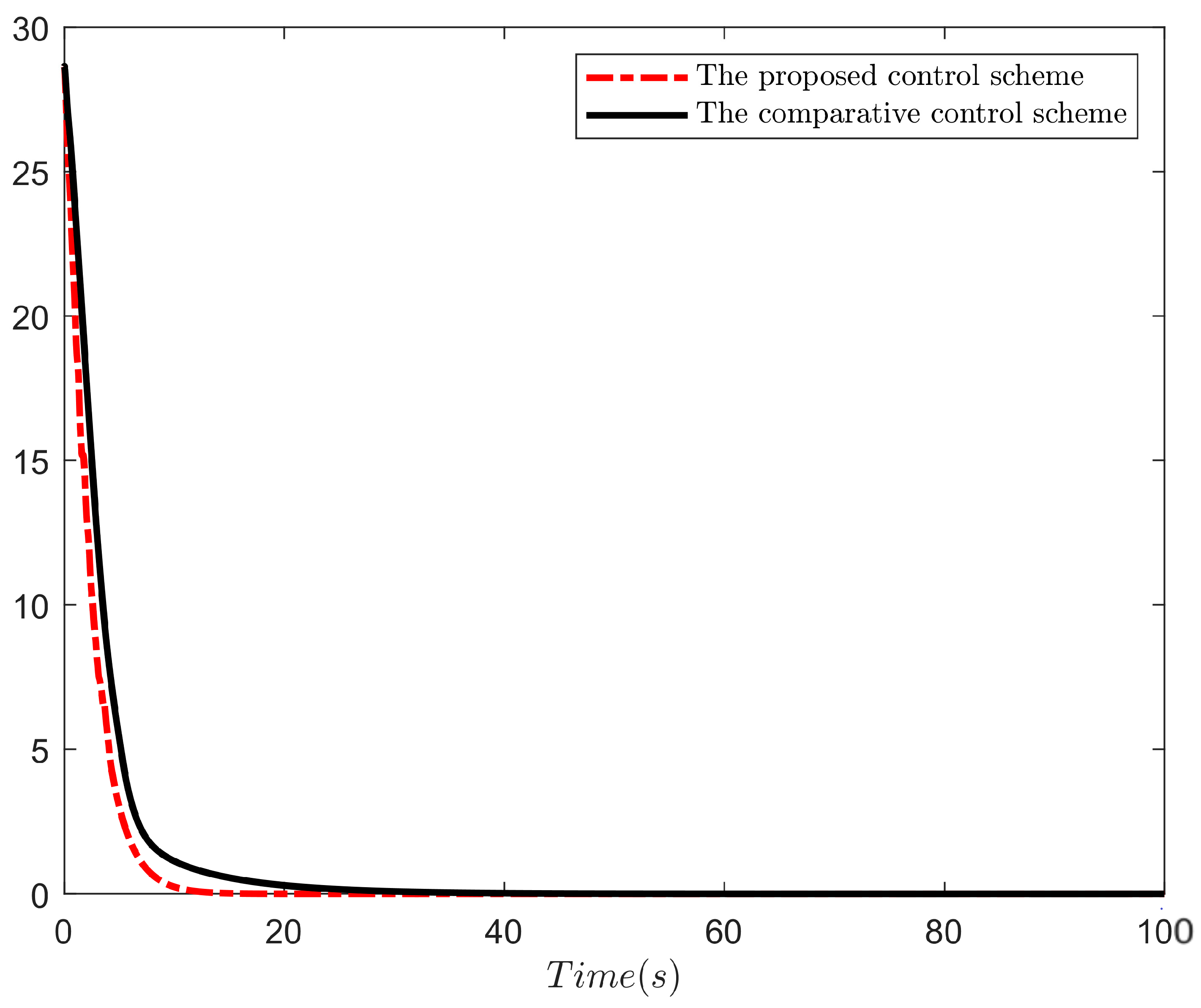
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| The communication topology diagram. | |
| The node of communication topology graph. | |
| The edge of communication topology graph. | |
| The set of neighbors of the th node. | |
| The adjacency matrix. | |
| The in-degree matrix. | |
| The Laplacian matrix. | |
| The incidence matrix. | |
| The rotation matrix. | |
| The inertial matrix. | |
| The prescribed performance function | |
| The nonlinear time-varying function. | |
| The observations of state observer. | |
| The filtering error. | |
| The kinematics control law. | |
| The dynamics control law. | |
| The state of compensator. |
References
- Chen, C.; Zou, W.; Xiang, Z. Event-Triggered Connectivity-Preserving Formation Control of Heterogeneous Multiple USVs. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7746–7755. [Google Scholar] [CrossRef]
- Fan, Y.; Li, Z.; Li, J.; Ma, G.; Bu, H. Fixed-time event-triggered distributed formation control for underactuated USVs considering actuator saturation. Ocean Eng. 2025, 316, 119829. [Google Scholar] [CrossRef]
- Wu, T.; Xue, K.; Wang, P. Leader-follower formation control of USVs using APF-based adaptive fuzzy logic nonsingular terminal sliding mode control method. J. Mech. Sci. Technol. 2022, 36, 2007–2018. [Google Scholar] [CrossRef]
- Chen, C.; Liao, Y.; Tang, X.; Sun, J.; Gu, J.; Li, H.; Ren, Z.; Zhai, Z.; Li, Y.; Wang, B.; et al. Research on double-USVs fuzzy-priority NSB behavior fusion formation control method for oil spill recovery. J. Field Robot. 2025, 42, 302–326. [Google Scholar] [CrossRef]
- Jiang, X.; Xia, G. Sliding mode formation control of leaderless unmanned surface vehicles with environmental disturbances. Ocean Eng. 2022, 244, 110301. [Google Scholar] [CrossRef]
- Fang, X.; Wen, G.; Yu, X.; Chen, G. Formation control for unmanned surface vessels: A game-theoretic approach. Asian J. Control 2022, 24, 498–509. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L. Coordination control for multiple unmanned surface vehicles using hybrid behavior-based method. Ocean Eng. 2021, 232, 109147. [Google Scholar] [CrossRef]
- Fan, J.; Liao, Y.; Li, Y.; Jiang, Q.; Wang, L.; Jiang, W. Formation control of multiple unmanned surface vehicles using the adaptive null-space-based behavioral method. IEEE Access 2019, 7, 87647–87657. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, W.; Li, J.; Zhang, X. A novel event-triggered robust neural formation control for USVs with the optimized leader–follower structure. Ocean Eng. 2021, 235, 109390. [Google Scholar] [CrossRef]
- Xie, M.; Wu, Z.; Huang, H. Low-complexity formation control of marine vehicle system based on prescribed performance. Nonlinear Dyn. 2024, 112, 18311–18332. [Google Scholar] [CrossRef]
- Liu, G.; Wen, N.; Long, F.; Zhang, R. A Formation Control and Obstacle Avoidance Method for Multiple Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 2346. [Google Scholar] [CrossRef]
- Zhen, Q.; Wan, L.; Li, Y.; Jiang, D. Formation control of a multi-AUVs system based on virtual structure and artificial potential field on SE(3). Ocean Eng. 2022, 253, 111148. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y. Neural adaptive performance guaranteed formation control for USVs with event-triggered quantized inputs. Ships Offshore Struct. 2024, 1–13. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Zheng, Z. Formation tracking control for underactuated surface vehicles with actuator magnitude and rate saturations. Ocean Eng. 2022, 260, 111935. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, H.; Li, P.; Zou, J. Formation control of multiple underactuated surface vessels with a disturbance observer. J. Mar. Sci. Eng. 2022, 10, 1016. [Google Scholar] [CrossRef]
- Ma, Y.; Ning, J.; Li, T.; Liu, L. Distributed extended state observer-based formation tracking control of under-actuated unmanned surface vehicles with input and state quantization. Ocean Eng. 2024, 311, 118872. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Qi, S.; Zhang, H.; Li, J.; Liu, Y. Autonomous cooperative formation control of underactuated USVs based on improved MPC in complex ocean environment. Ocean Eng. 2023, 270, 113633. [Google Scholar] [CrossRef]
- Dong, C.; Ye, Q.; Dai, S.L. Neural-network-based adaptive output-feedback formation tracking control of USVs under collision avoidance and connectivity maintenance constraints. Neurocomputing 2020, 401, 101–112. [Google Scholar] [CrossRef]
- Peng, H.; Huang, B.; Jin, M.; Zhu, C.; Zhuang, J. Distributed finite-time bearing-based formation control for underactuated surface vessels with Levant differentiator. ISA Trans. 2024, 147, 239–251. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Z.; Chen, F. Adaptive output-constrained finite-time formation control for multiple unmanned surface vessels with directed communication topology. Ocean Eng. 2024, 292, 116552. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Fixed-time formation fault tolerant control for unmanned surface vehicle systems with intermittent actuator faults. Ocean Eng. 2023, 281, 114813. [Google Scholar] [CrossRef]
- An, S.; Liu, Y.; Wang, X.; Fan, Z.; Zhang, Q.; He, Y.; Wang, L. Distributed Event-Triggered Fixed-Time Leader–Follower Formation Tracking Control of Multiple Underwater Vehicles Based on an Adaptive Fixed-Time Observer. J. Mar. Sci. Eng. 2023, 11, 1522. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Li, J.; Song, S. Prescribed-time collision-free trajectory tracking control for spacecraft with position-only measurements. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4035–4043. [Google Scholar] [CrossRef]
- Wu, G.X.; Ding, Y.; Tahsin, T.; Atilla, I. Adaptive neural network and extended state observer-based non-singular terminal sliding mode tracking control for an underactuated USV with unknown uncertainties. Appl. Ocean Res. 2023, 135, 103560. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q.; Dong, S.; Yu, H. Dynamic surface control for tracking of unmanned surface vessel with prescribed performance and asymmetric time-varying full state constraints. Ocean Eng. 2022, 253, 111319. [Google Scholar] [CrossRef]
- Sui, B.; Zhang, J.; Liu, Z. Extended state observer based prescribed-time trajectory tracking control for USV with prescribed performance constraints and input saturation. Ocean Eng. 2025, 316, 120005. [Google Scholar] [CrossRef]
- Li, J.; Fan, Y.; Liu, J. Distributed fixed-time formation tracking control for multiple underactuated USVs with lumped uncertainties and input saturation. ISA Trans. 2024, 154, 186–198. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T.I.; Kokotović, P.V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 2005, 41, 289–298. [Google Scholar] [CrossRef]
- Li, J.; Fu, M.; Wang, L. Formation control for underactuated surface vehicles in the presence of ocean current. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- Fu, M.; Yu, L. Finite-time extended state observer-based distributed formation control for marine surface vehicles with input saturation and disturbances. Ocean Eng. 2018, 159, 219–227. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y.; Zhang, X. Extended state observer-based fixed-time trajectory tracking control of autonomous surface vessels with uncertainties and output constraints. ISA Trans. 2022, 128, 174–183. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, B.; Zhang, J.; Liu, Z. Prescribed-Time Formation Tracking Control for Underactuated USVs with Prescribed Performance. J. Mar. Sci. Eng. 2025, 13, 480. https://doi.org/10.3390/jmse13030480
Sui B, Zhang J, Liu Z. Prescribed-Time Formation Tracking Control for Underactuated USVs with Prescribed Performance. Journal of Marine Science and Engineering. 2025; 13(3):480. https://doi.org/10.3390/jmse13030480
Chicago/Turabian StyleSui, Bowen, Jianqiang Zhang, and Zhong Liu. 2025. "Prescribed-Time Formation Tracking Control for Underactuated USVs with Prescribed Performance" Journal of Marine Science and Engineering 13, no. 3: 480. https://doi.org/10.3390/jmse13030480
APA StyleSui, B., Zhang, J., & Liu, Z. (2025). Prescribed-Time Formation Tracking Control for Underactuated USVs with Prescribed Performance. Journal of Marine Science and Engineering, 13(3), 480. https://doi.org/10.3390/jmse13030480




