Surface Wave Effects on Storm Surge: A Case Study of Typhoon Doksuri (2023)
Abstract
1. Introduction
2. Numerical Experiments
2.1. Data
2.2. Model Setup
3. Results
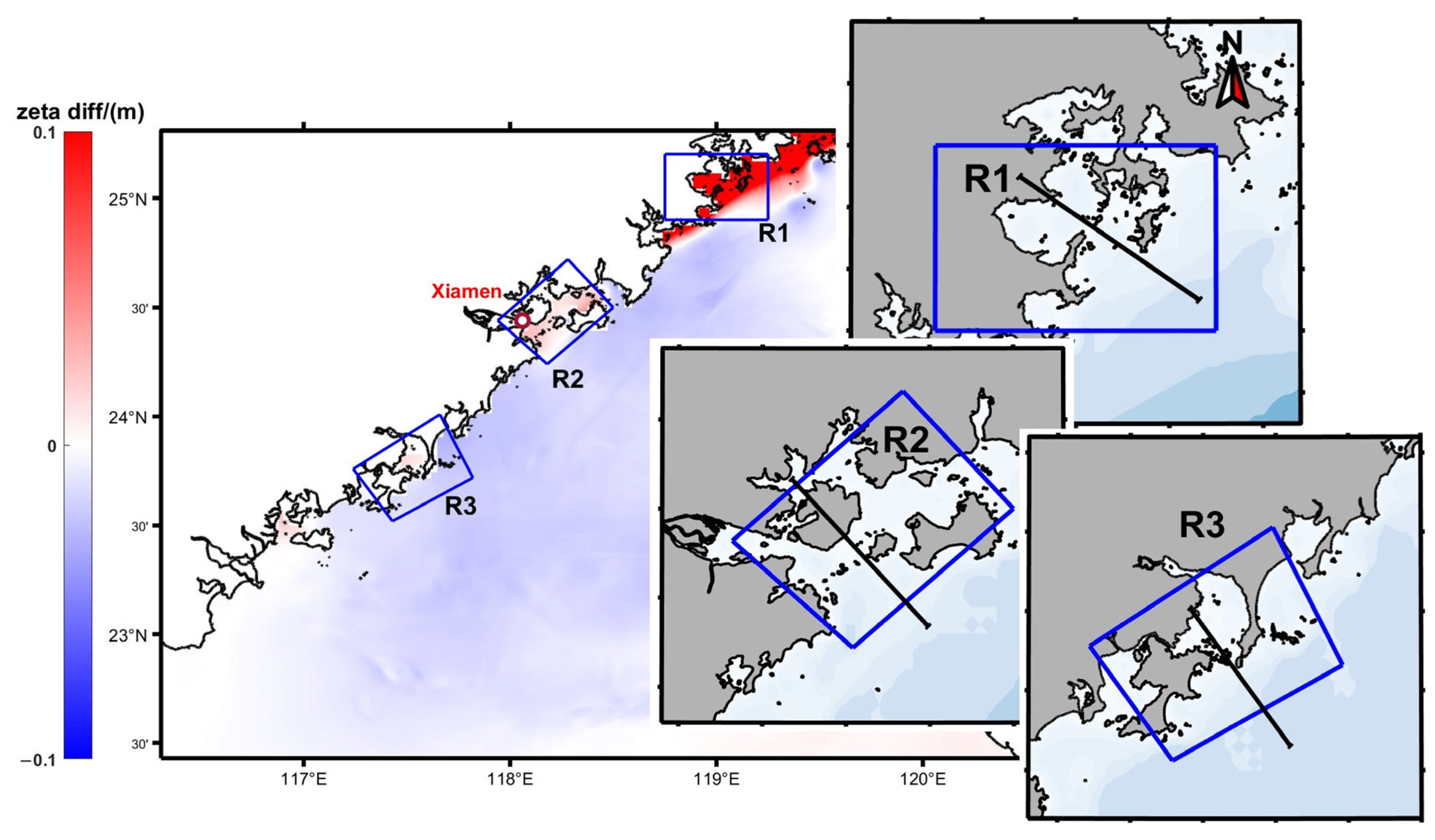
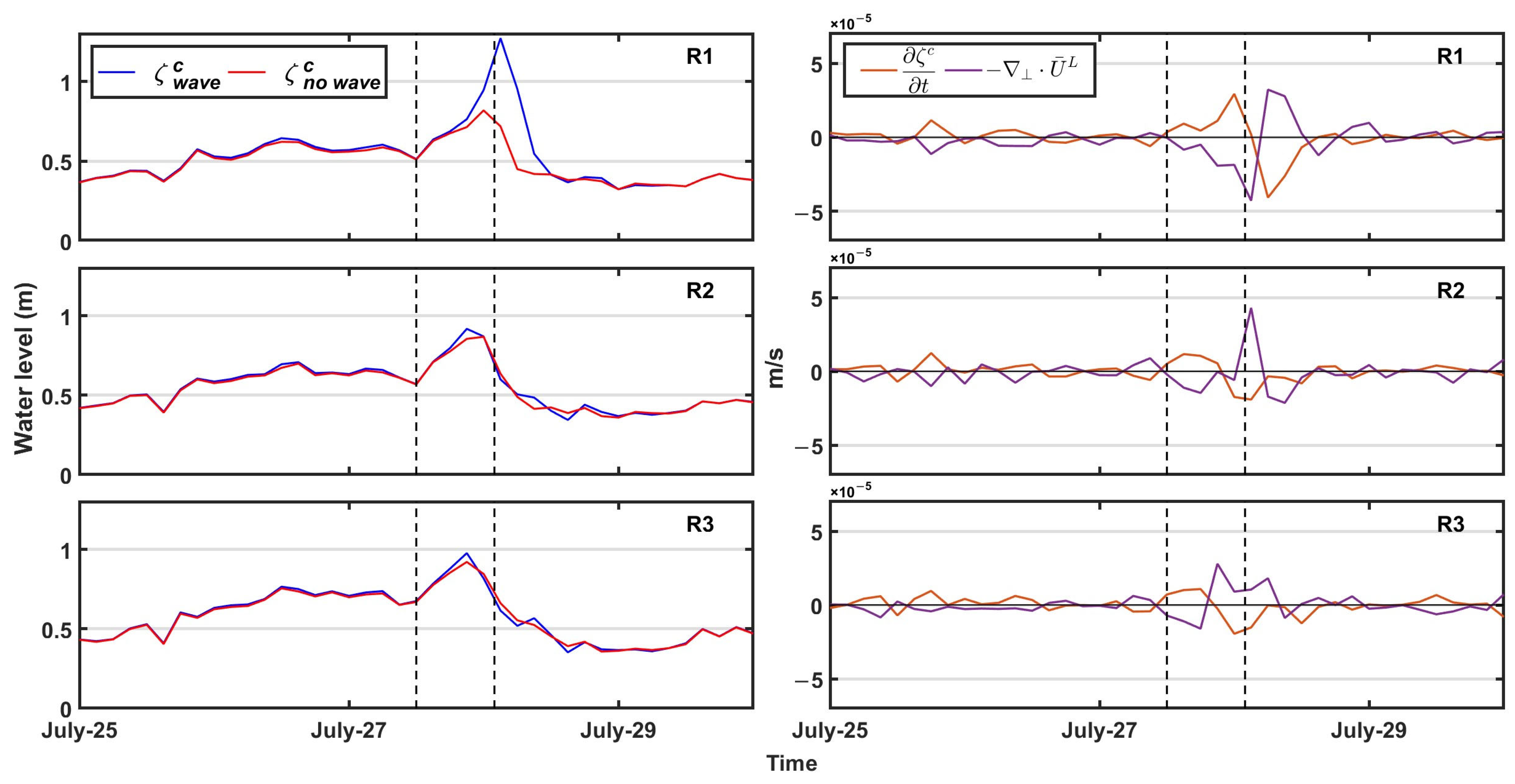
3.1. Nearshore Water Level Change
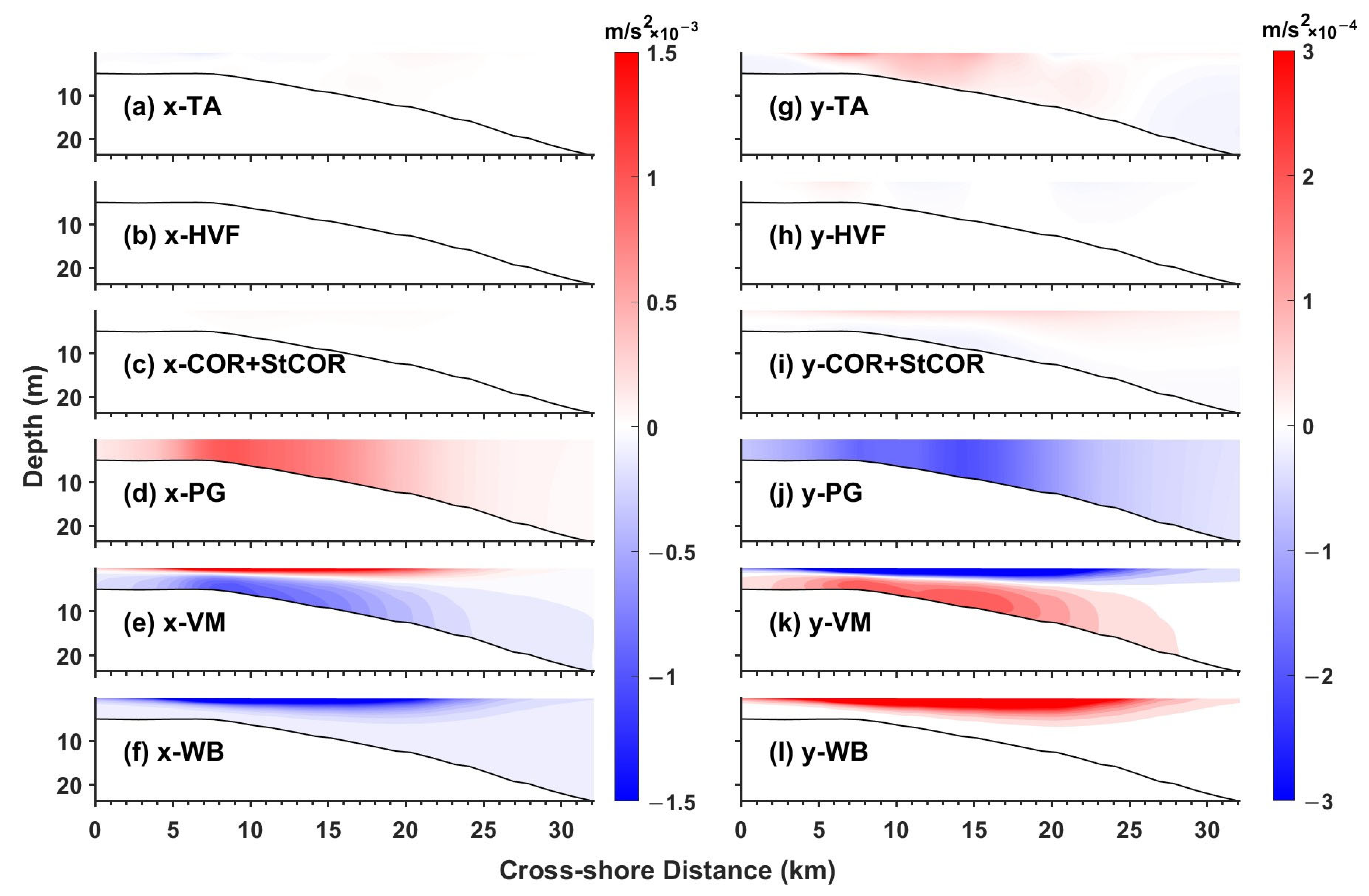
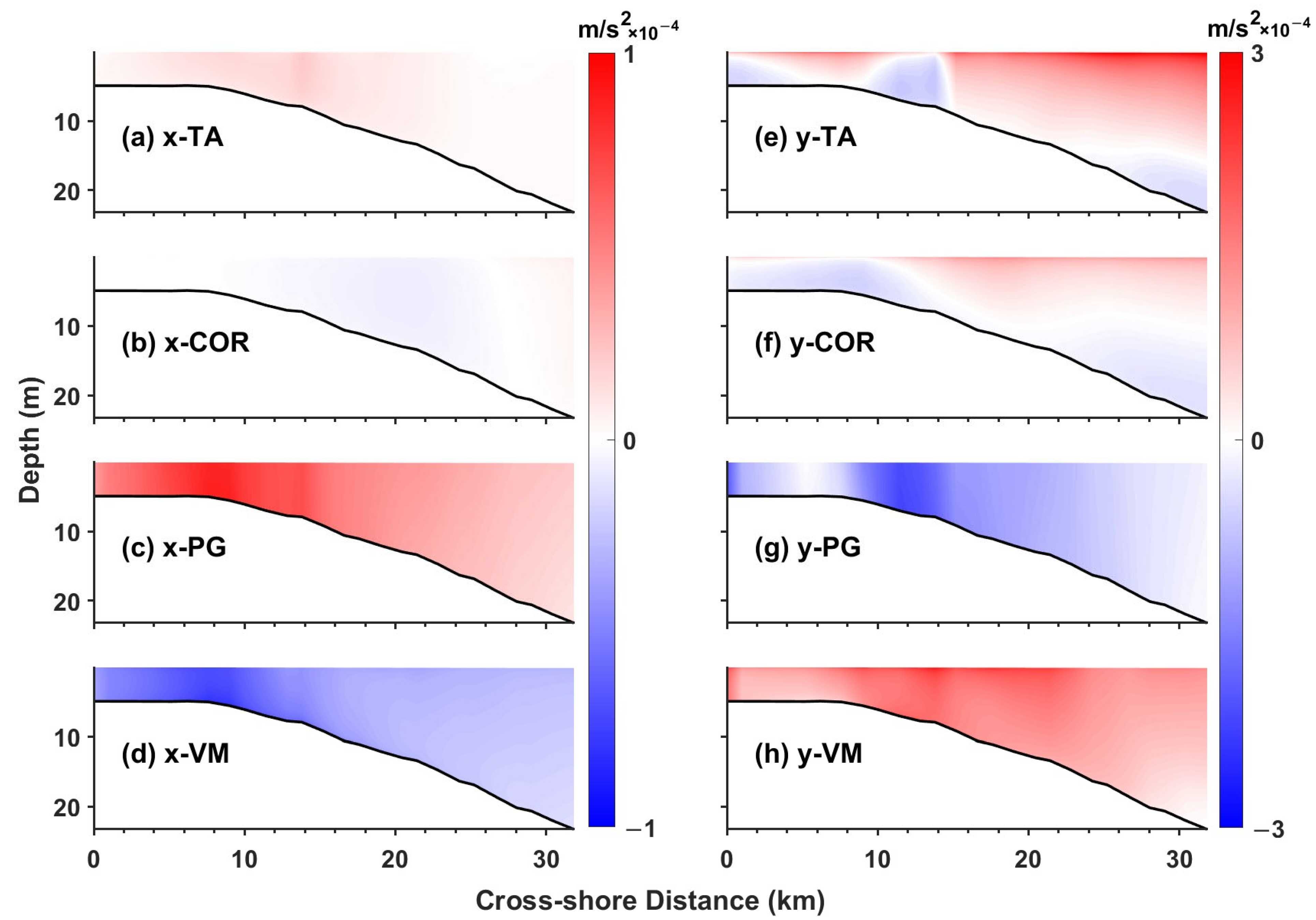
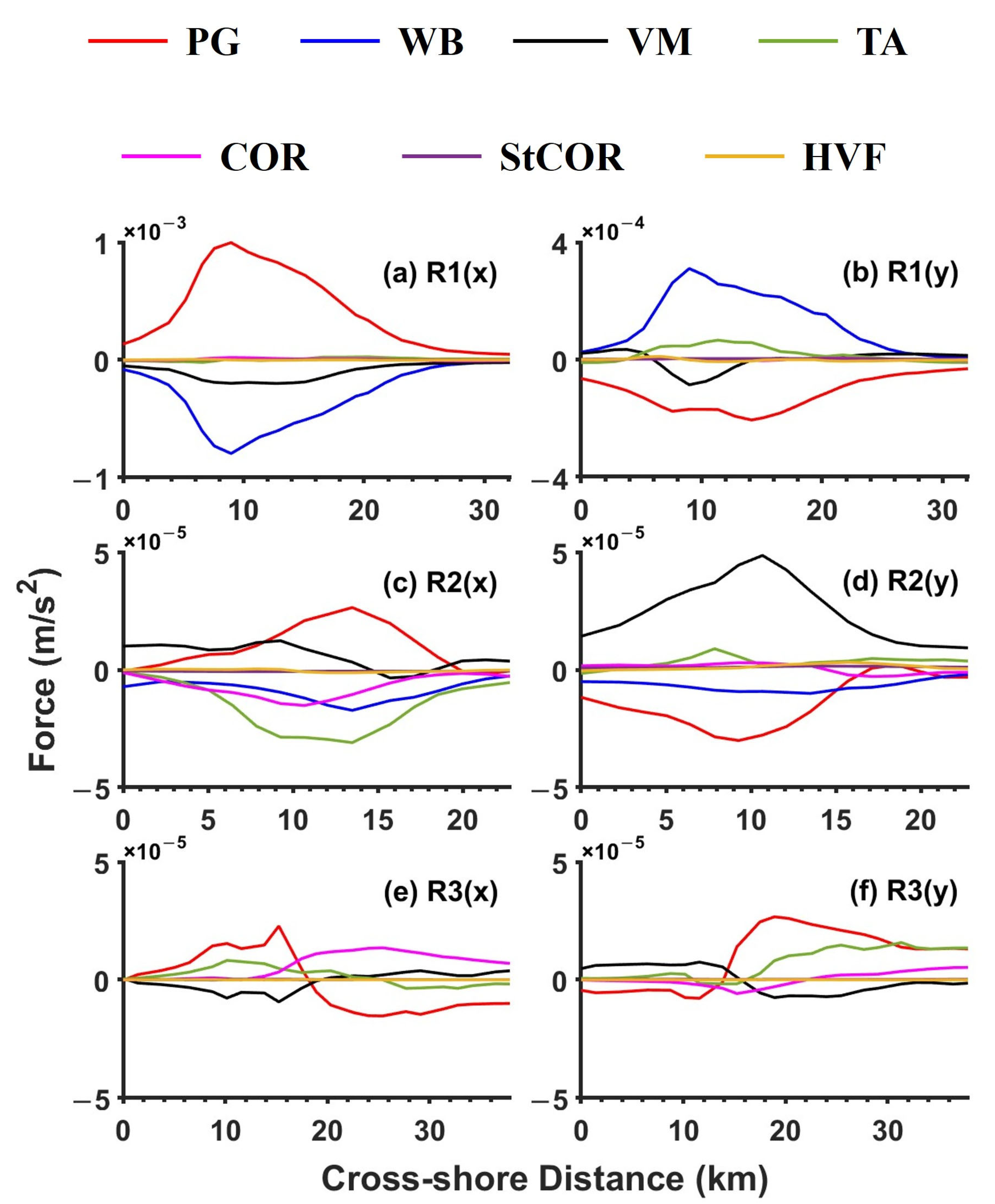
3.2. Momentum Balance in the Nearshore Shallow Water
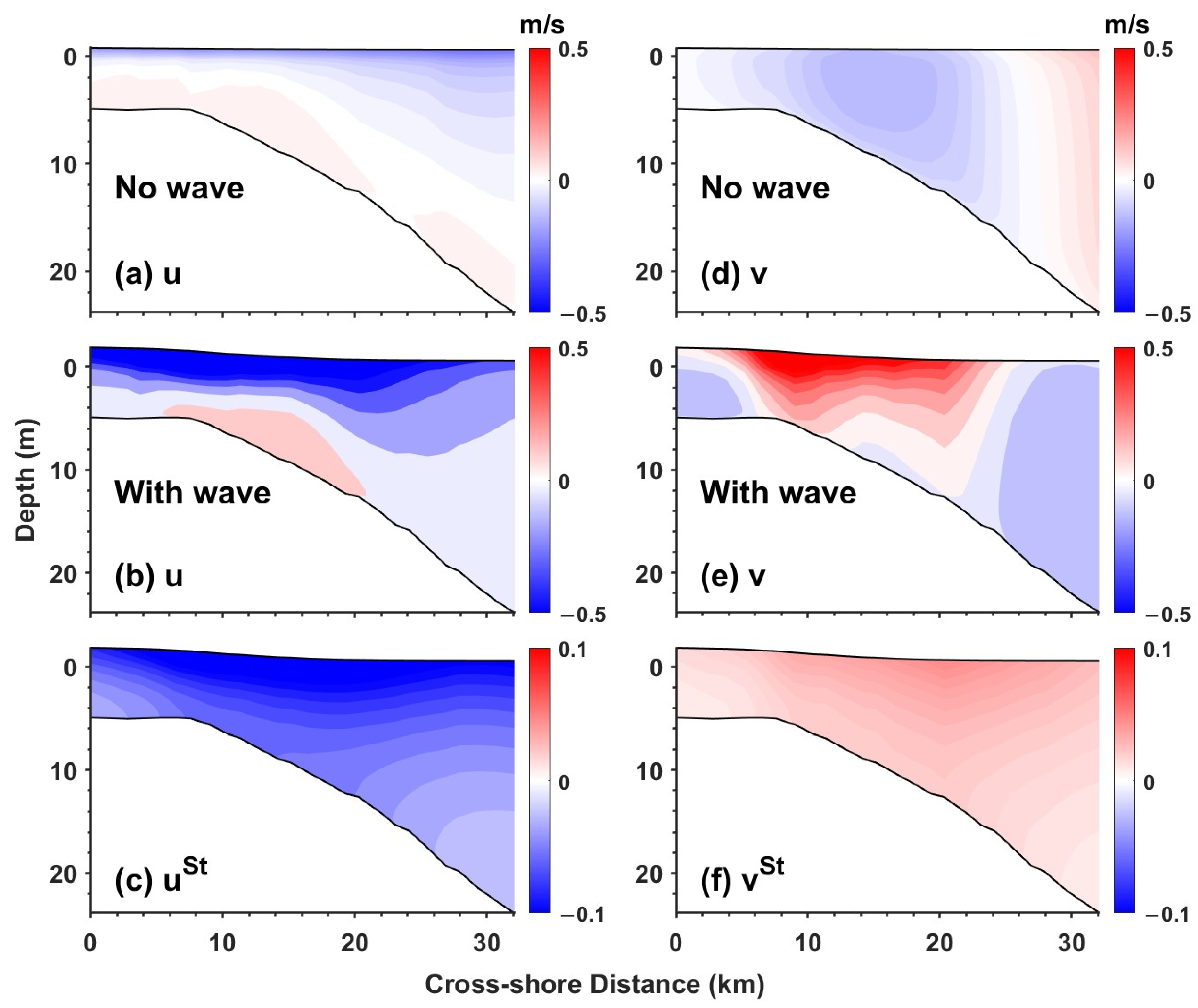
3.3. Nearshore Flow Structures
4. Discussion and Conclusions
- Previous studies have shown that ERA5 reanalysis data tend to underestimate the intensity of tropical cyclones [43,44,45], which directly leads to simulated water levels being lower than the observed maximum surge. This limitation may affect the accuracy of storm surge simulations in the present study.
- In this study, we used the spectrum peak values from CMEMS data to calculate wave–current interactions. This monochromatic assumption is commonly employed to obtain quick, rough estimates of wave characteristics and their effects in shallow and deep water conditions and is often applied in ocean engineering and coastal engineering [46]. However, it is important to highlight the limitations of this modeling approach; that is, the simplification of wave characteristics prevents the model from capturing the second-order nonlinear properties of surface gravity waves. In contrast, considering the full wave spectrum provides crucial information about the distribution of energy across a broad range of frequencies and directions. This is essential for accurately modeling wave–current interactions, such as Langmuir circulation and rip currents [47]. Therefore, coupling the wave–current model with a finer grid resolution would better capture nearshore wave spectrum dynamics and improve the representation of wave-induced contributions to storm surge processes.
- Other non-conservative wave effects, such as wave streaming and wave-enhanced bottom stress, were not considered in this study. For example, previous studies showed that wave streaming enhances onshore transport near the bottom, which can potentially affect the nearshore water level [26]. In addition, wave-enhanced bottom stress is also a critical factor influencing storm surge, particularly in shallow water depths [17,48].
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GB/T 30746-2014; Technical Directives for the Disaster Prevention and Mitigation of Storm Surge. Chinese National Standard: Beijing, China, 2014.
- Harris, D.L. Characteristics of the Hurricane Storm Surge; Department of Commerce, Weather Bureau: Washington, DC, USA, 1963. [Google Scholar]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L.J.C.D. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 47, 3171–3190. [Google Scholar] [CrossRef]
- von Storch, H.; Woth, K. Storm surges: Perspectives and options. Sustain. Sci. 2008, 3, 33–43. [Google Scholar] [CrossRef]
- Kim, S.Y.; Yasuda, T.; Mase, H. Numerical analysis of effects of tidal variations on storm surges and waves. Appl. Ocean. Res. 2008, 30, 311–322. [Google Scholar] [CrossRef]
- García-León, M.; Sotillo, M.G.; Mestres, M.; Espino, M.; Fanjul, E.Á. Improving Operational Ocean Models for the Spanish Port Authorities: Assessment of the SAMOA Coastal Forecasting Service Upgrades. J. Mar. Sci. Eng. 2022, 10, 149. [Google Scholar] [CrossRef]
- Sotillo, M.G.; Mourre, B.; Mestres, M.; Lorente, P.; Aznar, R.; García-León, M.; Liste, M.; Santana, A.; Espino, M.; Álvarez, E. Evaluation of the Operational CMEMS and Coastal Downstream Ocean Forecasting Services During the Storm Gloria (January 2020). Front. Mar. Sci. 2021, 8, 644525. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R. Radiation stresses in water waves; A physical discussion, with applications. In Deep Sea Research and Oceanographic Abstracts; Elsevier: Amsterdam, The Netherlands, 1964; pp. 529–562. [Google Scholar]
- McWilliams, J.C.; Restrepo, J.M.; Lane, E.M. An asymptotic theory for the interaction of waves and currents in coastal waters. J. Fluid Mech. 2004, 511, 135–178. [Google Scholar] [CrossRef]
- Mellor, G. The Three-Dimensional Current and Surface Wave Equations. J. Phys. Oceanogr. 2003, 33, 1978–1989. [Google Scholar] [CrossRef]
- Uchiyama, Y.; McWilliams, J.C.; Shchepetkin, A.F. Wave–current interaction in an oceanic circulation model with a vortex-force formalism: Application to the surf zone. Ocean. Model. 2010, 34, 16–35. [Google Scholar] [CrossRef]
- Xie, L.; Liu, H.; Peng, M. The effect of wave–current interactions on the storm surge and inundation in Charleston Harbor during Hurricane Hugo 1989. Ocean. Model. 2008, 20, 252–269. [Google Scholar] [CrossRef]
- Beardsley, R.C.; Chen, C.; Xu, Q. Coastal flooding in Scituate (MA): A FVCOM study of the 27 December 2010 nor’easter. J. Geophys. Res. Ocean. 2013, 118, 6030–6045. [Google Scholar] [CrossRef]
- Rong, Z.; Hetland, R.D.; Zhang, W.; Zhang, X. Current–wave interaction in the Mississippi–Atchafalaya river plume on the Texas–Louisiana shelf. Ocean Model. 2014, 84, 67–83. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, C.; Beardsley, R.C.; Xu, Q.; Qi, J.; Lin, H. Impact of current-wave interaction on storm surge simulation: A case study for Hurricane Bob. J. Geophys. Res. Ocean. 2013, 118, 2685–2701. [Google Scholar] [CrossRef]
- Lavaud, L.; Bertin, X.; Martins, K.; Arnaud, G.; Bouin, M.-N. The contribution of short-wave breaking to storm surges: The case Klaus in the Southern Bay of Biscay. Ocean Model. 2020, 156, 101710. [Google Scholar] [CrossRef]
- Mo, D.; Hu, P.; Li, J.; Hou, Y.; Li, S. Effect of Wave-Dependent Mechanisms on Storm Surge and Current Simulation during Three Extreme Weather Systems. J. Phys. Oceanogr. 2024, 54, 1519–1543. [Google Scholar] [CrossRef]
- Feng, J.; Lu, X.; Yu, H.; Zhang, W.; Ying, M.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Leibovich, S. On wave-current interaction theories of Langmuir circulations. J. Fluid Mech. 1980, 99, 715–724. [Google Scholar] [CrossRef]
- Hasselmann, K. On the mass and momentum transfer between short gravity waves and larger-scale motions. J. Fluid Mech. 1971, 50, 189–205. [Google Scholar] [CrossRef]
- Wang, P.; McWilliams, J.C.; Wang, D.; Yi, D.L. Conservative Surface Wave Effects on a Wind-Driven Coastal Upwelling System. J. Phys. Oceanogr. 2023, 53, 37–55. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; MacMahan, J.H.; Reniers, A.J.; Nelko, V.J. Rip currents. Annu. Rev. Fluid Mech. 2011, 43, 551–581. [Google Scholar] [CrossRef]
- MacMahan, J.H.; Thornton, E.B.; Reniers, A.J.H.M. Rip current review. Coast. Eng. 2006, 53, 191–208. [Google Scholar] [CrossRef]
- Uchiyama, Y.; McWilliams, J.C.; Akan, C. Three-dimensional transient rip currents: Bathymetric excitation of low-frequency intrinsic variability. J. Geophys. Res. Ocean. 2017, 122, 5826–5849. [Google Scholar] [CrossRef]
- Wang, P.; McWilliams, J.C.; Uchiyama, Y.; Chekroun, M.D.; Yi, D.L. Effects of Wave Streaming and Wave Variations on Nearshore Wave-Driven Circulation. J. Phys. Oceanogr. 2020, 50, 3025–3041. [Google Scholar] [CrossRef]
- Wang, P.; McWilliams, J.C.; Uchiyama, Y. A Nearshore Oceanic Front Induced By Wave Streaming. J. Phys. Oceanogr. 2021, 51, 1967–1984. [Google Scholar] [CrossRef]
- Yu, X.; Pan, W.; Zheng, X.; Zhou, S.; Tao, X. Effects of wave-current interaction on storm surge in the Taiwan Strait: Insights from Typhoon Morakot. Cont. Shelf Res. 2017, 146, 47–57. [Google Scholar] [CrossRef]
- Romero, L.; Hypolite, D.; McWilliams, J.C. Representing wave effects on currents. Ocean Model. 2021, 167, 101873. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Reppucci, A.; Alvarez Fanjul, E.; Aouf, L.; Behrens, A.; Belmonte, M.; Bentamy, A.; Bertino, L.; Brando, V.E.; Kreiner, M.B.; et al. From Observation to Information and Users: The Copernicus Marine Service Perspective. Front. Mar. Sci. 2019, 6, 00234. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) Modeling System. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Kumar, N.; Voulgaris, G.; Warner, J.C.; Olabarrieta, M. Implementation of the vortex force formalism in the coupled ocean-atmosphere-wave-sediment transport (COAWST) modeling system for inner shelf and surf zone applications. Ocean Model. 2012, 47, 65–95. [Google Scholar] [CrossRef]
- Jenkins, A.D. The use of a wave prediction model for driving a near-surface current model. Dtsch. Hydrogr. Z. 1989, 42, 133–149. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R.T. Transformation of wave height distribution. J. Geophys. Res. Ocean. 1983, 88, 5925–5938. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R.T. Surf Zone Longshore Currents and Random Waves: Field Data and Models. J. Phys. Oceanogr. 1986, 16, 1165–1178. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.; Duan, Y.; Wang, H.; Sun, Z.; Xu, Y. Observational fine-scale evolutionary characteristics of concentric eyewall Typhoon Doksuri (2023). Atmos. Res. 2024, 310, 107630. [Google Scholar] [CrossRef]
- Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Alymov, V.; Paramygin, V.A. Simulation of storm surge, wave, currents, and inundation in the Outer Banks and Chesapeake Bay during Hurricane Isabel in 2003: The importance of waves. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Dulac, W.; Cattiaux, J.; Chauvin, F.; Bourdin, S.; Fromang, S. Assessing the representation of tropical cyclones in ERA5 with the CNRM tracker. Clim. Dyn. 2023, 62, 223–238. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Bourdin, S.; Vrac, M.; Thao, S.; Riboldi, J.; Fromang, S.; Yiou, P. Correcting biases in tropical cyclone intensities in low-resolution datasets using dynamical systems metrics. Clim. Dyn. 2023, 61, 4393–4409. [Google Scholar] [CrossRef]
- Slocum, C.J.; Razin, M.N.; Knaff, J.A.; Stow, J.P. Does ERA5 Mark a New Era for Resolving the Tropical Cyclone Environment? J. Clim. 2022, 35, 7147–7164. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; Volume 2. [Google Scholar]
- Craik, A.D.D.; Leibovich, S. A rational model for Langmuir circulations. J. Fluid Mech. 1976, 73, 401–426. [Google Scholar] [CrossRef]
- Bertin, X.; Li, K.; Roland, A.; Bidlot, J.-R. The contribution of short-waves in storm surges: Two case studies in the Bay of Biscay. Cont. Shelf Res. 2015, 96, 1–15. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Wang, P. Surface Wave Effects on Storm Surge: A Case Study of Typhoon Doksuri (2023). J. Mar. Sci. Eng. 2025, 13, 478. https://doi.org/10.3390/jmse13030478
Peng Z, Wang P. Surface Wave Effects on Storm Surge: A Case Study of Typhoon Doksuri (2023). Journal of Marine Science and Engineering. 2025; 13(3):478. https://doi.org/10.3390/jmse13030478
Chicago/Turabian StylePeng, Zhiyong, and Peng Wang. 2025. "Surface Wave Effects on Storm Surge: A Case Study of Typhoon Doksuri (2023)" Journal of Marine Science and Engineering 13, no. 3: 478. https://doi.org/10.3390/jmse13030478
APA StylePeng, Z., & Wang, P. (2025). Surface Wave Effects on Storm Surge: A Case Study of Typhoon Doksuri (2023). Journal of Marine Science and Engineering, 13(3), 478. https://doi.org/10.3390/jmse13030478





