1. Introduction
During navigation, a ship is primarily influenced by three types of resistance: frictional resistance, viscous pressure resistance, and wave-making resistance. Injecting air beneath the hull during transit creates a uniform and stable gas–liquid two-phase flow. This approach effectively reduces the ship’s resistance by leveraging the differences in density and viscosity between water and air. Air lubrication drag reduction technology has long been of interest to researchers [
1].
As illustrated in
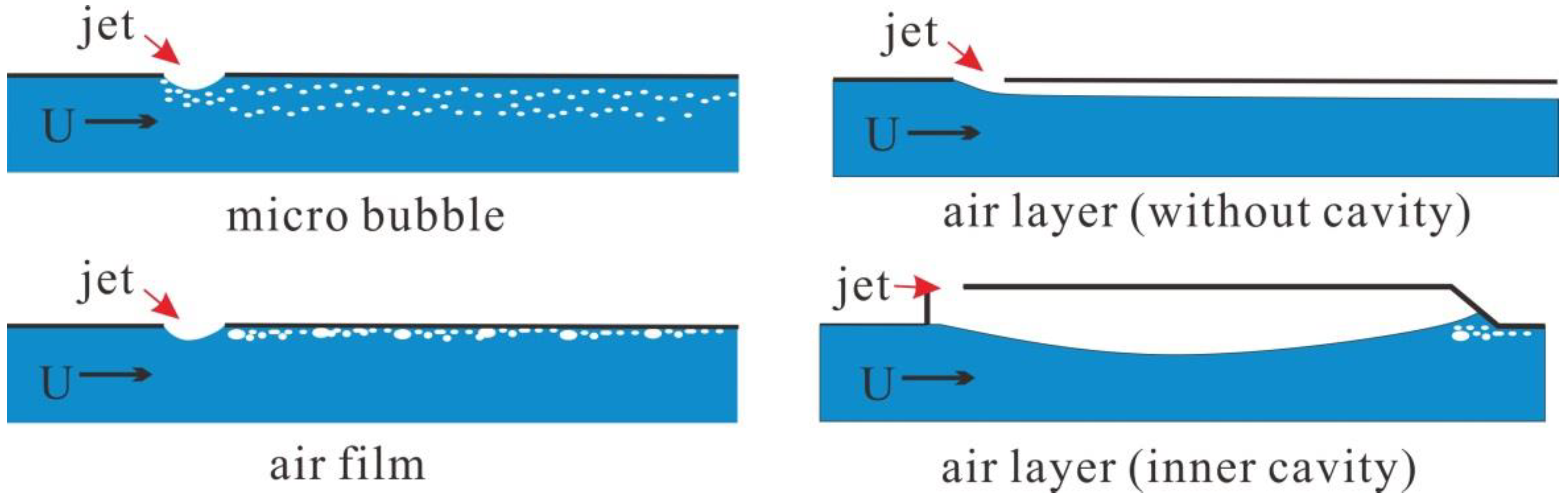
Figure 1, the methods of air lubrication drag reduction can be categorized into two main types based on their mechanisms and gas distribution forms: bubble drag reduction (BDR) and air-layer drag reduction (ALDR). BDR encompasses various techniques, including microbubble drag reduction, bubble drag reduction, transitional air-layer drag reduction, and air curtain drag reduction. A defining characteristic of BDR is the mixing of gas and liquid without a distinct interface, which typically requires minimal modifications to the hydrodynamic shape of the hull. The majority of vessels using the BDR technology do not need to set up extra cavity structures.
Elbing et al. [
2] investigated the transition relationships between bubble, transitional, and air-layer drag reductions, revealing that at higher airflow rates, the drag reduction mechanism shifts to ALDR, which offers greater efficiency.
A hull bottom, designed with a proper cavity, can facilitate the development of a stable air layer. Typically, air cavities are introduced at the bottom of the hull to facilitate the generation of an air layer. In contrast, the sidewalls of these cavities help prevent airflow from escaping along the sides of the hull, thereby maintaining the stability of the air layer. This method, which employs air cavities for drag reduction in the air layer, is referred to by some researchers as partial cavity drag reduction (PCDR) or air cavity drag reduction (ACDR) [
3,
4]. Implementing this approach usually necessitates modifying the hull shape by adding cavity structures at its base.
As early as 1968, Butuzov [
5] conducted theoretical studies on flat-plate air cavities. After 2000, many researchers began investigating the application of air-layer drag reduction (ALDR) technology for high-speed hulls. Matveev et al. [
6,
7] conducted experimental studies on air injection drag reduction and cavity length using a simplified flat-bottom ship model measuring 0.56 m long and featuring longitudinal grooves on its bottom. Their findings showed good agreement between the linear potential flow theoretical model and experimental results, indicating that hull geometry changes significantly influence the air-layer distribution. In 2022, Matveev [
8] carried out research on the air cavity system of a planing hull with two steps in the bottom. Computational fluid dynamics was used to model an air cavity system. Simulations of the modified hull at various speeds and center of gravity positions were conducted, obtaining data on resistance, trim, heave, and air cavity shapes, and a favorable loading condition was identified. Shallow water simulation studies showed that in the steady state, the performance drops significantly near the critical speed, while the performance improves in the supercritical regime. Fang et al. [
9] conducted a study on an air cavity ship derived from a 3 m long and 0.85 m wide planing hull, employing both CFD methods and experimental approaches. They analyzed how the ventilation rate and heel angle affected its performance. As the ventilation rate increased, the air cavity changed from meniscus growth to the stable, bottleneck type. Excessive ventilation changed the tail leakage opening size, not air coverage. Differences in air coverage and bottom pressure between the two types of air cavities influenced the ship’s trim, sinkage, and heeling stability, and the air cavity negatively affected heeling stability.
Vincenzo Sorrentino et al. [
10] conducted a study on the application of the air lubrication system (ALS) to the planing hull equipped with the double interceptor system (DIS). They compared the situation without ventilation, analyzed the effectiveness of air lubrication on the DIS using natural and forced ventilation methods, and carried out experiments within a specific Froude number range and air flow rate range. The results showed that the ventilated DIS had better performance. The improvement of resistance using natural ventilation at low speeds was limited, and two key regions of hull resistance change under different air flow rates were identified, providing a basis for optimizing this type of hull.
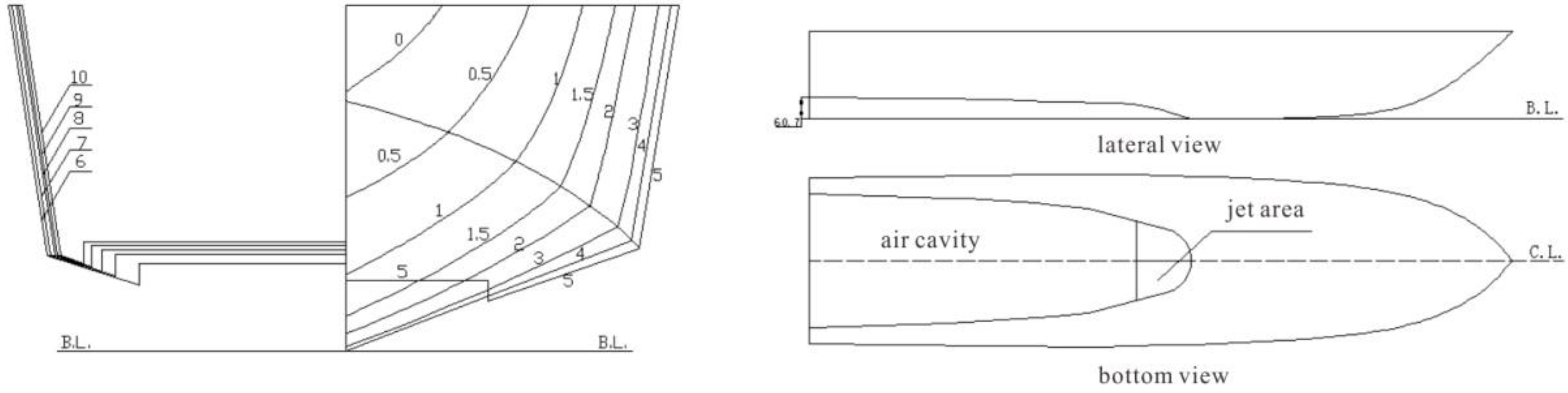
In China, Dong Wencai and Ou Yongpeng [
11,
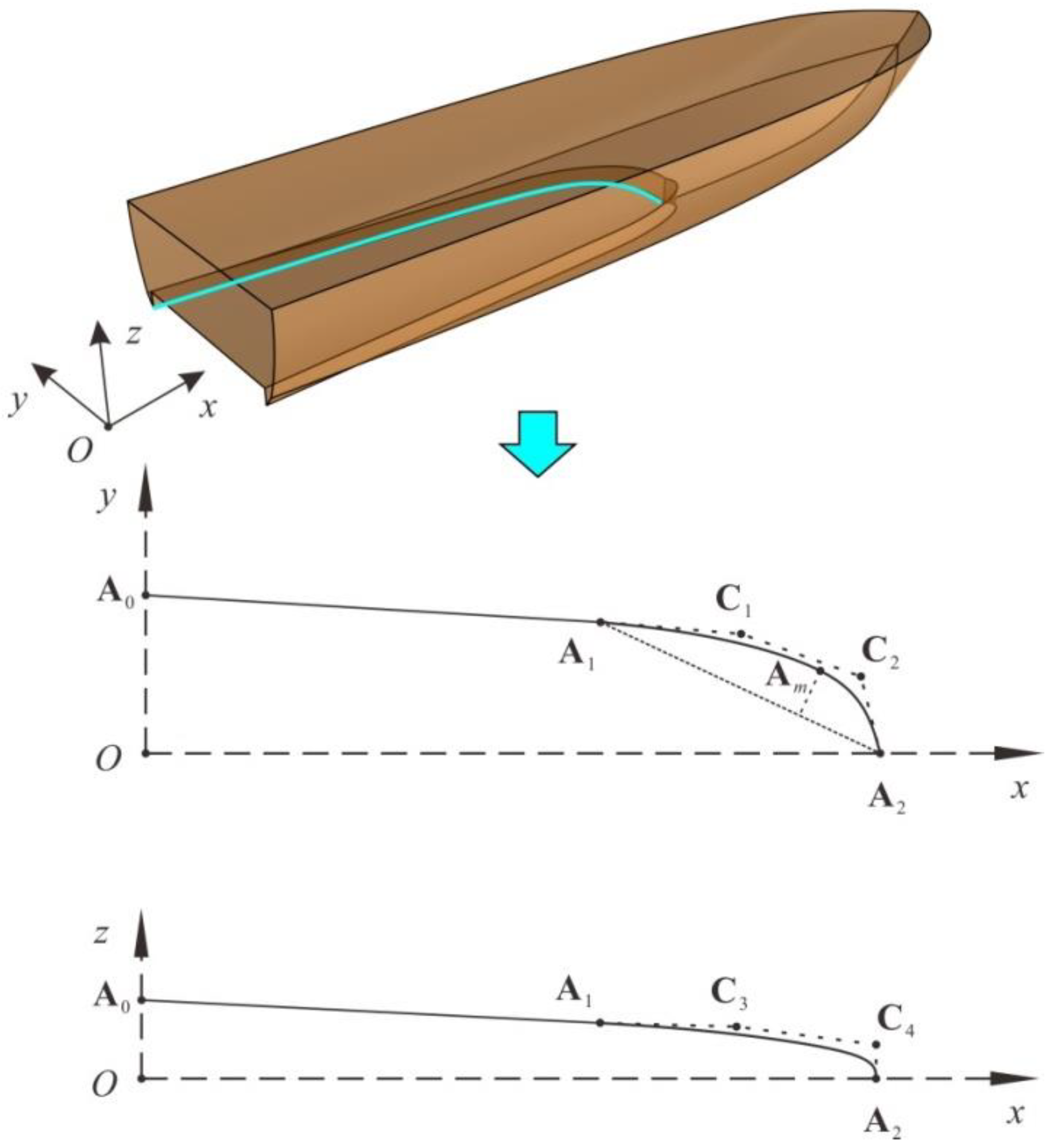
12] from the Naval University of Engineering conducted experimental studies on air injection drag reduction for a B.H-type air-lubricated planing craft under calm water and wave conditions. As illustrated in
Figure 2, the prototype vessel featured a non-stepped, deep-V planing hull designed with grooved regions extending from the midsection to the stern. The leading edge of the groove was arc-shaped when projected onto the horizontal plane, with the groove width gradually widening toward the stern. The groove bottom comprised either planar or folded planar surfaces, forming a developable surface. Their experiments examined the effects of speed, air injection rate, and waves on the hydrodynamic performance of the hull. Comparing two grooved hull designs with different groove depth transitions near the stepped region revealed that groove depth significantly affected navigation performance without air injection. The study concluded that the parameterized design of an air-lubricated planing craft is a promising and impactful avenue for future research in ALDR for planing vessels.
For low-speed, full-form ships, introducing localized air cavity structures generally has minimal impact on the navigation attitude of the vessel. Therefore, when implementing ALDR technology in these ships, the design and optimization of the air cavity structure can often be conducted independently. In contrast, adding air cavities in a planing craft significantly affects the flow field at the bottom of the hull. Additionally, since the air cavity substantially reduces the planing surface that provides dynamic lift, the craft’s running attitude is inevitably altered. Given the strong coupling effect between the air cavity and the hull, designing an air-lubricated planing craft from a hydrodynamic performance perspective requires not only the localized optimization of the air cavity structure but also a coordinated adjustment of the baseline planing hull’s lines based on air cavity parameters. Therefore, a holistic optimization approach that concurrently considers the design parameters of the air cavity and the planing hull is likely to enhance the overall optimal hydrodynamic performance of the air-lubricated planing craft.
With advancements in computational and CFD (computational fluid dynamics) technologies, integrating CFD-based numerical evaluation techniques with optimization theory and parameterized hull design methods has led to a new paradigm in hull design known as simulation-based design (SBD) [
13]. This approach has been widely applied in the field of ship design. For air-lubricated planing hulls, SBD facilitates the exploration and optimization of the design space for vessel configurations through optimization techniques and geometric reconstruction methods, ultimately resulting in hydrodynamically optimal hull designs that operate under specific constraints. A key aspect of the SBD approach is hull parameterization.
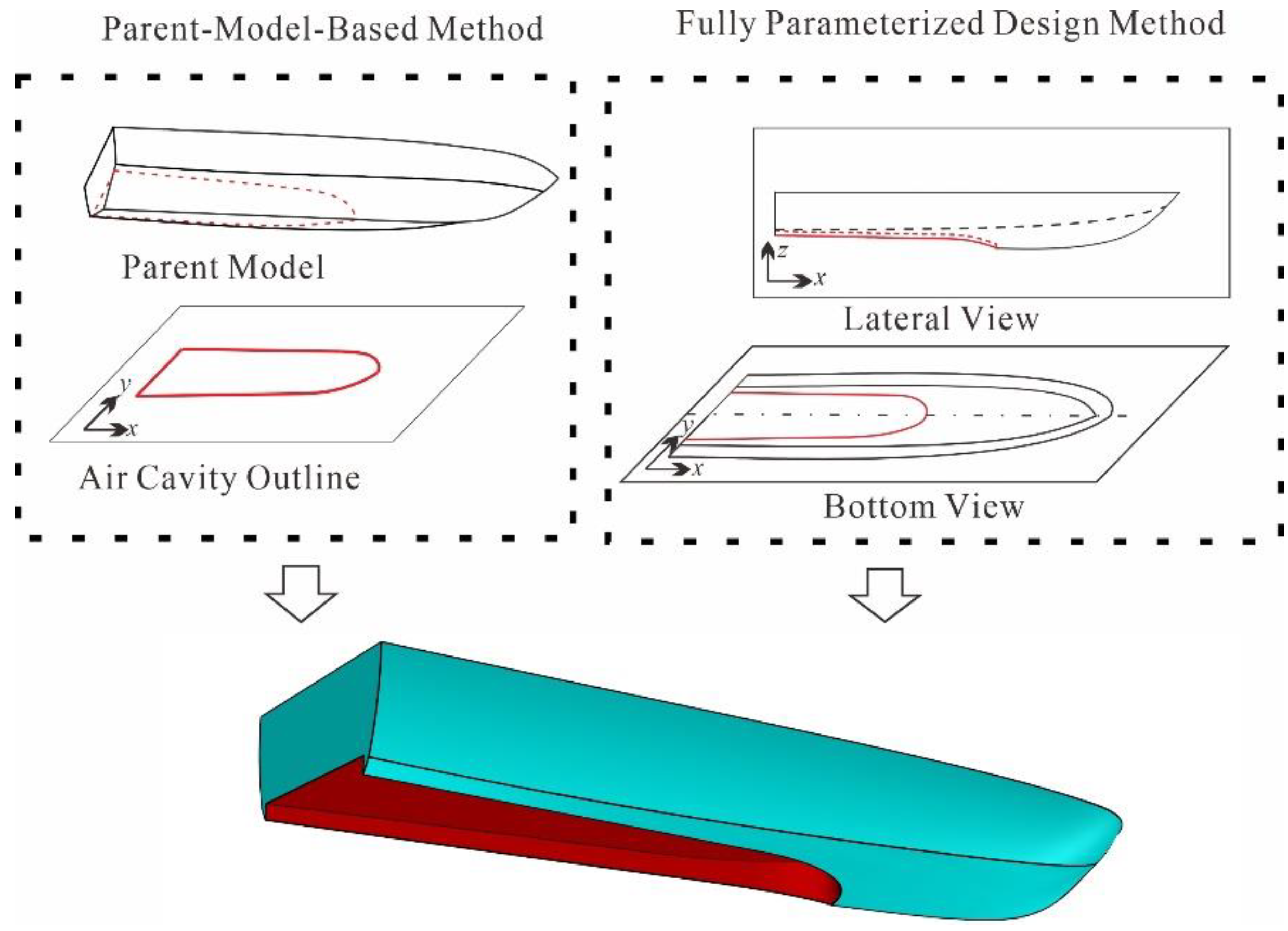
Rapid hull generation: In the SBD approach, many model samples must be computed. By developing an automated platform that integrates geometry generation, simulation, and optimization, the efficiency of the optimization process can be significantly enhanced [
14]. As illustrated in
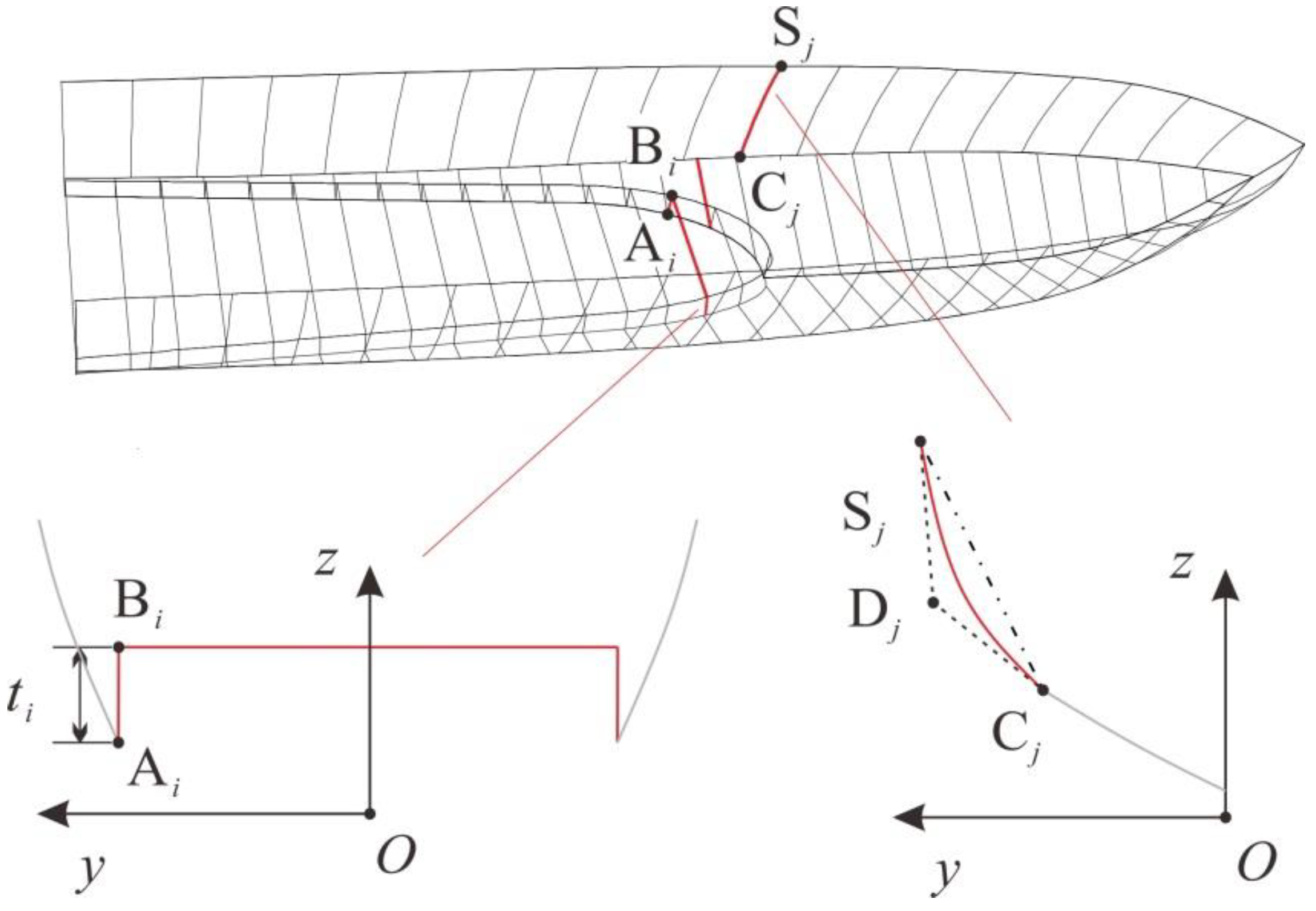
Figure 3, the majority of air cavity planing hulls are derived through cutting and modification in the horizontal projection based on the parent model. When using this approach to generate a model for SBD, due to the extensive cutting of the running surface, a portion of the original design parameters becomes redundant. On the other hand, the spatial position of the air cavity edge line cannot be completely defined by the design parameters.
A fully parameterized modeling method entails sequentially defining and constructing the geometric model of the target vessel, from points to lines to surfaces, based on predetermined design parameter constraints. Notably, this method does not rely on an initial baseline hull and achieves a comprehensive definition of the vessel’s geometric features solely through design parameters. Consequently, a fully parameterized design of air-lubricated planing hulls offers several potential advantages.
Larger design space exploration: Traditional planing hulls, particularly those modified with air cavities, typically have design parameters confined to localized features associated with these cavities. In contrast, the fully parameterized design method allows for the direct definition of multiple geometric parameters of characteristic contour lines, including air cavity edge lines, across multiple sections. This enables the exploration and creation of a broader range of planing hull designs.
In the 1970s, Kuiper pioneered employing digital methods to represent hull surfaces [
15]. From the 1990s onward, extensive research focused on parameterized hull modeling. Harries [
16,
17,
18] proposed a parameterization method by developing F-spline curves and the corresponding design software CAESES. This software enables the deformation of hull lines based on specified parameters and has been extensively used to optimize hull hydrodynamic performance. Building on NURBS theory, Zhang et al. [
19,
20] identified longitudinal characteristic curves through feature parameters. They employed optimization methods to generate sectional station lines that were subsequently utilized to construct the hull surface.
Stemming from this representation, Lu [
21] used NURBS functions to represent hull surfaces and explored critical issues in ship design. Kostas [
22] employed T-splines in the Rhino modeling environment to develop hull surfaces with bulbous bows, achieving second-order continuity across the surface except at extraordinary points. Additionally, Mancuso [
23] focused on a sailboat hull and establishing the keel and waterlines under parameter constraints while smoothing the hull surface using B-spline surfaces for parameterized modeling.
Zhou et al. [
24] introduced a NURBS-based parameterization method for surface ships by using classifications of geometric feature parameters and designing characteristic curves to parameterize the hull surface. This method applied NURBS techniques to model hull curves and surfaces parametrically, enabling geometry-driven hull deformation and the development of the corresponding software.
Paérez-Arribas [
25,
26,
27] adopted B-spline methods to parameterize various ship types, including surface ships, planing crafts, and small-waterplane-area twin hulls (SWATHs). Shahroz Khan [
28] segmented yacht hulls into three regions and parameterized each section independently to produce a diverse array of hull designs. Ghassabzadeh [
29] utilized three different geometric line types—parabolic, circular arcs, and NURBS curves—to design planing tunnel hulls.
Although substantial research has focused on the geometric parameterization of traditional hull types, studies focusing on fully parameterized modeling methods for air-lubricated planing crafts remain relatively scarce.
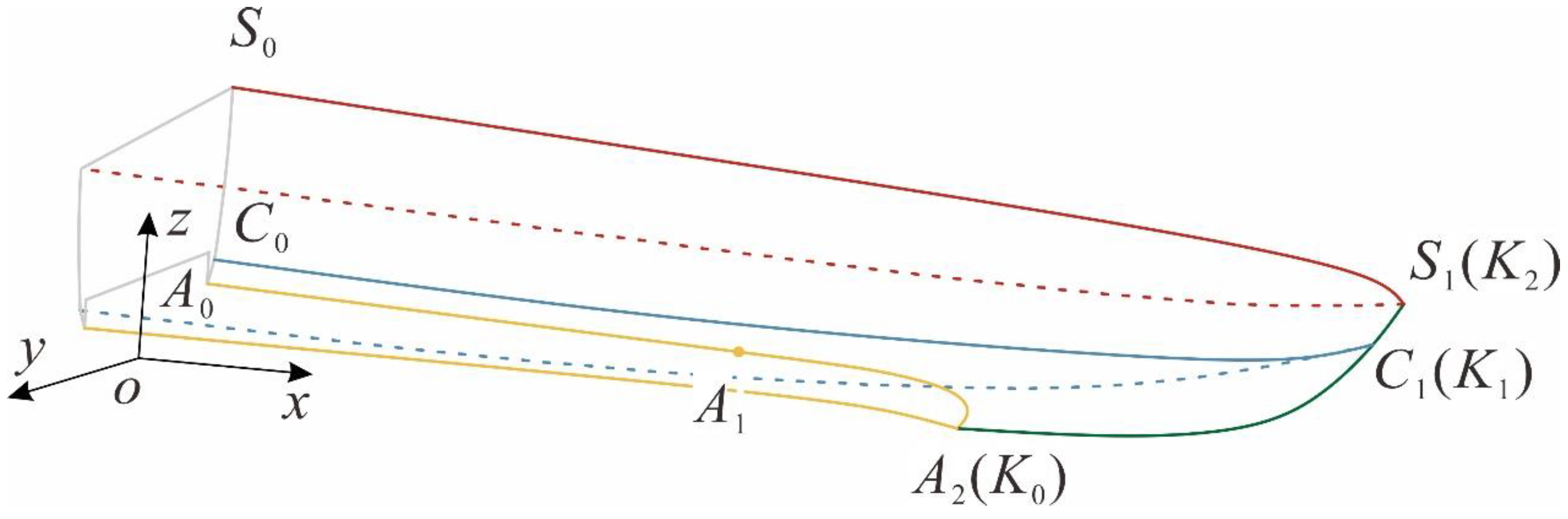
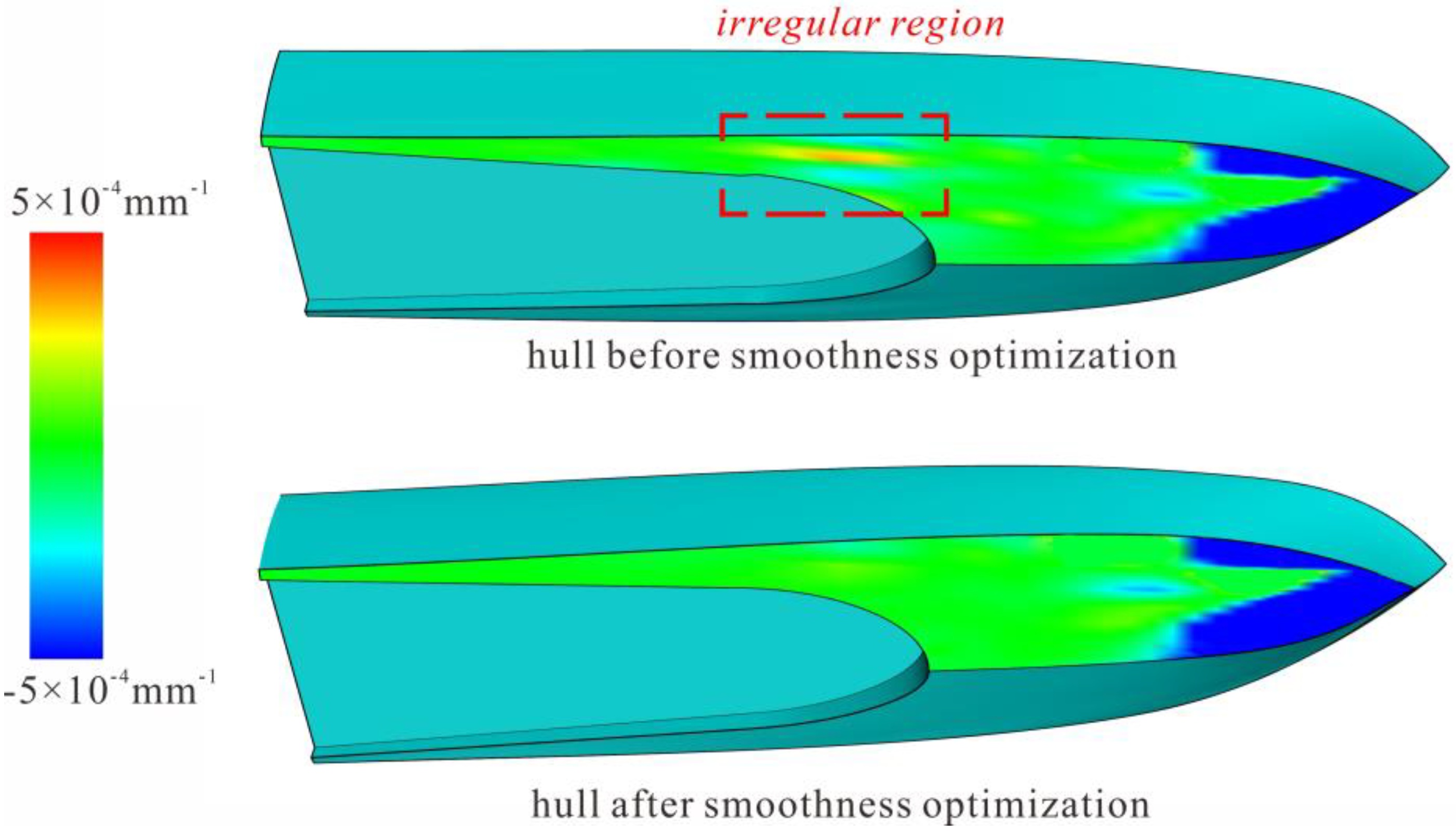
This study proposes a fully parameterized modeling method for air-lubricated planing crafts with air cavities. Unlike traditional techniques that involve adding grooves to traditional planing hulls to form an air-cavity hull, this approach defines a set of geometrically meaningful and mutually independent design parameters. These parameters are then utilized to construct the primary contour lines of the hull. Longitudinal functions associated with these design parameters generate sectional station lines for the major hull surfaces. Once the primary framework of the hull is established, an initial hull surface is fitted, followed by surface fairness optimization based on the principle of minimum strain energy.
As a demonstration, the proposed method is applied to the B.H-type air-lubricated planing hull [
11,
12] for modeling and deformation. The approach rapidly generates various smooth hull forms with distinct characteristics.
4. Modeling Example
As illustrated in
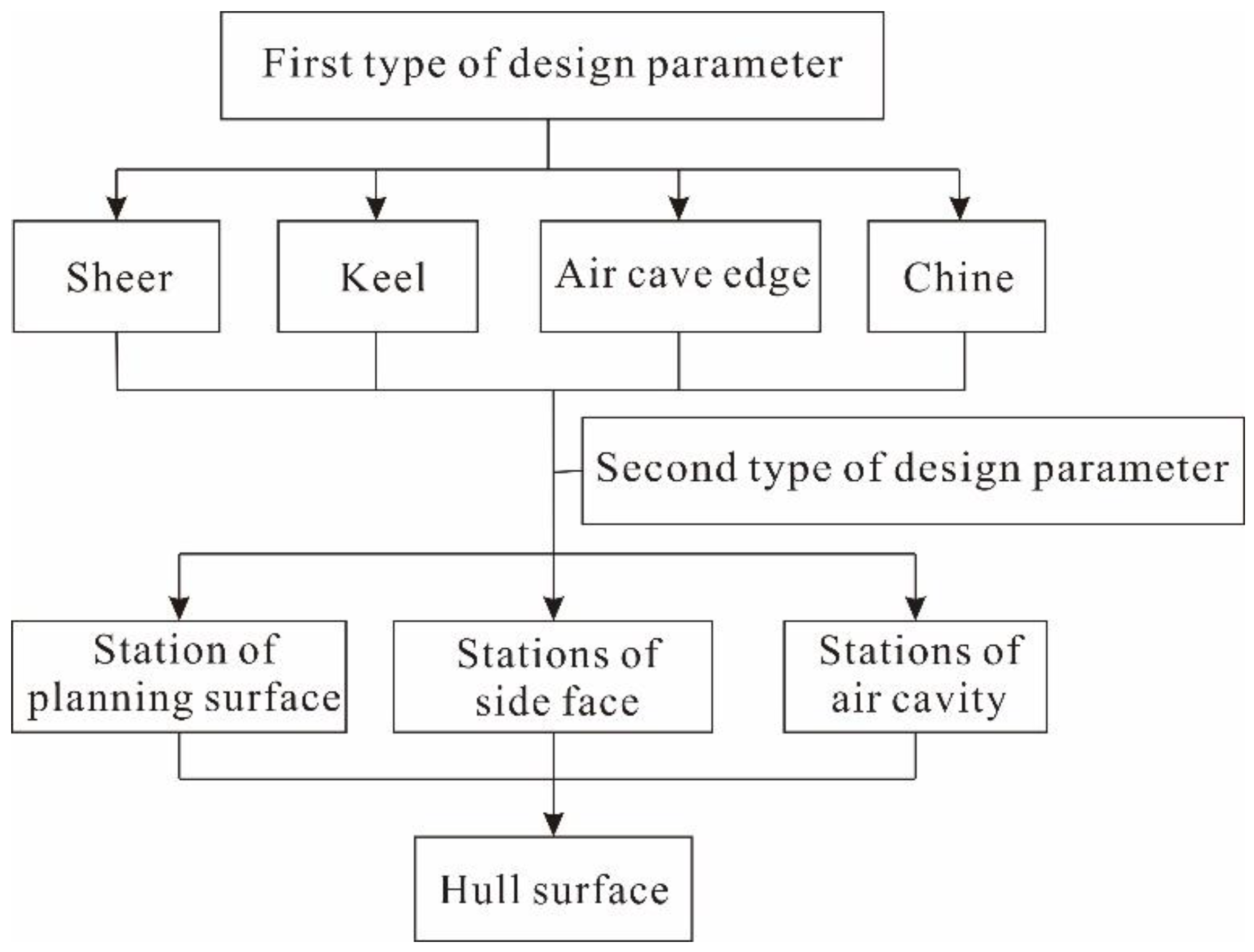
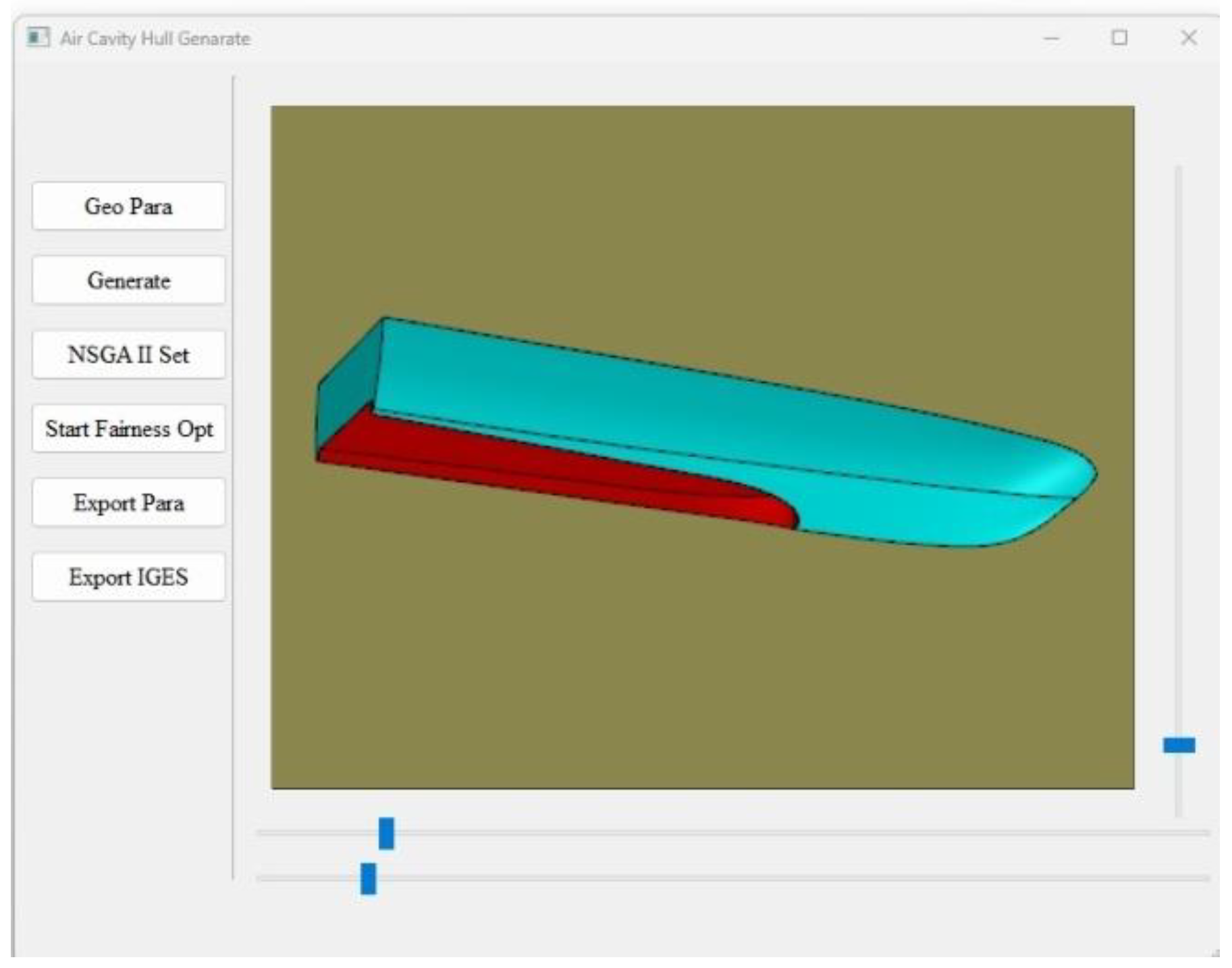
Figure 13, a modeling program for air-lubricated planing hull has been developed based on the methods described in this paper. The user interface (UI) is built on Qt, a cross-platform development framework, while the core modeling and smoothness optimization functions are implemented in backend C++ files. The program comprises two key functionalities: fully parameterized modeling and local parameter optimization.
Following the content in
Section 2, users can define the first and second types of parameters to generate the initial hull form through the point-line-surface process sequentially. According to the content in
Section 3, users can define the relevant parameter settings for the NSGA-II algorithm to achieve smoothness optimization for the hull.
The primary application of the parametric modeling of the air-lubricated planing hull lies in providing effective geometric models for the overall hull parameter optimization design, as illustrated in
Figure 14. By adjusting specific geometric parameters, hull forms with different characteristics can be generated, validating the effectiveness of the proposed modeling method.
Model 1: this model closely resembles the original hull form, with its parameter values listed in
Table 2 and
Table 3.
Model 2: This design adopts a style similar to a flat-bottomed high-speed boat. The modified parameters are outlined in
Table 6, while the other parameters remain the same as those in Model 1. The height of the air cavity edge line has been reduced, and the aft transverse deadrise angle is decreased, resulting in a lower side angle. The mid-to-aft section of the hull becomes lower and smoother, providing relatively more internal arrangement space. Additionally, the air cavity depth is smaller and uniformly distributed, which is expected to reduce the form drag resistance in non-air-lubricated conditions. Model 1 is modified into Model 2 with the parent-model-based method, as illustrated in
Figure 14. Since there are only the parameters of the horizontal projection curve of the cavity edge, the parameters in the height direction such as
HA0,
HA1, and
γA cannot be defined; that is, the parameters related to the side view of the air groove cannot be defined. On the other hand, since a considerable part of the planing surface will be cut off, many design parameters set for the original surface fail to be fully utilized. These redundant parameters not only augment the intricacy of the design process, but they also have the potential to impose unwarranted encumbrances on the optimization endeavors of the hydrodynamic performance.
Model 3: This model incorporates a longer air cavity design, with the significant modifications specified in
Table 7, while
and other parameters remain the same as those in Model 1. Compared to Models 1 and 2, the step location is moved forward, and the keel design in the forward section is steeper. This configuration is expected to create a larger stable air-layer area.