Novel Load Forecasting and Optimal Dispatching Methods Considering Demand Response for Integrated Port Energy System
Abstract
1. Introduction
2. Port Load Forecasting Based on SADSs
2.1. The Operation Model of Port Machinery
2.2. Port Load Forecasting Model
2.3. Simulation Results and Analysis
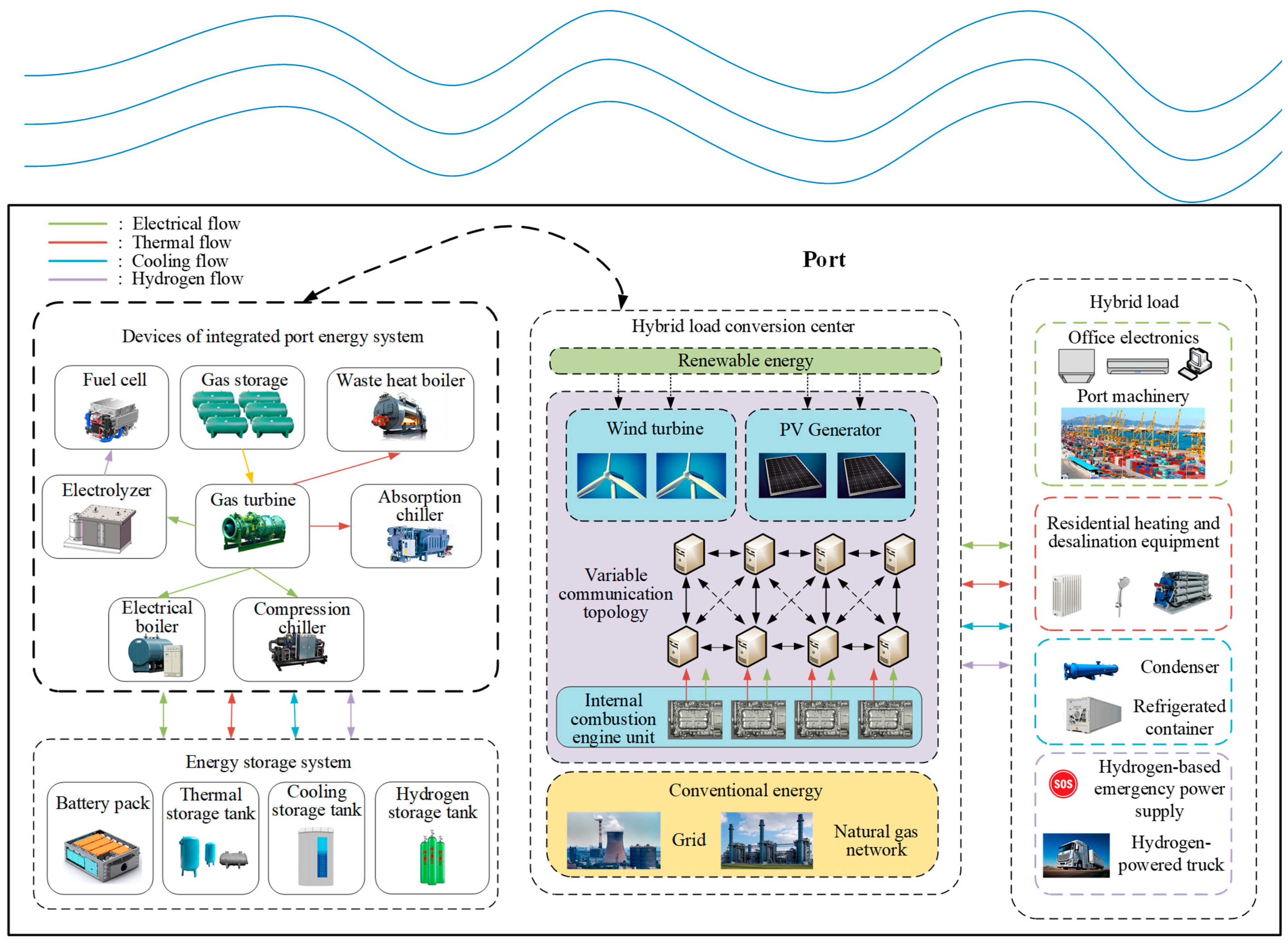
3. Structure and Optimal Dispatching Model for IPESs
3.1. The Structure of the IPES
3.2. The Equipment Model of the IPES
3.2.1. Energy Production Equipment
- (1)
- Wind turbine (WT)
- (2)
- Photovoltaic (PV) cells
3.2.2. Energy Conversion Equipment
- (1)
- Gas turbine (GT)
- (2)
- Waste heat boiler/Absorption chiller (WHB/AC)
- (3)
- Electric boiler (EB)
- (4)
- Compression chiller (CC)
- (5)
- Electrolyzer (EL)
- (6)
- Fuel cell (FC)
3.2.3. Energy Storage Devices (ESDs)
- (1)
- The capacity constraints of the ESD can be represented by Equation (20):
- (2)
- The maximum charging/discharging power constraints can be formulized as shown in Equation (21):
- (3)
- The constraint of prohibiting charging and discharging simultaneously can be described as shown in Equation (22):
- (4)
- The SOC terminal state constraint is shown in Equation (23):
3.3. The Dispatching Model of the IPES
3.3.1. The Objective Function
- (1)
- Electricity grid exchange cost
- (2)
- Fuel cost
- (3)
- The maintenance cost of the equipment
- (4)
- The cost of purchasing hydrogen energy
- (5)
- The cost of carbon emission
3.3.2. The Constraint Function
- (1)
- The electricity energy balance constraint
- (2)
- The thermal energy balance constraint
- (3)
- The cold energy balance constraint
- (4)
- The hydrogen energy balance constraint
- (5)
- The power exchange constraint with the grid
4. Experimental Results and Analysis
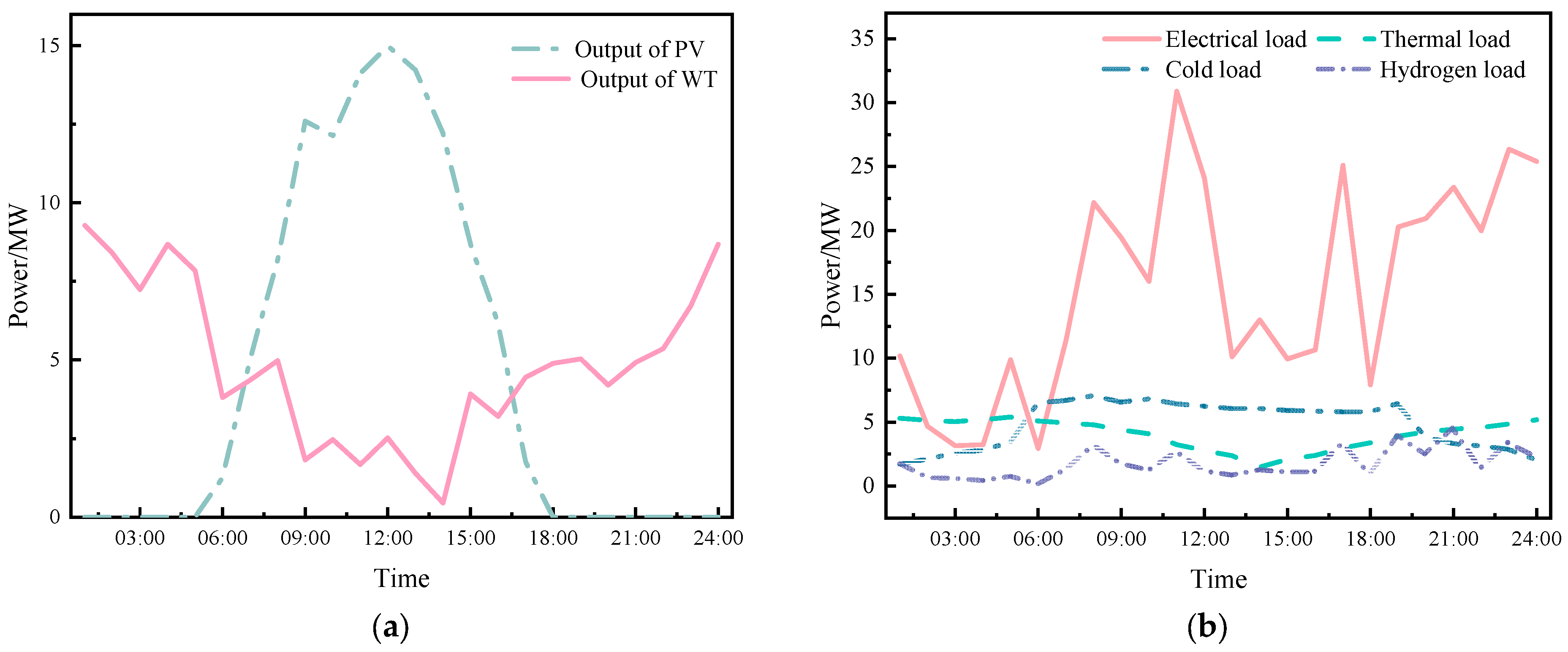
4.1. Parameter Settings
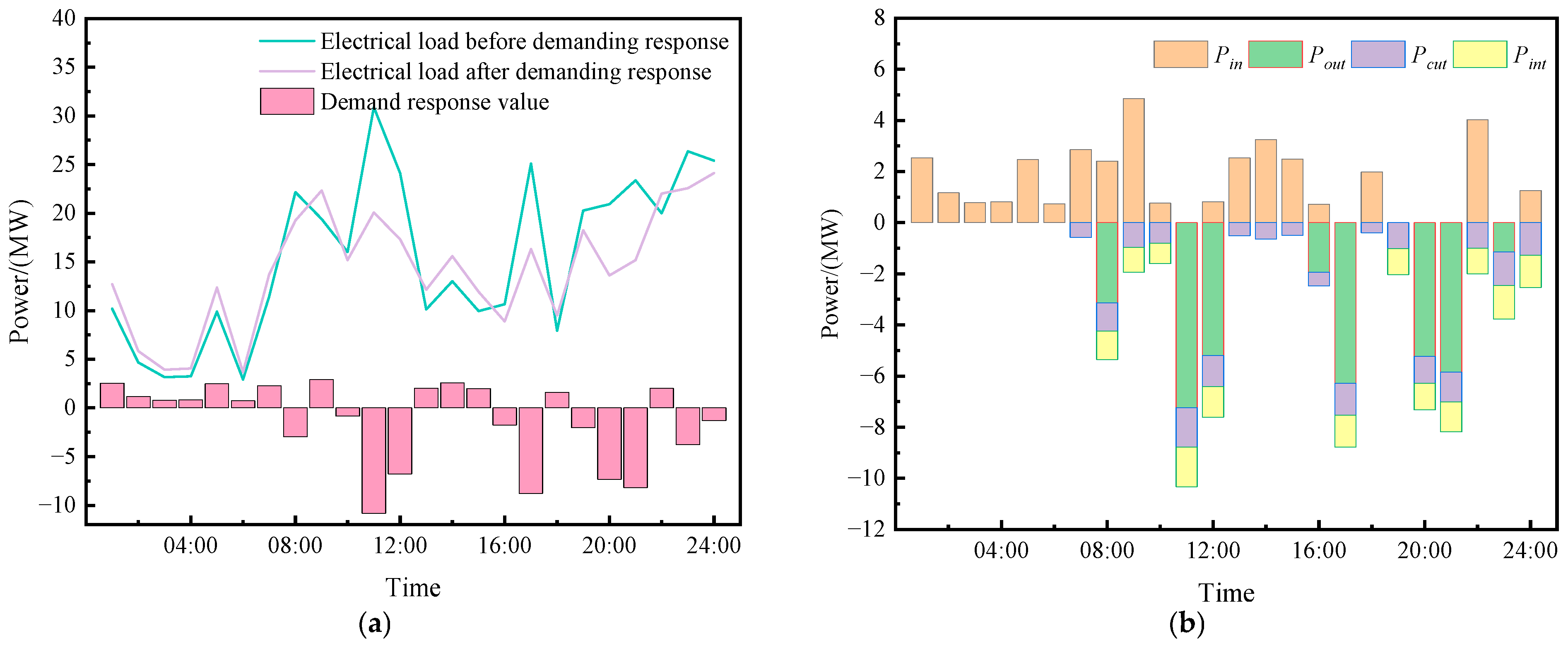
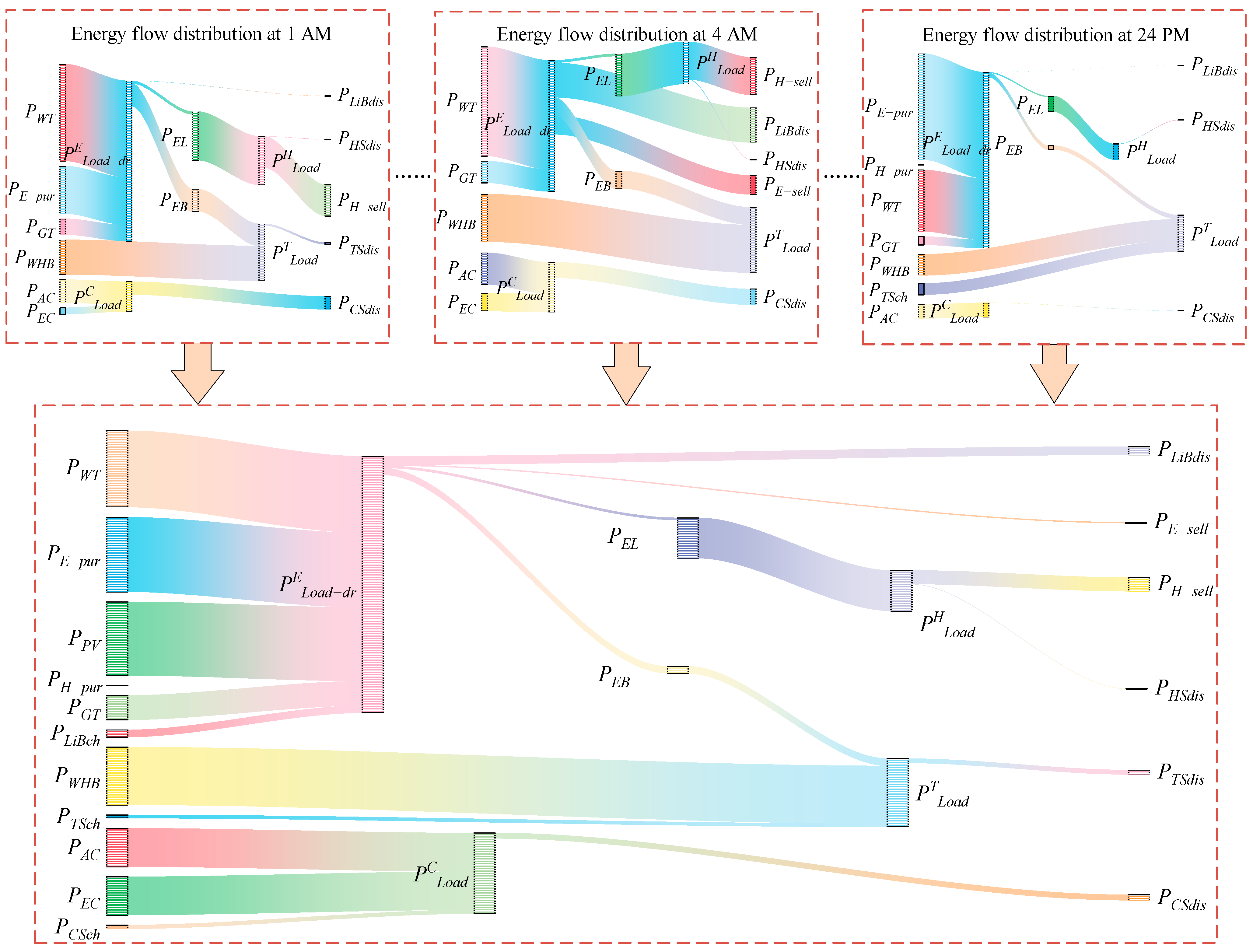
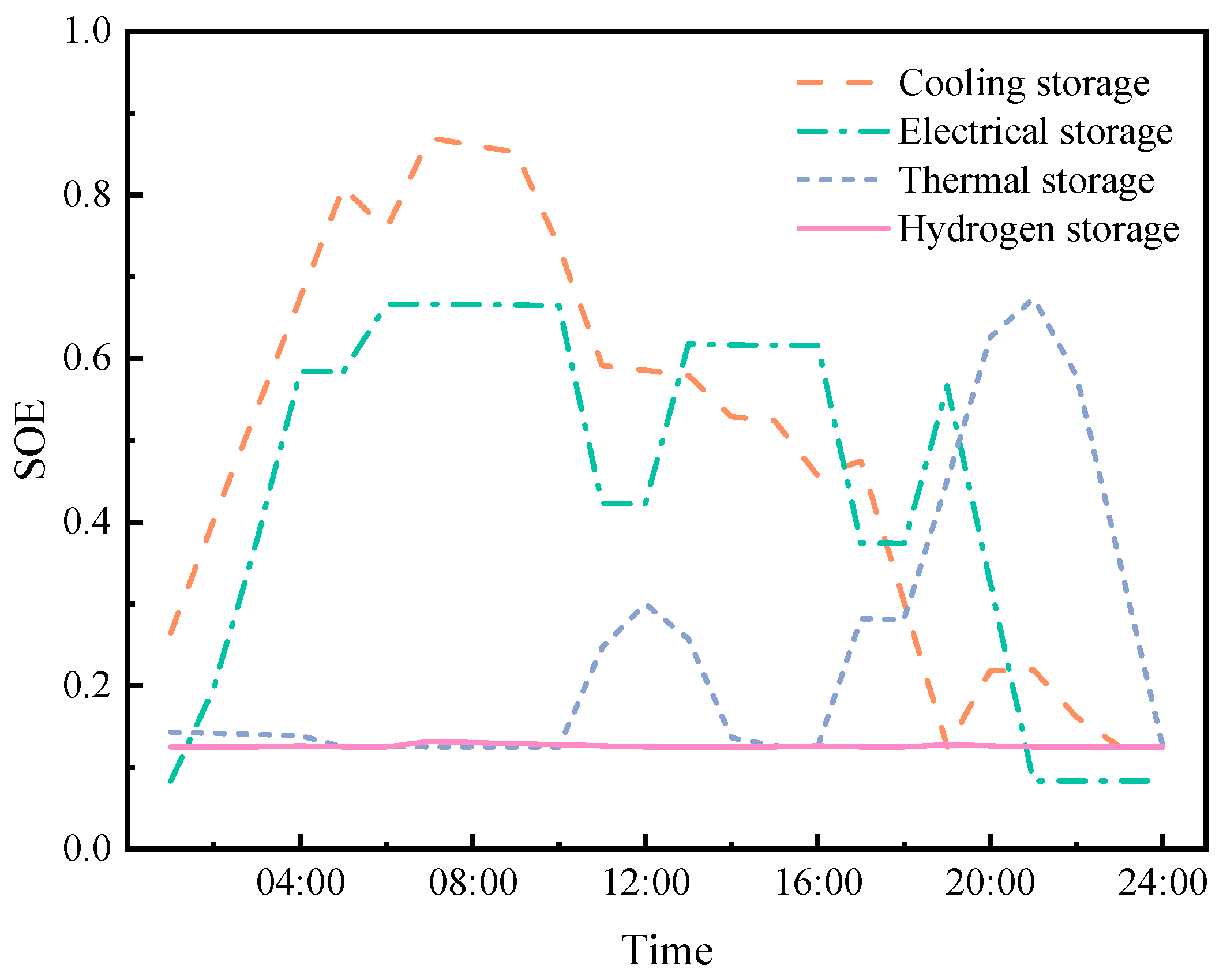
4.2. Experimental Results and Analysis
4.3. Carbon Emission Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviations | |||
|---|---|---|---|
| IPES | Integrated port energy system | CCHP | Combined cooling, heating and power |
| RES | Renewable energy system | WT | Wind turbine |
| ESS | Energy storage system | PV | Photovoltaic generation system |
| IES | Integrated energy system | GT | Gas turbine |
| SADS | Ship arrival and departure schedule | WHB | Waste heat boiler |
| GP | General purpose | AC | Absorption chiller |
| TEU | Twenty-foot equivalent unit | EB | Electric boiler |
| FEU | Forty-foot equivalent unit | EL | Electrolyzer |
| CC | Compression chiller | ESD | Energy storage system |
| FC | Fuel cell | TSD | Thermal storage system |
| LIB | Lithium battery | HSD | Hydrogen storage system |
| CSD | Cooling storage device | ||
| Arrival Time | Departure Time | Purpose | Shipload |
|---|---|---|---|
| 00:30 | 22:00 | Load/Unload | Load: 54 20 GP Full Containers Unload: 25 20 GP Empty Containers/5 40 GP Empty Containers/33 40 GP Full Containers/3 20 GP Full Containers |
| 01:00 | 09:00 | Load/Unload | Load: 41 20 GP Empty Containers/116 40 GP Empty Containers Unload: 96 40 GP Empty Containers/115 20 GP Empty Containers |
| 03:00 | 08:00 | Load/Unload | Load: 7 20 GP Full Containers/22 40 GP Full Containers Unload: 60 20 GP Empty Containers/30 40 GP Empty Containers |
| 04:00 | 16:00 | Load/Unload | Load: 10 20 GP Full Containers/150 20 GP Empty Containers/5 40 GP Full Containers/50 40 GP Empty Containers Unload: 144 20 GP Full Containers |
| 05:30 | 16:00 | Load/Unload | Load: 107 20 GP Full Containers/20 20 GP Empty Containers Unload: 115 20 GP Empty Containers/146 20 GP Full Containers/38 40 GP Full Containers |
| 06:30 | 14:00 | Load/Unload | Load: 20 20 GP Full Containers/90 40 GP Empty Containers Unload: 10 40 GP Full Containers/20 20 GP Empty Containers/40 40 GP Empty Containers |
| 07:00 | 19:30 | Load/Unload | Load: 84 20 GP Full Containers/121 40 GP Full Containers Unload: 43 20 GP Empty Containers Unload: 25 40 GP Full Containers/120 20 GP Full Containers/50 40 GP Empty Containers |
| 07:30 | -- | Load/Unload | Load: 44 20 GP Full Containers/74 40 GP Full Containers Unload: 54 20 GP Empty Containers/16 20 GP Full Containers/27 40 GP Full Containers/71 40 GP Empty Containers |
| 08:30 | 23:45 | Load/Unload | Load: 100 20 GP Full Containers/185 40 GP Full Containers Unload: 37 20 GP Full Containers/18 40 GP Full Containers/17 40 GP Empty Containers |
| 08:30 | 23:45 | Load/Unload | Load: 120 20 GP Full Containers Unload: 8 20 GP Full Containers/540 20 GP Empty Containers/2 40 GP Full Containers |
| 09:00 | 21:00 | Load/Unload | Load: 91 40 GP Full Containers Unload: 35 20 GP Full Containers/50 20 GP Empty Containers/90 40 GP Empty Containers/4 40 GP Full Containers |
| 16:00 | 23:00 | Load/Unload | Load: 2 20 GP Full Containers/9 40 GP Full Containers Unload: 51 20 GP Full Containers/60 40 GP Full Containers |
| 16:30 | 22:00 | Load/Unload | Load: 80 20 GP Full Containers/20 40 GP Full Containers Unload: 8 20 GP Full Containers/80 20 GP Empty Containers/2 40 GP Full Containers |
| 17:00 | 23:45 | Load/Unload | Load: 300 20 GP Full Containers Unload: 260 20 GP Full Containers/20 40 GP Full Containers |
| 18:30 | 23:45 | Load/Unload | Load: 290 20 GP Full Containers Unload: 60 20 GP Full Containers/280 20 GP Empty Containers/100 40 GP Full Containers |
| 20:30 | -- | Load/Unload | Load: 26 20 GP Full Containers/99 40 GP Full Containers Unload: 4 20 GP Full Containers/31 40 GP Full Containers/134 40 GP Empty Containers |
| 21:00 | -- | Load/Unload | Load: 100 20 GP Full Containers Unload: 100 20 GP Full Containers |
| 11:30 | -- | Load/Unload | Load: 117 20 GP Full Containers 25/40 GP Full Containers Unload: 210 20 GP Full Containers |
| 15:00 | -- | Load/Unload | Load: 80 20 GP Empty Containers/150 40 GP Empty Containers Unload: 190 20 GP Full Containers/18 40 GP Full Containers |
| 13:30 | -- | Load/Unload | Load: 13 20 GP Full Containers Unload: 23 20 GP Full Containers/67 20 GP Empty Containers/10 40 GP Full Containers/134 40 GP Empty Containers |
| 10:00 | -- | Load/Unload | Load: 25 20 GP Full Containers/42 40 GP Full Containers Unload: 44 20 GP Full Containers/23 20 GP Empty Containers/19 40 GP Full Containers/10 40 GP Empty Containers |
| 11:00 | -- | Load/Unload | Load: 270 20 GP Full Containers/25 40 GP Full Containers Unload: 20 20 GP Full Containers/200 20 GP Empty Containers/10 40 GP Full Containers |
| 12:00 | -- | Load/Unload | Load: 290 20 GP Full Containers/12 40 GP Full Containers Unload: 91 20 GP Empty Containers/215 20 GP Full Containers/79 40 GP Full Containers |
| 13:00 | -- | Load/Unload | Load: 70 20 GP Full Containers/158 20 GP Empty Containers/20 40 GP Full Containers/400 40 GP Empty Containers Unload: 502 20 GP Full Containers/48 20 GP Empty Containers/106 40 GP Full Containers/119 40 GP Empty Containers |
| 14:00 | -- | Load/Unload | Load: 300 20 GP Full Containers/50 40 GP Full Containers Unload: 400 20 GP Full Containers/200 40 GP Full Containers |
References
- Zhang, J.; Song, Y. Mathematical model and algorithm for the reefer mechanic scheduling problem at seaports. Discret. Dyn. Nat. Soc. 2017, 2017, 4730253. [Google Scholar] [CrossRef]
- Fiadomor, R. Assessment of Alternative Maritime Power (Cold Ironing) and Its Impact on Port Management and Operations. Master’s Thesis, World Maritime University, Malmö, Sweden, 2009. [Google Scholar]
- Huang, W.; Yu, M.; Li, H.; Tai, N. Energy Management of Integrated Energy System in Large Ports; Springer Nature: Singapore, 2023. [Google Scholar]
- Zhao, J.; Mi, H.; Cheng, H.; Chen, S. A planning model and method for an integrated port energy system considering shore power load flexibility. J. Shanghai Jiaotong Univ. 2021, 55, 1577. [Google Scholar]
- Wang, C.; Chen, Q.; Huang, R. Locating dry ports on a network: A case study on Tianjin Port. Marit. Policy Manag. 2018, 45, 71–88. [Google Scholar] [CrossRef]
- Pu, Y.; Chen, W.; Zhang, R.; Liu, H. Optimal operation strategy of port integrated energy system considering demand response. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; IEEE: Wuhan, China, 2020; pp. 518–523. [Google Scholar]
- Song, T.; Li, Y.; Zhang, X.-P.; Wu, C.; Li, J.; Guo, Y.; Gu, H. Integrated port energy system considering integrated demand response and energy interconnection. Int. J. Electr. Power Energy Syst. 2020, 117, 105654. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Zhao, Q.; Wang, S.; Fu, L. A multi-energy load prediction model based on deep multi-task learning and ensemble approach for regional integrated energy systems. Int. J. Electr. Power Energy Syst. 2021, 126, 106583. [Google Scholar]
- Fan, G.-F.; Han, Y.-Y.; Wang, J.-J.; Jia, H.-L.; Peng, L.-L.; Huang, H.-P.; Hong, W.-C. A new intelligent hybrid forecasting method for power load considering uncertainty. Knowl.-Based Syst. 2023, 280, 111034. [Google Scholar] [CrossRef]
- Tan, Z.; De, G.; Li, M.; Lin, H.; Yang, S.; Huang, L.; Tan, Q. Combined electricity-heat-cooling-gas load forecasting model for integrated energy system based on multi-task learning and least square support vector machine. J. Clean. Prod. 2020, 248, 119252. [Google Scholar] [CrossRef]
- Kim, G.; Lee, G.; An, S.; Lee, J. Forecasting future electric power consumption in Busan New Port using a deep learning model. Asian J. Shipp. Logist. 2023, 39, 78–93. [Google Scholar] [CrossRef]
- Duan, J.; Tian, Q.; Liu, F.; Xia, Y.; Gao, Q. Optimal scheduling strategy with integrated demand response based on stepped incentive mechanism for integrated electricity-gas energy system. Energy 2024, 313, 133689. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.; Fang, Y.; Yang, Y.; Ren, H.; Fan, L.; Tai, N. Optimization scheduling of community integrated energy system considering integrated demand response. J. Build. Eng. 2024, 98, 111230. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Huo, Y. A distributionally robust optimization approach of multi-park integrated energy systems considering shared energy storage and Uncertainty of Demand Response. Electr. Power Syst. Res. 2025, 238, 111116. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, J.; Zhen, L. Optimization of integrated energy system considering multi-energy collaboration in carbon-free hydrogen port. Transp. Res. Part E Logist. Transp. Rev. 2023, 180, 103351. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Shen, W.; Zeng, B.; Zeng, M. Multi-timescale rolling optimization dispatch method for integrated energy system with hybrid energy storage system. Energy 2023, 283, 129006. [Google Scholar] [CrossRef]
- Zhao, N.; Gu, W. Low-carbon planning and optimization of the integrated energy system considering lifetime carbon emissions. J. Build. Eng. 2024, 82, 108178. [Google Scholar] [CrossRef]
- Bakar, N.N.A.; Guerrero, J.M.; Vasquez, J.C.; Bazmohammadi, N.; Yu, Y.; Abusorrah, A.; Al-Turki, Y.A. A Review of the Conceptualization and Operational Management of Seaport Microgrids on the Shore and Seaside. Energies 2021, 14, 7941. [Google Scholar] [CrossRef]
- Parise, G.; Parise, L.; Malerba, A.; Pepe, F.M.; Honorati, A.; Chavdarian, P. Comprehensive Peak-Shaving Solutions for Port Cranes. IEEE Trans. Ind. Appl. 2017, 53, 1799–1806. [Google Scholar] [CrossRef]
- Tang, G.; Qin, M.; Zhao, Z.; Yu, J.; Shen, C. Performance of peak shaving policies for quay cranes at container terminals with double cycling. Simul. Model. Pract. Theory 2020, 104, 102129. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Liu, X. Distributionally robust optimization scheduling of port energy system considering hydrogen production and ammonia synthesis. Heliyon 2024, 10, e27615. [Google Scholar] [CrossRef] [PubMed]
- Nondy, J. 4E analyses of a micro-CCHP system with a polymer exchange membrane fuel cell and an absorption cooling system in summer and winter modes. Int. J. Hydrogen Energy 2024, 52, 886–904. [Google Scholar] [CrossRef]
- Ouyang, T.; Tan, X.; Tuo, X.; Qin, P.; Mo, C. Performance analysis and multi-objective optimization of a novel CCHP system integrated energy storage in large seagoing vessel. Renew. Energy 2024, 224, 120185. [Google Scholar] [CrossRef]
- NI, L.; Liu, W.; Wen, F.; Xue, Y.; Dong, Z.; Zheng, Y.; Zhang, R. Optimal operation of electricity, natural gas and heat systems considering integrated demand responses and diversified storage devices. J. Mod. Power Syst. Clean Energy 2018, 6, 423–437. [Google Scholar] [CrossRef]
- Sunderland, K.; Woolmington, T.; Blackledge, J.; Conlon, M. Small wind turbines in turbulent (urban) environments: A consideration of normal and Weibull distributions for power prediction. J. Wind Eng. Ind. Aerodyn. 2013, 121, 70–81. [Google Scholar] [CrossRef]
- Tang, R.; Wu, Z.; Li, X. Optimal operation of photovoltaic/battery/diesel/cold-ironing hybrid energy system for maritime application. Energy 2018, 162, 697–714. [Google Scholar] [CrossRef]
- Shen, X.; Han, Y.; Zhu, S.; Zheng, J.; Li, Q.; Nong, J. Comprehensive power-supply planning for active distribution system considering cooling, heating and power load balance. J. Mod. Power Syst. Clean Energy 2015, 3, 485–493. [Google Scholar]
- Tavana, M.; Deymi-Dashtebayaz, M.; Gholizadeh, M.; Ghorbani, S.; Dadpour, D. Optimizing building energy efficiency with a combined cooling, heating, and power (CCHP) system driven by boiler waste heat recovery. J. Build. Eng. 2024, 97, 110982. [Google Scholar] [CrossRef]
- Ibrahim, N.I.; Yahiaoui, A.; Garkuwa, J.A.; Ben Mansour, R.; Rehman, S. Solar cooling with absorption chillers, thermal energy storage, and control strategies: A review. J. Energy Storage 2024, 97, 112762. [Google Scholar] [CrossRef]
- Zhao, P.; Gou, F.; Xu, W.; Shi, H.; Wang, J. Multi-objective optimization of a hybrid system based on combined heat and compressed air energy storage and electrical boiler for wind power penetration and heat-power decoupling purposes. J. Energy Storage 2023, 58, 106353. [Google Scholar] [CrossRef]
- Moghaddas-Zadeh, N.; Farzaneh-Gord, M.; Bahnfleth, W.P. Optimal design and operation of the hybrid absorption-compression chiller plants—Energy and economic analysis. J. Build. Eng. 2024, 82, 108182. [Google Scholar] [CrossRef]
- Bornemann, L.; Lange, J.; Kaltschmitt, M. Optimizing temperature and pressure in PEM electrolyzers: A model-based approach to enhanced efficiency in integrated energy systems. Energy Convers. Manag. 2025, 325, 119338. [Google Scholar] [CrossRef]
- Amirkhalili, S.A.; Zahedi, A.; Ghaffarinezhad, A.; Kanani, B. Design and evaluation of a hybrid wind/hydrogen/fuel cell energy system for sustainable off-grid power supply. Int. J. Hydrogen Energy 2025, 100, 1456–1482. [Google Scholar] [CrossRef]
- Villamarín-Jácome, A.; Saltos-Rodríguez, M.; Espín-Sarzosa, D.; Haro, R.; Villamarín, G.; Okoye, M.O. Deploying renewable energy sources and energy storage systems for achieving low-carbon emissions targets in hydro-dominated power systems: A case study of Ecuador. Renew. Energy 2025, 241, 122198. [Google Scholar] [CrossRef]
- Ju, L.; Lu, X.; Li, F.; Bai, X.; Li, G.; Nie, B.; Tan, Z. Two-stage optimal dispatching model and benefit allocation strategy for hydrogen energy storage system-carbon capture and utilization system-based micro-energy grid. Energy Convers. Manag. 2024, 313, 118618. [Google Scholar] [CrossRef]
- Patel, D.; Matalon, P.; Oluleye, G. A novel temporal mixed-integer market penetration model for cost-effective uptake of electric boilers in the UK chemical industry. J. Clean. Prod. 2024, 446, 141156. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L. Energy flow modeling and optimal operation analysis of the micro energy grid based on energy hub. Energy Convers. Manag. 2017, 133, 292–306. [Google Scholar] [CrossRef]
- Sadeghian, O.; Shotorbani, A.M.; Mohammadi-Ivatloo, B.; Ghassemzadeh, S. Fuel cell preventive maintenance in an electricity market with Hydrogen storage and Scenario-Based risk management. Sustain. Energy Technol. Assess. 2024, 61, 103587. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, J.; Cai, X.; Wang, L.; Zhao, Y.; Zhang, X.; Chen, W. Joint active and reactive for allocation of renewable energy and energy storage under uncertain coupling. Appl. Energy 2021, 302, 117582. [Google Scholar] [CrossRef]
- Dou, X. Comprehensive Energy System Optimization and Operation, Effectiveness Evaluation and Application Research. Master’s Thesis, North China Electric Power University, Beijing, China, 2024. [Google Scholar]
- Farah, S.; Andresen, G. Investment-based optimisation of energy storage design parameters in a grid-connected hybrid renewable energy system. Appl. Energy 2024, 355, 122384. [Google Scholar] [CrossRef]



| Sequence Number | Operating Procedures | Transport Direction |
|---|---|---|
| 1 | Main cranes lift and translate containers | Ship to platform |
| 2 | Main cranes lower and translate containers | Ship to platform |
| 3 | Vice cranes lift and translate containers | Platform to shore |
| 4 | Vice cranes lower and translate containers | Platform to shore |
| 5 | Empty main cranes lift and translate themselves | Platform to ship |
| 6 | Empty main cranes lower and translate themselves | Platform to ship |
| 7 | Empty vice cranes lift and translate themselves | Shore to platform |
| 8 | Empty vice cranes lower and translate themselves | Shore to platform |
| Parameter | Meaning | Value | Parameter | Meaning | Value |
|---|---|---|---|---|---|
| Nf | Number of 40 GP containers | 38 | Nt | Number of 20 GP containers | 388 |
| Ni | Quay crane operation steps | 8 | ri | Random deviation of the i-th operation of quay crane | N (, /10) |
| Ex | Peak-shaving rate | 0.2 | Ee | Peak-shaving efficiency | 0.88 |
| 1st operation of quay crane | 1.6 (MW) | 2nd operation of quay crane | −1.4 (MW) | ||
| 3rd operation of quay crane | 0.7 (MW) | 4th operation of quay crane | −0.65 (MW) | ||
| 5th operation of quay crane | 1.0 (MW) | 6th operation of quay crane | −0.8 (MW) | ||
| 7th operation of quay crane | 0.6 (MW) | 8th operation of quay crane | −0.5 (MW) | ||
| ηsp | The conversion coefficient of cold-ironing power | 0.2082 | ηothers | The conversion coefficient of refrigerated container power | 0.0211 |
| ηfb | The conversion coefficient of the other load power | 0.4644 | ηreefers | The conversion coefficient of yard gantry crane power | 0.3217 |
| Name | Input Energy | Output Energy | Efficiency | Unit Construction Cost/(RMB/MW) | Useful Life/Year |
|---|---|---|---|---|---|
| PV | Renewable | Electricity | 0.17 | 5,000,000 | 20 |
| WT | Renewable | Electricity | 0.39 | 6,500,000 | 20 |
| GT | Electricity | Thermal | 0.48 | 1,000,000 | 20 |
| EB | Electricity | Thermal | 0.98 | 1,200,000 | 10 |
| EL | Electricity | Hydrogen | 0.83 | 600,000 | 10 |
| FC | Hydrogen | Electricity | 0.65 | 200,000 | 1 |
| CC | Electricity | Cooling | 3.00 | 600,000 | 20 |
| AC | Thermal | Cooling | 0.80 | 600,000 | 20 |
| WHB | Thermal | Thermal | 0.90 | 960,000 | 10 |
| LIB | Electricity | Electricity | 0.98 | 780,000 | 15 |
| TSD | Thermal | Thermal | 0.90 | 90,000 | 10 |
| CSD | Cooling | Cooling | 0.90 | 90,000 | 10 |
| HSD | Hydrogen | Hydrogen | 0.95 | 669,000 | 15 |
| Name | Capacity/(MWh) | Self-Loss Rate | Initial SOE | Charging/Discharging Efficiency | Maintenance Cost/(RMB/MWh) | Max Charging/Discharging Ramping Rate/(MW/h) |
|---|---|---|---|---|---|---|
| LIB | 8 | 0.01 | 0.1 | 0.9/0.95 | 96 | 0.6/0.6 |
| TSD | 6 | 0.02 | 0.12 | 0.9/0.9 | 16 | 0.6/0.6 |
| CSD | 6 | 0.02 | 0.25 | 0.9/0.9 | 16 | 0.6/0.6 |
| HSD | 3 | -- | 0.13 | 0.9/0.9 | 18 | 0.6/0.6 |
| Name | Capacity/(MWh) | Ramping Rate/(MW/h) | Maintenance Cost/(RMB/MWh) |
|---|---|---|---|
| PV | 18 | -- | 23.5 |
| WT | 20 | -- | 19.6 |
| GT | 8 | −1.0/1.0 | 25 |
| EB | 6 | −1.0/1.0 | 16 |
| EL | 5 | −1.0/1.0 | 24 |
| FC | 5 | −1.0/1.0 | 26 |
| CC | 6 | −1.0/1.0 | 20 |
| AC | 6 | −1.0/1.0 | 20 |
| WHB | 6 | −1.0/1.0 | 17 |
| Time | Purchasing Electricity/(RMB/MWh) | Selling Electricity/(RMB/MWh) | Purchasing Gas/(RMB/MWh) | Purchasing Hydrogen Energy/(RMB/MWh) | Selling Hydrogen Energy/(RMB/MWh) |
|---|---|---|---|---|---|
| Off-peak period | 300 | 250 | 320 | 498 | 340 |
| Standard period | 780 | 680 | 320 | 498 | 340 |
| Peak period | 1200 | 900 | 320 | 498 | 340 |
| Scenario | Purchased Electricity Costs (RMB) | Purchased Gas Costs (RMB) | Purchased Thermal Costs (RMB) | Purchased Cooling Costs (RMB) | Purchased Hydrogen Costs (RMB) | Total Costs (RMB) |
|---|---|---|---|---|---|---|
| I (Traditional system) | 211,083 | — | 19,340 | 19,902 | 18,473 | 268,798 |
| II (IPES) | 119,851 | 37,624 | — | — | — | 5 |
| III (ESS + IPES) | 94,293 | 37,624 | — | — | — | 131,916 |
| Scenario | Calculate Area | Daily Carbon Emissions/kg |
|---|---|---|
| I (Traditional system) | Port area | — |
| Power plant area | 613,718 | |
| Total | 613,718 | |
| II (IPES) | Port area | 86,051 |
| Power plant area | 290,497 | |
| Total | 376,548 | |
| III (ESS + IPES) | Port area | 62,313 |
| Power plant area | 286,146 | |
| Total | 348,459 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Ning, S.; Ren, Z.; Li, X.; Zhang, Y. Novel Load Forecasting and Optimal Dispatching Methods Considering Demand Response for Integrated Port Energy System. J. Mar. Sci. Eng. 2025, 13, 421. https://doi.org/10.3390/jmse13030421
Tang R, Ning S, Ren Z, Li X, Zhang Y. Novel Load Forecasting and Optimal Dispatching Methods Considering Demand Response for Integrated Port Energy System. Journal of Marine Science and Engineering. 2025; 13(3):421. https://doi.org/10.3390/jmse13030421
Chicago/Turabian StyleTang, Ruoli, Siwen Ning, Zongyang Ren, Xin Li, and Yan Zhang. 2025. "Novel Load Forecasting and Optimal Dispatching Methods Considering Demand Response for Integrated Port Energy System" Journal of Marine Science and Engineering 13, no. 3: 421. https://doi.org/10.3390/jmse13030421
APA StyleTang, R., Ning, S., Ren, Z., Li, X., & Zhang, Y. (2025). Novel Load Forecasting and Optimal Dispatching Methods Considering Demand Response for Integrated Port Energy System. Journal of Marine Science and Engineering, 13(3), 421. https://doi.org/10.3390/jmse13030421





