Extraction of Tsunami Signals from Coupled Seismic and Tsunami Waves
Abstract
1. Introduction
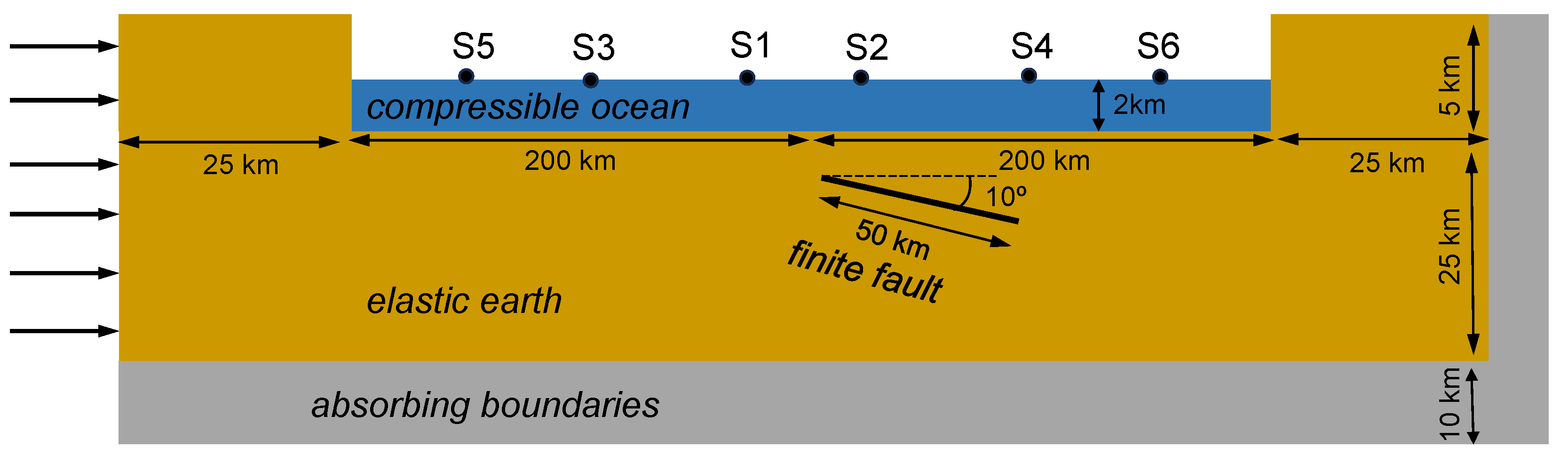
2. Numerical Generation of the Seismic and Tsunami Waves and Their Decoupling
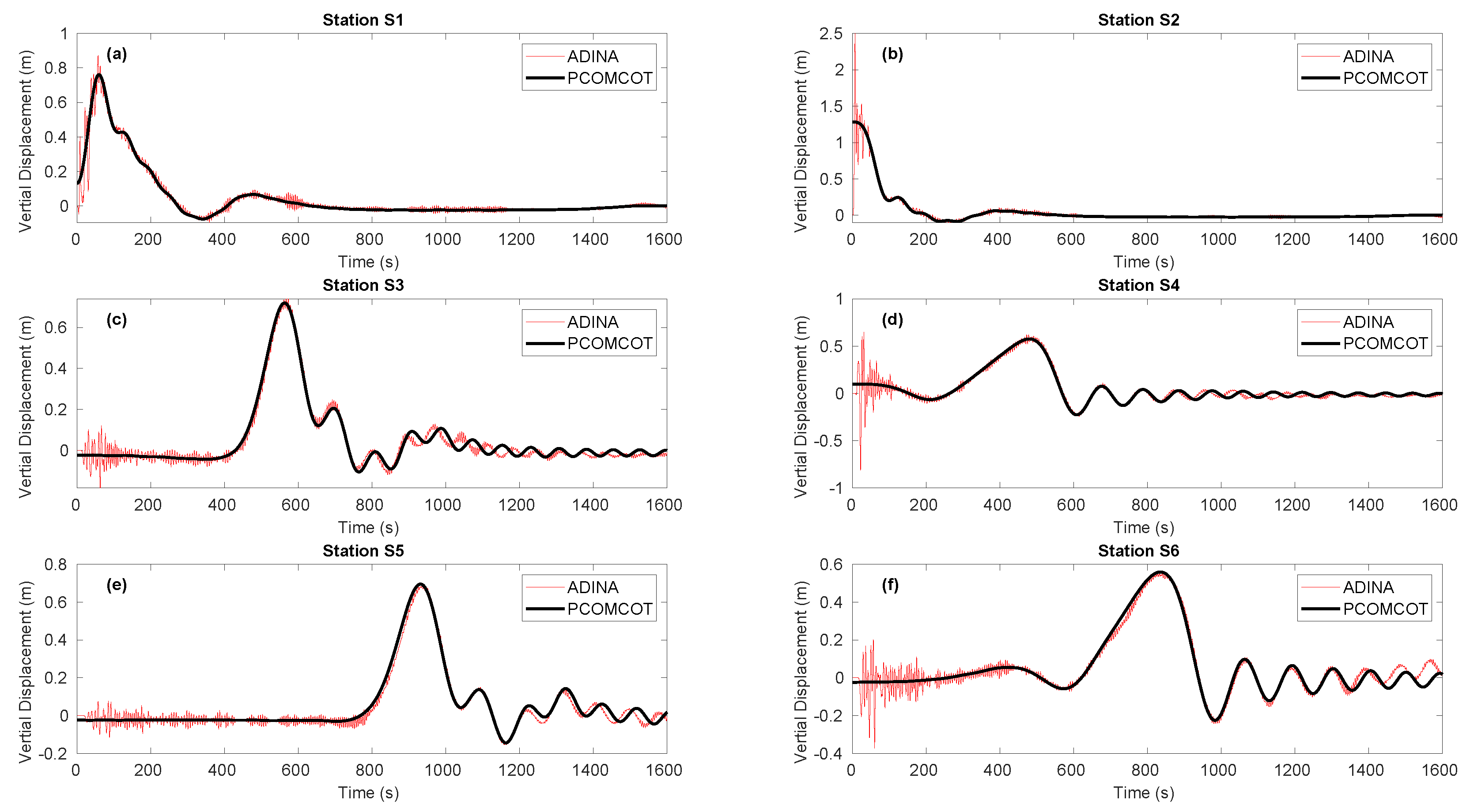
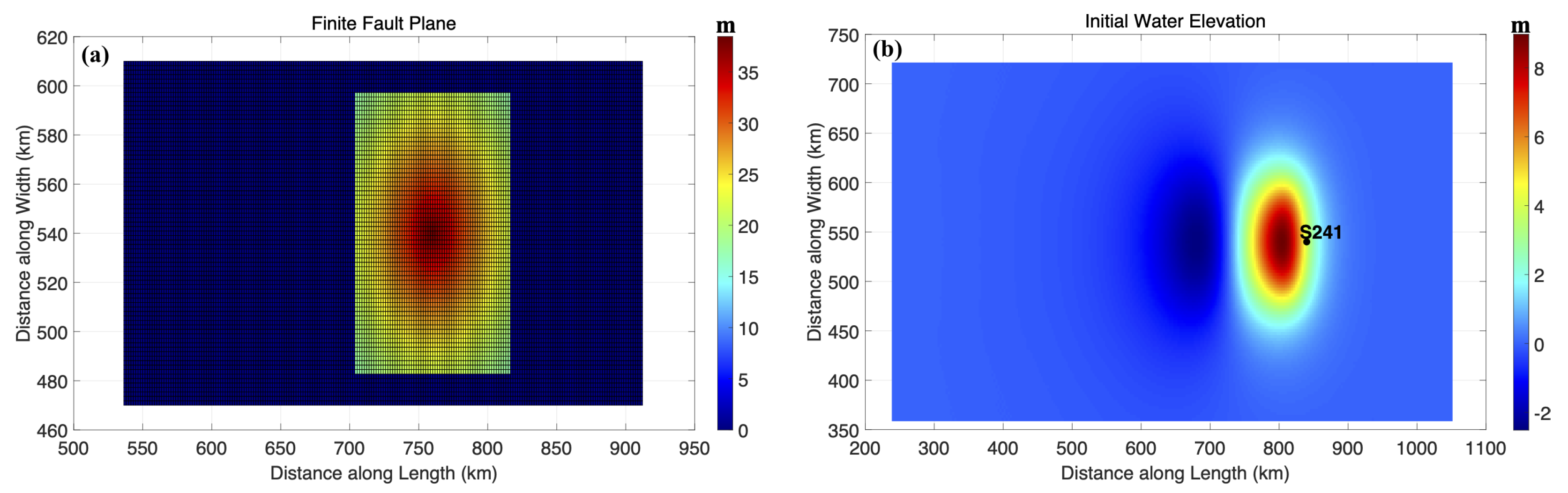
3. Simulation of Synthetic Seismic and Tsunami Waves
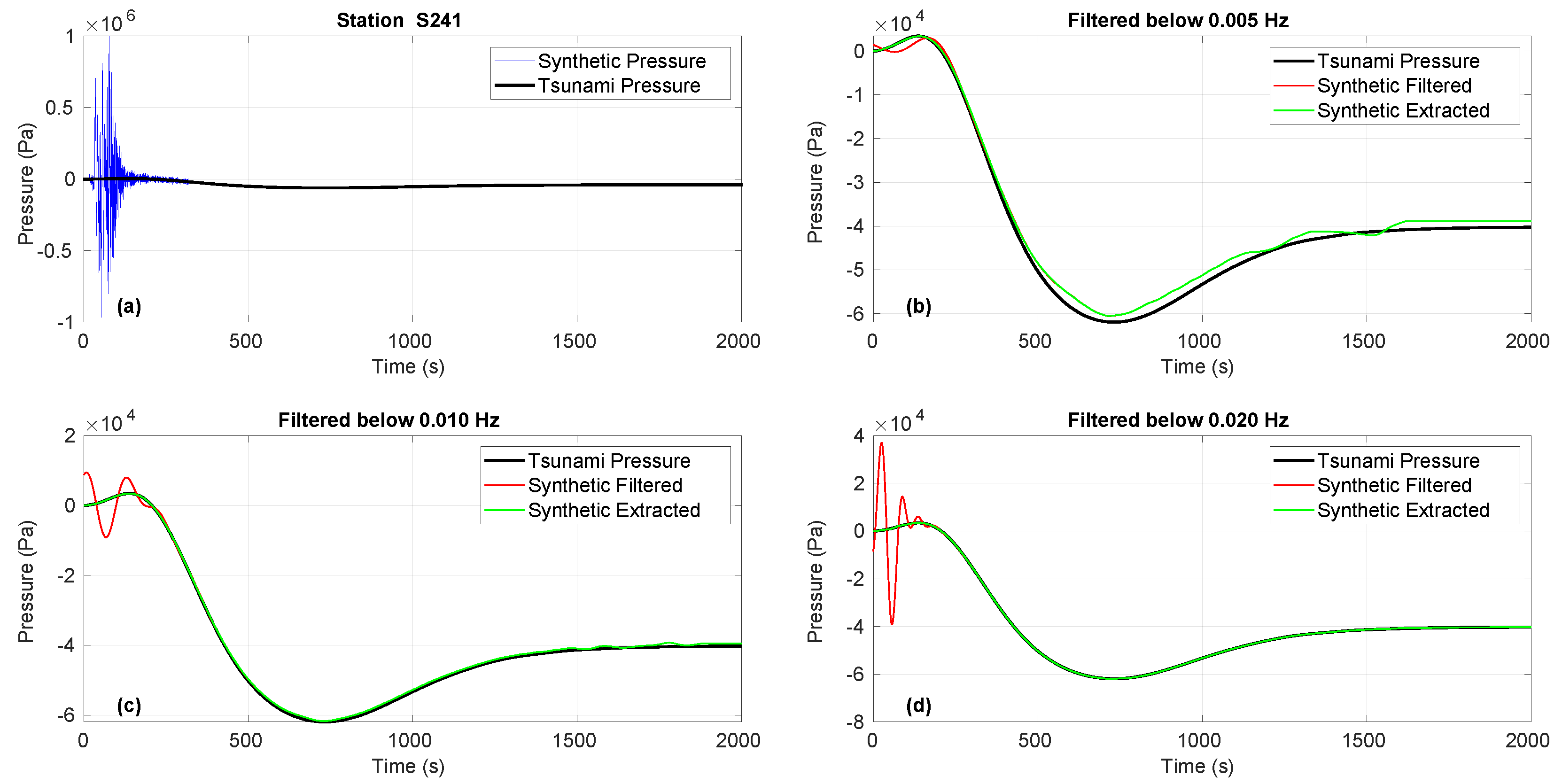
4. Extraction of Tsunami Signals
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maeda, T.; Furumura, T. FDM simulation of seismic waves, ocean acoustic waves, and tsunamis based on tsunami-coupled equations of motion. Pure Appl. Geophys. 2013, 170, 109–127. [Google Scholar] [CrossRef]
- Lotto, G.C.; Dunham, E.M. High-order finite difference modeling of tsunami generation in a compressible ocean from offshore earthquakes. Comput. Geosci. 2015, 19, 327–340. [Google Scholar] [CrossRef]
- Nosov, M.A.; Kolesov, S.V. Combined numerical model of tsunami. Math. Model. Comput. Simulations 2019, 11, 679–689. [Google Scholar] [CrossRef]
- Nosov, M.; Kolesov, S. Elastic oscillations of water column in the 2003 Tokachi-oki tsunami source: In-situ measurements and 3-D numerical modelling. Nat. Hazards Earth Syst. Sci. 2007, 7, 243–249. [Google Scholar] [CrossRef]
- Lotto, G.C.; Jeppson, T.N.; Dunham, E.M. Fully coupled simulations of megathrust earthquakes and tsunamis in the Japan Trench, Nankai Trough, and Cascadia Subduction Zone. Pure Appl. Geophys. 2019, 176, 4009–4041. [Google Scholar] [CrossRef]
- Kanamori, H. Mechanism of tsunami earthquakes. Phys. Earth Planet. Inter. 1972, 6, 346–359. [Google Scholar] [CrossRef]
- Saito, T. Tsunami Generation and Propagation; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ben-Menahem, A.; Smith, S.W.; Teng, T.L. A procedure for source studies from spectrums of long-period seismic body waves. Bull. Seismol. Soc. Am. 1965, 55, 203–235. [Google Scholar] [CrossRef]
- Boxberger, T.; Picozzi, M.; Parolai, S. Shallow geology characterization using Rayleigh and Love wave dispersion curves derived from seismic noise array measurements. J. Appl. Geophys. 2011, 75, 345–354. [Google Scholar] [CrossRef]
- An, C.; Liu, P.L.F. Characteristics of leading tsunami waves generated in three recent tsunami events. J. Earthq. Tsunami 2014, 8, 1440001. [Google Scholar] [CrossRef]
- Titov, V.V.; Gonzalez, F.I.; Bernard, E.; Eble, M.C.; Mofjeld, H.O.; Newman, J.C.; Venturato, A.J. Real-time tsunami forecasting: Challenges and solutions. Nat. Hazards 2005, 35, 35–41. [Google Scholar] [CrossRef]
- Lay, T.; Wallace, T.C. Modern Global Seismology; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Satake, K. Tsunamis. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 2002; Volume 81, pp. 437–451. [Google Scholar]
- Kubota, T.; Hino, R.; Inazu, D.; Ito, Y.; Iinuma, T. Complicated rupture process of the Mw 7.0 intraslab strike-slip earthquake in the Tohoku region on 10 July 2011 revealed by near-field pressure records. Geophys. Res. Lett. 2015, 42, 9733–9739. [Google Scholar] [CrossRef]
- Ho, T.C.; Satake, K.; Watada, S.; Fujii, Y. Source estimate for the 1960 Chile earthquake from joint inversion of geodetic and transoceanic tsunami data. J. Geophys. Res. Solid Earth 2019, 124, 2812–2828. [Google Scholar] [CrossRef]
- Iwasaki, T.; Horikawa, K. Tsunami caused by Chile earthquake in May, 1960 and outline of disasters in northeastern coasts of Japan. Coast. Eng. Jpn. 1960, 3, 33–48. [Google Scholar] [CrossRef]
- Levin, B.W.; Nosov, M. Physics of Tsunamis; Springer: Berlin/Heidelberg, Germany, 2009; Volume 327. [Google Scholar]
- Kassaras, I.; Kazantzidou-Firtinidou, D. Tectonic hazards: Earthquakes. J. Environ. Hazards Methodol. Risk Assess. Manag. 2017, 7, 378. [Google Scholar]
- Woo, G. Downward counterfactual search for extreme events. Front. Earth Sci. 2019, 7, 340. [Google Scholar] [CrossRef]
- Goda, K.; Abilova, K. Tsunami hazard warning and risk prediction based on inaccurate earthquake source parameters. Nat. Hazards Earth Syst. Sci. 2016, 16, 577–593. [Google Scholar] [CrossRef]
- Uchida, N.; Bürgmann, R. A decade of lessons learned from the 2011 Tohoku-Oki earthquake. Rev. Geophys. 2021, 59, e2020RG000713. [Google Scholar] [CrossRef]
- Song, L.; An, C. Finite-fault Slip Distribution and Initial Water Elevation of the 2024 Noto Peninsula, Japan Earthquake Estimated from Tsunami Waveforms. J. Earthq. Tsunami 2024, 2450033. [Google Scholar] [CrossRef]
- Fujii, Y.; Satake, K. Slip distribution of the 2024 Noto Peninsula earthquake (MJMA 7.6) estimated from tsunami waveforms and GNSS data. Earth Planets Space 2024, 76, 44. [Google Scholar] [CrossRef]
- Pakoksung, K.; Suppasri, A.; Imamura, F. Preliminary modeling and analysis of the Tsunami generated by the 2024 Noto Peninsula earthquake on 1 January: Wave characteristics in the Sea of Japan. Ocean. Eng. 2024, 307, 118172. [Google Scholar] [CrossRef]
- Shirai, T.; Enomoto, Y.; Haga, K.; Tokuta, T.; Arikawa, T.; Mori, N.; Imamura, F. Potential for tsunami detection via CCTV cameras in northeastern Toyama Prefecture, Japan, following the 2024 Noto Peninsula earthquake. Geosci. Lett. 2024, 11, 28. [Google Scholar] [CrossRef]
- Mulia, I.E.; Gusman, A.R.; Heidarzadeh, M.; Satake, K. Sensitivity of Tsunami Data to the Up-Dip Extent of the July 2021 Mw 8.2 Alaska Earthquake. Seismol. Soc. Am. 2022, 93, 1992–2003. [Google Scholar] [CrossRef]
- Wang, Y.; Satake, K.; Maeda, T.; Shinohara, M.; Sakai, S. A method of real-time tsunami detection using ensemble empirical mode decomposition. Seismol. Res. Lett. 2020, 91, 2851–2861. [Google Scholar] [CrossRef]
- Kubota, T.; Saito, T.; Tsushima, H.; Hino, R.; Ohta, Y.; Suzuki, S.; Inazu, D. Extracting near-field seismograms from ocean-bottom pressure gauge inside the focal area: Application to the 2011 Mw 9.1 Tohoku-Oki earthquake. Geophys. Res. Lett. 2021, 48, e2020GL091664. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite elements in CAD and ADINA. Nucl. Eng. Des. 1986, 98, 57–67. [Google Scholar] [CrossRef]
- An, C.; Cai, Y. The effect of beach slope on the tsunami run-up induced by thrust fault earthquakes. Procedia Comput. Sci. 2010, 1, 645–654. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Y.; An, C.; Liu, H. A numerical study of tsunami generation by horizontal displacement of sloping seafloor. J. Earthq. Tsunami 2020, 14, 2050018. [Google Scholar] [CrossRef]
- An, C.; Liu, H.; Ren, Z.; Yuan, Y. Prediction of tsunami waves by uniform slip models. J. Geophys. Res. Ocean. 2018, 123, 8366–8382. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P.L.F. An analysis of 2004 Sumatra earthquake fault plane mechanisms and Indian Ocean tsunami. J. Hydraul. Res. 2006, 44, 147–154. [Google Scholar] [CrossRef]
- Zhu, Y.; An, C.; Yu, H.; Zhang, W.; Chen, X. High-resolution tsunami hazard assessment for the Guangdong-Hong Kong-Macao Greater Bay Area based on a non-hydrostatic tsunami model. Sci. China Earth Sci. 2024, 67, 2326–2351. [Google Scholar] [CrossRef]
- Kajiura, K.; Shuto, N. 11. TSUNAMIS. Ocean. Eng. Sci. 1990, 9, 395. [Google Scholar]
- Saito, T. Tsunami generation: Validity and limitations of conventional theories. Geophys. J. Int. 2017, 210, 1888–1900. [Google Scholar] [CrossRef]
- Peter, D.; Komatitsch, D.; Luo, Y.; Martin, R.; Le Goff, N.; Casarotti, E.; Le Loher, P.; Magnoni, F.; Liu, Q.; Blitz, C.; et al. Forward and adjoint simulations of seismic wave propagation on fully unstructured hexahedral meshes. Geophys. J. Int. 2011, 186, 721–739. [Google Scholar] [CrossRef]
- Tromp, J.; Komatitsch, D.; Liu, Q. Spectral-element and adjoint methods in seismology. Commun. Comput. Phys. 2008, 3, 1–32. [Google Scholar]
- Blaser, L.; Krüger, F.; Ohrnberger, M.; Scherbaum, F. Scaling relations of earthquake source parameter estimates with special focus on subduction environment. Bull. Seismol. Soc. Am. 2010, 100, 2914–2926. [Google Scholar] [CrossRef]
- Murotani, S.; Miyake, H.; Koketsu, K. Scaling of characterized slip models for plate-boundary earthquakes. Earth Planets Space 2008, 60, 987–991. [Google Scholar] [CrossRef]
- Murotani, S.; Satake, K.; Fujii, Y. Scaling relations of seismic moment, rupture area, average slip, and asperity size for M~9 subduction-zone earthquakes. Geophys. Res. Lett. 2013, 40, 5070–5074. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar] [CrossRef]
- Cormier, V.F. The effect of attenuation on seismic body waves. Bull. Seismol. Soc. Am. 1982, 72, S169–S200. [Google Scholar]
- Mi, B.; Xia, J.; Shen, C.; Wang, L. Dispersion energy analysis of Rayleigh and Love waves in the presence of low-velocity layers in near-surface seismic surveys. Surv. Geophys. 2018, 39, 271–288. [Google Scholar] [CrossRef]
- Rabinovich, A.B.; Eblé, M.C. Deep-ocean measurements of tsunami waves. Pure Appl. Geophys. 2015, 172, 3281–3312. [Google Scholar] [CrossRef]
- An, C.; Cai, C.; Zheng, Y.; Meng, L.; Liu, P. Theoretical solution and applications of ocean bottom pressure induced by seismic seafloor motion. Geophys. Res. Lett. 2017, 44, 10–272. [Google Scholar] [CrossRef]
- Deng, H.; An, C.; Cai, C.; Ren, H. Theoretical solution and applications of ocean bottom pressure induced by seismic waves at high frequencies. Geophys. Res. Lett. 2022, 49, e2021GL096952. [Google Scholar] [CrossRef]
- Kubota, T.; Saito, T.; Suzuki, W.; Hino, R. Estimation of seismic centroid moment tensor using ocean bottom pressure gauges as seismometers. Geophys. Res. Lett. 2017, 44, 10–907. [Google Scholar] [CrossRef]
- Nosov, M.; Karpov, V.; Kolesov, S.; Sementsov, K.; Matsumoto, H.; Kaneda, Y. Relationship between pressure variations at the ocean bottom and the acceleration of its motion during a submarine earthquake. Earth Planets Space 2018, 70, 100. [Google Scholar] [CrossRef]
- Iannaccone, G.; Pucciarelli, G.; Guardato, S.; Donnarumma, G.P.; Macedonio, G.; Beranzoli, L. When the hydrophone works as an accelerometer. Seismol. Soc. Am. 2021, 92, 365–377. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; An, C. Extraction of Tsunami Signals from Coupled Seismic and Tsunami Waves. J. Mar. Sci. Eng. 2025, 13, 419. https://doi.org/10.3390/jmse13030419
Song L, An C. Extraction of Tsunami Signals from Coupled Seismic and Tsunami Waves. Journal of Marine Science and Engineering. 2025; 13(3):419. https://doi.org/10.3390/jmse13030419
Chicago/Turabian StyleSong, Linjian, and Chao An. 2025. "Extraction of Tsunami Signals from Coupled Seismic and Tsunami Waves" Journal of Marine Science and Engineering 13, no. 3: 419. https://doi.org/10.3390/jmse13030419
APA StyleSong, L., & An, C. (2025). Extraction of Tsunami Signals from Coupled Seismic and Tsunami Waves. Journal of Marine Science and Engineering, 13(3), 419. https://doi.org/10.3390/jmse13030419





