Passivity-Based Sliding Mode Control for the Robust Trajectory Tracking of Unmanned Surface Vessels Under External Disturbances and Model Uncertainty

Abstract

This study uses a port-Hamiltonian framework to address trajectory tracking control for unmanned surface vessels (USVs) under unknown disturbances. A passivity-based sliding mode controller is designed, integrating adaptive disturbance estimation and an RBFNN-based uncertainty estimator. Stability is rigorously proven, and simulations confirm superior tracking performance, strong disturbance rejection, and accurate uncertainty estimation.

1. Introduction

In recent decades, unmanned surface vessels (USVs) have been widely adopted due to their simple mechanical design and operational efficiency. By integrating various mission modules, USVs can be adapted for use in diverse applications, including scientific research, environmental monitoring, marine resource exploration, and military operations. However, operating in complex marine environments requires high maneuverability and reliability. To achieve autonomous, safe, and efficient mission execution, USVs must have adaptive and precise control capabilities. The inherent nonlinear, multivariable, strongly coupled, and time-varying dynamics of USVs pose significant challenges for traditional control methods. Additionally, these systems are subject to external disturbances, nonlinearities, and modeling uncertainties. Addressing these challenges necessitates advanced motion control strategies based on nonlinear control theory to ensure robust and optimal performance.

The port-Hamiltonian system (PHS) framework [1,2,3] provides a systematic approach to modeling, analyzing, and controlling nonlinear systems across various domains, including electrical and chemical systems [4,5,6], and it is particularly effective in mechanical applications [7,8]. It captures energy exchange and system dynamics using Hamilton’s canonical equations, offering a clear physical interpretation of control strategies based on energy conservation and dissipation [9,10]. To stabilize PHS-based systems, passivity-based control (PBC) techniques leverage the system’s inherent passivity, using the Hamiltonian function as a Lyapunov candidate and shaping it to achieve stability while preserving physical interpretability [11,12,13,14,15]. Many studies have been dedicated to passivity-based control for USV control. For fully actuated marine vehicles, an IDA-PBC controller with integral action [16] was proposed in [17]. For under-actuated USVs, a hybrid backstepping and passivity-based control approach using the LOS method was introduced in [18]. Additionally, the authors of [19] proposed a family of trajectory tracking controllers for fully actuated marine crafts in the port-Hamiltonian framework using virtual differential passivity-based control (v-dPBC).

Sliding mode control (SMC) is a robust nonlinear approach for handling uncertainties and disturbances [20,21,22]. SMC confines the system state to a sliding surface with desired dynamics through high-gain feedback, although it may introduce chattering effects that could potentially harm the system. One approach to mitigate this is higher-order sliding mode control [23,24], which extends conventional sliding modes to achieve smooth control signals while preserving robustness. Another method is boundary layer smoothing [25], where a thin boundary layer around the sliding surface is introduced, replacing the discontinuous control with a continuous approximation to reduce chattering. It has been widely utilized in USV control for its effectiveness in addressing complex dynamics and ensuring reliable performance [26,27,28].

Recent studies [29,30,31] have introduced a passivity-based sliding mode controller that is tailored for mechanical and electromechanical PHSs. A nonsmooth function serves as an artificial potential in kinetic–potential energy shaping to realize SMC. Basing a design on the PBC framework guarantees that the closed-loop system has Lyapunov stability, even when the discontinuous SMC input is replaced with a smooth approximation to reduce chattering.

The main contribution of this study is the proposal of an energy-based sliding mode control approach for trajectory tracking in USVs that are subject to external disturbances. A PHS model of a USV in inertial reference frames is presented to effectively capture its physical dynamics for control design. To address system uncertainties, a radial basis function neural network (RBFNN) [32,33] was employed to estimate the dynamic uncertainties effectively. The RBFNN was chosen for its universal approximation capability and fast convergence properties, making it particularly suitable for modeling highly nonlinear uncertainties in real time. The RBFNN provides accurate and computationally efficient estimations that improve the overall control performance by approximating the uncertainties as a weighted sum of radial basis functions. Additionally, an adaptive estimator [34] was incorporated to iteratively adjust and refine the disturbance estimates, continuously improving the control system’s precision and reliability. We established asymptotic stability in a closed-loop system, ensuring robust performance. The simulation results confirm the approach, showing that the USV accurately tracks desired trajectories and effectively rejects disturbances.

This article is structured as follows: Section 2 provides the preliminaries, including an overview of the PHS, momentum transformation, and kinetic–potential energy shaping. In Section 3, the problem is formulated by introducing the mathematical model and dynamics of the USV, along with its port-Hamiltonian representation in inertial co-ordinates. Section 4 focuses on the control design, where an RBFNN is utilized for uncertainty estimation, an adaptive disturbance estimator is introduced, and the energy-based sliding mode tracking control for the USV is presented. In Section 5, the simulation results that validate the proposed approach are presented.

2. Preliminaries

PHSs effectively model multi-physical interactions, such as the energy conversion in an electrically driven USV. Passivity-based control utilizes these energy exchanges to facilitate the design of controllers with clear physical interpretations, enhancing the closed-loop stability and robustness. This section briefly reviews PHSs, which are widely used to model fully actuated mechanical systems.

2.1. Port-Hamiltonian System

A fully actuated mechanical system can be expressed in a port-Hamiltonian form, as outlined in [10]:

$$\left[\begin{array}{c}\dot{q}\\ \dot{p}\end{array}\right]=\left[\begin{array}{cc}0& I_n\\ -I_n& -D_0(q,p)\end{array}\right]\left[\begin{array}{c}{\nabla }_q{H}_0(q,p)\\ {\nabla }_p{H}_0(q,p)\end{array}\right]+\left[\begin{array}{c}0\\ G_0\left(q\right)\end{array}\right]\mathbf{u}$$

(1)

$$H_0(q,p)={\displaystyle \frac{1}{2}}{p}^{T}M{\left(q\right)}^{-1}p$$

(2)

In this formulation, the state vector is given by ${[q^T,p^T]}^T\in {\mathbb{R}}^{2m}$, where $q\in {\mathbb{R}}^m$ represents the configuration, and $p\in {\mathbb{R}}^m$ represents the momentum. The input vector is $u\in {\mathbb{R}}^m$. The inertia matrix $M\left(q\right)\in {\mathbb{R}}^{m\times m}$ is symmetric and positive definite, whereas the damping matrix $D_0(q,p)\in {\mathbb{R}}^{m\times m}$ is positive semi-definite. The full-rank matrix $G_0\left(q\right)\in {\mathbb{R}}^{m\times m}$ maps the input to the system. The Hamiltonian function $H_0(q,p)\in \mathbb{R}$ captures the total system’s energy.

2.2. Momentum Transformation and Kinetic–Potential Energy Shaping

A momentum transformation is commonly applied to decouple kinetic energy from the configuration variable q in the study of fully actuated mechanical PHSs. This technique is central to the kinetic–potential energy shaping approach [35], which allows for the design of a potential function depending on the configuration and momentum variables. To achieve this, we introduce the following co-ordinate transformation:

$$\left[\begin{array}{c}q\\ \xi \end{array}\right]=\left[\begin{array}{c}q\\ T{\left(q\right)}^{T}p\end{array}\right],$$

(3)

where $\xi =T{\left(q\right)}^{T}p$ is the transformed momentum and $T\left(q\right)\in {\mathbb{R}}^{m\times m}$ is a nonsingular matrix that fulfills the following condition:

$$T\left(q\right)T{\left(q\right)}^{-1}=M{\left(q\right)}^{-1}.$$

(4)

The system in (1) can be rewritten with a quadratic Hamiltonian function, $H\left(\eta \right)={\displaystyle \frac{1}{2}}{\xi }^T\xi$, as follows:

$$\left[\begin{array}{c}\dot{q}\\ \dot{\xi }\end{array}\right]=\left[\begin{array}{cc}0& T\left(q\right)\\ -T{\left(q\right)}^T& -D(q,\xi )\end{array}\right]\left[\begin{array}{c}{\nabla }_{q}H\left(\xi \right)\\ {\nabla }_{\xi }H\left(\xi \right)\end{array}\right]+\left[\begin{array}{c}0\\ G\left(q\right)\end{array}\right]\mathbf{u},$$

(5)

where $G\left(q\right)=T{\left(q\right)}^T{G}_0\left(q\right)$ and $D(q,\xi )$ is a matrix satisfying $D(q,\xi )+D{(q,\xi )}^T\ge 0$. The matrix $D(q,\xi )$ includes both gyroscopic and damping terms. This co-ordinate transformation removes the $M{\left(q\right)}^{-1}$ dependency in the original Hamiltonian function $H_0(q,p)$, resulting in a new Hamiltonian, $H\left(\xi \right)$, which is independent of q. By adjusting the upper-left block of the structure matrix $J\left(x\right)$, a potential function can then be defined to depend on both q and $\xi$ without affecting the system’s kinematics.

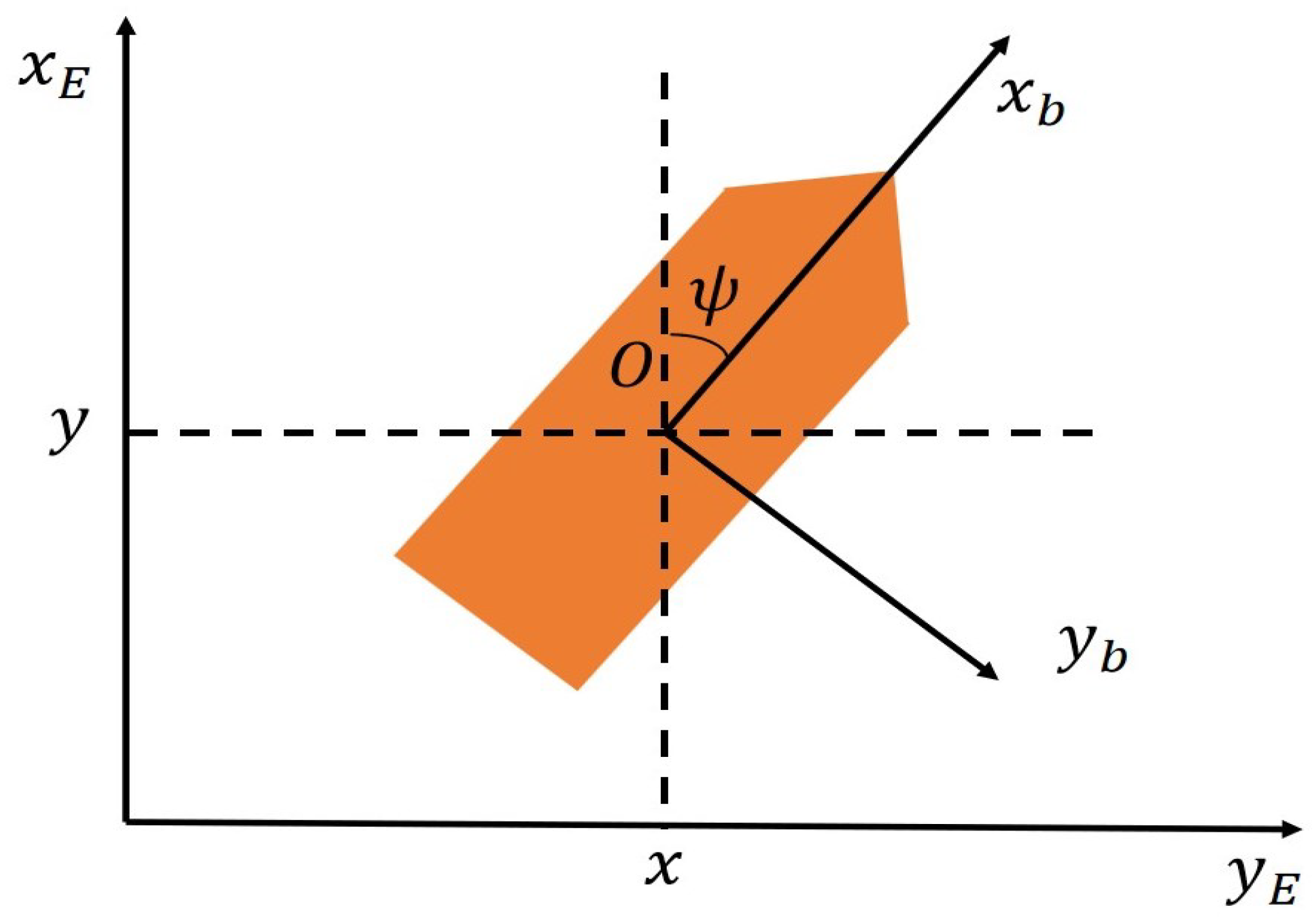
3. Problem Statement

In marine craft modeling, as depicted in Figure 1, the body frame is a moving co-ordinate system that is fixed at the vessel’s center of gravity, with axes $x_b$, $y_b$, and $z_b$ representing the surge, sway, and upward directions. The inertial frame, fixed to the Earth, uses $x_E$, $y_E$, and $z_E$ for the north, east, and downward directions.

The mathematical model of a marine craft [36,37] typically describes a rigid body that is influenced by external forces and torques.

$$\left\{\begin{array}{c}\dot{q}=J\left(q\right)v,\hfill \\ M_u\dot{\nu }=-C\left(v\right)-D\left(v\right)v+{\tau }_c+{\tau }_d\hfill \end{array}\right.$$

(6)

where $q={\left[\begin{array}{ccc}x& y& \psi \end{array}\right]}^T$ represents the surge displacement, sway displacement, and yaw angle along $x_E$ and $y_E$ in the Earth frame. $\nu ={\left[\begin{array}{ccc}u& v& r\end{array}\right]}^T$ denotes the surge, sway, and yaw velocities with respect to the body-fixed frame. $M_u=\mathrm{diag}(m_{11},m_{22},m_{33})$ is the inertia matrix, accounting for the added mass, where $m_{11}$, $m_{22}$, and $m_{33}$ correspond to the added mass in the surge, sway, and yaw directions, respectively.${\tau }_c\in {\mathbb{R}}^3$ denotes the control vector, consisting of forces and moments, and ${\tau }_d\in {\mathbb{R}}^3$ represents the external disturbance vector.

The matrix $J\left(q\right)\in {\mathbb{R}}^{3\times 3}$ represents a transformation matrix related to the yaw Euler angle and is expressed as

$$J\left(q\right)=\left[\begin{array}{cc}R\left(\psi \right)& 0_{2\times 1}\\ 0_{1\times 2}& 1\end{array}\right],R\left(\psi \right)=\left[\begin{array}{cc}cos\left(\psi \right)& -sin\left(\psi \right)\\ sin\left(\psi \right)& cos\left(\psi \right)\end{array}\right],$$

(7)

where the matrix $C\left(v\right)$ represents the combined Coriolis and centripetal forces, while the damping matrix $D\left(v\right)$ accounts for motion-related damping effects.

$$C\left(v\right)=\left[\begin{array}{ccc}0& 0& -m_{22}v\\ 0& 0& m_{11}u\\ m_{22}v& -m_{11}u& 0\end{array}\right],D\left(v\right)=\left[\begin{array}{ccc}{d}_{11}& 0& 0\\ 0& d_{22}& 0\\ 0& 0& d_{33}\end{array}\right].$$

(8)

where $d_{11}$, $d_{22}$, and $d_{33}$ represent the linear damping coefficients in the surge, sway, and yaw directions, respectively.

The port-Hamiltonian model in body-fixed co-ordinates is widely used for passivity-based control of marine vehicles. In contrast, the inertial co-ordinate model [17], related to the NED representation in [36], has not been applied (for control purposes). This model resembles the general port-Hamiltonian framework for mechanical systems (1), and both require a co-ordinate-dependent mass matrix. Since passivity-based sliding mode control [29] employs the general port-Hamiltonian model, we adopted the inertial co-ordinate model for USV control to implement this approach.

$$\left[\begin{array}{c}\dot{q}\\ \dot{p}\end{array}\right]=\left[\begin{array}{cc}0& I_n\\ -I_n& -D_0(q,p)\end{array}\right]\left[\begin{array}{c}{\nabla }_q{H}_0(q,p)\\ {\nabla }_p{H}_0(q,p)\end{array}\right]+\left[\begin{array}{c}0\\ J^{-1}\left(q\right)\end{array}\right]\mathbf{u},$$

(9)

where $q={\left[\begin{array}{ccc}x& y& \psi \end{array}\right]}^T$, and $p=J^{-1}{M}_{u}v$ with $\nu ={\left[\begin{array}{ccc}u& v& r\end{array}\right]}^T$. The matrix $D_0={({\displaystyle \sum _{i=1}^n}{\nabla }_{q_i}\left[J^{-1}\right]Mv{e}_i^T)}^T-{\displaystyle \sum _{i=1}^n}{\nabla }_{q_i}\left[J^{-1}\right]Mv{e}_i^T+J^{-T}C\left(v\right)J^{-1}+J^{-T}D\left(v\right)J^{-1}$ is positive semi-definite and denotes the damping matrix of the system, input mapping matrix, $G_0\left(q\right)=J^{-1}\left(q\right)$, and the input vector, $\mathbf{u}=({\tau }_c+{\tau }_d)$.

The Hamiltonian in this model is defined by the kinetic energy:

$$\begin{array}{ccc}\hfill H_0(q,p)& =& {\displaystyle \frac{1}{2}}{p}^{T}J\left(q\right)M_u{\left(q\right)}^{-1}J{\left(q\right)}^{T}p,\hfill \end{array}$$

(10)

$$\begin{array}{cc}=& {\displaystyle \frac{1}{2}}{p}^{T}M{\left(q\right)}^{-1}p\hfill \end{array}$$

(11)

Remark 1. 

The Hamiltonian functions, linked by $M{\left(q\right)}^{-1}=J\left(q\right)M_u^{-1}J{\left(q\right)}^T$, are equivalent, with the former using J to factorize the mass matrix. Based on kinetic co-energy, expressed via q, this factorization inspires momentum transformations to achieve a port-Hamiltonian model with a constant mass matrix in body-fixed co-ordinates. Such transformations are widely used to simplify controller and observer designs for mechanical systems.

This section presents the unmanned surface vessel (USV) model. We formulate the problem within the port-Hamiltonian system (PHS) framework, setting up the system dynamics in a way that facilitates energy-based control design in the subsequent sections.

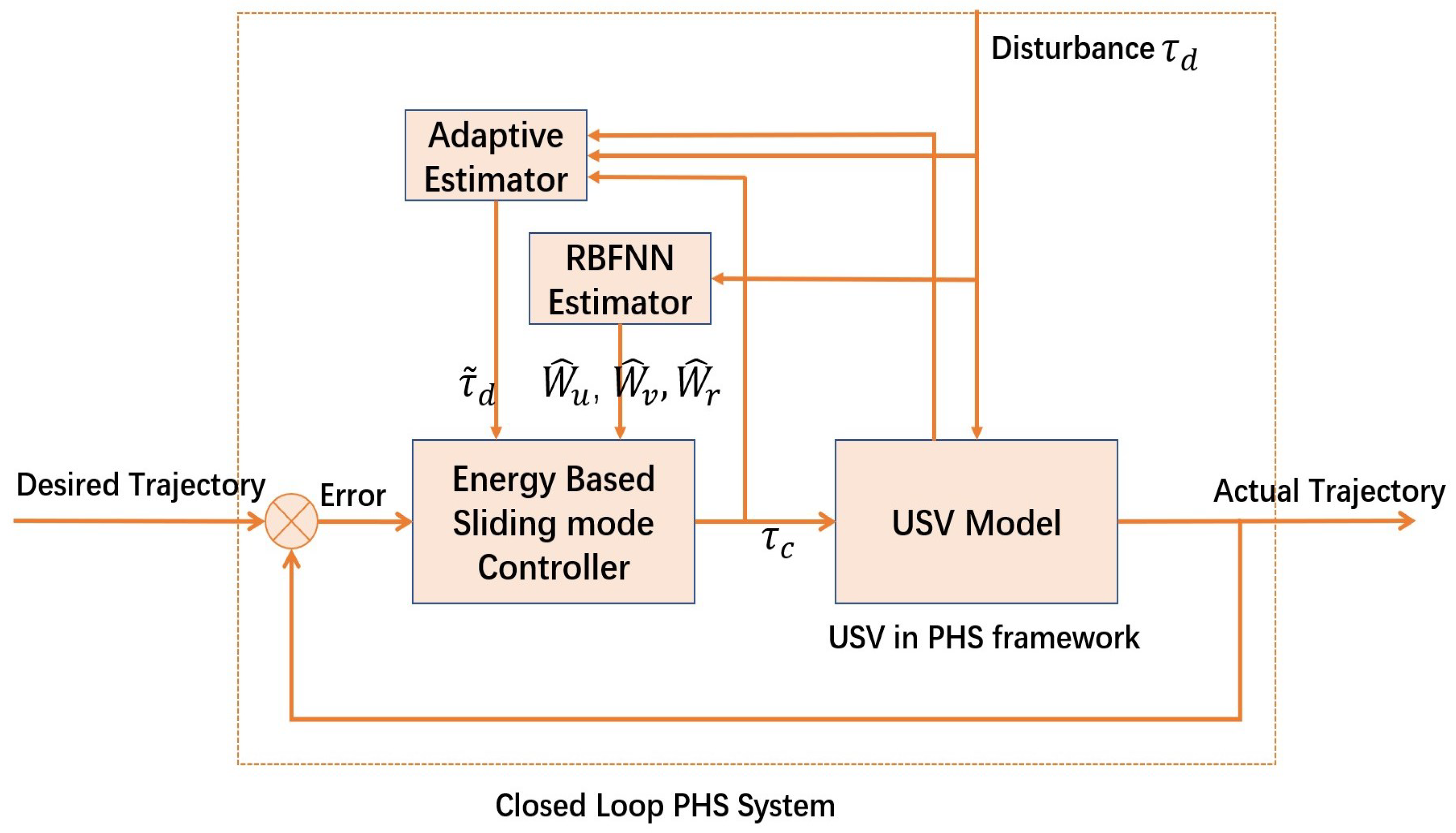
4. Control Design

This section presents the controller design for USVs, aiming to guide the USV along smooth reference paths, ${\xi }_{rd}$, by regulating the control input, ${\tau }_c$. An energy-based sliding mode controller is utilized, while an RBFNN addresses the model uncertainties of the USV. Additionally, the unknown disturbances are estimated using an adaptive estimator. The complete control architecture is illustrated in Figure 2.

4.1. Radial Basis Function Neural Network-Based Uncertainty Estimator

The velocity tracking errors are defined as $u_e=u-u_d,v_e=v-v_d,r_e=r-r_d$, with $u_d$, $v_d$, and $r_d$ representing the desired surge, sway, and yaw velocities, respectively. The velocity tracking error system can be expressed based on the model in (6) as follows:

$$\begin{array}{cc}\hfill & m_{110}{\dot{u}}_e=m_{220}vr-d_{11}u-m_{110}{\dot{u}}_d+{\delta }_u+{\tau }_u,\hfill \\ \hfill & m_{220}{\dot{v}}_e=m_{110}ur-d_{22}v-m_{220}{\dot{v}}_d+{\delta }_v+{\tau }_v,\hfill \\ \hfill & m_{330}{\dot{r}}_e=(m_{110}-m_{220})uv-d_{330}r-m_{330}{\dot{r}}_d+{\delta }_r+{\tau }_r,\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill {\delta }_u& =\Delta m_{220}vr-\Delta d_{11}u-\Delta m_{110}{\dot{u}}_e-\Delta m_{110}{\dot{u}}_d,\hfill \\ \hfill {\delta }_v& =\Delta m_{110}ur-\Delta d_{22}v-\Delta m_{220}{\dot{v}}_e-\Delta m_{220}{\dot{u}}_d,\hfill \\ \hfill {\delta }_r& =(\Delta m_{110}-\Delta m_{220})uv-\Delta d_{33}r-\Delta m_{330}{\dot{r}}_e-\Delta m_{330}{\dot{r}}_d,\hfill \end{array}$$

represent the model uncertainties. Here, $m_{110},m_{220},m_{330},d_{110},d_{220},$ and $d_{330}$ are the nominal parameters of the USV, and the differences between the actual parameters and the nominal parameters are defined as

$$\begin{array}{cc}\hfill \Delta m_{110}& =m_{11}-m_{110},\Delta m_{220}=m_{22}-m_{220},\Delta m_{330}=m_{33}-m_{330},\hfill \\ \hfill \Delta d_{11}& =d_{11}-d_{110},\Delta d_{22}=d_{22}-d_{220},\Delta d_{33}=d_{33}-d_{330}.\hfill \end{array}$$

The system can be expressed in matrix form as

$$M_{un}\dot{\tilde{v}}=-C_n\left(v\right)-D_n\left(v\right)v+{\tau }_C+{\tau }_d+\Delta ,$$

(13)

where $M_{un}$, $C_n\left(v\right)$, and $D_n\left(v\right)$ represent the nominal inertia matrix, Coriolis matrix, and damping matrix, respectively, and $\Delta$ encapsulates the uncertainties in the kinetic system of the USV, with $\Delta ={\left[\begin{array}{ccc}{\delta }_u& {\delta }_v& {\delta }_r\end{array}\right]}^{\top }$.

To address these uncertainties, three RBFNNs, ${\delta }_u$, ${\delta }_v$, and ${\delta }_r$, are utilized to approximate the kinetic system’s uncertainties as follows:

$$\begin{array}{ccc}\hfill {\delta }_u& =& W_u^{\top }{\Psi }_u\left({\chi }_u\right)+{ϵ}_u,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill {\delta }_v& =& W_v^{\top }{\Psi }_v\left({\chi }_v\right)+{ϵ}_v,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\delta }_r& =& W_r^{\top }{\Psi }_r\left({\chi }_r\right)+{ϵ}_r,\hfill \end{array}$$

(16)

where $W_u$, $W_v$, and $W_r$ are the weight vectors; ${\Psi }_u\left({\chi }_u\right)$, ${\Psi }_v\left({\chi }_v\right)$, and ${\chi }_u={[u,v,r,\dot{u},{\dot{u}}_d]}^T$ are the input vectors; $W_u,W_r\in {\mathbb{R}}^l$ represents the RBFNN output weight vectors; ${\Psi }_u\left({\chi }_u\right)=\left[\begin{array}{c}{\psi }_{u_1}\left({\chi }_u\right),\dots ,{\psi }_{u_h}\left({\chi }_u\right)\end{array}\right]$, ${\Psi }_v\left({\chi }_v\right)=\left[\begin{array}{c}{\psi }_{v_1}\left({\chi }_v\right),\dots ,{\psi }_{v_h}\left({\chi }_v\right)\end{array}\right]$, and ${\Psi }_r\left({\chi }_r\right)=\left[\begin{array}{c}{\psi }_{r_1}\left({\chi }_r\right),\dots ,{\psi }_{r_h}\left({\chi }_r\right)\end{array}\right]$ are the radial basis function (RBF) vectors; ${ϵ}_u$, ${ϵ}_v$, and ${ϵ}_r$ represent the approximation residual errors, with the upper bounds of ${\overline{ϵ}}_u$, ${\overline{ϵ}}_v$, and ${\overline{ϵ}}_r$; h is the designed number of hidden layer nodes; and

$$\begin{array}{ccc}\hfill {\psi }_{u_i}\left({\chi }_u\right)& =& exp\left({\displaystyle \frac{-\left|\right|{\chi }_u-{\mu }_{ui}\left|\right|}{{\sigma }_{ui}^2}}\right),\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\psi }_{v_i}\left({\chi }_v\right)& =& exp\left({\displaystyle \frac{-\left|\right|{\chi }_v-{\mu }_{vi}\left|\right|}{{\sigma }_{vi}^2}}\right),\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\psi }_{r_i}\left({\chi }_r\right)& =& exp\left({\displaystyle \frac{-\left|\right|{\chi }_r-{\mu }_{ri}\left|\right|}{{\sigma }_{ri}^2}}\right),\hfill \end{array}$$

(19)

where $i=1,2,\dots ,h,1,2,h,{\mu }_{ui},{\mu }_{vi},{\mu }_{ri}\in {\mathbb{R}}^5$ are the centers of the receptive fields. ${\sigma }_{ui}$, ${\sigma }_{vi}$, and ${\sigma }_{ri}$ are the widths of the RBFs.

The adaptive law of the RBFNN output matrices is designed as

$$\begin{array}{ccc}\hfill {\dot{\hat{W}}}_u& =& {\Gamma }_u({\Psi }_u\left({\chi }_u\right)u_e-k_{wu}{\hat{W}}_u),\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\dot{\hat{W}}}_v& =& {\Gamma }_v({\Psi }_v\left({\chi }_v\right)v_e-k_{wv}{\hat{W}}_v),\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill {\dot{\hat{W}}}_r& =& {\Gamma }_r({\Psi }_r\left({\chi }_r\right)r_e-k_{wr}{\hat{W}}_r),\hfill \end{array}$$

(22)

where ${\hat{W}}_u$, ${\hat{W}}_v$, and ${\hat{W}}_r$ are the estimated weight matrices of $W_u$, $W_v$, and $W_r$, respectively, and ${\Gamma }_u$, ${\Gamma }_v$, ${\Gamma }_r$, $k_{wu}$, and $k_{wv}$, $k_{wr}$ are the designed positive constants.

The system’s uncertainty can be considered alongside external disturbances, resulting in the control input, expressed as

$$\mathbf{u}={\tau }_c+{\tau }_d+\Xi ,$$

(23)

with $\Xi ={\left[\begin{array}{ccc}{W}_u^{\top }{\Psi }_u\left({\chi }_u\right)& W_v^{\top }{\Psi }_v\left({\chi }_v\right)& W_r^{\top }{\Psi }_r\left({\chi }_r\right)\end{array}\right]}^T$.

The control is then designed directly for u to account for these disturbances.

4.2. Adaptive Disturbance Estimation

The estimation of unknown disturbances is based on the immersion and invariance method [38] for a linear PHS. This method has been extended to nonlinear PHSs and applied to a USV system in [34] and is summarized as follows:

Proposition 1. 

For the USV system (6), the estimated disturbance ${\overline{\tau }}_d$ converges to the actual disturbance under the given adaptive law.

$${\overline{\tau }}_d=-\alpha p+\alpha \int (-J{\xi }^T{\displaystyle \frac{\partial H}{\partial \xi }}-J_2{\displaystyle \frac{\partial H}{\partial p}}+{\tau }_c-{\overline{\tau }}_d)dt,$$

(24)

where $\alpha >0$ is a tuning parameter.

For a detailed demonstration, readers are encouraged to refer to [34]. With the adaptive disturbance estimator and the RBF estimator, the control input torque ${\tau }_c$ for the USV is expressed in accordance with (23):

$${\tau }_c=\mathbf{u}-{\overline{\tau }}_d-\Xi$$

(25)

4.3. Energy-Based Sliding Mode Tracking Control of USV

For the purpose of energy-based sliding mode control, the model in (9) must be transformed into a square form. This transformation follows the method outlined in Section 2.2. For the USV system, the matrix $T\left(q\right)$ is computed as follows:

$$T\left(q\right)=J\left(q\right)\sqrt{M_u^{-1}}$$

(26)

Then, the system (9) is transformed into the following one with a square Hamiltonian function $H\left(\xi \right)={\displaystyle \frac{1}{2}}{\xi }^T\xi$:

$$\left[\begin{array}{c}\dot{q}\\ \dot{\xi }\end{array}\right]=\left[\begin{array}{cc}0& T\left(q\right)\\ -T{\left(q\right)}^T& -D(q,\xi )\end{array}\right]\left[\begin{array}{c}{\nabla }_{q}H\left(\xi \right)\\ {\nabla }_{\xi }H\left(\xi \right)\end{array}\right]+\left[\begin{array}{c}0\\ G\left(q\right)\end{array}\right]\mathbf{u}$$

(27)

with $G\left(q\right)=J^T\left(q\right)\sqrt{M_u^{-T}}{J}^{-1}\left(q\right)$, and $D=D_0{M}^{-1}$

We define the tracking errors in the momentum-transformed framework as follows:

$$\left[\begin{array}{c}\tilde{q}\\ \tilde{\xi }\end{array}\right]=\left[\begin{array}{c}q-q_d\left(t\right)\\ \xi -{\xi }_d(q,t)\end{array}\right]$$

(28)

where the desired momentum ${\xi }_d(q,t)$ is defined by

$${\xi }_d(q,t)=T{\left(q\right)}^{-1}{\dot{q}}_d\left(t\right)$$

(29)

The controller transforms the system into the following closed-loop PHS, ensuring the desired tracking error dynamics:

$$\left[\begin{array}{c}\dot{\tilde{q}}\\ \dot{\tilde{\xi }}\end{array}\right]=\left[\begin{array}{cc}-T{\displaystyle \frac{\partial {\mathbf{S}}^T}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial {\mathbf{S}}^{-T}}{\partial \tilde{q}}}& T\\ -T^T& -{\displaystyle \frac{\partial {\mathbf{S}}^{-1}}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial \mathbf{S}}{\partial \tilde{q}}}T\end{array}\right]\left[\begin{array}{c}{\nabla }_{\tilde{q}}{H}_{smc}\\ {\nabla }_{\tilde{\xi }}{H}_{smc}\end{array}\right]$$

(30)

$$H_{smc}={\displaystyle \frac{1}{2}}\left|\right|\tilde{\xi }{\left|\right|}^2+U\left(\mathbf{S}(\tilde{q},\tilde{\xi })\right)$$

(31)

Note that $\mathbf{S}$ is the sliding variable, and the desired Hamiltonian comprises kinetic energy and sliding-variable-dependent potential energy.

To develop the proposed passivity-based sliding mode controller, we begin by introducing the following assumptions:

Assumption 1. 

The matrix $\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi })$ is defined as

$$\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi })={\displaystyle \frac{\partial \mathbf{S}(\tilde{q},\tilde{\xi })}{\partial \tilde{q}}}T\left(q\right){\displaystyle \frac{\partial \mathbf{S}{(\tilde{q},\tilde{\xi })}^T}{\partial \tilde{\xi }}}+{\displaystyle \frac{\partial \mathbf{S}(\tilde{q},\tilde{\xi })}{\partial \tilde{\xi }}}T\left(q\right){\displaystyle \frac{\partial \mathbf{S}{(\tilde{q},\tilde{\xi })}^T}{\partial \tilde{q}}},$$

(32)

which is uniformly positive definite, i.e., there exists a constant $ϵ>0$ so that

$$\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi })>ϵI_m,\forall q,\tilde{q}.\tilde{\xi }.$$

(33)

Assumption 2. 

Let $U:{\mathbb{R}}^m\to \mathbb{R}$ be a positive definite function so that

$$\left|\right|{\nabla }_{\zeta }U\left(\zeta \right)\left|\right|\ge \kappa U{\left(\zeta \right)}^{\rho },\forall \zeta \ne 0,$$

(34)

where $\kappa >0$ and $0\le \rho <{\displaystyle \frac{1}{2}}$.

Remark 2. 

The matrix $\tilde{\mathbf{L}}$ is a positive definite matrix, defined based on the sliding variable $\mathbf{S}$, where the tilde ($˜$) indicates the tracking error that is required for trajectory following. Similarly, U is also a positive definite matrix. Both $\tilde{\mathbf{L}}$ and U are control parameters. Assumptions 1 and 2 are not just technical conditions for the proof but specifically constrain the selection of $\tilde{\mathbf{L}}$ and U. These assumptions ensure that the Lyapunov stability analysis holds, meaning that the proposed control law remains valid. Stability can only be guaranteed when $\tilde{\mathbf{L}}$ and U satisfy these conditions.

Proposition 2. 

For the full actuated USV system (9), the control law

$$\begin{array}{ccc}\hfill \mathbf{u}& =& G{\left(q\right)}^{-1}\{D(q,\xi ){\xi }_d(q,t)+{\displaystyle \frac{\partial {\xi }_d(q,t)}{\partial q}}T\left(q\right)\xi +T{\left(q\right)}^{-1}{\ddot{q}}_d\left(t\right)\hfill \\ & & -\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi }{\nabla }_{\zeta }U\left(\zeta \right)+D(q,\xi )\tilde{\xi }-{\displaystyle \frac{\partial \mathbf{S}{(\tilde{q},\tilde{\xi })}^{-1}}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial \mathbf{S}(\tilde{q},\tilde{\xi })}{\partial \tilde{q}}}T\left(q\right)\tilde{\xi }\}\hfill \end{array}$$

(35)

ensures asymptotic stability of the closed-loop system with respect to disturbances ${\tau }_d$ and guarantees robust trajectory tracking control.

Remark 3. 

With the inclusion of the adaptive disturbance estimator and the RBFNN-based uncertainty estimator, the control input torque, ${\tau }_c$, for the USV is defined in accordance with (23) as ${\tau }_c=w-{\tilde{\tau }}_d-\Xi$.

It is important to note that the control input w, as introduced in the earlier proposition, is not the final control variable. The actual control torque, ${\tau }_c$, accounts for the adaptive disturbance estimation, ${\tilde{\tau }}_d$, and the modeled system uncertainty, Ξ, ensuring accurate trajectory tracking under external disturbances and system uncertainties.

Remark 4. 

The controller that is described in the proposition includes the free parameters $\mathbf{S}(\tilde{q},\tilde{\xi })$ and $U\left(\zeta \right)$. Here, $\mathbf{S}(\tilde{q},\tilde{\xi })$ represents the sliding variable, while $U\left(\zeta \right)$ defines the potential energy associated with the sliding variable.

Proof. 

The proof consists of three parts:

1.

Transformation of the Error System

Using the control law,

$$\mathbf{u}=G{\left(q\right)}^{-1}(D(q,\xi ){\xi }_d(q,t)+{\displaystyle \frac{\partial {\xi }_d(q,t)}{\partial q}}T\left(q\right)\xi +T{\left(q\right)}^{-1}{\ddot{q}}_d\left(t\right)+\mathbf{v})$$

(36)

the closed-loop error PHS is transformed into

$$\left[\begin{array}{c}\dot{\tilde{q}}\\ \dot{\tilde{\xi }}\end{array}\right]=\left[\begin{array}{cc}0& T\left(q\right)\\ -T{\left(q\right)}^T& -D(q,\xi )\end{array}\right]\left[\begin{array}{c}{\nabla }_{\tilde{q}}\tilde{H}\left(\tilde{\xi }\right)\\ {\nabla }_{\tilde{\xi }}\tilde{H}\left(\tilde{\xi }\right)\end{array}\right]+\left[\begin{array}{c}0\\ I\end{array}\right]\mathbf{v}$$

(37)

The time derivative of ${\xi }_d(q,t)$ can be expressed as

$${\dot{\xi }}_d(q,t)={\displaystyle \frac{\partial {\xi }_d(q,t)}{\partial q}}\dot{q}+T{\left(q\right)}^{-1}\ddot{q_d}\left(t\right)={\displaystyle \frac{\partial {\xi }_d(q,t)}{\partial q}}T\left(q\right)\xi +T{\left(q\right)}^{-1}\ddot{q_d}\left(t\right)$$

(38)

For the time derivative of $\tilde{q}$, we have

$$\dot{\tilde{q}}=\dot{q}-\dot{q_d}\left(t\right)=T\left(q\right)(\xi -{\xi }_d\left(t\right))=T\left(q\right)\tilde{\xi }$$

(39)

By substituting the control law (30) into the system dynamics (9) and incorporating the expression for ${\dot{\xi }}_d(q,t)$ from (38), the resulting equation for $\dot{\tilde{\xi }}$ becomes

$$\dot{\tilde{\xi }}=-D(q,\xi )\tilde{\xi }+\mathbf{v}$$

(40)

Equations (39) and (40) are consistent with the closed-loop system Equation (37). Therefore, the control input given by Equation (36) modifies the original system (9) to yield the closed-loop system (37). The first part of the proof is thus established.

2.

Further Transformation Using the Auxiliary Control Input v

By using the auxiliary control input,

$$\mathbf{v}=-\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi }){\nabla }_{\zeta }U\left(\zeta \right)+D(q,\xi )\tilde{\xi }-{\displaystyle \frac{\partial \mathbf{S}{(\tilde{q},\tilde{\xi })}^{-1}}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial \mathbf{S}{(\tilde{q},\tilde{\xi })}^{-1}}{\partial \tilde{q}}}T\left(q\right)\tilde{\xi }$$

(41)

the system is converted into the closed-loop port-Hamiltonian form:

$$\left[\begin{array}{c}\dot{\tilde{q}}\\ \dot{\tilde{\xi }}\end{array}\right]=\left[\begin{array}{cc}-T{\displaystyle \frac{\partial {\mathbf{S}}^T}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial {\mathbf{S}}^{-T}}{\partial \tilde{q}}}& T\\ -T^T& -{\displaystyle \frac{\partial {\mathbf{S}}^{-1}}{\partial \tilde{\xi }}}{\displaystyle \frac{\partial \mathbf{S}}{\partial \tilde{q}}}T\end{array}\right]\left[\begin{array}{c}{\nabla }_{\tilde{q}}{\tilde{H}}_{smc}\\ {\nabla }_{\tilde{\xi }}{\tilde{H}}_{smc}\end{array}\right]$$

(42)

The partial derivatives of $U(\mathbf{S}\left(\tilde{q}\right),\tilde{\xi })$ regarding $\tilde{q}$ and $\tilde{\xi }$ are computed as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial U\left(\mathbf{S}(\tilde{q},\tilde{\xi })\right)}{\partial \tilde{q}}}& =& {\displaystyle \frac{\partial U\left(\zeta \right)}{\partial \zeta }}{\displaystyle \frac{\partial \mathbf{S}(\tilde{q},\tilde{\xi })}{\partial \tilde{q}}}\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial U\left(\mathbf{S}(\tilde{q},\tilde{\xi })\right)}{\partial \tilde{\xi }}}& =& {\displaystyle \frac{\partial U\left(\zeta \right)}{\partial \zeta }}{\displaystyle \frac{\partial \mathbf{S}(\tilde{q},\tilde{\xi })}{\partial \tilde{\xi }}}\hfill \end{array}$$

(44)

By applying the input (41) to the error system (37) and utilizing the derived expressions for ${\displaystyle \frac{\partial U\left(\mathbf{S}(\tilde{q},\tilde{\xi })\right)}{\partial \tilde{q}}}$ and ${\displaystyle \frac{\partial U\left(\mathbf{S}(\tilde{q},\tilde{\xi })\right)}{\partial \tilde{\xi }}}$, it is demonstrated that (37) transitions into the system (30). The second part of the proof is thus established.

3.

Stability Analysis

Finally, we prove that the closed-loop error system (42) is asymptotically stable using the Lyapunov function ${\tilde{H}}_{smc}$.

In order to establish the finite time convergence of the sliding variable $\zeta$, we introduce the following co-ordinate transformation:

$$\left[\begin{array}{c}\tilde{q}\\ \tilde{\xi }\end{array}\right]\to \left[\begin{array}{c}\zeta \\ \tilde{\xi }\end{array}\right]=\left[\begin{array}{c}\mathbf{S}(\tilde{q},\tilde{\xi })\\ \tilde{\xi }\end{array}\right]$$

(45)

With the co-ordinate transformation applied, the closed-loop system is then expressed as

$$\left[\begin{array}{c}\dot{\zeta }\\ \dot{\tilde{\xi }}\end{array}\right]=\left[\begin{array}{cc}-\tilde{\mathbf{L}}& 0\\ -{\displaystyle \frac{\partial {\mathbf{S}}^{-1}}{\partial \xi }}\mathbf{L}& -{\displaystyle \frac{\partial {\mathbf{S}}^{-1}}{\partial \xi }}{\displaystyle \frac{\partial \mathbf{S}}{\partial q}}T\end{array}\right]\left[\begin{array}{c}{\nabla }_{\zeta }{\tilde{H}}_{smc}\\ {\nabla }_{\tilde{\xi }}{\tilde{H}}_{smc}\end{array}\right]$$

(46)

With the Hamiltonian, it is expressed as

$$H_{smc}={\displaystyle \frac{1}{2}}\left|\right|\tilde{\xi }{\left|\right|}^2+U\left(\zeta \right)$$

(47)

The dynamic of the sliding variables, $\zeta$, is then

$$\dot{\zeta }=-\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi }){\nabla }_{\zeta }U\left(\zeta \right)$$

(48)

The designed energy function, $U\left(\zeta \right)$, can be considered a Lyapunov candidate function according to Assumption 2. Since $U\left(\zeta \right)$ is positive definite, we initially treat it as a Lyapunov candidate function. The specific condition $U\left(0\right)=0$ will be addressed and computed in the subsequent proofs.

In the closed-loop system (30), the reaching mode and sliding mode are analyzed separately to establish the upper bound of $U\left(\zeta \right)$.

Initially, during the reaching mode (${\zeta }_i\ne 0\forall i$), we studied the time derivative of $U\left(\zeta \right)$.

$$\begin{array}{ccc}\hfill \dot{U}& =& {\nabla }_{\zeta }U{\left(\zeta \right)}^T(-\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi }){\nabla }_{\zeta }U\left(\zeta \right)\hfill \\ & \le & -ϵ\left|\right|{\nabla }_{\zeta }U\left(\zeta \right){\left|\right|}^2\hfill \\ & \le & -ϵ{\kappa }^2{\nabla }_{\zeta }U{\left(\zeta \right)}^{2\rho }\hfill \end{array}$$

(49)

The above equation holds true under Assumptions 1 and 2.

In the case of sliding modes, consider scenarios where some ${\zeta }_i$ are equal to zero. Specifically, assume that there are k sub-sliding modes and $m-k$ sub-reaching modes. This implies that k components of $\zeta$ are constrained to zero, while the remaining $m-k$ components have yet to reach zero, with $1\le k\le m-1$. Define ${\zeta }_{sm}={({\zeta }_1,\dots ,{\zeta }_k)}^T$ to represent the sliding mode components and ${\zeta }_{rm}={({\zeta }_{k+1},\dots ,{\zeta }_m)}^T$ to represent the reaching mode components. For simplicity, let ${\zeta }_{sm}={\dot{\zeta }}_{sm}=0$ and ${\zeta }_{rm}\ne 0$. Under these conditions, the dynamics of ${\zeta }_i$ (48) can be expressed as

$${\displaystyle \frac{d}{dt}}\left(\begin{array}{c}{\zeta }_{sm}\\ {\zeta }_{rm}\end{array}\right)=-\left(\begin{array}{cc}{\tilde{\mathbf{L}}}_{11}(q,\tilde{q},\tilde{\xi })& {\tilde{\mathbf{L}}}_{12}(q,\tilde{q},\tilde{\xi })\\ {\tilde{\mathbf{L}}}_{12}{(q,\tilde{q},\tilde{\xi })}^{\top }& {\tilde{\mathbf{L}}}_{22}(q,\tilde{q},\tilde{\xi })\end{array}\right)\left(\begin{array}{c}{\nabla }_{{\zeta }_{sm}}U\left(\zeta \right)\\ {\nabla }_{{\zeta }_{rm}}U\left(\zeta \right)\end{array}\right)=\left(\begin{array}{c}0\\ \ast \end{array}\right),$$

(50)

where ∗ represents an arbitrary value. Based on (50) and Assumption 2, the following holds:

$$\begin{array}{ccc}\hfill \kappa U{\left(\zeta \right)}^p& \le & \left|\right|{\nabla }_{\zeta }U(\mathbf{S}(\tilde{q},\tilde{\xi })\left|\right|\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& =& ∥\underset{{\Theta }^k(q,\xi )}{\underbrace{\left(\begin{array}{c}-{\tilde{\mathbf{L}}}_{11}{(q,\tilde{q},\tilde{\xi })}^{-1}{\tilde{\mathbf{L}}}_{12}(q,\tilde{q},\tilde{\xi })\\ I_{m-k}\end{array}\right)}}{L}^{*}(q,\xi ){\nabla }_{{\zeta }_m}U\left(\zeta \right)∥\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& =& \parallel {\Theta }^k(q,\xi )\parallel \parallel {\nabla }_{{\zeta }_m}U\left(\zeta \right)\hfill \end{array}$$

(53)

$$\begin{array}{ccc}& \le & {\theta }_{max}^k\parallel {\nabla }_{{\zeta }_m}U\left(\zeta \right)\parallel \hfill \end{array}$$

(54)

In this context, ${\theta }_{max}^k\ge 1$ denotes the maximum value of $\parallel {\Theta }^k(q,\xi )\parallel$ in the vicinity of the origin. The resulting system is characterized as

$${\dot{\zeta }}_{rm}=-\underset{\tilde{\mathbf{L}}/{\tilde{\mathbf{L}}}_{11}(q,\tilde{q},\tilde{\xi })}{\underbrace{({\tilde{\mathbf{L}}}_{22}-{\tilde{\mathbf{L}}}_{12}^T{\tilde{\mathbf{L}}}_{11}^{-1}{\tilde{\mathbf{L}}}_{12})}}{\nabla }_{{\zeta }_m}U\left(\zeta \right)$$

(55)

By calculating the time derivative of $U\left(\zeta \right)$, we obtain the following:

$$\begin{array}{ccc}\hfill \dot{U}& =& \left(\begin{array}{cc}{\displaystyle \frac{\partial U\left(\zeta \right)}{\partial {\zeta }_{sm}}}& {\displaystyle \frac{\partial U\left(\zeta \right)}{\partial {\zeta }_{rm}}}\end{array}\right)\left(\begin{array}{c}{\dot{\zeta }}_{sm}\\ {\dot{\zeta }}_{rm}\end{array}\right)\hfill \\ & =& -{\nabla }_{{\zeta }_m}^T(\tilde{\mathbf{L}}/{\tilde{\mathbf{L}}}_{11}){\nabla }_{{\zeta }_m}U\hfill \\ & \le & -ϵ\parallel {\nabla }_{{\zeta }_m}{U\left(\zeta \right)\parallel }^2\le -{\displaystyle \frac{{ϵ}^2}{{\left(l_{max}^k\right)}^2}}U{\left(\zeta \right)}^{2p}\hfill \end{array}$$

(56)

$\tilde{\mathbf{L}}/{\tilde{\mathbf{L}}}_{11}(q,\tilde{q},\tilde{\xi })>ϵI_{m-k}$ follows from Assumption 1, and $\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi })$ is as shown below:

$$\tilde{\mathbf{L}}=\left(\begin{array}{cc}{I}_k& {\tilde{\mathbf{L}}}_{12}{\tilde{\mathbf{L}}}_{11}^{-1}\\ 0& I_{m-k}\end{array}\right)\left(\begin{array}{cc}{\tilde{\mathbf{L}}}_{11}& 0\\ 0& \tilde{\mathbf{L}}/{\tilde{\mathbf{L}}}_{11}(q,\tilde{q},\tilde{\xi })\end{array}\right)\left(\begin{array}{cc}{I}_k& {\tilde{\mathbf{L}}}_{11}^{-1}{\tilde{\mathbf{L}}}_{12}\\ 0& I_{m-k}\end{array}\right)$$

(57)

From (49) and (56), we can conclude that the inequality holds for a constant $\alpha \le 0$:

$$\dot{U}\le -{\displaystyle \frac{ϵ{\kappa }^2}{{\alpha }^2}}{U}^{2\rho }$$

(58)

In the reaching mode, $\alpha =1$, whereas in the sliding mode, $\alpha ={\theta }_{\max }^k$.

Thus, inequality (58) applies to the two cases, ensuring that the time derivative of $U\left(\zeta \right)$ is upper-bounded.

By integrating (58) with respect to time, the designed energy function $U\left(\zeta \right)$ is

$$U\left(\zeta \left(t\right)\right)\le {\left({\displaystyle \frac{-ϵ{\kappa }^2}{{\alpha }^2}}(t-t_0)+U{\left(\zeta \left(t_0\right)\right)}^{1-2\rho }\right)}^{{\displaystyle \frac{1}{1-2\rho }}}.$$

(59)

$U\left(\zeta \right)$ reaches zero in finite time $t_0+{\alpha }^{2}U{\left(\zeta \left(t_0\right)\right)}^{1-2\rho }/\left(ϵ{\kappa }^2\right)$, which leads to the finite time convergence of $\zeta$ to zero.

Finally, we prove the asymptotic stability of the closed-loop system. The derivative of the Hamilton function $H_{smc}$ in the reaching mode ${\zeta }_i\ne 0$ is computed as

$${\dot{H}}_{smc}=-{\displaystyle \frac{1}{4}}{∥{\displaystyle \frac{\partial {\zeta }^{\top }}{\partial \tilde{\xi }}}\tilde{\xi }+2{\nabla }_{\zeta }U∥}_{\tilde{\mathbf{L}}}^2-{\displaystyle \frac{1}{4}}{∥{\displaystyle \frac{\partial {\zeta }^{\top }}{\partial \tilde{\xi }}}∥}_{\tilde{\mathbf{L}}}^2<0.$$

(60)

If sub-sliding modes satisfy ${\dot{\zeta }}_{sm}=0,{\dot{\zeta }}_{rm}\ne 0$, then we have that

$${\dot{H}}_{smc}=-{\displaystyle \frac{1}{4}}{∥{\displaystyle \frac{\partial {\mathbf{S}}^{\top }}{\partial \tilde{\xi }}}\xi +2\left(\begin{array}{c}0\\ {\dot{\zeta }}_{rm}\end{array}\right)∥}_{{\tilde{\mathbf{L}}}^{-1}}^2-{\displaystyle \frac{1}{4}}{∥{\displaystyle \frac{\partial {\mathbf{S}}^{\top }}{\partial \tilde{\xi }}}\tilde{\xi }∥}_{\tilde{\mathbf{L}}}^2<0,$$

(61)

In the state space of the equivalent system with ${\dot{\zeta }}_{sm}=0$, it also holds that in the sliding mode $\zeta =0$,

$$\dot{\zeta }=\tilde{\mathbf{L}}(q,\tilde{q},\tilde{\xi }){\nabla }_{\zeta }U\left(\zeta \right)=0.$$

(62)

The dynamic of $H_{smc}$ is then

$${\dot{H}}_{smc}=-{\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{\partial {\mathbf{S}}^{\top }}{\partial \tilde{\xi }}}\tilde{\xi }∥}_{\tilde{\mathbf{L}}}^2<0,$$

(63)

In conclusion, the above equation for the sliding surface $\zeta =0$ ensures the asymptotic stability of the tracking errors.

□

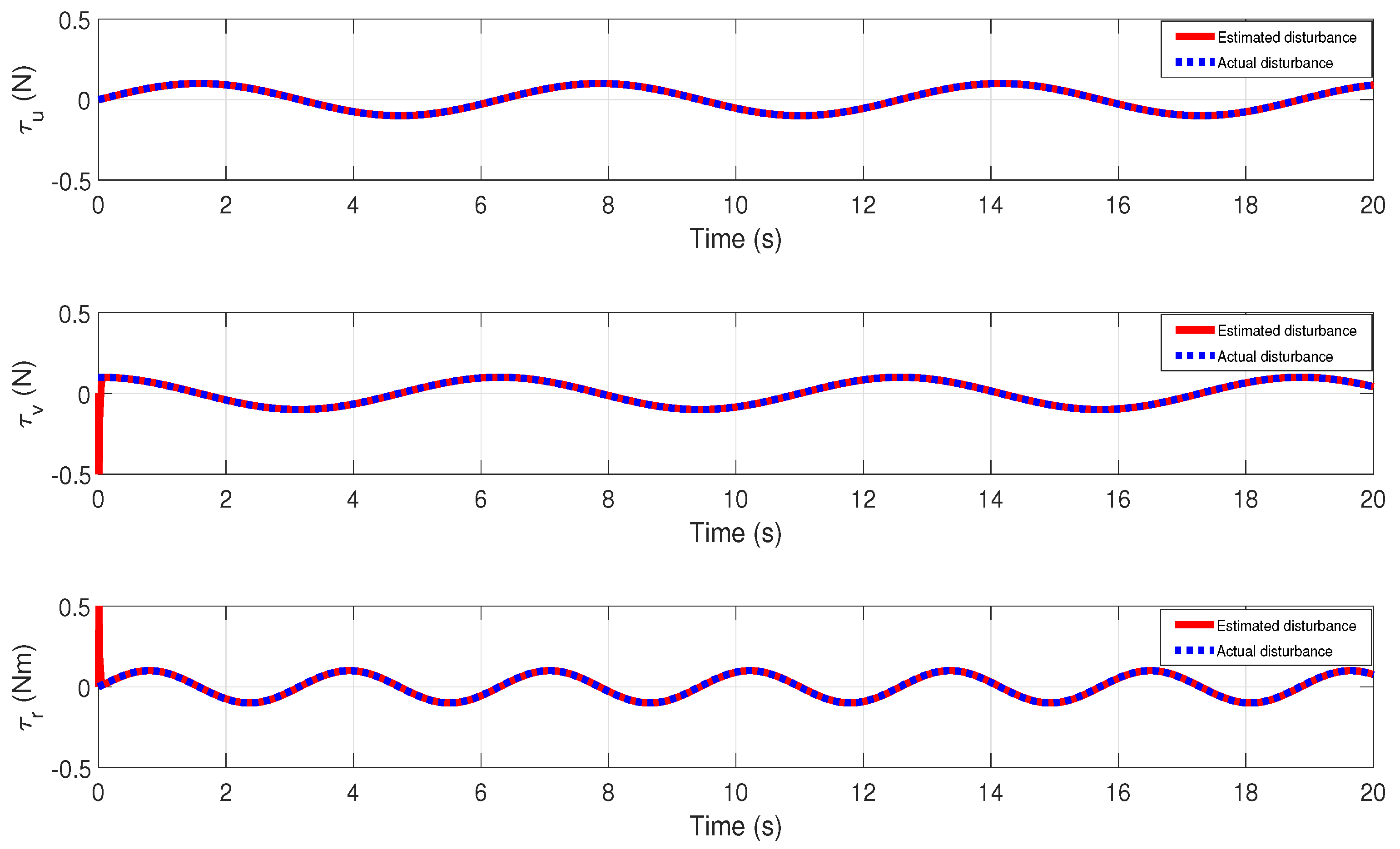
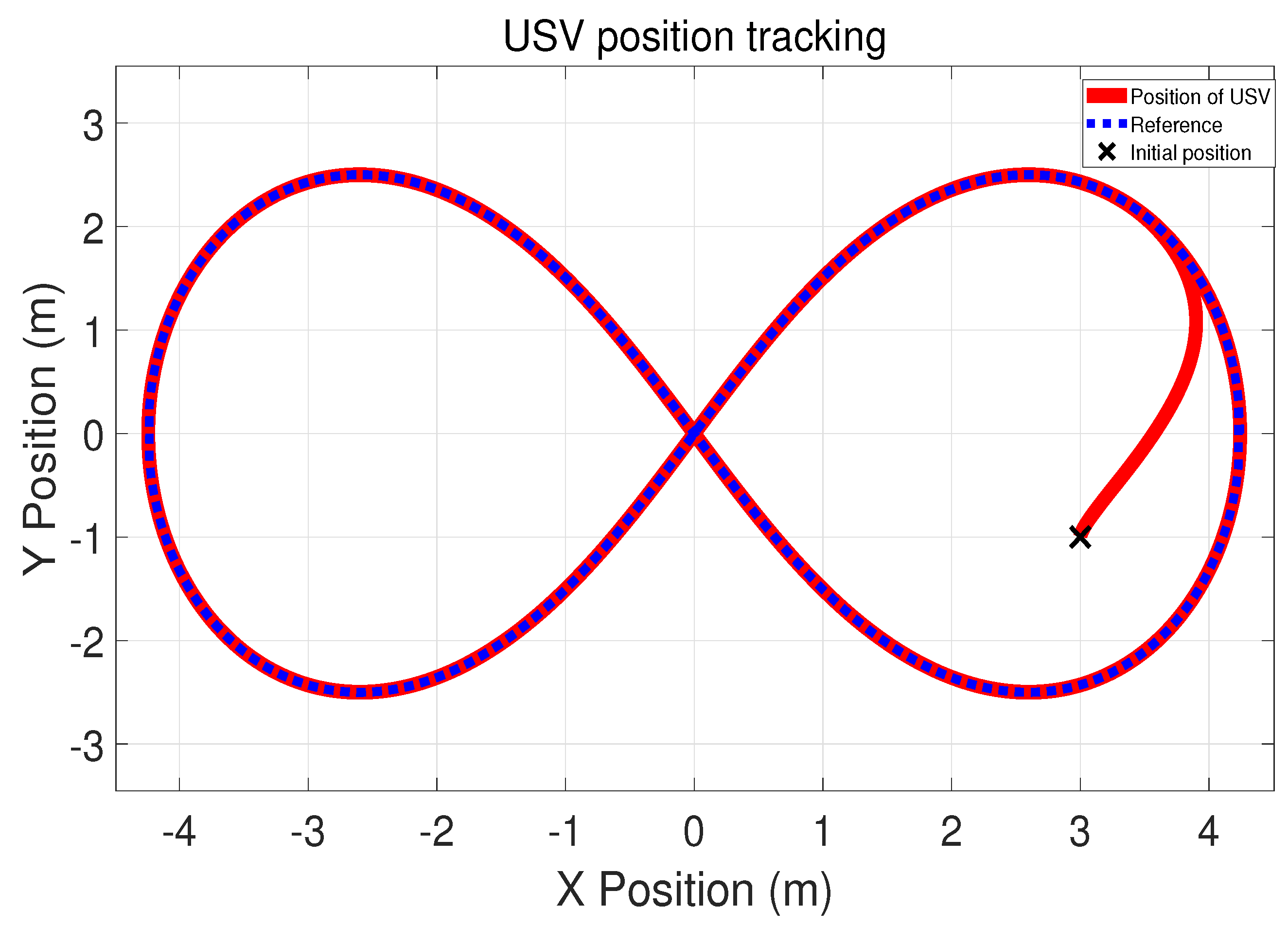
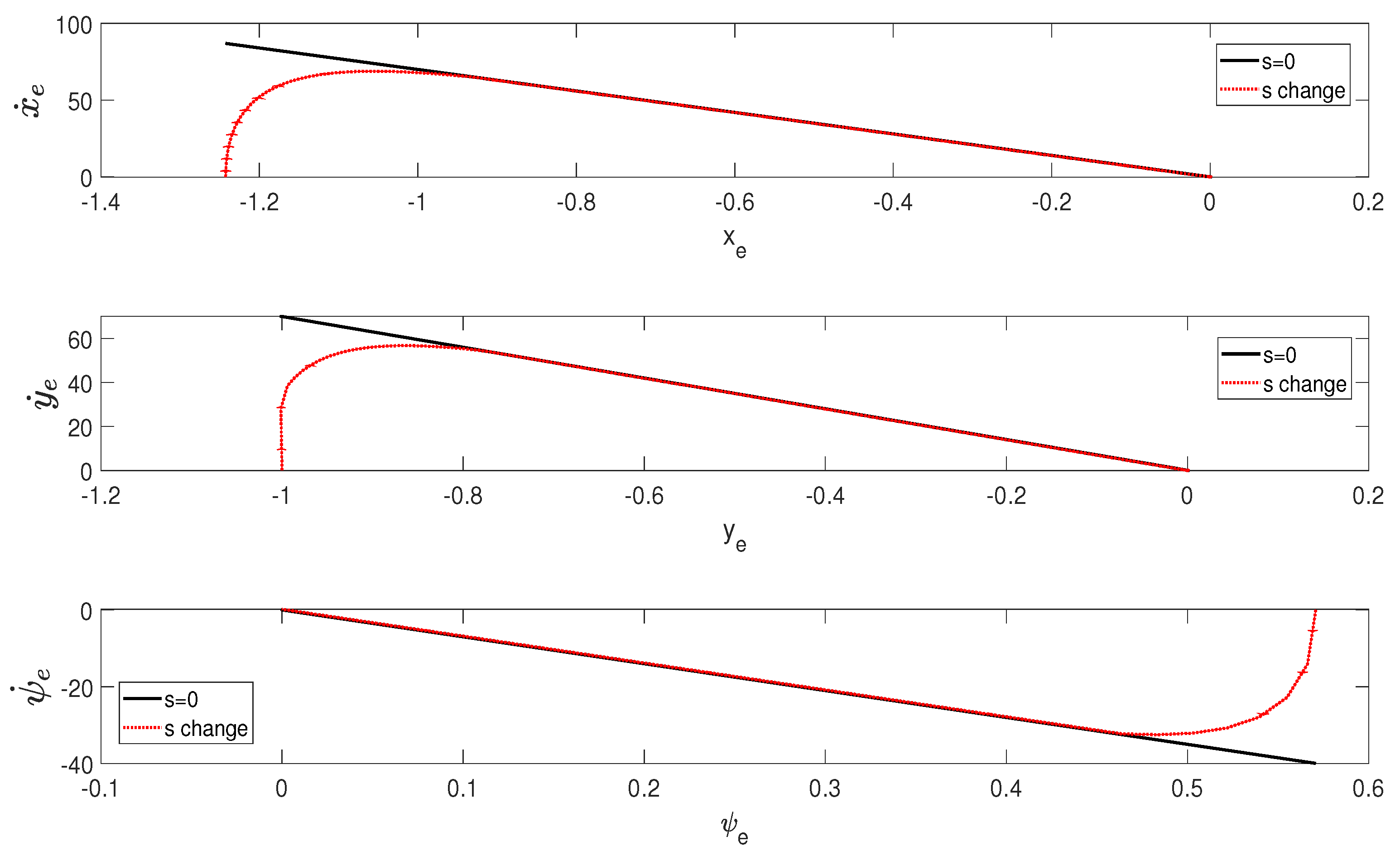
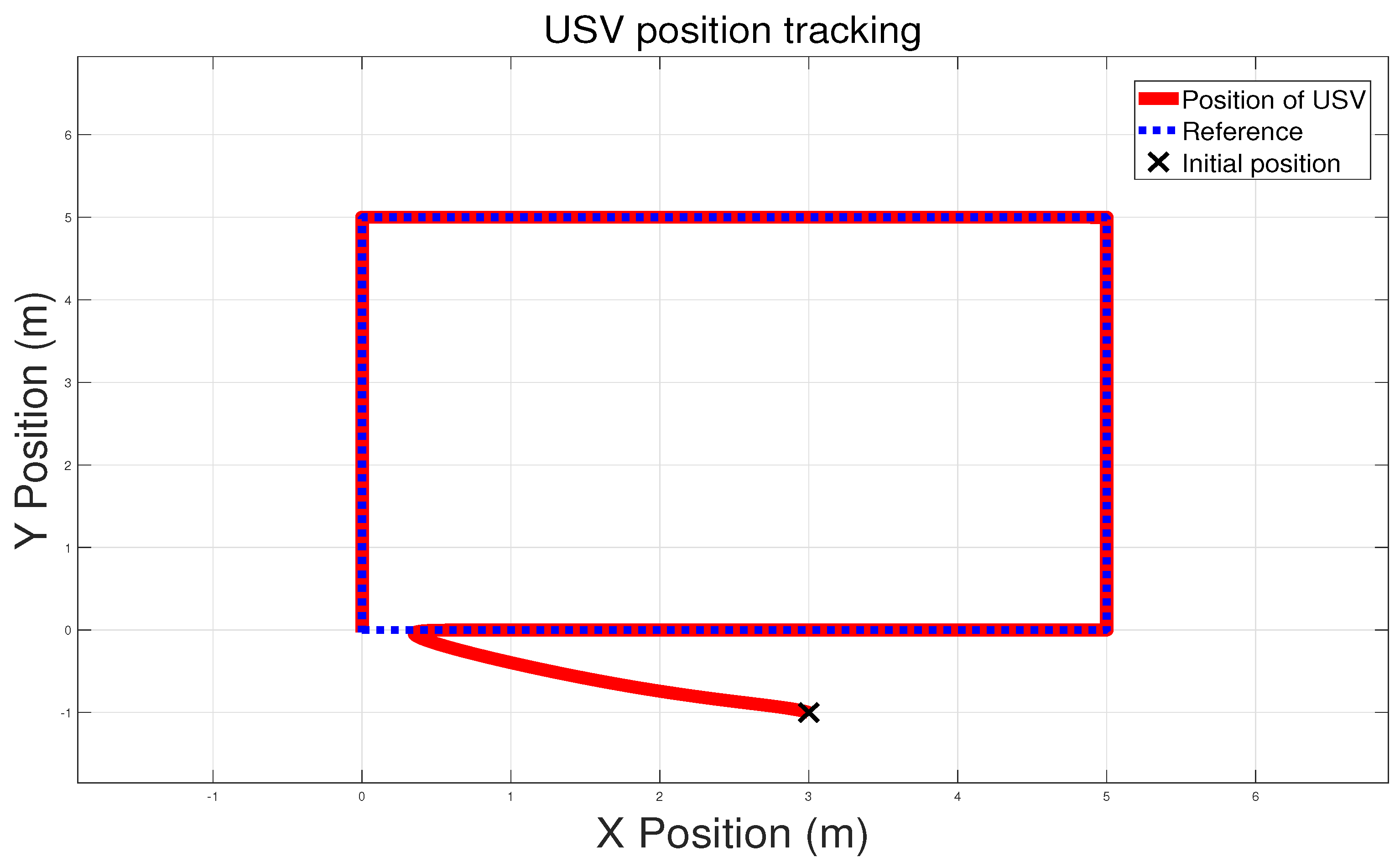
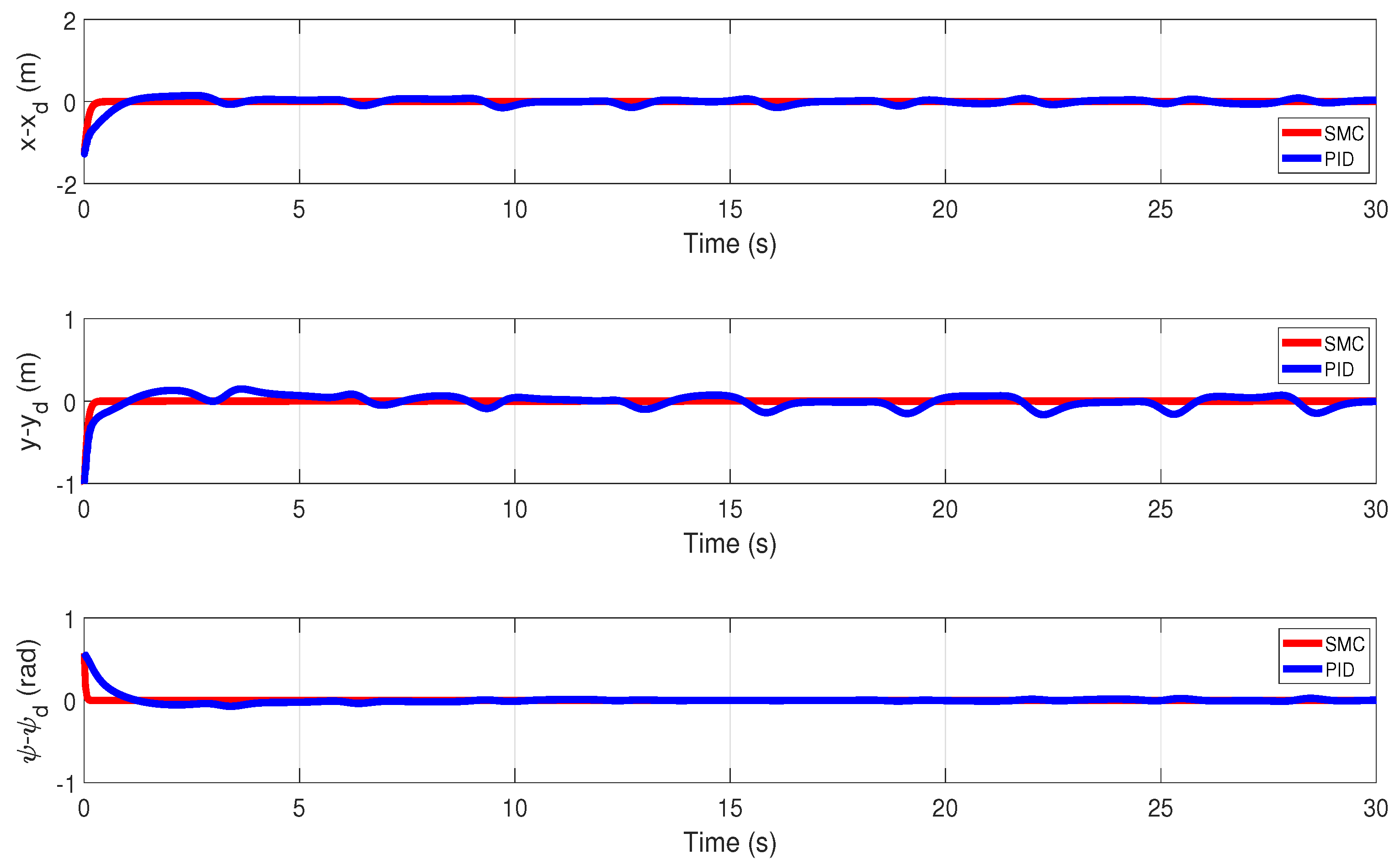
5. Simulation

This section details the application of passivity-based sliding mode control to enable a USV to track a specified trajectory. The objective is to ensure precise trajectory tracking using the control law. The proposed control strategy was validated using numerical simulations.

The initial position is defined as $\left[\begin{array}{c}-3\mathrm{m},-1\mathrm{m}\end{array}\right]$. The simulation uses a figure-eight trajectory as the reference to evaluate the controller’s ability to handle bidirectional rotations. This trajectory effectively represents the dynamic behavior of two circular paths while introducing additional complexity, making it a more comprehensive test of control performance:

$$\left[\begin{array}{c}{x}_d\\ y_d\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{3\sqrt{2}cos\left(t\right)}{1+si{n}^2\left(t\right)}}\\ {\displaystyle \frac{5\sqrt{2}sin\left(t\right)cos\left(t\right)}{1+si{n}^2\left(t\right)}}\end{array}\right]$$

(64)

We first estimate the unknown disturbance ${\tau }_d$ using (24), obtaining ${\tilde{\tau }}_d$. Then, the control law (35) is applied, with all parameters being determined using MatLab R2023b. The disturbance caused by slowly varying winds, currents, and waves affecting the USV system is modeled by the following equation:

$${\tau }_d=\left[\begin{array}{c}0.1sin\left(0.1t\right)\\ 0.1cos\left(0.1t\right)\\ 0.1sin\left(0.2t\right)\end{array}\right]$$

(65)

We consider the estimator gain $\alpha =\mathrm{diag}[70,70,70]$. Figure 3 illustrates the difference in the estimated disturbances, $\widetilde{{\tau }_d}$, and the actual environmental forces, ${\tau }_d$, in the $x_b$, $y_b$, and rotational directions. The results clearly demonstrate that the proposed disturbance observer accurately tracks the unknown disturbances, with the error rapidly converging to zero.

An RBFNN with 128 nodes ($m=128$) is employed, where the Gaussian function’s width is $c_{ij}=0.6$, and the nodes are uniformly distributed in the range of $[-10,10]$. The model uncertainty estimations obtained by the RBFNN, denoted as ${\delta }_u$, ${\delta }_v$, and ${\delta }_r$, are illustrated in Figure 4.

The control strategy outlined in (35) was applied to stabilize the USV and ensure that it tracks the desired trajectory (64) in the presence of disturbances. In (35), the control input u is expressed as $u={\tau }_c+\widetilde{{\tau }_d}$, where $\widetilde{{\tau }_d}$ is the estimation of external disturbances. Importantly, ${\tau }_c$ represents the actual control variables that can be directly applied to the USV for maneuvering and stabilization. The design parameters are set as follows:

$$\zeta =\tilde{\mathbf{S}}(\tilde{q},\tilde{\xi })=\left[\begin{array}{cc}2& 0\\ 2& 2\end{array}\right]\left[\begin{array}{c}{\tilde{q}}_1\\ {\tilde{q}}_2\end{array}\right]+\tilde{\xi }$$

(66)

$$U\left(\zeta \right)={\alpha \left|\right|\zeta \left|\right|}_1+{\displaystyle \frac{\beta }{2}}{\left|\right|\alpha \left|\right|}^2,with \alpha =10,\beta =5$$

(67)

Figure 5, Figure 6 and Figure 7 depict the system’s performance in tracking the desired trajectory. In Figure 5, the displacement variables in the x and y axes directions and $\psi$ demonstrate asymptotic convergence, with the controlled variables aligning perfectly with their desired counterparts. Correspondingly, Figure 6 highlights the rapid and steady decay of the errors, confirming that they asymptotically converge to zero. Figure 7 offers a clearer view in the X-Y plane, demonstrating precise convergence.

Figure 8 illustrates the behavior of the sliding variables. When comparing this with Figure 5, we can observe that the sliding variables rapidly converge to zero at the initial stage (in $0.5$ s), indicating the controller’s effectiveness in quickly initiating trajectory tracking. Subsequently, the sliding variables exhibit transient instability during abrupt changes in either x or y-axis displacement. However, through controller adjustment, they promptly return to zero, demonstrating the system’s robustness in maintaining accurate trajectory tracking despite sudden variations.

Figure 9 illustrates the phase portraits of x, y, and $\psi$. The figure shows that the trajectories of x, y, and $\psi$ eventually converge with the sliding surface $s=0$. This behavior indicates that the system transitions into the sliding mode as expected under the designed control law. As the reaching phase drives the system toward the sliding surface, the system dynamics are constrained along the surface. The convergence of x, y, and $\psi$ to $s=0$ ensures robust performance and stability; this demonstrates effective tracking and control.

We included a rectangular trajectory in the simulation to better assess the controller’s ability to handle sharp turns.

As depicted in Figure 10, the controller effectively tracks the rectangular trajectory, showcasing its ability to manage sudden direction changes while ensuring stability and accuracy throughout rapid transitions.

To further validate the advantages of our proposed method, we implemented a PID controller for comparison and conducted an error analysis. We linearized the USV model and then used the MATLAB PID Tuning Toolbox to obtain the PID control parameters.

Figure 11 and Figure 12 show that our controller achieves lower tracking errors, particularly during USV turning maneuvers. In contrast, the PID controller exhibits noticeably larger errors, while our method maintains accuracy, with the errors approaching zero.

6. Conclusions

In conclusion, this study successfully addressed the trajectory tracking control problem for USVs under unknown environmental disturbances. This was achieved by integrating sliding mode control with the port-Hamiltonian framework into a unified passivity-based sliding mode control strategy. By formulating the USV dynamics in the inertial co-ordinates within the port-Hamiltonian framework, the proposed method preserves the system’s passivity properties while ensuring robustness to external disturbances. An adaptive disturbance estimation mechanism was incorporated into the sliding mode controller to accurately identify and compensate for environmental forces affecting USV motion. This approach maintains the Hamiltonian structure and guarantees robust trajectory tracking. The stability of the closed-loop system was rigorously analyzed and proven. The simulation results demonstrate the proposed control scheme’s strong performance, precisely tracking figure-eight and square trajectories. Our method shows clear quantitative advantages over the PID controller in disturbance rejection and tracking accuracy.

The proposed passivity-based sliding mode control framework holds significant potential for extension to under-actuated USVs. These systems, characterized by fewer control inputs than degrees of freedom, pose additional challenges in trajectory tracking and disturbance rejection. Adapting this unified control strategy to under-actuated configurations would involve leveraging the passivity-based sliding mode approach to fully exploit the system’s natural dynamics while addressing its control limitations. Future research will focus on extending this framework to under-actuated USVs, broadening its applicability to a wider range of marine systems.