Application of Hexagonal Reference Maps in Gravity-Assisted Inertial Navigation

Abstract

High-resolution and high-precision marine gravity reference maps are core prerequisites for the practical application of gravity-assisted inertial navigation algorithms, and their accuracy directly determines the performance of the navigation system. In view of the problems existing in the current geographic rectangular grid gravity reference map, such as severe polar deformation, poor adjacent consistency, and low positioning accuracy in high latitudes, this study introduces a hexagonal grid system to construct a gravity reference map. It systematically analyzes its compatibility and accuracy in navigation applications. A multi-resolution hexagonal grid scheme with a 7-aperture structure is further proposed to meet the characterization requirements of gravitational fields with different complexities. Experimental verification shows that the accuracy of the gravity-assisted inertial navigation algorithm improved by 0.4%, while that of gravity sequence matching improved by 50%. The proposed hybrid resolution grid can achieve a maximum gravity data compression rate of 68% while ensuring navigation accuracy, especially with regard to the computational efficiency and accuracy requirements of gravity-assisted inertial navigation.

1. Introduction

Gravity anomaly reference maps are key to implementing gravity-assisted inertial navigation. Reference map errors are a major concern in gravity-assisted inertial navigation, together with gravity measurement error and navigation algorithm error. The reference map error includes raw data error and quantization error (linearization error). The original data for constructing the benchmark map of marine gravity anomalies include satellite altimetry data, aerial gravity measurements, and marine gravity measurements. Their errors are coupled with each other and not easy to separate. However, quantification errors can be alleviated by simply changing the organization method used for gravity data. Since field gravity measurements in practice are not uniformly distributed, conducting regular discrete quantification of the measured Earth’s gravity field data is necessary. Geographical rectangular grids are commonly used as an organizational method. The definition of the coordinates as well as the horizontal and vertical arrangement of these grids are better attuned with people’s thinking patterns, providing advantages such as data storage management and multi-resolution analysis. However, notable disadvantages include high-latitude degradation and lack of adjacent consistency.

In recent years, many scholars have focused their research on other spherical standard grid systems to address the problems associated with geographical rectangular grids. Hexagonal grids, with their better adjacent consistency, greater angular resolution, and globally uniform isovolume, have become vital to the construction of global data integration systems.

Previous studies [1,2] have employed hexagonal grids in the spherical harmonic synthesis theory of the Earth’s gravitational field. Numerical experiments proved that the numerical integration discretization errors of the three types of kernel functions—Stokes, Hotine, and Poisson—in the hexagonal grid were superior to those in the same number of quadrilateral geographic grids. Gravity-assisted inertial navigation uses local linearization for nearby grid points to construct the observation equation; therefore, the discretization error of numerical differentiation needs to be considered. A previous study [3] used hexagonal grid-like gravity data to solve the gravity field model. The results show that the order error is smaller than that obtained by solving the quadrilateral grid data. Additionally, fewer datasets are used, indicating a certain degree of information redundancy in the gravity data organized by quadrilateral grids. For the isotropic gravitational field of Earth, the adoption of global hexagonal mesh partitioning can enhance the theoretical accuracy of data processing. Previous studies have applied multi-resolution hexagonal grids to terrain data analyses [4], including the statistical calculation of terrain parameters. Moreover, the results demonstrate that analysis based on multi-resolution hexagonal grids has relatively high computational efficiency. A study [5] found that the representation error of the numerical model of gravity anomaly under the hexagonal grid was smaller than that of the quadrilateral geographic grid, and the difference in representation error between the two became smaller as the subdivision level increased. The representative error expresses the difference between the reference map data and the actual gravity measurement (that is, the magnitude of the reference map error). The smaller the representative error of the gravity anomaly reference map, the better the accuracy for gravity-assisted inertial navigation. In addition to constructing the reference map with the original measurement data, appropriately interpolating, reconstructing, and refining the existing gravity reference map [6,7,8] can improve spatial resolution and thus enhance the positioning accuracy of gravity-assisted inertial navigation.

Additionally, rotation transformation can be adopted in the solution associated with spherical harmonic synthesis of gravitational fields to enhance computational efficiency [9] and eliminate the influence of non-equal latitude distribution of numerous hexagonal grid points. Hexagonal grids are widely used in wargame simulation [10], the construction of marine contour maps [11], and spatial data visualization [12]. In addition, hexagonal grids can also be combined with artificial intelligence technologies such as machine learning and deep learning [13,14], such as hexagonal convolutional neural networks.

The organization and application of global gravity reference maps will inevitably involve a large amount of data. If a fixed resolution is uniformly adopted for all, a large amount of data redundancy will occur in areas with gentle gravity changes. Consequently, expressing its complexity and sudden changes in an evolving gravitational field environment will be impossible. For geographical rectangular grids, the expression of multi-resolution grids is possible. For hexagonal grids with their particular structure, however, one hexagon cannot be split into multiple hexagons and can only be composed of multiple small hexagons spliced together to form a “generalized balanced triplet.” This limits the multi-resolution applications based on hexagonal grids. The existing multi-level hexagons can be classified into 3-aperture, 4-aperture, and 7-aperture types based on the area ratio of their upper and lower levels. A study [15] has proposed a multi-resolution hexagonal global mesh partitioning and address coding method, which can seamlessly handle and represent global meshes.

Therefore, constructing a high-precision gravity reference map is of great significance for high-precision autonomous navigation of underwater vehicles. The existing gravity-assisted inertial navigation algorithm based on geographic rectangular grids can almost be equivalently applied to hexagonal grids, creating favorable conditions for historical algorithmic achievements. In this study, the ISEA7H (Icosahedral Snyder Equal Area aperture 7 Hexagon) grid system was generated by H3 through spherical center projection, and the regional geographic rectangular grid and hexagonal grid data were constructed using the DTU [16] (Technical University of Denmark) marine gravity anomaly data. Subsequently, a random linearization method was proposed for gravity-assisted inertial navigation based on the hexagonal grid model. Combined with the functions of the known analytical expressions, experiments were designed to verify the discretization accuracy of the two grids, and the gravity-assisted inertial navigation algorithms were experimentally compared by combining inertial navigation data and gravity measurement data. For the construction problem of multi-resolution hexagonal grids, a local subdivision method based on representative error is proposed. Since there is only a 19.10° rotation angle between adjacent layers of the 7-aperture hexagonal grid, the formed gap is the smallest. Therefore, a 7-aperture hexagonal grid was used to construct a hybrid multi-level multi-resolution gravity reference map for the analysis and research of gravity-assisted inertial navigation. Accordingly, experiments were conducted to verify the efficacy of this approach. The main contribution of this paper lies in introducing hexagonal grids into the field of gravity-assisted inertial navigation. Moreover, by discussing the principles of the two types of algorithms, filtering and matching, from the perspective of grids and verifying the effectiveness of actual matching experiments, the improvement effect of using hexagonal grids for different algorithms in gravity-assisted inertial navigation is specifically analyzed. For the first time, the issue of hexagonal multi-resolution grids was explored, and hexagonal multi-resolution grids were applied to the compression representation of gravitational field data.

The structure of this paper is organized as follows. First, the method for generating hexagonal grids and the characteristics of global data representation using hexagonal grids are introduced. Since the construction of the observation function in the filtering algorithm requires the solution of discrete derivatives on the grids, the performance differences in solving discrete derivatives between geographic rectangular grids and hexagonal grids are compared. Then, the filtering and matching algorithms in gravity-assisted inertial navigation are, respectively, implemented on hexagonal grids and geographic rectangular grids for experiments, and the experimental results are statistically analyzed to draw conclusions. Finally, the generation algorithm of multi-resolution hexagonal grids and its application in data compression for gravity-assisted inertial navigation are discussed.

2. Materials and Methods

2.1. Global Hexagonal Grid Construction

To construct a global hexagonal grid, it is necessary to recursively perform hierarchical subdivision on the selected regular icosahedral surface to form a multi-resolution hexagonal grid. Subsequently, each grid is encoded and indexed. Since the closed polyhedral surface is equivalent to the spherical surface in terms of topological relationship, mapping the planar grid to the spherical surface completes the construction. Different levels of partitioning correspond to different numbers and areas of the grids. The relationship between the number and area of grid cells in H3 is summarized in

Table 1. Statistics of H3 grid parameters.

Resolution	Grid Number	Average Grid Area (km2)	Average Grid Side Length (km)
0	122	4,357,449.416078381	1281.256011
1	842	609,788.441794133	483.0568391
2	5882	86,801.780398997	182.5129565
3	41,162	12,393.434655088	68.97922179
4	288,122	1770.347654491	26.07175968
5	2,016,842	252.903858182	9.854090990
6	14,117,882	36.129062164	3.724532667
7	98,825,162	5.161293360	1.406475763
8	691,776,122	0.737327598	0.531414010
9	4,842,432,842	0.105332513	0.200786148

.

Table 1 shows different numbers of spherical hexagonal grids at different resolution levels. As the H3 system adopts a 7-aperture hexagon, the overall parameters between its adjacent layers vary significantly. The existing highest-resolution gravity reference map is 1′ × 1′, which corresponds to the 7–9-layer grids in H3.

To demonstrate the results under different partition grids on a spherical surface, geographic rectangular grids and hexagonal grids were adopted for partitioning (Figure 1).

As the grid division level of the global terrain data in Figure 1 is relatively low, significant differences between using hexagonal grids and geographic rectangular grids in local areas can be observed. The resolution of geographic rectangular grids increases with latitude, and their shapes undergo obvious deformation, particularly in the regions close to the poles. However, the use of hexagonal grids will not cause deformation in the polar regions, and the resolution remains consistent throughout the global distribution.

From Figure 2, it can be seen that the ratio of the circumference to the area of a hexagon is closer to a circle than that of a rectangle. This means that at the same circumference, the area of a hexagon will be larger, or in other words, at the same area, the circumference of a hexagon will be shorter. Due to their smaller ratio of perimeter to area, hexagons are closer to a circle and are more conducive to reducing deviations caused by edge effects.

2.2. Grid Performance Analysis

In gravity-assisted inertial navigation, conducting random linearization on the gravity reference map to construct the observation equation is essential. The most important part of random linearization is to solve the derivatives of gravity observations with respect to the longitude and latitude directions. This establishes the relationship between the observations and state quantities. The accuracy of solving the derivatives determines the positioning and navigation accuracy of gravity-assisted inertial navigation.

2.3. Grid Discretization Modeling

Owing to the constraints offered by traditional operation habits, existing data processing algorithms, and other factors, the vast majority of current global gravity field numerical model products are still presented in the form of geographic rectangular grids. Their sampling modes and spatial references are significantly different from those of hexagonal grids. Therefore, it is necessary to re-discretize and sample the hexagonal grids from the original observational data. When a function with an analytical expression is used to discretize and model the local regional grid, the derivative can be accurately analyzed as the true value for comparison. Therefore, the PEAKS function was adopted in the present study for discretization modeling. To make the numerical differences significant, the function was scaled as follows:

$$Z(X,Y)=100\cdot \left(3{\left(1-X\right)}^2{e}^{-X^2-{\left(Y+1\right)}^2}-10\left({\displaystyle \frac{X}{5}}-X^3-Y^5\right)e^{-X^2-Y^2}-{\displaystyle \frac{1}{3}}{e}^{-{\left(X+1\right)}^2-Y^2}\right)$$

(1)

where Z is the function value, and X and Y are independent variables. Subsequently, the PEAKS function is used to perform grid quantization. To facilitate a comprehensive comparison between rectangular and hexagonal grids, hierarchical partitioning of ISEA4H was not adopted. Function value quantization was performed at the grid center as follows:

First, the quantities of rectangular and hexagonal grids were calculated separately. In the same local area, differences in planar geometric relationships were divided into four conditions: same quantity, same area, same radius of the circumscribed circle, and same distance between adjacent elements. The dimensions of rectangular and hexagonal grids in the specified area under the four conditions were calculated. Second, rectangular and hexagonal grids with the specified parameters were generated in the specified area. Third, the PEAKS function was used to calculate the function values at the centers of the rectangular and hexagonal grids, which were subsequently bound to the grid attributes. Finally, the derivatives of adjacent elements in the rectangular grid and the hexagonal grid were obtained, and the errors between the discretized derivative and the analytical derivative were statistically analyzed. The statistical experiments were repeated for the four conditions.

3. Results

Figure 3 shows the discrete quantization results of the two grids. Although the number of grids is the same, the resolution of the hexagonal grid is higher than that of the geographic rectangular grid due to the higher angular resolution of the hexagonal grid.

3.1. Discretization Derivative Solution

In gravity-assisted inertial navigation, random linearization [17,18] is often adopted; that is, known low-order equations are used to approximate the nonlinear surface equations and thus accurately solve the derivative relationship between the observed values and the estimated parameters, while controlling computational complexity. Random linearization methods include the use of average point selection, full plane fitting, improved full plane fitting, nine-point fitting, average tangent, and first-order Taylor expansion. 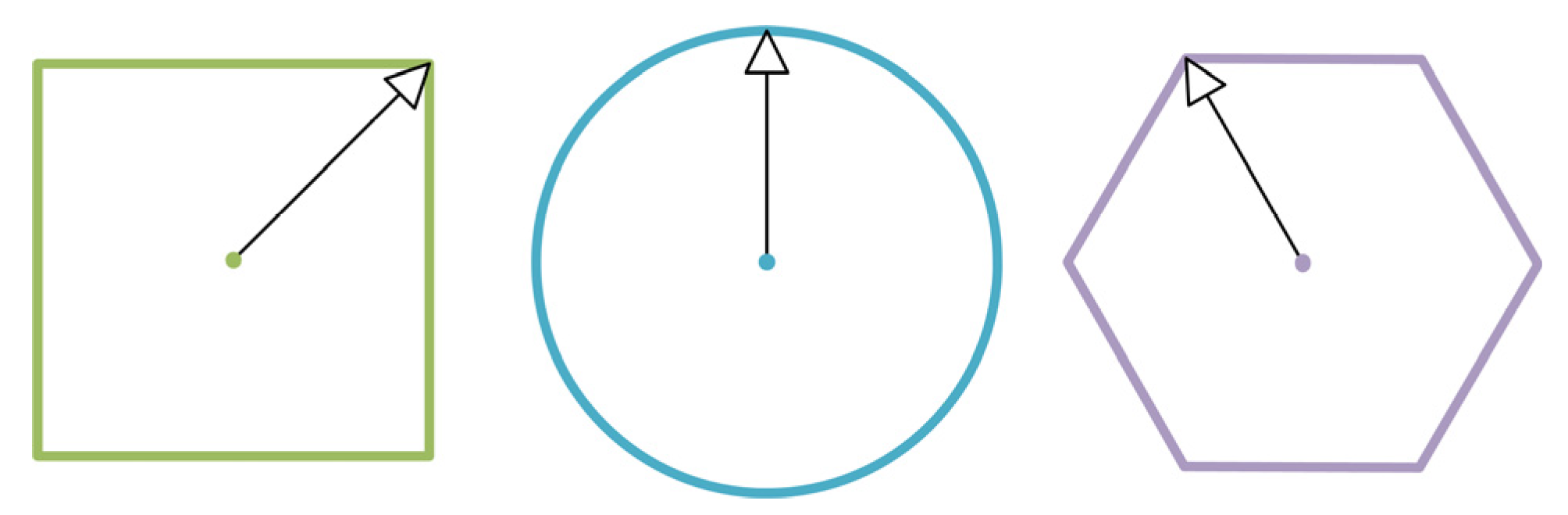Owing to the highly nonlinear relationship between gravity measurements and the position of underwater vehicles, the validity of assuming local random linearization depends on the complexity of the marine gravity field [19]. The errors produced by the linearization of gravity fields with different complexities vary. In the flat distribution of the marine gravity field, observability for the estimated state is poor despite low linearization error. In the rough marine gravitational field, observability for the estimated state is strong despite a high linearization error. In this study, full plane fitting is adopted to fit 8 and 6 elements around the selected indicator points of the rectangular and hexagonal grids, respectively. Their relationships are shown in Figure 4.

According to the relationship between the function values and coordinates in the elements shown in Figure 4, the least squares equation for solving the discretized derivative corresponding to two types of grids can be listed as follows:

$$R=\left[\begin{array}{c}{r}_1-r_0\\ ⋮\\ r_8-r_0\end{array}\right]=\left[\begin{array}{cc}{x}_1-x_2& y_1-y_2\\ ⋮& ⋮\\ x_3-x_2& y_3-y_2\end{array}\right]\left[\begin{array}{c}{k}_x\\ k_y\end{array}\right]+\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right]b=A_{r}K+B$$

(2)

$$H=\left[\begin{array}{c}{h}_1-h_0\\ ⋮\\ h_6-h_0\end{array}\right]=\left[\begin{array}{cc}0& y_1-y_3\\ ⋮& ⋮\\ x_1-x_2& y_2-y_3\end{array}\right]\left[\begin{array}{c}{k}_x\\ k_y\end{array}\right]+\left[\begin{array}{c}1\\ ⋮\\ 1\end{array}\right]b=A_{h}K+B$$

(3)

In the above Equations (2) and (3), R and H are the data difference vectors in two different grids, $A_r$ and $A_h$ are the coefficient matrices composed of the coordinate difference vectors in the two grids, $K$ is the gradient vector to be estimated, and $B$ is the bias vector to be estimated. In Equations (2) and (3) corresponding to the two grids (rectangular (R) and horizontal (H), respectively), only the coefficient matrix is different and represents the distribution of the observed data.

3.2. Grid Discretization Derivative Experiment

The rectangular and hexagonal grids were discretized and differentiated under four design conditions: same quantity, same area, same radius of the circumscribed circle, and same distance between adjacent elements. The errors between them and the true value of the analytical derivative were statistically analyzed. The results are shown in

Table 2. Statistics representing derivative performance for discretization numerical solution of geographic rectangular and hexagonal grids.

	Statistics	Root Mean Square Error (RMSE)	Mean Error	Maximum Absolute Error
Conditions
Same quantity	Geographical rectangular grid	6.9097	4.1777	24.2000
	Hexagonal grid	5.1188	2.8098	19.5485
Same area	Geographical rectangular grid	8.5234	5.1734	29.7726
	Hexagonal grid	5.5387	3.0398	21.0920
Same radius of the circumscribed circle	Geographical rectangular grid	5.6202	3.3965	19.7007
	Hexagonal grid	4.7448	2.6048	18.0600
Distance between adjacent elements of the same size	Geographical rectangular grid	9.6890	5.8785	33.1485
	Hexagonal grid	5.2859	2.8157	20.7683

.

The statistical results in Table 2 show that the discretization derivative accuracy of the hexagonal grid under the four conditions is higher than that of the geographic rectangular grid, with average discretization derivative accuracy increasing by 30%. This is due to the consistent distribution of the hexagonal grid, which makes the local solution of the discretization derivative more accurate.

3.3. Gravity-Assisted Inertial Navigation Based on Hexagonal Grids

Mathematical Model

Gravity-assisted inertial navigation algorithm is a process of correcting navigation parameters based on the difference between gravity measurement values and the values of inertial navigation indicator points on the gravity reference map. According to the processing flow, the algorithms can be divided into two categories: real-time and post-event. Real-time algorithms need to correct the real-time output of inertial navigation based on current observations and are generally represented by the extended Kalman filter algorithm. Conversely, post-event algorithms require the matching of multiple gravity observations collected over a period of time with the positions of inertial navigation indicator points on the graph to obtain corrected inertial navigation position information. Related extremum algorithms are usually present.

In the gravity-assisted inertial navigation extended Kalman filter algorithm, a two-dimensional longitude and latitude position vector is generally selected as the state quantity $X_k={\left[\begin{array}{cc}{B}_k& L_k\end{array}\right]}^T$, and its state equation and observation equation can be expressed in the form of error state variables as follows:

$$\left\{\begin{array}{c}\delta {\breve{X}}_k=A_k\delta {\widehat{X}}_{k-1}+G_k{W}_k\\ Y_k=H_k\delta {\breve{X}}_k+V_k\end{array}\right.$$

(4)

Among them, $\delta {\widehat{X}}_{k-1}$ is the posterior state at time k − 1; $\delta {\breve{X}}_k$ is the prior state at time k; $A_k$ is the coefficient matrix at time k, constructed by the inertial navigation error equation; and $W_k$ is the noise vector of the state process at time k, composed of the white noise of the angular velocity of the gyroscope and the white noise of the comparison of the accelerometer. $G_k$ is the noise transfer matrix at time k, $Y_k$ is the observed value at time k (the difference between the gravity anomaly observation and the gravity anomaly at the inertial navigation indication point on the reference map). $H_k$ is the observation matrix at time k, which is constructed by the local random linearization method. $V_k$ is the observed noise vector at time k. The mathematical model of the extended Kalman filter algorithm can be summarized into five formulae (Equation (5)).

$$\left\{\begin{array}{c}\delta {\breve{X}}_k=A_k\delta {\widehat{X}}_{k-1}\\ {\breve{P}}_k=A_k{\widehat{P}}_{k-1}{A}_k^T+Q_k\\ K_k={\breve{P}}_k{H}_k^T(H_k{\breve{P}}_k{H}_k^T+R_k{)}^{-1}\\ \delta {\widehat{X}}_k=\delta {\breve{X}}_k+K_k\left(Y_k-H_k\delta {\breve{X}}_k\right)\\ {\widehat{P}}_k=(I-K_k{H}_k){\breve{P}}_k\end{array}\right.$$

(5)

Among them, ${\widehat{P}}_{k-1}$ is the posterior state covariance of the previous moment; ${\breve{P}}_k$ is the prior state covariance of the current moment; $Q_k$ is the process noise matrix set according to the error level of the inertial component; $R_k$ is the observation noise; and $K_k$ is the Kalman filter gain matrix.

In the gravity matching extremum algorithm, the position of the carrier on the reference map cannot be uniquely determined by a single gravity anomaly observation due to the continuous and random characteristics of the Earth’s gravitational field. Therefore, collecting the inertial navigation indicator points and the sequence of gravity anomaly measurement values within a certain period of time is necessary. The gravity anomaly measurement values and the sequence of inertial indication points during the period from time i to j are denoted as $\mathsf{\Delta }{g}_{ij}^{measure}$ and $\mathsf{\Delta }{X}_{ij}$, respectively, and are specifically expressed as:

$$\left\{\begin{array}{c}\mathsf{\Delta }{g}_{ij}^{measure}={\left[\begin{array}{cccc}\mathsf{\Delta }{g}_i^{measure}& \mathsf{\Delta }{g}_{i+1}^{measure}& \cdots & \mathsf{\Delta }{g}_j^{measure}\end{array}\right]}^T\\ \mathsf{\Delta }{X}_{ij}={\left[\begin{array}{cccc}{X}_i& X_{i+1}& \cdots & X_j\end{array}\right]}^T\end{array}\right.$$

(6)

The gravity anomaly at each indicator point in the inertial navigation indicator point sequence $\mathsf{\Delta }{X}_{ij}$ can be found on the gravity reference map to form sequence $\mathsf{\Delta }{g}_{ij}^{map}={\left[\begin{array}{cccc}\mathsf{\Delta }{g}_i^{map}& \mathsf{\Delta }{g}_{i+1}^{map}& \cdots & \mathsf{\Delta }{g}_j^{map}\end{array}\right]}^T$. By applying a certain correlation extremum matching algorithm to the measurement value and indicator point value sequences, the optimal estimate of the current position $\left(\begin{array}{cc}B& L\end{array}\right)$ of the carrier can be obtained. The commonly used correlation extremum algorithms include cross-correlation, mean absolute value difference correlation, and mean square deviation correlation algorithms. Their mathematical models are represented in Equations (7)–(9).

Cross-correlation algorithm:

$$J_{cor}(B_j,L_j)={\displaystyle \frac{1}{(j-i+1)}}\sum _{k=i}^j\mathsf{\Delta }{g}_k^{measure}\cdot \mathsf{\Delta }{g}_k^{map}$$

(7)

Mean absolute value difference correlation algorithm:

$$J_{mad}(B_j,L_j)={\displaystyle \frac{1}{(j-i+1)}}\sum _{k=i}^j\left|\mathsf{\Delta }{g}_k^{measure}-\mathsf{\Delta }{g}_k^{map}\right|$$

(8)

Mean square deviation correlation algorithm:

$$J_{msd}(B_j,L_j)={\displaystyle \frac{1}{(j-i+1)}}\sum _{k=i}^j{\left(\mathsf{\Delta }{g}_k^{measure}-\mathsf{\Delta }{g}_k^{map}\right)}^2$$

(9)

By selecting different grid points around the inertial navigation indicator points, multiple sequences of indicator point values can be formed. According to the correlation extremum algorithm, when the cross-correlation $J_{cor}(B_j,L_j)$ is the maximum or the mean absolute value difference $J_{mad}(B_j,L_j)$ and the mean square deviation $J_{msd}(B_j,L_j)$ are the minimum among multiple sequences of indicator point values, this sequence of indicator points is considered the true track of the carrier, and the inertial navigation is corrected at the corresponding positions of the sequence points.

3.4. Experiment on Gravity-Assisted Inertial Navigation EKF Algorithm Based on Hexagonal Grids

To verify the performance of hexagonal grids in gravity-assisted inertial navigation, a 24-h underwater track was designed, and gravity reference maps of hexagonal and geographic matrix grids were generated. The relevant parameters of the simulated flight path are shown in the following

Table 3. Trajectory parameter setting.

	Initial Attitude	Initial Velocity	Initial Position	Track Duration
Parameters	Pitch: 0°	Eastward: 0 m/s	Longitude: 111° E	24 h
	Roll: 0°	Northward: 0 m/s	Latitude: 7° N
	Yaw: 0°	Upward: 0 m/s	Altitude: −100 m

.

The initial acceleration of the submersible on its path was 0.017 knots per second (0.009 m/s²), the acceleration time was 600 s, and the speed was 10.2 knots (5.4 m/s). The submersible first sailed northward for 8 h, then turned westward for 8 h, and finally adjusted its course to northward for the last 8 h.

The submersible was made to navigate on the two reference maps, and the extended Kalman filtering algorithm was adopted. The difference between the gravity measurement and inertial indicator point values on the gravity reference map was taken as the observation quantity. Real-time correction of the navigation parameters output was obtained by inertial navigation. Based on the accuracy level of the existing instruments, the parameters of the inertial components and the gravimeter were set (

Table 4. Parameter settings of inertial components.

INS Error Term	Gyroscope	Accelerometer
	(x, y, z Axis)	(x, y, z Axis)
Constant zero bias	0.002°/$\mathrm{h}\mathrm{r}$	10 mGal
Random walk	0.001°/$\sqrt{\mathrm{h}\mathrm{r}}$	5 mGal/$\sqrt{\mathrm{H}\mathrm{z}}$
Gravimeter Error Term	Horizontal accelerometer	Vertical accelerometer
	(x, y, z axis)	(x, y, z axis)
Constant zero bias	50 mGal	3 mGal
Random walk	5 mGal/$\sqrt{\mathrm{H}\mathrm{z}}$	0.3 mGal/$\sqrt{\mathrm{H}\mathrm{z}}$

).

Based on the set parameters of the inertial components, the 24-h simulation track and the inertial navigation angular velocity and acceleration data on the track were generated. The H3 7th layer hexagonal grid was generated in the navigation area, and the DTU marine gravity anomaly data were used to conduct discrete sampling for each hexagonal grid center (Figure 5).

Gravity-assisted inertial navigation experiments were conducted under four conditions using geographic rectangular and hexagonal grids. The numerical derivatives calculated from geographic rectangular grids and hexagonal grids were used to construct observation equations to correct the inertial navigation positions. The statistical results of the experiments are displayed in

Table 5. Gravity matching navigation accuracy statistics.

	Statistics	Longitude RMSE (nmiles)	Latitude RMSE (nmiles)	Position RMSE (nmiles)	Average Position Error (nmiles)
Conditions
Same quantity	Hexagonal grid	1.2682	1.6106	2.0500	1.8249
	Geographical rectangular grid	1.2699	1.6279	2.0647	1.8388
Same area	Hexagonal grid	0.9170	1.7103	1.9407	1.6777
	Geographical rectangular grid	0.9138	1.7237	1.9510	1.6815
Same radius of the circumscribed circle	Hexagonal grid	1.2192	1.3878	1.8472	1.6398
	Geographical rectangular grid	1.2204	1.3890	1.8489	1.6422
Same distance between adjacent elements of the same size	Hexagonal grid	0.9800	1.4152	1.7119	1.5047
	Geographical rectangular grid	0.9822	1.4158	1.7200	1.5114

.

The statistical results in Table 5 show that under the four conditions, the position RMSE of gravity-assisted inertial navigation based on hexagonal grids is better than that based on rectangular grids. For the same quantity, the position RMSE of hexagonal grids is 0.7% lower than that of rectangular grids. Under the same area, position RMSE decreases by 0.5% for the hexagonal grids. When the radius of the circumscribed circle is the same, the position RMSE of hexagonal grids decreases by 0.09%. When the distances between adjacent elements are equal, the position RMSE of hexagonal grids decreases by 0.4%. In all four cases, the accuracy of gravity-assisted inertial navigation based on hexagonal grids is, on average, 0.4% higher than that based on rectangular matrix grids. The results show that using hexagonal grids can improve the calculation accuracy of discretized derivatives, thereby enhancing gravity-assisted inertial navigation.

3.5. Gravity Matching Extremum Algorithm Based on Hexagonal Grid

The gravity matching algorithm based on correlation-extremum navigation requires that each gravity anomaly sampling point on the observation sequence be searched and matched on the gravity anomaly map within a certain range around the inertial navigation indication track. The range is jointly determined by the error of the inertial navigation component and the time. Figure 4 shows that in the rectangular matrix grid, nine grids around the inertial indicator point need to be selected; meanwhile, in the hexagonal matrix grid, only six grids around need to be selected. However, in the rectangular matrix grid, the surrounding nine grids and the central grid are not evenly spaced or equidirectionally distributed, which implies that they are not evenly distributed around the inertial indicator points. There will be 9ⁿ sequence values corresponding to n indicator points in the rectangular matrix grid. Meanwhile, in the hexagonal matrix grid, the surrounding six grids and the central grid are both evenly spaced and equidirectionally distributed; thus, there will be 6ⁿ sequence values corresponding to n indicator points, which not only significantly reduce the computational load but also distribute it around the indicator points with equal probability.

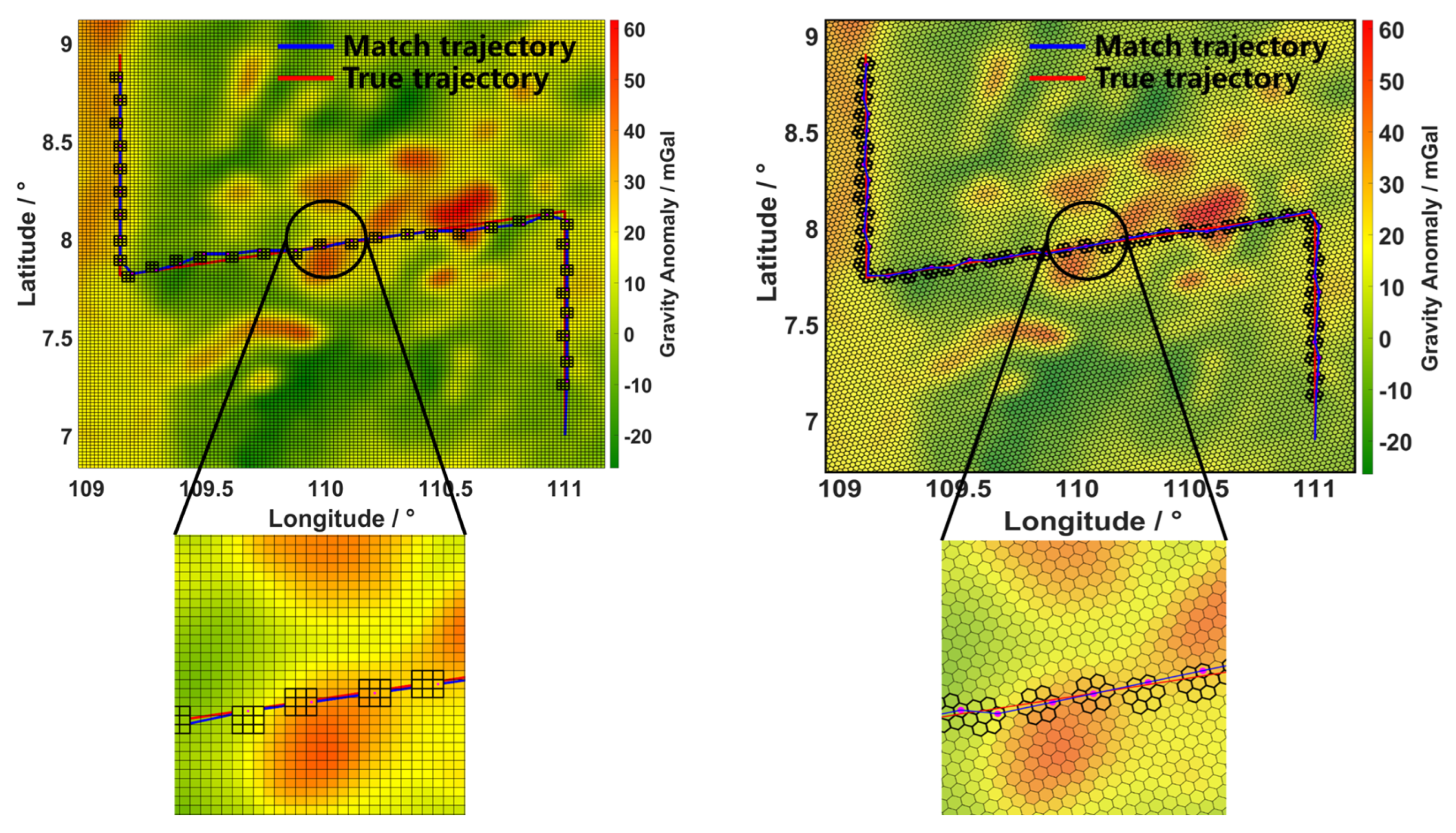
In the matching navigation experiment, this area was also selected as reference map. Relevant extreme value matching was performed on the gravity reference maps of the geographic matrix and hexagonal grids for the 24-h inertial navigation track, as shown in Figure 6.

From Figure 6, it can be seen that the process of matching using the geographic matrix grid and hexagonal grid is carried out separately, and the coordinate points determined after matching are marked with magenta dots, which are located at the center of the discrete grid. However, due to the different centers of the hexagonal grid and the geographic rectangular grid, the matching results are also different. Since the number of matching sequences for gravity matching in hexagonal grids and rectangular grids was different, they were determined for cases having the same number of matching points and the same computational load. Under the same computational load, the relationship between the number of matching points (n1) corresponding to the hexagonal grid and the number of matching points (n2) of the rectangular grid was 6ⁿ¹–9ⁿ². The accuracy performance after gravity matching in these two cases was statistically analyzed.

The statistical results in

Table 6. Gravity matching navigation accuracy statistics.

	Statistics	Position RMSE (nmiles)	Average Position Error (nmiles)	Maximum Position Error (nmiles)
Conditions
Same matching points	Hexagonal grid	0.8963	0.7829	1.1226
	Geographical rectangular grid	2.1681	1.8347	4.2281
Same number of computations	Hexagonal grid	0.8539	0.7267	1.0504
	Geographical rectangular grid	2.1004	1.8168	3.7142

show that the accuracy of gravity matching using hexagonal grids is much higher than that using geographic rectangular grids, with an average improvement of 50% compared to that using geographic rectangular grids. Moreover, the accuracy of the correlation extremum matching algorithm under hexagonal grids is also higher than that of the real-time extended Kalman filter algorithm. Hexagonal grids are more suitable for matching algorithms due to their higher angular resolution and the equal probability distribution of their adjacent grids. When the number of matching points equals 9, the data volume of the rectangular grid increases exponentially due to its proximity distribution. In contrast, using a hexagonal grid can not only increase the number of matching points but also effectively control the computational load.

3.6. Hybrid Resolution Hexagonal Gravity Reference Grid

The use of a multi-resolution hexagonal grid can reduce the global gravity field data storage without significantly lowering the accuracy of gravity-assisted inertial navigation on the reference map. Additionally, it helps to clearly determine the observation covariance matrix in the filtering algorithm, reducing the observation variance in high-resolution regions and increasing it in low-resolution regions. Thus, the computational efficiency and accuracy of the real-time algorithm for gravity-assisted inertial navigation can be simultaneously improved.

Since the 7-aperture hexagon has a clearer and more definite correspondence between its upper and lower layers than the 3-aperture and 4-aperture hexagons, and the gaps formed between the layers are the smallest, this section uses Uber’s open-source H3 grid system to construct a global 7-aperture hexagon grid gravity reference map. First, determining the construction area range and generating different levels of grids within this area is necessary. Owing to the excessive error in the representative area of the lower-level hexagon, the lowest section layer is selected as the 4th layer, and the highest section layer is the 7th layer (based on the existing standard of the highest 1′ × 1′ resolution gravity reference map).

After generating the highest-level hexagonal grid of the specified area, the next level of hexagonal grids is generated successively from the highest level to ensure a clear mapping relationship among the hexagonal grids of different resolution levels (Figure 7). As seen in Figure 7, the spherical 7-aperture hexagon projected onto the plane needs to be expanded outward to fully include the specified area, as it does not strictly align with the rectangular area. To obtain the gravity outlier values in each level of the hexagon, the average value sampled within the DTU geographic rectangular grid in the hexagonal area is taken as the grid gravity outlier value and represents the position at the grid center.

Based on the multi-resolution hexagonal grid constructed in the designated area, the highest-level hexagon is traversed, and the standard deviation of the 7 sub-level grids in each hexagon is counted. If the standard deviation is greater than the set representative error threshold, the subdivision continues until the set highest level is reached and then stops. The overall algorithm process is listed in Algorithm 1.

From the algorithm process listed in Algorithm 1, a hybrid hexagonal grid that meets the specified standard deviation threshold conditions can be obtained. Since there is no interdependence among different high-level hexagons, different hexagons can be subjected to parallel recursive partitioning to accelerate the generation speed of the hybrid resolution hexagonal grid [20].

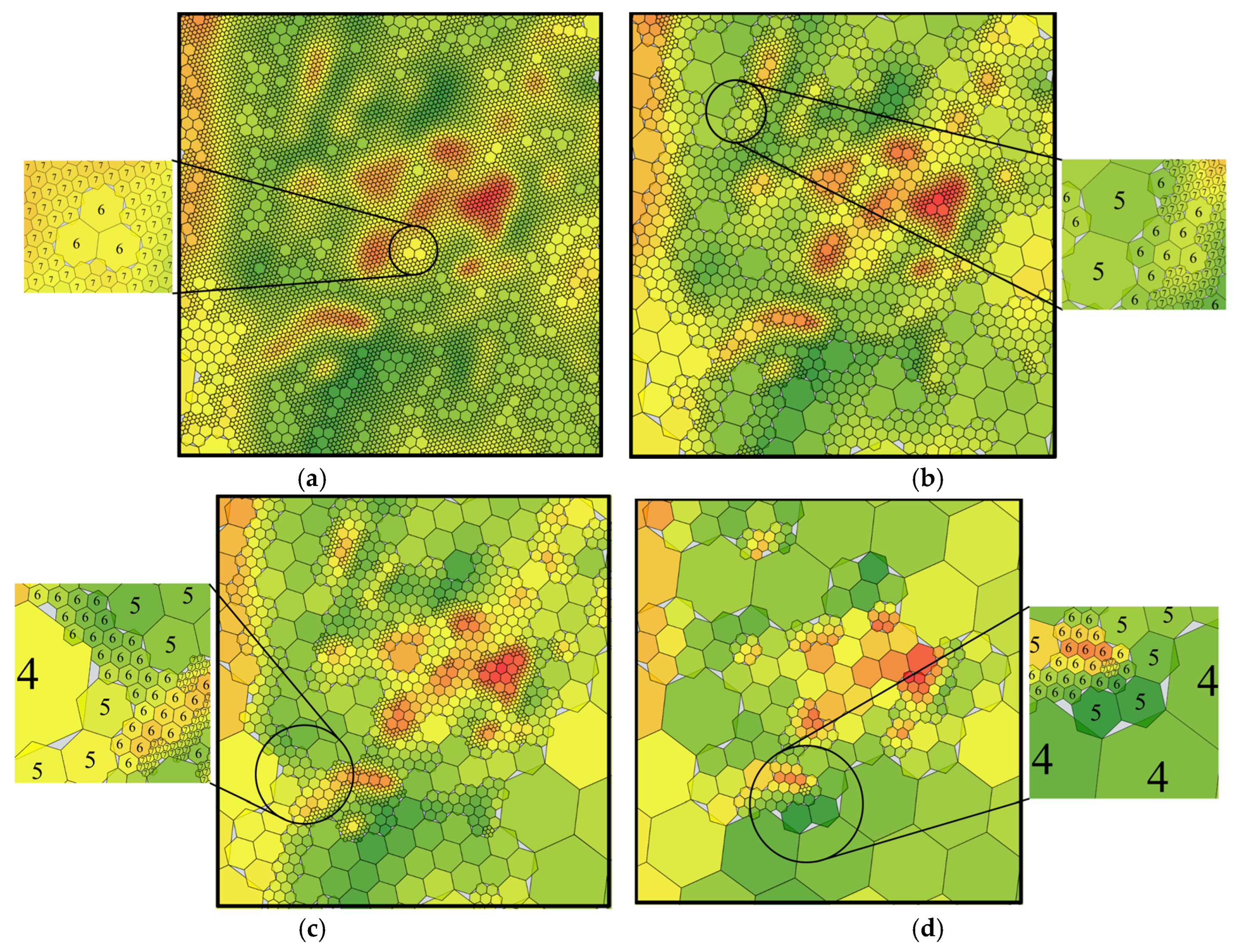
When the threshold values of the standard deviation of the hierarchical subdivision representative error were set to 1 mGal, 3 mGal, 5 mGal, and 10 mGal, the resulting multi-hexagonal grid was plotted (Figure 8a–d).

Algorithm 1 Multi-Resolution Hexagonal Grid Partition

Input: DTU geographic rectangular grid gravity anomaly model, specifying the longitude and latitude coordinates of the designated area Output: multi-resolution hexagonal grid data 1: Grav = [∆g1…∆gn]; Lat = [B1…Bn]; Lng = [L1…Ln]; // Initialize the geographic rectangular grid dots and gravity outliers 2: Hex = [h1…hn]; // Initialize the highest-level 7-aperture hexagonal grid 3: HexMix = []; // Initialize an empty list for storing multi-resolution hexagons 4: for (i = 1 to n) do // Loop through all the hexagons at the highest level in the specified area 5:   hi = Hex(i); 6:   if (std(hi) < Threshold) then // Determine whether the standard deviation of its internal gravity anomaly is less than the representative error threshold 7:    HexMix = [HexMix; hi]; 8:   end if 9:   [hi1, hi2, hi3, hi4, hi5, hi6, hi7] = Hex_To_Children(hi); // Obtain the sub-level split hexagon 10:   for (j = 1 to 7) do 11:     if(Variance(hij) < Threshold) then 12:       HexMix = [HexMix; hij]; 13:     end if 14:     [hij1, hij2, hij3, hij4, hij5, hij6, hij7] = Hex_To_Children(hij); 15:     for (k = 1 to 7) do 16:       if (Variance(hijk) < Threshold) then 17:         HexMix = [HexMix; hijk]; 18:       end if 19:       [hijk1, hijk2, hijk3, hijk4, hijk5, hijk6, hijk7] = Hex_To_Children(hijk); 20:        for (m = 1 to 7) do 21:         HexMix = [HexMix; hijkm]; 22:        end for 23:       end for 24:     end for 25: end for 26: return HexMix // Return the multi-resolution hexagonal grid data

As shown in Figure 8, the threshold rises with the number of low-level hexagonal grids, with the compression ratio of the gravity reference map data also increasing. The level numbers corresponding to the multi-resolution hexagons in Table 1 are marked in the thumbnail. Under the corresponding requirements of gravity measurement tasks, choosing an appropriate threshold can retain the original significant features of the gravity reference map to the greatest extent while compressing the original data.

The accuracy of gravity-assisted inertial navigation is strongly correlated with the roughness of the gravity reference map. In areas where gravity significantly changes due to the “lighthouse effect”, gravity measurement values are more likely to match the correct position of the submersible on the reference map. When a multi-resolution hexagonal grid is adopted, it becomes more convenient to distinguish the seaworthiness areas with significant gravitational changes from the graph. In addition, the confidence level of the matching position can also be divided based on the grid level. The higher the level of the grid matched, the more reliable the result. However, the confidence level of the position is also lower in lower-level grids due to the flatter change in gravity within the area. Therefore, constructing a multi-resolution hexagonal grid plays an important role in gravity-assisted inertial navigation. The number of multi-resolution hexagonal grids and the magnitude of their average representative errors under different representative error thresholds were statistically analyzed (

Table 7. Number of hexagonal grids and the average representative error under different thresholds.

	Statistics	Number of Hexagons	Average Representative Error (mGal)
Threshold
1 mGal		8682	0.7902
2 mGal		5333	1.0955
3 mGal		3342	1.4494
5 mGal		1445	2.2937
10 mGal		244	5.0255

).

The hybrid-resolution hexagonal grid can compress the data size as much as possible while ensuring data accuracy. As shown in Table 7, the results show that the average representative error of the hybrid resolution hexagonal grid constructed at each threshold is much smaller than the set threshold; the ratio of the average representative error to the set threshold is, on average, 55%, indicating that the gravity data constructed by the hybrid resolution hexagonal grid is closer to the original data.

4. Conclusions

This study focused on the defects of the rectangular grid gravity reference map, systematically investigated the application of hexagonal grids in gravity-assisted inertial navigation, analyzed the advantages and characteristics of hexagonal grids compared with those of geographic rectangular grids, discussed and tested both real-time and post hoc algorithms, and proposed a hybrid resolution hexagonal grid generation algorithm. To ensure the accuracy of the gravitational field reference map, the data have been effectively compressed. The main conclusions drawn through experimental verification are as follows:

• Since the angular resolution is higher for the gravitational field reference map constructed by hexagons than that for the geographic matrix grid, the accuracy of calculating the discretized derivative is higher. The accuracy of the discretization derivative solved by the hexagonal grid is 30% higher than that of the geographic rectangular grid. Therefore, the construction accuracy of the observation function can be improved in the real-time extended Kalman filtering algorithm, enhancing the accuracy of navigation and positioning.
• Owing to its characteristic equal probability distribution, the gravity anomaly sequence matching is much higher for the hexagonal grid than for the rectangular grid. According to the results, the accuracy improvement in the hexagonal grid using the filtering algorithm compared to the geographic rectangular grid is only 0.4%. However, after using the matching algorithm, the accuracy improvement in the hexagonal grid compared to the geographic rectangular grid can reach nearly 50%. Moreover, as the number of matching points gradually increases, its computational load becomes lower than that of the geographic rectangular grid, indicating that the hexagonal grid is more suitable for the matching algorithms of discrete grids.
• The multi-resolution hexagonal grid can achieve data compression under the condition of the set reference graph representing the error threshold. After using multi-resolution hexagonal grid compression, the average accuracy can reach 55% of the set threshold. In gravity-assisted inertial navigation, the hexagonal grid accuracy has a strong correlation with the roughness of the gravity reference map. In areas where gravity changes significantly because of the “lighthouse effect”, the gravity measurement values are more likely to match the correct position of the submersible on the reference map. When a multi-resolution hexagonal grid is used, the adapted and non-adapted areas of gravity-assisted inertial navigation can be significantly distinguished.