Effect of Following Current on the Hydroelastic Behavior of a Floating Ice Sheet near an Impermeable Wall

Abstract

A theoretical model of the interaction between a following current and a semi-infinite floating ice sheet under compressive stress near a vertical impermeable wall is developed, within the scope of linear water wave theory, to study the hydroelastic behavior. The conceptual framework defining the buoyant ice structure incorporates the tenets of elastic beam theory. The associated fluid dynamics are governed by strict adherence to the potential flow paradigm. To resolve the undetermined parameters appearing in the Fourier series decomposition of the potential functions, investigators systematically apply higher-order criteria detailing the coupling relationships between modes. The current results are compared with a specific case of results available in the literature, and the convergence analysis of the analytical solution is made for computational accuracy. Further, the free edge conditions are applied at the edge of the floating ice sheet, and the effects of current speed, compressive stress, the thickness of the ice sheet, flexural rigidity, water depth on the strain, displacements, reflection wave amplitude, and the horizontal force on the rigid vertical wall are analyzed in detail. It is found that the higher values of the following current heighten the strain, displacements, reflection amplitude, and force on the wall. The study’s outcomes are considered to benefit not just cold region design applications but also the engineering of resilient floating structures for oceanic and offshore environments, and to the design of marine structures.

1. Introduction

The massive sheets of ocean ice in the Arctic and Antarctic are used as important natural platforms. They are key for travel across the ice, for building short-term airstrips, and for aiding other transportation needs in these extreme marine environments [1,2,3,4]. On the other hand, when hydrodynamic forces—specifically combined swells and currents—impinge upon an ice-covered sea, the resulting wave propagation is fundamentally dictated by the structural stiffness inherent to the ice sheet surface [5]. The ice sheet possesses a significantly large horizontal dimension, allowing it to be approximated as infinite for many practical cases. Due to the continuous excitation of a small-amplitude wave–current, the overall performance characteristics of the component are overwhelmingly driven by recoverable deformation.

Therefore, the mechanical response of expansive floating ice to the combined forcing of waves and currents is critically governed by the principles of hydroelasticity. Hence, it is necessary to gain deeper insight into the impact of wave–current–/structure/ice interactions [6]. The present investigation addresses a problem in which a vertical wall is placed near a compressed FIS with semi-infinite extent and its interaction with a following current (FC) application to breakwater in the Arctic region. A detailed review of the latest advancements of the nonlinear hydroelastic models associated with sea ice interactions with floating ice sheets and ship structures [3] application to Arctic and offshore engineering is presented. A 2D FEM-DEM is applied to determine the maximum ice load values that occur when sea ice breaks against a sloped marine structure [7]. Ni et al. [8] provided a review that presented the ice deformation, focusing on the defining attributes of waves driven by combined bending and gravitational forces.

To address some important aspects of floating sea ice interaction with marine structures under varying sea ice properties, a significant amount of work has been conducted by many researchers using numerical simulations or numerical methodologies. An experimental study on the ice–structure interaction for offshore wind turbines with a monopile foundation is presented in [9]. Shi et al. [10] evaluated how the specific physical configuration and thermal condition of the ice structure modulated the dynamics of the collision event based on the elastic-plastic iceberg material model. Tsuprik et al. [11] presented a mathematical model of sea ice failure by assessing the mechanics governing the interaction between traveling sea ice masses and fixed marine architecture. Ni et al. [12] studied the ice deformation based on the propagation of elastic-gravitational waves through a full ice cover, resulting from the dynamic application of a traveling object. Song et al. [13] utilized an established multi-yield-surface plasticity approach to simulate stress states and fracture initiation in ice. This model was subsequently applied to predict the mechanical failure of three distinct forms.

A new physical modeling approach was adopted to examine the wave-ice interaction for determining an elastic stiffness in [14]. Yiew et al. [15] carried out a scaled experiment to analyze wave damping and the scattering of wave energy when encountering diverse icy environments. The wave interaction with a floating structure close to the marginal ice zone in 2D is examined, where the linear velocity potential theory and the thin elastic plate are utilized for fluid flow and the analysis of ice sheet deflection, respectively [16]. A numerical simulation of a very large floating interconnected rectangular structure under current and wind [17], along with theoretical floating flexible rectangular [18] and floating interconnected rectangular model [19] subjected to current using Timoshenko-Mindlin Beam theory, are presented, during the execution of a study focused on how the velocity of the fluid flow dictates the resultant stresses within the physical infrastructure and the parametric metrics characterizing the generated wave system. Korobkin and Khabakhpasheva [20] studied the response of floating ice using a model that accounts for both ice properties and its interaction with the underlying water. Van den Berg et al. [21] analyzed ice forces and structural response on a vertical cylindrical pile using ice basin test data. The impact response of an upright ocean structure to the forces exerted by a drifting ice floe was numerically simulated and is documented in [22]. A review of ice–structure modeling, focused on predicting interactions between ships or floating platforms with broken ice fields, is conducted [23]. Using a deployed array of ice-drifting buoys, Hutchings et al. [24] studied the temporal and spatial scaling of sea ice deformation. A review focusing on the mechanical failure and discontinuous nature of sea ice using the DEM approach is conducted in [25], while Sayeed et al. [26] focused on the review of hydrodynamic influence and motion statistics of large, discrete glacial ice features (icebergs) impacting marine structures.

Huang et al. [27] used the Open-FOAM solver to model the hydroelastic response of a large ice sheet under wave actions. Under the potential flow hydroelastic model and nonlinear numerical FE solver, Hartmann et al. [28] studied the ice sheet’s bending and deformation under the consideration of the Kirchhoff–Love theory applied to model the behavior of the linear elastic plate. Tavakoli et al. [29] presented a viscoelastic wave–ice interactions model using the fluid–solid dynamic model. Xue et al. [30] utilized a hybrid method to analyze the hydroelastic response of a floating ice sheet due to pressure under constant water depth and potential linear flow theory. Huang and Thomas [31] adopted a 3D CFD model to analyze the nonlinear interaction between the regular waves and a circular ice floe.

Staroszczyk [32] analyzed the sea ice–structure interaction based on numerical simulation under thermal expansion, in which sea ice was modeled as a rectangular plate with uniform thickness and axial compressive force. Hu et al. [33] proposed a fluid structure interaction Scheme to model the collision dynamics impact of ice and water by employing a penalty function technique. Sinsabvarodom et al. [34] detailed established probabilistic methodologies for sea ice used to predict the load uncertainty impacting various offshore structures. Using the discrete element method and physical modeling, the forces and effects resulting from the contact between a cylindrical object and ice fragments were studied [35]. The radiation of waves from a submerged structure covered with ice at the surface was studied in 3D under deep-water conditions [36]. A virtual buoy was created based on the numerical WW3 to study the wave propagation under ice covers [37]. The DEM numerical methodology is used to investigate the icebreaking performance of a single leg Jacket platform under different ice conditions [38]. The local ice pressure magnitude and its dependency on various factors were studied using experimental tests and theoretical analysis [39].

Squire [40] focused on the hydroelastic coupling relevant to sea ice mechanics and the behavior of VLFS. The wave quantities were investigated by utilizing two methods from the framework of generalized Polynomial Chaos (gPC) in [41]. Timco and Weeks [42] extensively reviewed sea ice engineering properties concerning personnel and environmental safety. Bennetts et al. [43] presented a 3D numerical model to study the wave energy dissipation in the marginal ice zone by simulating how waves are scattered by arrays of large elastic thin plates.

Based on the assumption of linear wave theory and thin plate theory, a considerable amount of work when accounting for all components of the analysis of floating ice sheet in different conditions has been carried out, which is discussed below. Brocklehurst et al. [44] analyzed the behavior of the flexural gravity waves over an ice sheet analytically, considering the clamped condition. Maiti and Mandal [45] addressed the 2D wave scattering phenomenon in which a thin, uniform ice cover interacts with a submerged rigid barrier. Korobkin et al. [46] examined the behavior of hydroelastic waves that develop within an ice-covered channel under the assumption of linear progressive waves and the linear elastic plate equation. Lu et al. [47] developed a coupled theoretical model between the ice and wide sloping structure to study the impact of ice breaking under spatial and temporal variations.

Zhao et al. [48] presented a brief overview of the mathematical framework and wave quantities associated with different ice characteristics. Hegarty and Squire [49] analyzed the response of a compliant, floating sea ice floe when subjected to the waves of large-amplitudes, and the solution was obtained using a perturbation expansion, boundary-integral method, and the results were compared with eigenfunction matching methods. Zhang and Zhao [50] studied the wave quantities by a finite ice cover under a viscoelastic sea ice model using the two-mode approximate method. Using an elastic plate model for the ice cover, Batyaev and Khabakhpasheva [51] examined the behavior of linear hydroelastic waves propagating through a channel. Qiu et al. [52] provided a theoretical solution for the steady-state response of a freely floating ice sheet to a moving load based on integral transforms and asymptotic methods. Wan et al. [53] presented the hydrodynamic analysis of an ice-covered domain based on a hybrid method that combines the BIEM and eigenfunction expansions.

Zhang et al. [54] studied the hydrodynamics of a floating body in the vicinity of a semi-infinite ice sheet using the eigenfunction expansions in conjunction with Green’s identity, analyzed within the framework of linear wave theory and the Kirchhoff–Love plate approximations. Wang et al. [55] studied the 3D elastic sea ice scattering model in irregular waves using thin plate theory. The solution of the nonlinear water wave equations with an ice sheet is presented based on BIEM, while different types of responses were analyzed [56]. Under nonlinear incident waves, Kostikov et al. [57] employed a combined Green–Naghdi and thin plate model to accurately predict the current-driven drift motion of an FIS.

In recent years, there have been a considerable amount of works carried out, specifically the hydroelastic analysis of floating structures [58,59], and floating and submerged structures based on thin elastic plate theory and linear water wave theory using an analytical approach [60,61,62]. Korobkin et al. [63] derived a theoretical framework for the 2D, linear, and unsteady hydroelastic interaction involving a moving vertical wall with spring-like constraints under the action of surface waves. A revised theoretical model based on shallow-water approximation is presented to analyze wave scattering by regions of randomly fluctuating water depth and areas covered by fragmented floating ice of irregular thickness [64]. A numerical framework is used to simulate the nonlinear propagation of waves as they traverse along fragmented sea ice fields [65]. The 3D complex phenomenon of wave propagation of an FIS with variable ice thickness and water depth is investigated in [66]. A viscoelastic model is developed to analyze the generation of gravity waves in different types of ice cover with finite thickness [67]. A review of the recently established theoretical and numerical techniques for assessing the uncertainties and sensitivities inherent in the hydrodynamic and hydroelastic behavior of floating structures. [68].

Beyond their role in quantifying the fluid structure interaction dynamics of mega-scale marine platforms, flexible plate models with unrestrained boundaries are a standard analytical tool for researchers investigating the influence of surface gravity waves on sea ice across high-latitude zones [69]. Floating ice sheets experience compressive stress from a variety of natural factors, including thermal expansion and contraction, and frictional forces exerted by wind and water currents underneath, as documented in [70]. The impact of surface waves on compressed ice edges in a constant-depth basin was analyzed in [71] by employing the conjugate gradient algorithm. The behavior of an ice sheet that is subjected to compression while it floats is investigated, specifically in relation to a moving load applied to the ice [72], which provided a study on the synergy between very large floating structures and sea ice research. Mohapatra et al. [73] utilized the BIEM to analyze the phenomenon of wave diffraction around a floating elastic plate under the influence of compressive force, and the critical compressive force was investigated and analyzed based on the phase and group velocities.

Although research on sea ice–structure interactions has progressed, existing literature still lacks a comprehensive theoretical model. This gap is particularly evident in the analysis of hydroelastic flexural gravity waves on an FIS with a vertical wall, where the inclusion of current velocity in both the formulation and solution techniques for current effects remains inadequately addressed, impacting its application to maritime activities. This paper, therefore, focuses on developing an FIS theoretical model for hydroelastic waves to provide solutions, the analysis of which will offer valuable insights into the current literature.

The sections of this manuscript are organized in the following manner. The theoretical framework is established in Section 2, where the problem is formulated based on the principles of linear wave theory, with the underlying physical phenomenon expressed mathematically through a model of flexural gravity wave scattering by a semi-infinite FIS with compressive force near an impermeable vertical wall in the presence of FC. In Section 3, the solution method, leveraging eigenfunction expansion and mode coupling relations, is discussed and utilized. In Section 4, the comparison results, convergence analysis, and impact of FC, along with the parameters of the FIS model on the strain, displacements, and reflection wave amplitude by a vertical rigid wall, are discussed. It is observed that the current speed significantly influences the strain, displacements, and reflection amplitude in addition to the horizontal force applied to the wall. At the end, the concluding remarks and limitations are highlighted in Section 5.

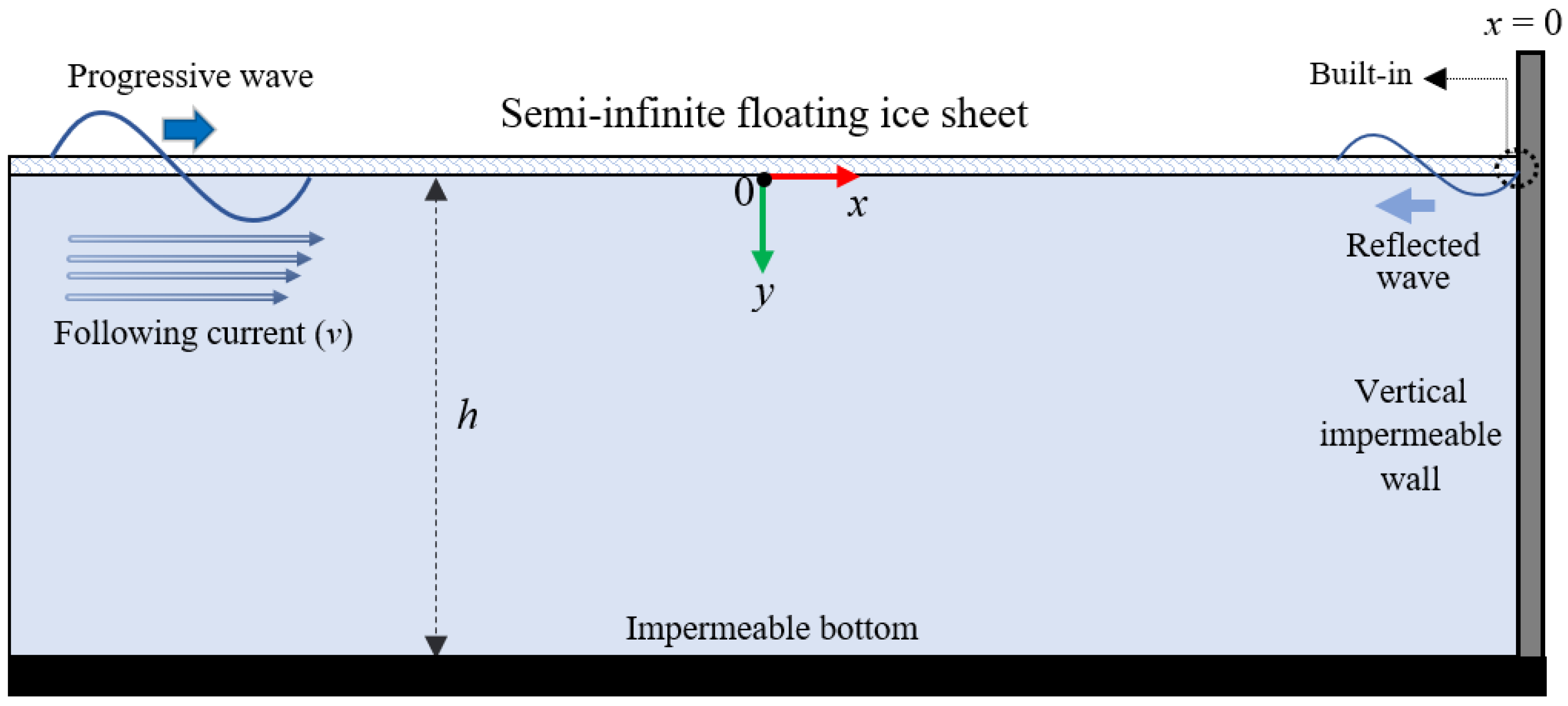
2. Model Definition

The underlying assumptions of the mathematical structure dictate the use of a standard Cartesian coordinate system, where the abscissa ($x$-axis) is defined horizontally. The ordinate ($y$-axis), conversely, features an unconventional polarity, establishing positive movement as an increase in the downward vertical direction. The physical configuration includes an impermeable vertical barrier positioned at $x=0$. To its left, an aquatic domain stretches indefinitely towards negative $x$-values $(-\infty < x < 0$), maintaining a constant depth ‘$h$’ (from $y=0$ to $y=h$). This water body’s upper interface is completely overlain by a semi-infinite ice sheet, which has an infinitesimally small thickness ‘$d$’ (illustrated in Figure 1). Consistent with the framework of linear water wave theory, a uniform current is prescribed to flow at a constant velocity $\nu$, and is oriented in the positive $x$-direction, aligning with the direction of wave propagation. Under the assumption of the linearized water wave theory, the fluid is considered to be incompressible, inviscid, and the motion is irrotational and time harmonic $t$ with angular frequency ω. There exists a velocity potential $\Phi \left(\dot{y},t\right)$ associated with FC, which is expressed as:

$$\Phi (\dot{y},t)=\nu x+\Psi (\dot{y},t),$$

(1)

where $\dot{y}=\left(x,y\right).$ We can express $\Psi \left(\dot{y},t\right)$ as $\Psi \left(\dot{y},t\right)=Re\left\{\phi \left(\dot{y}\right)e^{-i\omega t}\right\}$. In this expression, Re stands for the real part, and $\phi \left(\dot{y}\right)$ represents the spatial potential. Consequently, the scalar potential field $\Psi$ is mathematically governed by the two-dimensional constraints intrinsic to the Laplace differential equation as:

$${\nabla }^2\Psi \left(\dot{y}\right)=0 \mathrm{in} \mathrm{the} \mathrm{whole} \mathrm{fluid} \mathrm{domain}$$

(2)

where ${\nabla }^2={\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}$.

The seabed state, taken precisely at the level $y = h$, implies the relationship:

$${\displaystyle \frac{\partial \Psi }{\partial y}}=0$$

(3)

As structural movement $\zeta (x,t)=Re\left\{\zeta \left(x\right)e^{-i\omega t}\right\}$ drives changes in fluid patterns, a linear kinematic condition is formulated to account for the effect of FC ($\nu$). This condition is given by:

$${\displaystyle \frac{\partial \zeta }{\partial t}}+\nu {\displaystyle \frac{\partial \zeta }{\partial x}}={\displaystyle \frac{\partial \Psi }{\partial y}} \mathrm{for} y=0$$

(4)

The thin ice sheet on the upper surface is treated as a component of the water surface, though its distinct physical characteristics are governed by its structural stiffness. Under compression and following the current, the dynamic boundary condition satisfies as:

$$\left\{EI{\partial }_{xxxx}+C{\partial }_{xx}+{\rho }_{i}d{\partial }_{tt}\right\}\zeta =-P_H(x,y,t),$$

(5)

where $P_H\left(x,y,t\right)= -\rho \left({\partial }_t+v{\partial }_x\right)\psi +\rho g\zeta$.

Eliminating the ice sheet deformation $\zeta$ from Equations (4) and (5), the linearized enclosed BC, via $\psi \left(x,y,t\right),$ is determined as:

$$\left\{EI{\partial }_{xxxx}+C{\partial }_{xx}+{\rho }_{i}d{\partial }_{tt}+\rho g\right\}{\psi }_y=\rho \left({\partial }_t+v{\partial }_x\right)\psi .$$

(6)

The fifth-order BC on the FIS via $\phi$ can be obtained by combining the kinetical, dynamic boundary conditions along with Equation (6) as:

$$\left\{\alpha {\partial }_{yyyyy}-\beta {\partial }_{yyy}+{\partial }_y\right\}\phi =-\gamma {(\omega -vp)}^2\phi .$$

(7)

where $\alpha =EI/(\rho g-{\rho }_{i}d{\omega }^2)$, $\beta =C/(\rho g-{\rho }_{i}d{\omega }^2)$, and $\gamma =\rho /(\rho g-{\rho }_{i}d{\omega }^2)$.

This may highlight that if we set $\beta =0$ and $\nu =0$ in Equation (7), the reduced expression will be the same as in Equation (3a) as previously found in [5].

The BC on the vertical impermeable wall can be provided as:

$${\displaystyle \frac{\partial \phi }{\partial x}}=0 \mathrm{on} x=0$$

(8)

The far-field BC adheres to the following mathematical conditions:

$$\phi \left(\dot{y}\right)=\left(I{e}^{-i{p}_{0x}}+R{e}^{i{p}_{0x}}\right){\mathcal{F}}_0\left(y\right), \mathrm{a}\mathrm{s} \left|x\right|\to \infty \mathrm{i}\mathrm{n} \mathrm{F}\mathrm{W}\mathrm{D},$$

(9)

where ${\mathcal{F}}_0\left(y\right)=\left[cosh\left\{p_0(h-y)\right\}\right]/cosh{(p}_{0}h)$ with the parameters $I$ and $R$ are the fixed scalar magnitudes corresponding to the progressive wave components traveling along the negative and positive x-axes, respectively, while the quantity $p_0$ designates the spatial frequency (wave number) intrinsic to the progressive flexural gravity waves.

The free edge at $x\to 0^{-}, y=0$ leads to the following mathematical conditions:

$${\displaystyle \frac{{\partial }^3\phi }{\partial x^2\partial y}}=0,$$

(10a)

$$EI{\displaystyle \frac{{\partial }^4\phi }{\partial x^3\partial y}}+C{\displaystyle \frac{{\partial }^2\phi }{\partial x\partial y}}=0.$$

(10b)

The stipulations for a built-in or fixed edge condition necessitate that the displacement and the gradient of deflection are nullified at $x\to 0^{-}$, $y=0$ and can be expressed as:

$${\displaystyle \frac{\partial \phi }{\partial y}}=0,$$

(11a)

$${\displaystyle \frac{{\partial }^2\phi }{\partial x\partial y}}=0.$$

(11b)

3. Solution Technique

Utilizing the Fourier expansion formulae, $\phi$, satisfies Equations (2), (9) and (10) and can be formulated as:

$$\phi \left(\dot{y}\right)=\left(I_0{e}^{-i{p}_{0}x}+R{e}^{i{p}_{0}x}\right)S\left(p_0,v\right){\mathcal{F}}_0\left(y\right)+ {\sum }_{n=I}^{II}{R}_n{S\left(p_n,v\right)e}^{i{p}_{n}x}{\mathcal{F}}_n\left(y\right)+{\sum }_{n=1}^{\infty }{R}_n{S\left(p_n,v\right)e}^{-p_{n}x}{\mathcal{F}}_n\left(y\right),$$

(12)

where $S\left({\lambda }_n,v\right)=ig/2\left(\omega -v{p}_n\right)$, ${\mathcal{F}}_0\left(y\right)$ being the same as defined in Equation (9), and the expression for ${\mathcal{F}}_n\left(y\right)$, for $n=I,II,\dots$ is obtained by replacing $p_0$ with $p_n$ in ${\mathcal{F}}_0\left(y\right)$. In addition, ${\mathcal{F}}_n\left(y\right)={\displaystyle \frac{cos{p}_n(h-y)}{cos{p}_{n}h}}$, for $n=\mathrm{1,2},\dots$.

The eigenvalues $p_0$ and $p_n$ satisfy the dispersion relations as:

$p_n\left(\alpha p_n^4-\beta p_n^2+1\right)tanh{p}_{n}h-\left(1/g\right){\left(\omega -v{p}_n\right)}^2=0$ for $n=0$ refer to the real root and

$p_n\left(\alpha p_n^4-\beta p_n^2+1\right)tanh{p}_{n}h-\left(1/g\right){\left(\omega -v{p}_n\right)}^2=0$ contain four complex roots, but due to the boundedness of the series solution, only two complex roots are considered in the expansion formula (12) of the form $a\pm ib$ for $n=I,II$. On the other hand, for $n=\mathrm{1,2},\dots$ there are infinitely many imaginary roots of the form $i{p}_n$. It is imperative to recognize that if we set compression $\beta =0$ and $v=0$, then the resultant will be consistent as previously obtained in [5]. ${\mathcal{F}}_n\left(y\right)$ satisfy the following orthogonal mode-coupling relation as:

$$\begin{gathered} <{\mathcal{F}}_m\left(y\right),{\mathcal{F}}_n\left(y\right)> ={\int }_0^h{\mathcal{F}}_m\left(y\right){\mathcal{F}}_n\left(y\right)dy+{\displaystyle \frac{g\alpha }{{(\omega -v{p}_n)}^2}}\left\{{\partial }_{yyy}{\mathcal{F}}_m\left(0\right){\partial }_y{\mathcal{F}}_n\left(0\right)+ \\ {\partial }_y{\mathcal{F}}_m\left(0\right){\partial }_{yyy}{\mathcal{F}}_n\left(0\right)\right\}-{\displaystyle \frac{g\beta }{{\left(\omega -v{p}_n\right)}^2}}\left\{{\partial }_y{\mathcal{F}}_m\left(0\right){\partial }_y{\mathcal{F}}_n\left(0\right)\right\}=\left\{\begin{array}{c}0, m\ne n\\ U_n, m=n\end{array}\right. \end{gathered}$$

(13)

where $U_n={\displaystyle \frac{2p_{n}h\left(\alpha p_n^4-\beta p_n^2+1\right)+\left(5\alpha p_n^4-3\beta p_n^2+1\right)sinh2\left(p_{n}h\right)}{4p_n\left(\alpha p_n^4-\beta p_n^2+1\right)cos{h}^2{p}_{n}h}}$.

Using (13), Equation (8), and edge condition (10), the coefficients $R_n$, are determined as:

$$R_n=I-{\displaystyle \frac{gtanh{p}_{n}h}{i{\left(\omega -vp\right)}^2{U}_n}}{p}_n\left[a(\alpha p_n^2-\beta )+b\alpha \right], n = I, II, III, IV, 1, 2,\dots$$

(14)

The ice sheet edge condition, detailed in Equation (10), allows for the determination of the two unknown parameters, $a$ and $b$. Applying the ice sheet edge condition (10) $\phi$ as in Equation (12), and replacing $R_n$ from Equation (14), results in:

$${\mathsf{{\rm Y}}}_{1}a+{\mathsf{{\rm Y}}}_{2}b={\mathsf{{\rm Y}}}_3$$

(15)

$${\mathsf{{\rm Y}}}_{4}a+{\mathsf{{\rm Y}}}_{5}b=0$$

(16)

Solving Equations (15) and (16), one can obtain:

$$a={\displaystyle \frac{{\mathsf{{\rm Y}}}_3{\mathsf{{\rm Y}}}_5}{{\mathsf{{\rm Y}}}_1{\mathsf{{\rm Y}}}_5-{\mathsf{{\rm Y}}}_2{\mathsf{{\rm Y}}}_4}} b={\displaystyle \frac{{-\mathsf{{\rm Y}}}_3{\mathsf{{\rm Y}}}_4}{{\mathsf{{\rm Y}}}_1{\mathsf{{\rm Y}}}_5-{\mathsf{{\rm Y}}}_2{\mathsf{{\rm Y}}}_4}} \mathrm{where}, {\mathsf{{\rm Y}}}_1{\mathsf{{\rm Y}}}_5-{\mathsf{{\rm Y}}}_2{\mathsf{{\rm Y}}}_4\ne 0$$

(17)

$${\mathsf{{\rm Y}}}_1=-gi\sum _{n=0,I,II,1}^N{\displaystyle \frac{{tanh}^2{p}_{n}h}{{\left(\omega -v{p}_n\right)}^2{U}_n}}{p}_n^3(\alpha p_n^2-\beta )$$

$${\mathsf{{\rm Y}}}_2=-gi\sum _{n=0,I,II,1}^N{\displaystyle \frac{\alpha }{{\left(\omega -v{p}_n\right)}^2{U}_n}}{p}_n^5{tanh}^2{p}_{n}h$$

$${\mathsf{{\rm Y}}}_3=-2p_n^{3}tanh{p}_{n}h$$

$${\mathsf{{\rm Y}}}_4=g\sum _{n=0,I,II,1}^N{\displaystyle \frac{{tanh}^2{p}_{n}h}{{\left(\omega -v{p}_n\right)}^2{U}_n}}{p}_n^4(\alpha p_n^2-\beta )$$

$${\mathsf{{\rm Y}}}_5=-g\sum _{n=0,I,II,1}^N{\displaystyle \frac{\alpha }{{\left(\omega -v{p}_n\right)}^2{U}_n}}{p}_n^6{tanh}^2{p}_{n}h$$

where, to successfully determine the values of the coefficients $a$ and $b$, the infinite mathematical progression detailed in Expressions (15) and (16) must be curtailed, utilizing only a finite set of components for the summation.

NB: It should be noted that, at $v=0$ and compression $\beta =0$ in Equations (15) and (16), the reduced expressions will be the same as in [5].

The surface strain $S$ for the flexural gravity waves along the FIS at $y = 0$ can be computed by the following formula:

$$S= {\displaystyle \frac{id}{2\omega }}{\displaystyle \frac{{\partial }^3\Psi }{\partial x^2\partial y}}.$$

(18)

$$\left({\partial }_t+\nu {\partial }_x\right)\zeta ={\Psi }_y.$$

(19)

It may be mentioned that although the underlying mathematical framework is fully capable of modeling both co-directional (following) and contra-directional (opposing) interactions between currents and waves, the findings presented here are confined solely to the co-directional scenario. This strategic limitation serves to proactively bypass wave blocking, an adverse physical condition exclusive to flow regimes featuring opposing currents which is crucial to exclude from the analysis.

4. Quantified Outcomes and Their Interpretive Analysis

By analyzing the numerical values of reflection amplitude for different current speeds with increasing the number of terms ($N$) in the series solution along with the range of parametric values provided in

Table 1. FIS key elements of the model.

Model Key Elements	Values	Units
Thickness (d)	0.14	[m]
Flexural rigidity (EI)	$0.47\times {10}^{0.4}$	[Nm2]
Current speed (v)	0.5	[m/s]
Water depth (h)	10	[m]
Water density ($\rho$)	1025	[kgm−3]
Gravitational constant (g)	9.8	[m/s]

, we demonstrate the numerical accuracy of the analytical results with $g=9.8 \mathrm{m}/{\mathrm{s}}^2$ and water density $\rho = 1000 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$ in

Table 2. Demonstration of convergence $R$ for various $v$.

N	$\left(\mathbf{a}\right) \mathit{v}=0.8 \mathbf{m}/\mathbf{s}$ R (m)	$\left(\mathbf{b}\right) \mathit{v}=1.4 \mathbf{m}/\mathbf{s}$ R (m)
6	0.8350	0.8524
9	0.8327	0.8508
13	0.7849	0.8497
15	0.7774	0.8478
17	0.7758	0.8481
19	0.7755	0.8483
20	0.7752	0.8485

. Further, it may be noted that the structural parameters provided in Table 1, especially a small thickness of the FIS, along with other parametric values, were selected to achieve computational accuracy in the numerical results relative to the analytical solution.

The numerical simulations derived from the analytical solution were executed using MATLAB R2023b (64-bit, Windows x64) on a desktop workstation equipped with an Intel Core i7-4790 CPU running at 3.60 GHz and boasting 16 GB of memory (Intel Corporation, Santa Clara, CA, USA). The time required to simulate a single case usually falls within the 8–10 min range.

4.1. Convergence of the Present Solution and Validation with Literature

Here, the infinite series sums (11) associated with the reflection amplitude $R$ is bounded such that it incorporates a maximum of $N=20$ elements to determine the coefficients ‘$a$’ and ‘$b$’. An analysis of reflection wave amplitudes ($R$) in Table 2, considering increasing $N$ and different current speed values, confirms their computational accuracy. Table 2 shows that the $R$ values are accurate to three decimal places for $N \ge 20$. Consequently, to maintain computational accuracy.

Figure 2 illustrates a comparison of the non-dimensional strain ($S$) along the non-dimensional length ($x$) of the FIS between the present solution under current loading and the results of [44]. For this comparison, the physical parameters are the same as in [44]. Overall, the two curves exhibit a qualitatively similar oscillatory pattern. However, the inclusion of current in the present model leads to noticeable changes in the phase of the strain response. Specifically, the present solution shows slightly reduced strain amplitudes and a phase shift relative to the no-current case in [44], indicating that the presence of current alters the hydrodynamic pressure distribution and modifies the FIS deformation characteristics.

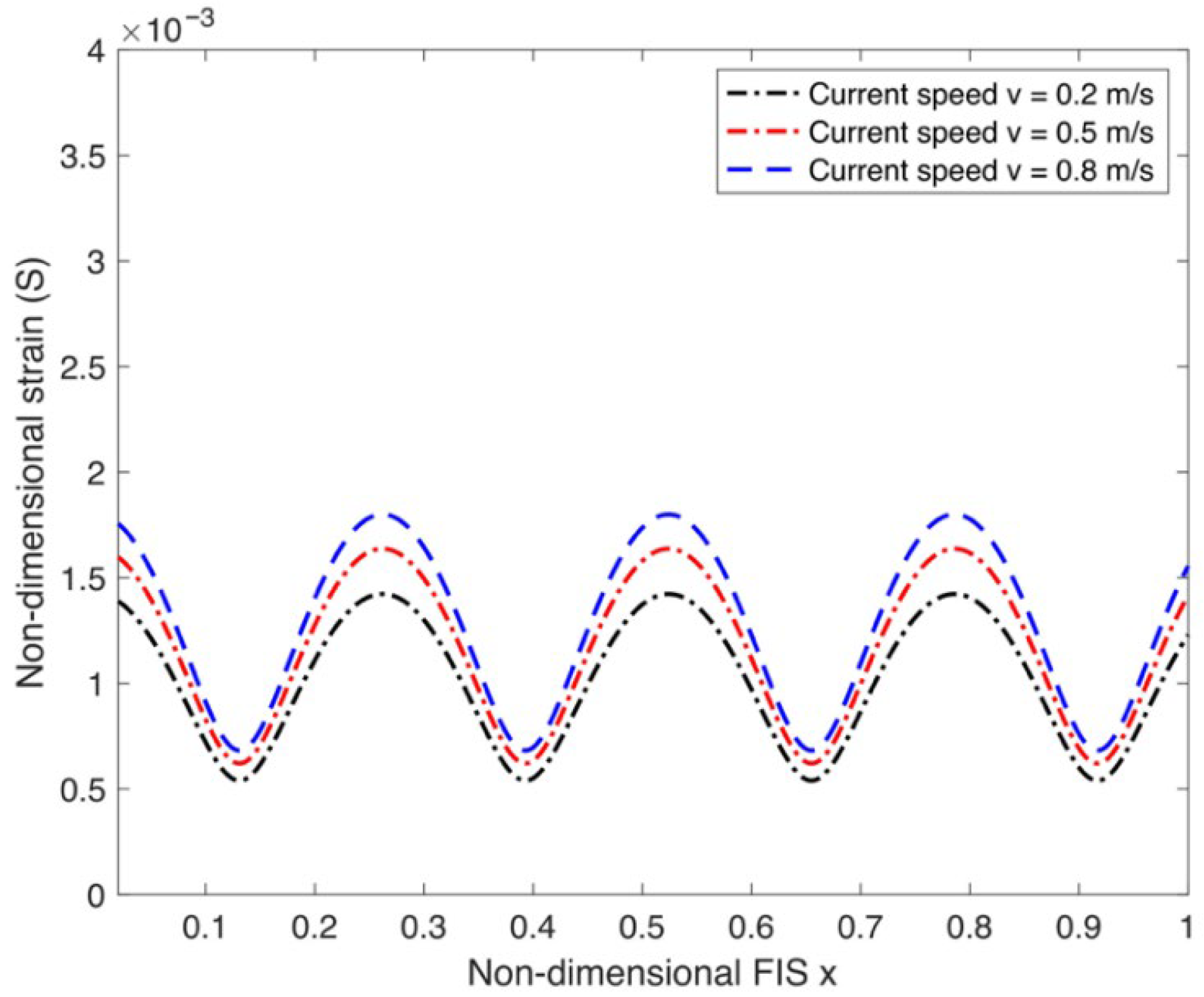
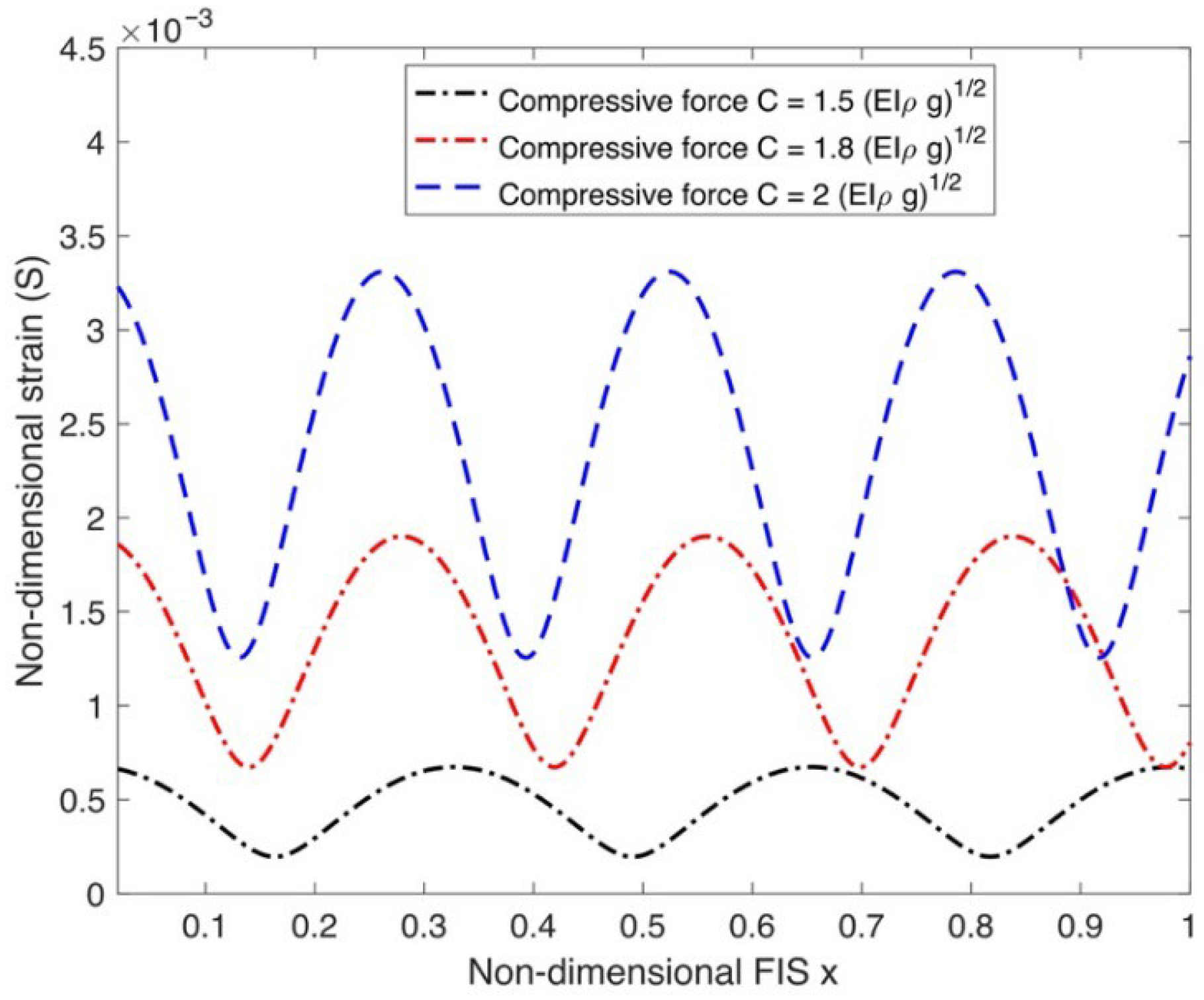
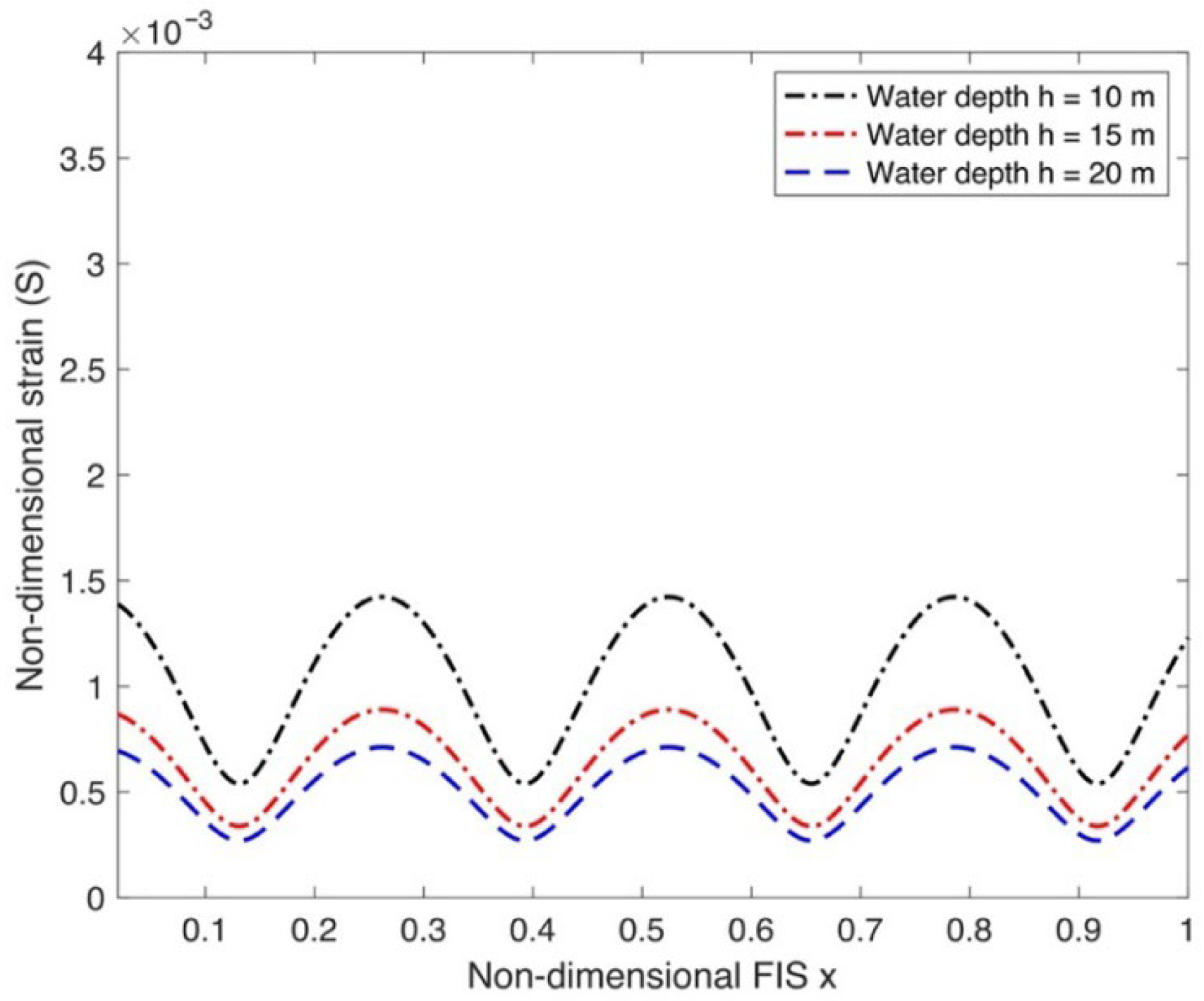
4.2. Impact of Current Speed and FIS Key Elements on Strain Along FIS

Figure 3 effectively demonstrates that in the present model, increasing the current speed significantly increases the magnitude of strain (S) over the length (x) of the FIS. This critical observation is primarily due to the exponential increase in the fluid excitation force imparted by the flow onto the FIS, highlighting the crucial role of current as a dominant and indispensable environmental parameter for accurately predicting the hydroelastic response of the FIS. This necessity is vital for applications such as assessing ice sheet stability and predicting ice-induced loading on coastal or offshore structures.

Figure 4 plots how the non-dimensional strain of the FIS changes over its non-dimensional length for different compressive forces ($C$). Increasing the magnitude of the compressive force leads to a significant amplification of the dynamic strain amplitude experienced by the FIS. The compressive force effectively reduces the flexural rigidity of the FIS, making it more susceptible to dynamic excitation loads like waves and currents.

Figure 5 illustrates an inverse relationship between the non-dimensional strain and the flexural rigidity $EI$ of the FIS. For the given non-dimensional length, an increase in the $EI$ results in a substantial decrease in the measured strain.. Essentially, the ice sheet’s higher flexural rigidity successfully mitigates the development of large non-dimensional strains along its length, thereby enhancing the integrity of the FIS.

Figure 6 illustrates the strain $S$ along $x$ the FIS for different $d$. The results confirm that thicker ice sheets are more rigid and are therefore better able to resist the applied wave–current load, resulting in less strain. Increasing the FIS thickness raises both the bending moment and the effective moment of inertia. In contrast, a thin FIS has much lower flexural rigidity and thus responds more readily to external loads. Its reduced rigidity allows wave and current loads to induce larger deflections and higher strain concentrations. These elevated strain levels make thin ice more vulnerable to mechanical failure, which magnifies tensile stresses at the ice surface, increasing the likelihood of crack initiation and propagation, leading to fracture or complete breakup when subjected to strong hydroelastic wave–current interactions.

From Figure 7, observations demonstrate that for deeper water, the amplitude of the non-dimensional strain decreases. Specifically, the highest strain values occur for the shallowest case ($h = 10 \mathrm{m}$), while the lowest correspond to the deepest case ($h = 20 \mathrm{m}$). As in shallower water, the velocity field beneath the FIS is constrained by the seabed, significantly increasing the hydrodynamic pressure and leading to a stronger interaction between the wave–current and the FIS.

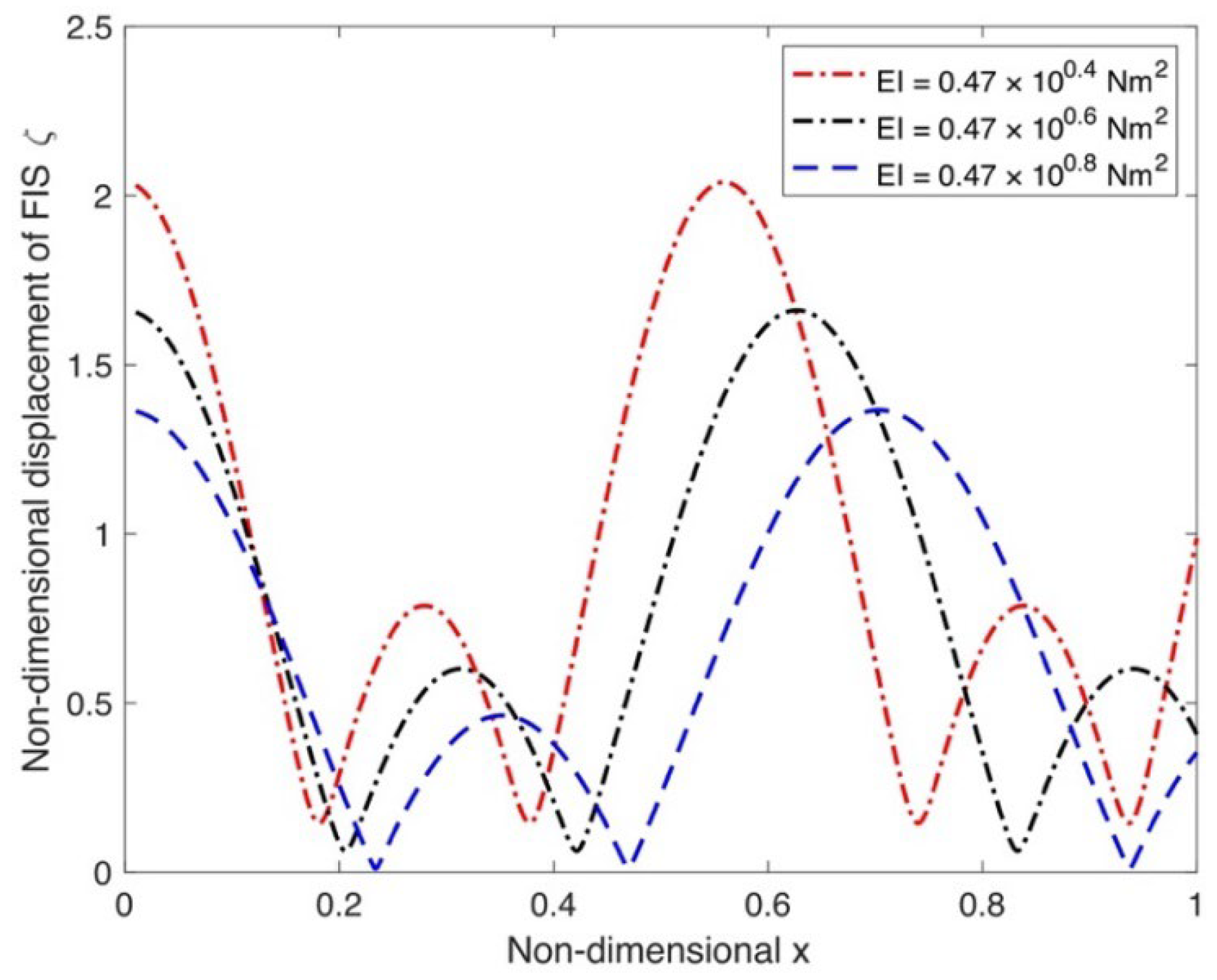
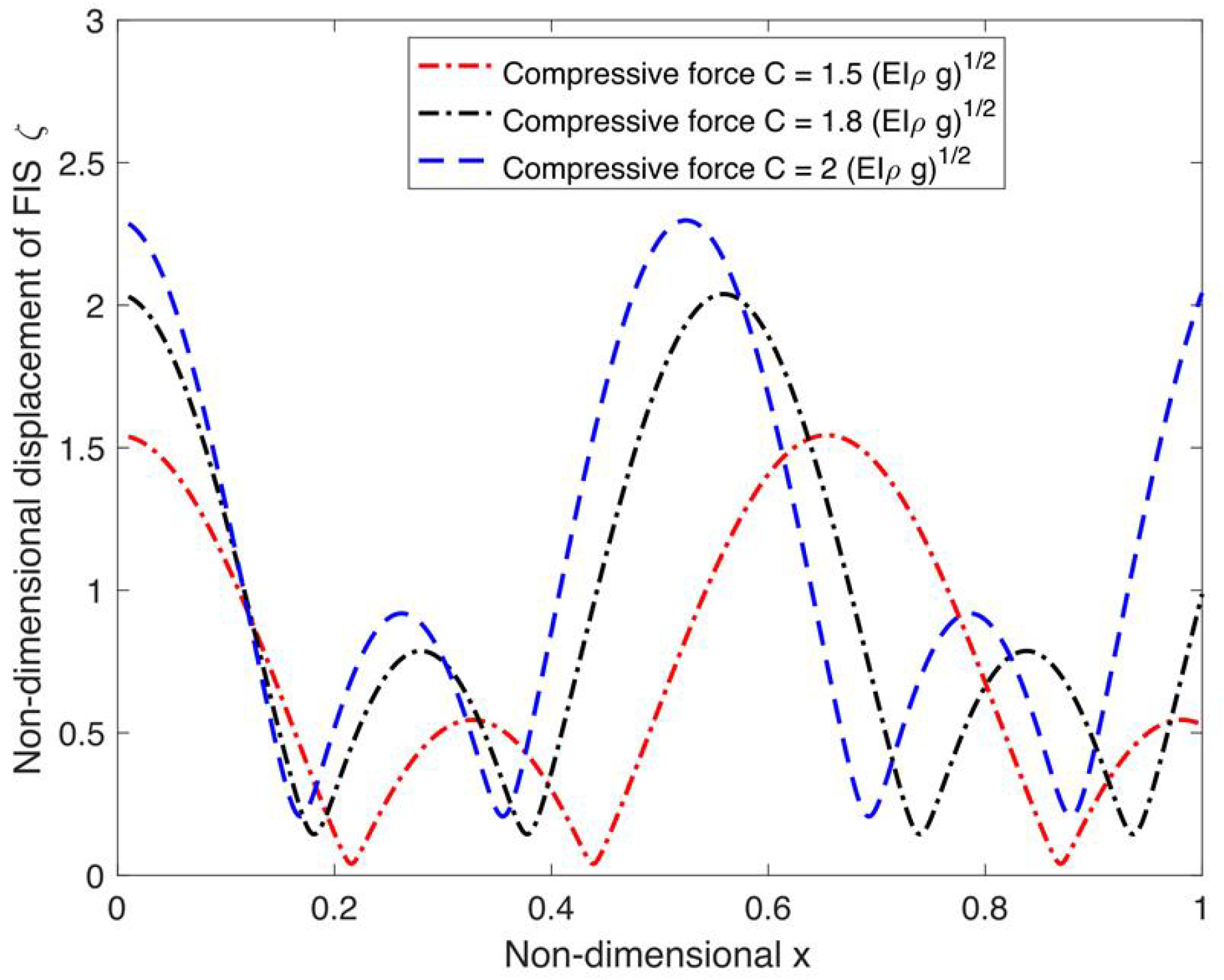
4.3. Effect of Physical and FIS Parameters on Displacement Along FIS

Figure 8 shows the impact of current speed on the FIS displacements against non-dimensional length and using the designated values for each parameter, as enumerated in Table 1. As the current speed increases, the magnitude of the non-dimensional displacement along the non-dimensional length of the FIS increases significantly. Higher current speed intensifies the hydrodynamic excitation acting on the FIS, thereby amplifying its hydroelastic response. This behavior highlights the sensitivity of the FIS to current-induced loading and demonstrates that the current plays a dominant and indeed indispensable role. Accurately capturing its influence is therefore essential for precise prediction and reliable assessment of the overall hydroelastic performance.

Figure 9 shows the non-dimensional displacements for various $EI$ versus the non-dimensional length of FIS, with other parametric values being the same as mentioned in Table 1. It is observed that with the increase in the $EI$, the displacement decreases since the ice sheet rigidity becomes higher. The same phenomenon is observed in Figure 5 for strain.

Figure 10 illustrates the variation of the non-dimensional displacement of the FIS along the non-dimensional length for various values of $C$. It is evident that the magnitude and spatial pattern of the displacement are influenced by the applied compressive force. As $C$ increases, the amplitude of the displacement also increases. This trend suggests that higher compressive loads promote larger displacements of the FIS and that the compressive force has a destabilizing effect on the FIS.

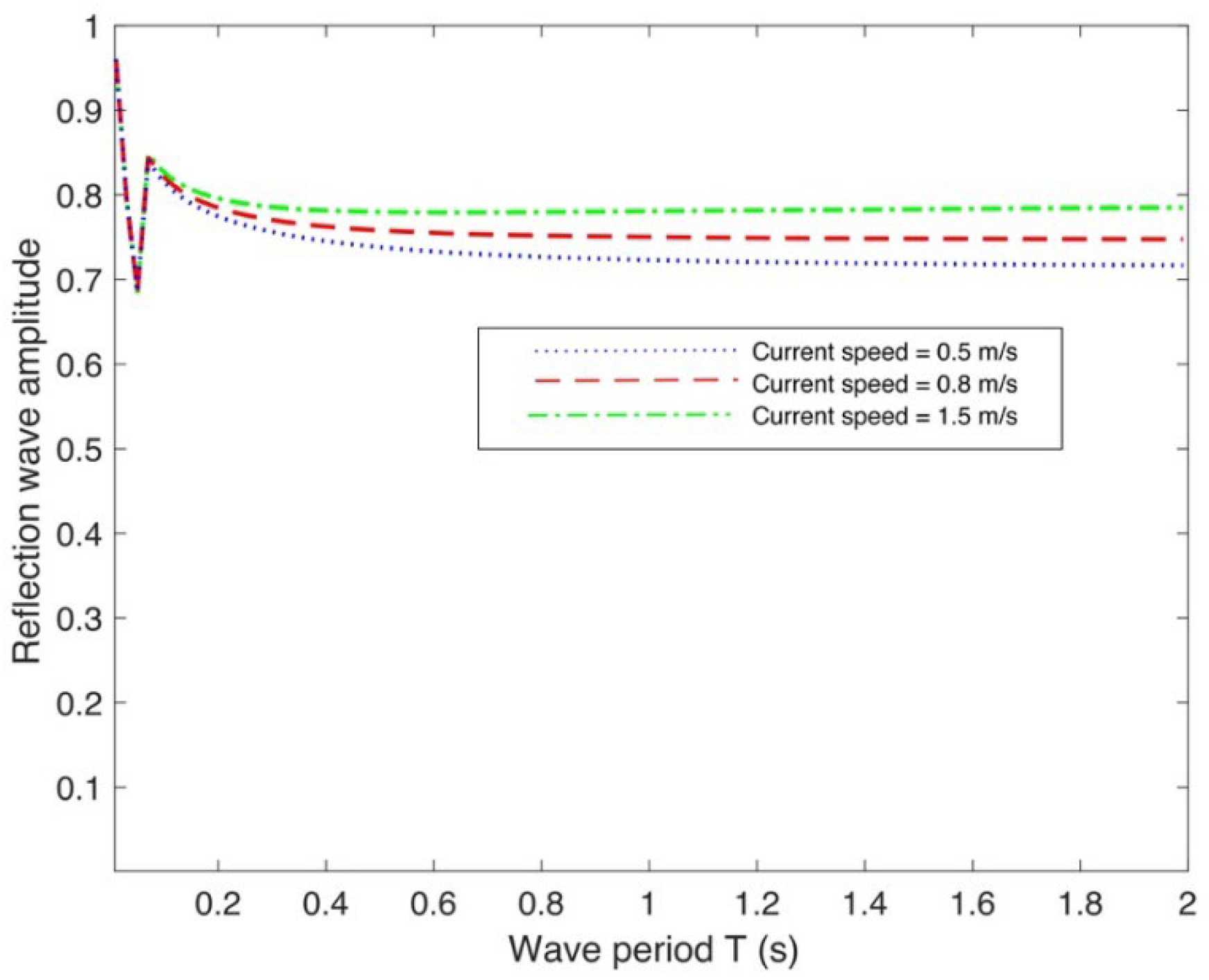
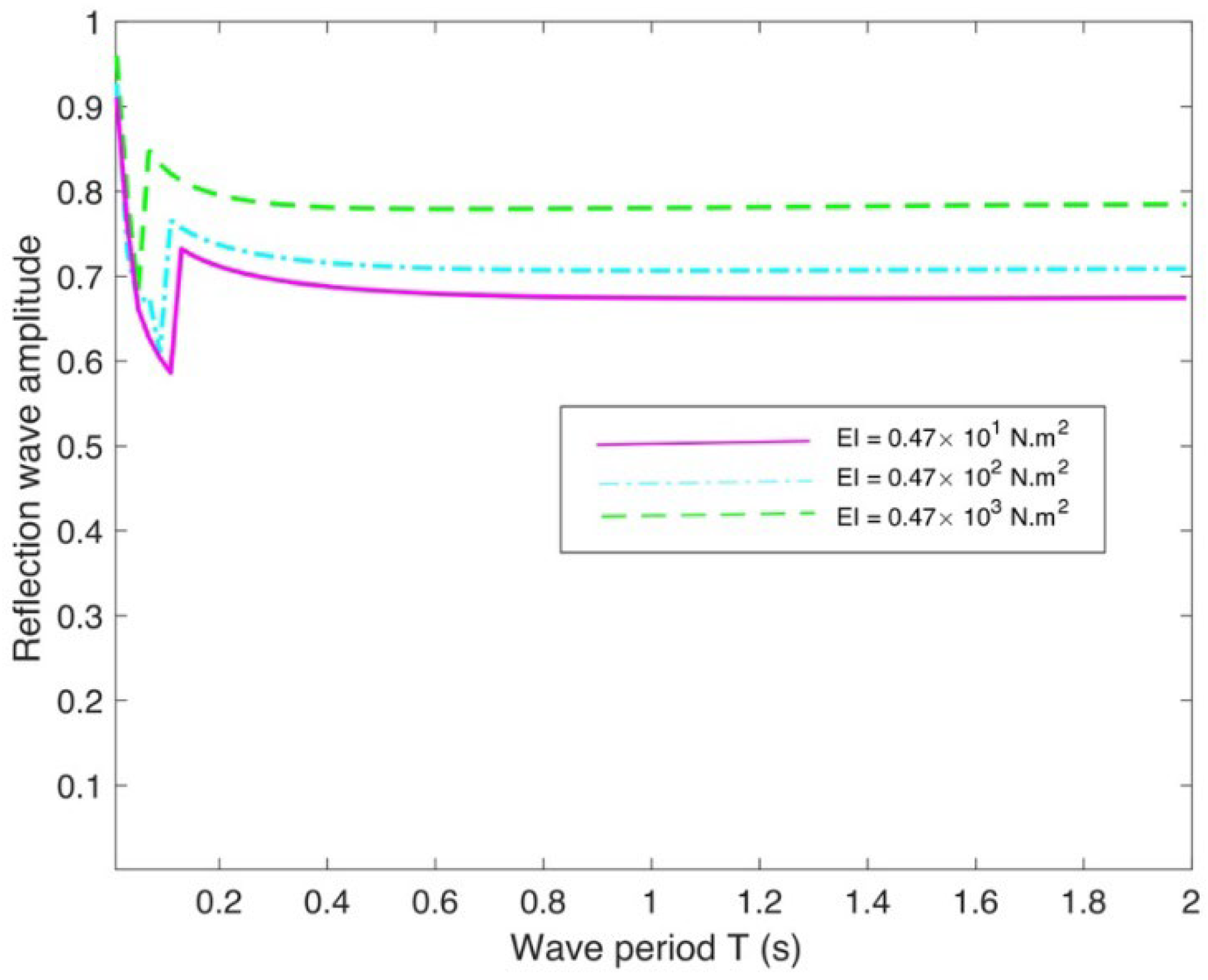
4.4. Effect of Current Speed and FIS Parameters on Reflection Wave Amplitude

In Figure 11, the differences in reflection wave amplitude for lower values of wave period for various current speeds generate a resonant pattern. Observations indicate that the magnitude of the reflected wave increases with flow velocity, with this growth becoming substantial for longer wave periods. As the current speed increases, the wave–current interaction intensifies for longer wave periods, increasing the dynamic pressure at the FIS edge boundary.

Figure 12 elucidates the relationship between flexural rigidity ($EI$) and wave reflection amplitude ($R$) as a function of wave period ($T\left(s\right)$), maintaining a constant current velocity of $v=0.8$ m/s. The data reveal that higher structural stiffness results in a more pronounced wave reflection. This observation stems from the fact that an increase in the structure’s rigidity renders the fluid-structure interface less compliant, consequently augmenting the reflection of incident waves by the now stiffer boundary. Furthermore, at shorter wave periods, the reflection amplitude consistently approaches unity ($R$ ≈ 1.0) across the entire range of flexural rigidities, a result that is entirely consistent with physical principles.

Figure 13 illustrates the relationship between $R$ and period, presenting how $R$’s values change across a spectrum of compressive forces ($C$), with the velocity consistently maintained at $v=0.8$ m/s. Changes in compressive force have a negligible impact on $R$. Conversely, an upward trend in $C$ directly correlates with an increase in $R$. Interestingly, the reflection wave amplitude remains close to one across all $C$ values when the wave period is low. This effect is likely due to a stiff, vertical wall that ensures wave energy is not lost near its surface.

Figure 14 illustrates the variation of the $F_H$ over a range of T for different v affected by a wall. The results show a clear increasing trend of the horizontal force with increasing current speed for the longer wave periods. This trend is consistent with theoretical expectations since longer wave periods are typically associated with higher wave energy, and the combined effects of increasing wave period and higher current speed result in an amplification of the hydrodynamic load on the FIS.

Figure 15 depicts the relationship between the $F_H$ and T for different h, considering the wave reflection by the vertical wall. It can be seen that the $F_H$ is higher for greater water depths and longer wave periods. This suggests that when the water depth is greater, especially in longer wave periods, effectively, the wave energy passes further below the FIS with less attenuation, resulting in a higher horizontal force on the vertical rigid wall.

5. Conclusions

The present work introduces novel mathematical formulations that include the following current interaction with a semi-infinite FIS near a vertical impermeable wall, and an analytical solution using free edge conditions along with orthogonal mode-coupling relation in FWD. Further, the effect of current, along with FIS parameters, on the strain, displacements, the reflection wave amplitude, and horizontal wave force on the wall are analyzed by studying numerical results created using a MATLAB implementation of the governing analytical expressions. The study presents these significant concluding observations.

• The consideration of FC and compressive force for the establishment of the mathematical model and its theoretical solution, along with the orthogonal mode-coupling relation, is an original contribution of this work. The current strain finding aligns with the result achieved in the literature.
• Analysis of the FIS’s strain pattern shows a consistent upward trend linked to increasing compressive force and current speed. In stark contrast, the influence of the FIS’s flexural rigidity and water depths exhibits an inverse relationship, causing strain to lessen as these values rise. Additionally, the observed displacement characteristics of the FIS, which are shaped by variables such as current velocity, applied compressive force, the material’s elastic modulus, and the prevailing water depth, demonstrate consistent alignment with the outcomes of strain analysis.
• Regarding numerical results, the current study examines how FIS affects the reflection wave amplitude and flexural gravity waves across various water depths with different structural and environmental parameters. In a semi-infinite FIS with a vertical rigid wall, the amplitude of the reflected wave was found to be larger for higher current speed, structural rigidity, and compressive force in larger wave periods. The present findings indicate that the reflection wave amplitude is contained within a physical limit of 1.0, consistent with expectations.
• The analysis of the horizontal force on the wall reveals that the higher values of current speed in deeper water increase the force on the vertical rigid wall.
• For marine engineering practical interests in polar regions, FISs often encounter vertical boundaries, ranging from natural continental shelves to man-made structures like drilling platforms and wharves, which effectively behave as a vertical wall. Consequently, studying the reflection of ice-coupled waves by a vertical impermeable wall becomes scientifically significant. Moreover, VLFSs are often deployed near shorelines or integrated with vertical breakwaters, directly exemplifying the interaction between flexural–gravity waves and vertical walls.
• The established framework exhibits specific limitations: the applicable ice sheet covered BC needs to be linear and of fifth-order, and the governing equation should be in 1D, 2D, 3D, and Helmholtz equation. Thus, the existing methodology is suitable for elastic structures that have straightforward shapes and are limited to linear analysis.