Research on Instantaneous Sediment Concentration in Muddy Coastal Waters Under Extreme Weather Conditions
Abstract
1. Introduction
2. Materials and Methods
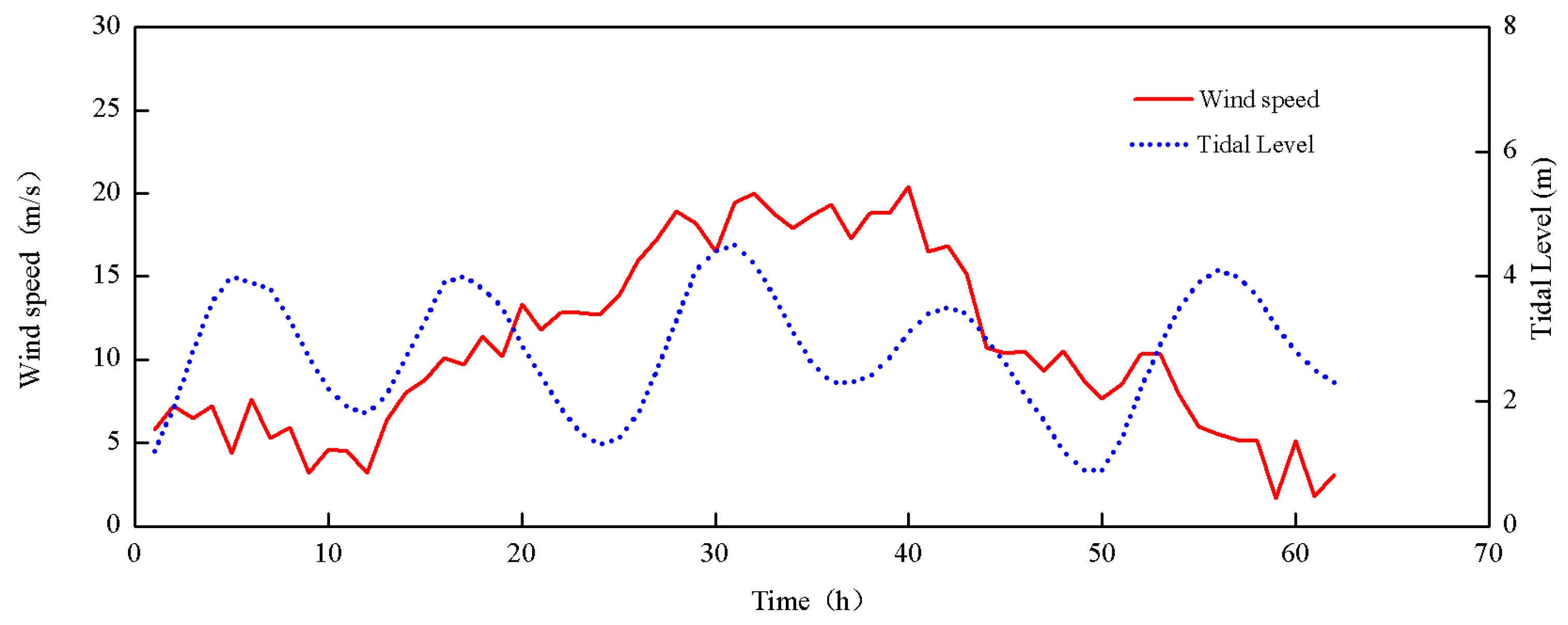
2.1. Data Sources and Monitoring Process
2.2. Relationship Between Sediment Concentration and Tidal Dynamics
2.3. Correlation Between Sediment Concentration and Wave Dynamics
- (1)
- Correlation between sediment concentration and wave height response
- (2)
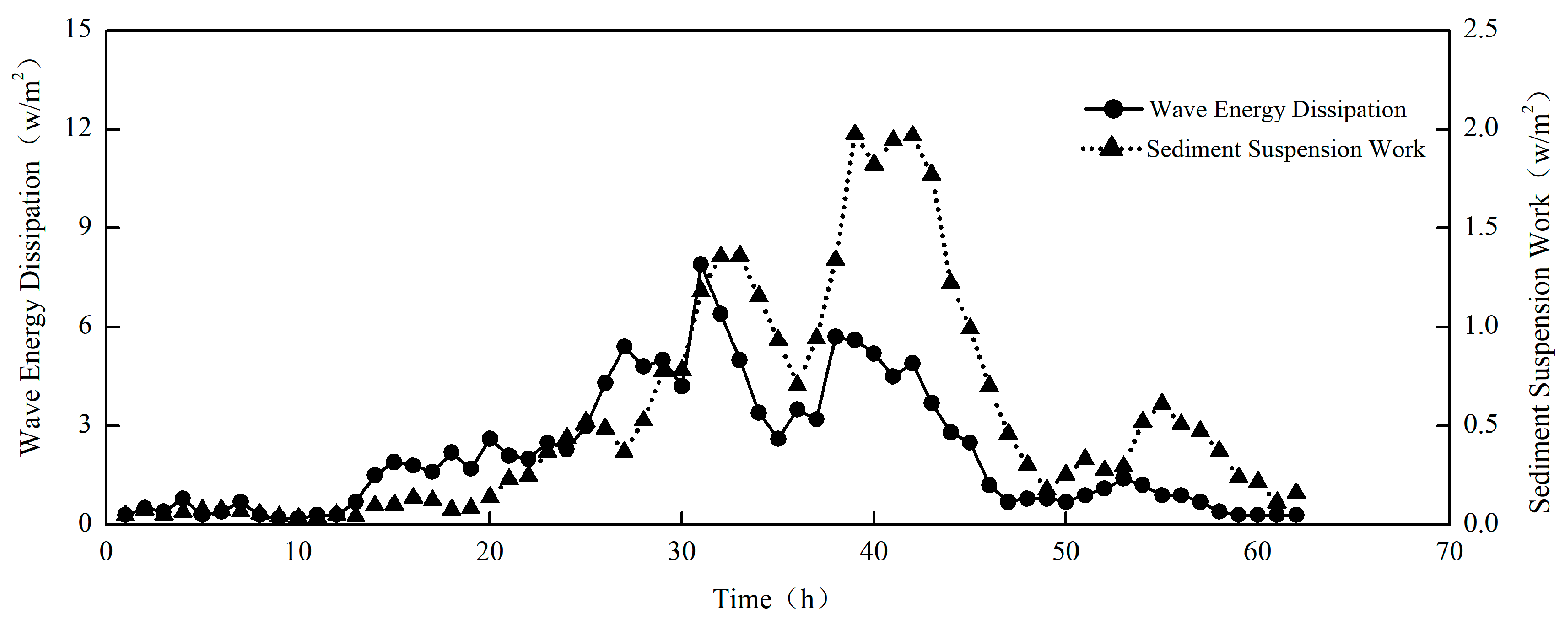
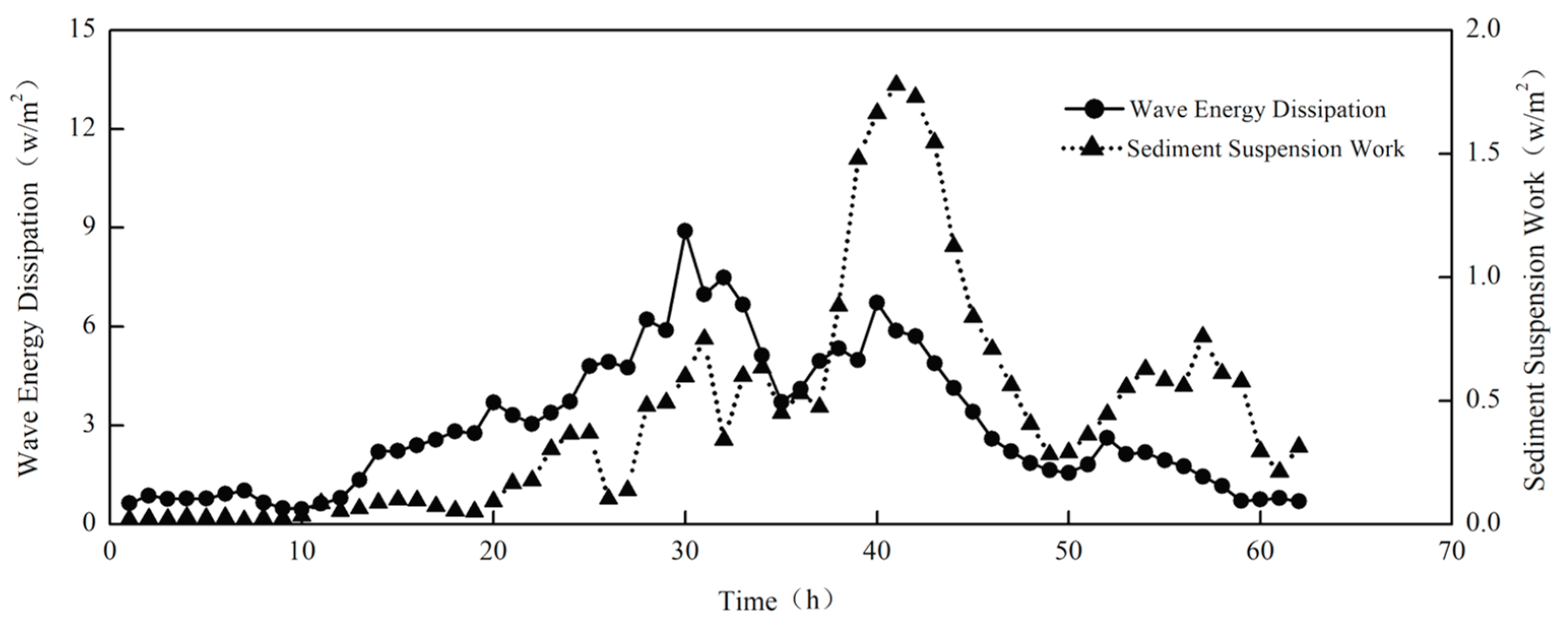
- Correlation between sediment concentration and wave energy dissipation
3. Results
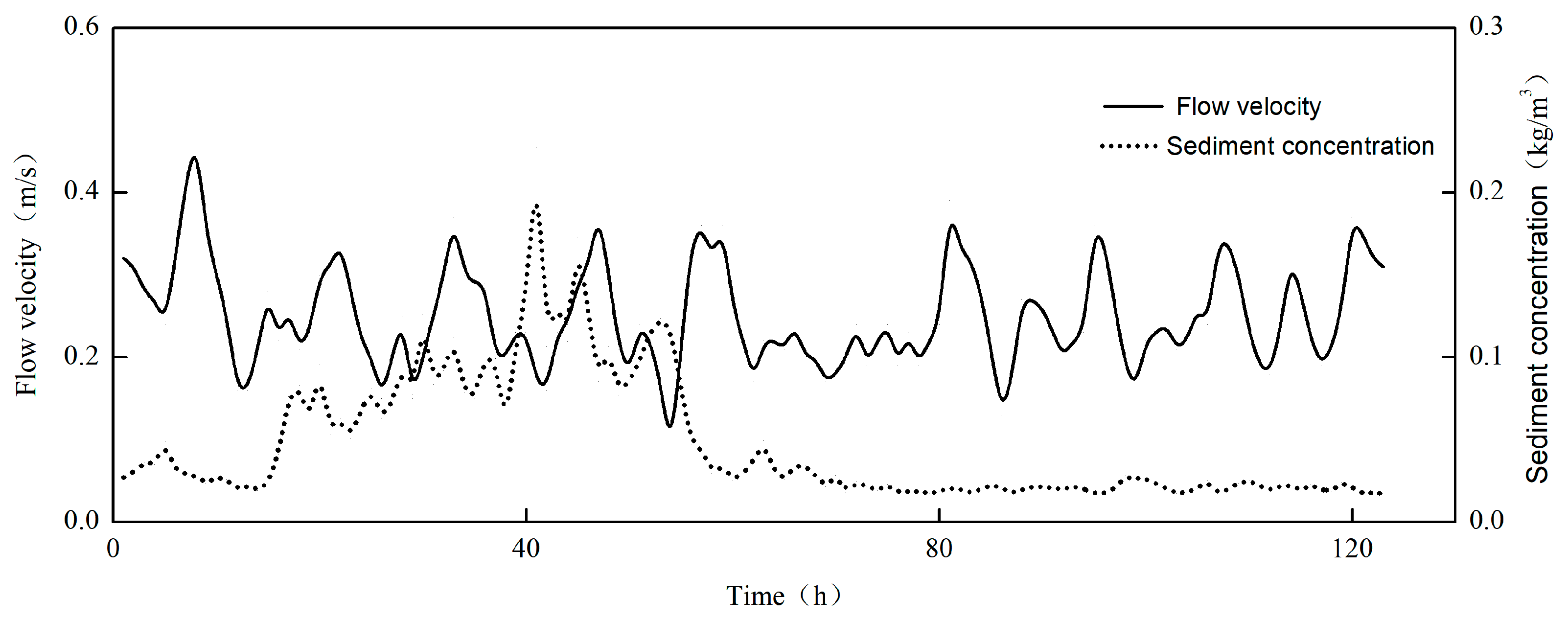
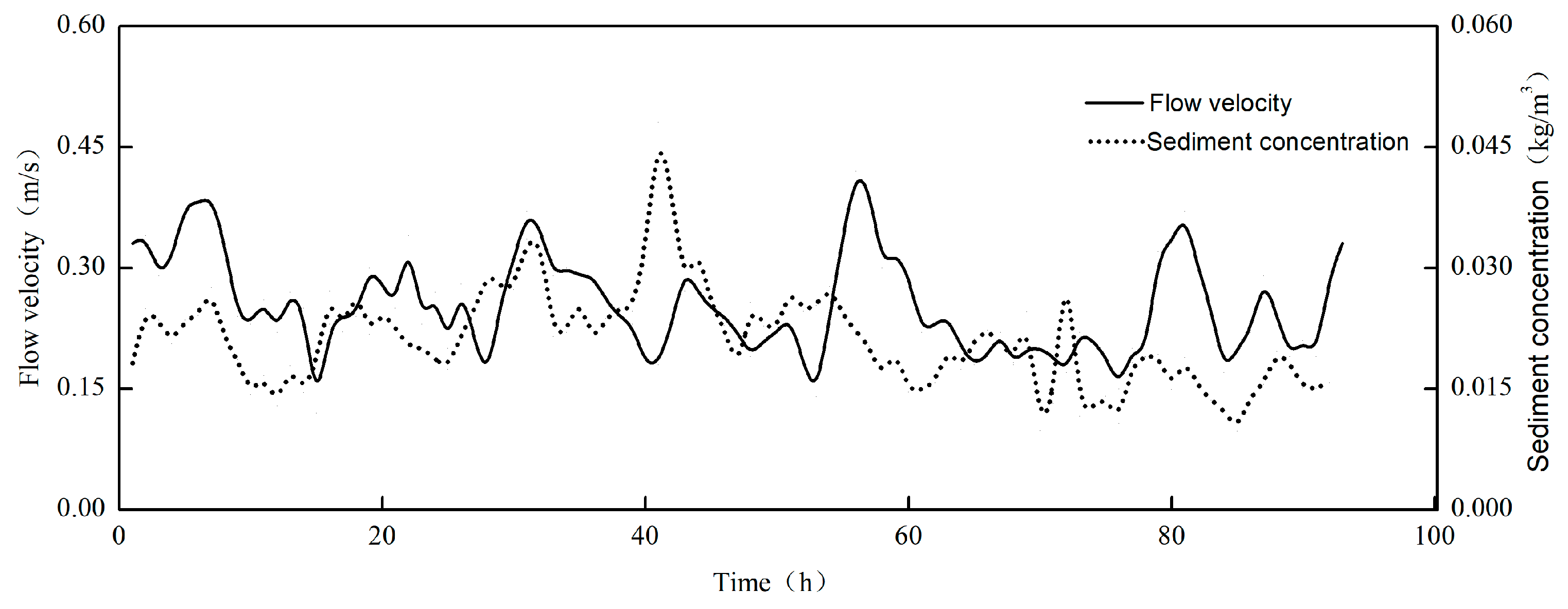
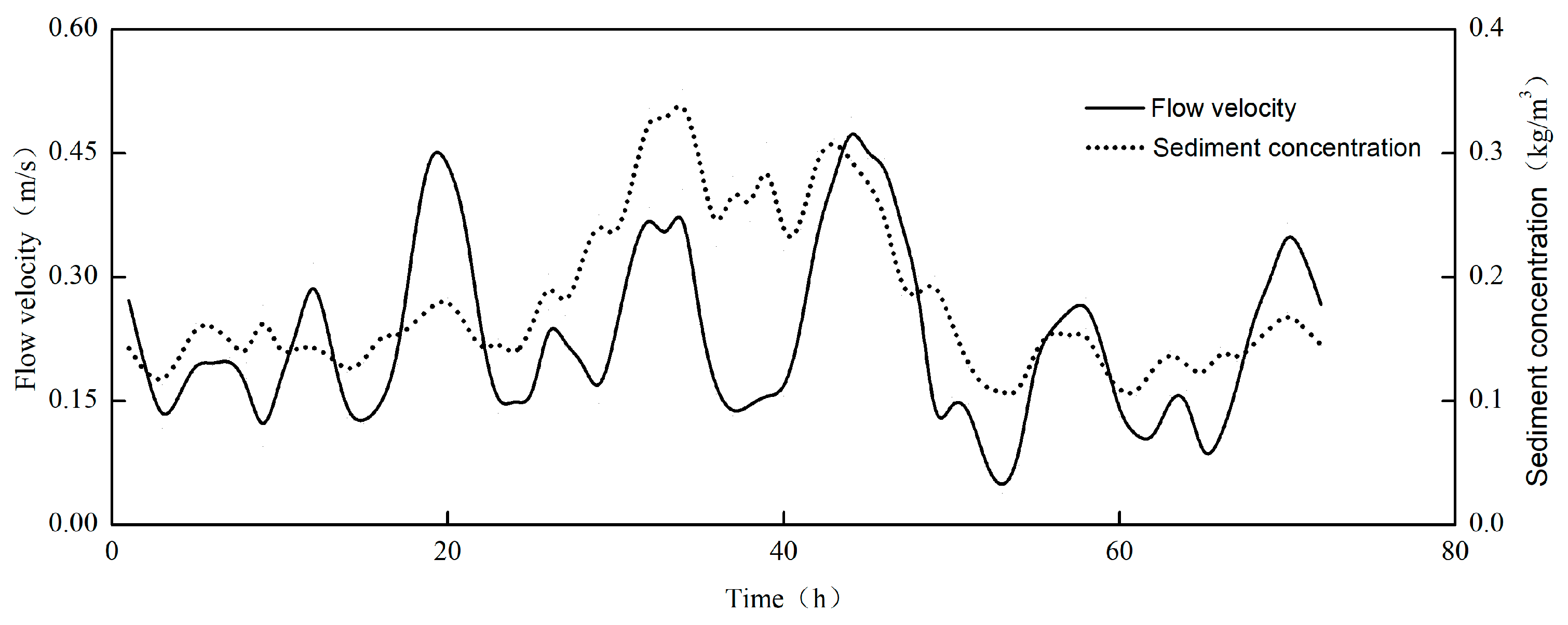
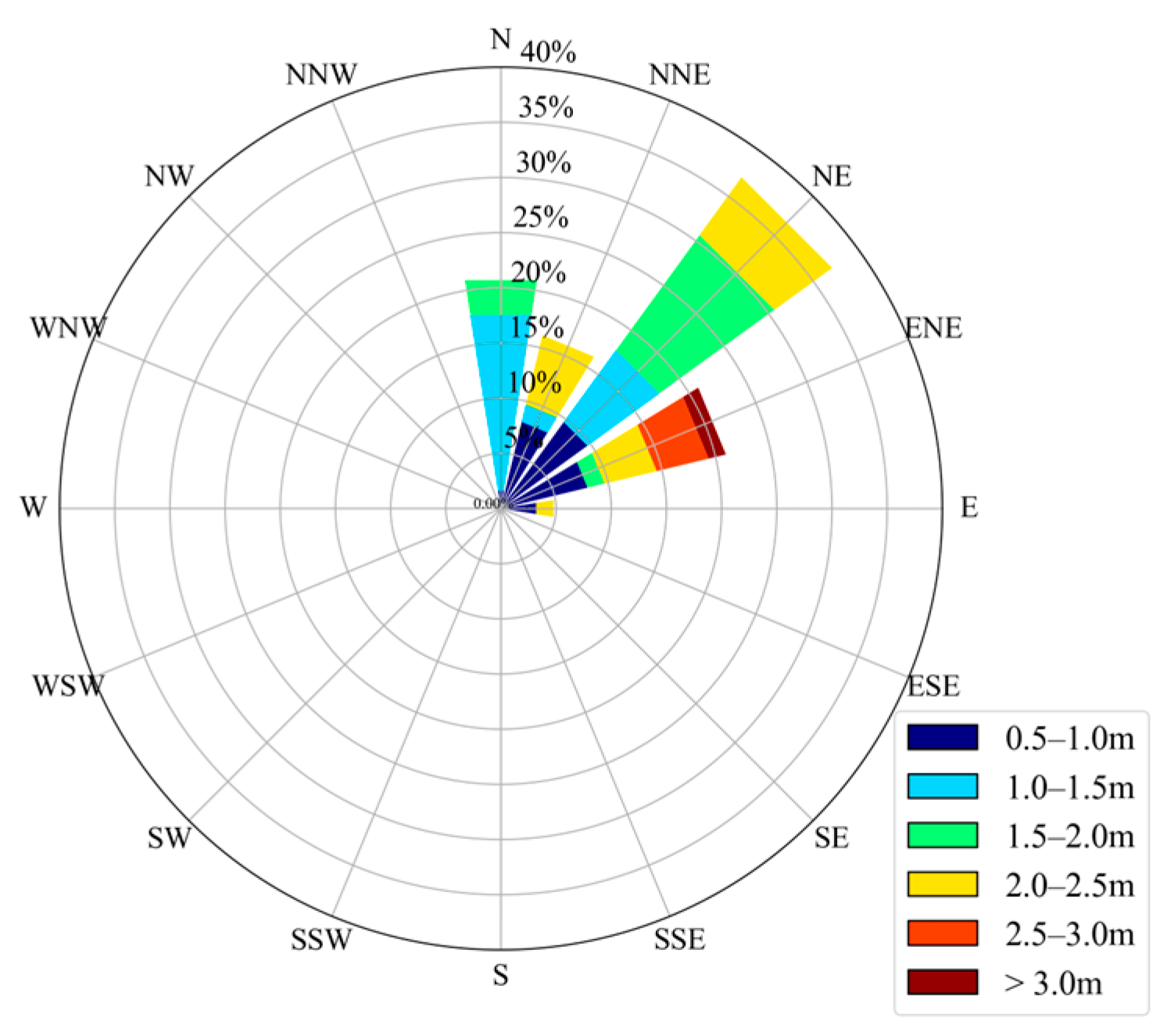
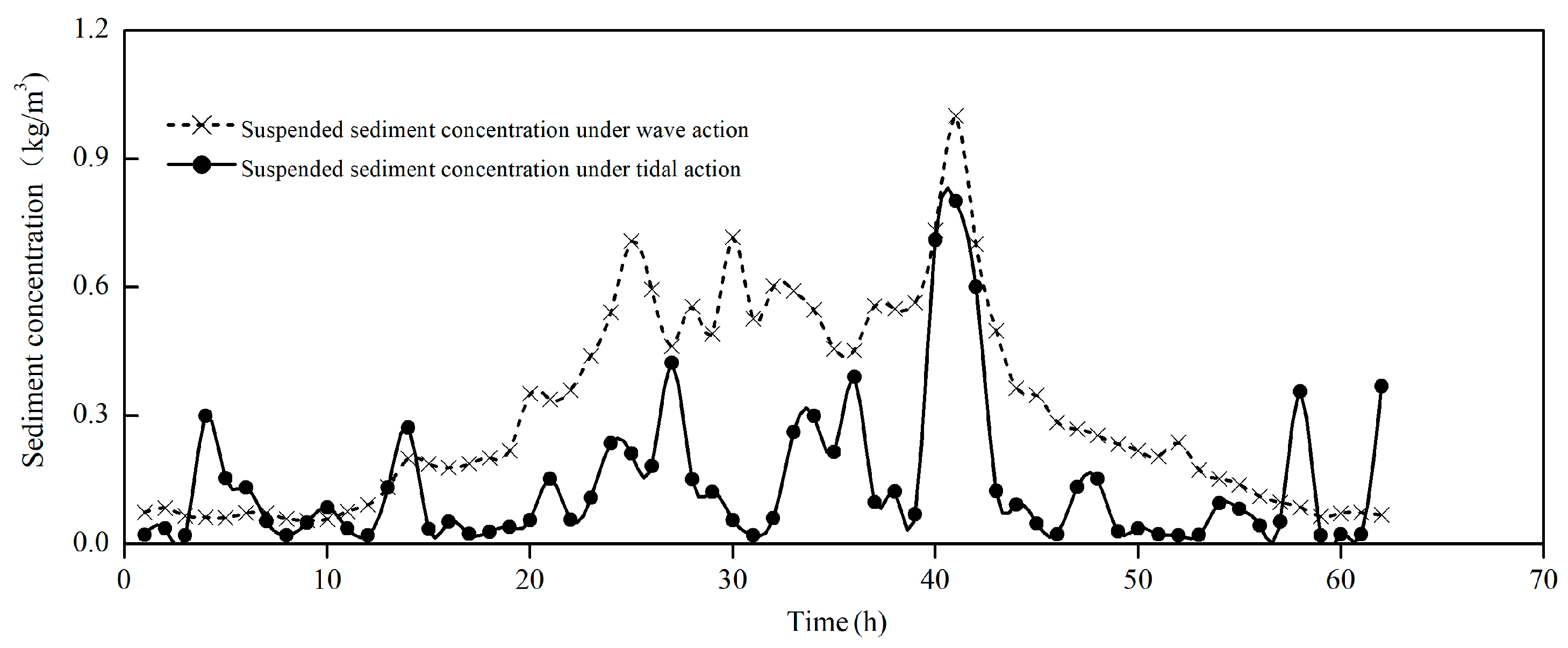
3.1. Analysis of Factors Influencing Instantaneous Sediment Concentration
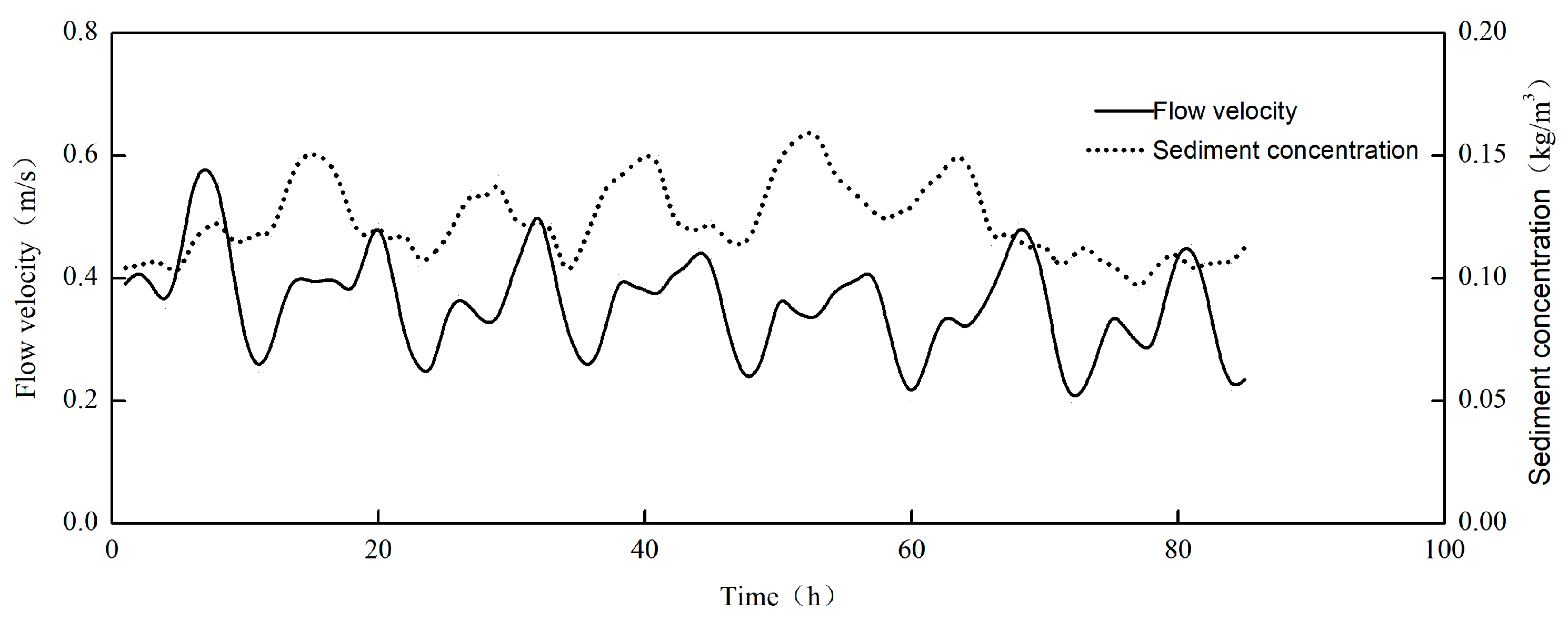
3.2. Instantaneous Sediment Concentration in the Context of Tidal Currents
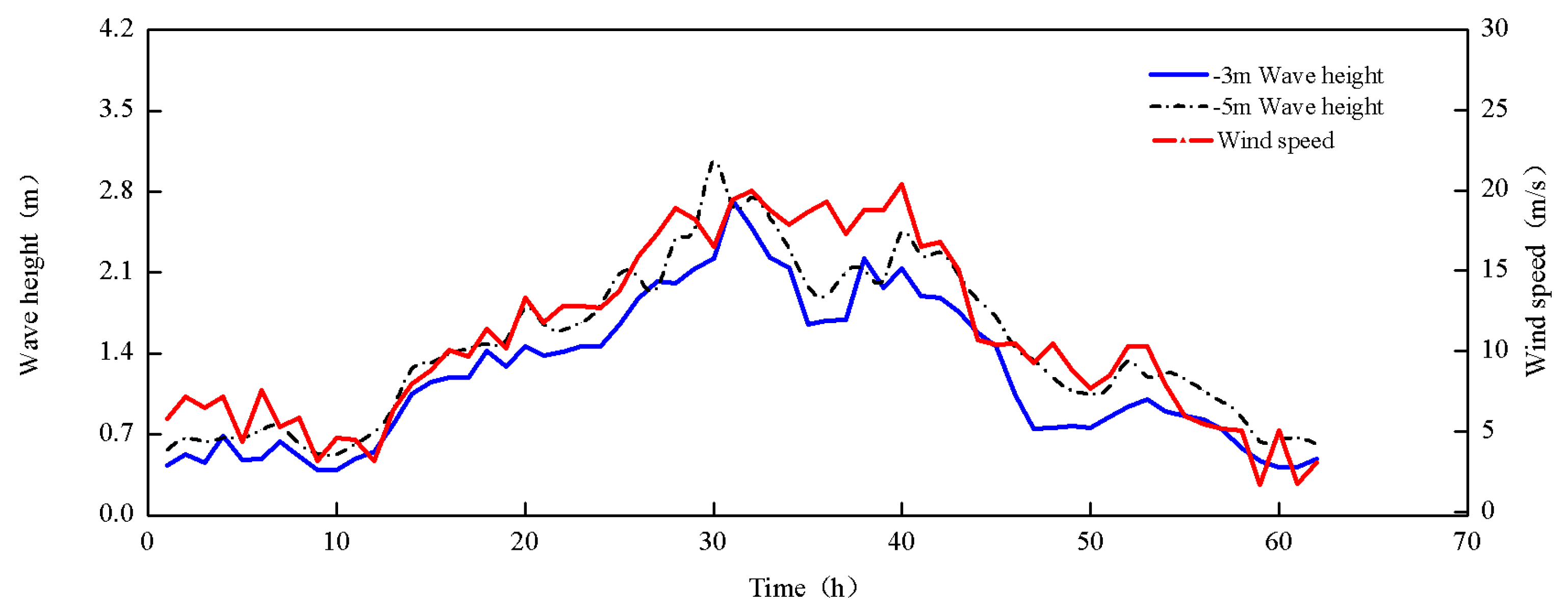
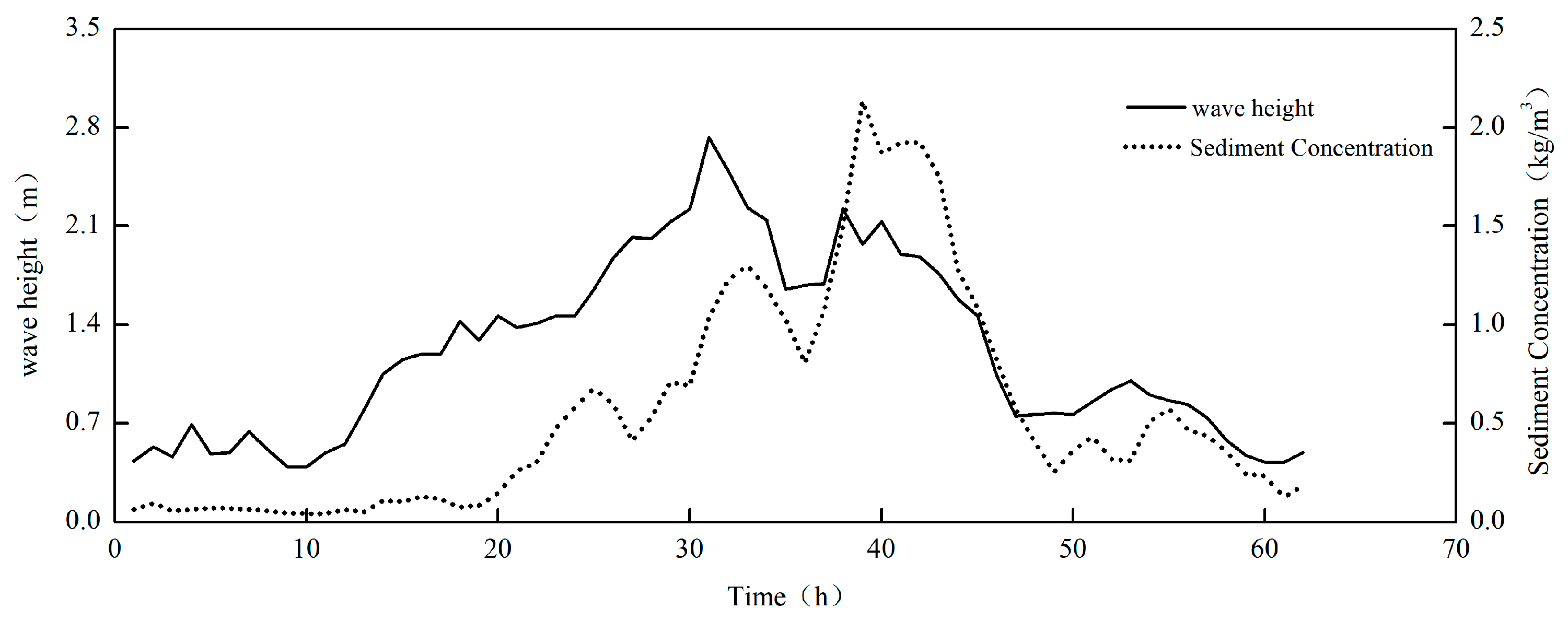
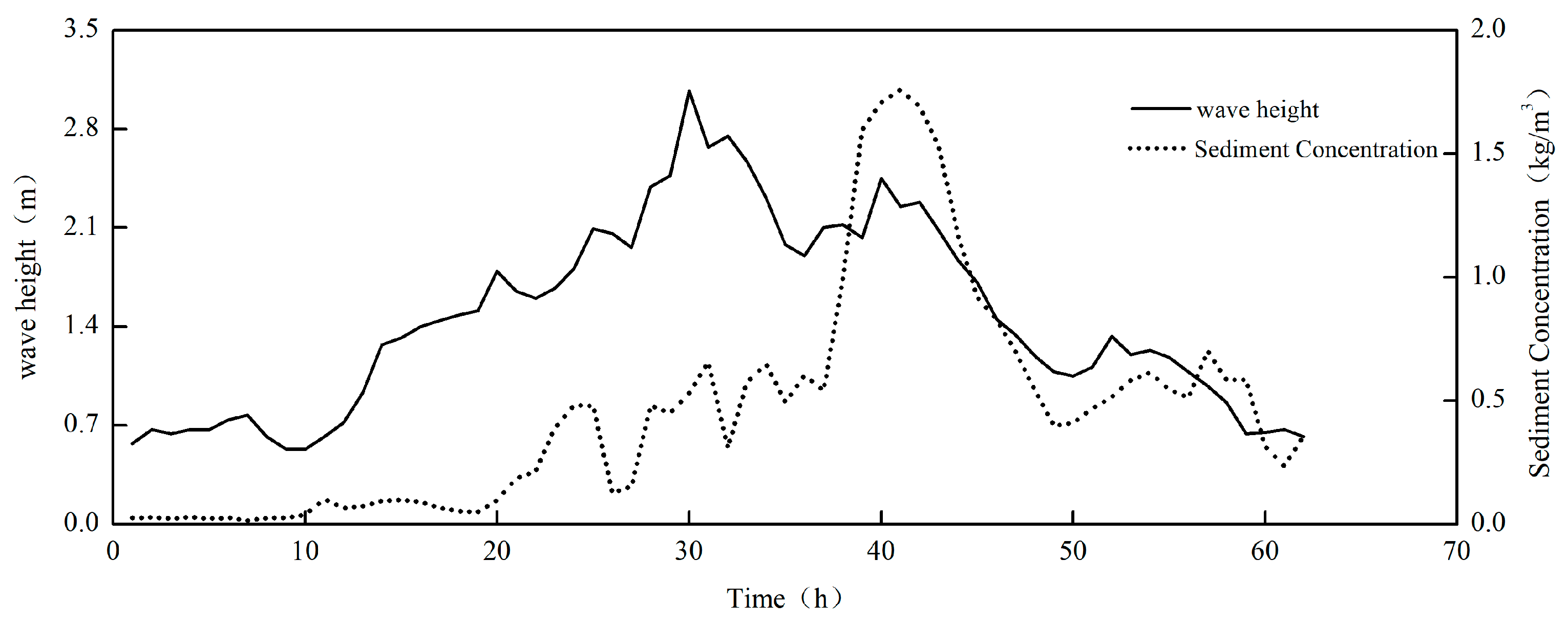
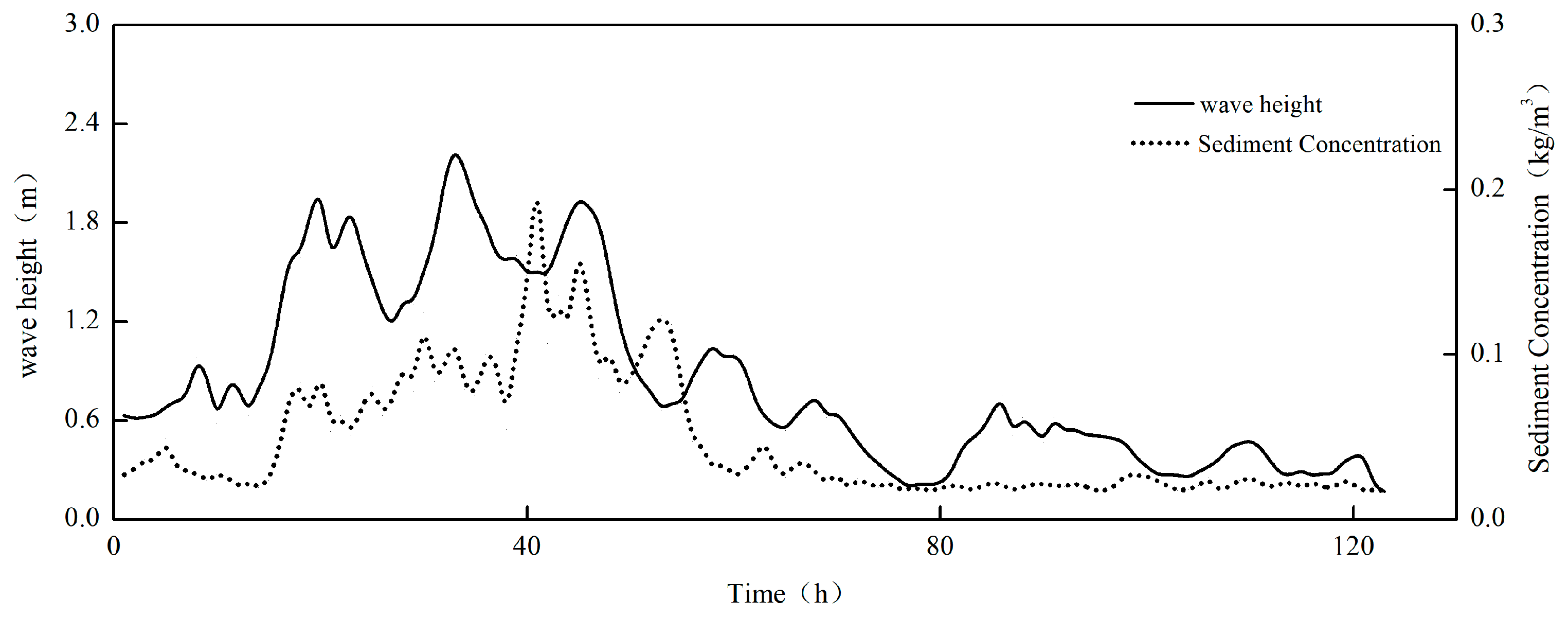
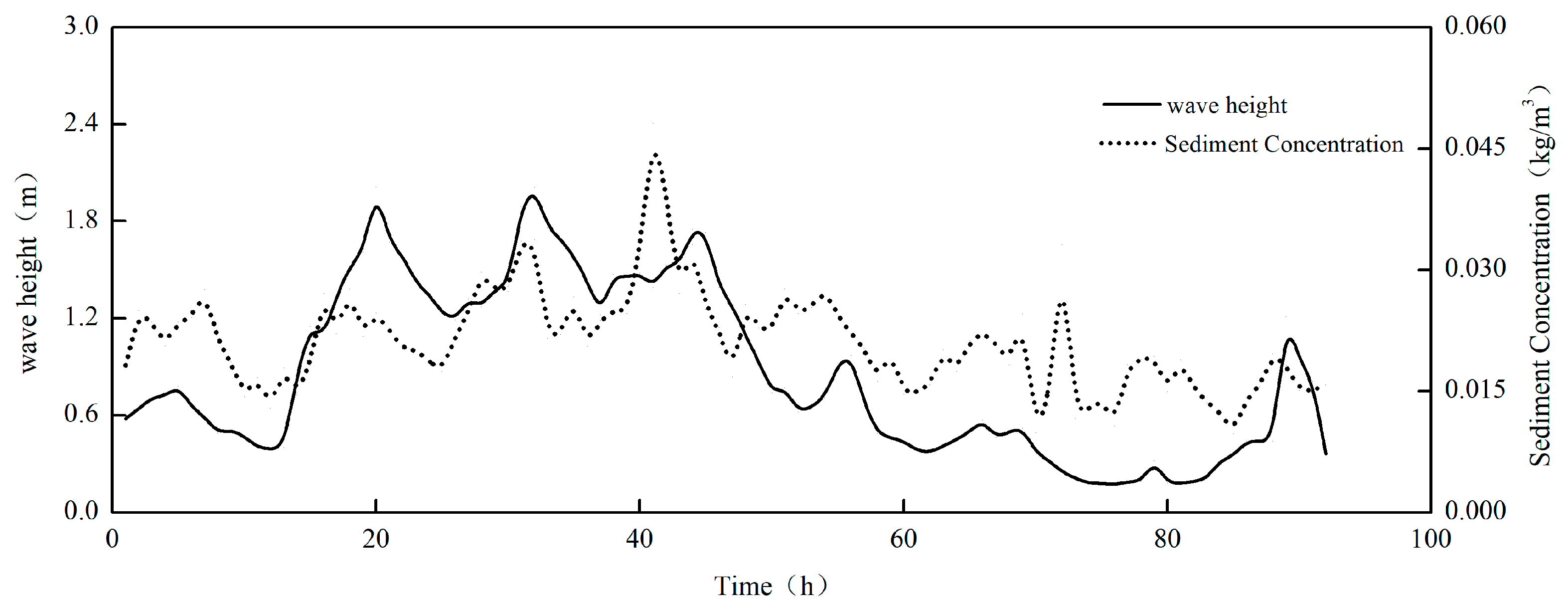
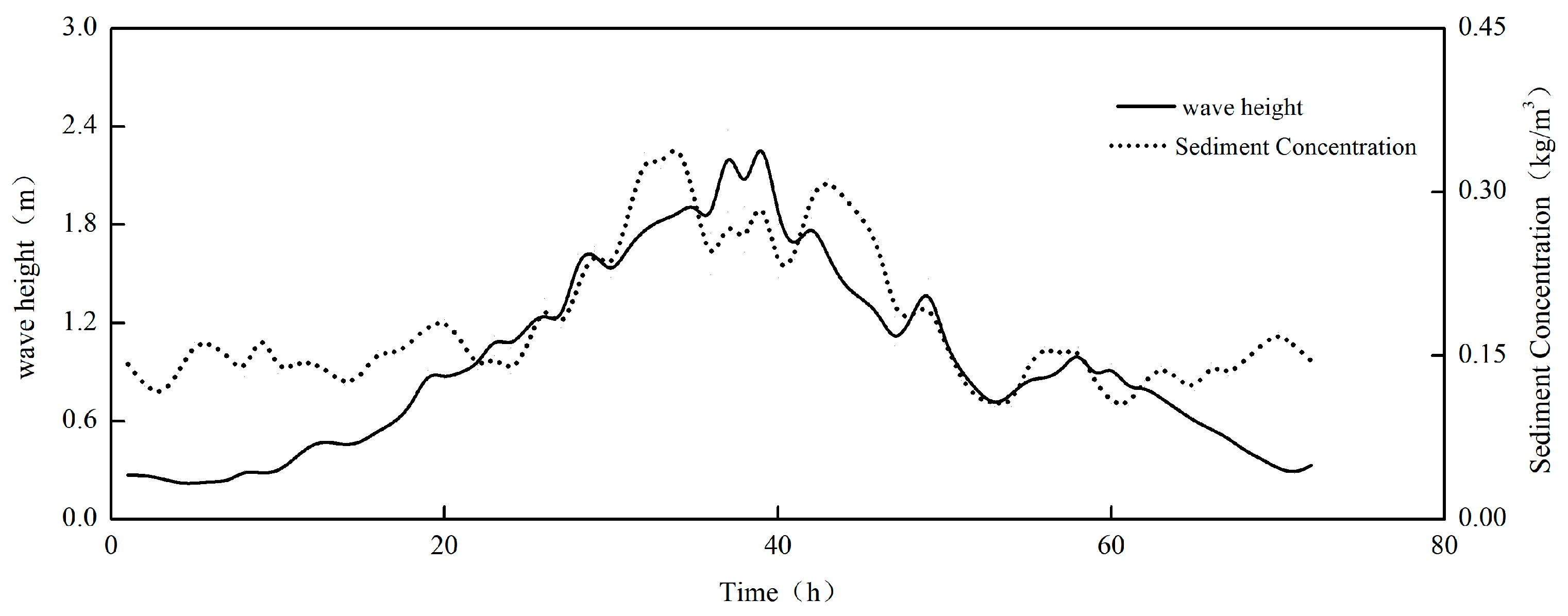
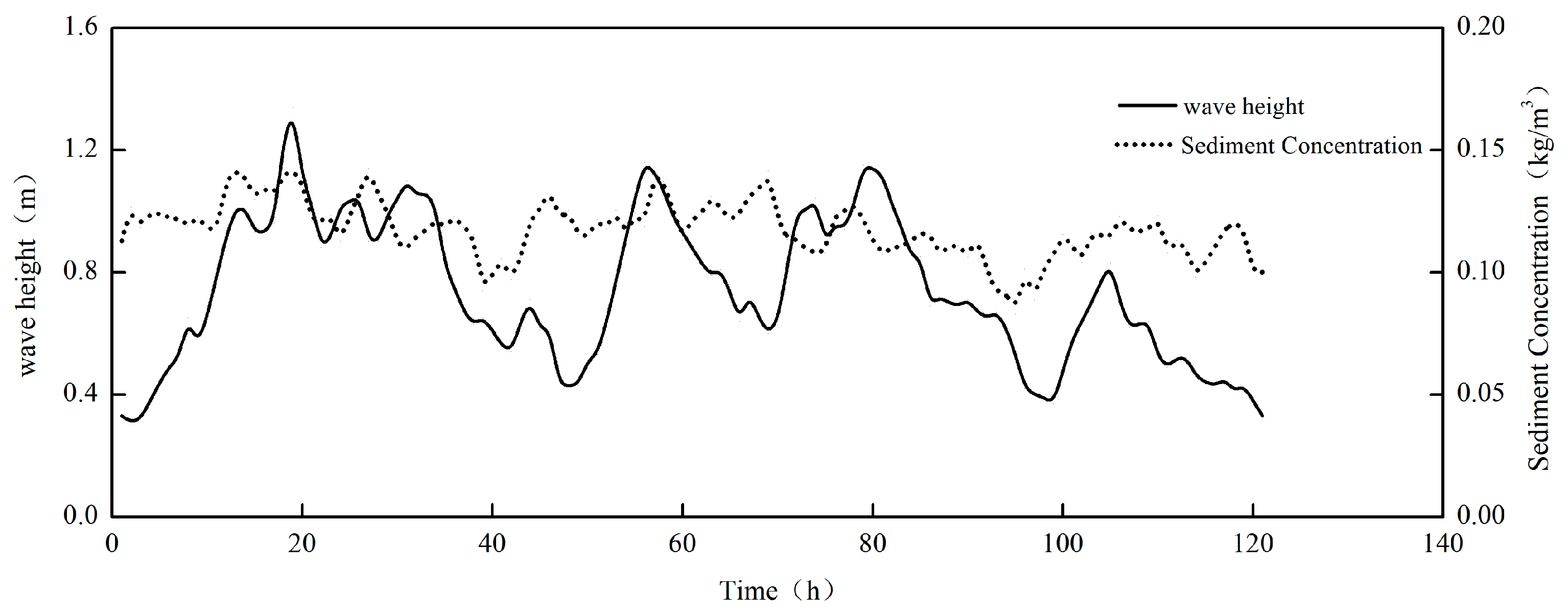
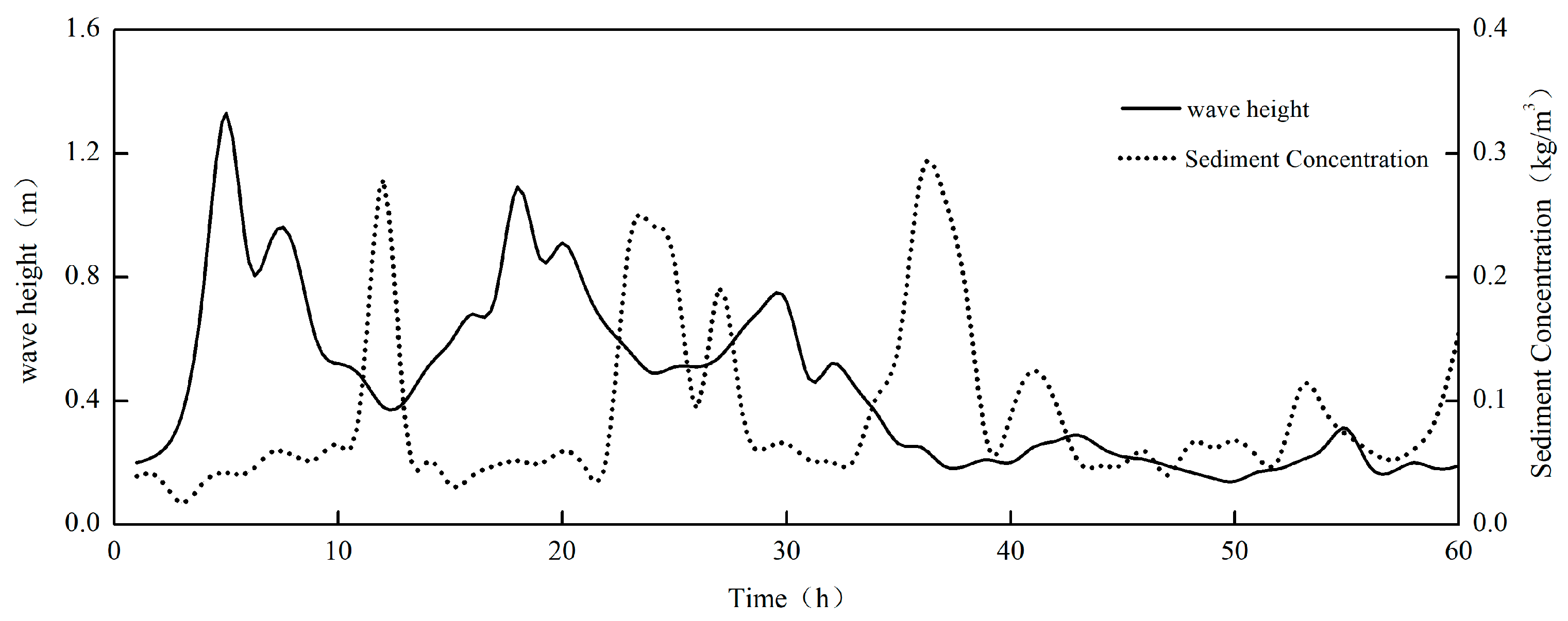
3.3. Instantaneous Sediment Concentration in the Presence of Wave Action
3.4. Research on Instantaneous Sediment Concentration Under the Combined Effect of Waves and Currents
3.4.1. Formula Establishment and Parameter Calibration
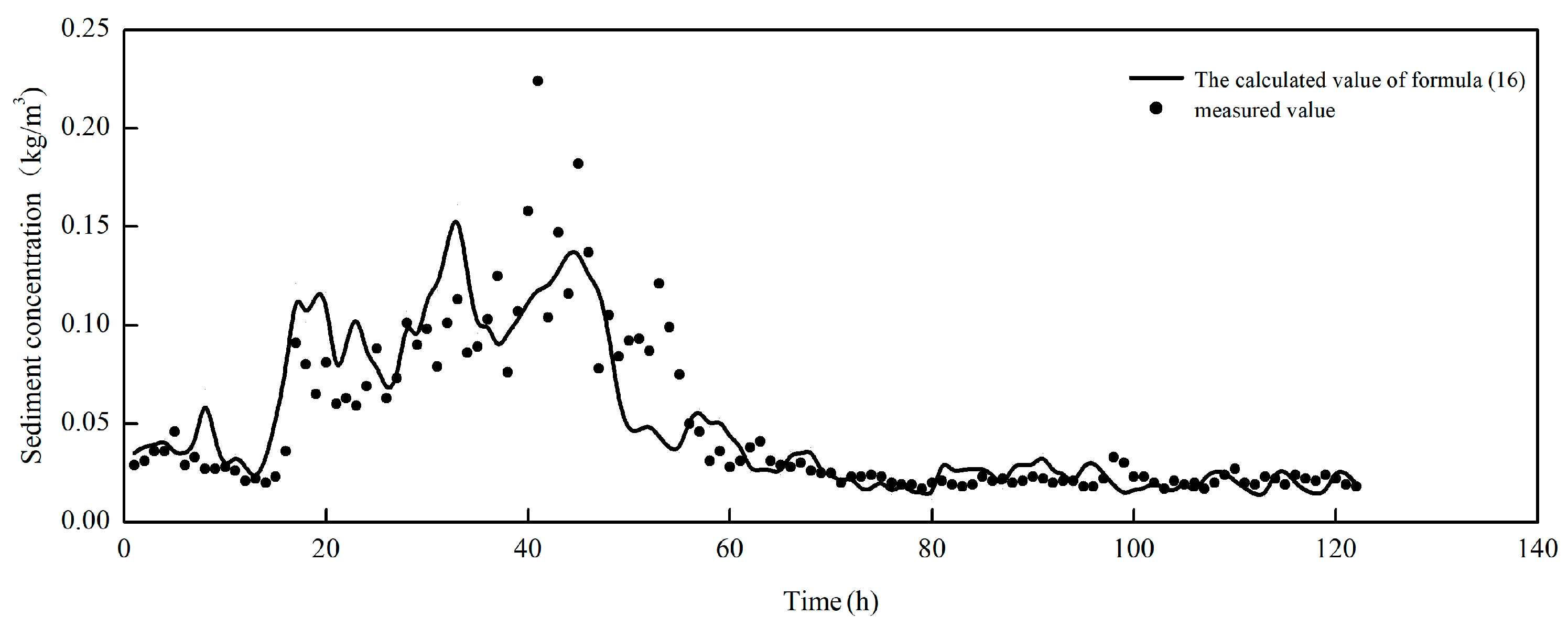
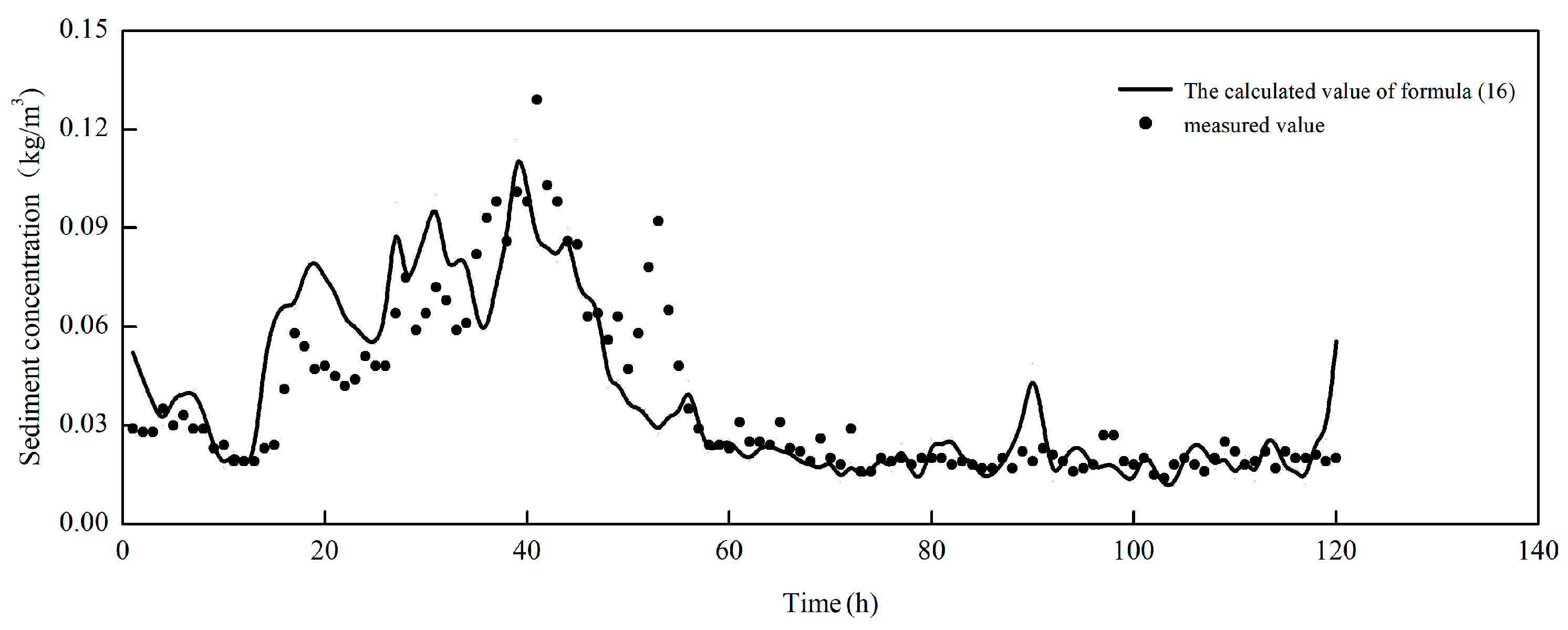
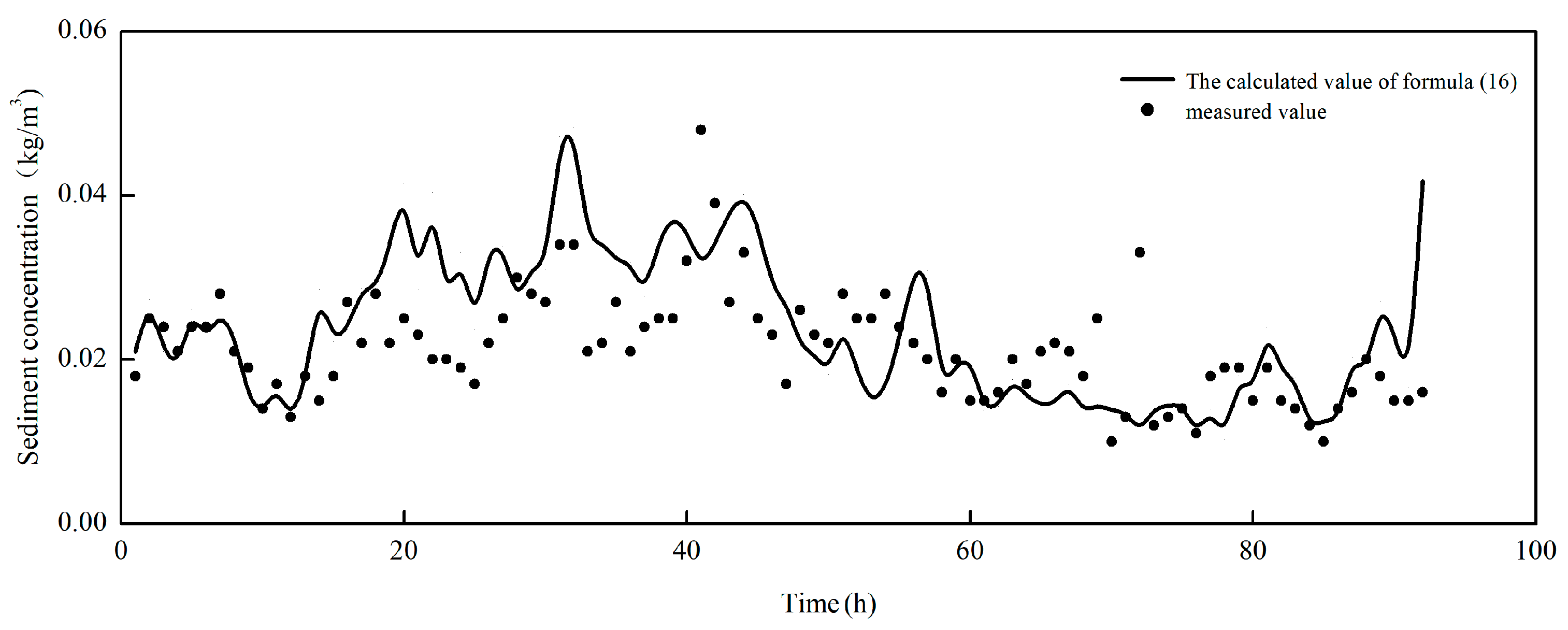
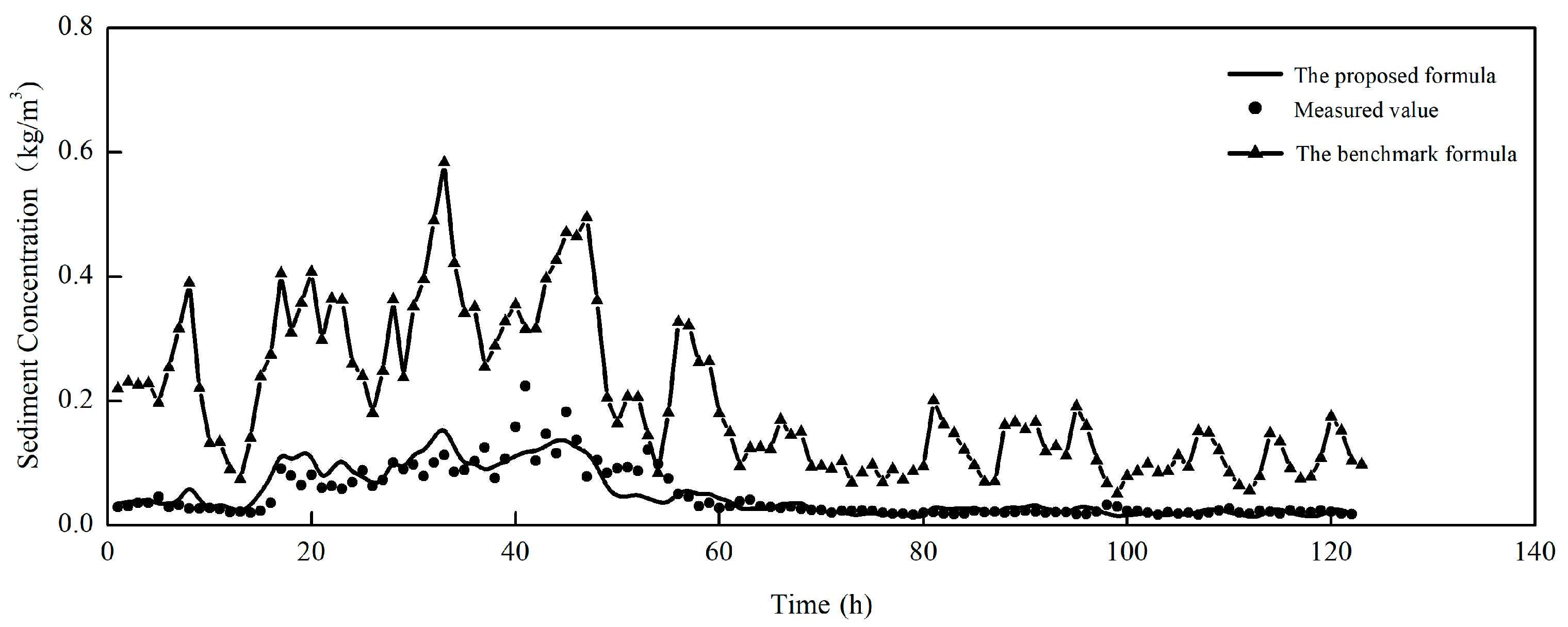
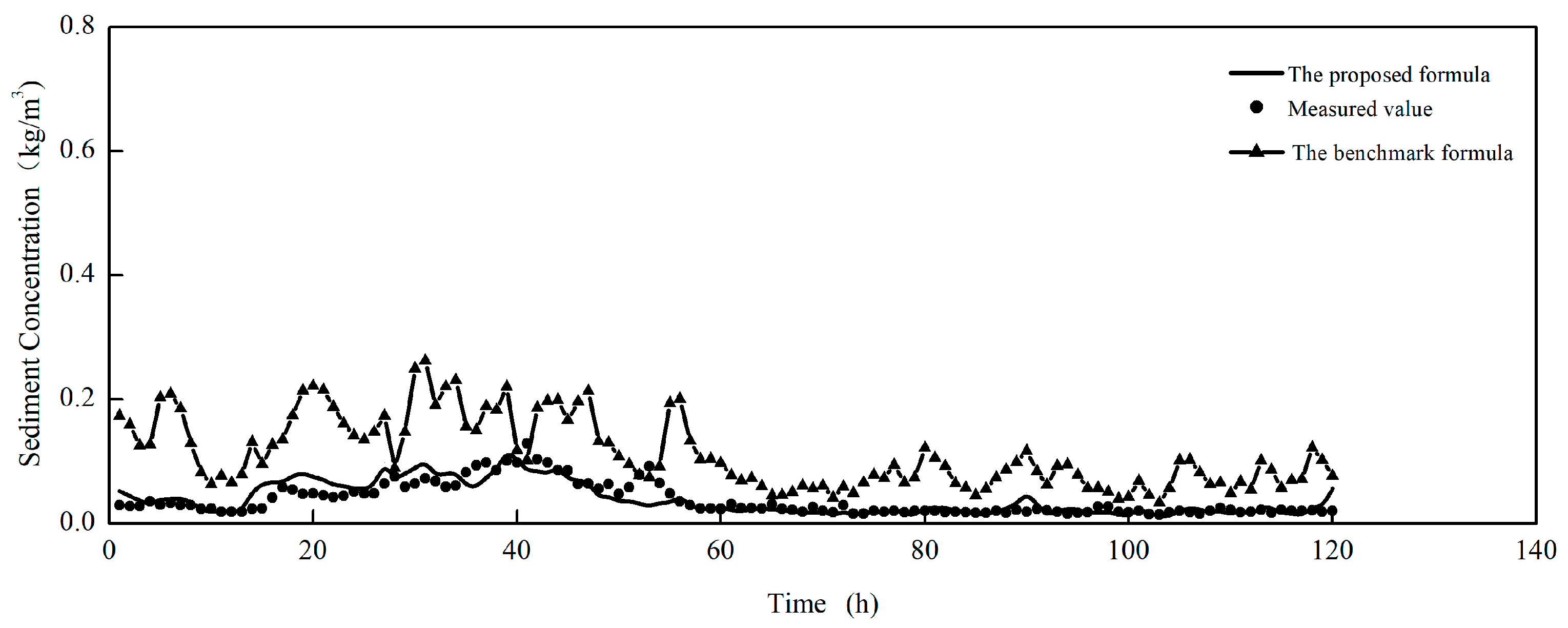
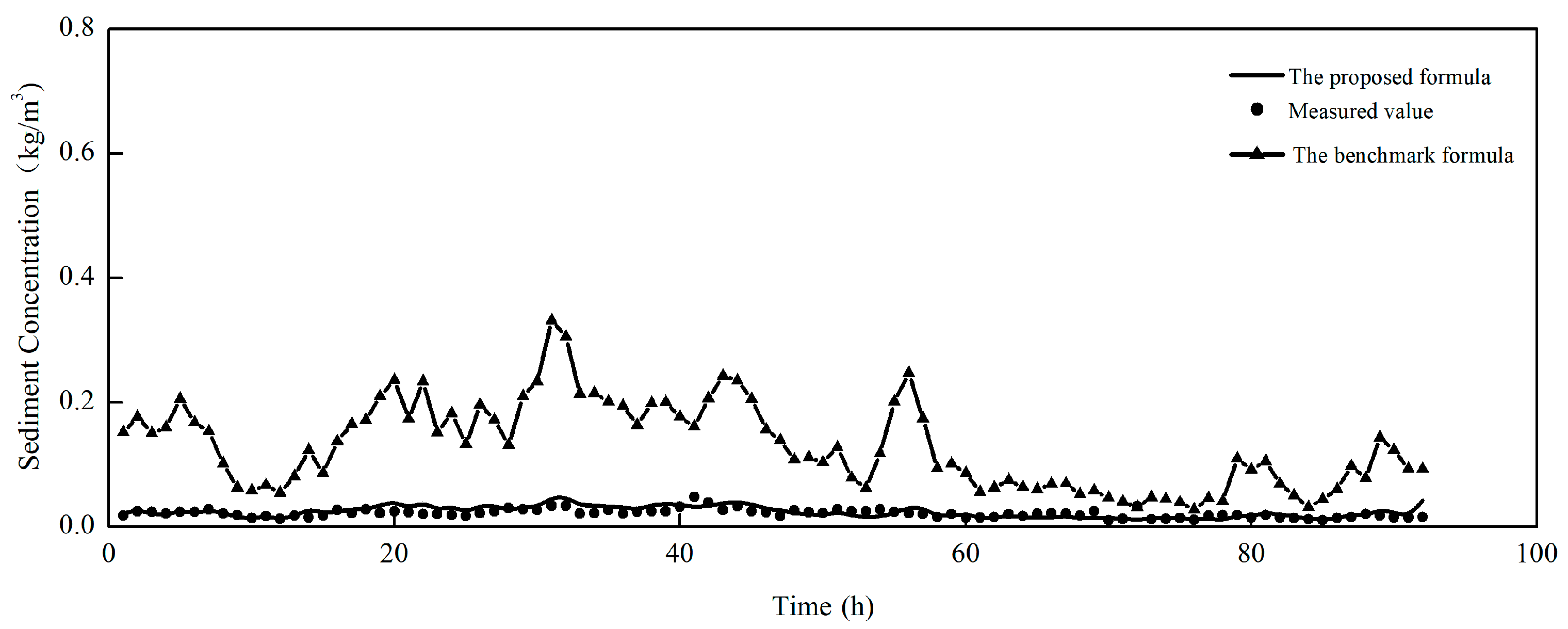
3.4.2. Verification of Formulas
4. Discussion
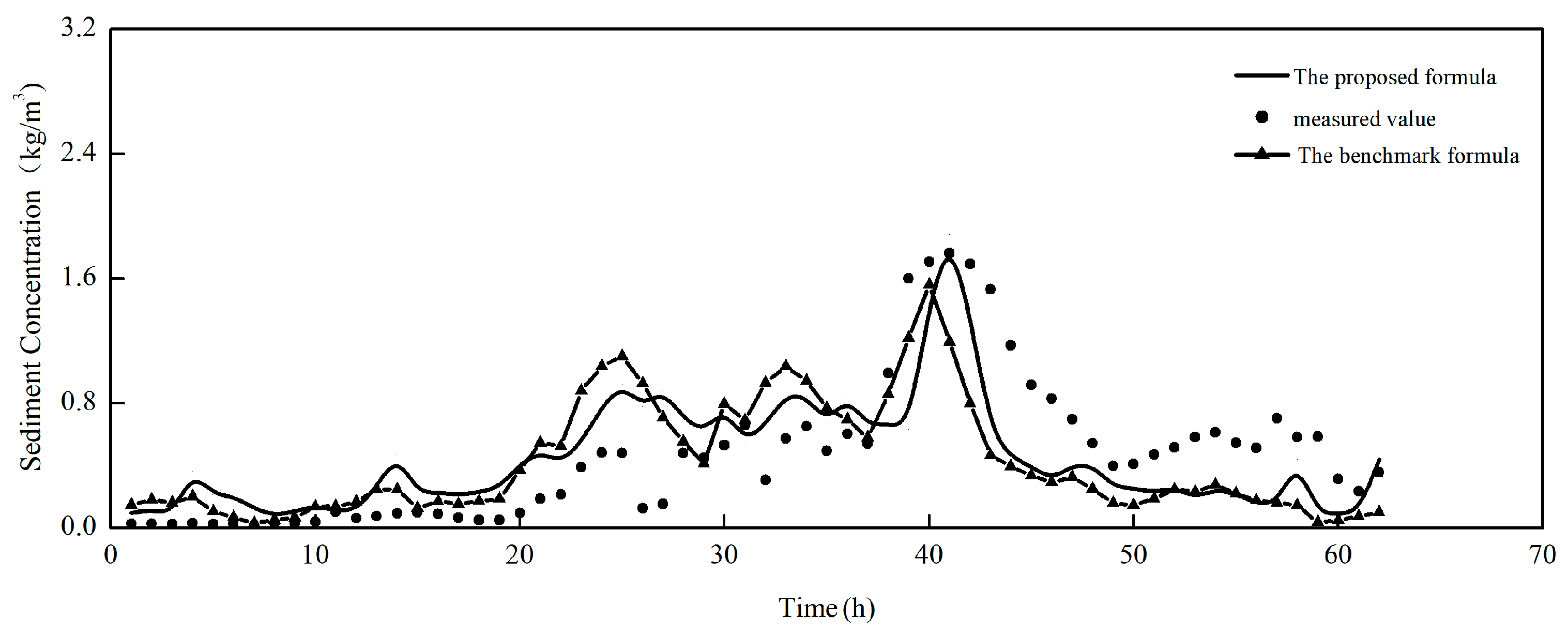
4.1. Comparison with Previous Studies
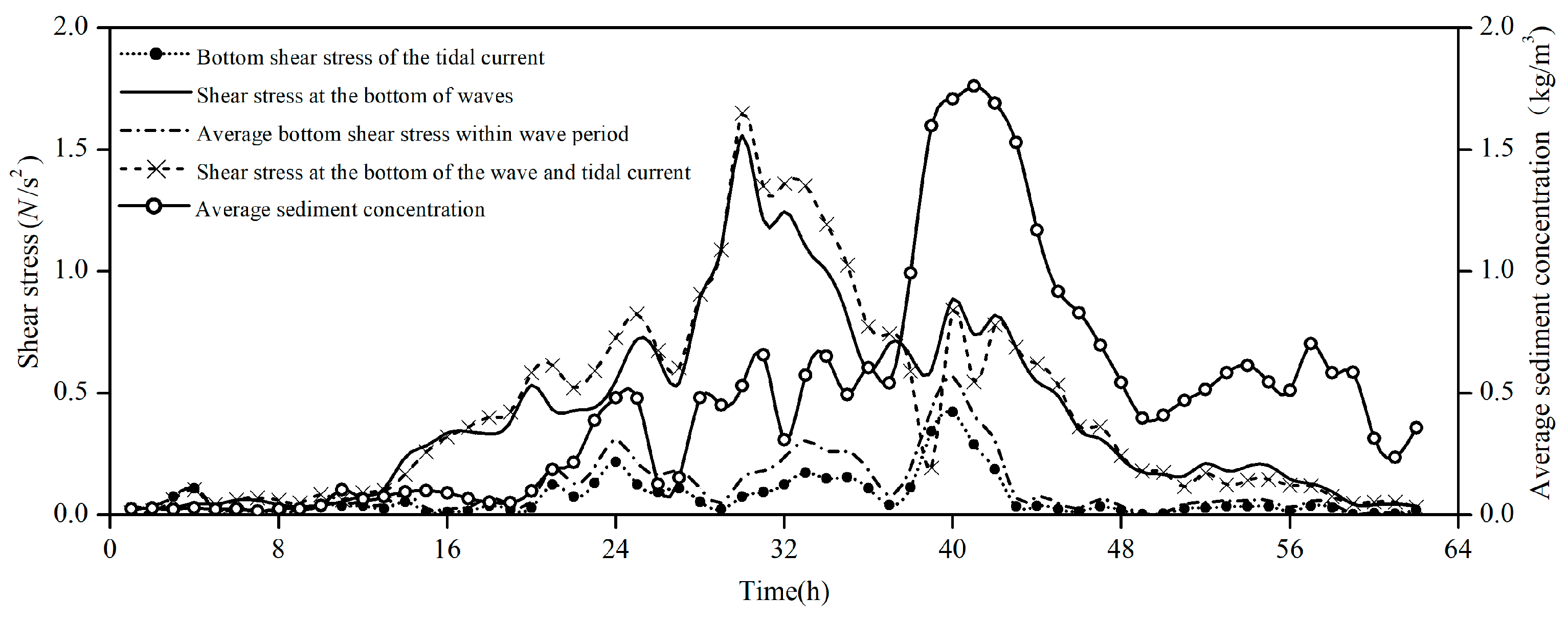
4.2. Research on the Influence Mechanism of Four Wave Flow Dynamics
5. Conclusions
- (1)
- Under extreme weather conditions, the instantaneous sediment concentration demonstrates a quasi-periodic distribution, which corresponds to the dynamic factors of waves and currents within a specific spatio-temporal domain. The temporal variation period of the instantaneous sediment concentration shows a notable lag in comparison to the dynamic factors of currents. There exists a positive correlation between wave energy loss and the instantaneous sediment concentration in the water body. Wave energy serves as the primary energy source for the initiation and suspension of sediment in the bottom bed.
- (2)
- In light of the phenomenon where the instantaneous sediment concentration in water during extreme weather exhibits a significant time lag in relation to the temporal variations in tidal dynamics, the analysis indicates that the time-varying characteristics of tidal flow velocity and wave energy serve as its intrinsic driving forces. Moreover, the formulas for tidal and wave horizontal velocity are refined. A computational formula for instantaneous sediment concentration under extreme weather conditions has been formulated, uncovering the response characteristics of instantaneous sediment concentration in muddy coastal waters to wave and tidal dynamics. The computed values of the formula exhibit a high degree of consistency with the measured values, which can offer precise sediment open boundary conditions for sediment mathematical models.
- (3)
- The parameterized formula for instantaneous sediment concentration under extreme wind conditions, as developed in this study, achieves an integrated representation and reasonable simplification of multiple physical processes including turbulence, flocculation, and salinity effects. To advance the understanding of sediment transport mechanisms, subsequent research will leverage controlled experimental data to systematically decouple the multi-physical field interactions, with the ultimate goal of establishing a three-dimensional formula for instantaneous sediment concentration grounded in well-defined physical principles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Corbett, D.R.; Dail, M.; McKee, B. High-frequency time-series of the dynamic sedimentation processes on the western shelf of the Mississippi River Delta. Cont. Shelf Res. 2007, 27, 1600–1615. [Google Scholar] [CrossRef]
- Baugh, J.; Feates, N.; Littlewood, M.; Spearman, J. The fine sediment regime of the Thames Estuary—A clearer understanding. Ocean. Coast. Manag. 2013, 79, 10–19. [Google Scholar] [CrossRef]
- Kineke, G.C.; Sternberg, R.W. Distribution of fluid muds on the Amazon continental shelf. Mar. Geol. 1995, 125, 193–233. [Google Scholar] [CrossRef]
- Cui, J.; Xia, Y. Analysis on the Application of Seaworthy Depth Technology in the Pearl River Estuary Channel and Port. Value Eng. 2012, 9, 65–66. [Google Scholar]
- Gilbert, G.K. The Transportation of Debris by Running Water; Professional Paper 86; U.S. Geological Survey: Washington, DC, USA, 1914; 263p. [Google Scholar]
- Bagnold, R.A. An Approach to the Sediment Transport Problem from General Physics; Professional Paper 422-1; U.S. Geological Survey: Washington, DC, USA, 1966; 37p. [Google Scholar]
- Yang, C.T. Unit Stream Power Equation and Sediment Transport. J. Hydraul. Div. 1972, 98, 1805–1826. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, J.; Gao, Z.; Zhang, W.; Yu, Z. Study on layout schemes of entrance channel in enclosed harbor basin along muddy coasts. Hydro-Sci. Eng. 2014, 1, 17–23. [Google Scholar]
- Yang, F.; Zhang, W. Effects of Typhoon Wipha on wave energy dissipation and suspended sediment concentration in typical waters of Lianyungang. Ocean Eng. 2012, 30, 82–89. [Google Scholar] [CrossRef]
- Dong, H.; Lu, Z. Field Observation Report on Waves, Tidal Currents, and Sediment in Lianyungang During the Passage of Typhoon “Wipha” in September 2007; Tianjin Research Institute for Water Transport Engineering; Ministry of Communications: Tianjin, China, 2008. [Google Scholar]
- Dong, H.; Lu, Z. Field Observation Results and Analysis of Waves, Tidal Currents, and Sediment in Lianyungang During a Cold Wave and Gale in December 2008; Tianjin Research Institute for Water Transport Engineering, Ministry of Communications: Tianjin, China, 2008. [Google Scholar]
- Pang, Q.; Yang, H. Report on Short-Term Continuous Observation and Analysis of Waves, Tidal Currents, and Sediment in the Xuwei Port Area of Lianyungang; Tianjin Research Institute for Water Transport Engineering, Ministry of Transport: Tianjin, China, 2010. [Google Scholar]
- Yang, F. Research on Wind-induced Waves and Wave-Induced Current Movement on Muddy Coast: A Case Study of Lianyungang. Master’s Thesis, Hohai University, Nanjing, China, 2012. [Google Scholar]
- Pang, Q. Study on the Formation and Movement Characteristics of Fluid Mud and Its Countermeasures. Ph.D. Dissertation, Tianjin University, Tianjin, China, 2011. [Google Scholar]
- Suhayda, J.N. Interaction of Surface Waves with Muddy Bed Sediments. Sci. Tech. Inf. Hohai Univ. 1988, 2, 16–29. [Google Scholar]
- Gao, Z. Study on Sediment Movement and Channel Siltation in the Surf Zone of Muddy Coasts; Nanjing Hydraulic Research Institute: Nanjing, China, 2014. [Google Scholar]
- Dou, G.; Dong, F.; Dou, X. Sediment transport capacity in fluvial and coastal environments. Chin. Sci. Bull. 1995, 40, 443–446. [Google Scholar]
- Liu, J.J. Study and Application of Coastal Sediment Movement; China Ocean Press: Beijing, China, 2009. [Google Scholar]
- Feng, Q.; Li, R.J.; Luo, F. A preliminary study on the estimation of instantaneous sediment concentration in tidal river reaches. J. Wuhan Univ. 2013, 46, 273–277. [Google Scholar]
- Li, R.; Zheng, J.; Zhang, W.; Cao, H. A general form of sediment-carrying capacity formula and its analysis. J. Sediment Res. 2014, 1, 1–7. [Google Scholar]
- Li, C. Study on Vertical Distribution of Nearshore Water-Sediment and Instantaneous Sediment Concentration; Hohai University: Nanjing, China, 2016. [Google Scholar]
- Drennan, W.M.; Donelan, M.A.; Terray, E.A.; Katsaros, K.B. On Waves, Oceanic Turbulence, and Their Interaction. Geophysical 1997, 33, 17–27. [Google Scholar]
- Dou, G.; Dou, X.; Li, T. Incipient motion of sediment under wave action. Sci. China Technol. Sci. 2001, 31, 566–573. [Google Scholar]
- Ma, J. Research on the Mathematical Model for Sediment Transport Under Joint Action of Waves and Currents in Muddy Coasts. PhD. Dissertation, Hohai University, Nanjing, China, 2009. [Google Scholar]
- Yan, B. Study on Sediment Movement and Channel Siltation Mechanism on Sandy Coasts. PhD. Dissertation, Tianjin University, Tianjin, China, 2008. [Google Scholar]

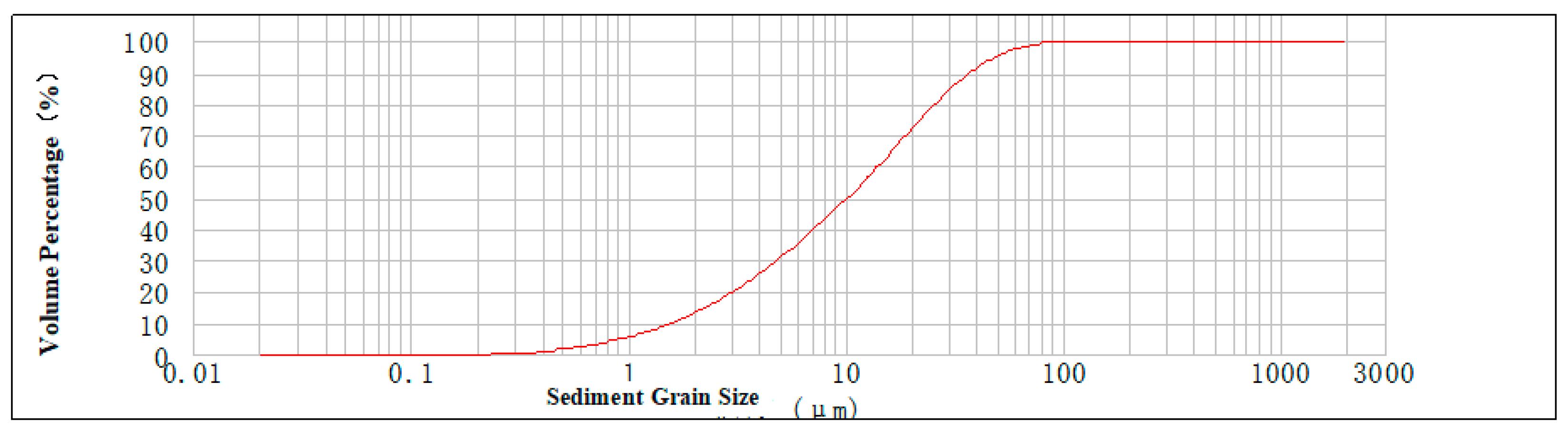
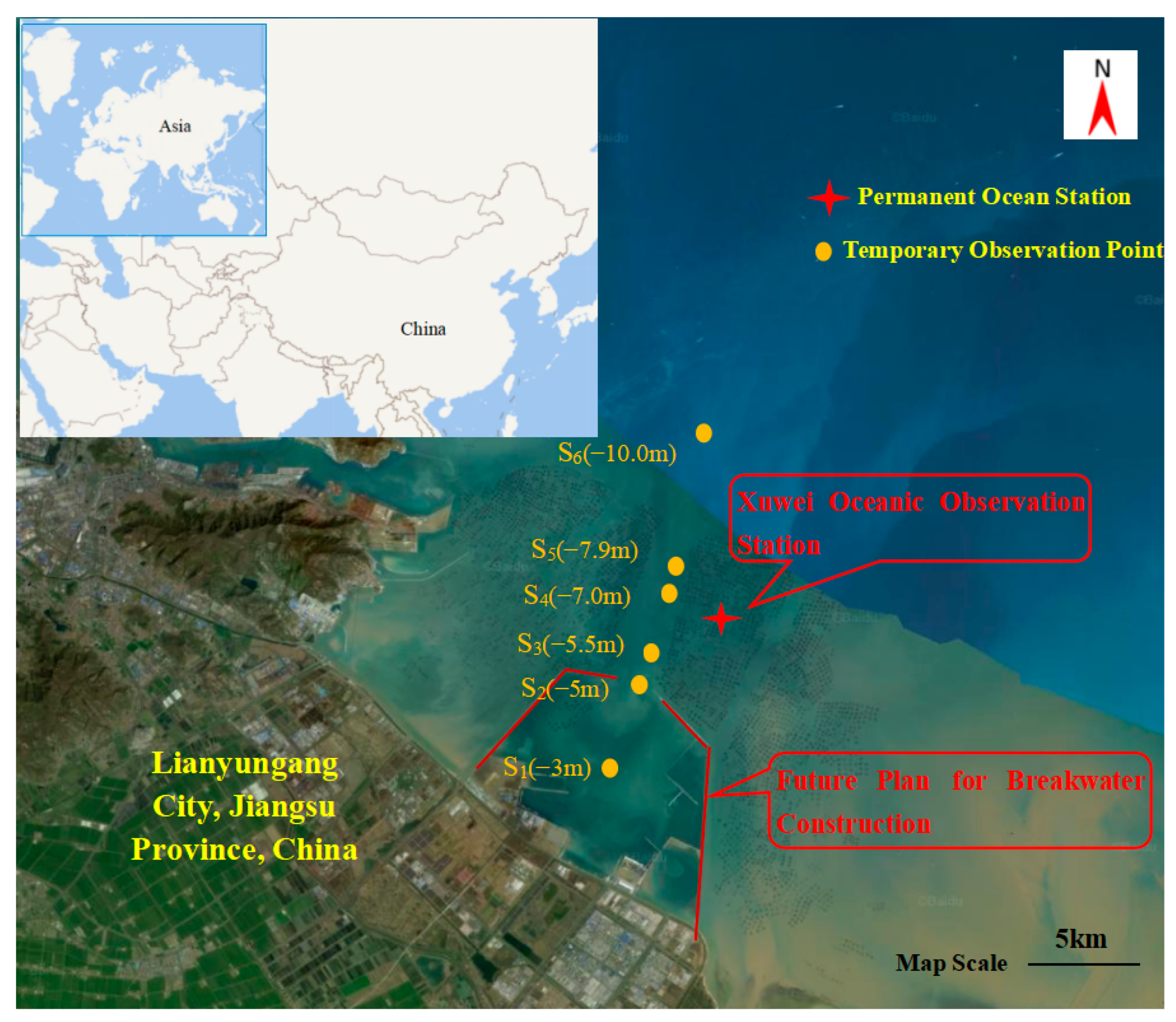
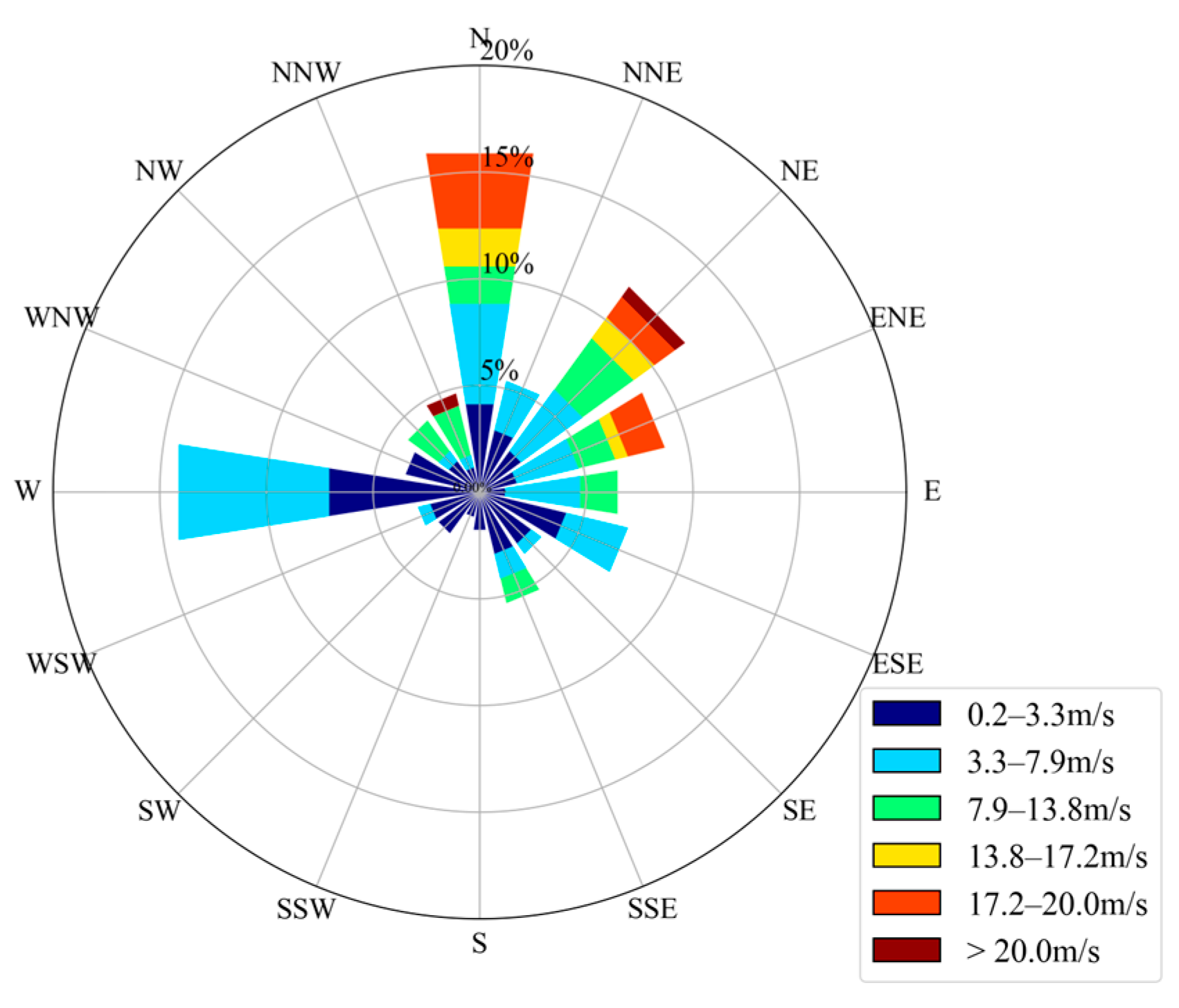
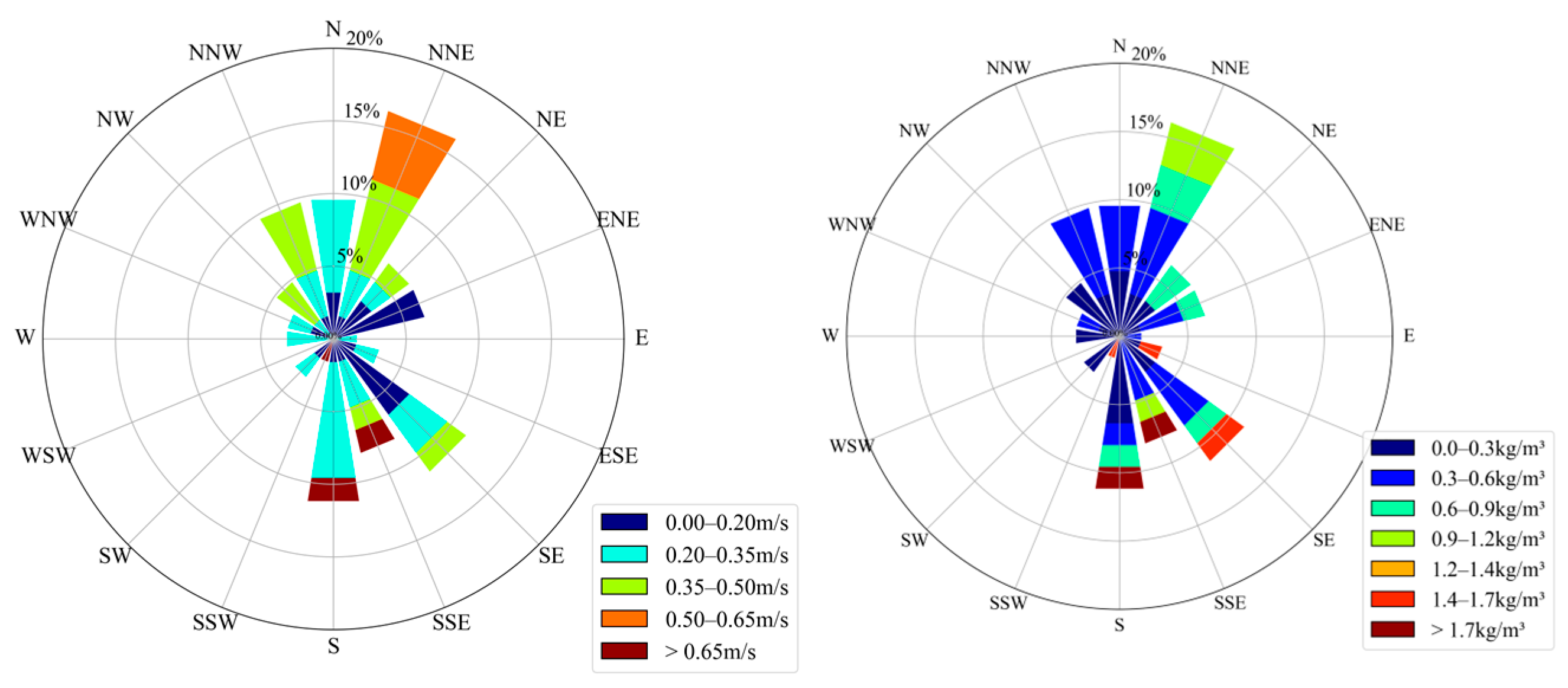











| Event Name | Temporary Station | Water Depth | Observation Equipment | Observation Period | Data Type |
|---|---|---|---|---|---|
| Typhoon “Wipha” | S1 | −3 m | 1 wave and tide gauge, 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 19 September 2007~21 September 2007 | W, Z, V, C |
| S2 | −5 m | 1 wave dragon, 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 19 September 2007~21 September 2007 | W, Z, V, C | |
| Cold Wave and Strong Wind in December 2008 | S1 | −3 m | 1 ADCP (for wave measurement), 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 3 December 2008~8 December 2008 | W, Z, V, C |
| S2 | −5 m | 1 wave dragon (for measuring waves and ocean currents), 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 3 December 2008~8 December 2008 | W, Z, V, C | |
| S5 | −7.9 m | 1 wave dragon, 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 3 December 2008~8 December 2008 | W, Z, V, C | |
| S6 | −10 m | 1 wave dragon, 2 RBR turbidity meters, 1 CTD instrument (sediment concentration) | 3 December 2008~8 December 2008 | W, Z, V, C | |
| Cold Wave and Strong Wind (August to November 2009) | S1 | −3 m | ADCP, OBS-3A self-contained turbidity meter | 13 August 2009~6 November 2009 | W, Z, V, C |
| S3 | −5.5 m | ADCP, OBS-3A self-contained turbidity meter, In Situ tide gauge | 2 September 2009~28 October 2009 | W, Z, V, C | |
| S4 | −7 m | Nortek AWAC 1 MHz (wave dragon), Nortek Aquadopp Profiler 2 MHz (broad dragon), OBS3A turbidity meter, OBS3plus turbidity meter | 5 August 2009~5 November 2009 | W, Z, V, C |
| Instrument Name | Model | Technical Specifications |
|---|---|---|
| In Situ Tide Gauge | LEVEL TROLL 500 | Measurement accuracy: ±6 cm Measurement range: 0–60 m |
| “OBS-3A” Turbidimeter | OBS-3A | Measurement accuracy: ±2% of the measured value Measurement range: 0.2–4000 NTU |
| RBR Turbidimeter | XR-420 | Measurement accuracy: ±1% of the measured value Measurement range: 0–2500 FTU |
| ALEC ATU75W Self-Contained Turbidimeter | ALEC ATU75W | Measurement accuracy: ±0.3 FTU Measurement range: 0–1000 FTU |
| Acoustic Doppler Current Profiler (ADCP) | Junma Sentinel Self-Contained ADCP (1200 KHz) | Current direction error: ±2 °Current velocity error: ±0.25% of the measured value ±2.5 mm/s Wave height accuracy: 1% of the measured value; Wave direction accuracy: ±2°Measurement range: Current velocity: 0.01–20 m/s; Current direction: 0–360°; Wave height: 0–20 m; Period: 2–30 s |
| Nortek AWAC 1 MHz (Wave Dragon) | Nortek AWAC 1 MHz | Measurement accuracy: Current velocity: 1% of the measured value ±0.5 cm/s Measurement range: Horizontal current velocity: ±10 m/s; Along-beam current velocity: ±5 m/s |
| Nortek Aquadopp Profiler 2 MHz (Broad Dragon) | Aquadopp Profiler | Measurement range: Current velocity: ±10 m/s (range extension required) Measurement accuracy: 1% of the measured value ±0.5 cm/s |
| Japanese COMPACT-CTD Temperature-Depth-Salinity-Sediment Gauge | COMPACT-CTD | Suspended sediment concentration: 0–5000 ppm Measurement accuracy: ±2% of the measured value |
| Time | Mean Value of the Measured Sediment Concentration (kg/m3) | Equation (16) Computes the Mean (kg/m3) | Mean Sediment Concentration Induced by Waves (kg/m3) | Mean Concentration of Tidal Sediment (kg/m3) | The Ratio of Sediment Concentration Induced by Waves and Currents |
|---|---|---|---|---|---|
| During the typhoon event spanning (8:00 on the 18th to 7:00 on the 21st | 0.46 | 0.43 | 0.29 | 0.14 | 2.1 |
| During the period of big waves (, From 12:00 on the 19th to 15:00 on the 20th) | 0.70 | 0.73 | 0.42 | 0.21 | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Q.; Xu, D.; Ding, Y. Research on Instantaneous Sediment Concentration in Muddy Coastal Waters Under Extreme Weather Conditions. J. Mar. Sci. Eng. 2025, 13, 2188. https://doi.org/10.3390/jmse13112188
Qi Q, Xu D, Ding Y. Research on Instantaneous Sediment Concentration in Muddy Coastal Waters Under Extreme Weather Conditions. Journal of Marine Science and Engineering. 2025; 13(11):2188. https://doi.org/10.3390/jmse13112188
Chicago/Turabian StyleQi, Qinghui, Dong Xu, and Youbin Ding. 2025. "Research on Instantaneous Sediment Concentration in Muddy Coastal Waters Under Extreme Weather Conditions" Journal of Marine Science and Engineering 13, no. 11: 2188. https://doi.org/10.3390/jmse13112188
APA StyleQi, Q., Xu, D., & Ding, Y. (2025). Research on Instantaneous Sediment Concentration in Muddy Coastal Waters Under Extreme Weather Conditions. Journal of Marine Science and Engineering, 13(11), 2188. https://doi.org/10.3390/jmse13112188






