Engineering Critical Assessment of IMO Type C Tanks: A Comparative Study of Shell and Solid Element Models
Abstract
1. Introduction
2. Research Background
2.1. Engineering Critical Assessment (ECA)
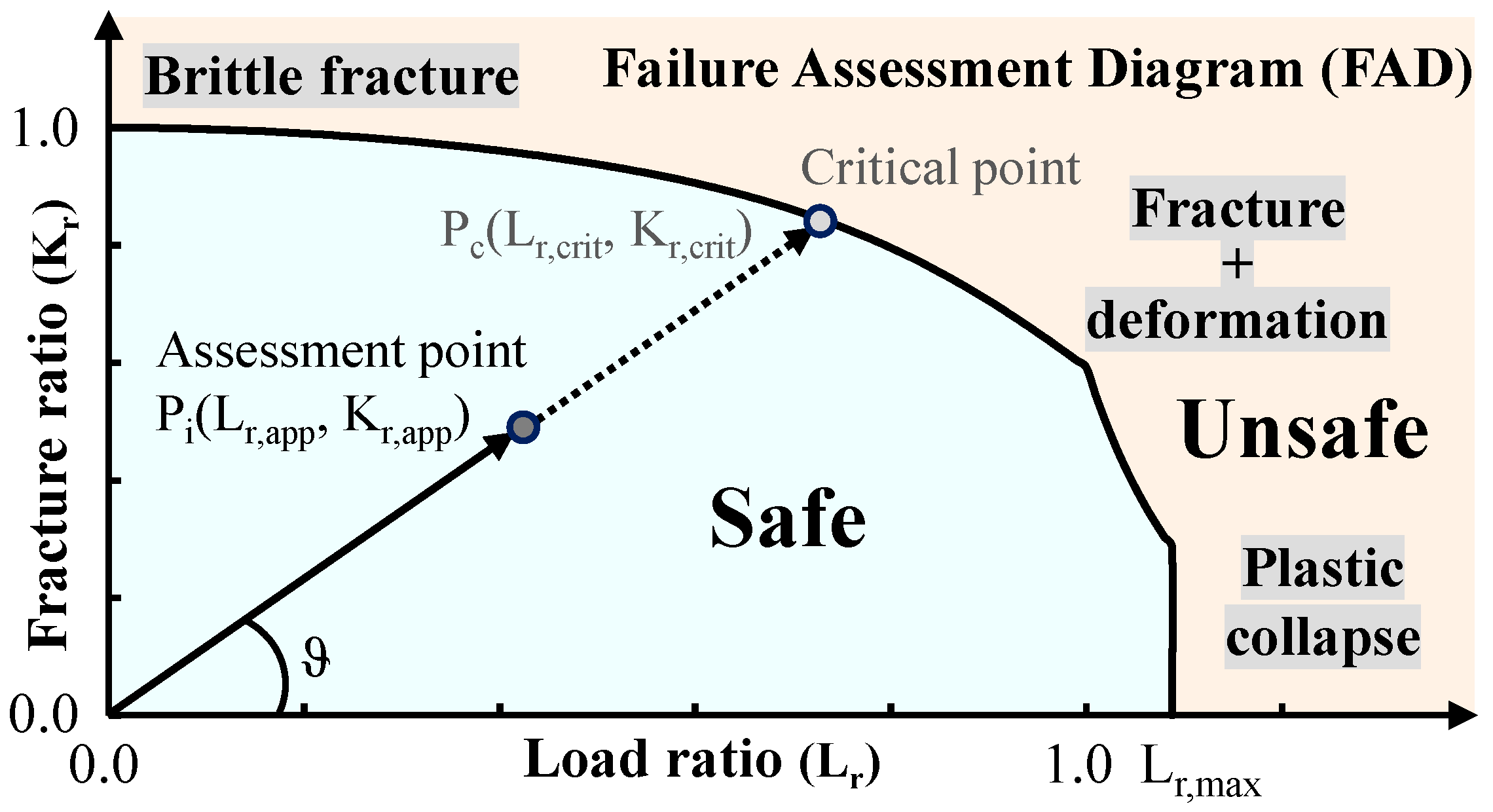
2.2. Failure Assessment Diagram (FAD)
2.3. Finite Element Configurations
3. Research Methodology
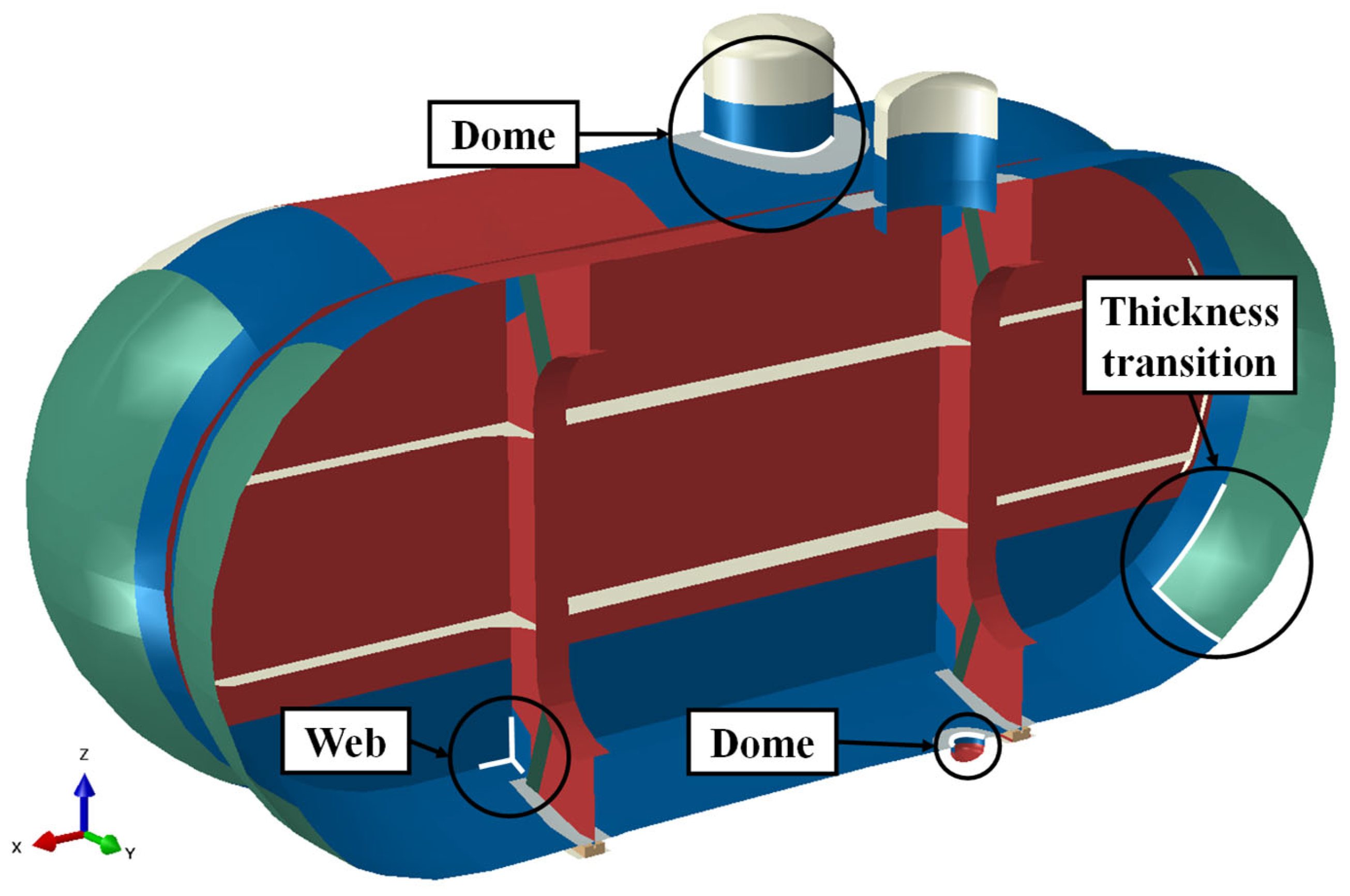
3.1. Applied Structure
3.1.1. Tank Specification
3.1.2. Material Properties
3.1.3. Loading Conditions
3.2. Finite Element Modelling
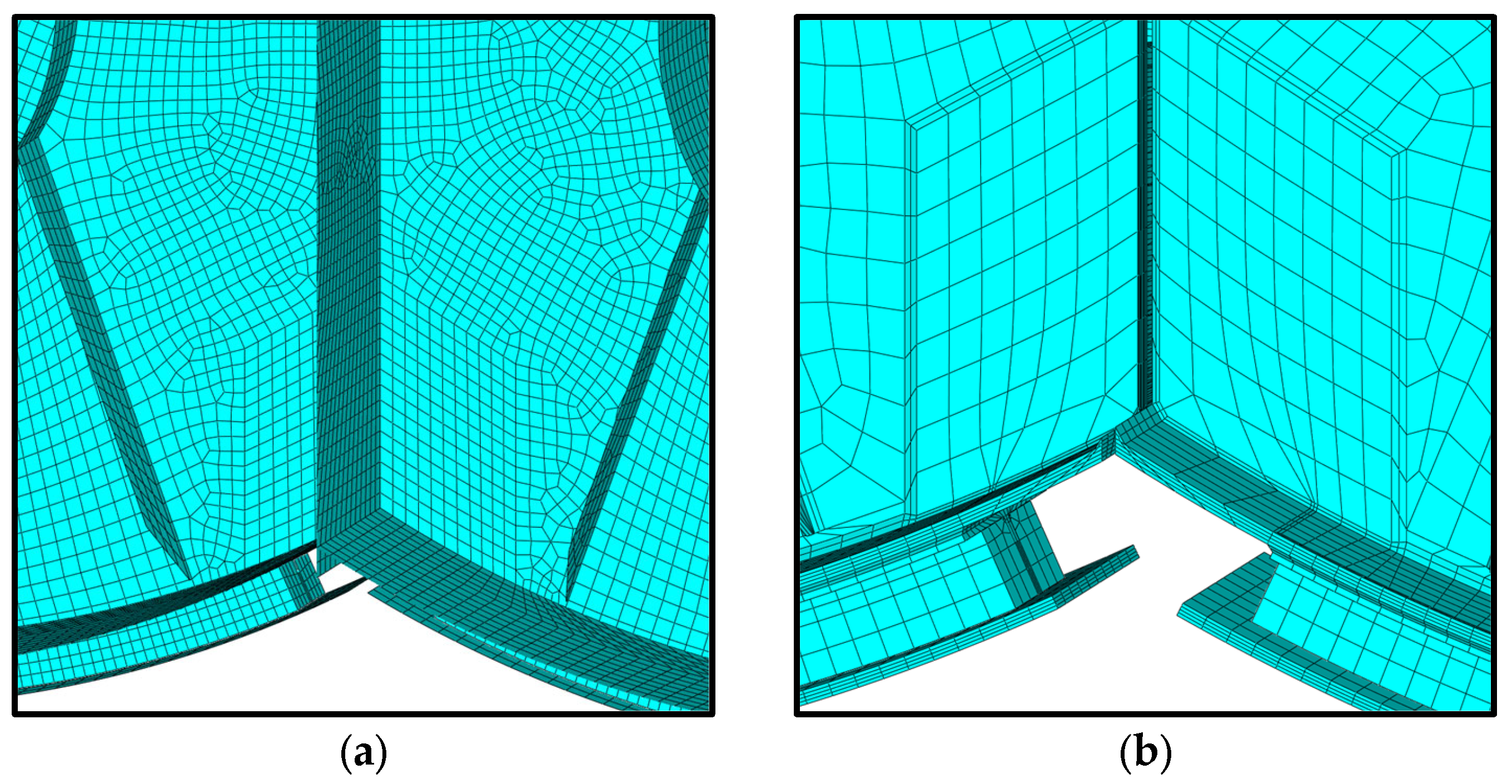
3.2.1. Shell and Solid Element
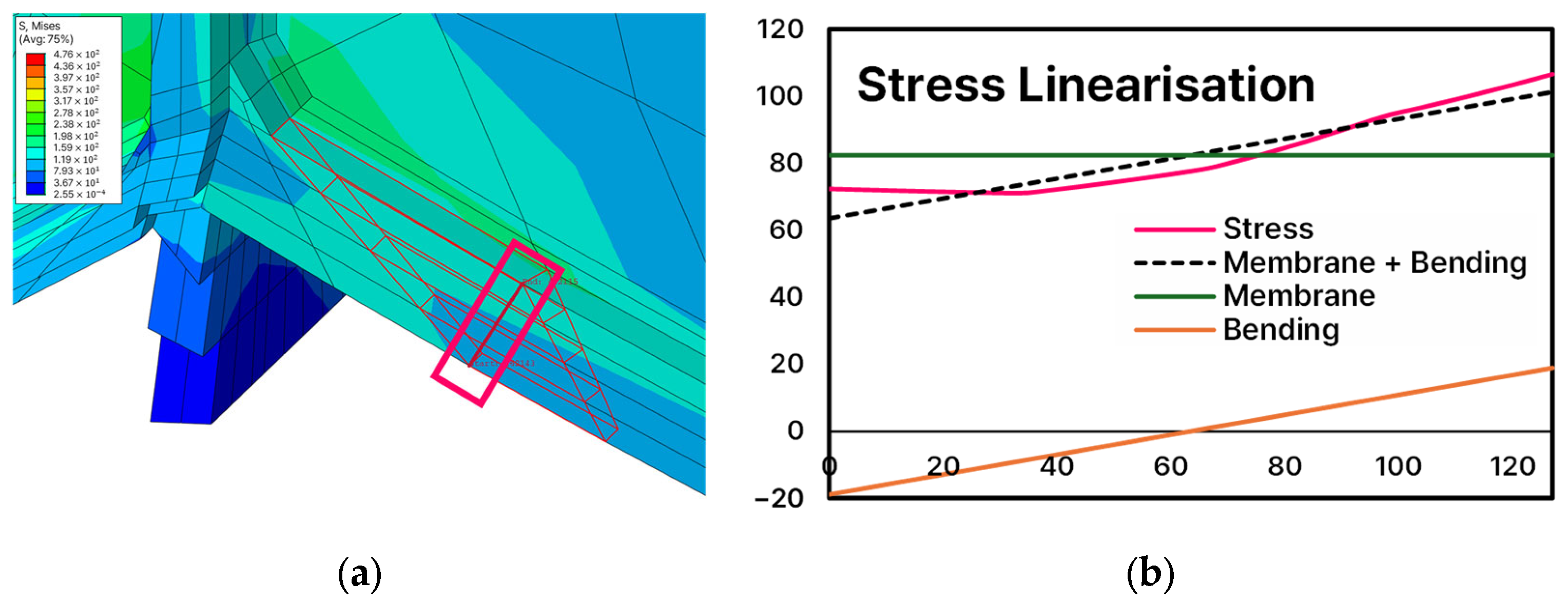
3.2.2. Stress Linearisation
3.3. Engineering Critical Assessment
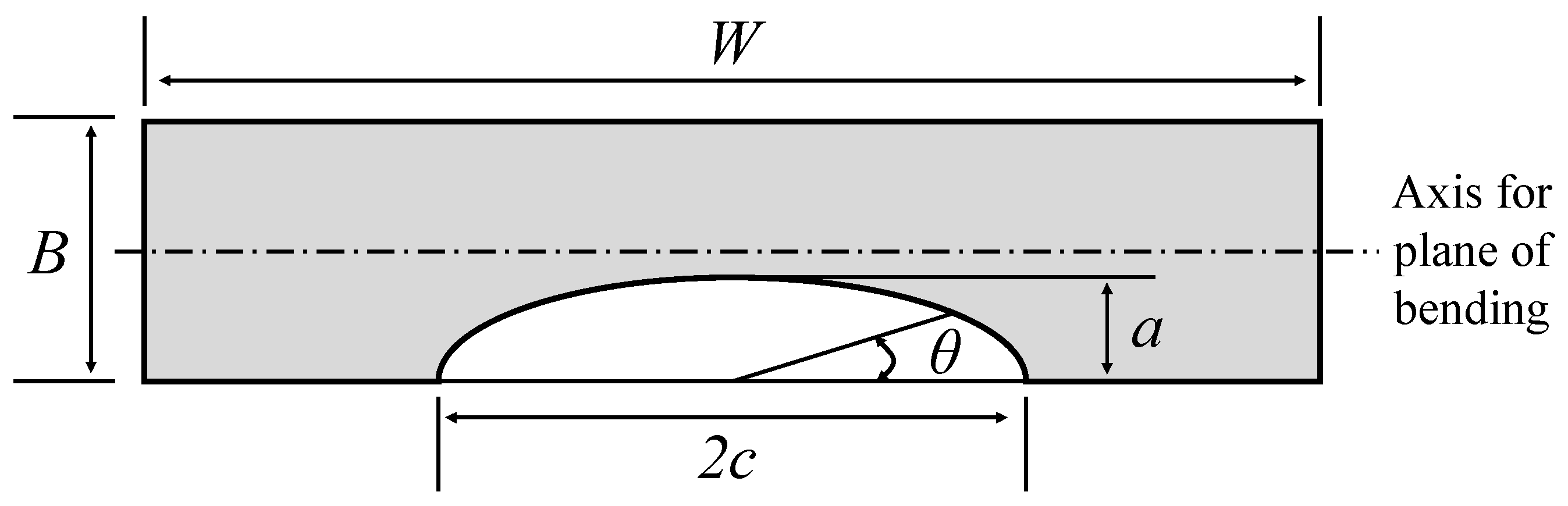
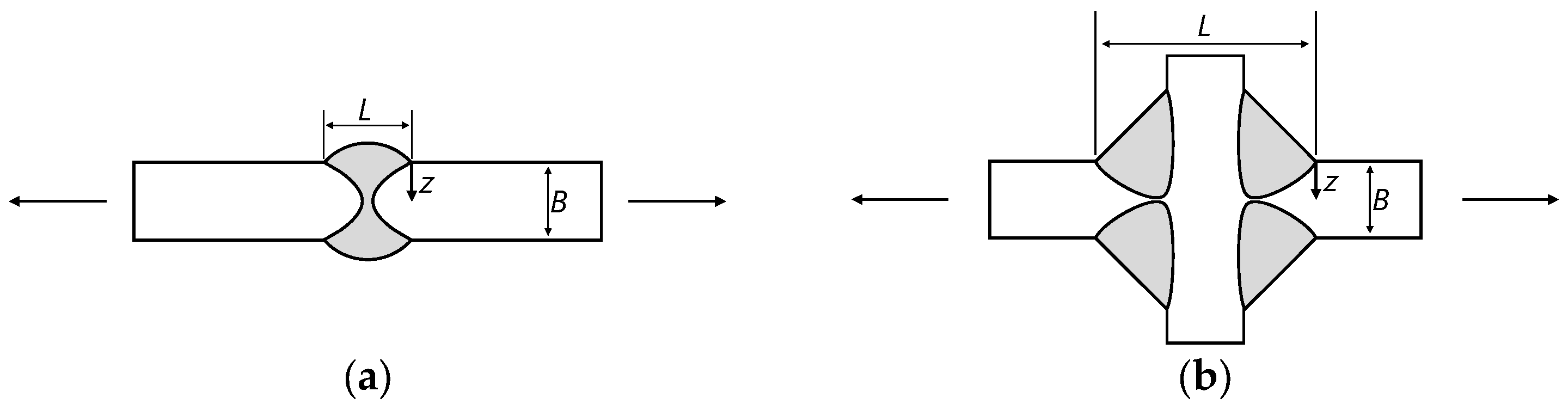
3.3.1. Flaw Characterisation
3.3.2. Fracture Assessment Methodology Using ECA
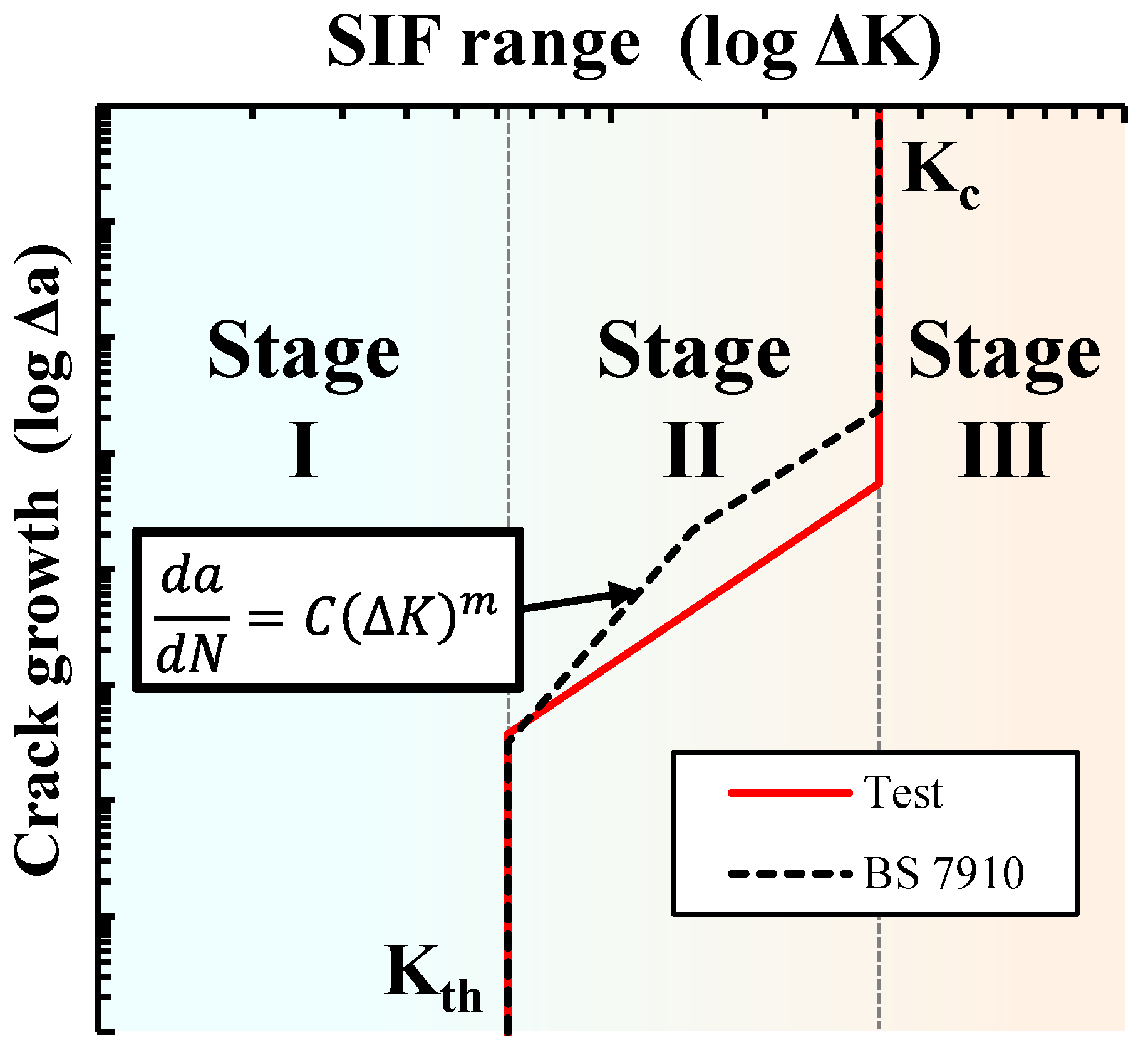
3.3.3. Fatigue Assessment Methodology Using ECA
4. Results
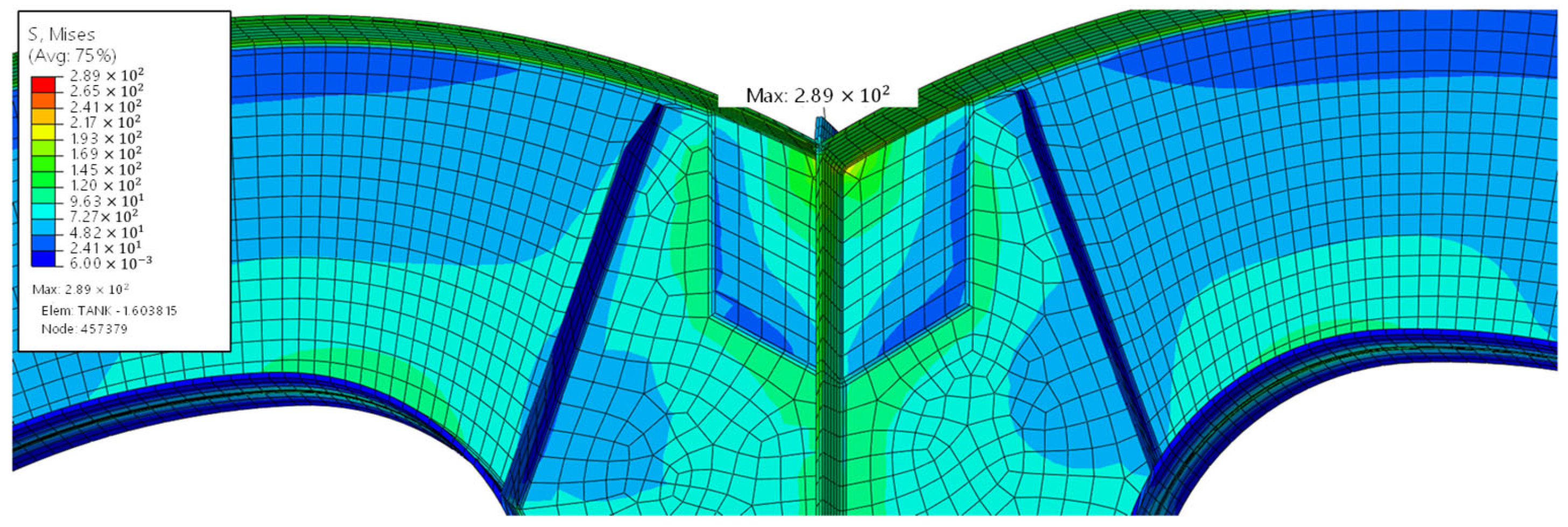
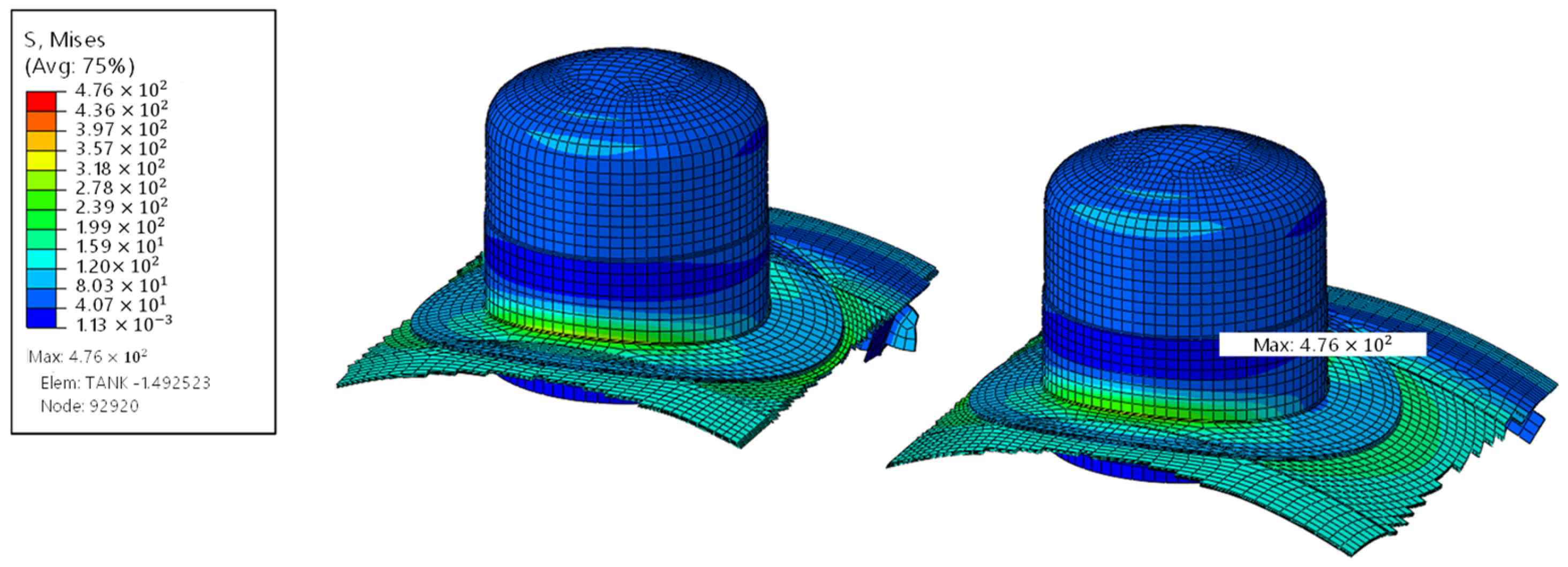
4.1. Stress Distribution
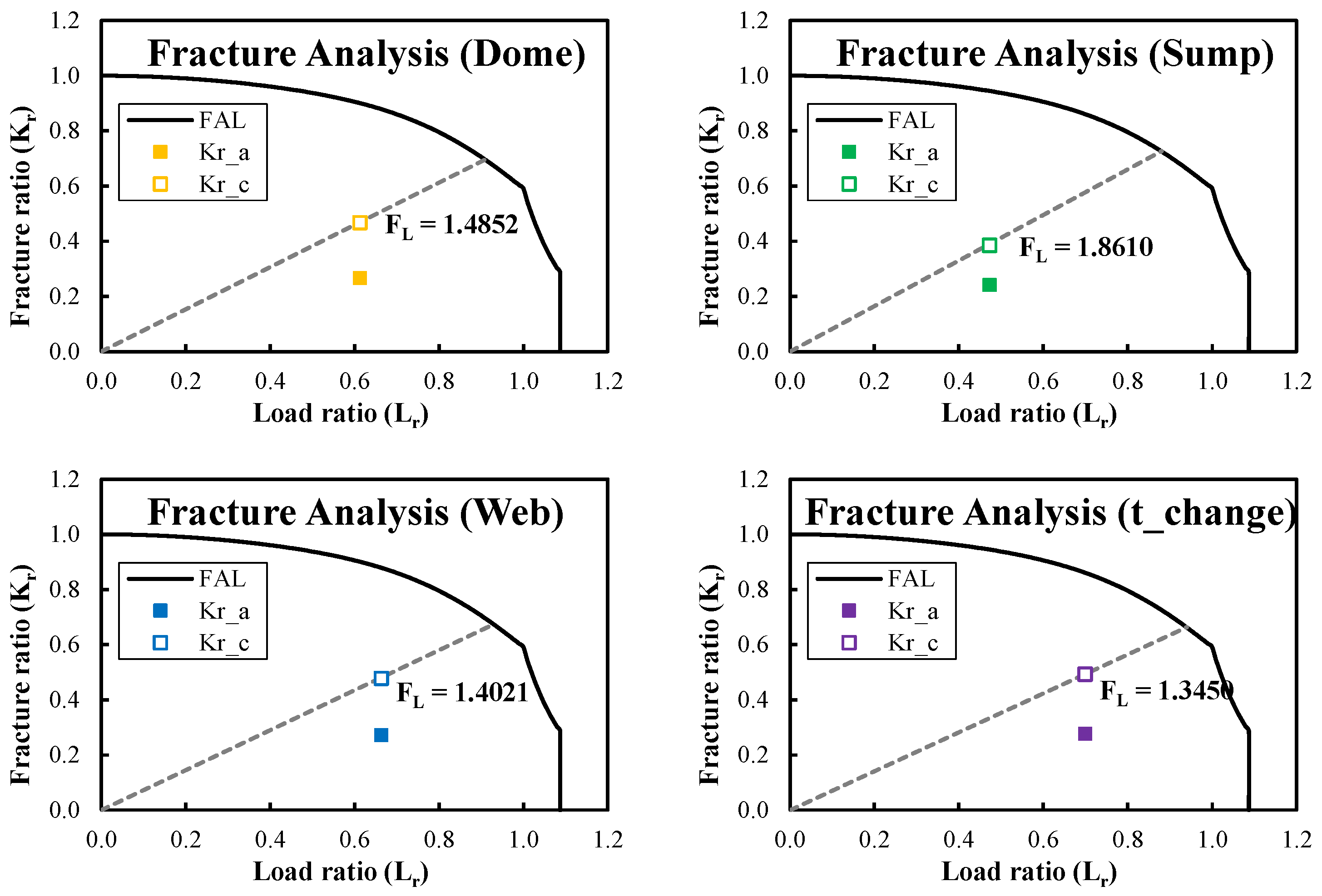
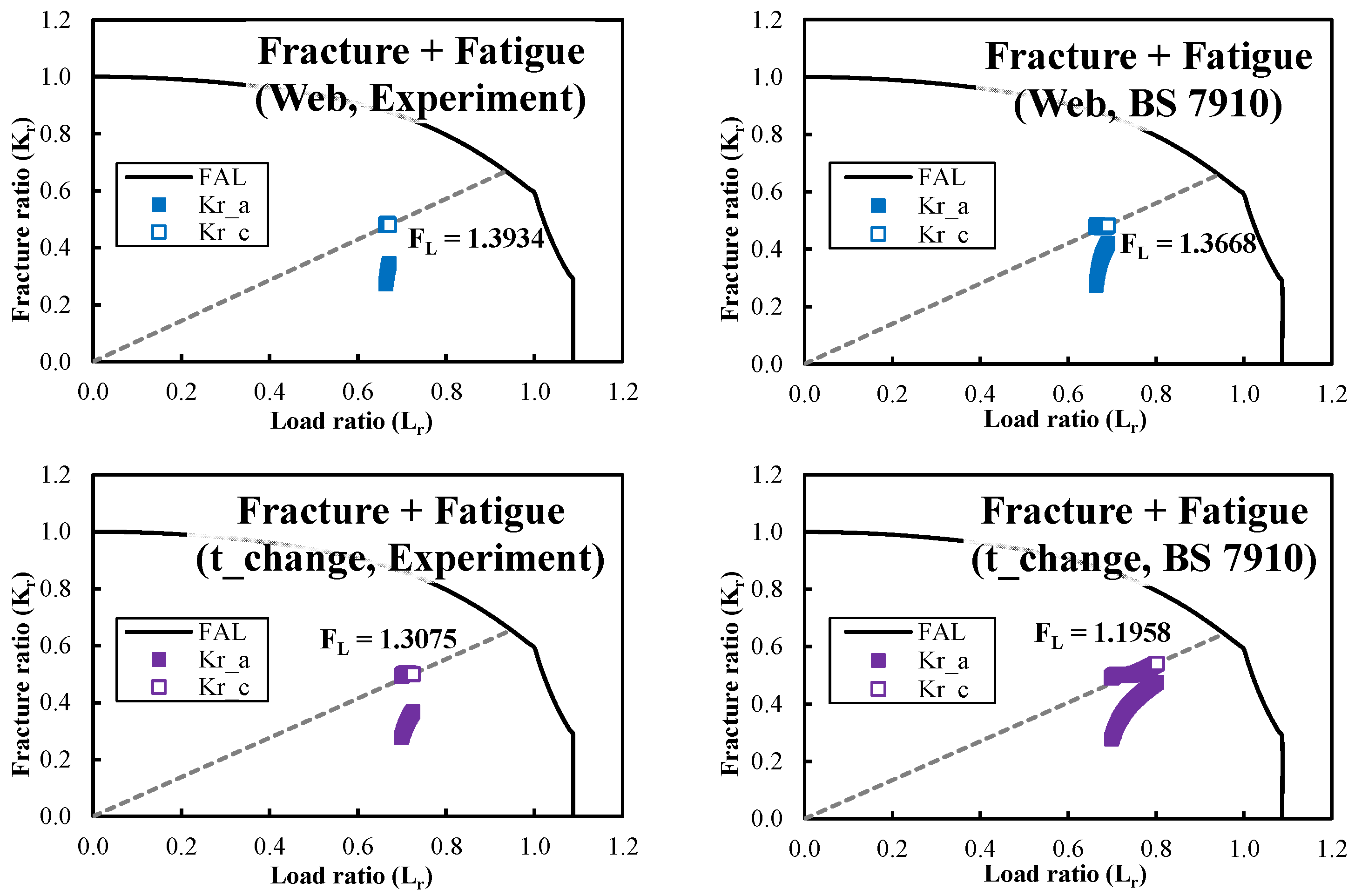
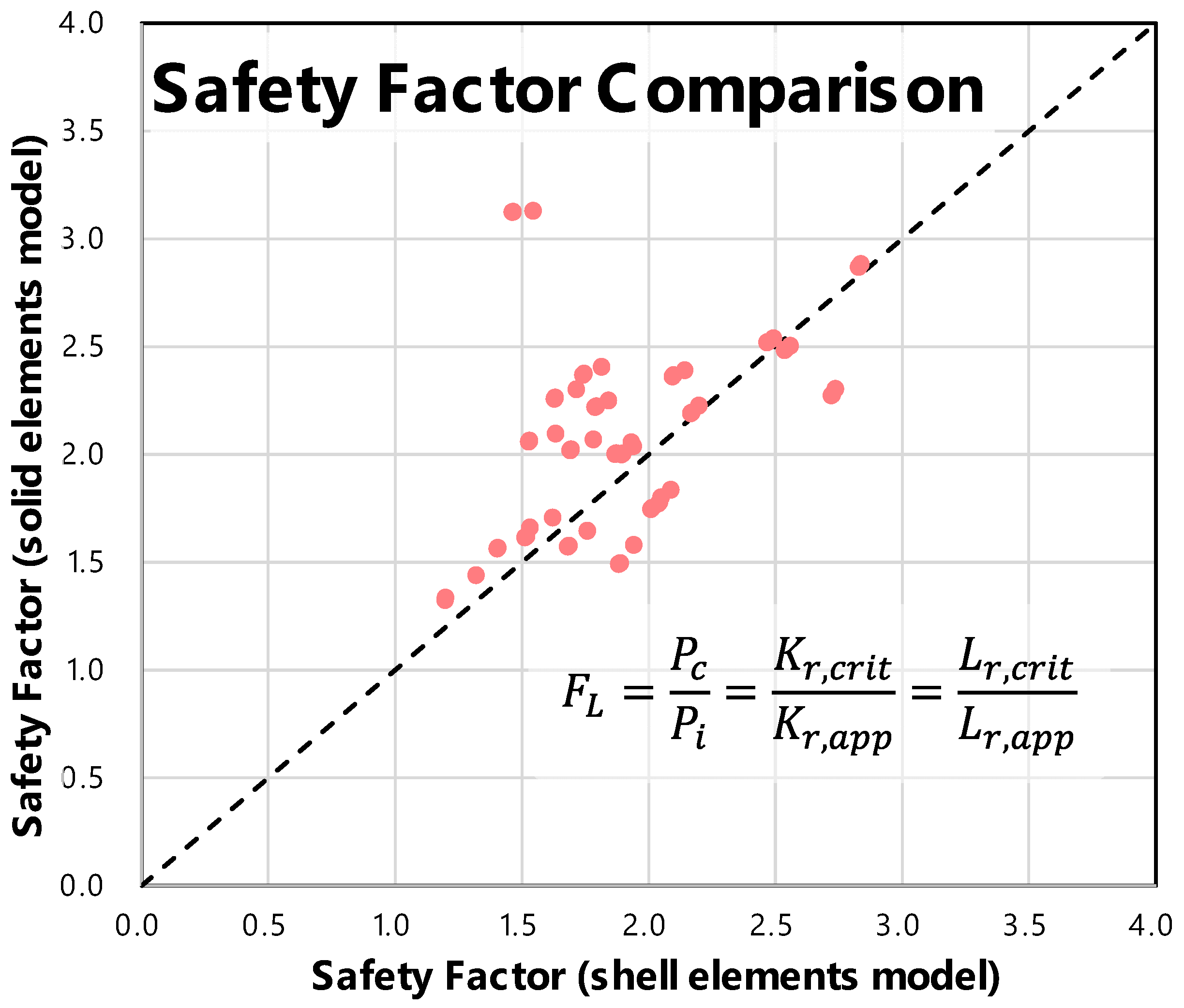
4.2. Fracture Assessment Results
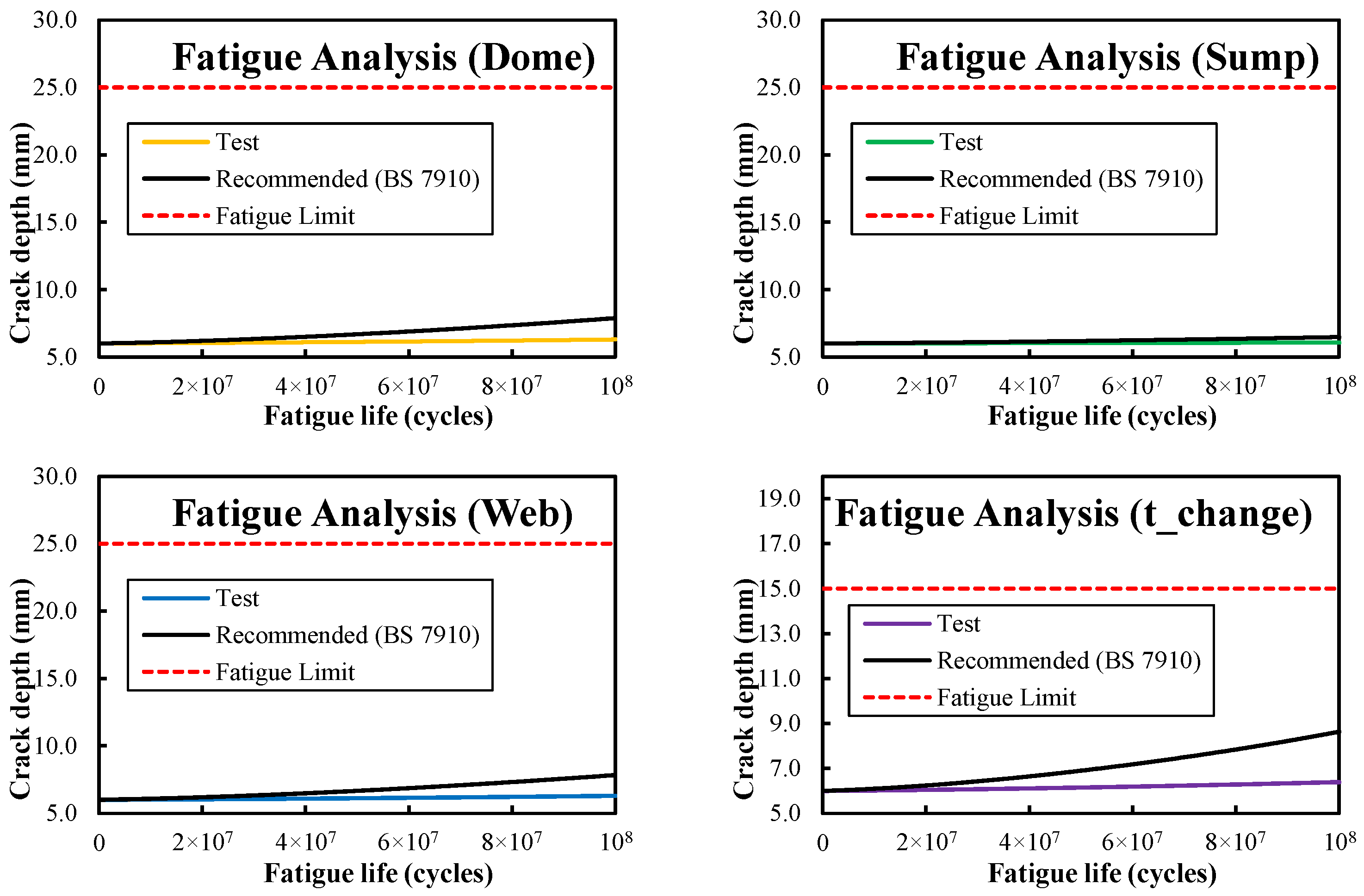
4.3. Fatigue Assessment Results
5. Discussion
6. Conclusions
- Accuracy and computational efficiency: The shell model required significantly fewer elements and reduced computation time, whereas the solid model increased computational cost by a factor of 4.78 to achieve improved local stress resolution.
- Stress distribution and Kr, Lr distribution: Both models exhibited similar global stress behaviour, but the solid model captured sharper local stress gradients, influencing the membrane/bending stress components and subsequently the fracture ratio (Kr), load ratio (Lr), and safety factor (FL).
- Fatigue and fracture assessment: While through-thickness crack growth was not predicted, the final crack depth showed sensitivity to FCGR datasets, indicating the importance of accurate crack growth and fracture toughness data for LCO2 tank steels (ex., LTFH36).
- Characteristics by location: The web and welded intersections of the bilobe shell were consistently identified as critical locations due to geometric and weld-induced stress concentrations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| Symbol | Description | Units |
| a | Flaw height | mm |
| a0 | Function of V, L0 used in acceleration calculation | |
| A | Function of z, L0, CB used in acceleration calculation | |
| ax, ay, az | Maximum dimensionless accelerations normalised by gravitational acceleration | |
| B | Section thickness | mm |
| Bs | Greatest moulded breadth of the ship | m |
| C | Material constant for crack growth relationship | |
| CB | Block coefficient of the ship | |
| c | Half flaw length | mm |
| Fatigue crack growth rate | mm/cycle | |
| FL | Safety factor defined by load ratio on FAD | |
| fw | Finite width correction factor | |
| K | Roll correction factor for acceleration calculation | |
| Kc | Critical stress intensity factor | |
| KI | Stress intensity factor for tensile load (mode I) | |
| Kmat | Material fracture toughness | |
| Kr | Fracture ratio | |
| Kth | Stress intensity factor for fatigue crack growth threshold | |
| km | Stress intensity factor due to misalignment | |
| ktb | Bending stress concentration factor | |
| ktm | Membrane stress concentration factor | |
| Lr | Load ratio | |
| L0 | Length of the ship for scantlings | |
| M | Bulging correction factor | |
| Mb | Bending stress intensity magnification factor for flaws | |
| Mm | Membrane stress intensity magnification factor for flaws | |
| Mkb | Bending stress intensity magnification factor for welded joints | |
| Mkm | Membrane stress intensity magnification factor for welded joints | |
| m | Exponent in flaw growth law | |
| N | Strain hardening coefficient | |
| nd | Number of total cycles | cycle |
| Pb | Primary bending stress | MPa |
| Pc | Critical assessment point on FAD | |
| Pi | Initial assessment point on FAD | |
| Pm | Primary membrane stress | MPa |
| P0 | Design pressure of the tank | MPa |
| Qb | Secondary bending stress | MPa |
| Qm | Secondary membrane stress | MPa |
| Tcargo | Design temperature of the tank | ℃ |
| Td | Design life in seconds | s |
| Troom | Room temperature (typically 40 °C) | ℃ |
| V | Service speed of the ship | knots |
| W | Structure width | mm |
| x | Longitudinal distance from midships to the centre of gravity of the tank | m |
| Y | Stress intensity correction factor | |
| (Yσ)p | Primary stress intensity correction | |
| (Yσ)s | Secondary stress intensity correction | |
| y | Transverse distance from centreline to the centre of gravity of the tank | m |
| z | Vertical distance from waterline to the centre of gravity of the tank | m |
| α″ | Parameter used in calculation of collapse stresses | |
| ΔK | Stress intensity factor range | |
| ϑ | Assessment angle on the FAD | ° |
| μ | Parameter for constructing FAL | |
| σbottom | Stress at the bottom surface of the plate | MPa |
| σref | Reference stress | MPa |
| σtop | Stress at the top surface of the plate | MPa |
| σu | Tensile strength | MPa |
| σY | Yield stress | MPa |
| υ0 | Average zero-crossing frequency | Hz |
References
- Deng, S.; Mi, Z. A review on carbon emissions of global shipping. Mar. Dev. 2023, 1, 4. [Google Scholar] [CrossRef]
- OECD. Maritime Transport CO2 Emissions. Available online: https://www.oecd.org/en/data/datasets/maritime-transport-co2-emissions.html (accessed on 20 July 2025).
- International Maritime Organization (IMO). 2023 IMO Strategy on Reduction of GHG Emissions from Ships; IMO Publishing: London, UK, 2023. [Google Scholar]
- BP. Energy Outlook: 2024 Edition. 2024. Available online: https://www.bp.com/en/global/corporate/energy-economics/energy-outlook.html (accessed on 11 October 2024).
- Al Baroudi, H.; Awoyomi, A.; Patchigolla, K.; Jonnalagadda, K.; Anthony, E.J. A review of large-scale CO2 shipping and marine emissions management for carbon capture, utilisation and storage. Appl. Energy 2021, 287, 116510. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). International Code of the Construction and Equipment of Ships Carrying Liquefied Gases in Bulk (IGC Code); IMO Publishing: London, UK, 2016. [Google Scholar]
- International Association of Classification Societies (IACS). UR W1: Material and Welding for Ships Carrying Liquefied Gases in Bulk and Ships Using Gases or Other Low-Flashpoint Fuels; International Association of Classification Societies: London, UK, 2021. [Google Scholar]
- BS 7910:2019; Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures. British Standards Institution: London, UK, 2019.
- EDF Energy. R6: Assessment of the Integrity of Structures Containing Defects; EDF Energy: Gloucester, UK, 2019. [Google Scholar]
- API 579-1/ASME FFS-1; Fitness-For-Service. American Petroleum Institute: Washington, DC, USA, 2021.
- Radu, D.; Sedmak, A.; Sedmak, S.; Li, W. Engineering critical assessment of steel shell structure elements welded joints under high cycle fatigue. Eng. Fail. Anal. 2020, 114, 104578. [Google Scholar] [CrossRef]
- Rezaie, Y.; Sharifi, S.M.H.; Rashed, G.R. Probabilistic fracture assessment of snake laid pipelines under high pressure/high temperature conditions by engineering critical assessment. Eng. Fract. Mech. 2022, 271, 108592. [Google Scholar] [CrossRef]
- He, M.; Pang, M.; Chen, N.Z. Engineering critical assessment (ECA) for monopile foundation of an offshore wind turbine subjected to pitting. Ocean Eng. 2023, 285, 115400. [Google Scholar] [CrossRef]
- Seo, J.H.; Park, K.S.; Cha, I.; Choung, J. Engineering Critical Assessement for an Independent Type-B LNG Cargo Tank. J. Soc. Nav. Archit. Korea 2023, 60, 213–221. [Google Scholar] [CrossRef]
- Kim, B.I.; Kim, K.T.; Islam, M.D.S. Development of Strength Evaluation Methodology for Independent IMO TYPE C Tank with LH2 Carriers. J. Ocean Eng. Technol. 2024, 38, 87–102. [Google Scholar] [CrossRef]
- Kim, J.; Park, K.S.; Cha, I.; Choung, J. Structural Integrity Assessments of an IMO Type C LCO2 Cargo Tank. J. Mar. Sci.Technol. 2025, 13, 1479. [Google Scholar] [CrossRef]
- Conti, F.; Aubert, J.-M. Engineering Critical Assessment for Alternative Materials to IGC Code for LCO2 Carriers Type-C Tanks. In Proceedings of the ASME 2024 43rd International Conference on Ocean, Offshore and Arctic Engineering, Singapore, 9–14 June 2024. [Google Scholar]
- Zhen, Y.; Cao, Y.; Li, F.; Li, W.; Wu, G. A Pressure Decompression Model-Based Finite Element Approach for Efficient Dynamic Fracture Analysis in CO2 Pipelines. Fatigue Fract. Eng. Mater. Struct. 2025, 48, 4245–4258. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Lin, Y.Y.; Jang, B.S.; Han, S.W.; Park, Y.H.; Hwang, J.; Kim, D.K. Cutting-edge insights: Crack growth rates in 9% Ni steel from room to cryogenic conditions influenced by crack closure and effective stress intensity factors. Eng. Fract. Mech. 2024, 301, 110014. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Park, K.S.; Hwang, J.; Cho, N.K.; Kim, D.K. Advanced techniques for residual stress measurement and data processing in fatigue crack growth rate tests of FH36 and 9% Ni steel at cryogenic temperatures. Ocean Eng. 2025, 316, 119942. [Google Scholar] [CrossRef]
- ASTM E1820-2024; Standard Test Method for Measurement of Fracture Toughness. ASTM International: West Conshohocken, PA, USA, 2024.
- BS 7448-1:1991; Fracture Mechanics Toughness Tests—Method for Determination of KIC, Critical CTOD and Critical J Values of Metallic Materials. British Standards Institution: London, UK, 1991.
- ISO 12135:2021; Metallic Materials—Unified Method of Test for the Determination of Quasistatic Fracture Toughness. International Organization for Standardization: Geneva, Switzerland, 2021.
- ASTM E647-24; Standard Test Method for Measurement of Fatigue Crack Growth Rates. ASTM International: West Conshohocken, PA, USA, 2024.
- Lin, Y.Y.; Kim, Y.-J.; Cho, N.-K.; Hwang, J.H.; Park, K.-S.; Kim, D.I.; Mehmanparast, A.; Kim, D.K. Technical Recommendations for Metallic C(T) and SEN(B) Fracture Toughness Test Specimens: Data-driven Insights from Literature. Results Eng. 2025, 28, 108117. [Google Scholar] [CrossRef]
- Abul Kashem Mohammad, Y.; Mohammad, S. Recent developments and challenges in fracture mechanics–based fatigue life prediction. ASRC Procedia Glob. Perspect. Sci. Scholarsh. 2025, 1, 1202–1237. [Google Scholar] [CrossRef]
- Tukeev, D.L.; Afanaseva, O.V.; Tulyakov, T.F. Realization of Statistical Models Based on Symmetric Unimodal Distributions. Int. J. Eng. 2026, 39, 407–419. [Google Scholar] [CrossRef]
- Saifi, Q. Novel probabilistic crack growth assessment method: Based on the realised PDF law for growing cracks. Eng. Fract. Mech. 2022, 276, 108931. [Google Scholar] [CrossRef]
- Fan, X.; Chen, S.; Steingrimsson, B.; Xiong, Q.; Li, W.; Liaw, P.K. Dataset for Fracture and Impact Toughness of High-Entropy Alloys. Sci. Data 2023, 10, 37. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.K.; Ban, I.; Poh, B.Y.; Shin, S.-C. A useful guide of effective mesh-size decision in predicting the ultimate strength of flat- and curved plates in compression. J. Ocean Eng. Sci. 2023, 8, 401–417. [Google Scholar] [CrossRef]
- Wang, Z.; Kong, W.; Wu, S.; Li, S.; Kim, D.K. A guidance of solid element application in predicting the ultimate strength of flat plates in compression. J. Ocean Eng. Sci. 2023, 10, 661–677. [Google Scholar] [CrossRef]






| Authors | Structure | Stress Intensity Factor Calculation | FE Analysis | Fracture Assessment |
|---|---|---|---|---|
| Radu et al. [11] | Antenna tower | Handbook (BS 7910) | Solid | O |
| He et al. [13] | Wind turbine monopile | XFEM | Solid | O |
| Seo et al. [14] | Type B (LNG) | Handbook (BS 7910) | Shell | O |
| Kim et al. [15] | Type C (LH2, single) | Handbook (BS 7910) | Shell | - |
| Kim et al. [16] | Type C (LCO2, single) | Handbook (BS 7910) | Shell | - |
| Present study | Type C (LCO2, bilobe) | Handbook (BS 7910) | Shell/Solid | O |
| Material Properties | LTFH36 | Supporting Wood |
|---|---|---|
| Elastic Modulus (MPa) | 206,000 | 30,000 |
| Poisson Ratio | 0.3 | 0.4 |
| Yield Stress (MPa) | 355 | - |
| Tensile Strength (MPa) | 490 | - |
| Density (kg/m3) | 7850 | 1300 |
| Thermal Expansion Coefficient (×10−6 °C) | 12 | 8 |
| Curve | Threshold (N/mm3/2) | A (Mean + 2SD) | m (Mean + 2SD) | Transition (N/mm3/2) | ||
|---|---|---|---|---|---|---|
| Stage A | Stage B | Stage A | Stage B | |||
| Recommended (Weld) | 63 | 2.10 × 10−17 | 1.19 × 10−12 | 5.10 | 2.88 | 144 |
| Experiment | 63 | 1.49 × 10−13 | 3.0 | - | ||
| L0 (m) | Bs (m) | CB | V (knot) | x (m) | y (m) | z (m) |
|---|---|---|---|---|---|---|
| 215.0 | 31.6 | 0.78 | 14 | 53.5 | 0.0 | 2.8 |
| Load Case | Internal Pressure | Static Loading | Acceleration | Temperature |
|---|---|---|---|---|
| Longitudinal (x, LC1) | P0 | hydrostatic pressure, gravity | ±ax | Tcargo |
| Transverse (y, LC2) | P0 | hydrostatic pressure, gravity | ±ay | Tcargo |
| Vertical (z, LC3) | P0 | hydrostatic pressure, gravity | ±az | Tcargo |
| Static (LC4) | - | gravity | - | Troom |
| Collision (LC5) | P0 | hydrostatic pressure, gravity | +0.5 g, −0.25 g | Tcargo |
| Analysis Information | Shell Element | Solid Element |
|---|---|---|
| Number of Elements | 372,999 | 1,037,272 |
| Number DOFs | 2,182,674 | 3,314,808 |
| CPU Time (s) | 34,681 | 165,847 |
| Shell Element Model | Solid Element Model | ||
|---|---|---|---|
| Membrane (MPa) | Bending (MPa) | Membrane (MPa) | Bending (MPa) |
| 150.5 | 163.5 | 109.0 | 95.1 |
| Shell Element Model | Solid Element Model | ||
|---|---|---|---|
| Membrane (MPa) | Bending (MPa) | Membrane (MPa) | Bending (MPa) |
| 266.0 | 96.7 | 238.8 | 93.7 |
| Shell Element Model | Solid Element Model | ||
|---|---|---|---|
| Membrane (MPa) | Bending (MPa) | Membrane (MPa) | Bending (MPa) |
| 328.7 | 172.3 | 314.5 | 103.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.I.; Cho, N.-K.; Hwang, J.-H.; Lin, Y.Y.; Kim, D.K. Engineering Critical Assessment of IMO Type C Tanks: A Comparative Study of Shell and Solid Element Models. J. Mar. Sci. Eng. 2025, 13, 2185. https://doi.org/10.3390/jmse13112185
Kim DI, Cho N-K, Hwang J-H, Lin YY, Kim DK. Engineering Critical Assessment of IMO Type C Tanks: A Comparative Study of Shell and Solid Element Models. Journal of Marine Science and Engineering. 2025; 13(11):2185. https://doi.org/10.3390/jmse13112185
Chicago/Turabian StyleKim, Dong In, Nak-Kyun Cho, Jin-Ha Hwang, Yu Yao Lin, and Do Kyun Kim. 2025. "Engineering Critical Assessment of IMO Type C Tanks: A Comparative Study of Shell and Solid Element Models" Journal of Marine Science and Engineering 13, no. 11: 2185. https://doi.org/10.3390/jmse13112185
APA StyleKim, D. I., Cho, N.-K., Hwang, J.-H., Lin, Y. Y., & Kim, D. K. (2025). Engineering Critical Assessment of IMO Type C Tanks: A Comparative Study of Shell and Solid Element Models. Journal of Marine Science and Engineering, 13(11), 2185. https://doi.org/10.3390/jmse13112185







