Investigation of the Internal Solitary Wave Influence on Subsea Equipment Lowering with a Continuous Lowering Analysis Model
Abstract
1. Introduction
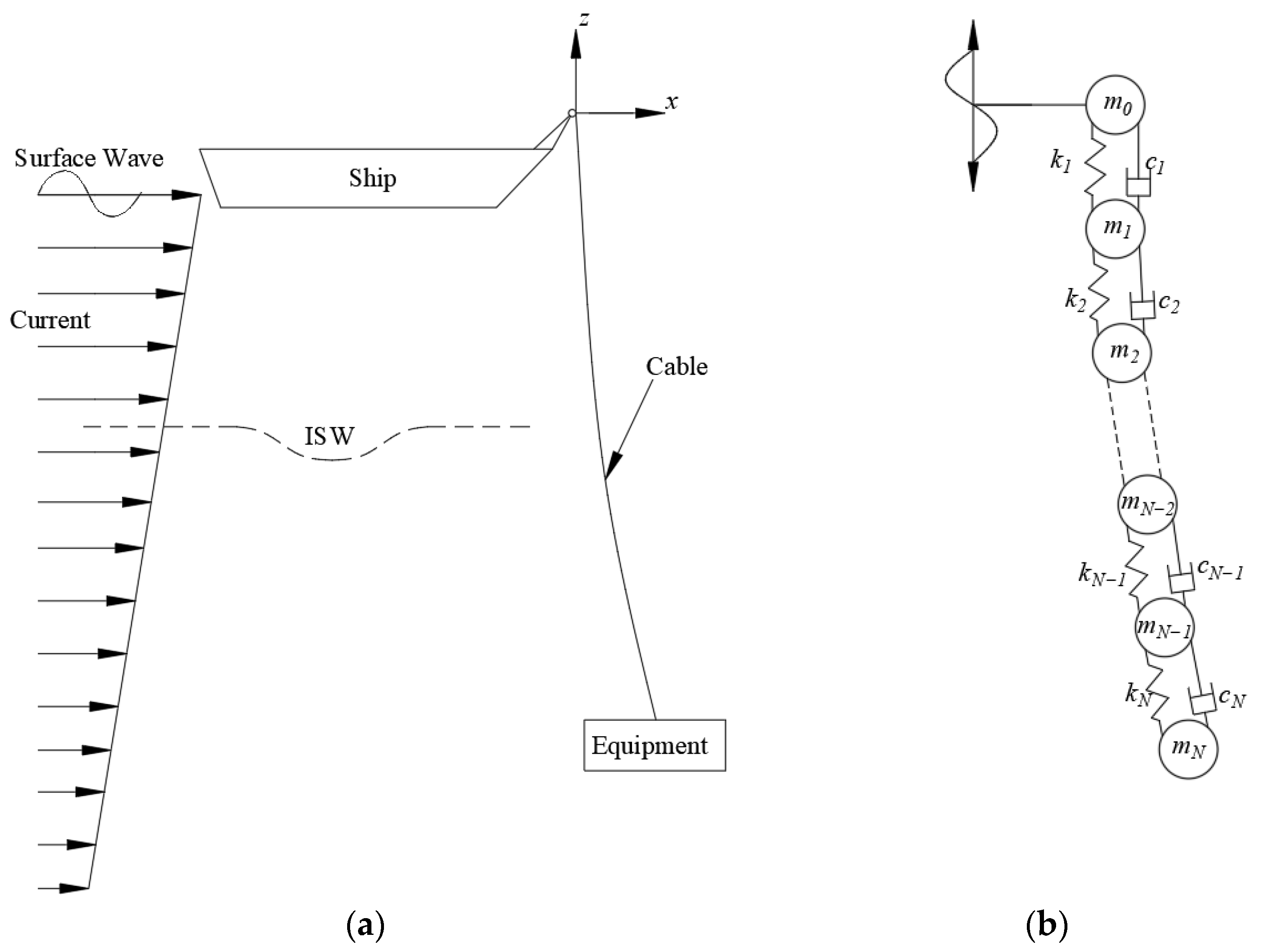
2. Methodology
2.1. Governing Equations
2.1.1. Kinetic Equations
2.1.2. External Loads
2.1.3. Internal Solitary Wave
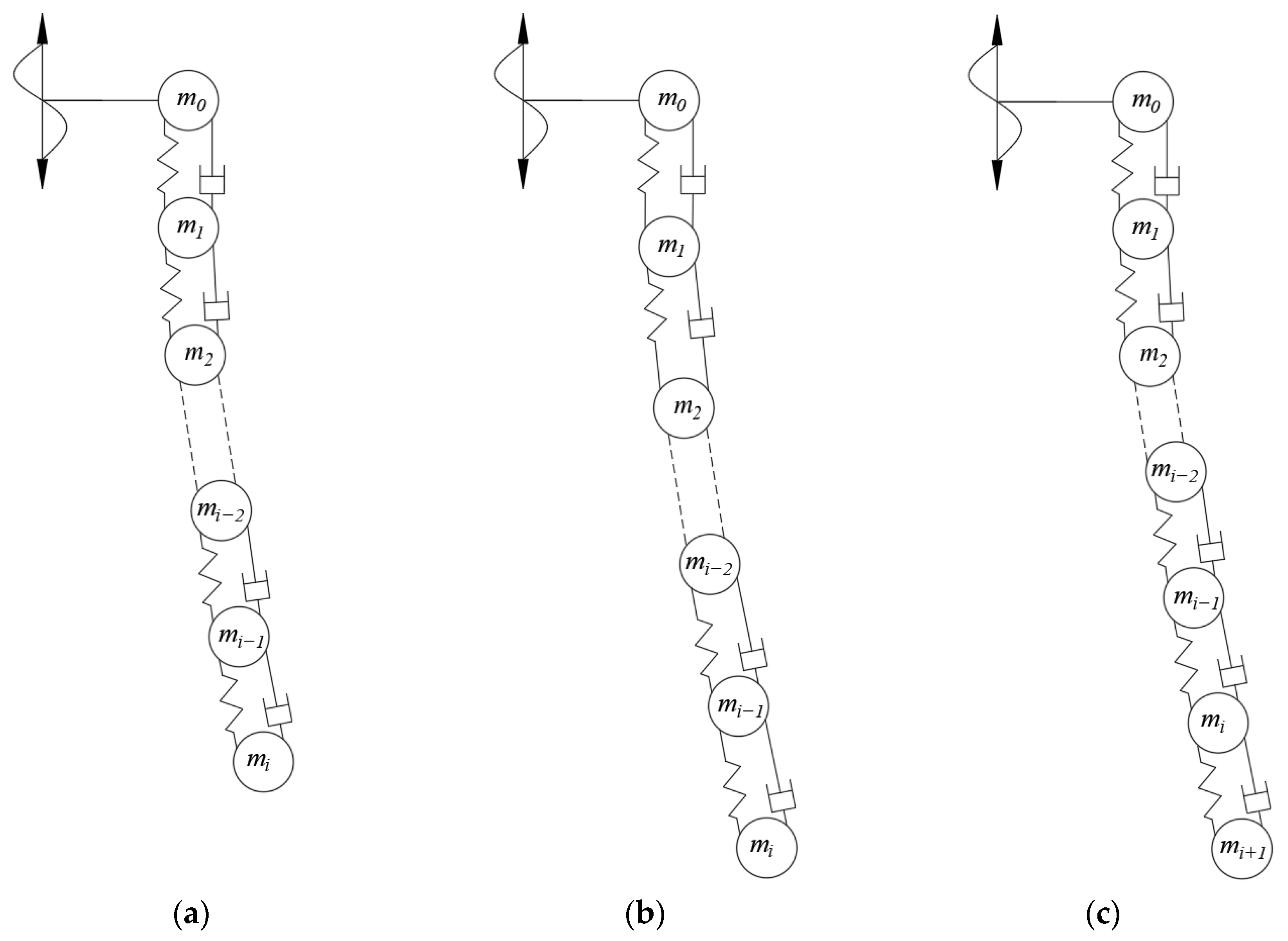
2.2. Lumped-Mass Disretization
2.2.1. Internal Force
2.2.2. External Force
2.3. Numerical Solution Algorithm with Variable Domain
- (1)
- Build cumulative arc-length along the old polyline, and form continuous maps ,
- (2)
- Generate new nodes: , .
- (3)
- Conduct position and velocity interpolation: , .
- (4)
- Recompute , , , and enforce .
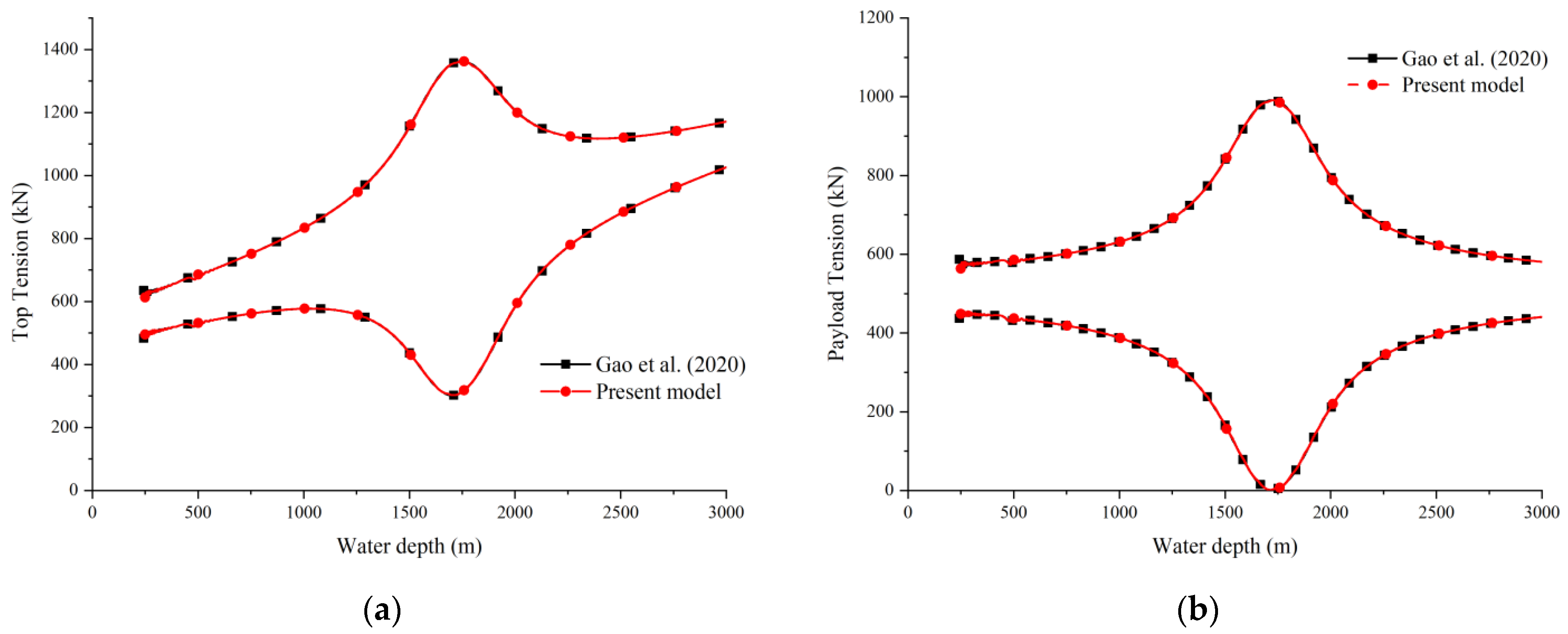
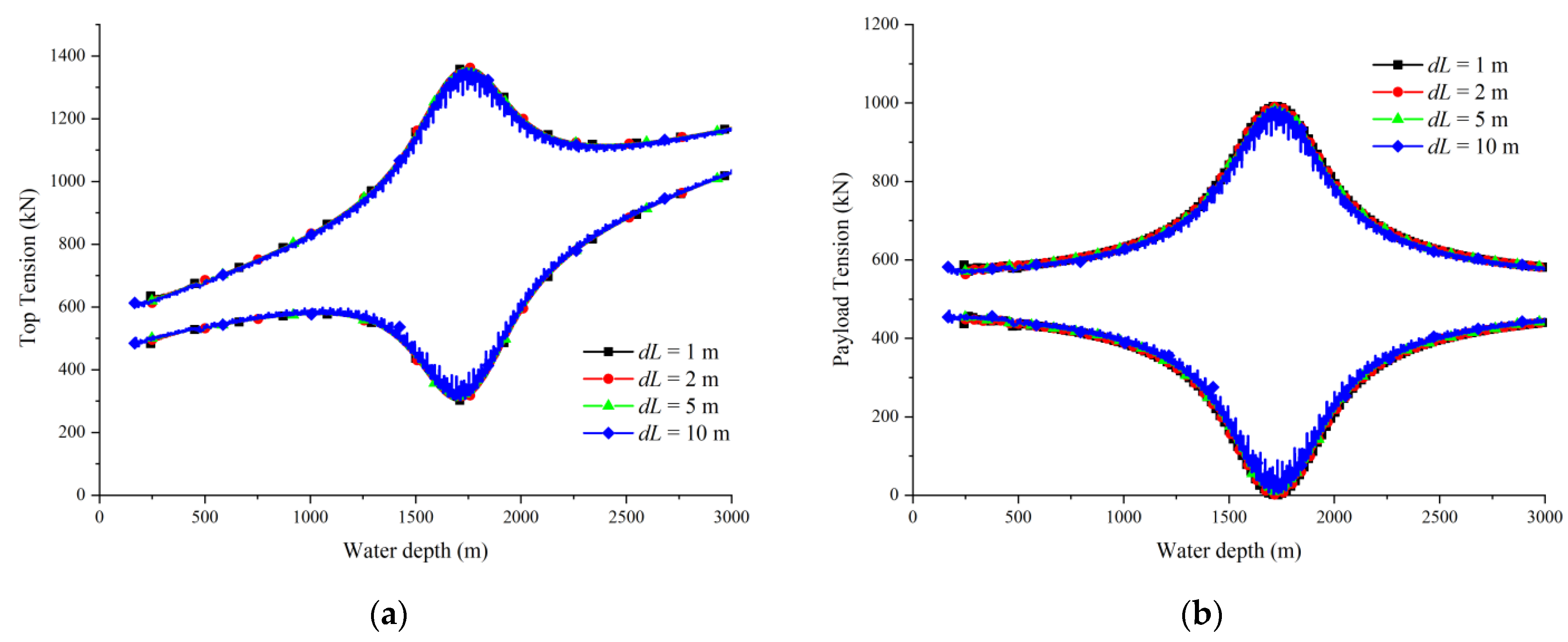
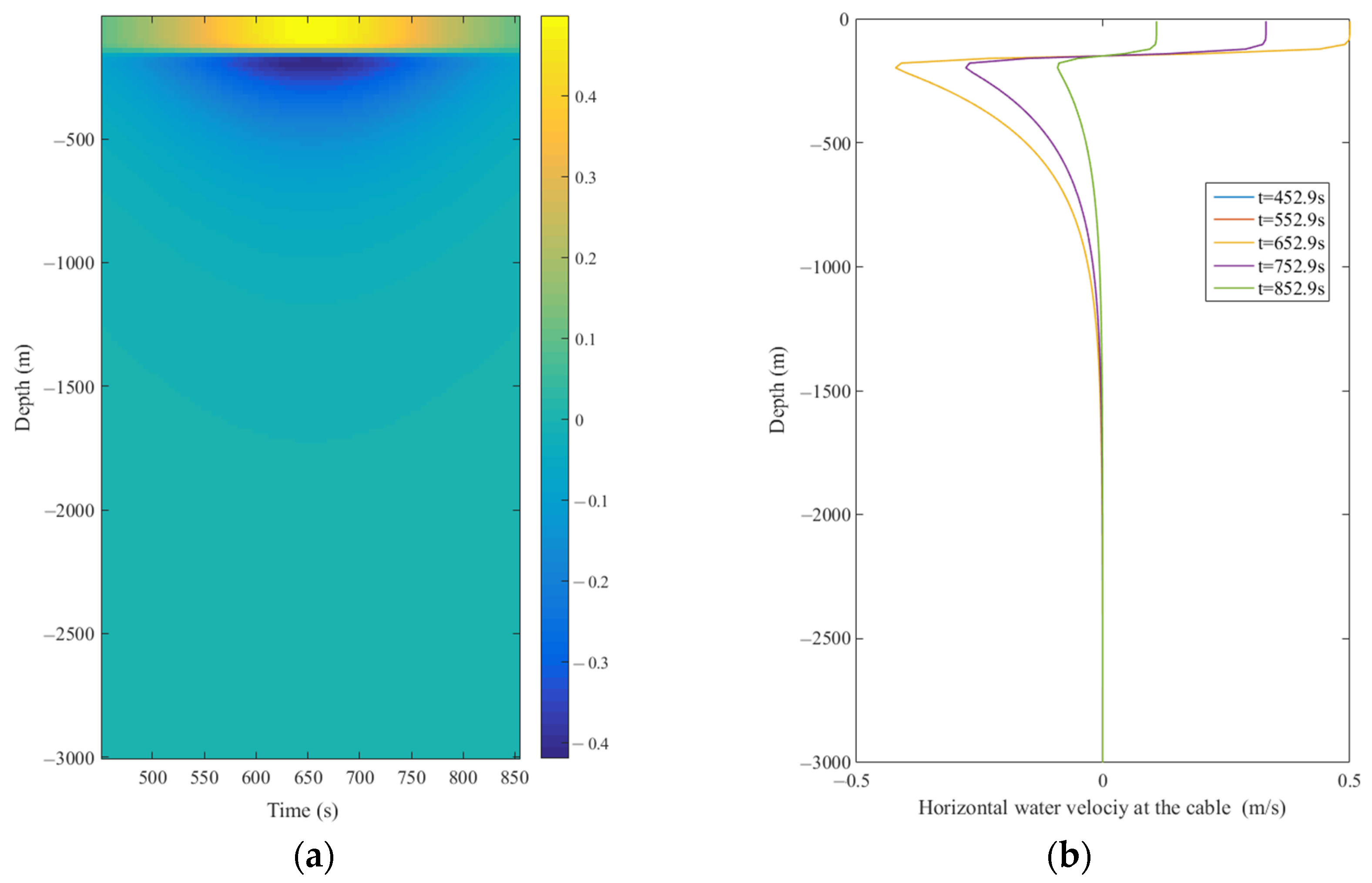
2.4. Model Validation
3. Results and Discussion
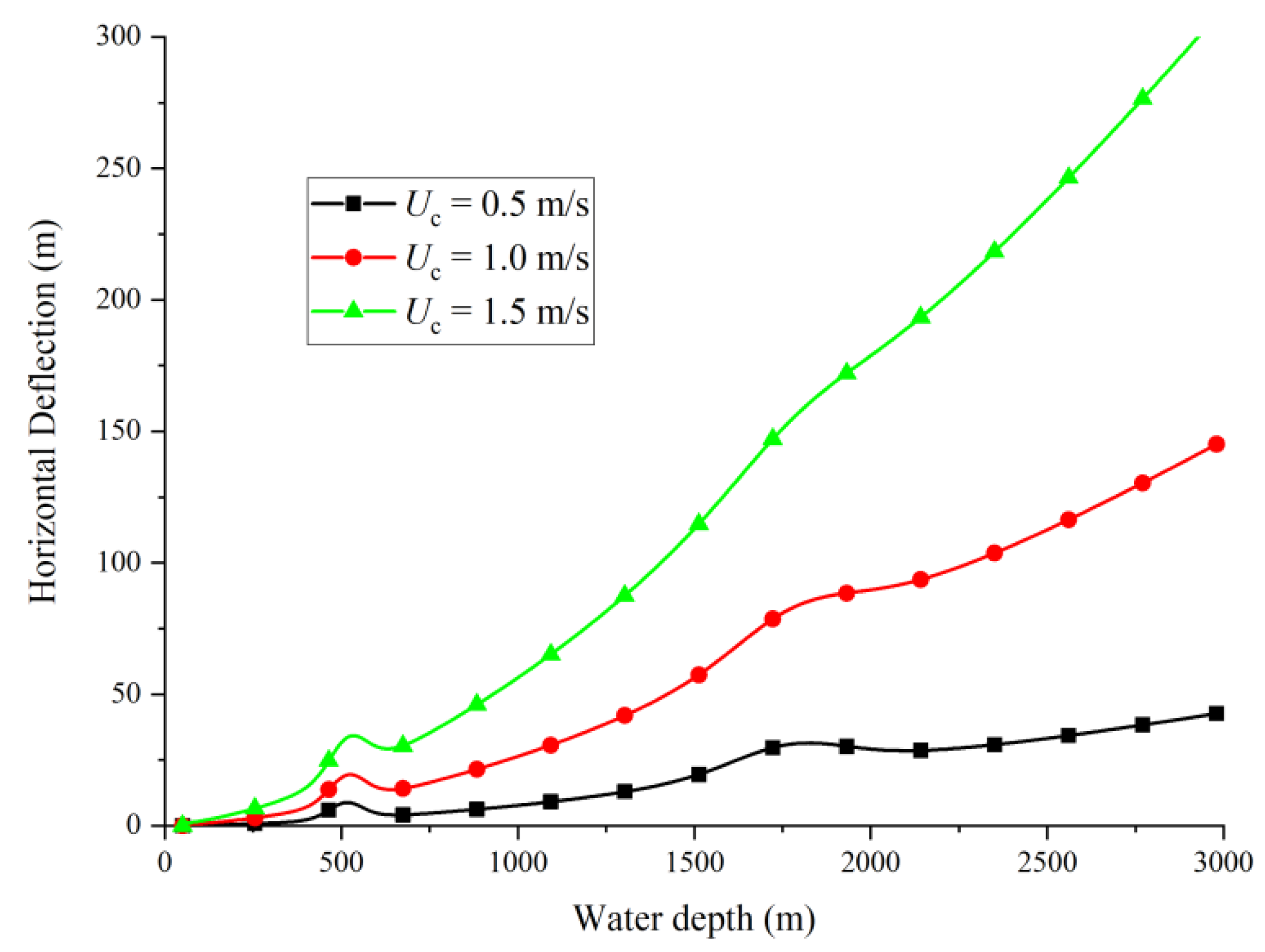
3.1. Effect of Cross Flow
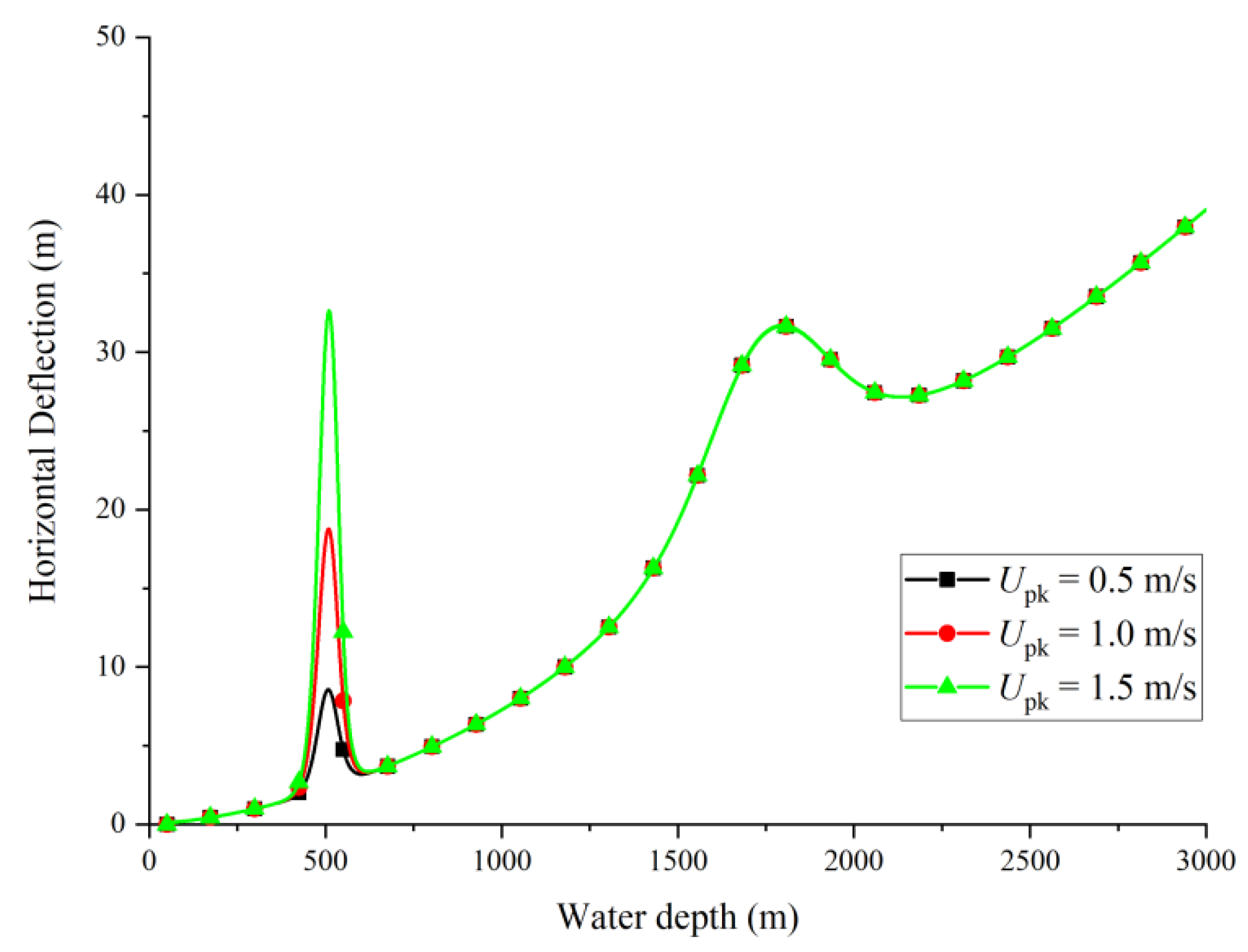
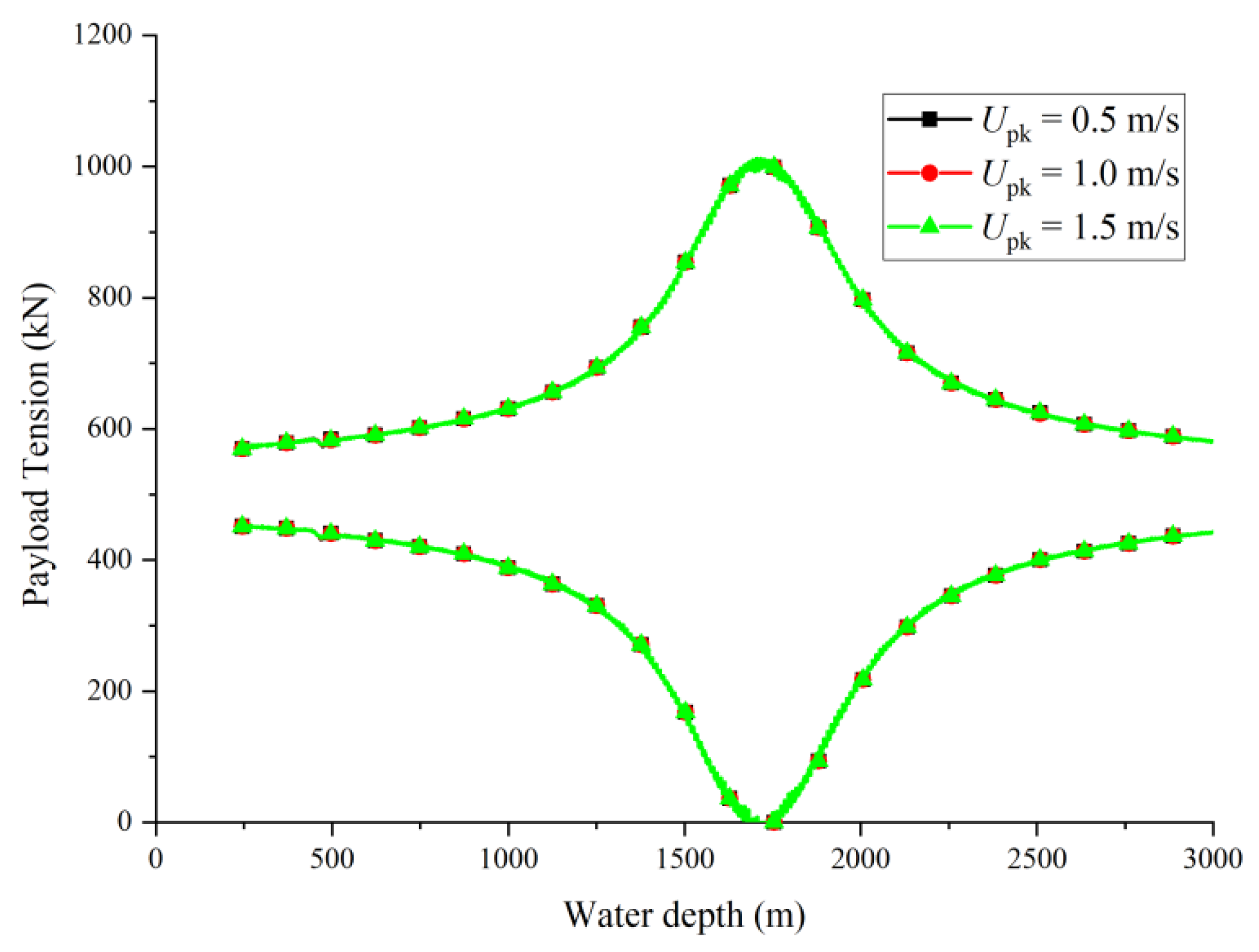
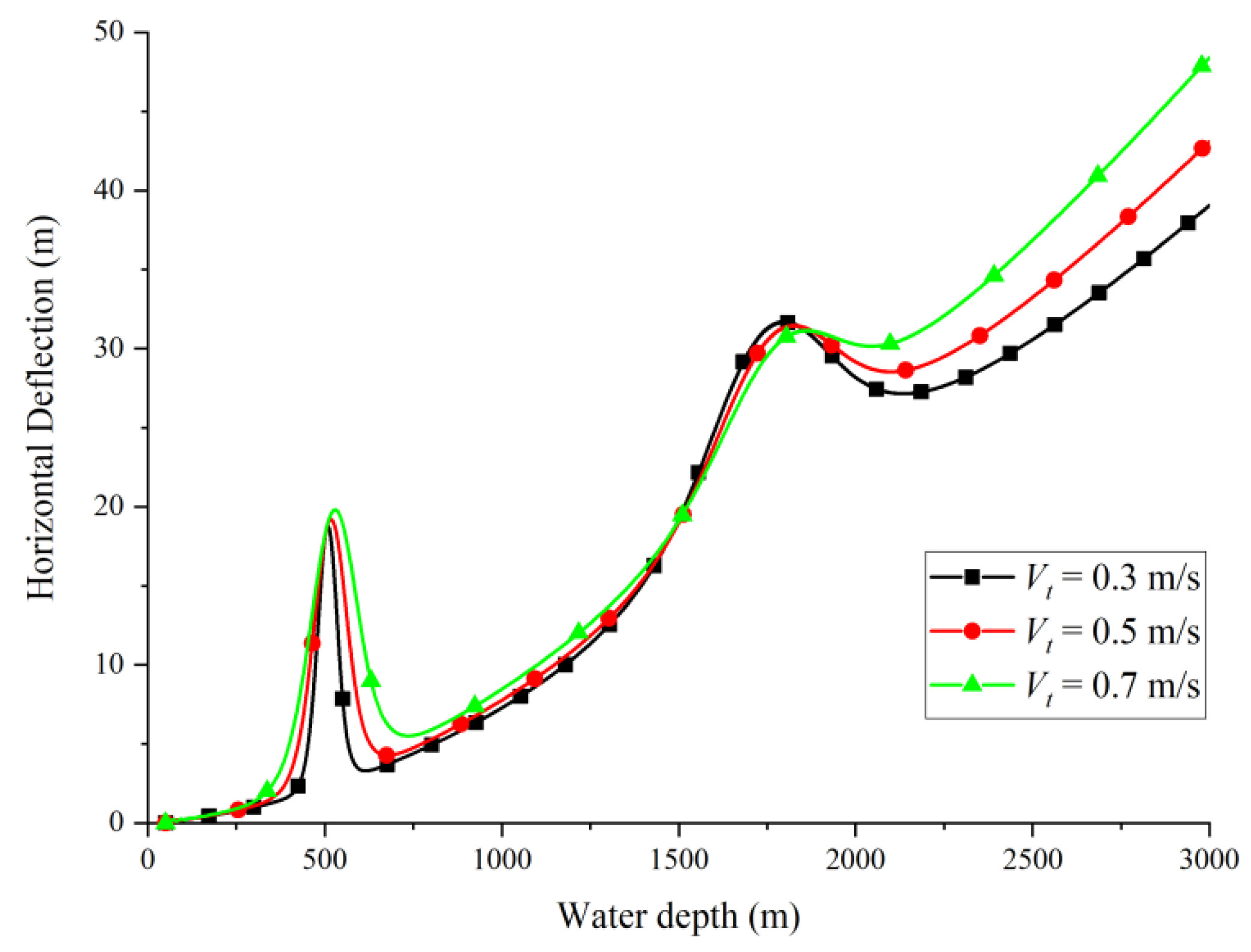
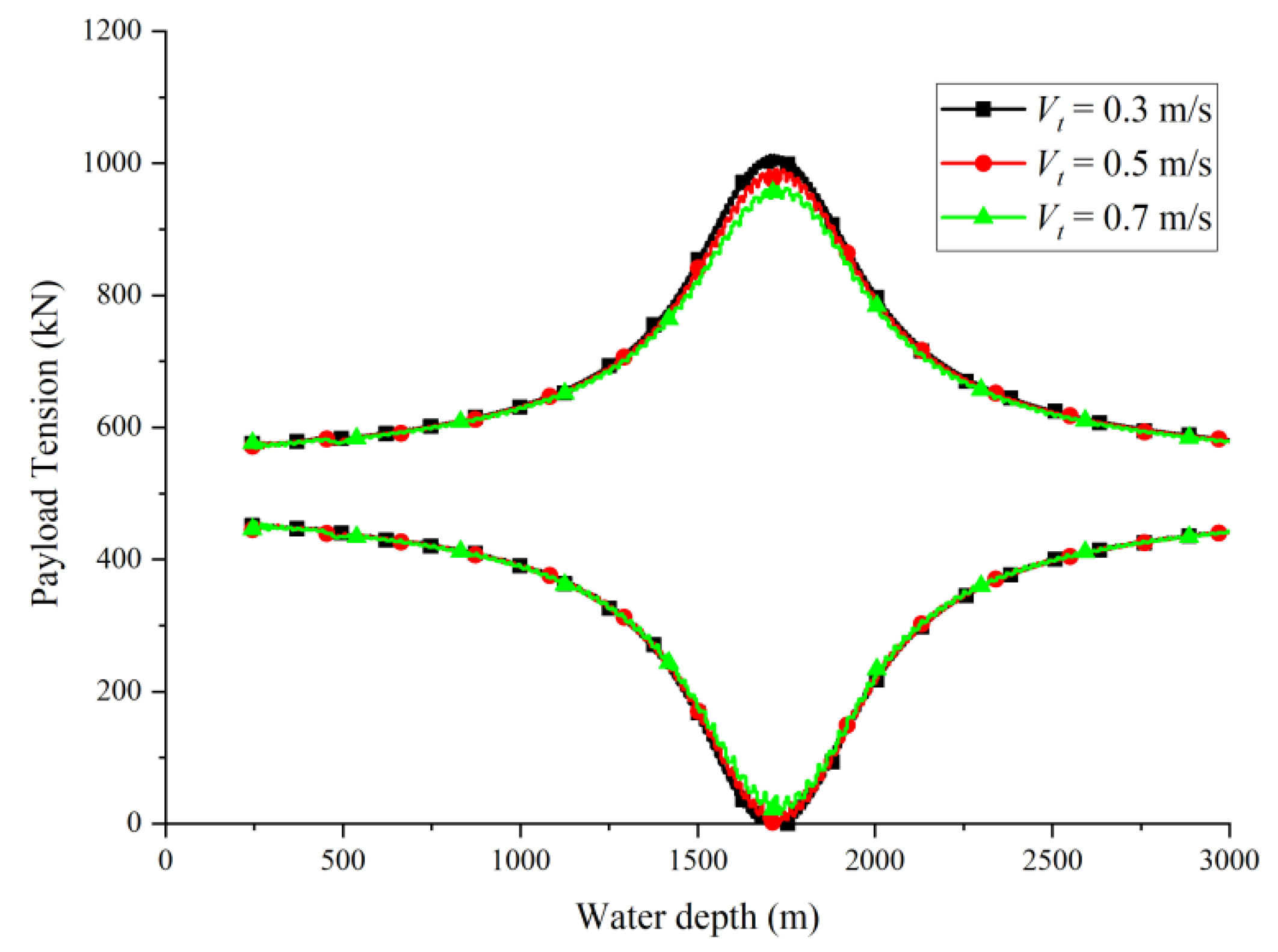
3.2. Effect of Lowering Velocity
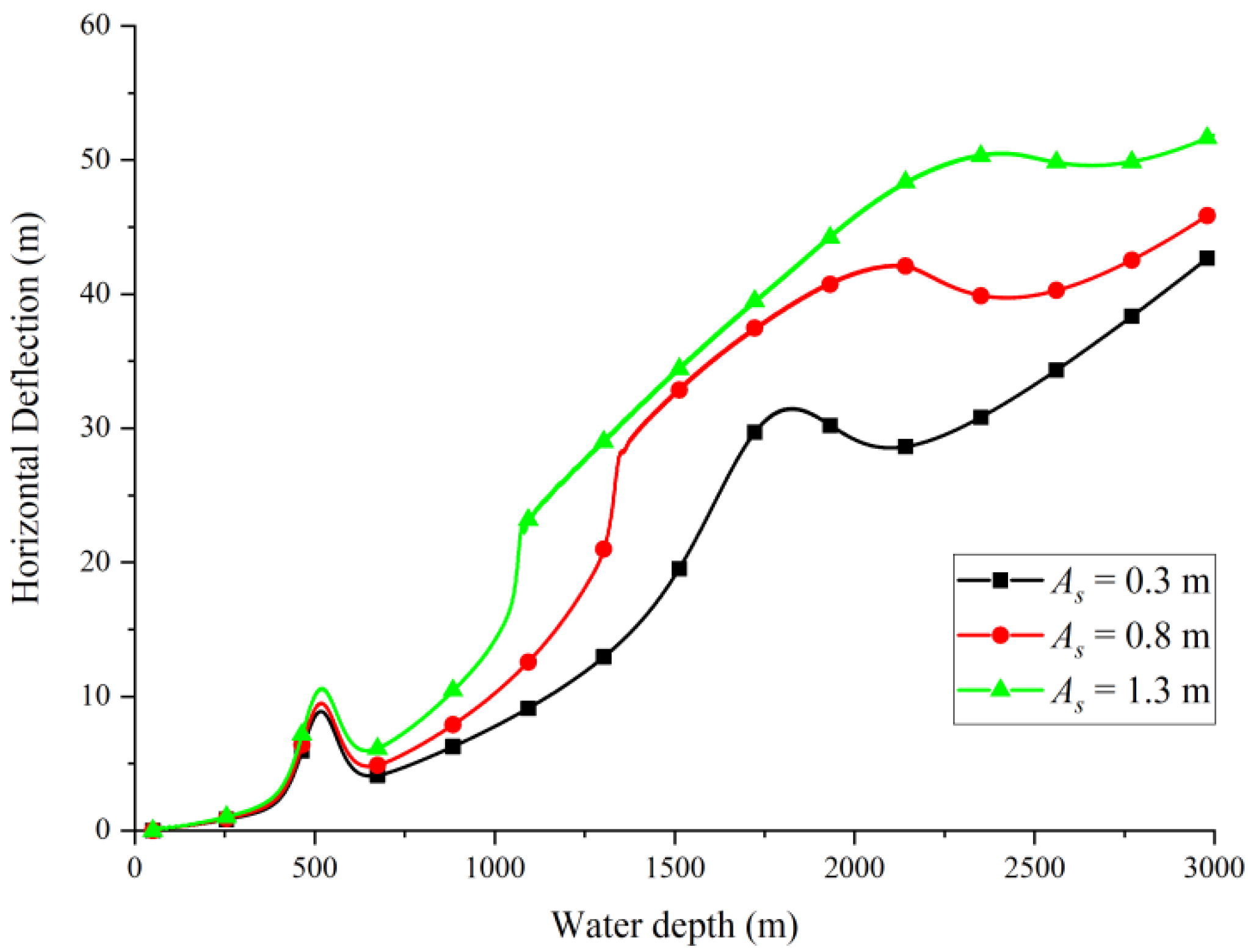
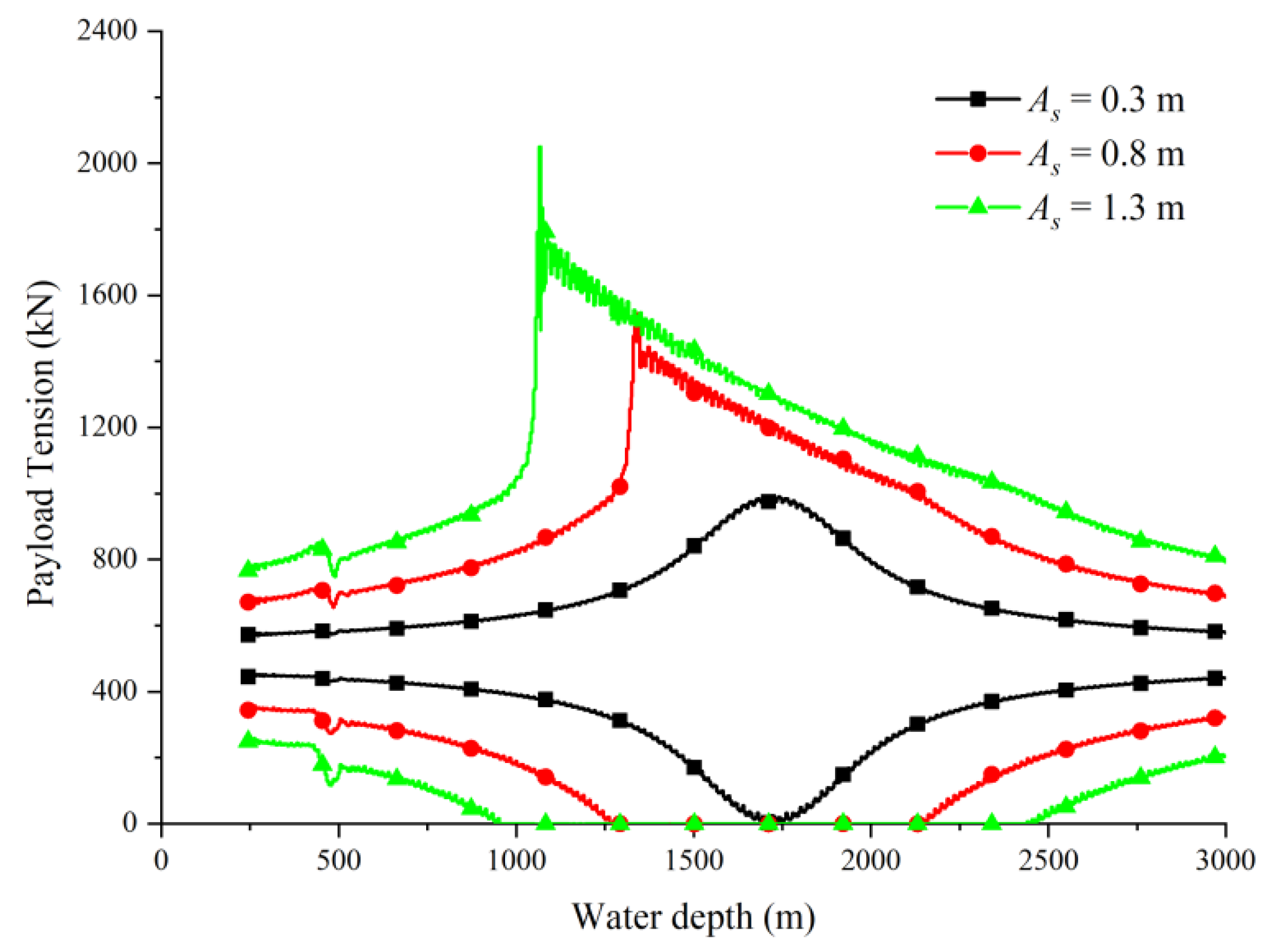
3.3. Effect of Top Heave
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| (, ) | Horizontal and vertical coordinates in 2D plane | m |
| Arc length along the cable | m | |
| Nodal displacement vector of lumped-mass model | m | |
| Number of active segments in the cable | – | |
| Suspended cable length | m | |
| Element (segment) length | m | |
| Linear mass density of cable | kg/m | |
| Dry mass of the payload | kg | |
| Added mass of the payload | kg | |
| Axial stiffness of cable | N | |
| Axial damping coefficient of cable | N·s/m | |
| Tangential unit vector of cable segment | – | |
| Normal unit vector of cable segment | – | |
| Cable tension | N | |
| Gravitational acceleration | m/s2 | |
| Drag coefficient on the cable | – | |
| Drag coefficient on the payload | m | |
| Seawater density | kg/m3 | |
| Horizontal water particle velocity | m/s | |
| Vertical water particle velocity | m/s | |
| Relative fluid velocity (structure vs. current) | m/s | |
| ISW interface displacement | m | |
| Vertical modal function of ISW | – | |
| Linear long-wave phase speed | m/s | |
| Modal-to-velocity scaling factor | – | |
| Dispersion coefficient in eKdV | – | |
| ISW half-width | m | |
| Peak ISW horizontal velocity | m/s | |
| Amplitude of surface heave | m | |
| Period of surface heave | s | |
| Lowering (payout) speed of cable | m/s | |
| Pycnocline thickness | m | |
| Total water depth | m |
References
- de Andrade, E.M.; de Oliveira Costa, D.; Fernandes, A.C.; Sales Junior, J.S. A Review on the Modeling of Subsea Lifting Operations. Ocean Eng. 2023, 275, 113293. [Google Scholar] [CrossRef]
- Tommasini, R.B.; Pavanello, R.; de Oliveira Carvalho, L. Prediction of Design Loads for Deep Water Subsea Lifting Operations Based on Non-Stationary Time Response. Mar. Struct. 2020, 74, 102818. [Google Scholar] [CrossRef]
- Li, L.; Parra, C.; Zhu, X.; Ong, M.C. Splash Zone Lowering Analysis of a Large Subsea Spool Piece. Mar. Struct. 2020, 70, 102664. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Yang, Z.; Zhao, X.; Yin, J.; Hu, Y. Dynamic Analysis of a Subsea Suspended Manifold Going through Splash-Zone During Installation. China Ocean Eng. 2022, 36, 553–564. [Google Scholar] [CrossRef]
- Amer, A.M.; Li, L.; Zhu, X. Dynamic Analysis of Splash-Zone Crossing Operation for a Subsea Template. Sust. Mar. Struct. 2022, 4, 18–39. [Google Scholar] [CrossRef]
- Zan, Y.; Guo, R.; Xue, Y.; Bai, X.; Liu, P.; Huang, F. Experimental and Numerical Investigations of Regular Head Wave Effects on Cable Tension of a Subsea Module during Lowering Operations. Ocean Eng. 2021, 239, 109822. [Google Scholar] [CrossRef]
- Zan, Y.; Guo, R.; Li, F.; Liu, P.; Huang, F.; Tian, L. Splash-Zone Dynamic Analysis of a Suspended Semi-Submerged Subsea Module for Irregular Waves. China Ocean Eng. 2023, 37, 258–271. [Google Scholar] [CrossRef]
- Guo, R.; Zan, Y.; Han, D.; Wang, Y.; Yuan, L.; Qi, B. Irregular-Wave Impact on Lowering of a Subsea Module with Large Cavity Shells. Ocean Eng. 2023, 271, 113743. [Google Scholar] [CrossRef]
- Tommasini, R.B.; Hill, T.L.; Macdonald, J.H.G.; Pavanello, R.; de Oliveira Carvalho, L. Nonlinear Dynamics of Deep Water Subsea Lifting Operations Considering KC-Dependent Hydrodynamic Coefficients. Ocean Eng. 2021, 233, 109172. [Google Scholar] [CrossRef]
- Gao, P.; Yan, K.; Ni, M.; Fu, X.; Liu, Z. A Dynamic Model for Continuous Lowering Analysis of Deep-Sea Equipment, Based on the Lumped-Mass Method. Appl. Sci. 2020, 10, 3177. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhu, K.; Jiang, H. Dynamic Analysis of Towed Cable with Variable Length during Turning Maneuvers. Sci. Rep. 2023, 13, 3525. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, G.; Lian, L. Numerical Model of Towed Cable-Body System Validation from Sea-Trial Data. Ocean Eng. 2021, 226, 108859. [Google Scholar] [CrossRef]
- Liu, Q.; Bao, J.; Shao, Y.; Zheng, L.; Xu, H. Dynamic Modeling and Underwater Configuration Analysis of fiber optic cable for UUV-launched UAV. Ocean Eng. 2024, 303, 117774. [Google Scholar] [CrossRef]
- Yang, S.; Ren, H.; Zhu, X. Dynamic Modeling of Cable Deployment/Retrieval Based on ALE-ANCF and adaptive step-size integrator. Ocean Eng. 2024, 309, 118517. [Google Scholar] [CrossRef]
- Kim, D.; Ku, N. Heave Compensation Dynamics for Offshore Drilling Operation. J. Mar. Sci. Eng. 2021, 9, 965. [Google Scholar] [CrossRef]
- Xie, T.; Huang, L.; Guo, Y.; Ou, Y. Modeling and Simulation Analysis of Active Heave Compensation Control System for Electric-Driven Marine Winch under Excitation of Irregular Waves. Meas. Control 2023, 56, 1004–1015. [Google Scholar] [CrossRef]
- Chen, S.; Xie, P.; Liao, J.; Huang, Z. Model Experimental Studies on Active Heave Compensation Control Strategy for Electric-Driven Offshore Cranes. Ocean Eng. 2024, 311, 118987. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B.; et al. The Formation and Fate of Internal Waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An Extreme Internal Solitary Wave Event Observed in the Northern South China Sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, Q.; Xiong, X.; Yuan, Y.; Xie, H.; Guo, Y.; Yu, L.; Yun, S. Dynamic and Statistical Features of Internal Solitary Waves on the Continental Slope in the Northern South China Sea Derived from Mooring Observations. J. Geophys. Res. Ocean. 2019, 124, 4078–4097. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Xu, J.; Xie, J.; Chen, Z.; He, Y.; Cai, S. An Internal Solitary Wave Forecasting Model in the Northern South China Sea (ISWFM-NSCS). Geosci. Model Dev. 2023, 16, 2851–2872. [Google Scholar] [CrossRef]
- Cui, J.; Dong, S.; Wang, Z.; Han, X.; Yu, M. Experimental Research on Internal Solitary Waves Interacting with Moored Floating Structures. Mar. Struct. 2019, 67, 102641. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, Y.; Li, Z.; Huang, Z.; Yang, Z.; Zhang, X.; Cui, Y.; Wu, J.; Liu, X.; Yu, J. The Influence of Internal Solitary Wave on Semi-Submersible Platform System Including Mooring Line Failure. Ocean Eng. 2022, 258, 111604. [Google Scholar] [CrossRef]
- Ruan, W.; Chen, M.; Nie, Q.; Xu, P.; Li, J.; Wang, X. Dynamic Response of Steel Lazy Wave Riser Considering the Excitation of Internal Solitary Wave and Ocean Currents. Ocean Eng. 2024, 294, 116708. [Google Scholar] [CrossRef]
- He, Z.; Wu, W.; Wang, J.; Ding, L.; Chang, Q.; Huang, Y. Investigations into Motion Responses of Suspended Submersible in Internal Solitary Wave Field. J. Mar. Sci. Eng. 2024, 12, 596. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Pelinovsky, E. Evolution and Statistical Analysis of Internal Random Wave Fields within the Benjamin–Ono Equation. J. Mar. Sci. Eng. 2023, 11, 1853. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Ostrovsky, L. Effects of rotation and topography on internal solitary waves governed by the rotating Gardner equation, Nonlin. Process. Geophys. 2022, 29, 207–218. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Poloukhina, O. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface, Nonlin. Process. Geophys. 2002, 9, 221–235. [Google Scholar] [CrossRef]
- Apel, J.R. A new analytical model for internal solitons in the ocean. J. Phys. Oceanogr. 2003, 33, 2247–2269. [Google Scholar] [CrossRef]
- Vlasenko, V.; Brandt, P.; Rubino, A. Structure of large-amplitude internal solitary waves. J. Phys. Oceanogr. 2000, 30, 2172–2185. [Google Scholar] [CrossRef]
- Grue, J. Generation, Propagation, and Breaking of Internal Solitary Waves. Chaos 2005, 15, 037110. [Google Scholar] [CrossRef] [PubMed]
- Flamarion, M.V.; Pelinovsky, E. Solitary Wave Interactions with an External Periodic Force: The Extended Korteweg-de Vries Framework. Mathematics 2022, 10, 4538. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| Cable | 24.6 kg/m | |
| 4098 mm2 | ||
| 325 MN | ||
| 72.23 mm | ||
| 0.7 | ||
| 0.1 | ||
| Equipment | 60 t | |
| 7.63 m3 | ||
| 56.95 m2 | ||
| 56.95 m2 | ||
| 300 ton | ||
| 0.1 | ||
| Parameter | Value |
|---|---|
| Peak ISW horizontal velocity, | 0.5, 1.0, 1.5 m/s |
| Interface thickness, | 40 m |
| Wave speed, | 1.5 m/s |
| Pycnocline depth, | −150 m |
| Influenced depth in the lower layer, | 300 m |
| Full Width at Half Maximum, | 600 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, J.; Chen, G.; He, M.; Gao, P. Investigation of the Internal Solitary Wave Influence on Subsea Equipment Lowering with a Continuous Lowering Analysis Model. J. Mar. Sci. Eng. 2025, 13, 2177. https://doi.org/10.3390/jmse13112177
Li M, Zhang J, Chen G, He M, Gao P. Investigation of the Internal Solitary Wave Influence on Subsea Equipment Lowering with a Continuous Lowering Analysis Model. Journal of Marine Science and Engineering. 2025; 13(11):2177. https://doi.org/10.3390/jmse13112177
Chicago/Turabian StyleLi, Mingjie, Junliang Zhang, Guosong Chen, Mengjie He, and Pan Gao. 2025. "Investigation of the Internal Solitary Wave Influence on Subsea Equipment Lowering with a Continuous Lowering Analysis Model" Journal of Marine Science and Engineering 13, no. 11: 2177. https://doi.org/10.3390/jmse13112177
APA StyleLi, M., Zhang, J., Chen, G., He, M., & Gao, P. (2025). Investigation of the Internal Solitary Wave Influence on Subsea Equipment Lowering with a Continuous Lowering Analysis Model. Journal of Marine Science and Engineering, 13(11), 2177. https://doi.org/10.3390/jmse13112177






