Comparative Analysis of Design Standards for Floating Offshore Wind Turbine Mooring Systems: A Focus on Line Tension Safety Factors

Abstract

The present study aims to conduct a comprehensive comparative analysis of international standards (DNV, ABS, BV, etc.) that regulate the design of mooring systems for floating offshore wind turbines. The comparative analysis focuses on the safety factors applied to the line tension of mooring systems. Firstly, an extensive literature review of the most-used floating platforms in the offshore wind industry and their corresponding mooring configurations is presented. Afterwards, a case study is presented using the VolturnUS floating substructure as a reference for analyzing the coupled dynamic response of mooring analysis through OrcaFlex 11.4, where the numerical model used for the coupled dynamic response of moorings is validated by benchmarking against the OC3 Hywind platform model. Within the scope of the comparative analysis, all-chain and semi-taut hybrid systems under various operational and survival load conditions are considered. The results demonstrate the similarities and discrepancies in line tension utilization among the standards, highlighting the comparative conservatism in different environmental conditions. Furthermore, the study underscores the need for tailored safety factors in mooring designs, given the variability in assessment methods across design guidelines, thereby making the design more flexible and encouraging innovative mooring system solutions.

1. Introduction

In recent decades, the energy demand of consumers has continuously increased; for instance, the total global primary energy consumption was 361 TWh in 1990, 572 TWh in 2000, 1174 TWh in 2010, and 2414 TWh in 2022 [1]. Simultaneously, renewable energy technologies have been adopted quite rapidly in the energy sector in order to reduce environmental impacts caused by the traditional oil and gas industry (i.e., climate change and air pollution) and meet the demand for clean and sustainable energy [2].

In this regard, the European Union (EU) has expressed its ambition of achieving 42.5% to 45.0% renewable energy in its new binding target by 2030; the United Kingdom has committed to 60% renewables by 2030 and China has established a target of 28% non-fossil energy by 2030 [3]. Many other nations, such as the USA and India, have also set their green energy targets [4,5]. There are many forms of renewable energy, including solar, wind, geothermal, hydropower, bioenergy, and ocean energy. Offshore wind energy, in particular, plays an essential role in the production of renewable energy; for instance, global offshore wind energy devices produced 5.3 GW in 2012, 14.3 GW in 2016, 28.3 GW in 2019, and 63.2 GW in 2022 [6].

Along with the rapid growth of offshore wind turbine (OWT) installations, there is a significant interest in the floating offshore wind turbine (FOWT) as a sustainable energy solution designed to harvest more stable and powerful wind energy at deeper waters and further from shore [7]. The mooring systems of FOWTs ensure the stability and safety of FOWTs, especially in challenging marine environments; thus, the robust and reliable design of mooring systems is of the utmost importance [8,9]. However, one of the key issues is the lack of standardized criteria for mooring system design, particularly concerning line tension safety factors. This discrepancy poses significant challenges, as different international guidelines, including those from DNV (Det Norske Veritas), ABS (American Bureau of Shipping), and BV (Bureau Veritas), offer varying prescriptions for these safety factors. Such variations can lead to inconsistencies in design practices and the operational reliability of FOWTs.

Furthermore, the diverse environmental conditions and the unique dynamics of floating platforms further complicate the design of a one-size-fits-all mooring system. Therefore, a comprehensive comparative analysis involving various environmental conditions and mooring configurations is of timely relevance and relevant as it bridges the gaps in standardization. Moreover, the present study’s motivation goes beyond an academic pursuit, as there is a practical necessity to advance the field of offshore wind energy. Various regulatory bodies have simultaneously developed codes and standards to regulate the mooring system design.

In light of the motivation discussed above, the present work aims to contribute to the field of FOWT mooring systems by providing a comprehensive comparative analysis of line-tension safety factors across various international standards through an extensive literature review, methodical dynamic mooring analysis, and case studies, particularly for the VolturnUS platform. The study aims to highlight the variations and similarities in safety factor prescriptions of the international standards. By doing so, it not only bridges the gap in understanding different mooring guidelines but also offers valuable insights for optimizing mooring system design and enhancing safety in OWT deployments.

The present study is structured into distinct sections, beginning with an extensive literature review of floating platforms of OWT and corresponding mooring configurations. This is followed by a detailed methodology section that delineates the performance of mooring systems based on coupled dynamic response analysis. Afterwards, a comprehensive case study of the VolturnUS platform and a meticulous analysis incorporating both validation and additional case studies are presented. The following section offers a thorough discussion of the findings, drawing critical insights and implications. Finally, a summary of the key outcomes and their relevance to the field concludes the study.

2. Literature Review

There are three common types of floating platforms used to support offshore wind turbines: Spar, Semisubmersible, and Tensioned Leg Platform (TLP) [10,11]. Spar tends to have a very deep draft, with ballast water ensuring a lower center of gravity than the center of buoyancy, leading to great stability, whilst the downside is that the ultra-deep draft means they can only be deployed in sufficiently deep water. Semisubmersibles are widely used in both renewables and the oil and gas (O&G) industry; the towage and installation process has been well established and optimized [12]. Semisubmersibles can be deployed across a wide range of water depths. They are particularly more suitable than spars or TLPs when the wind farm is close to shore and the water depth is shallow [13].

TLP has multiple vertical tendons (tethers) connected to the anchors on the seabed, which means that the footprint of the installation is minimized compared to spars or semisubmersibles that need larger mooring ranges [14]. TLPs can also offer excellent heave motion control due to their tendons. However, the installation, maintenance, repair, and decommission process can be more cumbersome than for the other two types of FOWT platforms [15]. Among these floater types, semi-submersibles are often used in both the O&G and renewable energy sectors due to their flexibility during installation and cost-effectiveness.

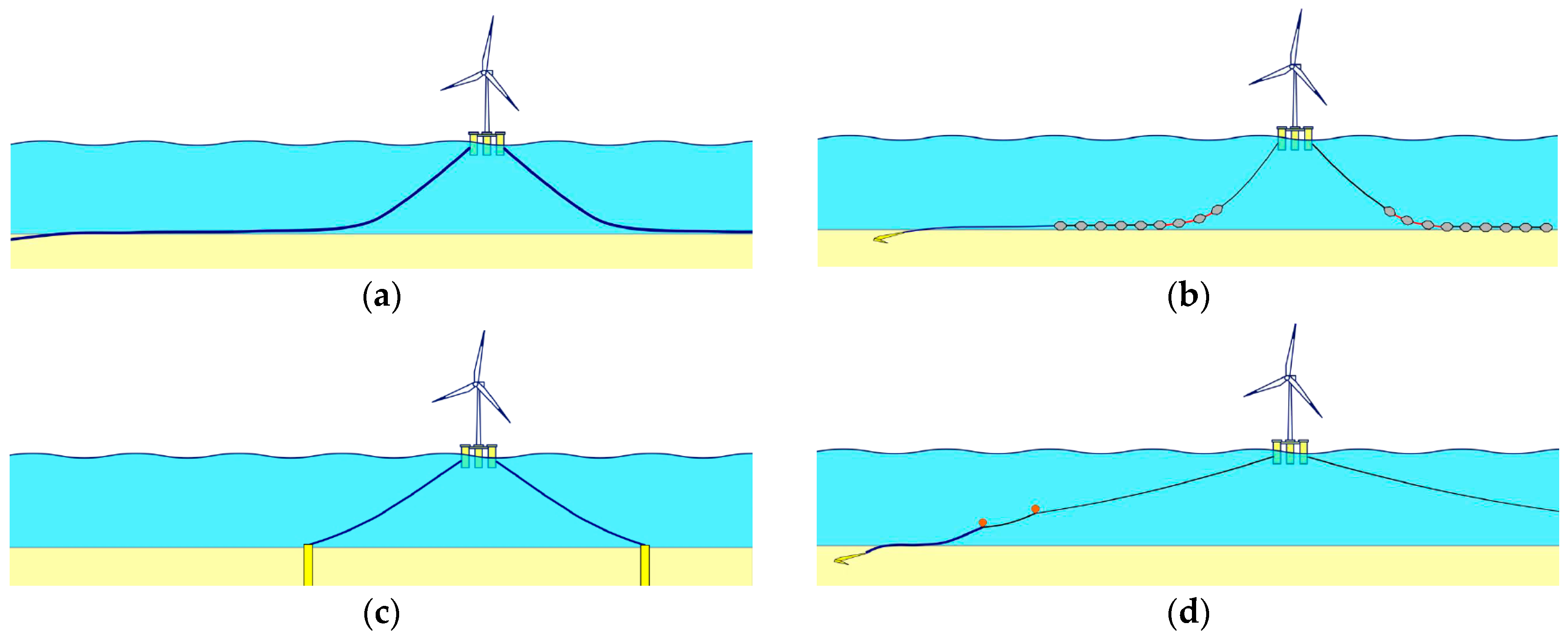
A series of the most typical mooring configurations for FOWT semi-submersibles is shown in Figure 1, and they can be summarized as follows:

• A conventional catenary mooring spread has all mooring lines made of a single component on each line; for instance, an all-chain system. It is easy and quick to install, with a relatively large footprint. It typically utilizes a drag embedment anchor at the end of the mooring line. The mooring restoring force (mooring stiffness) is ensured by the weight of the suspended chain [16].
• The multi-catenary spread is a modified solution to the conventional catenary, with clump weights attached at certain sections on the mooring line. Due to the increased line weight, the mooring system stiffness is improved, leading to an enhanced vessel offset/excursion [17].
• Taut leg mooring is unsuitable for use with drag embedment anchors due to the undesirable vertical loading characteristics. A pile anchor or a vertical loading anchor can be deployed [18]. The anchor range is more compact than the conventional catenary mooring since it does not require a grounded chain length. It has minimal contact with the seabed, which is particularly beneficial when the subsea layout is congested.
• Semi-taut mooring spread can be considered as a combination of a taut leg and a conventional catenary [19]. A synthetic fiber rope may be used in the middle section of the mooring line, with optional buoyancy at both ends. Such a configuration provides good vertical clearance, energy absorption (leading to an improved factor of safety), and the ability to deploy drag-embedment anchors. The downside is that due to the relatively low axial stiffness of the fiber rope, a larger offset/excursion may be expected.

In addition to the above, a hybrid taut leg mooring system can be suggested, involving segments of clump weights at the anchor side and/or sub-surface buoys near the water surface, with the aim of reducing the vessel excursion, anchor range, and potential anchor uplifts [20]. In this regard, the test presented in [20] has shown improvement in vessel offset without significantly increasing tension if a sub-surface buoy is deployed.

Figure 1. Mooring types (adapted from [21]): (a) conventional catenary, (b) multi-catenary, (c) taut leg, and (d) semi-taut.

Figure 1. Mooring types (adapted from [21]): (a) conventional catenary, (b) multi-catenary, (c) taut leg, and (d) semi-taut.

There are usually two approaches to conducting a dynamic response analysis of moorings: time-domain analysis [22] and frequency-domain analysis [23]. The two approaches each have their own merits; frequency-domain analysis is often used when cost-efficient and quick computation is required, while time-domain analysis offers a more accurate method due to its ability to accurately solve non-linear problems, such as load coupling, the vessel’s low-frequency motions, and large deformation of the mooring lines [24,25].

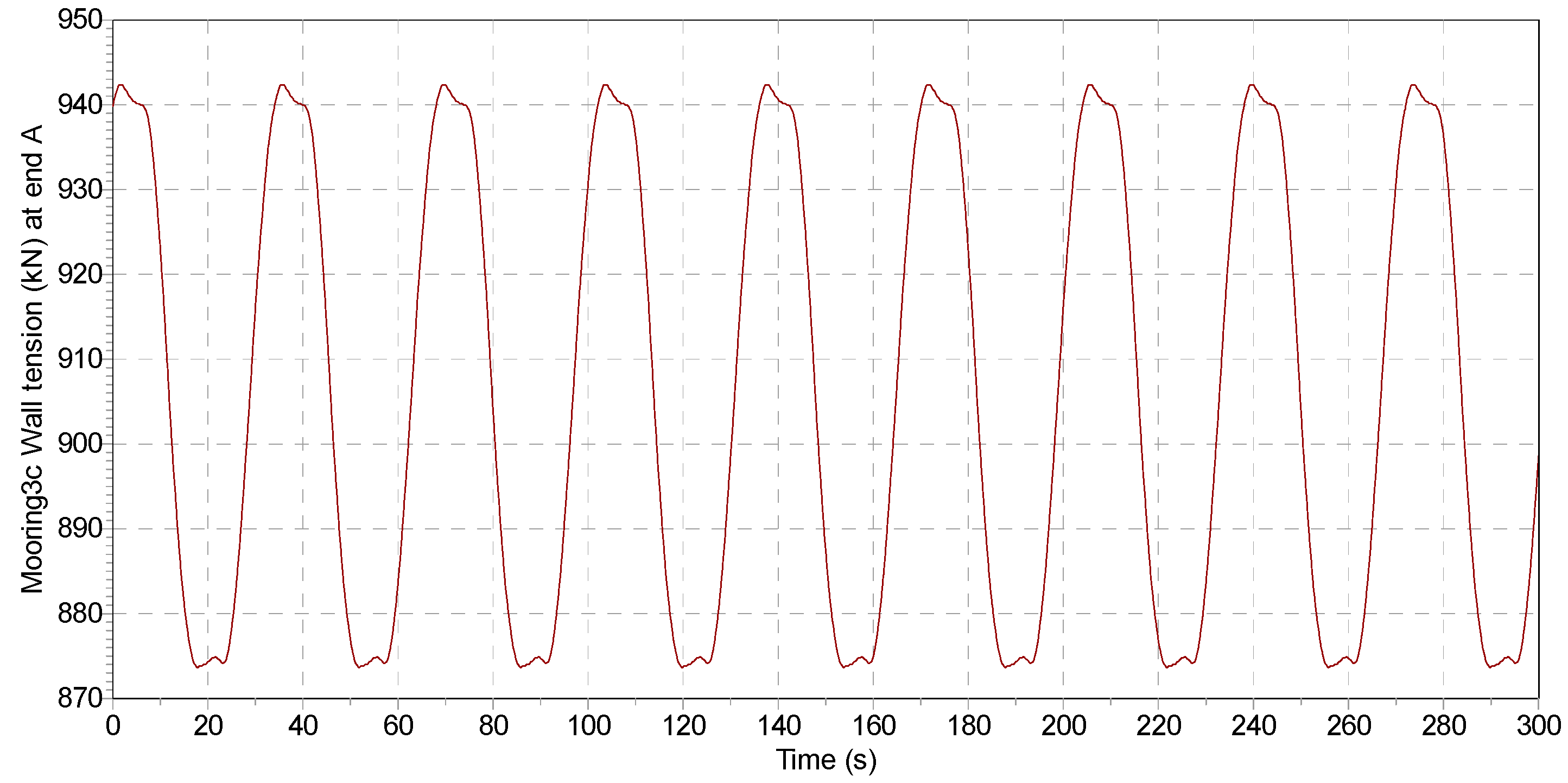
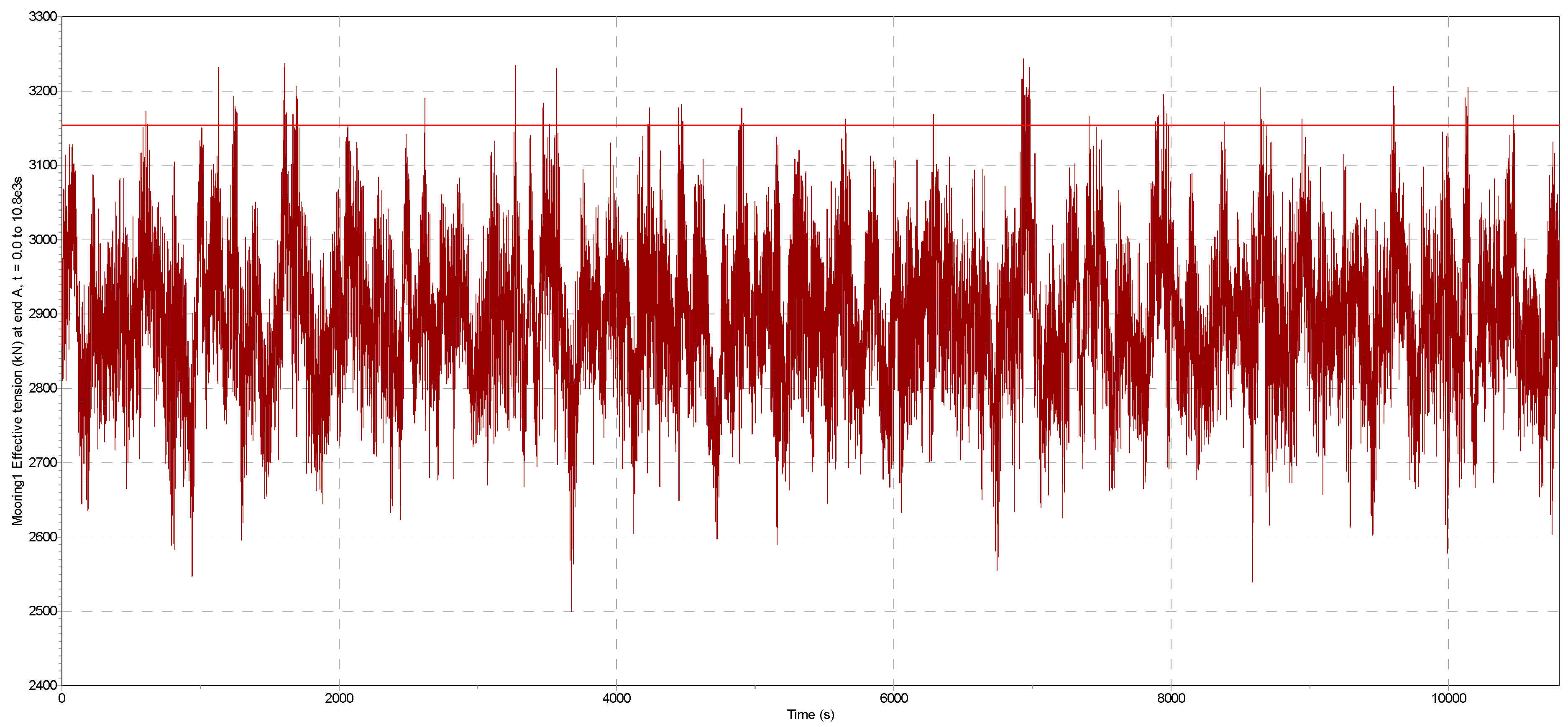
For a time-domain dynamic mooring analysis, it is critical to properly extract the most probable maximum (MPM) tensions or the extreme value (EV) tensions [26,27]. Some software packages have EV analysis features already built in, such as OrcaFlex [28,29,30]. It has three built-in methods for obtaining MPM from a line-tension time-history output: the Rayleigh distribution method, the Weibull distribution method, and the generalized Pareto distribution (GPD) method. 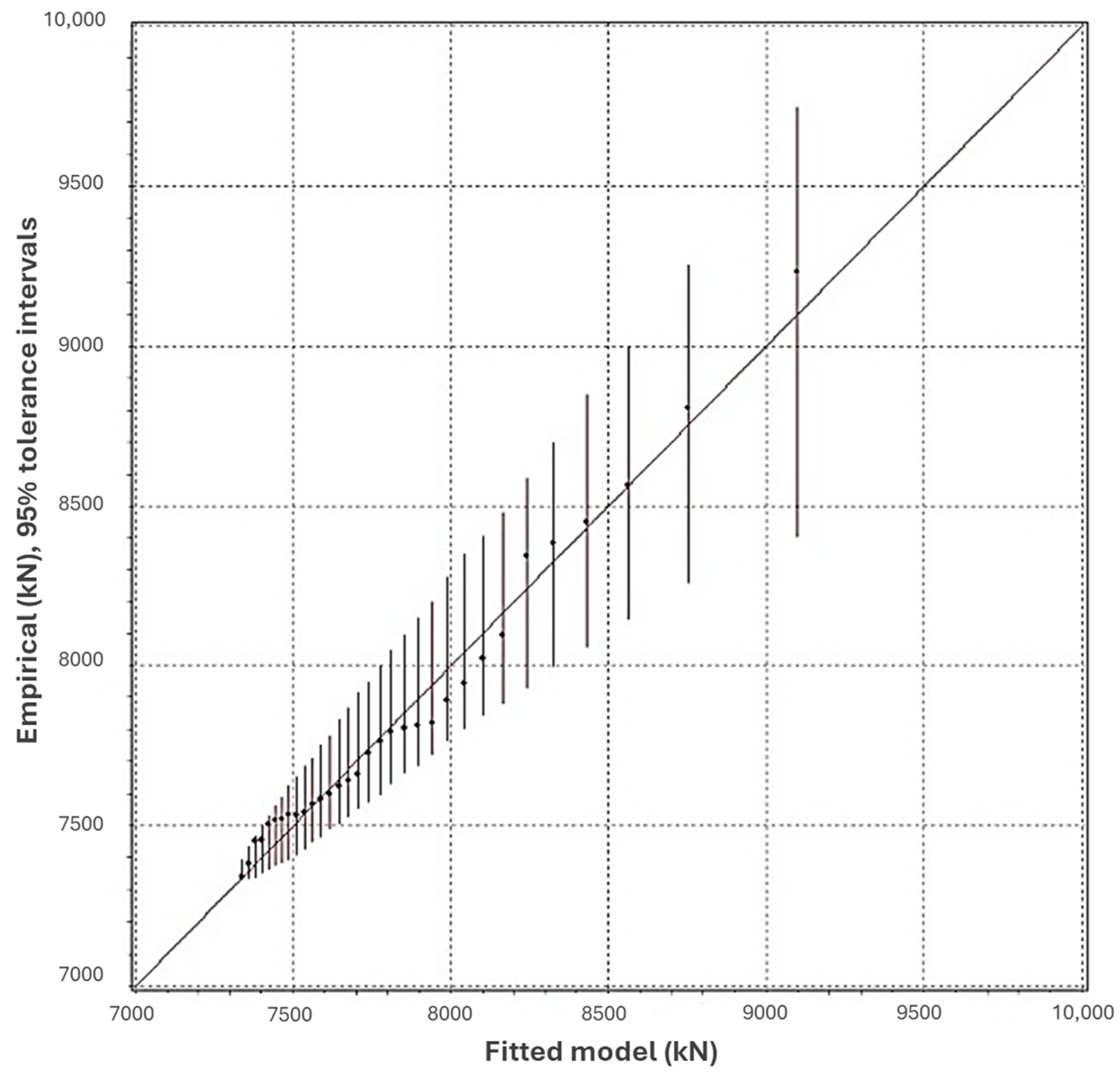The Rayleigh distribution shall be carefully used when extracting the line tensions, since the peak responses must follow a Gaussian process [31]. The Weibull distribution method is a general-purpose statistical model, whereas the GPD is mainly used in EV extractions. In practice, the GPD-fitted model in OrcaFlex appears to be more robust than the Weibull-fitted model, which occasionally results in convergence issues.

In the offshore industry, from a practical point of view, the guideline of the American Petroleum Institute, as API RP 2SK—Design and Analysis of Station Keeping Systems for Floating Structures [32]—summarizes three methods of determining the extreme response from a stochastic time history, as follows:

• Probability density function (PDF) of a selected distribution model: API points out that this approach requires a considerable amount of simulation realizations, from which the extreme responses are to be extracted and fitted into a statistical distribution model, then the most probable maximum (MPM) is the maximum PDF of such a fitted model. To ensure the validity of the model, many realizations are required, which is time-consuming and not always practical [33,34].
• Average of extreme responses: There are five to ten realizations often required for this approach. The extreme responses are then extracted from each realization, and the MPM is then taken from the average of such extreme responses. This approach is commonly used in the O&G industry, is easy to apply, and is considered acceptable by the class [35].
• Fitted probability distribution model: In this method, a probability distribution model with peak probabilities, such as Rayleigh, Normal, Gumbel, Weibull, and Exponential, is chosen. The model parameters are then determined using available response time histories. Subsequently, the anticipated extreme response is calculated based on the adjusted model. Although this method might require fewer iterations than Method 2, in practice, the fitted parametric model often fails to accurately capture the true upper-tail behavior, leading to biased predictions of extreme responses. To enhance accuracy, some analysts employ specialized techniques, such as fitting the upper tail or averaging predictions from multiple iterations [36,37]. Such a description might appear somewhat vague, yet acceptable if the time domain analysis is conducted with one realization only, from which the MPM is to be determined using a statistical model such as Rayleigh, Weibull, and Exponential distributions. However, a single realization may lead to biased results, and therefore, multiple realizations are preferable with MPMs that are then fitted into, for example, a Gumbel distribution to eliminate the bias. Alternatively, take the average of the MPMs to improve accuracy.

There have been ongoing discussions about obtaining MPM/EV within the research community, and numerous publications have addressed this topic from various perspectives. The uncertainty in extreme mooring loads due to various statistical models has been assessed by Zhao and Dong [38], including average conditional exceedance rate, global maxima, peak-over-threshold methods with Gumbel distribution, generalized extreme value distribution, generalized Pareto distribution, and three-parameter Weibull distribution. The work concluded that the uncertainties/deviations introduced by different statistical models could be significant and recommended calibration for the line safety factors. A novel methodology was proposed in [39], attempting to give a robust distribution of extremes using the peaks over threshold (POT) method.

A detailed discussion was given in [40] to predict long-term mooring tensions with multiple statistical models, with the potential to reduce the number of realizations required in a time domain mooring analysis. The study demonstrated several common definitions of peaks in response time history and validated a two-parameter Weibull distribution for upper-tail behavior in mooring tension, which is appropriate for representing long-term structural response under extreme conditions [41]. In addition, the study also covered some approaches to conduct the estimation of the parameters for the Weibull distribution.

Furthermore, research has been undertaken to demonstrate the equations to calculate the line catenary based on the water depth and top tension. The complexity of solving the equation is increased when there are multiple components involved in the line, i.e., the combination of chain, wire, fiber rope [42,43], buoyancy module, and clump weight. A numerical mooring model was developed for an offshore floating platform [44] based on the vector form of the intrinsic finite elements method. Such a method of catenary calculation was validated against multiple validated codes and shows good accuracy.

A study on the mooring line dynamics response was conducted in [45], where research catenary equations were given for single and multi-component mooring lines/cables, with seabed slope considered. A validation was performed against the model test and OrcaFlex results, which showed agreement.

The vessel position is determined mainly by the environmental forces and the mooring system stiffness matrix. Usually, iterative simulations were undertaken to find the equilibrium vessel position and mooring stiffness with environmental forces as variables. For the mooring of an offshore floating structure, the literature is available [46,47] to give solutions to the vessel position and environmental loads.

The basic principles of conducting a time-domain mooring analysis are briefly discussed here. However, many other factors are involved in the calculation process. For instance, low-frequency and wave frequency motions, added mass and damping matrices, seabed frictions and geometries, and the riser system are not covered in this study.

3. Methodology

3.1. Standards’ Provisions for Mooring Line Design

Several class societies, such as DNV, BV, ABS, etc., have released their mooring guidelines in the offshore wind industry in recent years. It could be challenging for floating offshore wind farm stakeholders to decide which code to follow, as most FOWT platforms are unclassed, and major guidelines have recently been developed with similarities in certain aspects. Therefore, comparing the major mooring codes and standards in the FOWT industry is highly informative. However, there have been few recent benchmarking studies of mooring guidelines in the floating offshore wind turbine structure industry in the research community.

A review of mooring design for floating wave energy converters was conducted, where a brief summary of design criteria from major guidelines and standards from different classes [48], such as ISO (ISO 19901-7, ISO 14909, ISO 18692), IEC (IEC TS 62600-10), BV (NR 493, NI 572), API (API RP 2SK, API RP 2SM, API SPEC 9A), and DNV (DNV OS E301-5), was provided. The summarized codes and standards are mostly applicable to offshore wind turbines as well. For a typical mooring design, the process generally follows the flow chart, as shown in Figure 2.

General mooring design criteria are listed below, among which, the line tension criteria are usually the most critical [32,49,50]:

• Line tension safety factors;
• Vessel excursion due to the limitations of drilling riser, flexible riser/cable, gangway stroke, vessel to adjacent structures, etc.;
• Vertical clearance to subsea assets in slack line scenario, horizontal clearance between touchdown point to subsea assets or cable hog-bend to vessel keel/sag-bend to seabed;
• Mooring system design life (mooring/structural fatigue criterion).

A detailed summary of the mooring design and analysis criteria is contained in [51] as well. The objective of this study is to compare and benchmark the mooring line tension criterion among DNV, BV, and ABS guidelines.

3.2. Mooring Model Setup

This present study aims to provide insight into the common FOWT platform mooring configurations, including redundancy options (with or without redundancy), and a comparison between all-chain systems and semi-taut hybrid systems, as discussed in Section 2 of this current study. The assessment is performed for the VolturnUS platform, and the Multiphysics model is built in OrcaFlex (see Figure 3). The present study primarily focuses on the comparison of line-tension safety factors, i.e., other criteria (e.g., offsets and clearances) that are not considered in the comparative analysis.

The mooring analysis is conducted using the OrcaFlex software package. The VolturnUS offshore wind turbine platform has been widely used within the research community for case studies and is selected for this current mooring tension code comparison study [52,53,54].

The basic OrcaFlex model of VolturnUS was produced by Orcina and made publicly available on their website. In this model, a 15 MW wind turbine is installed on the VolturnUS platform, from which some adjustments were then made [55]:

• There are four models developed from the base model: All-chain system with redundancy, all-chain system without redundancy, semi-taut hybrid system with redundancy, and semi-taut hybrid system without redundancy.
• The mooring line length in the base model is 850 m; after a few preliminary analysis iterations with typical extreme weather in the North Sea, the mooring line length of 850 m is considered insufficient. Therefore, the line length in the analysis model is increased to 1050 m for the all-chain system.
• The wind and current coefficients and load on the turbine are included in addition to the base model.

3.3. Load Cases

Each of the four analysis models has operational and survival conditions with down-line and between-line weather directions. In addition, for the hybrid systems, both new and old ropes have been considered due to their long-term elongation behavior. In total, 24 load cases are considered as seen in

Table 1. VolturnUS mooring analysis load cases.

Case ID	Load Condition	Line Make-Up	Redundancy	Weather Direction	Note
LC01	Operational	All chain	No	Down Line
LC02	Operational	All chain	No	Between Line
LC03	Operational	All chain	Yes	Down Line
LC04	Operational	All chain	Yes	Between Line
LC05	Operational	400 m Fiber	No	Down Line	Old rope
LC06	Operational	400 m Fiber	No	Between Line	Old rope
LC07	Operational	400 m Fiber	No	Down Line	New rope
LC08	Operational	400 m Fiber	No	Between Line	New rope
LC09	Operational	400 m Fiber	Yes	Down Line	Old rope
LC10	Operational	400 m Fiber	Yes	Between Line	Old rope
LC11	Operational	400 m Fiber	Yes	Down Line	New rope
LC12	Operational	400 m Fiber	Yes	Between Line	New rope
LC13	Survival	All chain	No	Down Line
LC14	Survival	All chain	No	Between Line
LC15	Survival	All chain	Yes	Down Line
LC16	Survival	All chain	Yes	Between Line
LC17	Survival	400 m Fiber	No	Down Line	Old rope
LC18	Survival	400 m Fiber	No	Between Line	Old rope
LC19	Survival	400 m Fiber	No	Down Line	new rope
LC20	Survival	400 m Fiber	No	Between Line	new rope
LC21	Survival	400 m Fiber	Yes	Down Line	Old rope
LC22	Survival	400 m Fiber	Yes	Between Line	Old rope
LC23	Survival	400 m Fiber	Yes	Down Line	New rope
LC24	Survival	400 m Fiber	Yes	Between Line	New rope

.

3.4. Mooring Line Setup

Several preliminary iterative analyses are conducted to size the mooring gear and optimize the configuration. The mooring chain and fiber are initially sized small, and the mooring analysis is conducted to determine the line safety factor, which is then found to be insufficient, and then larger sizes are introduced. The above practice is carried out for a few iterations until a potential “workable solution” is found, as per

Table 2. All-chain line properties; mooring system with redundancy.

Parameter	Value	Unit
No. of Lines	6	-
Line Type	All Chain	-
- Chain Grade	R4 Studlink	-
- Chain Size	137	mm
- Chain MBL	1732	te
Total Line Payout	1050	m
Pretension	200	te
Drag Coefficient, Normal	2.6	-
Drag Coefficient, Axial	1.4	-
Added Mass Coefficient, Normal	1.0	-
Added Mass Coefficient, Axial	0.5	-

,

Table 3. All-chain line properties; mooring system without redundancy.

Parameter	Value	Unit
No. of Lines	3	-
Line Type	All Chain	-
- Chain Grade	R4 Studlink	-
- Chain Size	162	mm
- Chain MBL	2275	te
Total Line Payout	1050	m
Pretension	200	te
Drag Coefficient, Normal	2.6	-
Drag Coefficient, Axial	1.4	-
Added Mass Coefficient, Normal	1.0	-
Added Mass Coefficient, Axial	0.5	-

,

Table 4. Fiber line properties; mooring system with redundancy.

Parameter	Value	Unit
No. of Lines	6	-
Line Type	Hybrid	-
- Chain Grade	R4 Studlink	-
- Chain Size	137	mm
- Chain MBL	1732	te
- Fiber Type	Dyneema	-
- Fiber Size	171	mm
- Fiber MBL	2083	te
Total Line Payout	1050 (50 m top chain + 400 m Fiber Inserts + 600 m anchor chain)	m
Pretension	200	te
Drag Coefficient, Normal	2.6	-
Drag Coefficient, Axial	1.4	-
Added Mass Coefficient, Normal	1.0	-
Added Mass Coefficient, Axial	0.5	-

and

Table 5. Fiber line properties; mooring system without redundancy.

Parameter	Value	Unit
No. of Lines	3	-
Line Type	Hybrid	-
- Chain Grade	R4 Studlink	-
- Chain Size	162	mm
- Chain MBL	2275	te
- Fiber Type	Dyneema	-
- Fiber Size	187	mm
- Fiber MBL	2529	te
Total Line Payout	1050 (50 m top chain + 400 m Fiber Inserts + 600 m anchor chain)	m
Pretension	200	te
Drag Coefficient, Normal	2.6	-
Drag Coefficient, Axial	1.4	-
Added Mass Coefficient, Normal	1.0	-
Added Mass Coefficient, Axial	0.5	-

.

The pretension value is taken from “Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-MW Offshore Reference Wind Turbine Technical Report” [56]. The added mass and drag coefficient are kept at OrcaFlex default values.

There is a 15-ton buoyancy module fitted to the lower end of the fiber rope inserts to lift the lower end of the Dyneema rope so that it will not touch down when slackened by a storm. The line catenary and vertical seabed clearance is, however, not a part of the current study.

Line component axial stiffness plays an important role in mooring analysis; therefore, it is critical to apply the appropriate parameters. Normally, for chain and steel wire, the axial stiffness is considered linear within the Minimum Breaking Load (MBL). For most synthetic ropes, the axial stiffness changes over time due to creeping behavior. New rope and used rope have different load–elongation curves, as per the graph given below, based on [57]. Both new and used rope curves, as in Figure 4, are therefore included in this study.

3.5. Metocean and Site Information

The operating condition is considered the maximum production metocean criteria, whereas the survival condition is the extreme storm condition (typically a 50-year return period for FOWT platforms). The metocean data presented in

Table 6. Metocean criteria used in mooring analysis.

	Operating	Survival	Unit
Wind Speed at 10 m MSL	20.8	37.7	m/s
Wind Speed at 150 m MSL	27.4	52.8	m/s
Wind Spectrum	NPD
Wave Hs	6.64	13.5	m
Wave Tz	9.4	12.2	s
Wave Spectrum	JONSWAP
Surface Current Speed	0.60	0.67	m/s
Water Depth	200		m

is used for the mooring analysis in this study and is extracted from First Marine Solutions Ltd.’s in-house metocean database for Gryphon Field in the North Sea.

3.6. Generalized Pareto Distribution

The final line-tension results are computed using extreme value analysis. A generalized Pareto distribution (GPD) is considered suitable for extracting extreme responses for mooring line tensions in time history, along with a peak-over-threshold (POT) approach [58,59,60,61]. The GPD can be expressed as [62]

$$F\left(y\right)=\left\{\begin{array}{c}1-{\left(1+\xi \times {\displaystyle \frac{y}{\sigma }}\right)}^{-{\displaystyle \frac{1}{\xi }}}\\ 1-\exp \left(-{\displaystyle \frac{y}{\sigma }}\right)\end{array}\right.{\displaystyle \genfrac{}{}{0pt}{}{,for \xi \ne 0 where\left(1+\xi \times \frac{y}{\sigma }\right)=max\left\{1+\xi \times \frac{y}{\sigma },0\right\}}{,for \xi =0}}$$

(1)

where $\sigma$ is the scale parameter, $\xi$ is the shape parameter, and $y$ is the peak value above the threshold. The determination of the threshold depends on the applications and typically requires sophisticated techniques and an analyst with experience. A sample size that is too high above the threshold may yield invalid and meaningless extreme value results, whereas a sample size that is too small may produce a biased extreme response. A discussion was given in [63] regarding applying the POT method for the extreme response of the mooring line, in which several empirical methods for selecting a threshold were summarized.

3.7. Other Considerations

The selection of DNV, ABS, and BV standards for this comparative analysis is driven by their widespread use and recognition in the offshore engineering industry. DNV provides a set of guidelines widely adopted for floating wind turbine structures, thanks to its comprehensive risk management and probabilistic load assessment approach. ABS standards, such as the ABS Guide for Building and Classing Floating Offshore Wind Turbines, are recognized for their prescriptive approach, offering clear criteria for different mooring configurations and environmental conditions. BV standards are known for their stringent requirements for synthetic mooring lines, which are increasingly used in modern offshore wind turbine installations due to their lightweight, high-strength properties. These standards represent a broad spectrum of design philosophies, making them ideal candidates for a comparative study aimed at understanding the variances in safety factor prescriptions and their implications for mooring system reliability.

The selection of load cases is critical to the robustness of the mooring analysis. The load cases considered in this study are chosen to reflect both operational and extreme survival conditions typical of offshore wind turbine environments. For operational conditions, moderate wind speeds of up to 27.4 m/s and wave heights of 6.64 m are selected to represent the maximum production conditions [64]. In contrast, survival conditions are based on extreme storm scenarios, with wind speeds reaching 52.8 m/s and wave heights of up to 13.5 m, which correspond to a 50-year return period event [38]. These environmental conditions are selected based on regional metocean data for the North Sea, a common location for offshore wind farms, and are intended to capture the range of forces the mooring system is expected to endure during its operational life. Alternatively the Inverse First-order Reliability Method can be employed in order to estimate the 25-, 50-, and 100-year return period events, as exemplified in [65].

The OrcaFlex model used in this study incorporates several assumptions to simplify the analysis without compromising accuracy. For instance, the mooring lines are assumed to have linear elastic properties up to their MBL, which is a common simplification in mooring system analysis [51,66]. Additionally, environmental loads are modeled as steady-state inputs, ignoring transient effects such as wave slamming or vortex-induced vibrations, which are generally considered secondary effects in the context of mooring line tension analysis [67]. These assumptions are necessary to manage the computational complexity of the model, yet are acknowledged as potential sources of error. The impact of these simplifications is mitigated using conservative safety factors and validation against empirical data.

The validation of the OrcaFlex mooring model was performed by benchmarking the simulation results against published data from the OC3 Hywind platform, a well-documented floating wind turbine model [68]. The validation process involved comparing the simulated line tensions and platform motions under identical environmental conditions, showing a close correlation with reported values [69]. This validation process provides confidence in the accuracy of the model and its applicability to the VolturnUS platform studied in this paper. Any discrepancies observed are within acceptable limits and are attributed to differences in the numerical methods used by different simulation tools.

The long-term environmental effects, such as fatigue and creep, are incorporated into the analysis using a time-domain simulation approach. Fatigue life estimation is performed based on cumulative damage models, which sum the damage from cyclic loads over the mooring system’s expected lifespan [39] deterministically. For a probabilistic fatigue life analysis, the structural reliability theory for components in series is required [70,71]. Creep in synthetic ropes, particularly in Dyneema, is modeled using time-dependent material properties that reflect the non-linear stress–strain behavior observed in laboratory tests [45]. These considerations are crucial for accurately predicting the long-term performance of mooring systems, ensuring that safety factors account not only for immediate loads but also for the degradation of material properties over time.

4. Mooring Analysis Case Study—Volturnus

4.1. Methodology Validation—OC3

A methodology validation process is conducted using the OC3 Hywind platform model, and mesh details are illustrated in Figure 5 and Figure 6, respectively. Furthermore, the properties of the OC3 mooring system are presented in

Table 7. OC3 mooring system properties (reproduced from [68,69]).

Parameter	Value	Unit
Water Depth	320	m
Diameter—Platform Base	9.4	m
Diameter—Platform Top	6.5	m
Draft	120	m
Depth	130	m
Center of Mass below SWL	−89.92	m
Mass	7466.33	te
Moment of Inertia—pitch and row	2.2 × 107	te·m2
Moment of Inertia—yaw	1.64 × 105	te·m2
Anchor Range	853.87	m
Total Line Length	902.2	m
Line Axial Stiffness	384,200	kN

.

A hydrodynamic analysis has been performed using the above-shown parameters with linear damping, as presented in

Table 8. OC3 linear damping matrix (reproduced from [68]).

Surge, kN/(m/s)	Sway, kN/(m/s)	Heave, kN/(m/s)	Roll, kNm/(rad/s)	Pitch, kNm/(rad/s)	Yaw, kNm/(rad/s)
100	0	0	0	0	0
0	100	0	0	0	0
0	0	130	0	0	0
0	0	0	0	0	0
0	0	0	0	0	0
0	0	0	0	0	13,000

, and restoring the force matrix in

Table 9. OC3 restoring force matrix (reproduced from [68]).

Surge, kN/m	Sway, kN/m	Heave, kN/m	Roll, kN/rad	Pitch, kNm/(rad/s)	Yaw, kNm/(rad/s)
41.18	0	0	0	−2821	0
0	41.18	0	2821	0	0
0	0	11.94	0	0	0
0	2816	0	311,100	0	0
−2816	0	0	0	311,100	0
0	0	0	0	0	11,560

as follows [68].

The diffraction analysis is performed using Orcawave 11.4 by Orcina, Ulverston, UK. The results are then verified against FAST and WAMIT analysis outcomes [72]. It shows good agreement with the FAST and WAMIT results, as shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. There appears to be, however, a minor shift in frequency, which could be due to the variance in the mooring system stiffness across these models.

Further validation is conducted and compared with a mooring analysis of the OC3 spar by Xu and Srinil [73]. One case is analyzed where the wind and waves aligned collinearly from the between-the-line direction. A wind speed of 11.4 m/s and a regular wave height of 2.56 m with a period of 34 s are applied, and the results are shown in Figure 13.

The dynamic loads are both approximately 65 kN, which indicates that the wave loads are in good agreement with each other. In the OrcaFlex analysis, the mean line tension is found to be approximately 5% higher than the results reported by Xu and Srinil [73]. This could be because of the variance of air density used in the software program (0.00128 te/m³) considered in OrcaFlex analysis). The validation outcomes using the OC3 model show general consistency with other studies.

4.2. VolturnUS Mooring Setup

A benchmarking study has been performed to investigate the discrepancy and gap in the safety factors of the FOWT mooring system among DNV, BV, and ABS. An example of the VolturnUS platform with a 15 MW turbine has been selected for this study. The selection of the VolturnUS platform for this case study is motivated by its innovative design and its relevance to the offshore wind industry. As one of the few floating platforms that have been extensively tested in both academic and commercial settings, VolturnUS serves as a suitable model for evaluating the effectiveness of different mooring standards [56]. Also, the platform has been used in several benchmark studies, making it a well-established reference for comparing mooring system performance under various environmental conditions.

Moreover, the VolturnUS platform’s hybrid mooring system, which combines chain and synthetic rope segments, presents a unique opportunity to explore the implications of using different materials in mooring systems. This is particularly relevant given the increasing adoption of synthetic ropes in the offshore wind industry, which offers advantages in terms of weight reduction and flexibility but also presents challenges related to long-term durability and creep [45].

The VolturnUS platform model has been widely used in the research community in recent years, patented by the University of Maine, and is an offshore floating concrete hull semi-submersible, with the capability to accommodate wind turbines in water depths over 45 m. The key properties of the VolturnUS platform are listed below, in

Table 10. VolturnUS platform key properties (reproduced from [56]).

Parameter	Value	Units
Displacement	20,206	m3
Hull Steel Mass	3914	te
Draft	20	m
Freeboard	15	m
VCG from SWL	−14.94	m
VCB from SWL	−13.63	m
Roll Inertia about CoG	1.251 × 1010	Kg·m2
Pitch Inertia about CoG	1.251 × 1010	Kg·m2
Yaw Inertia about CoG	2.367 × 1010	Kg·m2

and

Table 11. Original proposed mooring setup (reproduced from [56]).

Parameter	Value	Unit
No. of Lines	3	-
Line Type	All Chain	-
-Chain Grade	R3 Studless	-
-Chain Size	185	mm
-Chain MBL	2272	te
Total Line Payout	850	m
Pretension	248	te
Drag Coefficient, Normal	2.6	-
Drag Coefficient, Axial	1.4	-
Added Mass Coefficient, Normal	1.0	-
Added Mass Coefficient, Axial	0.5	-

.

In comparison with [56], the design metocean data considered in this benchmarking study is more conservative, i.e., wind speed in this benchmarking is 52.8 m/s at hub height, whereas it is 47.5 m/s in [56]; significant wave height H_s is 13.5 m compared to 10.7 m in [56], and current speed and current load are also considered in this current study. Therefore, the anchor range has been extended by 200 m to accommodate this.

4.3. Criteria of Acceptance

The DNV definition of consequence class is as follows:

• Consequence class 1, where failure is unlikely to lead to unacceptable consequences such as loss of life, collision with an adjacent structure, and environmental impacts;
• Consequence class 2, where failure may well lead to unacceptable consequences of these types.

For floating wind turbine platforms with redundancy components, Consequence Class 1 is required, whereas for a floating wind turbine mooring system without redundancy, Consequence Class 2 shall be applied as per DNV (see

Table 12. DNV partial safety factors (adapted from [74]).

Limit State	Partial Load Factor	Consequence Class 1	Consequence Class 2
ULS	γmean	1.3	1.5
ULS	γdyn	1.75	2.2

).

The partial safety factors are applied in the following way:

$$Sc=0.95\times MBL$$

(2)

$$Sc-Tmean\times \gamma mean-Tdyn\times \gamma dyn>0$$

(3)

where MBL is the minimum breaking load, Sc is the characteristic strength, Tmean is the mean tension, and Tdyn is the dynamic tension. For the sake of code comparison, DNV utilization has been defined as

$$Utilizatio{n}_{DNV}={\displaystyle \frac{Tmean\times \gamma mean-Tdyn\times \gamma dyn}{Sc}}$$

(4)

The BV baseline safety factor is 1.67 in the intact condition [75]. For a system without redundancy, the safety factor is required to be increased by 20%. In addition, for synthetic ropes, a 10% increase is required for polyester ropes, and a 20% increase is needed for other types of materials.

For the sake of code comparison, the BV utilization has been defined as

$$Utilizatio{n}_{BV}=Maximum\left({\displaystyle \frac{Factored Load on Chain}{Chain MBL}},{\displaystyle \frac{Factored Load on Fibre Rope}{Rope MBL}}\right)$$

(5)

Table 13. ABS safety factors.

Line Component	Redundancy	Condition	Safety Factor
Steel	Redundancy	Intact	1.67
	Non-redundancy		2.0
Fiber Rope	Redundancy		1.82
	Non-redundancy		1.82 × 1.2

presents the ABS safety factors [76,77] for mooring lines in intact condition.

The ABS tension utilization is defined in the following way:

$$Utilizatio{n}_{ABS}=\mathrm{ }Maximum\left({\displaystyle \frac{Factored Load on Chain}{Chain MBL}},{\displaystyle \frac{Factored Load on Fibre Rope}{Rope MBL}}\right)$$

(6)

A simulation time of 3 h has been considered in the analysis, which aligns with the best industry practices. Both operating and survival conditions have been analyzed for the OC3 mooring analysis, including both all-chain and chain–fiber mooring systems. Mooring systems with and without line redundancy have also been investigated and compared. In summary, the following load cases have been assessed.

4.4. Implications of Findings

The findings from this case study have significant implications for the design and safety of floating offshore wind turbines. The analysis underscores the importance of selecting appropriate mooring materials and configurations based on the specific environmental conditions of the deployment site. For instance, the use of synthetic ropes in the VolturnUS platform, while advantageous in terms of weight and flexibility, requires careful consideration of long-term creep and fatigue characteristics to ensure the system’s reliability over its operational life. Furthermore, the comparison with the OC3 Hywind platform highlights the need for tailored mooring system designs that consider the unique challenges posed by different floating platform types. The results suggest that a one-size-fits-all approach may not be appropriate for FOWT mooring systems and that industry standards should evolve to reflect the specific needs of different platform designs. This study also points to the potential benefits of integrating more sophisticated modeling techniques, such as time-domain simulations that account for non-linear material behaviors and environmental interactions, into the design and analysis process. Such approaches could lead to more accurate predictions of mooring line tensions and, consequently, more reliable and cost-effective mooring system designs.

5. Analysis Results

5.1. Simulations Outcomes

Dynamic analysis is conducted to extract the time history of the line tension, as illustrated in Figure 14, red line representing the threshold for the peaks. The 3 h return level line tension is computed with a generalized Pareto distribution with maximum likelihood fitting [78].

The dynamic tension for each analysis case is extracted by the following equation:

$$Dynamic Tension=3 hour return level-mean tension$$

(7)

The mean tension, standard deviation, and 3 h return level line tension over the simulation period is calculated by OrcaFlex, and the analysis output for each load case is presented in

Table 14. Analysis output and threshold selection.

Case ID	No. of Peaks	3 h Return Level, kN	Mean Tension, kN	Std. Dev. Tension, kN	Dynamic Tension, kN	Utilization
						DNV	BV	ABS
LC01	42	3239.3	2894.3	97.2	345.0	0.24	0.29	0.29
LC02	42	2820.9	2511.9	79.5	309.0	0.21	0.25	0.25
LC03	42	2048.8	1841.5	57.6	207.3	0.17	0.20	0.20
LC04	42	1959.4	1715.1	56.5	244.2	0.16	0.19	0.19
LC05	42	2595.1	1489.8	224.4	1105.4	0.22	0.25	0.23
LC06	42	1963.4	1248.3	154.7	715.1	0.16	0.19	0.18
LC07	42	2307.6	1488.5	190.8	819.0	0.19	0.22	0.21
LC08	42	1821.6	1242.5	127.8	579.1	0.15	0.18	0.16
LC09	42	1455.4	810.7	125.3	644.7	0.14	0.14	0.14
LC10	42	1696.8	976.8	149.1	720.0	0.16	0.17	0.17
LC11	42	1299.6	809.3	102.5	490.3	0.12	0.13	0.13
LC12	42	1526.5	969.0	120.5	557.6	0.14	0.15	0.15
LC13	32	8885.2	5091.8	750.7	3793.5	0.75	0.80	0.78
LC14	32	6529.7	4282.4	406.6	2247.4	0.54	0.59	0.57
LC15	32	4899.6	2946.0	384.4	1953.6	0.45	0.48	0.48
LC16	32	4471.2	2783.3	311.2	1687.9	0.41	0.44	0.44
LC17	32	11,240.4	3941.3	1654.1	7299.0	1.04	1.09	0.99
LC18	32	7309.0	3389.3	855.9	3919.7	0.65	0.71	0.64
LC19	32	9546.6	3941.5	1311.2	5605.1	0.86	0.93	0.84
LC20	32	6430.6	3361.2	704.0	3069.4	0.56	0.62	0.57
LC21	32	6727.1	2128.0	987.4	4599.1	0.67	0.66	0.66
LC22	32	6572.4	2669.5	890.3	3902.9	0.64	0.65	0.65
LC23	32	5726.8	2123.3	803.3	3603.5	0.56	0.56	0.56
LC24	32	5628.7	2643.3	710.9	2985.4	0.54	0.55	0.55

and Figure 15. The number of peaks is the number of tension peaks in the time history above the selected threshold, which are then fitted into the generalized Pareto distribution.

From the analysis results table, the following conclusions can be summarized:

• Fiber inserts, in general, have a positive impact on mooring line tensions.
• New fiber ropes exhibited lower dynamic tensions than old ropes. In theory, the mooring tension gradually increases for a hybrid line as the synthetic rope ages.
• All-chain system sees higher mean tensions but lower dynamic tension in comparison to a hybrid system, which helps the mooring system designer to determine what types of mooring work are favorable based on the site metocean data.

The goodness of the distribution fit is assessed by the review and analysis of quantile plots. For all cases analyzed, the goodness of fit appears to be reasonably good, with all the points sitting between a 95% confidence level and close to the diagonal theoretical line. Two examples from LC01 and LC13 are demonstrated below, in Figure 16 and Figure 17.

The analysis of safety factors across the DNV, ABS, and BV standards reveals significant differences in how these organizations approach the design of mooring systems for floating offshore wind turbines. Specifically, DNV employs a probabilistic approach, incorporating both mean and dynamic tensions to calculate safety factors that account for the variability in environmental loads.

In contrast, ABS adopts a more deterministic approach, using fixed safety factors that are adjusted based on the presence or absence of redundancy in the mooring system. BV, on the other hand, applies additional factors for synthetic ropes, reflecting the unique challenges posed by these materials, such as creep and fatigue. For example, in the case study involving the VolturnUS platform, the safety factors calculated using the DNV standard are generally lower than those calculated using ABS and BV standards under operational conditions. This suggests that DNV’s approach may be less conservative in these scenarios, potentially leading to more cost-effective designs. However, under survival conditions, the BV standard resulted in the highest safety factors, particularly for mooring lines incorporating synthetic ropes, which highlights BV’s emphasis on the long-term material behavior and additional uncertainties associated with synthetic materials.

5.2. Interpretation of Mooring Line Tensions

The calculation of mooring line tensions for the VolturnUS platform under various environmental conditions provides critical insights into the relative conservatism of each standard. Under operational conditions, the mean tensions are relatively consistent across all standards, with the DNV-based calculations showing slightly lower tensions due to the probabilistic treatment of dynamic loads [38]. However, under survival conditions, the tensions calculated using the BV standard are significantly higher, particularly in scenarios involving synthetic ropes.

This disparity can be attributed to the higher safety factors required by BV for synthetic materials, which are designed to account for potential long-term degradation and creep effects. The ABS standard also produces relatively high-tension values in survival scenarios but is more aligned with DNV in operational conditions. These results suggest that while all three standards provide robust guidelines for mooring system design, BV may offer greater conservatism in scenarios involving extreme environmental loads and synthetic materials [39].

5.3. Discussion of Material-Specific Considerations

The use of different materials in mooring lines, such as traditional steel chains and modern synthetic ropes, has a significant impact on the tension results and the associated safety factors. Steel chains, known for their high strength and predictable behavior under load, generally result in lower calculated tensions and safety factors across all standards. In contrast, synthetic ropes, while offering advantages in terms of weight and flexibility, introduce additional challenges due to their non-linear stress–strain behavior and susceptibility to long-term degradation [51].

In the case study, the hybrid mooring system of the VolturnUS platform, which incorporates both steel chains and synthetic ropes, demonstrated higher tension variability under extreme conditions. This finding underscores the importance of carefully selecting mooring materials based on the specific environmental conditions and the intended lifespan of the installation. BV’s higher safety factors for synthetic ropes reflect a more cautious approach, acknowledging the uncertainties associated with these materials.

6. Discussion

The results indicate that tension calculations according to the DNV, BV, and ABS standards are broadly comparable, despite some differences. Notably, Load Case 17 (LC17) failed under DNV and BV standards but passed marginally under ABS. Overall, BV tends to yield more conservative (i.e., higher) tension safety factors, while DNV generally predicts lower tension safety factors, particularly in calm conditions. These variations arise from differing approaches to safety and risk assessment among the classification societies, and there is no absolute standard of correctness. This study focuses on benchmarking these standards under normal operational conditions and does not address damaged scenarios or Accidental Limit States, as defined by DNV. For simplicity, only one wave condition is considered, though a comprehensive mooring analysis would typically involve multiple sea states to statistically determine the most probable maximum line tensions.

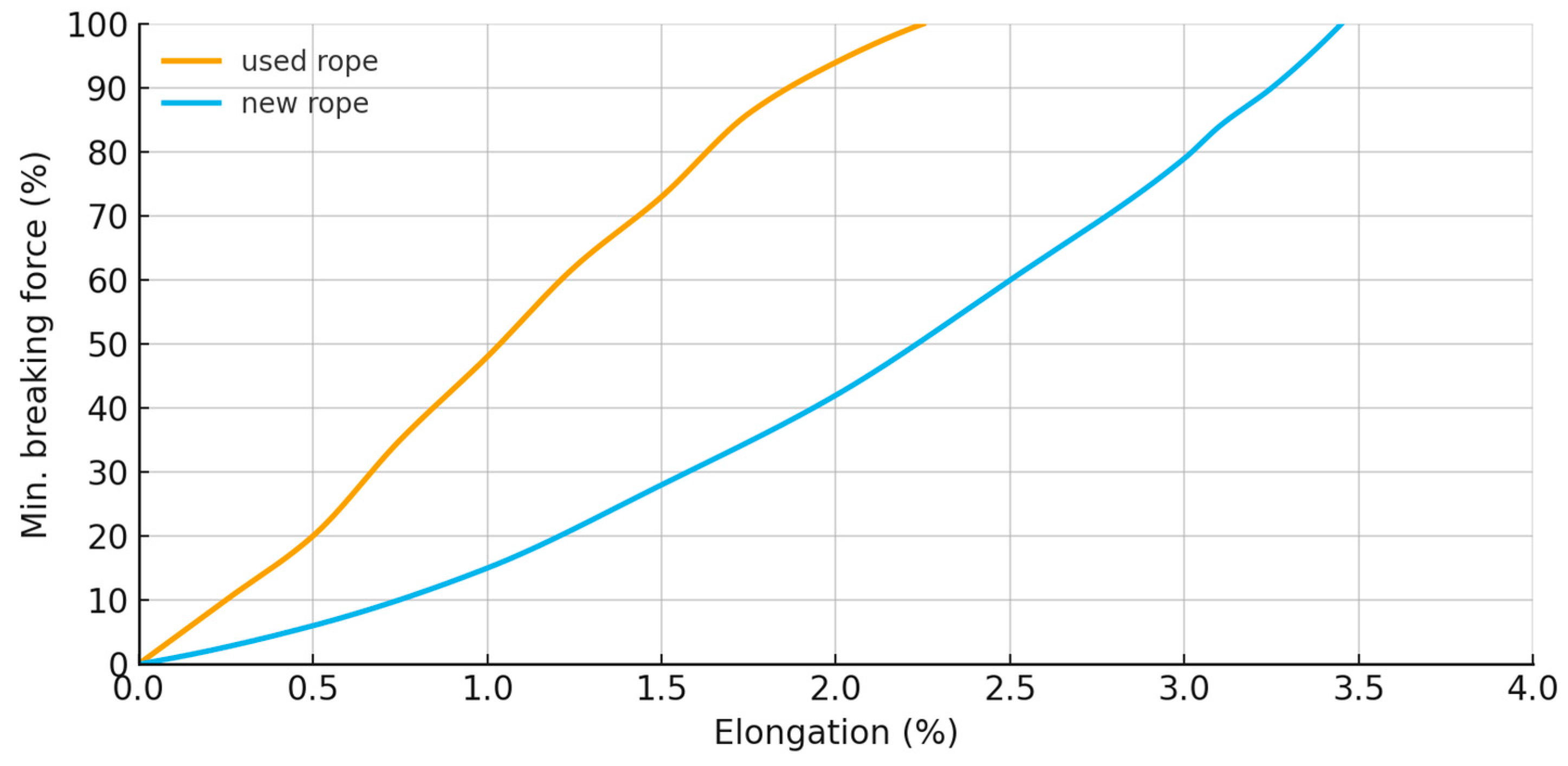
The analysis incorporates the non-linear behavior of Dyneema fiber ropes, although the long-term creep behavior is simplified by considering only “new” and “aged” rope conditions. Intermediate stages and time-dependent changes are not explicitly modeled. Similarly, while the peak-over-threshold method is used to identify characteristic maximum tensions, it involves subjective decisions that depend on the analyst’s experience. Extreme value analysis applied to the time-history data generally produced reliable fits, though some load cases showed wider confidence intervals that could be refined with threshold adjustments and additional data. The practical implications of these findings are significant for the offshore wind industry.

The variations in safety factors across different standards suggest that the choice of guidelines can have a considerable impact on the design and cost of mooring systems. For example, adhering to BV standards may result in higher initial costs due to the more conservative safety factors, particularly when synthetic ropes are used. However, this can be justified by the increased safety margin and potentially lower long-term maintenance costs, as these standards account more rigorously for material fatigue and creep.

Furthermore, the results indicate that hybrid mooring systems, such as those used in the VolturnUS platform, can offer superior performance under certain conditions but require careful design consideration to ensure long-term reliability. The higher tension variances observed in synthetic ropes under extreme conditions highlight the need for ongoing monitoring and maintenance to mitigate the risks associated with material degradation over time.

Several limitations of the current study should be acknowledged. The environmental conditions analyzed are specific to the North Sea and may not generalize to all offshore sites. Furthermore, the simplified modeling of rope stiffness and environmental interactions, along with the exclusion of transient phenomena such as wave slamming, may lead to the underestimation of actual mooring loads. These limitations suggest that caution is needed when interpreting the results.

Future research should focus on performing a more detailed evaluation of synthetic rope performance, including long-term fatigue and creep under real conditions. Expanding the scope to include damaged scenarios and more complex environmental interactions—potentially through stochastic and transient modeling—would improve design reliability. Additionally, integrating the strengths of DNV, BV, and ABS into a hybrid or harmonized standard may offer a more balanced and robust framework for mooring system design.

7. Conclusions

This study has made a critical advancement in the understanding of FOWT mooring systems by conducting a detailed comparative analysis of safety factors in line with tensions as prescribed by DNV, ABS, and BV guidelines. Utilizing the VolturnUS platform as a case study, the research employed dynamic mooring analysis through sophisticated simulation tools. This approach not only revealed the nuances and similarities between different standards but also provided a benchmark against which current and future mooring systems could be evaluated. The methodology, grounded in both theoretical and practical aspects, strengthens the study’s credibility and relevance to real-world applications.

This study assessed the effectiveness of international standards—DNV, ABS, and BV—in predicting mooring line safety for offshore wind turbines. The analysis, based on a single-wave condition, effectively demonstrated differences in mooring line behavior but did not capture the full complexity of material responses. Additionally, the subjectivity in identifying maximum line tensions highlights the need for more rigorous and standardized evaluation methodologies.

While broad alignment was observed, discrepancies emerged in specific cases, reflecting the distinct risk assessment frameworks embedded within each standard. The study does not intend to favor any classification society, as there is no absolute standard of correctness. Nonetheless, the study urges comprehensive structural reliability and risk analysis to define a partial safety or target reliability index for the next generation of floating structures.

The findings of this study have important implications for the design of reliable and cost-effective mooring systems not only for floating offshore wind turbines (FOWTs) but also for other floating offshore renewables systems, such as wave energy converters with similar risk profiles (likelihood × consequence). By revealing differences in safety factor requirements across standards, the research supports more informed design decisions that balance safety with economic considerations. In particular, the methodology presented to conduct a comparative analysis of different standards can be used by developers of innovative floating structures to make better-informed decisions in the long and arduous technology qualification process.

The study also emphasizes the need for the continuous refinement of mooring guidelines to meet the evolving demands of offshore wind applications. Future research should investigate damaged-state scenarios and the non-linear mechanical behavior of synthetic ropes to further improve mooring system resilience.