Investigation of Cavitation Flow Field and Flow Loss in Shaftless Water-Jet Propulsion Pump Under Different Acceleration Conditions
Abstract
1. Introduction
2. Numerical Method and Entropy Production Theory
2.1. Governing Equations
2.2. Turbulence Model
2.3. Cavitation Model
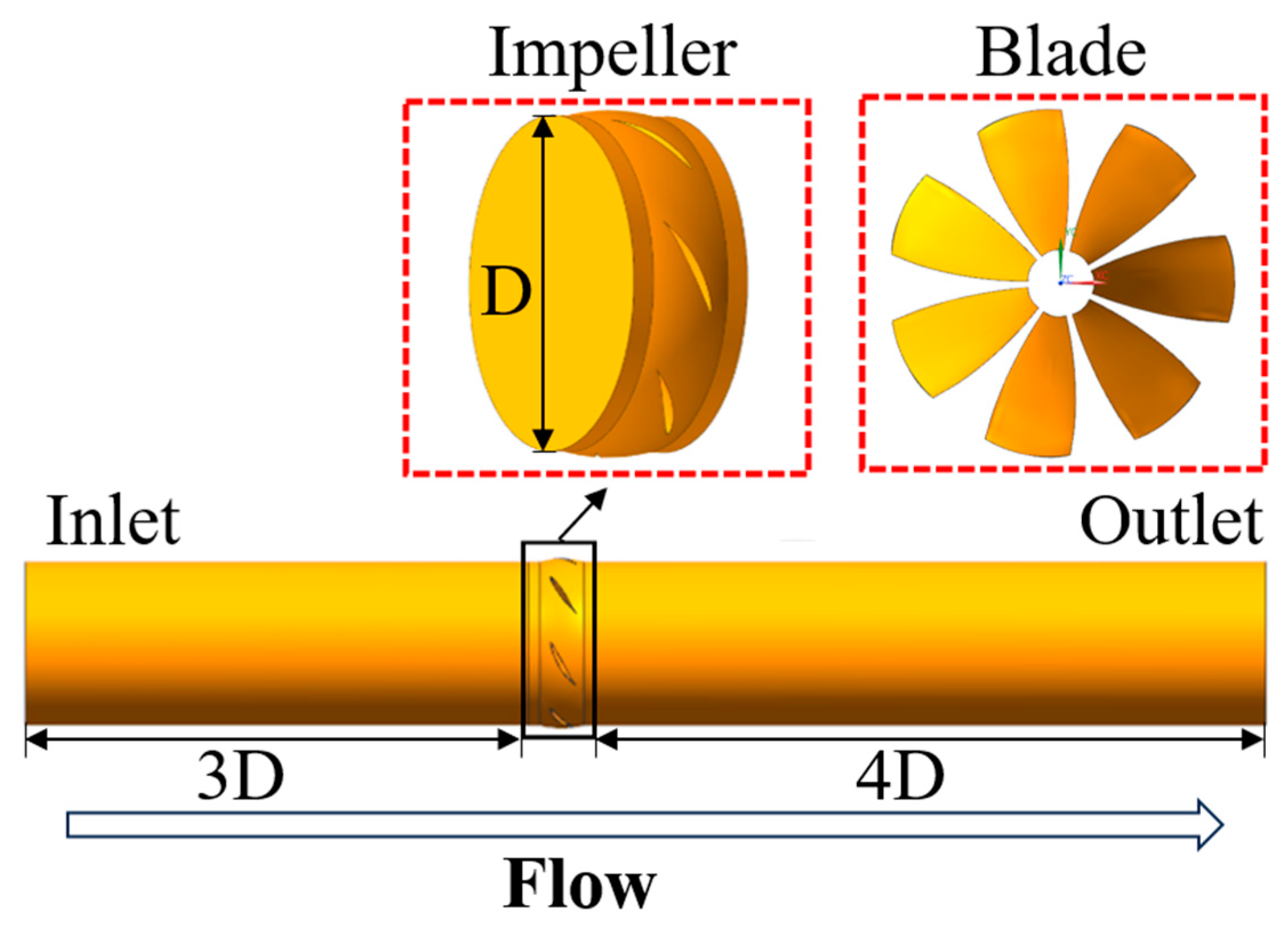
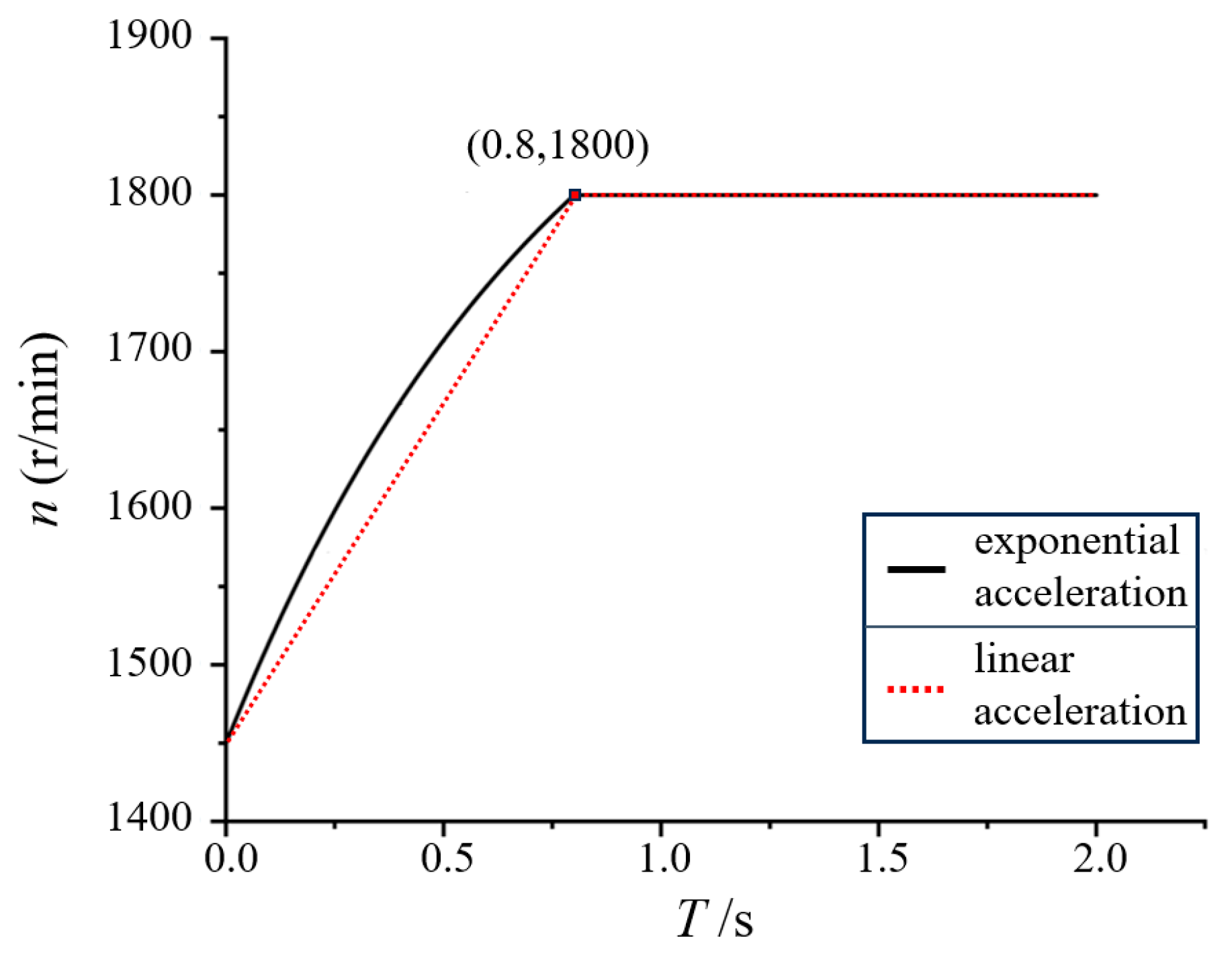
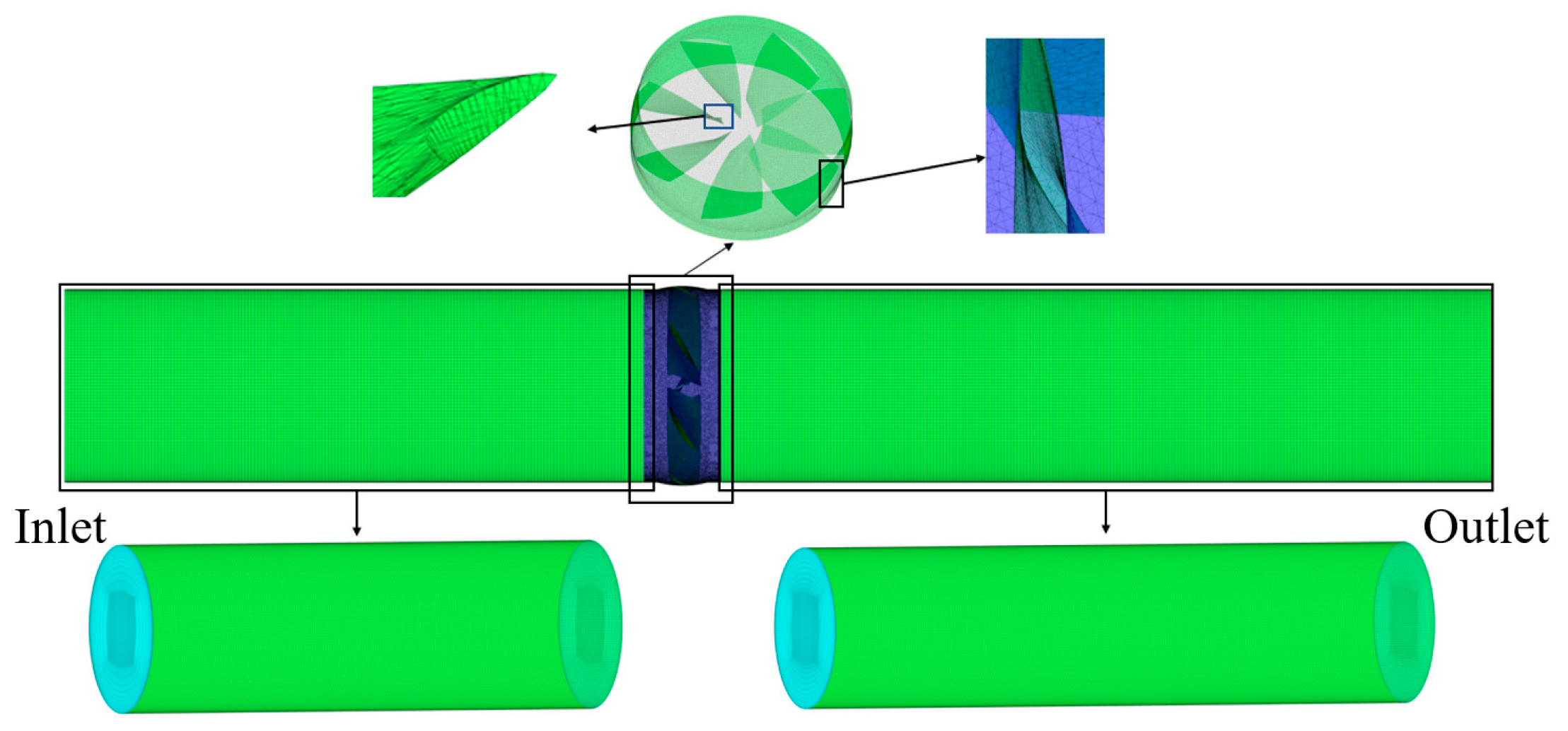
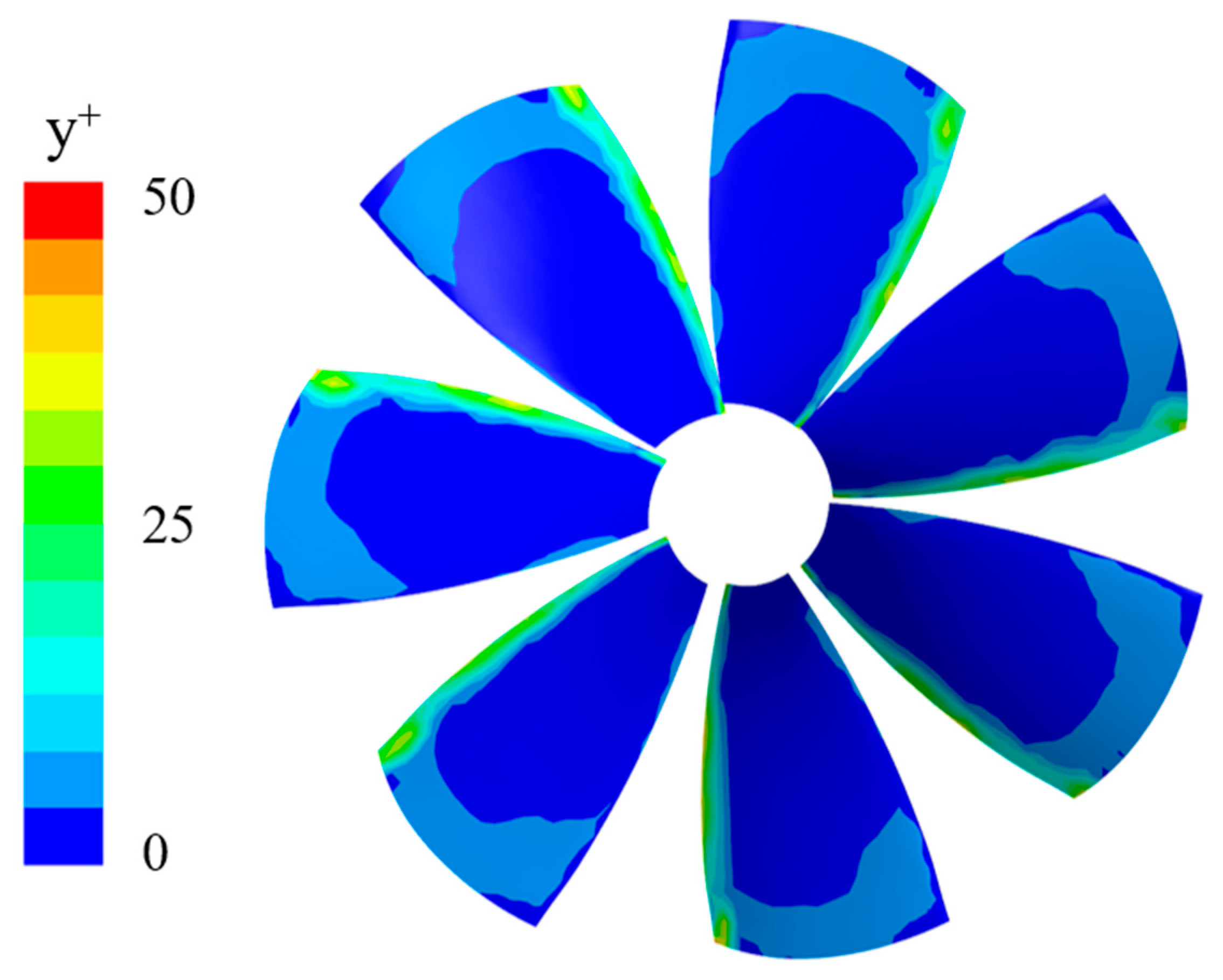
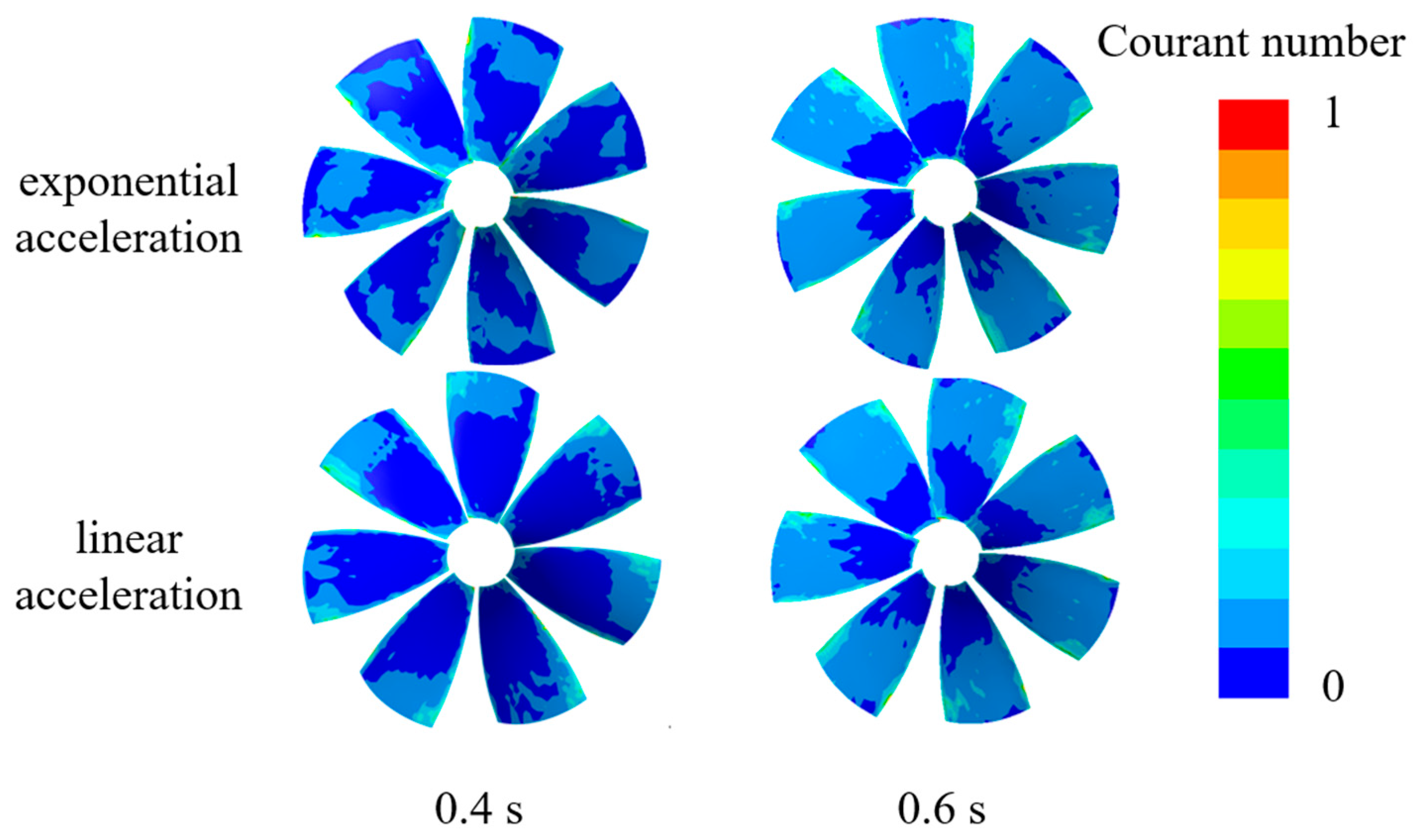
2.4. Simulation Setup
2.5. Entropy Production Theory
3. Results and Discussion
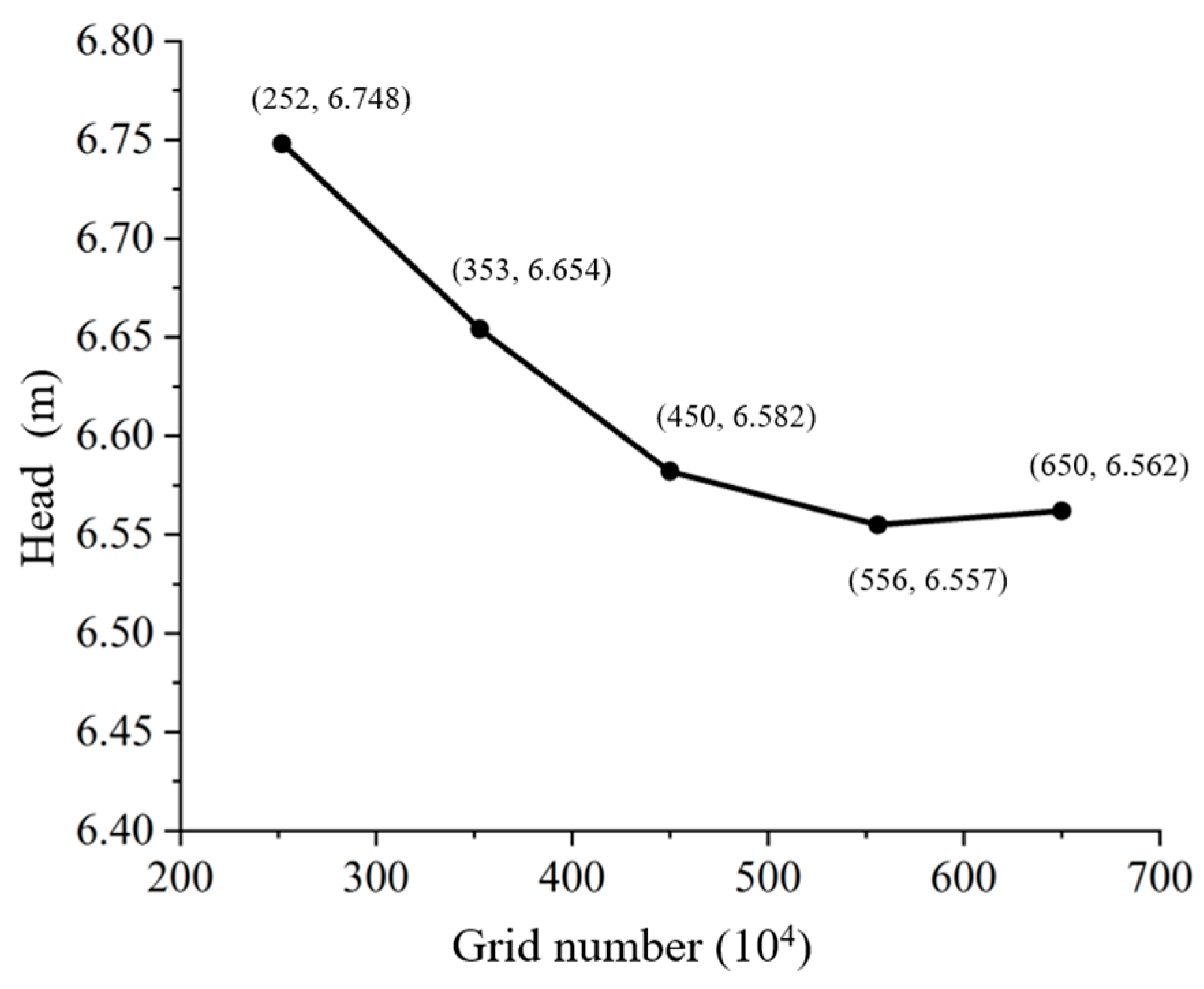
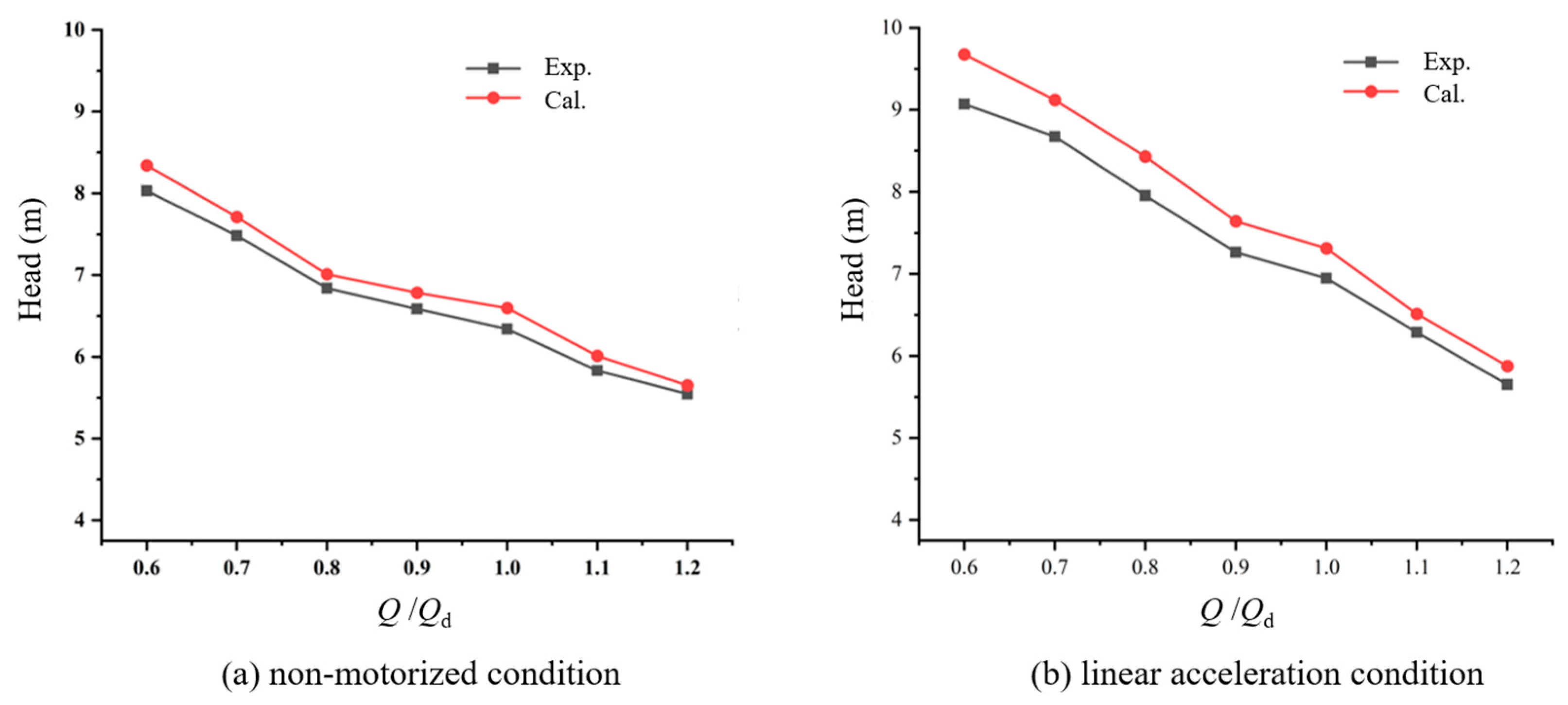
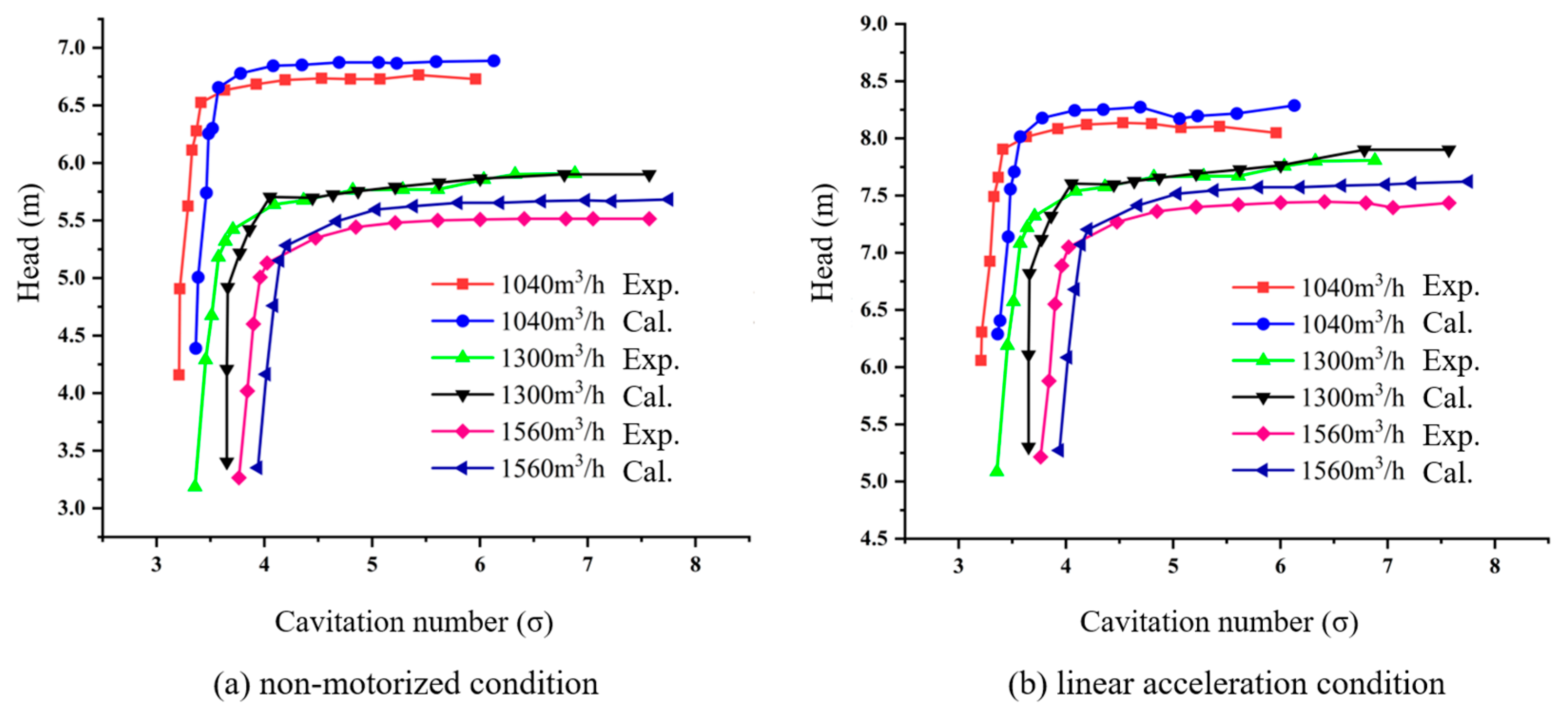
3.1. Accuracy Validation of Numerical Methods
3.2. Comparison of Cavitation Flow Field
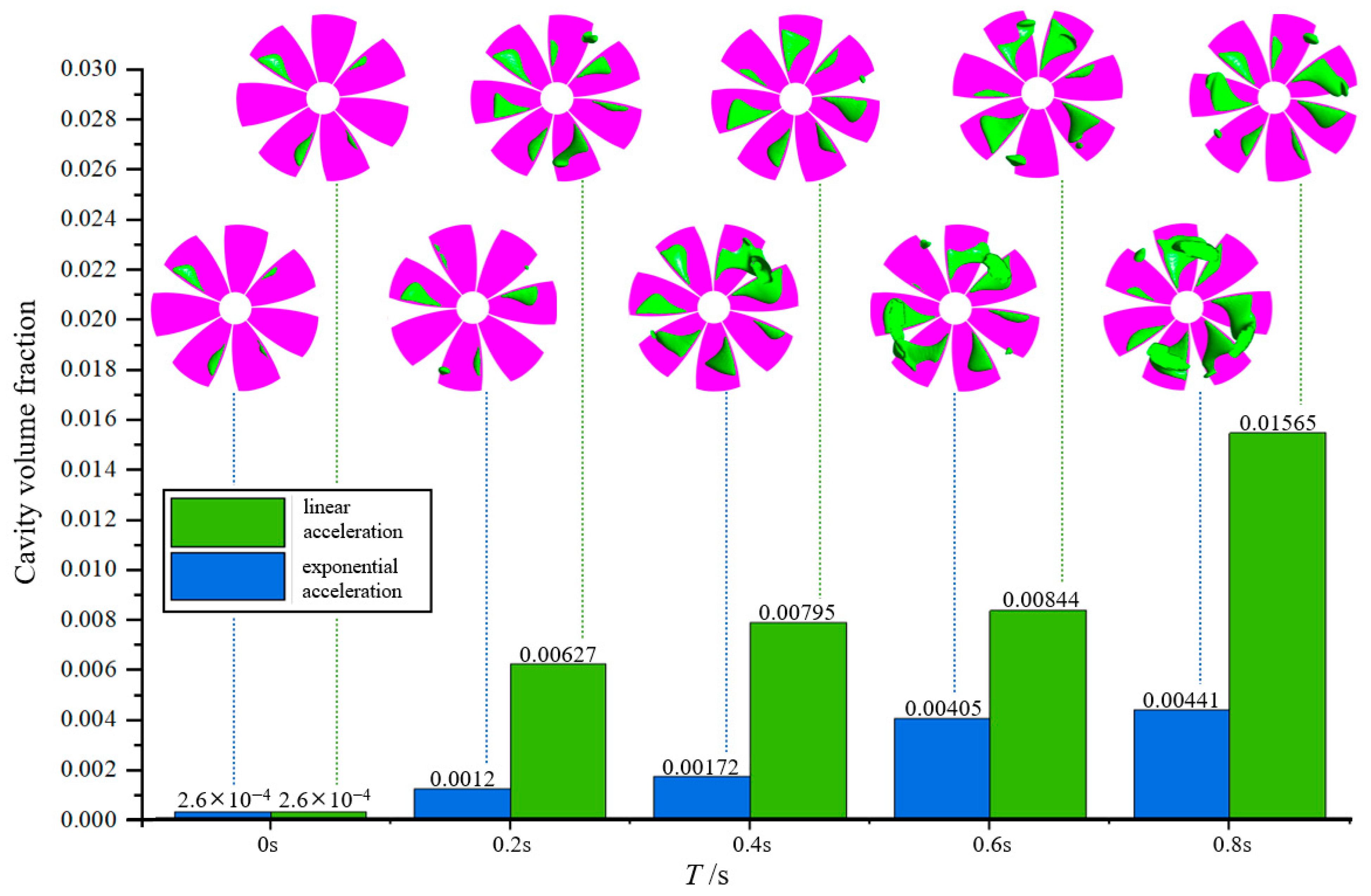
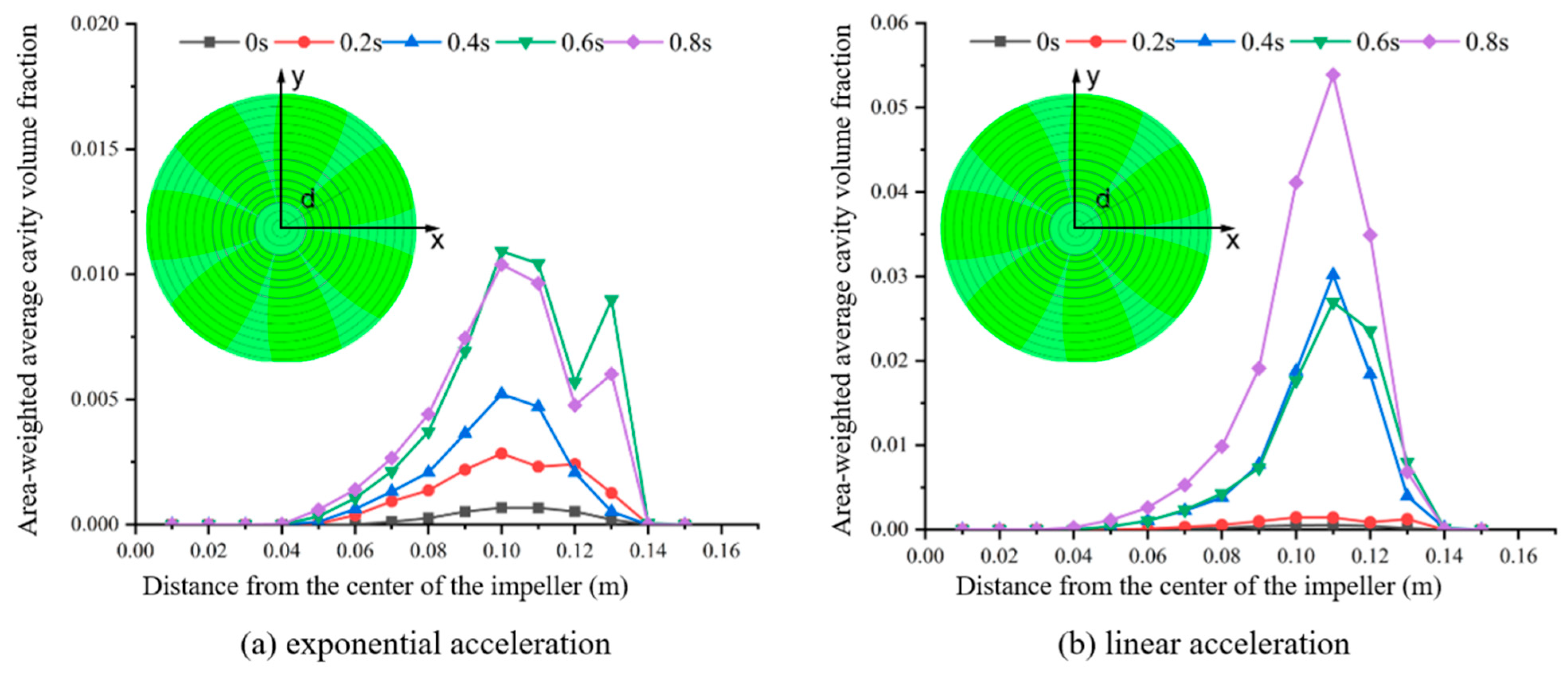
3.2.1. Cavity Distribution Comparison
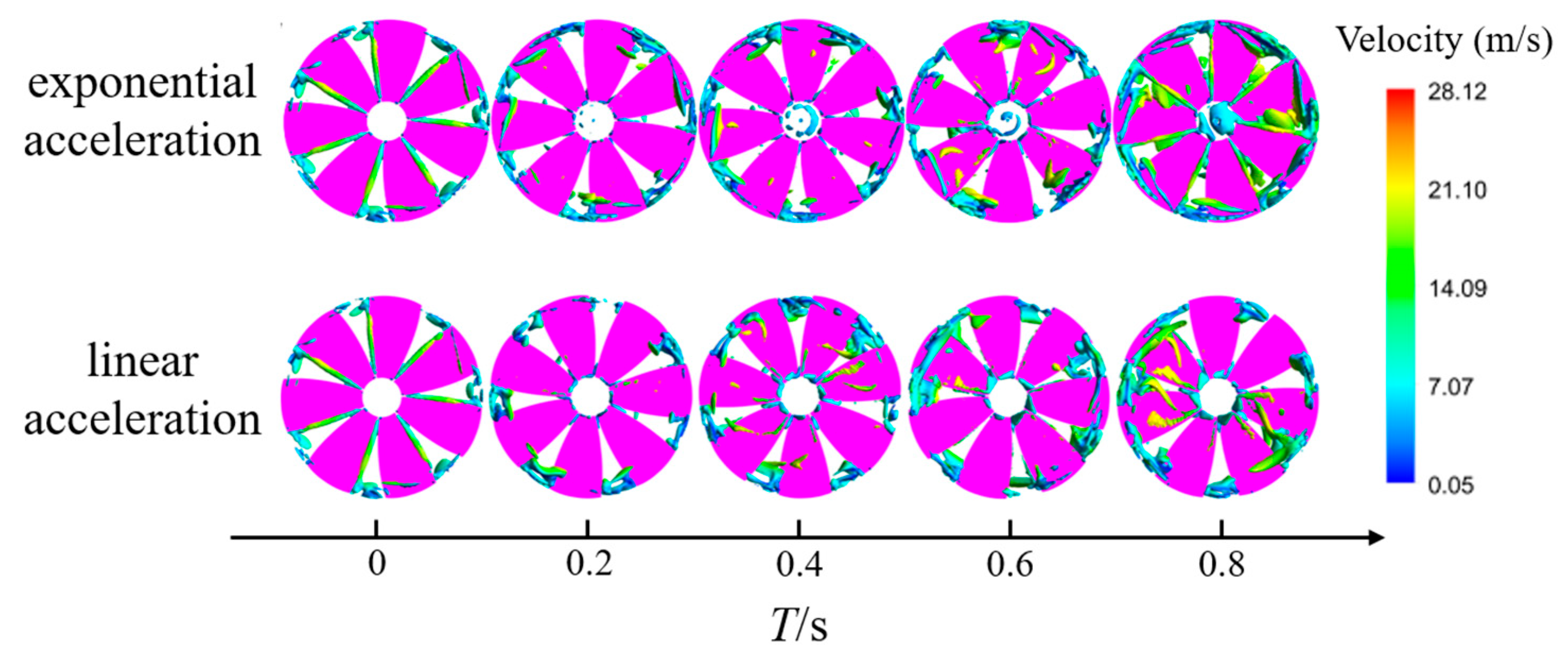
3.2.2. Impeller Velocity Comparison
3.2.3. Impeller Pressure Comparison
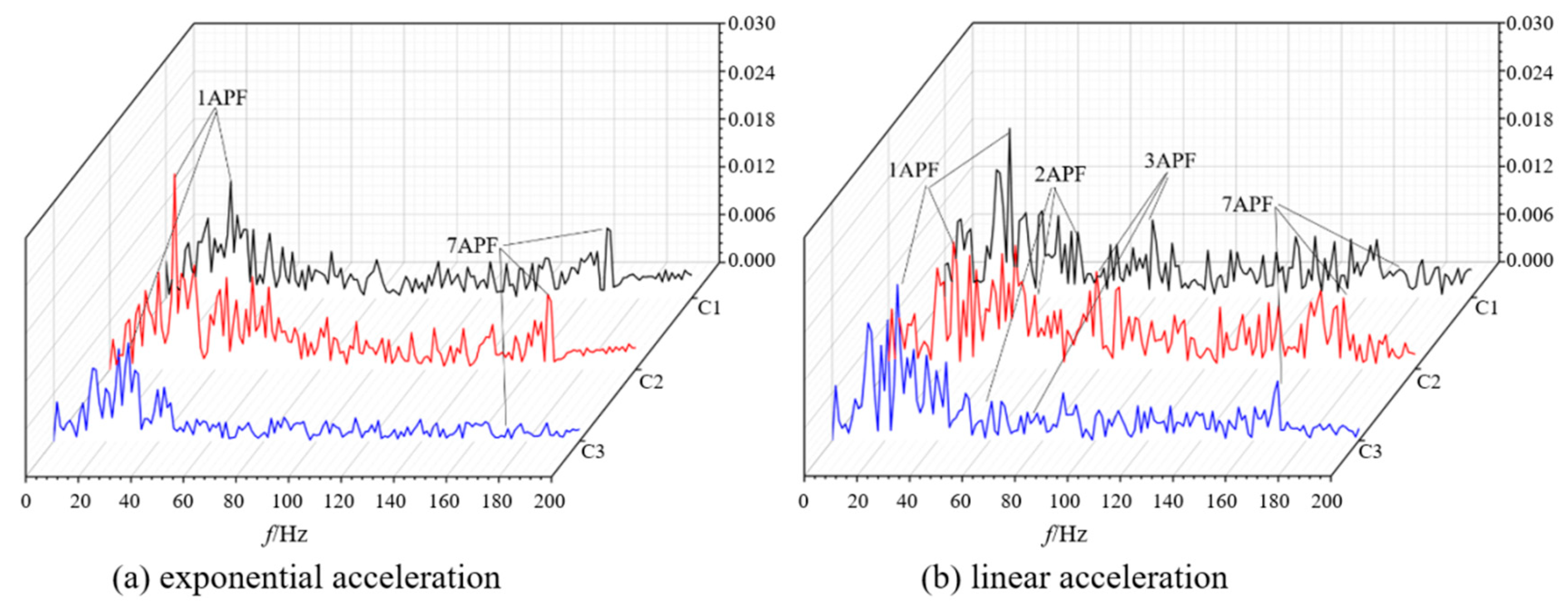
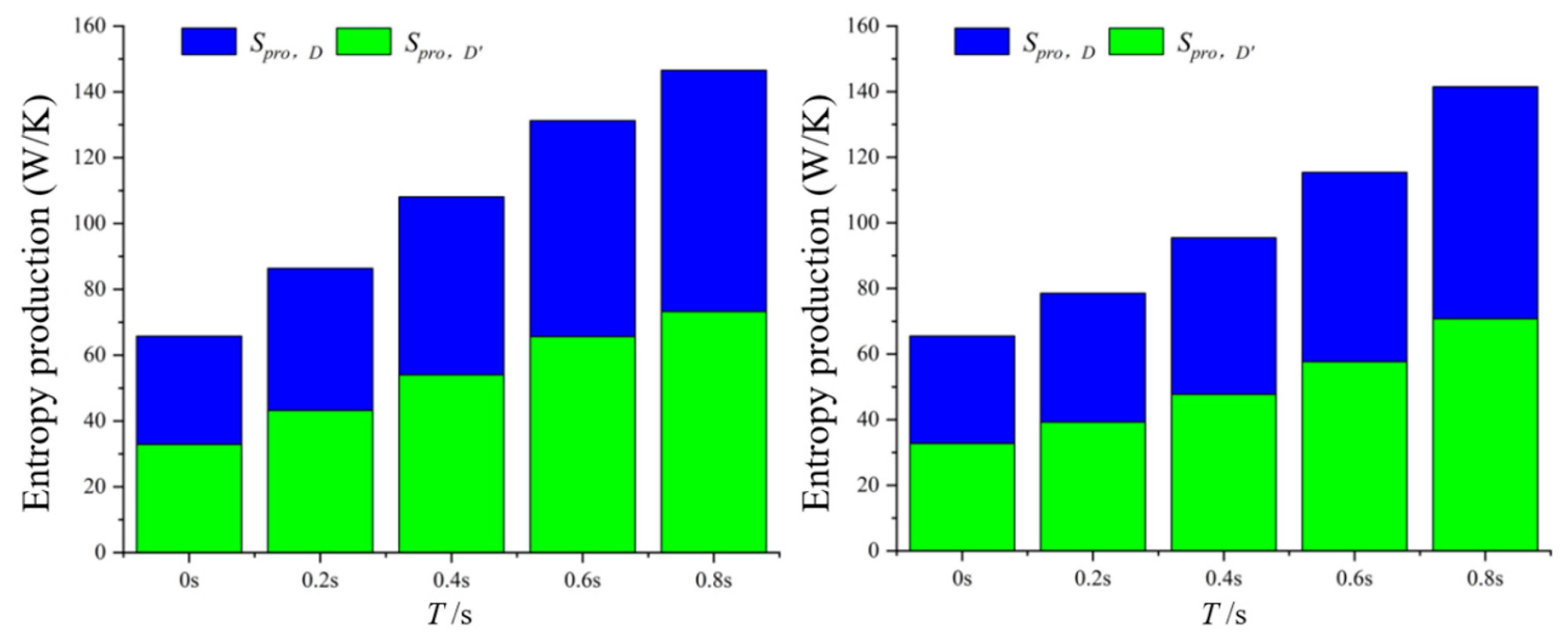
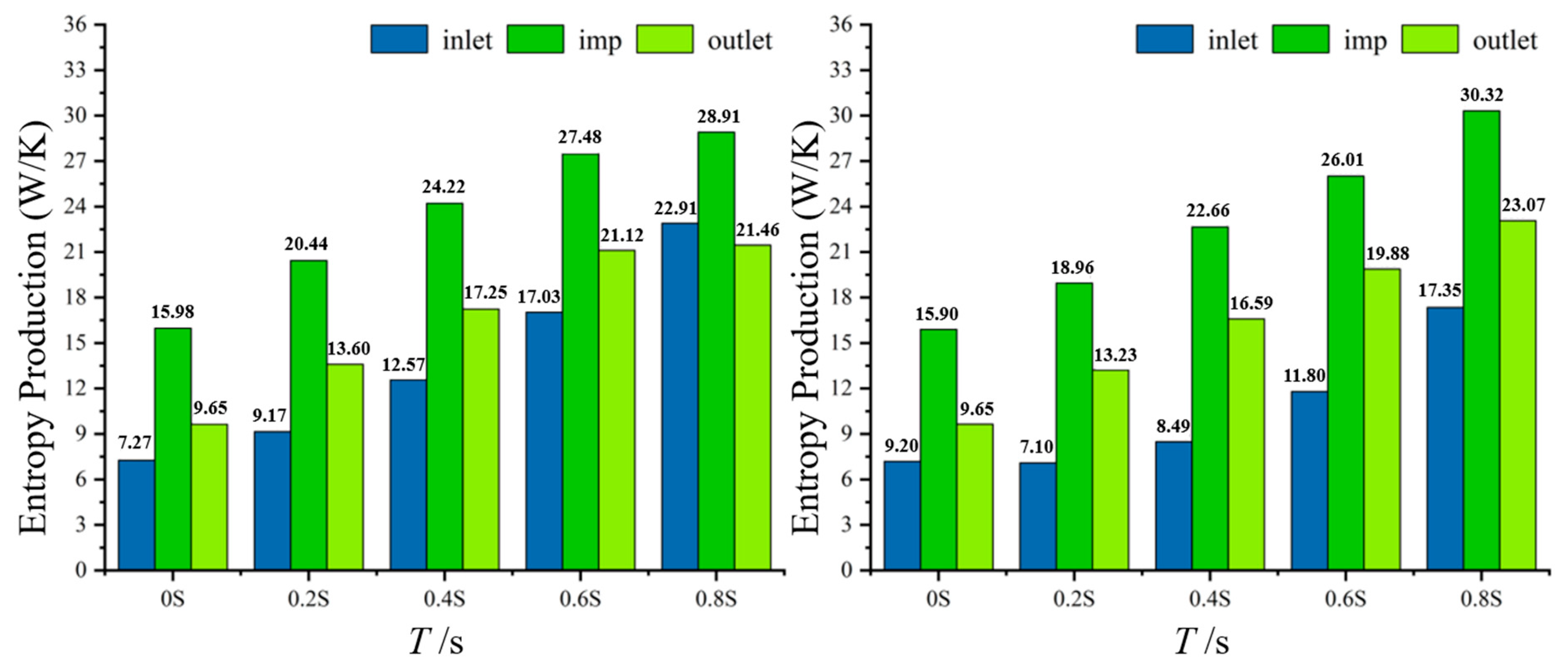
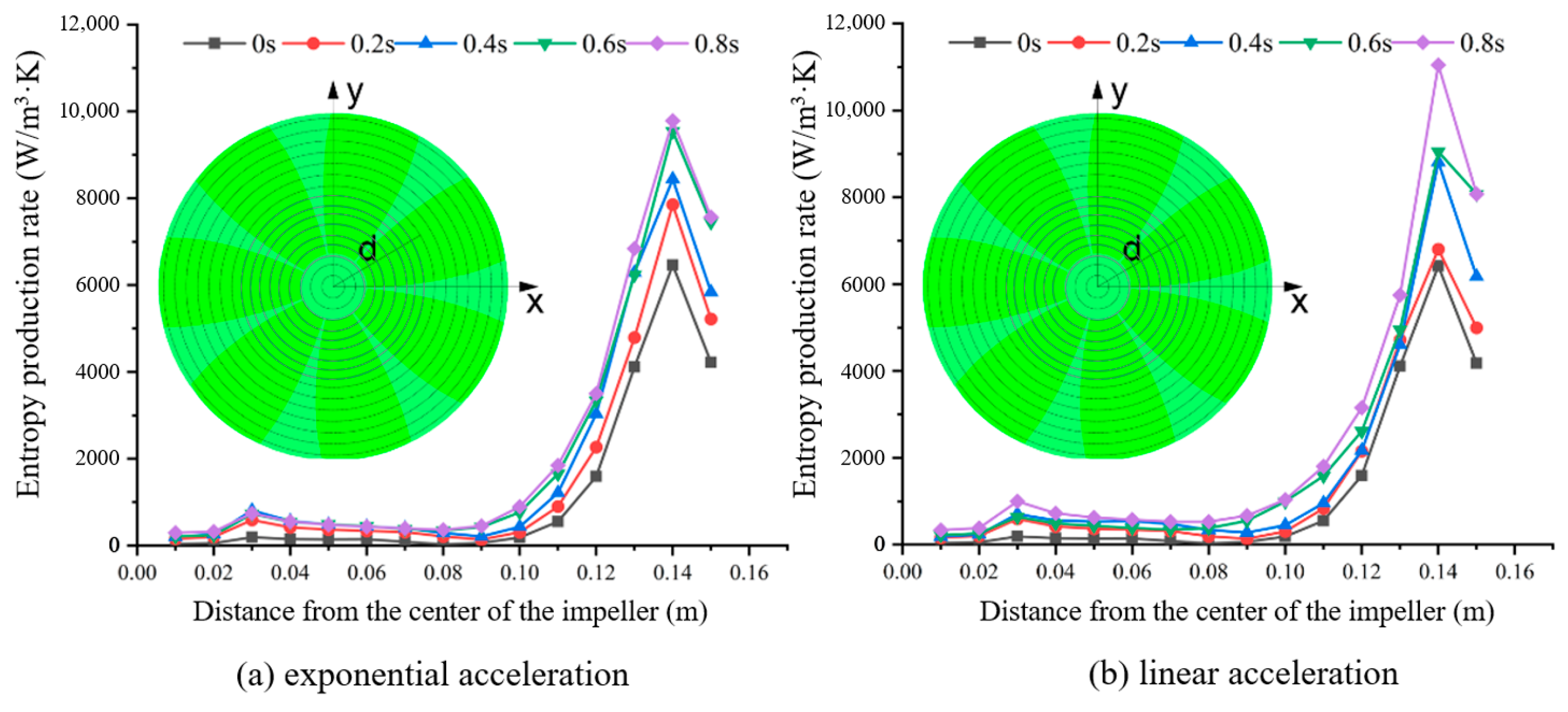
3.3. Comparison of Cavitation Flow Loss
4. Conclusions
5. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Qd | Designed flow (m3/h) |
| H | Designed head (m) |
| n | Rated speed (r/min) |
| ns | Specific speed |
| Z | Number of impeller blades |
| D | Impeller diameter (mm) |
| ρ | Density of the fluid medium |
| Mc | Mass of the reduced cavities (kg/(m3·s)) |
| Mv | Mass of the increased cavities (kg/(m3·s)) |
| p | Pressure (Pa) |
| pv | Vaporization pressure (Pa) |
| psat | saturated vapor pressure (Pa) |
| μ | Viscosity coefficient |
| FD | Interphase drag force |
| FTD | Turbulent diffusion force |
| Pk | Production term |
| Dk | Dissipation term |
| αv | Vapor phase volume fraction |
| αl | Liquid phase volume fraction |
| αnuc | Volume fraction of the cavitating nucleon |
| RB | Cavity radius |
| Evaporation rate | |
| Condensation rate | |
| x0 | Initial speed of the impeller (r/min) |
| xa | Acceleration of the impeller (r/min) |
| t | A certain time during the acceleration (s) |
| t0 | Total time for the impeller to accelerate (s) |
| TK | Temperature (K) |
| ω | Turbulent eddy viscosity frequency (s−1) |
| k | Turbulent kinetic energy (m2/s2) |
| β | Empirical coefficient |
Abbreviations
| CFD | Computational Fluid Dynamics |
| SST | Shear stress transport |
| GGI | General Grid Interface |
| RANS | Reynolds Average Navier-Stokes |
| CFL | Courant Friedrichs Lewy |
References
- Kim, C.; Chun, H. Experimental Investigation into the performance of the Axial-Flow-Type Waterjet according to the Variation of Impeller Tip Clearance. Ocean Eng. 2005, 34, 275–283. [Google Scholar] [CrossRef]
- Chen, W.; Chen, P.; Zhou, Y.; Zhang, C. The effect of tip rake distribution on the hydrodynamic performance of shaftless rim-driven contra-rotating thruster. Ocean Eng. 2023, 285, 115454. [Google Scholar] [CrossRef]
- Cao, L.; Che, X.; Hu, J. Design method of water jet pump towards high cavitation performances. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Hangzhou, China, 20–23 May 2016; Volume 129, p. 012067. [Google Scholar]
- Tan, Z.; Yan, P.; Liu, L. Technology development and prospect of shaftless rim-driven propulsion system. J. Wuhan Univ. Technol. 2015, 39, 601–605. [Google Scholar]
- Ni, Y.; Liu, M. Overview on research of water-jet propulsion. Ship Ocean Eng. 2013, 42, 1–5. [Google Scholar]
- Miorini, L.; Wu, X.; Katz, J. The internal structure of the tip leakage vortex within the rotor of an axial waterjet pump. J. Turbomach. 2012, 134, 031018. [Google Scholar] [CrossRef]
- Jiao, X.; Wang, Q.; Cheng, L.; Zhao, H. Experimental study on thrust pulsation characteristics of water jet propulsion pump units. Ocean Eng. 2023, 284, 115079. [Google Scholar] [CrossRef]
- Gong, B.; Zhang, C.; Yi, L. Experimental study on the cavitation flow and the induced vibration characteristics of a mixed-flow water-jet pump. J. Vib. Shock 2024, 43, 42–45. [Google Scholar]
- Dong, Q.; Yang, J. Experimental study on effect of cavitation on fluctuating pressure on the duct of waterjet. Ship Boat 2023, 34, 35–42. [Google Scholar]
- Yan, P.; Zhang, Z.; Meng, Y.; Geng, H. Numerical investigation of internal flow characteristics in an azimuth waterjet propulsion at different ship speeds. Appl. Ocean Res. 2025, 154, 104406. [Google Scholar] [CrossRef]
- Gong, J.; Wu, W.; Ding, M. Numerical analysis on the transom-stern wake with a horizontal plunging jet. Ocean Eng. 2023, 285, 115465. [Google Scholar] [CrossRef]
- Liu, H.; Cao, Y.; Wang, Y. Hydrodynamic characteristics of shaft-less waterjet pump. J. Drain. Irrig. Mach. Eng. 2015, 33, 380–386. [Google Scholar]
- Zhu, H.; Jin, B.; Wang, D. Open-water characteristics of shaftless pump-jet thruster. Acta Armamentarii 2021, 42, 835–841. [Google Scholar]
- Du, W.; Yuan, G.; Cai, L. Analysis on hydrodynamic performance of shaftless waterjet based on CFD. Ship Sci. Technol. 2022, 44, 20–25. [Google Scholar]
- Wang, C.; Zhang, Y.; Yang, J. Influence of pump shaft on flow performance of inlet duct and waterjet propulsion. Ship Eng. 2023, 45, 22–27. [Google Scholar]
- Soltanmohamadi, R.; Lakzian, E. Improved design of Wells turbine for wave energy conversion using entropy generation. Meccanica 2015, 51, 1713–1722. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Li, Y. Experimental and numerical investigations of head-flow curve instability of a single-stage centrifugal pump with volute casing. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 633–647. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W. Energy characteristics of mixed-flow pump under different tip clearances based on entropy production analysis. Energy 2020, 199, 117447. [Google Scholar] [CrossRef]
- Shen, S.; Qian, Z.; Ji, B. Numerical analysis of mechanical energy dissipation for an axial-flow pump based on entropy generation theory. Energies 2019, 12, 4162. [Google Scholar] [CrossRef]
- Shim, H.; Kim, K. Effects of the cross-sectional area of a volute on suction recirculation and cavitation in a centrifugal pump. J. Fluids Eng. 2022, 142, 051204. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Liu, L. Cavitation characteristics of rotational hydrodynamic cavitation generator. J. Drain. Irrig. Mach. Eng. 2023, 41, 160–165. [Google Scholar]
- Ruan, H.; Guo, C.; Yu, L. Cavitation induced flow instability mechanism of pump turbine under pump conditions. J. Drain. Irrig. Mach. Eng. 2023, 41, 779–786. [Google Scholar]
- Singhal, K.; Athavale, M.; Li, H. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Chen, T.; Huang, B.; Wang, G. Numerical study of cavitating flows in a wide range of water temperatures with special emphasis on two typical cavitation dynamics. Int. J. Heat Mass Transf. 2016, 101, 886–900. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Luo, K. Analysis of cavitation characteristics of marine centrifugal pump based on modified Kunz model. J. Drain. Irrig. Mach. Eng. 2017, 35, 381–386. [Google Scholar]
- Ghorani, M.; Haghighi, M.; Maleki, A. A numerical study on mechanisms of energy dissipation in a pump as turbine (PAT) using entropy generation theory. Renew. Energy 2020, 162, 1036–1053. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Y.; Tang, Q. Energy analysis of Francis turbine for various mass flow rate conditions based on entropy production theory. Renew. Energy 2022, 183, 447–458. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Designed flow Qd (m3/h) | 1300 |
| Designed head H (m) | 6.5 |
| Rated speed n (r/min) | 1450 |
| Specific speed ns | 781 |
| Number of impeller blades Z | 7 |
| Impeller diameter D (mm) | 300 |
| Hub ratio dh/D | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Wang, Y.; Liu, H.; Li, M.; Pi, Q. Investigation of Cavitation Flow Field and Flow Loss in Shaftless Water-Jet Propulsion Pump Under Different Acceleration Conditions. J. Mar. Sci. Eng. 2025, 13, 2165. https://doi.org/10.3390/jmse13112165
Lei J, Wang Y, Liu H, Li M, Pi Q. Investigation of Cavitation Flow Field and Flow Loss in Shaftless Water-Jet Propulsion Pump Under Different Acceleration Conditions. Journal of Marine Science and Engineering. 2025; 13(11):2165. https://doi.org/10.3390/jmse13112165
Chicago/Turabian StyleLei, Jianing, Yong Wang, Houlin Liu, Ming Li, and Qing Pi. 2025. "Investigation of Cavitation Flow Field and Flow Loss in Shaftless Water-Jet Propulsion Pump Under Different Acceleration Conditions" Journal of Marine Science and Engineering 13, no. 11: 2165. https://doi.org/10.3390/jmse13112165
APA StyleLei, J., Wang, Y., Liu, H., Li, M., & Pi, Q. (2025). Investigation of Cavitation Flow Field and Flow Loss in Shaftless Water-Jet Propulsion Pump Under Different Acceleration Conditions. Journal of Marine Science and Engineering, 13(11), 2165. https://doi.org/10.3390/jmse13112165





