A DRC-TCN Model for Marine Vessel Track Association Using AIS Data

Abstract

Accurate vessel track association is a key requirement for maritime traffic monitoring and collision-avoidance systems, yet the Automatic Identification System (AIS) records commonly contain noise, missing intervals, and overlapping trajectories in congested coastal waters. We propose a Dilated Residual Connection Temporal Convolutional Network (DRC-TCN) tailored to AIS sequences; residual dilated blocks with layer normalization enable stable training while capturing long-range temporal dependencies under imperfect data. Beyond kinematic inputs, we augment AIS with buoy-based meteorological variables (wind direction and speed, gust, pressure, air temperature, and sea surface temperature) via time-aligned nearest-station fusion, allowing the model to account for environmental effects on vessel motion. Experiments on New York coastal AIS data show that DRC-TCN outperforms CNN-LSTM and vanilla TCN baselines, improving F1 score by up to 99.3% and achieving 99.7% accuracy. The results indicate that environment-aware temporal modeling strengthens the robustness of track association and supports situational awareness for next-generation intelligent navigation and ocean engineering applications.

1. Introduction

Maritime transportation is the backbone of the global economy, carrying more than 80% of goods by volume across international waters. Safe navigation in congested waterways and coastal regions depends critically on accurate vessel monitoring and reliable trajectory association, which provide the foundation for collision avoidance, traffic management, and the development of Maritime Autonomous Surface Ships (MASSs) [1]. The Automatic Identification System (AIS), mandated by the International Maritime Organization (IMO), has become the dominant source of vessel trajectory data, providing information such as position, speed, course, and heading at frequent intervals [2,3]. Despite its ubiquity, AIS suffers from various imperfections, including noise, message loss, and fragmented trajectories due to equipment failure, multipath interference, or deliberate manipulation [4,5].  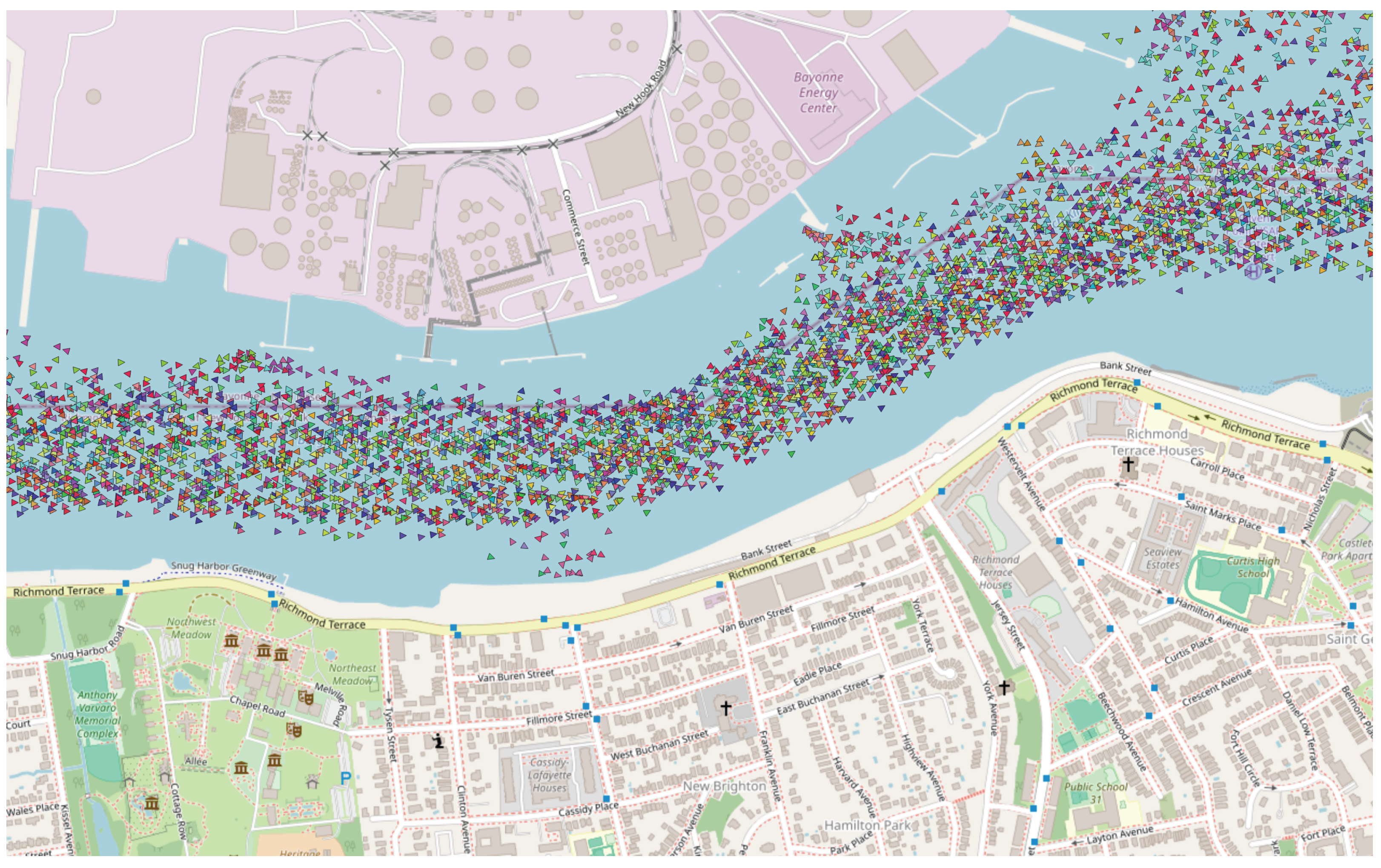Figure 1 illustrates an example of AIS tracks in a busy harbor, where each color represents a different vessel’s route and many paths intermingle, making it non-trivial to distinguish which points belong to which vessel. These issues hinder the accurate association of track fragments belonging to the same vessel, particularly in busy ports and coastal areas.

Numerous approaches have been explored for track association in maritime domains. Traditional methods such as probabilistic filters [6,7] and multi-hypothesis tracking [8,9] provide principled frameworks, but they often struggle with the scale and density of modern AIS streams. More recent studies have explored machine learning and deep learning for trajectory modeling. Recurrent neural networks, especially Long Short-Term Memory (LSTM) models, have been widely used for sequence prediction and classification due to their ability to capture temporal dependencies [10,11]. Hybrid CNN–LSTM architectures have been proposed to extract both local motion features and sequential context and have shown competitive results in vessel trajectory classification [12]. Temporal Convolutional Networks (TCNs) have also emerged as efficient alternatives, offering large receptive fields through dilated convolutions and stable training dynamics compared to recurrent architectures [13]. However, vanilla TCNs may still degrade in deeper layers and exhibit unstable convergence when trained on noisy, fragmented AIS sequences.

Beyond trajectory kinematics, environmental conditions such as wind, pressure, and sea surface temperature significantly affect vessel dynamics [14]. Yet, most existing works on AIS-based vessel tracking overlook the integration of environmental data sources. In parallel, deep representation learning has shown that properly designed loss functions can enforce identity-discriminative embeddings. For instance, triplet loss has been found to be successful in face recognition [15] and other sequence domains but has not yet been systematically applied to vessel track association tasks.

To address these challenges, this study introduces a Dilated Residual Connection Temporal Convolutional Network (DRC-TCN) framework for AIS-based vessel track association. The DRC-TCN backbone leverages residual dilated temporal convolutions with layer normalization to robustly capture long-range temporal dependencies while maintaining stable optimization under noisy data. In addition, we propose an environmental augmentation strategy that fuses buoy-based meteorological variables from NOAA coastal stations [16] with AIS kinematics, thereby enabling the model to learn environment-aware trajectory representations. To further enhance discriminability in the learned embedding space, we adopt a joint cross-entropy and triplet loss strategy, encouraging the model to separate vessel identities in latent space more effectively.

The main contributions of this paper are summarized as follows:

• A DRC-TCN backbone for AIS track association, leveraging dilated residual temporal convolutions for efficient long-range sequence modeling [13]. Unlike conventional TCNs or LSTM-based networks, our design maintains training stability and achieves high accuracy with fewer parameters.
• A novel environmental augmentation scheme incorporating buoy-based meteorological variables to account for external conditions affecting vessel motion [14,16]. To the best of our knowledge, this is the first attempt to fuse meteorological data with AIS trajectories for vessel identity discrimination.
• A joint CE + triplet loss strategy to produce identity-discriminative embeddings, enhancing the separability of vessel trajectories in latent space [15]. This dual-loss approach enforces stronger intra-class compactness and inter-class separability than classification-only baselines.
• Extensive evaluation on a NOAA MarineCadastre AIS dataset from the New York coastal region [17], demonstrating superior performance over a strong CNN-LSTM baseline [12].

Despite prior efforts, existing AIS-based track association studies still face two key limitations: (1) instability under noisy or incomplete trajectory sequences, and (2) lack of environmental awareness in modeling vessel dynamics. This study directly addresses these issues through the proposed DRC-TCN architecture and buoy-based meteorological fusion, enabling both stable optimization and environment-aware discrimination.

The remainder of this paper is structured as follows. Section 2 reviews related work on vessel track association and deep learning for trajectory modeling. Section 3 details the proposed DRC-TCN architecture, the buoy–AIS fusion process, and the joint loss design. Section 4 describes the dataset and experimental setup. Section 5 presents the results and comparative analyses. Finally, Section 6 concludes the paper with discussions and future directions.

Software and Tools. All analyses and model training were conducted in Python (Version 3.10; Python Software Foundation, Wilmington, DE, USA) using open-source scientific computing libraries: PyTorch (Version 2.1.0; PyTorch Foundation, San Francisco, CA, USA), Torchvision (Version 0.16.0; PyTorch Foundation, San Francisco, CA, USA), Torchaudio (Version 2.1.0; PyTorch Foundation, San Francisco, CA, USA), NumPy (Version 1.21.0; NumFOCUS, Austin, TX, USA), Pandas (Version 1.3.0; pandas development team, USA), Matplotlib (Version 3.4.0; Matplotlib Development Team, USA), Seaborn (Version 0.11.0; Seaborn Development Team, USA), scikit-learn (Version 1.0.0; INRIA, Paris, France), TQDM (Version 4.62.0; Open Source Contributors, USA), Jupyter (Version 1.0.0; Project Jupyter, Berkeley, CA, USA), and IPyKernel (Version 6.0.0; IPython Development Team, USA). The experiments were performed on a workstation equipped with an NVIDIA GPU (GeForce RTX 4090, NVIDIA Corporation, Santa Clara, CA, USA) and CUDA Toolkit (Version 12.1; NVIDIA Corporation, Santa Clara, CA, USA).

2. Related Work

Classical MOT on Maritime Targets. Multi-object tracking (MOT) algorithms from radar and vision have long served as the foundation for observation-to-track association. Global Nearest Neighbor (GNN) [18] and Joint Probabilistic Data Association (JPDA) [19] assign measurements via cost matrices or probabilistic weighting. Multiple Hypothesis Tracking (MHT) [8,20] expands track trees to handle ambiguities, and random finite set (RFS) filters [21,22] model uncertain target births and deaths. Yet AIS-specific issues—long occlusions, unknown and varying vessel counts, and highly non-linear maneuvering—limit their effectiveness, since most rely on linear motion models (e.g., Kalman filtering) or single-best hypothesis pruning.

Physics-Based Vessel Motion Models. Ship kinematic and dynamic models [23] have been employed in simulation, control, and navigation-assist contexts. While physically interpretable, they require detailed vessel parameters and struggle to account for environmental and operator-dependent variability (currents, wind, routing decisions, helmsman habits). Extending them to multi-vessel association incurs high calibration costs.

Trajectory Prediction with Conventional ML. Classical ML methods such as Gaussian Processes, SVMs, and PCA variants have been applied for short-term vessel trajectory extrapolation. These approaches can capture local structure but fail to model long-term dependencies and abrupt regime shifts in vessel motion. Hybrid methods (physics + ML) have been proposed, though often limited by the constraints of both worlds.

Deep Learning for AIS Sequences. Deep sequence models have recently emerged as powerful tools for AIS-based tasks. RNNs, particularly LSTMs and GRUs, capture long-range dependencies and have been applied to trajectory forecasting [24,25] and vessel behavior modeling [26]. CNNs are strong at extracting local motion signatures, while variational autoencoders (VAEs/VRAEs) provide latent representations useful for clustering [27] or anomaly detection. However, the majority of these works emphasize next-position prediction or anomaly detection [28] rather than explicit vessel identification. A comprehensive survey on predictive modeling for vessel traffic flow—from traditional statistical approaches to AI-based frameworks—was presented by Wang et al.  [29], providing an extensive overview of data-driven maritime prediction methods relevant to AIS sequence modeling.

Track Association from AIS. Direct formulations of AIS track association remain sparse. Syed and Ahmed [12] cast the problem as a closed-set multivariate time-series classification task, introducing a CNN-LSTM that integrates local (CNN) and long-term (LSTM) cues. Their model achieved ∼0.89 accuracy on 327 vessels, surpassing CNN- and LSTM-only baselines, but residual confusion persisted in overlapping routes and sparse data settings. Ahmed et al. [30] proposed a spatio-temporal algorithm for AIS association, but it still relied heavily on handcrafted motion similarity metrics. These studies demonstrated feasibility but highlighted remaining limitations: sensitivity to sequence length/windowing, vulnerability under high traffic density, and difficulty extending context beyond a few minutes without large computational costs. In addition, Siddique and Ahmed [31] recently proposed a multi-model LSTM architecture for AIS-based track association, further demonstrating the growing use of deep recurrent structures for vessel identity classification. More recently, Wang et al. [32] developed a deep learning–based vessel trajectory association algorithm using trajectory similarity measures, further validating the effectiveness of data-driven approaches for maritime track association.

Exogenous/Contextual Signals and Multi-Sensor Fusion. While multisensor fusion (AIS with radar, sonar, etc.) has been studied [33] for maritime situational awareness, relatively few works systematically integrate environmental signals into AIS-based association. Minssen et al. [14] showed that contextual weather variables can enhance predictive maritime models, and recent efforts [34] highlight robustness gains under AIS outages using auxiliary cues. Yet most applications use environmental context for anomaly detection or ETA prediction, not for identity discrimination. Reports of buoy-based augmentation specifically aligned with AIS sequences are limited, and structured evaluations on its ability to disambiguate vessels with visually similar tracks remain scarce. In addition, Chen et al.  [35] introduced an orientation-aware ship detection framework based on rotation feature decoupling, highlighting the relevance of deep learning approaches to maritime perception tasks. This gap in environment-aware vessel association is especially relevant in congested coastal waters, where currents, winds, and wave conditions exert systematic influences on vessels’ speed and course-over-ground profiles.

Temporal Convolutional Networks (TCNs) for Long-Range Dependencies. Temporal Convolutional Networks [13] employ dilated, causal 1D convolutions with residual connections, enabling exponential receptive field growth, parallelization, and stability advantages over RNNs. Variants (Attention-TCN, hybrid TCN-transformers) have shown success in diverse sequence domains, but maritime AIS association tasks remain underexplored. Compared to CNN-LSTM backbones, TCNs naturally cover longer contexts with fewer parameters and maintain training efficiency on sequences ranging from 50 to over 200 time steps. To our knowledge, no prior work has systematically applied a Dilated Residual Connection TCN (DRC-TCN) to the AIS track association problem.

Position of This Work. Building upon the above, our work contributes in two unique directions: (1) integration of buoy-based meteorological augmentation—wind, gust, pressure, air and water temperature—aligned via nearest-buoy and temporal interpolation; and (2) application of a DRC-TCN backbone for AIS association, enabling stable long-range dependency modeling without recurrent bottlenecks. Together with a discriminative CE+triplet loss, this closes a gap in the previous literature where AIS association relied solely on trajectory shape. By embedding vessels’ environmental responses into the feature space, our method sharpens class boundaries under crowded and overlapping conditions. Compared with previous CNN-LSTM [30] and vanilla TCN [13] architectures, the proposed DRC-TCN introduces residual-dilated connections and buoy-based feature fusion, which together stabilize long-range temporal modeling and capture external environmental influences on vessel motion. This integration effectively overcomes the convergence instability and limited contextual awareness observed in prior AIS association studies.

3. Methodology

The proposed model is a deep neural network that classifies an AIS trajectory segment into a specific vessel identity. The input to the network is a sequence of AIS readings of length $T=50$, where each reading consists of five features: the change in latitude $\Delta \mathrm{lat}$, change in longitude $\Delta \mathrm{lon}$, vessel heading degree (Heading), speed over ground (SOG), and course over ground (COG). To capture the influence of environmental conditions, six additional features are appended from the nearest ocean buoy: wind direction (WDIR), wind speed (WSPD), gust speed (GST), atmospheric pressure (PRES), air temperature (ATMP), and water temperature (WTMP). Thus, each time step is represented as a vector ${\mathbf{x}}_t\in {\mathbb{R}}^{11}$, and the full input sequence is denoted as ${\mathbf{x}}_{1:T}=[{\mathbf{x}}_1,\mathbf{x}2,\dots ,\mathbf{x}T]$. The model processes this sequential data and outputs a probability distribution over C possible vessel IDs, ultimately predicting the identity of the vessel that generated the trajectory. At the core of the model is a Temporal Convolutional Network (TCN) composed of multiple dilated residual convolutional blocks. The TCN extracts high-level temporal features from the AIS sequence while respecting the temporal order (causality) of the data. The final feature representation of the entire sequence is given by a fixed-length embedding vector $\mathbf{z}$, obtained via a global pooling over the TCN outputs. This embedding $\mathbf{z}$ is fed into a classification head (a fully connected layer with softmax) to produce the vessel ID prediction. In addition to the classification output, the embedding is also used in a metric learning objective: a triplet loss that encourages $\mathbf{z}$ to be more discriminative (i.e., trajectories from the same vessel result in similar embeddings, while those from different vessels are well-separated). The network is trained end-to-end using a combination of the standard cross-entropy loss for classification and the triplet loss on the embedding, as detailed below.

3.1. Data Acquisition and Preprocessing

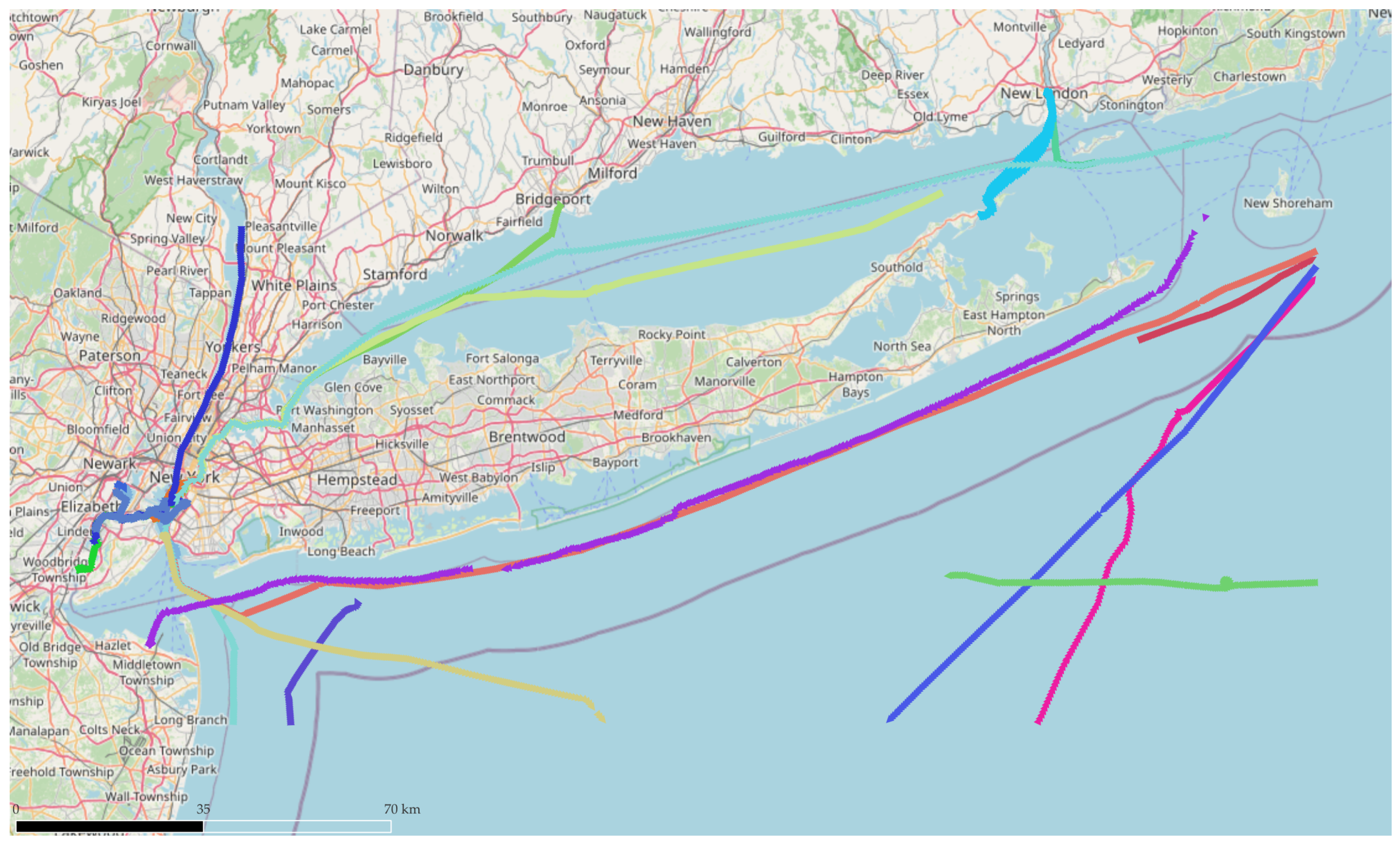
We evaluated our proposed approach on a corpus of real AIS data obtained from NOAA’s MarineCadastre database, augmented with meteorological observations from NOAA’s fixed coastal buoys. We focused on the coastal waterways surrounding Long Island, New York, a region with high vessel density and diverse vessel types. The observation area was bounded by the following: latitude: ${40.3}^{\circ }$ N to ${41.5}^{\circ }$ N, longitude: −${74.3}^{\circ }$ E to −${71.5}^{\circ }$ E. Examples of real-world vessel trajectories are shown in Figure 2.

The preprocessing pipeline was structured as follows:

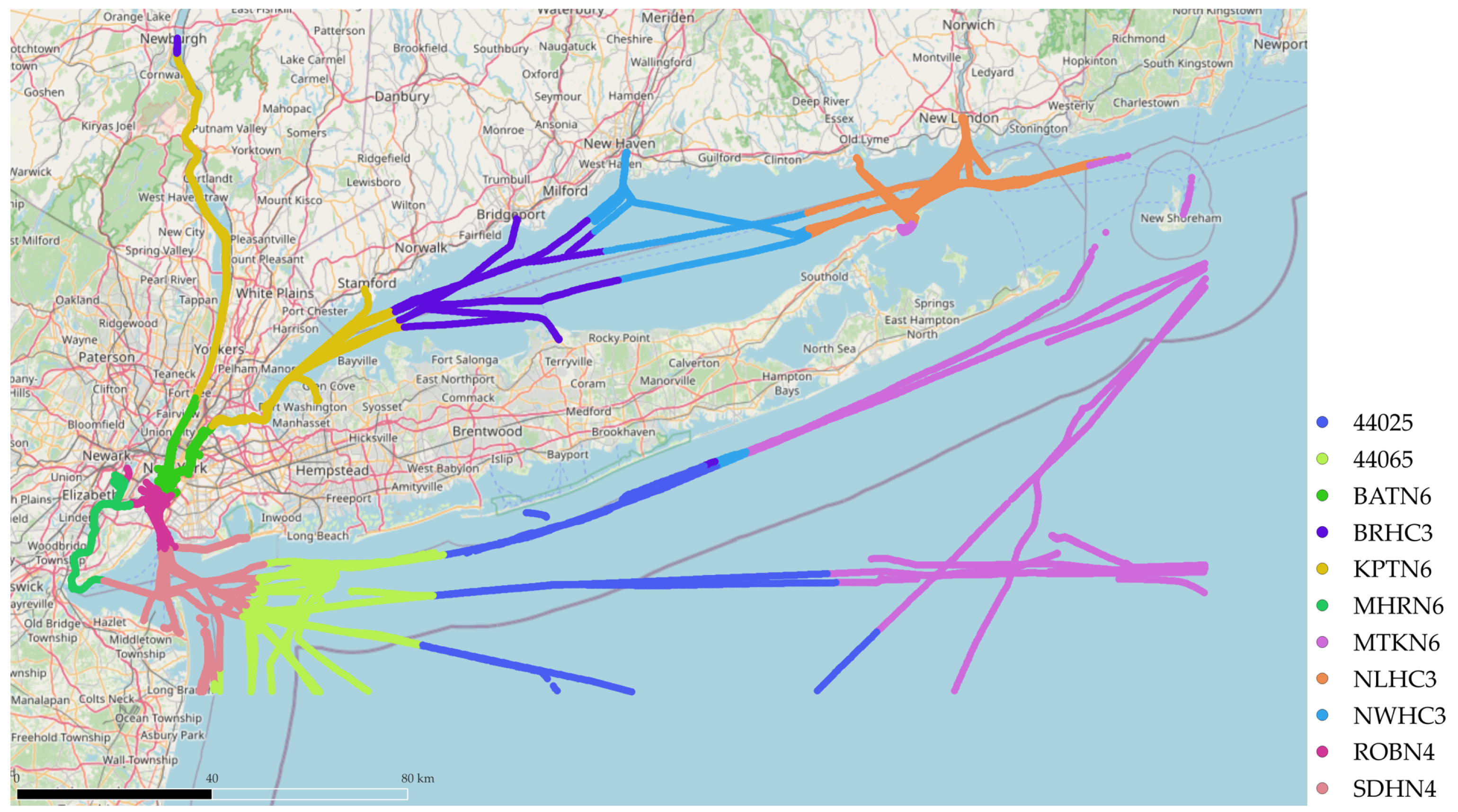
Step 1. Raw AIS Filtering: Remove invalid coordinates, speeds, and MMSI values (MMSI = 0). Step 2. Selection of vessels: Retain only Class-A moving vessels with more than 10 valid points. Step 3. Buoy Data Mapping: Assign each AIS record to its nearest NOAA buoy station using the Haversine distance (see Figure 3). Step 4. Temporal Alignment: Match the AIS timestamps with the buoy observations at a fixed 10-min interval using linear interpolation. Step 5. Feature Normalization: Normalize all 11 features (5 AIS + 6 buoys) to zero-mean and unit-variance for stable training.

3.1.1. AIS Dataset Overview

We collected AIS records for vessels operating within the study area. Each AIS record contains MMSI, timestamp, position (latitude, longitude), speed over ground (SOG), course over ground (COG), heading, and vessel type. After preprocessing, we retained approximately 574 unique vessels and $\mathrm{393,815}$ AIS records. The filtering process was as follows:

• Only moving vessels were included (SOG > 0.5 knots).
• Only Class A AIS messages were retained.
• Tugboats (VesselType = 52) were excluded.
• Records with MMSI = 0 were removed.
• Vessels with fewer than 10 AIS points were discarded.
• Records with Heading = 511 (undefined) were removed.

3.1.2. Buoy Data Integration

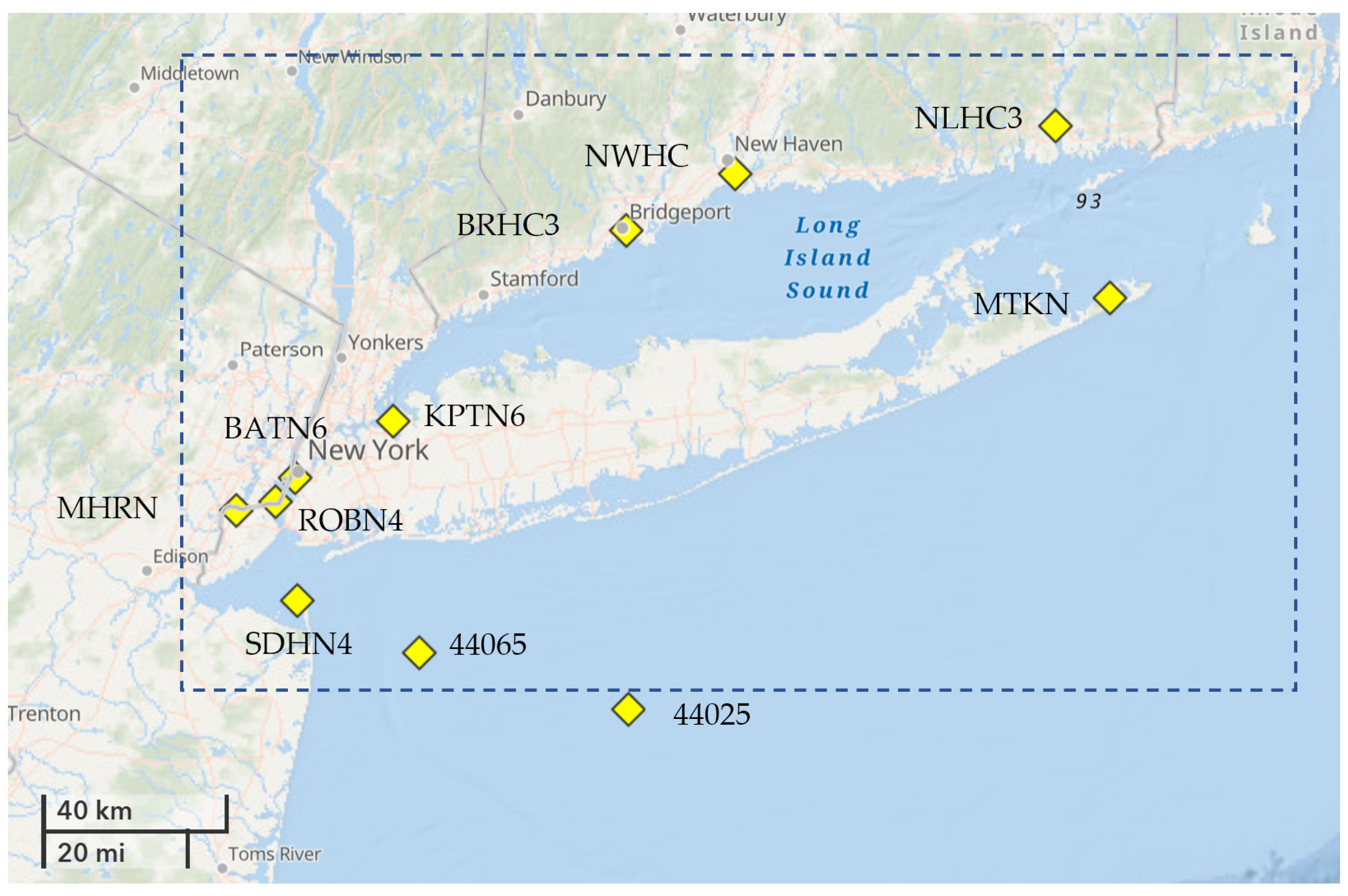
We augmented AIS tracks with environmental conditions from fixed NOAA buoys located in and around Long Island Sound. The buoys used in this study are as follows:

• 44025, 44065, BATN6, BRHC3, KPTN6, MHRN6,
• MTKN6, NLHC3, NWHC3, ROBN4, SDHN4

The location of each buoy is shown in Figure 4. These buoys typically provide six environmental parameters:

• WDIR—Wind Direction;
• WSPD—Wind Speed;
• GST—Gust Speed;
• PRES—Atmospheric Pressure;
• ATMP—Air Temperature;
• WTMP—Water Temperature.

Some buoys did not report all parameters at all times. Missing values were supplemented using data from the nearest buoy for the same time period. The nearest buoy for each AIS position was determined using the Haversine formula. The spatial mapping results of this buoy–AIS integration are illustrated in Figure 3, where each vessel route is assigned to the nearest buoy based on the Haversine distance. Distinct colors indicate the trajectories associated with each buoy, showing the spatial grouping used for data augmentation.

If a given buoy station did not report a particular environmental parameter at a timestamp, we substituted the reading from the nearest available buoy rather than discarding the data. This nearest-station substitution preserves a complete feature vector for each AIS time step at the cost of a small approximation error. We considered this trade-off acceptable because the study region is geographically compact, meaning conditions at neighboring buoys are likely similar. By filling gaps with the closest buoy’s readings, we minimized information loss due to missing sensor data—albeit at the risk of introducing minor noise or bias, as discussed in the Limitations section.

3.1.3. Temporal Alignment

AIS data were not resampled and were kept at their original reporting intervals. Only buoy meteorological data were resampled to a fixed 10-min interval. AIS records were matched to the nearest buoy reading in time, using linear interpolation when exact timestamps were not available.

3.1.4. Final Feature Set

Each final training sample consisted of 11 features (

Table 1. Summary of the fused AIS–buoy feature set and the ground-truth vessel identity label.

Column	Description	Unit	Notes
MMSI	Maritime Mobile Service Identity (vessel ID)	–	Serves as the ground-truth label
LAT	Latitude	degree	WGS84
LON	Longitude	degree	WGS84
SOG	Speed Over Ground	knot	From AIS
COG	Course Over Ground	degree	$[0,360)$
Heading	Vessel heading	degree	511 denotes undefined in some AIS
WDIR	Wind direction	degree	From buoy
WSPD	Wind speed	m/s	From buoy
GST	Gust speed	m/s	From buoy
PRES	Atmospheric pressure	hPa	From buoy
ATMP	Air temperature	°C	From buoy
WTMP	Water temperature	°C	From buoy

):

• AIS-derived features (5): Longitude, Latitude, COG, SOG, and Heading.
• Buoy-derived features (6): WDIR, WSPD, GST, PRES, ATMP, and WTMP.

The resulting dataset contains $\mathrm{366,428}$ samples across 574 unique vessels, with all features aligned in time and space.

3.1.5. Resulting Dataset

The final dataset contains a total of $\mathrm{393,815}$ AIS position reports from 574 unique vessels. Each record is represented by an 11-dimensional feature vector, consisting of 5 AIS-derived features (Longitude, Latitude, COG, SOG, Heading) and 6 buoy-derived environmental features (WDIR, WSPD, GST, PRES, ATMP, WTMP). All buoy observations were resampled to a fixed 10-min interval and matched to AIS records via nearest-neighbor temporal matching with linear interpolation.

3.1.6. Buoy-Derived Feature Distributions

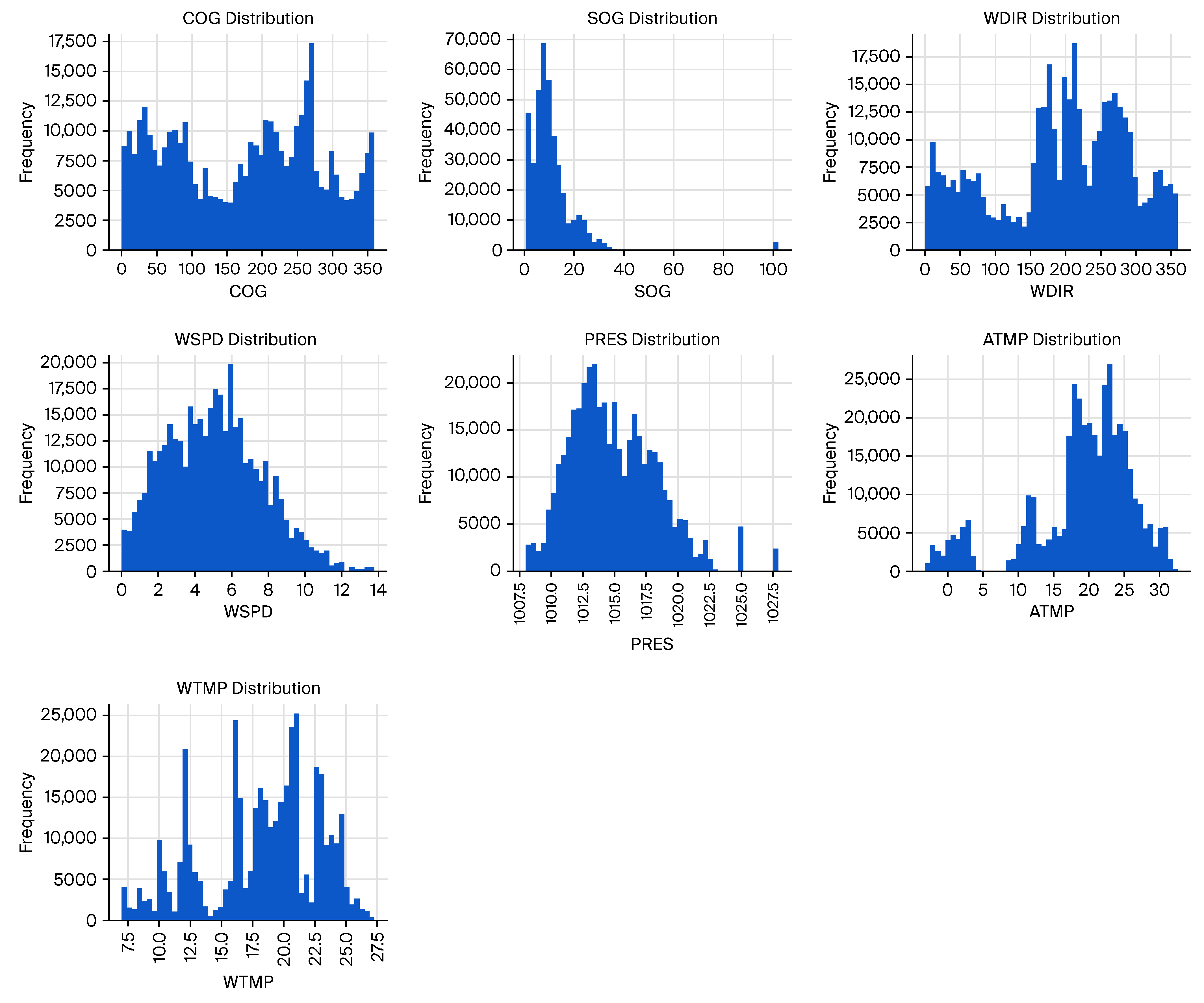
Figure 5 shows the distributions of selected AIS and buoy-derived features. Notably, COG and WDIR exhibit multimodal patterns reflecting dominant navigation routes and prevailing wind directions. SOG and WSPD distributions indicate that most vessels operate at moderate speeds under relatively calm wind conditions. PRES, ATMP, and WTMP distributions are narrower, reflecting stable atmospheric conditions during the observation period.

3.1.7. Sequential Characteristics

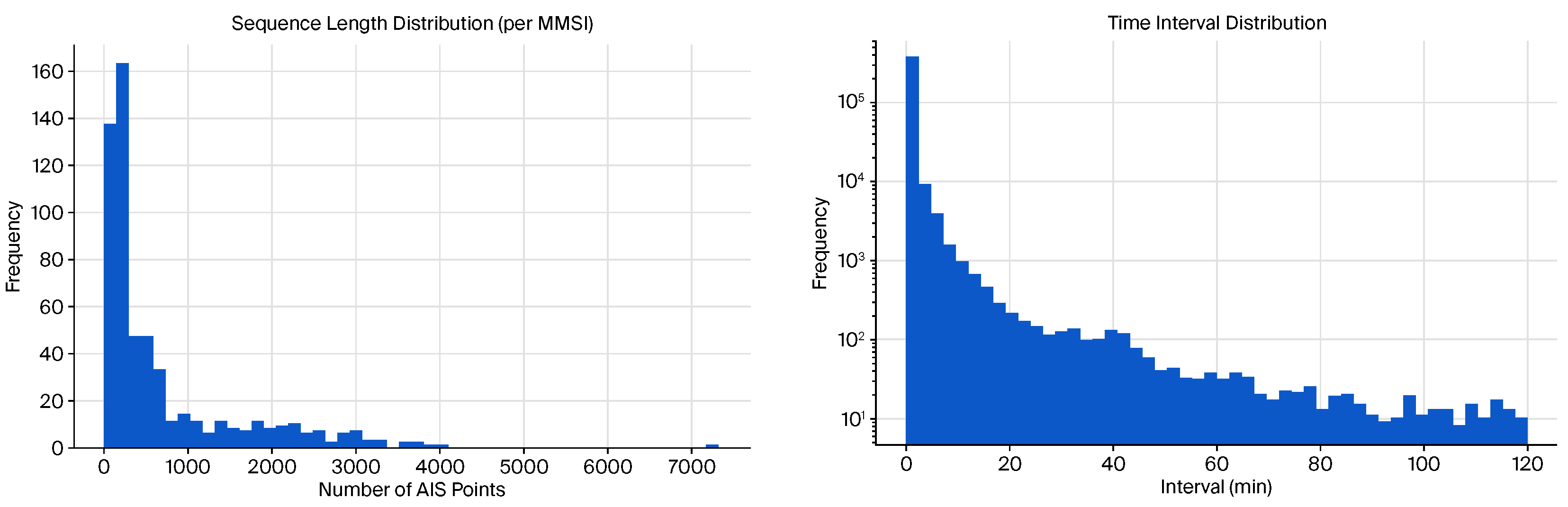
In addition to static feature distributions, we analyzed the sequential characteristics of the AIS dataset. Figure 6 presents the distribution of sequence lengths per vessel (MMSI) and the inter-message time intervals. Most vessels have between 300 and 1000 position reports in the dataset, though some have significantly longer or shorter sequences. The majority of AIS reports are separated by 2–10 min, which is consistent with Class A AIS transmission intervals for moving vessels.

3.1.8. Dataset Utility

This enriched dataset enables trajectory modeling that accounts for both navigational and environmental factors. The inclusion of environmental conditions allows for improved differentiation of vessel behaviors in congested waterways, particularly when spatial trajectories alone are insufficient to separate distinct movement patterns.

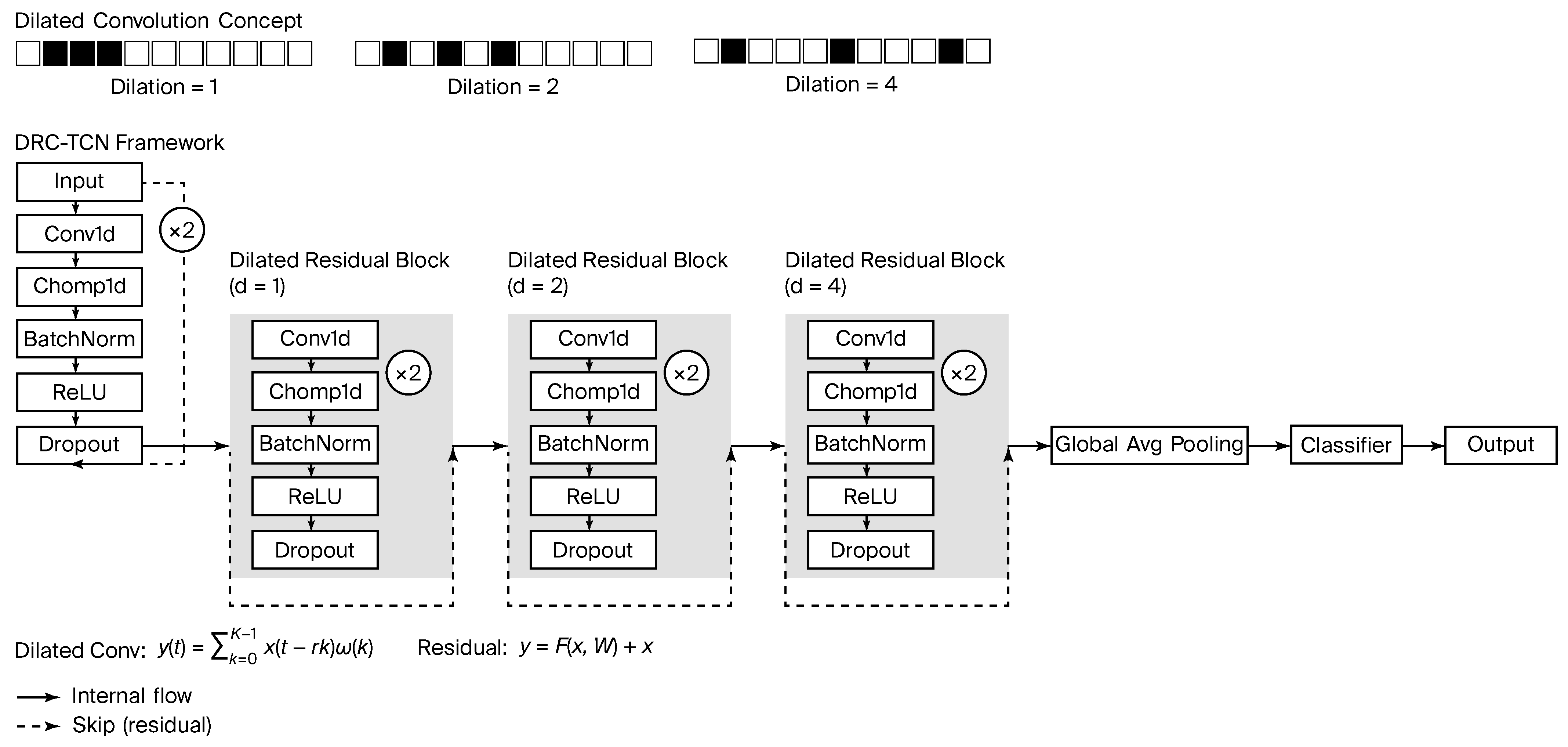
3.2. Dilated Residual Temporal Convolutional Network

The sequence modeling backbone of our architecture is a Dilated Residual Temporal Convolutional Network. A TCN is a 1D convolutional network designed for sequential data, characterized by the use of causal and dilated convolutions. Causal convolution means that, at any time step t, the convolutional filters only access inputs from time t and earlier, never from the future, thereby preserving the temporal causality in the sequence. Dilated convolution refers to convolutional filters that skip over certain time steps, allowing the network to have a larger receptive field without a proportional increase in the number of layers. Formally, a 1D dilated convolution with filter weights $w=[w_0,\dots ,w_{k-1}]$ and dilation factor d computes an output at time t as follows:

$$\left(x{\ast }_{d}w\right)\left(t\right)=\sum _{i=0}^{k-1}{w}_i,x(t-i·d)$$

(1)

where ${\ast }_d$ denotes a 1D dilated convolution operation, and k is the kernel size. In a causal convolution, $x(t-i·d)$ for $i·d>t$ is out of range (often effectively padded with zeros), ensuring no future values are used. By increasing the dilation factor d in successive convolutional layers, the TCN exponentially expands its temporal receptive field, enabling it to capture long-range dependencies in the AIS sequence even with relatively few layers. Our TCN is composed of L stacked convolutional blocks. Each block is a residual block with dilated causal convolutions. Specifically, within a single TCN block, the input passes through two consecutive dilated causal convolution layers (each followed by a non-linear activation such as ReLU, and, optionally, normalization and dropout for regularization). Let ${\mathbf{h}}^{(l-1)}$ denote the input to the l-th block (with ${\mathbf{h}}^{\left(0\right)}$ being the original input $\mathbf{x}1:T$). The block computes an intermediate activation ${\mathbf{u}}^{\left(l\right)}=\mathrm{ReLU}\left(\mathrm{Conv}{d_l}^{\left(1\right)}\left({\mathbf{h}}^{(l-1)}\right)\right)$; then, another convolution $\mathrm{Conv}{d_l}^{\left(2\right)}$ produces ${\mathbf{v}}^{\left(l\right)}=\mathrm{ReLU}\left(\mathrm{Conv}{d_l}^{\left(2\right)}\left({\mathbf{u}}^{\left(l\right)}\right)\right)$. Here, ${\mathrm{Conv}}_{d_l}^{\left(j\right)}$ denotes a 1D convolution with dilation $d_l$ in block l. A residual connection adds the block’s input to the output of the convolution layers, yielding the final output of the block:

$${\mathbf{h}}^{\left(l\right)}={\mathbf{h}}^{(l-1)}+{\mathbf{v}}^{\left(l\right)}$$

(2)

If needed, a linear projection is applied to ${\mathbf{h}}^{(l-1)}$ prior to addition to match dimensionality. This residual addition enables the model to propagate information across layers and facilitates stable training of deep networks. The dilation factor $d_l$ is typically doubled for each subsequent block (e.g., $d_1=1,d_2=2,d_3=4,\dots$), so that the receptive field grows exponentially with the depth L. With an appropriate number of blocks, the TCN can effectively model patterns spanning the full length of the input sequence (50 time steps in our case). The overall layer configuration of the DRC-TCN is listed in

Table 2. Architecture summary of the Dilated Residual Connection Temporal Convolutional Network (DRC-TCN).

Stage	In→Out Ch.	Kernel	Dilation	Notes
Input	T × F	–	–	Sequence length T = 50, feature dim F = 11
TCN Block 1	$11\to 48$	5	1	Dilated residual block + BN, ReLU, Dropout
TCN Block 2	$48\to 96$	5	2	Dilated residual block + BN, ReLU, Dropout
TCN Block 3	$96\to 192$	5	4	Dilated residual block + BN, ReLU, Dropout
Global Avg Pool	$192\to 192$	–	–	Pool over time axis
Classifier (FC)	$192\to 64\to C$	–	–	ReLU, Dropout, Linear to C classes

, and its structural overview is illustrated in Figure 7.

3.3. Embedding and Classification Head

After passing through the stacked TCN blocks, the model produces a sequence of high-level feature maps over time. We then aggregate these time-dependent features into a single vector representation for the entire sequence. Specifically, we apply a global pooling operation across the time dimension of the TCN output. In our implementation, Global average pooling was applied, which computes the mean of each feature channel over the T time steps, producing a fixed-length embedding vector $\mathbf{z}\in {\mathbb{R}}^D$. This embedding $\mathbf{z}$ is intended to capture the salient characteristics of the vessel’s trajectory segment in a compact form. The embedding vector $\mathbf{z}$ is fed into the classification head to predict the vessel ID (MMSI). The classification head consists of a fully connected layer (or equivalently, a $D\times C$ weight matrix plus a bias term) that maps the embedding to C logits (scores), one for each possible vessel identity. We denote the vector of logits as $\mathbf{o}\in {\mathbb{R}}^C$. A softmax function is then applied to $\mathbf{o}$ to produce a probability distribution over the C classes:

$${\widehat{p}}_c={\displaystyle \frac{\exp \left(o_c\right)}{{\sum }_{j=1}^C\exp \left(o_j\right)}}$$

(3)

Here, ${\widehat{p}}_c$ denotes the predicted probability for class c (for $c=1,\dots ,C$). The class with the highest probability, ${max}_c{\widehat{p}}_c$, is taken as the model’s predicted vessel ID. The parameters of both the TCN layers and the classification head are learned jointly during training.

3.4. Loss Function: Cross-Entropy and Triplet Loss

To train the network, we utilize a composite loss function that combines a classification loss and a metric learning loss. The primary classification loss is the softmax cross-entropy, which encourages the network to output the correct vessel ID for each input sequence. Given the ground-truth class label y for an input sequence (expressed as a one-hot vector over C classes) and the predicted probability vector $\widehat{\mathbf{p}}=[\widehat{p}1,\dots ,\widehat{p}C]$ from the softmax, the cross-entropy loss is defined as follows:

$${\mathcal{L}}_{\mathrm{CE}}=-\sum _{c=1}^C{y}_c\log \left({\widehat{p}}_c\right)$$

(4)

which is minimized when the model assigns a high probability to the correct class. While the cross-entropy loss trains the model to be accurate in classifying known vessels, it does not explicitly enforce that the learned embedding space $\mathbf{z}$ is well-structured in terms of similarity between trajectories. We therefore introduce a triplet loss on the embedding $\mathbf{z}$ to improve the discriminative quality of the features. The triplet loss operates on triplets of samples, consisting of an anchor (a), a positive (p), and a negative (n). For a given anchor trajectory (with embedding ${\mathbf{z}}_a$) belonging to a certain vessel, we take a positive sample ${\mathbf{z}}_p$ which is another trajectory from the same vessel, and a negative sample $\mathbf{z}n$ which is a trajectory from a different vessel. The triplet loss is formulated as follows:

$${\mathcal{L}}_{\mathrm{triplet}}=max\left(0,|{\mathbf{z}}_a-{\mathbf{z}}_p{|}_2^2-{|{\mathbf{z}}_a-{\mathbf{z}}_n|}_2^2+\alpha \right)$$

(5)

where ${|·|}_2$ denotes the Euclidean distance, and $\alpha >0$ is a margin parameter. This loss drives the network to reduce the distance between the anchor and positive embeddings (making same-vessel trajectories more similar) and to increase the distance between the anchor and negative embeddings by at least the margin $\alpha$. Only triplets that violate this margin condition (i.e., those for which $|{\mathbf{z}}_a-{\mathbf{z}}_p{|}_2^2+\alpha >{|{\mathbf{z}}_a-{\mathbf{z}}_n|}_2^2$) contribute a non-zero loss. This focuses the training on the more challenging examples (often referred to as hard or semi-hard triplets). The total training objective is a weighted sum of the cross-entropy and triplet losses:

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{CE}}+\lambda ·{\mathcal{L}}_{\mathrm{triplet}}$$

(6)

where $\lambda$ is a tunable hyperparameter that controls the trade-off between the classification accuracy and the embedding discriminability. By optimizing ${\mathcal{L}}_{\mathrm{total}}$, the network learns to accurately classify vessel IDs while simultaneously producing embeddings that cluster trajectories of the same vessel and repel those of different vessels.

3.5. Training Configuration

We train the model end to end using mini-batch stochastic gradient descent. Each mini-batch consists of a set of trajectory sequences (of length 50) along with their vessel ID labels. To effectively utilize the triplet loss, we ensure that each batch contains multiple trajectories from some of the same vessels so that anchor–positive pairs can be formed. During training, triplets are chosen from each mini-batch (either by random sampling or using an online mining strategy to select hard examples) to compute ${\mathcal{L}}_{\mathrm{triplet}}$. The margin $\alpha$ for the triplet loss is treated as a hyperparameter (e.g., $\alpha =0.2$), and the weight $\lambda$ for the triplet term is adjusted on a validation set to balance the two loss components. We use the Adam optimizer to minimize ${\mathcal{L}}_{\mathrm{total}}$, with an initial learning rate (e.g., ${10}^{-3}$) that may decay as training progresses. The network weights are initialized randomly, and we apply regularization techniques such as dropout within the TCN blocks and $L_2$ weight decay to prevent overfitting. Training is run for a fixed number of epochs or until convergence based on validation performance. Throughout training, the combined loss drives the model to improve both classification accuracy and the quality of the embedding space for vessel trajectory representations.

4. Experiments

4.1. AIS Dataset and Preprocessing

We evaluated the proposed approach on a corpus of real AIS data obtained from NOAA’s MarineCadastre database. We focused on a specific geographic region with heavy vessel traffic (a major port area) and extracted AIS records from the first day of each month. Then, we identified a set of 574 distinct vessels that were consistently present in the area and used their data for our experiments. These vessels represent a mix of cargo ships, tankers, and passenger ferries, providing a diverse set of motion patterns.

Each AIS record contains the MMSI, timestamp, latitude, longitude, speed over ground, and course/heading. For data where MMSI was available, we treated it as the ground-truth identity label (during training and evaluation, MMSI is withheld from the input features). We preprocessed the data by first filtering obviously erroneous points (e.g., invalid coordinates or speeds). We then segmented each vessel’s continuous AIS feed into trajectory segments of a fixed length, i.e., $T=50$ timestamps. This segment length was chosen to capture roughly several hours of movement (given typical 2–5-min AIS reporting intervals for moving vessels). If a vessel had a continuous trajectory longer than T, we slid a window to create multiple samples (with 50% overlap between consecutive windows to augment the training data). If a trajectory segment was shorter than T due to the vessel leaving the region or a long gap, we discarded that segment to avoid excessive padding. In total, we obtained about $\mathrm{366,428}$ labeled sequence segments across the 574 vessels.

The vector of features of each input time step ${\mathbf{x}}_t$ consisted of four features: the vessel’s $\Delta$latitude and $\Delta$longitude (difference in position from the previous time step, in kilometers, in a local projection of the tangent plane), speed over the ground and course over the ground. Using position-difference features was observed to improve normalization of the data for spatial location and focus the model on movement patterns rather than absolute location (since some vessels always stay in certain channels, the absolute position could inadvertently cue the identity; using the differences reduces this bias and forces the model to rely on how the vessel moves). We normalized each feature to zero-mean and unit-variance values based on the training set.

The dataset was split into training, validation, and test sets at a ratio of 70%, 20%, and 10%, respectively. Unlike vessel-level splitting, we first constructed fixed-length sequences of 50 AIS messages with 50% overlap from all vessels, and then randomly assigned these sequences into the three sets. As a result, different sequences from the same vessel may appear across training, validation, and test sets, but the overall split ratio was strictly maintained.

Notably, we ensured that no overlapping trajectory segments from the same continuous vessel track were allocated to different sets. This step prevents any identical AIS observations from appearing in both training and test partitions (i.e., no direct data leakage). It is important to note, however, that the test set vessel identities were also seen during training (a closed-set assumption). Thus, the model’s near-perfect accuracy reflects performance in a scenario with known vessel classes, and not necessarily an open-world setting. We acknowledge this evaluation context in our discussion and emphasize in the Limitations section that generalization to entirely unseen vessels remains an area for future study.

4.2. Baseline Models

We compared the TCN model against a CNN-LSTM baseline based on the LSTM architecture:

• LSTM: A standard LSTM-based classifier. Long Short-Term Memory (LSTM) networks [11] extend the original recurrent neural network formulation [36,37] to mitigate the vanishing gradient problem and capture long-range temporal dependencies. Instead of relying on a standalone LSTM, we used a CNN-LSTM baseline, detailed in the next section.
• CNN-LSTM: A hybrid model inspired by [12] and earlier convolutional recurrent architectures [38,39]. We implemented a one-dimensional CNN with two convolutional layers (each with 32 filters, kernel size 3, ReLU activation) that transforms the sequence of four-dimensional feature vectors into higher-level features. These features are then fed into an LSTM (with 128 hidden units) followed by a dense layer for classification. The CNN-LSTM can capture short-term local patterns (e.g., sudden turns or stops) via convolution before the LSTM models the longer sequence context.
• Vanilla TCN: A baseline temporal convolutional model composed of stacked causal and dilated 1-D convolutions without residual shortcuts, providing a minimal configuration for capturing temporal dependencies across multiple receptive fields.
• Attention TCN: Enhances the vanilla TCN by introducing a temporal self-attention mechanism that dynamically re-weights hidden activations across time steps, enabling the network to focus on salient motion intervals within AIS sequences.
• Graph TCN: Incorporates graph-convolutional operations between temporal layers to capture spatial dependencies among trajectory attributes (e.g., $\Delta$lat–$\Delta$lon–SOG–COG), thus modeling both temporal and spatial correlations simultaneously.
• MS-TCN-RF (Multi-Stage TCN with Residual Fusion): Applies a multi-stage refinement strategy where each stage progressively refines the predictions from the previous one through residual fusion blocks, improving temporal smoothness and prediction consistency across stages.
• Proposed DRC-TCN: Combines dilated residual blocks with layer normalization and dropout (p = $0.15$) for robust optimization under noisy AIS inputs. This design maintains the exponential receptive-field growth of TCNs while stabilizing training through residual connections.

4.3. Training Setup

All models were trained using the Adam optimizer with an initial learning rate of 0.001. We applied early stopping based on the validation $F1$ score: if the validation score did not improve for 10 epochs, training was stopped to prevent overfitting. The batch size was set to 64 sequence segments. We trained for a maximum of 250 epochs.

To ensure a fair comparison, an identical preprocessing pipeline was applied across all models. AIS trajectories were segmented into fixed-length sequences of 50 messages with 50% overlap, and all features were normalized using a Min–Max scaler—a standard technique in time-series modeling to ensure convergence stability and balanced feature contribution [40,41,42]. In contrast to prior works that employ trajectory reversal or synthetic noise injection, we deliberately refrained from such augmentations (e.g., adding Gaussian noise to simulate sensor variability [43] or applying geographical perturbations via in-circle/on-circle schemes [44,45]), in order to evaluate model discriminative power under realistic AIS conditions. Moreover, our framework enriches input data with contextual environmental cues derived from coastal buoy measurements, thereby enhancing robustness beyond AIS-only baselines.

4.4. Evaluation Metrics

We evaluated track association performance using standard classification metrics: Accuracy, Precision, Recall, and F1-score [46,47,48]. Since our test set contains one sample (trajectory segment) labeled with a true vessel ID, we compute these metrics across all samples, treating each vessel ID as a class. In a multi-class setting with fairly balanced data per class, accuracy and $F1$-score tend to be similar; however, $F1$-score is more informative if there is variation in class support. We report the macro-averaged Precision, Recall, and F1-score (i.e., average of per-vessel metrics) to ensure that performance is not dominated by a few vessels with many samples.

5. Results and Discussion

5.1. Quantitative Performance

Table 3. Comparison of track association performance and model size on the AIS dataset. All methods use the same preprocessing and train/validation/test split built from fixed-length AIS trajectory segments. Accuracy, Precision, Recall, and F1-score are reported on the held-out test set (%). #Params indicates the number of trainable weights. All results in this table were obtained using the 5-dimensional AIS-only feature configuration without buoy-based inputs. The proposed DRC-TCN achieves the best overall performance while maintaining a parameter budget comparable to that of other models, including the vanilla TCN, highlighting a favorable accuracy–efficiency trade-off.

Model	#Params	Accuracy	Precision	Recall	F1-Score
CNN-LSTM (Baseline) [12]	275,542	92.61	88.97	85.93	86.44
TCN	452,934	93.54	92.99	90.79	91.43
Attention TCN	601,158	89.27	89.46	85.24	86.26
Graph TCN	440,890	90.44	89.91	86.96	87.35
MS-TCN-RF	607,690	90.93	96.22	85.02	85.97
DRC-TCN (Proposed)	405,178	99.16	98.12	97.94	97.96

summarizes the performance of the proposed TCN model in comparison to the baseline CNN-LSTM, evaluated on the test set comprising 574 vessels (10% of the entire dataset, approximately 36,642 trajectory segments). The TCN achieved the highest accuracy and $F1$ score among the models.

As shown in Table 3, the CNN-LSTM baseline achieved 92.6% accuracy (F1 = 86.4%), validating the benefit of incorporating convolutional layers as reported in [12]. In contrast, our proposed DRC-TCN increased the accuracy to 99.1% (F1 = 97.9%), yielding a nearly one-order-of-magnitude reduction in error rate compared to the CNN-LSTM. This substantial improvement demonstrates that the modified TCN state empowers the network to capture highly discriminative features for reliable vessel track association.

As numerical results already demonstrate extremely high accuracy (Table 3), a detailed confusion-matrix visualization is omitted for brevity. Nevertheless, the model exhibited clear class separability, with errors restricted to a few vessels operating on nearly identical routes, while the majority of trajectories were correctly associated, consistent with standard interpretations of confusion-matrix analysis [49].

To further examine the effect of environmental features,

Table 4. Comparison of DRC-TCN performance under different input dimensionalities. All methods use the same preprocessing and train/validation/test split built from fixed-length AIS trajectory segments. Accuracy, Precision, Recall, and F1-score are reported on the held-out test set (%). This table compares the 5-dimensional AIS-only configuration with the 11-dimensional AIS + Buoy configuration to illustrate the effect of environmental features on association performance.

Model/Input	Accuracy	Precision	Recall	F1-Score
DRC-TCN (5D, AIS-only)	99.16	98.12	97.94	97.96
DRC-TCN (11D, AIS + Buoy)	99.75	99.34	99.31	99.31

Note. The 11-dimensional AIS + Buoy setting augments the 5 AIS-derived kinematic features with 6 buoy-based meteorological variables (WDIR, WSPD, GST, PRES, ATMP, WTMP) via nearest-station time alignment.

compares the model performance between the 5-dimensional AIS-only and 11-dimensional AIS + Buoy configurations. The inclusion of buoy-based meteorological variables led to slightly improved accuracy and faster convergence, demonstrating that environmental context enhances the robustness of vessel trajectory association.

The proposed DRC-TCN demonstrates consistently higher classification performance compared to CNN-LSTM. In particular, the latent feature space learned by DRC-TCN exhibits clearly separated and well-formed identity clusters, as illustrated by the t-SNE visualization in Figure 8. This indicates that the model not only improves prediction accuracy but also enhances the intrinsic separability of vessel representations in the embedding space, leading to more reliable identity discrimination.

The precision and recall values for TCN are also well balanced (92.9% and 90.7%, respectively), suggesting that the model is not biased toward over-predicting certain vessel classes at the expense of others. In contrast, the other baselines generally showed lower recall, meaning they missed more true associations (likely predicting another vessel instead), whereas CNN-LSTM exhibited relatively balanced precision and recall overall.

Although the DRC-TCN contains a slightly larger number of trainable parameters (≈4.05 × ${10}^5$) than the CNN-LSTM baseline (≈2.75 × ${10}^5$), this increase results from the additional residual and dilated layers that enhance temporal coverage and training stability. The difference is moderate relative to the achieved improvement in accuracy and does not impose substantial computational overhead. In practice, a single forward inference on a mid-range GPU (e.g., RTX 2060) incurs only a few milliseconds of latency (typically 3–10 ms for the sequence lengths used in this study). Hence, the DRC-TCN provides a favorable balance between predictive performance and practical deployability for near-real-time maritime surveillance.

5.2. Vessel Behavior Analysis

To better understand the types of errors made by each model, we qualitatively examined vessel-specific behavior patterns in the test set. The plain CNN-LSTM exhibited broader class overlap, often mixing up vessels that followed highly similar trajectories. In contrast, the TCN demonstrated clearer class separation, with remaining ambiguities confined to a few cases of nearly identical operational routes.

For instance, two passenger ferries that shuttle along nearly identical routes were frequently misidentified by the CNN-LSTM, achieving only about 60% recall for each vessel and often swapping their identities. This relatively low recall was not common across the dataset, but occurred specifically for this pair of vessels whose trajectories overlapped almost entirely, making them particularly challenging to distinguish. The TCN, however, distinguished them correctly in most instances, improving recall to over 80% for both. This observation suggests that the temporal convolutional representation helped capture subtle differences in their movement timing or speed profiles that recurrent models tended to smooth over.

Another case where all models exhibited difficulty involved a pair of medium-sized cargo ships that occasionally follow each other at close range. Because their AIS tracks can overlap both spatially and temporally, even a human observer might struggle to differentiate them without additional contextual information. Consequently, the models sometimes misassigned trajectory segments between the two. These findings indicate that some ambiguities in vessel identity stem from inherent limitations of AIS-only data, which might be alleviated by incorporating auxiliary features such as vessel dimensions or dynamic motion characteristics in future work.

5.3. Dilated Residual Connection TCN

The proposed DRC-TCN model was designed to effectively capture both short- and long-range dependencies within vessel trajectory data. A key advantage of this architecture lies in its use of dilated convolutions, which exponentially expand the receptive field without a proportional increase in the number of parameters. This allows the model to detect motion patterns across varying temporal scales, from rapid local changes such as sudden turns to long-term behaviors such as cruising or loitering. Furthermore, the incorporation of residual connections mitigates gradient vanishing and stabilizes optimization, enabling deeper network construction while preserving efficient convergence.

Experimental results demonstrate that DRC-TCN consistently outperforms both standard LSTM-based models and conventional TCN baselines in terms of classification accuracy and F1-score. In particular, the dilated residual connections enhance the model’s ability to disambiguate overlapping trajectories and noisy AIS inputs, which are common in congested maritime environments. This improvement is evident in the t-SNE analysis, where DRC-TCN achieves more distinct class boundaries compared to the blurred decision surfaces of recurrent models. The reduction in misclassification among vessels with highly similar movement patterns underscores the model’s strength in capturing subtle temporal dependencies.

Another important finding is the favorable balance between performance and efficiency. Unlike CNN-LSTM-based architectures that require sequential processing of each time step, DRC-TCN benefits from parallelizable convolutional operations, resulting in significantly reduced training and inference times. Combined with the residual connections, this architecture provides both robustness and scalability, making it well suited for large-scale trajectory association tasks in real-world AIS systems.

Overall, the DRC-TCN not only advances accuracy but also provides a practical foundation for future extensions, such as integrating attention modules or incorporating external contextual information (e.g., weather, geographic constraints). These findings validate the architectural choice of dilated residual connections as a critical factor in achieving state-of-the-art performance in multi-vessel track association.

5.4. Ablation Study

To further investigate the effectiveness of the proposed DRC-TCN, we conducted an ablation study focusing on structural variations and parameter changes, as summarized in

Table 5. Ablation study of the proposed DRC-TCN model. Performance is compared across (i) channel and kernel size variations, (ii) dropout rate settings, (iii) different loss function types, and (iv) weighting factor $\lambda$ in the combined loss ${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{CE}}+\lambda ·{\mathcal{L}}_{\mathrm{Triplet}}$. All experiments were conducted under the same 5-dimensional AIS-only feature setting described in Table 3.

Aspect	Configuration	#Params	Accuracy	Precision	Recall	F1
Channels & Kernel	$[32,64,128]$, kernel size = 3	150,646	96.32	95.05	93.78	94.15
	$[48,96,192]$, kernel size = 5 (Proposed)	405,178	99.16	98.12	97.94	97.96
Dropout Rate	0.10	*	97.86	97.47	97.40	97.42
	0.35	*	92.25	89.90	87.76	87.90
	0.50	*	74.25	76.60	69.62	70.29
Loss Function	CE + Triplet ($\lambda$ablation, combined)
	CE only ($\lambda =0$)	*	96.42	95.63	95.02	95.13
	Triplet only ($\lambda =1$)	*	97.01	95.69	95.71	95.48
	$\lambda =0.10$	*	97.88	96.78	96.50	96.48
	$\lambda =0.35$	*	96.35	95.93	95.22	95.40
	$\lambda =0.50$	*	96.36	95.74	95.28	95.35

* For all Dropout Rate and Loss Function configurations, the number of parameters is identical to the proposed setting (except the first row, which has fewer parameters). The proposed DRC-TCN used a dropout rate of 0.15 and a loss weighting factor of $\lambda$ = 0.15.

. Four aspects were examined: (i) channels and kernel size; (ii) dropout rate; (iii) loss function type; and (iv) the weighting factor $\lambda$ in the combined loss ${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{CE}}+\lambda ·{\mathcal{L}}_{\mathrm{Triplet}}$.

Channels and Kernel Configuration: Increasing the number of channels and kernel size substantially improved classification performance. With a smaller configuration of [32, 64, 128] channels and kernel size 3, the model achieved 96.32% accuracy (Precision 95.05%, Recall 93.78%, F1 94.15). In contrast, the proposed configuration of [64, 128, 192] channels with kernel size 5 reached 99.16% accuracy, 98.12% precision, 97.94% recall, and 97.96 F1, demonstrating the benefit of larger capacity (405 K parameters vs. 150 K).

Dropout Rate: Performance degraded as the dropout rate increased. At 0.10, the model maintained high accuracy (97.86%) with balanced metrics (Precision 97.47%, Recall 97.40%, F1 97.42). Increasing dropout to 0.35 reduced accuracy to 92.25% (Precision 89.90%, Recall 87.76%, F1 87.90), while a dropout of 0.50 caused a collapse to 74.25% accuracy (Precision 76.00%, Recall 69.62%, F1 70.29). These results indicate that moderate dropout (≈0.10) provides regularization without harming feature learning.

Loss Function: Using only cross-entropy (CE) loss or only triplet loss yielded lower performance than combining them. CE-only training ($\lambda$ = 0) produced 96.42% accuracy (Precision 95.63%, Recall 95.02%, F1 95.13), while triplet-only training ($\lambda$ = 1) achieved 97.01% accuracy (Precision 95.69%, Recall 95.71%, F1 95.48). When both were combined, the best results were obtained with $\lambda =0.1$, yielding 97.88% accuracy, 96.78% precision, 96.50% recall, and 96.48 F1. This outperforms either CE or triplet loss alone.

Loss Weighting ($\mathbf{\lambda }$): Within the combined loss, the weighting factor significantly influenced performance. While $\lambda =0.1$ produced the highest metrics (97.88% accuracy, 96.48 F1), larger $\lambda$ values (0.35 or 0.5) reduced accuracy to ≈96.35% and slightly decreased precision and recall. This indicates that a relatively small weight on the triplet loss (around 0.1) is optimal, whereas excessive emphasis on the triplet term degrades overall performance.

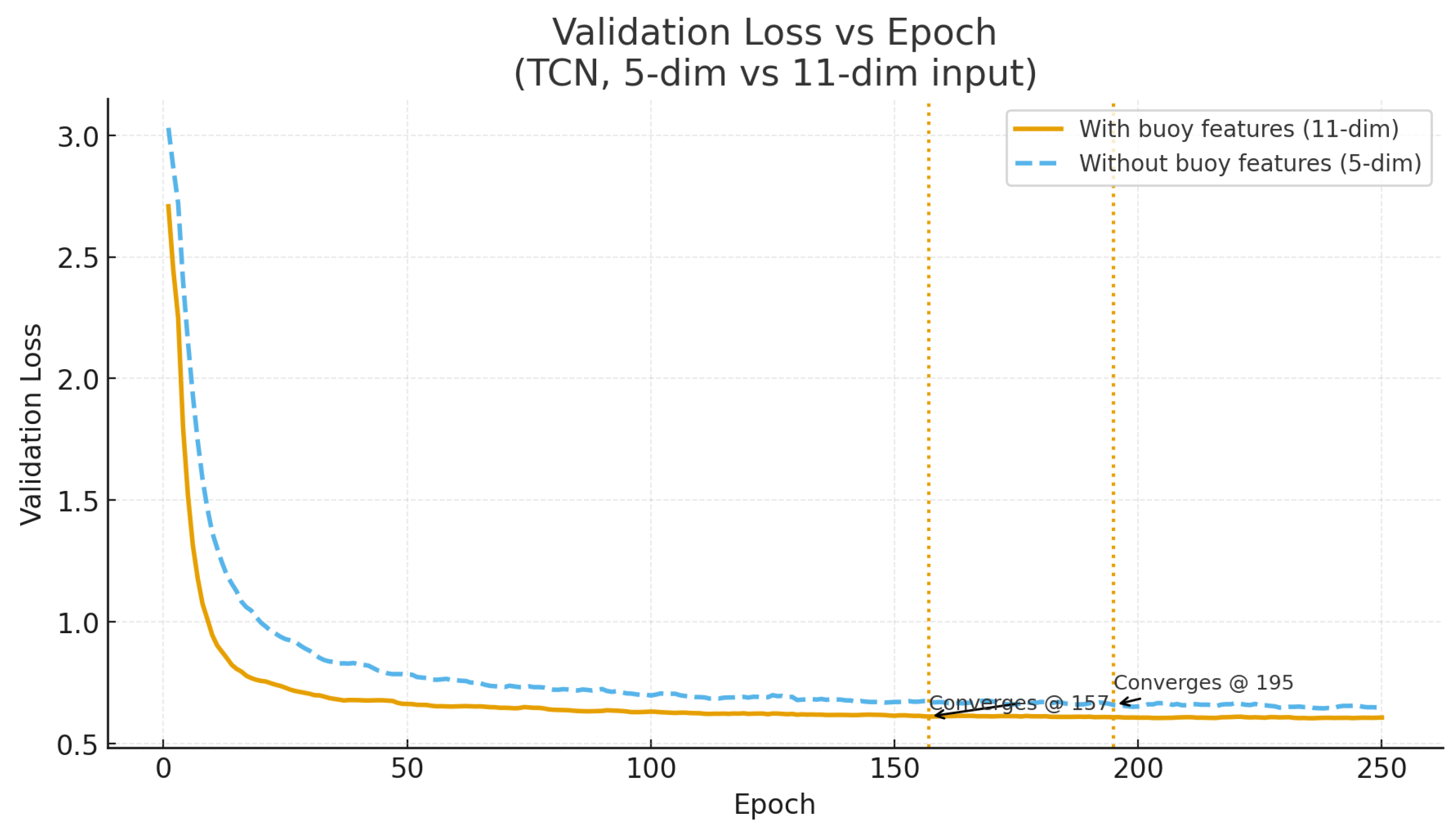
Effect of Input Dimensionality (AIS-only vs. AIS + Buoy). In addition to architectural variations, we examined how environmental augmentation affects training dynamics. Figure 9 compares the validation-loss evolution between models trained with AIS-only (5-dimensional) and AIS + buoy (11-dimensional) inputs. The model incorporating buoy-derived meteorological variables reached a stable validation loss approximately 40 epochs earlier (195 → 157), confirming that environmental context accelerates convergence and enhances generalization stability. This finding supports the hypothesis that weather-aware features improve the learning efficiency of temporal models by encoding external forces influencing vessel motion dynamics.

In summary, Table 5 confirms that the proposed [64, 128, 192] channel configuration with kernel size 5, a dropout rate of 0.10–0.15, and a combined loss with $\lambda \approx 0.1$ achieves the best trade-off between accuracy and generalization.

6. Conclusions

In this paper, we presented the Dilated Residual Connection Temporal Convolutional Network (DRC-TCN) for multi-vessel track association using AIS data. Unlike recurrent architectures that rely on sequential processing, the proposed model employs dilated convolutions to efficiently capture both short- and long-range dependencies, while residual connections stabilize training and accelerate convergence.

Through extensive experiments, DRC-TCN consistently outperformed the conventional CNN-LSTM baseline across all evaluation metrics, including accuracy, precision, recall, and F1-score. The model demonstrated particular effectiveness in distinguishing overlapping trajectories and mitigating the impact of noisy AIS signals, both of which are common challenges in congested maritime environments. Moreover, the parallelizable structure of TCN renders DRC-TCN computationally efficient and scalable, enabling deployment in large-scale surveillance systems.

The findings from this work suggest several promising avenues for future research. One direction is to extend DRC-TCN to the open-set track association problem, where previously unseen vessels must be detected and classified as unknown. Another is to integrate complementary modalities, such as radar, environmental data, or geographic constraints, to further enhance robustness under ambiguous or degraded conditions. Finally, combining DRC-TCN with probabilistic tracking frameworks (e.g., multi-hypothesis tracking or particle filtering) may yield hybrid systems that exploit the strengths of both deep learning and traditional statistical inference.

In summary, DRC-TCN demonstrates a strong balance of accuracy, efficiency, and robustness for vessel track association, providing a practical foundation for real-world maritime monitoring. By enabling continuous and reliable vessel identification, this approach has the potential to improve maritime safety, support regulatory compliance, and help prevent illegal activities at sea. Ultimately, the proposed model represents a step toward more intelligent and trustworthy surveillance systems that safeguard both commercial operations and global maritime security.

Limitations and Future Work. Although the proposed DRC-TCN achieved outstanding accuracy (99.7%) and F1-score (99.3%), these results were obtained under a closed-set assumption, in which the vessel identities in the test set were also present during training. Therefore, the generalization capability to previously unseen vessels remains an open challenge and will be further investigated in future studies.

The present work focuses on a single coastal region (New York area) to ensure controlled evaluation, and the model’s cross-regional robustness has not yet been verified. Future work will extend validation to multiple geographic and environmental settings to examine the model’s adaptability.

While the integration of buoy-based meteorological variables qualitatively improved stability, a more systematic ablation analysis comparing models with and without environmental augmentation will be conducted to quantify this effect. Furthermore, the current approach assumes genuine AIS messages; handling spoofed or corrupted signals lies outside the present scope but will be incorporated in future versions to improve data integrity.

Finally, although the proposed AIS–buoy fusion strategy aligns each vessel trajectory with its nearest buoy station, several practical challenges remain. These include cases where a vessel passes between multiple buoy coverage zones, temporary sensor outages, or mismatches caused by sparse buoy networks. Future work will explore adaptive buoy selection, uncertainty modeling, and enhanced spatio-temporal fusion techniques to address such real-world issues. To address generalizability, we will extend our evaluation to AIS data from other coastal regions that exhibit different vessel traffic densities and movement patterns. By testing DRC-TCN on diverse waterways and open-world scenarios (where some vessels in the test set were never seen during training), we will be able to assess the model’s robustness beyond the New York Harbor dataset. These future studies will determine how well the approach adapts to varying traffic conditions and previously unseen vessels.