Analysis of Carbon Impacts of the Sanya Bay Ecological Restoration Project
Abstract
1. Introduction
2. Study Area
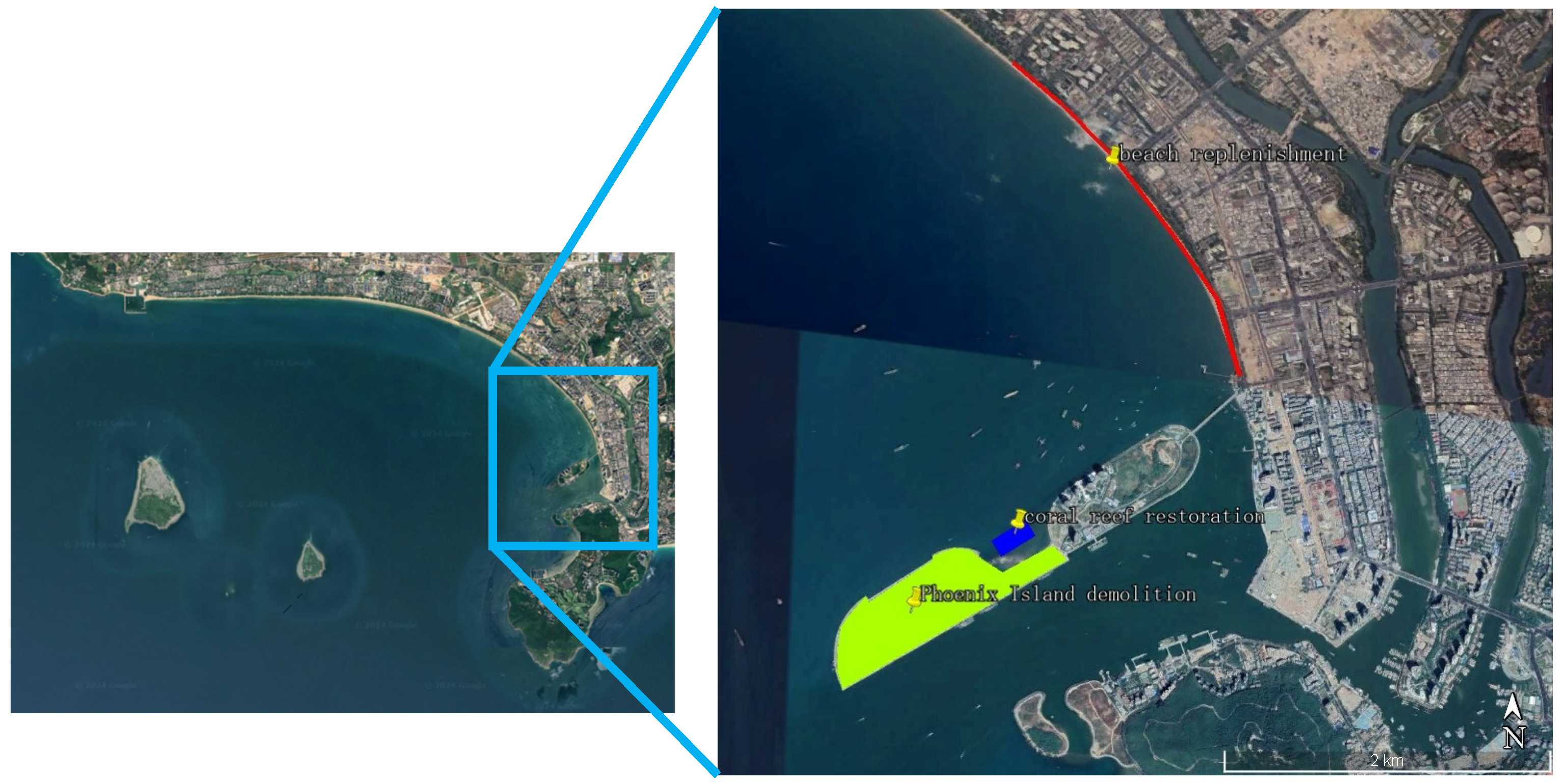
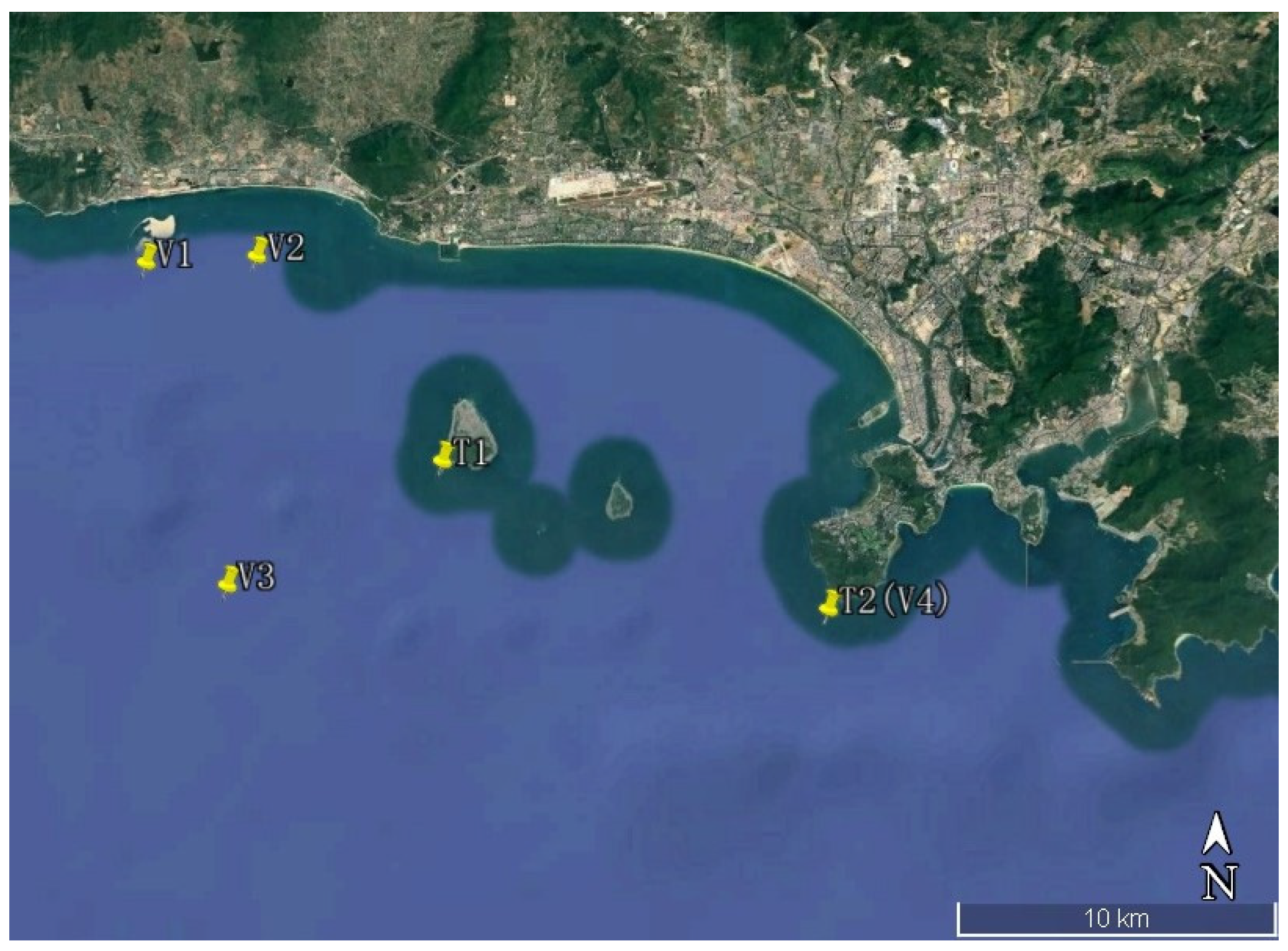
2.1. Natural Conditions
2.2. Ecological Restoration Project
3. Mathematical Model
3.1. Hydrodynamic Model
3.2. Ecological Dynamics Model
4. Model Setup and Verification
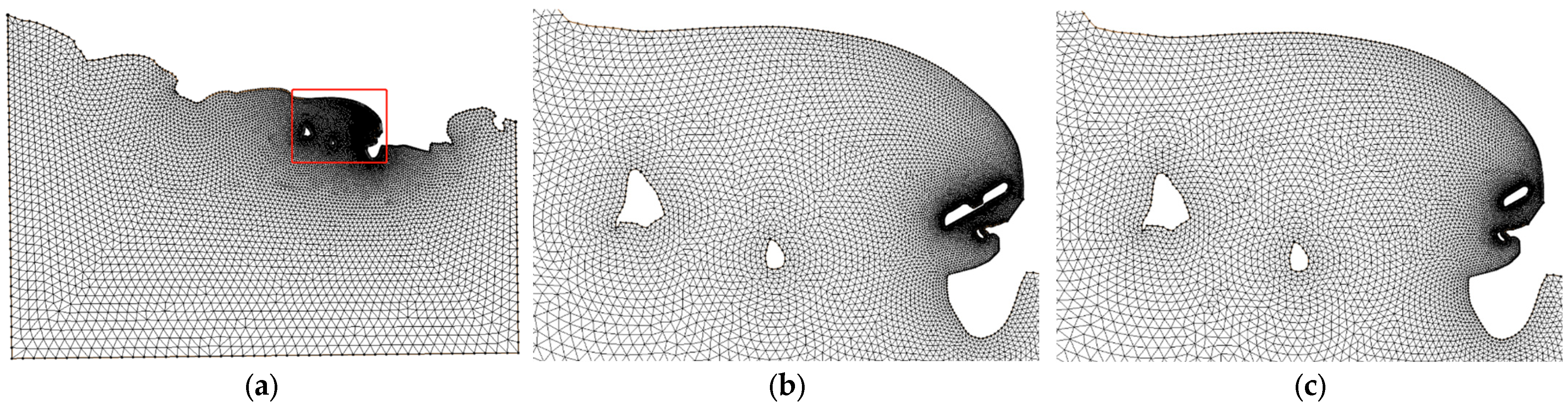
4.1. Model Setup
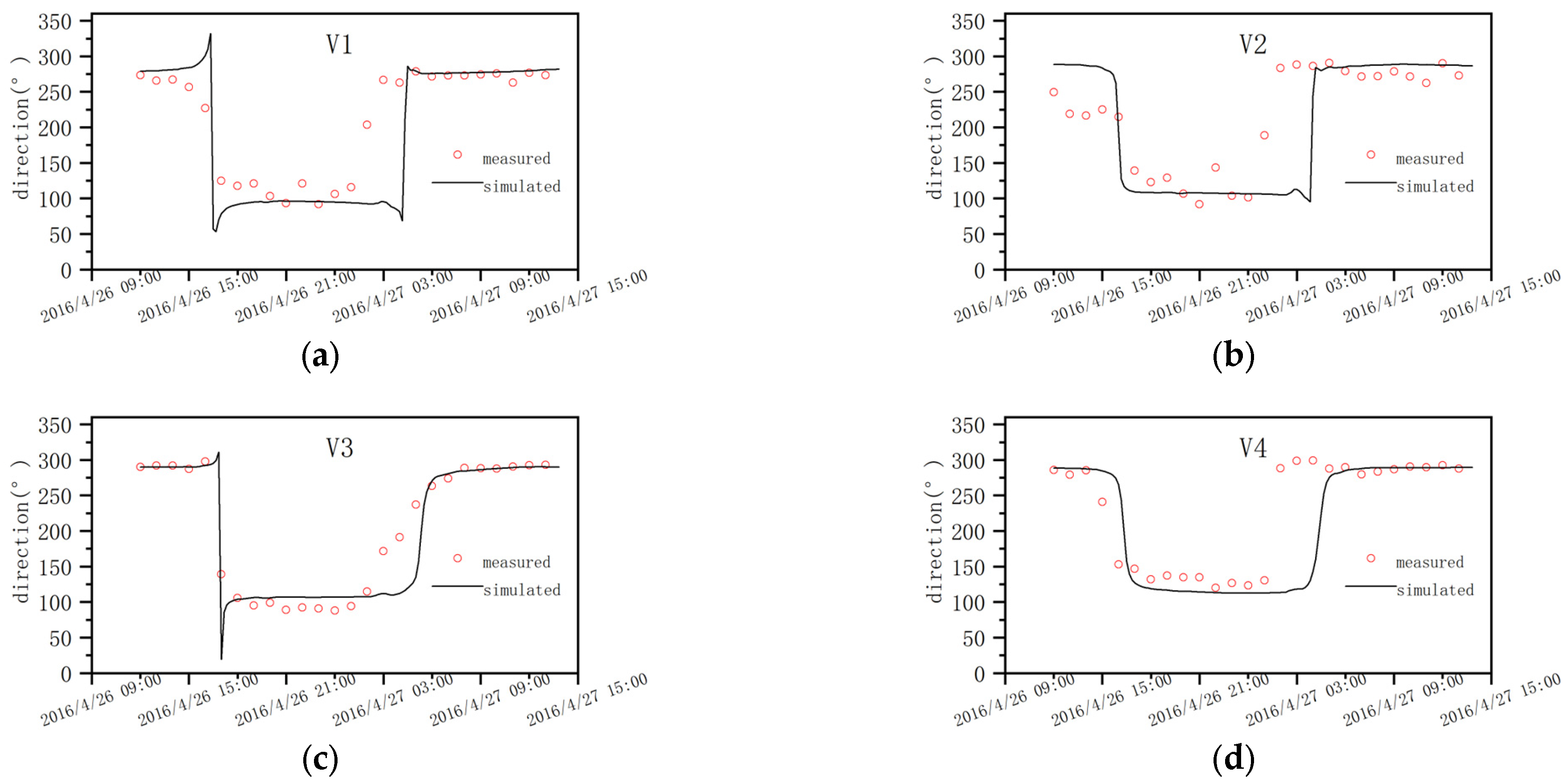
4.2. Model Verification
5. Results and Discussions
5.1. Overall Assessment
5.2. Effects to Seagrass Carbon Sink
5.2.1. Model and Initial Conditions
5.2.2. Results
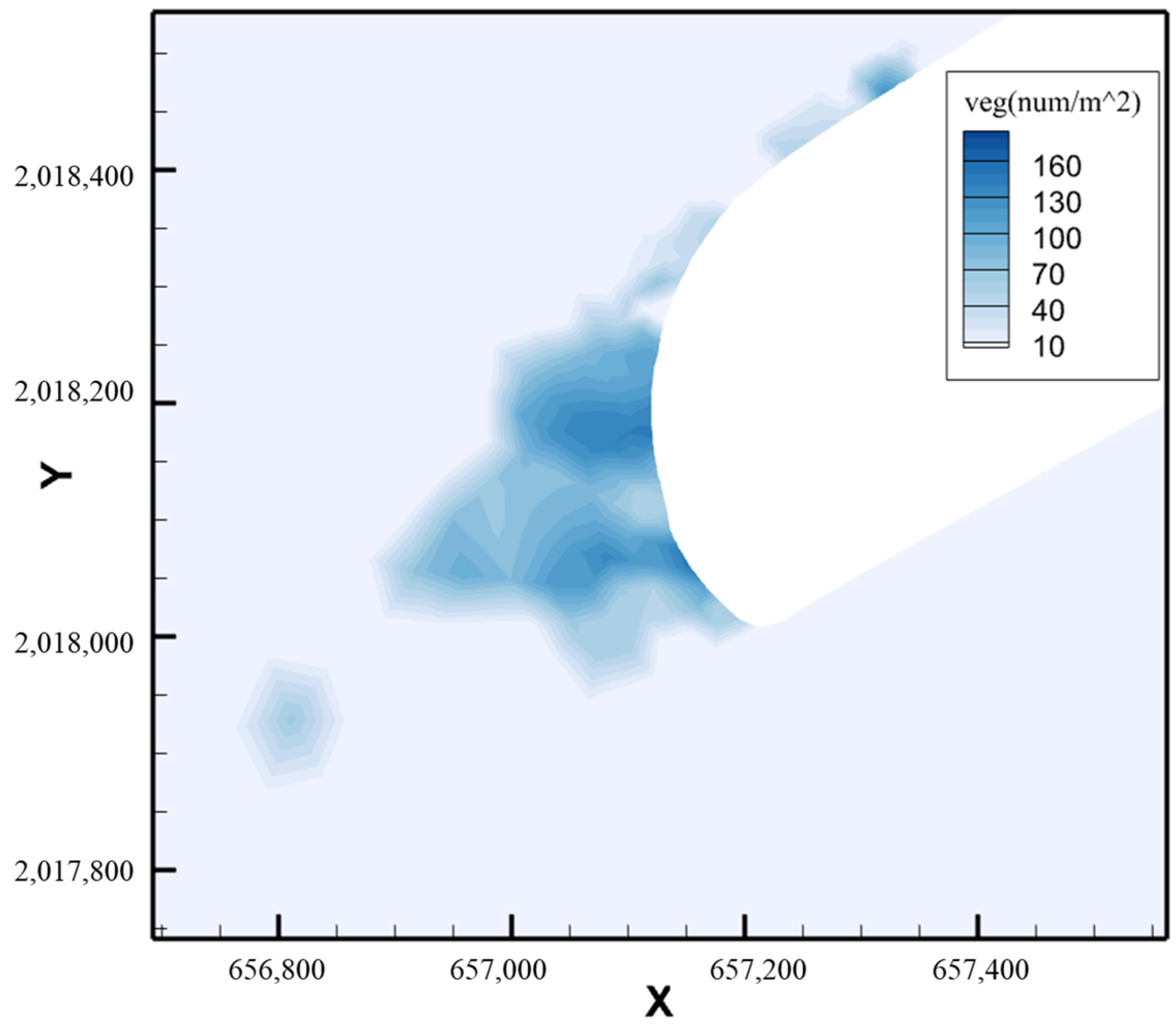
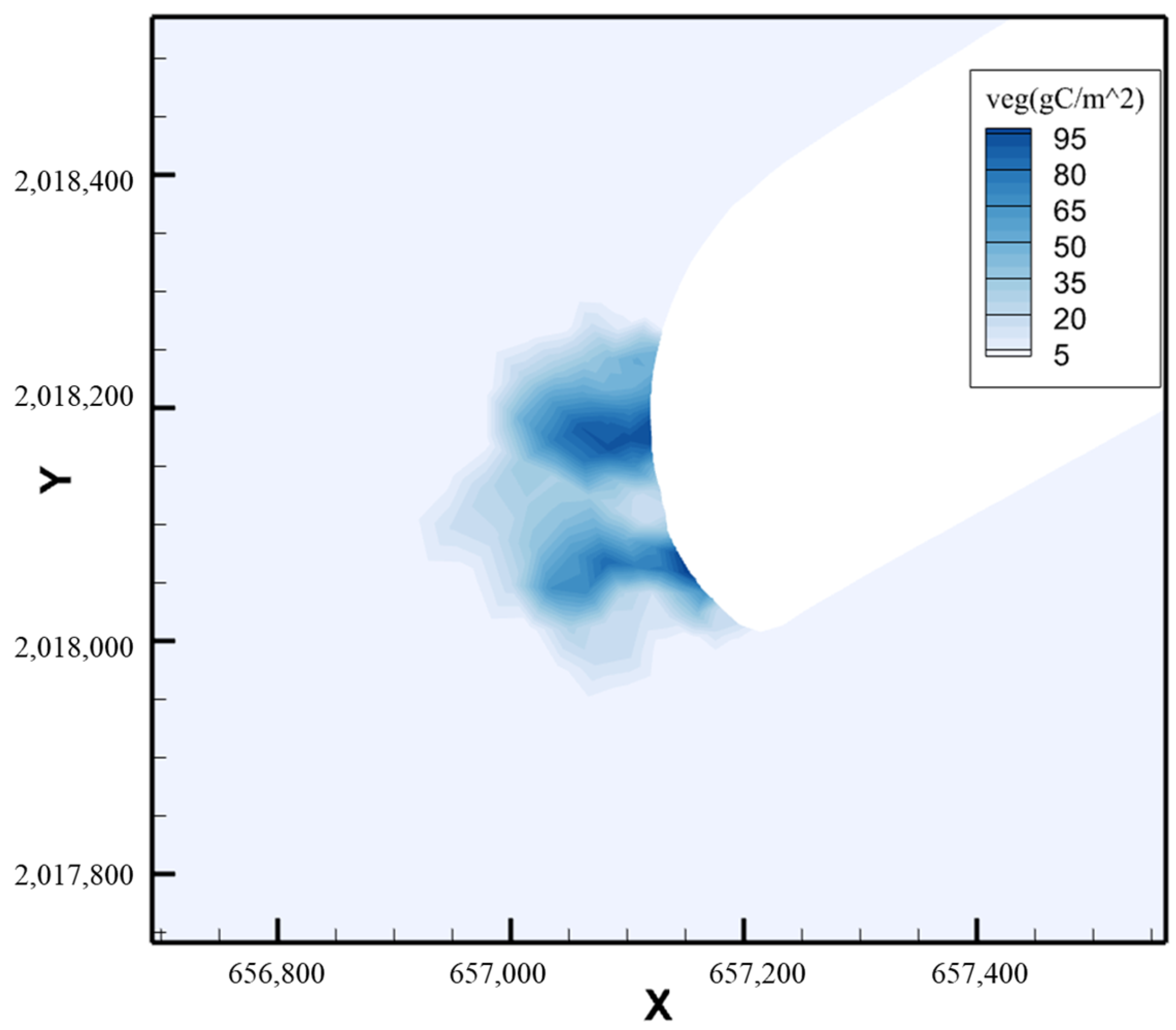
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Friedlingstein, P.; Jones, M.; O’Sullivan, M.; Andrew, R.M.; Bakker, D.C.; Hauck, J.; Le Quéré, C.; Peters, G.P.; Peters, W.; Pongratz, J.; et al. Global Carbon Budget 2021. Earth Syst. Sci. Data 2022, 14, 1917–2005. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Cai, H.Y.; Yan, Y.; Wang, B.Z.; Pan, H.M.; Zhang, P.; Li, B.; Zhao, T.T.G. Regime shifts in the thermal dynamics of offshore China due to accelerated global warming. Sci. Total Environ. 2024, 949, 174882. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.Y.; He, Y.L.; Guan, X.D. Increasing trends of land and coastal heatwaves under global warming. Atmos. Res. 2025, 318, 108007. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Q.; Wang, L.; Chen, Y.Z.; Wang, J.S. A review of the port carbon emission sources and related emission reduction technical measures. Environ. Pollut. 2023, 320, 121000. [Google Scholar] [CrossRef]
- Ge, M.; Ren, L.; Yang, D.; Li, X.Z.; Huang, Y.; Tang, J.W.; Hans, B. Invasion of Spartina species enhance blue carbon functions by increasing CO2 uptake and reducing methane emissions in Chinese and Danish coastal wetlands. J. Clean. Prod. 2025, 508, 145596. [Google Scholar] [CrossRef]
- Jiao, N.Z. Developing ocean negative carbon emission technology to support national carbon neutralization. Bull. Chin. Acad. Sci. 2021, 36, 179–187. [Google Scholar]
- Wang, W.L.; Fu, W.W.; Moigne, F.A.C.; Letscher, R.T.; Liu, Y.; Tang, J.M.; Primeau, F.W. Biological carbon pump estimate based on multidecadal hydrographic data. Nature 2023, 624, 579–585. [Google Scholar] [CrossRef]
- Yang, X.Y.; Wang, C.J.; Liu, C.; Liu, Z.; Liu, B.Q.; Xu, C.X. Assessing the spatio evolution of carbon sequestration and optimizing ecological restoration strategies using the InVEST model: A case study of the Yellow River Estuary, China. Mar. Environ. Res. 2025, 209, 107204. [Google Scholar] [CrossRef]
- Tang, Q.S.; Zhang, J.H.; Fang, J.G. Shellfish and seaweed mariculture increase atmospheric CO2 absorption by coastal ecosystems. Mar. Ecol. Prog. Ser. 2011, 424, 97–104. [Google Scholar] [CrossRef]
- Han, T.T.; Shi, R.J.; Qi, Z.H.; Liu, Q.X.; Huang, H.H. Role of intensive mariculture on CO2 absorption and carbon burial, and the carbon sink potential of Sanggou Bay, China. Aquaculture 2025, 597, 741936. [Google Scholar] [CrossRef]
- Mao, Y.J.; Sun, J.; Guo, C.C.; Yang, S.; Wei, Y.Q. Sinking rates of phytoplankton in response to cell size and carbon biomass: A case study in the northeastern South China Sea. J. Mar. Syst. 2023, 240, 103885. [Google Scholar] [CrossRef]
- Wang, N.; Li, J.M.; Zhou, Y.F. Mechanism of action of marine ecological restoration on ecological, economic, and social benefits—An empirical analysis based on a structural equation model. Ocean Coast. Manag. 2024, 248, 106950. [Google Scholar] [CrossRef]
- Gao, J.Z.; Ding, J.; Gu, X.Y.; Li, G.Q.; Yang, X.; Sun, M.; Zhang, K.C. Developing ecological restoration strategies based on carbon storage assessment. J. Sea Res. 2024, 202, 102539. [Google Scholar] [CrossRef]
- Wu, Y.J.; Su, J.F.; Yang, Y.; Fan, D.D. Artificial island construction exacerbates storm-induced loss of buried estuarine carbon. Limnol. Oceanogr. Lett. 2025, 10, 782–791. [Google Scholar] [CrossRef]
- Google Earth. Google Earth [Software], Google Earth: Mountain View, CA, USA, 2024. Available online: https://www.google.com/earth/ (accessed on 1 October 2024).
- Fasham, M.J.R.; Ducklow, H.W.; McKelvie, S.M. A nitrogen-based model of plankton dynamics in the oceanic mixed layer. J. Mar. Res. 1990, 48, 591–639. [Google Scholar] [CrossRef]
- Heinle, A.; Slawig, T. Internal dynamics of NPZD ecosystem models. Ecol. Model. 2013, 254, 33–42. [Google Scholar] [CrossRef]
- Fennel, K.; Losch, M.; Schröter, J.; Manfred, W. Testing a marine ecosystem model: Sensitivity analysis and parameter optimization. J. Mar. Syst. 2001, 28, 45–63. [Google Scholar] [CrossRef]
- Thi, N.Y.; Hang, M.; Cao, N.Y.; Hiroyuki, Y.; Kenichi, K. Applications of a new ecosystem model to study the dynamics of phytoplankton and nutrient in the Ariake Sea west coast of Kyushu Japan. J. Mar. Syst. 2009, 75, 1–16. [Google Scholar] [CrossRef]
- Fulton, E.A.; Smith, A.D.M.; Johnson, C.R. Effect of complexity on marine ecosystem models. Mar. Ecol. Prog. Ser. 2003, 253, 1–16. [Google Scholar] [CrossRef]
- Raick, C.; Soetaert, K.; Grégoire, M. Model complexity and performance: How far can we simplify? Prog. Oceanogr. 2006, 70, 27–57. [Google Scholar] [CrossRef]
- Seawater Quality Monitoring Information Disclosure System. 2025. [Website]. Available online: http://ep.nmemc.org.cn:8888/Water/ (accessed on 1 October 2024).
- Gao, Y.P.; Fang, J.G.; Tang, W.; Zhang, J.H.; Ren, L.H.; Du, M.R. Seagrass meadow carbon sink and amplification of the carbon sink for eelgrass bed in Sanggou Bay. Prog. Fish. Sci. 2013, 34, 17–21. (In Chinese) [Google Scholar]
- Wu, Z.J.; Chen, S.Q.; Shi, Q.; Cai, Z.F.; Shen, J.; Luo, L.Z.; Wang, D.R. Analysis of distribution change and restoration suggestion of the seagrass beds in Hainan Island. Mar. Environ. Sci. 2021, 4, 542–549. [Google Scholar]



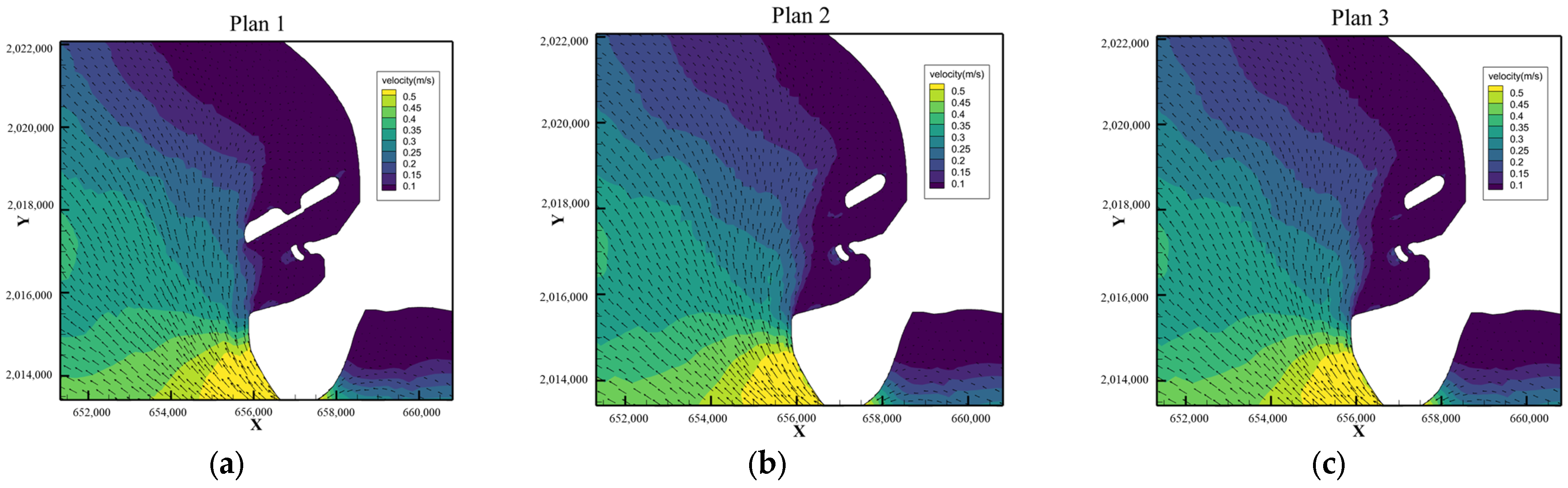
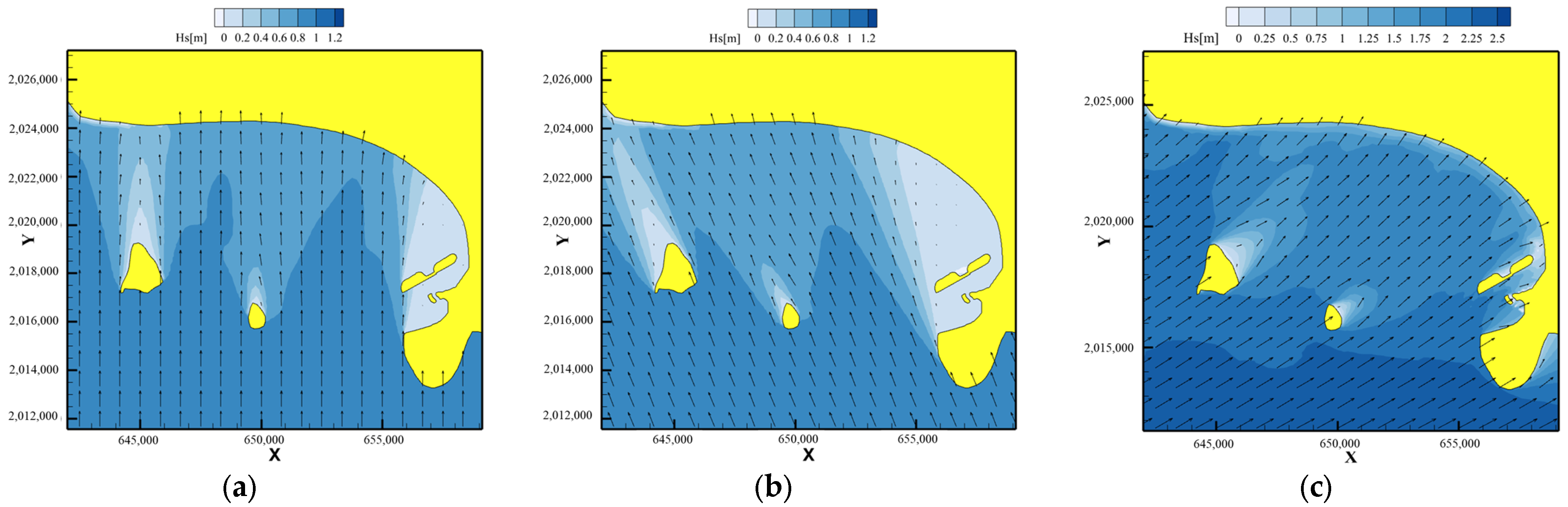
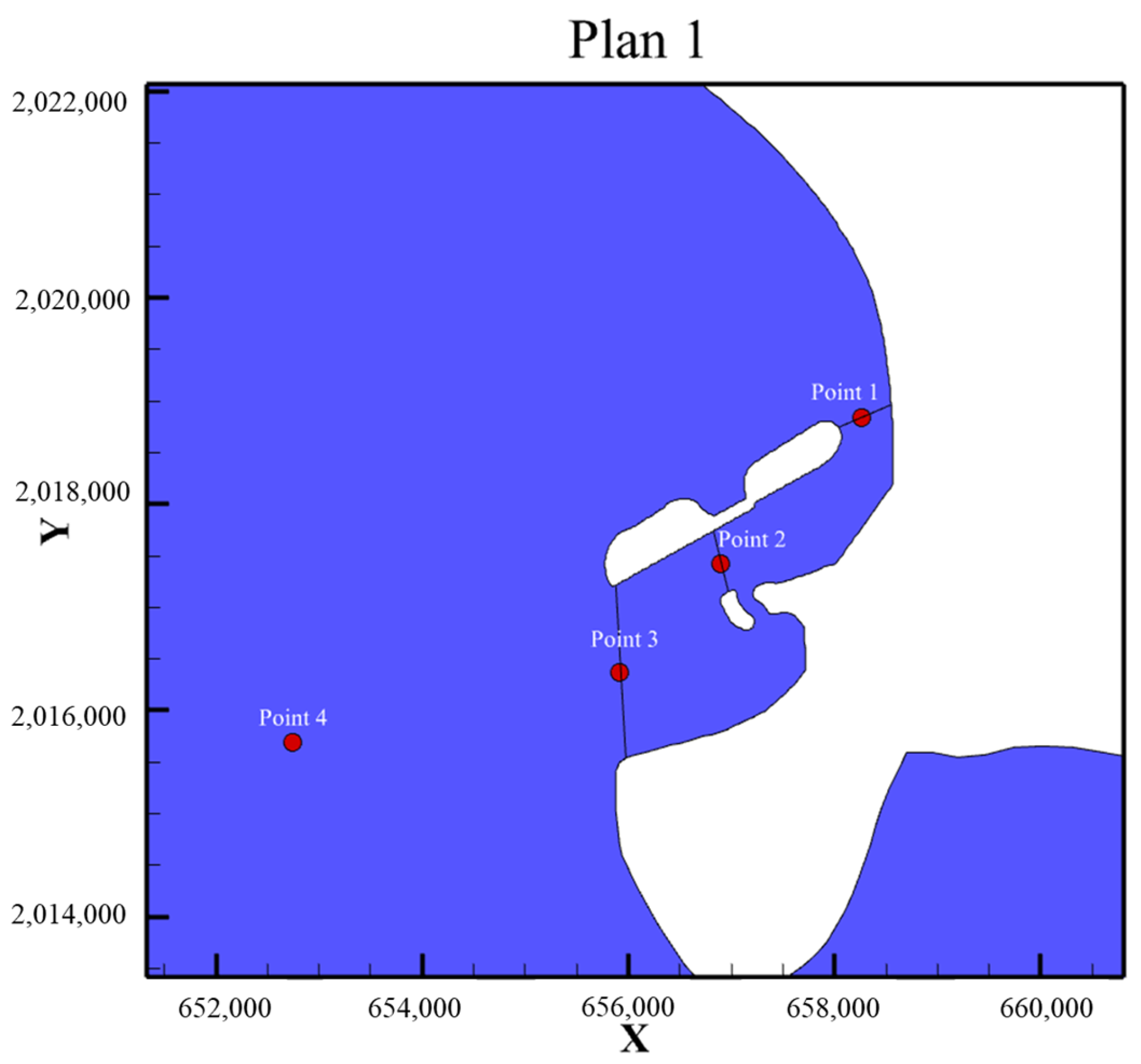
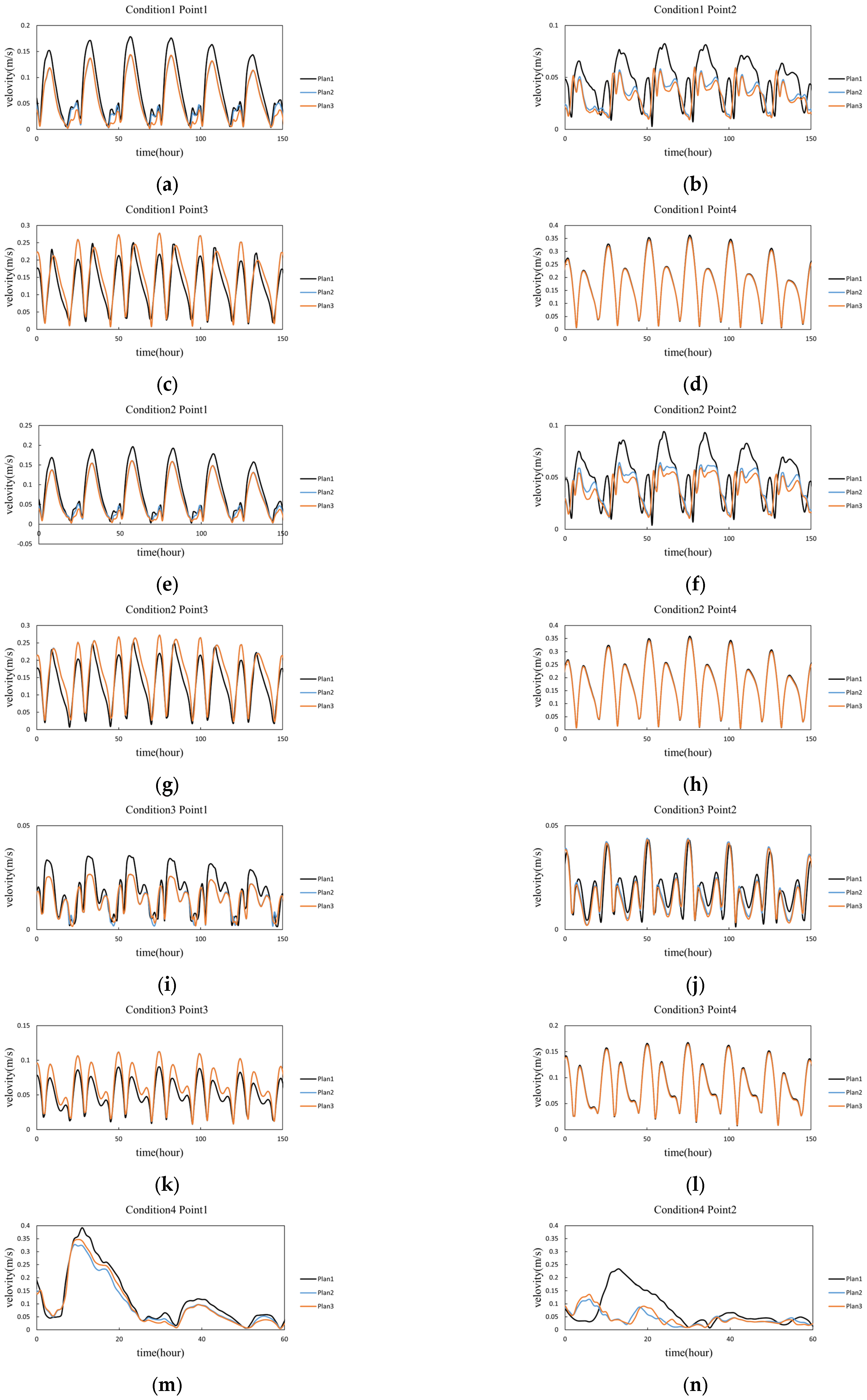

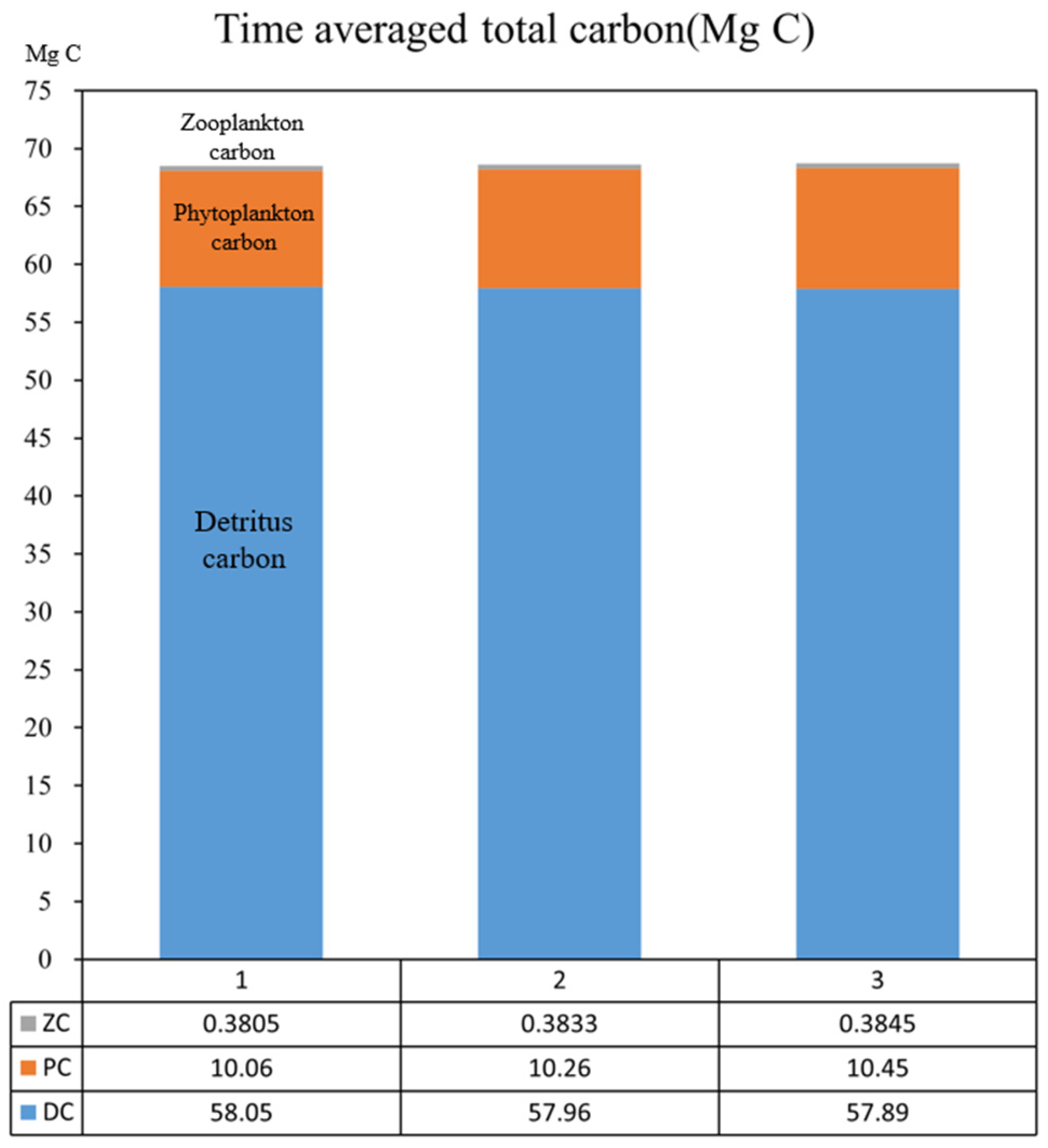
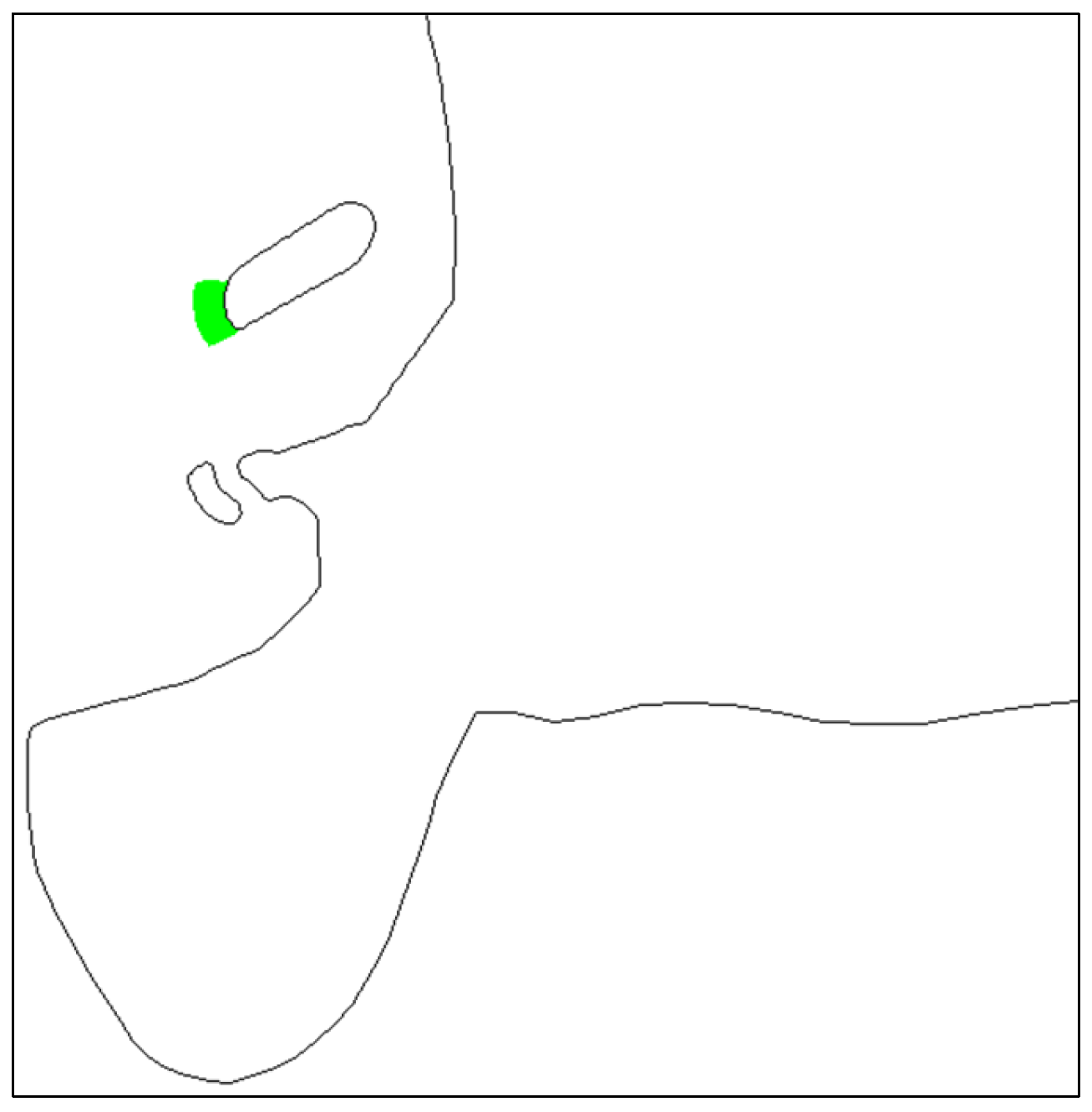
| Plan | Plan 1 | Plan 2 | Plan 3 | Plan2-Plan1 | Plan3-Plan1 |
|---|---|---|---|---|---|
| Pure tide | 12.55 | 12.79 | 12.89 | 0.245 | 0.347 |
| Tide + S | 11.74 | 11.89 | 11.85 | 0.155 | 0.110 |
| Tide + SSE | 12.14 | 12.30 | 12.27 | 0.170 | 0.134 |
| Tide + typhoon | 6.96 | 6.95 | 6.94 | −0.0148 | −0.0255 |
| Plan 1 | Carbon Sink (Mg C) | |||
|---|---|---|---|---|
| Plan | 1 | 2 | 3 | |
| Pure tide | 51.3 | 2349.92 | 2394.86 | 2413.59 |
| Tide + S | 20 | 857.02 | 867.97 | 865.05 |
| Tide + SSE | 26 | 1152.09 | 1167.27 | 1164.42 |
| Tide + typhoon | 2.7 | 68.59 | 68.49 | 68.39 |
| Total | 100 | 4427.62 | 4498.60 | 4511.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, Q.; Lu, F.; Guo, G.; Zhang, J.; Yan, F.; Liu, G. Analysis of Carbon Impacts of the Sanya Bay Ecological Restoration Project. J. Mar. Sci. Eng. 2025, 13, 2126. https://doi.org/10.3390/jmse13112126
Wang L, Zhang Q, Lu F, Guo G, Zhang J, Yan F, Liu G. Analysis of Carbon Impacts of the Sanya Bay Ecological Restoration Project. Journal of Marine Science and Engineering. 2025; 13(11):2126. https://doi.org/10.3390/jmse13112126
Chicago/Turabian StyleWang, Lulu, Qinghe Zhang, Feng Lu, Gaogui Guo, Jinfeng Zhang, Fei Yan, and Guangwei Liu. 2025. "Analysis of Carbon Impacts of the Sanya Bay Ecological Restoration Project" Journal of Marine Science and Engineering 13, no. 11: 2126. https://doi.org/10.3390/jmse13112126
APA StyleWang, L., Zhang, Q., Lu, F., Guo, G., Zhang, J., Yan, F., & Liu, G. (2025). Analysis of Carbon Impacts of the Sanya Bay Ecological Restoration Project. Journal of Marine Science and Engineering, 13(11), 2126. https://doi.org/10.3390/jmse13112126






