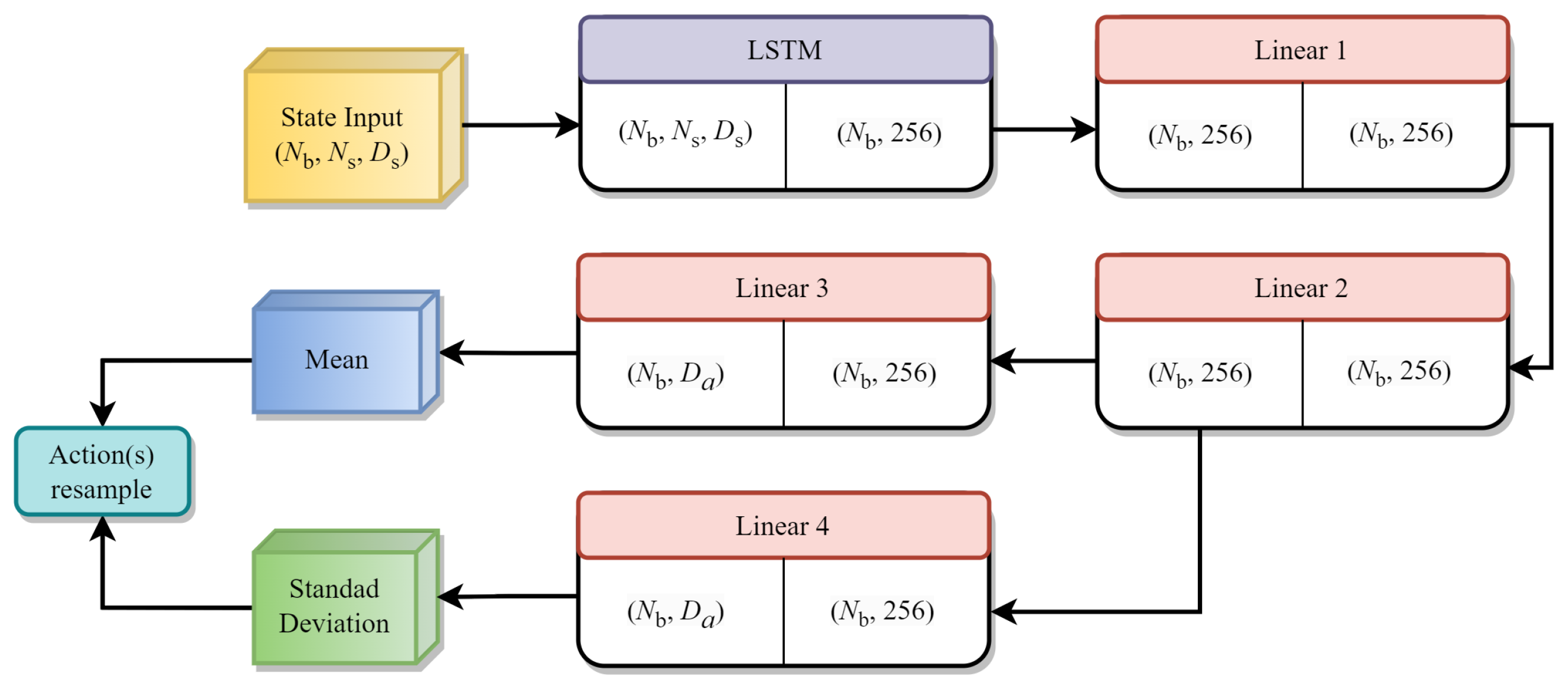
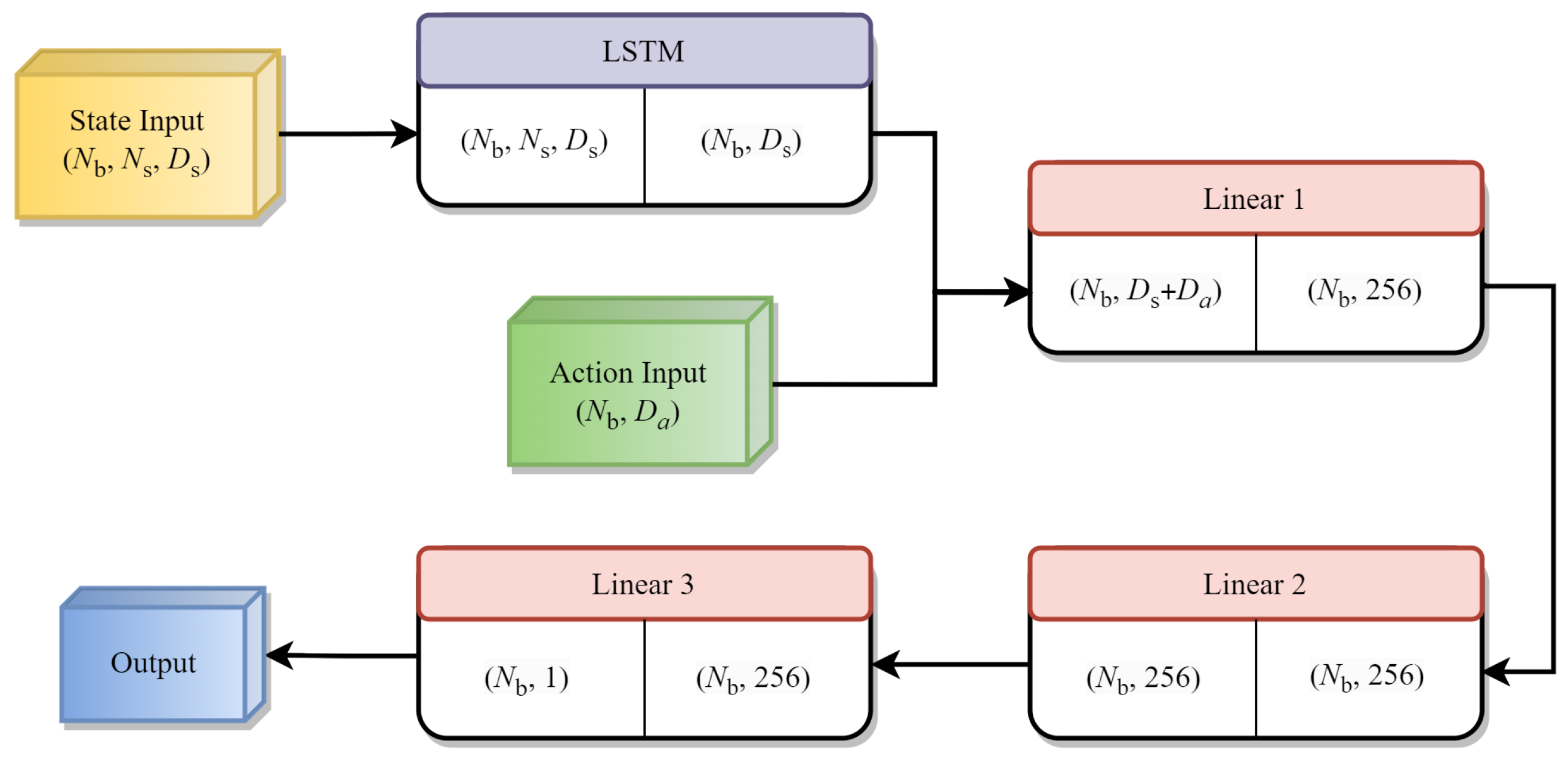
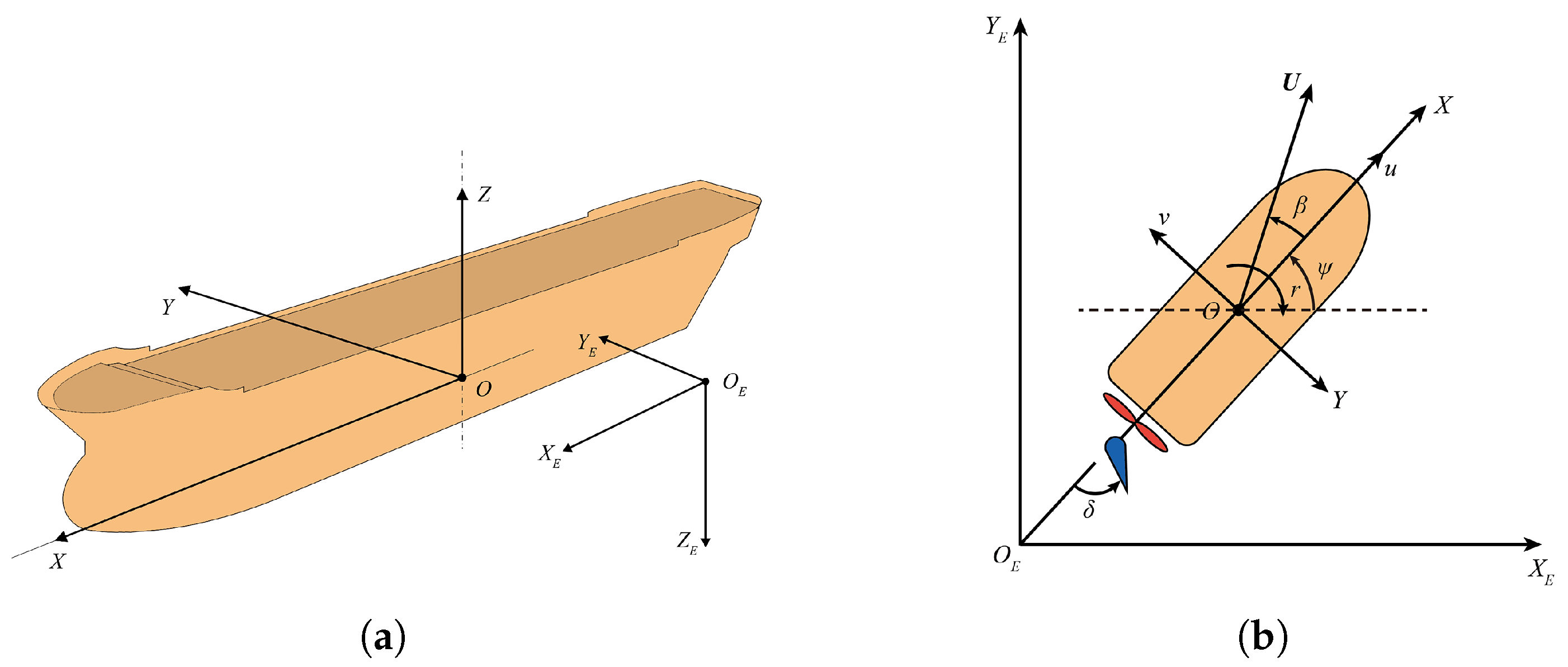
Figure 1.
The reference coordinate systems. (a) The Earth and body-fixed coordinate systems in the six-DOF scenario. The original point O is located at the mass center of the ship. (b) The three-DOF horizontal Earth and body-fixed coordinate systems.
Figure 1.
The reference coordinate systems. (a) The Earth and body-fixed coordinate systems in the six-DOF scenario. The original point O is located at the mass center of the ship. (b) The three-DOF horizontal Earth and body-fixed coordinate systems.
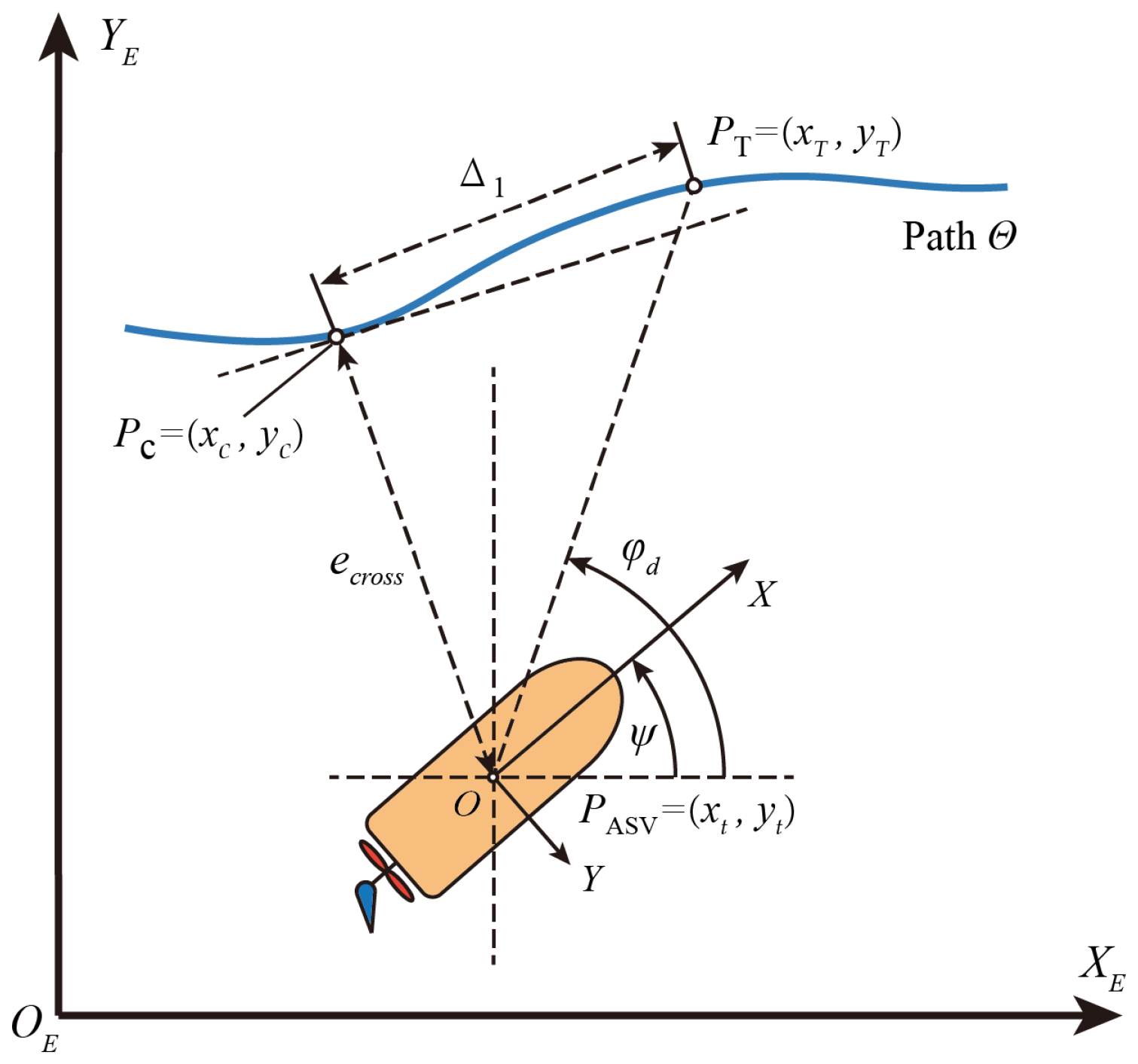
Figure 2.
The general view of the path-following task in three-DOF horizontal plane, which is based on course tracking control.
Figure 2.
The general view of the path-following task in three-DOF horizontal plane, which is based on course tracking control.
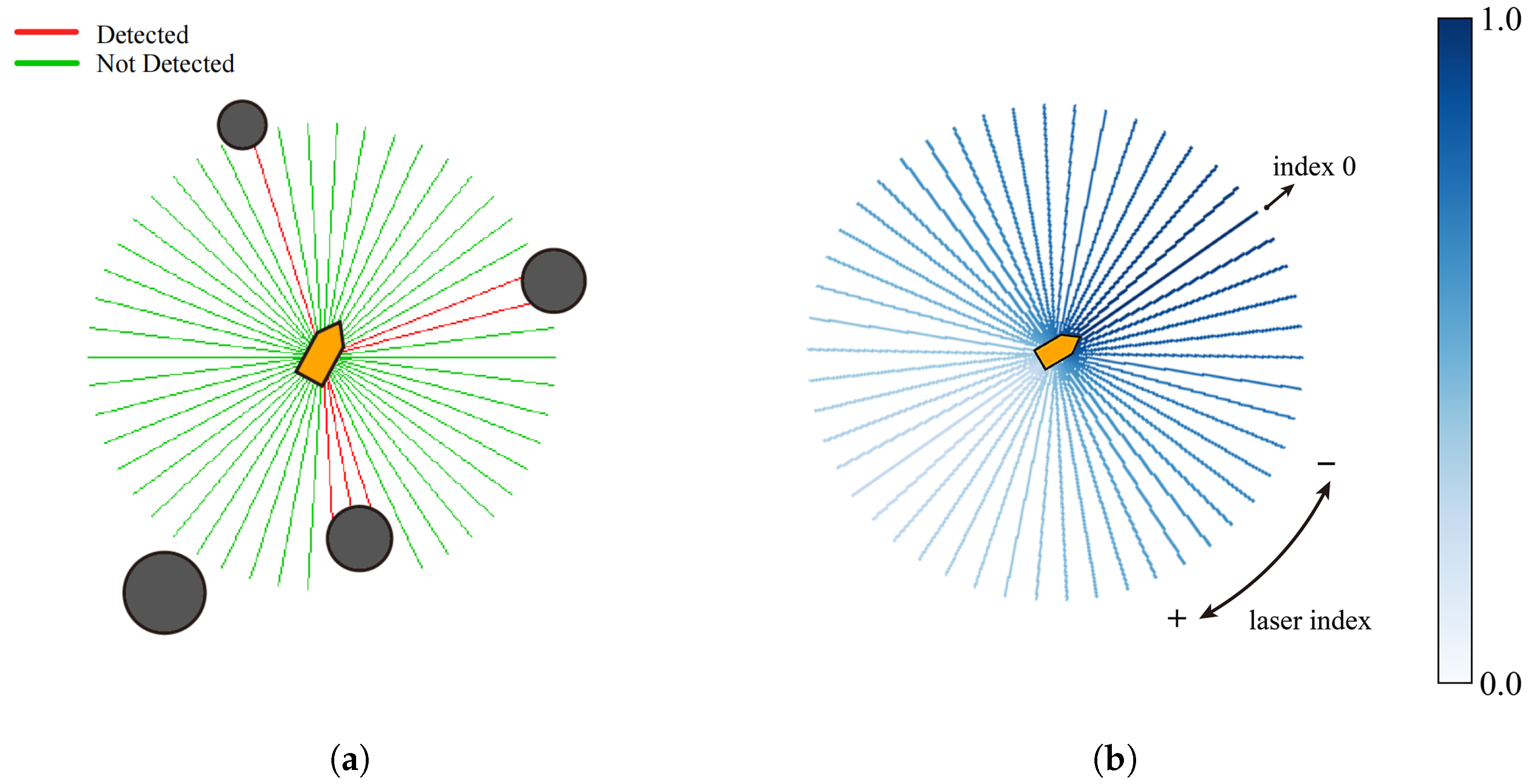
Figure 3.
The schematic views of LiDAR on ASV. (a) A LiDAR on an ASV is emitting laser beams in two-dimensional space. (b) The weight distribution of LiDAR laser beams. The beams located in front of the ASV possess a higher weight value showing a higher collision risk, whereas those directed backwards hold a lower weight value of collision risk.
Figure 3.
The schematic views of LiDAR on ASV. (a) A LiDAR on an ASV is emitting laser beams in two-dimensional space. (b) The weight distribution of LiDAR laser beams. The beams located in front of the ASV possess a higher weight value showing a higher collision risk, whereas those directed backwards hold a lower weight value of collision risk.
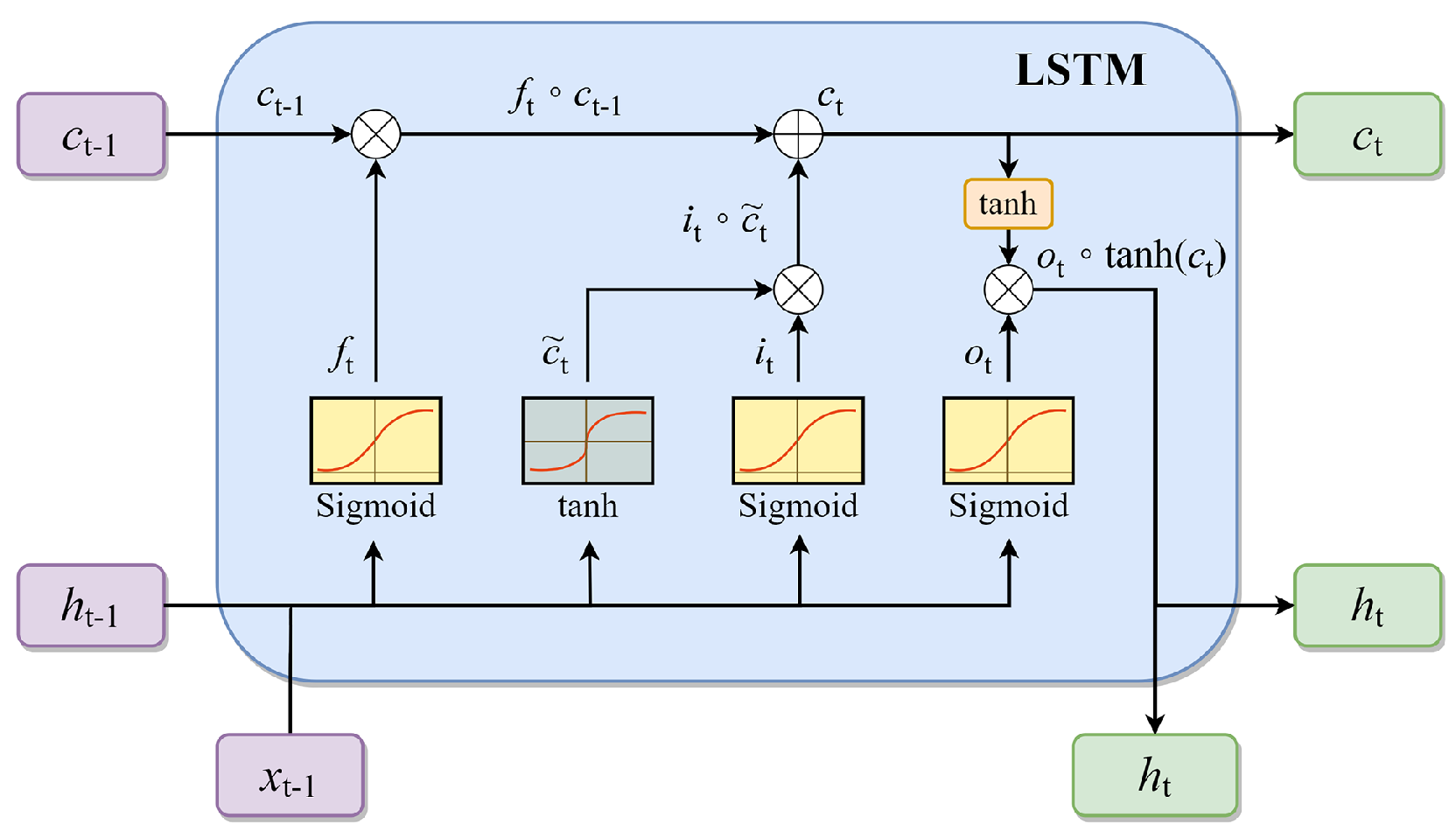
Figure 4.
In the structure of the LSTM unit, c represents the memory cell’s stored value, h denotes the output value of the LSTM, and x is the input value from the user. The LSTM unit has four inputs and one output. The inputs consist of the vector along with the activation signals for the forget gate , the input gate , and the output gate .
Figure 4.
In the structure of the LSTM unit, c represents the memory cell’s stored value, h denotes the output value of the LSTM, and x is the input value from the user. The LSTM unit has four inputs and one output. The inputs consist of the vector along with the activation signals for the forget gate , the input gate , and the output gate .
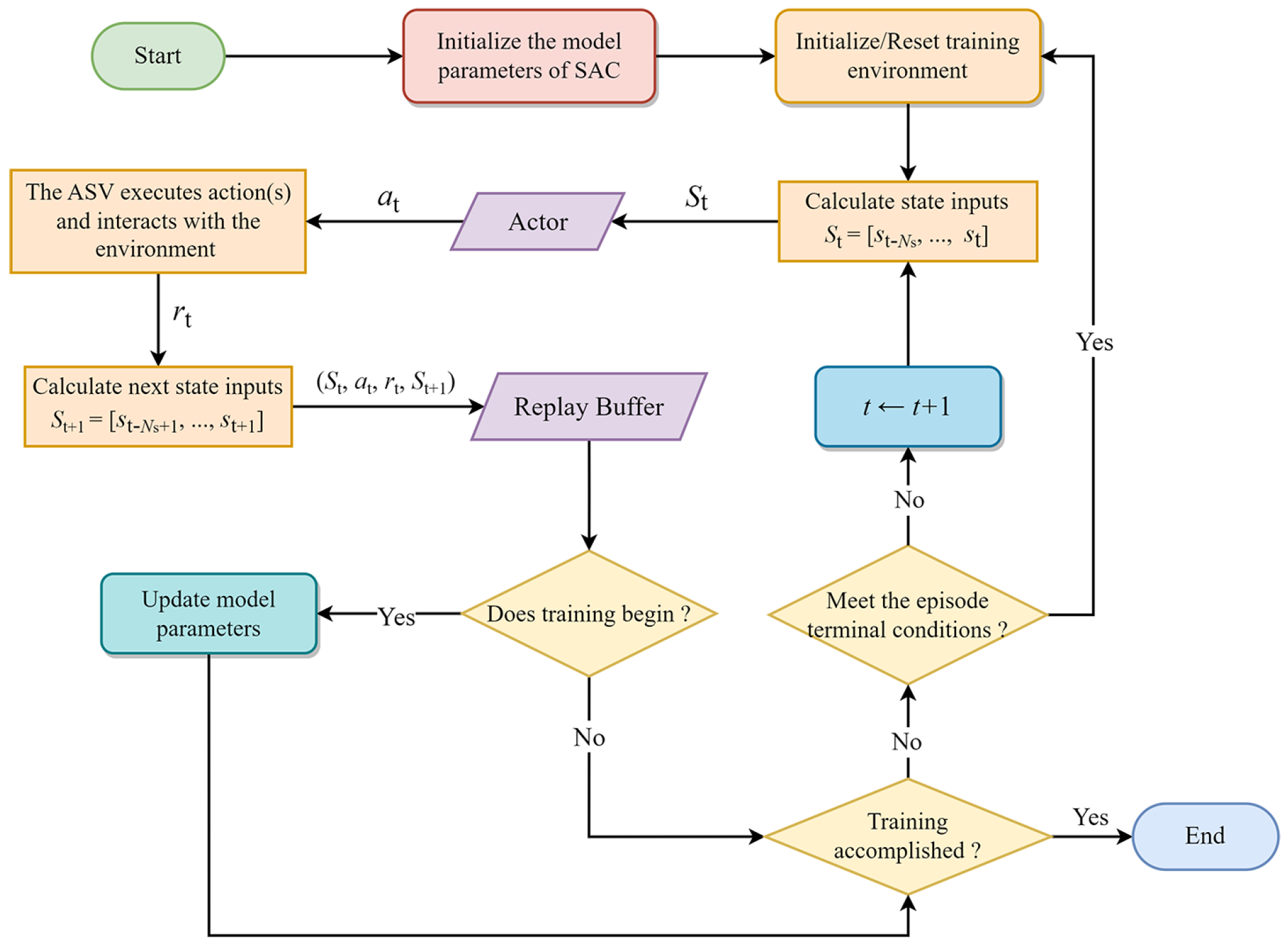
Figure 5.
The flowchart of the policy training process. If the current iterative step is larger than the policy training start step, the model training commences.
Figure 5.
The flowchart of the policy training process. If the current iterative step is larger than the policy training start step, the model training commences.
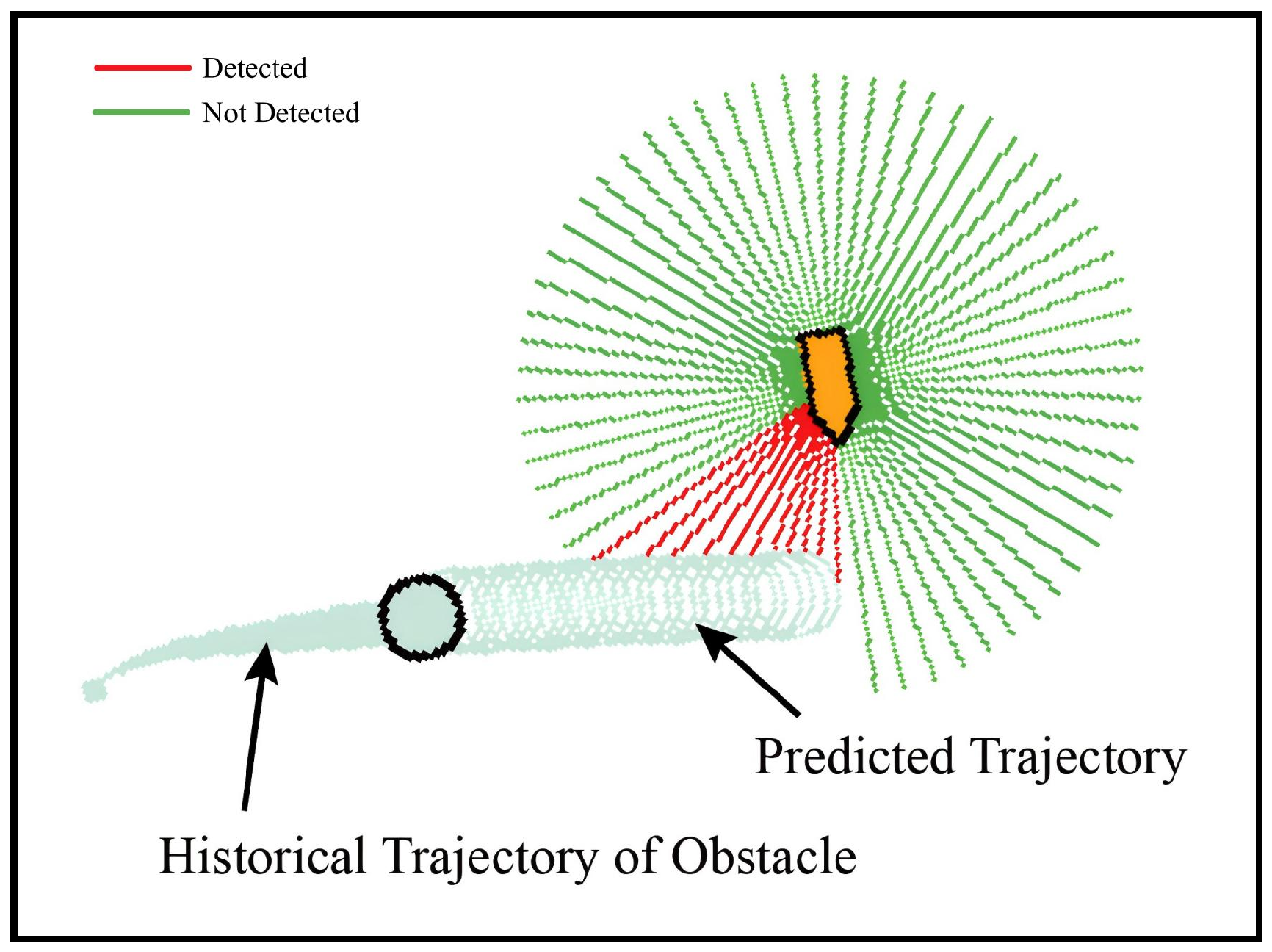
Figure 6.
The points in the predicted trajectory are considered as virtual obstacles that the ASV needs to avoid.
Figure 6.
The points in the predicted trajectory are considered as virtual obstacles that the ASV needs to avoid.
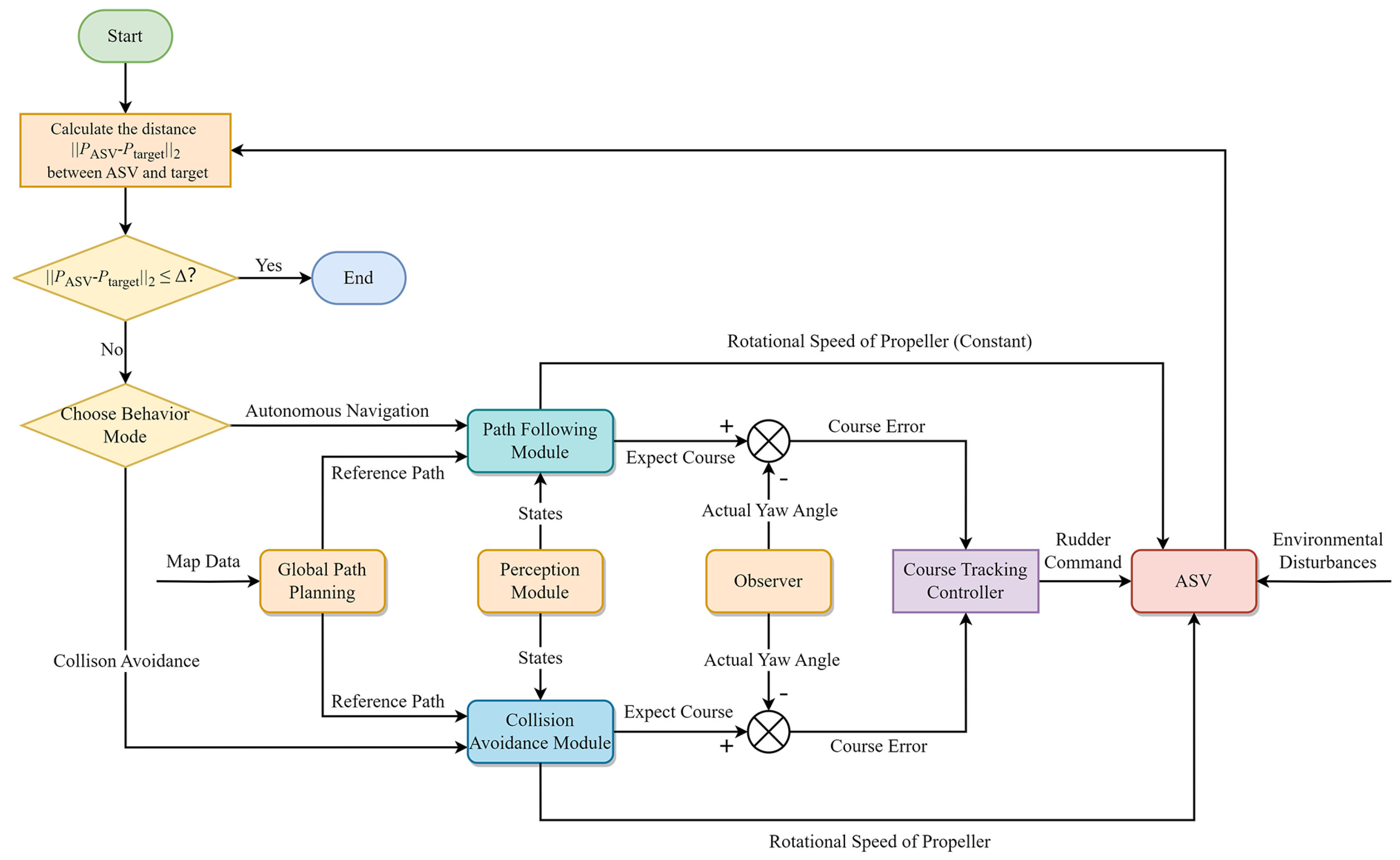
Figure 7.
The flowchart of the hybrid system, where represents the coordinates of the final target point. is the distance threshold.
Figure 7.
The flowchart of the hybrid system, where represents the coordinates of the final target point. is the distance threshold.
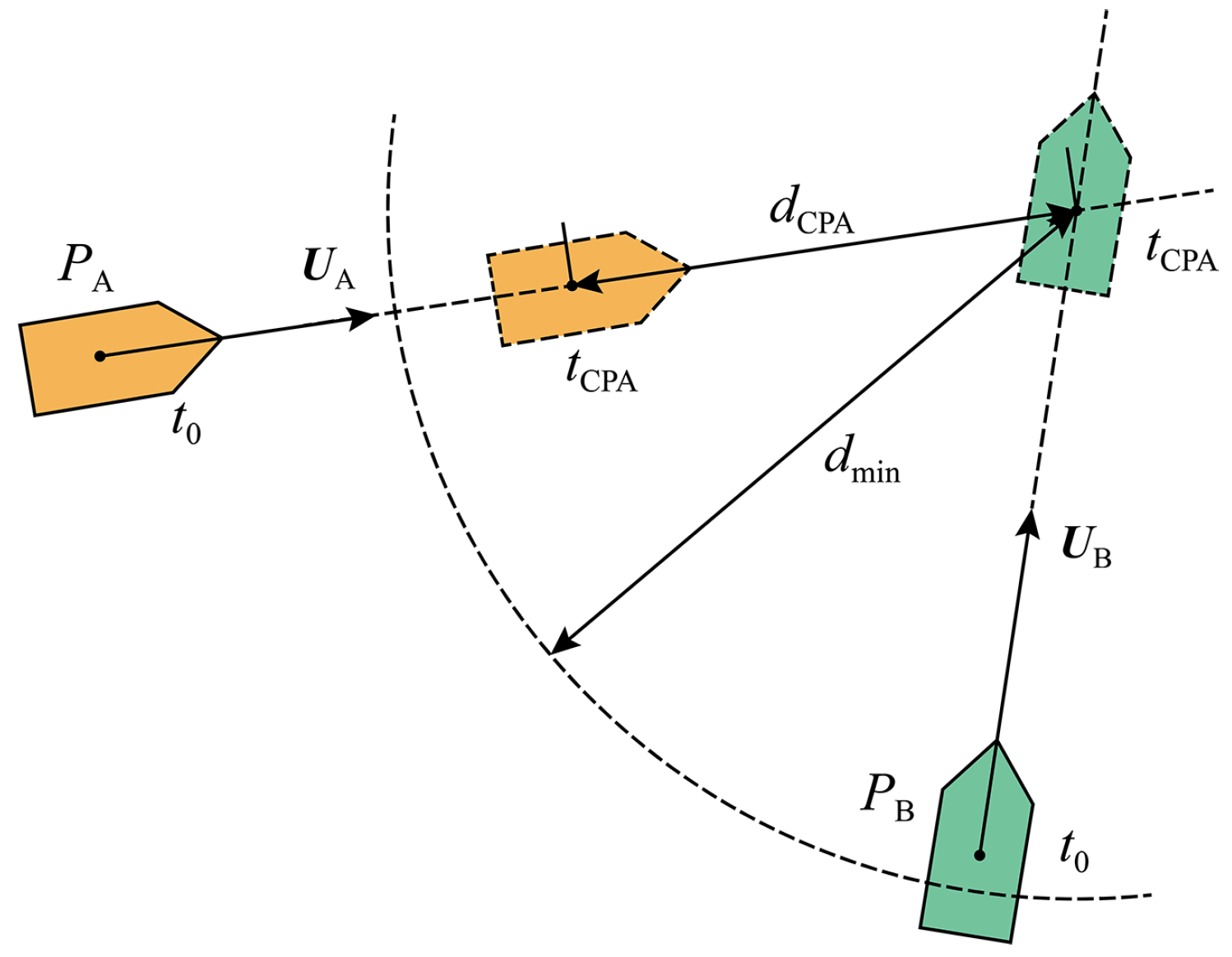
Figure 8.
The schematic view of CPA, where and are the resultant velocities.
Figure 8.
The schematic view of CPA, where and are the resultant velocities.
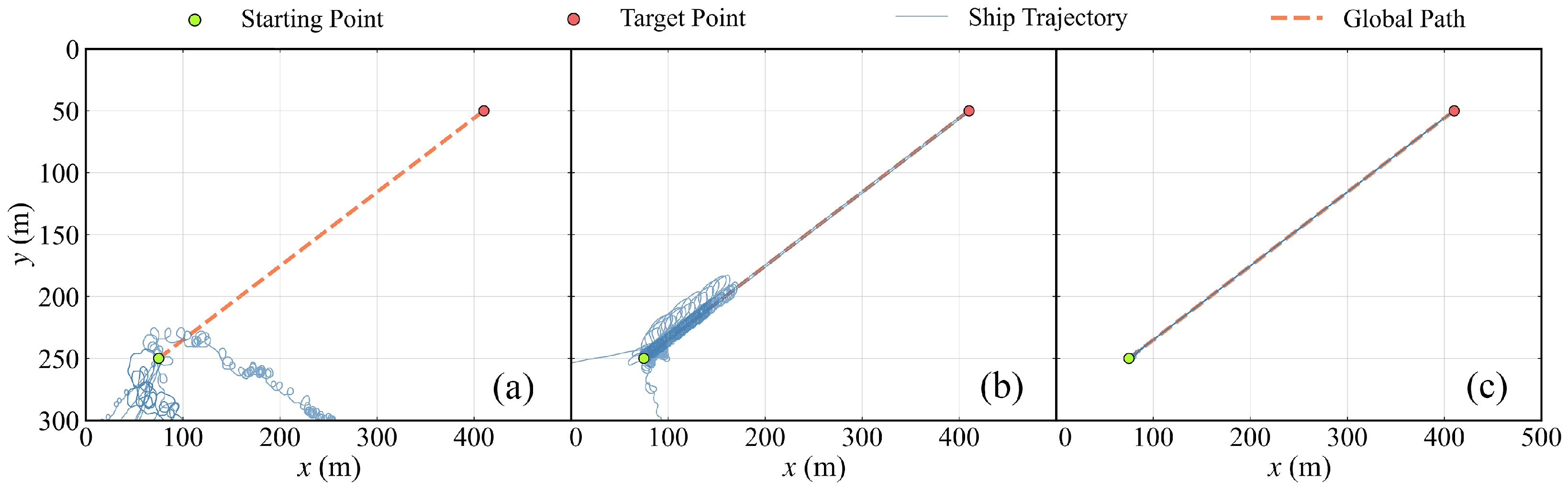
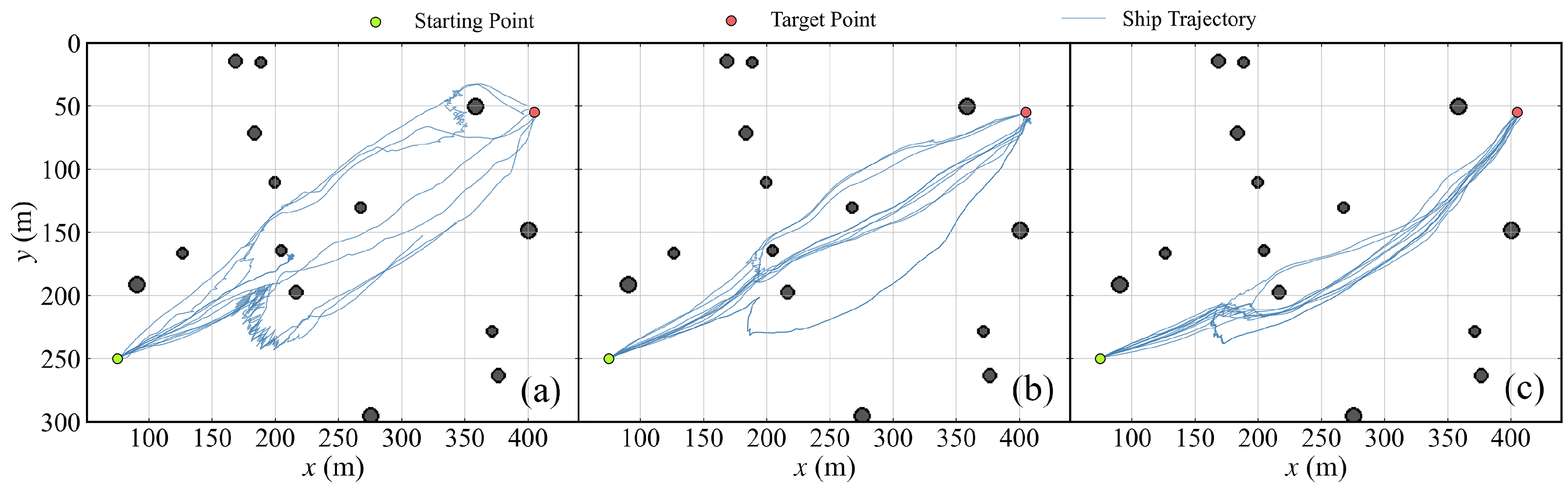
Figure 9.
Visualization of the path-following policy training process in different training stages. The epoch of each sub-figure (a–c) is 1, 20, and 175, respectively.
Figure 9.
Visualization of the path-following policy training process in different training stages. The epoch of each sub-figure (a–c) is 1, 20, and 175, respectively.
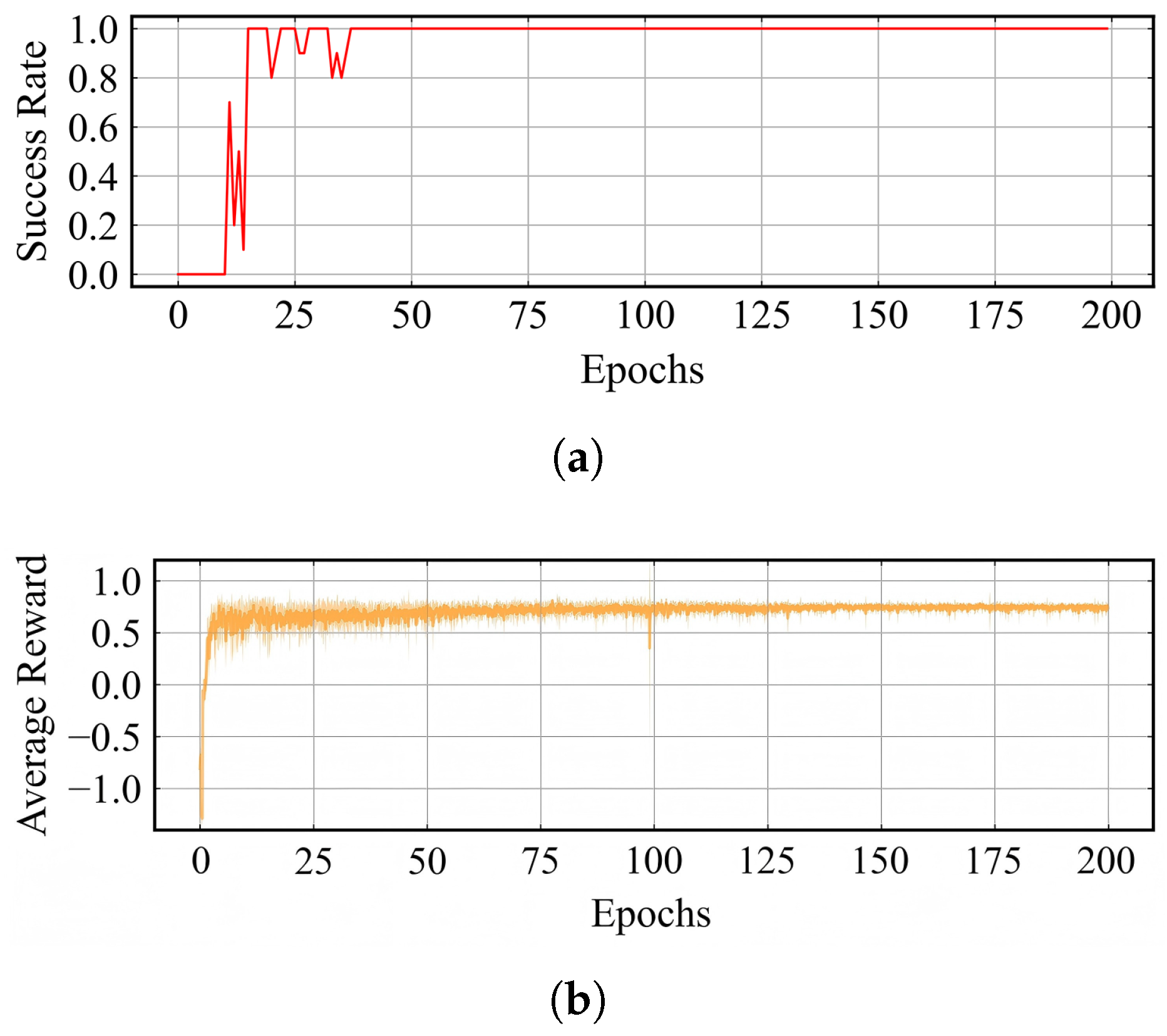
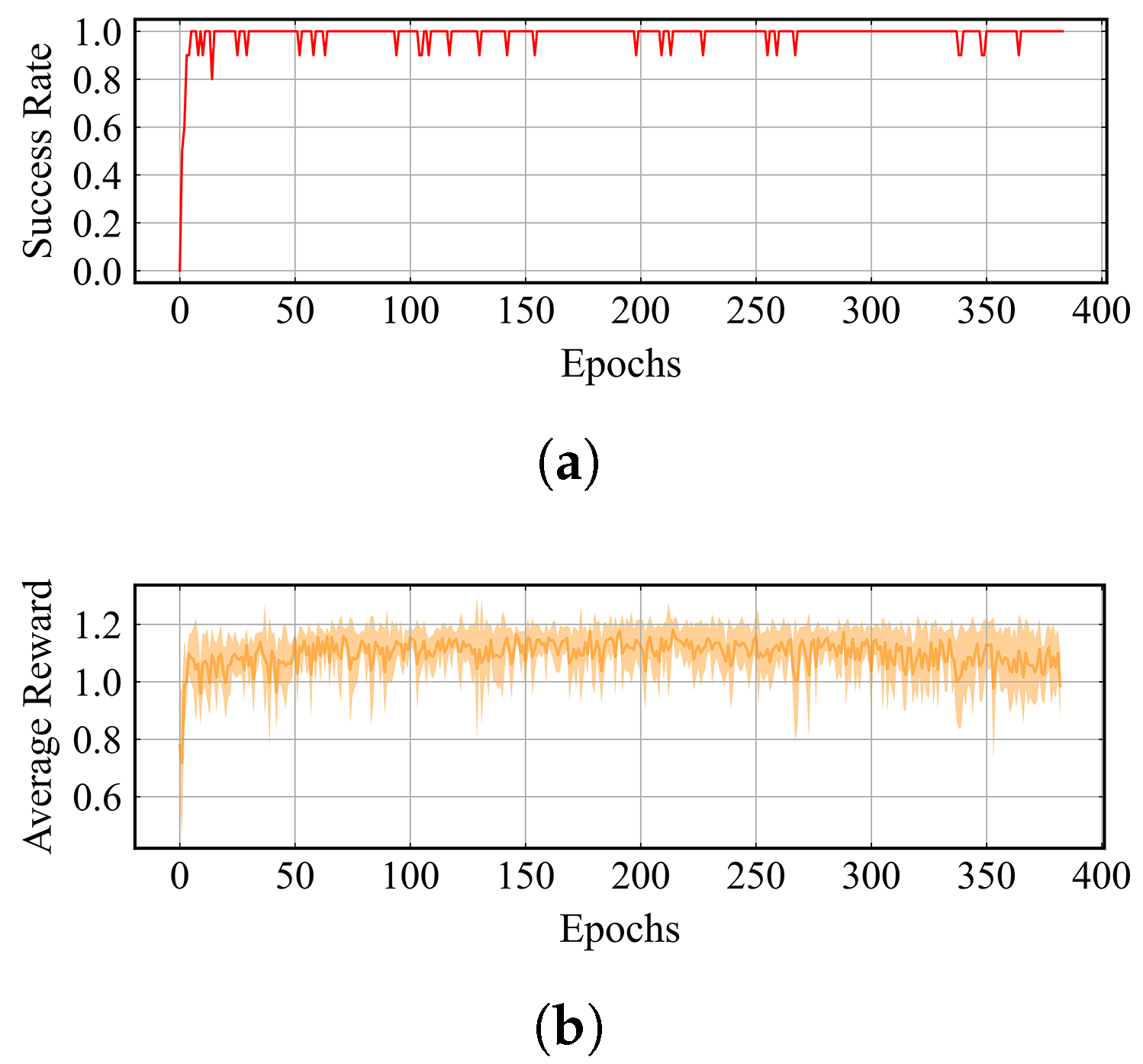
Figure 10.
The training results of the path-following policy. (a) Success rate per epoch. (b) Average return and standard deviation per step in each epoch.
Figure 10.
The training results of the path-following policy. (a) Success rate per epoch. (b) Average return and standard deviation per step in each epoch.
Figure 11.
Visualization of the collision avoidance policy training process in different training stages. The epoch of each sub-figure (a–c) is 1, 25, and 300, respectively.
Figure 11.
Visualization of the collision avoidance policy training process in different training stages. The epoch of each sub-figure (a–c) is 1, 25, and 300, respectively.
Figure 12.
The training results of the collision avoidance policy. (a) Success rate per epoch. (b) Average return and standard deviation per step in each epoch.
Figure 12.
The training results of the collision avoidance policy. (a) Success rate per epoch. (b) Average return and standard deviation per step in each epoch.
Figure 13.
Visualization of the AIS trajectory data.
Figure 13.
Visualization of the AIS trajectory data.
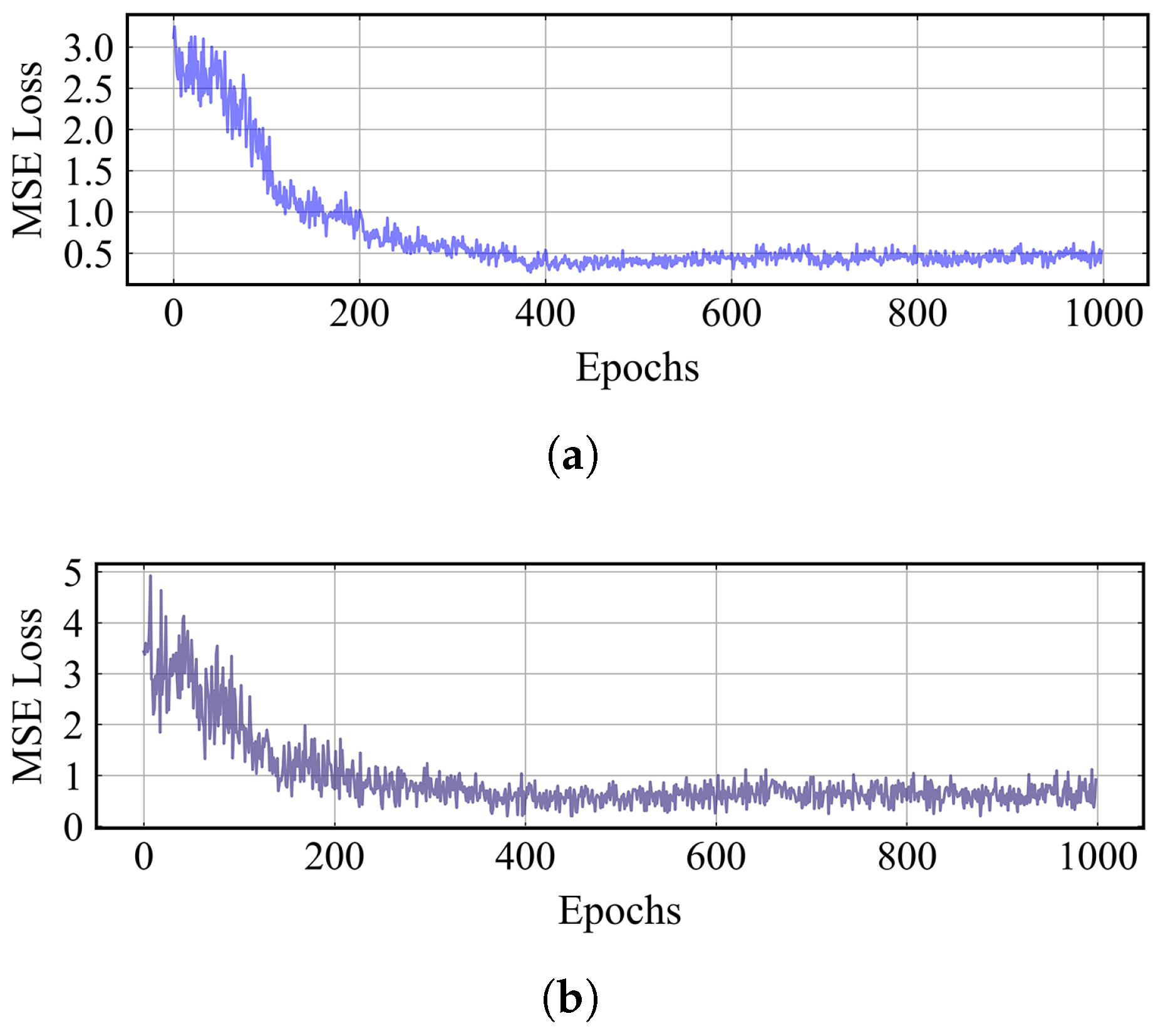
Figure 14.
MSE loss of KF-LSTM trajectory predictor. (a) Average training loss in each epoch. (b) Average validation loss in each epoch.
Figure 14.
MSE loss of KF-LSTM trajectory predictor. (a) Average training loss in each epoch. (b) Average validation loss in each epoch.
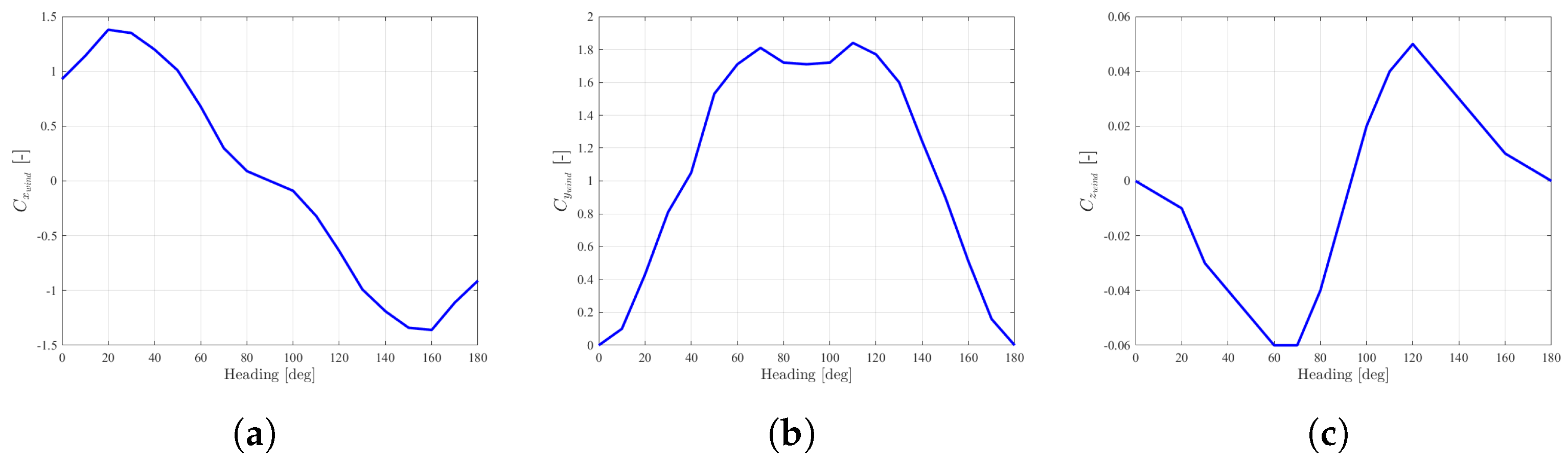
Figure 15.
Wind load coefficients of the ASV in different headings. (a) . (b) . (c) .
Figure 15.
Wind load coefficients of the ASV in different headings. (a) . (b) . (c) .
Figure 16.
Path-following task results in different scenarios. (a) Simulation results in static water. (b) Simulation results in water with external disturbances.
Figure 16.
Path-following task results in different scenarios. (a) Simulation results in static water. (b) Simulation results in water with external disturbances.
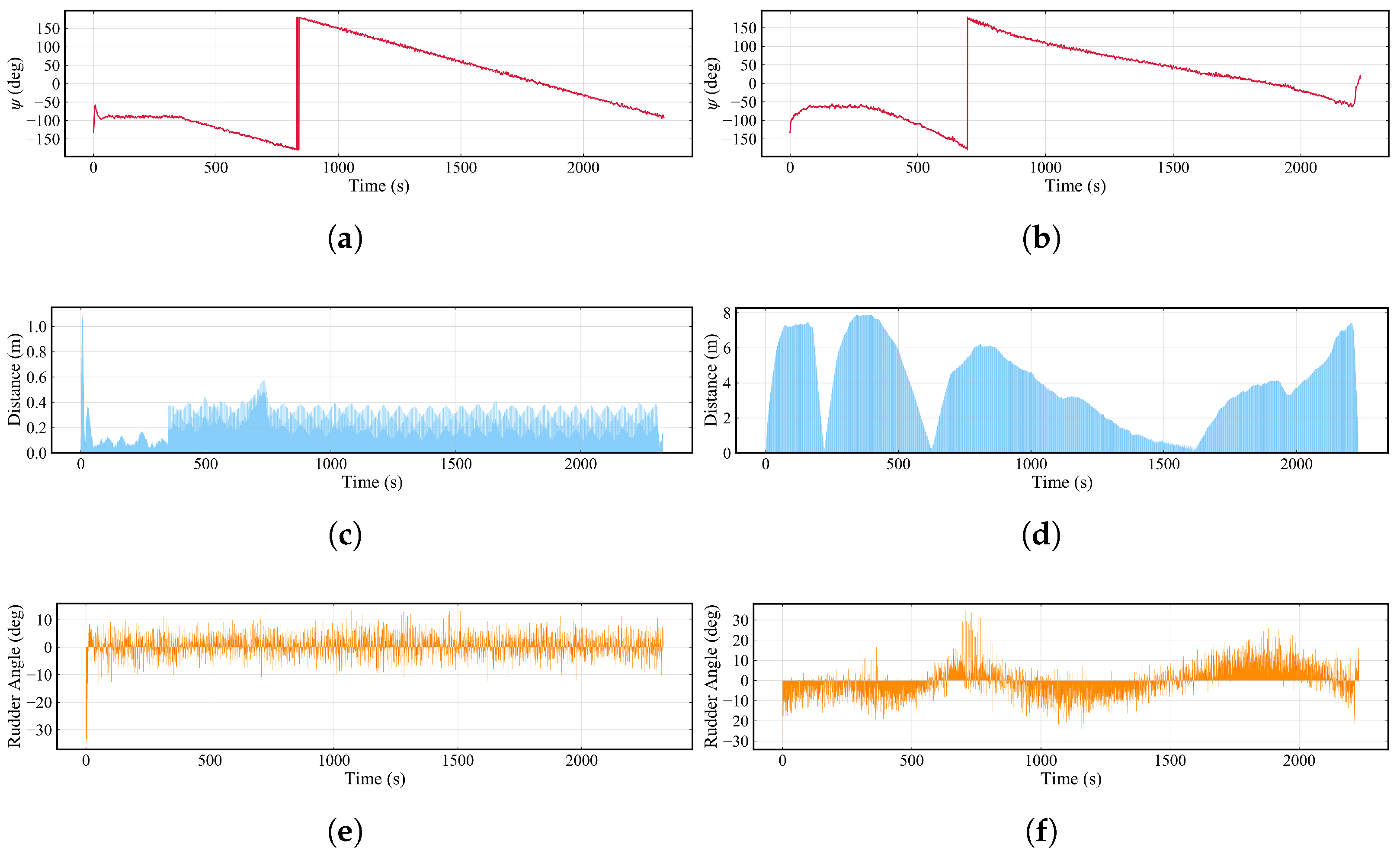
Figure 17.
Time domain curves of yaw angle, path-following error, and rudder angle in scenarios and . (a) Yaw angle (Scenario ). (b) Yaw angle (Scenario ). (c) Path-following error (Scenario ). (d) Path following error (Scenario ). (e) Rudder angle (Scenario ). (f) Rudder angle (Scenario ).
Figure 17.
Time domain curves of yaw angle, path-following error, and rudder angle in scenarios and . (a) Yaw angle (Scenario ). (b) Yaw angle (Scenario ). (c) Path-following error (Scenario ). (d) Path following error (Scenario ). (e) Rudder angle (Scenario ). (f) Rudder angle (Scenario ).
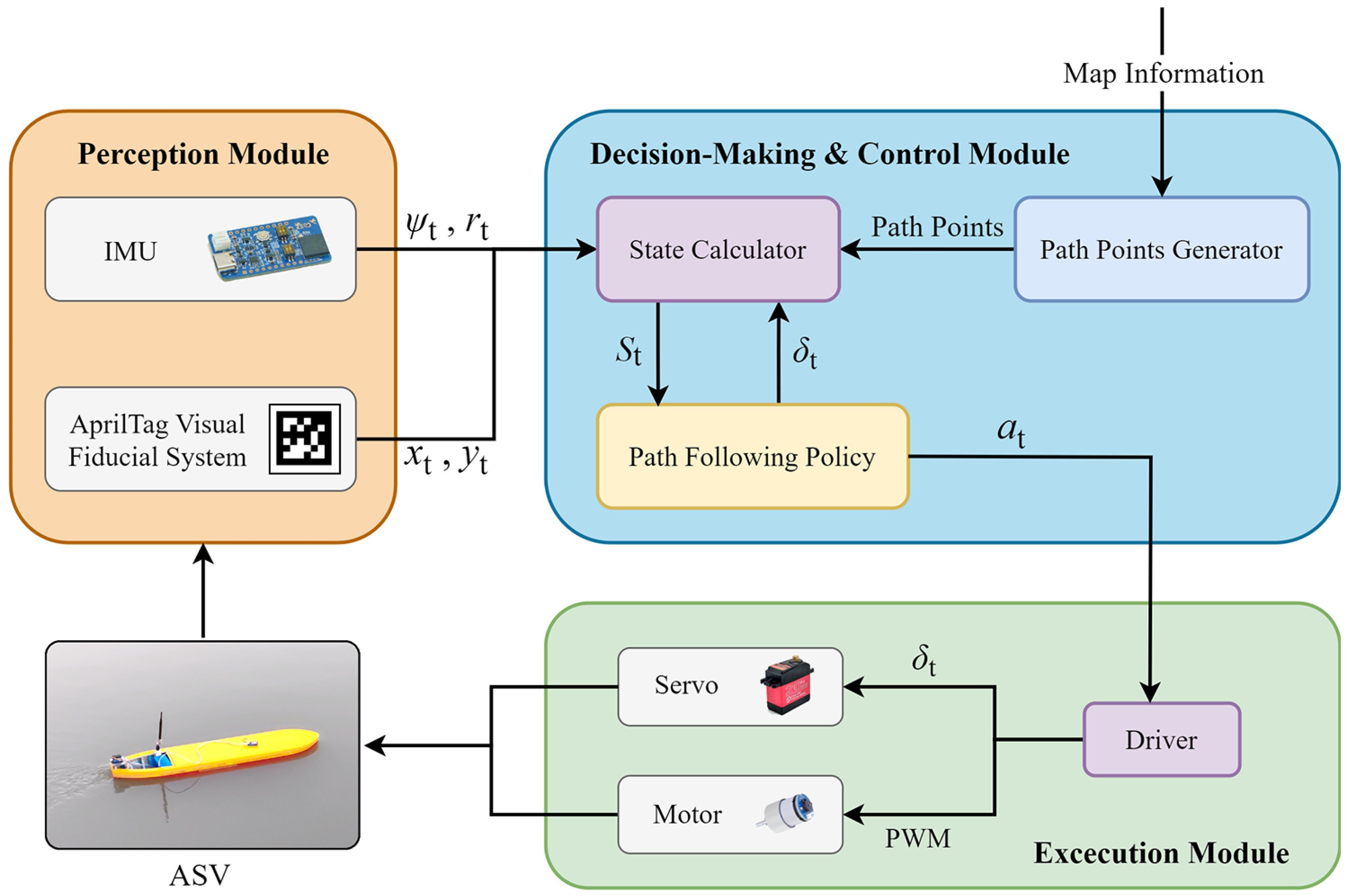
Figure 18.
The automatic behavior system of the under-actuated ASV state calculator.
Figure 18.
The automatic behavior system of the under-actuated ASV state calculator.
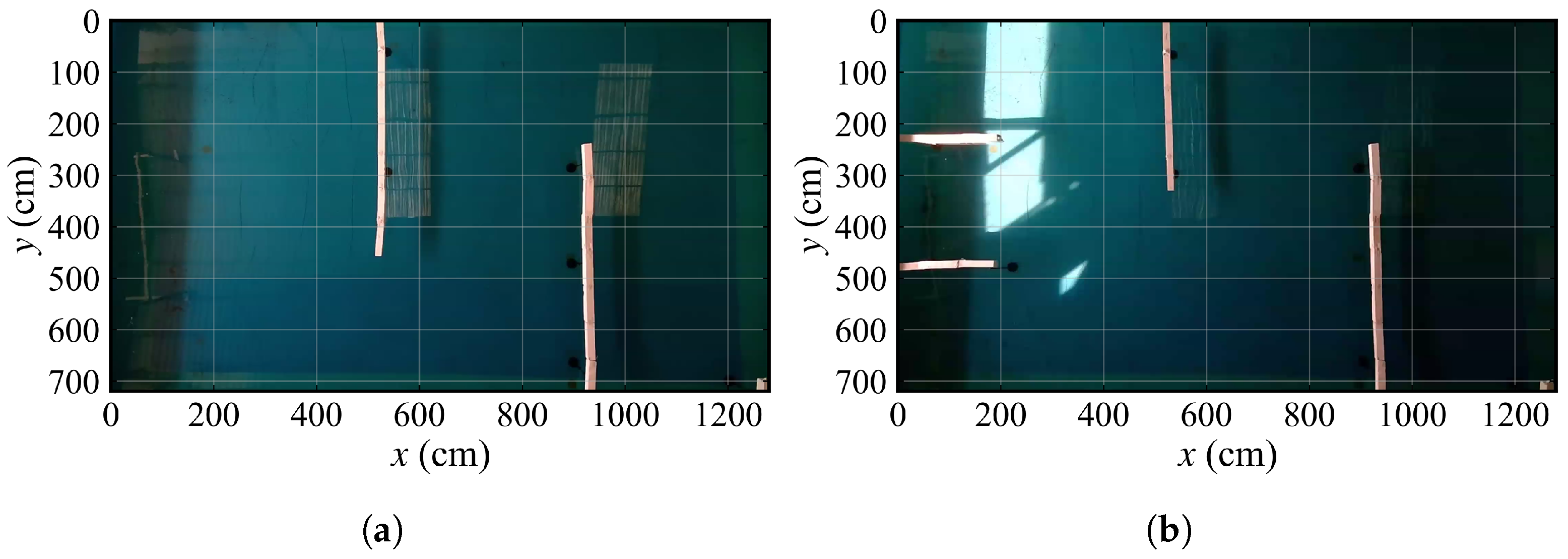
Figure 19.
The overview of two maps for model tests. (a) The map for test 1-1 and 1-2. (b) The map for test 2-1 and 2-2.
Figure 19.
The overview of two maps for model tests. (a) The map for test 1-1 and 1-2. (b) The map for test 2-1 and 2-2.
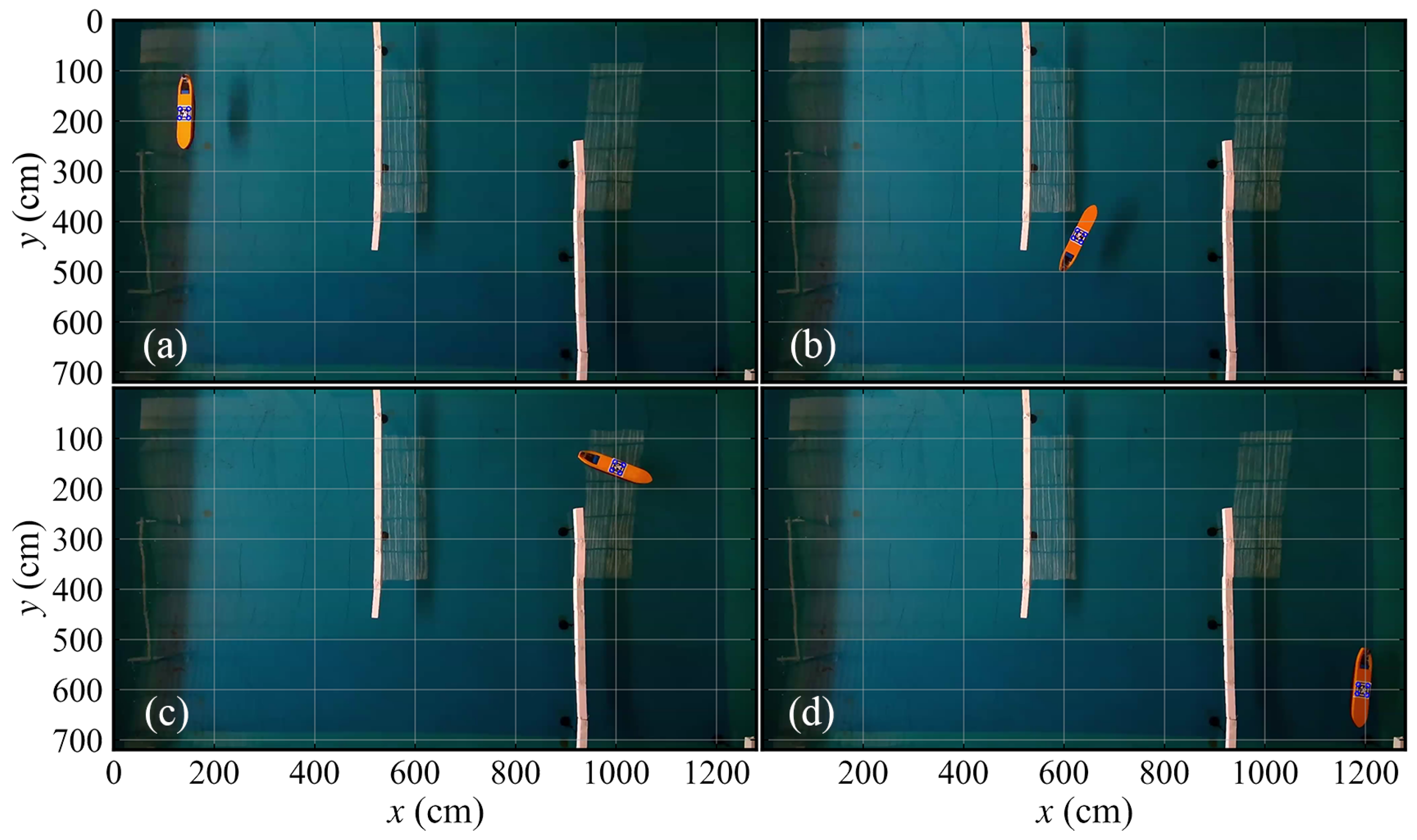
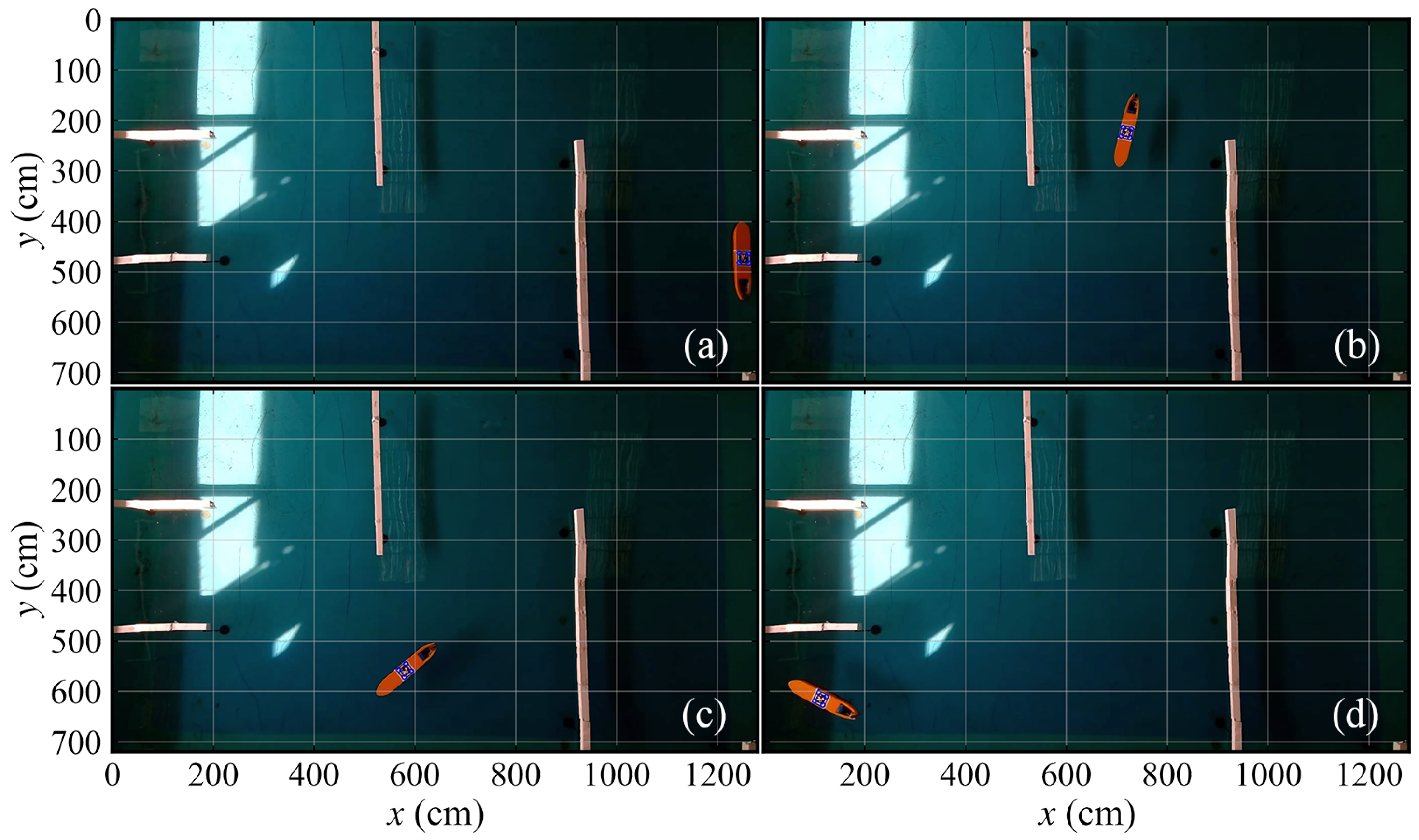
Figure 20.
Crucial navigation snapshots of test 1-2 in map 1. (a) Initial status. (b) During the navigation. (c) During the navigation. (d) Final stage.
Figure 20.
Crucial navigation snapshots of test 1-2 in map 1. (a) Initial status. (b) During the navigation. (c) During the navigation. (d) Final stage.
Figure 21.
Crucial navigation snapshots of test 2-1 in map 2. (a) Initial status. (b) During the navigation. (c) During the navigation. (d) Final stage.
Figure 21.
Crucial navigation snapshots of test 2-1 in map 2. (a) Initial status. (b) During the navigation. (c) During the navigation. (d) Final stage.
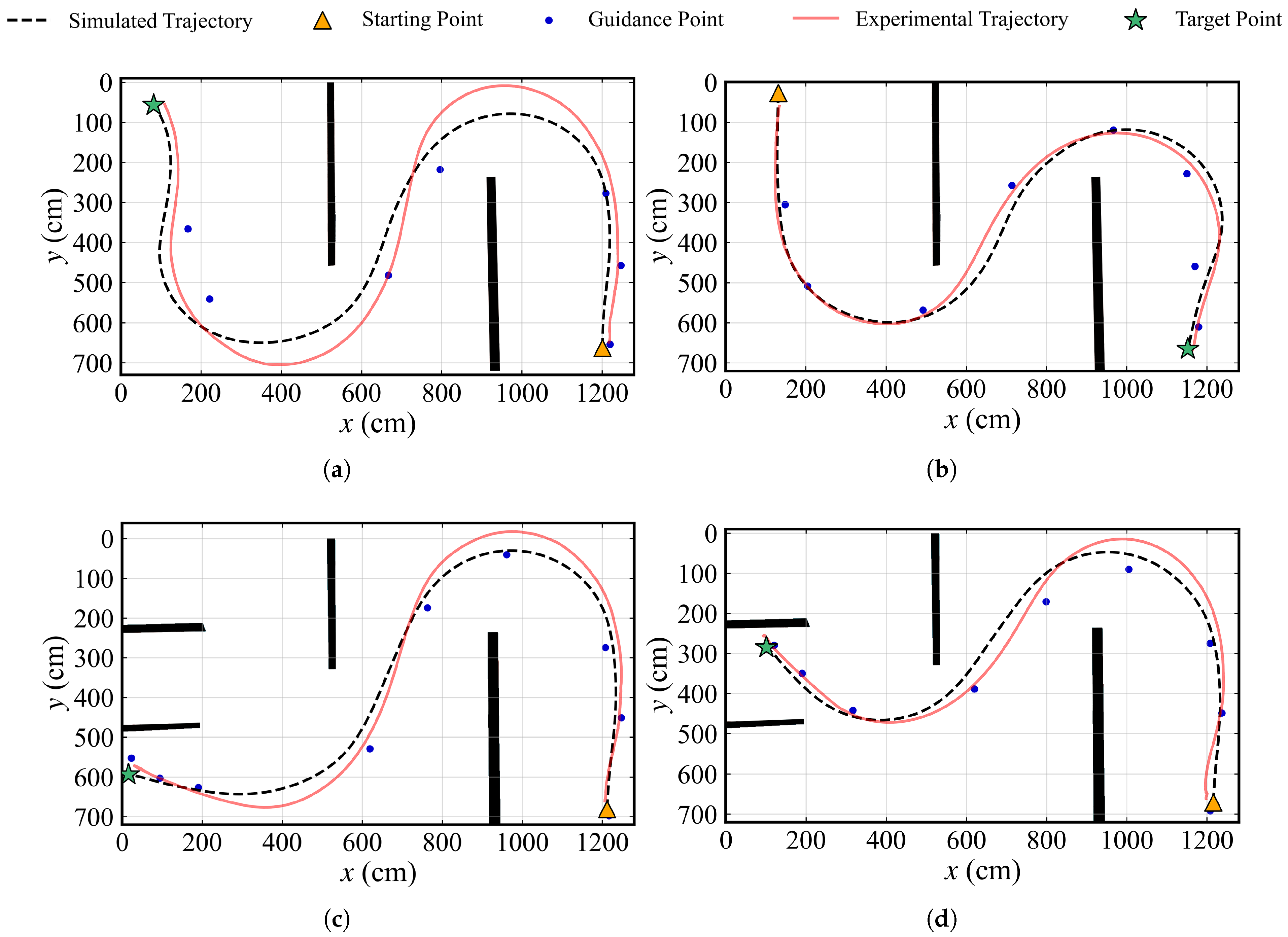
Figure 22.
Comparisons between experimental trajectory and simulated trajectory. (a) Test 1-1. (b) Test 1-2. (c) Test 2-1. (d) Test 2-2.
Figure 22.
Comparisons between experimental trajectory and simulated trajectory. (a) Test 1-1. (b) Test 1-2. (c) Test 2-1. (d) Test 2-2.
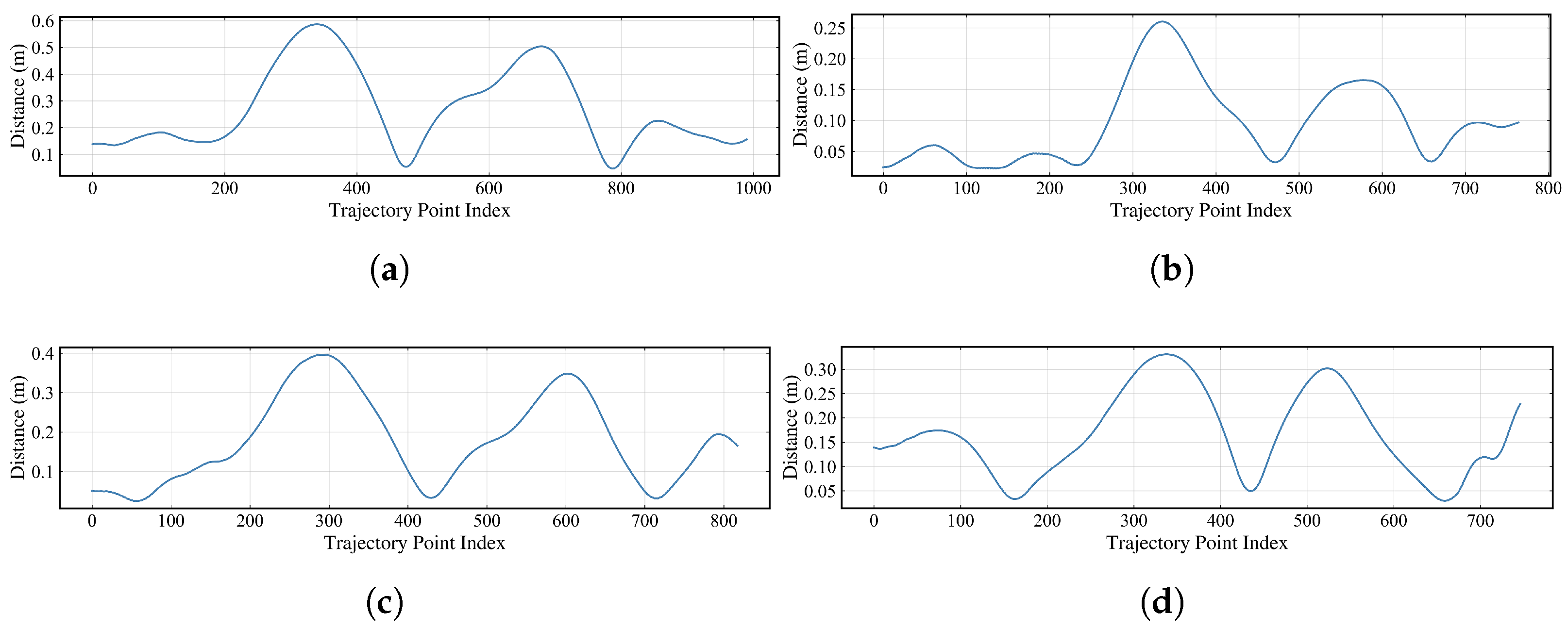
Figure 23.
Distance errors between experimental trajectory and simulated trajectory. The x-axis denotes the index of experimental trajectory points. (a) Test 1-1. (b) Test 1-2. (c) Test 2-1. (d) Test 2-2.
Figure 23.
Distance errors between experimental trajectory and simulated trajectory. The x-axis denotes the index of experimental trajectory points. (a) Test 1-1. (b) Test 1-2. (c) Test 2-1. (d) Test 2-2.
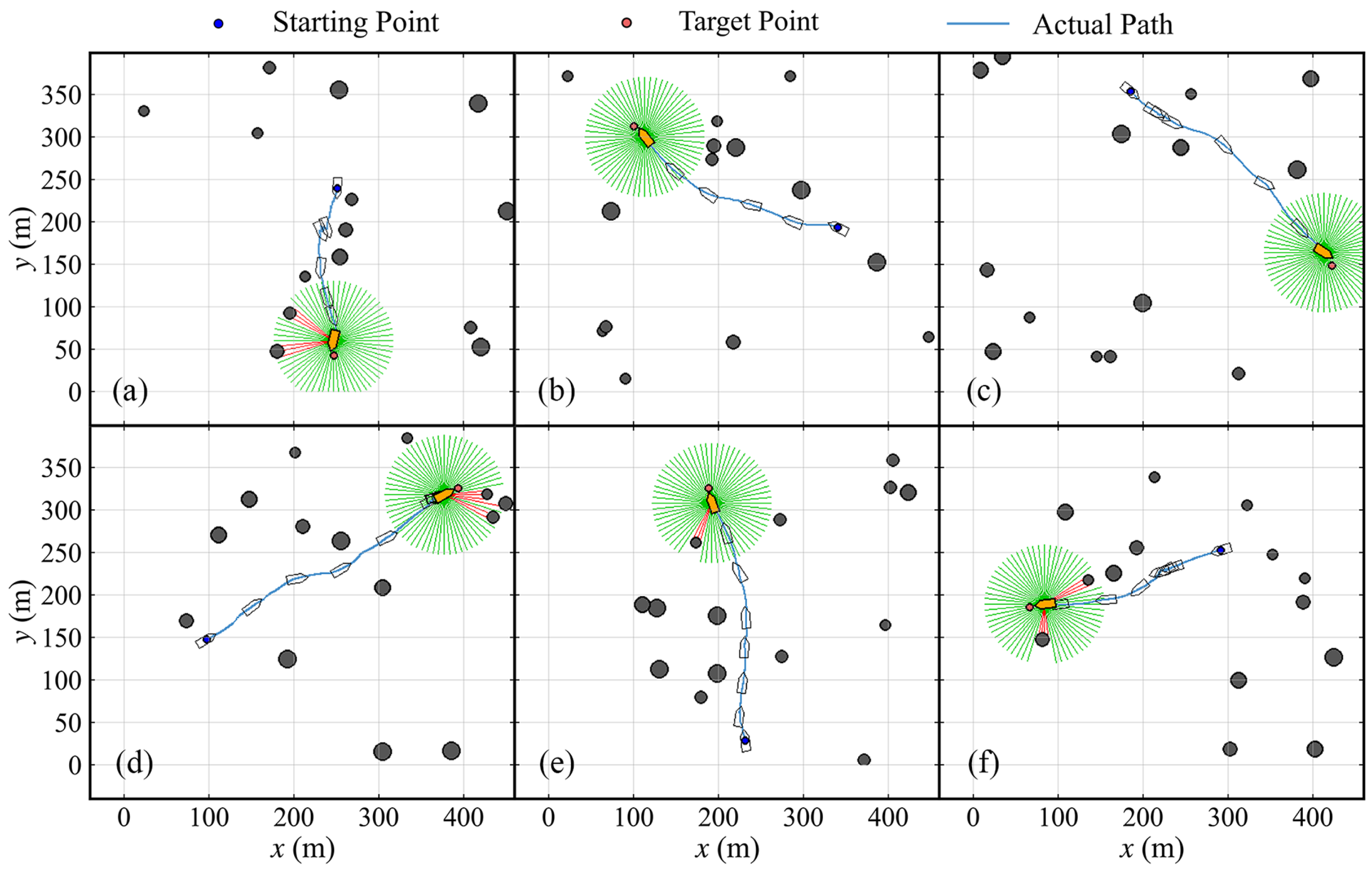
Figure 24.
Trajectories of the ASV in autonomous collision avoidance tasks. (a) Task 1. (b) Task 2. (c) Task 3. (d) Task 4. (e) Task 5. (f) Task 6.
Figure 24.
Trajectories of the ASV in autonomous collision avoidance tasks. (a) Task 1. (b) Task 2. (c) Task 3. (d) Task 4. (e) Task 5. (f) Task 6.
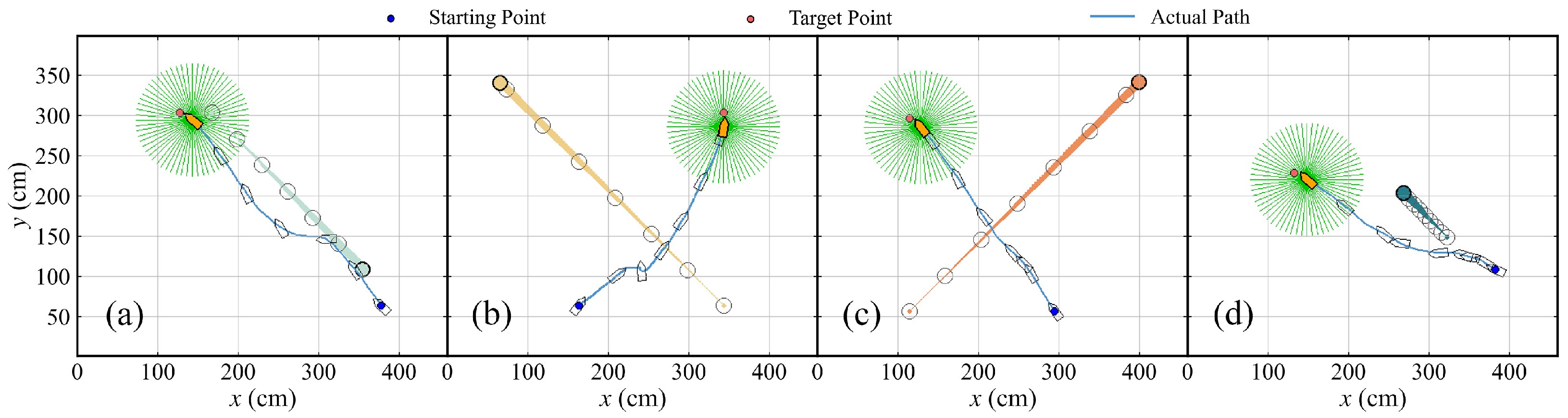
Figure 25.
The schematic representations of the ASV successfully avoiding four dynamic obstacles in calm water. (a) Task 1. (b) Task 2. (c) Task 3. (d) Task 4.
Figure 25.
The schematic representations of the ASV successfully avoiding four dynamic obstacles in calm water. (a) Task 1. (b) Task 2. (c) Task 3. (d) Task 4.
Figure 26.
The variation in distance between the vessel and obstacles. (a) Single dynamic obstacle in different encounter scenarios. (b) Multiple dynamic obstacles scenario.
Figure 26.
The variation in distance between the vessel and obstacles. (a) Single dynamic obstacle in different encounter scenarios. (b) Multiple dynamic obstacles scenario.
Figure 27.
The schematic representations of the ASV successfully avoiding four dynamic obstacles under environmental disturbances.
Figure 27.
The schematic representations of the ASV successfully avoiding four dynamic obstacles under environmental disturbances.
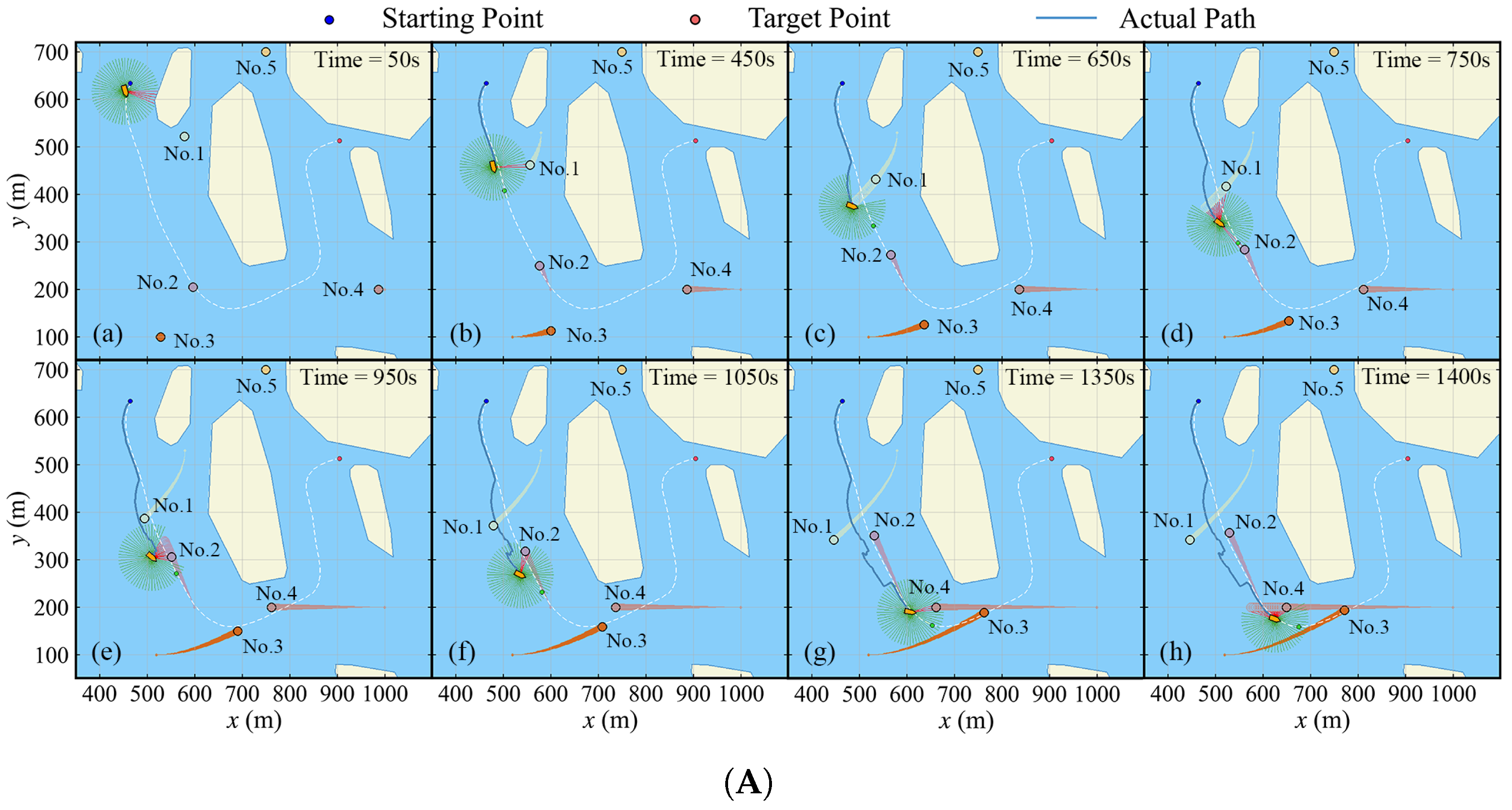
Figure 28.
The general views of the ASV navigating in a complex environment. (A) The navigation between 50 s and 1400 s. (B) The navigation between 1550 s and terminal time step.
Figure 28.
The general views of the ASV navigating in a complex environment. (A) The navigation between 50 s and 1400 s. (B) The navigation between 1550 s and terminal time step.
Figure 29.
The variation in distance between the ASV and the obstacles and the motion parameters change in a complicated environment. (a) The variation in distance between the ASV and dynamic obstacles. (b) The distance between ship actual path and global path. (c) Rudder angle. (d) Propeller PWM.
Figure 29.
The variation in distance between the ASV and the obstacles and the motion parameters change in a complicated environment. (a) The variation in distance between the ASV and dynamic obstacles. (b) The distance between ship actual path and global path. (c) Rudder angle. (d) Propeller PWM.
Table 1.
Major parameters of the model-scale VLCC.
Table 1.
Major parameters of the model-scale VLCC.
| Parameter | Unit | Value |
|---|
| Overall length | m | 1.11 |
| Overall width | m | 0.165 |
| Draft | m | 0.068 |
| Displacement | kg | 10 |
| m | 0.562 |
| m | 0 |
| m | 0.058 |
| m | 0.052 |
| m | 0.26 |
| m | 0.26 |
Table 2.
Hyperparameters of algorithms.
Table 2.
Hyperparameters of algorithms.
| Parameter | Value | Parameter | Value |
|---|
| Time step (s) | 0.5 | Learning rate | 3 × 10−4 |
| Soft-update coefficient | 5 × 10−3 | Batch size of policy training | 256 |
| Batch size of KF-LSTM training | 128 | Discount factor | 0.99 |
| Actor and critic network update interval | 1 | Target network update interval | 1 |
| Policy training start step | 1 × 104 | Replay buffer size | 1 × 106 |
| Historical states horizon | 6 | KF-LSTM historical horizon | 8 |
| KF-LSTM prediction horizon | 30 | Maximum CPA time (s) | 50 |
| Minimum CPA distance (m) | 200 | Threshold distance (m) | 10.0 |
| Forward viewing distance (m) | 8.0 | Forward viewing distance (m) | 30.0 |
| Coefficient | 1.0 | Coefficient | 1.0 |
| Coefficient | −0.1 | Coefficient | 1.0 |
| Coefficient | 1.0 | Coefficient | 0.6 |
| Coefficient | 5.0 | - | - |
Table 3.
Parameters of environmental disturbances.
Table 3.
Parameters of environmental disturbances.
| Parameter | Value | Parameter | Value |
|---|
| Wind speed (m/s) | 1.5 | Wind angle (rad) | −3/4 |
| Wave angle (rad) | −3/4 | Current speed (m/s) | 0.2 |
| Current angle (rad) | −3/4 | Air density (kg/) | 1.29 |
| Fluid density (kg/) | 1030 | Gravitational acceleration g (m/) | 9.8 |
| Frontal projection area () | 0.0066 | Lateral projection area () | 0.0444 |
Table 4.
The path-following errors in scenarios and .
Table 4.
The path-following errors in scenarios and .
| Parameter | Value | Parameter | Value |
|---|
| Average error in Scenario (m) | 0.210 | Average error in Scenario (m) | 3.979 |
| Maximum error in Scenario (m) | 1.098 | Maximum error in Scenario (m) | 7.886 |
| Time for maximum error in Scenario (s) | 5.5 | Time for maximum error in Scenario (s) | 396.5 |
Table 5.
The trajectory deviation values for each model test.
Table 5.
The trajectory deviation values for each model test.
| Test | Average Error (m) | Maximum Error (m) | Actual Trajectory Index of Maximum Error |
|---|
| 1-1 | 0.270 | 0.587 | 340 |
| 1-2 | 0.096 | 0.260 | 336 |
| 2-1 | 0.178 | 0.396 | 291 |
| 2-2 | 0.165 | 0.331 | 338 |
Table 6.
The minimum distances between the ASV and obstacles in different encounter scenarios.
Table 6.
The minimum distances between the ASV and obstacles in different encounter scenarios.
| Encounter Scenario | Minimum Distance (m) | Time (s) |
|---|
| Head on | 40.658 | 488.0 |
| Crossing 1 | 42.769 | 285.0 |
| Crossing 2 | 55.493 | 342.0 |
| Overtaking | 47.239 | 645.5 |
Table 7.
The minimum distances between the ASV and obstacles in multiple dynamic obstacles scenario.
Table 7.
The minimum distances between the ASV and obstacles in multiple dynamic obstacles scenario.
| Obstacle Index | Minimum Distance (m) | Time (s) |
|---|
| No.1 | 56.869 | 722.5 |
| No.2 | 59.884 | 727.0 |
| No.3 | 58.246 | 480.0 |
| No.4 | 22.741 | 839.5 |
Table 8.
The minimum distances between the ASV and dynamic obstacles in complicated water.
Table 8.
The minimum distances between the ASV and dynamic obstacles in complicated water.
| Obstacle Index | Minimum Distance (m) | Time (s) |
|---|
| No.1 | 76.321 | 665.0 |
| No.2 | 37.078 | 989.5 |
| No.3 | 56.530 | 2041.0 |
| No.4 | 30.866 | 1421.0 |
| No.5 | 25.081 | 2650.0 |