Exploring Time-Series Deep Learning Models for Ship Fuel Consumption Prediction
Abstract
1. Introduction
- We theoretically analyzed the possible effect factors of predicting SFC based on ship energy efficiency data, including the traditional propulsion power, resistance, and time-series dependency factors.
- We implemented in total nine time-series deep learning models for the SFC prediction task, including three RNN-based time series models, four attention-based models, and two RNN–attention mixed models. Among them, we applied models such as Transformer, iTransformer, and Informer to the prediction of ship fuel consumption for the first time and discovered their significance in improving the prediction accuracy.
- We also implemented the promising XGBoost as a representative of traditional machine learning methods for the SFC prediction task and then comprehensively compared the total ten machine learning models and evaluated their respective applicability and accuracy for SFC prediction.
2. Preliminaries
2.1. Problem Definition
2.2. Evaluation Metrics
- The mean square error (MSE) refers to the expected value of the squared error or loss and is calculated using the following equation:
- The root mean square error (RMSE) is closely related to the previously mentioned MSE and is equal to the square root of the MSE. This property brings it back to the scale of the target variable and makes it easier to interpret and understand.
- The mean absolute error (MAE) is the arithmetic average of the absolute errors and is calculated as follows:
- Mean absolute percentage error (MAPE) refers to the average relative error between the predicted value and the true value, expressed as a percentage, and is calculated as follows:
- The R-square score ( score) pertains to the coefficient of determination. It quantifies the model’s capability to predict unseen data and is computed using the following equation:
3. Related Work
4. Methodology
4.1. Ship Energy Efficiency Data
4.1.1. Characteristics of Ship Energy Efficiency Data
- In cruising conditions, the adjacent data records have similar states, leading to similar SFCs as well.
- Under changing circumstances, such as ship acceleration or deceleration, the SFC is a reflection of both the current state and the previous state. For instance, if the current speed through water is 12 knots, and the previous speed through water is higher or lower than 12 knots, i.e., the ship is accelerating or decelerating, the SFC values should not be the same.
- Under some circumstances, the noise or outlier data record contained in the data can only be identified by analyzing multiple adjacent data records, which cannot be identified solely in the data itself.
- As the frequency of ship energy efficiency data is relatively high, many changes occur gradually, including short-term subtle variations and long-term trends, with potential non-linear and lag effects between them.
4.1.2. Data Preparation for Modeling
- Based on the drafts recorded from the four sides of the ship, we calculated the average draft of the bow and astern draft and the difference between the bow and astern draft as trim. On one hand, the average draft reflects the loading conditions of ships; heavier loads lead to a deeper average draft, which requires more fuel to support the transportation of more goods. On the other hand, trim is another factor that has been proven to be able to influence ship fuel consumptions [48]. The draft difference of the ship’s left and right side is considered to have minor effects on SFC and can be neglected.
- The ships’ slip ratio can be calculated to reflect the overall situation that a ship is currently in, since it indicates the theoretical and practical distance difference a ship can move forward when the propeller makes a turn.
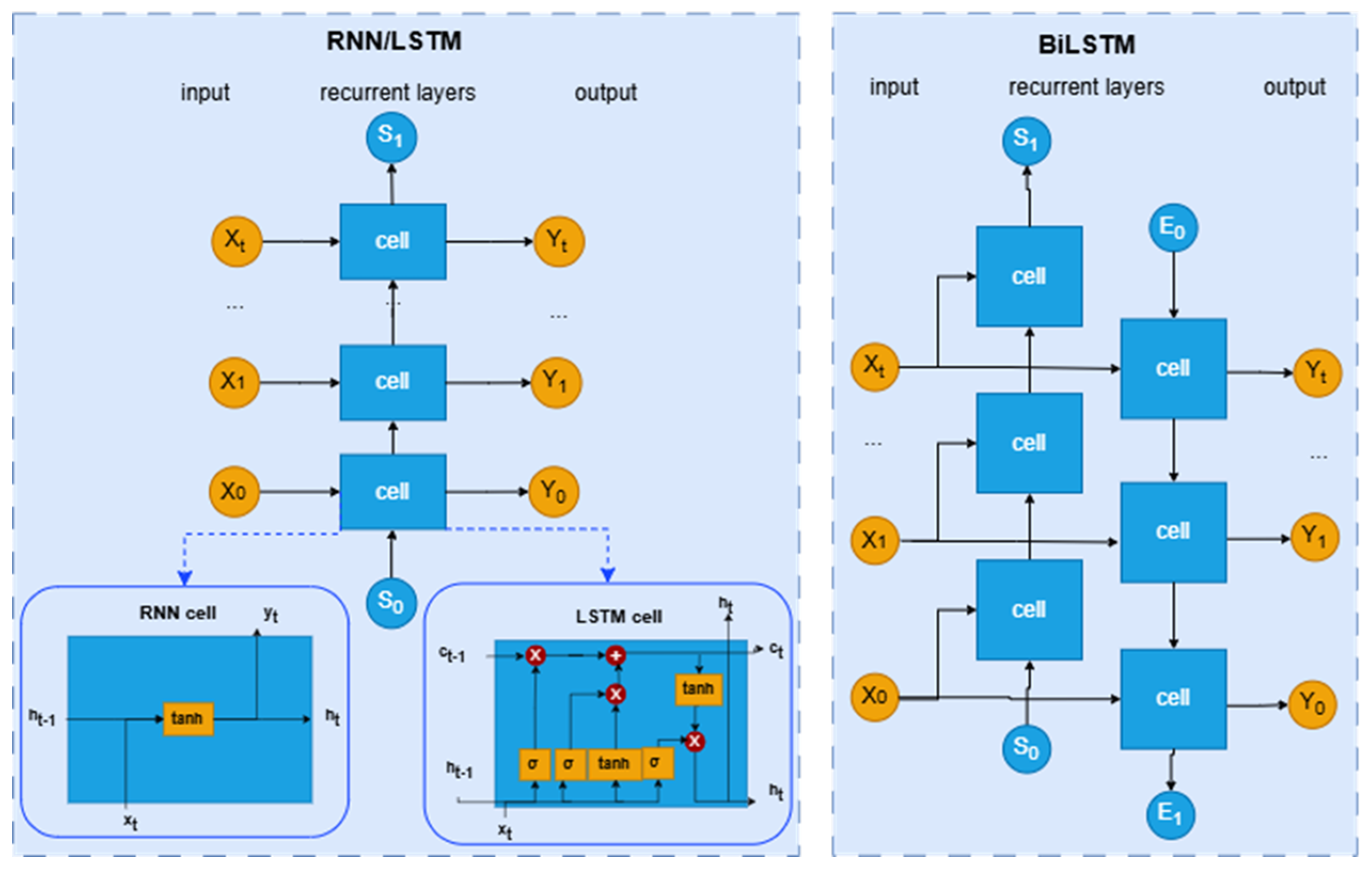
4.2. Predicting SFC Using Time-Series Deep Learning Models

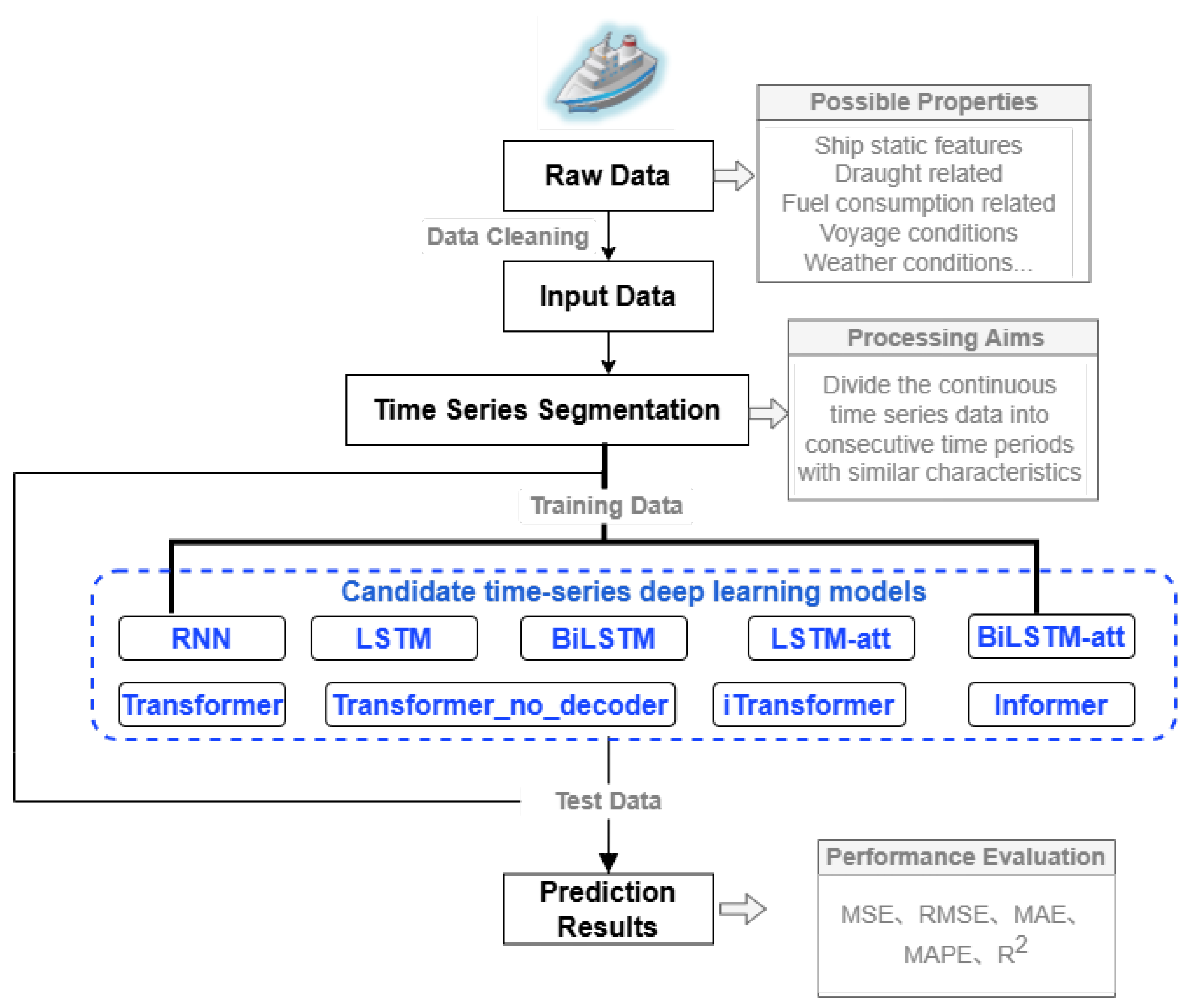
5. Experimental Evaluation
5.1. Experimental Setting
5.1.1. Datasets Used and Experimental Environment
5.1.2. Experimental Design
5.2. Experimental Results
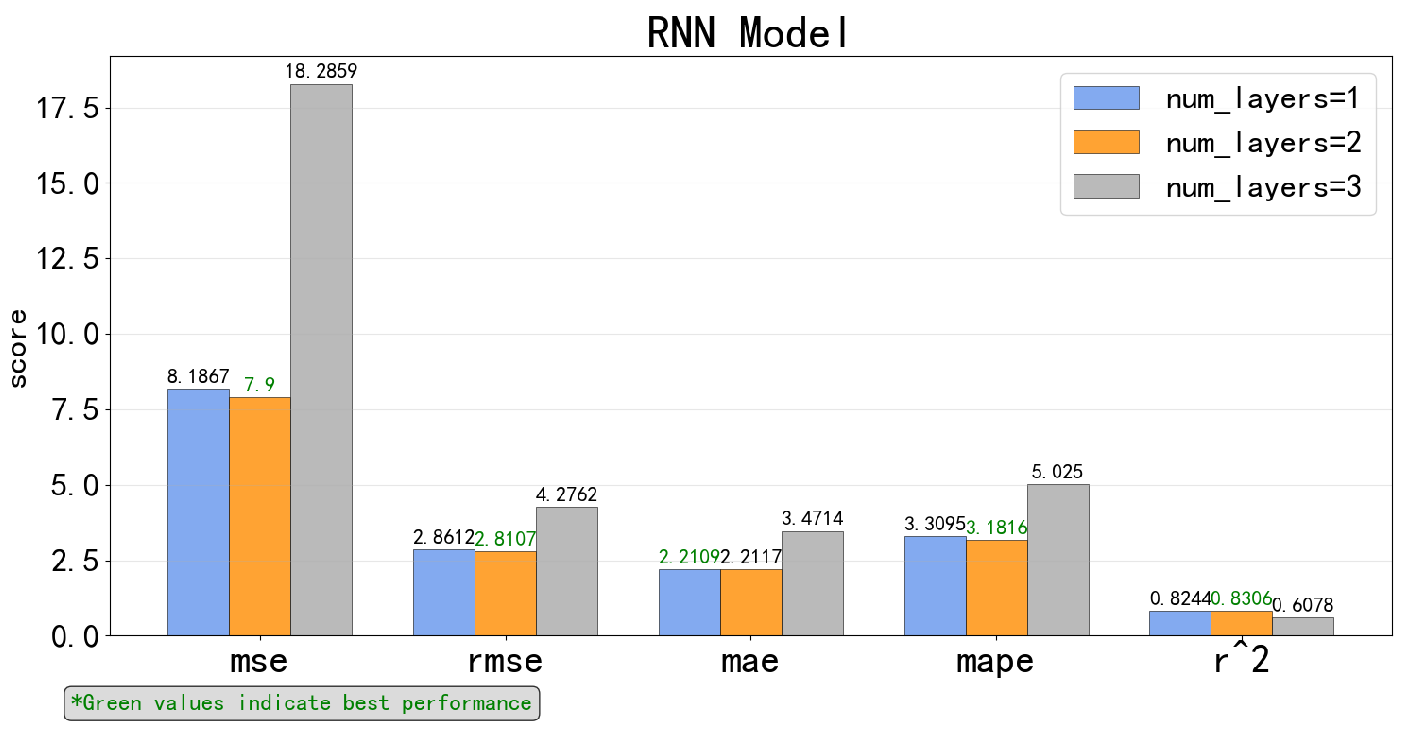
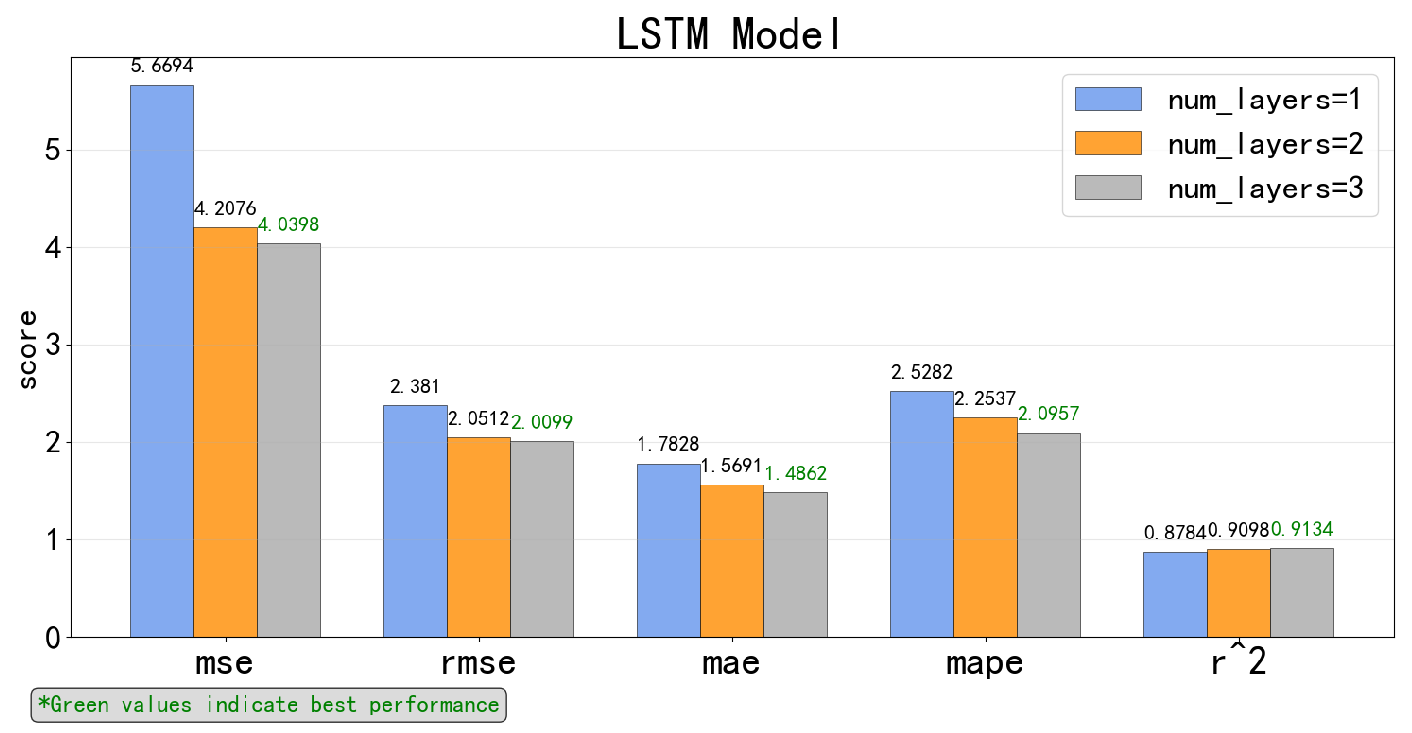
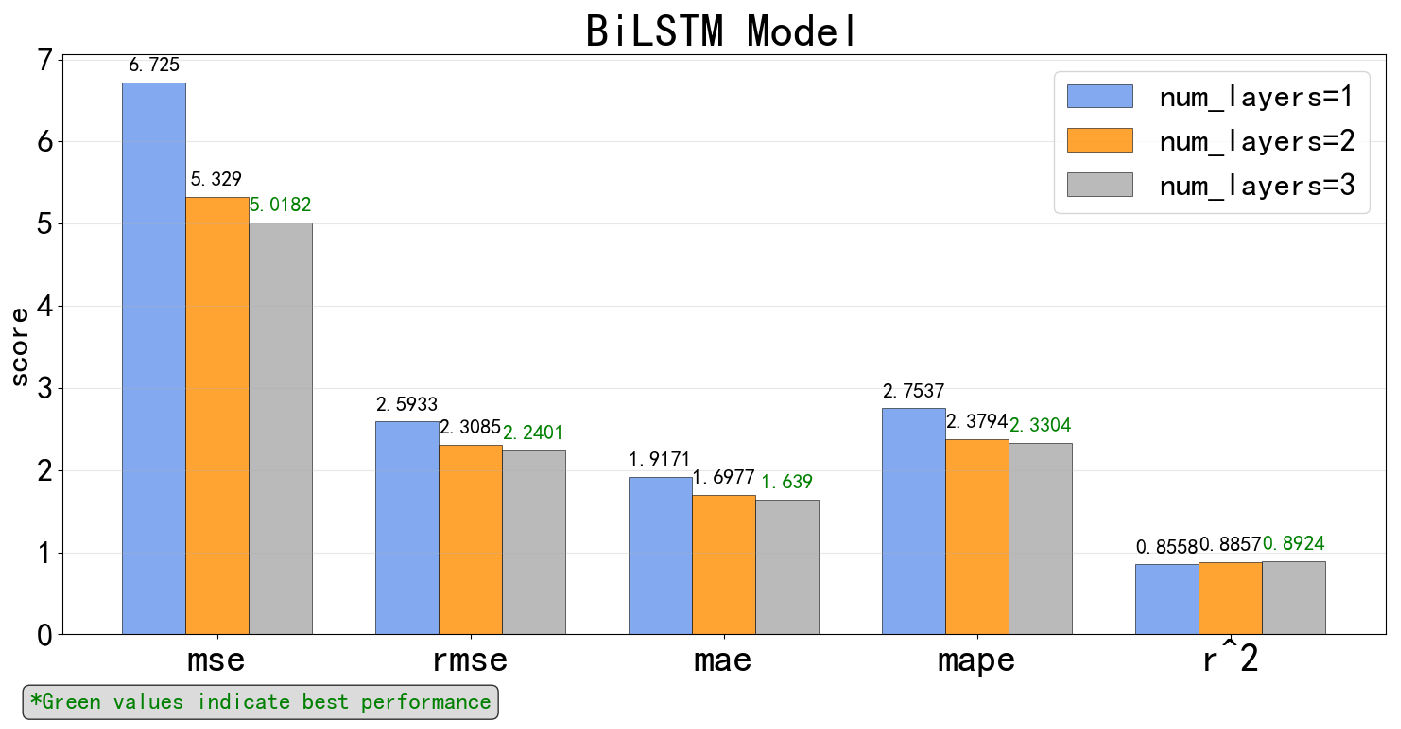
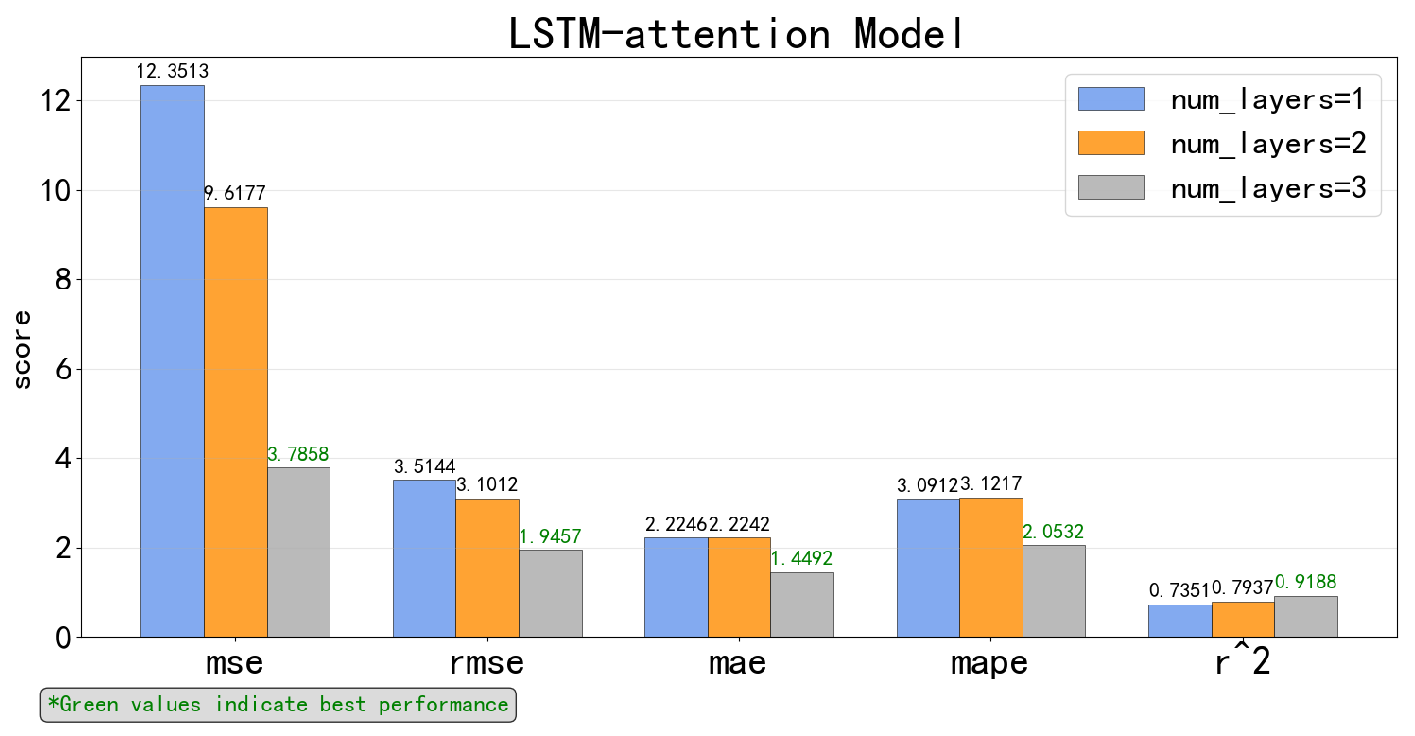
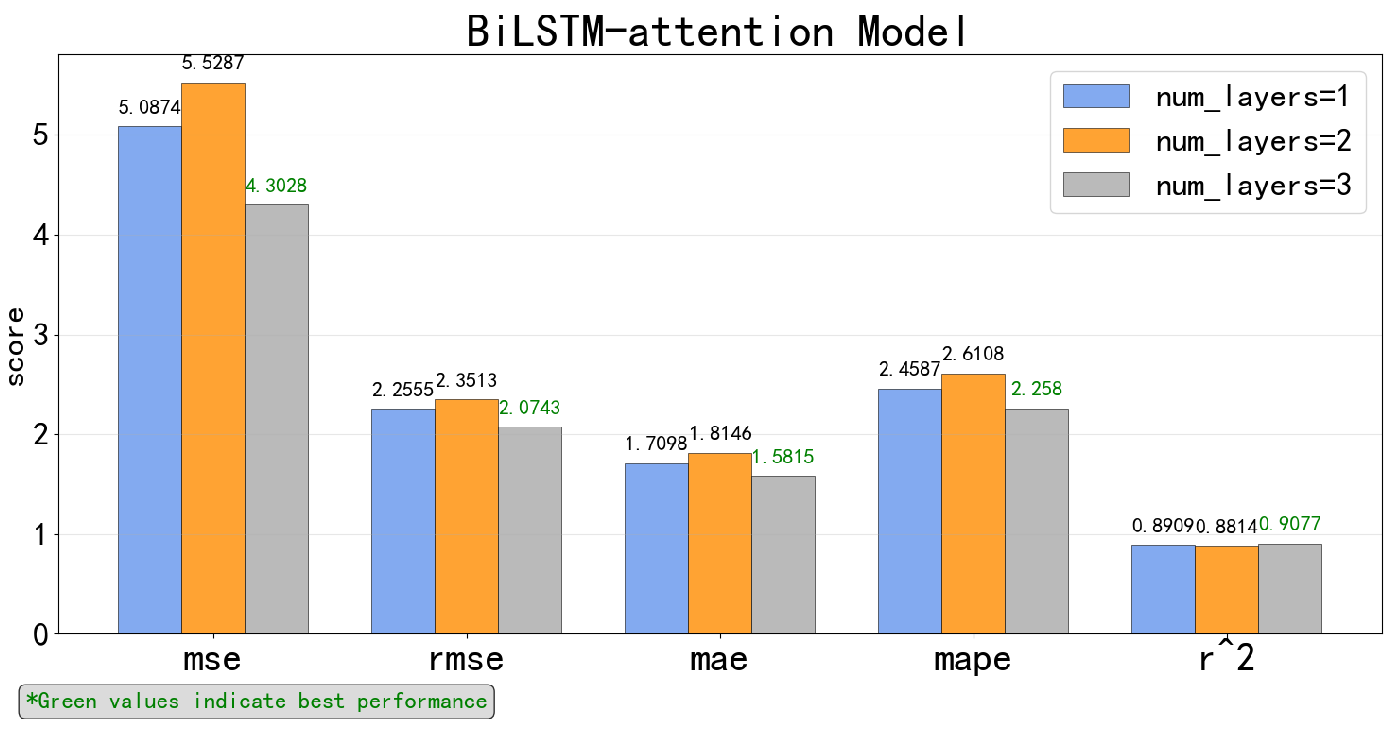
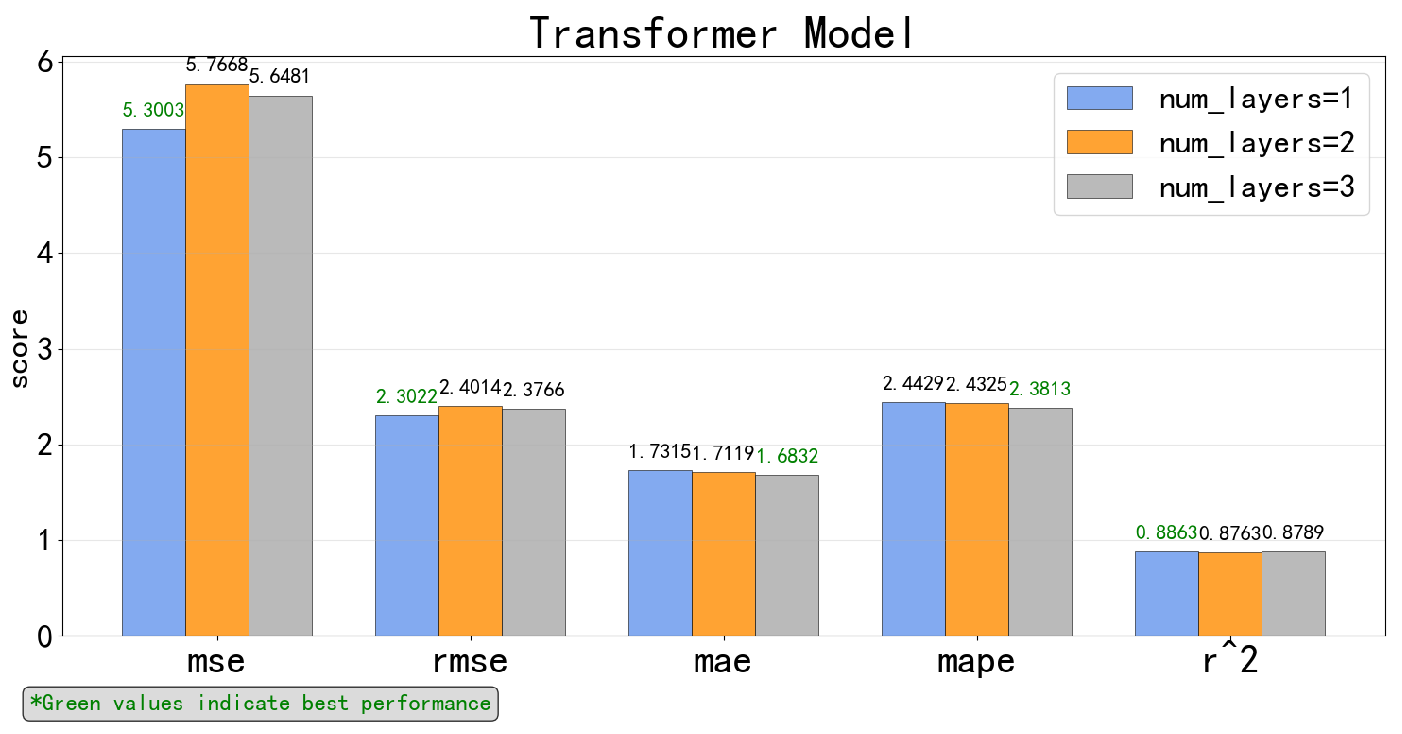
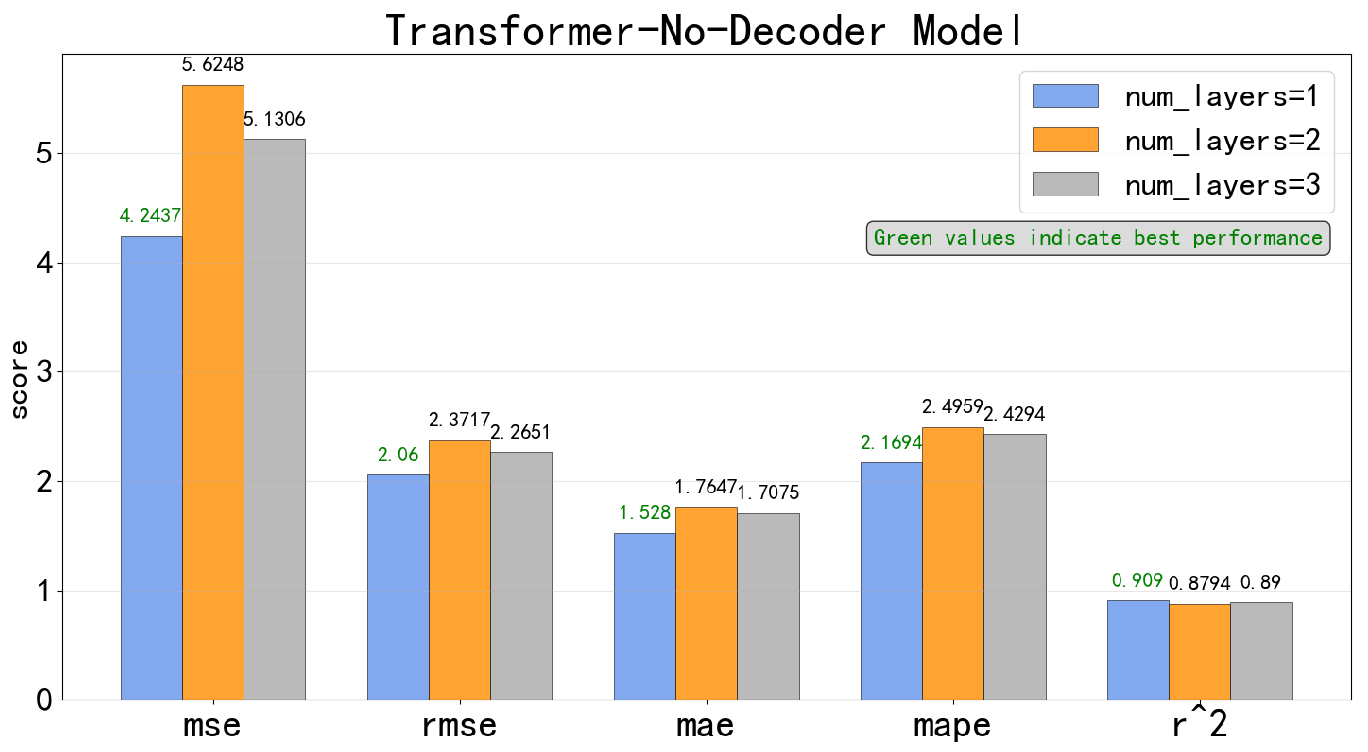
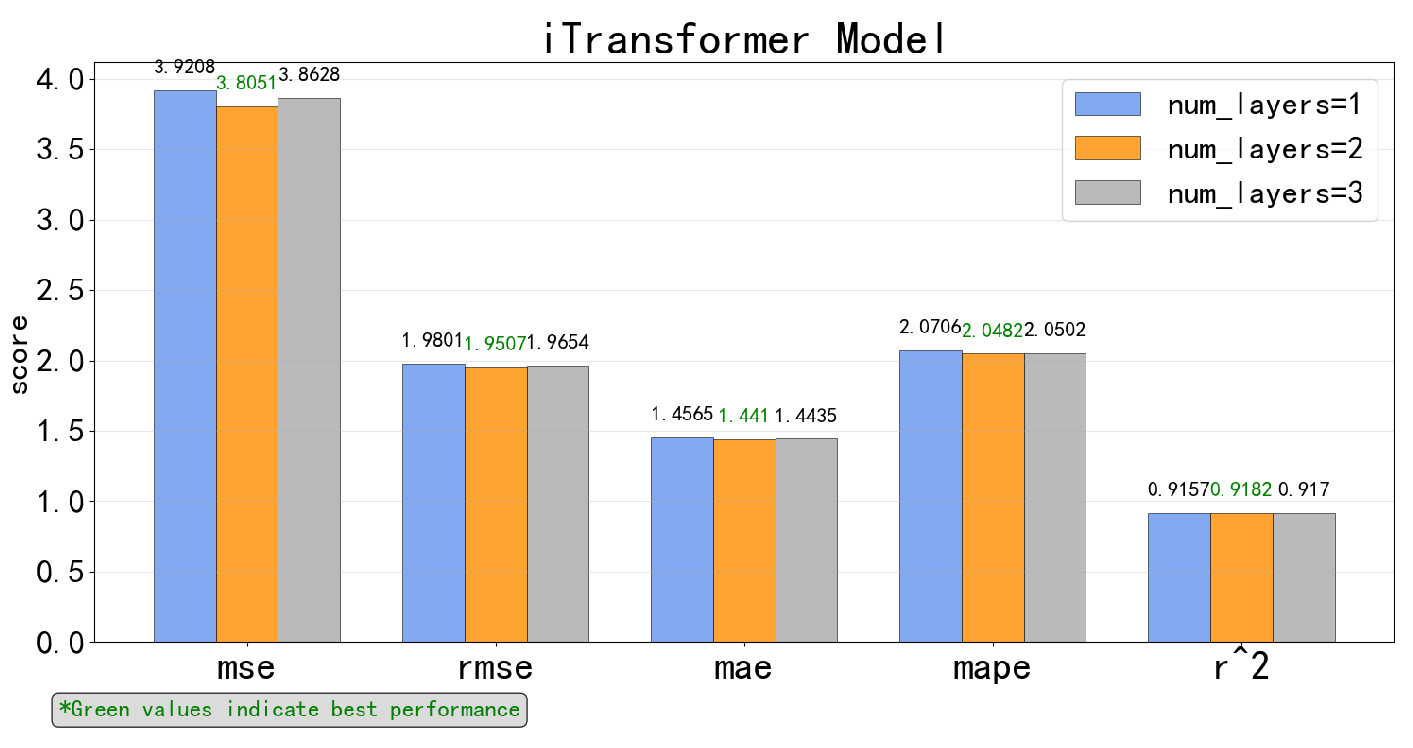
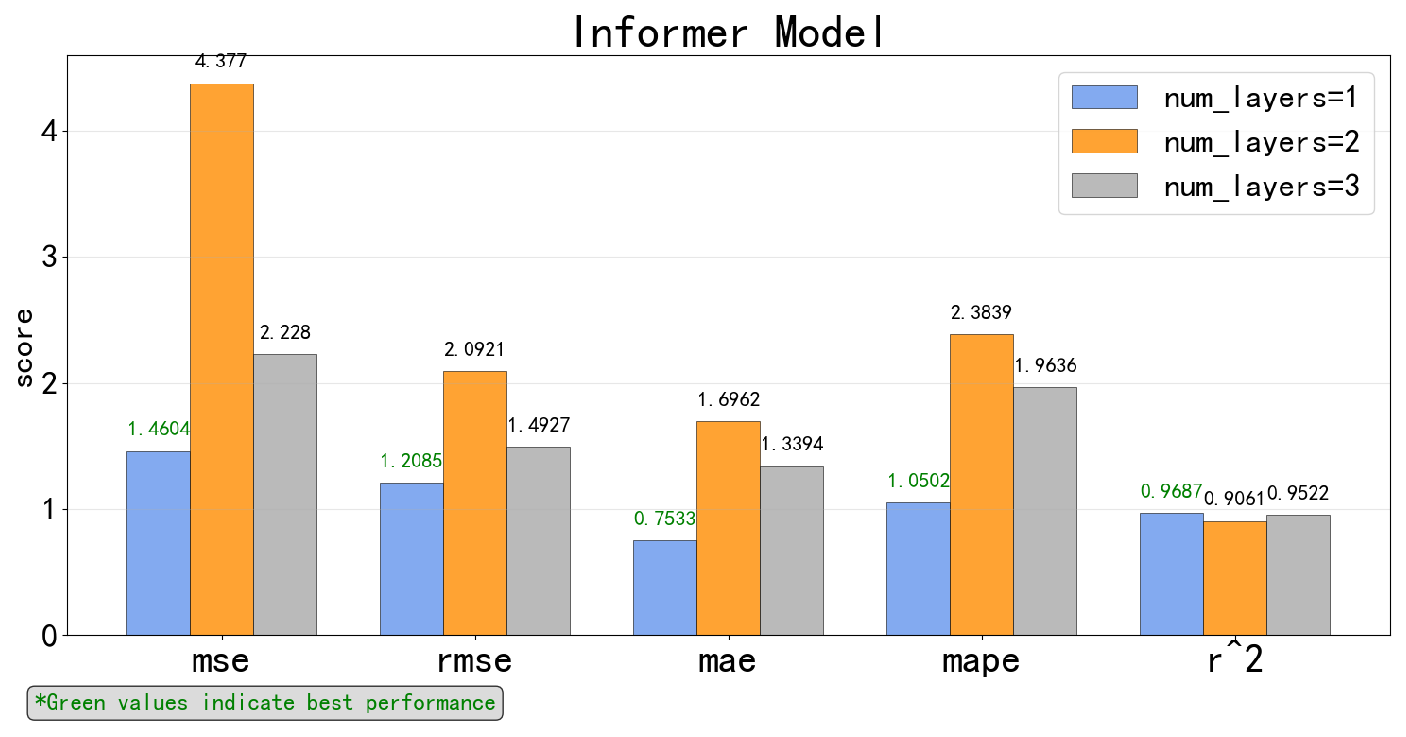
5.2.1. Respective Results of Each Time-Series Deep Learning Model
5.2.2. Comparison of Different Algorithms for SFC Prediction
5.2.3. Visualization of the SFC Prediction Result for Different Models
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agand, P.; Kennedy, A.; Harris, T.; Bae, C.; Chen, M.; Park, E.J. Fuel consumption prediction for a passenger ferry using machine learning and in-service data: A comparative study. Ocean. Eng. 2023, 284, 115271. [Google Scholar] [CrossRef]
- Eide, M.S.; Longva, T.; Hoffmann, P.; Endresen, Ø.; Dalsøren, S.B. Future cost scenarios for reduction of ship CO2 emissions. Marit. Policy Manag. 2011, 38, 11–37. [Google Scholar] [CrossRef]
- Zeng, X.; Chen, M. A novel big data collection system for ship energy efficiency monitoring and analysis based on BeiDou system. J. Adv. Transp. 2021, 2021, 9914720. [Google Scholar] [CrossRef]
- IMO. IMO Regulations to Introduce Carbon Intensity Measures Enter into Force on 1 November 2022; Manifold Times: Singapore, 2022. [Google Scholar]
- Zeng, X.; Chen, M.; Li, H.; Wu, X. A data-driven intelligent energy efficiency management system for ships. IEEE Intell. Transp. Syst. Mag. 2022, 15, 270–284. [Google Scholar] [CrossRef]
- Mou, X.; Yuan, Y.; Yan, X.; Zhao, G. A Prediction Model of Fuel Consumption for Inland River Ships Based on Random Forest Regression. J. Transp. Inf. Saf. 2017, 35, 100–105. [Google Scholar]
- Hu, Z.; Zhou, T.; Osman, M.T.; Li, X.; Jin, Y.; Zhen, R. A novel hybrid fuel consumption prediction model for ocean-going container ships based on sensor data. J. Mar. Sci. Eng. 2021, 9, 449. [Google Scholar] [CrossRef]
- Yan, R.; Wang, S.; Du, Y. Development of a two-stage ship fuel consumption prediction and reduction model for a dry bulk ship. Transp. Res. Part Logist. Transp. Rev. 2020, 138, 101930. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean. Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Chen, Z.S.; Lam, J.S.L.; Xiao, Z. Prediction of harbour vessel fuel consumption based on machine learning approach. Ocean. Eng. 2023, 278, 114483. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Anguita, D. Vessels fuel consumption forecast and trim optimisation: A data analytics perspective. Ocean. Eng. 2017, 130, 351–370. [Google Scholar] [CrossRef]
- Xie, X.; Sun, B.; Li, X.; Olsson, T.; Maleki, N.; Ahlgren, F. Fuel consumption prediction models based on machine learning and mathematical methods. J. Mar. Sci. Eng. 2023, 11, 738. [Google Scholar] [CrossRef]
- Bialystocki, N.; Konovessis, D. On the estimation of ship’s fuel consumption and speed curve: A statistical approach. J. Ocean. Eng. Sci. 2016, 1, 157–166. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Transp. Res. Part Transp. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Soner, O.; Akyuz, E.; Celik, M. Statistical modelling of ship operational performance monitoring problem. J. Mar. Sci. Technol. 2019, 24, 543–552. [Google Scholar] [CrossRef]
- Soner, O.; Akyuz, E.; Celik, M. Use of tree based methods in ship performance monitoring under operating conditions. Ocean. Eng. 2018, 166, 302–310. [Google Scholar] [CrossRef]
- Tran, T.A. Comparative analysis on the fuel consumption prediction model for bulk carriers from ship launching to current states based on sea trial data and machine learning techniquec. J. Ocean. Eng. Sci. 2021, 6, 317–339. [Google Scholar] [CrossRef]
- Kim, Y.R.; Jung, M.; Park, J.B. Development of a fuel consumption prediction model based on machine learning using ship in-service data. J. Mar. Sci. Eng. 2021, 9, 137. [Google Scholar] [CrossRef]
- Zhou, T.; Hu, Q.; Hu, Z.; Zhen, R. An adaptive hyper parameter tuning model for ship fuel consumption prediction under complex maritime environments. J. Ocean. Eng. Sci. 2022, 7, 255–263. [Google Scholar] [CrossRef]
- Karagiannidis, P.; Themelis, N. Data-driven modelling of ship propulsion and the effect of data pre-processing on the prediction of ship fuel consumption and speed loss. Ocean. Eng. 2021, 222, 108616. [Google Scholar] [CrossRef]
- Jeon, M.; Noh, Y.; Shin, Y.; Lim, O.K.; Lee, I.; Cho, D. Prediction of ship fuel consumption by using an artificial neural network. J. Mech. Sci. Technol. 2018, 32, 5785–5796. [Google Scholar] [CrossRef]
- Bui-Duy, L.; Vu-Thi-Minh, N. Utilization of a deep learning-based fuel consumption model in choosing a liner shipping route for container ships in Asia. Asian J. Shipp. Logist. 2021, 37, 1–11. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Tadros, M.; Ventura, M.; Soares, C.G. Strategy for ship energy efficiency based on optimization model and data-driven approach. Ocean. Eng. 2023, 279, 114397. [Google Scholar] [CrossRef]
- Zhu, Y.; Zuo, Y.; Li, T. Predicting ship fuel consumption based on lstm neural network. In Proceedings of the 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Guangzhou, China, 13–15 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 310–313. [Google Scholar]
- Panapakidis, I.; Sourtzi, V.M.; Dagoumas, A. Forecasting the fuel consumption of passenger ships with a combination of shallow and deep learning. Electronics 2020, 9, 776. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, J.; Zhang, Q.; Liu, Y.; Yuan, Y.; Li, Z. Prediction and optimisation of fuel consumption for inland ships considering real-time status and environmental factors. Ocean. Eng. 2021, 221, 108530. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, B.; Xie, X.; Li, X.; Li, Y.; Zhao, Y. Short-term forecasting for ship fuel consumption based on deep learning. Ocean. Eng. 2024, 301, 117398. [Google Scholar] [CrossRef]
- Zhang, M.; Tsoulakos, N.; Kujala, P.; Hirdaris, S. A deep learning method for the prediction of ship fuel consumption in real operational conditions. Eng. Appl. Artif. Intell. 2024, 130, 107425. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Scikit Learn. Metrics and Scoring: Quantifying the Quality of Predictions. 2023. Available online: https://scikit-learn.org/stable/modules/model_evaluation.html (accessed on 28 October 2025).
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Lewinson, E. A Comprehensive Overview of Regression Evaluation Metrics. 2023. Available online: https://developer.nvidia.com/blog/a-comprehensive-overview-of-regression-evaluation-metrics/ (accessed on 28 October 2025).
- Fan, A.; Yang, J.; Yang, L.; Wu, D.; Vladimir, N. A review of ship fuel consumption models. Ocean. Eng. 2022, 264, 112405. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Sailing speed optimization for container ships in a liner shipping network. Transp. Res. Part Logist. Transp. Rev. 2012, 48, 701–714. [Google Scholar] [CrossRef]
- Wei, N.; Yin, L.; Li, C.; Li, C.; Chan, C.; Zeng, F. Forecasting the daily natural gas consumption with an accurate white-box model. Energy 2021, 232, 121036. [Google Scholar] [CrossRef]
- Baldi, F. Modelling, Analysis and Optimisation of Ship Energy Systems; Chalmers University of Technology Gothenburg: Göteborg, Sweden, 2016. [Google Scholar]
- Kim, Y.; Emery, S.L.; Vera, L.; David, B.; Huang, J. At the speed of Juul: Measuring the Twitter conversation related to ENDS and Juul across space and time (2017–2018). Tob. Control 2021, 30, 137–146. [Google Scholar] [CrossRef]
- Yan, R.; Wang, S.; Psaraftis, H.N. Data analytics for fuel consumption management in maritime transportation: Status and perspectives. Transp. Res. Part Logist. Transp. Rev. 2021, 155, 102489. [Google Scholar] [CrossRef]
- Aldous, L.G. Ship Operational Efficiency: Performance Models and Uncertainty Analysis. Ph.D. Thesis, UCL (University College London), London, UK, 2016. [Google Scholar]
- Weiqiang, Y.; Honggui, L. Application of grey theory to the prediction of diesel consumption of diesel generator set. In Proceedings of the 2013 IEEE International Conference on Grey systems and Intelligent Services (GSIS), Macao, China, 15–17 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 151–153. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference (ICML’96), Bari, Italy, 3–6 July 1996; Volume 96, pp. 148–156. [Google Scholar]
- Han, P.; Ellefsen, A.L.; Li, G.; Æsøy, V.; Zhang, H. Fault Prognostics Using LSTM Networks: Application to Marine Diesel Engine. IEEE Sens. J. 2021, 21, 25986–25994. [Google Scholar] [CrossRef]
- Liu, Y.; Gan, H.; Cong, Y.; Hu, G. Research on fault prediction of marine diesel engine based on attention-LSTM. Proc. Inst. Mech. Eng. Part J. Eng. Marit. Environ. 2023, 237, 508–519. [Google Scholar] [CrossRef]
- Park, H.J.; Lee, M.S.; Park, D.I.; Han, S.W. Time-Aware and Feature Similarity Self-Attention in Vessel Fuel Consumption Prediction. Appl. Sci. 2021, 11, 11514. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. Acm Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Du, Y.; Meng, Q.; Wang, S.; Kuang, H. Two-phase optimal solutions for ship speed and trim optimization over a voyage using voyage report data. Transp. Res. Part Methodol. 2019, 122, 88–114. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF models for sequence tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. NIPS’17. pp. 6000–6010. [Google Scholar]
- Li, Z.; Rao, Z.; Pan, L.; Xu, Z. Mts-mixers: Multivariate time series forecasting via factorized temporal and channel mixing. arXiv 2023, arXiv:2302.04501. [Google Scholar] [CrossRef]
- Lin, S.; Lin, W.; Wu, W.; Wang, S.; Wang, Y. Petformer: Long-term time series forecasting via placeholder-enhanced transformer. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 9, 1189–1201. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Gong, M.; Zhao, Y.; Sun, J.; Han, C.; Sun, G.; Yan, B. Load forecasting of district heating system based on Informer. Energy 2022, 253, 124179. [Google Scholar] [CrossRef]
- Zhu, Q.; Han, J.; Chai, K.; Zhao, C. Time series analysis based on informer algorithms: A survey. Symmetry 2023, 15, 951. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, L.; Li, N.; Tian, J. Time series forecasting of motor bearing vibration based on informer. Sensors 2022, 22, 5858. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 19–21 May 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar]



| Name | Unit | Calculation Equation |
|---|---|---|
| kg/km | ||
| ShipSlip | % | |
| ShipTrim | m | |
| ShipHeel | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, X.; Luo, Y.; Zeng, X. Exploring Time-Series Deep Learning Models for Ship Fuel Consumption Prediction. J. Mar. Sci. Eng. 2025, 13, 2102. https://doi.org/10.3390/jmse13112102
Chen X, Liu X, Luo Y, Zeng X. Exploring Time-Series Deep Learning Models for Ship Fuel Consumption Prediction. Journal of Marine Science and Engineering. 2025; 13(11):2102. https://doi.org/10.3390/jmse13112102
Chicago/Turabian StyleChen, Xiao, Xiaosheng Liu, Yuxia Luo, and Xiangming Zeng. 2025. "Exploring Time-Series Deep Learning Models for Ship Fuel Consumption Prediction" Journal of Marine Science and Engineering 13, no. 11: 2102. https://doi.org/10.3390/jmse13112102
APA StyleChen, X., Liu, X., Luo, Y., & Zeng, X. (2025). Exploring Time-Series Deep Learning Models for Ship Fuel Consumption Prediction. Journal of Marine Science and Engineering, 13(11), 2102. https://doi.org/10.3390/jmse13112102