Abstract
While battery-powered propulsion represents a promising pathway for inland waterway freight, its widespread adoption is hindered by range anxiety and high investment costs. Strategic energy replenishment has emerged as a critical and cost-effective solution to extend voyage endurance and mitigate these barriers. This paper introduces a novel approach to optimize energy replenishment strategies for inland electric ships that considers the possibility of adopting multiple technologies (charging and battery swapping) and partial replenishment. The proposed approach not only identifies optimal replenishment ports but also determines the technology to employ and the corresponding amount of energy to replenish for each operation, aimed at minimizing total replenishment costs. This problem is formulated as a mixed-integer linear programming model. A case study of a 700-TEU electric container ship operating on two routes along the Yangtze River validates the effectiveness of the proposed approach. The methodology demonstrates superior performance over existing approaches by significantly reducing replenishment costs and improving solution feasibility, particularly in scenarios with tight schedules and limited technology availability. Furthermore, a sensitivity analysis examines the impacts of key parameters, offering valuable strategic insights for industry stakeholders.
1. Introduction
Inland waterway transport plays a fundamental role in the transportation sector by providing a cost-effective and energy-efficient alternative to conventional road and rail transport [1]. However, the associated emission issues are of significant concern, particularly in the context of escalating environmental challenges and stricter regulations, as they pose significant threats to public health and exacerbate climate change [2,3].
Given that propulsion systems constitute the primary source of vessel emissions, and considering that over 95% of inland ships still utilize conventional diesel engines, a transformation in propulsion technology is both imperative and inevitable [4,5,6]. Recently, battery power has emerged as a promising solution for greening inland waterway freight transportation, with the potential to achieve zero emissions, higher energy efficiency, and greater operational flexibility [7,8,9]. Despite the numerous advantages of electric ships, their adoption in inland waterway freight transportation has progressed at a relatively slow pace. This can be attributed to two primary challenges. First, the energy density of onboard batteries (about 0.18–0.26 kWh/kg) is significantly lower than that of conventional fuels (about 11.1 kWh/kg for heavy fuel oil), leading to reduced cargo efficiency and range anxiety [10]. Second, the high initial investment cost of batteries poses a significant barrier, which is difficult to recover through subsequent operational savings [11].
Strategic energy replenishment offers a direct solution to these challenges. For instance, by charging at port-side stations along their routes, electric ships can break down a long voyage into several shorter, navigable segments, thereby extending their operational range. Moreover, en-route charging reduces the demand for large-capacity onboard batteries, which in turn frees up valuable cargo space, leading to lower investment costs and higher freight income. However, energy replenishment through conventional plug-in charging, such as slow charging and fast charging, remains significantly time-consuming. To illustrate, a 1600-kWh battery requires over ten hours to fully recharge with a 150-kW slow charger, or around four hours with a 400-kW fast charger. In time-sensitive freight shipping operations, such as inland liner services, such prolonged replenishment durations represent a major operational drawback. To address this limitation, battery swapping emerges as a time-efficient alternative, enabling rapid energy replenishment for electric ships. This method involves exchanging depleted batteries for fully charged ones at port-side battery swapping stations, a process that takes only about ten minutes per battery. While battery swapping is remarkably fast, it is also considerably more expensive than charging [12]. Given that the prevailing industry practice is to employ a single technology for an entire voyage, the distinct cost and efficiency characteristics of charging and battery swapping force operators to choose between a low-cost, time-intensive strategy and a high-cost, rapid one.
In addition, existing energy replenishment strategies are often based on the principle of full replenishment (FR), which requires that the ship’s total energy level be restored to its maximum after each operation. This practice, though straightforward, can result in extended replenishment durations and unnecessarily high costs, as it fails to account for critical operational factors like task-specific energy demand and replenishment rates [13].
This paper addresses an enhanced energy replenishment optimization problem for inland electric ships by introducing two primary advancements. First, we propose a multi-technology (MT) replenishment strategy, in contrast to conventional single-technology (ST) approaches. Under this strategy, ships have the flexibility to select from various technologies, such as slow charging, fast charging, and battery swapping, whenever they replenish energy. This strategic flexibility is practically viable, as newly built electric ships with containerized batteries can utilize both charging and battery swapping. Second, we refine the traditional FR policy by incorporating partial replenishment (PR), thereby enabling ships to determine the replenishment amount during each operation.
The main contributions of this study are summarized as follows: First, to the best of our knowledge, this is the first study to integrate MT and PR strategies for inland electric ships. While growing research has focused on planning economic and efficient energy replenishment strategies, existing studies primarily focus on whether to replenish energy at candidate ports (port selection). The critical aspects of how to replenish (technology choice) and how much energy to replenish (amount determination) have largely been overlooked. Second, we propose a new mixed-integer nonlinear programming (MINLP) model to address the problem. Our model introduces several distinctive features that are not present in previous studies, such as the priorities of battery discharging, charging, and swapping, as well as the logical and operational constraints governing three key decision-making aspects. To overcome the challenges of nonlinearity, the model is reformulated as a mixed-integer linear programming (MILP) one, ensuring the efficient computation of globally optimal solutions for practical-scale instances within seconds. Third, a case study is conducted to demonstrate how the proposed model determines the optimal energy replenishment strategies for inland electric ships and investigates the effects of key parameters on decision-making. The results show significant improvements in cost efficiency and operational feasibility compared to existing methods. Based on these findings, we provide stakeholders with strategic recommendations and actionable insights to support infrastructure planning and operational decision-making.
2. Literature Review
Prior studies have extensively examined the energy replenishment optimization problem for inland electric ships. Wang et al. [14] proposed a comprehensive optimization framework that addresses multiple aspects, including the location of charging stations, charging planning, route planning, ship scheduling, and ship deployment. The objective function was to minimize total costs associated with station construction, charging operations, and fixed ship deployment. The emergence of battery swapping technology has prompted a growing interest in developing cost-effective battery swapping strategies [9,15,16]. For instance, Gu et al. [15] focused on selecting the optimal battery swapping stations for a ship to visit from candidates along its route, aimed at minimizing the total battery swapping cost. Building on this work, Zhang et al. [16] incorporated time-of-use pricing instead of fixed pricing for battery swapping. In a subsequent study, they formulated a more comprehensive bilevel optimization framework. The upper-level addresses strategic infrastructure planning, such as station siting, while the lower-level optimizes tactical ship scheduling, which involves selecting the optimal stations during a voyage [9].
Methodologically, these problems are formulated as mixed-integer programming models. MILP models can be efficiently solved to global optimality using commercial solvers such as CPLEX and Gurobi for typical problem scales [14]. However, most real-world problems are instead formulated as MINLP models due to factors such as nonlinear power–speed relationship or physical constraints. Such models pose significant challenges due to their non-convex nature and computational complexity. To address this, a classical approach involves linearizing the nonlinear terms to reformulate the problem as an MILP model. This approach has been widely adopted in energy replenishment optimization for both conventional diesel-driven ships and emerging electric ships, demonstrating its suitability for addressing such problems [15,17,18,19]. Nevertheless, when the problem structure becomes highly complex or the problem scale grows excessively large, the linearized MILP approach may become impractical. In such cases, heuristic or metaheuristic algorithms are commonly employed to efficiently find high-quality, near-optimal solutions for the original MINLP model [9,16]. However, these methods can trade precision and robustness for computational efficiency, as they typically provide suboptimal solutions and exhibit sensitivity to parameter settings.
These studies have contributed to developing energy replenishment strategies for inland electric ships. Given that the unit energy replenishment price usually differs across stations, most existing studies focus on selecting the optimal stations among candidates to minimize total replenishment costs, reflecting ships’ preferences in replenishing at cheaper stations. However, such strategies present two major limitations.
First, most strategies rely on the simplified assumption of FR, an approach consistent with early research on the Green/Electric Vehicle Routing Problem. This strategy, which mandates that vehicles recharge to their maximum capacity at charging stations, overlooks the optimization of replenishment amounts and is often suboptimal in practice [20]. The primary drawback of FR is that it can lead to prolonged total charging durations, resulting in distribution delays and higher operational costs. Consequently, the PR strategy was introduced, allowing vehicles to recharge with variable energy levels [21]. The advantages of PR have been empirically validated, including significant reductions in costs, time, and energy consumption, along with enhanced solution feasibility under complex scenarios [22,23,24,25,26]. Given these benefits, adapting PR for electric ships is crucial. However, a key distinction arises when applying this concept to electric ships. Conventional PR has exclusively been applied to the charging of vehicles, as single-battery electric vehicles do not involve decisions regarding the number of batteries to be swapped. In contrast, current inland electric ships are typically equipped with multiple batteries to enhance endurance. For example, the “Alphenaar” is equipped with two batteries, the “Jiangyuanbaihe” with three, and the “N997” with 36. The multi-battery configuration therefore makes it essential to develop a PR strategy for electric ships that addresses both charging and battery swapping.
Second, existing strategies have typically focused on either charging or battery swapping exclusively, neglecting the potential advantages of selecting from multiple available technologies for each replenishment operation. The superiority of adopting MT strategies has been demonstrated in studies developing energy replenishment strategies for alternative fuel vehicles. For instance, Felipe et al. [21] investigated a model for alternative fuel vehicles that incorporated three distinct charging technology options with varying levels of charging speed and cost. Their comprehensive testing on diverse technology combinations revealed that no single technology consistently outperforms the others or their combinations across all scenarios. Paz et al. [24] proposed three MILP models for electric vehicles to address scenarios involving charging-only, battery swapping-only, or a combination of both. Their findings demonstrated that the integration of the two technologies offers enhanced operational flexibility. Similarly, Verma et al. [13] found that allowing electric vehicles to replenish energy through both charging and battery swapping enables the development of more efficient delivery routes with reduced overall costs, particularly in scenarios where the unit cost of battery swapping decreases.
To bridge these gaps, this study proposes an innovative energy replenishment optimization model for inland electric ships that integrates both MT and PR strategies. This is challenging for two primary reasons. First, charging and battery swapping are fundamentally distinct technologies requiring different modelling approaches. Second, the PR strategy for inland electric ships, owing to their multi-battery configuration, differs substantially from existing strategies for electric vehicles. By addressing these complexities, the proposed approach is expected to significantly enhance the flexibility of energy replenishment strategies, thereby offering substantial potential for cost reduction and improved solution feasibility.
3. Problem Formulation
3.1. Problem Description
Consider an inland electric ship powered entirely by onboard batteries, with the total number of batteries and their unit capacity denoted by and (in kWh), respectively. The number of batteries remains fixed throughout the voyage. These batteries supply power for both propulsion loads and service loads. The propulsion power, a function of the ship’s sailing speed, is commonly modeled using either the classic cubic relationship or a more comprehensive empirical third-order polynomial function [9,15,16]. The service power is assumed to be constant and known throughout the voyage.
To ensure operational safety and prolong battery life, the state of charge (SOC) of each battery must remain within prescribed limits [16], denoted by . For simplicity, we assume that batteries are discharged sequentially, with each battery being discharged until its SOC reaches , after which the next battery begins discharging. The discharging sequence follows an ascending order based on the initial SOC of the batteries. Based on their SOC, we classify the batteries into three primary groups:
- Fully charged batteries: Batteries with an SOC equal to the upper limit, ;
- Partially charged batteries: Batteries with an SOC in the open range ;
- Depleted batteries: Batteries with an SOC equal to the lower limit, .
The ship performs cargo transportation tasks along a predefined inland round-trip shipping route, and the entire voyage is required to be completed within a reasonable time frame, denoted as (in hours) [27]. Let denote the total number of ports along the route. The route is represented as a symmetric sequence of port nodes: , where forms the forward sub-route, and forms the backward sub-route. Each port node is indexed by (). Specifically, for , nodes and represent the same physical port, with on the forward sub-route and on the backward sub-route. Node refers to the destination port.
A leg () is defined as the directed edge connecting node to node . Each leg is characterized by its length (in nautical miles) and water speed (in km/h). The symmetry of the route ensures: , . The sign of indicates the impact of the streamflow: when the ship sails along the streamflow, and when the ship sails against the streamflow. For each leg , the ship’s sailing speed (in knots) and its corresponding propulsion power (in kW) are assumed to be known constants. This simplification is justified by the common practice of shipping companies operating under typical conditions (e.g., sailing speed, cargo amount), where power consumption data is available from performance trials or historical operational data [16].
Based on the above discussions, an example sailing route is illustrated in Figure 1, with two groups of port nodes highlighted:
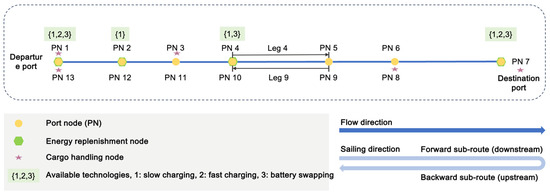
Figure 1.
An illustrated example of the sailing route.
- Cargo handling nodes (): These are ports where the ship is scheduled to load or unload cargo. For the specific network illustrated in Figure 1, we have . These specific ports are predetermined as part of transportation plans to ensure customer convenience [14]. A visit to a node incurs a fixed and known port time (in hours), accounting for pilotage, cargo handling, and waiting times [1]. For nodes , no such time exists by definition. However, to ensure mathematical consistency in the model, is assigned a value of 0 for all
- Energy replenishment nodes (): These are ports equipped with facilities where the ship can optionally stop to replenish its energy. For the specific network illustrated in Figure 1, we have . This model includes a set of energy replenishment options, , consisting of both charging and battery swapping.
- Charging is defined as the continuous replenishment of energy by connecting to chargers. Multiple charging options, differentiated by their power levels, are typically available, such as slow charging and fast charging (as shown in Figure 1). These charging options are collectively denoted as the set ().
- Battery swapping is a discrete process of replacing onboard batteries with fully charged ones at battery swapping stations. This model considers a single battery swapping option, denoted by the singleton set ().
Let represent the set of available technologies at node . For each energy replenishment operation, the ship has the flexibility to select a technology . Each technology has distinct cost and efficiency characteristics. Specifically, the unit cost of using technology at node is denoted by (in CNY/kWh). The replenishment efficiency is defined differently for charging and battery swapping. For charging, efficiency is measured by the charging power (in kW), which reflects the capacity of the charging facilities. For battery swapping, efficiency is measured by the time (in hours) required to replace a single battery. It is assumed that , , and are all fixed and known as parameters. Furthermore, the model incorporates PR for both charging and battery swapping, offering flexibility in determining the replenishment amount. To implement this strategy, two key variables are defined: , representing the amount of energy replenishment (in kWh), and , representing the number of batteries to be swapped. The role of differs depending on the technology used. For , serves as a direct decision variable that specifies the charging amount. In contrast, for , it becomes a dependent variable, whose value is determined by . For simplicity, the following assumptions are established regarding energy replenishment:
- Replenishment at stations in the set is limited to a single visit per station and must strictly follow the forward progression of the ship’s route.
- A voyage is complete after the ship returns to its departure port, finishes cargo handling, and undergoes an FR in preparations for the subsequent voyage.
- During charging, batteries are charged sequentially in descending order of their initial SOC. The process involves charging each battery to before proceeding to the next. This process continues sequentially until the cumulative energy charged reaches the target value. For battery swapping, batteries are also replaced sequentially, but in ascending order of their initial SOC. Only depleted batteries can be swapped at intermediate battery swapping stations.
- When a cargo handling node is also equipped with replenishment facilities, it is advantageous for the ship to replenish energy at the port to enhance berth time utilization and reduce dedicated stops, thereby minimizing disruptions to voyage schedules. The concurrency of these two operations depends on the technology employed: charging can occur simultaneously with cargo handling, enabling the efficient use of the ship’s time at berth. In contrast, battery swapping must be conducted as a separate activity due to security considerations.
Two key conclusions can be derived based on the preceding assumptions:
- A direct consequence of the sequential battery charging, discharging, and swapping is that there can be at most one partially charged battery at any given time. All other non-fully charged batteries are, by definition, depleted ones.
- Replenishing energy at node 1 is unnecessary as the ship has performed FR at the conclusion of the preceding voyage. The model’s replenishment strategy therefore involves three distinct rules: no replenishment at node 1, a mandatory FR at node , and optional PR at intermediate stations in the set .
Additionally, certain port nodes, such as nodes 5, 6, 9, and 11 in Figure 1, do not serve as cargo handling nodes or energy replenishment nodes. These nodes are included in the route to divide it into adjacent segments with distinct navigational environments [16]. In this study, this distinction is based specifically on water speed.
The objective function of our model is to minimize the total energy replenishment costs, which represent the primary variable operating expense in inland shipping [1,28,29]. Notably, the cost associated with battery degradation is not included in this model. This exclusion is justified by the adoption of the “Battery-as-a-Service” or battery leasing business model, which first emerged in the electric vehicle market and has been embraced by industry leaders such as Tesla and NIO [30]. This innovative solution is becoming increasingly attractive for ship electrification because it eliminates the high upfront capital investment in batteries and transfers the risk of degradation to the service provider. In China, for instance, battery manufacturers such as CATL and Qiyuan Green Power are already acting as both battery lessors and operators of charging and battery swapping stations, providing services to inland shipping companies. Such operations realize the separation of ship and batteries, whereby the degradation cost has been internalized by the providers within their pricing structure, for example, through a fixed leasing fee or as a part of the energy replenishment price. Consequently, our objective function reflects the perspective of ship operators, aiming to minimize the explicit energy replenishment costs. However, to provide a more comprehensive analysis, a preliminary investigation into battery degradation is conducted in the case study.
To minimize the total replenishment costs, our study develops an optimal strategy by considering three interdependent factors within an integrated framework:
- Port selection: Identifying the optimal ports for energy replenishment from a set of candidates ;
- Technology choice: Selecting the best replenishment technology from the available options at each selected port;
- Replenishment amount: Determining the optimal charging amount or the number of batteries to be swapped.
Accordingly, the problem is to determine an optimal energy replenishment strategy for an inland electric ship on a given route, which involves jointly optimizing port selection, technology choice, and replenishment amount. The objective is to minimize the total energy replenishment costs, subject to constraints on round-trip time, energy endurance, and a series of logical and operational constraints governing these decisions.
Notably, the model can accommodate any combination of replenishment technologies. In scenarios where ships are limited to only battery swapping or charging due to onboard limitations or the lack of replenishment infrastructure, the corresponding variables and constraints can be directly excluded from the model without affecting its usability. Thus, the proposed approach is general and adaptable to handle simplified problems involving different replenishment technologies (see Section 4.2).
3.2. Mathematical Model
The problem is formulated as an MINLP model. All notations are listed in Table 1, where and serve as indices for port nodes, for voyage legs, and for technologies.

Table 1.
Summary of notations used in the model.
The model is given as follows:
subject to
The objective Function (1) minimizes the total energy replenishment costs. The constraints are detailed as follows.
- Replenishment port and technology constraints: Constraints (2) and (3) govern the selection of replenishment ports and technologies through the binary variable . Specifically, Constraint (2) ensures that a ship can select at most one technology from the available options at any candidate replenishment node. Constraint (3) ensures that the ship replenishes energy upon returning to the departure port.
- Battery swapping number constraints: Constraint (4) ensures that the number of batteries to be swapped at intermediate battery swapping stations does not exceed the number of depleted batteries, which is calculated using the floor function . Constraint (5) mandates that if the ship swaps batteries upon returning to the departure port, all of its non-fully charged batteries must be swapped, with the required number determined by the ceiling function .
- Energy replenishment amount constraints: Constraint (6) ensures that the energy replenished using technology at node is positive and does not exceed the ship’s maximum energy capacity when technology is selected; otherwise, it is zero. Constraint (7) ensures that the ship is fully replenished to its maximum energy capacity upon returning to the departure port. Constraint (8) establishes the relationship between the amount of energy replenished and the number of batteries swapped at intermediate battery swapping stations.
- Round-trip time constraints: Constraint (9) defines the charging time as a function of the charging amount and the effective charging power, which is limited by the minimum of the charging facility’s capacity and the ship’s maximum allowable charging power. The use of the max operator prevents double counting of time by recognizing that charging and cargo handling operations can occur concurrently. Constraint (10) defines the time required for swapping batteries. Constraint (11) sets an upper limit on the total round-trip time, including port time at cargo handling nodes, additional pilotage and waiting time for replenishing energy at non-cargo handling nodes, sailing time, and energy replenishment time.
- Energy conservation constraints: Constraint (12) defines the ship’s remaining energy upon arriving at a port node. Constraint (13) sets lower and upper bounds on the ship’s total remaining energy, based on the SOC limits of each battery.
- Constraints defining variables: Constraints (14)–(18) specify the ranges of variables.
3.3. Solution Method
Given the manageable problem scale and structure, a linearization technique is applied to reformulate it into an MILP model, which can be efficiently solved to global optimality using standard commercial solvers such as Gurobi. The nonlinearities in the original MINLP model arise in Constraints (4)–(7) and (9).
First, to address the specific nonlinearities arising from the floor and ceiling functions, we introduce two auxiliary integer variables: and .
The integer variable is introduced to replace the floor function. This is achieved by enforcing the following linear constraint:
Similarly, the integer variable replaces the ceiling function, governed by the inequality:
Consequently, by employing these auxiliary variables and their corresponding linear constraints, the original nonlinear Constraints (4) and (5) are reformulated into the linear forms shown in (22) and (23):
Next, we address the nonlinearity arising from the product of binary variable with integer variables in Constraints (22) and (23). We employ the big-M method to linearize these terms. This technique introduces a sufficiently large constant, , to reformulate each nonlinear product into a set of linear inequalities whose logic is controlled by the binary variable. Specifically, the value of is used to either enforce or relax the relationship between the variables. As a result, Constraints (22) and (23) are transformed into the following equivalent linear forms.
Similarly, we again employ the big-M method to linearize Constraints (6) and (7). The nonlinearities in these constraints arise from the product of the binary variable and expressions involving the continuous variable . This is achieved by introducing another sufficiently large constant, , which transforms Constraints (6) and (7) into their equivalent linear forms (26) and (27), respectively:
The final nonlinearity in Constraint (9) arises from the max operator. We linearize this expression by introducing an auxiliary binary variable, , and applying the big-M method. This procedure replaces the original max function with the equivalent set of linear Constraint (28) and the binary variable definition (29):
where is a sufficiently large constant.
With all nonlinearities resolved, the problem is reformulated as an equivalent MILP model that minimizes the total replenishment costs, as previously defined in Equation (1), subject to Constraints (2), (3), (8), (10)–(21), and (24)–(29).
4. Case Study
The case study is carried out on a laptop equipped with an Intel Core i5-1135G7 processor (2.40 GHz) and 16 GB of memory. The model is implemented in Python (Version 3.12.9) and solved using Gurobi (Version 12.0.2).
4.1. Case Description and Parameter Setting
The proposed model and solution approach are applied to two service routes along the Yangtze River, with total lengths of approximately 500 and 1200 nautical miles, respectively, as detailed in Table 2 [1]. The two routes are as follows:

Table 2.
Basic information on the ports and legs of the two service routes 1.
- The Nanjing–Yangshan (NJ-YS) route involves non-stop freight transport between Nanjing Port and Yangshan Port, with a port time of 20 h for each port call.
- The Wuhan–Yangshan (WH-YS) route involves freight transport between Wuhan Port and Yangshan Port, with cargo replenishment at Anqing Port on the forward sub-route. The port times are 8 h at Anqing Port () and 20 h for other port calls (, , and 19).
Three replenishment technology options are considered: slow charging, fast charging, and battery swapping. The unit cost for slow charging at each port node is adopted as the baseline. The corresponding unit costs for fast charging and battery swapping are set at 1.5 and 2.0 times the baseline value, respectively [13]. For analytical convenience, the costs of all three technologies, though may unavailable, are listed for each port node in Table 2.
The target ship sailing on the two routes is a 700-TEU container ship. Its principal dimensions and other specifications are detailed in Table 3. Based on our field investigation at the shipyard, two key characteristics of the ship are its flexible battery configuration and grouped battery arrangement. First, the ship can be configured with 12, 24, or 36 batteries for different voyages, as its energy management system is designed to accommodate these discrete setups. In current operations, the ship is equipped with 24 batteries for the NJ-YS route and 36 batteries for the WH-YS route. These configurations ensure voyage feasibility within acceptable time limits while reducing energy redundancy. Second, the ship implements a common engineering strategy by evenly arranging the batteries into six parallel groups to reduce cabling, simplify switchboard design and system control. Each group is managed by a switchgear, ensuring that only one battery in each group is active at a time. Operationally, one battery from each of the six groups is activated simultaneously, forming an “operating set” that discharges in unison, with the power demand evenly distributed among these batteries. The maximum power output of the operating set should exceed the ship’s maximum power demand. Once these active batteries reach the lower SOC limit, a “batch switch” is performed, where all groups simultaneously transition to their next standby battery, creating a new operating set. Therefore, through conceptual abstraction, the battery system is treated as a collection of independent “equivalent battery units”. Each unit consists of six batteries (one from each group) and collectively provides an energy capacity of 9600 kWh. Consequently, the target ship is configured with four such equivalent units for the NJ-YS route and six for the WH-YS route, which are directly applied to our proposed model.

Table 3.
Principal dimensions and key specifications of the target ship.
Table 4 summarizes the remaining principal simulation parameters, which are derived from field data surveys, the shipping company’s technical documentation, and relevant literature [16].

Table 4.
Simulation parameters.
4.2. Result Analysis
4.2.1. Comparative Analysis with Varying Availability of Technologies
The availability of replenishment technologies is a key consideration in developing effective energy replenishment strategies. This availability varies across technology options and service routes, influenced by differences in technological maturity and deployment priorities. We define as the ratio of the number of replenishment stations for a specific technology to the total number of ports along the route. Four distinct availability levels are defined as follows:
- Level 0 (No availability): ;
- Level 1 (Limited availability): ;
- Level 2 (Moderate availability): ;
- Level 3 (Complete availability): .
The specific deployment patterns for each technology, availability level, and route are treated as predetermined and are further detailed in Table A1.
Let () represent the availability level of technology . A set of 26 technology availability scenarios is then generated based on the following criteria:
- Level 0 is permitted for at most one technology to encourage the adoption of multiple technologies.
- The availability level of slow charging must not be lower than those of fast charging and battery swapping (, ), reflecting its role as the most fundamental replenishment option.
From these 26 scenarios, a total of 52 instances are created by applying each scenario to both the NJ-YS route (numbered 1–26) and the WH-YS route (numbered 27–52). To evaluate performance under different shipping efficiency requirements, each of these 52 base instances is then optimized under two distinct time constraints (): 150 and 200 h for the NJ-YS route, and 250 and 300 h for the WH-YS route. The detailed information and results of each scenario are summarized in Table 5. The results reveal that enhancing the availability of replenishment technologies yields significant cost savings, reaching up to 6.95% for the NJ-YS route and 3.15% for the WH-YS route. This underscores the importance of developing a widespread energy replenishment infrastructure.

Table 5.
Comparative analysis of outcomes across technology availability scenarios.
Additionally, the findings highlight the indispensable role of battery swapping in ensuring voyage feasibility. Notably, even with maximum availability of both slow and fast charging, operations remain infeasible when battery swapping is entirely absent (, see instances 23 and 49). This infeasibility stems from the inherent power limitations of charging technologies, which are insufficient to provide timely replenishment to meet the voyage schedule. In contrast, having sufficient battery swapping stations () guarantees feasible solutions across all tested instances, even when fast charging is absent (see instances 5 and 31). This reveals a crucial strategic insight: focusing investment on the battery swapping network is more critical than diversifying replenishment technologies when resources are constrained. Without a well-established battery swapping network, the latter strategy often leads to infeasibility or forces efficiency trade-offs (see instances 24 and 50).
4.2.2. Comparative Analysis Between Single- and Multi- Technology Strategies
This subsection compares the performance of our proposed MT strategy against three ST benchmarks: slow charging-only, fast charging-only, and battery swapping-only. To ensure a fair comparison, the analysis focuses on the 14 instances per route where all three replenishment technologies are available. Each instance is solved under all four strategies. The strategies are evaluated based on two primary metrics: solution feasibility, measured as the fraction of successfully solved instances (), and economic efficiency, measured by the average total cost (, in thousand CNY) over those feasible solutions.
As shown in Table 6, the trade-offs of ST strategies are evident. The slow charging-only strategy, for instance, is consistently infeasible under the specified time constraints. It achieves feasibility only with impractically long round-trip times (700 h for the NJ-YS route and 1500 h for the WH-YS route), which severely compromises shipping efficiency. The battery swapping-only strategy, on the other hand, can provide feasibility even under tight schedules. However, its feasibility depends on sufficient battery swapping stations (), and it usually comes with a significantly higher replenishment costs.

Table 6.
Comparative analysis of outcomes across ST and MT strategies.
In contrast, the proposed MT strategy effectively overcomes these trade-offs by leveraging complementarity on two fronts. It not only combines the technological strengths of different options (e.g., the low cost of slow charging and the high time-efficiency of battery swapping) but also exploits the unit infrastructure available at each port along the route. This creates a level of operational flexibility that ST strategies lack, which in turn enables superior feasibility and significant cost savings, with reductions reaching 14.16% for the NJ-YS route and 5.93% for the WH-YS route.
4.2.3. Comparative Analysis Between Full and Partial Replenishment Strategies
Another key innovation of the proposed strategy is the incorporation of PR. This subsection evaluates the advantages of this extension over the traditional FR adopted in prior research. To this end, all 26 instances for each route are solved under both FR and PR frameworks. The comparative results are detailed in Table 7.

Table 7.
Comparative analysis of outcomes between PR and FR strategies.
The results demonstrate that the PR strategy’s flexibility provides a significant advantage over the rigid FR strategy in both feasibility and cost. The FR strategy’s strict requirement to either fully charge or swap all batteries during each operation often causes excessive delays, especially when charging technologies are heavily used, leading to violations of voyage time limits, which result in solution infeasibility. In contrast, the PR strategy’s ability to determine optimal replenishment amounts allows it to successfully identify feasible solutions where the FR strategy fails. Moreover, the PR strategy’s flexibility translates directly into notable cost savings, with maximum reductions of 8.24% and 4.54% for the NJ-YS and WH-YS routes, respectively.
4.3. Sensitivity Analysis
4.3.1. Effects of Technology Cost and Efficiency Parameters
The selection of energy replenishment technologies is governed by the fundamental trade-off between cost and efficiency. This subsection, therefore, investigates how variations in these critical parameters affect key outcomes: solution feasibility, strategic choices, and total replenishment costs.
Building upon the baseline scenario (BAS) from Section 4.1, we construct a series of scenarios by adjusting cost or efficiency parameters. First, five cost scenarios (CSs) are created by varying the parameters and/or , which represent the unit cost ratio of fast charging and battery swapping relative to slow charging. Second, three efficiency scenarios (ESs) are created by adjusting the parameters and/or . To facilitate a systematic comparison, our analysis concentrates on the 14 instances per route where all technologies are available. The nine scenarios and their corresponding results are summarized in Table 8.

Table 8.
Comparative analysis of outcomes across cost and efficiency scenarios.
The results reveal that total replenishment costs are highly sensitive to both cost and efficiency parameters. Comparing the CSs with the BAS, we observe that a 25% decrease in the unit cost of battery swapping leads to savings of up to 9.1% (CS2). When this is further combined with a 20% decrease in the unit cost of fast charging, the savings reach nearly 25% (CS1).
Comparing the ESs with the BAS, we find that doubling fast charging efficiency (ES2) proves more effective in cost reduction than doubling battery swapping efficiency (ES1), yielding cost savings of over 14%. More importantly, efficiency improvements are also critical for determining solution feasibility. This trend is clearly demonstrated in Table A2, where the improved efficiency scenarios (ES1–ES3) generally outperform the BAS in terms of solution feasibility. Such superior performance indicates that enhanced replenishment efficiency effectively addresses the challenges of time-constrained operations and facilitates more efficient inland shipping.
We further analyze how cost and efficiency parameters shape the specific energy replenishment strategies. Our analysis focuses on instances where all technologies are fully available at all ports (instances 26 and 52), as these are expected to reveal the most pronounced variations across scenarios.
As illustrated in Figure 2, the NJ-YS route exhibits remarkable strategic consistency under varying cost parameters (BAS and CS1–CS5), with only minor fluctuations in replenishment amounts across ports. In contrast, the WH-YS route shows considerably greater sensitivity to cost variations, affecting all aspects of its decision-making. A similar significant impact on strategy is observed in the comparative analysis of efficiency parameters (BAS and ES1–ES3), as depicted in Figure 3.
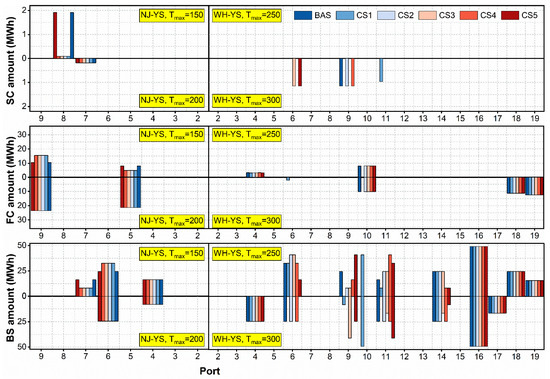
Figure 2.
Optimal energy replenishment strategies across cost scenarios.
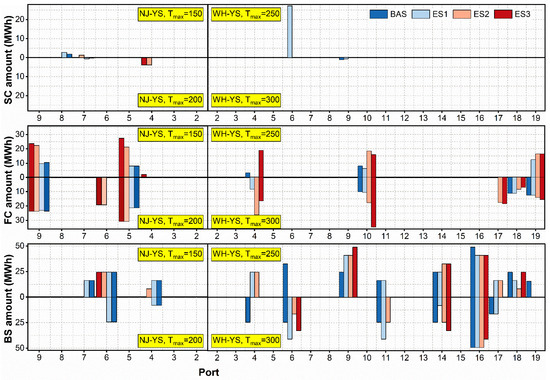
Figure 3.
Optimal energy replenishment strategies across efficiency scenarios.
Of particular interest are the shifts in energy replenishment mix, as these serve as a direct indicator of strategic trade-offs under varying cost and efficiency conditions. This direct comparison is possible because the total energy replenishment remains constant across all scenarios, a value equal to the total energy consumption and determined solely by the sailing speed according to the model’s assumptions. As detailed in Table 9, scenarios with increased fast charging power (ES2 and ES3) trigger a decisive shift in replenishment patterns on both routes. Specifically, a significant proportion of the energy previously replenished by battery swapping is reallocated to fast charging. This trend is clearly demonstrated by instance 26 under a 200-h time constraint: while the BAS yields a mix of 0.23% slow charging, 57.71% fast charging, and 42.05% battery swapping, ES2 prompts an almost complete pivot to fast charging (94.96%). This efficiency-driven strategic realignment is also economically significant, as it leverages the lower unit cost of fast charging to achieve considerable cost reductions (Table 8).

Table 9.
Energy replenishment mix (%) by technology across cost and efficiency scenarios 1.
4.3.2. Effects of Maximum Allowable Round-Trip Time
This subsection examines how the maximum allowable round-trip time influences the optimal energy replenishment strategies. Table 5 reveals a strong negative correlation between total replenishment costs and maximum allowable round-trip time, with cost reductions reaching up to 10.13% for the NJ-YS route and 5.66% for the WH-YS route.
As shown in Table 10, battery swapping emerges as the main method under more stringent time constraints, owing to its superior replenishment efficiency. It consistently constitutes the largest share across all instances. However, as the allowable duration extends, the energy replenishment mix gradually shifts away from battery swapping and towards charging. Specifically, on the short-distance route, fast charging becomes the preferred replenishment option under a 200-h time constraint, provided certain conditions of technology availability are met (i.e., , , ). Conversely, on the long-distance route, battery swapping remains dominant even with a 50-h extension, although the share of fast charging gradually increases.

Table 10.
Energy replenishment mix (%) by technology under various time constraints 1.
4.4. Preliminary Discussion on Battery Degradation
The analysis thus far has relied on a “ship-battery separation” simplification, which is facilitated by business models such as “Battery-as-a-Service” or battery leasing. Within these frameworks, shipping companies do not need to consider battery maintenance and degradation costs [31]. This section builds upon the main model to address battery degradation, a critical consideration when the shipping company owns the batteries and must therefore account for asset depreciation [32].
4.4.1. Effects of Allowable SOC Ranges
As indicated in Table 4, the default operational SOC range for batteries is , which aims to fully utilize their capacity while adhering to the maximum depth of discharge specified in Table 3. However, ship operators can adopt narrower SOC ranges to mitigate battery degradation from overcharging and over-discharging. For instance, we consider three SOC ranges: , , and . Theoretically, the range is the most favorable from a battery health perspective, as it is characterized by the lowest average SOC and the shallowest depth of discharge [33]. Conversely, the range is the least favorable for long-term battery lifespan. However, a narrower range is often suboptimal from an operational standpoint. The reduction in usable energy capacity can render voyages infeasible within acceptable time limits, as illustrated by the decreasing number of feasible solutions in Table 11. Additionally, a more constrained SOC range can necessitate more frequent energy replenishment operations, which disrupt the voyage plan and are often unfavorable in practice. For example, in instance 52 under the 300-h constraint, shifting from the original range to and results in one and three additional port calls for energy replenishment, respectively.

Table 11.
Comparative analysis of solution feasibility under various allowable SOC ranges.
4.4.2. Effects of C-Rates
Although fast charging at higher C-rates offers greater replenishment efficiency, it is widely recognized that it accelerates battery degradation compared to slow charging at lower C-rates [34]. This subsection incorporates a simplified battery degradation cost, modeled solely as a function of the C-rate of the replenishment technology, into the original model. The objective function is given as:
where represents the unit battery degradation cost for technology .
To estimate this cost, we model and compare three primary replenishment technologies: 0.1C charging, 0.25C charging, and battery swapping, with their replenishment cost and availability adopted from Table 2 and Table 5 for the purpose of this analysis. The 0.25C rate corresponds to the maximum charging rate supported by the onboard batteries, as specified in Table 3, with a 4000-cycle lifespan serving as the baseline for estimating degradation costs. The 0.1C rate is selected to represent a slower, more battery-friendly charging option. To quantify the benefits of slower 0.1C charging compared to 0.25C charging, we introduce three degradation scenarios (DS1–DS3) for 0.1C charging, each corresponding to a progressively longer battery lifespan. For simplicity, the degradation cost for battery swapping is assumed to be equal to that of 0.1C charging in each respective scenario. This simplification is supported by the centralized battery management at battery swapping stations, which can extend the battery cycle life [31]. With an initial investment cost of approximately CNY 3 million per battery, the unit degradation cost estimates for 0.1C and 0.25C charging under different scenarios are summarized in Table A3.
To illustrate, we compare the optimal strategies for instance 52 derived from the original model (No-Degradation Scenario, NDS) and those from the new model incorporating degradation costs (DS1–DS3). The results, summarized in Table 12, indicate that battery degradation cost is a significant factor, consistently accounting for over 20% of the total costs in DS1–DS3. Including degradation costs causes a strategic shift from higher C-rate charging to more battery-friendly options, such as lower C-rate charging and battery swapping. When comparing various degradation scenarios, the new model effectively balances the trade-off between replenishment cost and degradation loss under the round-trip time constraint. Under a tight 250-h time constraint, a shift occurs at DS2: battery swapping begins to be adopted, despite its higher replenishment cost, to avoid the greater degradation cost associated with higher C-rate charging. However, with a relaxed 300-h schedule, the model avoids the expensive battery swapping until DS3.

Table 12.
Comparative analysis of optimal strategies and cost structures under various battery degradation scenarios (instance 52) 1.
We acknowledge that the degradation cost function used in this subsection is a simplified form. The purpose is to facilitate a preliminary investigation into the strategic impact of degradation costs, rather than to precisely model the underlying electrochemical processes. Battery degradation is a highly complex mechanism influenced by multiple factors, such as temperature, the depth of discharge, and average SOC [32]. Moreover, the waterborne environment introduces additional adverse conditions, including high humidity and constant vibration and shock from ship motion, creating significant uncertainties not captured by standard degradation models developed for land-based applications [35,36]. Therefore, future work should develop or integrate more advanced degradation models to capture the complex nonlinear and environment-specific degradation behavior of onboard batteries [37,38].
4.5. Computational Efficiency Analysis
The results summarized in Figure 4 demonstrate the computational performance of the proposed MILP model, as all instances are solved to global optimality within acceptable time limits. This finding highlights the model’s computational efficiency and suggests its suitability for solving such practical-sized problems.
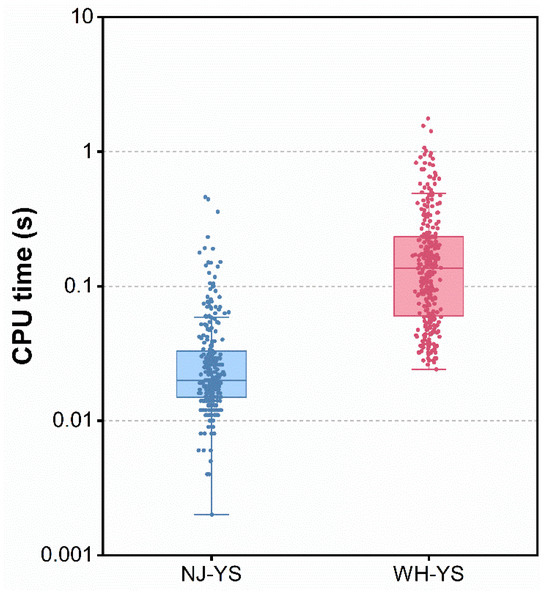
Figure 4.
CPU times for successful computational runs.
4.6. Managerial Implications
Our analysis of two representative routes along the Yangtze River yields three key findings with actionable implications for stakeholders.
- Our analysis demonstrates that comprehensively utilizing charging and battery swapping during a voyage significantly enhances operational feasibility and reduces replenishment costs. To implement this strategy, we recommend that shipping companies adopt electric ships equipped with containerized batteries, as this design enables the integration of both charging and battery swapping.
- Battery swapping plays a key role in extending electric ships to long-distance routes and enhancing operational efficiency. In light of this, we propose a phased investment and development strategy for policymakers and port operators. Building upon the existing slow charging network, the strategy prioritizes the development of battery swapping stations due to their critical role in enabling long-distance voyages and achieving high operational efficiency. The network is then completed with the integration of fast charging facilities, which introduces a lower-cost option for scenarios that require rapid energy replenishment. However, in terms of technological upgrades, improving fast charging efficiency represents the preferable strategic choice over a comparable enhancement of battery swapping efficiency.
- The preliminary discussion on battery degradation highlights a fundamental conflict between shipping efficiency and battery lifespan. Managing a large number of onboard batteries with complex degradation mechanisms poses a significant challenge for shipping companies, as it requires tracking the state of health of individual batteries. This challenge becomes even greater with the adoption of battery swapping, which involves frequent exchanges of batteries between ships and stations. “Battery-as-a-Service” or battery leasing models offer promising solutions to mitigate this challenge, allowing shipping companies to focus exclusively on their core operations without directly managing battery degradation. However, the success of such business models relies on the development of an effective pricing mechanism, which requires further investigation. Factors such as battery degradation dynamics, infrastructure maintenance, replenishment demand, and electricity sources should be comprehensively considered.
5. Conclusions
This study investigates the energy replenishment problem for inland electric ships, extending existing methods by considering the possibility of using multiple replenishment technologies and partial battery swapping or charging. With the objective of minimizing total replenishment costs, an MILP model is developed to determine the optimal energy replenishment strategy, including decisions on port selection, technology choice, and replenishment amount. The model is validated through a case study of a 700-TEU electric container ship operating on the NJ-YS route and the WH-YS route along the Yangtze River, with slow charging, fast charging, and battery swapping considered for energy replenishment. The results highlight the critical importance of a well-established energy replenishment network and emphasize the key role of battery swapping in enabling the electrification of inland shipping. The proposed strategy’s effectiveness is demonstrated by its superior performance compared to conventional ST and FR strategies, leading to significant cost reductions and enhanced feasibility. Additionally, sensitivity analyses of key parameters provide valuable insights for stakeholders in the shipping industry.
This study also has several limitations that can be addressed in future research. First, the model focuses only on energy replenishment decisions and does not account for sailing speed optimization. A crucial direction for future research is to incorporate sailing speed as a decision variable alongside more advanced power consumption models that account for ship dynamics, maneuverability, and realistic operational and environmental conditions [27,39]. Second, the model focuses on minimizing replenishment costs. While it is consistent with prior studies and establishes a clear performance baseline, a valuable extension would involve developing a multi-objective model that balances costs with competing factors such as shipping efficiency, emissions, and long-term battery degradation, thereby offering more comprehensive decision support.
Author Contributions
Conceptualization, L.D., H.H. and S.G.; methodology, S.G. and L.D.; software, S.G. and M.Y.; validation, S.G. and Y.W.; writing—original draft preparation, S.G.; writing—review and editing, S.F., S.Z. and L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant numbers 52477108, 72004132. The APC was funded by 52477108.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Detailed deployment of replenishment facilities across technologies, levels, and routes.
Table A1.
Detailed deployment of replenishment facilities across technologies, levels, and routes.
| Availability Level | Deployment on the NJ-YS Route | Deployment on the WH-YS Route | |
|---|---|---|---|
| Slow charging | 1 | Wuhan, Yangshan | Wuhan, Anqing, Jingjiang, Yangshan |
| 2 | Wuhan, Nantong, Yangshan | Wuhan, Jiujiang, Anqing, Jingjiang, Zhenjiang, Yangshan | |
| Fast charging | 1 | Wuhan, Yangshan | Wuhan, Wuhu, Nantong, Yangshan |
| 2 | Wuhan, Jingjiang, Yangshan | Wuhan, Huangshi, Wuhu, Nanjing, Nantong, Yangshan | |
| Battery swapping | 1 | Wuhan, Yangshan | Wuhan, Anqing, Nantong, Yangshan |
| 2 | Wuhan, Nantong, Yangshan | Wuhan, Huangshi, Anqing, Nantong, Yangshan | |

Table A2.
Feasibility across efficiency scenarios.
Table A2.
Feasibility across efficiency scenarios.
| (h) | NJ-YS | (h) | WH-YS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BAS | ES1 | ES2 | ES3 | BAS | ES1 | ES2 | ES3 | ||
| 150 | 8/14 | 8/14 | 11/14 | 11/14 | 250 h | 8/14 | 8/14 | 8/14 | 14/14 |
| 152 | 8/14 | 8/14 | 11/14 | 11/14 | 252 h | 8/14 | 14/14 | 8/14 | 14/14 |
| 154 | 8/14 | 8/14 | 11/14 | 11/14 | 254 h | 8/14 | 14/14 | 8/14 | 14/14 |
| 156 | 8/14 | 8/14 | 11/14 | 11/14 | 256 h | 8/14 | 14/14 | 14/14 | 14/14 |
| 158 | 8/14 | 11/14 | 11/14 | 11/14 | 258 h | 8/14 | 14/14 | 14/14 | 14/14 |

Table A3.
Unit battery degradation cost under different charging technologies and scenarios.
Table A3.
Unit battery degradation cost under different charging technologies and scenarios.
| Scenario 1 | 0.25C Charging 2 (Baseline) | 0.1C Charging 3 | ||
|---|---|---|---|---|
| Cycle Life (Cycles) | Unit Battery Degradation Cost (CNY/kWh) 4 | Cycle Life (Cycles) | Unit Battery Degradation Cost (CNY/kWh) | |
| DS1 | 4000 | 0.55 | 4400 | 0.50 |
| DS2 | 5200 | 0.42 | ||
| DS3 | 6000 | 0.37 | ||
1 Scenarios DS1, DS2, and DS3 describe cases where 0.1C charging extends battery cycle life by 10%, 30%, and 50% respectively, compared to the 4000-cycle baseline of 0.25C charging. 2,3 Since the target ship employs a grouped battery management architecture, the corresponding charging power levels corresponding to 0.25C and 0.1C for the 9600-kWh equivalent battery unit are 2.4 MW and 960 kW, respectively. These power levels are practically feasible, as the updated charging technology can support MW-scale charging. 4 The unit degradation cost for fast charging is calculated by dividing the total investment cost by the total energy throughput over the battery’s lifetime: battery investment cost/(battery capacity × depth of discharge × cycle life).
References
- Tan, Z.; Wang, Y.; Meng, Q.; Liu, Z. Joint Ship Schedule Design and Sailing Speed Optimization for a Single Inland Shipping Service with Uncertain Dam Transit Time. Transp. Sci. 2018, 52, 1570–1588. [Google Scholar] [CrossRef]
- Eger, P.; Mathes, T.; Zavarsky, A.; Duester, L. Measurement Report: Inland Ship Emissions and Their Contribution to NOx and Ultrafine Particle Concentrations at the Rhine. Atmos. Chem. Phys. 2023, 23, 8769–8788. [Google Scholar] [CrossRef]
- Li, D.-C.; Yang, H.-L.; Xing, Y.-W. Economic and Emission Assessment of LNG-Fuelled Ships for Inland Waterway Transportation. Ocean. Coast. Manag. 2023, 246, 106906. [Google Scholar] [CrossRef]
- Ammar, N.R.; Seddiek, I.S. Evaluation of the Environmental and Economic Impacts of Electric Propulsion Systems Onboard Ships: Case Study Passenger Vessel. Environ. Sci. Pollut. Res. 2021, 28, 37851–37866. [Google Scholar] [CrossRef]
- Fan, A.; Wang, J.; He, Y.; Perčić, M.; Vladimir, N.; Yang, L. Decarbonising Inland Ship Power System: Alternative Solution and Assessment Method. Energy 2021, 226, 120266. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Y.; Dai, L.; Hu, H. All-Electric Ship Operations and Management: Overview and Future Research Directions. eTransportation 2023, 17, 100251. [Google Scholar] [CrossRef]
- Feng, Y.; Dai, L.; Yue, M.; Hu, H.; Fang, S. Assessing the Decarbonization Potential of Electric Ships for Inland Waterway Freight Transportation. Transp. Res. Part D Transp. Environ. 2024, 129, 104151. [Google Scholar] [CrossRef]
- Ling, G.; Han, C.; Yang, Z.; He, J. Energy Consumption and Emission Analysis for Electric Container Ships. Ocean. Coast. Manag. 2025, 261, 107505. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, L.; Sun, W.; Ma, F.; Xiao, R.; Wu, Y.; Huang, H. Bilevel Optimal Infrastructure Planning Method for the Inland Battery Swapping Stations and Battery-Powered Ships. Tsinghua Sci. Technol. 2024, 29, 1323–1340. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Huang, W.; Tao, H.; Xu, W.; Tai, N.; Li, C. Accelerating Green Shipping with Spatially Optimized Offshore Charging Stations. Nat. Energy 2025, 10, 243–254. [Google Scholar] [CrossRef]
- Kersey, J.; Popovich, N.D.; Phadke, A.A. Rapid Battery Cost Declines Accelerate the Prospects of All-Electric Interregional Container Shipping. Nat. Energy 2022, 7, 664–674. [Google Scholar] [CrossRef]
- Karimi, S.; Zadeh, M.; Suul, J.A. Shore Charging for Plug-In Battery-Powered Ships: Power System Architecture, Infrastructure, and Control. IEEE Electrific. Mag. 2020, 8, 47–61. [Google Scholar] [CrossRef]
- Verma, A. Electric Vehicle Routing Problem with Time Windows, Recharging Stations and Battery Swapping Stations. EURO J. Transp. Logist. 2018, 7, 415–451. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Zhen, L.; Wang, H. How to Deploy Electric Ships for Green Shipping. J. Mar. Sci. Eng. 2022, 10, 1611. [Google Scholar] [CrossRef]
- Gu, M.; Wen, S.; Zhu, M.; Chen, C.; Huang, Y. Voyage Optimization for All-Electric Vessels Integrated with Swappable Containerized Battery. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; pp. 586–591. [Google Scholar]
- Zhang, Y.; Sun, L.; Fan, T.; Ma, F.; Xiong, Y. Speed and Energy Optimization Method for the Inland All-Electric Ship in Battery-Swapping Mode. Ocean. Eng. 2023, 284, 115234. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Robust Bunker Management for Liner Shipping Networks. Eur. J. Oper. Res. 2015, 243, 789–797. [Google Scholar] [CrossRef]
- Yao, Z.; Ng, S.H.; Lee, L.H. A Study on Bunker Fuel Management for the Shipping Liner Services. Comput. Oper. Res. 2012, 39, 1160–1172. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q.; Liu, Z. Bunker Consumption Optimization Methods in Shipping: A Critical Review and Extensions. Transp. Res. Part E Logist. Transp. Rev. 2013, 53, 49–62. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A Heuristic Approach for the Green Vehicle Routing Problem with Multiple Technologies and Partial Recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A Variable Neighborhood Search Branching for the Electric Vehicle Routing Problem with Time Windows. Electron. Notes Discret. Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. A Matheuristic Method for the Electric Vehicle Routing Problem with Time Windows and Fast Chargers. Comput. Oper. Res. 2018, 100, 172–188. [Google Scholar] [CrossRef]
- Paz, J.; Granada-Echeverri, M.; Escobar, J. The Multi-Depot Electric Vehicle Location Routing Problem with Time Windows. Int. J. Ind. Eng. Comput. 2018, 9, 123–136. [Google Scholar] [CrossRef]
- Schiffer, M.; Walther, G. The Electric Location Routing Problem with Time Windows and Partial Recharging. Eur. J. Oper. Res. 2017, 260, 995–1013. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Gunawan, A. An Adaptive Large Neighborhood Search for the Green Mixed Fleet Vehicle Routing Problem with Realistic Energy Consumption and Partial Recharges. Appl. Soft Comput. 2021, 105, 107251. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, C.; He, Z.; Chen, H.; Xiang, Q.; Chu, X. Optimization of Sailing Speed for Inland Electric Ships Based on an Improved Multi-Objective Particle Swarm Optimization (MOPSO) Algorithm. J. Mar. Sci. Eng. 2024, 12, 1417. [Google Scholar] [CrossRef]
- Gelareh, S.; Meng, Q. A Novel Modeling Approach for the Fleet Deployment Problem within a Short-Term Planning Horizon. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 76–89. [Google Scholar] [CrossRef]
- Ronen, D. The Effect of Oil Price on Containership Speed and Fleet Size. J. Oper. Res. Soc. 2011, 62, 211–216. [Google Scholar] [CrossRef]
- Hu, X.; Yang, Z.; Sun, J.; Zhang, Y. Optimal Pricing Strategy for Electric Vehicle Battery Swapping: Pay-per-Swap or Subscription? Transp. Res. Part E Logist. Transp. Rev. 2023, 171, 103030. [Google Scholar] [CrossRef]
- Cui, D.; Wang, Z.; Liu, P.; Wang, S.; Dorrell, D.G.; Li, X.; Zhan, W. Operation Optimization Approaches of Electric Vehicle Battery Swapping and Charging Station: A Literature Review. Energy 2023, 263, 126095. [Google Scholar] [CrossRef]
- Gao, J.; Lan, H.; Cheng, P.; Hong, Y.-Y.; Yin, H. Optimal Scheduling of an Electric Propulsion Tugboat Considering Various Operating Conditions and Navigation Uncertainties. J. Mar. Sci. Eng. 2022, 10, 1973. [Google Scholar] [CrossRef]
- Yu, K.; Yan, P.; Liu, Y.; Chen, Z.; Kong, X.T.R. Battery Degradation Mitigation-Oriented Strategy for Optimizing e-Hailing Electric Vehicle Operations. Transp. Res. Part E Logist. Transp. Rev. 2025, 196, 104006. [Google Scholar] [CrossRef]
- Zhou, R.; Zhu, R.; Huang, C.-G.; Peng, W. State of Health Estimation for Fast-Charging Lithium-Ion Battery Based on Incremental Capacity Analysis. J. Energy Storage 2022, 51, 104560. [Google Scholar] [CrossRef]
- Pang, B.; Liu, S.; Zhu, H.; Feng, Y.; Dong, Z. Real-Time Optimal Control of an LNG-Fueled Hybrid Electric Ship Considering Battery Degradations. Energy 2024, 296, 131170. [Google Scholar] [CrossRef]
- Kong, L.; Luo, Y.; Fang, S.; Niu, T.; Chen, G.; Yang, L.; Liao, R. State Estimation of Lithium-Ion Battery for Shipboard Applications: Key Challenges and Future Trends. Green Energy Intell. Transp. 2025, 4, 100192. [Google Scholar] [CrossRef]
- Li, L.; Yi, P.; Wu, S.; Huang, S.; Li, T. Analysis of Impact of Control Strategies on Integrated Electric Propulsion System Performance During Icebreaking Process. J. Mar. Sci. Eng. 2024, 12, 1888. [Google Scholar] [CrossRef]
- Song, Q.; Yang, X.; Tang, T.; Liu, Y.; Chen, Y.; Liu, L. Capacity Prognostics of Marine Lithium-Ion Batteries Based on ICPO-Bi-LSTM Under Dynamic Operating Conditions. J. Mar. Sci. Eng. 2024, 12, 2355. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Lee, J.-H.; Oh, J.-H.; Oh, J.-S. A Comparative Study on Energy Consumption Forecast Methods for Electric Propulsion Ship. J. Mar. Sci. Eng. 2022, 10, 32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).