Adaptive Sampling of Marine Submesoscale Features Using Gaussian Process Regression with Unmanned Platforms
Abstract
1. Introduction
2. Materials and Methods
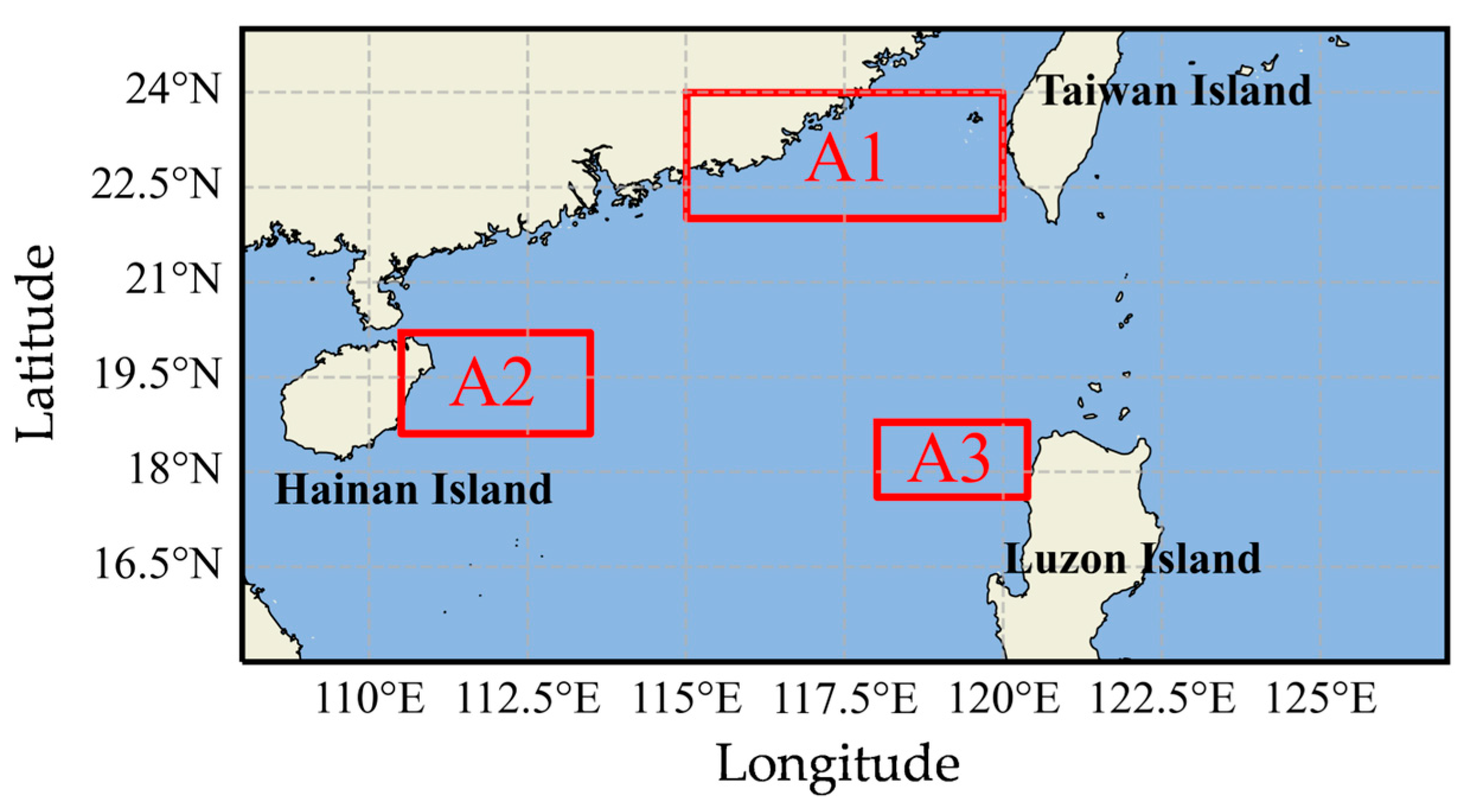
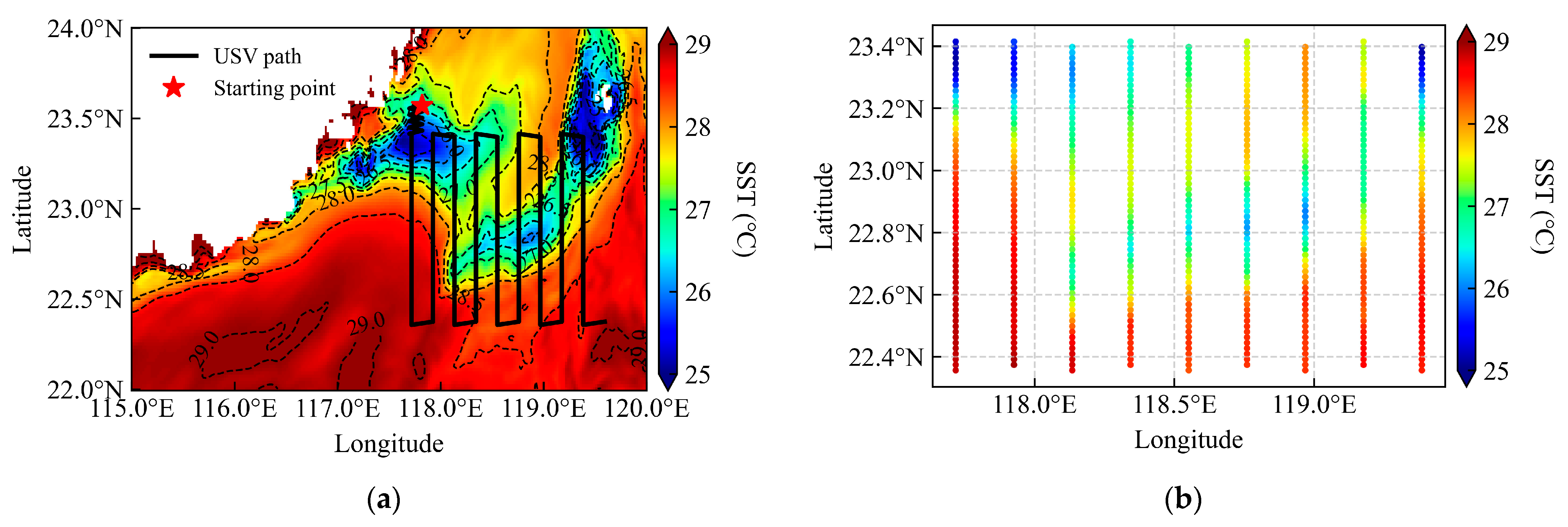
2.1. Data and Study Area
2.2. Gaussian Process Regression Modeling
- : Mean function, describing the global trend of the function. For the purposes of simplification, the mean function is typically taken to be 0 [19].
- : Kernel function, governing the local behavior of the function.
- and represent any two spatial data.
2.3. Multilayer Perceptron Model
2.4. Adaptive Sampling Framework
2.4.1. Frontal Identification Using the Coupled Gradient Indicator
2.4.2. Adaptive Path Planning Strategy
2.4.3. Submesoscale Confirmation Based on Rossby Number Threshold
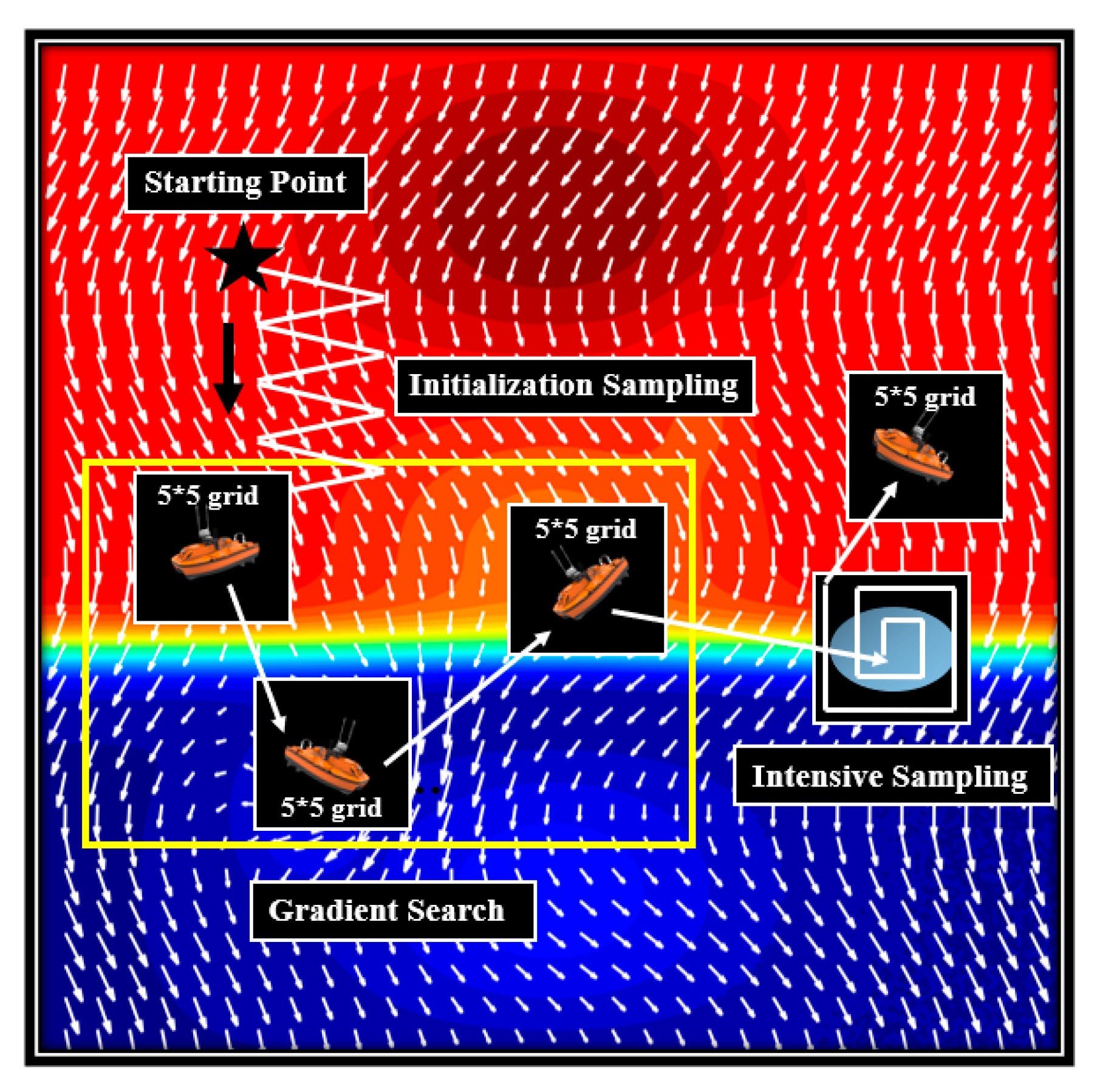
2.4.4. Integrated Implementation Workflow
- (1)
- Initialization: A random starting point is selected for the USV, which performs zigzag transect sampling along a predefined orientation (e.g., north to south) at a uniform velocity to collect initial field data including SST, U, and V. The USV is assumed to sample at each grid point it traverses.
- (2)
- Model Training: Optimal kernel functions and hyper-parameters are configured. All collected data are used to train three separate GPR models—each dedicated to predicting SST, U, and V within the local field—with hyper-parameter optimization performed concurrently for each model.
- (3)
- Local Field Prediction: The trained GPR models are used to predict SST, U, and V within a local unknown region, defined as a 5 × 5 grid centered on the USV’s current position.
- (4)
- Adaptive Sampling: The CGI and Ro are calculated across the 5 × 5 grid. The grid point with the maximum CGI value is selected as the next target, and the USV navigates to this location to conduct sampling.
- (5)
- Intensive Sampling: If the Ro value at any grid point meets the predefined Ro threshold, submesoscale activity is considered probable. If over 60% of the points within the local area satisfy the threshold, the region is classified as actively submesoscale, triggering a spiral-pattern intensive sampling routine. If these conditions are not met, intensive sampling is not activated.
3. Results
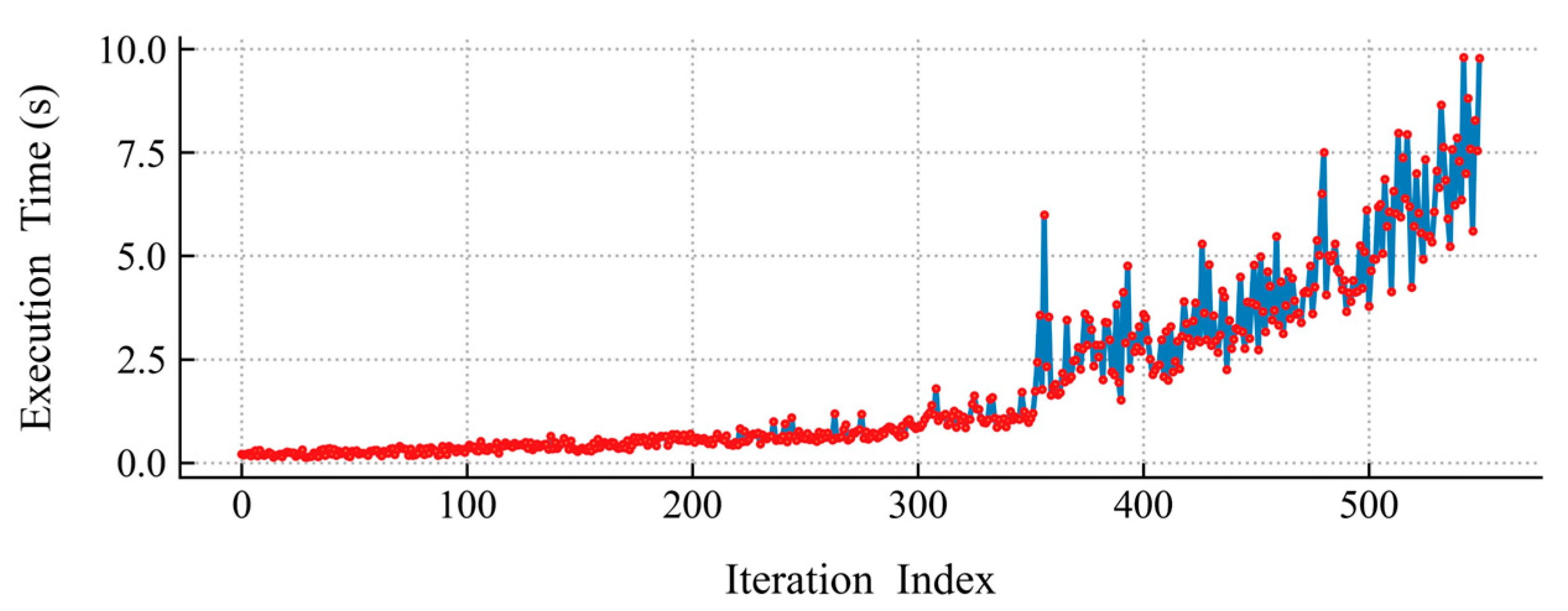
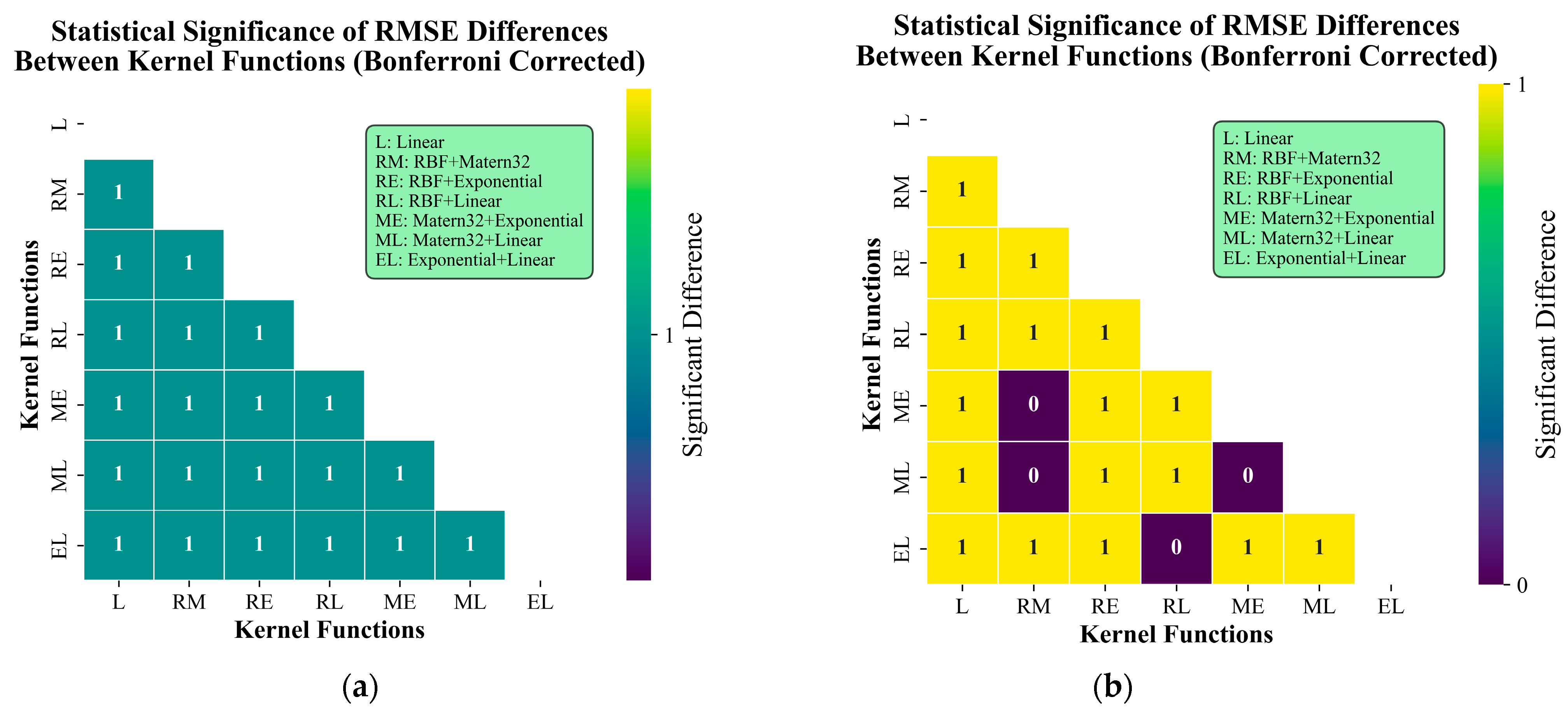
3.1. Optimization of GPR Kernel Functions
3.1.1. Local Field Prediction Performance
3.1.2. Global Field Reconstruction Accuracy
3.1.3. GPR vs. MLP
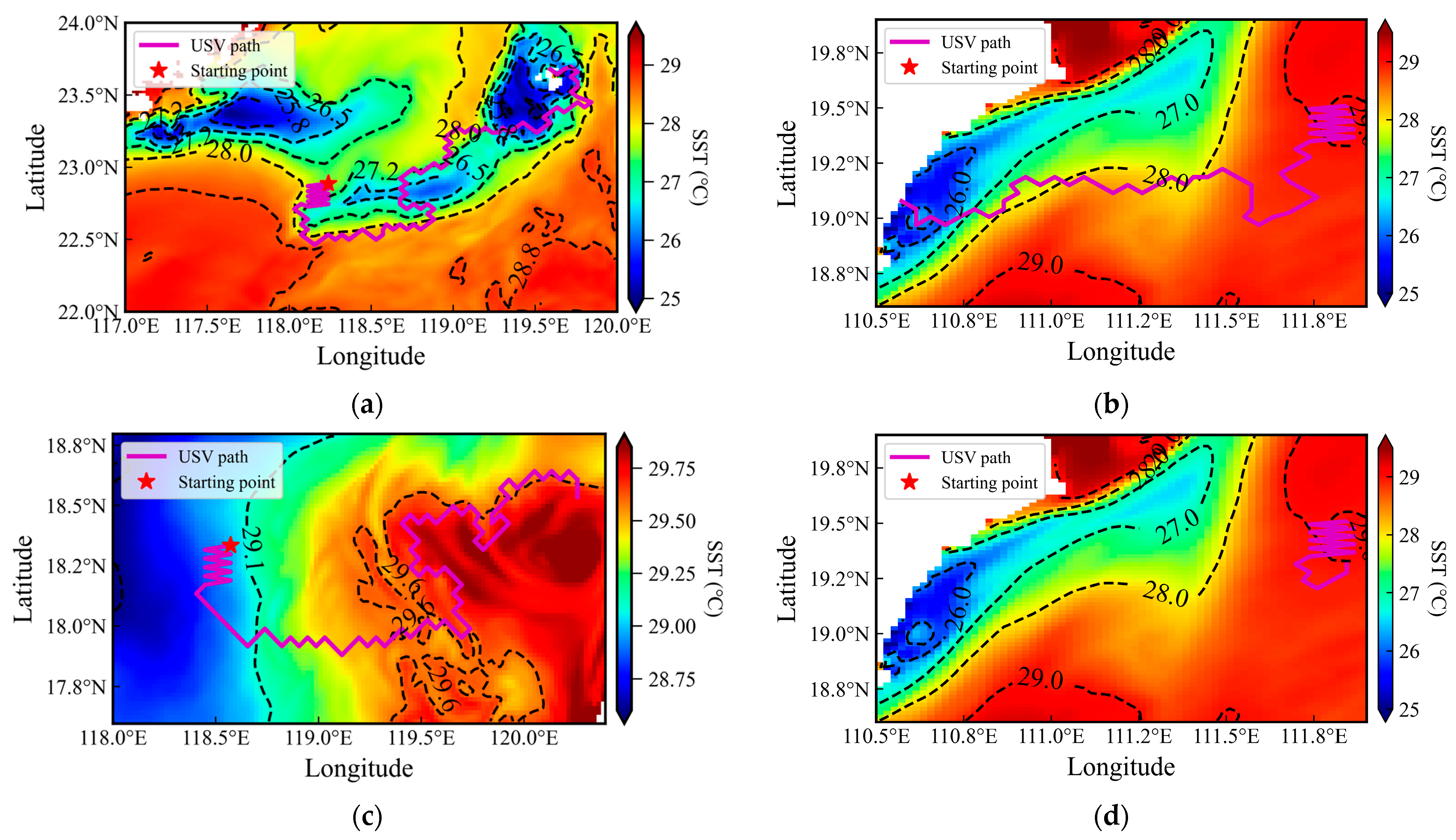
3.2. Performance of the Adaptive Sampling Strategy
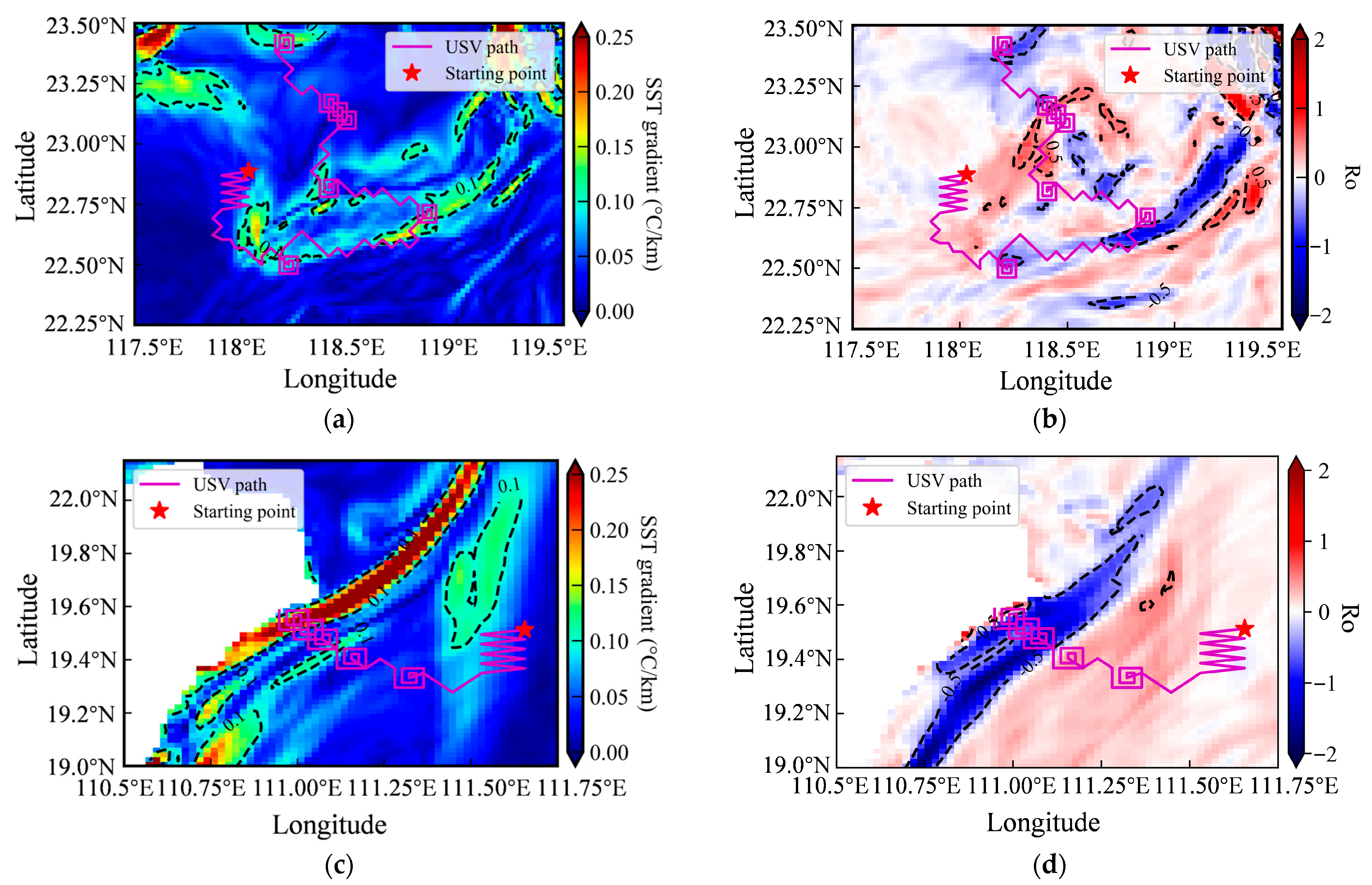
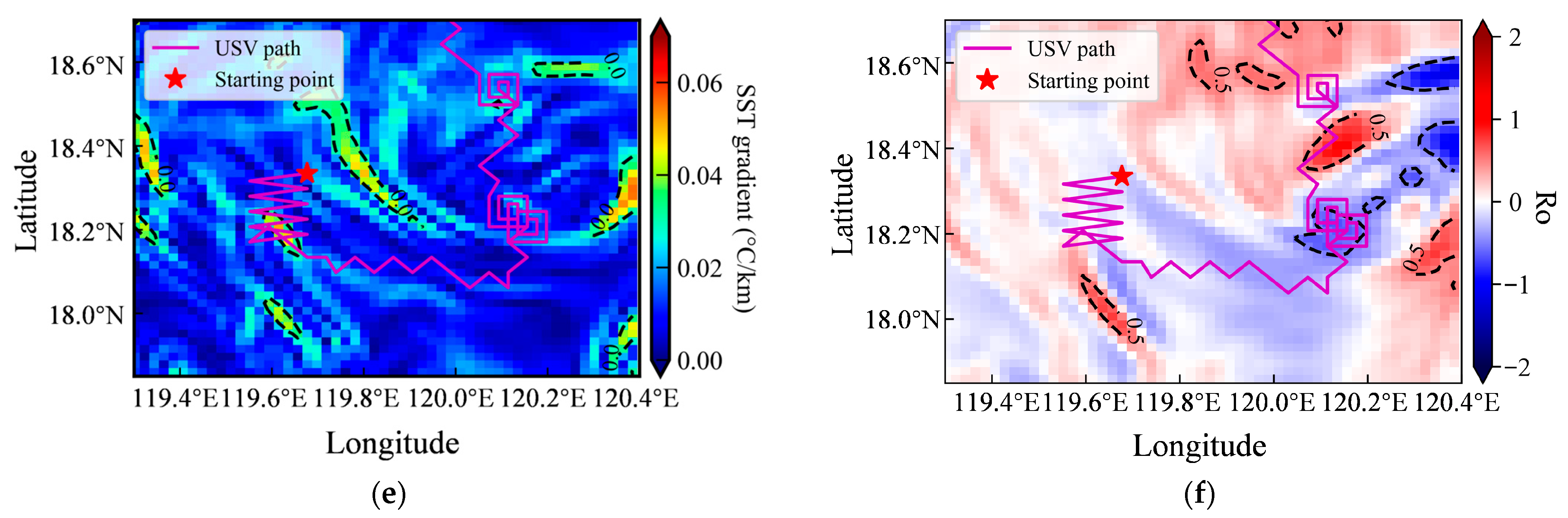
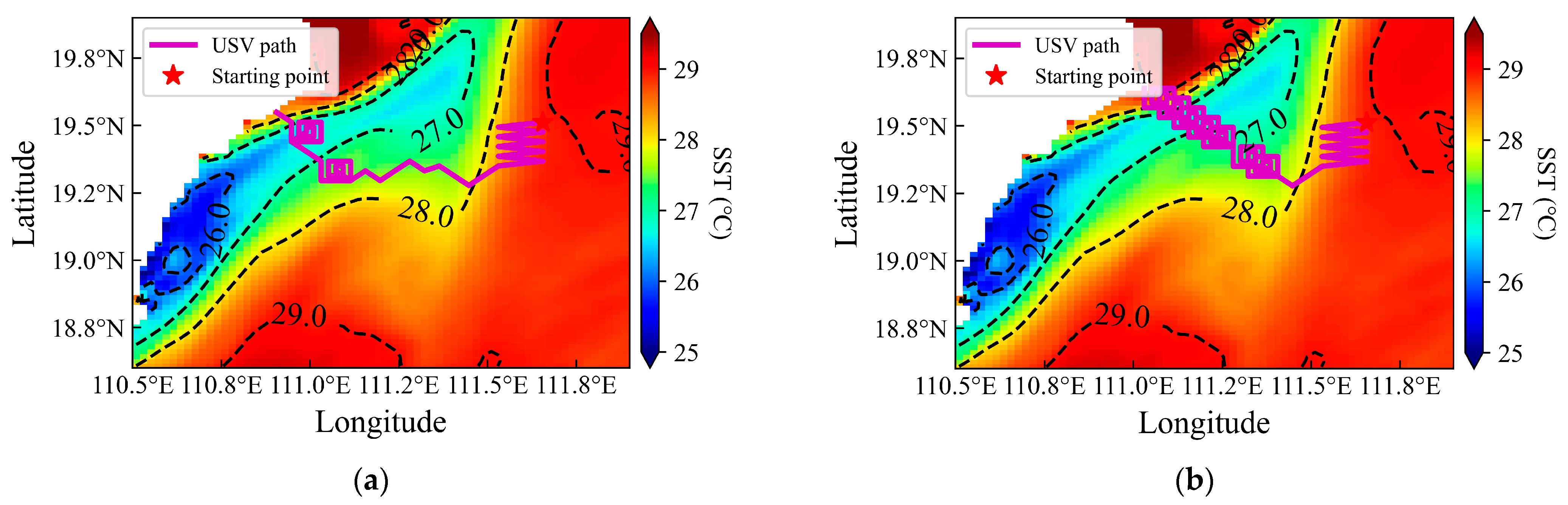
3.2.1. Gradient-Based Frontal Search
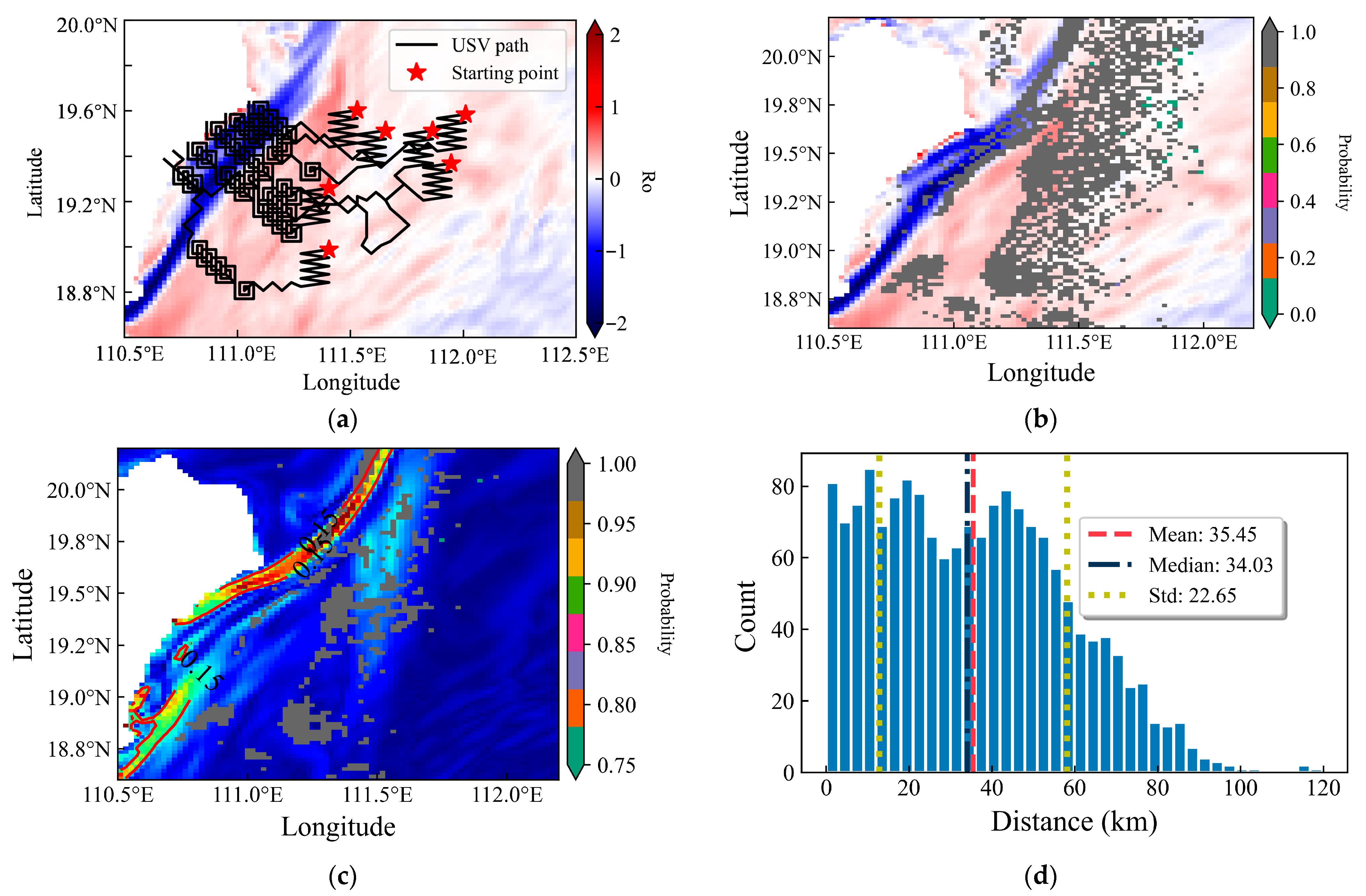
3.2.2. Triggered Intensive Sampling of Submesoscale Features
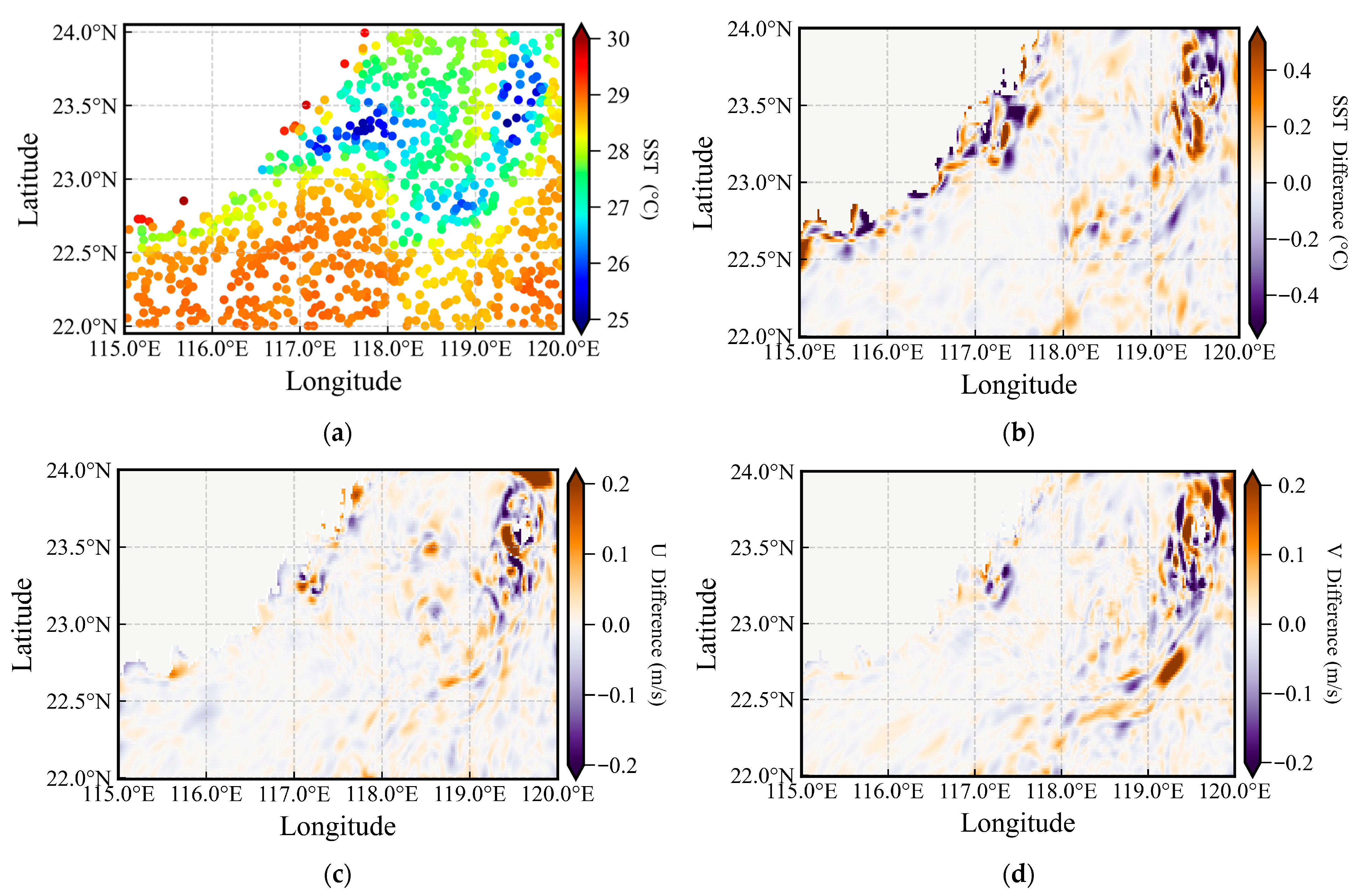
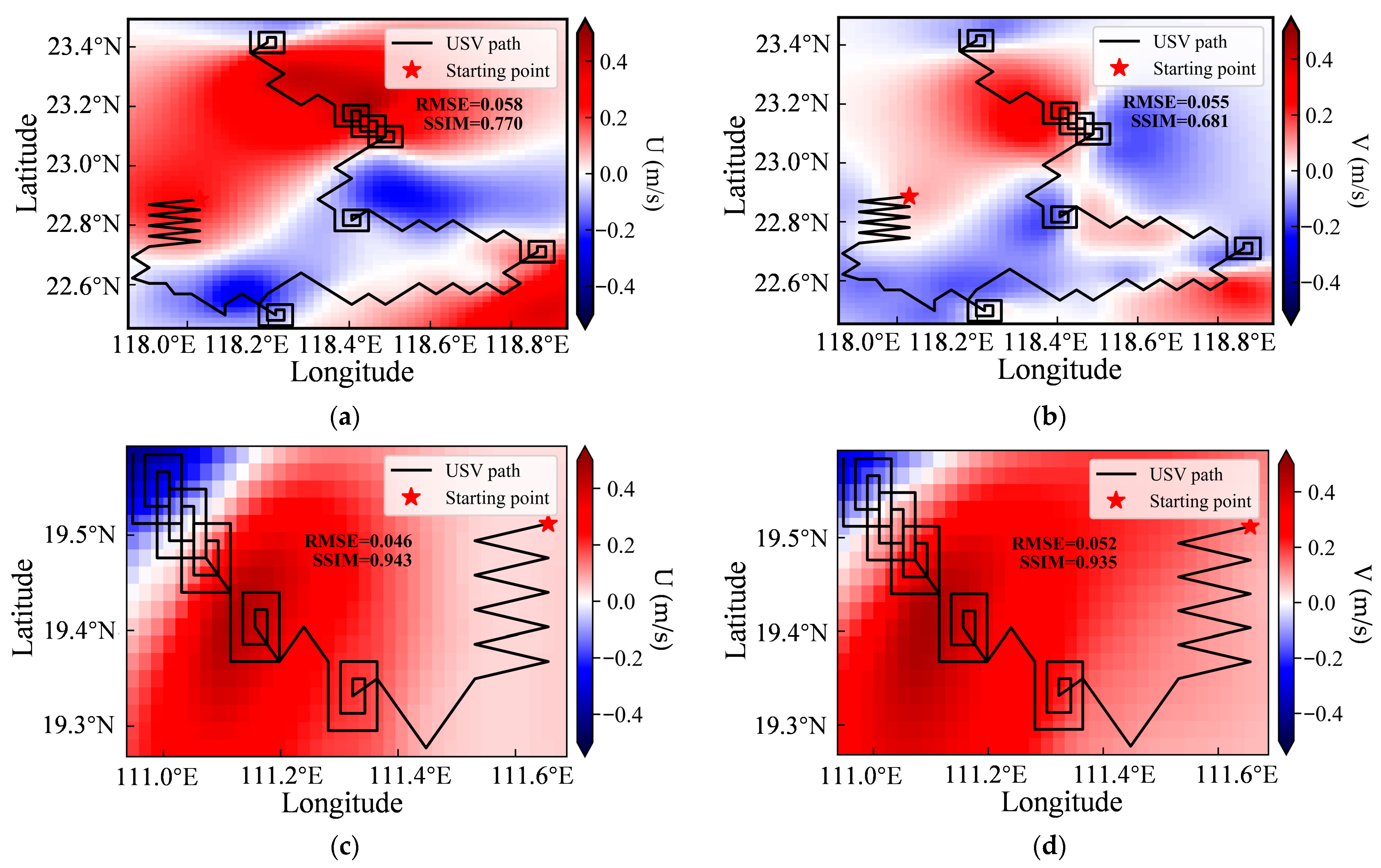
3.2.3. Post-Mission Environmental Field Reconstruction
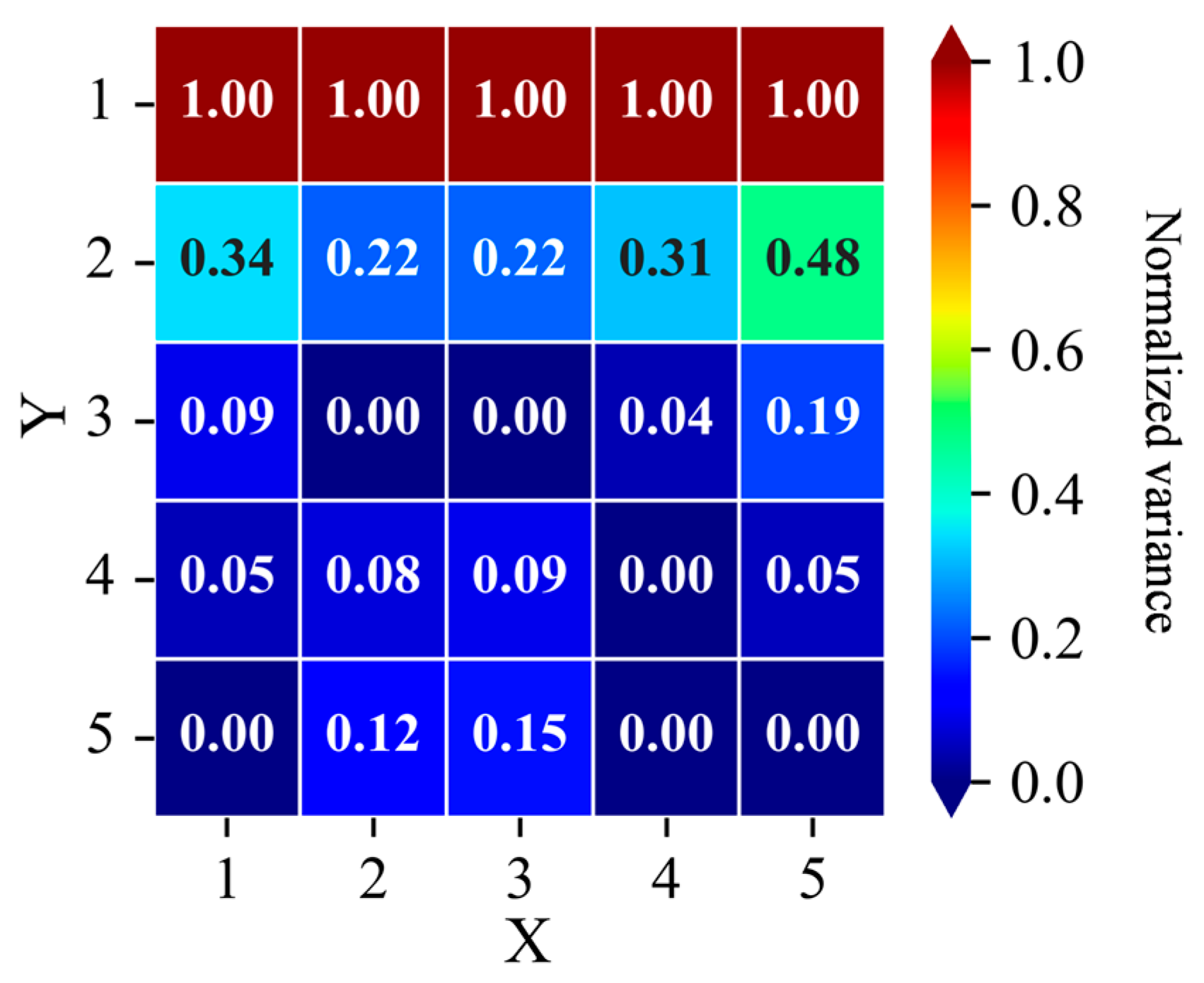
3.3. Analysis of Initial Deployment Locations
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Ing Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Thomas, L.N.; Tandon, A.; Mahadevan, A. Submesoscale Processes and Dynamics; Hecht, M.W., Hasumi, H., Eds.; American Geophysical Union: Washington, DC, USA, 2008; pp. 17–35. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Qiu, B.; Zhao, W.; Zhou, C.; Huang, X.; Tian, J. Submesoscale Currents in the Subtropical Upper Ocean Observed by Long-Term High-Reso lution Mooring Arrays. J. Phys. Oceanogr. 2021, 51, 187–206. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to Submesoscale Transition in the California Current System. Part III: Energy Balance and Flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- D’Asaro, E.; Lee, C.; Rainville, L.; Harcourt, R.; Thomas, L. Enhanced Turbulence and Energy Dissipation at Ocean Fronts. Science 2011, 332, 318–322. [Google Scholar] [CrossRef]
- Guo, M.; Xing, X.; Xiu, P.; Dall’oLmo, G.; Chen, W.; Chai, F. Efficient biological carbon export to the mesopelagic ocean induced by submesoscale fronts. Nat. Commun. 2024, 15, 580. [Google Scholar] [CrossRef]
- Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale Eddies Detected by SWOT and Moored Observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Z.; Sun, S.; Li, M.; Cai, W.; Wu, L.; Cai, J.; Sun, B.; Ma, K.; Ma, X.; et al. Observations Reveal Intense Air-Sea Exchanges Over Submesoscale Ocean Front. Geophys. Res. Lett. 2024, 51, e2023GL106840. [Google Scholar] [CrossRef]
- Dong, J.; Fox-Kemper, B.; Zhang, H.; Dong, C. The Scale and Activity of Symmetric Instability Estimated from a Global Submesoscale-Permitting Ocean Model. J. Phys. Oceanogr. 2021, 51, 1655–1670. [Google Scholar] [CrossRef]
- Nagano, A.; Ando, K. Saildrone-observed atmospheric boundary layer response to winter mesoscale warm spot along the Kuroshio south of Japan. Prog. Earth Planet. Sci. 2020, 7, 43. [Google Scholar] [CrossRef]
- Tang, H.; Wang, D.; Shu, Y.; Yu, X.; Shang, X.; Qiu, C.; Yu, J.; Chen, J. Vigorous Forced Submesoscale Instability Within an Anticyclonic Eddy During Tropical Cyclone “Haitang” from Glider Array Observations. J. Geophys. Res. Ocean. 2025, 130, e2024JC021396. [Google Scholar] [CrossRef]
- Nagano, A.; Geng, B.; Richards, K.J.; Cronin, M.F.; Taniguchi, K.; Katsumata, M.; Ueki, I. Coupled Atmosphere–Ocean Variations on Timescales of Days Observed in the Western Tropical Pacific Warm Pool During Mid-March 2020. J. Geophys. Res. Ocean. 2022, 127, e2022JC019032. [Google Scholar] [CrossRef]
- Belkin, I.; de Sousa, J.B.; Pinto, J.; Mendes, R.; Lopez-Castejon, F. A new front-tracking algorithm for marine robots. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Mitarai, S.; McWilliams, J.C. Wave glider observations of surface winds and currents in the core of Typhoon Danas. Geophys Ical Res. Lett. 2016, 43, 11312–11319. [Google Scholar] [CrossRef]
- Woithe, H.C.; Kremer, U. Feature based adaptive energy management of sensors on autonomous underwater vehicles. Ocean Eng. 2015, 97, 21–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Godin, M.A.; Bellingham, J.G.; Ryan, J.P. Using an Autonomous Underwater Vehicle to Track a Coastal Upwelling Front. IEEE J. Ocean. Eng. 2012, 37, 338–347. [Google Scholar] [CrossRef]
- Petillo, S.; Schmidt, H.; Lermusiaux, P.; Yoerger, D.; Balasuriya, A. Autonomous & adaptive oceanographic front tracking on board autonomous underwater vehicles. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005; ISBN 978-0-262-25683-4. Available online: https://direct.mit.edu/books/oa-monograph/2320/Gaussian-Processes-for-Machine-Learning (accessed on 19 July 2025).
- Ma, K.C.; Ma, Z.; Liu, L.; Sukhatme, G.S. Multi-robot Informative and Adaptive Planning for Persistent Environmental Monitoring. In Proceedings of the Distributed Autonomous Robotic Systems: The 13th International Symposium, London, UK, 7–9 November 2016; pp. 285–298. [Google Scholar] [CrossRef]
- Ma, K.C.; Liu, L.; Heidarsson, H.K.; Sukhatme, G.S. Data-driven learning and planning for environmental sampling. J. Field Robot. 2018, 35, 643–661. [Google Scholar] [CrossRef]
- Fossum, T.O.; Eidsvik, J.; Ellingsen, I.; Alver, M.O.; Fragoso, G.M.; Johnsen, G.; Mendes, R.; Ludvigsen, M.; Rajan, K. Information-driven robotic sampling in the coastal ocean. J. Field Robot. 2018, 35, 1101–1121. [Google Scholar] [CrossRef]
- Wang, S.; Song, Z.; Ma, W.; Shu, Q.; Qiao, F. Mesoscale and submesoscale turbulence in the Northwest Pacific Ocean revealed by numerical simulations. Deep Sea Res. Part II Top. Stud. Oceanogr. 2022, 206, 105221. [Google Scholar] [CrossRef]
- Gallmeier, K.; Prochaska, J.X.; Cornillon, P.; Menemenlis, D.; Kelm, M. An evaluation of the LLC4320 global-ocean simulation based on the submesoscale structure of modeled sea surface temperature fields. Geosci. Model Dev. 2023, 16, 7143–7170. [Google Scholar] [CrossRef]
- Lin, H.; Liu, Z.; Hu, J.; Menemenlis, D.; Huang, Y. Characterizing meso- to submesoscale features in the South China Sea. Prog. Oceanogr. 2020, 188, 102420. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Qiu, B.; Luo, Y.; Cai, W.; Yuan, Q.; Liu, Y.; Zhang, H.; Liu, H.; Miao, M.; et al. Submesoscale inverse energy cascade enhances Southern Ocean eddy heat transport. Nat. Commun. 2023, 14, 1335. [Google Scholar] [CrossRef]
- Stachniss, C.; Plagemann, C.; Lilienthal, A.J.; Burgard, W. Gas Distribution Modeling Using Sparse Gaussian Process Mixture Models. In Robotics: Science and Systems IV; MIT Press: Cambridge, MA, USA, 2008; pp. 310–317. Available online: https://ieeexplore.ieee.org/document/6284842 (accessed on 26 July 2025).
- He, Z.; Liu, G.; Zhao, X.; Yang, J. Temperature Model for FOG Zero-Bias Using Gaussian Process Regression. In Intelligence Computation and Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–45. [Google Scholar]
- Zhang, Y.; Feng, M.; Zhang, W.; Wang, H.; Wang, P. A Gaussian process regression-based sea surface temperature interpolation algorithm. J. Ocean. Limnol. 2021, 39, 1211–1221. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Zheng, Q.; Xie, L.; Xiong, X.; Hu, X.; Chen, L. Progress in research of submesoscale processes in the South China Sea. Acta Ocean. Sin. 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, B.; Li, X. Internal solitary waves in the China seas observed using satellite remote-sensing techniques: A review and perspectives. Int. J. Remote Sens. 2014, 35, 3926–3946. [Google Scholar] [CrossRef]
- Aravind, H.M.; Özgökmen, T.M.; Allshouse, M.R. Lagrangian analysis of submesoscale flows from sparse data using Gaussian Process Regression for field reconstruction. Ocean Model. 2025, 193, 102458. [Google Scholar] [CrossRef]
- Neural Computing: NeuralWorks Professional II/PLUS and Neural Works Explorer.—Ben-Gurion University of the Negev. Available online: https://primo.bgu.ac.il/discovery/fulldisplay/alma990019863950204361/972BGU_INST:972BGU (accessed on 24 October 2025).
- Citarella, A.A.; Carrino, L.; De Marco, F.; Di Biasi, L.; Perna, A.S.; Viscusi, A.; Tortora, G. AI Data-Driven Optimization of Cold Spray Coating Manufacturing. IEEE Trans. Ind. Inform. 2025, 21, 7848–7858. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, C.; Yang, W.; Liang, X.; Zhang, L.; Wang, X.; Dai, R. Improving prediction of groundwater quality in situations of limited monitoring data based on virtual sample generation and Gaussian process regression. Water Res. 2024, 267, 122498. [Google Scholar] [CrossRef]
- Katsaros, K.B.; Soloviev, A.V.; Weisberg, R.H.; Luther, M.E. Reduced Horizontal Sea Surface Temperature Gradients Under Conditions of Clear Skies and Weak Winds. Bound. Layer Meteorol 2005, 116, 175–185. [Google Scholar] [CrossRef]
- Melkumyan, A.; Ramos, F. A sparse covariance function for exact Gaussian process inference in large datasets. In Proceedings of the 21st International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2009; pp. 1936–1942. Available online: https://studylib.net/doc/13900740/a-sparse-covariance-function-for-exact-gaussian-process-i (accessed on 26 July 2025).
- Lawrence, N.; Seeger, M.; Herbrich, R. Fast sparse Gaussian process methods: The informative vector machine. In Proceedings of the 16th International Conference on Neural Information Processing Systems, Bangkok, Thailand, 1–5 December 2009; MIT Press: Cambridge, MA, USA, 2002; pp. 625–632. Available online: https://proceedings.neurips.cc/paper_files/paper/2002/file/d4dd111a4fd973394238aca5c05bebe3-Paper.pdf (accessed on 26 July 2025).


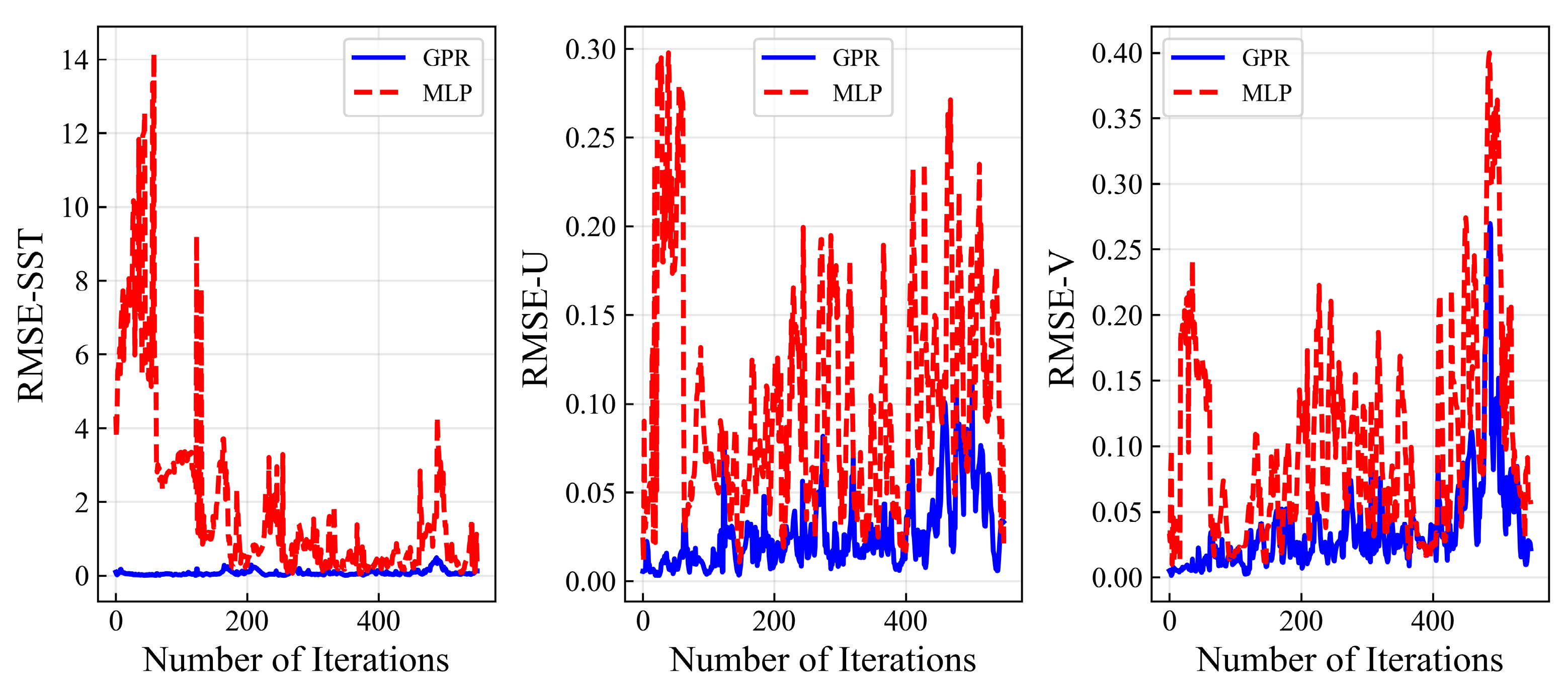




| Mean RMSE | ||||||
|---|---|---|---|---|---|---|
| Variables and 95% Confidence Interval | ||||||
| Kernel Function | SST | 95%CI | U | 95%CI | V | 95%CI |
| Linear | 3.701 | [3.545, 3.858] | 0.123 | [0.117, 0.130] | 0.120 | [0.110, 0.129] |
| RBF + Matérn32 | 0.078 | [0.071, 0.083] | 0.026 | [0.025, 0.028] | 0.036 | [0.033, 0.039] |
| RBF + Exponential | 0.181 | [0.176, 0.202] | 0.029 | [0.027, 0.031] | 0.037 | [0.034, 0.040] |
| RBF + Linear | 0.385 | [0.352, 0.377] | 0.340 | [0.032, 0.036] | 0.042 | [0.038, 0.045] |
| Matérn32 + Exponential | 0.080 | [0.074, 0.086] | 0.026 | [0.024, 0.028] | 0.036 | [0.033, 0.039] |
| Matérn32 + Linear | 0.080 | [0.076, 0.089] | 0.026 | [0.025, 0.028] | 0.036 | [0.033, 0.039] |
| Exponential + Linear | 0.102 | [0.095, 0.108] | 0.032 | [0.031, 0.034] | 0.040 | [0.037, 0.043] |
| RMSE (50-Run Average) | Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Sampling Points and 95% Confidence Interval | |||||||||
| Kernel Function | 100 | 95%CI | 200 | 95%CI | 500 | 95%CI | 1000 | 95%CI | |
| Linear | 9.875 | [9.875, 9.875] | 9.844 | [9.844, 9.844] | 9.849 | [9.849, 9.849] | 9.823 | [9.823, 9.823] | 9.848 |
| RBF + Matérn32 | 0.373 | [0.371, 0.374] | 0.281 | [0.279, 0.284] | 0.170 | [0.170, 0.170] | 0.102 | [0.102, 0.102] | 0.232 |
| RBF + Exponential | 0.380 | [0.380, 0.380] | 0.293 | [0.292, 0.293] | 0.181 | [0.181, 0.181] | 0.110 | [0.110, 0.110] | 0.241 |
| RBF + Linear | 0.566 | [0.566, 0.566] | 0.544 | [0.544, 0.544] | 0.224 | [0.224, 0.224] | 0.172 | [0.172, 0.172] | 0.377 |
| Matérn32 + Exponential | 0.376 | [0.376, 0.376] | 0.294 | [0.294, 0.294] | 0.172 | [0.172, 0.172] | 0.103 | [0.103, 0.103] | 0.236 |
| Matérn32 + Linear | 0.394 | [0.394, 0.394] | 0.326 | [0.326, 0.326] | 0.174 | [0.174, 0.174] | 0.104 | [0.104, 0.104] | 0.250 |
| Exponential + Linear | 0.376 | [0.376, 0.376] | 0.294 | [0.294, 0.294] | 0.181 | [0.181, 0.181] | 0.110 | [0.110, 0.110] | 0.240 |
| RMSE (50-Run Average) | Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Sampling Points and Confidence Interval | |||||||||
| Kernel Function | 100 | 95%CI | 200 | 95%CI | 500 | 95%CI | 1000 | 95%CI | |
| Linear | 0.151 | [0.151, 0.151] | 0.147 | [0.147, 0.147] | 0.147 | [0.147, 0.147] | 0.147 | [0.147, 0.147] | 0.148 |
| RBF + Matérn32 | 0.085 | [0.085, 0.085] | 0.075 | [0.075, 0.075] | 0.040 | [0.040, 0.040] | 0.034 | [0.034, 0.034] | 0.059 |
| RBF + Exponential | 0.086 | [0.086, 0.086] | 0.078 | [0.070, 0.070] | 0.042 | [0.042, 0.042] | 0.038 | [0.038, 0.038] | 0.061 |
| RBF + Linear | 0.099 | [0.099, 0.099] | 0.077 | [0.077, 0.072] | 0.074 | [0.074, 0.074] | 0.036 | [0.036, 0.036] | 0.072 |
| Matérn32 + Exponential | 0.086 | [0.086, 0.086] | 0.070 | [0.070, 0.070] | 0.042 | [0.042, 0.042] | 0.034 | [0.034, 0.034] | 0.058 |
| Matérn32 + Linear | 0.085 | [0.085, 0.085] | 0.070 | [0.070, 0.070] | 0.041 | [0.041, 0.041] | 0.034 | [0.034, 0.034] | 0.058 |
| Exponential + Linear | 0.086 | [0.086, 0.086] | 0.070 | [0.070, 0.070] | 0.042 | [0.042, 0.042] | 0.038 | [0.038, 0.038] | 0.059 |
| RMSE (50-Run Average) | Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Sampling Points and Confidence Interval | |||||||||
| Kernel Function | 100 | 95%CI | 200 | 95%CI | 500 | 95%CI | 1000 | 95%CI | |
| Linear | 0.149 | [0.149, 0.149] | 0.142 | [0.142, 0.142] | 0.142 | [0.142, 0.142] | 0.142 | [0.142, 0.142] | 0.144 |
| RBF + Matérn32 | 0.101 | [0.101, 0.101] | 0.101 | [0.101, 0.101] | 0.052 | [0.052, 0.052] | 0.037 | [0.037, 0.037] | 0.073 |
| RBF + Exponential | 0.099 | [0.099, 0.099] | 0.093 | [0.093, 0.093] | 0.055 | [0.055, 0.055] | 0.040 | [0.040, 0.040] | 0.072 |
| RBF + Linear | 0.104 | [0.104, 0.104] | 0.105 | [0.105, 0.105] | 0.090 | [0.090, 0.090] | 0.040 | [0.040, 0.040] | 0.085 |
| Matérn32 + Exponential | 0.099 | [0.099, 0.099] | 0.093 | [0.093, 0.093] | 0.055 | [0.055, 0.055] | 0.040 | [0.040, 0.040] | 0.072 |
| Matérn32 + Linear | 0.101 | [0.101, 0.101] | 0.101 | [0.101, 0.101] | 0.052 | [0.052, 0.052] | 0.037 | [0.037, 0.037] | 0.073 |
| Exponential + Linear | 0.099 | [0.099, 0.099] | 0.093 | [0.093, 0.093] | 0.055 | [0.055, 0.055] | 0.040 | [0.040, 0.040] | 0.072 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tang, H.; Song, W.; Fan, S.; Wang, D. Adaptive Sampling of Marine Submesoscale Features Using Gaussian Process Regression with Unmanned Platforms. J. Mar. Sci. Eng. 2025, 13, 2088. https://doi.org/10.3390/jmse13112088
Wang W, Tang H, Song W, Fan S, Wang D. Adaptive Sampling of Marine Submesoscale Features Using Gaussian Process Regression with Unmanned Platforms. Journal of Marine Science and Engineering. 2025; 13(11):2088. https://doi.org/10.3390/jmse13112088
Chicago/Turabian StyleWang, Wenbo, Haibo Tang, Wei Song, Shuangshuang Fan, and Dongxiao Wang. 2025. "Adaptive Sampling of Marine Submesoscale Features Using Gaussian Process Regression with Unmanned Platforms" Journal of Marine Science and Engineering 13, no. 11: 2088. https://doi.org/10.3390/jmse13112088
APA StyleWang, W., Tang, H., Song, W., Fan, S., & Wang, D. (2025). Adaptive Sampling of Marine Submesoscale Features Using Gaussian Process Regression with Unmanned Platforms. Journal of Marine Science and Engineering, 13(11), 2088. https://doi.org/10.3390/jmse13112088









