Abstract
Storm surge dynamics in coastal zones and estuaries are complex, driven by coupled oceanic and terrestrial interactions that enhance the risk of coastal disasters. This study investigates storm surge characteristics and mechanisms in the Macao Cross Tidal Channel (MCTC), located in the Macao Sea Area (MSA). A tide-surge coupled numerical model was established using the unstructured grid Finite Volume Community Ocean Model (FVCOM). The model was rigorously validated against tide gauge data from Typhoon Hato, demonstrating strong performance, with a skill score of 0.95 and a correlation coefficient exceeding 0.94. The spatiotemporal characteristics and mechanisms of storm surge dynamics in the MCTC were elucidated. The results show that the MCTC’s complex geometry induces a geometric funneling effect, which substantially amplifies the storm surge compared with adjacent locations in the estuary and open sea. During the typhoon period, coastal geomorphology affects winds, tide levels, currents, and waves, which in turn spatially and temporally modulate the storm surge. Wind is the primary driver, but its effect is modulated by nonlinear interactions with waves, including enhanced bottom friction and wave set-down. In isolation, the wind-induced component contributed approximately 106% of the peak total surge. This overestimation quantitatively highlights the critical role of nonlinear interactions, where wave-enhanced bottom friction acts as a major energy sink, and wave set-down directly suppresses the water level at the channel entrance. The individual peak contributions from atmospheric pressure and wave were approximately 5% and 17%, respectively, but these peaks occurred out of phase with the storm surge. Energy transformation analysis based on the Bernoulli principle revealed a distinct conversion from potential to kinetic energy in the constricted transverse waterway, while the longitudinal waterway exhibited a more gradual energy change. These findings enhance the mechanistic understanding of storm surges in complex, constricted estuaries and can inform targeted strategies for coastal hazard mitigation in the Macao region.
1. Introduction
Storm surge is an anomalous rise in sea level caused by a strong atmospheric disturbance [1]. Storm surges are one of the most significant natural hazards in coastal areas [2]. These events have caused severe harm to the safety and property of residents in coastal areas of China [3]. The damage is particularly significant in shallow, densely populated areas with complex geomorphology. In China, storm surges are the most economically destructive marine disasters, accounting for over 90% of all direct economic losses from marine-related disasters [4]. The Pearl River Estuary (PRE) region, characterized by a high concentration of population and economic assets in low-lying coastal areas, exhibits exceptional vulnerability and is a national hotspot for storm surge risk [5]. Historical data indicates that in years with significant storm activity, economic losses in this region can constitute a substantial majority of the national total [6].
Macao Sea Area (MSA) is located in the Pearl River Delta (PRD) and interacts with the South China Sea (SCS). Macao Cross Tidal Channel (MCTC) is located on the west bank of the PRE, between the PRE and the Modaomen Estuary (Figure 1e). The MCTC encompasses the Maliuzhou Waterway (Hongwan Waterway), Shizimen Waterway, Qianshan Waterway, and Macao Waterway. Its unique geographical location makes it an important frontline for storm surge defense, which is of great strategic significance for buffering the impact of storm surge on inland areas and ensuring the safety and stability of the PRE and surrounding cities. The PRD is among the areas most severely affected by typhoons on China’s southeastern coast. The coastline of the MSA is complex, and the storm surge often leads to overtopping, which seriously affects the social economy and ecological environment. Furthermore, the PRD is also one of the most complex estuarine deltas in the world. It presents typical hydrological characteristics and seasonal changes [7]. However, the complex dynamics of the PRE pose challenges to hydrodynamic research [8]. Storm surge prevention and flood control in this area remain high priorities for the government.
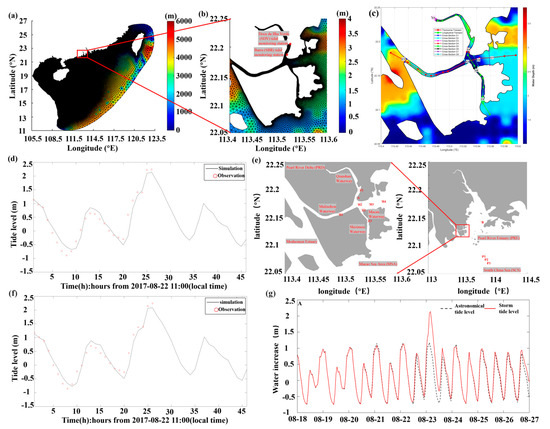
Figure 1.
(a) Large domain grid; (b) High-resolution grid of the MCTC and the two tide gauge stations used for model validation (Barra (SBR) and Doca da Ilha Verde (SDV) tidal monitoring stations); (c) Locations of the main transects and cross-sections for junction analysis. Red line: Transverse waterway; Green line: Longitudinal waterway; Colored lines with labels C1–C8: Cross-sections for analyzing flow partitioning at the junction; (d) Tide level of SBR station during Typhoon Hato; (e) 12 stations (A, Z1–Z3, H1–H4, B and P1–P3) in the MSA; (f) Tide level of SDV station during Typhoon Hato; (g) The astronomical tide-storm surge time sequence at station A.
While regions such as the U.S. Gulf Coast, the Bay of Bengal, and the Philippines are globally recognized for their vulnerability to large-scale storm surge inundation across open coastlines [9], the MCTC offers a distinct and complementary research opportunity. The MCTC serves as a natural laboratory for studying storm surge dynamics within a highly complex, constricted, and geometrically intricate estuarine system. Understanding the physical mechanisms of surge amplification and modulation at this finer scale is a key challenge in coastal science, as such systems are common worldwide but are often poorly resolved in large-scale models. Therefore, a detailed investigation of the MCTC provides transferable insights into the nonlinear processes governing storm surges in similarly complex estuarine environments globally.
At present, domestic and foreign scholars have studied the hydrodynamic processes in PRE from the aspects of hydrometeorological and storm surge characteristics under the influence of typhoon. The storm surge in Hengmen and its upstream is mainly affected by typhoons, astronomical tides and upstream inflow [10]. The severity of storm surge and coastal inundation in Macao and the broader PRE is deterministically linked to typhoon characteristics, particularly its track, landing point, and forward speed. The total water level, which dictates inundation, is a function of the astronomical tide and the storm surge, amplified by nonlinear tide-surge interactions that can contribute 5–25% to the total water level in the waters near Macao [11]. The most severe inundation events are typically associated with slow-moving typhoons whose tracks place the PRE on the dangerous side of the storm during a high astronomical tide [12]. Regarding numerical models, the river mouth morphology and runoff of PRE have a significant impact on the storm surge. When the typhoon lands on the west bank of the PRE, the nonlinear effect of storm surge-astronomical tide is the largest [13]. While reclamation may offer localized protection by reducing wave heights, it also constricts the estuary, creating a funneling effect that can amplify storm surge levels, increase current velocities, and aggravate coastal inundation in adjacent and upstream areas [14]. However, the storm surge characteristics and mechanisms inside the MCTC still need further investigation, due to the complex bathymetry and coastlines characteristic of estuarine systems.
To overcome this limitation, this study employs the unstructured grid Finite Volume Community Ocean Model (FVCOM) to accurately resolve the complex bathymetry and coastlines in MCTC-estuarine system, and numerically simulate the storm surge processes in the MCTC during the Typhoon Hato. This study aims to: (1) investigate the characteristics of storm tides and assess the impacts of Typhoon Hato on tides, storm surges, currents, and waves in the MSA and MCTC; (2) quantify the amplification of storm surge within the MCTC due to its unique geomorphology, provide theoretical guidance for disaster prevention and mitigation; and (3) elucidate the underlying physical mechanisms, with a particular focus on the nonlinear interactions between wind, atmospheric pressure, and wave that govern the total storm surges.
2. Materials and Methods
2.1. Typhoon Hato
Typhoon Hato (No. 13, 2017) formed on 20 August and then moved northwestward. Around 12:50 on 23 August 2017, it made landfall on the coast near Jinwan, Zhuhai, Guangdong Province as a strong typhoon. After landfall, it continued moving to the NW direction, and the intensity gradually weakened. Hato was characterized by high intensity, rapid movement speed, and a wide area of influence. From the morning of 23 August, there were strong winds and heavy rainfall along the coast of Guangdong. The accumulated precipitation in some areas of Zhuhai is more than 200 mm, and the maximum point precipitation reached approximately 250 mm in Zhuhai. Moreover, Hato is one of the strongest typhoons that have landed in the PRE for more than half a century. It broke the historical record in terms of affected areas with storm surges [15]. The strong winds and floods of Hato caused 22 deaths and direct economic losses of USD 3.5 billion [16].
The selection of Typhoon Hato as the case study for this research is predicated on its unprecedented intensity and catastrophic impact, which provide a unique and critical dataset for studying extreme storm surge dynamics. Critically for this study, Hato generated a record-breaking storm surge; the maximum recorded sea level at the Barra (SBR) tidal monitoring station reached 5.58 m, the highest recorded since 1925. The maximum inundation depth in the inner harbor area reached 3.1 m. This extreme event offers an opportunity to validate the storm tide model under extreme conditions and to investigate the upper limits of storm surge amplification within the complex geometry of the MCTC. Due to its severity, Typhoon Hato has been the focus of numerous scientific investigations, making it a well-documented event for comparative analysis.
2.2. Governing Equations
The three-dimensional hydrodynamic numerical model of the MSA with finite volume method and the unstructured grid is well-suited for resolving the complex shoreline and underwater terrain changes in the nearshore area [17]. The FVCOM has been widely used in hydrodynamic numerical simulation of coastal areas [18,19,20,21]. The model uses a coordinate system in the vertical direction. The coordinate transformation of the coordinate system is defined as follows:
In the formula, is the vertical coordinate in the Cartesian coordinate system, is the water depth relative to the average sea level, is the tide level, is the total water depth , and the value range of is −1 (seabed)–0 (sea surface).
In the coordinate system, the original control equations are as follows:
Continuity equation:
The momentum equation:
Here, and represent the east and north coordinates in the Cartesian coordinate system, respectively, is the Coriolis force parameter, , and are the velocity components in the , and directions, respectively, is the gravitational acceleration, and are the sea water density and the reference density. and are horizontal diffusion terms, and is vertical eddy viscosity coefficient. Horizontal mixing was parameterized using the Smagorinsky turbulence closure scheme of the model [22], and the Mellor-Yamada level 2.5 (MY-2.5) turbulence closure scheme is used in the vertical mixing calculation [23]. The FVCOM fully couples wave and current dynamics. Radiation stress terms from the wave model are incorporated into the momentum equations (Equations (3) and (4)), and the currents and water levels from the hydrodynamic model in turn affect wave propagation. This two-way coupling is essential for capturing nonlinear processes like wave-enhanced bottom friction and wave set-up.
2.3. Model Setting
The grid and water depth topography of the model cover most of the SCS (Figure 1a,b). The calculation domain is 105.50–123.50° E, 11.00–27.00° N, and the key calculation area is the MCTC, ranging from 113.40–113.60° E, 22.05–22.25° N. The overall water depth ranges from less than 10 m in the channel to over 5000 m in the open sea. The computational domain grid includes 86,441 nodes and 167,732 triangular elements. The open boundary was located in the deep ocean where the bathymetric slope is gentle to minimize boundary reflections. Following the model settings, the grid resolution was refined to improve accuracy in key areas. The resolution outside channel was set to 40 km while the grid in the key research area was refined to a resolution of 40 m. The model employs a wetting-drying algorithm to accurately simulate the inundation and exposure of intertidal zones, which is crucial for modeling storm surge in complex estuarine topographies like the MCTC. A 3-day spin-up period was implemented to allow the model to reach a stable state, ensuring that initial transient errors from the cold start were eliminated prior to the analysis period. Then the data were extracted for result analysis.
Model forcing included tidal elevation, wind, atmospheric pressure, and river runoff. Open boundary tidal forcing was derived from the TPXO7.2 global ocean tide model [24]. The model was forced at the open boundaries by 13 principal tidal constituents (M2, S2, K1, O1, etc.) derived from the TPXO7.2 global tide model (Table 1). Based on annual runoff data for the PRE from Bulletin of River Sediment in China (http://www.mwr.gov.cn/sj/tjgb/zghlnsgb/ (accessed on 7 February 2024)), we specified the constant runoff of the main river boundaries. The wind and atmospheric pressure field data in general weather conditions are derived from the reanalysis data provided by the European mesoscale forecasting center ECMWF (http://apps.ecmwf.int/datasets/ (accessed on 7 February 2024)). The wind speed at a distance of 10 m from the sea surface and the sea surface atmospheric pressure are selected. The temporal resolution was 6 h and the spatial resolution was 0.125°.

Table 1.
Model configuration parameters.
2.4. Model Verification
The FVCOM model is a well-established tool that has been widely and successfully applied to simulate storm surge events in this region and globally, including for violent typhoons such as Mangkhut and Hato, demonstrating its robustness for hydrodynamic research in the PRE [25,26]. In this study, Measured tide level data for model verification were obtained from the SBR station (113.550° E, 22.167° N) and SDV station (113.538° E, 22.208° N). Their specific locations are marked in Figure 1b) and the comparison between the simulated data and the measured data is shown in Figure 1d,f). These three statistical metrics were selected as they provide complementary perspectives on model performance: indicates magnitude of error, measures linear correlation, and assesses overall model skill relative to a reference [27].
Here, and are the model simulation and measured data, respectively. and are the averages of the simulated and measured values, respectively. The correlation coefficient () approaching unity indicates a stronger linear relationship between simulation and observation. Model reliability is considered modest when the skill score () exceeds 0.2 and strong when it surpasses 0.5 [28]. The of the model for the tide level data at SBR station was 0.337, was 0.942 and the was 0.955. The of the model for the tide level data at SDV station was 0.356, was 0.943 and the was 0.949. The validation results confirm that the model accurately simulates the tidal dynamic processes in the MCTC during the Typhoon Hato.
3. Results
Taking the established astronomical tide-storm surge-wave coupling model (Case0) as the control condition (Table 2), four numerical experiments were designed to quantify the contribution rate of each factor to the impact of storm surge. The spatial and temporal variations of the storm surge in and outside the MCTC are analyzed using the model results (Case0). 12 stations with 8 stations (A, Z1–Z3, H1–H4) in the channel, 3 stations (P1–P3) outside the channel and 1 station in the PRE (B) are selected to illustrate the spatial and temporal variations of the storm surge in and outside the MCTC (Figure 1e).

Table 2.
Configuration of the numerical experiments.
3.1. Tides and Storm Surges
In the spatial distribution across the PRE and MCTC, the maximum tide level and storm surge were higher in areas with complex terrain (Figure 2). At station A, located in the center of the MCTC, the maximum tide level was 2.14 m at 05:00 on 23 August (Figure 1e).
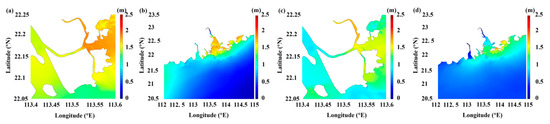
Figure 2.
(a) The tide level in MCTC; (b) The tide level in PRE; (c) The storm surge of maximum tide level in MCTC; (d) The storm surge of maximum tide level in PRE.
At the maximum tide level time, the overall distribution range of the tide level in the MCTC is between 1.0 m and 2.2 m, and the overall distribution range of the storm surge is between 0.3 m and 1.2 m (the purple line in Figure 3). The maximum tide levels of the 8 stations (A, H1–H4, Z1–Z3) range from 2.00 m to 2.15 m. The average value of the maximum tide level is 2.12 m, with a variation of ±0.12 m. In general, the tide level of the longitudinal stations is higher than that of the transverse stations, and the maximum tide level at station Z2 is the largest, while station H1 is the smallest. By comparing the tide level results of Case0 and Case4, the storm surge magnitude can be calculated. The maximum storm surge in the MCTC ranges from 0.98 m to 1.20 m. The average value of the maximum storm surge is 1.13 m with a variation of less than ±0.15 m. The maximum storm surge at station Z2 is the largest, while station H1 is the smallest, and station H2 is the closest to the average value. Because station B is located far from stations P1–P3, its maximum tide level and storm surge values were substantially different. The maximum tide level at station B is 1.63 m, and the maximum storm surge is 1.11 m. The maximum tide level at stations P1–P3 are 1.16 m, 1.12 m and 1.07 m; the average value of the maximum tide level is 1.12 m; the maximum storm surge values are 0.34 m, 0.31 m and 0.30 m; and the average value of total storm surge is 0.32 m.
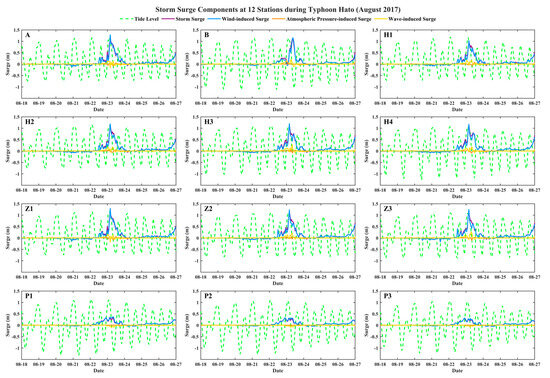
Figure 3.
Storm surge components at 12 stations during Typhoon Hato (August 2017). Green line: tide level, purple line: storm surge, blue line: wind-induced surge, orange line: atmospheric pressure-induced surge and yellow line: wave-induced surge.
A significant amplification of the storm surge occurs within the MCTC. The narrow geometry of the MCTC is prone to water accumulation. The wind, waves and currents are transmitted to the shoreline for refraction during typhoon, which will also affect the maximum storm surge. In contrast, the storm surge dynamics outside the channel are less complex, showing reduced influence from features such as islands and coastal constrictions. Under the influence of Typhoon Hato, storm surge of MCTC is a typical single-peaked storm surge hydrograph: the storm surge hydrograph was small during the precursor stage, increased rapidly during the main stage, and produced a small residual surge during the final stage. The maximum storm surge at each station in the channel occurred at the astronomical high-slack tides, which led to a further increase in the extreme tide level and amplified the disaster of typhoon storm surge in the MSA.
3.2. Currents
The main period of the hydrodynamic influence of Typhoon Hato in the MCTC is from 21 August to 25 August 2017 (Figure 4a,b). Four characteristic time points were selected for flow field analysis at an interval of 4 h. The distribution of surface flow field in the MCTC and the PRE during storms are studied. In the figure, color represents flow velocity and arrows indicate flow direction.
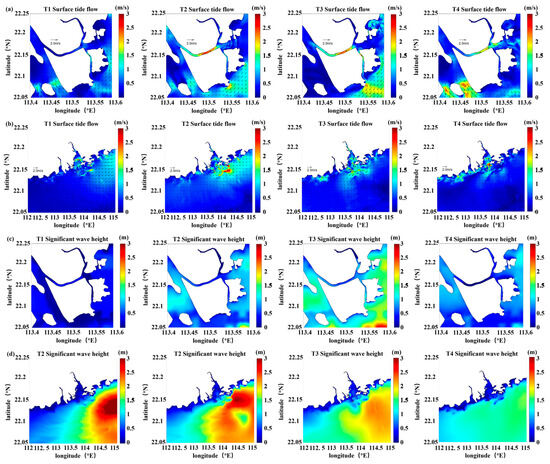
Figure 4.
(a) Surface flow fields in the MCTC (characteristic moments T1–T4); (b) Surface flow fields in the PRE (T1–T4); (c) Significant wave height (T1–T4) in the MCTC; (d) Significant wave height in the PRE (T1–T4).
During the T1 ebb slack moment, the surface current field in the MCTC exhibited an offshore ebb current, with relatively low flow velocities in the channel, distributed between 0.5–1.0 m/s. At T2, the moment of maximum flood current, when the typhoon advanced to the MCTC, MCTC is already under a southeast-to-northwest flood current due to the effect of wind stress. The overall flow velocity was the highest at this time. Influenced by the water depth and terrain, a high-velocity zone formed in the narrow section on the west side of the transverse channel, reaching 1.5–2.5 m/s. The surface current field under the action of the storm surge was consistent with the typhoon wind field, both forming a counterclockwise circulation around the typhoon center. At this moment, the current field on the left side of the typhoon center was stronger than other areas, because the flow velocity direction was consistent with the overall ebb current direction of the sea area, and their superposition resulted in a larger velocity. Notably, the circulation center of the current field did not coincide with the typhoon center of the wind field at the same moment, and the current field exhibited a certain lag relative to the wind field. During the T3 flood slack moment, the surface current field still exhibited an onshore flood current, but the flow velocity decreased and the tide level rose slowly. At this moment, the high-velocity zone continued to appear in the narrow section on the west side of the transverse channel in the Cross channel. During the T4 ebb maximum moment, the surface current field was a northwest-to-southeast ebb current, with relatively high overall flow velocity. The narrow and long section on the west side of the transverse channel had larger flow velocities, ranging from 1–1.5 m/s.
3.3. Waves
Typhoon Hato maintained a high intensity when it was close to the PRE, and the maximum significant wave height reached 10 m (Figure 4d). The distribution of significant wave height corresponds well to the movement and development process of typhoon. In the process of typhoon advance, waves were driven by wind and the wave height developed rapidly. At T1, in the open sea, the wave height near the typhoon center is larger, and the wave height in the right sea area is larger than that in the left sea area. This is because the wind speed on the right side is consistent with the direction of the typhoon, and its speed is larger than that on the left side, so it is more conducive to the development of waves. At this time, the distribution of significant wave height has a more regular oval shape. At T2, as the typhoon moves toward the coast of the PRD, the wave height in the southeastern part of the PRE increases first. At this time, the significant wave height shows an irregular elliptical distribution, and the typhoon center wave height gradually decreases. At T3, due to the influence of the terrain factors of the PRE, the distribution of wave height field becomes more irregular, and it accumulates along the southern coastline, which makes the wave height value of the offshore area larger. Under the reflection of the terrain, the wave along the coastline propagates to the northeast, which is easy to cause the wave disaster in the range. At T4, as the typhoon passes through the PRD, the intensity of the typhoon continues to weaken, and the significant wave height is within 5 m.
In the nearshore area, the shallow water depth causes wave breaking and energy dissipation, resulting in smaller wave heights than those in the open sea (Figure 4c). Due to the limitation of the water depth of the coastal topography, when the typhoon passes through the MCTC, the significant wave height along the contour line is distributed in blocks. The significant wave height in the channel is not more than 1 m, and the significant wave height in the open sea can reach more than 3 m. When the typhoon enters the MSA, the significant wave height is the largest due to the influence of the large onshore wind. When the typhoon is about to leave the MSA, the waves are arranged neatly and distributed regularly due to the influence of swells.
In summary, the wave height within the radius of maximum wind speed is larger and decreases with distance from it. The centroid of the entire wave field, derived from the spatial distribution of significant wave height, is located in the right-front quadrant of the typhoon center. In the open sea, the wave height is mainly affected by the wind field, the wave distribution has a more regular oval shape, and the energy is relatively concentrated. In the nearshore area, wave height is influenced by both the coastline and water depth, and the significant wave height tends to be relatively smaller and follows the depth contours.
3.4. Wind-Induced Surge
By comparing the storm surges of Case2 and Case0, the magnitude of the increase caused by the wind can be calculated. The wind field was the main factor affecting the storm surge, accounting for about 106% of the peak values of the total storm surge. The maximum wind-induced surge is at 05:00 on 23 August 2017, which is the same as that under the Case0. In general, the temporal evolution of the wind-induced surge closely mirrored that of the total storm surge (the blue line in Figure 3). At the time of the peak total surge, the wind-induced component slightly exceeded the total surge. This is likely because the wind speed in the MSA was highest at this time, which leads to the increase of surge, while the effect of atmospheric pressure and wave will reduce the surge before and after this time.
At the stations within the channel (A, H1–H4, Z1–Z3), the maximum wind-induced surge ranges from 1.03 m to 1.30 m (Table 3). This represents a contribution ranging from 101.20% to 114.31% of the total storm surge. The average value of wind-induced surge in the channel is 1.21 m, which is 106.54% of the average value of the storm surge. The maximum wind-induced surge at stations (B, P1–P3) outside the channel (Table 3) are 1.16 m, 0.38 m, 0.33 m, and 0.32 m, which are 104.40%, 111.88%, 105.00%, and 105.89% of the storm surge.

Table 3.
Contributions of individual forcing components to the total storm surge at the time of peak surge.
3.5. Atmospheric Pressure-Induced Surge
The atmospheric pressure-induced surge accounted for approximately 5% of the total storm surge and exerted a suppressive effect at the time of the peak surge. By comparing the storm surges of Case3 and Case0, the magnitude of storm surge caused by atmospheric pressure can be calculated (the orange line in Figure 3). Due to the small range of the MCTC, the atmospheric pressure remained basically unchanged in the MSA. The extreme value of the storm surge caused by the atmospheric pressure at T1–T4 were at the same time, which appeared at 13:00 on 23 August 2017. Compared with the maximum storm surge, it was delayed by 8 h, and atmospheric pressure exerted a suppressive effect on the maximum storm surge at 05:00 on 23 August 2017.
At the stations within the channel (A, H1–H4, Z1–Z3), the maximum atmospheric pressure-induced surge ranges from 0.03 m to 0.08 m (Table 3). This represents a contribution ranging from 2.65% to 8.31% of the storm surge. The average value of the maximum atmospheric pressure-induced surge in the channel is 0.06 m, which is 5.29% of the average value of maximum storm surge. The maximum atmospheric pressure-induced at stations (B, P1–P3) outside the channel (Table 3) are 0.01 m, which is 0.52%, 1.80%, 1.77% and 2.03% of the maximum storm surge.
At its peak at 13:00 on 23 August, the atmospheric pressure-induced surge ranged from −0.15 m to 0.15 m across the study area, and the atmospheric pressure-induced surge in a small part of the area is almost 0 due to the small water depth. At this time, the distribution of atmospheric pressure-induced surge is basically consistent with the distribution of atmospheric pressure field. The low atmospheric pressure area is in the southwest direction of the PRE, and the atmospheric pressure-induced surge in the open sea is less distributed between 0–0.02 m.
3.6. Wave-Induced Surge
The wave-induced surge accounts for about 17% of the storm surge at the peak surge moment and has a negative effect on the maximum total surge. By comparing the storm surges of Case1 and Case0, the increase in tide level caused by waves can be calculated (the yellow line in Figure 3). Due to the small MCTC, the maximum wave-induced surge is 09:00 on 23 August 2017, which is delayed by 4 h compared with the maximum storm surge. The reason for the delay is that the coastline of the MCTC has a certain blocking effect on the propagation of waves, which made the influence of the wave-induced surge delayed, and it exerted a suppressive effect at the time of the maximum storm surge.
At the stations within the channel (A, H1–H4, Z1–Z3), the maximum wave-induced surge ranges from 0.136 m to 0.281 m (Table 3). This corresponds to a contribution ranging from 12.13% to 24.13% of the maximum storm surge. The average value of the maximum wave-induced surge in the channel is 0.201 m, which is 17.74% of the average value of the maximum storm surge. The maximum wave-induced surge at stations (B, P1–P3) outside the channel (Table 3) are 0.192 m, 0.013 m, 0.010 m and 0.009 m, which are 17.33%, 3.72%, 3.21% and 3.07% of the storm surge.
At the maximum wave-induced surge (09:00 on 23 August 2017), the wave showed a surge effect on the east side of the MCTC, and a negative effect on the west side of the channel. The range of wave-induced surge from west to east is distributed between −0.2 m and 0.2 m, and the surge generated by the wave on the north side of the longitudinal channel is almost 0 due to the small water depth. The wave-induced surge in the open sea is less distributed between −0.1 m and 0.1 m. There is a wave breaking zone under the influence of water depth in the nearshore of the PRE. The wave breaks up in this area, resulting in a reduction in wave height. At the same time, the wave reduction value reaches the maximum near the breaking zone. When the waves broke, the loss of momentum flux was converted to a shoreward-directed radiation stress gradient, which caused a water level setup in the nearshore area.
4. Discussions
4.1. Mechanisms of Storm Surge in the MCTC
Storm surge in the MCTC is modulated by its unique and complex topography through a dynamic interplay of multiple physical processes. The primary amplification mechanism is a geometric funneling effect, a phenomenon well-documented in convergent estuaries where advancing storm waters are forced into a confined, narrowing cross-sectional area, leading to a pile-up of water [29,30,31]. This constriction of flow is evident in our model results, which show the formation of high-velocity zones reaching up to 2.5 m/s in the narrowest sections of the channel.
While geometric constriction initiates the surge amplification, the final water level is modulated by a complex interplay of energy transformation and dissipation. To deconstruct these competing processes, an analysis of the energy balance along the channel is necessary. To quantitatively assess how energy is converted and dissipated as the storm surge propagates through the MCTC, an analysis based on the Bernoulli equation was conducted using the model results.
4.1.1. Energy Transformation
The total energy head () at any point along the channel can be expressed using the Bernoulli equation for open channel flow, which represents the conservation of energy along a streamline. For an ideal, frictionless flow along a streamline, the Bernoulli equation states that the sum of potential energy head () and kinetic energy head () remains constant. In real open channel flows with bottom friction, the equation is defined as [32,33]:
where is the total energy head (m), is the potential energy head equivalent to the water level ζ (m), is the kinetic energy head (m), is the velocity magnitude (m/s), driven by tides, wind, and wave-current interactions, is the gravitational acceleration (9.81 m/s2), and is the cumulative frictional energy loss (m) along the flow path.
We first analyzed the along-channel variations of key parameters along two representative transects following the thalweg (Figure 1c): the transverse waterway (red line) and the longitudinal waterway (green line). Figure 5 reveals distinct energy dynamics during the peak storm surge at the reference station H2. The transverse waterway exhibits a classic signature of energy conversion consistent with the Bernoulli principle. A notable depression in the water level (Figure 5a) correlates with the peaks in velocity magnitude (Figure 5a) and (Figure 5a) at the 2–3 km constriction. This spatial correlation demonstrates the fundamental energy transformation mechanism: as the flow enters the constricted zone, the decreases from approximately 2.1 m to 1.8 m, while simultaneously, the increases from 0.05 m to 0.15 m. This indicates a conversion from potential to kinetic energy as the flow is constricted and accelerated. However, this energy conversion is not conservative—the decreases from 2.15 m to 1.95 m over this same section (Figure 5a), indicating that energy dissipation occurs concurrently with the -to- conversion. The steepest declines in occur in the constricted zone (8–12 km), correlating with high bottom friction (Figure 5a), which converts both kinetic and potential energy into heat through turbulent dissipation.
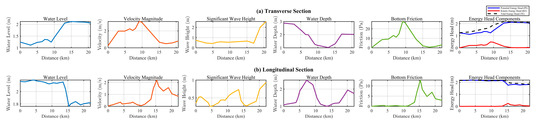
Figure 5.
Along-channel variations of key hydrodynamic and energy parameters along the (a) transverse and (b) longitudinal waterways during the peak storm surge (05:00 on 23 August 2017). Parameters include: Water Level, Velocity Magnitude, Significant Wave Height, Water Depth, Bottom Friction, the bottom friction stress presented here is the dynamic bed shear stress (in Pa), and Energy Head Components (Potential Energy Head, ; Kinetic Energy Head, ; and Total Energy Head, ).
In contrast, the longitudinal waterway exhibits smaller variations in both potential and kinetic energy components. The shows only minor fluctuations of approximately 0.1–0.2 m (Figure 5b), and the remains relatively low and steady at 0.02–0.05 m (Figure 5b). Consequently, the in this waterway (Figure 5b) shows a less pronounced decline compared to the transverse waterway. The relatively stable balance between PE and KE, combined with lower flow velocities, results in reduced bottom friction and therefore less energy dissipation along the longitudinal pathway. This distinction highlights that energy dissipation is not uniform across the MCTC but is concentrated in regions where both high flow velocities and geometric constriction combine to enhance bottom friction and flow separation.
To pinpoint the mechanisms and locations of this energy loss, we conducted a quantitative analysis of the flow and friction at eight cross-sections (C1–C8) surrounding the central junction (Figure 1c), with the spatial distribution of key hydrodynamic parameters visualized in Figure 6 and Figure 7. The data reveal a highly asymmetrical flow pattern at the junction. The dominant inflow occurred through the eastern transverse waterway (C8), which then diverged, exiting primarily westward through C2 and southward through C6. This flow partitioning created a complex, multi-directional flow field at the junction, characterized by flow separation, lateral momentum exchange, and flow deflection. These processes induce turbulent mixing and flow instabilities, which act as major sources of energy dissipation beyond the bottom friction [34,35].
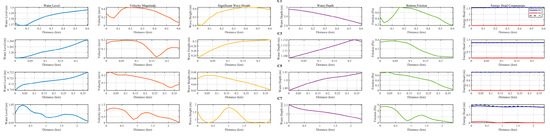
Figure 6.
Hydrodynamic characteristics across the peripheral cross-sections (C1, C3, C5, C7) during the peak storm surge.
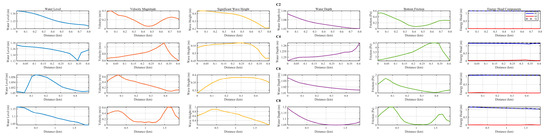
Figure 7.
Hydrodynamic characteristics across the primary confluence cross-sections (C2, C4, C6, C8) during the peak storm surge.
The hydrodynamic conditions at the key outlets elucidate the dissipation process. Section C2 (Western Transverse Outflow) was the primary energy dissipation hotspot. It carried the largest outflow, and as a direct consequence, exhibited the most intense hydrodynamic conditions observed among all cross-sections, characterized by the highest mean velocity (1.52 m/s) and the greatest mean bottom friction stress (8.45 Pa). The co-occurrence of high velocity and shallow depth in this constricted pathway created a primary zone for converting kinetic energy into heat through friction. The kinetic energy in the northward pathway (C4) was small, with a mean velocity of only 0.06 m/s. The blockage of the northern channel (C4) intensified this effect by forcing the high-energy inflow from C8 to be funneled predominantly through the narrow C2 outlet. In contrast, Section C6 (Southern Longitudinal Outflow), while a major exit, operated in a lower energy dissipation regime (mean friction 4.14 Pa).
The energy dynamics in the MCTC are governed by a two-stage process: the initial geometric constriction in the transverse waterway forces a conversion of potential energy to kinetic energy, as described by the Bernoulli principle [36]. Subsequently, this kinetic energy is efficiently dissipated at the channel junction, which acts as a energy sink due to the complex flow partitioning and the resulting intense bottom friction [37], particularly in the western outlet (C2). This finding, of energy dissipation modulating the surge peak, is consistent with studies in other shallow, complex estuaries [28,38,39]. This combined analysis of along-channel energy transformation and junction flow partitioning provides a mechanistic explanation for the non-conservative energy behavior, underscoring that the peak surge is ultimately limited by the system’s capacity to dissipate energy at critical nodes like the cross-channel junction.
4.1.2. Wave Set-Up/Set-Down
The wave-induced set-up and set-down are governed by the radiation stress theory [40]. The mean water level change due to waves can be expressed as:
where is the cross-shore component of radiation stress, is water density, is gravitational acceleration, is the total water depth (with as the still water depth and as the total mean water level from Equation (8)), and is the wave-induced adjustment to the mean water level (positive for set-up, negative for set-down).
To verify that such wave-breaking conditions occurred in the MCTC, we applied the ratio criterion from the foundational studies of wave set-down and breaking [41,42]. The onset of depth-induced wave breaking is commonly predicted when the local wave height exceeds a critical fraction of the water depth, a relationship often formalized as:
where is the breaking wave height, is the local water depth, and is the breaker index, which typically ranges from 0.6 to 0.8 for spilling breakers on mild slopes [43,44].
Applying this criterion to our model results, we find that along the eastern entrance of the transverse waterway, where water depths () range from 2.1 to 4.3 m and significant wave heights reach 1.8–2.4 m, the ratio exceeds this 0.6–0.8 threshold. Specifically, at the 3 m isobath, the modeled ratio reaches 0.73, confirming that active breaking was occurring, which is a prerequisite for the set-down mechanism.
This effect is most pronounced at the channel entrance, where wave set-down acts as a direct suppressive force, counteracting the wind-driven pile-up. This explains the observation that waves exerted an overall suppressive influence at the peak surge [45]. Therefore, waves play a dual role: wave shoaling generates set-down (modeled values of −0.2 to −0.15 m), which directly suppresses the mean water level, while post-breaking wave set-up (0.1–0.2 m) occurs in the inner harbor. Both processes combine to modulate the peak surge height.
4.1.3. Nonlinear Interactions
The numerical experiments revealed a critical nonlinearity in the storm surge dynamics: the wind-induced surge component, when simulated in isolation (Case 2), accounted for approximately 106% of the total surge simulated in the fully coupled simulation (Case 0) at its peak. This result serves as a direct quantitative measure of the integrated suppressive effect of the wave-induced processes that are absent in the wind-only scenario. The discrepancy is conclusively explained by the two key mechanisms elucidated in the previous sections: The energy dissipation via wave-enhanced bottom friction, which removed kinetic energy from the system that would otherwise contribute to water level rise. The direct water level suppression via wave set-down, which counteracted the wind-driven surge at the channel entrance.
Furthermore, the nonlinear system response was compounded by significant phase lags. The peak contributions of wave-induced and atmospheric pressure-induced surge occurred 4 and 8 hours after the total surge peak, respectively. The phase lags meant that at the time of peak total surge, the wave and pressure-induced components were not at their maxima but were instead exerting a suppressive effect, reducing the overall surge. Therefore, the 106% wind contribution is a diagnostic of the system’s nonlinearity. It represents the potential surge in a simplified, single-process model, while the fully coupled simulation reveals the lower, actual surge height due to the counteracting effects of wave-current interactions. This underscores that the peak storm surge in a complex system like the MCTC is not a simple sum of its parts, but a result of their dynamically competing and phase-shifted interactions.
4.2. The Uncertainties
The model validation is conducted only at two stations and only for the total surge, which may lead to uncertainties. Field instruments, such as tide gauges and pressure sensors, measure the total integrated water level at a single point. This measured sea surface level is the sum of all forcing components occurring simultaneously. For example, the effect of wind stress is dependent on the total water depth, which is itself a function of the tide and the other surge components. These components are not linearly summation in nature, and their individual effects cannot be disentangled from a single observational time series of the total water level. This inherent limitation of field measurement and the limited number of field stations may cause uncertainties to the model results.
The model is only validated using one typhoon, which may lead to uncertainties. It should be noted that this study focuses on a single, albeit extreme, storm event. While Typhoon Hato provides a critical case study for maximum surge potential, the dynamics may vary under different typhoon tracks and intensities.
Furthermore, the model results are subject to inherent uncertainties in the available bathymetric data and the resolution of the meteorological forcing fields. Future research should aim to apply this validated model to a broader ensemble of historical and synthetic typhoon events to develop a more comprehensive probabilistic storm surge risk assessment for the MCTC.
5. Conclusions
Using a validated three-dimensional storm surge model, this study analyzes the storm surge dynamics in the MSA during Typhoon Hato, identifying key mechanisms and factors influencing surge behavior in the MCTC. The main conclusions are as follows:
- (1)
- Wind forcing was the dominant driver of the storm surge in the MCTC during Typhoon Hato. However, its contribution was nonlinear; simulations of wind forcing in isolation yielded a peak surge equal to 106% of the total observed peak. This over-prediction is a key diagnostic, quantifying the combined suppressive effect of wave-enhanced bottom friction (a major energy sink) and wave set-down that are only captured in a fully coupled model.
- (2)
- The unique geomorphology of the MCTC acts as a natural funnel, making it a region of heightened vulnerability to storm surge disasters. This geometry induces storm surge amplification compared with the adjacent open coast, driven by a combination of geometric constriction and flow convergence. Energy transformation analysis based on the Bernoulli principle revealed distinct behaviors between the transverse and longitudinal waterways, with the constricted transverse waterway exhibiting a pronounced conversion from potential to kinetic energy, while the longitudinal waterway showed more gradual energy changes.
- (3)
- The total storm surge was governed by strong nonlinear interactions. Phase lags between the peak effects of wind, waves, and atmospheric pressure meant their contributions were not additive. Critically, wave-induced processes exerted a net suppressive effect at the time of the peak surge; this was primarily due to wave set-down generated by depth-induced breaking at the MCTC, which counteracted the wind-induced Surge. These findings highlight the critical need for fully coupled, high-resolution models to accurately predict storm surges in complex coastal environments, as they emphasize that wave-induced processes can significantly modulate the final water level in constricted estuarine channels.
These findings highlight the critical need for fully coupled, high-resolution models to accurately predict storm surges in complex coastal environments. Additionally, they emphasize the importance of site-specific, geometry-aware surge defenses in Macao, as traditional open-coast design criteria may fail to capture the intricate surge dynamics in constricted estuarine channels where wave-induced processes can significantly modulate the final water level.
Author Contributions
Conceptualization, L.L. and B.Z.; methodology, L.L. and J.G.; software, L.L. and Y.Z.; validation, L.L. and Z.H.; formal analysis, L.L. and B.Z.; investigation, L.L. and Y.X.; resources, L.L.; data curation, B.Z.; writing—original draft preparation, L.L. and B.Z.; writing—review and editing, L.L. and B.Z.; visualization, J.G.; supervision, Y.Z.; project administration, Y.X.; funding acquisition, Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Key Research and Development Program of China (2023YFC3008100), the National Natural Science Foundation of China (42476154), and the Science and Technology Bureau of Zhoushan (2023C81006, 2023C03003). This study was partially supported by UN Ocean Decade Project No. 78.7. Building Coastal Resilience Against Climate Change and the International Space Science Institute (ISSI) in Bern through ISSI International Team project #23–598. Data and samples were partially collected onboard of R/V Ke Xue San (Bo Hai Ke, Chuang Xin Yi), implementing the open research cruise NORC2023−03+NORC2023−302 supported by the NSFC Shiptime Sharing Project (42249903).
Data Availability Statement
The original contributions presented in this study are included in the article material. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Resio, D.T.; Westerink, J.J. Modeling the physics of storm surges. Phys. Today 2008, 61, 33–38. [Google Scholar] [CrossRef]
- Dan, M.; Yueming, L.; Zhihua, W.; Xiaoliang, L.; Junyao, Z.; Ku, G. Decreasing Vulnerability of Storm Surge Disasters in Coastal Cities of China over the Past 30 Years. J. Mar. Sci. Eng. 2023, 11, 128. [Google Scholar] [CrossRef]
- Irish, J.L.; Resio, D.T. A hydrodynamics-based surge scale for hurricanes. Ocean Eng. 2010, 37, 69–81. [Google Scholar] [CrossRef]
- Han, R.; Yin, K.; Dai, X.; Li, H.; Zhou, S. Economic Footprint Assessment of Storm Surge Disasters in China Based on Disastrously—Extended Input-Output Analysis. Front. Mar. Sci. 2025, 12, 1673928. [Google Scholar] [CrossRef]
- Yang, L.; Scheffran, J.; Qin, H.; You, Q. Climate-Related Flood Risks and Urban Responses in the Pearl River Delta, China. Reg. Environ. Change 2015, 15, 379–391. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Wang, Z.; Yang, X.; Zeng, X.; Meng, D. Comprehensive Assessment of Vulnerability to Storm Surges in Coastal China: Towards a Prefecture-Level Cities Perspective. Remote Sens. 2023, 15, 4828. [Google Scholar] [CrossRef]
- Wang, G. Study on the Characteristics of Tidal Current and Mass Transport in the Pearl River Estuary. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- He, L.; Li, G.; Li, K.; Zhang, Y.; Guo, T. Profit and loss analysis of engineering adaptation to storm surge disaster in the Pearl River Delta. Dili Yanjiu 2019, 38, 427–436. [Google Scholar] [CrossRef]
- Needham, H.F.; Keim, B.D.; Sathiaraj, D. A review of tropical cyclone-generated storm surges: Global data sources, observations, and impacts. Rev. Geophys. 2015, 53, 545–591. [Google Scholar] [CrossRef]
- Chen, W. Analysis of the impact of severe typhoons on water enhancement in the Pearl River Estuary-Hengmen and its upstream from 2008 to 2018. Guangdong Shuili Shuidian 2019, 5, 28–31. [Google Scholar]
- Guo, J.; Huang, S.; Ge, M.; Lee, J.H.W. A Comprehensive Investigation of Storm Surge-Induced Urban Flooding in Macao during Typhoon Hato in 2017. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2394641. [Google Scholar] [CrossRef]
- Du, M.; Hou, Y.; Hu, P.; Wang, K. Effects of Typhoon Paths on Storm Surge and Coastal Inundation in the Pearl River Estuary, China. Remote Sens. 2020, 12, 1851. [Google Scholar] [CrossRef]
- Hu, S.; Liu, B.; Qiu, J.; Zeng, H.; Zhang, M. Study on the nonlinear superposition effect of storm surge in the Pearl River Estuary. Haiyang Kexue 2023, 47, 1–12. [Google Scholar]
- Du, M.; Hou, Y.; Guo, Y.; Wang, K. Numerical simulation and risk analysis of coastal inundation in land reclamation areas: A case study of the Pearl River Estuary. J. Ocean Univ. China 2020, 19, 1221–1234. [Google Scholar] [CrossRef]
- Yang, J.; Li, L.; Zhao, K.F.; Liu, Z.Z.; Chan, P.W. A comparative study of Typhoon Hato (2017) and Typhoon Mangkhut (2018)—Their impacts on coastal inundation in Macau. J. Geophys. Res. Oceans 2019, 124, 9590–9619. [Google Scholar] [CrossRef]
- Li, L.; Yang, J.; Lin, C.Y.; Chua, C.T.; Wang, Y.H.; Zhao, K.F.; Wu, Y.T.; Liu, Z.Z.; Song, Y.S.; Wang, T.P.; et al. Field survey of Typhoon Hato (2017) and a comparison with storm surge modeling in Macau. Nat. Hazards Earth Syst. Sci. 2018, 18, 3167–3178. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Shi, X.; Chen, B.; Qiu, J.; Kang, X.; Ye, T. Simulation of inundation caused by typhoon-induced probable maximum storm surge based on numerical modeling and observational data. Stoch. Environ. Res. Risk Assess. 2021, 35, 2273–2286. [Google Scholar] [CrossRef]
- Ying, X.; Zheng, Z.; Ni, J.; Li, W.; Wang, C. Numerical simulation study on the dynamic impact of typhoon “Mangkhut” storm surge on the sea area near the Hong Kong-Zhuhai-Macao bridge. Phys. Chem. Earth 2022, 128, 103282. [Google Scholar] [CrossRef]
- Yue, X.; Li, C.; Miao, Q.; Liu, Y. Effects of coastal reclamation on the storm surge in the Bohai Bay. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012053. [Google Scholar] [CrossRef]
- Valdez, J.J.; Shibayama, T.; Takabatake, T.; Esteban, M. Simulated flood forces on a building due to the storm surge by Typhoon Haiyan. Coast. Eng. J. 2023, 65, 21–38. [Google Scholar] [CrossRef]
- Makris, C.; Mallios, Z.; Androulidakis, Y.; Krestenitis, Y. CoastFLOOD: A high-resolution model for the simulation of coastal inundation due to storm surges. Hydrology 2023, 10, 103. [Google Scholar] [CrossRef]
- Hutchings, G.; Sansó, B.; Gattiker, J.; Francom, D.; Higdon, D. Comparing emulation methods for a high-resolution storm surge model. Environmetrics 2023, 34, e2796. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Zheng, P.; Li, M.; Wang, C.; Wolf, J.; Chen, X.; De Dominicis, M.; Yao, P.; Hu, Z. Tide-Surge Interaction in the Pearl River Estuary: A Case Study of Typhoon Hato. Front. Mar. Sci. 2020, 7, 236. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Song, Z.; Chen, P.; Liu, F.; Zhang, D. A numerical study of storm surge behavior in and around Lingdingyang Bay, Pearl River Estuary, China. Nat. Hazards 2022, 111, 1507–1532. [Google Scholar] [CrossRef]
- Murphy, A.H. Climatology, Persistence, and Their Linear Combination as Standards of Reference in Skill Scores. Weather Forecast. 1992, 7, 692–698. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; He, Z.; Yu, Z.; Ren, Y. Investigation of storm tides induced by super typhoon in macro-tidal Hangzhou Bay. Front. Mar. Sci. 2022, 9, 890285. [Google Scholar] [CrossRef]
- As-Salek, J.A. Coastal trapping and funneling effects on storm surges in the Meghna Estuary in relation to cyclones hitting Noakhali–Cox’s Bazar coast of Bangladesh. J. Phys. Oceanogr. 1998, 28, 227–249. [Google Scholar] [CrossRef]
- Deb, M.; Benedict, J.J.; Sun, N.; Yang, Z.; Hetland, R.D.; Judi, D.R.; Wang, T. Estuarine hurricane wind can intensify surge-dominated extreme water level in shallow and converging coastal systems. Nat. Hazards Earth Syst. Sci. 2024, 24, 2461–2479. [Google Scholar] [CrossRef]
- Dykstra, S.L.; Talke, S.A.; Yankovsky, A.E.; Torres, R.; Viparelli, E. Reflection of storm surge and tides in convergent estuaries with dams, the case of Charleston, USA. J. Geophys. Res. Oceans 2024, 129, e2023JC020498. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Macmillan: New York, NY, USA, 1966. [Google Scholar]
- Mokrzycka-Olek, A.; Kałuża, T.; Hämmerling, M. Impact of Channel Confluence Geometry on Water Velocity Distributions in Channel Junctions with Inflows at Angles α = 45° and α = 60°. Water 2025, 17, 2890. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Shaheed, A.M. Numerical Simulation of Turbulent Flow in River Bends and Confluences Using the k-ω SST Turbulence Model and Comparison with Standard and Realizable k-ε Models. Hydrology 2025, 12, 145. [Google Scholar] [CrossRef]
- Guo, W.; Wang, X.H.; Ding, P.; Ge, J.; Song, D. A system shift in tidal choking due to the construction of Yangshan Harbour, Shanghai, China. Estuar. Coast. Shelf Sci. 2018, 206, 49–60. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave-current interaction in vertically sheared flows. Coastal Eng. 1993, 21, 41–99. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, T.; Zhang, S.; Wang, H. Effect of nonlinear tide–surge interaction in the Pearl River Estuary during Typhoon Nida (2016). Ocean Sci. 2025, 21, 1891–1908. [Google Scholar] [CrossRef]
- Nordio, G.; Fagherazzi, S. Storm Surge and Tidal Dissipation in Deltaic Wetlands: The Role of Vegetation and Bathymetry in South Louisiana. J. Geophys. Res. Oceans 2022, 127, e2021JC017655. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. Oceanogr. Abstr. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Bowen, A.J.; Inman, D.L.; Simmons, V.P. Wave ‘set-down’ and set-up. J. Geophys. Res. 1968, 73, 2569–2577. [Google Scholar] [CrossRef]
- Hsu, T.-W.; Hsu, J.R.-C.; Weng, W.-K.; Wang, S.-K.; Ou, S.-H. Wave setup and setdown generated by obliquely incident waves. Coastal Eng. 2006, 53, 865–877. [Google Scholar] [CrossRef]
- Goda, Y. Reanalysis of regular and random breaking wave statistics. J. Coast. Eng. 2010, 52, 71–106. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due to Breaking of Random Waves. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; American Society of Civil Engineers: Reston, VA, USA, 1978; pp. 569–587. [Google Scholar] [CrossRef]
- Pedreros, R.; Idier, D.; Muller, H.; Lecacheux, S.; Paris, F.; Yates-Michelin, M.; Dumas, F.; Pineau-Guillou, L.; Senechal, N. Relative contribution of wave setup to the storm surge: Observations and modeling based analysis in open and protected environments (Truc Vert beach and Tubuai island). J. Coast. Res. 2018, 85, 1046–1050. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).