An Affordable Wave Glider-Based Magnetometry System for Marine Magnetic Measurement
Abstract
1. Introduction
2. Equipment and Principles
2.1. Wave Glider Platform Overview
2.2. GNSS Module Integration
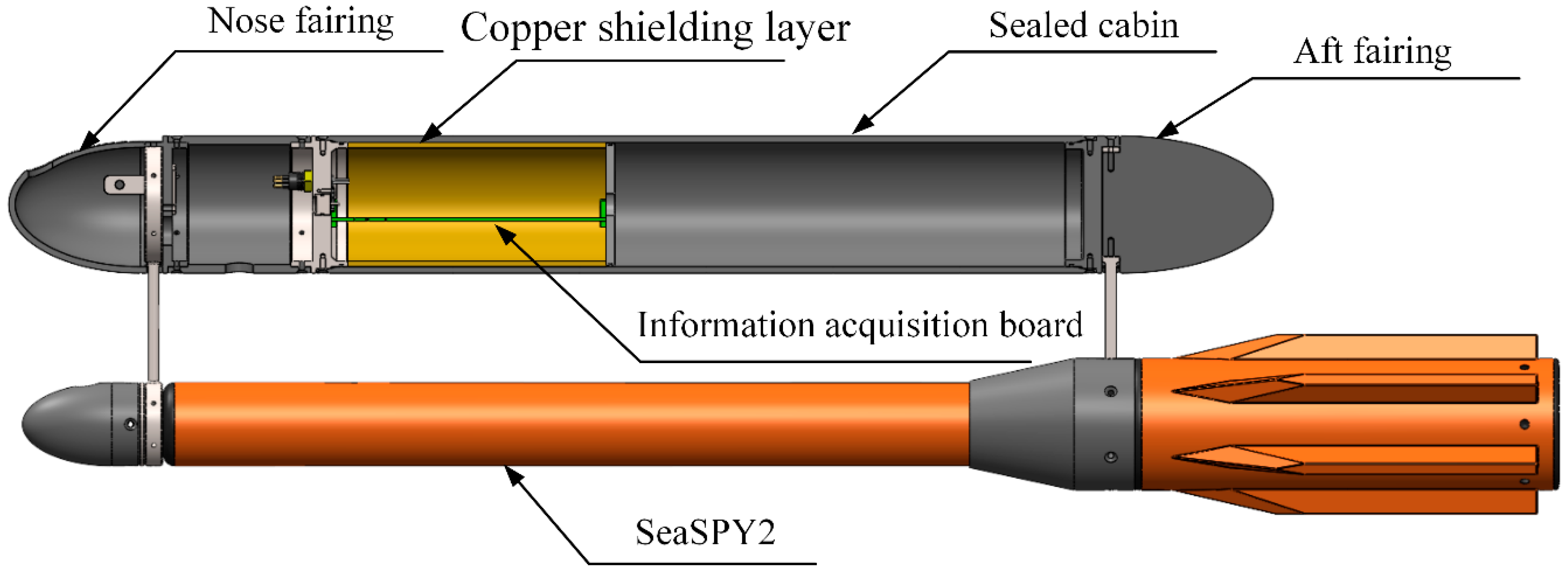
2.3. SeaSPY2 Magnetometer Towed Body
3. Engineering Design of a Wave Glider-Based Magnetic Survey System
3.1. Modification of the Magnetometer Towed Body
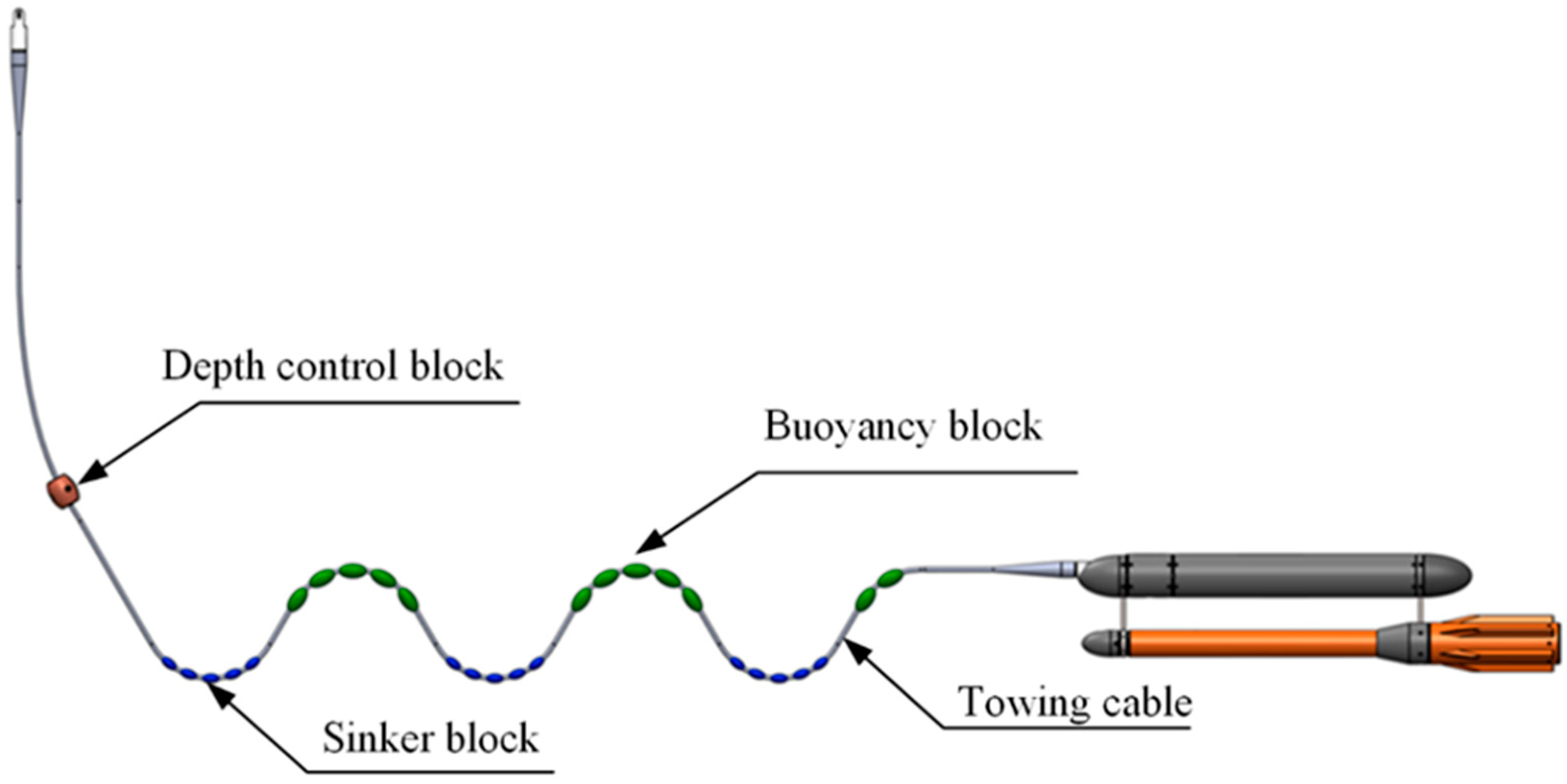
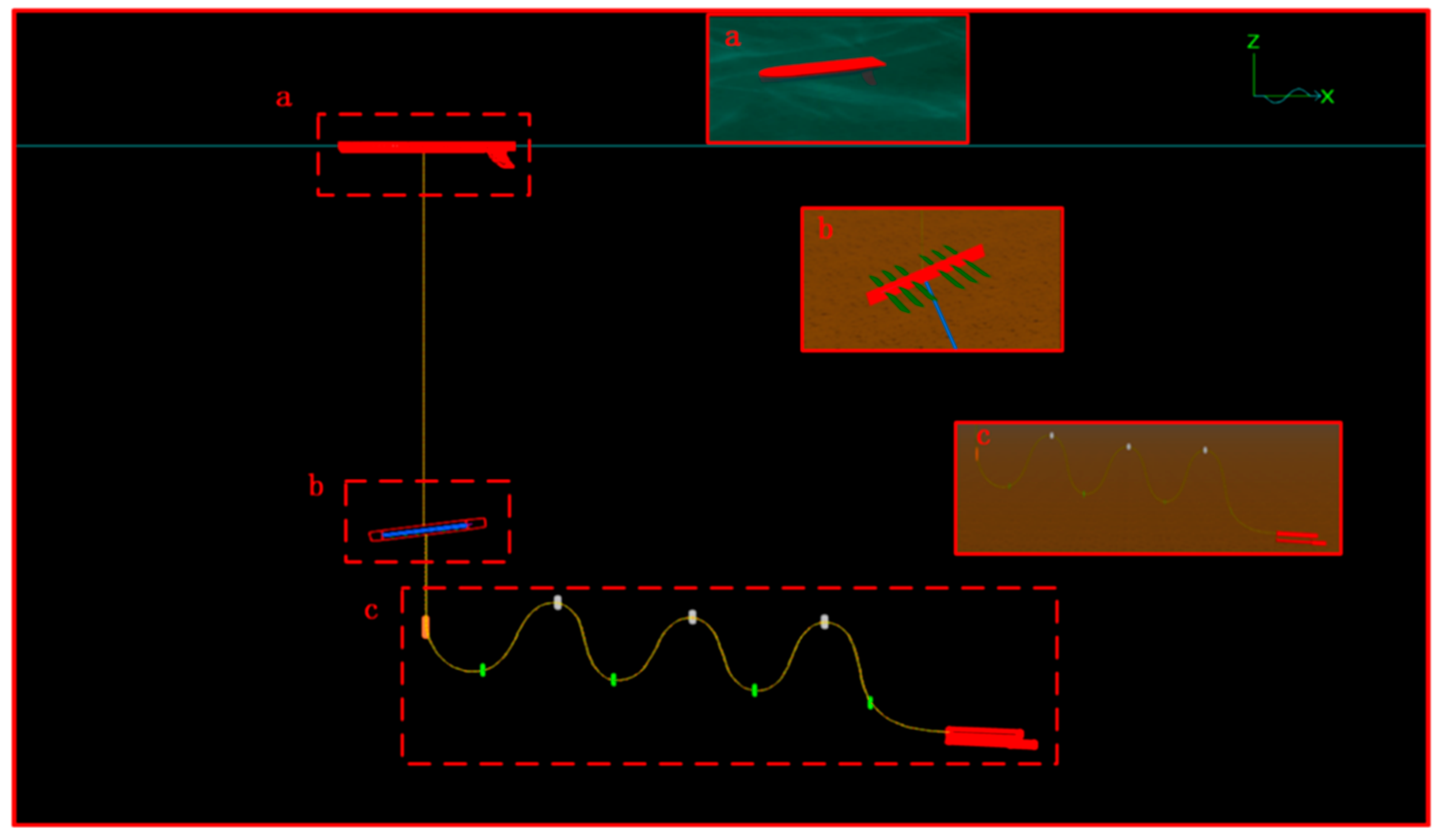
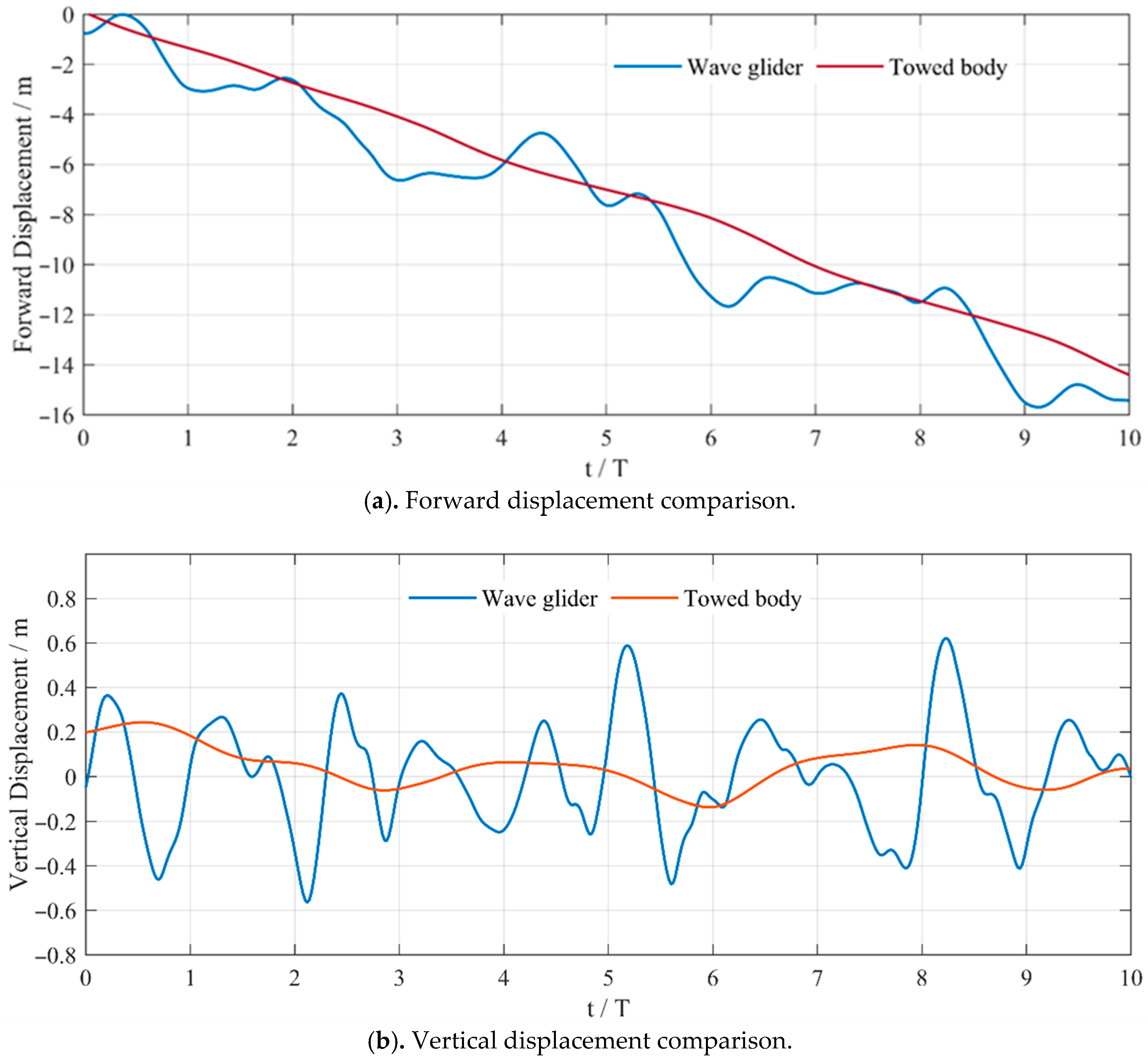
3.2. Towing Cable Shock Absorption and Disturbance Mitigation Design
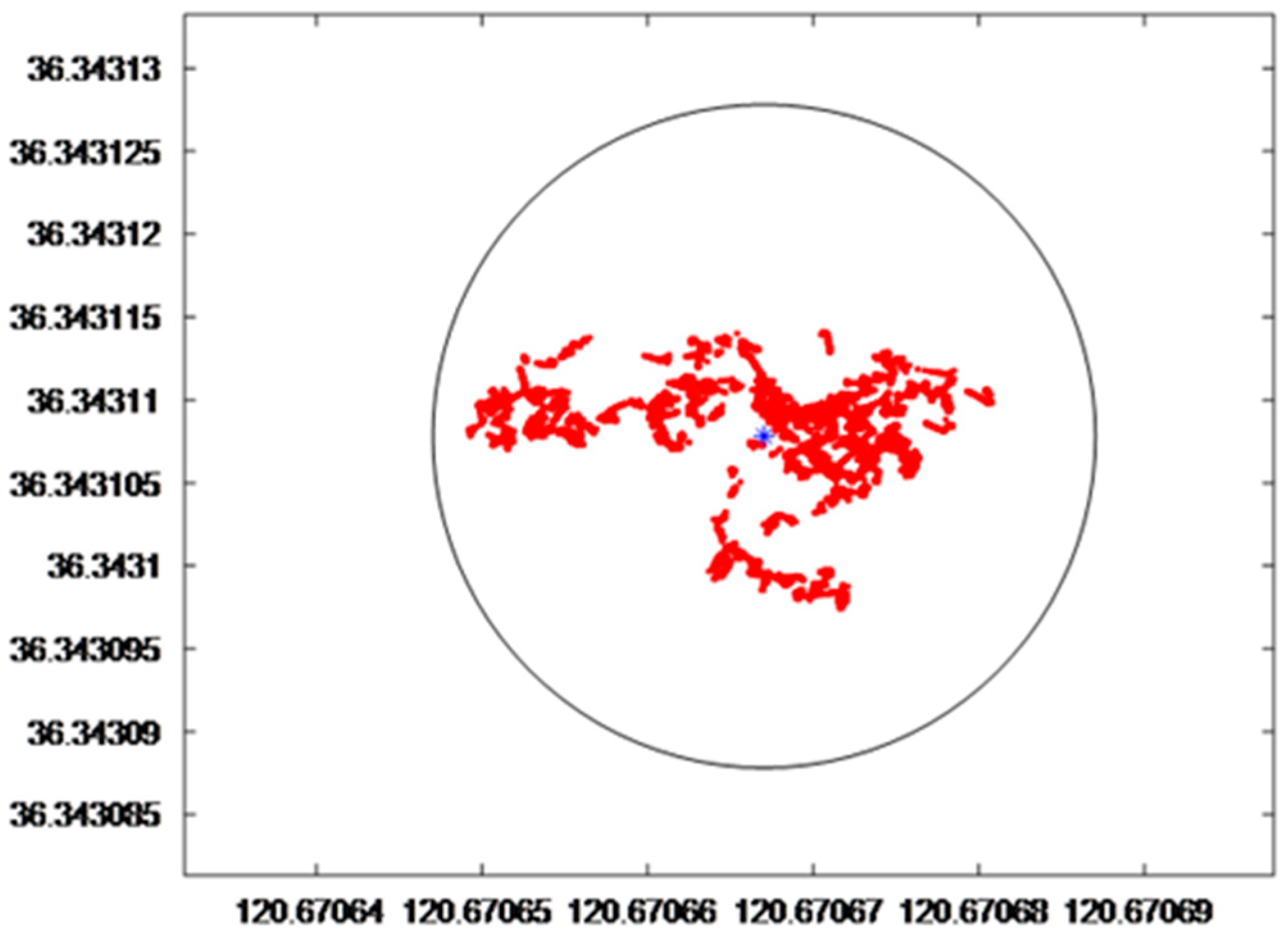
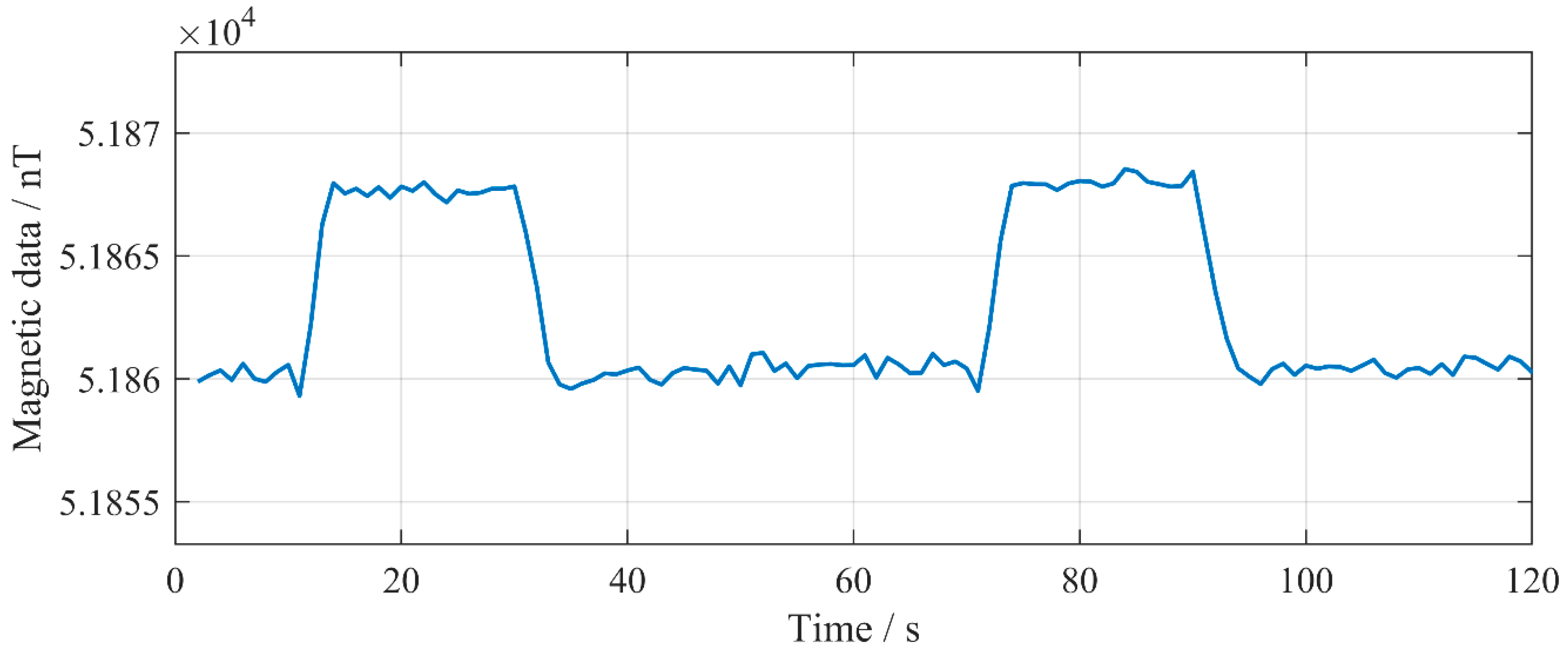
3.3. Instrument Self-Noise
4. Results and Discussions
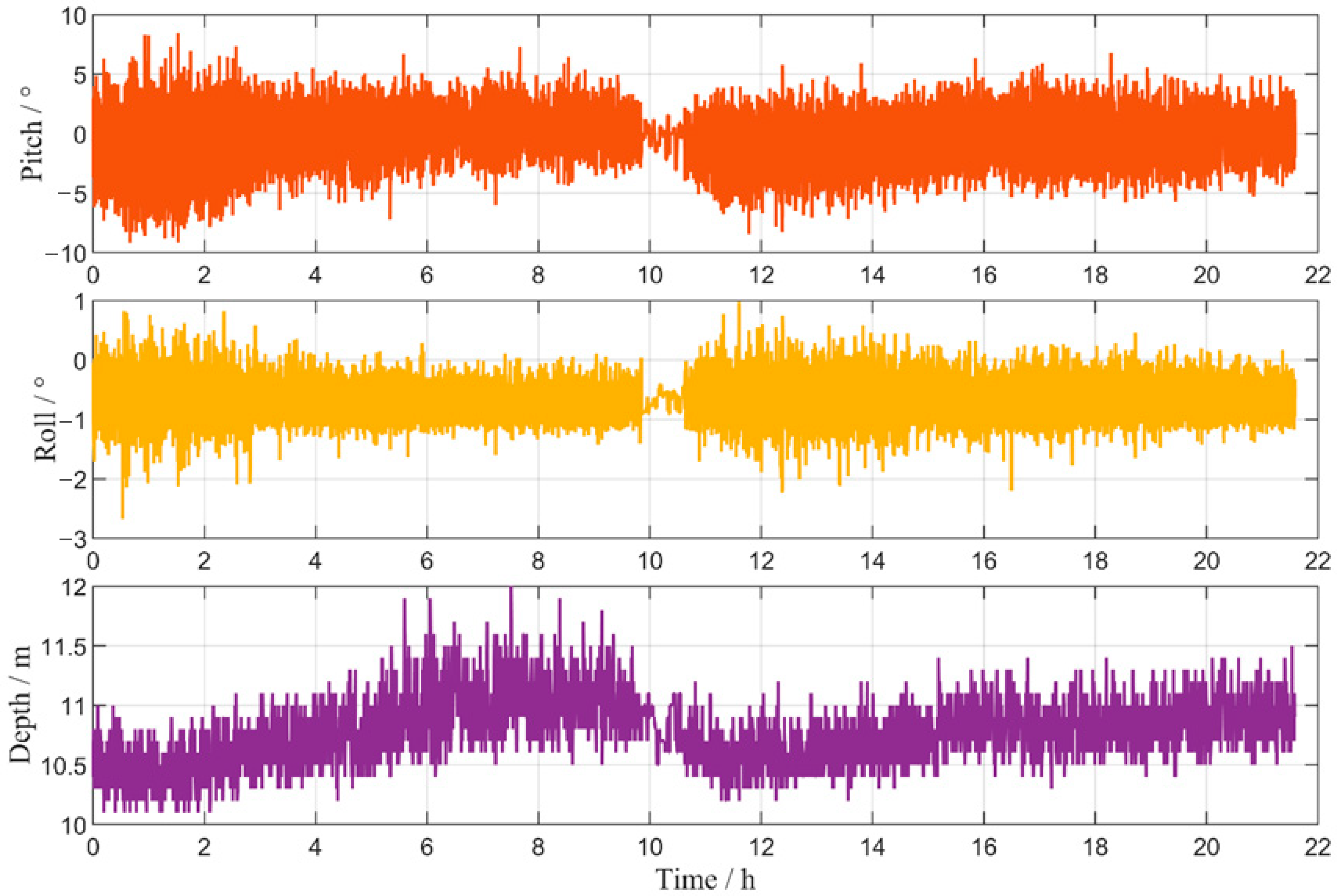
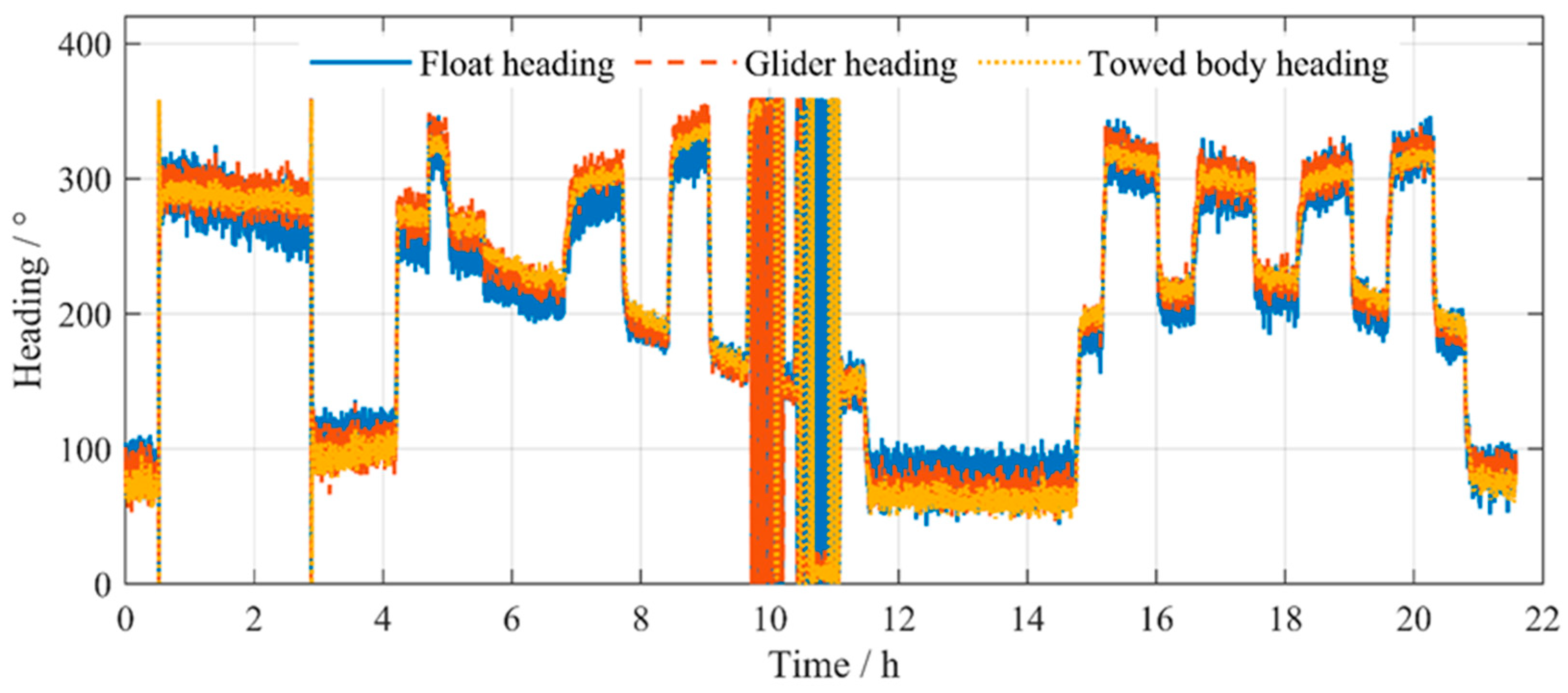
4.1. Sea Trial Overview
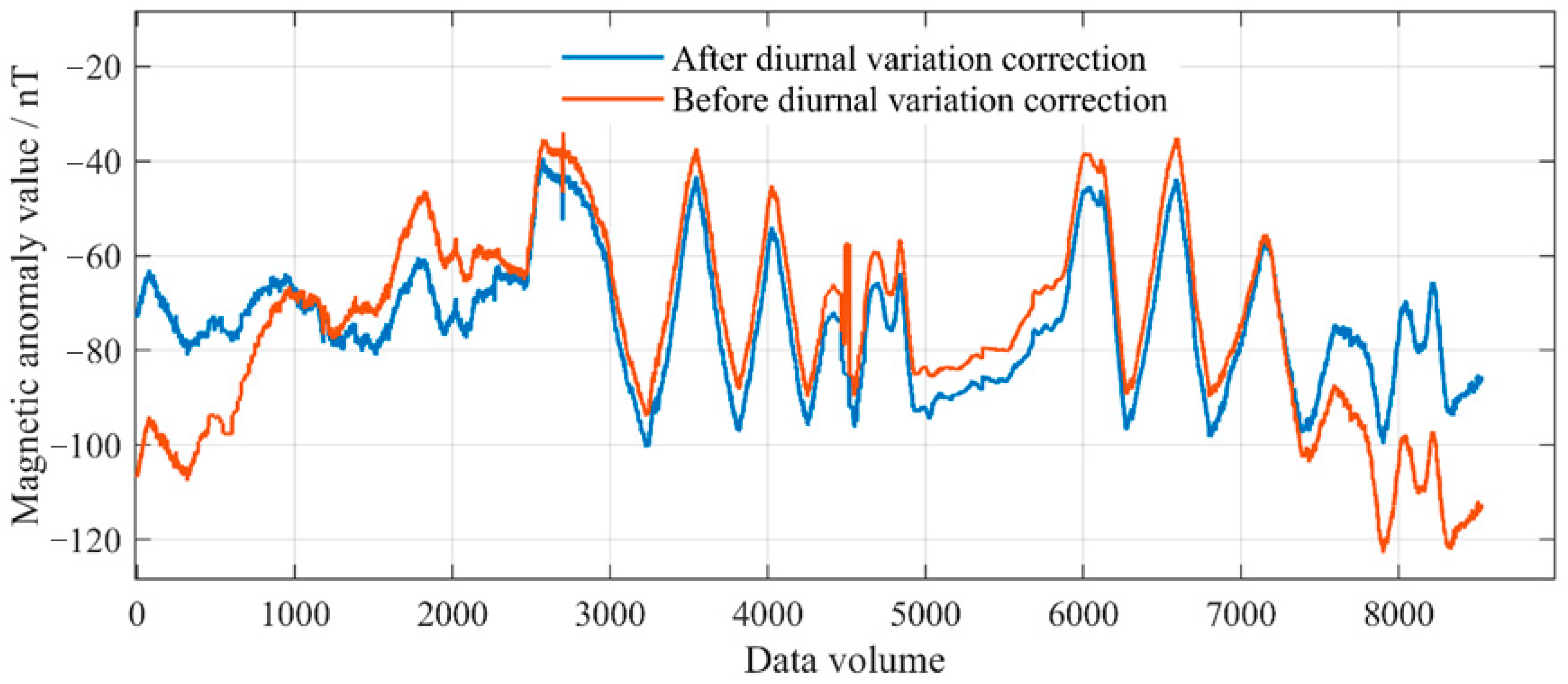
4.2. Diurnal Variation Correction and IGRF Removal
4.3. Dynamic Noise Assessment
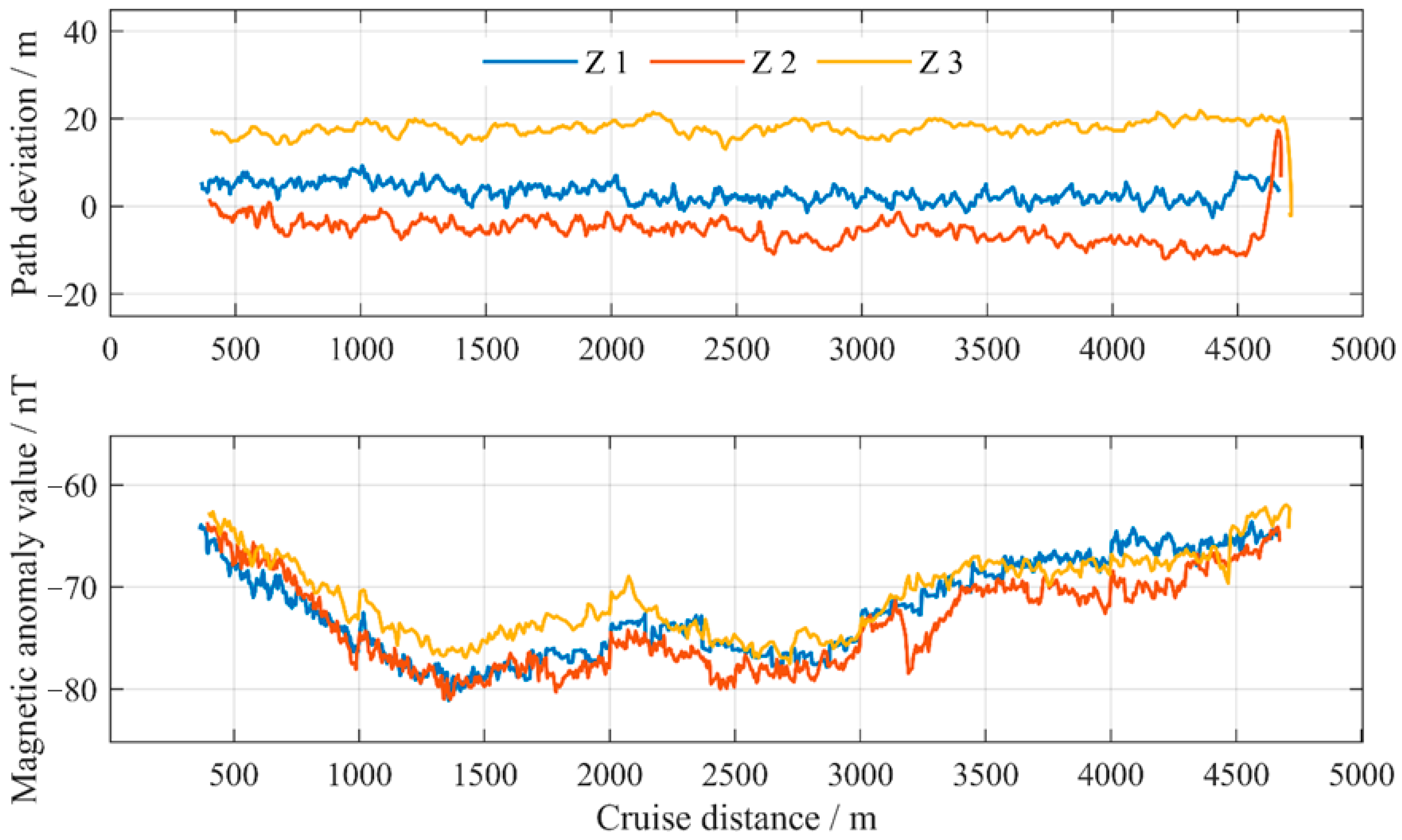
4.4. Repeat Line Internal Consistency Accuracy Calculation
4.5. Crossing Point Internal Consistency Accuracy Calculation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Engels, M.; Barckhausen, U.; Gee, J.S. A New Towed Marine Vector Magnetometer: Methods and Results from a Central Pacific Cruise. Geophys. J. Int. 2008, 172, 115–129. [Google Scholar] [CrossRef][Green Version]
- Banerjee, B.; Rao, P.B.V.S.; Gupta, G.; Joseph, E.J.; Singh, B.P. Results from a Magnetic Survey and Geomagnetic Depth Sounding in the Post-Eruption Phase of the Barren Island Volcano. Earth Planets Space 1998, 50, 327–338. [Google Scholar] [CrossRef]
- De Ritis, R.; Cocchi, L.; Passaro, S.; Chiappini, M. Giant Landslide, Hidden Caldera Structure, Magnetic Anomalies and Tectonics in Southern Tyrrhenian Sea (Italy). Geomorphology 2024, 466, 109445. [Google Scholar] [CrossRef]
- Uhm, J.; Jeong, S.; Bang, M.; Yi, M.-J. Joint Interpretation of Aero-Radiometric and Magnetic Survey Data for Ultramafic Rocks in the Yugu Area, South Korea. J. Appl. Geophys. 2025, 241, 105843. [Google Scholar] [CrossRef]
- Koyama, T.; Kanda, W.; Utsugi, M.; Kaneko, T.; Ohminato, T.; Watanabe, A.; Tsuji, H.; Nishimoto, T.; Kuvshinov, A.; Honda, Y. Aeromagnetic Survey in Kusatsu-Shirane Volcano, Central Japan, by Using an Unmanned Helicopter. Earth Planets Space 2021, 73, 139. [Google Scholar] [CrossRef]
- Shahsavani, H.; Smith, R.S. Aeromagnetic Gradiometry with UAV, a Case Study on Small Iron Ore Deposit. Drone Syst. Appl. 2024, 12, 1–9. [Google Scholar] [CrossRef]
- Petersen, J.T.; Døssing, A. Addressing Magnetometer Inconsistencies in Drone-Borne Total Field Gradiometer Surveys: Case Study from Rånbogen, Arctic Norway. Geophys. J. Int. 2024, 239, 1617–1628. [Google Scholar] [CrossRef]
- Lipovský, P.; Draganová, K.; Novotňák, J.; Szőke, Z.; Fiľko, M. Indoor Mapping of Magnetic Fields Using UAV Equipped with Fluxgate Magnetometer. Sensors 2021, 21, 4191. [Google Scholar] [CrossRef] [PubMed]
- Bronner, A.; Munschy, M.; Sauter, D.; Carlut, J.; Searle, R.; Maineult, A. Deep-Tow 3C Magnetic Measurement: Solutions for Calibration and Interpretation. Geophysics 2013, 78, J15–J23. [Google Scholar] [CrossRef]
- Oehler, J.-F.; Schifano, V.; Marquis, G.; Reiller, H.; Lucas, S.; Bougeault, C. Processing of Unmanned Underwater Vehicle Vector Magnetometer Data. Geophys. Prospect. 2024, 72, 2902–2918. [Google Scholar] [CrossRef]
- Teixeira, F.C.; Quintas, J.; Pascoal, A. Experimental Validation of Magnetic Navigation of Marine Robotic vehicle. IFAC-PapersOnLine 2016, 49, 273–278. [Google Scholar] [CrossRef]
- Jung, J.; Park, J.; Choi, J.; Choi, H.-T. Autonomous Mapping of Underwater Magnetic Fields Using a Surface Vehicle. IEEE Access 2018, 6, 62552–62563. [Google Scholar] [CrossRef]
- Choi, S.; Kim, M.; Park, Y.; Moon, G.; Choe, H. Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys. Sensors 2025, 25, 4511. [Google Scholar] [CrossRef] [PubMed]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The Thirteenth Generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Laiping, R.; Gengfeng, W.; Zhe, Z.; Yueyuan, M.; Zhongxiao, G. Test and Analysis of Marine Magnetometer Performance. Hydrogr. Surv. Charting 2016, 36, 38–42. [Google Scholar]
- Jiangang, L.; Haibing, L.; Jingxiao, L.; Haihu, L.; Cheng, L. FU Bibo Accuracy evaluation of marine magnetic measurement based on small unmanned ship. Hydrogr. Surv. Charting 2022, 42, 25–29. [Google Scholar]













| Parameters | Scale | Unit |
|---|---|---|
| Mass of the surface float | 72 | kg |
| Mass of the submerged glider | 80 | kg |
| Total mass of the wave glider | 152 | kg |
| Float dimension | 2.88 × 0.65 × 0.23 | m |
| Submerged glider dimension | 2.2 × 1.4 × 0.215 | m |
| Float maximum displacement | 270 | kg |
| Submerged glider displacement | 20 | kg |
| Length of the umbilical | 8 | m |
| Absolute Accuracy | 0.1 nT |
|---|---|
| Sensor sensitivity | 0.01 nT (standard), 0.02 nT (optional) |
| Counter sensitivity | 0.001 nT |
| Resolution | 0.001 nT |
| Range | 18,000 nT–120,000 nT |
| Gradient Tolerance | Over 10,000 nT/m |
| Sampling range | 4 Hz–0.1 Hz |
| Communications | RS-232, 9600 bps |
| Power supply | 24 VDC |
| Number | Z1 | Z2 | Z3 | Number | Z1 | Z2 | Z3 |
|---|---|---|---|---|---|---|---|
| 1 | −54.4 | −58.24 | −54.94 | 24 | −72.34 | −73.82 | −75.72 |
| 2 | −56.17 | −58.4 | −55.9 | 25 | −73.74 | −74.45 | −75.54 |
| 3 | −56.09 | −59.04 | −57.53 | 26 | −74.57 | −74.21 | −76.3 |
| 4 | −57.62 | −61.13 | −61.04 | 27 | −72.64 | −74.23 | −76.55 |
| 5 | −59.47 | −63.1 | −60.85 | 28 | −73.35 | −73.13 | −74.86 |
| 6 | −60.39 | −63.94 | −62.15 | 29 | −72.12 | −73.27 | −73.91 |
| 7 | −62.76 | −65.51 | −64.33 | 30 | −71.51 | −72.22 | −73.5 |
| 8 | −64.15 | −67.63 | −67.17 | 31 | −69.95 | −71.57 | −77.89 |
| 9 | −66.52 | −69.7 | −69.43 | 32 | −68.72 | −70.59 | −74 |
| 10 | −69.55 | −72.25 | −72.11 | 33 | −67.98 | −70.02 | −70.29 |
| 11 | −69.79 | −72.48 | −73.95 | 34 | −67.38 | −68.75 | −69.85 |
| 12 | −72.07 | −73.68 | −74.26 | 35 | −67.74 | −66.89 | −70.05 |
| 13 | −71.75 | −74.94 | −74.6 | 36 | −67.93 | −66.96 | −71.18 |
| 14 | −70.76 | −74.25 | −75.24 | 37 | −68.52 | −67.48 | −70.09 |
| 15 | −69.71 | −72.69 | −72.61 | 38 | −67.61 | −66.52 | −71.4 |
| 16 | −69.05 | −72.37 | −72.21 | 39 | −68.7 | −67.77 | −71.02 |
| 17 | −68.54 | −71.99 | −75.29 | 40 | −69.28 | −66.89 | −72.66 |
| 18 | −68.76 | −71.75 | −73.29 | 41 | −69.79 | −67.85 | −72.1 |
| 19 | −68.15 | −71.39 | −73.41 | 42 | −68.2 | −67.95 | −69.77 |
| 20 | −68.29 | −71.22 | −73.13 | 43 | −68.06 | −67.01 | −68.76 |
| 21 | −70.77 | −71.51 | −73.06 | 44 | −66.22 | −67.3 | −69.24 |
| 22 | −71.57 | −72.33 | −74.1 | 45 | −64.42 | −66.41 | −68.03 |
| 23 | −73.23 | −73.99 | −74.99 |
| Line | L1 | L3 | L5 | L7 | L9 | L11 | L13 | L15 | L7 |
|---|---|---|---|---|---|---|---|---|---|
| Z1 | −3.03 | −2.51 | −1.85 | −3.84 | −2.87 | −3.72 | −7.47 | −3.39 | |
| Z2 | −7.18 | −1.59 | −2.28 | −4.38 | −2.93 | −1.38 | −3.12 | −1.78 | 0.48 |
| Z3 | −3.38 | −1.57 | −1.54 | −2.24 | −1.71 | −0.63 | −3.27 | −2.95 | |
| Line | L2 | L4 | L6 | L8 | L10 | L12 | L14 | L16 | L18 |
| Z1 | −0.74 | −2.03 | −1.36 | −0.99 | −5 | −2.27 | −1.97 | ||
| Z2 | −3.68 | −3.7 | −1.53 | 1.16 | −0.21 | 1.66 | 1.2 | 0.92 | |
| Z3 | 1.38 | −1.08 | −1.23 | 0.37 | 0.82 | −0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Li, C.; Sun, X. An Affordable Wave Glider-Based Magnetometry System for Marine Magnetic Measurement. J. Mar. Sci. Eng. 2025, 13, 2089. https://doi.org/10.3390/jmse13112089
Ma S, Li C, Sun X. An Affordable Wave Glider-Based Magnetometry System for Marine Magnetic Measurement. Journal of Marine Science and Engineering. 2025; 13(11):2089. https://doi.org/10.3390/jmse13112089
Chicago/Turabian StyleMa, Siyuan, Can Li, and Xiujun Sun. 2025. "An Affordable Wave Glider-Based Magnetometry System for Marine Magnetic Measurement" Journal of Marine Science and Engineering 13, no. 11: 2089. https://doi.org/10.3390/jmse13112089
APA StyleMa, S., Li, C., & Sun, X. (2025). An Affordable Wave Glider-Based Magnetometry System for Marine Magnetic Measurement. Journal of Marine Science and Engineering, 13(11), 2089. https://doi.org/10.3390/jmse13112089






