Numerical Investigation of Hydrodynamic Characteristics of Circular Cylinder with Surface Roughness at Subcritical Reynolds Number
Abstract
1. Introduction
2. Control Equations and Numerical Model
2.1. Control Equations
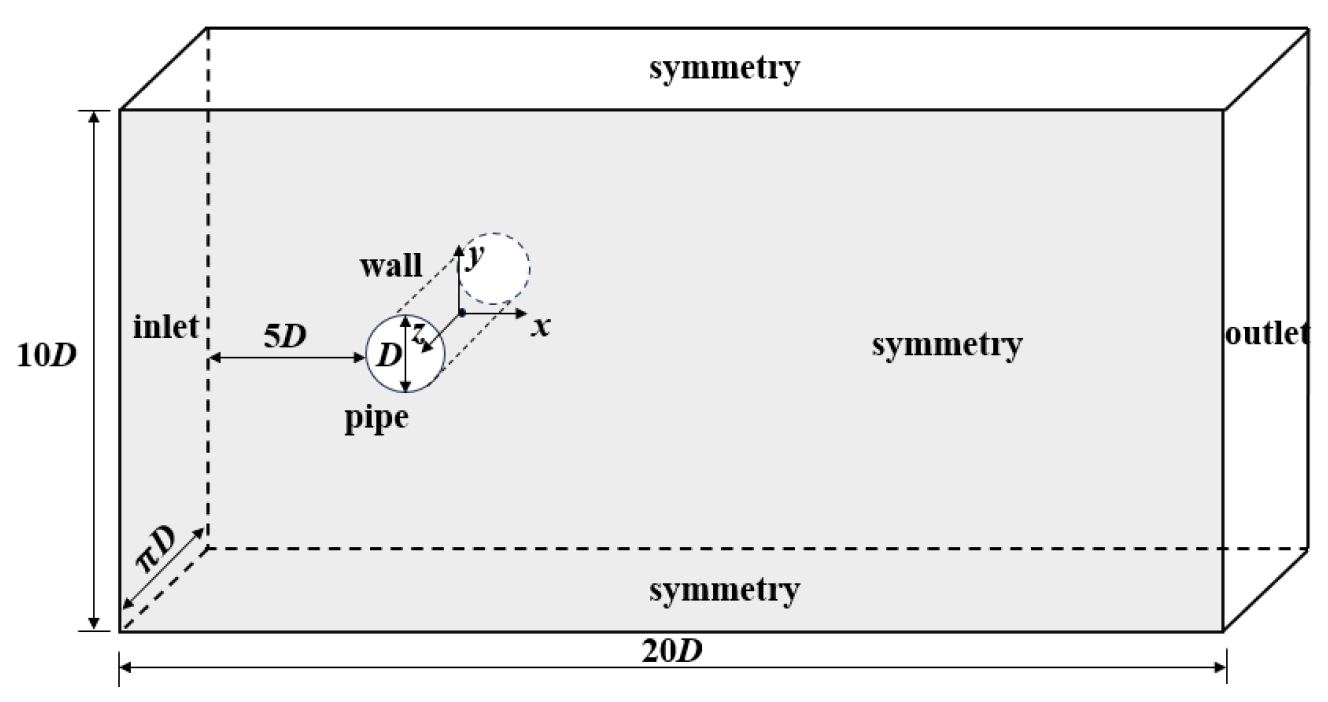
2.2. Computational Domain and Definite Solution Conditions
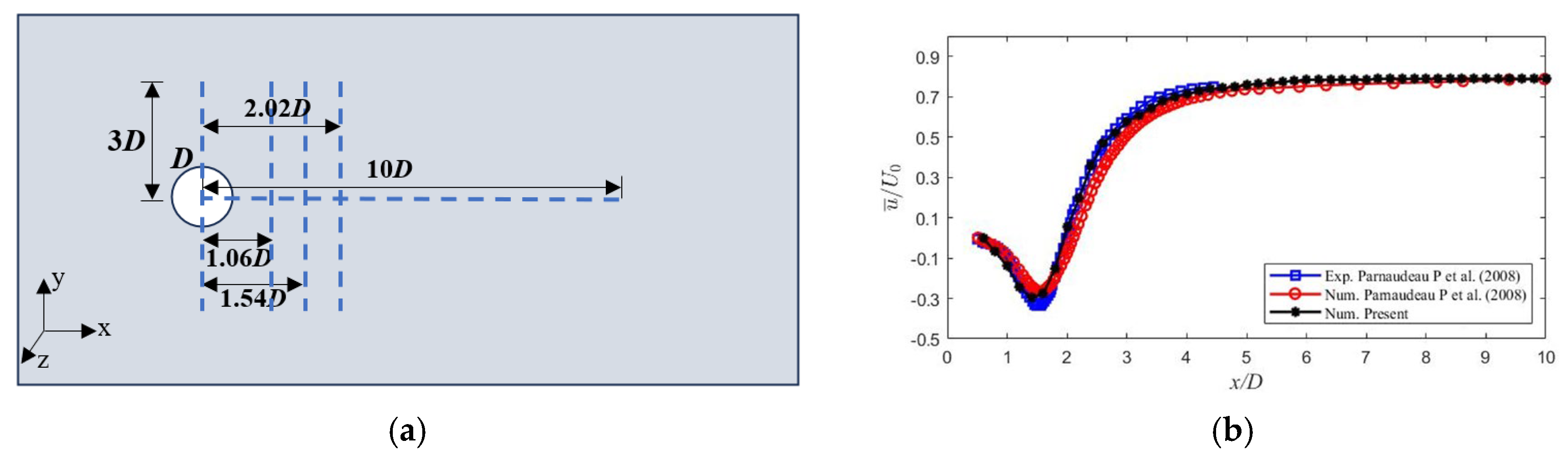
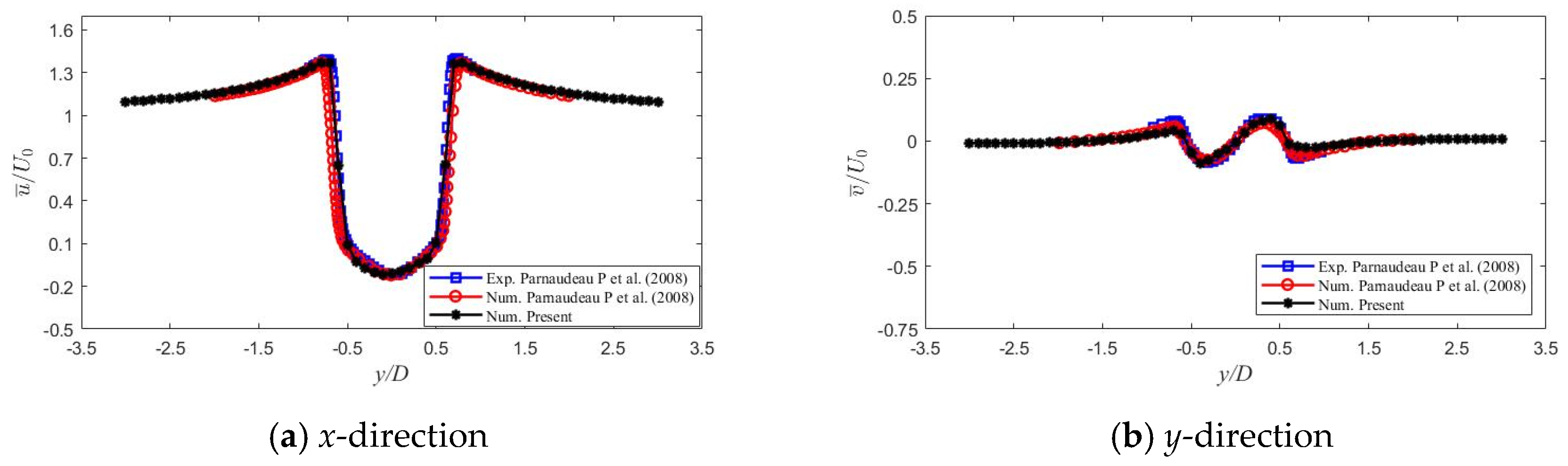
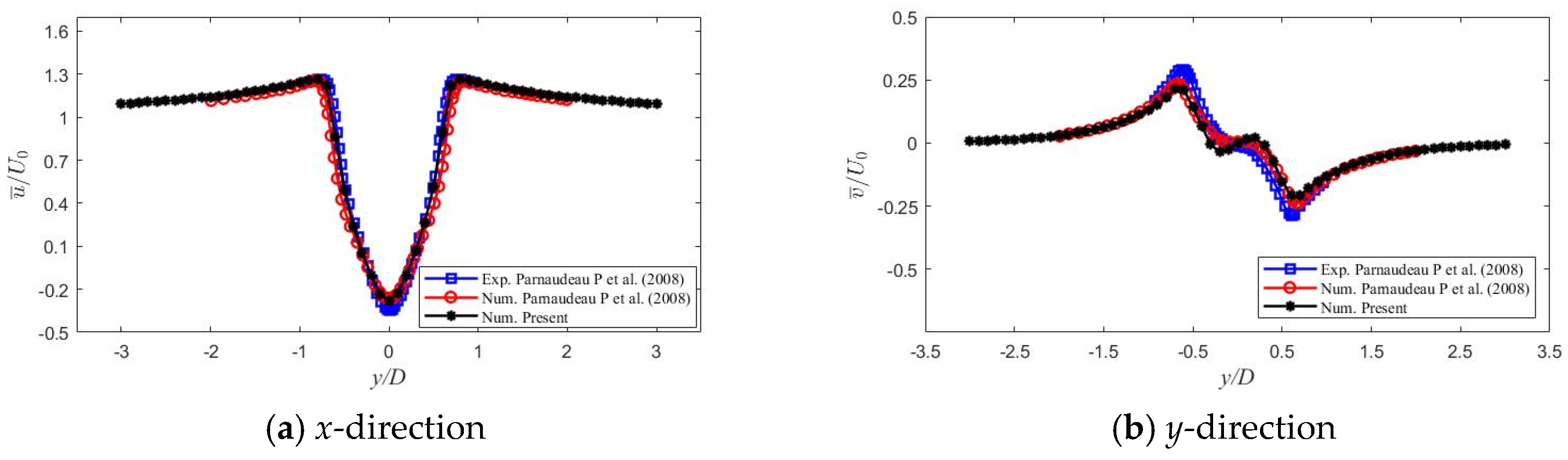
2.3. Verification of Convergence and Accuracy of the Numerical Model
3. Results and Discussion
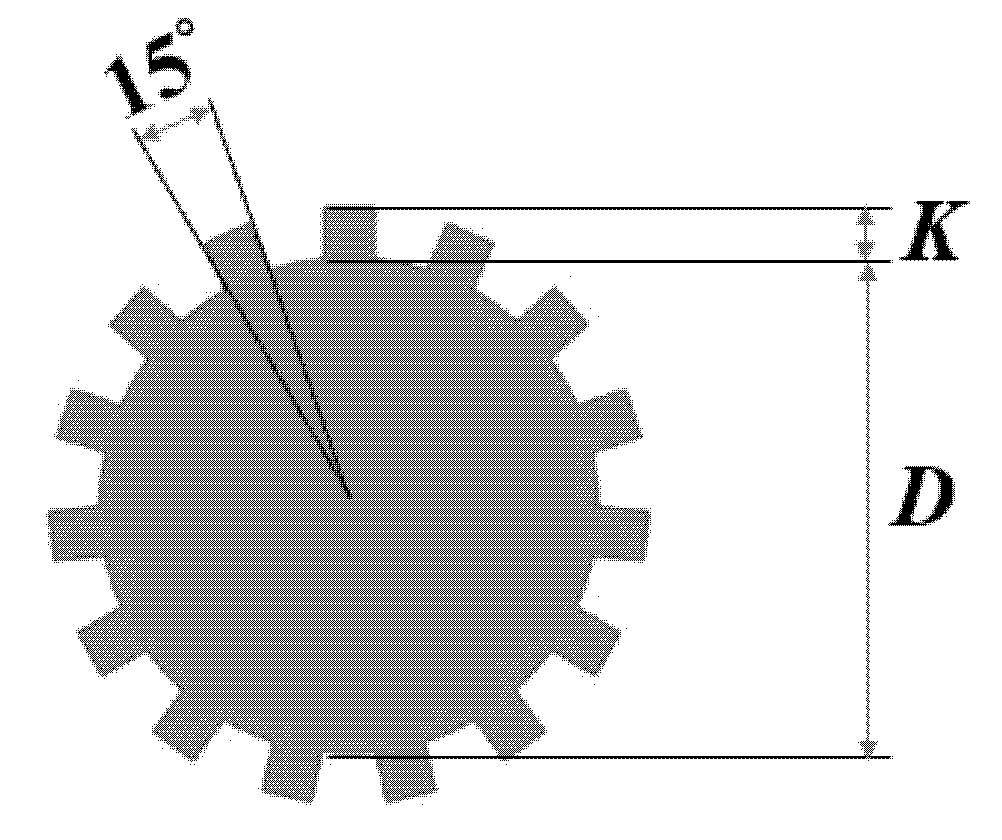
3.1. Calculation Condition Settings
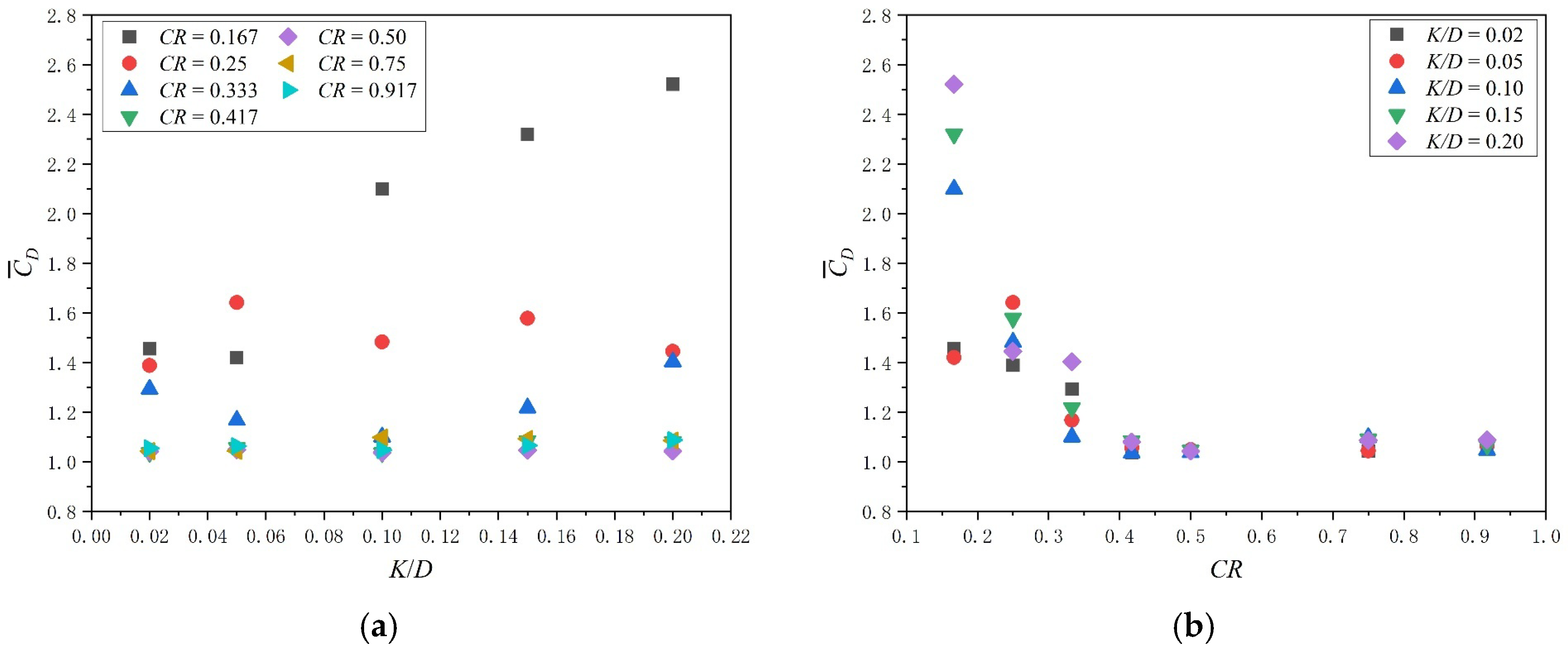
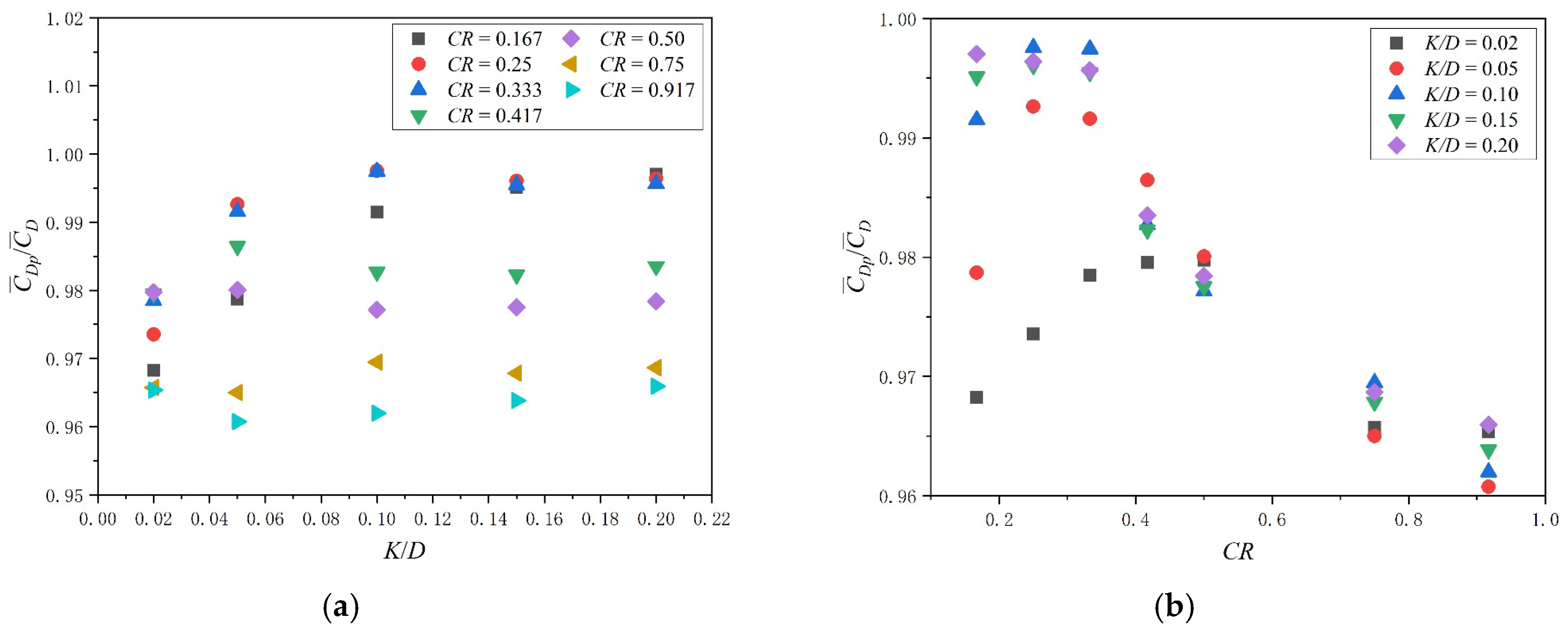
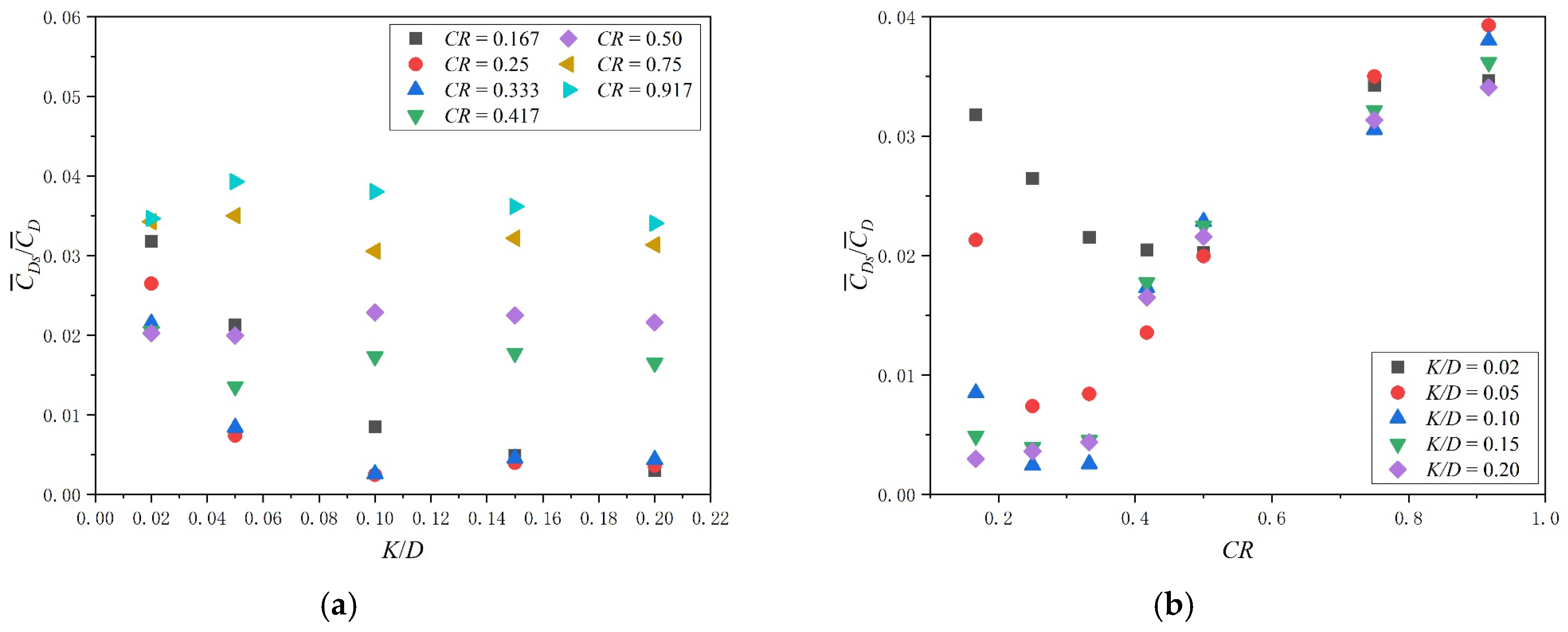
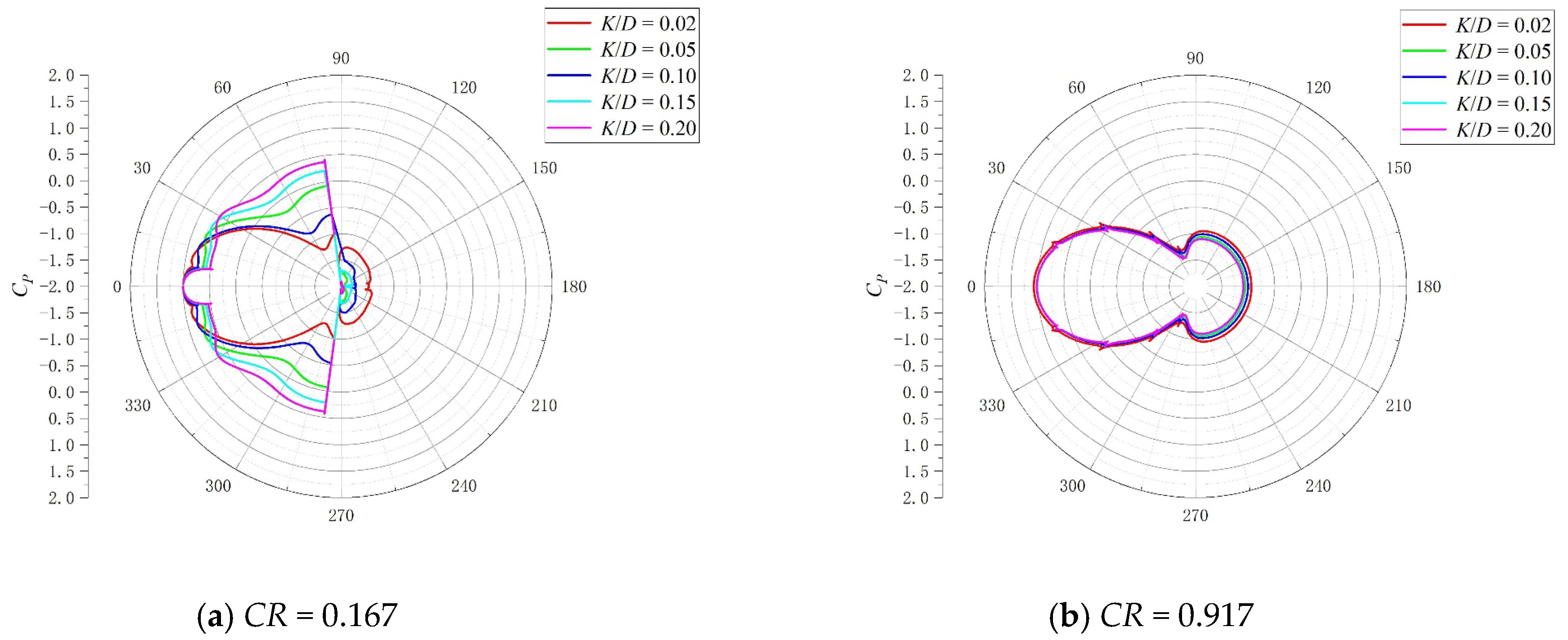
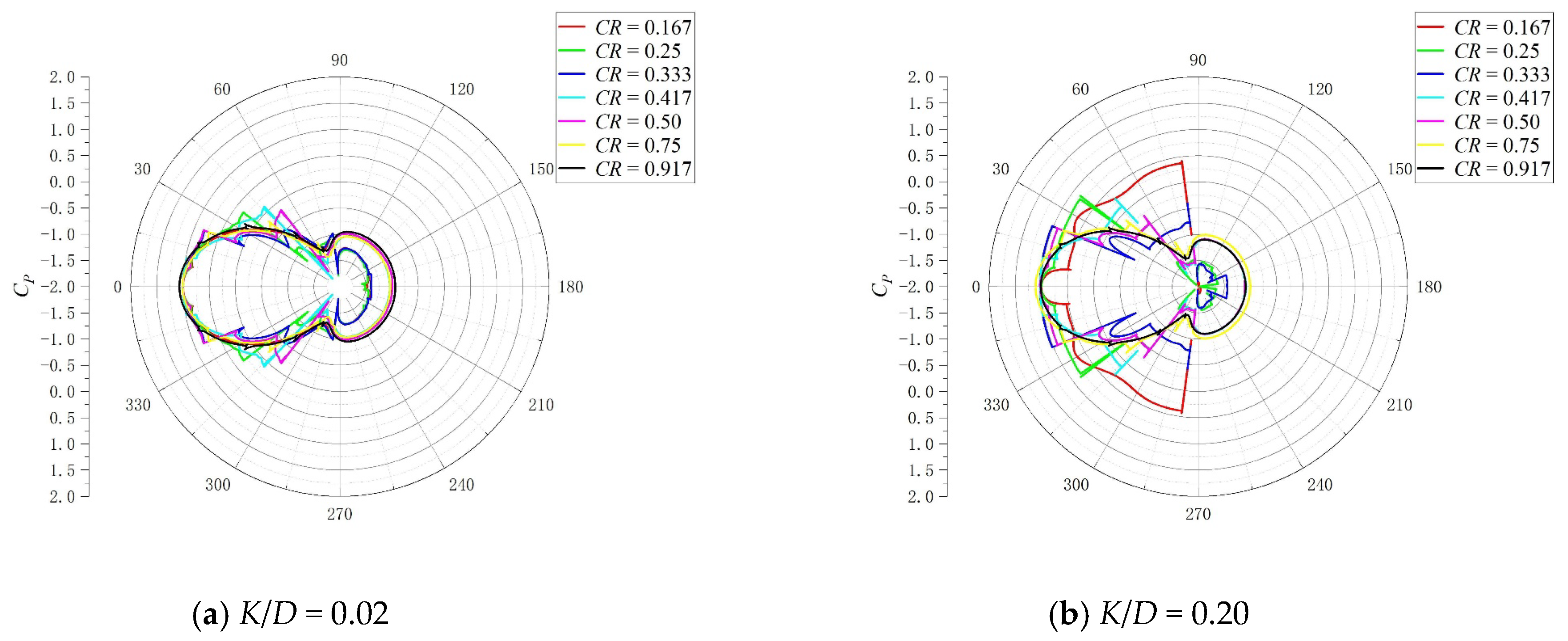
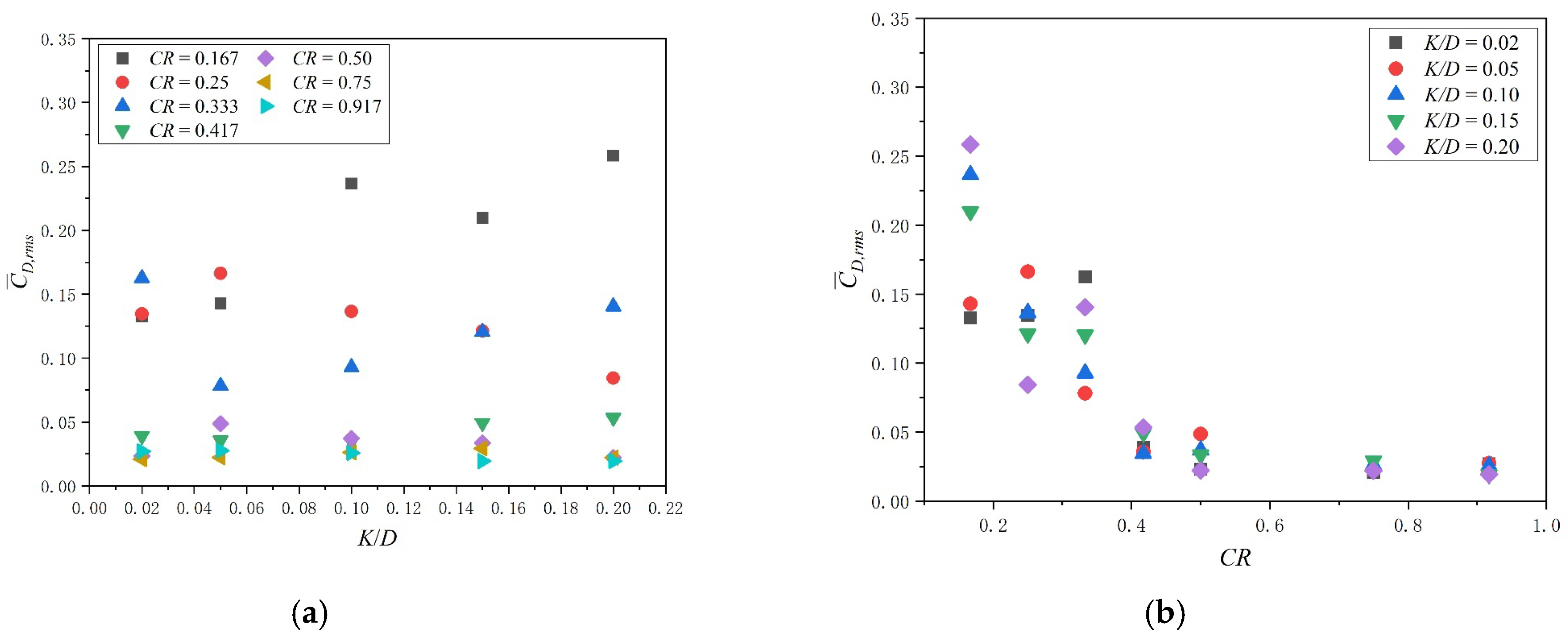
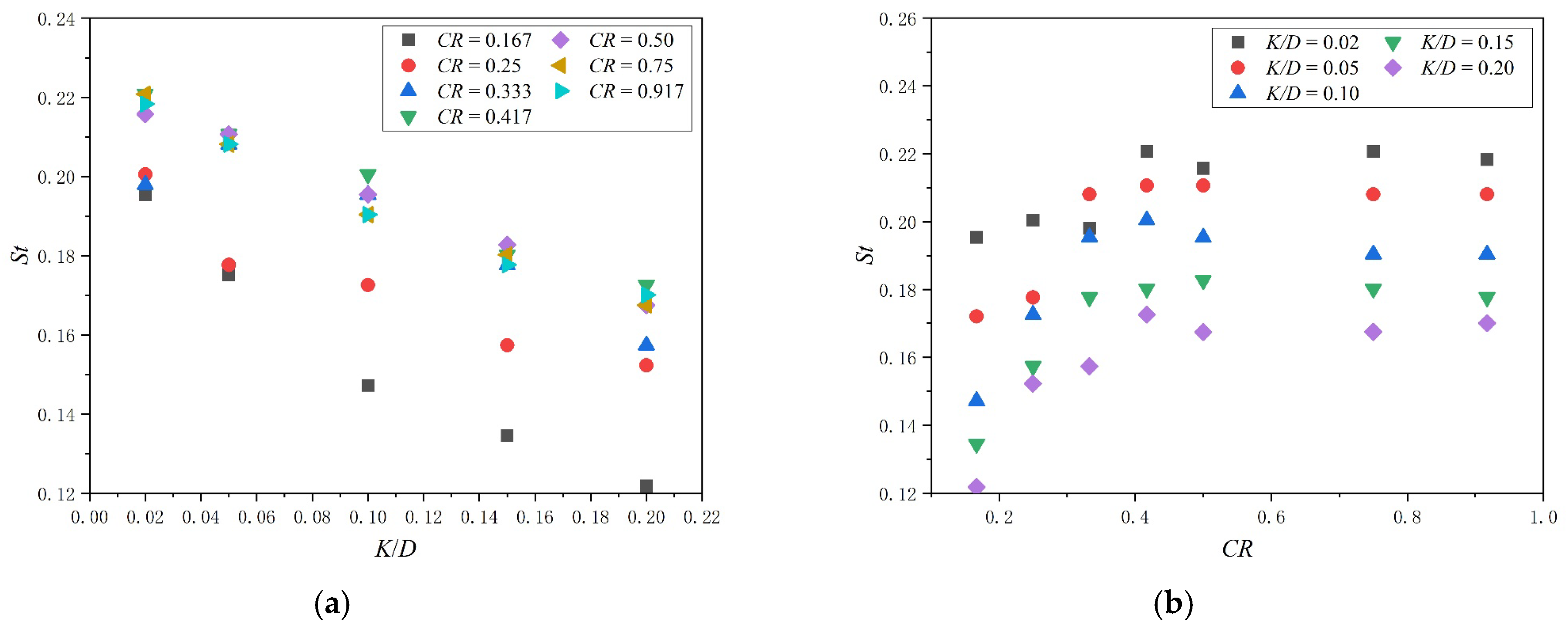
3.2. Hydrodynamic Coefficients
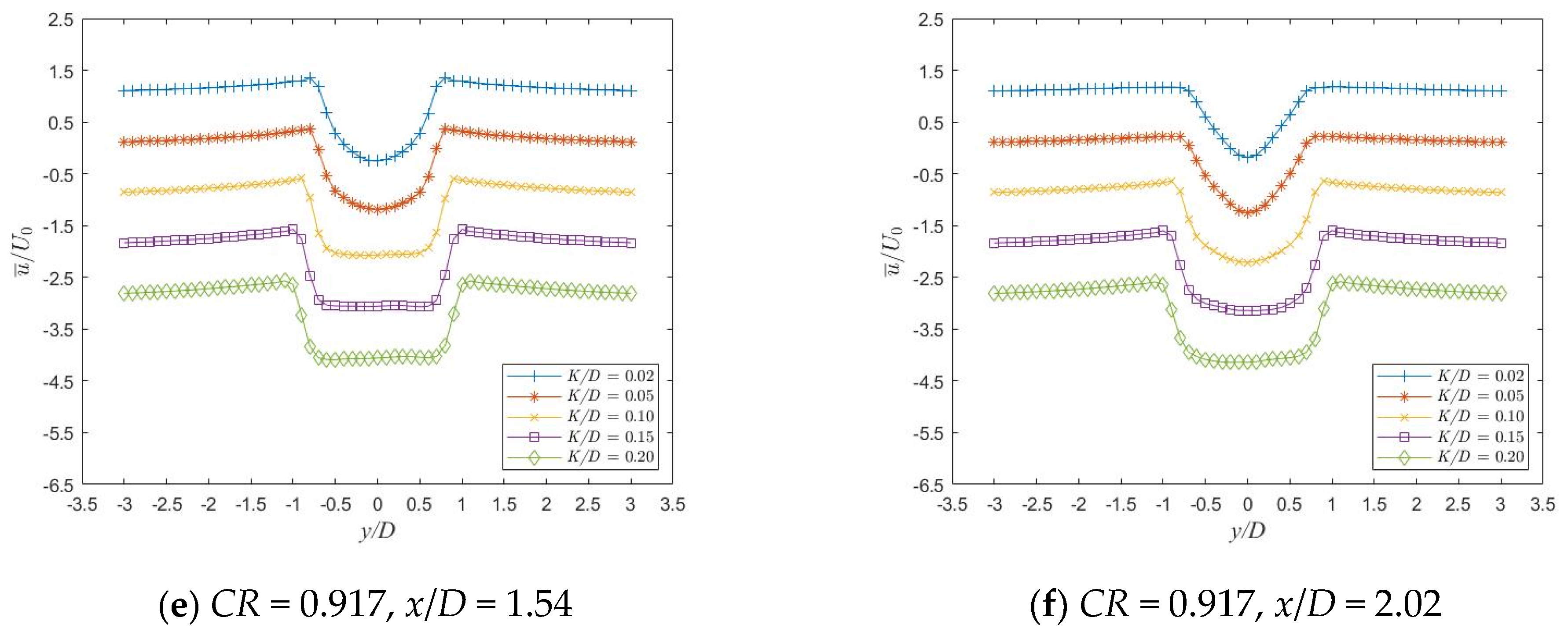
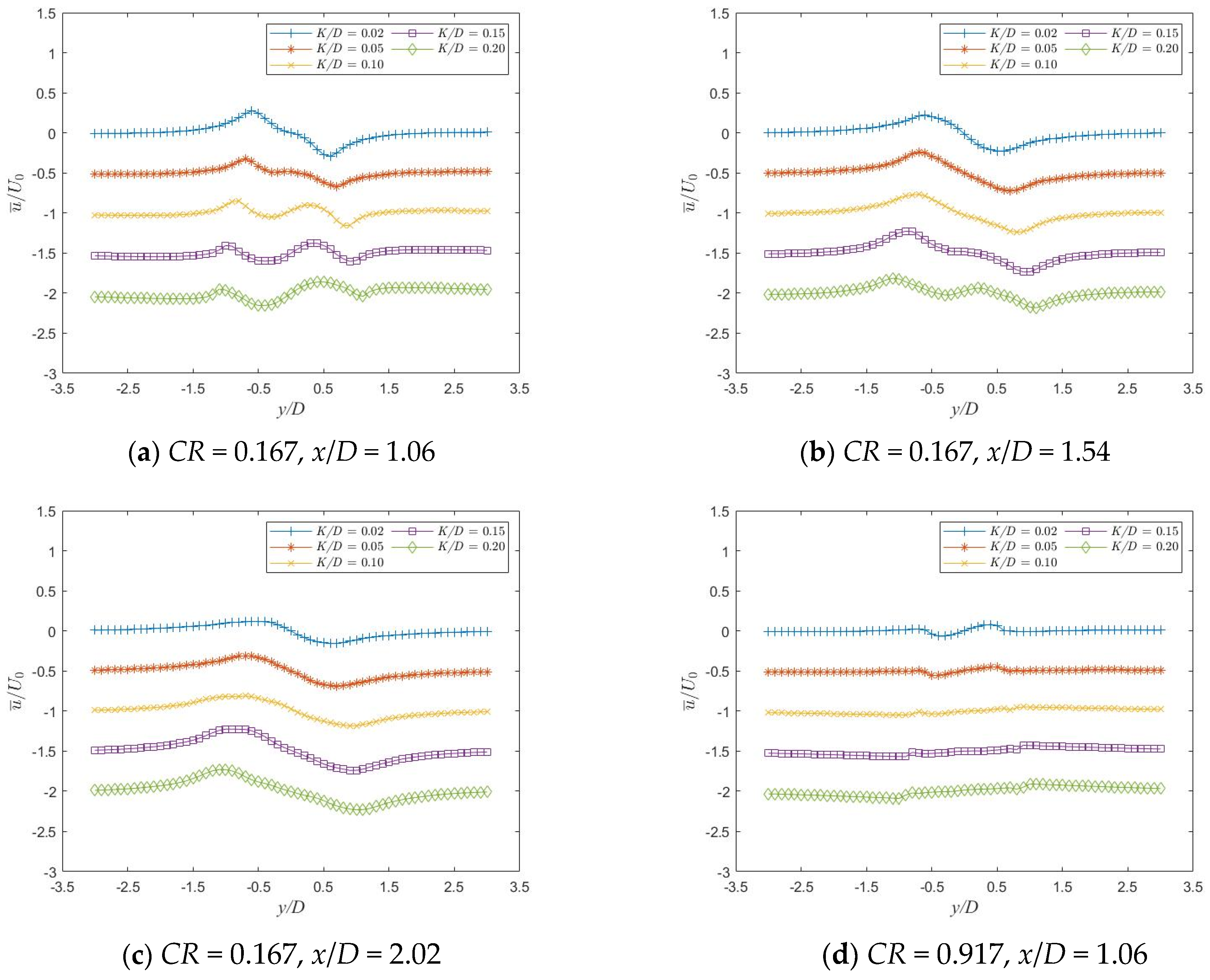
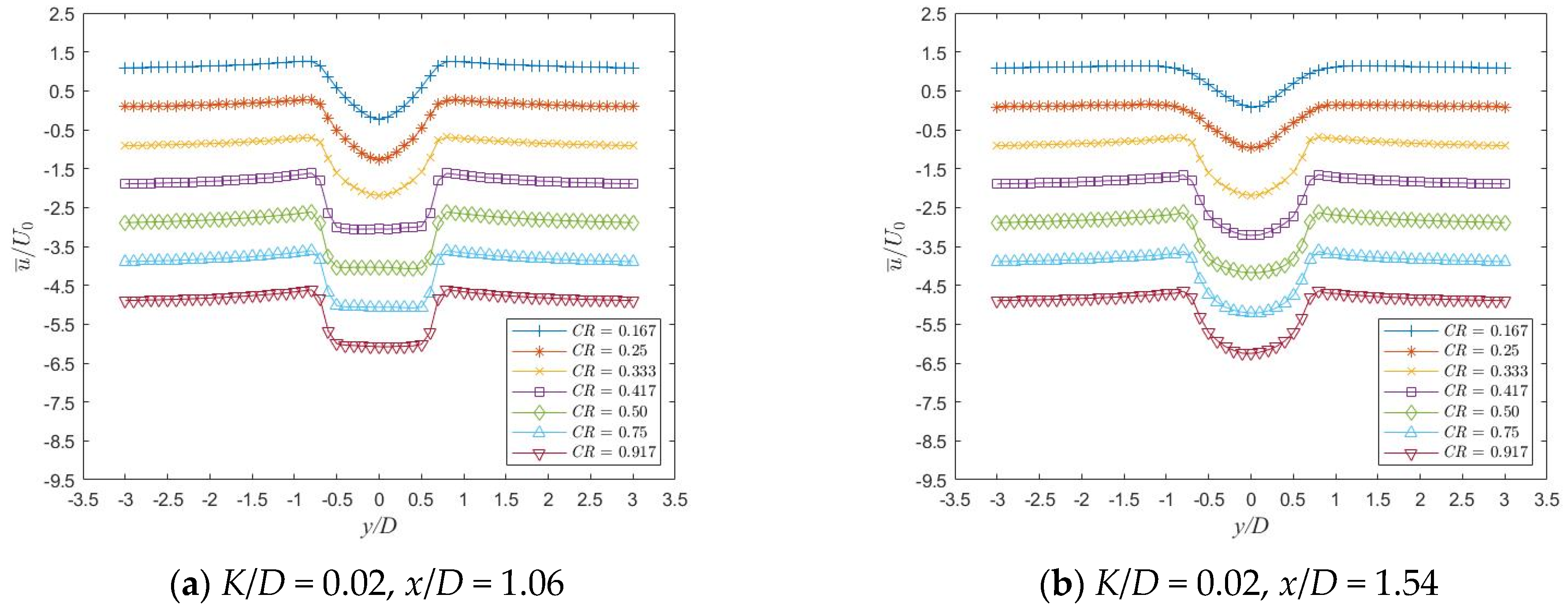
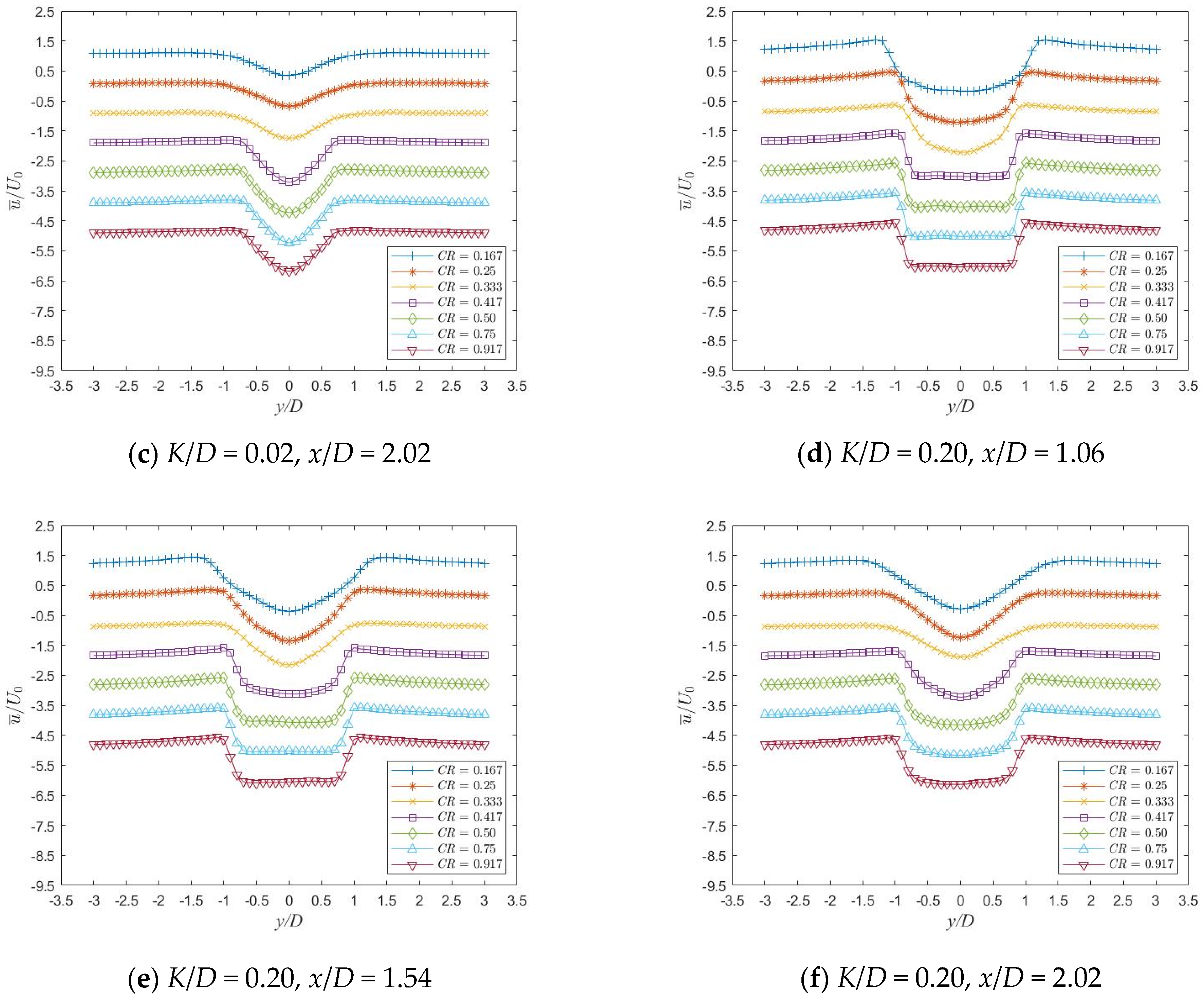
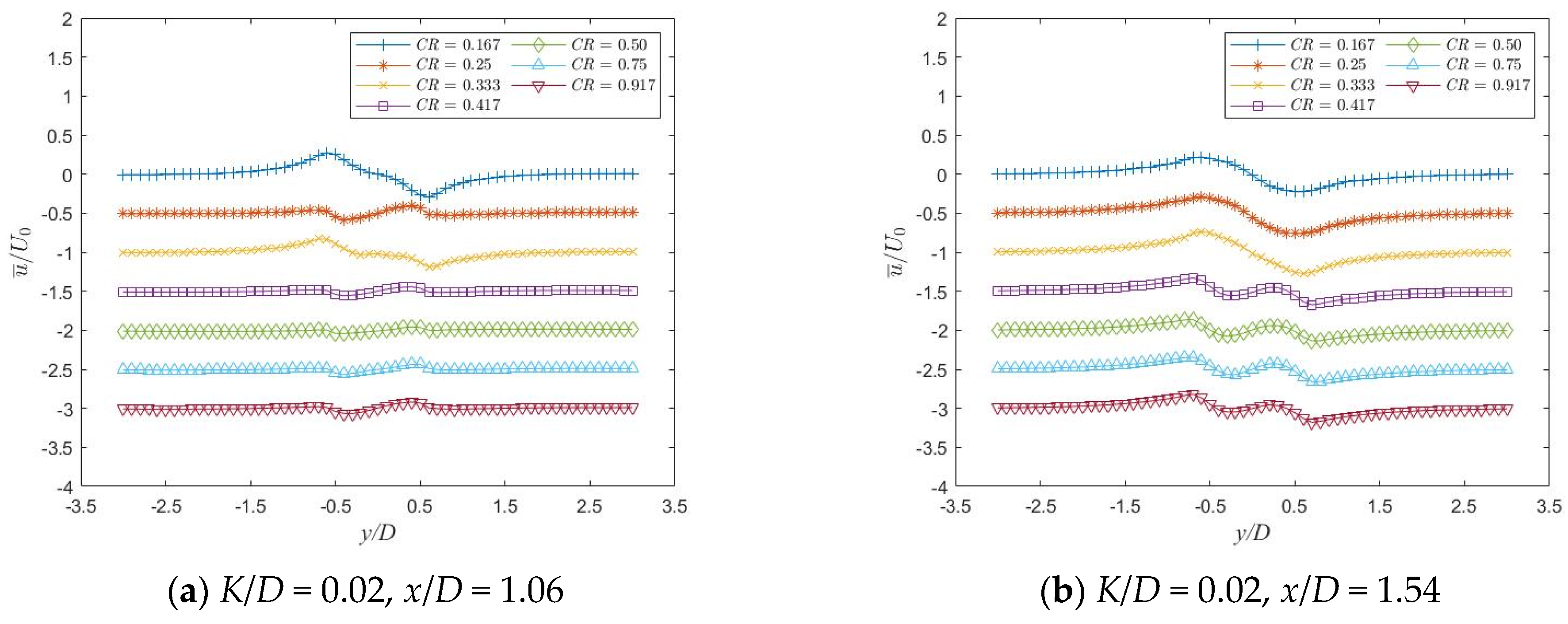
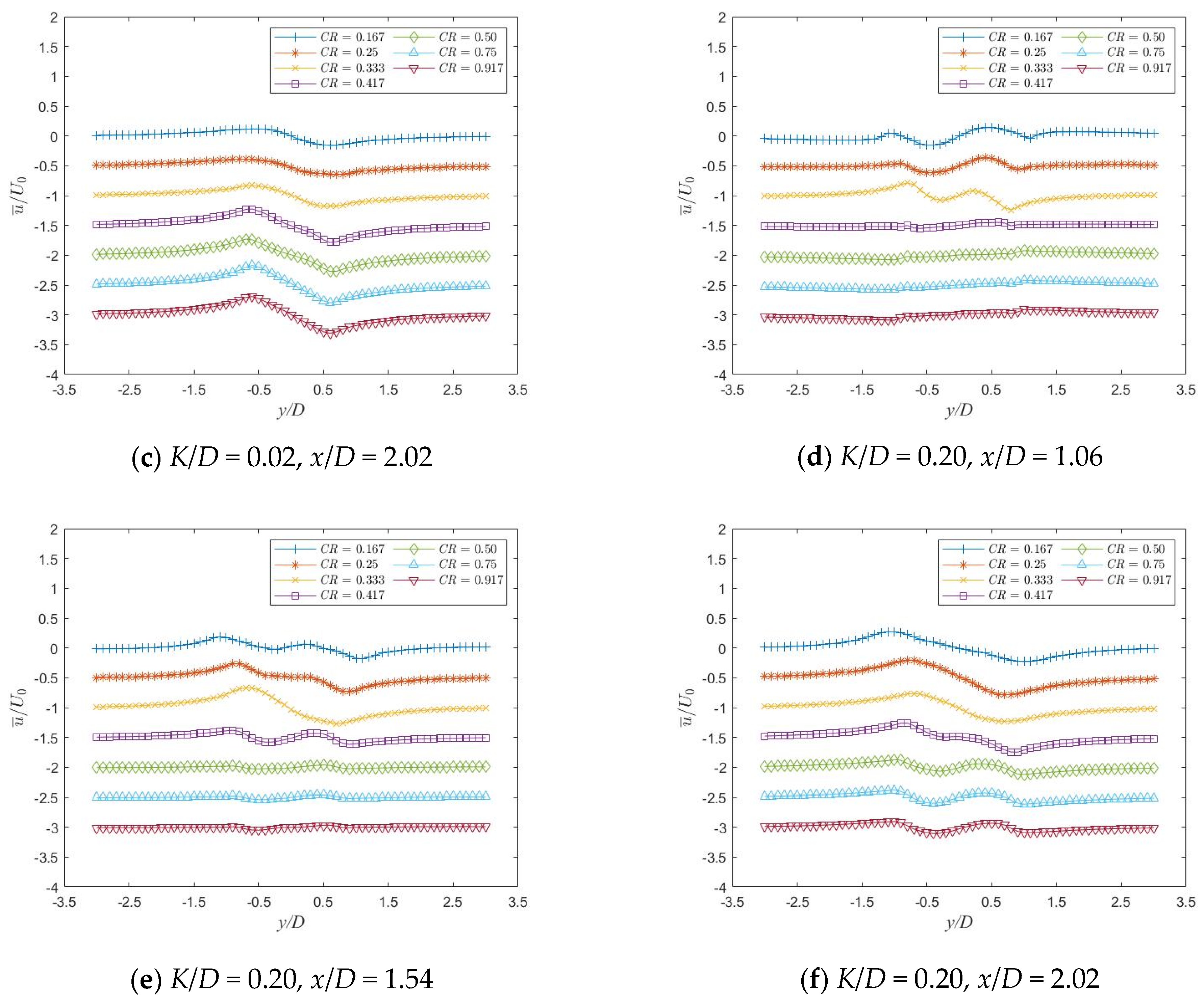
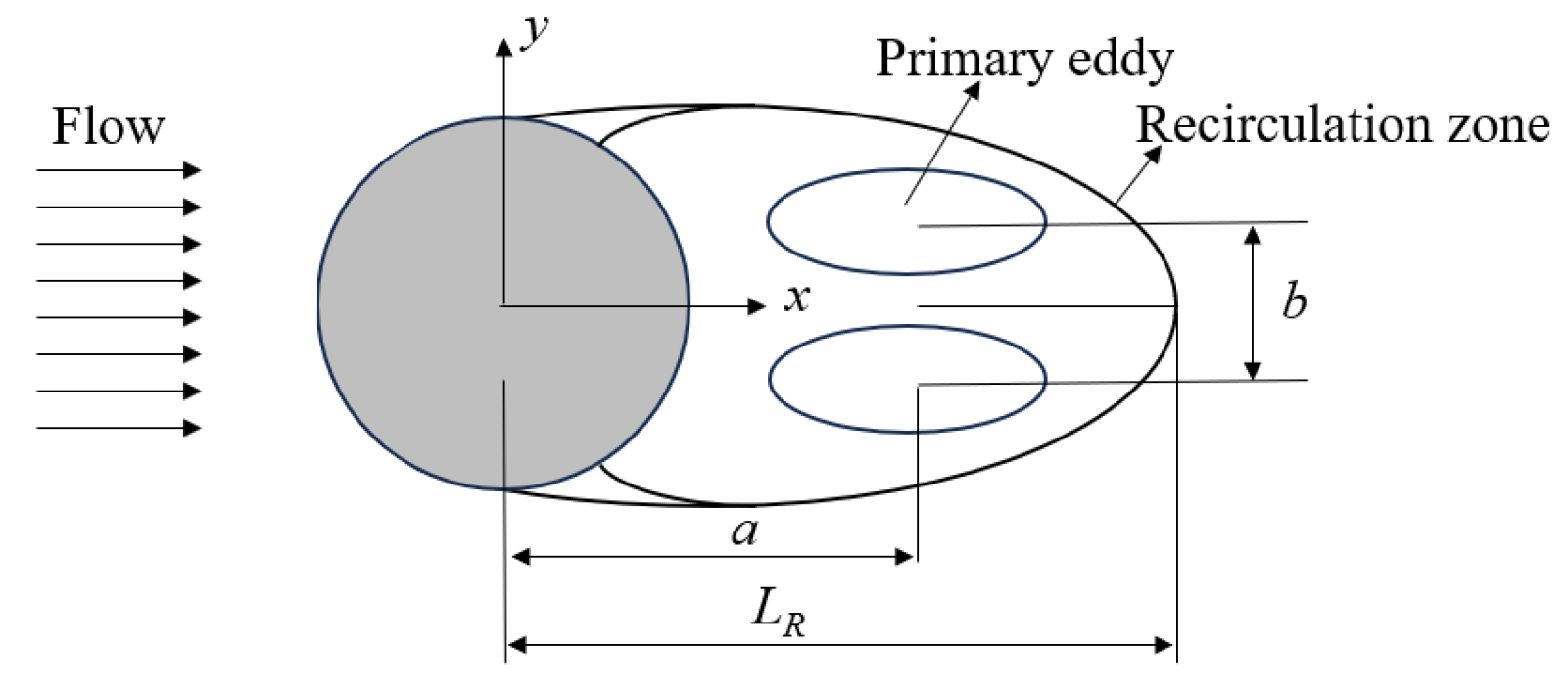
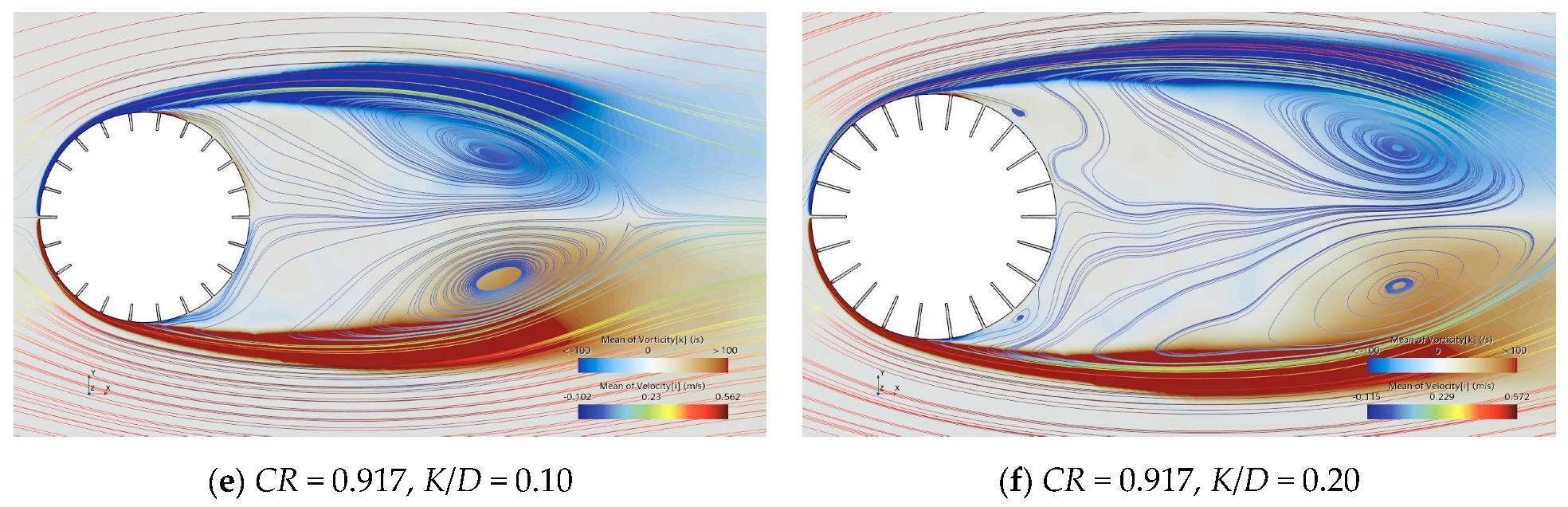
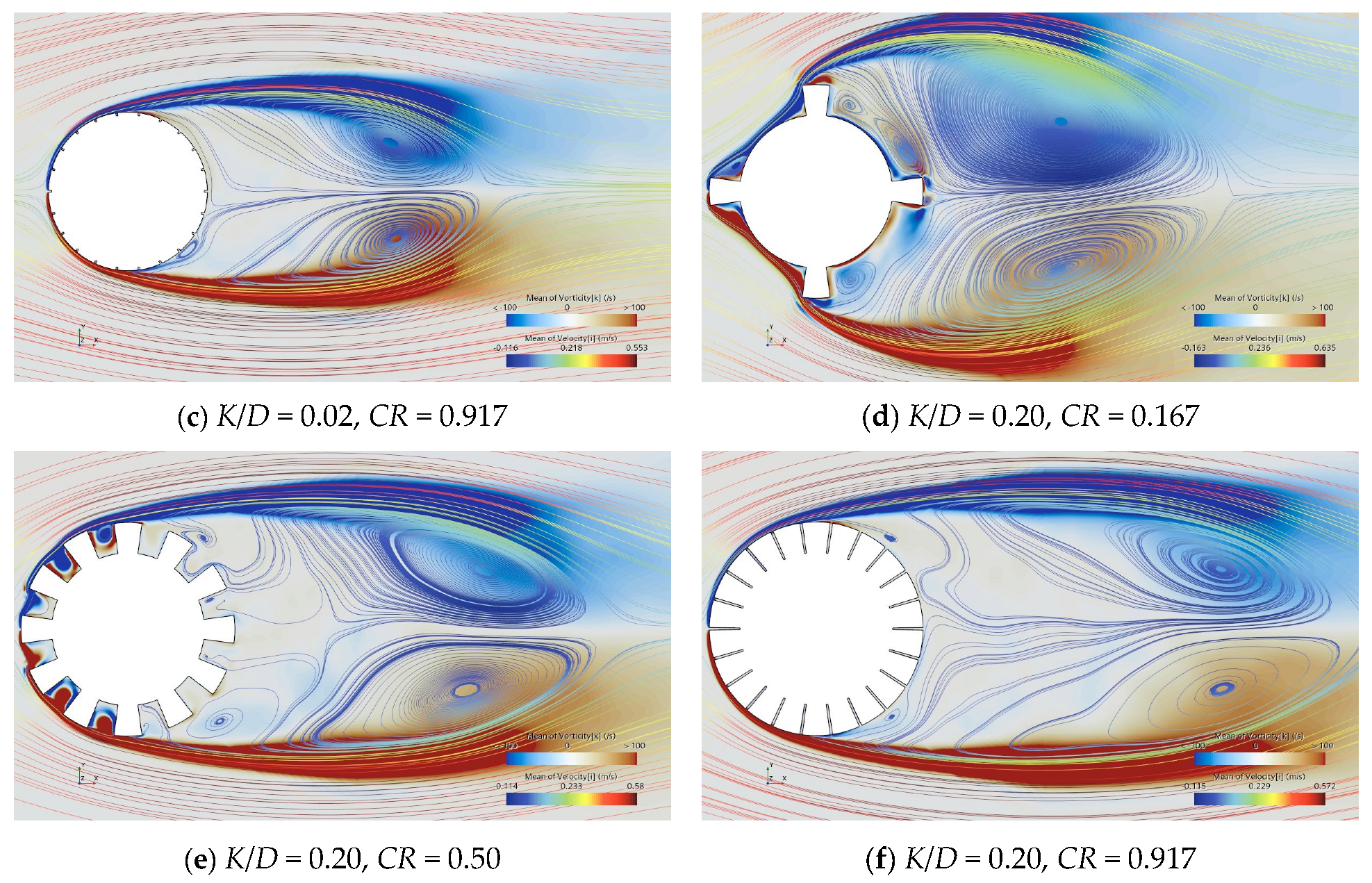
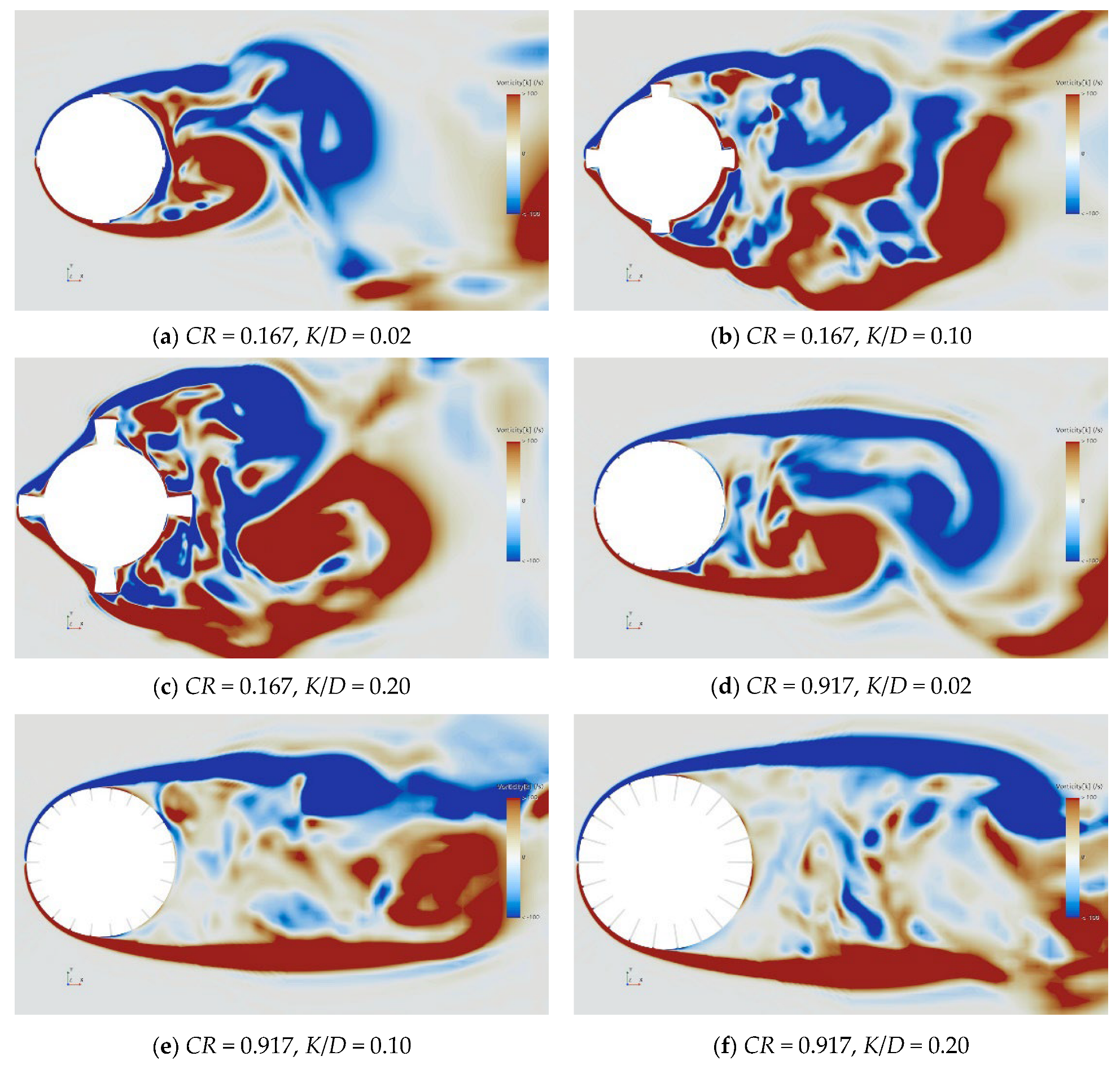
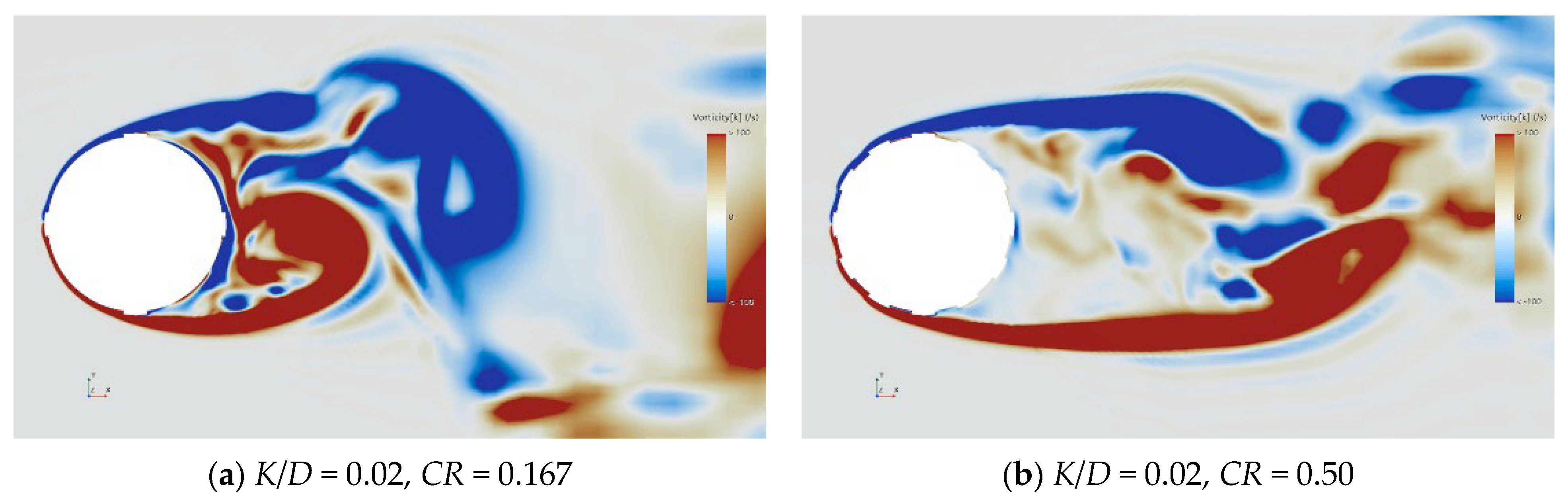
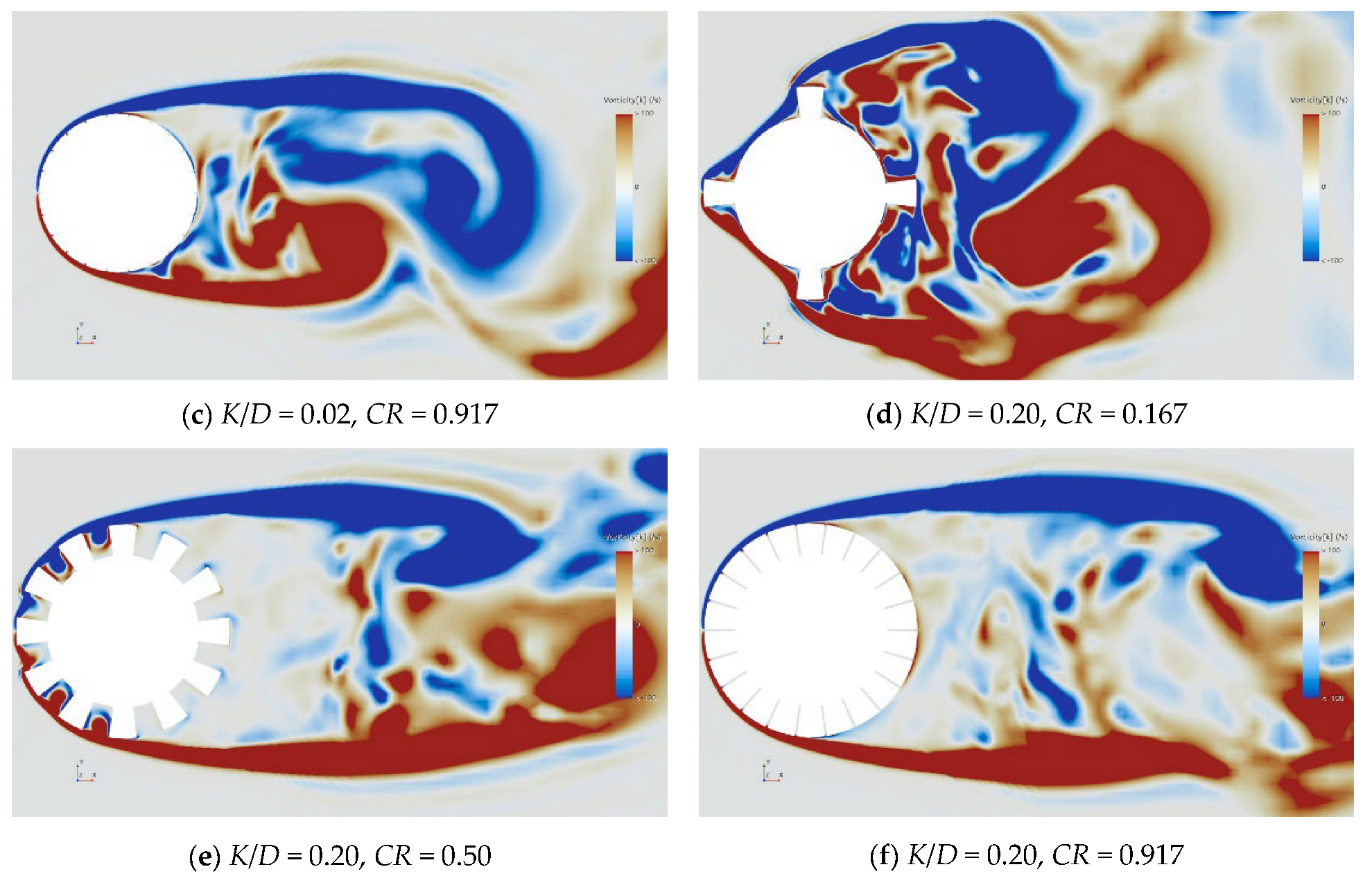
3.3. Flow Field Characteristic Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LES | Large-Eddy Simulation |
| PIV | Particle Image Velocimetry |
| RMS | Root Mean Square |
| CR | Coverage Ratio |
References
- Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Brede, M.; Eckelmann, H.; Rockwell, D. On secondary vortices in the cylinder wake. Phys. Fluids 1996, 8, 2117–2124. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 1988, 31, 2742–2744. [Google Scholar] [CrossRef]
- Catalano, P.; Wang, M.; Iaccarino, G.; Moin, P. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow. 2003, 24, 463–469. [Google Scholar] [CrossRef]
- Ong, M.C.; Utnes, T.; Holmedal, L.E.; Myrhaug, D.; Pettersen, B. Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers. Mar. Struct. 2009, 22, 142–153. [Google Scholar] [CrossRef]
- Marty, A.; Berhault, C.; Damblans, G.; Facq, J.-V.; Gaurier, B.; Germain, G.; Soulard, T.; Schoefs, F. Experimental study of hard marine growth effect on the hydrodynamical behaviour of a submarine cable. Appl. Ocean Res. 2021, 114, 102810. [Google Scholar] [CrossRef]
- Marty, A.; Schoefs, F.; Soulard, T.; Berhault, C.; Facq, J.-V.; Gaurier, B.; Germain, G. Effect of roughness of mussels on cylinder forces from a realistic shape modelling. J. Mar. Sci. Eng. 2021, 9, 598. [Google Scholar] [CrossRef]
- Nasr Esfahani, V.; Rajavarothayam, V.; Quan, K.; Hanson, R.; Lavoie, P. Effect of roughness and trips on the drag of a circular cylinder at subcritical flow. J. Wind Eng. Ind. Aerod. 2024, 253, 105847. [Google Scholar] [CrossRef]
- Kiu, K.Y.; Stappenbelt, B.; Thiagarajan, K.P. Effects of uniform surface roughness on vortex-induced vibration of towed vertical cylinders. J. Sound Vib. 2011, 330, 4753–4763. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Gho, W.M.; Tan, S.K. Force and flow characteristics of a circular cylinder with uniform surface roughness at subcritical Reynolds numbers. Appl. Ocean Res. 2015, 49, 20–26. [Google Scholar] [CrossRef]
- Hover, F.S.; Tvedt, H.; Triantafyllou, M.S. Vortex-induced vibrations of a cylinder with tripping wires. J. Fluid Mech. 2001, 448, 175–195. [Google Scholar] [CrossRef]
- Fage, A.; Warsap, J.H. The Effects of Turbulence and Surface Roughness on the Drag of a Circular Cylinder. Aeronautical Research Committee. No. 1283. 1929. Available online: https://reports.aerade.cranfield.ac.uk/bitstream/handle/1826.2/1414/arc-rm-1283.pdf?sequence=1&isAllowed=y (accessed on 1 October 2025).
- Güven, O.; Farell, C.; Patel, V.C. Surface-roughness effects on the mean flow past circular cylinders. J. Fluid Mech. 1980, 98, 673–701. [Google Scholar] [CrossRef]
- Sarpkaya, T. In-Line and Transverse Forces on Smooth and Rough Cylinders in Oscillatory Flow at High Reynolds Numbers; Interim Report; Naval Postgraduate School: Monterey, CA, USA, 4 July 1986. [Google Scholar]
- Achenbach, E. Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 1971, 46, 321–335. [Google Scholar] [CrossRef]
- Adachi, T.; Ono, H.; Matsuuchl, K.; Kawai, T.; Cho, T. Flow around a circular cylinder in the high Reynolds number range. Effect of surface roughness. Trans. JSME Part B 1989, 55, 685–692. [Google Scholar] [CrossRef][Green Version]
- Wolfram, J.; Naghipour, M. On the estimation of Morison force coefficients and their predictive accuracy for very rough circular cylinders. Appl. Ocean Res. 1999, 21, 311–328. [Google Scholar] [CrossRef]
- Huang, S.; Clelland, D.; Day, S.; James, R. Drag reduction of deepwater risers by the use of helical grooves. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering 2007, OMAE2007, San Deigo, CA, USA, 10–15 June 2007. [Google Scholar]
- Sun, C.; Zhou, T.; An, H.; Zhu, H.; Cheng, L. On the study of vortex-induced vibration of circular cylinders covered with different roughness. Appl. Ocean Res. 2022, 124, 103215. [Google Scholar] [CrossRef]
- de Moraes, P.G.; de Oliveira, M.A.; de Andrade, C.L.; Bimbato, A.M.; Pereira, L.A.A. Effects of surface roughness and wall confinement on bluff body aerodynamics at large-gap regime. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 397. [Google Scholar] [CrossRef]
- Suzuki, M.; Ikoma, T.; Rheem, C.; Aida, Y. Experimental investigation of roughness effect on flow field around cylinder in steady flow. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering, Volume 4: Ocean Space Utilization, Hamburg, Germany, 5–10 June 2022. [Google Scholar]
- Wang, Z.; Liu, K.; Liu, F.; Wei, H.; Liu, Q. A comprehensive numerical study of the effects of surface roughness on a finite-length cylinder with an aspect ratio of 1.5 for Reynolds numbers ranging from 3.9 × 103 to 4.8 × 105. Phys. Fluids 2024, 36, 055114. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1998, 3, 1760–1765. [Google Scholar] [CrossRef]
- Addad, Y.; Gaitonde, U.; Laurence, D.; Rolfo, S. Optimal unstructured meshing for large eddy simulations. In Quality & Reliability of Large Eddy Simulations; Springer: Dordrecht, The Netherlands, 2008; pp. 93–103. [Google Scholar]
- Vreman, B.; Geurts, B.; Kuerten, H. Realizability conditions for the turbulent stress tensor in large-eddy simulation. J. Fluid Mech. 1994, 278, 351–362. [Google Scholar] [CrossRef]
- Balaras, E.; Benocci, C.; Piomelli, U. Two-layer approximate boundary conditions for large-eddy simulations. AIAA J. 2012, 34, 1111–1119. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at ReD = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-Eddy Simulation of the Flow Over a Circular Cylinder at Reynolds Number 3900 Using the OpenFOAM Toolbox. Flow Turbul. Combust. 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Khan, N.B.; Ibrahim, Z.; Badry, A.B.B.M.; Jameel, M.; Javed, M.F. Numerical investigation of flow around cylinder at Reynolds number = 3900 with large eddy simulation technique: Effect of spanwise length and mesh resolution. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018, 233, 417–427. [Google Scholar] [CrossRef]
- Wornom, S.; Ouvrard, H.; Salvetti, M.V.; Koobus, B.; Dervieux, A. Variational multiscale large-eddy simulations of the flow past a circular cylinder: Reynolds number effects. Comput. Fluids 2011, 47, 44–50. [Google Scholar] [CrossRef]
- Ouvrard, H.; Koobus, B.; Dervieux, A.; Salvetti, M.V. Classical and variational multiscale LES of the flow around a circular cylinder on unstructured grids. Comput. Fluids 2010, 39, 1083–1094. [Google Scholar] [CrossRef]
- Dong, S.; Karniadakis, G.E.; Ekmekci, A.; Rockwell, D. A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 2006, 569, 185–207. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]







| Case | Grid Node ) | St | ||
|---|---|---|---|---|
| A1 | 60 | 1.052 | 0.070 | 0.228 |
| A2 | 60 | 1.061 | 0.084 | 0.228 |
| A3 | 60 | 1.054 | 0.078 | 0.228 |
| B1 | 60 | 1.064 | 0.090 | 0.226 |
| B2 | 60 | 1.038 | 0.055 | 0.226 |
| B3 | 60 | 1.043 | 0.064 | 0.226 |
| C2 | 70 | 1.031 | 0.057 | 0.223 |
| C3 | 80 | 1.042 | 0.059 | 0.223 |
| Case | Time Step | St | ||
|---|---|---|---|---|
| D1 | 0.01 | 1.037 | 0.062 | 0.216 |
| D2 | 0.005 | 1.031 | 0.057 | 0.223 |
| D3 | 0.002 | 1.034 | 0.088 | 0.216 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, E.; Yu, S.; Feng, H.; Jiao, Z.; Tang, G. Numerical Investigation of Hydrodynamic Characteristics of Circular Cylinder with Surface Roughness at Subcritical Reynolds Number. J. Mar. Sci. Eng. 2025, 13, 2075. https://doi.org/10.3390/jmse13112075
Zeng E, Yu S, Feng H, Jiao Z, Tang G. Numerical Investigation of Hydrodynamic Characteristics of Circular Cylinder with Surface Roughness at Subcritical Reynolds Number. Journal of Marine Science and Engineering. 2025; 13(11):2075. https://doi.org/10.3390/jmse13112075
Chicago/Turabian StyleZeng, Erxian, Songsong Yu, Heng Feng, Zhihui Jiao, and Guoqiang Tang. 2025. "Numerical Investigation of Hydrodynamic Characteristics of Circular Cylinder with Surface Roughness at Subcritical Reynolds Number" Journal of Marine Science and Engineering 13, no. 11: 2075. https://doi.org/10.3390/jmse13112075
APA StyleZeng, E., Yu, S., Feng, H., Jiao, Z., & Tang, G. (2025). Numerical Investigation of Hydrodynamic Characteristics of Circular Cylinder with Surface Roughness at Subcritical Reynolds Number. Journal of Marine Science and Engineering, 13(11), 2075. https://doi.org/10.3390/jmse13112075





