Multiscale Numerical Modeling of Wave Overtopping for Pedestrian Hazard Classification and Risk Assessment
Abstract
1. Introduction
2. Numerical Modeling
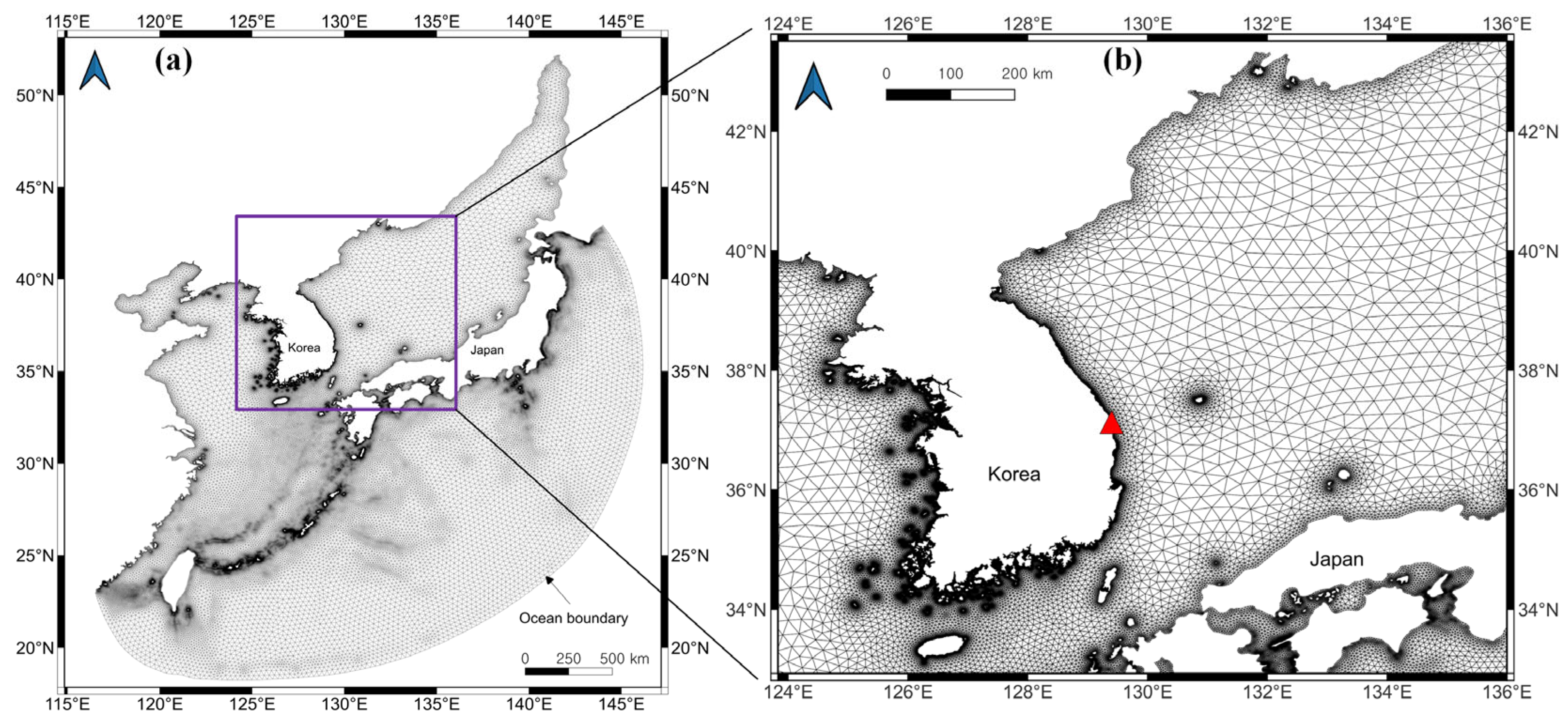
2.1. ADCIRC-UnSWAN Model
2.2. DualSPHysics Model Simulation
3. Hazard and Risk Assessment
3.1. Overtopping Hazard Rating
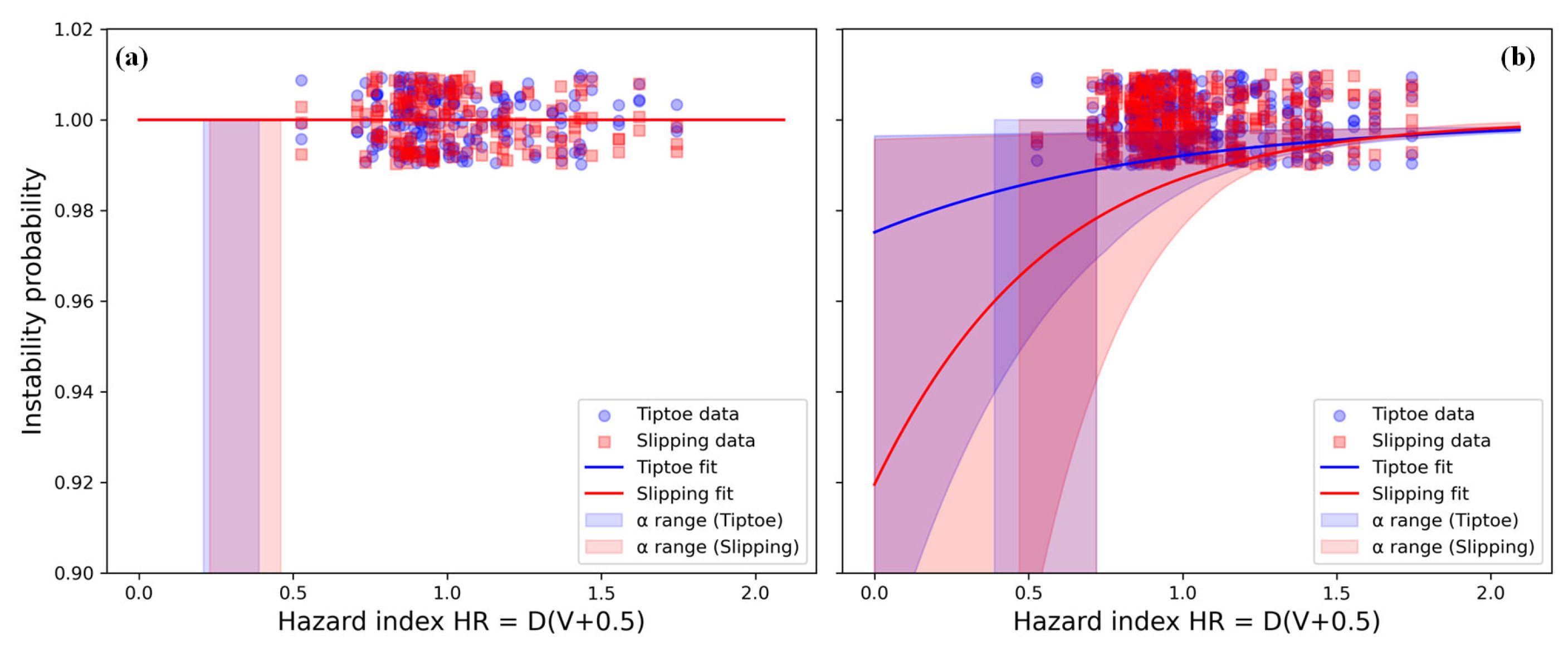
3.2. Risk Analysis for Pedestrians
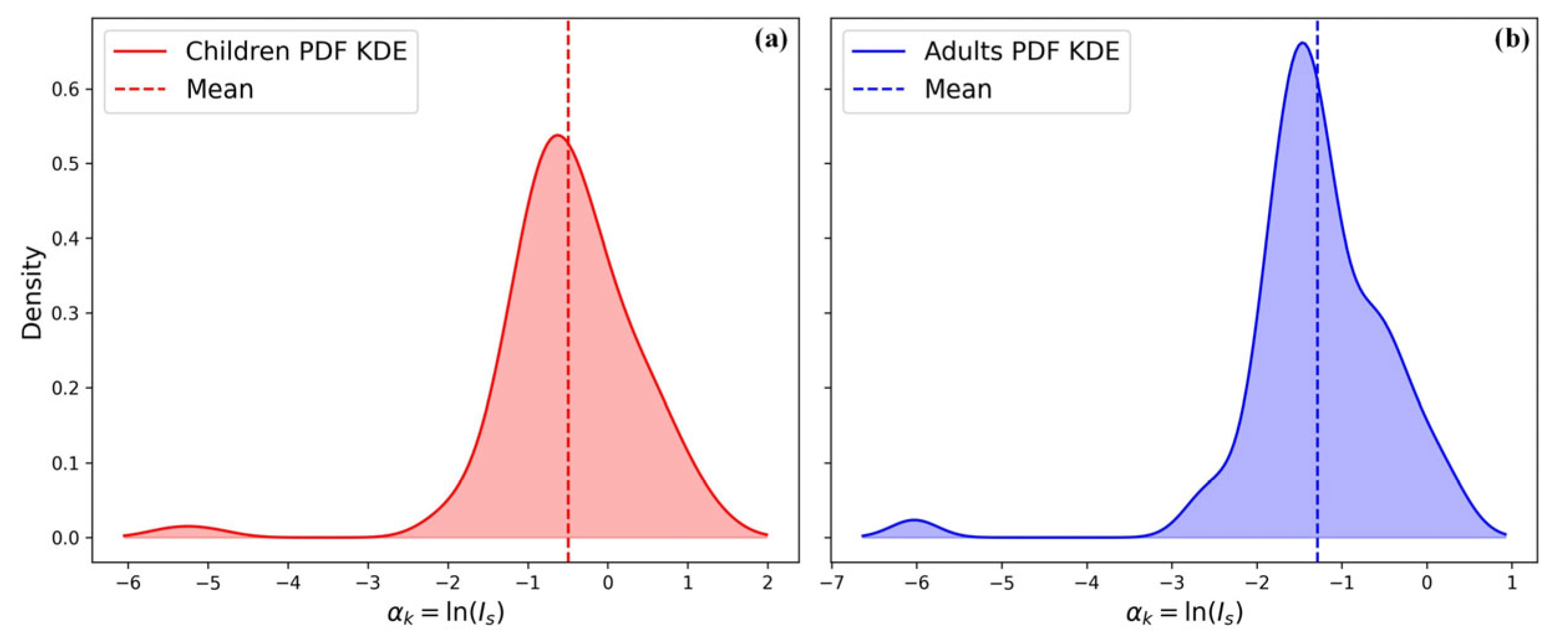
3.3. Probabilistic Risk Assessment for Pedestrians
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Almar, R.; Ranasinghe, R.; Bergsma, E.W.J.; Diaz, H.; Melet, A.; Papa, F.; Vousdoukas, M.; Athanasiou, P.; Dada, O.; Almeida, L.P.; et al. A Global Analysis of Extreme Coastal Water Levels with Implications for Potential Coastal Overtopping. Nat. Commun. 2021, 12, 3775. [Google Scholar] [CrossRef] [PubMed]
- Koosheh, A.; Etemad-Shahidi, A.; Cartwright, N.; Tomlinson, R.; van Gent, M.R.A. Individual Wave Overtopping at Coastal Structures: A Critical Review and the Existing Challenges. Appl. Ocean Res. 2021, 106, 102476. [Google Scholar] [CrossRef]
- Koosheh, A.; Etemad-Shahidi, A.; Cartwright, N.; Tomlinson, R.; van Gent, M.R.A. Wave Overtopping Layer Thickness on the Crest of Rubble Mound Seawalls. Coast. Eng. 2024, 188, 104441. [Google Scholar] [CrossRef]
- Garzon, J.L.; Ferreira; Reis, M.T.; Ferreira, A.; Fortes, C.J.E.M.; Zózimo, A.C. Conceptual and Quantitative Categorization of Wave-Induced Flooding Impacts for Pedestrians and Assets in Urban Beaches. Sci. Rep. 2023, 13, 7251. [Google Scholar] [CrossRef] [PubMed]
- Gruwez, V.; Altomare, C.; Suzuki, T.; Streicher, M.; Cappietti, L.; Kortenhaus, A.; Troch, P. Validation of RANS Modelling for Wave Interactions with Sea Dikes on Shallow Foreshores Using a Large-Scale Experimental Dataset. J. Mar. Sci. Eng. 2020, 8, 650. [Google Scholar] [CrossRef]
- Westerink, J.J.; Luettich, R.A.; Blain, C.A. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries; Report 2. User’s Manual for ADCIRC-2DDI; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1994. [Google Scholar]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves Coasts and Estuaries; Report 1: Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL, Dredging Research Program Technical Report DRP-92-6; Coastal Engineering Research Center (U.S.): Duck, NC, USA; Engineer Research and Development Center (U.S.): Vicksburg, MS, USA, 1992. [Google Scholar]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A Third-Generation Wave Model for Coastal Regions 2. Verification. J. Geophys. Res. Oceans 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-Generation Wave Model for Coastal Regions 1. Model Description and Validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Wang, N.; Hou, Y.; Mo, D.; Li, J. Hazard Assessment of Storm Surges and Concomitant Waves in Shandong Peninsula Based on Long-Term Numerical Simulations. Ocean Coast. Manag. 2021, 213, 105888. [Google Scholar] [CrossRef]
- Yin, C.; Huang, H.; Wang, D.; Liu, Y. Tropical Cyclone-Induced Wave Hazard Assessment in Hainan Island, China. Nat. Hazards 2022, 113, 103–123. [Google Scholar] [CrossRef]
- Mun, J.-Y.; Cho, W.-H.; Rehman, K. Hazard Classification and Risk Evaluation for Pedestrians at Sea Dikes Due to Wave Overtopping. In Proceedings of the 35th International Ocean and Polar Engineering Conference, Seoul, Republic of Korea, 1–6 June 2025; p. ISOPE-I-25-446. [Google Scholar]
- McCall, R.T.; Masselink, G.; Poate, T.G.; Roelvink, J.A.; Almeida, L.P.; Davidson, M.; Russell, P.E. Modelling Storm Hydrodynamics on Gravel Beaches with XBeach-G. Coast. Eng. 2014, 91, 231–250. [Google Scholar] [CrossRef]
- Ibrahim, M.S.I.; Baldock, T.E. Swash Overtopping on Plane Beaches – Reconciling Empirical and Theoretical Scaling Laws Using the Volume Flux. Coast. Eng. 2020, 157, 103668. [Google Scholar] [CrossRef]
- Akbari, H. Simulation of Wave Overtopping Using an Improved SPH Method. Coast. Eng. 2017, 126, 51–68. [Google Scholar] [CrossRef]
- Ryu, K.H.; Shin, C.H.; Jeong, W.M.; Baek, W.D. Applicability of Swash Model for Wave Field Data Reproduction in Namhangjin Coastal Area. In APAC 2019—Proceedings of the 10th International Conference on Asian and Pacific Coasts, Hanoi, Vietnam, 25–28 September 2019; Springer: Singapore, 2020; pp. 945–951. [Google Scholar] [CrossRef]
- Umesh, P.A.; Behera, M.R. On the Improvements in Nearshore Wave Height Predictions Using Nested SWAN-SWASH Modelling in the Eastern Coastal Waters of India. Ocean Eng. 2021, 236, 109550. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-Source Parallel CFD Solver Based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Altomare, C.; Gironella, X.; Crespo, A.J.C. Simulation of Random Wave Overtopping by a WCSPH Model. Appl. Ocean Res. 2021, 116, 102888. [Google Scholar] [CrossRef]
- Vanneste, D.F.A.; Altomare, C.; Suzuki, T.; Troch, P.; Verwaest, T. Comparison of Numerical Models for Wave Overtopping and Impact on a Sea Wall. Coast. Eng. Proc. 2014, 1, 5. [Google Scholar] [CrossRef]
- Bae, H.U.; Yun, K.M.; Yoon, J.Y.; Lim, N.H. Human Stability with Respect to Overtopping Flow on the Breakwater. Int. J. Appl. Eng. Res. 2016, 11, 111–119. [Google Scholar]
- Maranzoni, A.; D’Oria, M.; Rizzo, C. Quantitative Flood Hazard Assessment Methods: A Review. J. Flood Risk Manag. 2023, 16, e12855. [Google Scholar] [CrossRef]
- Cao, D.; Tan, W.; Yuan, J. Assessment of Wave Overtopping Risk for Pedestrian Visiting the Crest Area of Coastal Structure. Appl. Ocean Res. 2022, 120, 102985. [Google Scholar] [CrossRef]
- Mun, J.-Y.; Cho, W.-H.; Rehman, K. Estimation of Overtopping Discharge Using Real-Time Monitoring, Numerical, Empirical, and Neural Network Methods. J. Korean Soc. Mar. Environ. Saf. 2024, 30, 527–540. [Google Scholar] [CrossRef]
- Gruwez, V.; Altomare, C.; Suzuki, T.; Streicher, M.; Cappietti, L.; Kortenhaus, A.; Troch, P. An Inter-Model Comparison for Wave Interactions with Sea Dikes on Shallow Foreshores. J. Mar. Sci. Eng. 2020, 8, 985. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary Conditions Generated by Dynamic Particles in SPH Methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-Crested Wave Generation and Absorption for SPH-Based DualSPHysics Model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Altomare, C.; Domínguez, J.M.; González-Cao, J.; Gómez-Gesteira, M. Towards Simulating Floating Offshore Oscillating Water Column Converters with Smoothed Particle Hydrodynamics. Coast. Eng. 2017, 126, 11–26. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. EurOtop: Manual on Wave Overtopping of Sea Defences and Related Structures; 2nd edition 2018. Available online: https://www.overtopping-manual.com/ (accessed on 19 October 2025).
- van der Meer, J.; Bruce, T. New Physical Insights and Design Formulas on Wave Overtopping at Sloping and Vertical Structures. J. Waterw. Port. Coast. Ocean Eng. 2014, 140, 04014025. [Google Scholar] [CrossRef]
- Franco, L.; de Gerloni, M.; van der Meer, J. Wave overtopping on vertical and composite breakwaters. In Proceedings of the 24th International Conference on Coastal Enegineering, Kobe, Japan, 23–28 October 1994; pp. 1030–1045. [Google Scholar]
- Allsop, N.W.H. Overtopping Performance of Vertical and Composite Breakwaters, Seawalls and Low Reflection Alternatives. In Paper to Final MAST-MCS Project Workshop; University of Hannover: Alderney, UK, 1995. [Google Scholar]
- Wade, S.; Ramsbottom, D.; Floyd, P.; Penning-rowsell, E.; Surendran, S. Risks to People: Developing New Approaches for Flood Hazard and Vulnerability Mapping. In Proceedings of the 40th DEFRA Flood and Coastal Management Conference, York, UK, 5–7 July 2005. [Google Scholar]









| Parameter Key | Value | Description |
|---|---|---|
| Boundary | 1 | DBC (Dynamic Boundary Condition) |
| StepAlgorithm | 2 | Step algorithm: 2: Symplectic |
| Kernel | 2 | Interaction kernel: 2 = Wendland |
| ViscoType | 1 | Viscosity formulation: 1 = Artificial viscosity |
| Visco | 0.01 | Artificial viscosity coefficient |
| DensityDiff | 2 | Density diffusion term: 2 = Fourtakas |
| RigidAlgorithm | 1 | Rigid body algorithm: 1 = SPH |
| CoefDtMin | 0.05 | Coefficient for minimum time step |
| TimeOut | 1 | Time step for data output (seconds) |
| Coefficients | Franco et al. [31] for Relatively Deep Water | Allsop [32] | Van der Meer et al. [23] | This Study |
|---|---|---|---|---|
| a | 0.2 | 0.05 | 0.047 | 0.03 |
| b | 4.3 | 2.78 | 2.12 | 1.47 |
| c | - | - | 1.3 | 0.93 |
| Hazard Category | Hazard Index HR = D(V + 0.5) | Severity Level | Description |
|---|---|---|---|
| HR1 | HR < 0.75 |  Low Low | Flood zone with shallow or slow-moving water (caution only) |
| HR2 | 0.75 ≤ HR < 1.25 |  Moderate Moderate | Flood zone with deeper/faster water, risk for children |
| HR3 | 1.2 ≤ HR < 2.5 |  Significant Significant | Flood zone with deep, fast water, hazardous for most adults |
| HR4 | HR ≥ 2.5 |  Extreme Extreme | Flood zone with deep, fast water, extremely dangerous for all |
| Subject ID | Age (yrs.) | Height (m) | Mass (kg) | H × M (m.kg) |
|---|---|---|---|---|
| C1 | 2~3 | 0.93 | 15 | 14 |
| C2 | 6~7 | 1.2 | 23 | 28 |
| C3 | 9~10 | 1.37 | 36 | 49 |
| A1 | 24 | 1.72 | 68 | 117 |
| A2 | 34 | 1.71 | 70 | 120 |
| A3 | 28 | 1.68 | 72 | 121 |
| A4 | 26 | 1.83 | 71 | 130 |
| A5 | 27 | 1.8 | 75 | 135 |
| A6 | 26 | 1.77 | 90 | 159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mun, J.Y.; Cho, W.H.; Rehman, K. Multiscale Numerical Modeling of Wave Overtopping for Pedestrian Hazard Classification and Risk Assessment. J. Mar. Sci. Eng. 2025, 13, 2022. https://doi.org/10.3390/jmse13102022
Mun JY, Cho WH, Rehman K. Multiscale Numerical Modeling of Wave Overtopping for Pedestrian Hazard Classification and Risk Assessment. Journal of Marine Science and Engineering. 2025; 13(10):2022. https://doi.org/10.3390/jmse13102022
Chicago/Turabian StyleMun, Jong Yoon, Wan Hee Cho, and Khawar Rehman. 2025. "Multiscale Numerical Modeling of Wave Overtopping for Pedestrian Hazard Classification and Risk Assessment" Journal of Marine Science and Engineering 13, no. 10: 2022. https://doi.org/10.3390/jmse13102022
APA StyleMun, J. Y., Cho, W. H., & Rehman, K. (2025). Multiscale Numerical Modeling of Wave Overtopping for Pedestrian Hazard Classification and Risk Assessment. Journal of Marine Science and Engineering, 13(10), 2022. https://doi.org/10.3390/jmse13102022








