From Kelvin Wave Patterns to Ship Displacement: An Inverse Prediction Framework Based on a Hull Form Database
Abstract
1. Introduction
2. Theory and Prediction of Kelvin Ship Waves
2.1. Analytical Formulation of Wave Elevation
2.2. Determination of the Wave Amplitude Function
2.3. Simplified Expression for the Kelvin Ship Waves
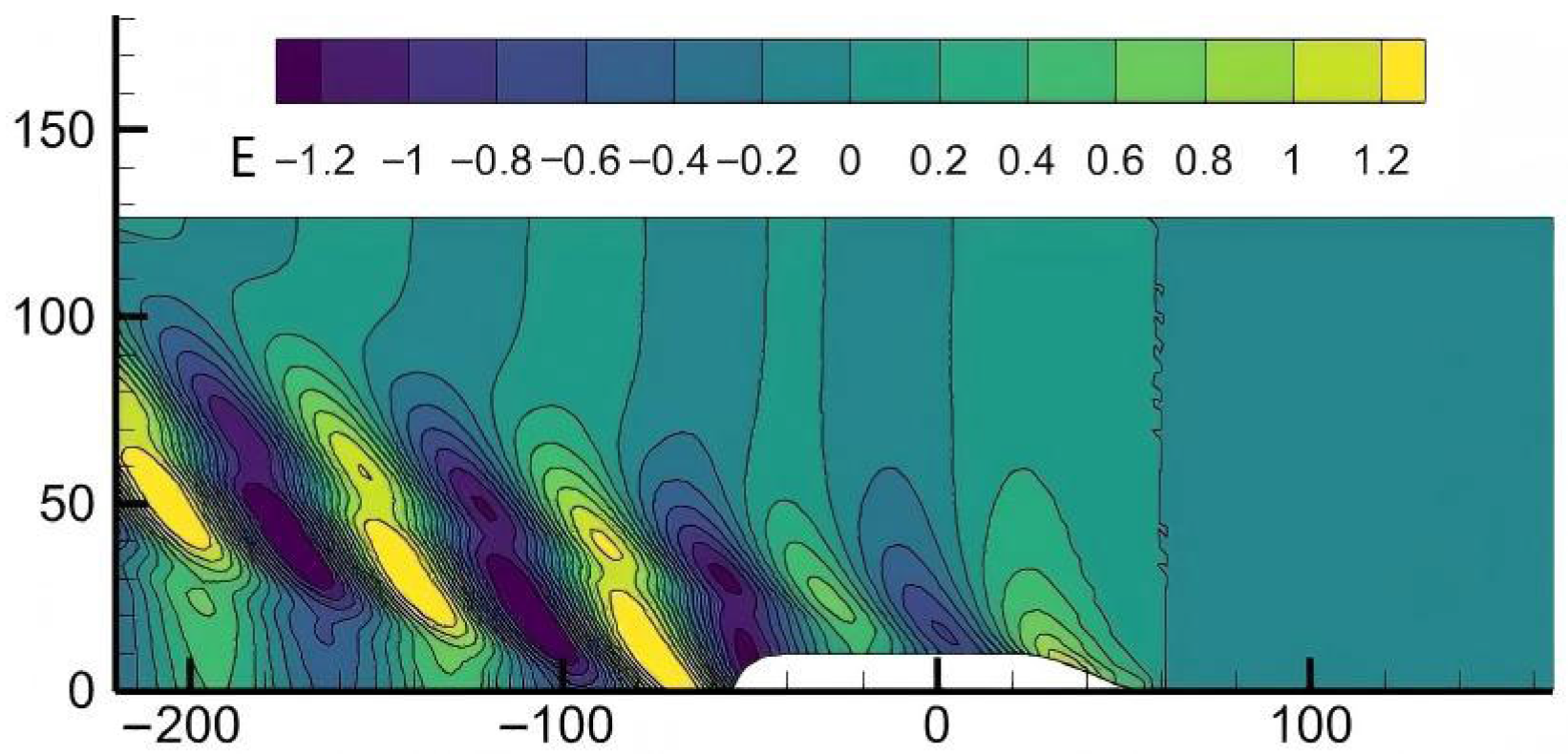
3. Fourier Series Representation of the Wave Elevation
3.1. Fourier Series Approximation of and
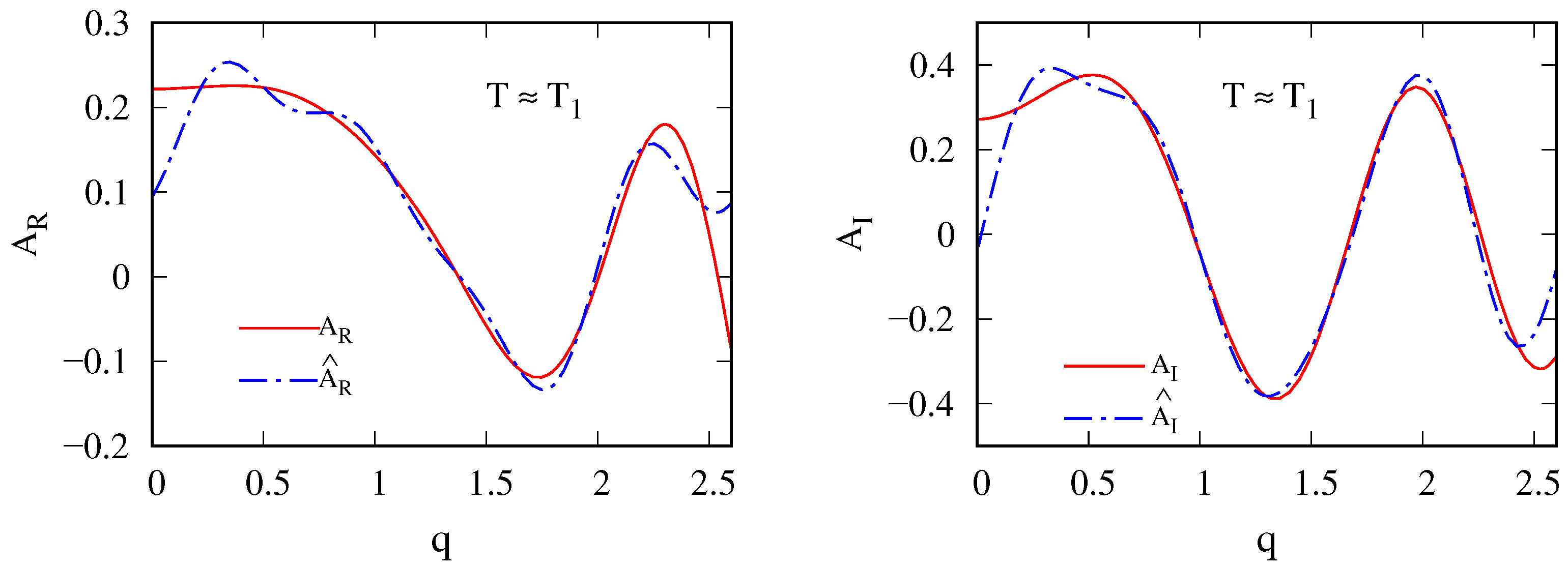
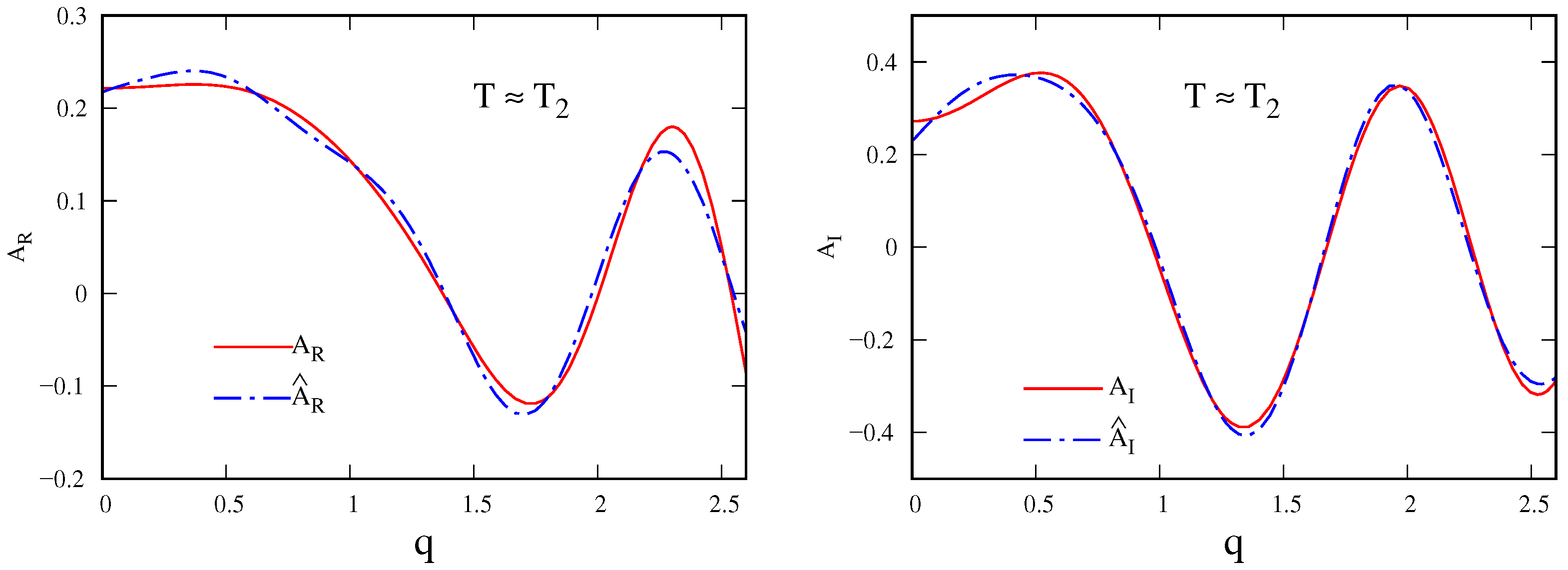
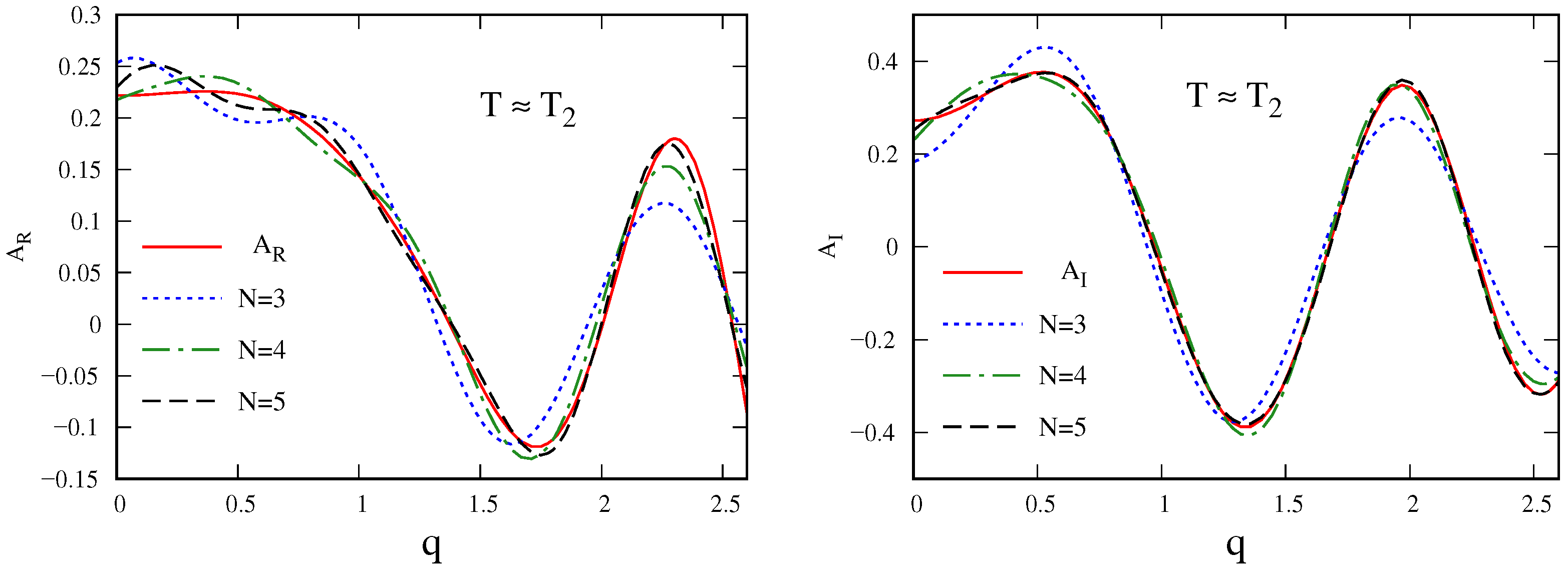
3.2. Realistic Determination of Parameters T And N
3.2.1. Extension of the Period T
3.2.2. Determination of the Number of Retained Terms N
3.3. Fourier Expansions of Wave Elevation
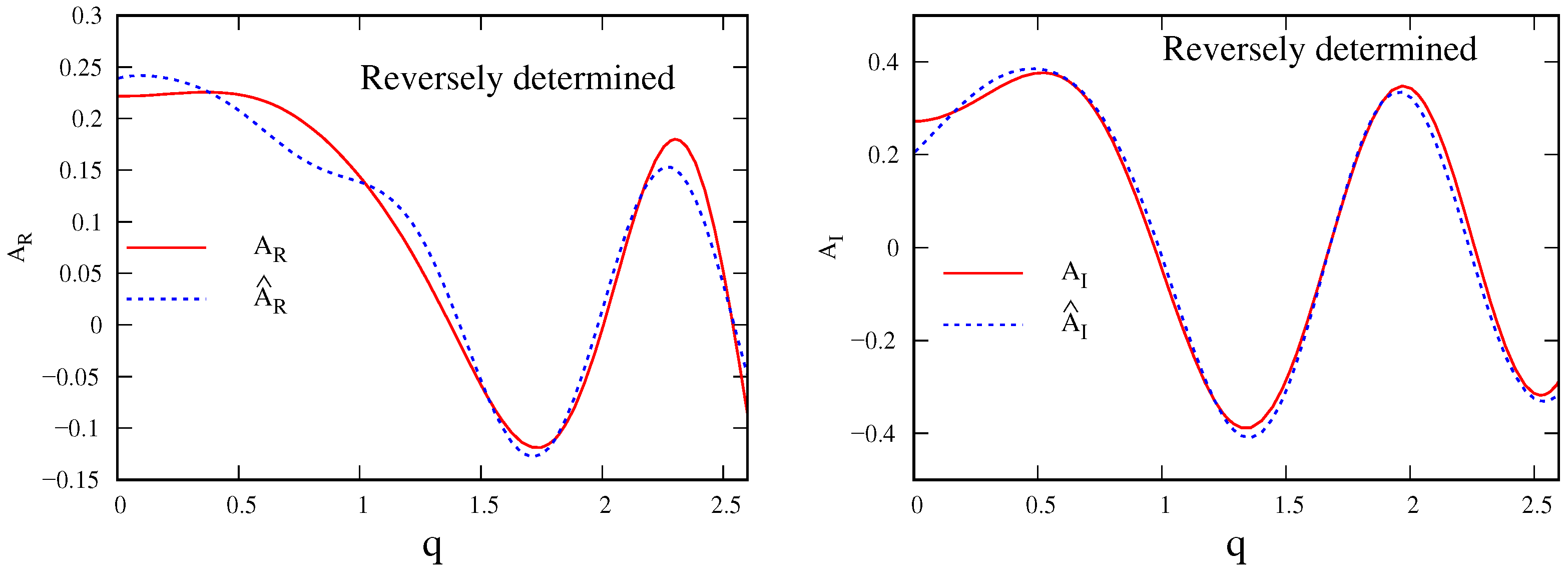
3.4. Inverse Estimation of the Wave Amplitude Function
4. Determination of Ship Displacement Volume
4.1. Candidate Hull Form Database
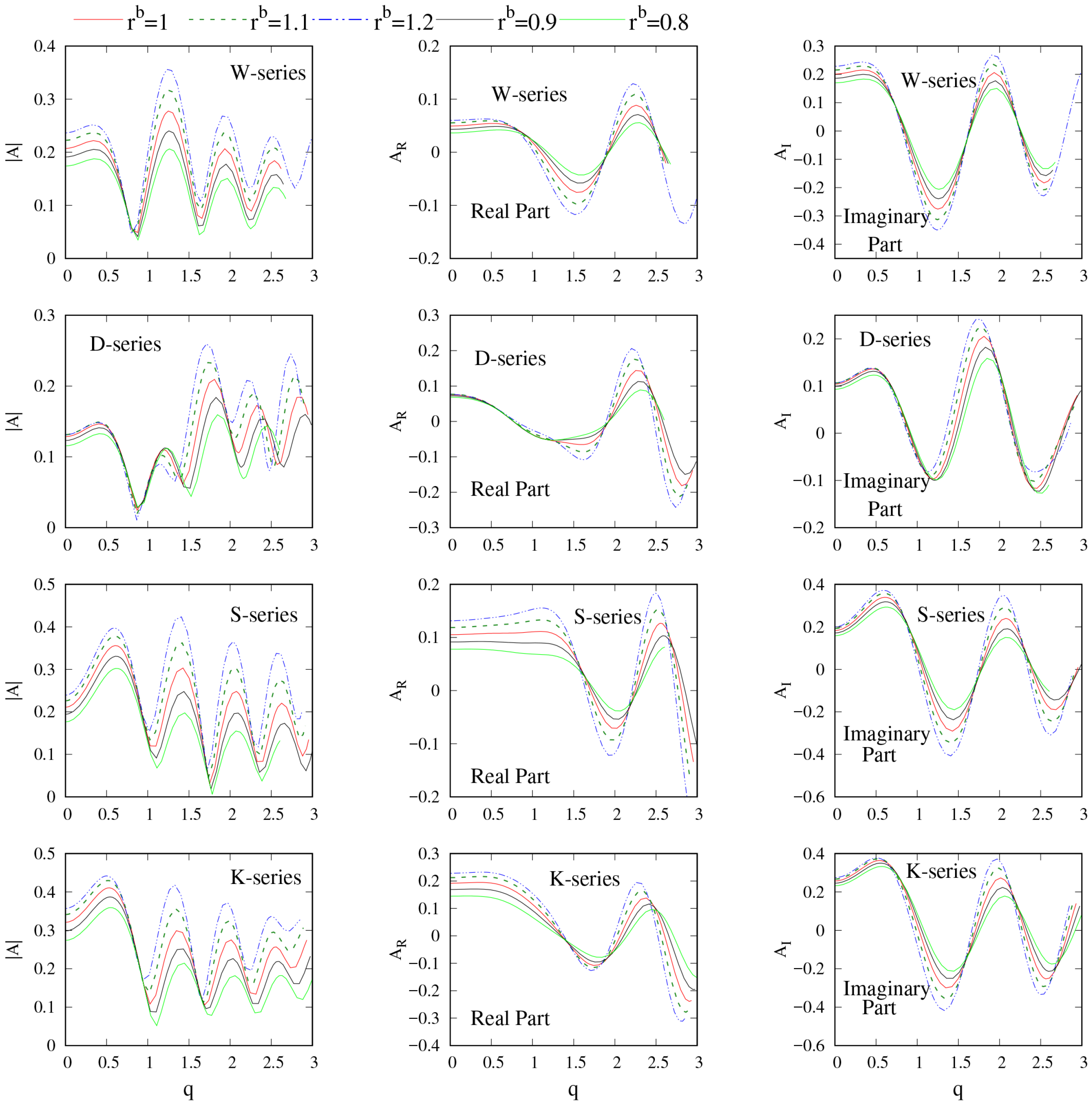
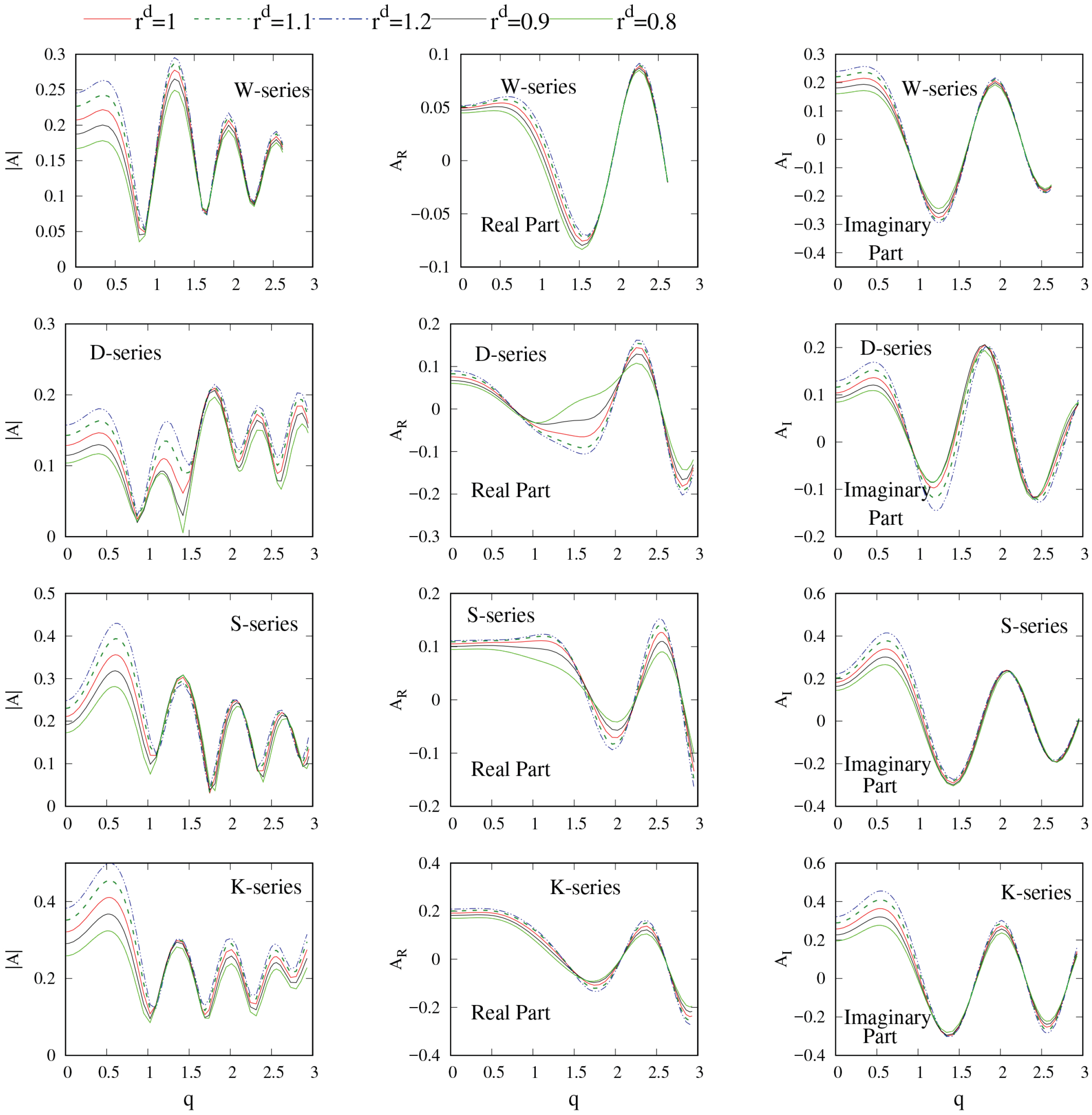
4.2. Characteristics of the Wave Amplitude Function
4.3. Inverse Prediction of Displacement Volume
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, K.; Zhang, H.; Liang, J.; Chen, P.; Xu, B.; Zhang, M. Analysis of ship wake features and extraction of ship motion parameters from SAR images in the Yellow Sea. Front. Earth Sci. 2019, 13, 588–595. [Google Scholar] [CrossRef]
- Shariati, S.; Hossein, M. Identification of underwater vehicles using surface wave pattern. Appl. Ocean. Res. 2018, 78, 281–289. [Google Scholar] [CrossRef]
- Newman, N. The Inverse Ship-Wave Problem. In Proceedings of the Sixth International Workshop on Water Waves and Floating Bodies, Manchester, UK, 25–28 March 1990; MIT: Cambridge, MA, USA, 1991; pp. 193–197. [Google Scholar]
- Wu, Z. On the Estimation of a Moving Ship’s Velocity and Hull Geometry Information from its Wave Spectra. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1991. [Google Scholar]
- Zilman, G.; Zapolski, A.; Marom, M. SAR Imaging of Ship Wakes and Inverse Ship Wake Problem; IWWWFB Workshop: Ramat-Aviv, Israel, 2004. [Google Scholar]
- Wang, J.; Guo, L.; Wei, Y.; Chai, S. Study on ship Kelvin wake detection in numerically simulated SAR images. Remote Sens. 2023, 15, 1089. [Google Scholar] [CrossRef]
- O’Connor, L.; Lecoanet, D.; Anders, E.H.; Augustson, K.C.; Burns, K.J.; Vasil, G.M.; Brown, B.P. Iterative methods for Navier-Stokes inverse problems. Phys. Rev. 2024, 109, 045108. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Gong, Y.; Zhang, X. An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR. Sensors 2025, 25, 4508. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Wang, S.; Zhao, P.; Chen, Y.; Wang, J. Modeling Kelvin wake imaging mechanism of visible spectral remote sensing. Appl. Ocean. Res. 2021, 113, 102712. [Google Scholar] [CrossRef]
- Xu, C.; Qi, R.; Wang, X.; Sun, Z. Identifiability of Kelvin wakes in SAR imageries: The role of time-varying characteristics and decoherence effect of wake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 20197–20213. [Google Scholar] [CrossRef]
- Hao, X. Inferring free surface disturbance properties from Kelvin wakes using convolutional neural network. Flow 2025, 5, E9. [Google Scholar] [CrossRef]
- Liang, H.; Li, Y.; Chen, X. An Earth-fixed observer to ship waves. J. Fluid Mech. 2024, 984, A14. [Google Scholar] [CrossRef]
- Gao, M.; Fang, S.; Wan, L.; Kang, W.; Ma, L.; He, Y.; Zhao, K. Ship-VNet: An algorithm for ship velocity analysis based on optical remote sensing imagery containing Kelvin wakes. Electronics 2024, 13, 3468. [Google Scholar] [CrossRef]
- Rizaev, G.; Achim, A. A Synthetic SAR dataset for deep learning classification of ships at sea. Remote Sens. 2022, 14, 3999. [Google Scholar] [CrossRef]
- Ma, C.; Liu, Z.; Yang, Y.; Zhan, C.; Chen, X.; Feng, B.; Chang, H. The reverse prediction of the ship principal dimensions based on the Kelvin ship waves. Ocean. Eng. 2023, 285, 115308. [Google Scholar] [CrossRef]
- Noblesse, F.; Huang, F.; Yang, C. The Neumann–Michell theory of ship waves. J. Eng. Math. 2013, 79, 51–71. [Google Scholar] [CrossRef]
- Noblesse, F.; He, J.; Zhu, Y.; Hong, L.; Zhang, C.; Zhu, R.; Yang, C. Why can ship wakes appear narrower than Kelvin’s angle. Eur. J. Mech. B Fluids 2014, 46, 164–171. [Google Scholar] [CrossRef]
- Huang, F.; Yang, C.; Noblesse, F. Numerical implementation and validation of the Neumann–Michell theory of ship waves. Eur. J. Mech. B Fluids 2013, 42, 47–68. [Google Scholar] [CrossRef]
- Ma, C.; Zhan, C.; Peng, S.; Wu, D.; Dong, Z.; Fan, L.; Liu, Z. The near-field wave interference of the steadily advancing monohull ships. Ocean. Eng. 2023, 275, 114147. [Google Scholar] [CrossRef]
- Zhang, C.; He, J.; Zhu, Y.; Li, W.; Noblesse, F.; Huang, F.; Yang, C. Stationary phase and numerical evaluation of far-field and near-field ship waves. Eur. J. Mech. B Fluids 2015, 52, 28–37. [Google Scholar] [CrossRef]


| B | D | ∇ | |
|---|---|---|---|
| 110 | 17.52 | 5.11 | 6337 |
| No. | E (m) | (m) | (m) |
|---|---|---|---|
| 1 | 1.335 | −214.138 | 56.796 |
| 2 | 1.485 | −210.228 | 54.214 |
| 3 | 0.201 | −208.24 | 23.235 |
| 4 | 0.376 | −206.289 | 30.98 |
| 5 | 0.113 | −206.253 | 2.582 |
| 6 | 0.335 | −204.312 | 18.071 |
| 7 | −1.456 | −180.893 | 49.051 |
| 8 | −0.088 | −178.839 | 23.235 |
| 9 | −1.322 | −175.027 | 49.051 |
| 10 | −0.547 | −169.001 | 15.49 |
| 11 | −1.108 | −161.24 | 30.98 |
| 12 | −0.263 | −159.311 | 36.143 |
| 13 | 0.551 | −157.383 | 41.306 |
| 14 | −0.414 | −155.271 | 15.49 |
| 15 | −0.428 | −151.381 | 20.653 |
| 16 | 0.236 | −147.478 | 23.235 |
| 17 | 0.092 | −145.41 | 7.745 |
| 18 | 0.34 | −141.541 | 15.49 |
| n | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0.143 | 0.097 | 0.029 | 0.077 | −0.036 | |
| - | 0.082 | 0.077 | −0.058 | −0.006 | |
| 0.096 | 0.161 | 0.135 | −0.177 | 0.036 | |
| - | 0.069 | 0.158 | −0.103 | 0.057 |
| Target Ship | |||||
|---|---|---|---|---|---|
| 4.41 | 4.11 | 3.35 | 3.16 | 1.39 | 1.25 |
| W-Series | |||||||
|---|---|---|---|---|---|---|---|
| No. | |||||||
| 1 | 2.22 | 2.78 | 2.07 | 2.07 | 0.49 | 0.75 | 7.29 |
| 2 | 1.78 | 2.49 | 1.93 | 1.67 | 0.36 | 0.8 | 8.64 |
| 3 | 2 | 2.65 | 2 | 1.87 | 0.45 | 0.78 | 7.92 |
| 4 | 2.43 | 2.88 | 2.12 | 2.27 | 0.51 | 0.74 | 6.72 |
| 5 | 2.63 | 2.95 | 2.17 | 2.45 | 0.53 | 0.74 | 6.2 |
| 6 | 1.88 | 2.06 | 1.51 | 1.74 | 0.35 | 0.45 | 9.68 |
| 7 | 2.05 | 2.4 | 1.78 | 1.91 | 0.41 | 0.61 | 8.51 |
| 8 | 2.37 | 3.17 | 2.36 | 2.22 | 0.51 | 0.92 | 6.12 |
| 9 | 2.52 | 3.56 | 2.68 | 2.36 | 0.46 | 1.08 | 5.01 |
| D-series | |||||||
| No. | |||||||
| 1 | 1.47 | 1.1 | 2.09 | 1.29 | 0.25 | 0.61 | 10.86 |
| 2 | 1.17 | 0.89 | 1.97 | 1.04 | 0.22 | 0.05 | 12.33 |
| 3 | 1.3 | 0.92 | 2.06 | 1.15 | 0.2 | 0.3 | 11.74 |
| 4 | 1.63 | 1.35 | 2.12 | 1.43 | 0.28 | 0.89 | 9.97 |
| 5 | 1.8 | 1.63 | 2.15 | 1.57 | 0.3 | 1.01 | 9.21 |
| 6 | 1.33 | 1.12 | 1.59 | 1.16 | 0.29 | 0.44 | 11.74 |
| 7 | 1.41 | 1.13 | 1.84 | 1.23 | 0.28 | 0.56 | 11.22 |
| 8 | 1.49 | 1.02 | 2.33 | 1.31 | 0.19 | 0.71 | 10.62 |
| 9 | 1.49 | 0.9 | 2.6 | 1.31 | 0.11 | 0.66 | 10.6 |
| S-series | |||||||
| No. | |||||||
| 1 | 3.56 | 3.03 | 2.48 | 2.11 | 1.19 | 0.3 | 5 |
| 2 | 2.81 | 3.08 | 2.34 | 1.73 | 0.76 | 0.37 | 6.58 |
| 3 | 3.18 | 3.09 | 2.43 | 1.92 | 0.99 | 0.38 | 5.68 |
| 4 | 3.94 | 2.96 | 2.5 | 2.3 | 1.21 | 0.33 | 4.43 |
| 5 | 4.3 | 2.88 | 2.5 | 2.48 | 1.23 | 0.41 | 3.87 |
| 6 | 3.02 | 1.98 | 1.55 | 1.76 | 0.68 | 0.06 | 8.62 |
| 7 | 3.31 | 2.48 | 1.97 | 1.94 | 0.91 | 0.18 | 6.88 |
| 8 | 3.78 | 3.62 | 3.04 | 2.26 | 1.34 | 0.44 | 3.19 |
| 9 | 3.98 | 4.23 | 3.65 | 2.39 | 1.54 | 0.6 | 2.41 |
| K-series | |||||||
| No. | |||||||
| 1 | 4.11 | 2.99 | 2.75 | 3.21 | 1.08 | 1.06 | 2.58 |
| 2 | 3.24 | 2.82 | 2.38 | 2.59 | 0.85 | 0.97 | 4.82 |
| 3 | 3.67 | 2.95 | 2.59 | 2.91 | 0.96 | 0.98 | 3.61 |
| 4 | 4.55 | 3.01 | 2.9 | 3.52 | 1.2 | 1.17 | 2.32 |
| 5 | 5 | 3.02 | 3.05 | 3.83 | 1.22 | 1.29 | 2.87 |
| 6 | 3.59 | 2.14 | 1.82 | 2.74 | 0.52 | 0.79 | 6.07 |
| 7 | 3.87 | 2.51 | 2.27 | 2.98 | 0.87 | 0.96 | 4.21 |
| 8 | 4.3 | 3.56 | 3.25 | 3.41 | 1.38 | 1.12 | 1.16 |
| 9 | 4.42 | 4.18 | 3.72 | 3.57 | 1.71 | 1.2 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Wang, L.; Zhao, Y.; Yang, H.; Huang, H.; Cao, B. From Kelvin Wave Patterns to Ship Displacement: An Inverse Prediction Framework Based on a Hull Form Database. J. Mar. Sci. Eng. 2025, 13, 2019. https://doi.org/10.3390/jmse13102019
Ma C, Wang L, Zhao Y, Yang H, Huang H, Cao B. From Kelvin Wave Patterns to Ship Displacement: An Inverse Prediction Framework Based on a Hull Form Database. Journal of Marine Science and Engineering. 2025; 13(10):2019. https://doi.org/10.3390/jmse13102019
Chicago/Turabian StyleMa, Chao, Linwei Wang, Yingjiang Zhao, Haolin Yang, Haoqing Huang, and Bohan Cao. 2025. "From Kelvin Wave Patterns to Ship Displacement: An Inverse Prediction Framework Based on a Hull Form Database" Journal of Marine Science and Engineering 13, no. 10: 2019. https://doi.org/10.3390/jmse13102019
APA StyleMa, C., Wang, L., Zhao, Y., Yang, H., Huang, H., & Cao, B. (2025). From Kelvin Wave Patterns to Ship Displacement: An Inverse Prediction Framework Based on a Hull Form Database. Journal of Marine Science and Engineering, 13(10), 2019. https://doi.org/10.3390/jmse13102019





