Dynamics of Offshore Wind Turbine Foundation: A Critical Review and Future Directions
Abstract
1. Introduction
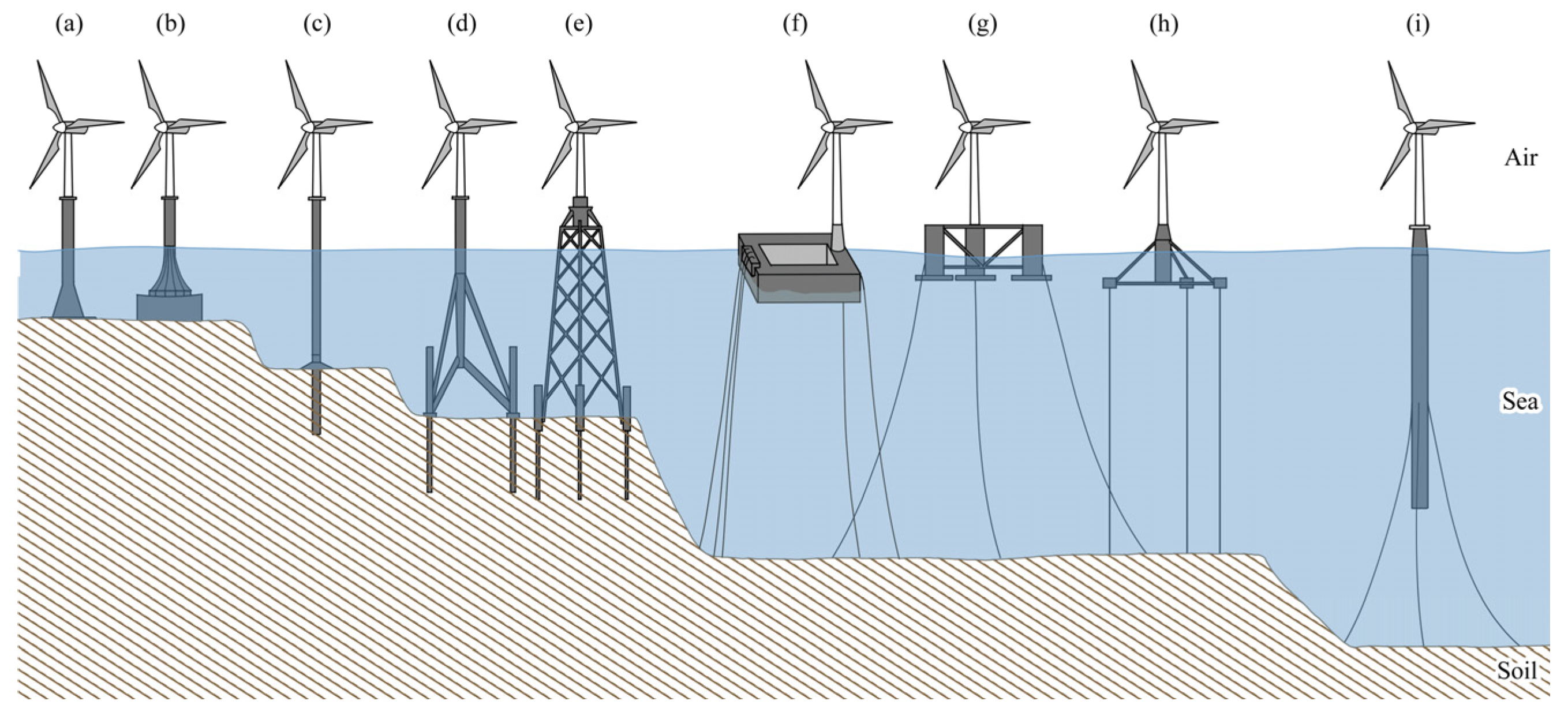
2. Structural Foundation Types of OWTs
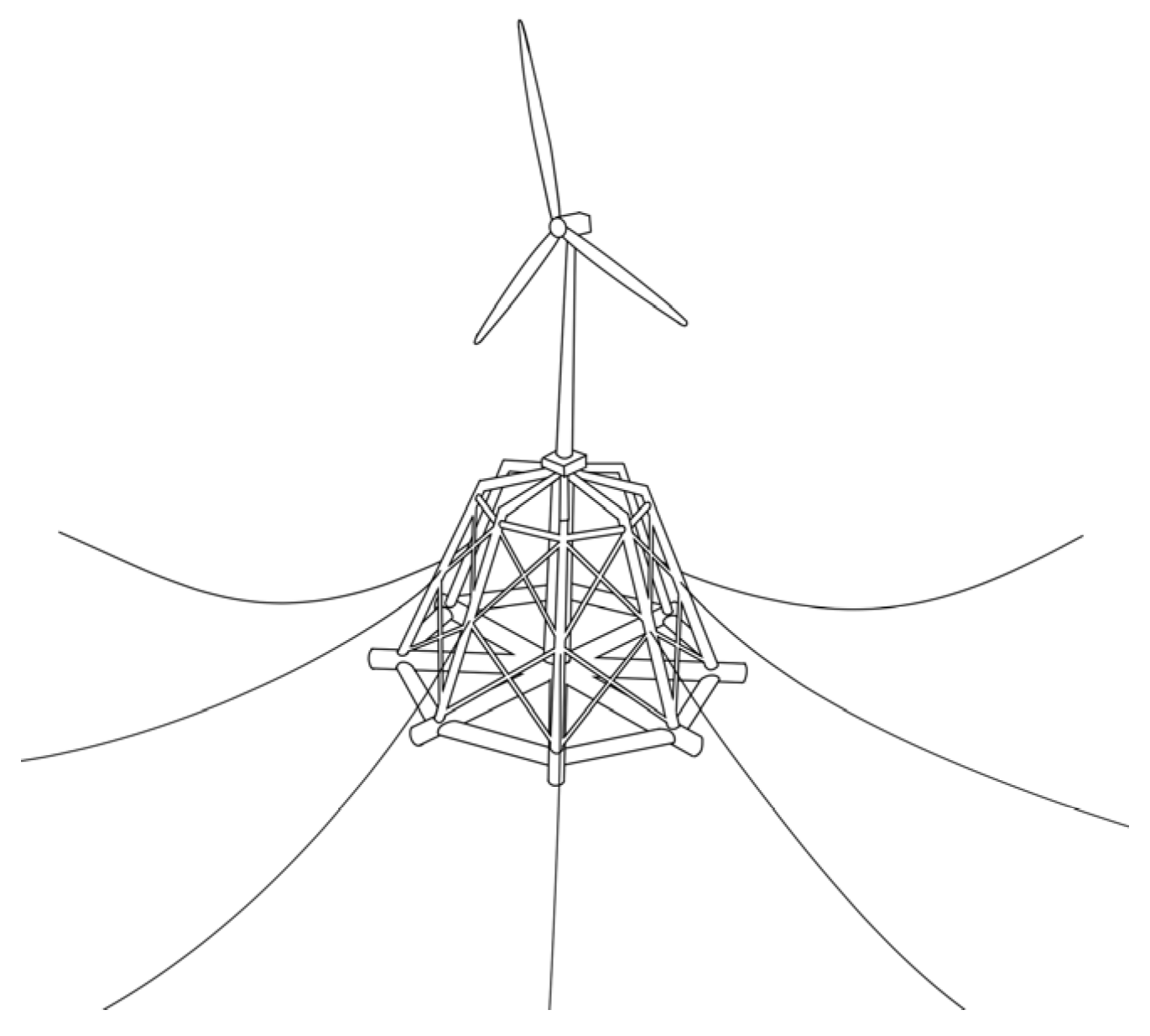
2.1. Foundation of Fixed Wind Turbines
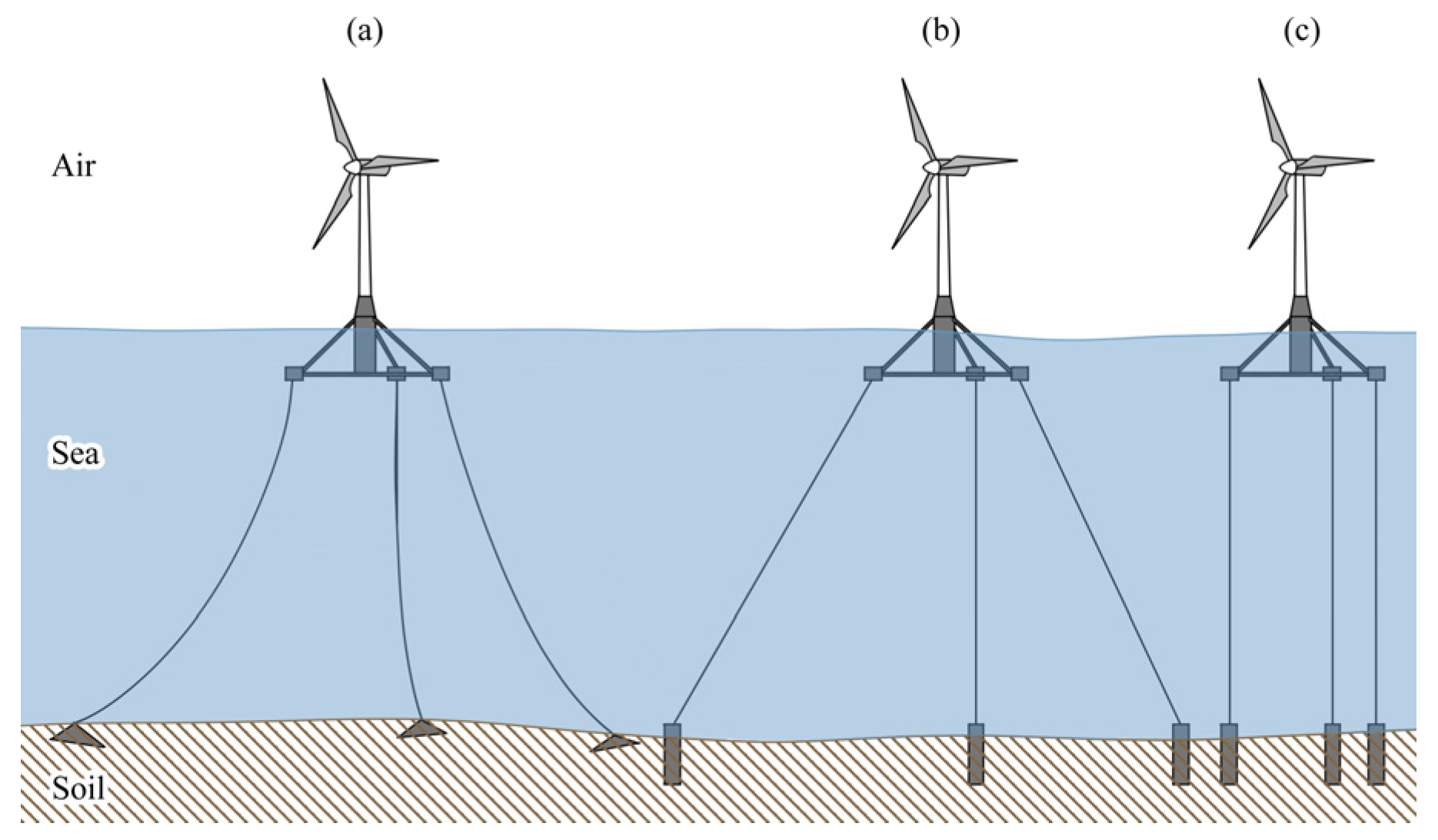
2.2. Floating Wind Turbine Foundation
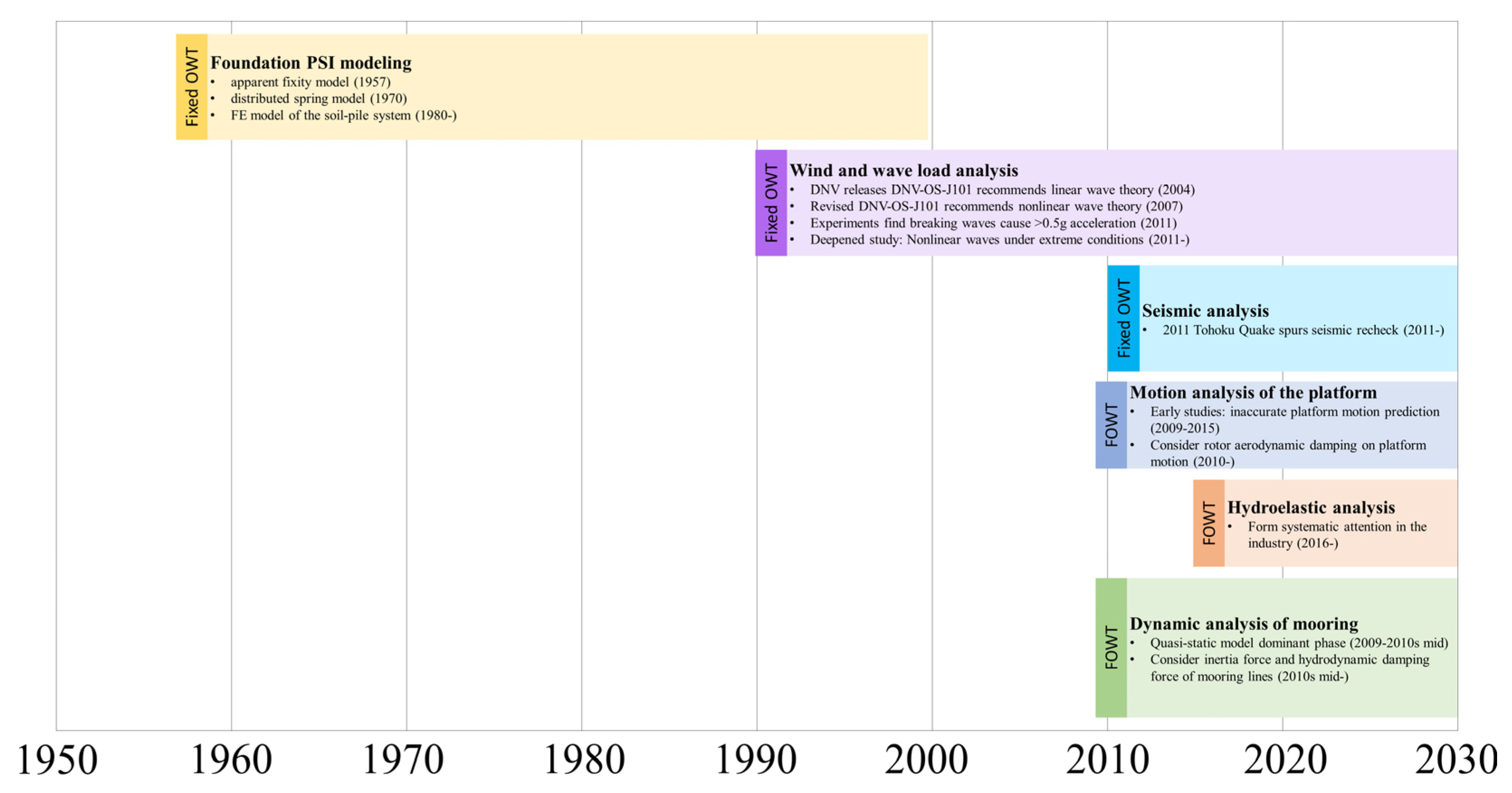
3. Dynamics of Fixed OWT Foundations
3.1. PSI Analysis
3.2. Wind and Wave Load Analysis
3.3. Seismic Analysis
4. Dynamics of FOWT Foundations
4.1. Motion Analysis of the Platform
4.2. Hydroelastic Analysis
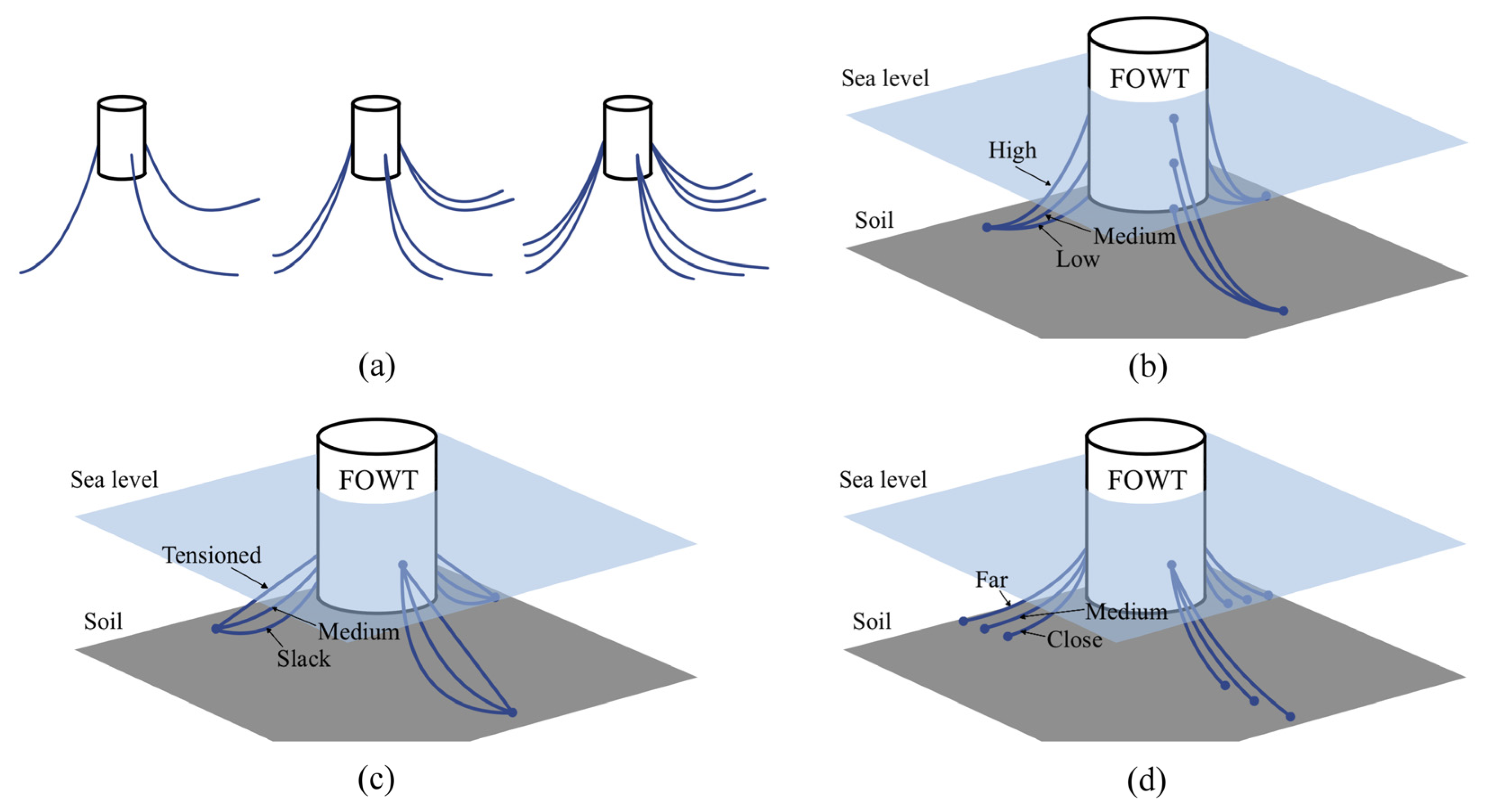
4.3. Dynamic Analysis of Mooring
5. Conclusions
- Under current technological conditions, the disadvantages of fixed offshore wind turbines appear when water depth exceeds 60 m, and FOWTs show higher engineering economic efficiency. However, FOWT has not realized industrial operation, and the stand-alone capacity of OWTs is increasing continuously. Optimizing and breaking mechanical performances of fixed offshore wind turbine foundations have been one of the key directions for industrial and academic studies.
- Uncertainty of soil properties may influence the dynamic response analysis of wind turbines significantly. Although there are many associated research achievements, it is still difficult to correct complicated soil models under cyclic loads and PSI parameters.
- The study of wave loads on OWTs, although some progress has been achieved, still faces some problems that involve the uncertainty of wave prediction and the multi-field load-coupling effect of wind, sea waves, and ice floes.
- Scouring and liquefaction are two major challenges against fixed wind turbine foundations under seismic effects. Studies about influences of scouring depth on dynamic responses are in the preliminary stage, lacking field verification and accurate evaluation. Liquefaction problems involve multi-field coupling effects, and it is difficult for experimental studies to simulate interactive effects in complicated marine environments completely.
- The highly stable and highly reliable dynamics of floating foundations are key to guaranteeing the long-term safe and stable services of FOWTs. Exploring and breaking the mechanical properties of the FOWT foundation are core problems in industry and academic circles. With references to marine engineering technologies, FOWTs have optimized the reliability and comprehensive economic benefits of the system. The stability principle and geometric size are used as major factors, and different technological ideas of stability optimization are adopted.
- Mechanical performances of foundations in academia and industry have insufficient understanding, resulting in disputes over structural safety and stability. Differences between FOWTs and traditional marine platforms in pneumatic loads should also be explored deeply.
- Lack of large-scale experimental data, full-size experimental platforms on practical OTWs foundation, and complicated marine environmental simulation technology of experiments need further improvement.
- Hydroelastic problems are an important problem that should be considered. Particularly, the mechanism and characteristics of hydroelastic behaviors in floating multi-unit platforms and VLFS have to be studied deeply.
- Technical schemes to optimize stability and reliability and promote the sustainable development of offshore OWT foundations should be the focus of future research in this field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z. Foundations of Offshore Wind Turbines: A Review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural Dynamics of Offshore Wind Turbines: A Review. Ocean Eng. 2022, 251, 111136. [Google Scholar] [CrossRef]
- Musial, W.; Ram, B. Large-Scale Offshore Wind Power in the United States: Assessment of Opportunities and Barriers; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2010.
- Li, J.; Guo, Y.; Lian, J.; Wang, H. Mechanisms, Assessments, Countermeasures, and Prospects for Offshore Wind Turbine Foundation Scour Research. Ocean Eng. 2023, 281, 114893. [Google Scholar] [CrossRef]
- Leung, D.Y.; Yang, Y. Wind Energy Development and Its Environmental Impact: A Review. Renew. Sustain. Energy Rev. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Hou, G.; Xu, K.; Lian, J. A Review on Recent Risk Assessment Methodologies of Offshore Wind Turbine Foundations. Ocean Eng. 2022, 264, 112469. [Google Scholar] [CrossRef]
- Chen, P.; Jia, C.; Ng, C.; Hu, Z. Application of SADA Method on Full-Scale Measurement Data for Dynamic Responses Prediction of Hywind Floating Wind Turbines. Ocean Eng. 2021, 239, 109814. [Google Scholar] [CrossRef]
- Rezaei, F.; Contestabile, P.; Vicinanza, D.; Azzellino, A. Towards Understanding Environmental and Cumulative Impacts of Floating Wind Farms: Lessons Learned from the Fixed-Bottom Offshore Wind Farms. Ocean Coast. Manag. 2023, 243, 106772. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Enevoldsen, P.; Koch, C.; Barthelmie, R.J. Cost Performance and Risk in the Construction of Offshore and Onshore Wind Farms. Wind Energy 2017, 20, 891–908. [Google Scholar] [CrossRef]
- Myhr, A.; Bjerkseter, C.; Ågotnes, A.; Nygaard, T.A. Levelised Cost of Energy for Offshore Floating Wind Turbines in a Life Cycle Perspective. Renew. Energy 2014, 66, 714–728. [Google Scholar] [CrossRef]
- Lu, F.; Long, K.; Zhang, C.; Zhang, J.; Tao, T. A Novel Design of the Offshore Wind Turbine Tripod Structure Using Topology Optimization Methodology. Ocean Eng. 2023, 280, 114607. [Google Scholar] [CrossRef]
- Zeng, X.; Shi, W.; Feng, X.; Shao, Y.; Li, X. Investigation of Higher-Harmonic Wave Loads and Low-Frequency Resonance Response of Floating Offshore Wind Turbine under Extreme Wave Groups. Mar. Struct. 2023, 89, 103401. [Google Scholar] [CrossRef]
- Ikoma, T.; Tan, L.; Moritsu, S.; Aida, Y.; Masuda, K. Motion Characteristics of a Barge-Type Floating Vertical-Axis Wind Turbine with Moonpools. Ocean Eng. 2021, 230, 109006. [Google Scholar] [CrossRef]
- Xie, J.; Wang, H.; Cai, X.; Xin, Z.; Ren, L.; Cai, M. Comprehensive Analysis of the Typhoon-Induced Impact on Large Offshore Wind Turbines Using Different Floating Platforms. Ocean Eng. 2025, 342, 122880. [Google Scholar] [CrossRef]
- Lian, J.; Ye, F.; Wang, P.; Guo, Y.; Wang, H.; Xiao, T.; Xiong, D. Integrated Transportation of Offshore Wind Turbine and Bucket Foundation Based on a U and K Shaped Assembled Platform. Ocean Eng. 2023, 275, 114096. [Google Scholar] [CrossRef]
- Johnston, B.; Foley, A.; Doran, J.; Littler, T. Levelised Cost of Energy, A Challenge for Offshore Wind. Renew. Energy 2020, 160, 876–885. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Ishihara, T. Comparison of Dynamic Response and Levelized Cost of Energy on Three Platform Concepts of Floating Offshore Wind Turbine Systems. J. Phys. Conf. Ser. 2020, 1452, 012035. [Google Scholar] [CrossRef]
- Zhou, B.; Zheng, Z.; Hong, M.; Jin, P.; Wang, L.; Chen, F. Dynamic and Power Generation Features of A Wind–Wave Hybrid System Consisting of A Spar-Type Wind Turbine and An Annular Wave Energy Converter in Irregular Waves. China Ocean Eng. 2023, 37, 923–933. [Google Scholar] [CrossRef]
- Chen, M.; Xiao, P.; Zhou, H.; Li, C.B.; Zhang, X. Fully Coupled Analysis of an Integrated Floating Wind-Wave Power Generation Platform in Operational Sea-States. Front. Energy Res. 2022, 10, 931057. [Google Scholar] [CrossRef]
- Wang, K.; Li, Y.; Ong, M.C.; Wan, L.; Li, L.; Cheng, Z. Extreme Responses of An Integrated System with A Semi-Submersible Wind Turbine and Four Torus-Shaped Wave Energy Converters in Different Survival Modes. China Ocean Eng. 2024, 38, 877–892. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Sun, J.; Tan, M.; Yang, S.; Ying, Y.; Qian, P.; Zhang, D.; Si, Y. Load Reduction of Semi-Submersible Floating Wind Turbines by Integrating Heaving-Type Wave Energy Converters with Bang-Bang Control. Front. Energy Res. 2022, 10, 929307. [Google Scholar] [CrossRef]
- Petracca, E.; Faraggiana, E.; Ghigo, A.; Sirigu, M.; Bracco, G.; Mattiazzo, G. Design and Techno-Economic Analysis of a Novel Hybrid Offshore Wind and Wave Energy System. Energies 2022, 15, 2739. [Google Scholar] [CrossRef]
- Jin, J.; Su, B.; Dou, R.; Luan, C.; Li, L.; Nygaard, I.; Fonseca, N.; Gao, Z. Numerical Modelling of Hydrodynamic Responses of Ocean Farm 1 in Waves and Current and Validation against Model Test Measurements. Mar. Struct. 2021, 78, 103017. [Google Scholar] [CrossRef]
- Lei, Y.; Zheng, X.Y.; Li, W.; Zheng, H.; Zhang, Q.; Zhao, S.; Cai, X.; Ci, X.; He, Q. Experimental Study of the State-of-the-Art Offshore System Integrating a Floating Offshore Wind Turbine with a Steel Fish Farming Cage. Mar. Struct. 2021, 80, 103076. [Google Scholar] [CrossRef]
- Serpetti, N.; Benjamins, S.; Brain, S.; Collu, M.; Harvey, B.J.; Heymans, J.J.; Hughes, A.D.; Risch, D.; Rosinski, S.; Waggitt, J.J.; et al. Modeling Small Scale Impacts of Multi-Purpose Platforms: An Ecosystem Approach. Front. Mar. Sci. 2021, 8, 694013. [Google Scholar] [CrossRef]
- Xu, H.; Rui, S.; Shen, K.; Jiang, L.; Zhang, H.; Teng, L. Shared Mooring Systems for Offshore Floating Wind Farms: A Review. Energy Rev. 2024, 3, 100063. [Google Scholar] [CrossRef]
- Pillai, A.C.; Gordelier, T.J.; Thies, P.R.; Cuthill, D.; Johanning, L. Anchor Loads for Shallow Water Mooring of a 15 MW Floating Wind Turbine—Part II: Synthetic and Novel Mooring Systems. Ocean Eng. 2022, 266, 112619. [Google Scholar] [CrossRef]
- Rongé, É.; Peyrard, C.; Venugopal, V.; Xiao, Q.; Johanning, L.; Benoit, M. Evaluation of Second and Third-Order Numerical Wave-Loading Models for Floating Offshore Wind TLPs. Ocean Eng. 2023, 288, 116064. [Google Scholar] [CrossRef]
- Li, X.; Dai, G.; Zhu, M.; Wang, L.; Liu, H. A Simplified Method for Estimating the Initial Stiffness of Monopile—Soil Interaction Under Lateral Loads in Offshore Wind Turbine Systems. China Ocean Eng. 2023, 37, 165–174. [Google Scholar] [CrossRef]
- Belabed, Z.; Tounsi, A.; Bousahla, A.A.; Tounsi, A.; Bourada, M.; Al-Osta, M.A. Free Vibration Analysis of Bi-Directional Functionally Graded Beams Using a Simple and Efficient Finite Element Model. Struct. Eng. Mech. 2024, 90, 233–252. [Google Scholar]
- Dauji, S. Axial Capacity of FRP Reinforced Concrete Columns: Empirical, Neural and Tree Based Methods. Struct. Eng. Mech. 2024, 89, 283–300. [Google Scholar]
- Shi, S.; Zhai, E.; Xu, C.; Iqbal, K.; Sun, Y.; Wang, S. Influence of Pile-Soil Interaction on Dynamic Properties and Response of Offshore Wind Turbine with Monopile Foundation in Sand Site. Appl. Ocean Res. 2022, 126, 103279. [Google Scholar] [CrossRef]
- Xie, S.; Gao, J.; Li, Y.; Jiang, S.; Zhang, C.; He, J. Aero-Hydro-Elastic-Servo Modeling and Dynamic Response Analysis of A Monopile Offshore Wind Turbine Under Different Operating Scenarios. China Ocean Eng. 2024, 38, 379–393. [Google Scholar] [CrossRef]
- Seed, H.B.; Lymon, C.; Reese, A.M.A. The Action of Soft Clay along Friction Piles. Trans. Am. Soc. Civ. Eng. 1957, 122, 731–754. [Google Scholar] [CrossRef]
- Matlock, H. Correlation for Design of Laterally Loaded Piles in Soft Clay. In Proceedings of the Offshore Technology Conference, Huston, TX, USA, 21–23 April 1970; p. OTC-1204. [Google Scholar]
- Galvín, P.; Romero, A.; Solís, M.; Domínguez, J. Dynamic Characterisation of Wind Turbine Towers Account for a Monopile Foundation and Different Soil Conditions. Struct. Infrastruct. Eng. 2017, 13, 942–954. [Google Scholar] [CrossRef]
- Yang, S.; Deng, X.; Yang, J. Modeling of Soil-Pile-Structure Interaction for Dynamic Response of Standalone Wind Turbines. Renew. Energy 2022, 186, 394–410. [Google Scholar] [CrossRef]
- Depina, I.; Le, T.M.H.; Eiksund, G.; Benz, T. Behavior of Cyclically Loaded Monopile Foundations for Offshore Wind Turbines in Heterogeneous Sands. Comput. Geotech. 2015, 65, 266–277. [Google Scholar] [CrossRef]
- Ma, H.; Yang, J.; Chen, L. Numerical Analysis of the Long-Term Performance of Offshore Wind Turbines Supported by Monopiles. Ocean Eng. 2017, 136, 94–105. [Google Scholar] [CrossRef]
- Yi, J.-H.; Kim, S.-B.; Yoon, G.-L.; Andersen, L.V. Natural Frequency of Bottom-Fixed Offshore Wind Turbines Considering Pile-Soil-Interaction with Material Uncertainties and Scouring Depth. Wind Struct. 2015, 21, 625–639. [Google Scholar] [CrossRef]
- Ren, X.; Xu, Y.; Shen, T.; Wang, Y.; Bhattacharya, S. Support Condition Monitoring of Monopile-Supported Offshore Wind Turbines in Layered Soil Based on Model Updating. Mar. Struct. 2023, 87, 103342. [Google Scholar] [CrossRef]
- Shirzadeh, R.; Devriendt, C.; Bidakhvidi, M.A.; Guillaume, P. Experimental and Computational Damping Estimation of an Offshore Wind Turbine on a Monopile Foundation. J. Wind Eng. Ind. Aerodyn. 2013, 120, 96–106. [Google Scholar] [CrossRef]
- Yeter, B.; Garbatov, Y.; Soares, C.G. Uncertainty Analysis of Soil-Pile Interactions of Monopile Offshore Wind Turbine Support Structures. Appl. Ocean Res. 2019, 82, 74–88. [Google Scholar] [CrossRef]
- DNV-OS-J101; Offshore Standard Design of Offshore Wind Turbine Structures. Det Norske Veritas: Høvik, Norway, 2004.
- Wedel-Heinen, J.; Ronold, K.O.; Madsen, P.H. Revision of DNV Design Standard for Offshore Wind Turbine Structures. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; Volume 42711, pp. 433–439. [Google Scholar]
- de Ridder, E.J.; Aalberts, P.; van den Berg, J.; Buchner, B.; Peeringa, J. The Dynamic Response of an Offshore Wind Turbine with Realistic Flexibility to Breaking Wave Impact. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 44373, pp. 543–552. [Google Scholar]
- Yu, D.; Ye, J.; Yin, C. Dynamics of Offshore Wind Turbine and Its Seabed Foundation under Combined Wind-Wave Loading. Ocean Eng. 2023, 286, 115624. [Google Scholar] [CrossRef]
- Chen, D.; Gao, P.; Huang, S.; Li, C.; Yu, X. Static and Dynamic Loading Behavior of a Hybrid Foundation for Offshore Wind Turbines. Mar. Struct. 2020, 71, 102727. [Google Scholar] [CrossRef]
- Cao, G.; Chen, Z.; Wang, C.; Ding, X. Dynamic Responses of Offshore Wind Turbine Considering Soil Nonlinearity and Wind-Wave Load Combinations. Ocean Eng. 2020, 217, 108155. [Google Scholar] [CrossRef]
- Charlton, T.S.; Rouainia, M. Geotechnical Fragility Analysis of Monopile Foundations for Offshore Wind Turbines in Extreme Storms. Renew. Energy 2022, 182, 1126–1140. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Xie, J. A Hybrid-Separate Strategy for Force Identification of the Nonlinear Structure under Impact Excitation. Struct. Eng. Mech. 2023, 85, 119–133. [Google Scholar]
- Jose, J.; Podrazka, O.; Obhrai, C.; Gudmestad, O.T.; Cieslikiewicz, W. Methods for Analysing Wave Slamming Loads on Truss Structures Used in Offshore Wind Applications Based on Experimental Data. Int. J. Offshore Polar Eng. 2016, 26, 100–108. [Google Scholar] [CrossRef]
- Paulsen, B.T.; de Sonneville, B.; van der Meulen, M.; Jacobsen, N.G. Probability of Wave Slamming and the Magnitude of Slamming Loads on Offshore Wind Turbine Foundations. Coast. Eng. 2019, 143, 76–95. [Google Scholar] [CrossRef]
- Wei, C.; Yu, S.; Du, J.; Wang, W. Model Test Method for Dynamic Responses of Bridge Towers Subjected to Waves. Struct. Eng. Mech. 2023, 86, 705–714. [Google Scholar]
- Lin, Y.-H.; Hasan, A.D. Transient Analysis of the Slamming Wave Load on an Offshore Wind Turbine Foundation Generated by Different Types of Breaking Waves. J. Renew. Sustain. Energy 2022, 14, 053302. [Google Scholar] [CrossRef]
- Zhu, J.; Gao, Y.; Wang, L.; Li, W. Experimental Investigation of Breaking Regular and Irregular Waves Slamming on an Offshore Monopile Wind Turbine. Mar. Struct. 2022, 86, 103270. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Goda, K. Use of Offshore Wind Farms to Increase Seismic Resilience of Nuclear Power Plants. Soil Dyn. Earthq. Eng. 2016, 80, 65–68. [Google Scholar] [CrossRef]
- Parate, K.; Kumbhar, O.; Kumar, R. Simplified Beam-Column Joint Model for Reinforced Concrete Moment Resisting Frames. Struct. Eng. Mech. 2024, 89, 77–91. [Google Scholar]
- Luco, J.E. Soil-Structure Interaction Effects on the Seismic Response of Tall Chimneys. Soil Dyn. Earthq. Eng. 1986, 5, 170–177. [Google Scholar] [CrossRef]
- Xi, R.; Xu, C.; Du, X.; Naggar, M.H.E.; Wang, P.; Liu, L.; Zhai, E. Framework for Dynamic Response Analysis of Monopile Supported Offshore Wind Turbine Excited by Combined Wind-Wave-Earthquake Loading. Ocean Eng. 2022, 247, 110743. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Y.; Zhang, X.; Xi, R.; Du, X. A Substructure Method for Seismic Responses of Offshore Wind Turbine Considering Nonlinear Pile-Soil Dynamic Interaction. Soil Dyn. Earthq. Eng. 2021, 144, 106684. [Google Scholar] [CrossRef]
- Panagoulias, S.; de Winter, C.; Navalkar, S.T.; Nernheim, A. Sensitivity of the Seismic Response of Monopile-Supported Offshore Wind Turbines to Soil Variability. Ocean Eng. 2023, 268, 113545. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Shi, W.; Li, X.; Li, Y. Dynamic Responses of Monopile Wind Turbine with Coupled Spring Boundaries in Bed Rock-Soil-Seawater Offshore Site under Offshore Ground Motions. Soil Dyn. Earthq. Eng. 2022, 158, 107311. [Google Scholar] [CrossRef]
- Ju, S.-H.; Huang, Y.-C. Analyses of Offshore Wind Turbine Structures with Soil-Structure Interaction under Earthquakes. Ocean Eng. 2019, 187, 106190. [Google Scholar] [CrossRef]
- Kaynia, A.M. Seismic Considerations in Design of Offshore Wind Turbines. Soil Dyn. Earthq. Eng. 2019, 124, 399–407. [Google Scholar] [CrossRef]
- Gao, B.; Ye, G.; Zhang, Q.; Xie, Y.; Yan, B. Numerical Simulation of Suction Bucket Foundation Response Located in Liquefiable Sand under Earthquakes. Ocean Eng. 2021, 235, 109394. [Google Scholar] [CrossRef]
- Ko, Y.-Y.; Li, Y.-T. Response of a Scale-model Pile Group for a Jacket Foundation of an Offshore Wind Turbine in Liquefiable Ground during Shaking Table Tests. Earthq. Eng. Struct. Dyn. 2020, 49, 1682–1701. [Google Scholar] [CrossRef]
- Hong-yan, D.; Jing-yi, L.I.; Cong-huan, L.E.; Chen, P.A.N.; Pu-yang, Z. Shaking Table Tests of Four-Bucket Jacket Foundation for Offshore Wind Turbines. China Ocean Eng. 2022, 36, 849–858. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Kim, J.; Jang, H.; Shen, Z.-R.; Koop, A.; Bunnik, T.; Yu, K. Validation of CFD Simulations of the Moored DeepCwind Offshore Wind Semisubmersible in Irregular Waves. Ocean Eng. 2022, 260, 112028. [Google Scholar] [CrossRef]
- Siegerstetter, L.A.; Kleinschroth, A. Wave Forces on Vertical Cylinders as a Basis for the Design of Offshore Structures. Appl. Math. Model. 1976, 1, 119–124. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; University of Colorado: Boulder, CO, USA, 2007; ISBN 0-549-31549-7. [Google Scholar]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The Force Exerted by Surface Waves on Piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Skaare, B.; Nielsen, F.G.; Hanson, T.D.; Yttervik, R.; Havmøller, O.; Rekdal, A. Analysis of Measurements and Simulations from the Hywind Demo Floating Wind Turbine. Wind Energy 2015, 18, 1105–1122. [Google Scholar] [CrossRef]
- Micallef, D.; Rezaeiha, A. Floating Offshore Wind Turbine Aerodynamics: Trends and Future Challenges. Renew. Sustain. Energy Rev. 2021, 152, 111696. [Google Scholar] [CrossRef]
- Tian, W.; Wang, Y.; Shi, W.; Michailides, C.; Wan, L.; Chen, M. Numerical Study of Hydrodynamic Responses for a Combined Concept of Semisubmersible Wind Turbine and Different Layouts of a Wave Energy Converter. Ocean Eng. 2023, 272, 113824. [Google Scholar] [CrossRef]
- Xu, B.; Kang, H.; Shen, X.; Li, Z.; Cai, X.; Hu, Z. Aerodynamic Analysis of a Downwind Offshore Floating Wind Turbine with Rotor Uptilt Angles in Platform Pitching Motion. Ocean Eng. 2023, 281, 114951. [Google Scholar] [CrossRef]
- Kang, T.-W.; Yun, J.-H.; Noh, H.-J.; Kim, E.; Yang, H.-I. Analysis of Contribution of Full Summation Hydrodynamic Load to Dynamic Response of Floating Offshore Wind Turbine Structure Operating in Extreme Environments. Int. J. Precis. Eng. Manuf. Green Technol. 2023, 10, 547–565. [Google Scholar] [CrossRef]
- Mello, P.C.; Malta, E.B.; da Silva, R.O.P.; Candido, M.H.O.; do Carmo, L.H.S.; Alberto, I.F.; Franzini, G.R.; Simos, A.N.; Suzuki, H.; Gonçalves, R.T. Influence of Heave Plates on the Dynamics of a Floating Offshore Wind Turbine in Waves. J. Mar. Sci. Technol. 2021, 26, 190–200. [Google Scholar] [CrossRef]
- Tan, L.; Ikoma, T.; Aida, Y.; Masuda, K. Mean Wave Drift Forces on a Barge-Type Floating Wind Turbine Platform with Moonpools. J. Mar. Sci. Eng. 2021, 9, 709. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, M.; Yuan, W.; Xu, K. Conceptual Design, Parameter Optimization and Performance Investigation of a 10MW Semi-Submersible Floating Wind Turbine in Shallow Water. Ocean Eng. 2023, 281, 114895. [Google Scholar] [CrossRef]
- Li, J.; Lian, J.; Guo, Y.; Wang, H. Concept Design and Floating Installation Method Study of Multi-Bucket Foundation Floating Platform for Offshore Wind Turbines. Mar. Struct. 2024, 93, 103541. [Google Scholar] [CrossRef]
- Tomás-Rodríguez, M.; Santos, M. Modelling and Control of Floating Offshore Wind Turbines. RIAI—Rev. Iberoam. Autom. Inform. Ind. 2019, 16, 381–390. [Google Scholar]
- Velino, J.; Kang, S.; Kane, M.B. Machine Learning Control for Floating Offshore Wind Turbine Individual Blade Pitch Control. J. Comput. Civ. Eng. 2022, 36, 6. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Teeuwisse, F.W.; Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind Plant Power Optimization through Yaw Control Using a Parametric Model for Wake Effects—A CFD Simulation Study. Wind Energy 2016, 19, 95–114. [Google Scholar] [CrossRef]
- Howland, M.F.; Ghate, A.S.; Quesada, J.B.; Pena Martinez, J.J.; Zhong, W.; Larranaga, F.P.; Lele, S.K.; Dabiri, J.O. Optimal Closed-Loop Wake Steering—Part 2: Diurnal Cycle Atmospheric Boundary Layer Conditions. Wind Energy Sci. 2022, 7, 345–365. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; Kern, S.; Maturu, S.; Kanev, S.; Salbert, B.; Schreiber, J.; Campagnolo, F.; Bottasso, C.L.; Schuler, S.; Wilts, F.; et al. Field Experiment for Open-Loop Yaw-Based Wake Steering at a Commercial Onshore Wind Farm in Italy. Wind Energy Sci. 2021, 6, 159–176. [Google Scholar] [CrossRef]
- Fleming, P.A.; Gebraad, P.M.O.; Lee, S.; van Wingerden, J.-W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Evaluating Techniques for Redirecting Turbine Wakes Using SOWFA. Renew. Energy 2014, 70, 211–218. [Google Scholar] [CrossRef]
- Lamei, A.; Hayatdavoodi, M. On Motion Analysis and Elastic Response of Floating Offshore Wind Turbines. J. Ocean Eng. Mar. Energy 2020, 6, 71–90. [Google Scholar] [CrossRef]
- Li, L. Full-Coupled Analysis of Offshore Floating Wind Turbine Supported by Very Large Floating Structure with Consideration of Hydroelasticity. Renew. Energy 2022, 189, 790–799. [Google Scholar] [CrossRef]
- Borg, M.; Hansen, A.M.; Bredmose, H. Floating Substructure Flexibility of Large-Volume 10MW Offshore Wind Turbine Platforms in Dynamic Calculations. J. Phys. Conf. Ser. 2016, 753, 082024. [Google Scholar] [CrossRef]
- Silva de Souza, C.E.; Bachynski, E.E. Effects of Hull Flexibility on the Structural Dynamics of a Tension Leg Platform Floating Wind Turbine. J. Offshore Mech. Arct. Eng. 2019, 142, 011903. [Google Scholar] [CrossRef]
- Mantadakis, N.; Loukogeorgaki, E.; Karimirad, M. Accounting for Hydroelasticity in the Analysis of Offshore Wind Turbine Spar-Type Platforms. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019; p. ISOPE-I. [Google Scholar]
- Leroy, V.; Delacroix, S.; Merrien, A.; Bachynski-Polić, E.E.; Gilloteaux, J.-C. Experimental Investigation of the Hydro-Elastic Response of a Spar-Type Floating Offshore Wind Turbine. Ocean Eng. 2022, 255, 111430. [Google Scholar] [CrossRef]
- Wang, H.; Ke, S.T.; Wang, T.G.; Zhu, S.Y. Typhoon-Induced Vibration Response and the Working Mechanism of Large Wind Turbine Considering Multi-Stage Effects. Renew. Energy 2020, 153, 740–758. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Wang, W.; Shi, W. Analysis of Dynamic Characteristics of an Ultra-Large Semi-Submersible Floating Wind Turbine. J. Mar. Sci. Eng. 2019, 7, 169. [Google Scholar] [CrossRef]
- Liu, B.; Yu, J. Effect of Mooring Parameters on Dynamic Responses of a Semi-Submersible Floating Offshore Wind Turbine. Sustainability 2022, 14, 14012. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Cai, X.; Xie, J.; Wang, Y.; Zhang, N. Novel Method for Designing and Optimising the Floating Platforms of Offshore Wind Turbines. Ocean Eng. 2022, 266, 112781. [Google Scholar] [CrossRef]
- Barrera, C.; Battistella, T.; Guanche, R.; Losada, I.J. Mooring System Fatigue Analysis of a Floating Offshore Wind Turbine. Ocean Eng. 2020, 195, 106670. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Long-Term Fatigue Damage Assessment for a Floating Offshore Wind Turbine under Realistic Environmental Conditions. Renew. Energy 2020, 159, 570–584. [Google Scholar] [CrossRef]
- Jard, T.; Snaiki, R. Real-Time Repositioning of Floating Wind Turbines Using Model Predictive Control for Position and Power Regulation. Wind 2023, 3, 131–150. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, W.; Li, D.; Li, X.; Duan, Y. Development of a Numerical Mooring Line Model for a Floating Wind Turbine Based on the Vector Form Intrinsic Finite Element Method. Ocean Eng. 2022, 253, 111354. [Google Scholar] [CrossRef]
- Chen, W.; Guo, S.; Li, Y.; Shen, Y. Impacts of Mooring-Lines Hysteresis on Dynamic Response of Spar Floating Wind Turbine. Energies 2021, 14, 2109. [Google Scholar] [CrossRef]

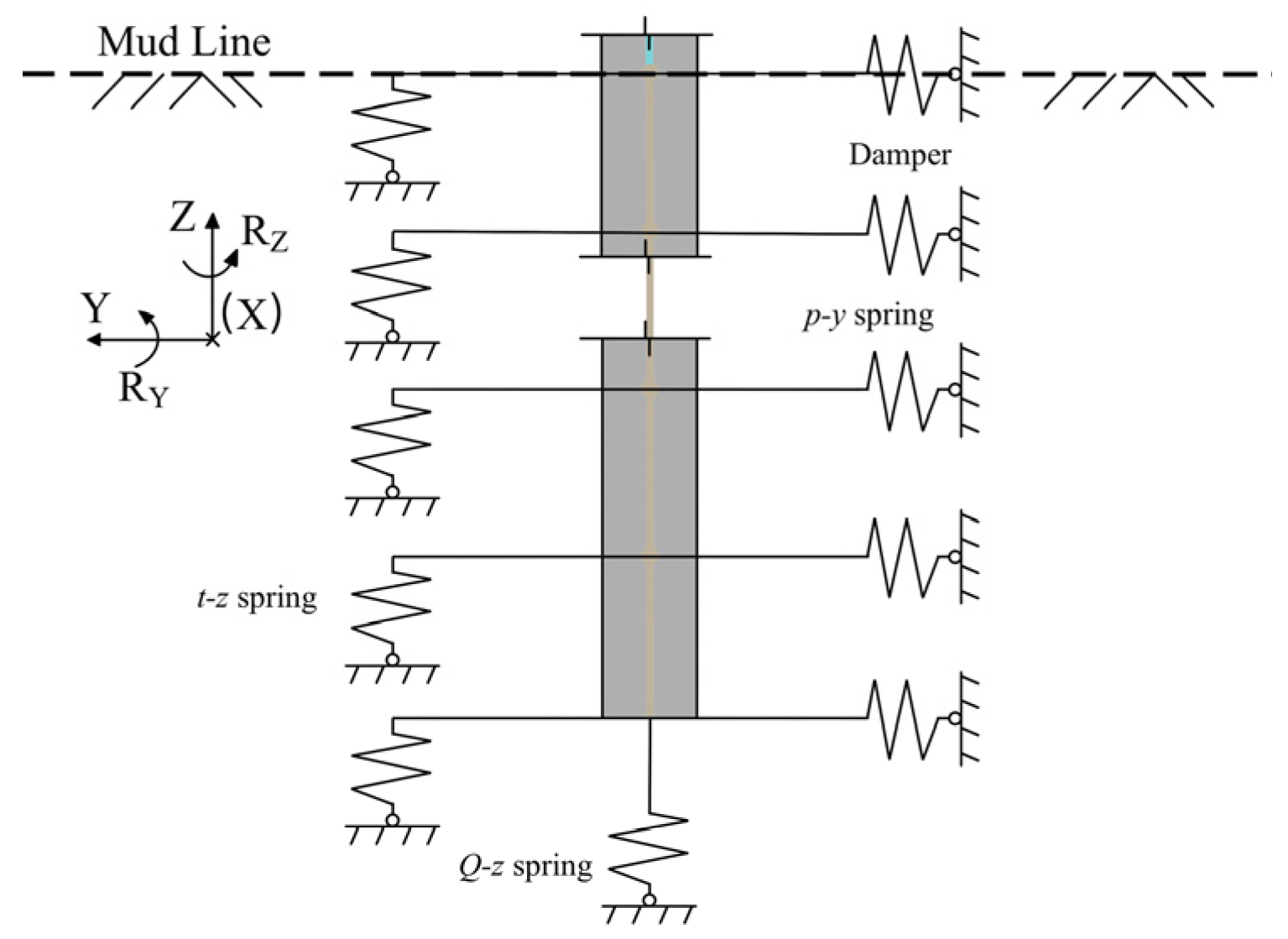
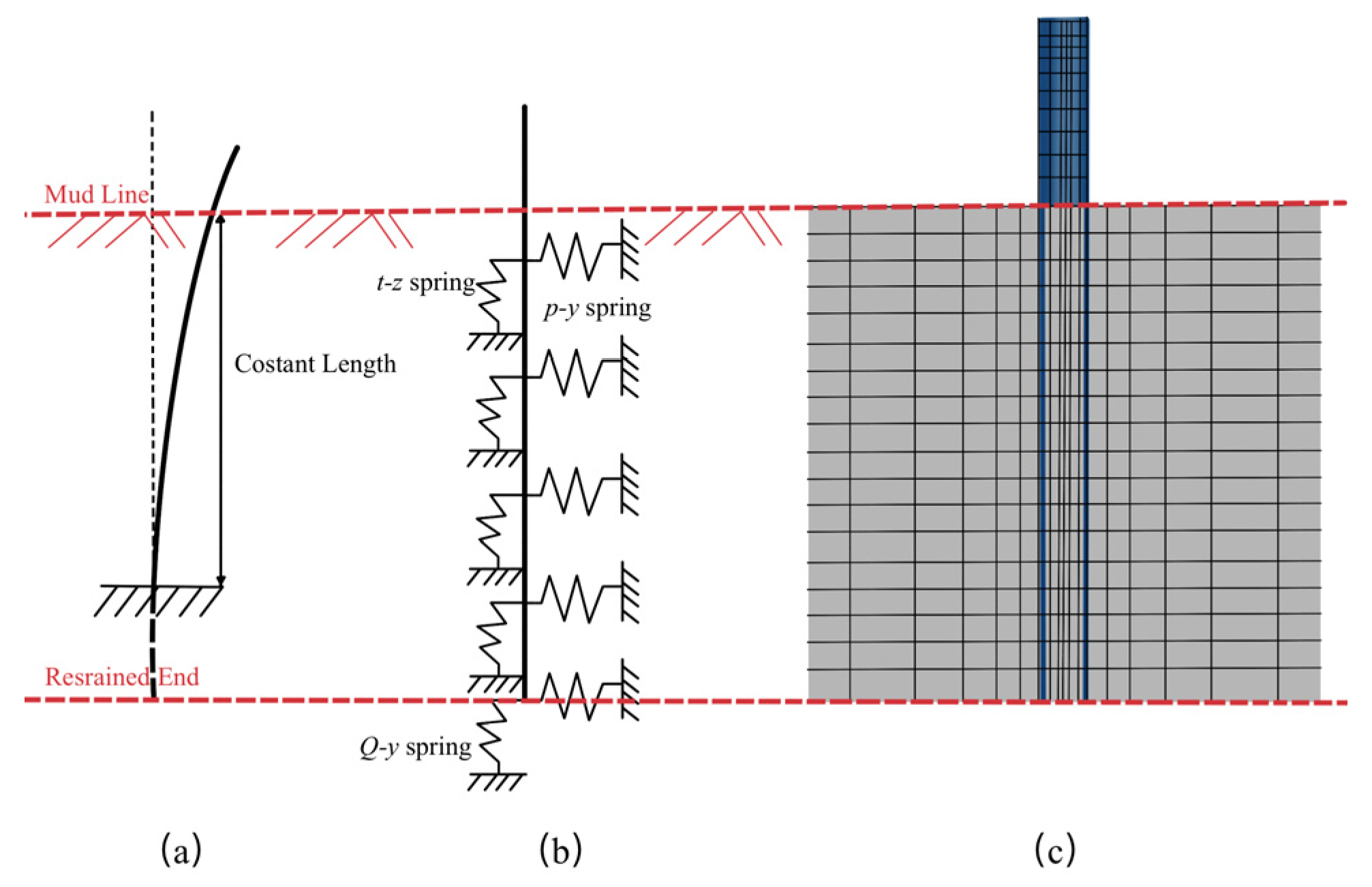
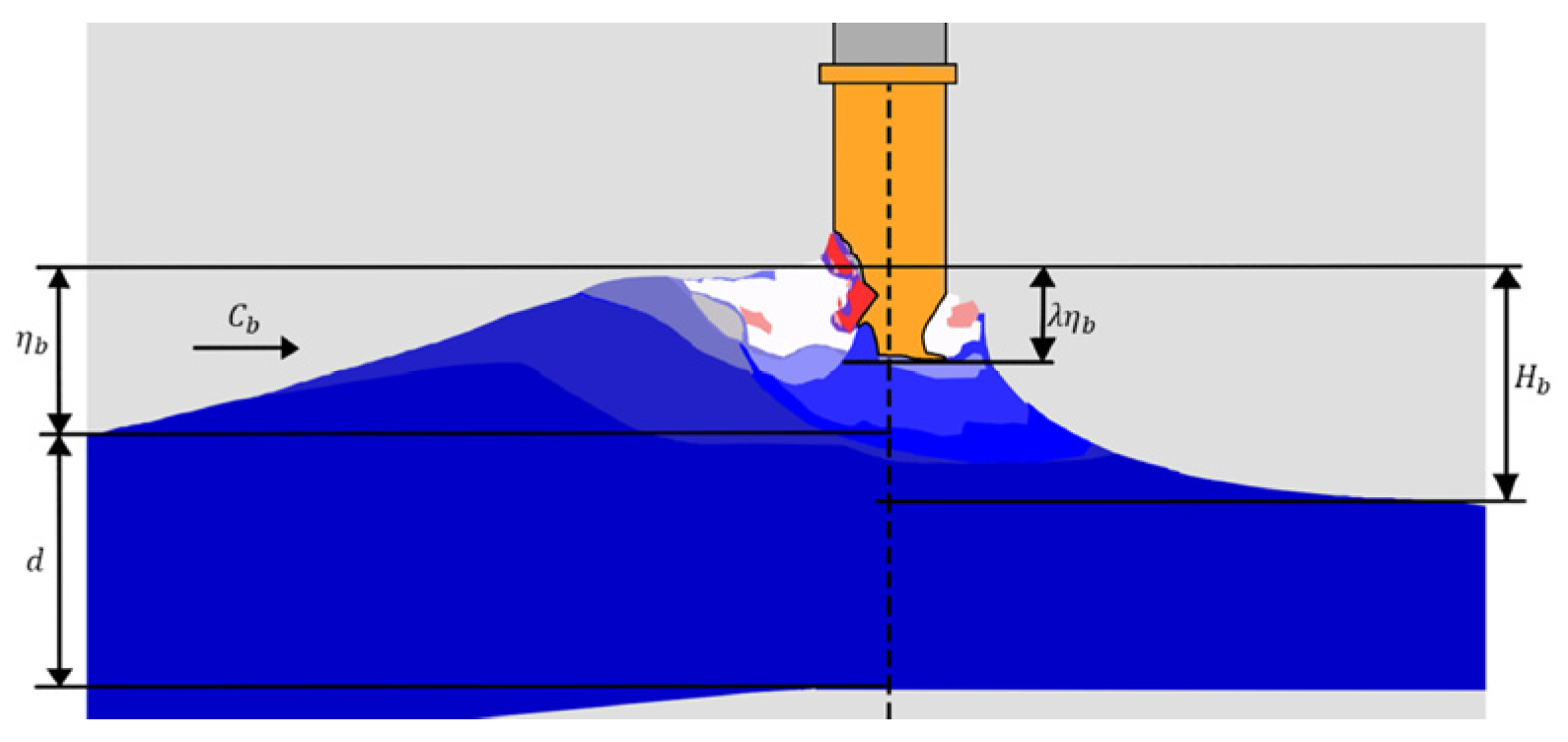

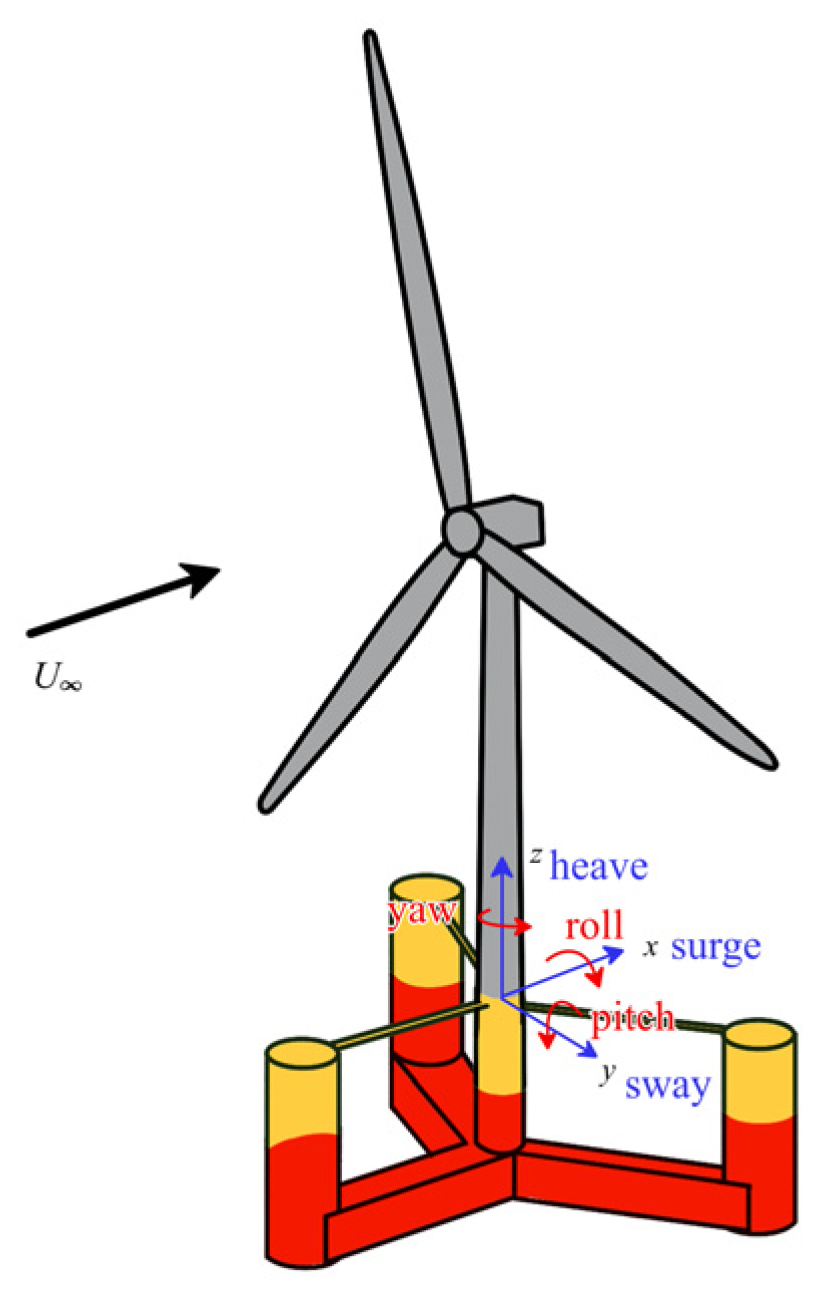




| Type of Foundation | Typical Projects | Water Depth | Per-Unit Capacity (MW) | Key Application Features |
|---|---|---|---|---|
| Monopile | Thanet Offshore Wind Power Field (2010) [5] | 20–25 m | 3 | First commercially operating offshore wind power field in the UK |
| Jacket | Beatrice Offshore Wind Power Field (2006) [6] | 56 m | 7 | Applied in a medium-deep water scenario |
| Semi-submersible | “The Three Gorges Leader” FOWT (2021) [7] | - | 5.5 | Typhoon-resistant; independently developed by China |
| Spar | Hywind Scotland Wind Power Field [7] (2017) | 95–120 m | 6 | First commercially operating deep-sea offshore wind power field worldwide |
| Type of Foundation | Cost of Quay-Side Lifts (EUR) | Cost of Transportation (EUR) | Cost of Substructure Installation (EUR) | Cost of Stationed Personnel (EUR) | Total Cost (EUR) |
|---|---|---|---|---|---|
| Monopile | 65 k | 47 k | 784 k | 63 k | 959 k |
| Jacket | 65 k | 47 k | 1176 k | 84 k | 1372 k |
| Type of Foundation | Working Principle | Foundation Soil Requirements | Advantages | Disadvantages |
|---|---|---|---|---|
| Gravity-based | Relies on self-weight and internal loading weight to balance upsetting moments and sliding force. | Wide soil adaptability. | Strong resistance to windstorms and high waves. | 1. Heavy structure, difficult to transport and install. 2. High material consumption, high initial cost. |
| Monopile | A single large-diameter steel pile is driven into the seabed. | Unsuitable for soft soil or hard rock, and highly sensitive to seabed scouring. | 1. Simple structure, easy to design and manufacture. 2. Low cost for shallow water (≤30 m). | 1. Not for deep water. 2. Prone to bending under horizontal loads. 3. Needs anti-scouring measures. |
| Tripod | Draws on offshore oil/gas experience, and tripod structure distributes loads to three legs. | Requires hard/firm seabeds. | 1. High rigidity and strength, and good resistance to horizontal loads. 2. Good anti-scouring performance. | 1. Strict soil requirements. 2. Complex on-site assembly. |
| Jacket | Steel truss structure fixed to seabed via piles. | Wide soil adaptability. | 1. High bearing capacity. 2. Mature construction, and less affected by marine loads. | 1. Complex structure, and difficult to design and manufacture. 2. High installation cost. |
| Bucket | Negative-pressure bucket: pump out internal air/water to suck it into seabed. | Soft soil may have internal liquefaction. | 1. Suitable for inshore/offshore areas. 2. Short construction time. | 1. Sensitive to seepage. 2. Risk of soil plug/liquefaction, leading to tilting. |
| Type of Foundation | Working Principle | Water Depth | Advantages | Disadvantages |
|---|---|---|---|---|
| Semi-submersible | Distributed buoy structures create large water plane changes. | 40–500 m | Minimal cost growth with deeper water [10], retains deep-sea economic benefits. | 1. Large water plane area, easily affected by wave loads. 2. High sensitivity to second-order low-frequency wave forces [12]. |
| barge | Increases damping pool to reduce structural lateral displacement [13]. | 40–500 m | 1. Relatively simple structure. 2. Low unit weight and cost. | 1. Large water plane area, easily affected by wave loads. 2. High sensitivity to second-order low-frequency wave forces [12]. |
| TLP | Generates stronger buoyancy than a dead load of wind turbines to balance off the tension of lines. | 30–500 m | Lower LCOE than other common floating foundations in shallow waters. | 1. High sensitivity to second-order high-frequency wave forces. 2. Structure cost surges with increasing water depth. |
| Spar | Stability supported by ballast center of gravity. | 75–500 m | 1. Suitable for large-scale FOWTs. 2. Economic benefits when water depth reaches 400–500 m. 3. Small water plane area reduces platform motion [14]. | High sensitivity to marine eddies. |
| Type of Foundation | Platform (EUR/kW) | Mooring Line (EUR/kW) | Total Cost (EUR/kW) |
|---|---|---|---|
| Semi-submersible | 1.27 k | 0.76 k | 644 k |
| Barge | 0.87 k | 0.77 k | 768 k |
| Spar | 0.65 k | 0.67 k | 786 k |
| Type of Foundation Models | Application Range | Advantages | Disadvantages |
|---|---|---|---|
| Apparent fixity model | Small subgrade stiffness and ignoring displacement of the tower top | The model is simple and has high sensitivity to pile diameter and pile thickness | Underestimates subgrade stiffness, and ignores influences of soil mass conditions on displacement response as well as changes in soil mass constraint caused by pile diameter |
| Distributed spring model | High subgrade stiffness | Predict subgrade stiffness accurately | Ignores continuity effect of soil bed [38] as well as effects of soil mass conditions on displacement responses |
| FE model of the soil–pile system | High subgrade stiffness | More sensitive to soil compaction and buried depth of piles | Heavy computation loads |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Wang, H.; Cai, X.; Zhang, H.; Ren, L.; Cai, M.; Xin, Z. Dynamics of Offshore Wind Turbine Foundation: A Critical Review and Future Directions. J. Mar. Sci. Eng. 2025, 13, 2016. https://doi.org/10.3390/jmse13102016
Xie J, Wang H, Cai X, Zhang H, Ren L, Cai M, Xin Z. Dynamics of Offshore Wind Turbine Foundation: A Critical Review and Future Directions. Journal of Marine Science and Engineering. 2025; 13(10):2016. https://doi.org/10.3390/jmse13102016
Chicago/Turabian StyleXie, Jiaojie, Hao Wang, Xin Cai, Hongjian Zhang, Lei Ren, Maowen Cai, and Zhiqiang Xin. 2025. "Dynamics of Offshore Wind Turbine Foundation: A Critical Review and Future Directions" Journal of Marine Science and Engineering 13, no. 10: 2016. https://doi.org/10.3390/jmse13102016
APA StyleXie, J., Wang, H., Cai, X., Zhang, H., Ren, L., Cai, M., & Xin, Z. (2025). Dynamics of Offshore Wind Turbine Foundation: A Critical Review and Future Directions. Journal of Marine Science and Engineering, 13(10), 2016. https://doi.org/10.3390/jmse13102016








