Research on Lightweight Design Performance of Offshore Structures Based on 3D Printing Technology
Abstract
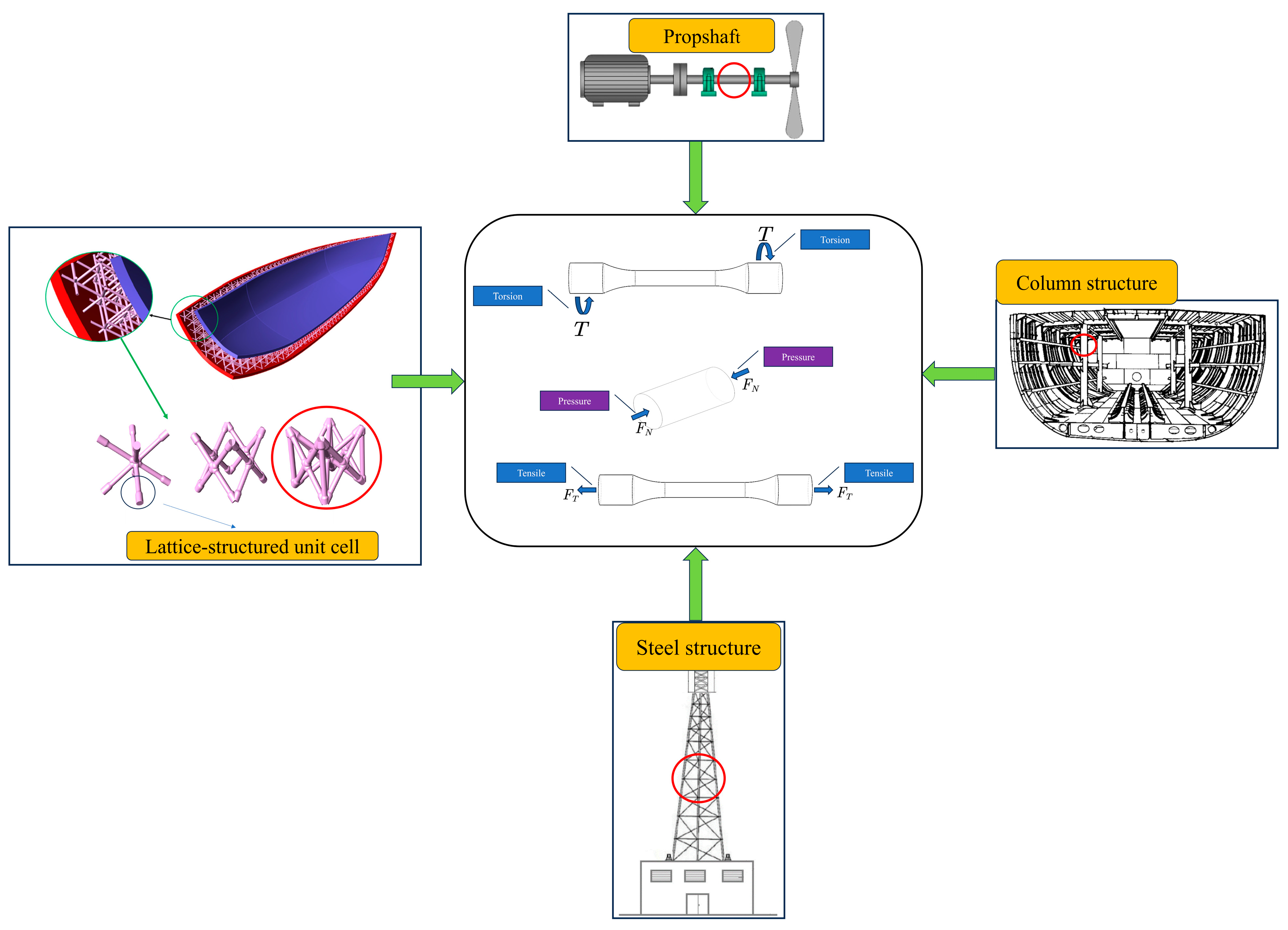
1. Introduction
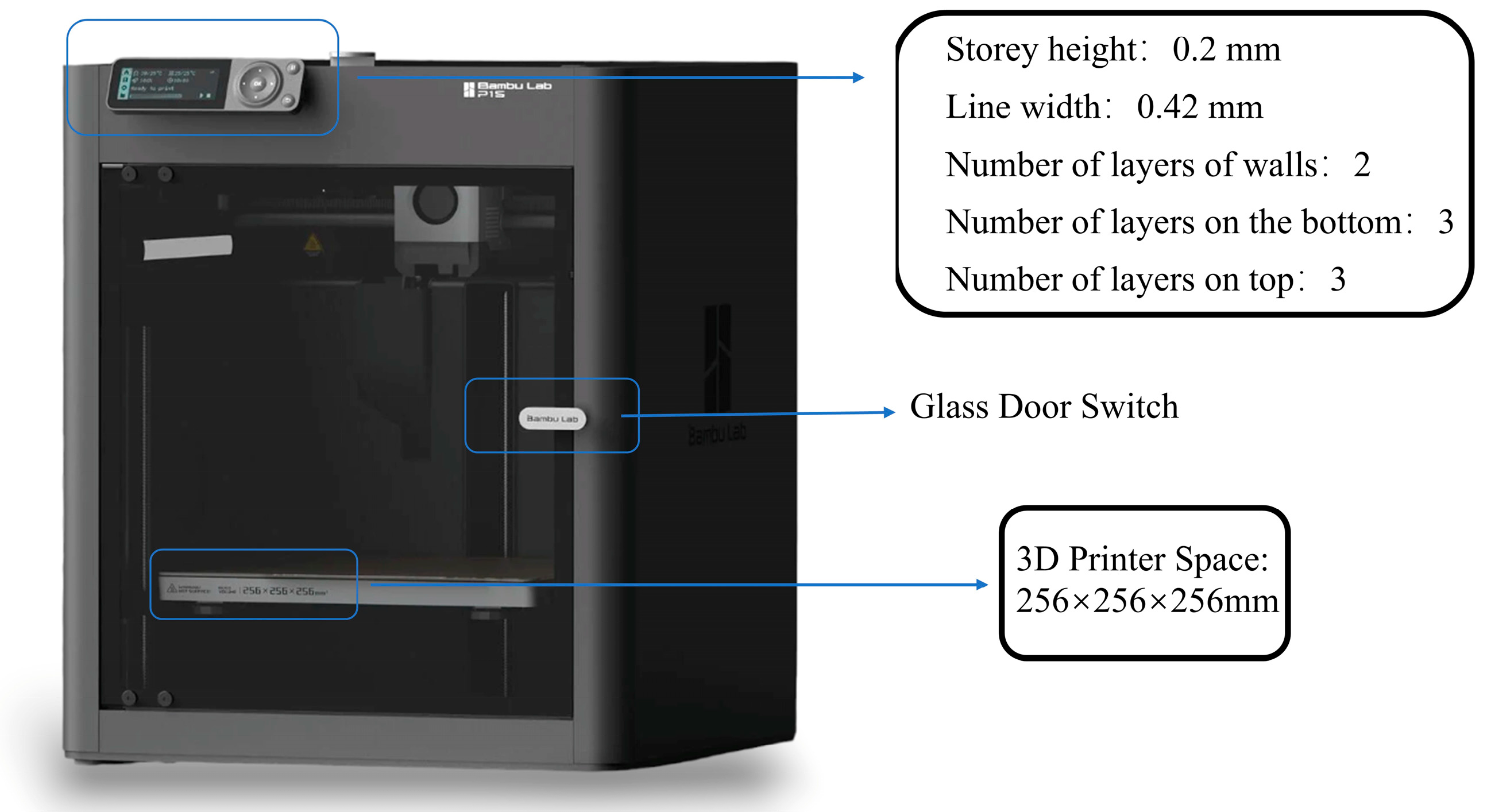
2. Experiment
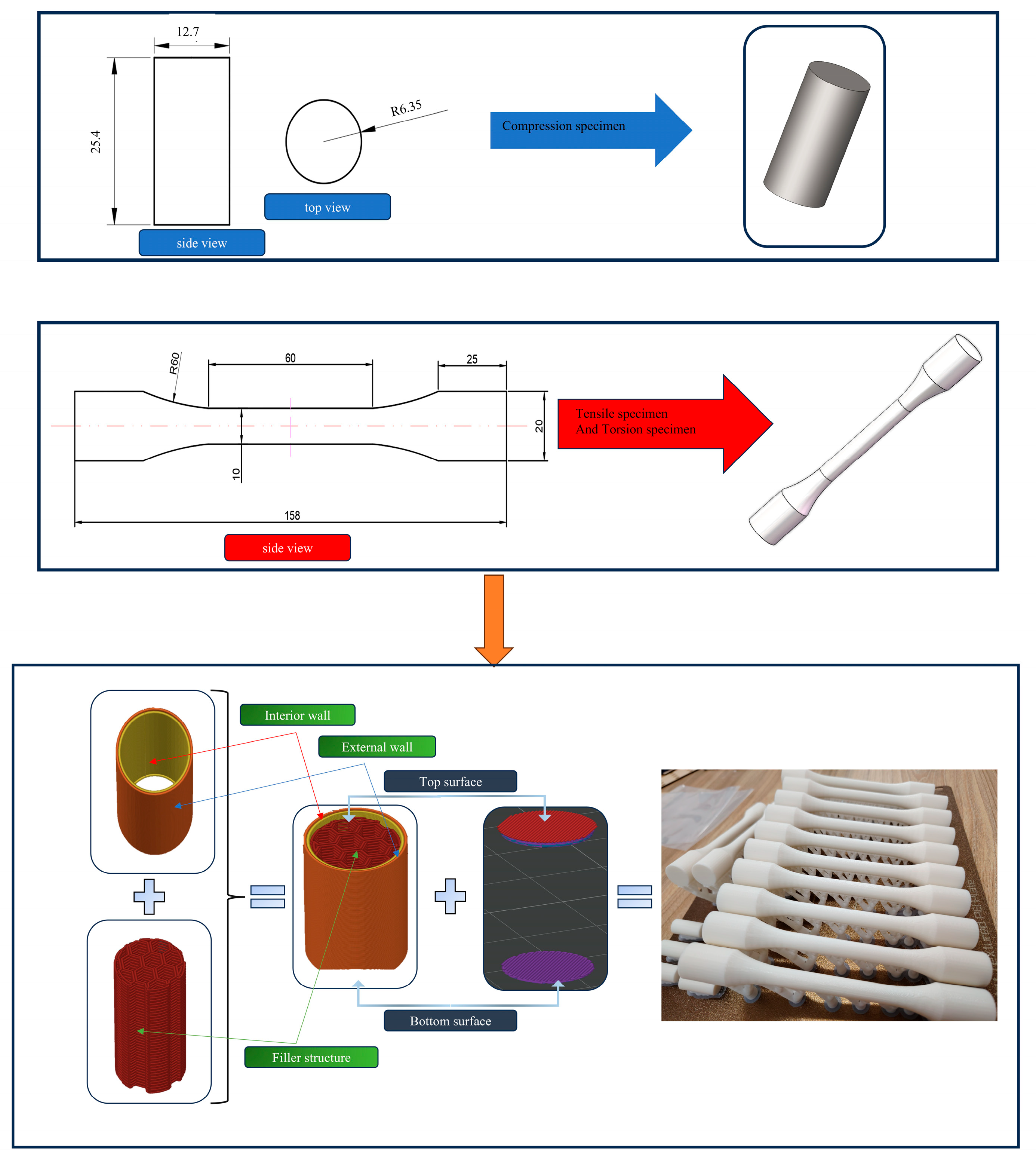
2.1. Specimen Size
2.2. Research Factors
2.3. Filling Structure and Filling Rates
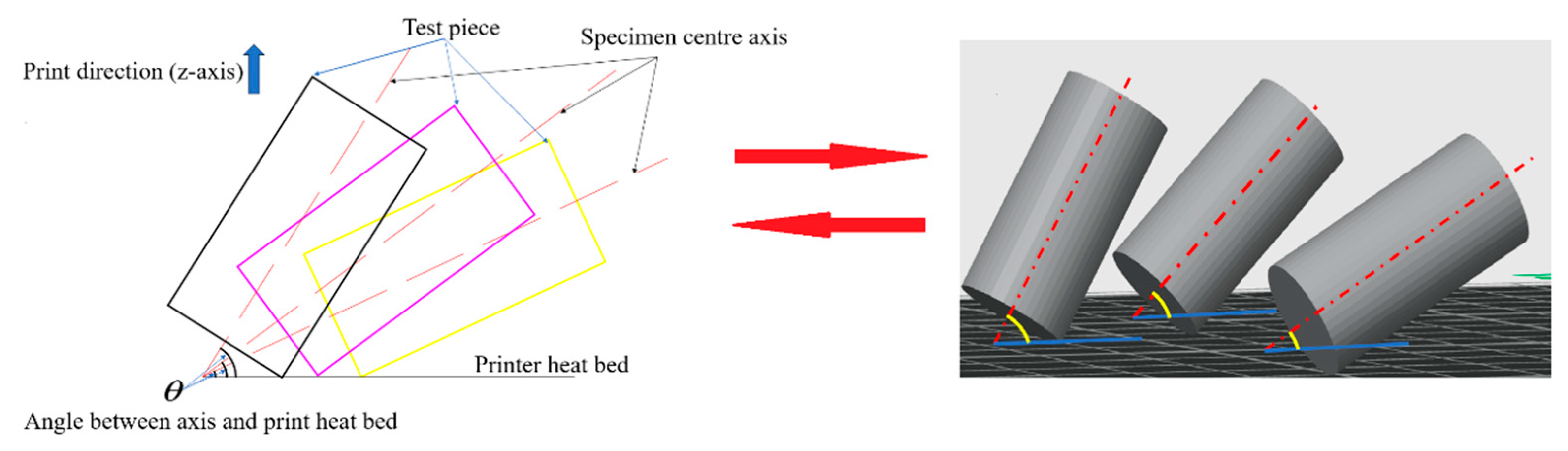
2.4. Specimen Inclination Angle
3. Theoretical Formulas
4. Tensile Experiment Analysis
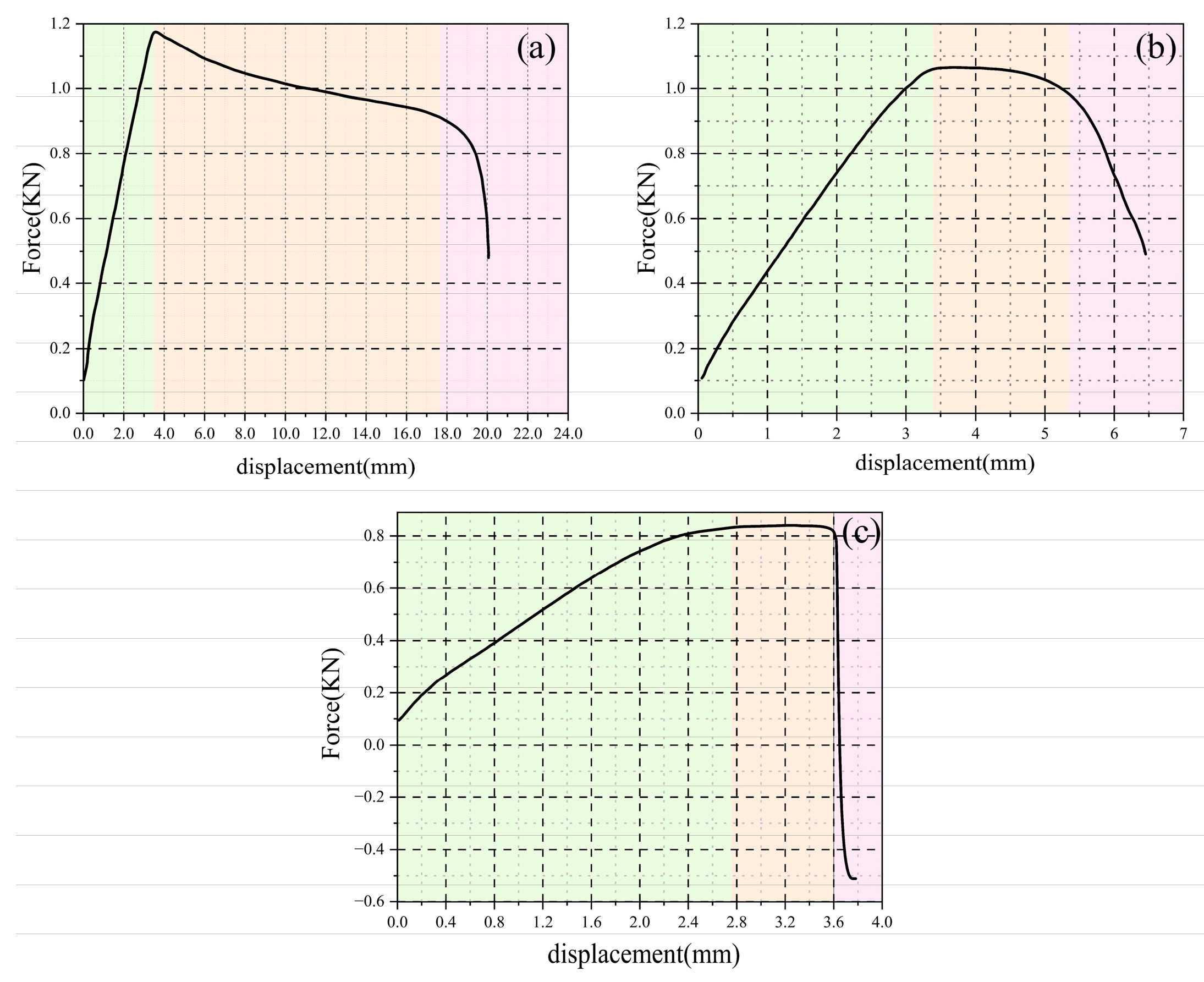
4.1. Curve Form of Tensile Specimen Load Variation with Specimen Length
4.2. Tensile Fracture Form
4.3. Tensile Strength Data Analysis
5. Compression Experiment
5.1. Compression Specimen Load Changes with the Specimen Length in the Form of a Curve
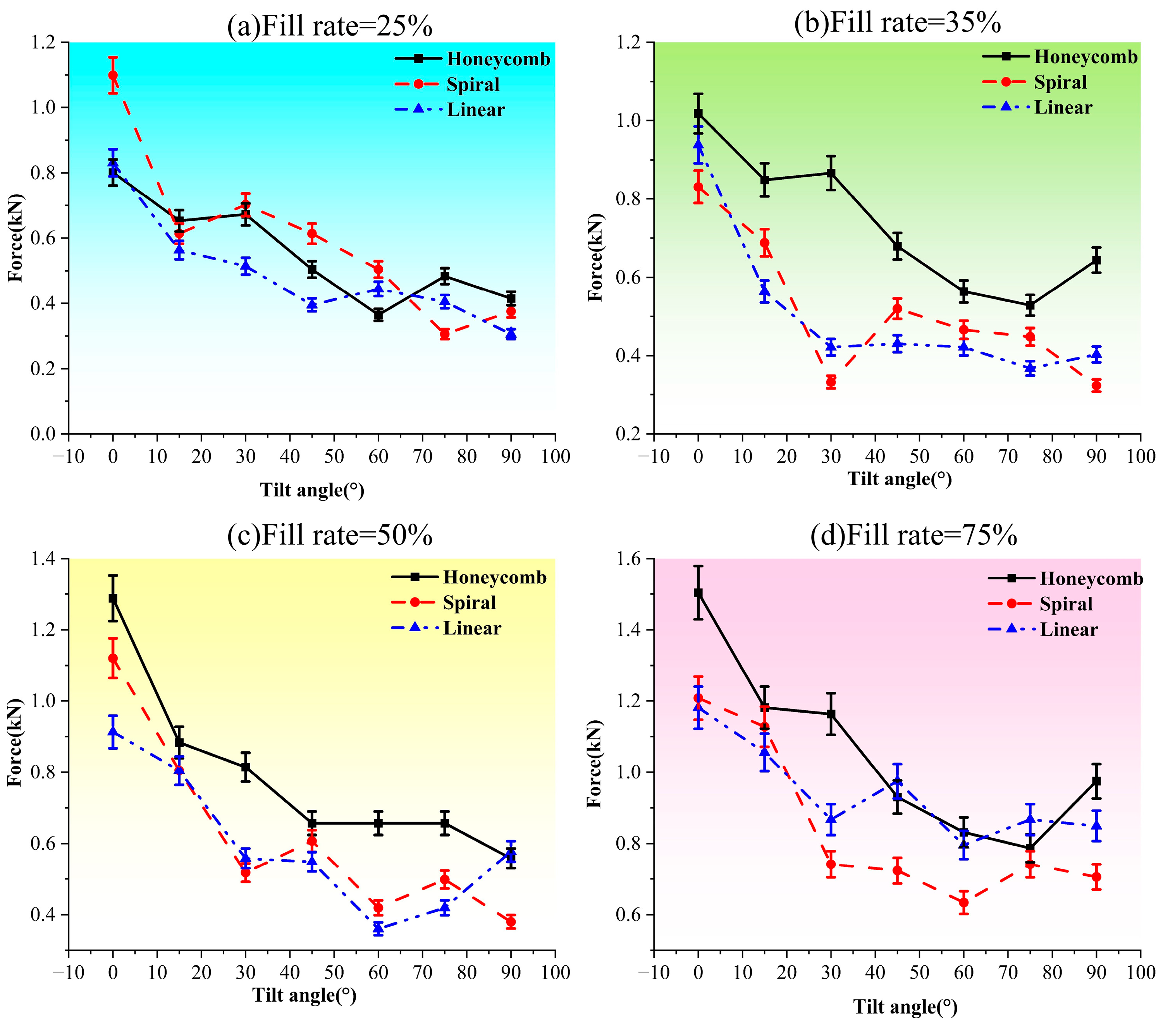
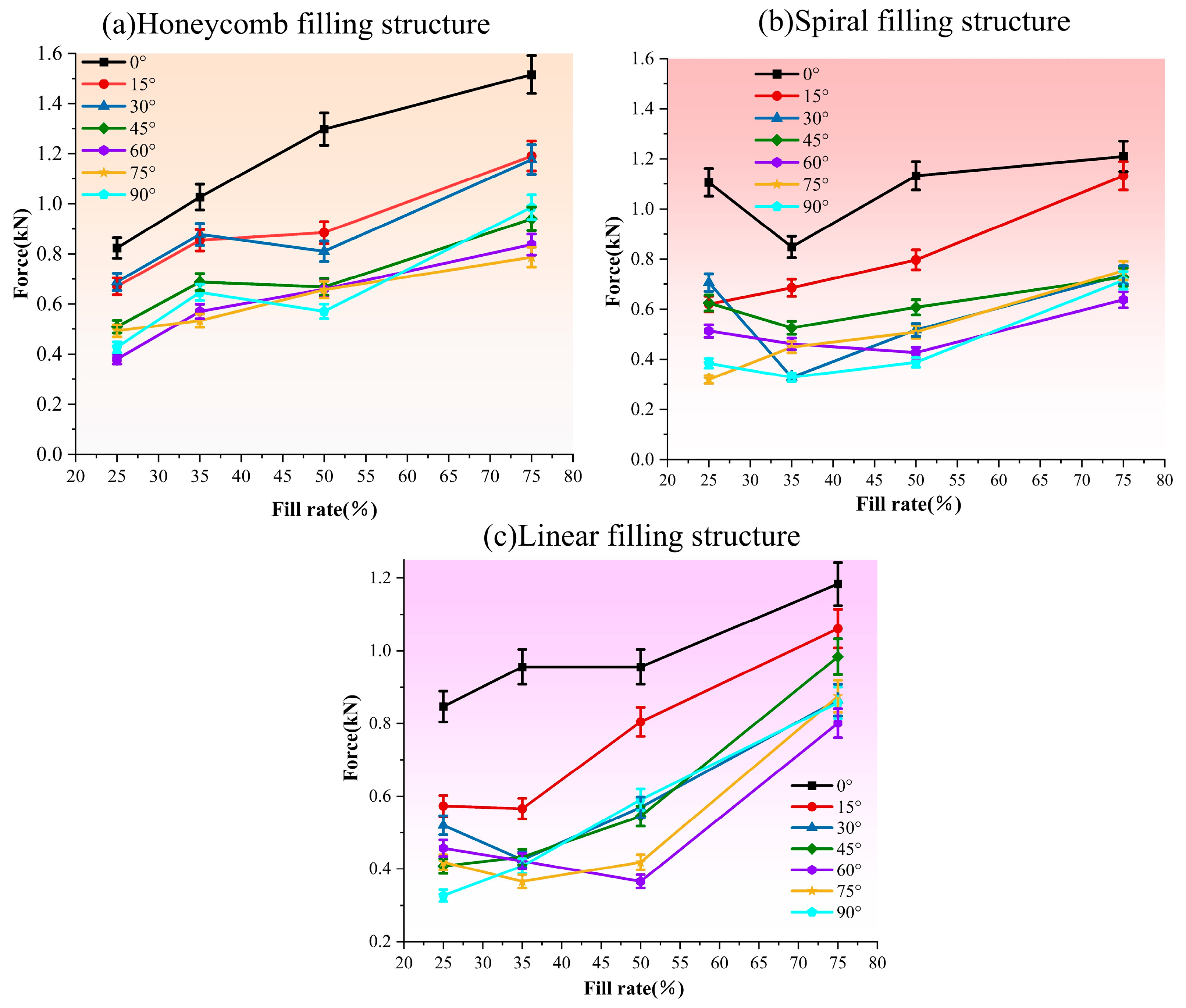
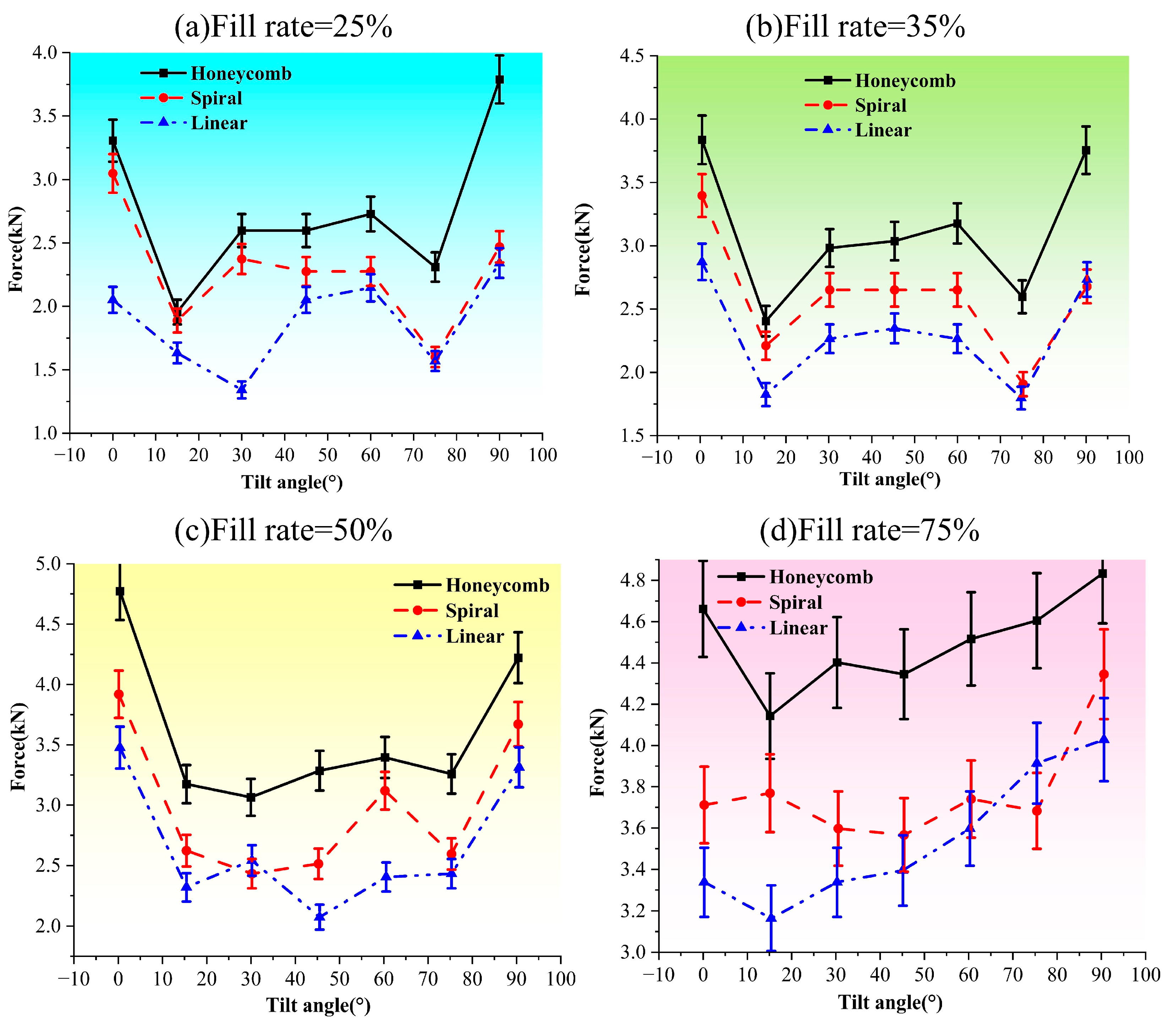
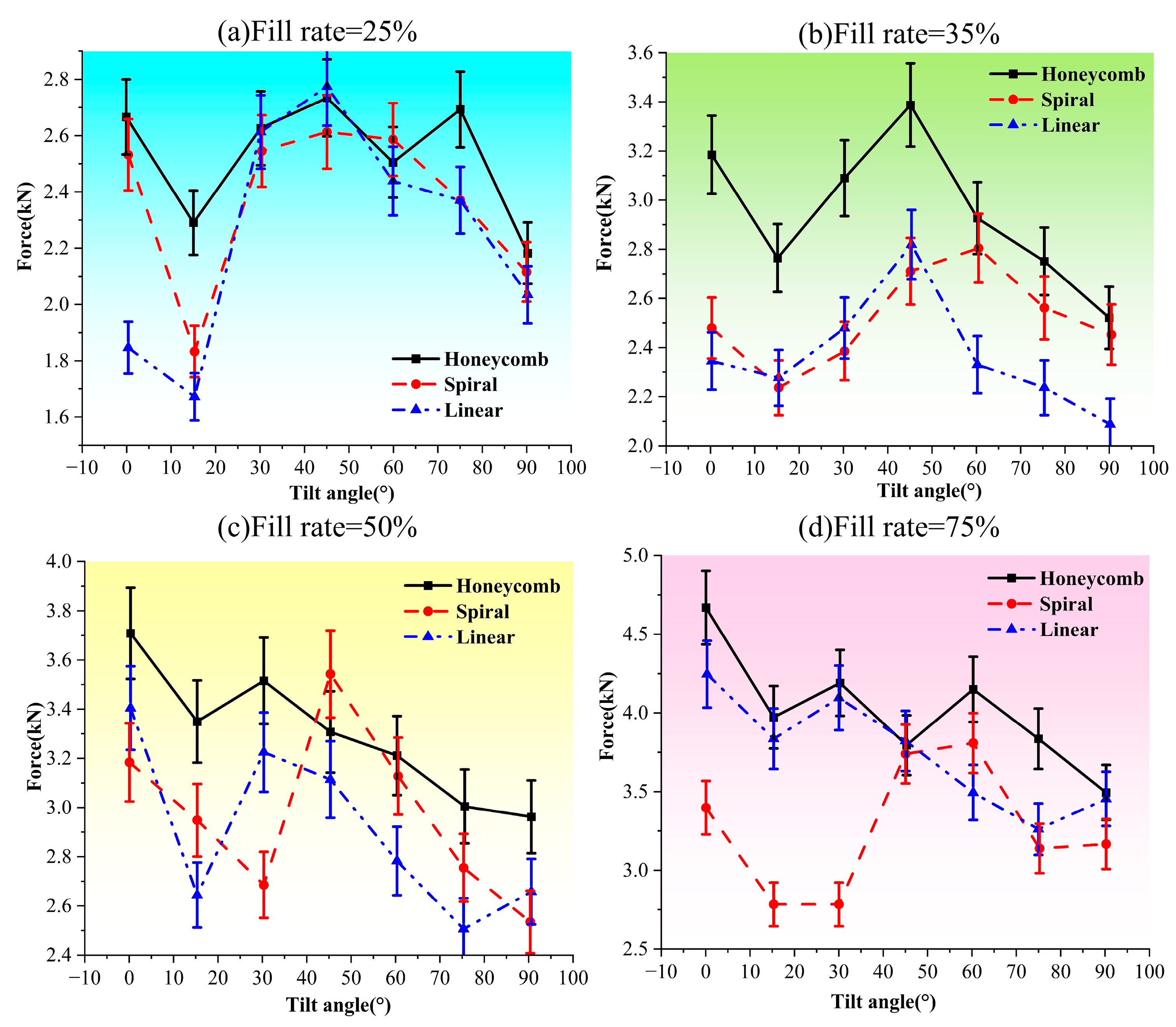
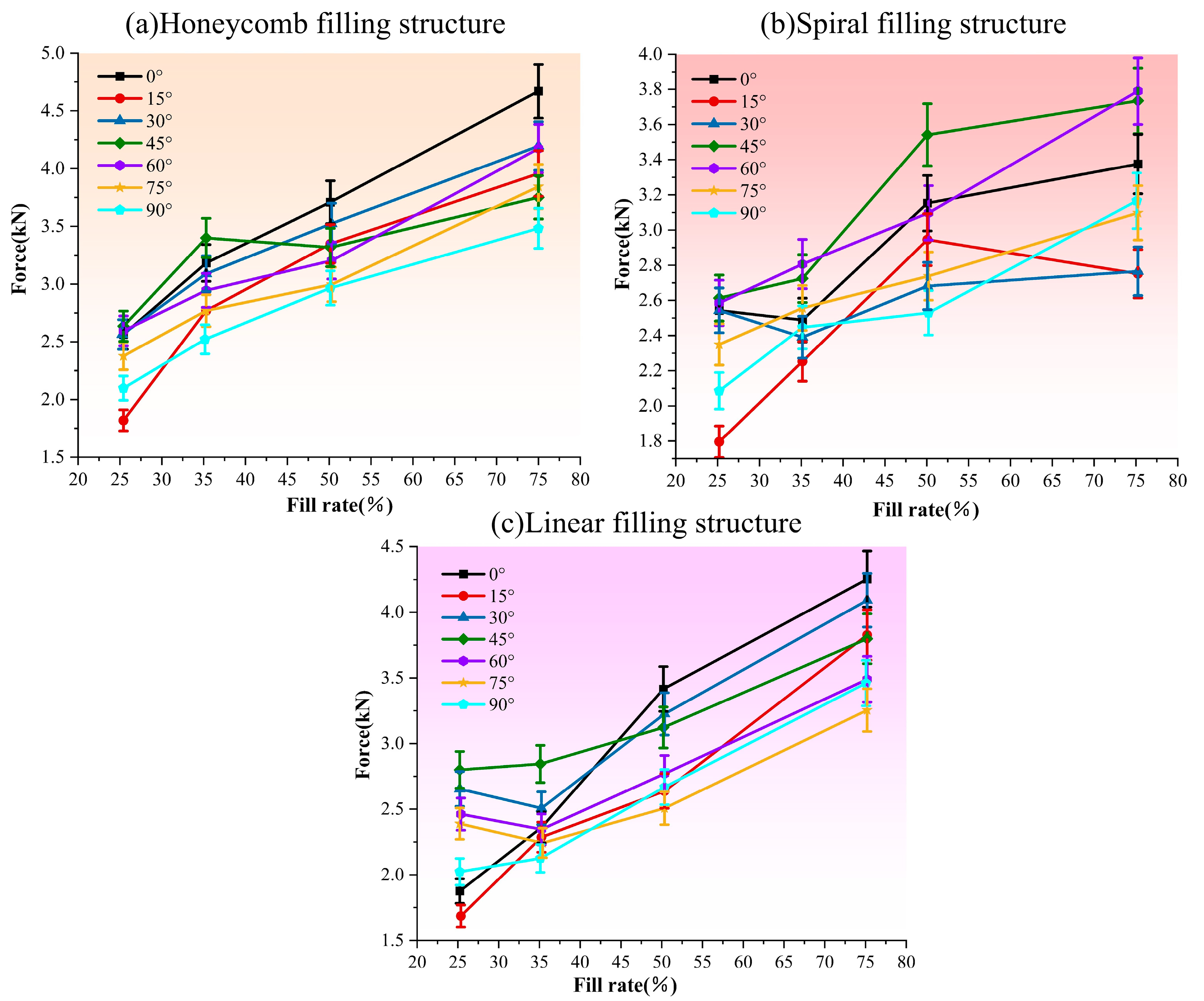
5.2. Compression of Experimental Data Analysis
6. Torsion Experiment
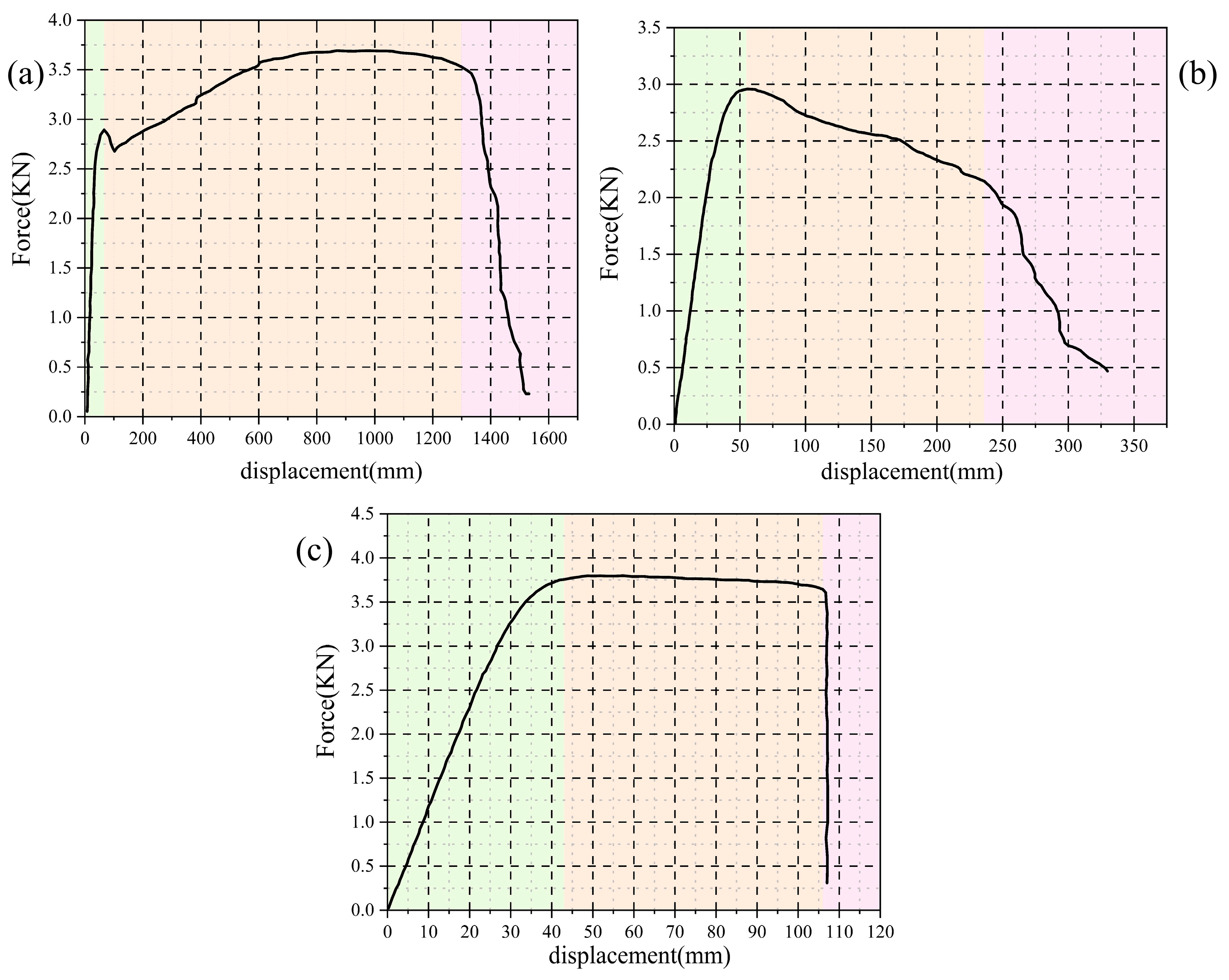
6.1. Curve Form
6.2. Torsional Experimental Fracture Forms
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, D.-P.; Li, P.-Y.; Ji, Y.-X.; Wen, D.-H.; Li, C. SA-ANN-based slag carry-over detection method and the embedded WME platform. IEEE Trans. Ind. Electron. 2012, 60, 4702–4713. [Google Scholar] [CrossRef]
- Wu, J.; Li, L.; Yin, Z.; Li, Z.; Wang, T.; Tan, Y.; Tan, D. Mass transfer mechanism of multiphase shear flows and interphase optimization solving method. Energy 2024, 292, 130475. [Google Scholar] [CrossRef]
- Soto-Rivas, K.; Richter, D.; Escauriaza, C. Flow effects of finite-sized tidal turbine arrays in the Chacao Channel, Southern Chile. Renew. Energy 2022, 195, 637–647. [Google Scholar] [CrossRef]
- Guo, X.; Wang, H.; Xiao, Y.; Liu, G.; Wang, W. Reassessing the cost of hydropower for multi-function hydropower bases: A case study from Sichuan. J. Clean. Prod. 2023, 413, 137422. [Google Scholar] [CrossRef]
- Comoglio, C.; Castelluccio, S.; Fiore, S. Environmental reporting in the hydropower sector: Analysis of EMAS registered hydropower companies in Italy. Front. Environ. Sci. 2023, 11, 1178037. [Google Scholar] [CrossRef]
- Wagner, B.; Hauer, C.; Habersack, H. Current hydropower developments in Europe. Curr. Opin. Environ. Sustain. 2019, 37, 41–49. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G.; Neill, S.P. The influence of waves on the tidal kinetic energy resource at a tidal stream energy site. Appl. Energy 2016, 180, 402–415. [Google Scholar] [CrossRef]
- Milford, C.; Martí, V.; Neill, S.P. Influence of the phase relationship between tidal currents and elevations on tidal energy conversion. Renew. Energy 2025, 247, 122774. [Google Scholar] [CrossRef]
- Rome, L.C.; Flynn, L.; Goldman, E.M.; Yoo, T.D. Generating electricity while walking with loads. Science 2005, 309, 1725–1728. [Google Scholar] [CrossRef]
- Donelan, J.M.; Li, Q.; Naing, V.; Hoffer, J.A.; Weber, D.J.; Kuo, A.D. Biomechanical energy harvesting: Generating electricity during walking with minimal user effort. Science 2008, 319, 807–810. [Google Scholar] [CrossRef]
- Cobb, B.R.; Sharp, K.V. Impulse (Turgo and Pelton) turbine performance characteristics and their impact on pico-hydro installations. Renew. Energy 2013, 50, 959–964. [Google Scholar] [CrossRef]
- Qi, Y.; Kim, J.; Nguyen, T.D.; Lisko, B.; Purohit, P.K.; McAlpine, M.C. Enhanced piezoelectricity and stretchability in energy harvesting devices fabricated from buckled pzt ribbons. Nano Lett. 2011, 11, 1331–1336. [Google Scholar] [CrossRef] [PubMed]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef]
- Qi, Y.; McAlpine, M.C. Nanotechnology-enabled flexible and biocompatible energy harvesting. Energy Environ. Sci. 2010, 3, 1275–1285. [Google Scholar] [CrossRef]
- Platt, S.; Farritor, S.; Garvin, K.; Haider, H. The use of piezoelectric ceramics for electric power generation within orthopedic implants. IEEE/ASME Trans. Mechatron. 2005, 10, 455–461. [Google Scholar] [CrossRef]
- Chen, X.; Xu, S.; Yao, N.; Shi, Y. 1.6 V nanogenerator for mechanical energy harvesting using PZT nanofibers. Nano Lett. 2010, 10, 2133–2137. [Google Scholar]
- Jeon, Y.; Sood, R.; Jeong, J.-H.; Kim, S.-G. MEMS power generator with transverse mode thin film PZT. Sens. Actuators A Phys. 2005, 122, 16–22. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, H.; Qin, X.; Jin, Y.; Li, Y.; Yang, S.; Yi, Z.; Gao, S.; Wang, S.; Wang, Z. Drinking-Bird-Enabled Triboelectric Hydrovoltaic Generator. Device 2024, 2, 100318. [Google Scholar] [CrossRef]
- Wei, L.; Nakamura, T.; Imai, K. Development and optimization of low-speed and high-efficiency permanent magnet generator for micro hydro-electrical generation system. Renew. Energy 2020, 147, 1653–1662. [Google Scholar] [CrossRef]
- Eick, B.; Brown, A.; Wilcoski, J.; Thurmer, C. Localization of flow-induced vibrations from wicket gates in hydropower generating units. J. Civ. Struct. Health Monit. 2023, 13, 811–825. [Google Scholar] [CrossRef]
- Yadav, G.; Chauhan, A.K. Design and development of pico micro hydro system by using house hold water supply. Int. J. Res. Eng. Technol. 2014, 3, 114–119. [Google Scholar]
- Ridzuan, M.J.M.; Hafis, S.; Azduwin, K.; Firdaus, K.; Zarina, Z. Development of pico-hydro turbine for domestic use. Appl. Mech. Mater. 2015, 695, 408–412. [Google Scholar] [CrossRef]
- Zainuddin, H.; Khamis, A.; Yahaya, M.S.; Basar, M.F.M.; Lazi, J.M.; Ibrahim, Z. Investigation on the performance of pico-hydro generation system using consuming water distributed to houses. In Proceedings of the 2009 1st International Conference on the Developements in Renewable Energy Technology (ICDRET), Dhaka, Bangladesh, 17–19 December 2009. [Google Scholar]
- Wang, C.X. Application of 3D printing technology in product styling design. Heilongjiang Sci. 2022, 13, 31–33. (In Chinese) [Google Scholar]
- Wu, Y.R. 3D Printing in aero engine manufacturing. China Sci. Technol. Inf. 2022, 11, 46–48. (In Chinese) [Google Scholar]
- Parwani, R.; Curto, M.; Kao, A.P.; Rowley, P.J.; Pani, M.; Tozzi, G.; Barber, A.H. Morphological and mechanical biomimetic bone structures. ACS Biomater. Sci. Eng. 2017, 3, 2761–2767. [Google Scholar] [CrossRef]
- Wong, K.V.; Hernandez, A. A review of additive manufacturing. Int. Sch. Res. Not. 2012, 2012, 208760. [Google Scholar] [CrossRef]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Lin, Z.; Shang, C.; Li, B. A review of the design methods of complex topology structures for 3D printing. Vis. Comput. Ind. Biomed. Art 2018, 1, 5. [Google Scholar] [CrossRef]
- Olsson, A.; Hellsing, M.S.; Rennie, A.R. New possibilities using additive manufacturing with materials that are difficult to process and with complex structures. Phys. Scr. 2017, 92, 053002. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- ISO 527-2-2012; Plastics–Determination of Tensile Properties–Part 2: Test Conditions for Moulding and Extrusion Plastics. The State Administration for Market Regulation of the People’s Republic of China, the Standardization Administration of the People’s Republic of China: Shanghai, China, 2013.
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2010.
- Liang, Z.; Xie, Y.; Zhang, Y.; Zhao, G.; Lin, Q.; Zhang, D.; Jiang, H.; Yang, K.; Si, K.; Yang, K.; et al. The Effect of the Support Mass in 3D Printing on the Forming Time of the Model. Eng. Solut. Mech. Mar. Struct. Infrastruct. 2024, 1, 7. [Google Scholar] [CrossRef]
- Yao, T.; Deng, Z.; Zhang, K.; Li, S. A method to predict the ultimate tensile strength of 3D printing polylactic acid (PLA) materials with different printing orientations. Compos. Part B Eng. 2019, 163, 393–402. [Google Scholar] [CrossRef]
- Manes, A.; Porcaro, R.; Ilstad, H.; Levold, E.; Langseth, M.; Børvik, T. The behaviour of an offshore steel pipeline material subjected to bending and stretching. Ships Offshore Struct. 2012, 7, 371–387. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhao, B.; Ma, Y.; Si, K. Exploring subsea dynamics: A comprehensive review of underwater pipelines and cables. Phys. Fluids 2024, 36, 101304. [Google Scholar] [CrossRef]
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Li, S.; Kim, D.K. Ultimate strength characteristics of unstiffened cylindrical shell in axial compression. Ocean Eng. 2022, 243, 110253. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Jiang, H. A review of offshore wind and wave installations in some areas with an eye towards generating economic benefits and offering commercial inspiration. Sustainability 2023, 15, 8429. [Google Scholar] [CrossRef]
- Buccino, F.; Martinoia, G.; Vergani, L.M. Torsion—Resistant structures: A nature addressed solution. Materials 2021, 14, 5368. [Google Scholar] [CrossRef] [PubMed]






| Research Factors | |||||||
|---|---|---|---|---|---|---|---|
| Filling structure | Honeycomb | Spiral | Linear | ||||
| Filling rate | 25% | 35% | 50% | 75% | |||
| Specimen tilt angle | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| Experimental load | Tensile load | Torsional load | Compressive load | ||||
| Tensile Experiments | Fill Rate | |||||
|---|---|---|---|---|---|---|
| 25% | 35% | 50% | 75% | |||
| Honeycomb filling structure | Maximum load (kN) | 0° | 0.80 | 1.02 | 1.28 | 1.50 |
| 15° | 0.65 | 0.85 | 0.88 | 1.18 | ||
| 30° | 0.68 | 0.87 | 0.81 | 1.16 | ||
| 45° | 0.50 | 0.69 | 0.65 | 0.93 | ||
| 60° | 0.35 | 0.58 | 0.65 | 0.83 | ||
| 75° | 0.47 | 0.53 | 0.65 | 0.78 | ||
| 90° | 0.40 | 0.64 | 0.55 | 0.97 | ||
| Spiral filling structure | 0° | 1.10 | 0.83 | 1.12 | 1.20 | |
| 15° | 0.60 | 0.69 | 0.80 | 1.12 | ||
| 30° | 0.69 | 0.3 | 0.51 | 0.74 | ||
| 45° | 0.62 | 0.52 | 0.60 | 0.72 | ||
| 60° | 0.51 | 0.46 | 0.41 | 0.63 | ||
| 75° | 0.29 | 0.44 | 0.49 | 0.74 | ||
| 90° | 0.39 | 0.32 | 0.37 | 0.70 | ||
| Linear filling structure | 0° | 0.84 | 0.93 | 0.91 | 1.18 | |
| 15° | 0.56 | 0.56 | 0.80 | 1.05 | ||
| 30° | 0.51 | 0.42 | 0.55 | 0.86 | ||
| 45° | 0.38 | 0.43 | 0.54 | 0.97 | ||
| 60° | 0.42 | 0.42 | 0.36 | 0.79 | ||
| 75° | 0.40 | 0.36 | 0.41 | 0.86 | ||
| 90° | 0.29 | 0.40 | 0.57 | 0.84 | ||
| Compression Experiment | Fill Rate | |||||
|---|---|---|---|---|---|---|
| 25% | 35% | 50% | 75% | |||
| Honeycomb filling structure | Maximum load (kN) | 0° | 3.30 | 3.83 | 4.77 | 4.66 |
| 15° | 1.95 | 2.40 | 3.17 | 4.14 | ||
| 30° | 2.59 | 2.98 | 3.06 | 4.40 | ||
| 45° | 2.59 | 3.03 | 3.28 | 4.34 | ||
| 60° | 2.72 | 3.17 | 3.39 | 4.51 | ||
| 75° | 2.30 | 2.59 | 3.25 | 4.60 | ||
| 90° | 3.78 | 3.75 | 4.22 | 4.83 | ||
| Spiral filling structure | 0° | 3.04 | 3.39 | 3.91 | 3.71 | |
| 15° | 1.88 | 2.21 | 2.62 | 3.76 | ||
| 30° | 2.37 | 2.65 | 2.43 | 3.59 | ||
| 45° | 2.27 | 2.65 | 2.52 | 3.56 | ||
| 60° | 2.27 | 2.65 | 3.11 | 3.74 | ||
| 75° | 1.60 | 1.90 | 2.59 | 3.68 | ||
| 90° | 2.46 | 2.67 | 3.67 | 4.34 | ||
| Linear filling structure | 0° | 2.05 | 2.87 | 3.47 | 3.33 | |
| 15° | 1.63 | 1.82 | 2.32 | 3.16 | ||
| 30° | 1.34 | 2.26 | 2.54 | 3.33 | ||
| 45° | 2.05 | 2.35 | 2.07 | 3.39 | ||
| 60° | 2.14 | 2.26 | 2.40 | 3.59 | ||
| 75° | 1.56 | 1.79 | 2.43 | 3.91 | ||
| 90° | 2.34 | 2.73 | 3.31 | 4.02 | ||
| Torsion Experiment | Fill Rate | |||||
|---|---|---|---|---|---|---|
| 25% | 35% | 50% | 75% | |||
| Honeycomb filling structure | Maximum load (kN) | 0° | 2.66 | 3.18 | 3.70 | 4.66 |
| 15° | 2.29 | 2.76 | 3.34 | 3.97 | ||
| 30° | 2.62 | 3.08 | 3.51 | 4.19 | ||
| 45° | 2.73 | 3.38 | 3.30 | 3.79 | ||
| 60° | 2.50 | 2.92 | 3.21 | 4.15 | ||
| 75° | 2.69 | 2.75 | 3.00 | 3.83 | ||
| 90° | 2.18 | 2.52 | 2.96 | 3.49 | ||
| Spiral filling structure | 0° | 2.53 | 2.47 | 3.18 | 3.39 | |
| 15° | 1.83 | 2.23 | 2.94 | 2.78 | ||
| 30° | 2.54 | 2.38 | 2.68 | 2.78 | ||
| 45° | 2.61 | 2.71 | 3.54 | 3.73 | ||
| 60° | 2.58 | 2.80 | 3.12 | 3.80 | ||
| 75° | 2.37 | 2.56 | 2.75 | 3.13 | ||
| 90° | 2.11 | 2.45 | 2.53 | 3.16 | ||
| Linear filling structure | 0° | 1.84 | 2.34 | 3.40 | 4.24 | |
| 15° | 1.67 | 2.27 | 2.64 | 3.83 | ||
| 30° | 2.61 | 2.47 | 3.22 | 4.09 | ||
| 45° | 2.77 | 2.81 | 3.11 | 3.82 | ||
| 60° | 2.43 | 2.33 | 2.78 | 3.49 | ||
| 75° | 2.37 | 2.23 | 2.50 | 3.26 | ||
| 90° | 2.03 | 2.08 | 2.65 | 3.45 | ||
| Torsional Strength | Stress Strength | Tensile Strength | |
|---|---|---|---|
| Filling method | Honeycomb filling outperforms the other two continuous filling methods. | ||
| Filling ratio | When the filling ratio exceeds 50%, all three properties of the component begin to increase significantly. | ||
| Print tilt angle | Specimens printed at 0° can withstand greater torque and do not fail at larger twist angles, whereas specimens with a 15° tilt exhibit poorer torsional performance. | Specimens with inclination angles of 0° and 90° exhibit superior compressive strength compared to those with other inclination angles. | The tensile properties of specimens with inclination angles of 0° and 15° are significantly greater than those of specimens with other inclination angles. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Xie, Y.; Zeng, S.; Guo, S.; Chen, Z.; Liang, Z.; Zhang, D. Research on Lightweight Design Performance of Offshore Structures Based on 3D Printing Technology. J. Mar. Sci. Eng. 2025, 13, 2007. https://doi.org/10.3390/jmse13102007
Jiang H, Xie Y, Zeng S, Guo S, Chen Z, Liang Z, Zhang D. Research on Lightweight Design Performance of Offshore Structures Based on 3D Printing Technology. Journal of Marine Science and Engineering. 2025; 13(10):2007. https://doi.org/10.3390/jmse13102007
Chicago/Turabian StyleJiang, Haoyu, Yifan Xie, Shengqing Zeng, Sixing Guo, Zehan Chen, Zhenjie Liang, and Dapeng Zhang. 2025. "Research on Lightweight Design Performance of Offshore Structures Based on 3D Printing Technology" Journal of Marine Science and Engineering 13, no. 10: 2007. https://doi.org/10.3390/jmse13102007
APA StyleJiang, H., Xie, Y., Zeng, S., Guo, S., Chen, Z., Liang, Z., & Zhang, D. (2025). Research on Lightweight Design Performance of Offshore Structures Based on 3D Printing Technology. Journal of Marine Science and Engineering, 13(10), 2007. https://doi.org/10.3390/jmse13102007






