Reducing Aerodynamic Interference Through Layout Optimization of Symmetrically Cambered Wingsails: A Comparative Study of In-Line and Parallel Configurations
Abstract
1. Introduction
2. Methods
2.1. Parameterization of Installation Layouts
2.2. Computational Method
2.3. Optimization Method
3. Results
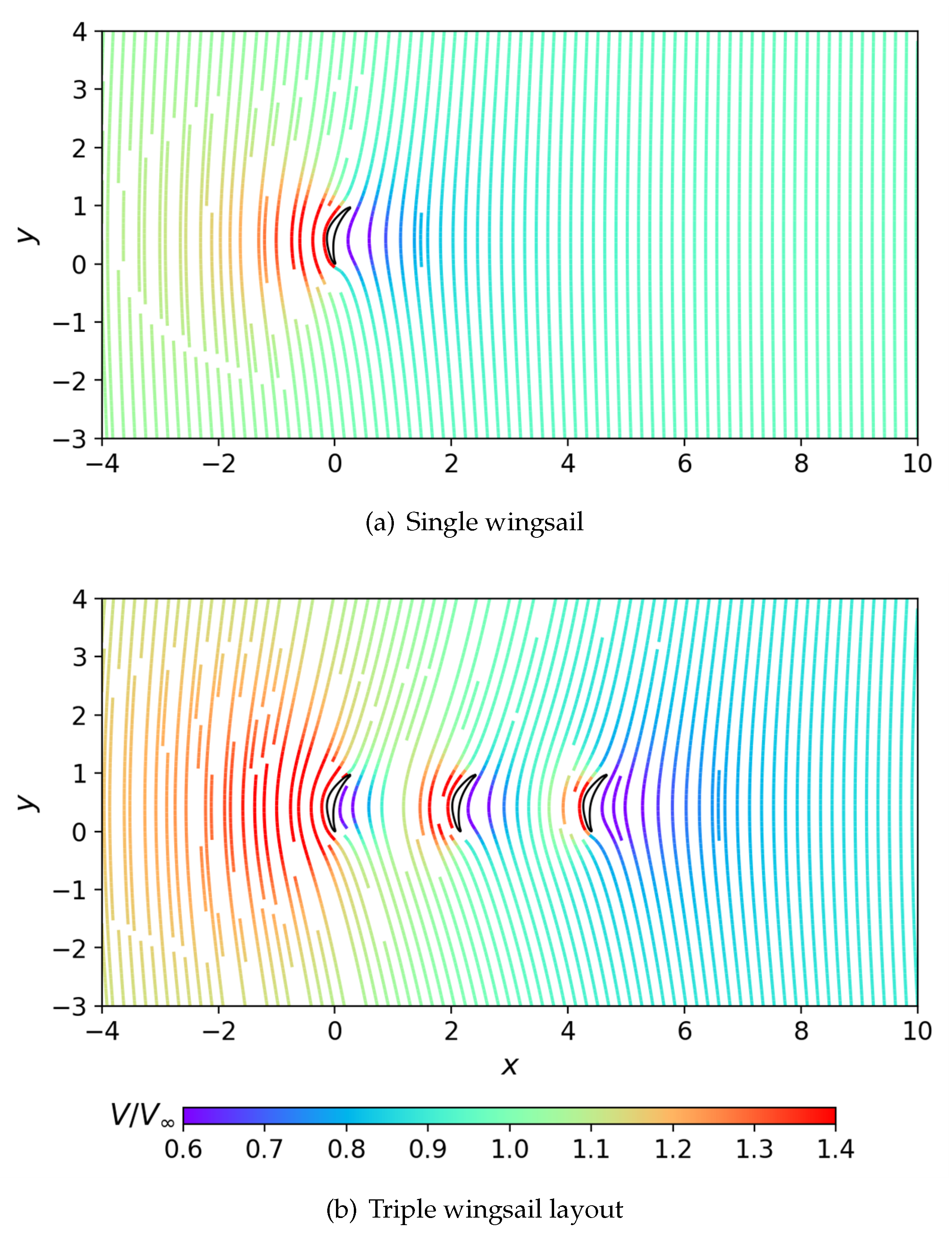
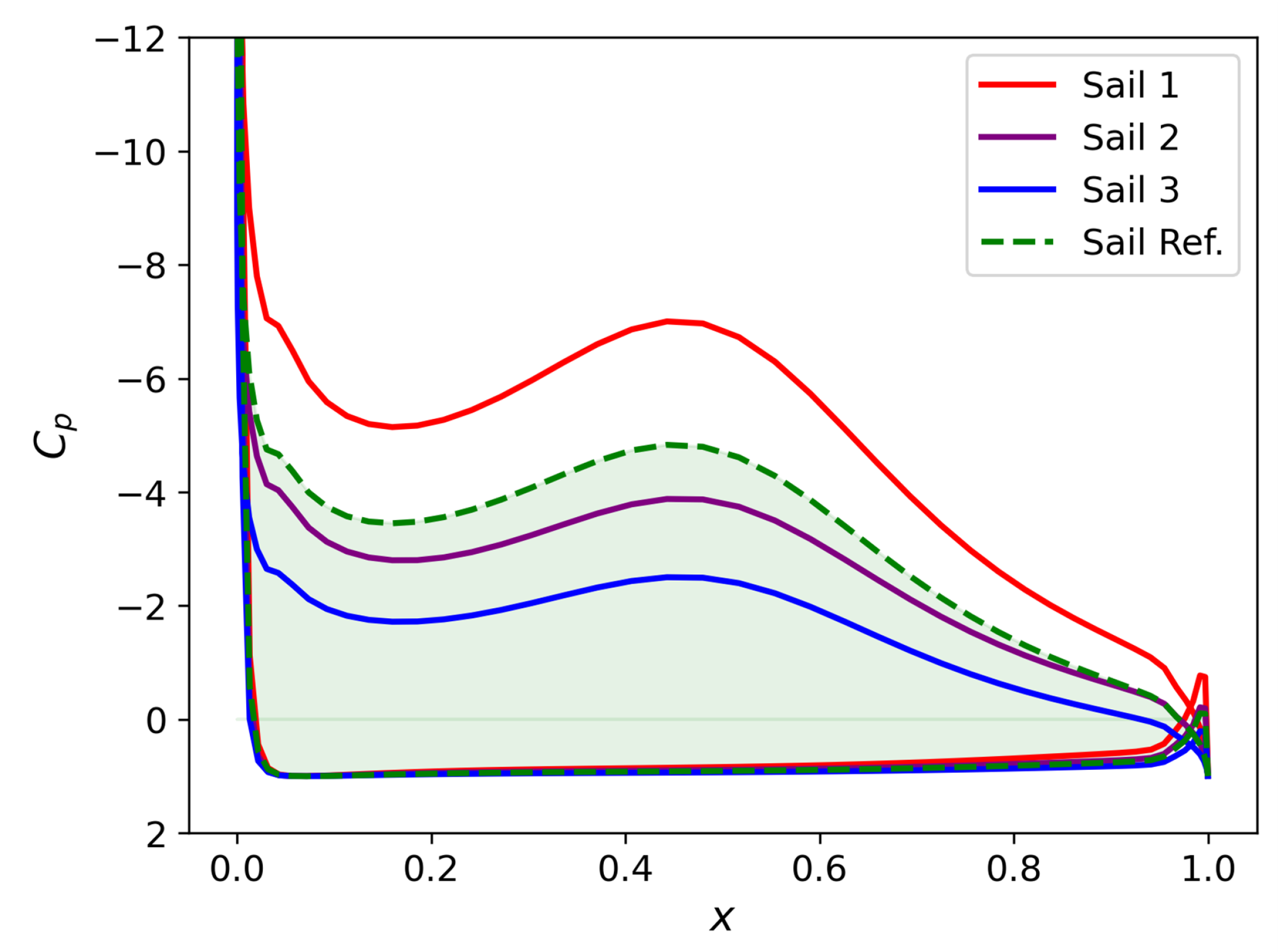
3.1. Triple-in-Line Layout
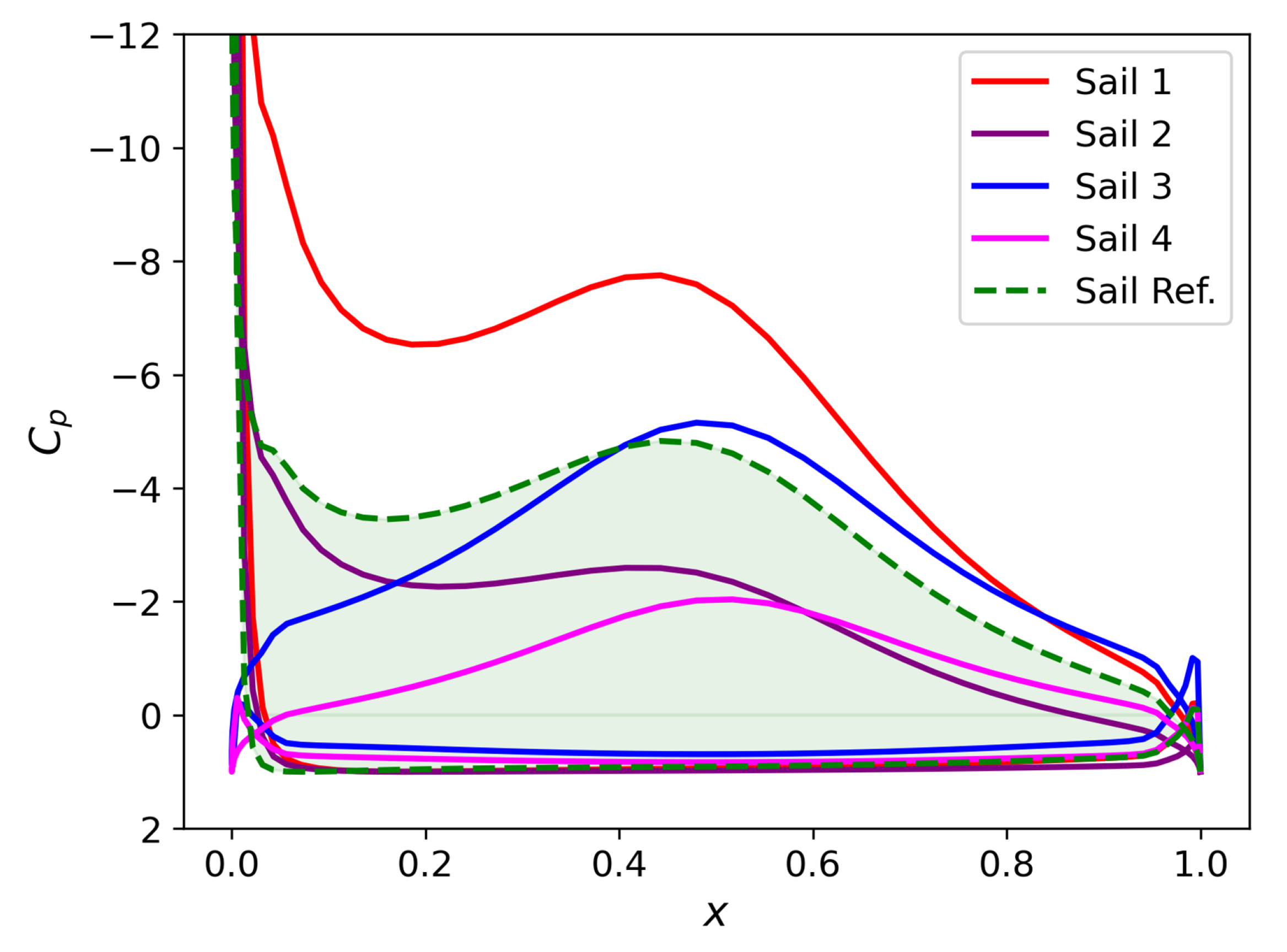
3.2. Quad-in-Parallel Layout
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AOA | Angle of attack |
| AWA | Apparent wind angle |
| Aspect ratio | |
| CFD | Computational fluid dynamics |
| FSI | Fluid–structure interaction |
| GA | Genetic algorithm |
| GHG | Greenhouse gases |
| IDDES | Improved Delayed Detached-Eddy Simulation |
| NACA | National Advisory Committee for Aeronautics |
| PSO | Particle swarm optimization |
| RANS | Reynolds-averaged Navier–Stokes |
| Re | Reynolds number |
| SC | Symmetrically Cambered (section/profile) |
| TL | Triple-in-line (layout) |
| QP | Quad-in-parallel (layout) |
| WT | Wind tunnel |
| WASP | Wind-assisted ship propulsion |
| Lift coefficient | |
| Drag coefficient | |
| Pressure coefficient | |
| Freestream velocity | |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
References
- International Maritime Organization. IMO Strategy on Reduction of GHG Emissions from Ships; IMO: London, UK, 2023. [Google Scholar]
- Kolodziejski, M.; Sosnowski, M. Review of Wind-Assisted Propulsion Systems in Maritime Transport. Energies 2025, 18, 897. [Google Scholar] [CrossRef]
- Huang, J.; Souppez, J.B.R.G. State of the Art in Wind Assisted Ship Propulsion for Maritime Decarbonisation and Sustainable Shipping: A Systematic Review. J. Sail. Technol. 2025, 10, 258–278. [Google Scholar] [CrossRef]
- Silva, M.F.; Friebe, A.; Malheiro, B.; Guedes, P.; Ferreira, P.; Waller, M. Rigid wing sailboats: A state of the art survey. Ocean Eng. 2019, 187, 106150. [Google Scholar] [CrossRef]
- Thies, F.; Fakiolas, K. Wind propulsion. In Sustainable Energy Systems on Ships; Elsevier: Amsterdam, The Netherlands, 2022; pp. 353–402. [Google Scholar]
- Čalić, A.; Jurić, Z.; Katalinić, M. Impact of Wind-Assisted Propulsion on Fuel Savings and Propeller Efficiency: A Case Study. J. Mar. Sci. Eng. 2024, 12, 2100. [Google Scholar] [CrossRef]
- International Maritime Organization. Resolution MEPC.328(76): 2021 Revised MARPOL Annex VI (Amendments to the Annex to the Protocol of 1997 to amend the International Convention for the Prevention of Pollution from Ships, 1973); IMO Resolution; International Maritime Organization: London, UK, 2021. [Google Scholar]
- International Maritime Organization. Resolution MEPC.352(78): 2022 Guidelines on Operational Carbon Intensity Indicators (CII Guidelines, G1); IMO Resolution; International Maritime Organization: London, UK, 2022. [Google Scholar]
- International Maritime Organization. Resolution MEPC.353(78): 2022 Guidelines on Reference Lines for Use with Operational Carbon Intensity Indicators (CII Reference Lines, G2); IMO Resolution; International Maritime Organization: London, UK, 2022. [Google Scholar]
- International Maritime Organization. Resolution MEPC.354(78): 2022 Guidelines on the Operational Carbon Intensity Rating of Ships (CII Rating Guidelines, G4); IMO Resolution; International Maritime Organization: London, UK, 2022. [Google Scholar]
- Bouman, E.A.; Lindstad, E.; Rialland, A.I.; Strømman, A.H. State-of-the-art technologies, measures, and potential for reducing GHG emissions from shipping—A review. Transp. Res. Part D Transp. Environ. 2017, 52, 408–421. [Google Scholar] [CrossRef]
- Mason, J.; Larkin, A.; Bullock, S.; van der Kolk, N.; Broderick, J.F. Quantifying Voyage Optimisation with Wind Propulsion for Short-Term CO2 Mitigation in Shipping. Ocean Eng. 2023, 289, 116065. [Google Scholar] [CrossRef]
- European Maritime Safety Agency. Potential of Wind-Assisted Propulsion for Shipping; Technical Report; EMSA: Lisbon, Portugal, 2023. [Google Scholar]
- International Maritime Organization. Reduction of GHG Emissions from Ships: White Paper on Wind Propulsion (MEPC 81/INF.39); Submitted by the Solomon Islands, IWSA, France, and Comoros; International Maritime Organization: London, UK, 2024. [Google Scholar]
- Lloyd’s Register. Guidance Notes on Wind Assisted Propulsion Systems; Guidance Notes; Lloyd’s Register: London, UK, 2024. [Google Scholar]
- ClassNK. Guidelines for Wind-Assisted Propulsion Systems (Edition 2.0); Guidelines; ClassNK: Vancouver, BC, Canada, 2023. [Google Scholar]
- Zhu, H.; Yao, H.D.; Thies, F.; Ringsberg, J.W.; Ramne, B. Propulsive performance of a rigid wingsail with crescent-shaped profiles. Ocean Eng. 2023, 285, 115349. [Google Scholar] [CrossRef]
- Ma, R.; Wang, Z.; Wang, K.; Zhao, H.D.; Jiang, B.; Liu, Y.; Xing, H.; Huang, L.Z. Evaluation Method for Energy Saving of Sail-Assisted Ship Based on Wind Resource Analysis of Typical Route. J. Mar. Sci. Eng. 2023, 11, 789. [Google Scholar] [CrossRef]
- Malmek, K.; Larsson, L.; Werner, S.; Ringsberg, J.W.; Bensow, R.; Finnsgård, C. Rapid aerodynamic method for predicting the performance of interacting wing sails. Ocean Eng. 2024, 293, 116596. [Google Scholar] [CrossRef]
- Hillenbrand, A.; Giovannetti, L.M.; Dhomé, U.; Kuttenkeuler, J. Wind Tunnel Tests of a Two-Element Wingsail with Focus on Near-Stall Aerodynamics. J. Sail. Technol. 2024, 9, 110–127. [Google Scholar] [CrossRef]
- Fang, S.; Tian, C.; Zhang, Y.; Xu, C.; Ding, T.; Wang, H.; Xia, T. Aerodynamic Analysis of Rigid Wing Sail Based on CFD Simulation for the Design of High-Performance Unmanned Sailboats. Mathematics 2024, 12, 2481. [Google Scholar] [CrossRef]
- Jiang, Y.; Cao, C.; Cui, T.; Yang, H.; Tian, Z. Numerical Study on Auxiliary Propulsion Performance of Foldable Three-Element Wingsail Utilizing Wind Energy. Energies 2024, 17, 3833. [Google Scholar] [CrossRef]
- Zhu, H.; Chernoray, V.; Yao, H.D.; Ringsberg, J.W.; Ramne, B. Fluid-structure interaction analysis of crescent-shaped wingsails. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Singapore, 9–14 June 2024. [Google Scholar]
- Zhu, H.; Chernoray, V.; Yao, H.D.; Ringsberg, J.W.; Ramne, B. Experimental study on structure responses of triple wing sails to turbulence flows at multiple apparent wind angles. In Proceedings of the 9th International Conference on Marine Structures (MarStruct), Gothenburg, Sweden, 3–5 April 2023. [Google Scholar]
- Ouchi, K.; Uzawa, K.; Kanai, A. Huge Hard Wing Sails for the Propulsor of Next Generation Sailing Vessel. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Ouchi, K.; Uzawa, K.; Kanai, A.; Katori, M. Wind Challenger: The Next Generation Hybrid Sailing Vessel. In Proceedings of the Third International Symposium on Marine Propulsors smp’13, Launceston, Tasmania, Australia, 5–8 May 2013. [Google Scholar]
- Yao, H.D. Hybrid Parametrization of Symmetrically Cambered (Crescent-Shaped) Airfoil Profiles for Rigid Wingsail Design in Wind-Assisted Ship Propulsion; Technical Report TR-2025-1; Chalmers University of Technology: Gothenburg, Sweden, 2025. [Google Scholar] [CrossRef]
- van Reen, S.; Serbülent, B.; Yao, H.D. Machine learning-based multipoint optimisation for improving aerodynamics of symmetrically cambered wing sails in wind-assisted ship propulsion. Ocean Eng. 2025, 342, 122829. [Google Scholar] [CrossRef]
- Giovannetti, L.M.; Dhome, U.; Malmek, K.; Persson, A.; Wielgosz, C. Multi-Wing Sails Interaction Effects. In Proceedings of the 24th Chesapeake Sailing Yacht Symposium, Annapolis, MD, USA, 10–11 June 2022. Paper No.: SNAME-CSYS-2022-006. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, W.; Zeng, Q. A Numerical Study on the Thrust and Interaction of a Three-Sail Wind-Assisted Propulsion System. In Proceedings of the ASME 2022 41st International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2022), Hamburg, Germany, 5–10 June 2022; p. V007T08A056. [Google Scholar] [CrossRef]
- Tian, F.; Huang, L.; Wang, Y.; Wang, K.; Ma, R. Numerical Simulation of the Aerodynamic Performance of A U-Shaped Sail. Proc. J. Phys. Conf. Ser. Iop Publ. 2023, 2508, 012029. [Google Scholar] [CrossRef]
- Wang, H.; Li, C.; Zuo, C.; Yuan, J.; Wu, B. Computational Fluid Dynamics Investigation of the Spacing of the Aerodynamic Characteristics for Multiple Wingsails on Ships. J. Mar. Sci. Eng. 2024, 12, 985. [Google Scholar] [CrossRef]
- Xu, K.; Malmek, K.; Bensow, R. Numerical investigation of multiple wingsails interaction under different apparent wind angles. Ocean Eng. 2025, 336, 121712. [Google Scholar] [CrossRef]
- Jo, Y.; Lee, H.; Choi, S.; Kwon, J.; Ahn, S. Aerodynamic Design Optimization of Wing-sails. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar] [CrossRef]
- Yasuda, A.; Taniguchi, T.; Katayama, T. Numerical Investigation of Aerodynamic Interactions between Rigid Sails Attached to Ship. J. Mar. Sci. Eng. 2024, 12, 1425. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, L.; Peng, G.; Ruan, Z.; Ma, R.; Wang, K.; Cao, J.; Wu, J.; Li, X. Investigation of aerodynamic performance and operational optimization of wing sails at varying spacings. Ocean Eng. 2025, 333, 121444. [Google Scholar] [CrossRef]
- Reche-Vilanova, M.; Kaltenbach, S.; Koumoutsakos, P.; Bingham, H.B.; Fluck, M.; Morris, D.; Psaraftis, H.N. Predictive Surrogates for Aerodynamic Performance and Independent Sail Trim Optimization of Multiple Wind Propulsion System Configurations. J. Sail. Technol. 2025, 10, 19–49. [Google Scholar] [CrossRef]
- Plessas, T.; Papanikolaou, A. Design Optimization and Assessment Platform for Wind-Assisted Ship Propulsion. J. Mar. Sci. Eng. 2025, 13, 1389. [Google Scholar] [CrossRef]
- Skinner, S.N.; Zare-Behtash, H. State-of-the-art in aerodynamic shape optimisation methods. Appl. Soft Comput. 2018, 62, 933–962. [Google Scholar] [CrossRef]
- Chiba, K.; Obayashi, S.; Nakahashi, K.; Morino, H. High-fidelity multidisciplinary design optimization of wing shape for regional jet aircraft. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 621–635. [Google Scholar]
- Zingg, D.W.; Nemec, M.; Pulliam, T.H. A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization. Eur. J. Comput. Mech./Rev. Eur. Mécanique Numérique 2008, 17, 103–126. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95: Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Wang, H.; Wang, S.; Zhuang, D.; Zhu, Z.; You, P.; Tang, Z.; Ding, G. Surrogate-based aerodynamic shape optimization of high-speed train heads: A review of four key technologies. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 907–920. [Google Scholar] [CrossRef]
- Hashimoto, A.; Jeong, S.; Obayashi, S. Aerodynamic optimization of near-future high-wing aircraft. Trans. Jpn. Soc. Aeronaut. Space Sci. 2015, 58, 73–82. [Google Scholar] [CrossRef]
- Hou, P.; Hu, W.; Soltani, M.; Chen, Z. Optimized placement of wind turbines in large-scale offshore wind farm using particle swarm optimization algorithm. IEEE Trans. Sustain. Energy 2015, 6, 1272–1282. [Google Scholar] [CrossRef]
- Zhu, H.; Yao, H.D.; Ringsberg, J.W. Unsteady RANS and IDDES studies on a telescopic crescent-shaped wingsail. Ships Offshore Struct. 2024, 19, 134–147. [Google Scholar] [CrossRef]
- Sharpe, P.D. Accelerating Practical Engineering Design Optimization with Computational Graph Transformations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2024. [Google Scholar]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics: Proceedings of the Conference, Notre Dame, Indiana, USA, 5–7 June 1989; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Sheldahl, R.E.; Klimas, P.C. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections Through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report; U.S. Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 1981. [Google Scholar]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]

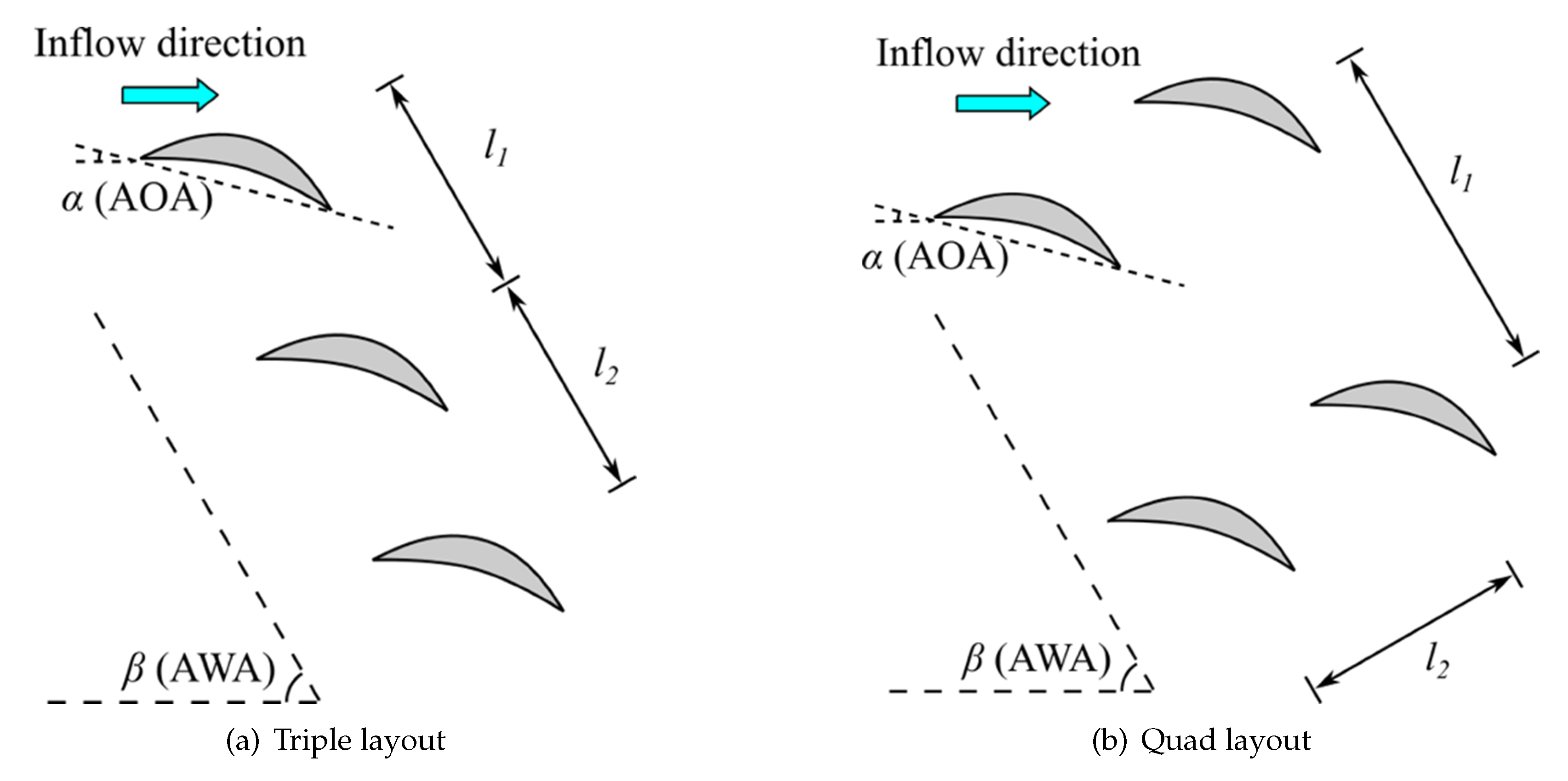


| Layout Type | AOA | AWA |
|---|---|---|
| TL | , , | |
| QP | , , |
| NACA0015 | D2R10 SC Foil | Present SC Foil | ||||
|---|---|---|---|---|---|---|
| Condition | Coeff. | Present Inviscid Method | WT Tests [49] | Present Inviscid Method | IDDES, 3D [46] | Present Inviscid Method |
| , Drag type | N/A | Profile drag | N/A | Profile + induced drag | N/A | |
| 0.609 | 0.550 | 2.278 | – | 2.924 | ||
| – | 0.007 | 0.129 | – | – | ||
| 1.208 | 1.100 | 2.862 | 1.685 | 3.479 | ||
| – | 0.010 | 0.163 | 0.177 | – | ||
| 1.792 | 1.414 | 3.409 | 1.980 | 3.988 | ||
| – | 0.019 | 0.194 | 0.330 | – | ||
| – | 1.333 | – | 2.243 | – | ||
| – | 0.026 | – | 0.388 | – | ||
| Equal spacing | 1.200 | 1.200 | 0.790 | 0.949 | 0.933 |
| Optimal | 1.151 | 1.249 | 0.961 | 0.949 | 0.933 |
| Equal spacing | 1.200 | 1.200 | 0.722 | 0.833 | 0.889 |
| Optimal | 1.132 | 1.268 | 0.722 | 0.833 | 0.910 |
| TL Layout | QP Layout | |
|---|---|---|
| Sail 1 | 0.165 | 0.182 |
| Sail 2 | −0.104 | −0.305 |
| Sail 3 | −0.218 | −0.0657 |
| Sail 4 | – | −0.525 |
| Total | −0.052 | −0.178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Reen, S.; Lin, J.; Niu, J.; Sharpe, P.; Li, X.; Yao, H.-D. Reducing Aerodynamic Interference Through Layout Optimization of Symmetrically Cambered Wingsails: A Comparative Study of In-Line and Parallel Configurations. J. Mar. Sci. Eng. 2025, 13, 1998. https://doi.org/10.3390/jmse13101998
van Reen S, Lin J, Niu J, Sharpe P, Li X, Yao H-D. Reducing Aerodynamic Interference Through Layout Optimization of Symmetrically Cambered Wingsails: A Comparative Study of In-Line and Parallel Configurations. Journal of Marine Science and Engineering. 2025; 13(10):1998. https://doi.org/10.3390/jmse13101998
Chicago/Turabian Stylevan Reen, Stephan, Jianfeng Lin, Jiqiang Niu, Peter Sharpe, Xiaodong Li, and Hua-Dong Yao. 2025. "Reducing Aerodynamic Interference Through Layout Optimization of Symmetrically Cambered Wingsails: A Comparative Study of In-Line and Parallel Configurations" Journal of Marine Science and Engineering 13, no. 10: 1998. https://doi.org/10.3390/jmse13101998
APA Stylevan Reen, S., Lin, J., Niu, J., Sharpe, P., Li, X., & Yao, H.-D. (2025). Reducing Aerodynamic Interference Through Layout Optimization of Symmetrically Cambered Wingsails: A Comparative Study of In-Line and Parallel Configurations. Journal of Marine Science and Engineering, 13(10), 1998. https://doi.org/10.3390/jmse13101998








